Abstract
Phytoplankton, as the foundation of primary production, is of great significant for the marine ecosystem. The vertical distribution of phytoplankton contains key information about marine ecology and the optical properties of water bodies related to remote sensing.The common methods to detect subsurface phytoplankton biomass are often in situ measurements and passive remote sensing; however, the bio-argo measurement is discrete and costly, and the passive remote sensing measurement is limited to obtain the vertical information. As a component of active remote sensing, lidar technology has been proved as an effective method for mapping the vertical distribution of phytoplankton. In the past years, there have been few studies on the phytoplankton layer extraction method for lidar data. The existing subsurface layer extraction algorithms are often non-automatic, which need manual intervention or empirical parameters to set the layer extraction threshold. Hence, an improved adaptive subsurface phytoplankton layer detection method was proposed, which incorporates a curve fitting method and a robust estimation method to determine the depth and thickness of subsurface phytoplankton scattering layer. The combination of robust estimation method can realize automatic calculation of layer detection threshold according to the characteristic of each lidar signal, instead of an empirical fixed value used in previous works. In addition, the noise jamming signal can also be effectively detected and removed. Lidar data and in situ spatio-temporal matching Chlorophyll-a profile data obtained in Sanya Bay in 2018 was used for algorithm verification. The example result of step-by-step process illustrates that the improved method is available for adaptive threshold determination for layer detection and redundant noise signals elimination. Correlation analysis and statistical hypothesis testing shows the retrieved subsurface phytoplankton maximum depth by the improved method and in situ measurement is highly relevant. The absolute difference of layer maximum depth between lidar data and in situ data for all stations is less than 0.75 m, and mean absolute difference of layer thickness difference is about 1.74 m. At last, the improved method was also applied to the lidar data obtained near Wuzhizhou Island seawater, which proves that the method is feasiable and robust for various sea areas.
1. Introduction
Marine ecosystems are complex entities [1] in which phytoplankton are the foundation and provide about half of the global primary production [2]. As the base of the food chain, phytoplankton plays an important role in the marine ecosystem [3,4]. The high concentration of phytoplankton forms phytoplankton layers [5,6,7], which affect the biogeochemical process of the upper ocean. Therefore, the study of phytoplankton is of great significance to the protection of marine ecosystems and the development and protection of fishery resources [4]. The vertical distribution of phytoplankton in the ocean not only contains information about marine ecology, but also contains key information about the optical properties of water bodies related to remote sensing.
Remote sensing technology has been investigated for the identification of phytoplankton community [8]. There are multiple algorithms for retrieving phytoplankton and are now available and applied in both coastal and open ocean environment [9,10,11,12]. However, passive remote sensing measurement is limited to obtain the vertical information of phytoplankton [13] and the bio-argo measurement is discrete and costly [14]. Lidar, as an active remote sensing observation method, has the advantages of high resolution, flexibility, and high efficiency [15,16], which is widely used in the detection of ocean interior [16,17,18,19,20,21]. Airborne lidar has been proved to be particularly useful for mapping the depth distribution of phytoplankton. Ocean laser remote sensing can obtain information on the vertical structure of phytoplankton and its associated primary productivity, carbon cycle, upwelling, and vortex on a large scale and periodically [22,23,24].
In the past years, there are a few studies on phytoplankton layer extraction based on lidar data. Goldin (2003) used airborne lidar to detect the underwater scattering layer in the Barents Sea [25]. Hill and Zimmerman (2010) [26] used the model results to show that the use of lidar can improve the estimation of primary productivity in the Arctic. Churnside and Marchbanks (2014) [27] used lidar to find phytoplankton thin layers in the Chukchi Sea and Beaufort Sea, and study the effect of ice floe on the depth and thickness of the layer. In 2017 [28], they conducted the lidar survey again in the Chukchi Sea and Beaufort Sea. Compared with the result in 2014, they inferred the mixing of phytoplankton and zooplankton from the power spectral density and acoustic scattering of lidar. Beherenfeld et al. (2017) [29] estimated the biomass of phytoplankton in the Arctic using the depth synthetic echo of space-based lidar.
In the investigation of detecting the subsurface layer by lidar, data-processing algorithms are an important step. Churnside and Tenningen compared three data processing algorithms for the lidar detection of mackerel in the Norwegian Sea [30]. The algorithms are manual identification, background signal-fitting algorithm, and median-filter algorithm, respectively. Chen et al. proposed a fast phytoplankton layer detection method. The depth of layer is obtained by the depth of the subsurface Chlorophyll-a maximum and the thickness is calculated by the full width at half maximum [23]. Until now, there were still few studies on phytoplankton extraction algorithms from lidar data. The existing subsurface layer extraction algorithms are often non-automatic, which need manual intervention or empirical parameters to set the extraction threshold.
In this paper, an improved adaptive subsurface phytoplankton layer detection method (IASPLDM) for ocean lidar data was proposed which can realize the automatic calculation of the layer detection threshold and redundant noise elimilation. Example results for the step-by-step process of IASPLDM were present firstly.Then, the data of lidar experiments carried on March 2018 was used for subsurface layer detection and shipborne in situ measurement was compared for algorithm verification. Finally, the improved method was also applied to subsurface layer detection in the seawater near Wuzhizhou Island.
2. Materials and Methods
2.1. Study Area
The data used in this paper were obtained from the observation experiment of subsurface plankton layer by airborne lidar in Sanya Bay, South China Sea (SCS). The airborne lidar (SIOM) comprised a frequency-doubled Nd:YAG laser and was operated at 532 nm with pulse duration of 1.5 ns and pulse repetition rate (PRF) of 1 kHz. The telescope diameter was 200 mm and field of view (FOV) was 40 mrad [24]. Two flight measurements were conducted in 11 March and 12 March 2018 in Sanya Bay, respectively. Simultaneously, an underwater hyperspectral absorption and attenuation meter (AC-S) and profile Chlorophyll-a fluorescent probe were used for shipboard in situ measurements. There are a total of four measurement stations, and the Chlorophyll-a concentration, absorption, and attenuation coefficient were measured. Figure 1 shows the flight tracks of airborne lidar and location of shipboard synchronous measurement stations.
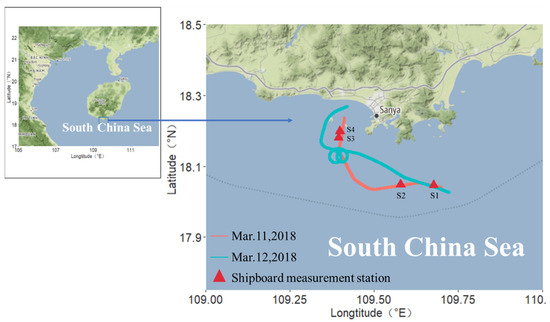
Figure 1.
Study area in Sanya Bay, South China Sea. The blue line is the lidar flight track on 11 March 2018 and the pink line is the flight track on 12 March 2018. The red triangles are shipboard measurement stations.
2.2. IASPLDM
The characteristics of subsurface plankton scattering were obtained by an improved adaptive subsurface phytoplankton layer detection method, IASPLDM. The improved method is based on the characteristics of depth, thickness, and intensity of subsurface plankton layer. A robust signal filtering calculation is employed to improve the accuracy of signal processing. Firstly, curve fitting is performed on the lidar logarithmic signal to obtain the depth-dependent background scattering signal and then the background scattering signal is subtracted; the subtraction result is considered to be the subsurface layer signal (SLS). After that, SLS is filtered by an robust estimation algorithm which is designed based on the median and the absolute deviations of sample [31]. SLS is standardized by the estimated positioning value and the scale estimation value, and the standardized signal is compaired with the set detection threshold. The points larger than the detection threshold are considered as subsurface plankton layer. Figure 2 is the flow chart of IASPLDM.
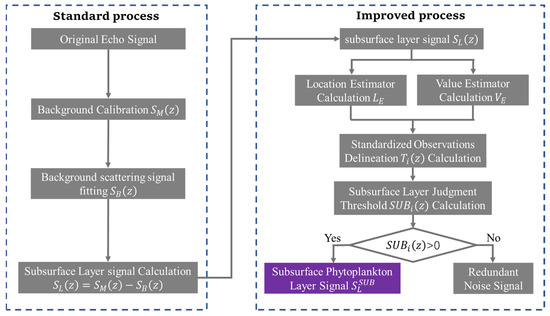
Figure 2.
Flow chart of IASPLDM.
Generally, the laser will decay exponentially in seawater, and the echo signal will also show an exponential decay trend. If the concentration of particulate matter increases or plankton appears, the echo signal will significantly enhance. When the signal reaches its maximum at a certain depth, it will begin to attenuate until the system cannot detect it. It is assumed that the optical properties of the near-surface water are uniformly distributed, and the laser diffuse attenuation coefficient is smaller than the attenuation of light by the subsurface layer. The original echo signal can be considered as the composition of background lidar signal and phytoplankton scattering layer lidar signal. The depth-dependent lidar signal is described by Equation (1).
The original echo contains kinds of noises such as background noise, random noise, and noise of the lidar system itself. It is necessary to remove noise from the original echo data to obtain echo data with a high signal-to-noise ratio (SNR). The average of the last one hundred pulse samples is considered as background noise signal and is subtracted. The noise-subtracted signal is logarithmically converted to obtain the lidar pre-processed signal SM. Then, the depth-dependent background scattering signal SB can be estimated as an exponential regression and be obtained from a linear function of depth z (Equation (2)).
For Airborne Lidar, the height H of the aircraft must be considered when calculating the laser light propagation distance D, and depth z is (Equation (3)).
where c is the propagation speed of the laser in vacuum, and n is the refractive index. The laser is refracted after entering the ocean from the air and the speed becomes c/n. Because of the high reflectivity of sea surface, those upper ocean data within the depth of 2 m are higher than the theoretical value and are considered as invalid data. Similarly, SNR will plummet with the increase in depth, so data below the depth of 0.8 times the maximum depth are also invalid data. Therefore, the effective range of regression depth is from 2 m below sea surface to a depth of 0.8 times the maximum depth.
After that, the subsurface layer signal is obtained by subtracting the depth-dependent lidar signal SB from SM (Equation (4)).
Although the background noise has been subtracted, the subsurface signal obtained in Equation (4) does not represent the true subsurface phytoplankton layer. It may contain other noise signals, such as some signals from the seabed, other organic debris in the water, bacteria, and inorganic particles. Further calculations are needed to remove that excess noise and extract the true subsurface layer signal. The location estimator and value estimator of are calculated through Equations (5) and (6). The total of 1.483 is a common correction factor to make the estimator consistent with the usual scale parameter of a normal distribution [31]. The location estimator is the median value of , and the value estimator is a new median value based on the absolute deviation between and its median value, which is called the median of all absolute deviations (MAD).
When estimators of location and scale are determined, the standardized observations are computed according to Equation (7). refers to the distance far from the location to scale .
At last, is put into Equation (8) for subsurface layer judgment threshold . When is greater than 0, the corresponding signal will be judged as the subsurface plankton layer signal.
The standardized observations and judgment threshold are dynamic. They will change according to the location estimator and value estimator of each group of signals, and the advantage of this step is adaptive computing. Some researchers use a fixed value as a denoising threshold, and the value is empirical [24]. When processing data from different stations or flight, they have to set the value based on the signal data each time; even sometimes, some data are need to be deleted artificially. Such processing may be inaccurate and time-consuming. A dynamic threshold can automatically calculate the subsurface layer signal and the result is more accurate.
3. Result
3.1. Example Results for Step-By-Step Process of IASPLDM
Figure 3 shows the example results for the step-by-step process of IASPLDM. Figure 3a shows the raw lidar echo signal SR. As the depth increases, the SR drops sharply from 480 to 260 and then rises; after reaching the peak at 8 m, SR decreases again. The original lidar signal is considered to be the sum of background signal and subsurface layer signal. Assuming that background signal is the lidar signal of vertical uniform phytoplankton water, which decay trend is exponential, this assumption implies and are constant over depth. Hence, SB can be obtained by linear fitting through Equation (2). Through Equation (4), SLS is calculated by subtracting background signal SB from logarithmically converted pre-processed lidar signal SM. Figure 3b shows that the subsurface layer is located at a depth of about 10–20 m. Here, the SLS is based on the hypothesis that original lidar signal is the sum of background signal and subsurface layer signal, so it may contain some noise signals. In Figure 3c, some noise signal can be seen from the vertical slice. At a distance of 1 to 10 km, depth below 30 m, there is a small amount of noise signals, and at a distance of 25 to 27 km, depth below 30 m, there are obvious strong noise signals. Therefore, it is necessary to set a threshold to remove the noise signal and extract the real subsurface signal. The blue line in Figure 3d is a subsurface layer judgment threshold which is calculated through Equation (8). is the result of subtracting the cutoff value from standardized observations (see Equation (7)). can also be called T scores, which have to be compared with the cutoff value. Here, the cutoff value is set as quartile after the absolute value of standardized observations. The black dotted line is the threshold which equals 0 and is used to compare with . Those values greater than 0 are the subsurface plankton layer signal (Figure 3e). The plus sign is the maximum value of SLS depth, which is defined as the subsurface chlorophyll-a maximum layer (SCML). The depth and thickness of is calculated based on the depth and half maximum width of SCML intensity, respectively. Figure 3f is the vertical slice of the subsurface layer. The result shows the layer varied from 7.89 m to 20.19 m; the average depth is 14.5 m and the thickness is 9.4 m.
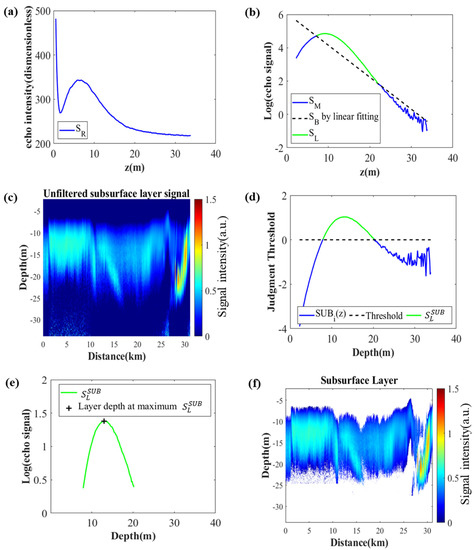
Figure 3.
An example result for step-by-step process of the subsurface phytoplankton layer detection method. (a) Raw lidar echo signal SR; (b) calculation process of SLS: blue line and black dotted line are logarithmic form of SM and SB, respectively. The green line is SL obtained by subtracting SB from SM. (c) vertical slice of unfiltered subsurface layer signal; (d) calculation process of the subsurface layer: the blue line is the judgment threshold , the black dotted line is threshold which equals to 0, and the green line is subsurface layer signal; (e) the filtered subsurface layer signal, and the plus sign is SCML; (f) vertical slice of extraction result of the subsurface layer.
3.2. Retrieval Comparisons between the Standard and the Improved Method
Figure 4 shows a vertical slice of the subsurface phytoplankton layer signal detection results measured by airborne lidar on 12 March 2018 through a step by step process. From Figure 4a, some strong signals caused by the high reflection of the sea surface can be seen near the surface, and these sea surface reflection signals are invalid. Therefore, the upper limit of effective range of regression depth is 2 m below the sea surface. The original signal consists of five discontinuous signal segments; the first segment of the signal starts at 20 m underwater and then rises to about 10 m. The remaining four segments of signals are located at 5–10 m, and the intensity is stronger than the first segment of the signal. The fitting method is used to calculate SB, and the result is shown in Figure 4b. After subtracting SB from the original signal by Equation (4), a continuous banded subsurface signal is obtained; the layer raised from 20 m to 10 m and remained at 10 m without significant depth change after 10 km. At the depth under 30 m, 0 to 10 km, there is a segment of strong signal followed by several weak signals. These signals may come from other creatures or seabed. If these noise signals are not removed, the calculation of SCML will be affected which will affect the calculation of depth and thickness of subsurface phytoplankton layer. Figure 4c shows the subsurface layer filtered by the standard method. Although the subsurface layer was extracted, the noise signal also remained. Figure 4d shows the schematic diagram of the subsurface phytoplankton layer detected according to Equations (5)–(8). In Figure 4d, the signal below 30 m is filtered and subsurface layer is extracted. The depth of subsurface layer changed significantly, rising from 20 m to 10 m. The layer located between the depth from 7.8 m to 12.9 m. had an average maximum depth of 10.11 m and a layer thickness of 5.2 m.
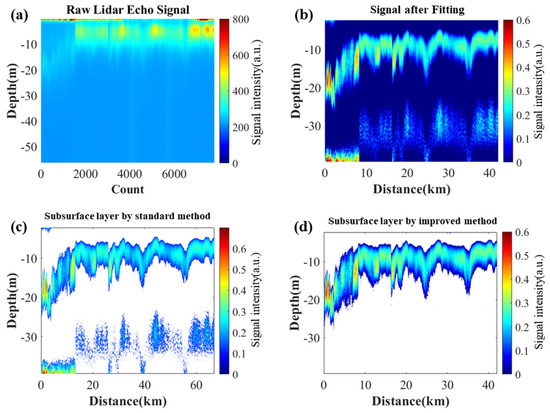
Figure 4.
Comparison of subsurface phytoplankton layer detection by the standard method and the improved method: (a) is a schematic diagram of the original signal profile, (b) is the result of subtracting the SB calculated by the linear fitting method from the original lidar, (c) is the subsurface phytoplankton layer filtered by a presupposed fixed threshold of the standard method, (d) is the subsurface phytoplankton layer detected by the improved method of the IASPLDM.
3.3. Algorithm Verification
The shipborne in situ measurement is utilized for the verification of IASPLDM. The location of shipboard synchronous measurement stations is shown in Figure 1, and the lidar signal was obtained from the flight on 12 March 2018. The comparison of subsurface phytoplankton layer detection results of IASPLDM and the unimproved method based on lidar data with in situ measurement results is shown in Figure 5. Figure 5a–d are the result of IASPLDM, and the maximum depth of subsurface layer and the maximum depth of Chlorophyll-a in the four stations are quite close. The absolute difference between Lidar-measured plankton layer depth and SCML depth of all stations is less than 0.75 m. Figure 5e,f is the result of unimproved method with an fixed threshold of 0.1. It can be seen that there are some redundant signals such as signals at the depth of 50 to 60 m in Figure 5e, signals at the depth about 5 m in Figure 5f, signals at the depth of 32 to 58 m in Figure 5g, and signals at the depth of about 5 m and that of 40 to 60 m in Figure 5h.
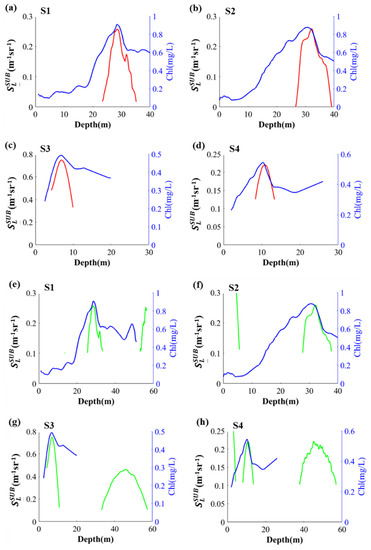
Figure 5.
Comparision between subsurface phytoplankton layer detection result of IASPLDM and unimproved method based on lidar data and shipborne in situ measurement. (a–d) are the result of IASPLDM and correspond to shipboard synchronous measurement stations S1 to S4, respectively. The red line is the subsurface plankton layer signal retrieved by lidar, and the blue line is the in situ Chlorophyll-a profile. (e–h) are the result of the unimproved method and correspond to shipboard synchronous measurement stations S1 to S4, respectively. The green line is subsurface plankton layer signal by fixed threshold of 0.1 and the blue line is the in situ Chlorophyll-a profile.
Statistical hypothesis testing and correlation analysis is applied for correlation detection of the maximum depth and thickness of Lidar-retrieved SCML with in situ-measured Chlorophyll-a profile. The statistical hypothesis testing result of maximum depth is shown in Table 1 and the result of layer thickness is shown in Table 2. p value refers to the probability of difference between the two groups of data; generally, a p value less than 0.05 indicates that there is difference between the data groups. The p value of maximum depth in Table 1 is 0.9751, and the p value of thickness in Table 2 is 0.3456, which means there is less difference between the maximum depth and thickness of airborne lidar-retrieved SCML and shipborne in situ measurement data. Figure 6 is the result of statistical analysis and correlation analysis of Lidar-retrieved SCML and in situ-measured Chlorophyll-a. In Figure 6a, the data dispersion of the two groups of data is similar and the error of S2 station is the largest. The absolute difference of layer maximum depth between lidar data and in situ data for all stations is less than 0.75 m. The lower boundary of Lidar-retrieved SCML is 1.44 m deeper than that of in situ-measured data, which is Å32.14 m and −30.70 m, respectively. In Figure 6b, there is a slight difference in the dispersion of the two sets of data. The thickness of in situ-measured Chlorophyll-a is thicker than that of lidar-retrieved SCML. The mean absolute difference of layer thickness difference between lidar data and in situ data is about 1.74 m. The layer thickness difference of the S2 station is the largest, with a difference of 3.30 m, and the smallest is the S1 station, with a difference of 0.53 m. Figure 6c,d is the result of correlation analysis, showing that data of Lidar-retrieved SCML and in situ measurement are highly correlated. The R2 of maximum depth is 0.9976 and the R2 of thickness is 0.916, respectively. The algorithm tends to underestimate the thickness of the layer; it maybe due to that the initial estimation of the lidar background signal is biased to higher values of β and α than actually exist by the presence of the subsurface layer, resulting in some of the signal contribution of the subsurface layer being subtracted out as “background”. An improved method to synthesize polarization information may be helpful for reducing the underestimation for layer thickness in the future.

Table 1.
ANOVA table of airborne lidar-retrieved SCML maximum depth and shipborne in situ measurement.

Table 2.
ANOVA table of thickness of airborne lidar-retrieved SCML and shipborne in situ measurement.
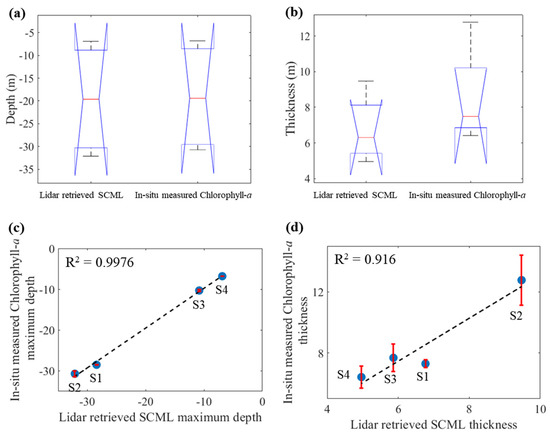
Figure 6.
Result of statistical analysis and correlation analysis of airborne lidar retrieval and shipborne measurement, (a,b) is the result of depth and thickness of statistical analysis, respectively. The black line segment represents the upper and lower boundaries of SCML, the red line segment represents the median value of the layer depth, and the blue line segment represents the quartile. (c,d) is the result of the SCML depth and thickness of statistical analysis correlation analysis; the red line segment represents the error.
3.4. Application in Lidar Track Data in the Seawater near Wuzhizhou Island
The IASPLDM is also applied to a set of new lidar data obtained in the seawater near Wuzhizhou Island. Six flight measurements were conducted, and the flight tracks shown in Figure 7, Figure 8 and Figure 9 are the result of the subsurface phytoplankton layer of six lidar flights and the comparison of depth and thickness of the subsurface phytoplankton layer, respectively. Figure 8a–f are the results of the subsurface phytoplankton layer corresponding to the lidar flight tracks 1 to 6, respectively. All six figures show the phytoplankton layer locate at the depths of 10 to 20 m. Compared with other figures, phytoplankton layer signal strength in Figure 8a is the weakest, followed by Figure 8f. From Figure 8b–e, the signal strength becomes concentrated and signal strength in Figure 8c is the strongest. This illustrates that there is a phytoplankton cluster, and track 3 may pass through the center of the center of the phytoplankton cluster near 18.31°N, 109.8°E. Figure 9 shows the depth and thickness of the subsurface layer of the six lidar flights, and the average depth of the six lidar flight tracks is −11.18 m, −17.16 m, −18.92 m, −15.79 m, −16.71 m, −14.37 m; the average thickness is 7.71 m, 8.69 m, 8.43 m, 10.49 m, 10.78 m, 8.58 m, respectively.
Figure 7.
Lidar flight tracks near Wuzhizhou Island. The six colors correspond to six tracks: the pink line is track 1, the gold line is track 2, the green line is track 3, the light blue line is track 4, the dark blue line is track 5, and the magenta line is track 6, respectively.
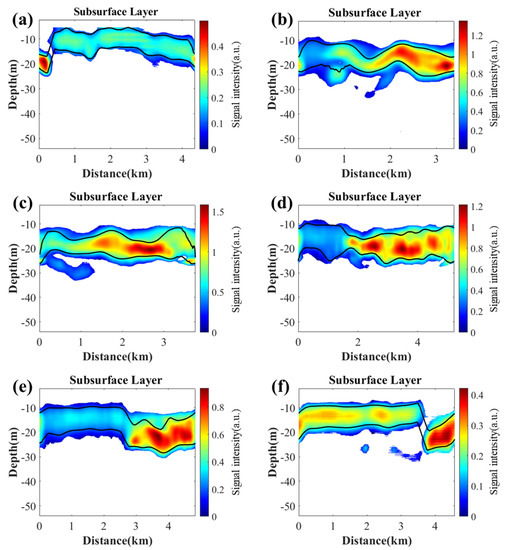
Figure 8.
Subsurface phytoplankton layer detection results of airborne lidar data near Wuzhizhou Island, (a–f) correspond to the results for the lidar flight tracks from the track 1 to the track 6, respectively.
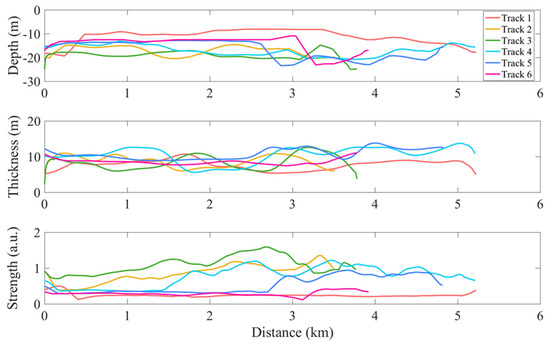
Figure 9.
Depth, thickness, and signal strength of the subsurface layer for the six lidar flights in the seawater near Wuzhizhou Island. The six different color lines correspond to the results of the six lidar flight tracks, respectively.
4. Discussion
One of the important improvements of IASPLDM is the dynamic threshold used for subsurface layer detection and denoising. The calculation of threshold is based on the principle of robust estimation. Robust estimation is designed based on the median and the absolute deviations of sample data and is widely used in denoising of water current data measured by the Acoustic Doppler velocimeter [32]. The essence of denoising is to detect and record/delete values that deviate far from the average value. Similarly, the subsurface layer signals can be considered as those signals that are extremely strong and vary far away from the average values. Therefore, they can be detected and recorded and the result obtained is the subsurface signal. The same principle can also be used to remove noise.
In the past, a preproposed fixed threshold was set for subsurface extraction; however, the choice of threshold is arbitrary or empirical. As shown in Figure 10, four signals are selected to illustrate the difference between the results using a fixed threshold and the dynamic threshold. Figure 10a shows the calculation result of the fixed threshold (set as 0.15). It can be seen clearly that each signal has different signal characteristics, such as signal 3 and 4 which raised after the depth of 25 m. Although the subsurface signal can be obtained by simply subtracting 0.15, there are some redundant noise signals. These noise signals may come from seabed and the vertical slice as shown in Figure 3c. If these signals are not removed, they will affect the subsequent calculation of depth and thickness and in the past studies, they are delated artificially. Figure 10b shows the dynamic threshold of 4 signals and Figure 10c is an enlarged part of Figure 10b in order to see more clearly. The dynamic threshold is calculated based on the characteristic and change trend of each signal. For signal 3 and signal 4, the raised part at depth of 30 m is considered as noise and is denoised so that the accuracy of subsurface extraction is improved.
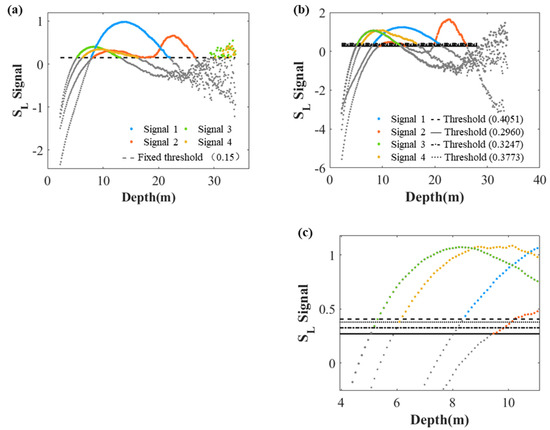
Figure 10.
An example of the subsurface layer signal extraction result by a fixed threshold and the dynamic threshold: (a,b) are both the example signal of data on 11 March 2018. (c) is an enlarged part of (b). The blue, green, orange, and yellow points correspond to the signals from the signal 1 to the signal 4, respectively. The black dotted line in (a) refers to the fixed threshold which is equal to 0.15, and four black dotted lines in (b) correspond to the dynamic thresholds of the signals from 1 to 4, respectively.
It should be noted that the fixed threshold cannot compared with dynamic threshold directly, because the fixed threshold is a simple value set as threshold, dynamic threshold is a converted value. It is calculated based on standardized observations (Equation (7)). , which is also called cutoff value in Equation (8), is the dynamic threshold that changes according to the location estimator and value estimator of each group of signals. In order to facilitate the calculation, the judgment threshold is defined as the result of subtracting the cutoff value from the standardized observation (Equation (8)). Then, when is greater than zero, the corresponding signal is the subsurface signal.
Figure 11 shows the determination threshold of two-flight experiment data. The change trend of threshold is basically consistent with that of layer. In Figure 11a, the threshold is mainly between 0.2 and 0.4; the threshold for the 4200th signal is relatively small, which is less than 0.1. The corresponding vertical slice of signals can be seen in Figure 3c; at the depth of 7 to 15 m and at 25 km, the layer is thin and signal strength is weak. In Figure 11b, the threshold is between 0.2 and 0.3 before the 1000th signal and the corresponding vertical slice of signal is shown in Figure 4d. At 0 to 3 km, the layer is located at 20 m, and then the depth increases, and the corresponding threshold increases. After that, the subsurface layer is maintained at 5 to 10 m and the threshold varied from 0.3 to 0.4.
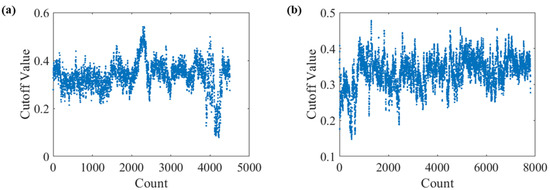
Figure 11.
Retrieved dynamic threshold for subsurface layer detection based on lidar signals. (a) is data on 11 March 2018, and (b) is data on 12 March 2018.
Figure 12 shows the comparision of the standard method and our improved method. The data used here is the airborne lidar data of track 2 near Wuzhizhou Island seen from Figure 7. Figure 12a is the vertical slice of the standard SLS; a clear subsurface profile can be seen at a depth of 10 to 20 m, There is a semi-circular aggregation at the beginning at the depth of 20 m, followed by a circular aggregation and banded aggregation at about 1 km. With the increase in distance, the intensity gradually increases, and the intensity is the strongest at 3 km. Figure 12b,c show the results of extracting the subsurface layer using different fixed thresholds in the standard method; the threshold of Figure 12b is 0.1 and Figure 12c is 0.2. The selection of 0.1 and 0.2 is arbitrary, and other values can also be selected (such as 0.15 or 0.25). At present, there is no studies on the impact of the selection of contrast threshold on the results. Compared with Figure 12b, the layer in Figure 12c is thinner because the threshold in Figure 12c is higher and more data are deleted. However, in both figures, there are noise signals at a depth of 50 m, which need to be deleted manually. Figure 12d is the result of subsurface layer by the improved method. The overall shape of the subsurface layer is similar to Figure 12b,c, but there are slight differences. In Figure 12a, at the depth of 20 to 30 m, distance between 1 to 2 km, The subsurface signal forms a hollow ring, but the signal is too weak so that it is not retained in Figure 12b,c. In Figure 12d, although it is not a complete ring, more signals are retained. The subsurface layer in Figure 12d is most consistent with that in Figure 12a.
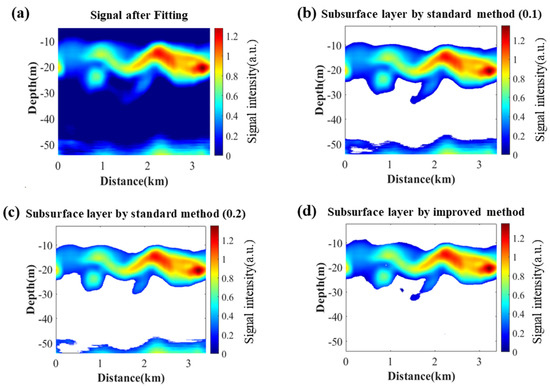
Figure 12.
Comparision of subsurface phytoplankton layer detection by the standard and the improved method. The airborne lidar data are from the lidar track 2 near Wuzhizhou Island. (a) is the result of subtracting the SB calculated by linear fitting method from original lidar data, (b) is the subsurface phytoplankton layer filtered by fixed threshold 0.1, (c) is the subsurface phytoplankton layer filtered by fixed threshold 0.2, (d) is the the subsurface phytoplankton layer detected by the IASPLDM.
In Equation (2), when linear function is used to calculate SB, the effective range of regression is set to 2 m below the surface to the depth of 0.8 times of the maximum depth. However, as shown in Figure 13, the linear fitting method does not work well due to the fact that the noise signal has a long tail phenomenon, which means that sometimes 0.8 times of the maximum depth as the lower limit is not optimal. The reason is that after a relative plummet, the signal has extremely little decrease after a certain depth due to signal-to-noise ratio. To solve this problem, a quadratic fitting method is used. We decide whether to use the quadratic fitting method based on calculating the attenuation α using the slope method, and count the number of the calculated α with the value of zero. If the number is larger than 20, we will used the quadratic fit in that case. The lower limits of layer mentioned above is determined by half maximum width of SCML intensity instead of the subtraction results between original and background signal. It can be seen from Figure 13 that the result of the quadratic fitting method is more appropriate. The depth of SLS varied from 14.32 m to 24.81 m, and its maximum intensity is 17.93 m.
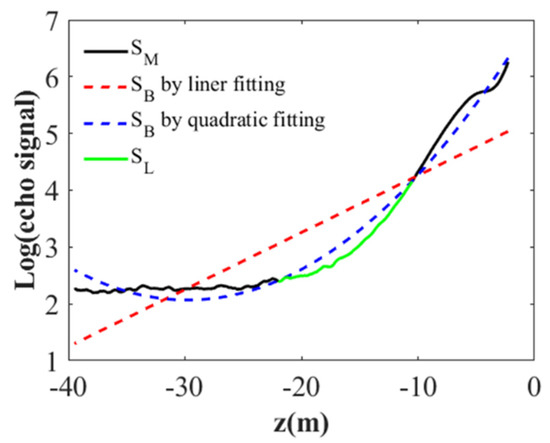
Figure 13.
Example SLS from lidar data at 109°25′E, 18°8′N. Two methods were compared to obtain the layer depth: the black solid line is the signal SM, the red dotted line and the blue dotted line are background signals by the linear fitting and signal by the quadratic fitting, respectively, and the green line is the subsurface layer signal.
The comparision of results based on the linear fitting and quadratic fitting is shown in Figure 14. Figure 14a is the result of subtracting the SB calculated by the linear fitting method from the original lidar data. At the distance of 0 to 10 km, there are obvious SLS at the depth of 20 m, but at the distance of 10 to 40 km, the signal above 10 m is connected to sea surface signal, and is incoherent with the previous signal. Meanwhile, signals appear below 30 m. This means that the liner fitting method is invalid. As an alternative, the quadratic fitting method is used to calculate SB and the result is shown in Figure 14b. After subtracting SB from original signal by Equation (4), a continuous banded subsurface layer signal is obtained. At first, the signal was located at 18 m and decreased slightly, then raised from 20 m to 10 m, and finally remained at 10 m. This change may be affected by wind-driven upwelling events.
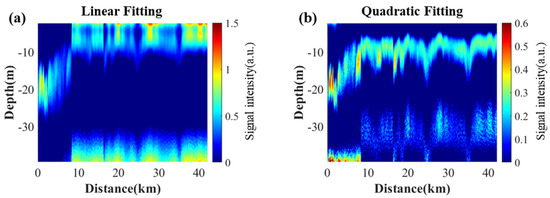
Figure 14.
Vertical slice of comparision between the SLS based on linear fitting and quadratic fitting. (a) is the result of subtracting the SB calculated by linear fitting method from the original lidar data; (b) is the result of subtracting the SB calculated by quadratic fitting method from the original lidar data.
5. Conclusions
The existing subsurface layer extraction algorithms are non-automatic, which need manual intervention or empirical parameters to set the extraction threshold. Hence, an improved adaptive subsurface phytoplankton layer detection method was proposed and was validated by the data of airborne lidar and in situ measurement in Sanya Bay. The results show that the subsurface phytoplankton layer could be effectively detected and the redundant noise could be reduced. Compared with the traditional method, IASPLDM can adaptively calculate the detection threshold, which is more efficient and faster. In the future, more lidar experiments will be carried out in various sea areas to verify and enhance the current methods to provide effective tools for the study of phytoplankton spatial distribution and seasonal changes. A lidar with a dual-polarization receiver will be developed, considering there is less surface reflection in the cross-polarized channel and better contrast with plankton layers.
Author Contributions
Methodology, C.Z.; Supervision, P.C.; Project Administration, D.P.; Writing—Original Draft, C.Z; Writing—Review and Editing, P.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Key Special Project for Introduced Talents Team of Southern Marine Science and Engineering Guangdong Laboratory (GML2019ZD0602), the National Natural Science Foundation (41901305; 61991453), and the Zhejiang Natural Science Foundation (LQ19D060003), the Scientific Research Fund of the Second Institute of Oceanography, Ministry of Natural Resources (QNYC1803).
Data Availability Statement
Not applicable.
Acknowledgments
We would like to thank our colleagues who made in-situ measurements, and thank the SIOM staff who provided airborne lidar data. We thank anonymous reviewers for their suggestions, which significantly improved the presentation of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hostetler, C.; Behrenfeld, M.J.; Hu, Y.; Hair, J.W.; Schulien, J.A. Spaceborne Lidar in the Study of Marine Systems. Annu. Rev. Mar. Sci. 2018, 10, 121–147. [Google Scholar] [CrossRef] [Green Version]
- Daniel, G.B.; Marlon, R.L.; Boris, W. Global phytoplankton decline over the past century. Nature 2011, 466, 591–596. [Google Scholar]
- Yue, C.; Zhibin, J.; Lu, S.; Genhai, Z.; Zhifu, W.; Yibo, L.; Yuexin, G. Distribution of net-collected phytoplankton and influence environmental factors in spring and autumn in the adjacent waters near Qinshan Nuclear Power Plant. Mar. Sci. Bull. 2018, 37, 31–39. [Google Scholar]
- Hongzhen, T.; Qinping, L.; Goes, J.I.; Gomes, H.D.R.; Mengmeng, Y. Temporal and spatial changes in chlorophyll a concentrations in the Bohai Sea in the past two decades. Hai Yang Xue Bao 2019, 41, 131–140. [Google Scholar]
- Dekshenieks, M.M.; Donaghay, P.L.; Sullivan, J.M.; Rines, J.E.B.; Osborn, T.R.; Twardowski, M.S. Temporal and spatial occurrence of thin phytoplankton layers in relation to physical processes. Mar. Ecol. Prog. 2001, 223, 61–71. [Google Scholar] [CrossRef]
- Chumside, J.H.; Donaghay, P.L. Thin scattering layers observed by airborne lidar. ICES J. Mar. Sci. 2009, 66, 778–789. [Google Scholar] [CrossRef]
- Sullivan, J.M.; Donaghay, P.L.; Rines, J.J.C.S.R. Coastal thin layer dynamics: Consequences to biology and optics. Cont. Shelf. Res. 2010, 30, 50–65. [Google Scholar] [CrossRef]
- Schulien, J.A.; Penna, A.D.; Gaube, P.; Chase, A.; Behrenfeld, M.J. Shifts in Phytoplankton Community Structure Across an Anticyclonic Eddy Revealed from High Spectral Resolution Lidar Scattering Measurements. Front. Mar. Sci. 2020, 7, 349. [Google Scholar] [CrossRef]
- Kostadinov, T.S.; Siegel, D.A.; Maritorena, S. Global variability of phytoplankton functional types from space: Assessment via the particle size distribution. Biogeosciences 2010, 7, 3239–3257. [Google Scholar] [CrossRef] [Green Version]
- Werdell, P.J.; Roesler, C.S.; Goes, J.I. Discrimination of Phytoplankton Functional Groups Using an Ocean Reflectance Inversion Model. Appl. Opt. 2014, 53, 4833–4849. [Google Scholar] [CrossRef]
- Uitz, J.; Stramski, D.; Reynolds, R.A.; Dubranna, J. Assessing phytoplankton community composition from hyperspectral measurements of phytoplankton absorption coefficient and remote-sensing reflectance in open-ocean environments. Remote Sens. Environ. 2015, 171, 58–74. [Google Scholar] [CrossRef]
- Mouw, C.B.; Hardman-Mountford, N.J.; Alvain, S.; Bracher, A.; Brewin, R.J.W.; Bricaud, A.; Ciotti, A.M.; Devred, E.; Fujiwara, A.; Hirata, T.; et al. A Consumer’s Guide to Satellite Remote Sensing of Multiple Phytoplankton Groups in the Global Ocean. Front. Mar. Sci. 2017, 4, 41. [Google Scholar] [CrossRef] [Green Version]
- Chen, P.; Pan, D. Ocean Optical Profiling in South China Sea Using Airborne LiDAR. Remote Sens. 2019, 11, 1826. [Google Scholar] [CrossRef] [Green Version]
- Peng, C.; Pan, D.; Mao, Z.; Hang, L. A Feasible Calibration Method for Type 1 Open Ocean Water LiDAR Data Based on Bio-Optical Models. Remote Sens. 2019, 11, 172. [Google Scholar]
- Xiao-long, L.; Chaofang, Z. Application and development of Lidar to detect the vertical distribution of marine materials. Infrared Laser Eng. 2020, 49, 24–32. [Google Scholar]
- Chen, P.; Jamet, C.; Mao, Z.; Pan, D. OLE: A Novel Oceanic Lidar Emulator. IEEE Trans. Geosci. Remote Sens. 2020, 99, 1–15. [Google Scholar] [CrossRef]
- Churnside, J.H.; Ostrovsky, L.A. Lidar observation of a strongly nonlinear internal wave train in the Gulf of Alaska. Int. J. Remote Sens. 2005, 26, 167–177. [Google Scholar] [CrossRef]
- Churnside, J.H.; Marchbanks, R.D.; Lee, J.H.; Shaw, J.A.; Weidemann, A.; Donaghay, P.L. Airborne lidar detection and characterization of internal waves in a shallow fjord. J. Appl. Remote Sens. 2012, 6, 063611. [Google Scholar] [CrossRef] [Green Version]
- Chen, P.; Pan, D.; Mao, Z.; Liu, H. Semi-Analytic Monte Carlo Model for Oceanographic Lidar Systems: Lookup Table Method Used for Randomly Choosing Scattering Angles. Appl. Sci. 2019, 9, 48. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Chen, P.; Mao, Z.; Pan, D. Iterative retrieval method for ocean attenuation profiles measured by airborne lidar. Appl. Opt. 2020, 59, C42–C51. [Google Scholar] [CrossRef]
- Chen, P.; Pan, D.; Mao, Z.; Liu, H. Semi-analytic Monte Carlo radiative transfer model of laser propagation in inhomogeneous sea water within subsurface plankton layer. Opt. Laser Technol. 2019, 111, 1–5. [Google Scholar] [CrossRef]
- Chen, P.; Jamet, C.; Zhang, Z.; He, Y.; Mao, Z.; Pan, D.; Wang, T.; Liu, D.; Yuan, D. Vertical distribution of subsurface phytoplankton layer in South China Sea using airborne lidar. Remote Sens. Environ. 2021, 263, 112567. [Google Scholar] [CrossRef]
- Chen, P.; Mao, Z.; Zhang, Z.; Liu, H.; Pan, D. Detecting subsurface phytoplankton layer in Qiandao Lake using shipborne lidar. Opt. Express 2020, 28, 558–569. [Google Scholar] [CrossRef]
- Liu, H.; Chen, P.; Mao, Z.; Pan, D.; He, Y. Subsurface plankton layers observed from airborne lidar in Sanya Bay, South China Sea. Opt. Express 2018, 26, 29134–29147. [Google Scholar] [CrossRef]
- Goldin, Y.A.; Vasilev, A.N.; Lisovskiy, A.S.; Chernook, V.I. Results of Barents Sea airborne lidar survey. In Current Research on Remote Sensing, Laser Probing, & Imagery in Natural Waters; International Society for Optics and Photonics: Bellingham, WA, USA, 2007. [Google Scholar]
- Zimmerman, R.C. Estimates of primary production by remote sensing in the Arctic Ocean: Assessment of accuracy with passive and active sensors. Deep Sea Res. Part I Oceanogr. Res. Pap. 2010, 57, 1243–1254. [Google Scholar]
- Churnside, J.H.; Marchbanks, R.D. Subsurface plankton layers in the Arctic Ocean. Geophys. Res. Lett. 2015, 42, 4896–4902. [Google Scholar] [CrossRef]
- Churnside, J.H.; Marchbanks, R.D.; Vagle, S.; Bell, S.W.; Stabeno, P.J. Stratification, plankton layers, and mixing measured by airborne lidar in the Chukchi and Beaufort seas. Deep Sea Res. Part II Top. Stud. Oceanogr. 2020, 177, 4742. [Google Scholar] [CrossRef]
- Behrenfeld, M.J.; Hu, Y.; O’Malley, R.T.; Boss, E.S.; Hostetler, C.A.; Siegel, D.A.; Sarmiento, J.L.; Schulien, J.; Hair, J.W.; Lu, X.; et al. Annual boom–bust cycles of polar phytoplankton biomass revealed by space-based lidar. Nat. Geosci. 2016, 10, 118–122. [Google Scholar] [CrossRef]
- Churnside, J.H.; Tenningen, E.; Wilson, J.J. Comparison of data-processing algorithms for the lidar detection of mackerel in the Norwegian Sea. ICES J. Mar. Sci. 2009, 66, 1023–1028. [Google Scholar] [CrossRef]
- Rousseeuw, P. Robust Estimation and Identifying Outliers. In Handbook of Statistical Methods for Engineers and Scientists; McGraw-Hill: New York, NY, USA, 1998; pp. 16.2–16.4. [Google Scholar]
- Zhong, C.; Yin, F.; Zhang, J.; Zhang, S.; Kitazawa, D. Optimized Algorithm for Processing Outlier of Water Current Data Measured by Acoustic Doppler Velocimeter. J. Mar. Sci. Eng. 2020, 8, 655. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).