Towards Robust Calculation of Interannual CO2 Growth Signal from TCCON (Total Carbon Column Observing Network)
Abstract
1. Introduction
2. Data
2.1. TCCON Observations
2.2. Copernicus Atmospheric Monitoring Service
2.3. CarbonTracker
2.4. Datasets with Global CO2 Growth Rate
2.5. Ancillary Datasets
3. Methodology for the CO2 Atmospheric Growth Rate Calculation
3.1. Calculation of CO2 Growth Rate at Monthly (MGR) and Annual (AGR) Scales
3.2. TCCON Data Sampling Strategy
4. Results
4.1. Estimating the Robustness of AGRTCCON Due to Data Sampling, Measurement Gaps and Irregularities in Time Series
4.1.1. Selected Sites (Garmisch, Park Falls and Tsukuba) Analysis: Time Series of Station-Wise XCO2, MGR and AGR
4.1.2. Station-Wise Analysis: Effects of Sub-Monthly XCO2 Variability on Station-Wise AGRTCCON Estimates
4.1.3. Station-Wise Analysis: Hidden Effects of CO2 Seasonality and Variability on Station-Wise AGRTCCON Estimates
4.1.4. Station-Wise Analysis: Effects of Irregularities in Data Sampling and Observation Abundances on Station-Wise AGRTCCON Estimates
4.1.5. Global AGRTCCON Analysis: Effects of Choosing “Daily Observation Threshold”
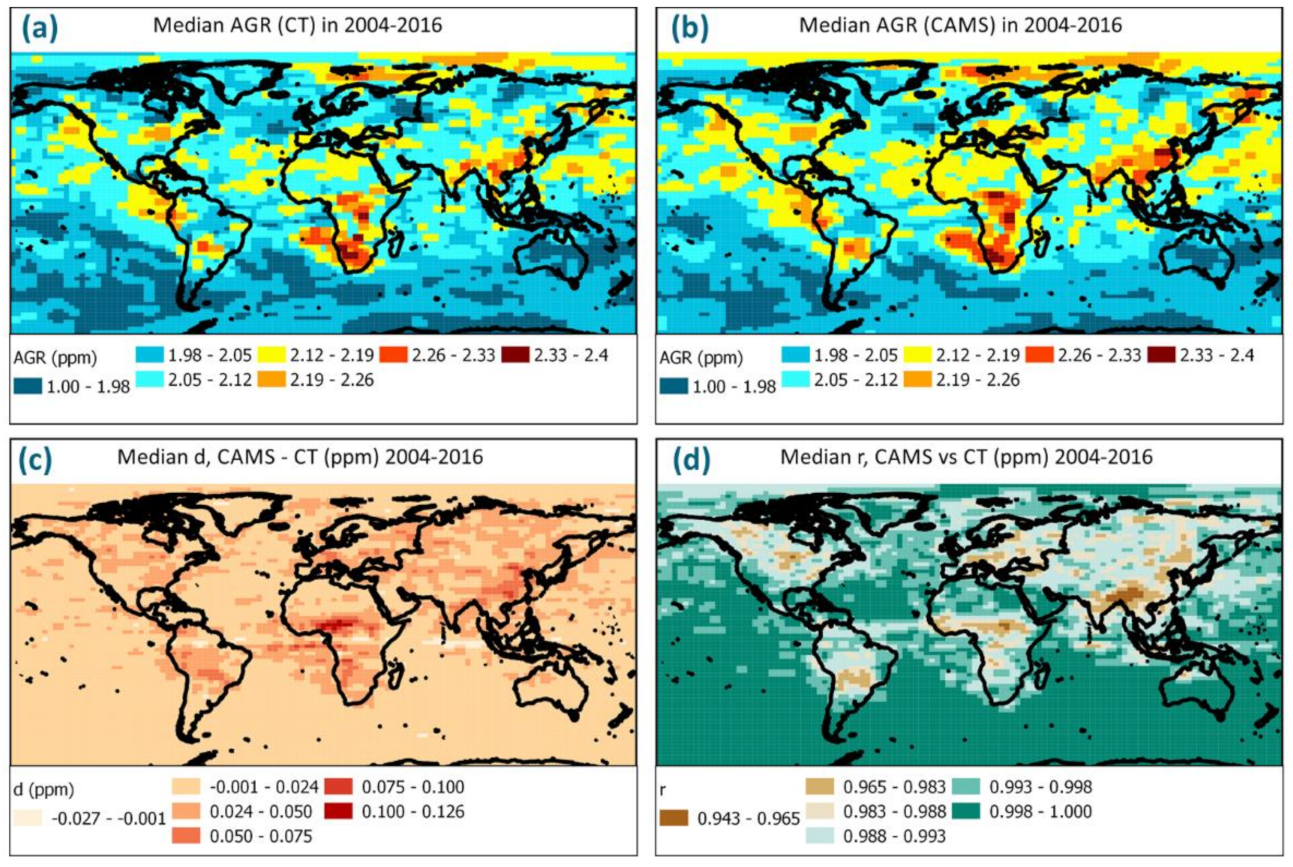
4.2. Retrieving Global Estimates of AGRTCCON and Comparing It with the Existing References
4.2.1. Comparing AGRTCCON with the References (Global Carbon Budget and Satellite Composite Estimates)
4.2.2. Evaluating the Factors Affecting AGRTCCON: ENSO
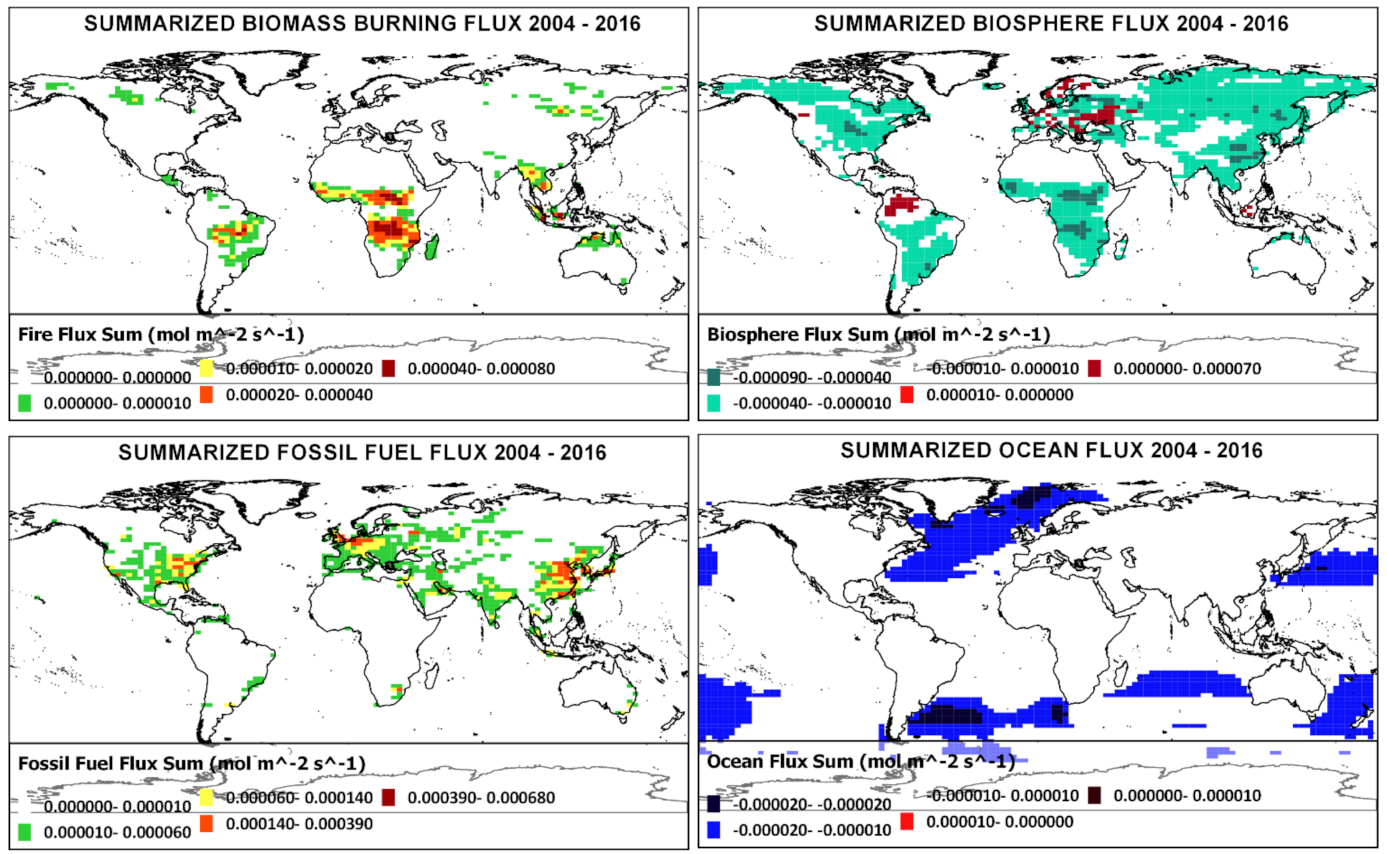
4.3. Additional Analyses: Examining Exposure of External Factors to TCCON CO2 Growth Data
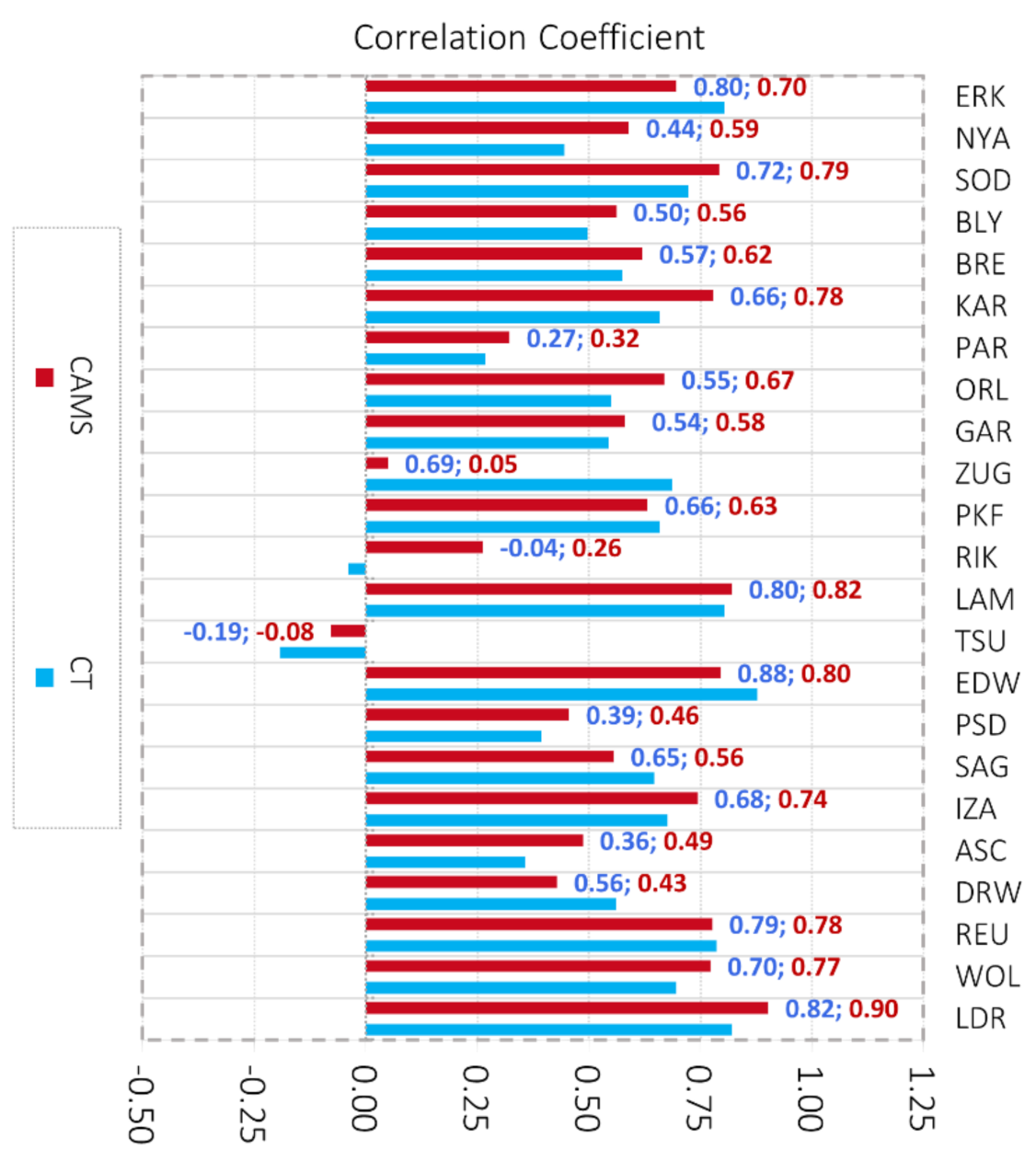
4.3.1. Identifying Local Influence in TCCON Interannual Signal. TCCON Versus CO2 Inverse Models at all TCCON Sites
4.3.2. Influence of the Urban CO2 Sites to TCCON Interannual Signal
4.3.3. Ascension Station: Data Gaps, Localized Influence of Atmospheric Mixing
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Betts, R.A.; Jones, C.D.; Knight, J.R.; Keeling, R.F.; Kennedy, J.J. El Niño and a record CO2 rise. Nat. Clim. Chang. 2016, 6, 806–810. [Google Scholar] [CrossRef]
- Stips, A.; Macias, D.; Coughlan, C.; Garcia-Gorriz, E.; Liang, X.S. On the causal structure between CO2 and global temperature. Sci. Rep. 2016, 6, 21691. [Google Scholar] [CrossRef] [PubMed]
- Canadell, J.G.; Le Quere, C.; Raupach, M.R.; Field, C.B.; Buitenhuis, E.T.; Ciais, P.; Conway, T.J.; Gillett, N.P.; Houghton, R.A.; Marland, G. Contributions to accelerating atmospheric CO2 growth from economic activity, carbon intensity, and efficiency of natural sinks. Proc. Natl. Acad. Sci. USA 2007, 104, 18866–18870. [Google Scholar] [CrossRef] [PubMed]
- Schneising, O.; Reuter, M.; Buchwitz, M.; Heymann, J.; Bovensmann, H.; Burrows, J.P. Terrestrial carbon sink observed from space: Variation of growth rates and seasonal cycle amplitudes in response to interannual surface temperature variability. Atmos. Chem. Phys. 2014, 14, 133–141. [Google Scholar] [CrossRef]
- Friedlingstein, P. Carbon cycle feedbacks and future climate change. Philos. Trans. R. Soc. A 2015, 373, 20140421. [Google Scholar] [CrossRef] [PubMed]
- Keenan, T.F.; Prentice, I.C.; Canadell, J.G.; Williams, C.A.; Wang, H.; Raupach, M.; Collatz, G.J. Recent pause in the growth rate of atmospheric CO2 due to enhanced terrestrial carbon uptake. Nat. Commun. 2016, 7, 13428. [Google Scholar] [CrossRef] [PubMed]
- Buchwitz, M.; Schneising, O.; Burrows, J.P.; Bovensmann, H.; Reuter, M.; Notholt, J. First direct observation of the atmospheric CO2 year-to-year increase from space. Atmos. Chem. Phys. 2007, 7, 4249–4256. [Google Scholar] [CrossRef]
- Buchwitz, M.; Reuter, M.; Schneising, O.; Noël, S.; Gier, B.; Bovensmann, H.; Burrows, J.P.; Boesch, H.; Anand, J.; Parker, R.J.; et al. Computation and analysis of atmospheric carbon dioxide annual mean growth rates from satellite observations during 2003–2016. Atmos. Chem. Phys. 2018, 18, 17355–17370. [Google Scholar] [CrossRef]
- Ekwurzel, B.; Boneham, J.; Dalton, M.W.; Heede, R.; Mera, R.J.; Allen, M.R.; Frumhoff, P.C. The rise in global atmospheric CO2, surface temperature, and sea level from emissions traced to major carbon producers. Clim. Chang. 2017, 144, 579–590. [Google Scholar] [CrossRef]
- Wang, W.; Ciais, P.; Nemani, R.R.; Canadell, J.G.; Piao, S.; Sitch, S.; White, M.A.; Hashimoto, H.; Milesi, C.; Myneni, R.B. Variations in atmospheric CO2 growth rates coupled with tropical temperature. Proc. Natl. Acad. Sci. USA 2013, 110, 13061–13066. [Google Scholar] [CrossRef]
- Kim, J.-S.; Kug, J.-S.; Jeong, S.-J. Intensification of terrestrial carbon cycle related to El Niño–Southern Oscillation under greenhouse warming. Nat. Commun. 2017, 8, 1674. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Bowman, K.W.; Schimel, D.S.; Parazoo, N.C.; Jiang, Z.; Lee, M.; Bloom, A.A.; Wunch, D.; Frankenberg, C.; Sun, Y.; et al. Contrasting carbon cycle responses of the tropical continents to the 2015–2016 El Niño. Science 2017, 358, eaam5690. [Google Scholar] [CrossRef] [PubMed]
- Chylek, P.; Tans, P.; Christy, J.; Dubey, M.K. The carbon cycle response to two El Nino types: An observational study. Environ. Res. Lett. 2018, 13, 024001. [Google Scholar] [CrossRef]
- Betts, R.A.; Jones, C.D.; Knight, J.R.; Keeling, R.F.; Kennedy, J.J.; Wiltshire, A.J.; Andrew, R.M.; Aragão, L.E.O.C. A successful prediction of the record CO2 rise associated with the 2015/2016 El Niño. Philos. Trans. R. Soc. B 2018, 373, 20170301. [Google Scholar] [CrossRef]
- Frölicher, T.L.; Joos, F.; Raible, C.C.; Sarmiento, J.L. Atmospheric CO2 response to volcanic eruptions: The role of ENSO, season, and variability: Volcanoes and the global carbon budget. Glob. Biogeochem. Cycles 2013, 27, 239–251. [Google Scholar] [CrossRef]
- Rafelski, L.E.; Piper, S.C.; Keeling, R.F. Climate effects on atmospheric carbon dioxide over the last century. Tellus B Chem. Phys. Meteorol. 2009, 61, 718–731. [Google Scholar] [CrossRef]
- Poulter, B.; Frank, D.; Ciais, P.; Myneni, R.B.; Andela, N.; Bi, J.; Broquet, G.; Canadell, J.G.; Chevallier, F.; Liu, Y.Y.; et al. Contribution of semi-arid ecosystems to interannual variability of the global carbon cycle. Nature 2014, 509, 600–603. [Google Scholar] [CrossRef]
- Piao, S.; Wang, X.; Wang, K.; Li, X.; Bastos, A.; Canadell, J.G.; Ciais, P.; Friedlingstein, P.; Sitch, S. Interannual variation of terrestrial carbon cycle: Issues and perspectives. Glob. Chang. Biol. 2020, 26, 300–318. [Google Scholar] [CrossRef]
- Dlugokencky, E.; Tans, P. Trends in Atmospheric Carbon Dioxide, National Oceanic & Atmospheric Administration, Earth System Research Laboratory (NOAA/ESRL). 2018. Available online: http://www.esrl.noaa.gov/gmd/ccgg/trends/global.html (accessed on 29 July 2020).
- Friedlingstein, P.; Jones, M.W.; O’Sullivan, M.; Andrew, R.M.; Hauck, J.; Peters, G.P.; Peters, W.; Pongratz, J.; Sitch, S.; Le Quéré, C.; et al. Global Carbon Budget 2019. Earth Syst. Sci. Data 2019, 11, 1783–1838. [Google Scholar] [CrossRef]
- Reuter, M.; Buchwitz, M.; Schneising, O.; Noël, S.; Bovensmann, H.; Burrows, J.P.; Boesch, H.; Di Noia, A.; Anand, J.; Parker, R.J.; et al. Ensemble-based satellite-derived carbon dioxide and methane column-averaged dry-air mole fraction data sets (2003–2018) for carbon and climate applications. Atmos. Meas. Tech. 2020, 13, 789–819. [Google Scholar] [CrossRef]
- Gaubert, B.; Stephens, B.B.; Basu, S.; Chevallier, F.; Deng, F.; Kor, E.A.; Patra, P.K.; Peters, W.; Rodenbeck, C.; Saeki, T.; et al. Global atmospheric CO2 inverse models converging on neutral tropical land exchange, but disagreeing on fossil fuel and atmospheric growth rate. Biogeosciences 2019, 16, 117–134. [Google Scholar] [CrossRef]
- Ciais, P.; Dolman, A.J.; Bombelli, A.; Duren, R.; Peregon, A.; Rayner, P.J.; Miller, C.; Gobron, N.; Kinderman, G.; Marland, G.; et al. Current systematic carbon-cycle observations and the need for implementing a policy-relevant carbon observing system. Biogeosciences 2014, 11, 3547–3602. [Google Scholar] [CrossRef]
- O’Dell, C.W.; Eldering, A.; Wennberg, P.O.; Crisp, D.; Gunson, M.R.; Fisher, B.; Frankenberg, C.; Kiel, M.; Lindqvist, H.; Mandrake, L.; et al. Improved retrievals of carbon dioxide from Orbiting Carbon Observatory-2 with the version 8 ACOS algorithm. Atmos. Meas. Tech. 2018, 11, 6539–6576. [Google Scholar] [CrossRef]
- Keppel-Aleks, G.; Wolf, A.S.; Mu, M.; Doney, S.C.; Morton, D.C.; Kasibhatla, P.S.; Miller, J.B.; Dlugokencky, E.J.; Randerson, J.T. Separating the influence of temperature, drought, and fire on interannual variability in atmospheric CO2. Glob. Biogeochem. Cycles 2014, 28, 1295–1310. [Google Scholar] [CrossRef]
- Belikov, D.A.; Maksyutov, S.; Ganshin, A.; Zhuravlev, R.; Deutscher, N.M.; Wunch, D.; Feist, D.G.; Morino, I.; Parker, R.J.; Strong, K.; et al. Study of the footprints of short-term variation in XCO2; observed by TCCON sites using NIES and FLEXPART atmospheric transport models. Atmos. Chem. Phys. 2017, 17, 143–157. [Google Scholar] [CrossRef]
- Chevallier, F.; Deutscher, N.M.; Conway, T.J.; Ciais, P.; Ciattaglia, L.; Dohe, S.; Fröhlich, M.; Gomez-Pelaez, A.J.; Griffith, D.; Hase, F.; et al. Global CO2 fluxes inferred from surface air-sample measurements and from TCCON retrievals of the CO2 total column: TWO CO2 FLUX INVERSIONS. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Lindqvist, H.; O’Dell, C.W.; Basu, S.; Boesch, H.; Chevallier, F.; Deutscher, N.; Feng, L.; Fisher, B.; Hase, F.; Inoue, M.; et al. Does GOSAT capture the true seasonal cycle of carbon dioxide? Atmos. Chem. Phys. 2015, 15, 13023–13040. [Google Scholar] [CrossRef]
- Messerschmidt, J.; Parazoo, N.; Wunch, D.; Deutscher, N.M.; Roehl, C.; Warneke, T.; Wennberg, P.O. Evaluation of seasonal atmosphere–biosphere exchange estimations with TCCON measurements. Atmos. Chem. Phys. 2013, 13, 5103–5115. [Google Scholar] [CrossRef]
- Wunch, D.; Wennberg, P.O.; Osterman, G.; Fisher, B.; Naylor, B.; Roehl, C.M.; O’Dell, C.; Mandrake, L.; Viatte, C.; Kiel, M.; et al. Comparisons of the Orbiting Carbon Observatory-2 (OCO-2) X CO2 measurements with TCCON. Atmos. Meas. Tech. 2017, 10, 2209–2238. [Google Scholar] [CrossRef]
- Sussmann, R.; Rettinger, M. Can We Measure a COVID-19-Related Slowdown in Atmospheric CO2 Growth? Sensitivity of Total Carbon Column Observations. Remote Sens. 2020, 12, 2387. [Google Scholar] [CrossRef]
- Peters, G.P.; Le Quéré, C.; Andrew, R.M.; Canadell, J.G.; Friedlingstein, P.; Ilyina, T.; Jackson, R.B.; Joos, F.; Korsbakken, J.I.; McKinley, G.A.; et al. Towards real-time verification of CO2 emissions. Nat. Clim. Chang. 2017, 7, 848–850. [Google Scholar] [CrossRef]
- Chevallier, F. On the parallelization of atmospheric inversions of CO2; surface fluxes within a variational framework. Geosci. Model Dev. 2013, 6, 783–790. [Google Scholar] [CrossRef]
- Wunch, D.; Toon, G.C.; Blavier, J.-F.L.; Washenfelder, R.A.; Notholt, J.; Connor, B.J.; Griffith, D.W.T.; Sherlock, V.; Wennberg, P.O. The Total Carbon Column Observing Network. Proc. R. Soc. A 2011, 369, 2087–2112. [Google Scholar] [CrossRef] [PubMed]
- Wunch, D.; Toon, G.C.; Wennberg, P.O.; Wofsy, S.C.; Stephens, B.B.; Fischer, M.L.; Uchino, O.; Abshire, J.B.; Bernath, P.; Biraud, S.C.; et al. Calibration of the Total Carbon Column Observing Network using aircraft profile data. Atmos. Meas. Tech. 2010, 3, 1351–1362. [Google Scholar] [CrossRef]
- Feist, D.G.; Arnold, S.G.; John, N.; Geibel, M.C. TCCON data from Ascension Island, Saint Helena, Ascension and Tristan da Cunha, Release GGG2014R0. TCCON Data Archive, Hosted by CaltechDATA; California Institute of Technology: Pasadena, CA, USA, 2014. [Google Scholar] [CrossRef]
- Deutscher, N.; Notholt, J.; Messerschmidt, J.; Weinzierl, C.; Warneke, T.; Petri, C.; Grupe, P.; Katrynski, K. TCCON Data from Bialystok, Poland, Release GGG2014R2. TCCON Data Archive, Hosted by CaltechDATA; California Institute of Technology: Pasadena, CA, USA, 2015. [Google Scholar] [CrossRef]
- Notholt, J.; Petri, C.; Warneke, T.; Deutscher, N.; Buschmann, M.; Weinzierl, C.; Macatangay, R.; Grupe, P. TCCON Data from Bremen, Germany, Release ggg2014r0. TCCON Data Archive, Hosted by the Carbon Dioxide Information Analysis Center; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2014. [Google Scholar] [CrossRef]
- Griffith, D.W.T.; Deutscher, N.; Velazco, V.A.; Wennberg, P.O.; Yavin, Y.; Aleks, G.K.; Washenfelder, R.; Toon, G.C.; Blavier, J.F.; Murphy, C.; et al. TCCON Data from Darwin, Australia, Release ggg2014r0. TCCON Data Archive, Hosted by the Carbon Dioxide Information Analysis Center; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2014. [Google Scholar]
- Iraci, L.; Podolske, J.; Hillyard, P.; Roehl, C.; Wennberg, P.O.; Blavier, J.-F.; Landeros, J.; Allen, N.; Wunch, D.; Zavaleta, J.; et al. TCCON Data from Armstrong Flight Research Center, Edwards, CA, USA, Release GGG2014R1. TCCON Data Archive, Hosted by CaltechDATA; California Institute of Technology: Pasadena, CA, USA, 2016. [Google Scholar] [CrossRef]
- Strong, K.; Mendonca, J.; Weaver, D.; Fogal, P.; Drummond, J.R.; Batchelor, R.; Lindenmaier, R. TCCON data from Eureka, Canada, Release GGG2014R2. TCCON Data Archive, Hosted by CaltechDATA; California Institute of Technology: Pasadena, CA, USA, 2017. [Google Scholar] [CrossRef]
- Sussmann, R.; Rettinger, M. TCCON Data from Garmisch (DE), Release GGG2014.R2. Available online: https://data.caltech.edu/records/956 (accessed on 23 May 2021).
- Blumenstock, T.; Hase, F.; Schneider, M.; Garcia, O.E.; Sepulveda, E. TCCON Data from Izana, Tenerife, Spain, Release GGG2014R1. TCCON Data Archive, Hosted by CaltechDATA; California Institute of Technology: Pasadena, CA, USA, 2017. [Google Scholar] [CrossRef]
- Hase, F.; Blumenstock, T.; Dohe, S.; Gross, J.; Kiel, M. TCCON Data from Karlsruhe, Germany, Release GGG2014R1. TCCON Data Archive, Hosted by CaltechDATA; California Institute of Technology: Pasadena, CA, USA, 2015. [Google Scholar] [CrossRef]
- Wennberg, P.O.; Wunch, D.; Roehl, C.; Blavier, J.F.; Toon, G.C.; Allen, N.; Dowell, P.; Teske, K.; Martin, C.; Martin, J. TCCON Data from Lamont, Oklahoma, USA, Release ggg2014r0. TCCON Data Archive, Hosted by the Carbon Dioxide Information Analysis Center; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2014. [Google Scholar]
- Sherlock, V.; Connor, B.; Robinson, J.; Shiona, H.; Smale, D.; Pollard, D. TCCON Data from Lauder, New Zealand, 125HR, Release GGG2014R0. TCCON Data Archive, Hosted by CaltechDATA; California Institute of Technology: Pasadena, CA, USA, 2014. [Google Scholar] [CrossRef]
- Pollard, D.; Robinson, J.; Shiona, H. TCCON Data from Lauder, New Zealand, 125HR, Release GGG2014R0. TCCON Data Archive, Hosted by CaltechDATA; California Institute of Technology: Pasadena, CA, USA, 2019. [Google Scholar] [CrossRef]
- Notholt, J.; Schrems, O.; Warneke, T.; Deutscher, N.; Weinzierl, C.; Palm, M.; Buschmann, M. AWI-PEV Station Engineers. TCCON Data from Ny Alesund, Spitzbergen, Norway, Release GGG2014R1. TCCON Data Archive, Hosted by CaltechDATA; California Institute of Technology: Pasadena, CA, USA, 2019. [Google Scholar] [CrossRef]
- Warneke, T.; Messerschmidt, J.; Notholt, J.; Weinzierl, C.; Deutscher, N.; Petri, C.; Grupe, P.; Vuillemin, C.; Truong, F.; Schmidt, M.; et al. TCCON Data from Orleans, France, Release GGG2014R1. TCCON Data Archive, Hosted by CaltechDATA; California Institute of Technology: Pasadena, CA, USA, 2014. [Google Scholar] [CrossRef]
- Te, Y.; Jeseck, P.; Janssen, C. TCCON Data from Paris, France, Release GGG2014R0. TCCON Data Archive, Hosted by CaltechDATA; California Institute of Technology: Pasadena, CA, USA, 2014. [Google Scholar] [CrossRef]
- Wennberg, P.O.; Roehl, C.; Wunch, D.; Toon, G.C.; Blavier, J.-F.; Washenfelder, R.; Keppel-Aleks, G.; Allen, N.; Ayers, J. TCCON Data from Park Falls, Wisconsin, USA, Release GGG2014R1. TCCON Data Archive, Hosted by CaltechDATA; California Institute of Technology: Pasadena, CA, USA, 2017. [Google Scholar] [CrossRef]
- Wennberg, P.O.; Wunch, D.; Roehl, C.; Blavier, J.-F.; Toon, G.C.; Allen, N. TCCON Data from California Institute of Technology, Pasadena, California, USA, Release GGG2014R1. TCCON Data Archive, Hosted by CaltechDATA; California Institute of Technology: Pasadena, CA, USA, 2015. [Google Scholar] [CrossRef]
- De Maziere, M.; Sha, M.K.; Desmet, F.; Hermans, C.; Scolas, F.; Kumps, N.; Metzger, J.-M.; Duflot, V.; Cammas, J.-P. TCCON Data from Réunion Island (La Réunion), France, Release GGG2014R0. TCCON Data Archive, Hosted by CaltechDATA; California Institute of Technology: Pasadena, CA, USA, 2017. [Google Scholar] [CrossRef]
- Shiomi, K.; Kawakami, S.; Ohyama, H.; Arai, K.; Okumura, H.; Taura, C.; Fukamachi, T.; Sakashita, M. TCCON Data from Saga, Japan, Release GGG2014R0. TCCON Data Archive, Hosted by CaltechDATA; California Institute of Technology: Pasadena, CA, USA, 2014. [Google Scholar] [CrossRef]
- Morino, I.; Matsuzaki, T.; Horikawa, M. TCCON Data from Tsukuba, Ibaraki, Japan, 125HR, Release GGG2014R2. TCCON Data Archive, Hosted by CaltechDATA; California Institute of Technology: Pasadena, CA, USA, 2018. [Google Scholar] [CrossRef]
- Kawakami, S.; Ohyama, H.; Arai, K.; Okumura, H.; Taura, C.; Fukamachi, T.; Sakashita, P. TCCON data from Saga (JP), Release GGG2014.R0. 2014. Available online: https://data.caltech.edu/records/288 (accessed on 23 May 2021).
- Kivi, R.; Heikkinen, P.; Kyro, E. TCCON Data from Sodankyla, Finland, Release GGG2014R0. TCCON Data Archive, Hosted by CaltechDATA; California Institute of Technology: Pasadena, CA, USA, 2014. [Google Scholar] [CrossRef]
- Kivi, R.; Heikkinen, P. Fourier transform spectrometer measurements of column CO2; at Sodankylä, Finland. Geosci. Instrum. Method. Data Syst. 2016, 5, 271–279. [Google Scholar] [CrossRef]
- Griffith, D.W.T.; Velazco, V.A.; Deutscher, N.; Murphy, C.; Jones, N.; Wilson, S.; Macatangay, R.; Kettlewell, G.; Buchholz, R.R.; Riggenbach, M. TCCON Data from Wollongong, Australia, Release ggg2014r0. TCCON Data Archive, Hosted by the Carbon Dioxide Information Analysis Center, Oak Ridge National Laboratory. Remote Sens. 2017, 9, 1033. [Google Scholar]
- Sussmann, R.; Rettinger, M. TCCON Data from Zugspitze, Germany, Release GGG2014R1. TCCON Data Archive, Hosted by CaltechDATA; California Institute of Technology: Pasadena, CA, USA, 2018. [Google Scholar]
- Wunch, D.; Toon, G.C.; Sherlock, V.; Deutscher, N.M.; Liu, C.; Feist, D.G.; Wennberg, P.O. The Total Carbon Column Observing Network’s GGG2014 Data Version, 42, n.d. (TCCON Data Reference) 2015. Dataset Identifier for TCCON. Available online: https://data.caltech.edu/records/249 (accessed on 23 May 2021).
- Griffith, D.W.T.; Deutscher, N.; Velazco, V.A.; Wennberg, P.O.; Yavin, Y.; Keppel Aleks, G.; Washenfelder, R.; Toon, G.C.; Blavier, J.-F.; Murphy, C.; et al. TCCON Data from Darwin, Australia, Release GGG2014R0. TCCON Data Archive, Hosted by CaltechDATA; California Institute of Technology: Pasadena, CA, USA, 2014. [Google Scholar] [CrossRef]
- Wennberg, P.O.; Roehl, C.; Blavier, J.-F.; Wunch, D.; Landeros, J.; Allen, N. TCCON Data from Jet Propulsion Laboratory, Pasadena, California, USA, Release GGG2014R1. TCCON Data Archive, Hosted by CaltechDATA; California Institute of Technology: Pasadena, CA, USA, 2007. [Google Scholar] [CrossRef]
- Wennberg, P.O.; Wunch, D.; Yavin, Y.; Toon, G.C.; Blavier, J.-F.; Allen, N.; Keppel-Aleks, G. TCCON Data from Jet Propulsion Laboratory, Pasadena, California, USA, Release GGG2014R0. TCCON Data Archive, Hosted by CaltechDATA; California Institute of Technology: Pasadena, CA, USA, 2014. [Google Scholar] [CrossRef]
- Dubey, M.; Henderson, B.; Green, D.; Butterfield, Z.; Keppel-Aleks, G.; Allen, N.; Blavier, J.-F.; Roehl, C.; Wunch, D.; Lindenmaier, R. TCCON Data from Manaus, Brazil, Release GGG2014R0. TCCON Data Archive, Hosted by CaltechDATA; California Institute of Technology: Pasadena, CA, USA, 2014. [Google Scholar] [CrossRef]
- Iraci, L.; Podolske, J.; Hillyard, P.; Roehl, C.; Wennberg, P.O.; Blavier, J.-F.; Landeros, J.; Allen, N.; Wunch, D.; Zavaleta, J.; et al. TCCON Data from Indianapolis, Indiana, USA, Release GGG2014R1. TCCON Data Archive, Hosted by CaltechDATA; California Institute of Technology: Pasadena, CA, USA, 2016. [Google Scholar] [CrossRef]
- Locatelli, R.; Bousquet, P.; Hourdin, F.; Saunois, M.; Cozic, A.; Couvreux, F.; Grandpeix, J.-Y.; Lefebvre, M.-P.; Rio, C.; Bergamaschi, P.; et al. Atmospheric transport and chemistry of trace gases in LMDz5B: Evaluation and implications for inverse modelling. Geosci. Model Dev. 2015, 8, 129–150. [Google Scholar] [CrossRef]
- Chevallier, F.; Fisher, M.; Peylin, P.; Serrar, S.; Bousquet, P.; Bréon, F.-M.; Chédin, A.; Ciais, P. Inferring CO2 sources and sinks from satellite observations: Method and application to TOVS data. J. Geophys. Res. 2005, 110, D24309. [Google Scholar] [CrossRef]
- Chevallier, F.; Ciais, P.; Conway, T.J.; Aalto, T.; Anderson, B.E.; Bousquet, P.; Brunke, E.G.; Ciattaglia, L.; Esaki, Y.; Fröhlich, M.; et al. CO2 surface fluxes at grid point scale estimated from a global 21 year reanalysis of atmospheric measurements. J. Geophys. Res. 2010, 115, D21307. [Google Scholar] [CrossRef]
- Krol, M.; Houweling, S.; Bregman, B.; Bergamaschi, P. The two-way nested global chemistry-transport zoom model TM5: Algorithm and applications. Atmos. Chem. Phys. 2005, 16, 417–432. [Google Scholar] [CrossRef]
- Oda, T.; Maksyutov, S.; Andres, R.J. The Open-source Data Inventory for anthropogenic CO2, version 2016 (ODIAC2016): A global monthly fossil fuel CO2 gridded emissions data product for tracer transport simulations and surface flux inversions. Earth Syst. Sci. Data 2018, 10, 87–107. [Google Scholar] [CrossRef] [PubMed]
- Jacobson, A.R.; Mikaloff Fletcher, S.E.; Gruber, N.; Sarmiento, J.L.; Gloor, M. A joint atmosphere-ocean inversion for surface fluxes of carbon dioxide: 1. Methods and global-scale fluxes: JOINT INVERSION-METHODS AND GLOBAL FLUXES. Glob. Biogeochem. Cycles 2007, 21. [Google Scholar] [CrossRef]
- Takahashi, T.; Sutherland, S.C.; Sweeney, C.; Feely, R.A.; Chipman, D.W.; Hales, B.; Friederich, G.; Chavez, F.; Sabine, C.; Watson, A.; et al. Climatological mean and decadal change in surface ocean pCO2, and net sea-air CO2 flux over the global oceans. Deep Sea Res. II 2009, 56, 554–577. [Google Scholar] [CrossRef]
- Zhao, X.; Marshall, J.; Hachinger, S.; Gerbig, C.; Frey, M.; Hase, F.; Chen, J. Analysis of total column CO2 and CH4 measurements in Berlin with WRF-GHG. Atmos. Chem. Phys. 2019, 19, 11279–11302. [Google Scholar] [CrossRef]
- Rodgers, C.D.; Connor, B.J. Intercomparison of remote sounding instruments. J. Geophys. Res 2003, 108, 4116. [Google Scholar] [CrossRef]
- Null, J. El Nino and La Niña Years and Intensities Based on Oceanic Nino Index (ONI), Golden GateWeather Services. 2013. Available online: http://ggweather.com/enso/oni.htm (accessed on 15 July 2020).
- Schneider, A.; Friedl, M.A.; Potere, D. A new map of global urban extent from MODIS satellite data. Environ. Res. Lett. 2009, 4, 044003. [Google Scholar] [CrossRef]
- Labzovskii, L.D.; Jeong, S.-J.; Parazoo, N.C. Working towards confident spaceborne monitoring of carbon emissions from cities using Orbiting Carbon Observatory-2. Remote Sens. Environ. 2019, 233, 111359. [Google Scholar] [CrossRef]
- Park, H.; Jeong, S.; Park, H.; Labzovskii, L.D.; Bowman, K.W. An assessment of emission characteristics of Northern Hemisphere cities using spaceborne observations of CO2, CO, and NO2. Remote Sens. Environ. 2021, 254, 112246. [Google Scholar] [CrossRef]
- Dlugokencky, E.J.; Mund, J.W.; Crotwell, A.M.; Crotwell, M.J.; Thoning, K.W. Atmospheric Carbon Dioxide Dry Air Mole Fractions from the NOAA GML Carbon Cycle Cooperative Global Air Sampling Network, 1968–2019; Version: 2020-07, 2020; Datasets Description; Available online: https://doi.org/10.15138/wkgj-f215 (accessed on 23 May 2021).
- Wang, X.; Piao, S.; Ciais, P.; Friedlingstein, P.; Myneni, R.B.; Cox, P.; Heimann, M.; Miller, J.; Peng, S.; Wang, T.; et al. A two-fold increase of carbon cycle sensitivity to tropical temperature variations. Nature 2014, 506, 212–215. [Google Scholar] [CrossRef]
- Yuan, Y.; Sussmann, R.; Rettinger, M.; Ries, L.; Petermeier, H.; Menzel, A. Comparison of Continuous In-Situ CO2 Measurements with Co-Located Column-Averaged XCO2 TCCON/Satellite Observations and CarbonTracker Model over the Zugspitze Region. Remote Sens. 2019, 11, 2981. [Google Scholar] [CrossRef]
- Paek, H.; Yu, J.-Y.; Qian, C. Why were the 2015/2016 and 1997/1998 extreme El Niños different? Contrasting 1997/1998 and 2015/2016 El Niños, Geophys. Res. Lett. 2017, 44, 1848–1856. [Google Scholar] [CrossRef]
- Graven, H.D.; Keeling, R.F.; Piper, S.C.; Patra, P.K.; Stephens, B.B.; Wofsy, S.C.; Welp, L.R.; Sweeney, C.; Tans, P.P.; Kelley, J.J.; et al. Enhanced Seasonal Exchange of CO2 by Northern Ecosystems Since 1960. Science 2013, 341, 1085–1089. [Google Scholar] [CrossRef]
- Uchino, O.; Sakai, T.; Nagai, T.; Izumi, T.; Shibata, T.; Morino, I.; Yoshida, Y.; Hiroshi, O.; Arai, K.; Bagtasa, G.; et al. Characteristics of Atmospheric Aerosols Observed by Lidar at Five TCCON Sites Extending from 43°N to 45°S. American Geophysical Union, Fall Meeting 2017 (December 2017)Conference Work 2017AGUFM.A21M..07U. Available online: https://ui.adsabs.harvard.edu/abs/2017AGUFM.A21M..07U/abstract (accessed on 23 May 2021).
- Fang, S.X.; Zhou, L.X.; Tans, P.P.; Ciais, P.; Steinbacher, M.; Xu, L.; Luan, T. In situ measurement of atmospheric CO2 at the four WMO/GAW stations in China. Atmos. Chem. Phys. 2014, 14, 2541–2554. [Google Scholar] [CrossRef]
- Cheng, Y.; Aa, X.; Yun, F.; Zhou, L.; Liu, L.; Fang, S.; Xu, L. Simulation of CO2 variations at Chinese background atmospheric monitoring stations between 2000 and 2009: Applying a CarbonTracker model. Chin. Sci. Bull. 2013, 58, 3986–3993. [Google Scholar] [CrossRef][Green Version]
- Nayak, R.K.; Deepthi, E.N.; Dadhwal, V.K.; Rao, K.H.; Dutt, C.B.S. Evaluation of NOAA Carbon Tracker Global Carbon Dioxide Products. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2014, XL-8, 287–290. [Google Scholar] [CrossRef]
- Le Quéré, C.; Andrew, R.M.; Friedlingstein, P.; Sitch, S.; Hauck, J.; Pongratz, J.; Pickers, P.A.; Korsbakken, J.I.; Peters, G.P.; Canadell, J.G.; et al. Global Carbon Budget 2018. Earth Syst. Sci. Data 2018, 10, 2141–2194. [Google Scholar] [CrossRef]
- Randerson, J.T.; Chen, Y.; van der Werf, G.R.; Rogers, B.M.; Morton, D.C. Global burned area and biomass burning emissions from small fires: Burned Area from Small Fires. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- Feist, D.G.; Burjack, I.; Niebling, S. TCCON measurements from Ascension Island: Lessons learned from the first of operation. In Proceedings of the EGU General Assembly 2013, Vienna, Austria, 7–12 April 2013. [Google Scholar]
- Palmer, P.I.; Feng, L.; Baker, D.; Chevallier, F.; Bösch, H.; Somkuti, P. Net carbon emissions from African biosphere dominate pan-tropical atmospheric CO2 signal. Nat. Commun. 2019, 10, 3344. [Google Scholar] [CrossRef]
- Denning, S.A.; Randall, D.A.; Collatz, G.J.; Sellers, P.J. Simulations of terrestrial carbon metabolism and atmospheric CO2 in a general circulation model. Tellus B Chem. Phys. Meteorol. 1996, 48, 543–567. [Google Scholar] [CrossRef][Green Version]
- Oh, Y.-S.; Kenea, S.T.; Goo, T.-Y.; Chung, K.-S.; Rhee, J.-S.; Ou, M.-L.; Byun, Y.-H.; Wennberg, P.O.; Kiel, M.; Di Gangi, J.P.; et al. Characteristics of greenhouse gas concentrations derived from ground-based FTS spectra at Anmyeondo, South Korea. Atmos. Meas. Tech. 2018, 11, 2361–2374. [Google Scholar] [CrossRef]
- Kulawik, S.; Wunch, D.; O’ Dell, C.; Frankenberg, C.; Reuter, M.; Oda, T.; Chevallier, F.; Sherlock, V.; Buchwitz, M.; Osterman, G.; et al. Consistent evaluation of ACOS-GOSAT, BESD-SCIAMACHY, CarbonTracker, and MACC through comparisons to TCCON. Atmos. Meas. Tech. 2016, 9, 683–709. [Google Scholar] [CrossRef]
- Lindenmaier, R.; Dubey, M.K.; Henderson, B.G.; Butterfield, Z.T.; Herman, J.R.; Rahn, T.; Lee, S.-H. Multiscale observations of CO2, 13CO2, and pollutants at Four Corners for emission verification and attribution. Proc. Natl. Acad. Sci. USA 2014, 111, 8386–8391. [Google Scholar] [CrossRef]
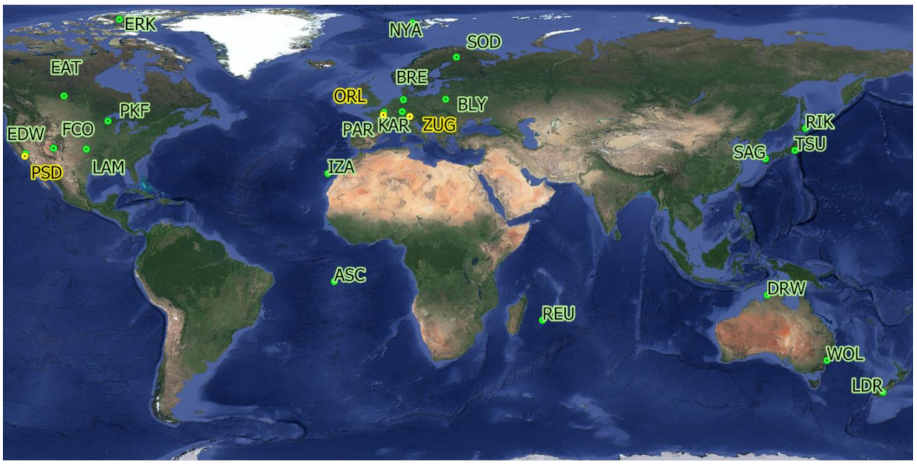
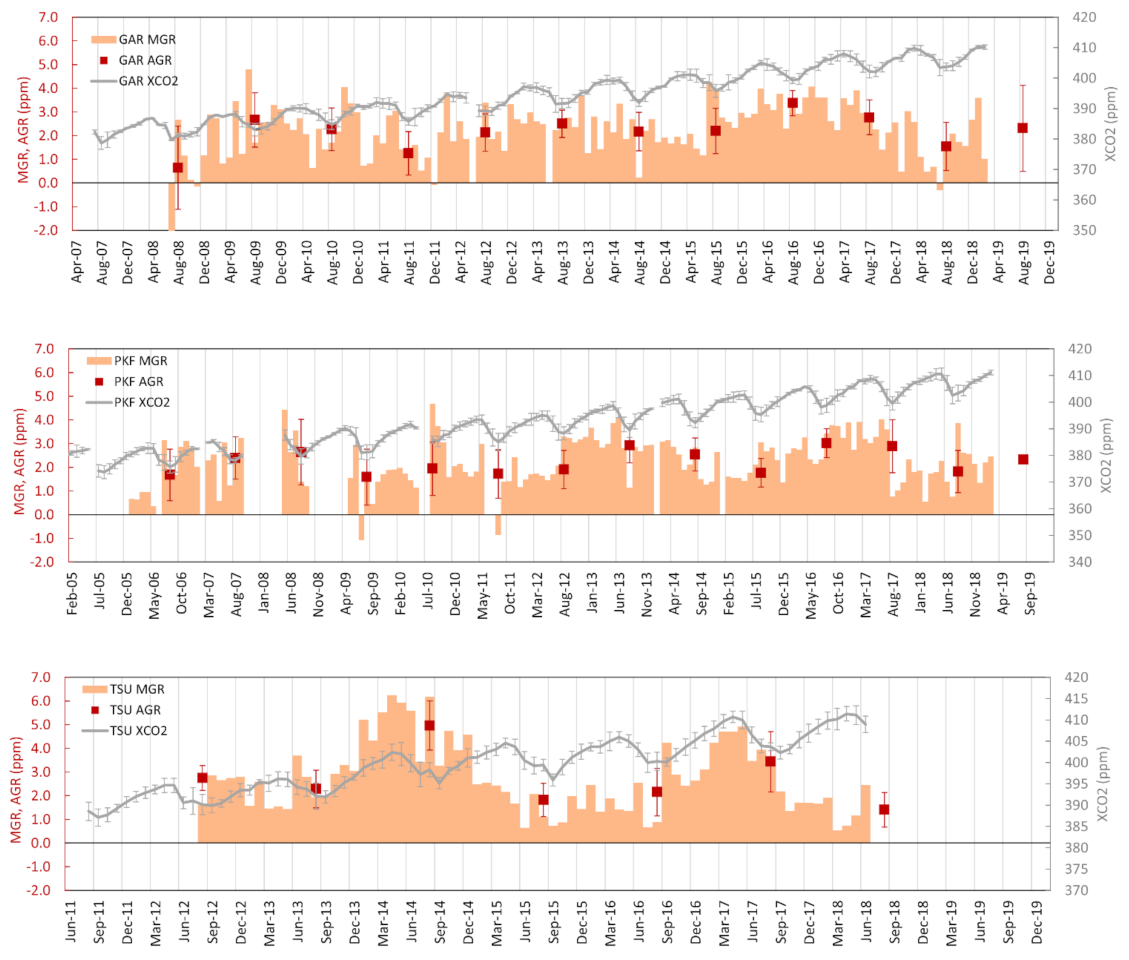
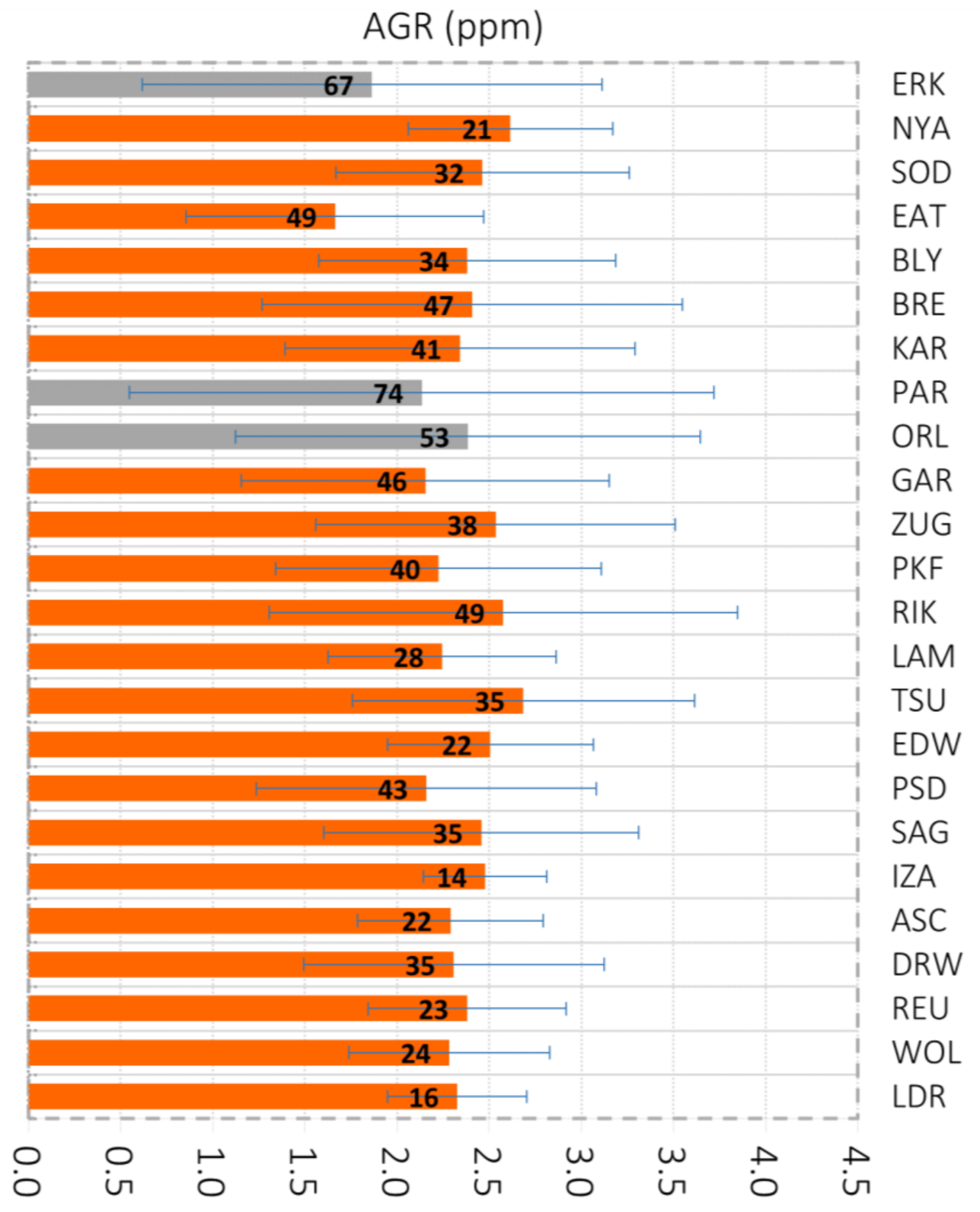
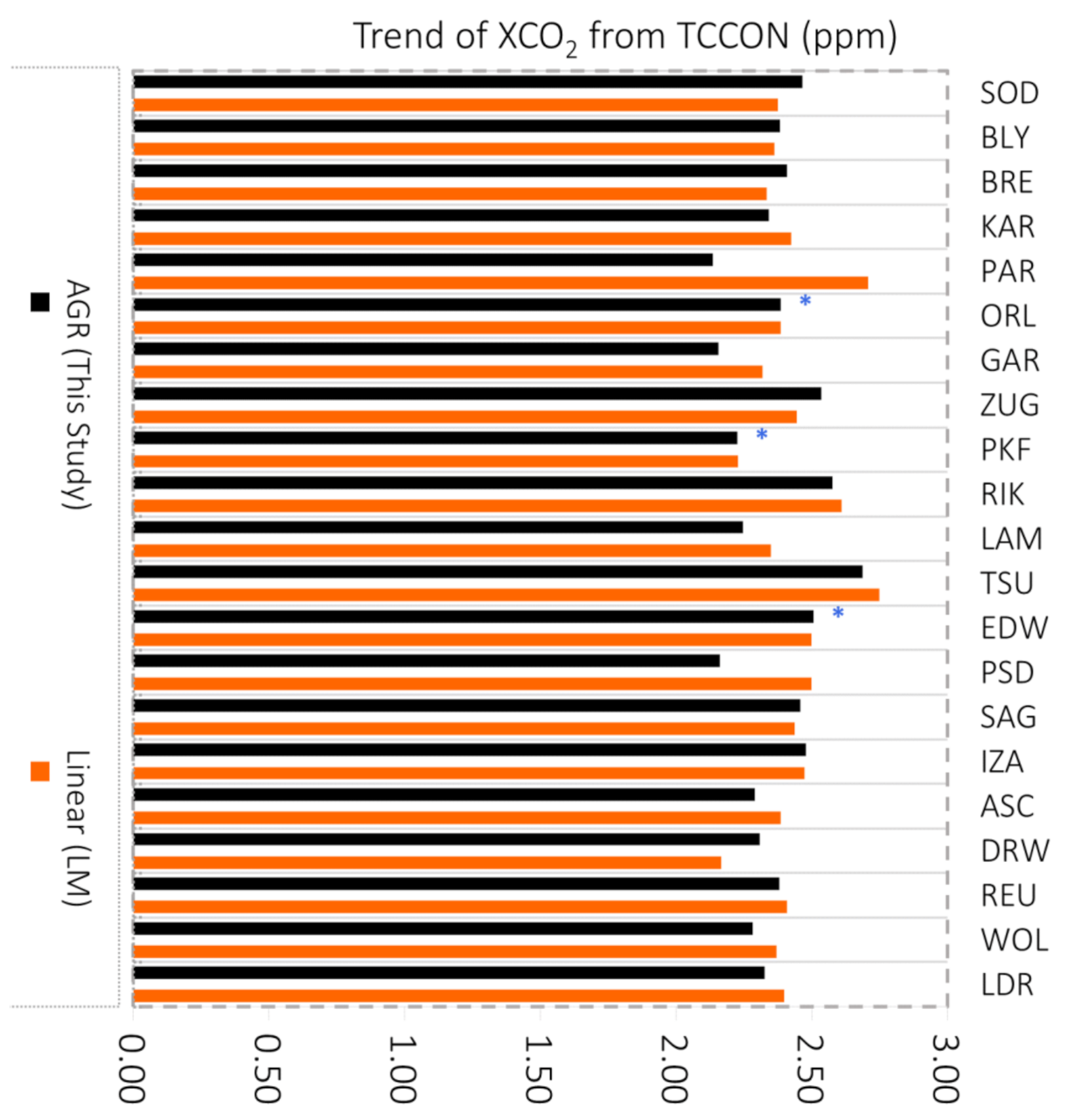
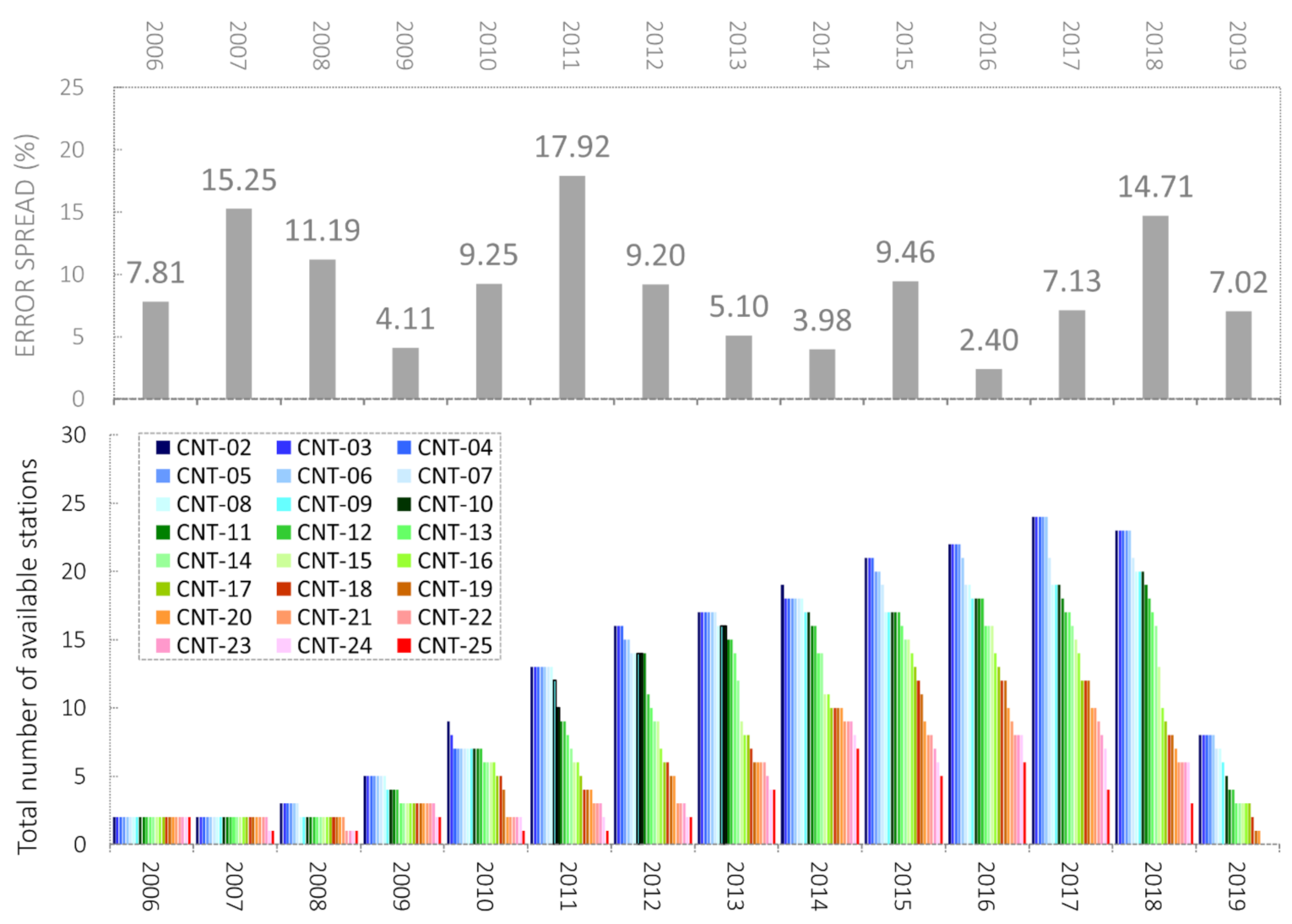
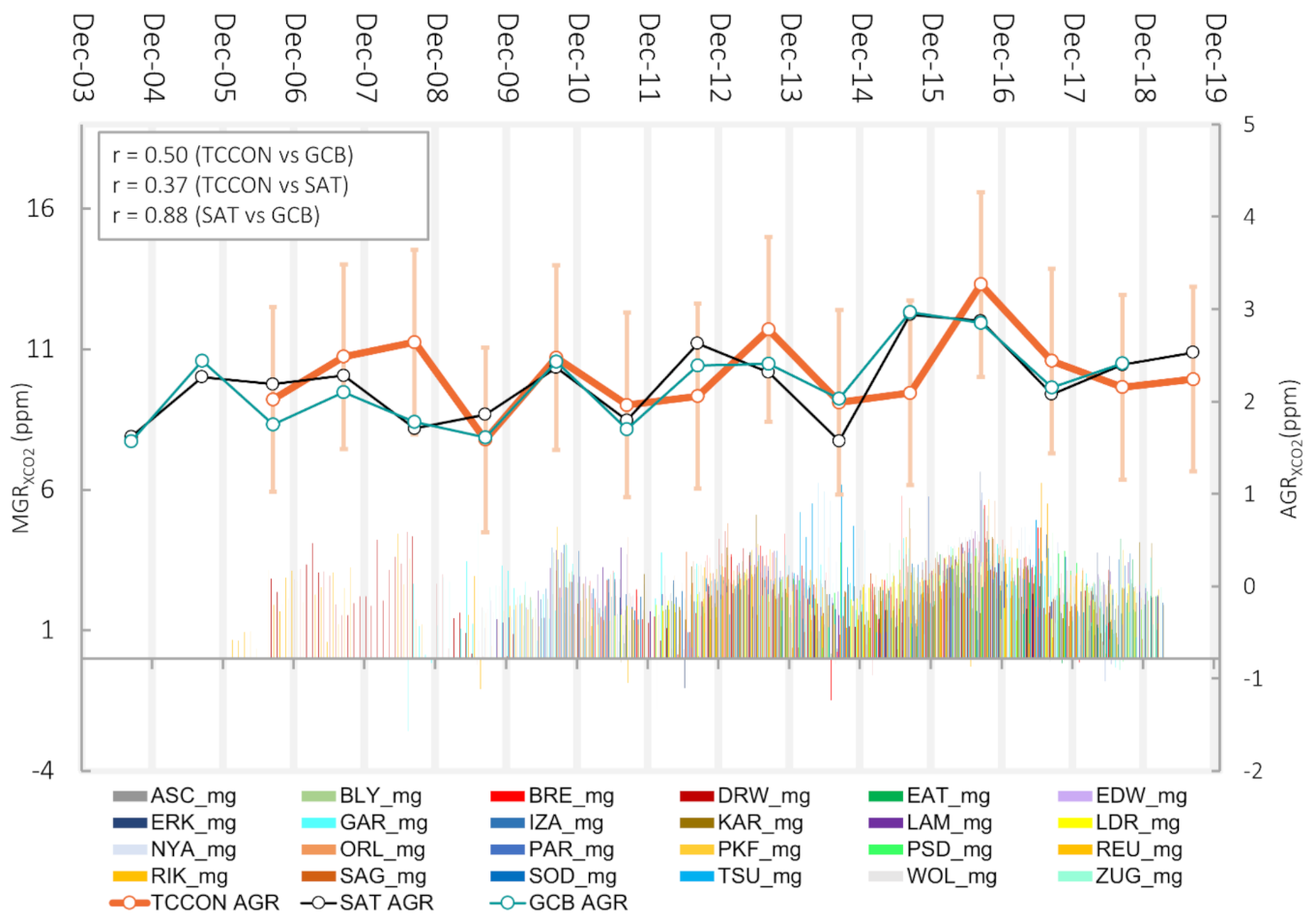
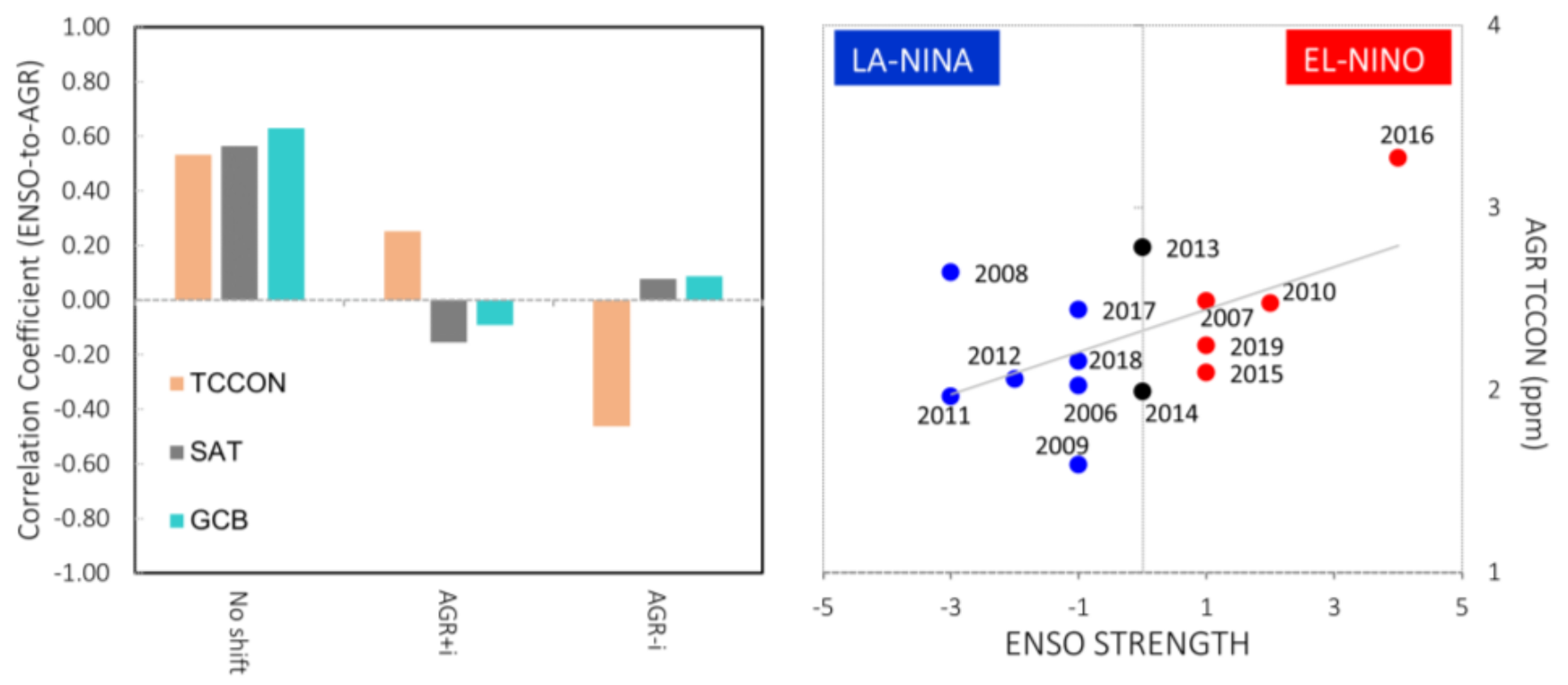
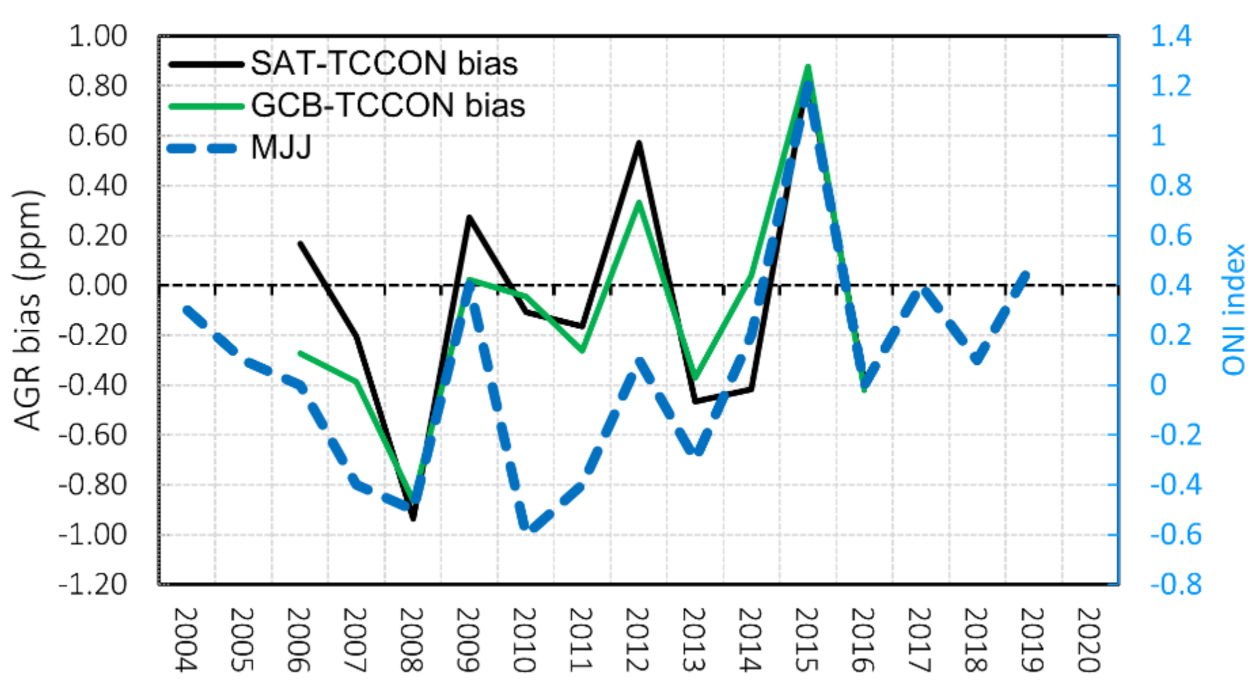
| Station | Daily(s) | Daily(f) | Daily(t) | MGR | AGR |
|---|---|---|---|---|---|
| PKF | 2340 | 2337 | 4677 | 136 | 14 |
| DRW | 2373 | 2417 | 4790 | 112 | 13 |
| LAM | 2522 | 2461 | 4983 | 112 | 11 |
| GAR | 1216 | 1257 | 2473 | 126 | 12 |
| WOL | 1420 | 1486 | 2906 | 98 | 10 |
| LDR | 1240 | 1307 | 2547 | 93 | 8 |
| SOD | 1243 | 1282 | 2525 | 75 | 9 |
| BLY | 1045 | 1015 | 2060 | 78 | 9 |
| ORL | 1041 | 1026 | 2067 | 75 | 9 |
| KAR | 849 | 921 | 1770 | 87 | 9 |
| PSD | 1537 | 1496 | 3033 | 65 | 7 |
| TSU | 815 | 824 | 1639 | 71 | 7 |
| REU | 1042 | 1066 | 2108 | 55 | 7 |
| SAG | 628 | 635 | 1263 | 68 | 7 |
| BRE | 386 | 393 | 779 | 70 | 8 |
| IZA | 383 | 447 | 830 | 52 | 8 |
| ASC | 579 | 610 | 1189 | 30 | 6 |
| EDW | 682 | 707 | 1389 | 28 | 4 |
| RIK | 213 | 235 | 448 | 42 | 4 |
| ERK | 202 | 200 | 402 | 25 | 7 |
| ZUG | 265 | 214 | 479 | 31 | 4 |
| PAR | 154 | 160 | 314 | 21 | 4 |
| NYA | 192 | 215 | 407 | 15 | 4 |
| EAT | 238 | 263 | 501 | 15 | 3 |
| Code. | dmegacity | Amegacity (km2) | dlarge | Alarge (km2) | danytown | Aanytown (km2) |
|---|---|---|---|---|---|---|
| ASC | 2488.4 | 3847.3 | 858.4 | 2170.6 | 20.6 | 1549.4 |
| BLY | 1533.0 | 436.5 | 863.2 | 174.2 | 147.0 | 9.8 |
| BRE | 8326.2 | 261.1 | 687.0 | 94.4 | 286.2 | 4.3 |
| DRW | 1540.3 | 2728.0 | 791.8 | 2612.2 | 100.2 | 3.2 |
| EAT | 1745.6 | 1617.3 | 525.9 | 717.3 | 57.3 | 136.3 |
| EDW | 6602.4 | 122.3 | 6602.4 | 122.3 | 253.1 | 42.1 |
| ERK | 1914.8 | 3918.3 | 1914.8 | 3918.3 | 10.9 | 2740.6 |
| FCO | 1745.6 | 448.8 | 593.4 | 248.7 | 81.1 | 27.2 |
| GAR | 5176.7 | 243.9 | 748.6 | 86.2 | 127.6 | 31.5 |
| IZA | 2715.9 | 1610.1 | 624.1 | 1033.2 | 18.0 | 312.0 |
| KAR | 4799.6 | 39.3 | 4799.6 | 39.3 | 4799.6 | 39.3 |
| LAM | 3647.8 | 408.8 | 529.1 | 111.3 | 33.4 | 37.5 |
| LDR | 1638.8 | 2023.2 | 1638.8 | 2023.2 | 20.7 | 111.5 |
| NYA | 2317.2 | 2986.9 | 584.5 | 2595.3 | 9.9 | 1040.9 |
| ORL | 3144.3 | 98.1 | 3144.3 | 98.1 | 173.9 | 16.7 |
| PAR | 3144.3 | 4.3 | 3144.3 | 4.3 | 3144.3 | 4.3 |
| PKF | 1914.8 | 257.8 | 1914.8 | 257.8 | 17.4 | 74.8 |
| PSD | 6602.4 | 32.4 | 6602.4 | 32.4 | 6602.4 | 32.4 |
| REU | 4136.9 | 2866.0 | 536.7 | 868.3 | 45.5 | 1.3 |
| RIK | 18,720.0 | 878.2 | 1148.6 | 631.6 | 52.8 | 37.8 |
| SAG | 5477.3 | 39.9 | 5477.3 | 39.9 | 5477.3 | 39.9 |
| SOD | 2088.0 | 1412.3 | 595.3 | 850.6 | 6.1 | 105.2 |
| TSU | 18,720.0 | 22.9 | 18,720.0 | 22.9 | 18,720.0 | 22.9 |
| WOL | 1638.8 | 59.5 | 1638.8 | 59.5 | 137.5 | 2.7 |
| ZUG | 5176.7 | 235.2 | 748.6 | 94.8 | 127.6 | 32.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Labzovskii, L.D.; Kenea, S.T.; Lindqvist, H.; Kim, J.; Li, S.; Byun, Y.-H.; Goo, T.-Y. Towards Robust Calculation of Interannual CO2 Growth Signal from TCCON (Total Carbon Column Observing Network). Remote Sens. 2021, 13, 3868. https://doi.org/10.3390/rs13193868
Labzovskii LD, Kenea ST, Lindqvist H, Kim J, Li S, Byun Y-H, Goo T-Y. Towards Robust Calculation of Interannual CO2 Growth Signal from TCCON (Total Carbon Column Observing Network). Remote Sensing. 2021; 13(19):3868. https://doi.org/10.3390/rs13193868
Chicago/Turabian StyleLabzovskii, Lev D., Samuel Takele Kenea, Hannakaisa Lindqvist, Jinwon Kim, Shanlan Li, Young-Hwa Byun, and Tae-Young Goo. 2021. "Towards Robust Calculation of Interannual CO2 Growth Signal from TCCON (Total Carbon Column Observing Network)" Remote Sensing 13, no. 19: 3868. https://doi.org/10.3390/rs13193868
APA StyleLabzovskii, L. D., Kenea, S. T., Lindqvist, H., Kim, J., Li, S., Byun, Y.-H., & Goo, T.-Y. (2021). Towards Robust Calculation of Interannual CO2 Growth Signal from TCCON (Total Carbon Column Observing Network). Remote Sensing, 13(19), 3868. https://doi.org/10.3390/rs13193868






