Abstract
Radar data are essential to convection nowcasting and nudging-based radar data assimilation through diabatic initialization is one of the most effective approaches for forecasting convective systems with numerical weather prediction (NWP) models, used at several advanced global weather centers. It is desired to assess the uncertainty and physical consistency of this assimilation process. This paper investigated impacts of relaxation coefficient, radar data update intervals and continuous assimilation time duration and addressed the key issues and possible solutions of the radar data assimilation based on the WRF hydrometeor and latent heat nudging (HLHN) developed at the National Center for Atmospheric Research (NCAR). It is revealed that excessively large relaxation coefficient forced the model to observations with a tendency greater than the physical terms of the convection, causing the dynamic imbalances and serious convection “ramp-down” right after the free forecast starts. Assimilating high update frequency radar data can make the tendency terms moderate and sustained thereby maintaining the assimilation effect and reducing fortuitous convection. HLHN requires a minimum continuous assimilation duration to contain the initial forced disturbance of the model. For a summer Meiyu precipitation case studied, the minimum duration is ~1 h. Appropriate selection of the HLHN parameters is able to effectively improve the temperature, humidity, and dynamic fields of the model. In addition, several issues still remain to be solved to further enhance HLHN.
1. Introduction
Convection is one of the most unstable chaotic and nonlinear components of atmospheric processes, and convection nowcasting has always been a hot and challenging research topic in meteorological research and operations. Traditional, nowcasting is usually considered to use the previously initiated model forecast or reanalysis data as a background, combined with observational information from different measurements, using a variety of methods to quickly forecast the weather conditions from the current moment to several hours later [1].
In the past few years, advances in weather radar observation techniques have led to valuable progress in methods based on numerical weather prediction (NWP) and radar echo extrapolation [2,3,4]. At present, weather radar is the only instrument that perform frequent and refined sampling of convective storms. But developing an accurate method to assimilate the radar observation into numerical models remains a difficult task [5]. Firstly, there are large uncertainties with the radar detection accuracy, formulation of forward operators, and/or cloud hydrometeors and latent heat retrieving. Although radars provide spatiotemporally high-resolution observations, at present, the assimilation of the refined detection data does not necessarily result in more accurate forecasts. The rapid growth of the small-scale errors, coupled with pre-existing large-scale errors may limit the effectiveness of such methods [6,7]. Secondly, it is inevitable to lose some small-scale precipitation information in the process of radar quality control and data upscaling to model grids. Therefore, it is necessary to improve the atmospheric thermodynamics and the microphysical fields at the same time during radar data assimilation to maintain the model dynamical and physical consistencies [6]. Finally, although weather radars allow measuring clouds in very high resolution, the occlusion of ground objects, non-meteorological echo and incomplete detection coverage often result in a lack of data in some spaces.
Since the 1990s, many data assimilation methods have been developed, including three-dimensional variational data assimilation (3D-VAR) [8,9,10,11], four-dimensional variational data assimilation (4D-VAR) [12,13,14,15], ensemble Kalman filter (EnKF) [16,17,18], Newtonian relaxation-based nudging method [19,20,21] and hybrid assimilation that combines variational and ensemble Kalman filtering (even hybrid methods including radar extrapolation techniques) [22,23,24]. These methods have been tested for radar data assimilation and showed encouraging impacts. However, there are still many problems that have not been solved.
In 3D-VAR technologies, a three-dimensional balance constraint that is imposed during minimization of the cost function often does not adequately represent the internal and peripheral balance of convection, or the consistency among the dynamical and thermodynamic state of convective storms. Therefore, the storms initialized with radar data assimilation often cannot be sustained in the model forecast [4]. In addition, the background error covariance required by 3D-VAR is typically assumed to be stationary, nearly homogeneous, and isotropic, and therefore cannot properly reflect the characteristics of a particular storm [25]. 4D-VAR relies on complex adjoint of atmospheric dynamical and physical equations. It requires massive calculation and thus limits its operational applications [12]. Meanwhile, the model errors are relatively larger at convection scales and convection systems evolve very fast, the linearity assumption required by 4D-VAR subjects to violation in many situations. The hybrid assimilation of variational and radar extrapolation effectively prolongs the forecast lead time, but due to the different weighting methods, the forecasting effect for different weathers is not stable [22]. Recently, several studies applied ensemble Kalman filter (EnKF) for radar data assimilation. EnKF makes use of a set of short-term ensembles to estimate the background error covariance, and then performs Kalman Filter to update the analysis and its error covariance [16]. EnKF is able to exploit flow-dependent background error covariances, but the effect of EnKF highly depends on the effectiveness of ensemble members in the representation of the convection and the errors, both of which contains large uncertainties. In fact, formulating high-quality model ensembles is one of the major research foci on EnKF. Recent studies have shown that variational and EnKF hybrid assimilation methods present a promising direction for future improvements in convective scale prediction of NWP [26,27].
Different data assimilation methods for convective-scale NWP have been adopted by major operational weather centers worldwide. Although variational and Kalman filtering methods have been adopted for assimilating general data, most centers continue to employ nudging technology to provide convection initialization. For nudging technology, the observation-based forcing tendency terms are introduced into the model and the observation information is digested by the model dynamics and physics during the process of forward integration, effectively interacting with the model dynamic, thermal, and microphysical variables. This method is a highly cost-effective way to promote the generation of mesoscale convective structures in areas where precipitation is continuously observed. National Oceanic and Atmospheric Administration (NOAA) and National Centers for Environmental Prediction (NCEP) in the United States currently executes two NWP systems to provide high-resolution convection-permitting forecasts for the United States, namely CONtiguous United States nest of North American Mesoscale system (CONUS-NAM) and High-Resolution Rapid Refresh system (HRRR). Both use hybrid 3DEnVAR technology to assimilate various data except for radar data which are assimilated by using a non-variational cloud analysis and a latent heat tendency derived from radar reflectivity factor (also called reflectivity: Z or ZH). For each forecast cycle, the initialization process lasts for 6 (or 1)-h, and then a 60 (or 18)-h continuous forecast is issued [11,28].
Similarly, in Europe, the United Kingdom Met Office employs 3DVAR and 4DVAR for data assimilation with its global and limited regional models, but the precipitation rate and radar data are added into the model through latent heat nudging (LHN) technology [29,30]. Deutscher Wetter Dienst (DWD) introduced an assimilation system based on Local Ensemble Transform Kalman Filter (LETKF) to the consortium for small scale modeling (COSMO) in 2016 and applies LHN derived from radar precipitation rate to initialize each ensemble member [21,31]. In addition, COSMO-DE (initially named LMK), a COSMO-based short-term forecasting system that focuses on convection scales, also uses the LHN technology to assimilate the latent heat derived from the surface precipitation. This algorithm considers the horizontal drift of falling hydrometeors and the latent heating time-lag, which significantly improves the forecast of short-term convection. In Canada, Environment and Climate Change Canada (ECCC) made use of LHN technology for large-area radar assimilation experiments over North America, and established a quality factor for radar reflectivity to reduce the representative error of radar data assimilation [32]. In Italy, the nudging technology based on humidity profile has also been tested in the Bologna Limited Area Model (BOLAM). As a result, the precipitation forecast in the Mediterranean area continues to show a significant improvement 10 h after the assimilation ends [33].
WRF-FDDA is a four-dimensional data assimilation scheme [34,35] based on the Newtonian relaxation principle. This scheme introduces artificial tendency terms into the model and gradually “nudge” the model towards the observations. Each observation has an influence radius, a time window, and a relaxation coefficient specified by the user. These determine where, when, and what extent the observation affects the model state, and generates an effective model analysis. On this basis, NCAR has developed a real-time four-dimensional data assimilation and short-term forecasting system RTFDDA that assimilates diverse observations into WRF for real-time rapid-update weather prediction on multi-scale mesoscale grids. The system adds the ability to assimilate radar reflectivity, that is, nudge hydrometeors and the latent heat (HLHN) retrieved from the reflectivity to the WRF hydrometeor and temperature prognostic equations for 4D continuous data assimilation. The system has been evaluated [36,37], and has proven a consistent positive impact in forecasting convection up to 9–12 h ahead.
One limitation of the nudging approach is that it relies on the empirical relationship between hydrometeor variables and radar reflectivity and a number of empirical assimilation parameters which requires careful evaluation and adjustments. In addition, hydrometeor nudging requires modifying the latent heat and/or water vapor to account for the diabatic effect and the dynamical and physical consistency among different model state variables. Despite these limitations, nudging based on diabatic initialization is, at present, still the most effective, efficient, and practical method for radar reflectivity and precipitation data assimilation for local short-term convective storm forecasting.
This paper aims at understanding and addressing several issues that have long been controversial with respect to the diabatic initialization method for radar data assimilation to maximize the performance of the process of assimilation. In particular, we quantitatively investigated the impact of the control parameters on HLHN, including the influence of relaxation coefficient on “ramp-down” issue, and the influence of radar data update intervals and continuous assimilation time duration for the forcing tendency. By selecting a typical Meiyu front precipitation event in Eastern China occurred in the summer of 2020, the forecast sensitivity and the model thermodynamic and dynamic response of these parameters were studied by conducting three sets of extensive sensitivity experiments. For the purpose of isolating the contribution of the individual factors, a large number of “observing system simulation experiments” (OSSEs) were also designed. Thereafter, the experiment obtained the highest forecast scores from the sensitivity experiments studied, was run to evaluate the ability of HLHN in improving the model convective storm clouds as well as temperatures, water vapor and winds.
In Section 2, we introduce the HLHN scheme, experimental configuration and some improvements to the radar reflectivity inversion for the hydrometeors and the calculation of forcing tendency terms. Section 3 briefly reports the assimilation effect in a simulation of the convective precipitation process using actual radar data. In Section 4, the results of the three sets of sensitivity experiments with different relaxation coefficients, radar data update intervals and continuous assimilation duration are analyzed and use the experiment with the highest forecast score to evaluate the assimilation effect. The conclusions and outlook are presented in Section 5.
2. Methodology and Experiment Design
2.1. Deriving Hydrometeors from Radar Reflectance Factor
WRF-FDDA uses the hydrometeor and latent heat nudging (HLHN) scheme to assimilate the radar reflectivity. HLHN is grid-based nudging scheme implemented in four-dimensional model state space along the model time integrations. In the process of observational nudging, the tendency term is first calculated from the difference between the observation and the model at the grid point (i.e., observation innovation), and then applied to the model equations during a time window around the observation time. The official WRF-FDDA HLHN scheme only retrieves two categories of precipitation particles, either rain or snow at a grid point, from radar reflectivity. Since most of the microphysical schemes available in WRF contain explicit predictions of ice crystals, snow, graupel, rain drops and cloud-droplets, it is beneficial to refine the radar reflectivity retrieving algorithm to obtain hydrometeor composition on the grid.
In HLHN, the radar data are interpolated on the model grids of each domain. In this study, regions with reflectivity less than 5 dBZ is judged as no-weather echo. The radar reflectivity is the logarithmic form of the equivalent radar reflectivity factor:
The equivalent reflectivity factor , is made up of four components:
where , , and are the contributions from rain, snow, hail and graupel. In the present research, we made improvements to the radar-based hydrometeor retrieval scheme according to Tong and Pan [17,38]. Firstly, the method of Albers et al. (1996) [39] is used to diagnose rain, snow and hail particles on the model three-dimensional grids with some modifications. Briefly, the reflectivity factor in each vertical grid column is inspected from the top grid point downwards and precipitate begins as snow if the echo top is in air colder than 0 °C, otherwise it starts as rain. As we track down the precipitate through radar echoes, if the ambient temperature is between 0 and 1.3 °C and there is already precipitate above this checking point diagnosed as rain, the precipitate will be diagnosed as rain, otherwise it will be diagnosed as wet snow. The reason for the melting threshold that is set to be slightly higher than 0 °C is to consider of the time lag for the snow to completely melt. If the precipitate once again falls into a layer below 0 °C, it becomes freezing rain. To diagnose hail, a simple threshold of >45 dBZ radar reflectivity is used. After that, we added the diagnosis of graupel based on the research of Lerach et al. (2010) [40]. When the previous diagnosis result satisfies one of the following conditions, the grid point precipitate is diagnosed as graupel: (i) The type of hydrometeor is pre-determined as snow, the reflectivity is between 32 and 41 dBZ, and the ambient temperature is below 0 °C; (ii) The type of hydrometeor is pre-determined as freezing rain, the reflectivity is between 41 and 54 dBZ, and the ambient temperature is below 0 °C; or (iii) The type of hydrometeor is pre-determined as hail if the reflectivity is between 41 and 54 dBZ, and the ambient temperature is below 0 °C. Accordingly, the reflectivity threshold to be used to identify hail is now set to 54 dBZ instead of 45 dBZ. After completing the classification of hydrometeor on the three-dimensional grid, the mixing ratio of the different hydrometeors detected by the 10 cm wavelength Doppler radar can be obtained by the formula showed in Table 1.

Table 1.
The hydrometer water mixing ratio diagnosed from radar reflectivity.
In the current radar data assimilation scheme, dry snow versus wet snow, and drain versus freezing rain are not distinguished when calculating the mixing ratio. Since the Thompson microphysical parameterization scheme was used in this study, which does not contain the hail variable, the diagnosed hail was classified as graupel or rain according to the ambient temperature. It is noted that the current algorithm only identifies one kind of hydrometeor types at each three-dimensional grid points. We will extend the algorithm to take account of the mixing existence of different hydrometeor types in future.
2.2. Hydrometeor and Latent Heat Nudging (HLHN)
Newtonian-Relaxation or nudging method adds artificial tendency terms based on difference between a model and an observation state to one or more model prediction equations, which relaxes the model state toward the observation state [41].
In WRF-FDDA, the hydrometeor mixing ratio calculated from radar reflectivity factor is used to calculate the nudging tendency terms, and the corresponding latent heat change term is also added to the thermal equation. The simplified equations for the nudging scheme can be written as follows:
where is the mixing ratios of rainwater, snow, hail and graupel. is the analysis value of , and are the close observations before and after the current moment, is the model state variable. is the source of mixing ratio from physical processes (microphysical conversion processes, land surface moisture flux, mixing, diffusion, etc.), is the source of air temperature from physical processes (latent heating, sensible heating, etc.). The relaxation coefficient determines the relative magnitude of the nudging tendency terms. It is noted that on one hand, one wishes to apply a relatively large to effectively force the model state toward the observed. On the other hand, one must avoid of introducing excessive disturbances to the model. Thus, the value of should be properly examined and determined. and are the nudging weighting coefficients of horizontal and vertical space, and latent heat tendency term, respectively. Since the radar reflectivity is interpolated on to the model grids, the spatial influence radius is limited to the action model grid, i.e., are set to 1 at the assimilation grid points and 0 for all others. is the specific latent heat, and is the specific heat of air at constant pressure. is the temporal weighting, accounting for the time inconsistency between the observation and the model integration time. The observations before and after the current time are used to calculate the tendency terms.
It should be noted that when a radar detects the echo, the precipitation cloud associated with it has been developed and the latent heat has already been released. Therefore, the temporal weighting coefficient is designed to reach a maximum at the moment of radar detection and decreases immediately thereafter. The temporal weighting coefficient changes in the assimilation window as shown in the Figure 1.
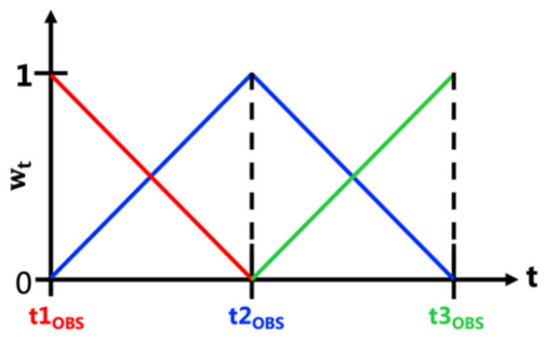
Figure 1.
Temporal weighting coefficient for assimilation of radar observations. t1OBS, t2OBS, and t3OBS mark the observation time and the color shades are temporal weighting corresponding to the observation in the same color.
The goal of radar data assimilation is to promote precipitation clouds that the model has failed to produce, and also to suppress factitious echoes and excessive water vapor developed in the model. To contain the factitious convection, is processed separately. First of all, cleanly separating zero-echo and missing-data areas is crucial. Thus, during the process of interpolating radar data onto the model grid points, the position information for each grid point is marked. If the grid point is within the radar detection range, it is marked as 1, otherwise it is 0. The value of is specified according to the following rules:
- (i)
- A grid is marked as 0:
- (ii)
- A grid is marked as 1, both and are 0:
- (iii)
- A grid is marked as 1, One of or is 0:
- (iv)
- A grid marked as 1, both and are not 0:
2.3. Model Configuration and Weather Case Description
The FDDA version used in this study is based on the Weather Research and Forecasting model (WRF), version 4.1.3. The model is configured with two nested-grid domains at 15- and 3-km horizontal grid spacings, respectively. The model domains and terrain height are shown in Figure 2. The Thompson microphysical parameterization scheme [42] is used in the two domains, and the Grell-Freitas cumulus parameterization scheme [43] is used in the 15-km coarse-grid domain and no cumulus scheme is activated in the 3-km fine-grid domain. The other physical parameterization schemes are the same in the two domains, including Yonsei University PBL physics scheme [44], RRTMG longwave and shortwave radiation scheme [45], Unified Noah land surface scheme, and revised MM5 Monin-Obukhov surface layer scheme [46]. The model initial and boundary conditions are driven from the NCEP-GFS data.
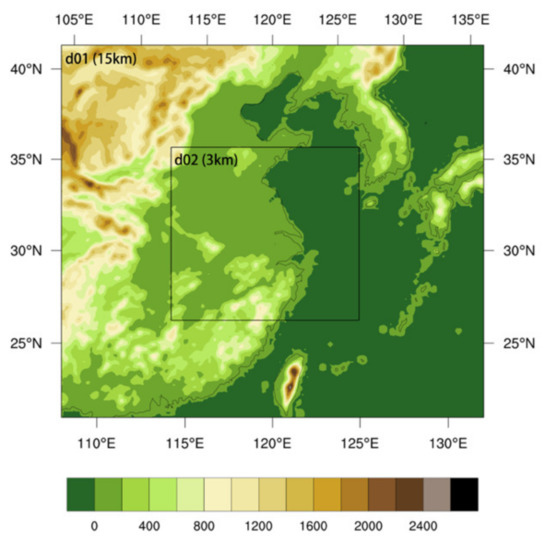
Figure 2.
Configuration of the model parent domain (D01: 15-km) and the nested domain (D02: 3-km) for the case study. Terrain heights (units: m) are shown in colored shades.
A Meiyu-front precipitation event occurred in the Eastern China on 27-28 June 2020, was selected for the modeling study. From 2000 UTC 27 June to 0600 UTC 28 June, the precipitation process was characterized by a mesoscale convective rainband with a large number of embedded convective cells. Such convection poses challenges for model assimilation and prediction. For the modeling study, firstly, an experiment with real radar reflectivity assimilation was conducted for four consecutive hours from 2000–0000 UTC in domain 2 with a horizontal spatial resolution of 3 km. The model predictions with and without radar data assimilation were compared with observation with a purpose of assessing the effectiveness of the radar data assimilation scheme.
2.4. Experiment Design
For the convenience of evaluating the impact of individual data assimilation parameters, an observing system simulation experiments (OSSEs) framework that assumes a “perfect model and perfect observation” is configured. Many previous studies have shown that OSSEs are a very helpful approach to understanding the behaviors and impacts of data assimilation methods and/or new observation data [17,47,48]. OSSEs include a natural run that mimics the real-world truth state (TRUE) and is used to extract observations, a baseline control forecast experiment (CTRL). Both were cold-started 20 h before the assimilation experiment (that is, 0000 UTC 27 June). Disturbances were artificially added during the start-up phase of CTRL to ensure sufficient difference from TRUE. The two have been integrated for 20 h to ensure the physical balance of the model and sufficient details of mesoscale and microscale clouds and hydrometeors. In addition, OSSEs contain three sets of sensitivity experiments, which are used to analyze the influence of relaxation coefficient , radar data update intervals, and continuous assimilation duration. The three sets of experiments use the forecast of CTRL as the experimental background field, and use TRUE as the real observation for assimilation. The time schedule of the three experimental groups is illustrated in Figure 3, and more details of the experimental design are described in Table 2.
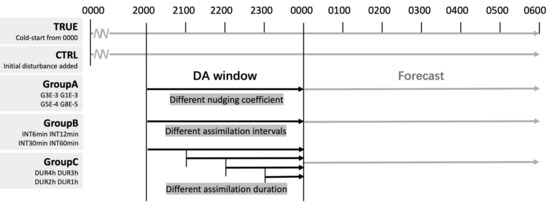
Figure 3.
The time schedule of observing system simulation experiments (OSSEs).

Table 2.
Specific grouping and configuration information of observing system simulation experiments (OSSEs).
2.5. Evaluation Method
In order to quantitatively and objectively evaluate the results of sensitivity experiments, Fractions Skill Score (FSS) [49] were calculated for different thresholds with a diameter of 15 km for hourly accumulated precipitation and radar reflectivity factor. In the WRF model, the calculation of reflectivity depends on the details of the microphysical scheme used, especially the treatment of liquid water and ice. The equivalent reflectivity factor is calculated under the assumption of Rayleigh scattering by using the particle number concentration and equivalent particle radius of different hydrometeors [50,51]. Then calculate the reflectivity factor by Formula (1). FSS is one of the neighborhood verification methods, which is appropriate for the evaluation of the precipitation simulations with fine resolution grids. The formulation of FSS is:
where is the number of grid points in the x and y directions of the domain, and are the observed fractions and model forecast fractions under the given threshold by each grid.
3. Baseline Radar Reflectivity Data Assimilation
This section reports the assimilation experiment using the mosaic radar reflectivity from the Severe Weather Automatic Nowcasting system (SWAN) of the China Meteorological Administration. The SWAN system collects observation data from the national radar network in real time, and integrates radar data quality control, data mapping, real-time monitoring and nowcasting. It began construction in 2008 and has undergone multiple version changes. It continues to be used in the Chinese Meteorological Center and most provincial weather forecasting offices.
The national radar network have a good coverage over the land and the shore areas in the studying domain. The mosaic radar data are updated every 6 min. Radar data assimilation is performed continuously for 4 h, continuously from 2000 UTC 27 to 0000 UTC 28.
The composite reflectivity from multiple radar observations and model forecast with/without radar DA are shown in Figure 4. It should be noted that the settings of WRF-FDDA parameters in this experiment are the default ones derived from previous experience. The results show that the radar DA produced an encouraging positive effect. It effectively shortened the spin-up time and improve the initialization of the model convection. After four hours of continuous radar assimilation, at 0000 UTC 28, the radar assimilation experiment simulated radar reflectivity with a good consistency with the observation. The rainband morphology, size, and the location of the convective cores were all simulated accurately, including the convective precipitation over the sea. However, the strength of the convective core is slightly underestimated. At 0300 UTC, (three-hour free forecast), the width of the rainband in the east of the domain rapidly strengthened, but the forecast of heavy rainfall is not good. It is caused by a variety of reasons, namely, radar observation error, errors in converting reflectivity to the nudging tendency terms, and errors caused by inappropriate nudging parameters. For the purpose of isolating the contribution of different factors and achieving the optimal effect of WRF-FDDA, we study the sensitivity of different HLHN parameters by building observing system simulation experiments (OSSEs).
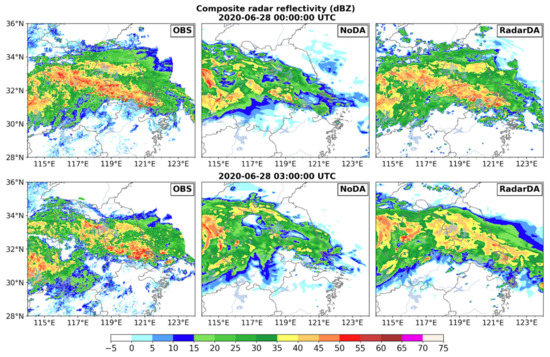
Figure 4.
Composite radar reflectivity (units: dBZ) of multiple radar observations (OBS), model forecasts without DA (NoDA) and with radar DA (RadarDA) at 0000 and 0300 UTC 28 June 2020.
4. Observing System Simulation Experiments (OSSEs)
4.1. The Correlation between Relaxation Coefficient and “Ramp-Down” Issue
In HLHN, the relaxation coefficient G determines the rate at which the model state is adjusted toward the observation state. Thus, G plays a key role in the HLHN-based radar data assimilation. The inverse of G is the e-folding time of the difference between the model and the observations assuming the model physical tendency terms are zero. For observational data available at different time intervals, G needs to be adjusted to maximize the nudging effect. In general, a larger G value will drive the model precipitation clouds towards the actual observations more rapidly. But meanwhile, it will also introduce a larger imbalance (“shock”) to the model dynamics and thermodynamics, which may cause unnecessary disturbances and development of factitious convection in the model. This may result in either assimilation divergence (i.e., oscillations with over-correction) or a rapid decline in the quality of model forecasts within a short period after the free forecasting starts. This phenomenon is known as the “ramp-down” issue in non-adiabatic initialization. Conversely, if G is too small, the radar data assimilation effect is small too.
For this reason, we conducted a large number of radar data assimilation experiments with an extensive variation of G to determine the optimal G value. Here, four sets of experiments with G values as 2E-3, 1E-3, 5E-4 and 2E-4, corresponding to very large, reasonable, small and weak G values respectively, were presented for analysis of the sensitivity.
Figure 5 shows the FSS of radar composite reflectivity and hourly accumulated precipitation of the modeling experiments throughout the data assimilation and forecast periods. The thresholds of 15 dBZ/2 mm and 40 dBZ/10 mm selected correspond to stratiform precipitation and convective precipitation, respectively. It can be seen that the FSS of the composite reflectivity and precipitation are in good agreement, and the decline rate of the convective precipitation FSS is much greater than the stratiform precipitation. Since radar reflectivity is computed directly from precipitation particles, the higher relaxation coefficient, the quicker the model hydrometeors are nudged to the actual observation. Again, the highest FSS score at the assimilation stage does not necessarily result in the best forecast effect. It is worth noting that G2E-3 gains the highest FSS at the assimilation stage, but it caused obvious “ramp-down” issues after the forecast starts, the FSS of the composite reflectivity and hourly accumulated precipitation both continued to decline and was lower than the FSS of G1E-3 within the first 3 h of free forecast. The FSS time series of G1E-3, G5E-4 and G2E-4 are relatively parallel, which indicates that the forcing tendency of the three G values does not cause an unbalanced disturbance of the mode state.
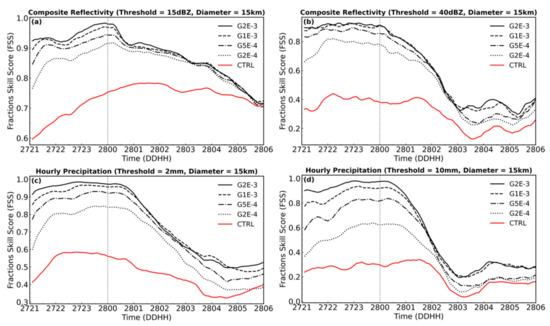
Figure 5.
Time series of forecast skill scores (FSS) of composite reflectivity with thresholds of 15 dBZ (a) and 40 dBZ (b), and FSS for hourly accumulated precipitation with thresholds of 2 mm (c), 10 mm (d) of Group A. The horizontal scale (diameter) used for FSS is 15-km.
To further study this procedure, the domain average of the rainwater content (Qrain) and the domain sum of the latent heat tendency terms for the four experiments were analyzed. Ideally, during the initialization phase of the radar data assimilation, the model state gradually approaches the observations, and the tendency terms shall gradually stabilize and approach zero. As shown in Figure 6a, at the beginning of assimilation, TRUE and CTRL’s averaged Qrain are similar. After 15 min, the precipitation of TRUE increased significantly. In order to make up for the insufficient precipitation in CTRL, latent heat cooling in G2E-3 was started at the same time (Figure 6b). To drive the change of the model state, an excessive amount of latent heat cooling is added in a short time. The latent heat tendency term in G1E-3 gradually decreases to −110 K/s, and G2E-3 to 280 K/s, resulting large disturbances. After the excessive latent cooling being added, Qrain increases until it exceeds TRUE, and reaches the maximum at 30 min. In subsequent nudging processes, the excessive latent heat cooling is gradually corrected. But in the subsequent period of assimilation, the latent heat tendency term of G2E-3 still kept significant fluctuations than other experiments. This overshooting correction also led to a faster decline in forecasting performance after the assimilation finished.
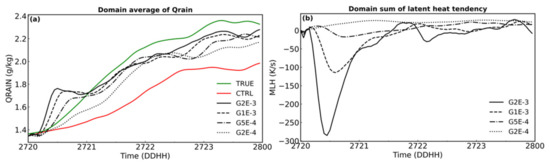
Figure 6.
Time series of domain-averaged Qrain (a) and domain-integrated latent heat tendency terms (b) of Group A.
Although G1E-3 was determined as the most reasonable G value in terms of modeling radar reflectivity, it’s Qrain is not coincident with TRUE. In order to stimulate the convection that did not existed in the model before, excessive latent heat needs to be nudged, excessive latent heat promotes the updraft, condensation of water vapor, and surface rain, resulting in a decrease in the rainwater mixing ratio in the clouds. The latent heat tendency term of experiment G2E-4 stays between 0 and 30 K/s in the assimilation window. The nudging forcing was insufficient to correct the Qrain deficit in the model and only 50% of the Qrain difference was corrected. The time evolution of Qsnow and Qgraup show similar performance (the figures were omitted).
4.2. Sensitivity on Data Update Intervals
It is known that high-frequency radar volume scans help capture the details of cloud development. Therefore it is of great interest to study the impact of radar data update intervals on HLHN on both cloud analysis and forecast. Hu & Xue (2003) used a 3D cloud analysis method to assimilate radar data. Their results showed that an update interval of 10 min performed better than 5 or 15 min ones [52]. They found that the cloud analysis scheme often takes at least 5 min to initialize the storm, and a 10-min analysis interval is required for the model to complete the balance adjustment to establish a sustainable convective storm. In a GSI (Grid Statistical Interpolation)-based Convection-Allowing Ensemble-Based assimilation experiment, Johnson et al., (2017) showed that a 10-min cycle of the radar DA provides more skillful short-term (0–6 h) forecasts than 5- or 15-min cycling [53]. These results were based on 3D cloud analysis and adjustment approaches. The impact of the assimilation intervals for 4D continuous nudging with HLHN has yet to be understood.
In this section, four experiments are designed to study the impact of different radar data update intervals. To mimic the current national radar network operations of 6-min volume scan, the four experiments with assimilation of 6, 12, 30, and 60-min data update intervals, named as INT6min, INT12min, INT30min and INT60min, respectively, were conducted. In these experiments, the relaxation coefficient G is set to 1E-3.
Figure 7 shows the time series of the FSS of the composite reflectivity and the hourly surface accumulated precipitation for the sets of experiments. It is noteworthy that INT6min and INT12min achieved similar great performance although the 6min update is slightly better than the 12 min update. Same as Figure 6, Figure 8 shows the domain average of Qrain and domain sum of latent heat tendency terms of this set of experiments. The latent heat tendency terms varied dramatically among these experiments. With longer data update intervals, a “sawtooth”-shaped latent heat tendency term becomes more obvious. Such discontinuous shocks increased the noise of the model and caused the FSS fluctuated with time. For INT60min, FSSs of both reflectivity and hourly precipitation have obvious “sawtooth”-shaped issue, and their FSS is significantly lower than the other experiments with shorter update intervals during the free forecast stage. The assimilation efficiency of HLHN depends on the balance of nudging forcing speed, data update interval, and system development speed. Therefore, for fast-developing and moving convection systems, a higher data update interval will provide a gentle and continuous nudging tendency to reduce the noise of the model system and improve the quality of the forecast.
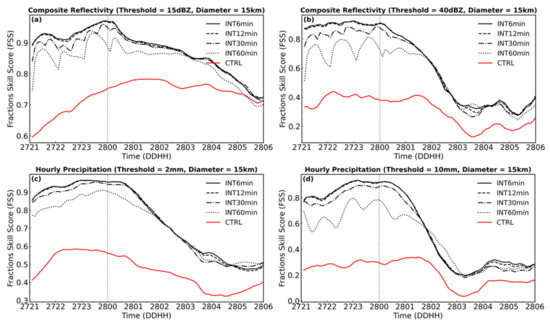
Figure 7.
Time series of forecast skill scores (FSS) of composite reflectivity with thresholds of 15 dBZ (a) and 40 dBZ (b), and FSS for hourly accumulated precipitation with thresholds of 2 mm (c), 10 mm (d) of Group B. The horizontal scale (diameter) used for FSS is 15-km.
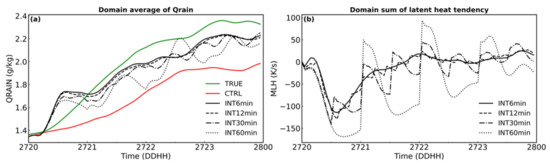
Figure 8.
Time series of domain-averaged Qrain (a) and domain-integrated latent heat tendency terms (b) of Group B.
4.3. Sensitivity on Time Duration of Continuous Assimilation
HLHN is a 4D continuous data assimilation scheme. Ideally, to minimize the cold-start “spin-up” effect, one would set up the model to continuously assimilate the data without a “break”. But in reality, due to the incomplete observations and measurement uncertainties, approximation of data assimilation schemes, and the non-linear model error growth, one has to reset “cold-starts” in certain time intervals for the 4D data assimilation cycles to get rid of the error accumulation in the system. For radar data assimilation, missing times/frames of radar observations is inevitable. Therefore, one wants to know how long an assimilation window is required to fully adjust the initial state of the model with HLHN radar data assimilation, and what is the maximum continuous assimilation duration during which the error accumulation of the model and assimilation is acceptable.
Four experiments, assimilating radar data continuously for 4 (DUR4H), 3 (DUR3H), 2 (DUR2H), and 1 (DUR1H) -hour respectively were conducted. The radar data is assimilated at 6-min update intervals. The time series of FSSs are shown in Figure 9. In general, the forecast from DUR4H and DUR3H is better than the forecast from DUR2H and DUR1H, although DUR1H has already effectively improved the forecast from CTRL. Figure 10 shows the domain average of Qrain and domain sum of latent heat tendency terms of the four experiments. Due to the difference between the model states of CTRL and TRUE (i.e., the error in the initial conditions) changes with time, the latent heat tendency terms in the initial assimilation window of the four assimilation experiments are different, which may affect the time required for the nudging tendency terms to spin up the cloud. Between 20:00 and 21:00 UTC, the difference in Qrain between TRUE and CTRL is relatively small. Therefore, starting assimilation at this time only takes 1 h to stabilize the mode state (DUR4H). As the difference between TRUE and CTRL model states increases, the radar assimilation duration needed to spin up the model is longer. This is why the FSS of DUR1H is significantly lower than other experiments with longer assimilation durations. The prediction skills of DUR2H increased significantly from DUR1H.
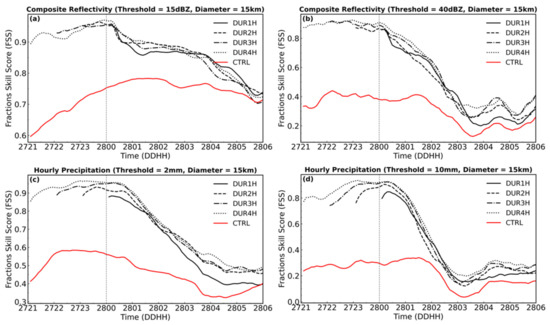
Figure 9.
Time series of forecast skill scores (FSS) of composite reflectivity with thresholds of 15 dBZ (a) and 40 dBZ (b), and FSS for hourly accumulated precipitation with thresholds of 2 mm (c), 10 mm (d) of Group C. The horizontal scale (diameter) used for FSS is 15-km.
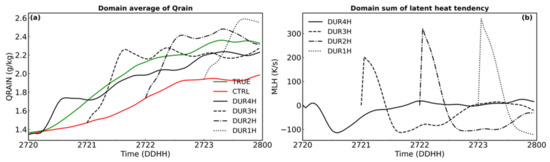
Figure 10.
Time series of domain-averaged Qrain (a) and domain-integrated latent heat tendency terms (b) of Group C.
After an assimilation duration is found to be able to fully spin up the model state, further increase of the assimilation duration only brings about some minor benefits. Since the spin-up process of the model state with the radar data assimilation depends on the size of the model error and the speed of convection development, the minimum duration required for fully spin up the model states can be different for the model initiated at different times. Fabry, F. & Sun, J. (2010) also found that different model variables should be assimilated with different durations [50]. A complex and fast-changing convection system desires a longer assimilation duration than a slowly evolving frontal stratiform cloud.
4.4. Respone of the Model Temprature, Moisture and Winds
HLHN can effectively reduce the “spin-up” issue of precipitation and improve the forecasting skills in the first few hours [21,54]. However, since the radar observed precipitation is an outcome of complex multi-scale atmospheric thermodynamic and dynamical processes, HLHN has an immediate direct positive impact on the model precipitate particles and temperature. The impact on all other weather variables were through the model thermodynamic and dynamical adjustments. Therefore, it is important to analyze whether HLHN reduces the errors of these other atmospheric state variables. In fact, the effect of HLHN on the model forecast heavily depends on the consistency among all model dynamic and thermodynamic fields. Hereby we look into this problem by analyzing the results of the experiment that obtained the highest forecast scores (i.e., G1E-3 or INT6min or DUR4H. Experiments with the same settings were used to participate in different groups of sensitivity analysis).
Figure 11 shows the radar composite reflectivity at the end of assimilation windows and the 3-h forecast. The precipitation system presents a typical Meiyu-season precipitation structure, with a 1000 km long west-east oriented rainband and abundant β or γ-mesoscale strong convection cores (of 20~50 km) embedded in. The strong convective system cores are mainly distributed in the southern part of the rainband, and to the north is relatively uniform stratiform precipitation. After 4 h of radar data assimilation, the experiment has made good adjustments to the precipitation in the entire domain and the rainband is very similar to TRUE. At this time, the FSS scores for strong convective precipitation and stratiform precipitation both reached a high of 0.9. Although RadarDA and CTRL used the same boundary conditions, in the first three hours of the free forecast, the rainband developed by the HLHN initialization was well maintained. The 15 dBZ rainband boundary of the forecast rainband is consistent with TRUE, and the FSS score of the 15 dBZ composite reflectivity is still high (0.879). The forecast score for convective precipitation is lower. The composite reflectivity FSS of 45 dBZ is 0.346, which is still about 1.5 higher than that of CTRL. More error information can be seen from the Taylor diagram of the composite reflectivity verification (Figure 15a). From 0000 to 0300 UTC, the correlation coefficients of the composite reflectivity have increased by 0.8, 0.6, 0.36, and 0.2, respectively, from CTRL, and RMSD (root-mean-square deviation) has also been significantly reduced (5.0, 10.2, 12.8, and 14.5, respectively).
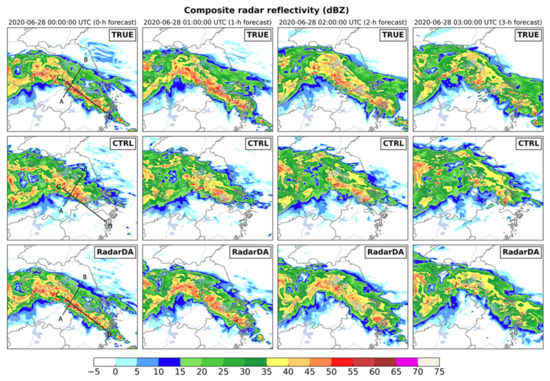
Figure 11.
Composite reflectivity (units: dBZ) at 0000–0300 UTC 28 June 2020. 1st row for simulated observations TRUE; 2nd row for control forecast CTRL; 3rd for radar assimilation forecast RadarDA. Thick solid lines in the panels of 0000 UTC (A–B, C–D) denote the location of cross section in Figure 12.
Jones and Macpherson [19] proposed a diabatic latent heat assimilation scheme that is based on the relationship between precipitation and latent heat release. They modified the model dynamics in a way that the model will respond by producing a rain rate close to the observed precipitation. This scheme was originally applied to the COSMO-DE model [21]. They found the scheme to be heavily dependent on microphysical parameterization. When the parameterization of evaporation and snowfall formation was improved, it unfortunately resulted in a significant overestimation of ground precipitation [31]. In order to investigate the impact of the HLHN radar data assimilation on the water vapor and total hydrometeors, vertical cross-sections of water mixing ratio of different hydrometeors for the experiments at 0000 UTC 28 June were plotted (Figure 12). The locations of the cross sections were marked as the thick solid lines in Figure 11.
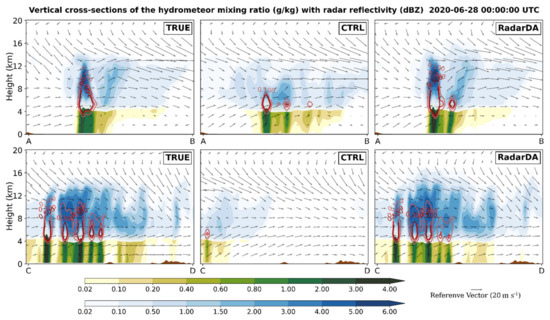
Figure 12.
Vertical cross-sections of the Qrain (green shading; units: g/kg), Qsnow (blue shading; units: g/kg), Qgraup (red contour; units: g/kg) overlaid with vertical wind (wind arrows; units: m/s) at 0000 UTC 28 June 2020. 1st row for cross-sections A–B; 2nd row for cross-sections C–D.
The cross-section A–B cuts through the main precipitation rainband, with heavy convective precipitation located mostly on the A side, and the stratiform precipitation on the B side. The positive impact of HLHN on the precipitation system is fabulous except for factitious convection stimulated on the B side of the main precipitation area, with a maximum Qrain of 0.8 g/kg, and a maximum Qgraup of 0.5 g/kg in the middle layer.
Cross-section C–D passes through the center of the convective precipitation rainband. It can be seen that the hydrometeor distribution of the convection in the truth run was reproduced precisely by HLHN RadarDA, including the locations, morphology and magnitudes of all precipitate particle categories. The impact of HLHN on the wind field is also evident. The RadarDA resulted in more accurate winds and stronger updrafts in the convection clouds. The inflow, outflow, and ascending and descending airflows associated with all convective cells were also well improved from CTRL.
It is worth noting that the cloud top heights of some convective cells simulated with RadarDA were higher than the truth run. The upper boundary of Qsnow at 1.5 g/kg was increased by about 1.5 km by RadarDA. This error is associated with an issue of the latent-heat nudging scheme. During the nudging process, the latent heat was added into the model where the observed convection was missing. To drive the model toward the amount of the hydrometeors derived from observed radar reflectivity, excessive latent heat might have been added. As the latent heat source is continuously added in, it keeps promoting the updrafts and condensation of the water vapor, resulting in an accumulation of heat and water vapor in the upper layers. This is an example indicating that we should take into account of the convection precipitation development stages for the design of HLHN, and properly reduce the rate of latent heat nudging in HLHN during the later development of convection.
The hourly precipitation accumulation of model forecasts is consistent with the observed (Figure 13), featured a heavy rainband in the center of the domain. The maximum 1-h accumulated precipitation of the truth run exceeded 40 mm. At the end of the DA window, the radar data assimilation accurately captured the rainband and the heavy precipitation core successfully. The FSS score for the 2 mm threshold of the hourly accumulated precipitation reaches 0.956, and that of 10mm reaches 0.923. Until the second hour of the forecast, the simulation of the precipitation center of the RadarDA was equally accurate. At 0300 UTC, the simulated precipitation center is shifted slightly northward, and the hourly accumulated precipitation FSS of 2 mm and 10 mm is 0.616 and 0.207, respectively. Figure 15c shows the Taylor diagram of relative humidity. Comparing with CTRL, the correlation coefficient increased by approximately 0.2 at 0000–0300 UTC, and the RMSD decreased from 13 to 10.5. For 1-h accumulated precipitation verification, the correlation coefficient and RMSD have been significantly improved from CTRL. The correlation coefficient at the end of assimilation increased from 0.13 to 0.92, and the RMSD decreased from 9.2 to 3.1 and by the end of three-hour forecasting, the correlation coefficient for RadarDA is still 0.25 higher than CTRL (Figure 15d).
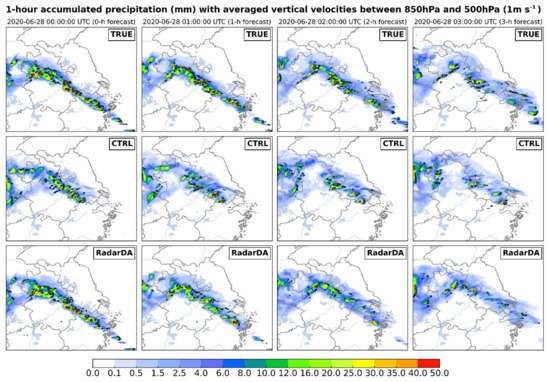
Figure 13.
1-h accumulated total precipitation (shading; units: mm) overlaid with the averaged vertical velocities between 850 hPa and 500 hPa (black contour; units: 1 m/s) at 0000–0300 UTC 28 June 2020. 1st row for simulated observations TRUE; 2nd row for control forecast CTRL; 3rd for radar assimilation forecast RadarDA.
The vertical velocities averaged between 850 hPa and 500 hPa (contour of 1 m/s shown in black in Figure 13) indicated that the latent heat nudging obviously promotes updrafts in the convection and precipitation development. As the forecast progresses, the model precipitation gradually decreases, and the updraft also gradually weakens. HLHN is able to adjust the convection updraft and maintain consistent the precipitation development.
A Meiyu front is typically characterized by a temperature field with a “sandwich” structure over the land [55,56]. That is, the air masses temperature of the north and south sides of the Meiyu front is higher than that in the front zone, which featured a frontal cold pool. Figure 14 shows that model that successfully reproduced such a structure. HLHN not only improved the vertical updraft, but also the temperature in the cold pool. During the free-forecasting phase, the area of the warm zone on the south side of the system has also been reduced, bringing it closer to TRUE. From 0000–0300 UTC, the correlation coefficient of 2-m perturbation potential temperature has been dramatically improved with the radar data assimilation (Figure 15b).
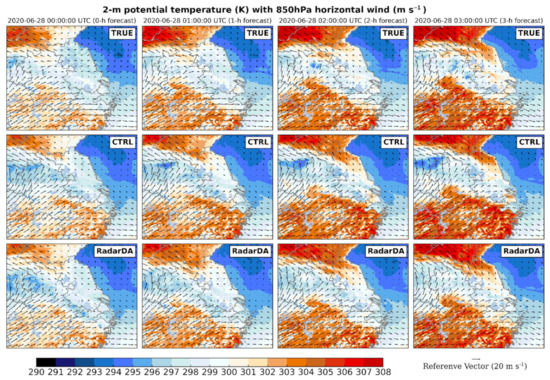
Figure 14.
2-m potential temperature (shading; units: K) overlaid with 850 hPa horizontal wind (wind arrows; units: m/s) at 0000–0300 UTC 28 June 2020. 1st row for simulated observations TRUE; 2nd row for control forecast CTRL; 3rd for radar assimilation forecast RadarDA.
The 850 hpa winds presents the characteristics of monsoon activity in the Meiyu season, and radarDA experiments simulated the wind field reasonably well. It captures the warm and humid air flowing northward above the cold pool, along with the shift in wind direction to the southeast. The radarDA experiment removed the excessive wind speed in CTRL. Figure 15e,f show the Taylor diagrams of the horizontal wind field at 10-m. The improvement of HLHN to the wind field reached the best effect at 1 h of free forecasting, with RMSD reduced by about 30% from CTRL. The improvement was still obvious at three hours of free forecasting.
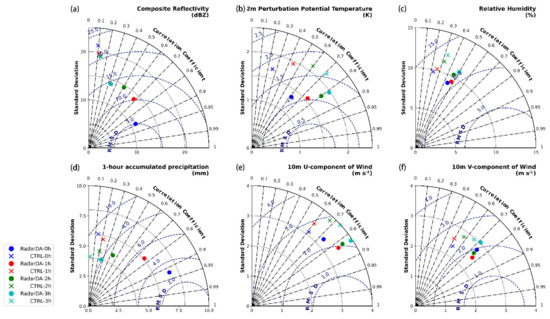
Figure 15.
Taylor Diagrams of (a) composite reflectivity (dBZ), (b) 2 m perturbation potential temperature (K), (c) relative humidity (%), (d) 1-h accumulated precipitation (mm), (e) U-component of 10 m wind (m s−1), and (f) V-component of 10 m wind (m s−1) at 0000–0300 UTC 28 June 2020. Each model variable is verified against TRUE.
5. Discussion and Conclusions
In this study, the NCAR WRF-based four-dimensional data assimilation system, WRF-FDDA, was used to evaluate the key control parameters of hydrometeor and latent-heat nudging (HLHN) for radar data assimilation and study the response of the model clouds, temperature, moisture, and winds to HLHN during the assimilation and forecast processes.
First, we improved the algorithm to suppress the excessive clouds in the model and classified the tendency term of the mixing ratio of hydrometeor into four cases. By selecting a typical Meiyu front precipitation process in eastern China, a radar data assimilation experiment and a series of observation system simulation experiments were carried out to test the impact of the key control parameters. The model result showed that:
- (1)
- The nudging relaxation coefficient G plays a key role in HLHN. For the summer Meiyu precipitation in China, 1E-3 was found as an appropriate value for G. Analysis shows that for more complex and rapidly changing weather systems, a larger G may be desired. In contrast, for relatively stable small and medium-scale weather, G should be set to a smaller value. Note that in general the nudging tendency term should not dominate the change of model variables in order for the adjustment not to damage the dynamic consistency. The imbalanced model states caused by overly strong HLHN forcing can lead to serious “ramp-down” issues right after the assimilation period ends.
- (2)
- The efficiency of HLHN depends on the balance between nudging coefficients, assimilation intervals, and the convection system’s evolving speed. For fast-developing and moving convection systems, a higher assimilation interval provides a gentle and smooth nudging effect.
- (3)
- HLHN requires a minimum assimilation duration to spin up the model clouds with dynamical and thermodynamical consistency. For the summer Meiyu precipitation studied, this time is ~1 h. When the assimilation duration is extended to 2 h, both analysis and forecasting gain proper assimilation effects. With a further increase of the assimilation duration, more improvement is seen but the improvement effect is gradually slowed down. It should be noted that the minimum duration depends on the initial model error and the development speed of the weather system.
- (4)
- In the first three hours of free forecasting, HLHN effectively improves the model clouds as well as temperatures, moisture, and winds of the model. Although HLHN does not directly adjust these model parameters, the spatiotemporal adjustment of the hydrometeors makes a positive effect on the overall model states. However, in order to spin up convection that was missed in the model, HLHN tends to add excessive latent heat into the model, resulting in an increase in upper-level updraft and snow content.
This study helps gain valuable insights about the model dynamical and thermodynamical adjustments with HLHN radar data assimilation. Nevertheless, we noticed that there are still several issues deserving further study. The performance of HLHN depends on nudging relaxation coefficients, data update intervals, and the convection development speed. For fast-developing and moving convection systems, a higher update interval may be desired to produce gentle nudging tendency and a smooth nudging effect. An adaptive nudging coefficient which varies with weather situations should be developed in the future. Unlike OSSEs, for real radar data assimilation, the observation errors can significantly affect the performance of HLHN. Furthermore, we point out that besides radar observations, there are several other platforms observing clouds, winds and other variables. Thus, joint assimilation of multiple platform observations, including convectional temperature, moisture, wind observations as well as lightning data and satellite cloud measurements, should be studied to achieve an optimal effect. In particular, the operational geostationary satellites detect clouds at spatial resolutions similar to the operational weather model grid (kilometers) and have a temporal resolution of 15 min or higher. Using satellite cloud observation data to complement radar observations has become a major direction of nowcasting research [57,58,59]. Finally, in the next few years, phased array weather radars, multi-wavelength cloud radars, lidars, satellite cloud observations and other new cloud instruments will be fielded for operation. Methods to assimilate these diverse, very high spatiotemporal resolution and rich information data shall be developed.
Author Contributions
Conceptualization, Z.H. and Y.L. (Yubao Liu); Data curation, Y.S. and C.F. Formal analysis, Z.H., M.W., Z.S. and Y.L. (Yang Li); Methodology, Z.H. and Y.L. (Yubao Liu); Writing—original draft, Z.H.; Writing—review & editing, Y.L. (Yubao Liu). All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Northwestern Region’s Artificial Weather Modification Capacity Building Project (ZQC-R1908) and partially supported by the SGCC Science and Technology Project: 5200-201955490A-0-0-00.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
NCEP GFS 0.25 Degree Global Forecast Grids data can be obtained from https://rda.ucar.edu/datasets/ds084.1/. SWAN radar data used in this paper can be provided by Zhaoyang Huo (zyhuo1@nuist.edu.cn) upon request.
Acknowledgments
The authors acknowledge NCAR data processing teams for making the GFS data available. And acknowledge Chinese Academy of Meteorological Sciences for providing SWAN radar data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wilson, J.W.; Crook, N.A.; Mueller, C.K.; Sun, J.; Dixon, M. Nowcasting Thunderstorms: A Status Report. Bull. Am. Meteorol. Soc. 1998, 79, 2079–2099. [Google Scholar] [CrossRef]
- Lilly, D. Numerical prediction of thunderstorm—Has its time come? Q. J. R. Meteorol. Soc. 1990, 116, 779–798. [Google Scholar]
- Wilson, J.; Megenhardt, D.; Pinto, J. NWP and Radar Extrapolation: Comparisons and Explanation of Errors. Mon. Weather Rev. 2020, 148, 4783–4798. [Google Scholar] [CrossRef]
- Sun, J.; Xue, M.; Wilson, J.W.; Zawadzki, I.; Ballard, S.P.; Onvlee-Hooimeyer, J.; Joe, P.; Barker, D.; Li, P.-W.; Golding, B.; et al. Use of NWP for Nowcasting Convective Precipitation: Recent Progress and Challenges. Bull. Am. Meteorol. Soc. 2014, 95, 409–426. [Google Scholar] [CrossRef]
- Sun, J. Convective-scale assimilation of radar data: Progress and challenges. Q. J. R. Meteorol. Soc. 2005, 131, 3439–3463. [Google Scholar] [CrossRef]
- Jacques, D.; Zawadzki, I. The Impacts of Representing the Correlation of Errors in Radar Data Assimilation. Part I: Experiments with Simulated Background and Observation Estimates. Mon. Weather Rev. 2014, 142, 3998–4016. [Google Scholar] [CrossRef]
- Jacques, D.; Zawadzki, I. The Impacts of Representing the Correlation of Errors in Radar Data Assimilation. Part II: Model Output as Background Estimates. Mon. Weather Rev. 2015, 143, 2637–2656. [Google Scholar] [CrossRef]
- Chandrasekar, R.; Balaji, C. Impact of physics parameterization and 3DVAR data assimilation on prediction of tropical cyclones in the Bay of Bengal region. Nat. Hazards 2016, 80, 223–247. [Google Scholar] [CrossRef]
- Xiao, Q.; Kuo, Y.-H.; Sun, J.; Lee, W.-C.; Lim, E.; Guo, Y.-R.; Barker, D. Assimilation of Doppler Radar Observations with a Regional 3DVAR System: Impact of Doppler Velocities on Forecasts of a Heavy Rainfall Case. J. Appl. Meteorol. 2005, 44, 768–788. [Google Scholar] [CrossRef]
- Sugimoto, S.; Crook, N.A.; Sun, J.; Xiao, Q.; Barker, D. An Examination of WRF 3DVAR Radar Data Assimilation on Its Capability in Retrieving Unobserved Variables and Forecasting Precipitation through Observing System Simulation Experiments. Mon. Weather Rev. 2009, 137, 4011–4029. [Google Scholar] [CrossRef]
- Benjamin, S.G.; Dévényi, D.; Weygandt, S.S.; Brundage, K.J.; Brown, J.M.; Grell, G.A.; Kim, D.; Schwartz, B.E.; Smirnova, T.G.; Smith, T.L.; et al. An Hourly Assimilation–Forecast Cycle: The RUC. Mon. Weather Rev. 2004, 132, 495–518. [Google Scholar] [CrossRef]
- Sun, J. Initialization and Numerical Forecasting of a Supercell Storm Observed during STEPS. Mon. Weather Rev. 2005, 133, 793–813. [Google Scholar] [CrossRef]
- Sun, J.; Chen, M.; Wang, Y. A Frequent-Updating Analysis System Based on Radar, Surface, and Mesoscale Model Data for the Beijing 2008 Forecast Demonstration Project. Weather Forecast. 2010, 25, 1715–1735. [Google Scholar] [CrossRef]
- Kawabata, T.; Kuroda, T.; Seko, H.; Saito, K. A Cloud-Resolving 4DVAR Assimilation Experiment for a Local Heavy Rainfall Event in the Tokyo Metropolitan Area. Mon. Weather Rev. 2011, 139, 1911–1931. [Google Scholar] [CrossRef]
- Sun, J.; Wang, H. Radar Data Assimilation with WRF 4D-Var. Part II: Comparison with 3D-Var for a Squall Line over the U.S. Great Plains. Mon. Weather Rev. 2013, 141, 2245–2264. [Google Scholar] [CrossRef]
- Snyder, C.; Zhang, F. Assimilation of Simulated Doppler Radar Observations with an Ensemble Kalman Filter*. Mon. Weather Rev. 2003, 131 Pt 1, 1663–1677. [Google Scholar] [CrossRef]
- Tong, M.; Xue, M. Ensemble Kalman Filter Assimilation of Doppler Radar Data with a Compressible Nonhydrostatic Model: OSS Experiments. Mon. Weather Rev. 2005, 133, 1789–1807. [Google Scholar] [CrossRef]
- Zhang, F.; Weng, Y.; Sippel, J.A.; Meng, Z.; Bishop, C. Cloud-Resolving Hurricane Initialization and Prediction through Assimilation of Doppler Radar Observations with an Ensemble Kalman Filter. Mon. Weather Rev. 2009, 137, 2105–2125. [Google Scholar] [CrossRef]
- Jones, C.D.; MacPherson, B. A latent heat nudging scheme for the assimilation of precipitation data into an operational mesoscale model. Meteorol. Appl. 1997, 4, 269–277. [Google Scholar] [CrossRef]
- Haase, G.; Crewell, S.; Simmer, C.; Wergen, W. Assimilation of radar data in mesoscale models: Physical initialization and latent heat nudging. Phys. Chem. Earth Part B Hydrol. Ocean. Atmos. 2000, 25, 1237–1242. [Google Scholar] [CrossRef]
- Stephan, K.; Klink, S.; Schraff, C. Assimilation of radar-derived rain rates into the convective-scale model COSMO-DE at DWD. Q. J. R. Meteorol. Soc. 2008, 134, 1315–1326. [Google Scholar] [CrossRef]
- Radhakrishnan, C.; Chandrasekar, V. CASA Prediction System over Dallas–Fort Worth Urban Network: Blending of Nowcasting and High-Resolution Numerical Weather Prediction Model. J. Atmos. Ocean Technol. 2020, 37, 211–228. [Google Scholar] [CrossRef]
- Tian, X.; Zhang, H.; Feng, X.; Xie, Y. Nonlinear Least Squares En4DVar to 4DEnVar Methods for Data Assimilation: Formulation, Analysis, and Preliminary Evaluation. Mon. Weather Rev. 2018, 146, 77–93. [Google Scholar] [CrossRef]
- Liu, C.; Xiao, Q.; Wang, B. An Ensemble-Based Four-Dimensional Variational Data Assimilation Scheme. Part I: Technical Formulation and Preliminary Test. Mon. Weather Rev. 2008, 136, 3363–3373. [Google Scholar] [CrossRef]
- Wang, X.; Snyder, C.; Hamill, T.M. On the Theoretical Equivalence of Differently Proposed Ensemble–3DVAR Hybrid Analysis Schemes. Mon. Weather Rev. 2007, 135, 222–227. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Xue, M. Assimilation of Radar Radial Velocity Data with the WRF Hybrid Ensemble–3DVAR System for the Prediction of Hurricane Ike (2008). Mon. Weather Rev. 2012, 140, 3507–3524. [Google Scholar] [CrossRef]
- Duda, J.D.; Wang, X.; Wang, Y.; Carley, J.R. Comparing the Assimilation of Radar Reflectivity Using the Direct GSI-Based Ensemble–Variational (EnVar) and Indirect Cloud Analysis Methods in Convection-Allowing Forecasts over the Continental United States. Mon. Weather Rev. 2019, 147, 1655–1678. [Google Scholar] [CrossRef]
- Benjamin, S.G.; Weygandt, S.S.; Brown, J.M.; Hu, M.; Alexander, C.R.; Smirnova, T.G.; Olson, J.B.; James, E.; Dowell, D.C.; Grell, G.A.; et al. A North American Hourly Assimilation and Model Forecast Cycle: The Rapid Refresh. Mon. Weather Rev. 2016, 144, 1669–1694. [Google Scholar] [CrossRef]
- Ingleby, N.B.; Lorenc, A.C.; Ngan, K.; Rawlins, F.; Jackson, D.R. Improved variational analyses using a nonlinear humidity control variable. Q. J. R. Meteorol. Soc. 2013, 139, 1875–1887. [Google Scholar] [CrossRef]
- Tang, Y.; Lean, H.W.; Bornemann, J. The benefits of the Met Office variable resolution NWP model for forecasting convection. Meteorol. Appl. 2013, 20, 417–426. [Google Scholar] [CrossRef]
- Stephan, K.; Schraff, C. Improvements of the operational latent heat nudging scheme used in COSMO-DE at DWD. COSMO Newsl. 2008, 9, 7–11. [Google Scholar]
- Jacques, D.; Michelson, D.; Caron, J.-F.; Fillion, L. Latent Heat Nudging in the Canadian Regional Deterministic Prediction System. Mon. Weather Rev. 2018, 146, 3995–4014. [Google Scholar] [CrossRef]
- Davolio, S.; Buzzi, A. A Nudging Scheme for the Assimilation of Precipitation Data into a Mesoscale Model. Weather Forecast. 2004, 19, 855–871. [Google Scholar] [CrossRef]
- Liu, Y.; Vandenberghe, F.; Low-Nam, S.; Warner, T.; Swerdlin, S. Observation-quality estimation and its application in the NCAR/ATEC real-time FDDA and forecast (RTFDDA) system. Bull. Am. Meteorol. Soc. 2004, 1, 31–40. [Google Scholar]
- Liu, Y.; Xu, M.; Roux, G.; Ge, M.; Sheu, R.; Hacker, J.; Swerdlin, S. A FDDA Based Operational Mesoscale Ensemble Analysis and Prediction System (E-RTFDDA) and a Comparison of MM5 and WRF. 2007. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.503.1545&rep=rep1&type=pdf (accessed on 22 September 2021).
- Liu, Y.; Warner, T.T.; Bowers, J.F.; Carson, L.P.; Chen, F.; Clough, C.A.; Davis, C.A.; Egeland, C.H.; Halvorson, S.F.; Huck, T.W.; et al. The Operational Mesogamma-Scale Analysis and Forecast System of the U.S. Army Test and Evaluation Command. Part I: Overview of the Modeling System, the Forecast Products, and How the Products Are Used. J. Appl. Meteorol. Clim. 2008, 47, 1077–1092. [Google Scholar] [CrossRef]
- Liu, Y.; Warner, T.T.; Astling, E.G.; Bowers, J.F.; Davis, C.A.; Halvorson, S.F.; Rife, D.L.; Sheu, R.-S.; Swerdlin, S.P.; Xu, M. The Operational Mesogamma-Scale Analysis and Forecast System of the U.S. Army Test and Evaluation Command. Part II: Interrange Comparison of the Accuracy of Model Analyses and Forecasts. J. Appl. Meteorol. Clim. 2008, 47, 1093–1104. [Google Scholar] [CrossRef][Green Version]
- Pan, Y.; Xue, M.; Ge, G. Incorporating Diagnosed Intercept Parameters and the Graupel Category within the ARPS Cloud Analysis System for the Initialization of Double-Moment Microphysics: Testing with a Squall Line over South China. Mon. Weather Rev. 2016, 144, 371–392. [Google Scholar] [CrossRef]
- Albers, S.C.; McGinley, J.A.; Birkenheuer, D.L.; Smart, J.R. The Local Analysis and Prediction System (LAPS): Analyses of Clouds, Precipitation, and Temperature. Weather Forecast. 1996, 11, 273–287. [Google Scholar] [CrossRef]
- Lerach, D.G.; Rutledge, S.A.; Williams, C.; Cifelli, R. Vertical Structure of Convective Systems during NAME 2004. Mon. Weather Rev. 2010, 138, 1695–1714. [Google Scholar] [CrossRef]
- Xu, M.; Liu, Y.; Davis, C.A.; Warner, T.T. 2002: Sensitivity of nudging parameters on the performance of a mesoscale FDDA system: A case study. In Proceedings of the 15th Conference on NumericaL Weather Prediction, San Antonio, TX, USA, 12–16 August 2002; pp. 127–130. [Google Scholar]
- Thompson, G.; Field, P.R.; Rasmussen, R.M.; Hall, W.D. Explicit Forecasts of Winter Precipitation Using an Improved Bulk Microphysics Scheme. Part II: Implementation of a New Snow Parameterization. Mon. Weather Rev. 2008, 136, 5095–5115. [Google Scholar] [CrossRef]
- Grell, G.A.; Freitas, S.R. A scale and aerosol aware stochastic convective parameterization for weather and air quality modeling. Atmos. Chem. Phys. 2014, 14, 5233–5250. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Noh, Y.; Dudhia, J. A New Vertical Diffusion Package with an Explicit Treatment of Entrainment Processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Iacono, M.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W. Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. Space Phys. 2008, 113, 1–8. [Google Scholar] [CrossRef]
- Fairall, C.W.; Bradley, E.F.; Hare, J.E.; Grachev, A.A.; Edson, J.B. Bulk parameterization of air-sea fluxes: Updates and verification for the COARE algorithm. J. Clim. 2003, 16, 571–591. [Google Scholar] [CrossRef]
- Pan, S.; Gao, J.; Stensrud, D.J.; Wang, X.; Jones, T.A. Assimilation of Radar Radial Velocity and Reflectivity, Satellite Cloud Water Path, and Total Precipitable Water for Convective-Scale NWP in OSSEs. J. Atmos. Ocean. Technol. 2018, 35, 67–89. [Google Scholar] [CrossRef]
- Zhu, K.; Xue, M.; Ouyang, K.; Jung, Y. Assimilating polarimetric radar data with an ensemble Kalman filter: OSSEs with a tornadic supercell storm simulated with a two-moment microphysics scheme. Q. J. R. Meteorol. Soc. 2020, 146, 1880–1900. [Google Scholar] [CrossRef]
- Roberts, N.M.; Lean, H.W. Scale-Selective Verification of Rainfall Accumulations from High-Resolution Forecasts of Convective Events. Mon. Weather Rev. 2008, 136, 78–97. [Google Scholar] [CrossRef]
- Han, M.; Braun, S.A.; Matsui, T.; Williams, C.R. Evaluation of cloud microphysics schemes in simulations of a winter storm using radar and radiometer measurements. J. Geophys. Res. Atmos. 2013, 118, 1401–1419. [Google Scholar] [CrossRef]
- Koch, S.E.; Ferrier, B.; Stoelinga, M.T.; Szoke, E.; Weiss, S.J.; Kain, J.S. The use of Simulated Radar Reflectivity Fields in the Diagnosis of Mesoscale Phenomena from High-Resolution WRF Model Forecasts. 2005. Available online: https://www.researchgate.net/publication/228873463_The_use_of_simulated_radar_reflectivity_fields_in_the_diagnosis_of_mesoscale_phenomena_from_high-resolution_WRF_model_forecasts (accessed on 22 September 2021).
- Hu, M.; Xue, M. Impact of configurations of rapid intermittent assimilation of wsr-88d radar data for the 8 may 2003 oklahoma city tornadic thunderstorm case. Mon. Weather Rev. 2007, 135, 507–525. [Google Scholar] [CrossRef]
- Johnson, A.; Wang, X. Design and Implementation of a GSI-Based Convection-Allowing Ensemble Data Assimilation and Forecast System for the PECAN Field Experiment. Part I: Optimal Configurations for Nocturnal Convection Prediction Using Retrospective Cases. Weather Forecast. 2017, 32, 289–315. [Google Scholar] [CrossRef]
- Hu, M.; Xue, M.; Brewster, K. 3DVAR and Cloud Analysis with WSR-88D Level-II Data for the Prediction of the Fort Worth, Texas, Tornadic Thunderstorms. Part I: Cloud Analysis and Its Impact. Mon. Weather Rev. 2006, 134, 675–698. [Google Scholar] [CrossRef]
- Ding, Y. Summer Monsoon Rainfalls in China. J. Meteorol. Soc. Jpn. 1992, 70, 373–396. [Google Scholar] [CrossRef]
- Kato, K. Airmass Transformation over the Semiarid Region around North China anc Abrupt Change in the Structure of the Baiu Front in Early Summer. J. Meteorol. Soc. Jpn. 1987, 65, 737–750. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, E.; Mahajan, R.; Thomas, C.; Groff, D.; Van Delst, P.; Collard, A.; Kleist, D.; Treadon, R.; Derber, J.C. All-Sky Microwave Radiance Assimilation in NCEP’s GSI Analysis System. Mon. Weather. Rev. 2016, 144, 4709–4735. [Google Scholar] [CrossRef]
- Qian, X.; Qiu, B.; Zhang, Y. Widespread Decline in Vegetation Photosynthesis in Southeast Asia Due to the Prolonged Drought During the 2015/2016 El Niño. Remote Sens. 2019, 11, 910. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L.; Guan, J.; Zhang, M. Evaluation of Combined Satellite and Radar Data Assimilation with POD-4DEnVar Method on Rainfall Forecast. Appl. Sci. 2020, 10, 5493. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).