1. Introduction
Glaciers are widely considered as a proxy for climate changes because of their high sensitivity to changes in atmospheric temperature [
1,
2,
3]. In particular, alpine glaciers are strongly suffering the consequences of the rising temperature. Most of them, in fact, are located in humid–temperate areas and at altitudes ranging between 2000 and 4800 m a.s.l., where the average air temperature in the past 100 years has increased almost two times faster than the global average [
4,
5]. Based on present trends, it was estimated that alpine glaciers may lose half of their volume, compared to that in 2017, by 2050 [
3].
Glaciological studies carried out with in situ measurements or analysis of time series of images allow for glacier inventory updates with a frequency on the order of the decade [
6,
7,
8,
9]. In situ glaciological measurements to quantify volume variations and mass balances, however, are extremely time consuming, and they usually require mountaineering expertise, as the environment is often dangerous. To overcome this limit, photogrammetry is a widely used technique for building 3D models of glacier surfaces by means of pairs (or groups) of overlapping images. These can be acquired either from terrestrial stations [
10], aerial platforms carrying photogrammetric cameras [
11,
12,
13] or satellites [
14,
15] and can be employed to carry out geometrically accurate and recurrent analyses on glaciers evolution.
Since early 2000s, the development of digital photogrammetric cameras for aerial platforms, combined with high-quality GNSS-INS sensors for the estimation of the camera location and attitude, has allowed surveys in remote and orographically complex areas to be georeferenced with fewer ground control points (GCPs), significantly reducing the required fieldwork [
16]. Moreover, in the past 10 years, the increasing development of unmanned aerial vehicles (UAVs), low-cost sensors and structure-from-motion (SfM) techniques have drastically reduced the need for highly specific and expensive equipment for large-scale glacier monitoring [
17]. High-spatial-resolution volume variation [
18,
19,
20,
21] as well as high-frequency displacement and surface velocity fields [
22,
23,
24,
25,
26] can be derived even by a single research group with simplified logistics and resource allocation.
Though there is currently a wide range of techniques that can be successfully applied to survey and monitor glaciers (with different spatial and temporal resolution), going back in time to retrace the evolution of a glacier is still a challenging task. To this end, historical aerial images, e.g., those acquired for regional cartographic purposes, are extremely valuable resources to study the evolution and the movement of a glacier in the past. Thanks to the state-of-the-art digital SfM techniques, historical aerial images can be employed to build geometrically accurate photogrammetric models of large-scale glaciers [
27,
28]. From such models, digital surface models (DSMs) and orthophotos can be retrieved to compute volumetric variations, surface displacements and velocities or to compute mass balances. However, historical images are clearly analog: films must be first digitalized with a photogrammetric scanner in such a way as to employ digital SfM algorithms to orient the images through aerial triangulation [
29].
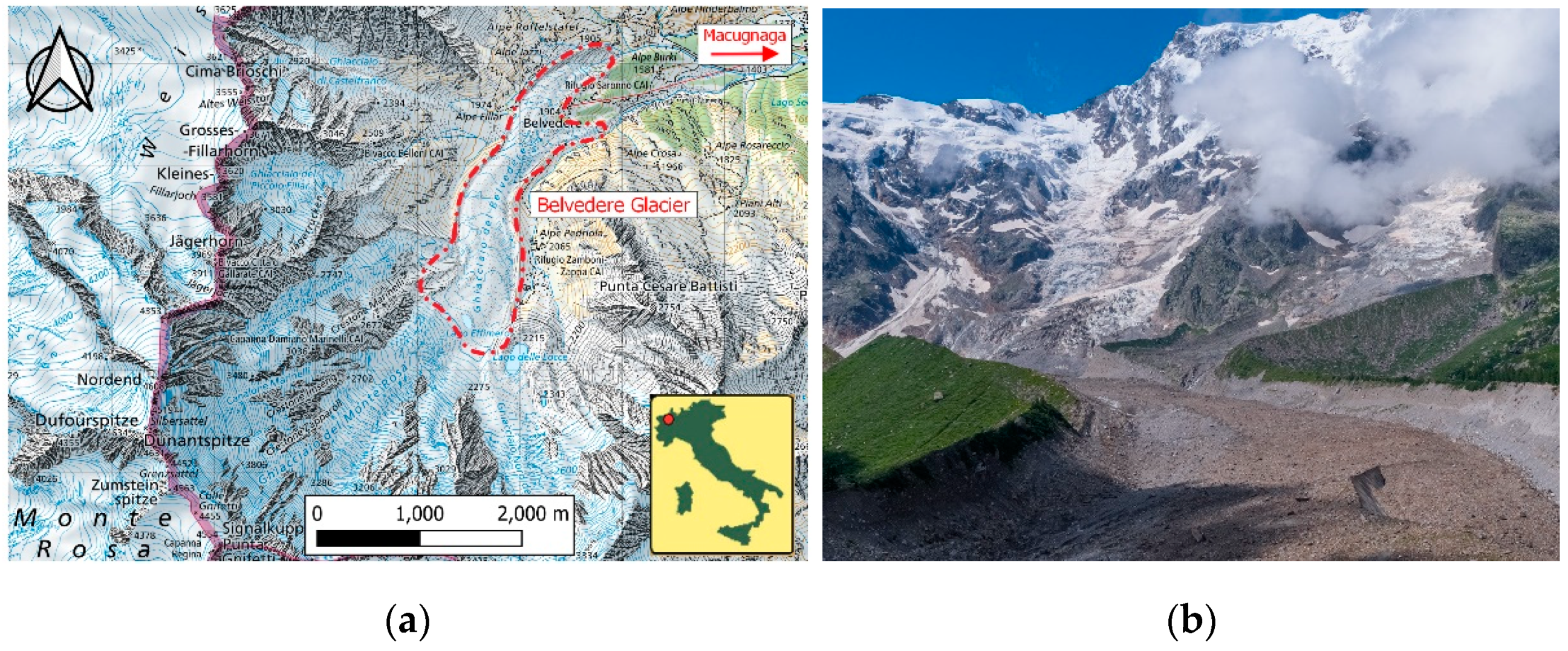
In this framework, the Belvedere Glacier was the object of study because of its peculiar characteristics. It is located at the base of the east side of Monte Rosa (see
Figure 1a), in the Anzasca Valley (Piedmont region, Italy). It extends from 1800 to about 2300 m a.s.l., near the municipality of Macugnaga. Belvedere Glacier is a typical dark, debris-covered glacier, almost completely covered by rocks and debris (see
Figure 1b), and it is fed by ice and snow avalanches falling from the steep Monte Rosa glacier, which is more than 4500 m high a.s.l. Particularly relevant is the fact that, until the first years of the 21st century, the Belvedere Glacier was one of the few alpine glaciers not retreating. By contrast, between 2000 and 2001, the Belvedere Glacier experienced an extraordinary surge phenomenon: a sudden increase of ice mass at the base of the Monte Rosa glacier propagated down to the valley in the form of a kinematic wave [
30,
31,
32,
33].
This work analyzed the evolution of the Belvedere Glacier by means of SfM techniques applied to digitalized historical aerial images combined with more recent digital surveys, either from aerial platforms or UAVs. This allowed the monitoring of an Alpine glacier with high resolution and geometrical accuracy over a long span of time, which is crucial for the considered application. In particular, the period 1977–2019 was considered with five different surveys. The surveys were carried out in different epochs, roughly well distributed in time, so as to capture the morphology of the glacier and quantify volume variations that occurred.
2. Photogrammetric Dataset Description
For the study, data acquired from five photogrammetric surveys performed over a time span ranging between 1977 and 2019 were considered. The earlier datasets (named hereafter
historical surveys) dated back to September 1977, August 1991 and September 2001. The images were acquired for regional mapping purposes by the Italian company CGR SpA (Compagnia Generale Ripreseaeree) with analogic photogrammetric cameras mounted aboard planes. The images were catalogued, and their metadata were organized in the SITAD (Sistema Informativo Territoriale Ambientale Diffuso) database [
34], now integrated with the GeoPortale Piemonte [
35]. Upon request, CGR SpA digitalized the images related to the Belvedere Glacier and made them available to the authors. The analogic films were digitalized by means of a photogrammetric scanner with a resolution of 21 µm/px. The 2009 dataset was also acquired by CGR SpA for mapping purposes (and made available to the authors), but at that time a digital photogrammetric camera was employed. The most recent dataset, from 2019, was directly acquired by the authors by using a fixed-wing UAV with a small and lightweight action camera mounted on board.
A summary of the characteristics of the cameras and flights for each of the five datasets are summarized in
Table 1 for immediate comparisons, and more details on these datasets are provided in the following subsections.
2.1. Analog Aerial Datasets of 1977, 1991 and 2001
The earliest dataset considered in the study was acquired by CGR SpA on 16/Sep/1977 with an analog photogrammetric camera Wild RC10, equipped with a 15 UAG I lens, with a focal length of 153.26 mm. The flight consisted of three stripes performed at an average altitude of 5600 m a.s.l., with approximately 60% along-flight overlap and transversal overlap varying from 30% to 60% because the stripes were not parallel. A total of 11 RGB images were acquired (see
Figure 2). Considering an average altitude of the glacier of 2000 m a.s.l., the scale of the images was about 1:23,000, leading to an average ground sample distance (GSD) of 0.5 m. The camera reference system was materialized on the film with four fiducial marks placed at the four corners of the image. As is visible in
Figure 2c, some of the fiducial marks were faded due to the aging of the films, but they were still identifiable in the digitalized images.
The 1991 survey was carried out on two different days: 3/Aug/1991 and 7/Aug/1991. Eleven grayscale images were taken with an analog photogrammetric camera, a Wild RC20 equipped with a 15/4 UAGA F lens (focal length of 153.26 mm). The flight consisted of only two stripes (
Figure 3), conducted at 8200 m a.s.l. and 8500 m a.s.l., leading to an average GSD for the images of about 0.9 m. The along-flight overlap was approximately between 70% and 80%, while the transversal overlap was about 50%. As in the images of 1977, four fiducial marks allowed for the definition of the camera reference system (
Figure 3c).
The most recent among the three historical datasets dated back to 2001. Images were acquired with a film camera Wild RC30 equipped with a 15/4 UAG-S lens (focal length of 153.928 mm). The flight consisted of three stripes acquired between 6/Sep/2001 and 11/Sep/2001, producing a total of 10 RGB images with overlaps of ~70% along flight and ~50% in the transversal direction (
Figure 4). The two external stripes were conducted at an altitude of about 6100 m a.s.l., while the central one was conducted at a lower altitude of about 4800 m a.s.l, for an average of 5800 m a.s.l. The mean scale of the images was 1:23,000, producing a GSD of 0.5 m, comparable to that of the 1977 flight. The camera reference frame was materialized by 8 fiducial marks, well identifiable on the digitalized images (
Figure 4c).
Analog images taken during the aerial surveys of 1977, 1991 and 2001 were digitalized by means of a photogrammetric scanner (PhotoScan2000, developed by Z/I Imaging and Carl Zeiss) capable of scanning analog film rolls. The Photoscan2000 scanner was equipped with a Kodak KLI trilinear CCD sensor with an optical scanning resolution of 7 µm. Pixels could be digitally aggregated to obtain resolutions of 14, 21, 28, 56, 112 or 224 µm. The scanner was designed to ensure a geometrical accuracy for the digitalized images of 2 µm. The images from the historical surveys were digitalized by CGR SpA with a resolution of 21 µm/px, producing eight-bit TIF images with dimensions of 12,098 × 11,144 px. In order to assess the quality of the digitalized images, the actual pixel size was empirically estimated as the ratio of the average distance, in millimeters, of the four fiducial marks at corners and the correspondent average distance in terms of pixels on the digitalized images. The estimated pixel size was 21 µm × 21 µm for each dataset, with computed standard deviations of about three orders of magnitude less, in agreement with the technical specifications of the scanner.
2.2. Digital Aerial and UAV Datasets of 2009 and 2019
During October 2009, a flight over Belvedere Glacier was carried out by CGR SpA for mapping purposes. This time, a digital photogrammetric camera was employed. A Z/I-Imaging DMC camera equipped with a 120 mm focal length lens and a CCD sensor with pixel size of 12 µm × 12 µm, acquiring RGB digital images at a resolution of 7680 × 13,824 pixels, was mounted on an airplane. Eleven images with along-flight and transversal overlaps of 70% and 50%, respectively, were gathered along two stripes with altitude between 5600 and 6000 m a.s.l (
Figure 5). The average image scale was 1:32,000, and the GSD was 0.4 m.
Images from the latest dataset were gathered by the authors during fieldwork on the Belvedere Glacier carried out between 29/Jul/2019 and 2/Aug/2019. A fixed-wing UAV Parrot Disco was adapted in such a way as to carry a low-cost and lightweight action camera, a HawkEye Firefly 8S. The action camera was equipped with a 12 Mpx 1/2.3″ CMOS sensor and had a pixel size of 1.34 µm × 1.34 µm and a focal length of 3.8 mm (90° field of view). The flights were conducted at an average height of 120 m a.g.l. (above ground level), in agreement with Italian UAV regulations, and images were taken with longitudinal and transversal overlap of 80% and 60%, respectively (except for a small portion in the middle of the glacier with a slightly smaller transversal overlap of ~50%; see
Figure 6a). The average image scale was therefore approximately 1:32,000, and the GSD was 5 cm, one order of magnitude smaller compared to those of the aerial datasets. Because of UAV technical limitations, the survey area was restricted to the glacier body only and five flights with the fixed-wing UAV were performed (
Figure 6).
The characteristics of the cameras and flights for each of the five datasets are summarized in
Table 1 for immediate comparison.
2.3. The GNSS Survey for Block Georeferencing
To constrain the UAV photogrammetric block from 2019, 36 squared targets, consisting of 50 cm × 50 cm polypropylene sheets with high color contrast, were deployed over the survey area, anchored to large rocks on both the glacier and the moraines. Among the 36 targets, 26 were used as ground control points (GCPs) and 10 as control points (CPs). The targets were measured on the field with a dual frequency (L1/L2) geodetic quality GNSS receiver Leica GS14. Because GSM internet connection was available in the lower part of the glacier, the targets were measured in nRTK with respect to the HxGN SmartNet network of permanent stations. All the points measured in nRTK were occupied for ~10 s at 1 Hz of acquisition rate. In the upper part of the glacier, where nRTK was not possible, the targets were measured by static positioning. For each of those points, carrier-phase raw observations were logged for a timespan of ~10 min (1 Hz sampling rate). These were postprocessed with respect to a local master station (Leica GPS1200) placed over a target located next to the Zamboni–Zappa hut (2070 m a.s.l.). Coordinates of the master station were repeatedly measured in different years with both static and nRTK measurements, and accuracy on the order of 0.5 cm in planimetry and 2 cm in height was obtained. GNSS observations were postprocessed with the software Leica Infinity (version 3.2.0) in the official Italian reference system ETRF2000 at epoch 2008.0. The resulting accuracies of the coordinates of the GCPs were 1.5 cm in planimetry and 3 cm in height, in terms of average RMSE.
3. Image Orientation and Point Cloud Generation
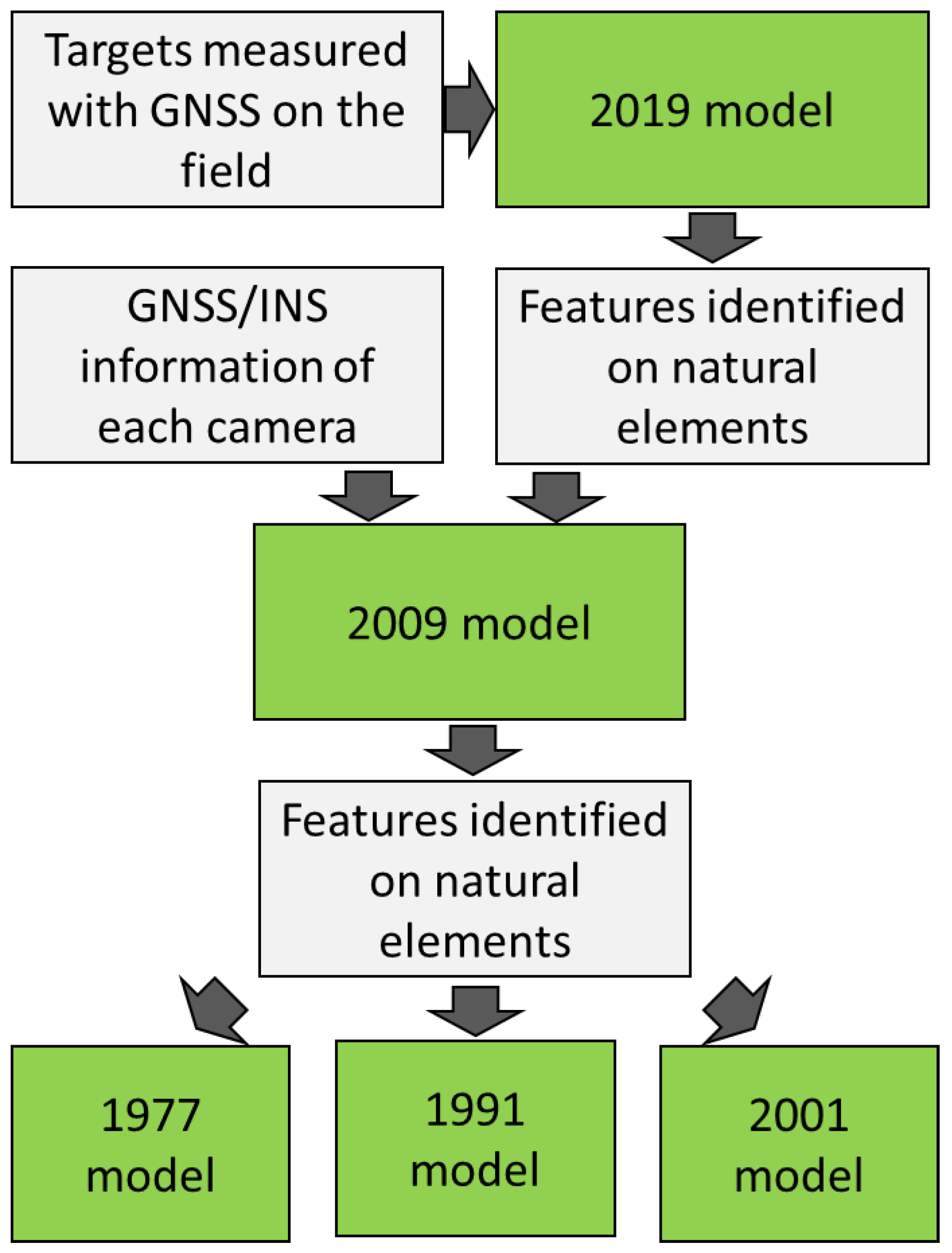
For image orientation and model reconstruction of all the datasets, the photogrammetric software Agisoft Metashape (version 1.7.2) was employed. A sketch of the followed workflow is provided in
Figure 7.
Concerning the most recent UAV survey, that from 2019, the 1486 images were oriented by traditional aerial triangulation on the basis of 26 targets spread over the survey (
Figure 8) area used as GCPs (see
Section 2.2) in the bundle block adjustment (BBA). The GCPs were manually collimated on the images. A collimation accuracy of 1 px was assumed as the a priori standard deviation of the observations within the BBA. Tie Points (TPs) were automatically detected and matched by Metashape on full resolution images. Camera internal orientation (IO) parameters of the Hawkeye Firefly 8S action camera was estimated during the BBA by self-calibration. To this end, approximated values of IO were precalibrated by using a traditional checkerboard. However, these initial values were adjusted for each flight because of the internal instability of the camera and thanks to the high density of the GCPs available.
Regarding the 2009 digital dataset, the DMC system described in
Section 2.2 included high-precision GNSS/INS instrumentations able to provide the camera with external orientation (EO) [
36]. The coordinates of the camera projection centers were provided with an accuracy of 30 cm, while the camera attitude angles had accuracies of 8 mgon for roll and pitch angles and 10 mgon for yaw [
37]. In order to improve the quality of the photogrammetric block within a small area such as that of Belvedere Glacier, 11 features clearly identifiable on the images (e.g., sharp rocks) were used as GCPs. Their coordinates were retrieved from the 2019 model, which had a significantly higher spatial resolution (see
Table 1). The EO of the images was estimated through assisted aerial triangulation (AAT) [
16]. The BBA was solved by combining GNSS/INS information with TPs automatically detected by the software and 11 GCPs manually collimated on the images. The quality of the photogrammetric model was assessed by means of six check points (CP) not used to solve the BBA.
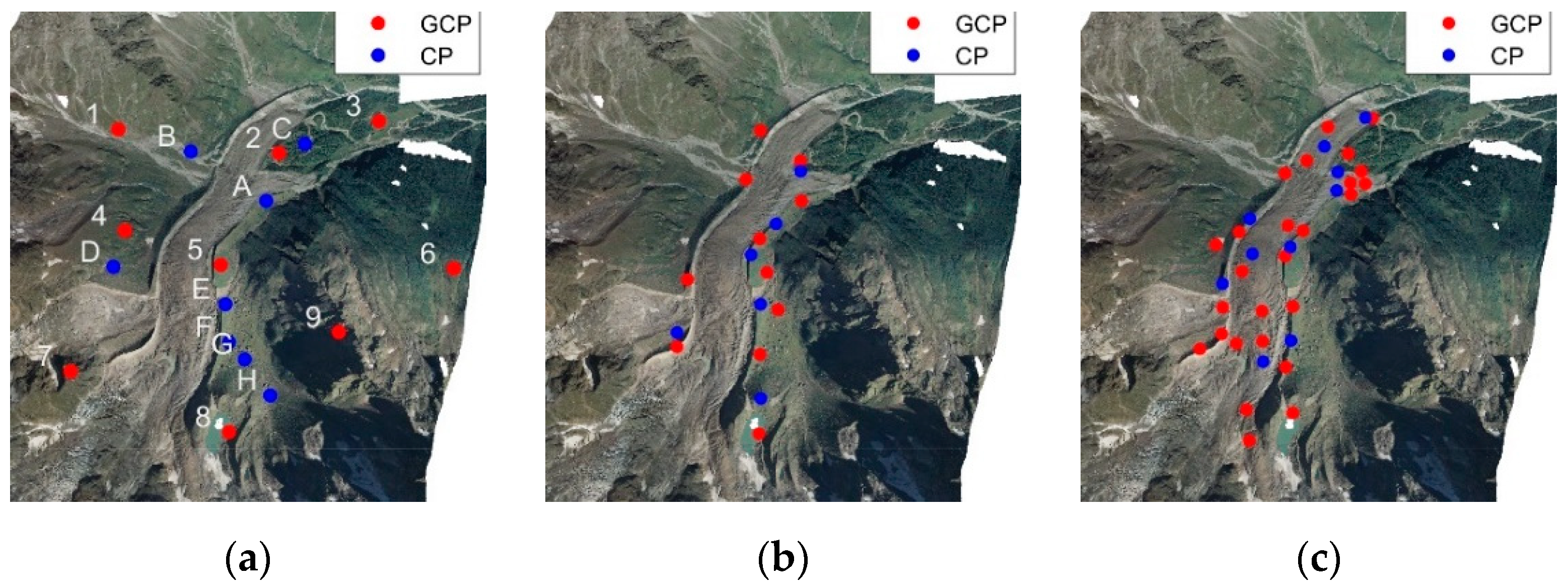
After the digitalization, the three historical datasets, those from 1977, 1991 and 2001 were oriented by aerial triangulation on the basis of the already-oriented 2009 survey. The coordinates of nine groups of GCPs (marked with numbers 1 to 9 in
Figure 8) and eight groups of CPs (marked with letters A to H), well distributed over the whole area, were retrieved from the aerial images acquired with the DMC digital photogrammetry system.
Points such as buildings edges, corners, sharp rocks along the glacier moraines and particular morphological patterns that remained reasonably unchanged over time were selected in such a way as to be clearly identified in most of the four datasets (1977, 1991, 2001 and 2009), as shown in
Figure 9.
Note that it was not always possible to identify the same point in all four of the datasets because of the different image scales, different image quality (e.g., RGB versus grayscale images) or changes in the morphology over 30 years. To overcome this problem, if one point was not visible in one dataset, another one was searched nearby. To clarify, if one point (e.g., Point 2) was not found in images from 1991 (e.g., because of the larger image scale), then another feature, named Point 2b, was searched for close to the original location of Point 2 in the 2009 images and used as GCP for the 1991 dataset. However, in the statistics, Points 2 and 2b were considered as one single point because of their spatial proximity.
The GCPs used to solve the BBA of the three historical datasets were properly weighted with their variance. An accuracy of 0.75 px was assumed as the collimation accuracy for a human operator dealing with high-quality digital images such as those from 2009. This assumption was confirmed by the image reprojection error of the manually collimated points, which was always smaller than one pixel. Therefore, an a priori accuracy of 0.3 m was given to the GCPs in the three datasets from 1977, 1991 and 2001.
Concerning the camera IO, the three analog cameras were calibrated in laboratory by the producer, and calibration certificates were available. Therefore, the calibrated value of focal length and the coordinates of the principal point were provided as initial values in the BBA. These were then adjusted based on the GCPs by using a self-calibration procedure [
38]. Additionally, two radial (k1 and k2) and tangential (p1 and p2) distortion parameters were estimated in order to correct the lens distortions of the photogrammetric cameras and the distortion introduced by external factors, e.g., the deterioration of the films over the years.
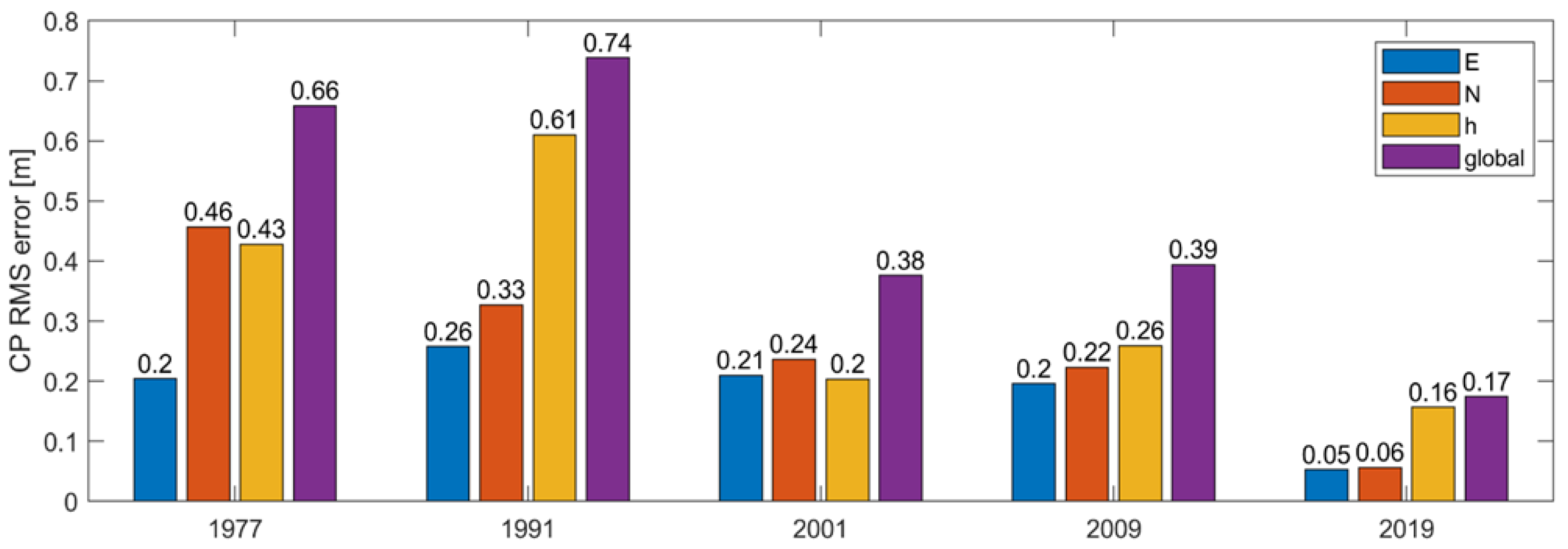
On the basis of the considered CPs, different model accuracies were obtained. The accuracy of the three historical models was assessed by using eight CPs, distributed mainly along the glacier moraines (see
Figure 8). Six CPs were used for the 2009 dataset. As reported in
Figure 10, the 1977 and 1991 models obtained global RMSEs of about 0.66 m and 0.74 m, respectively, while the 2001 and 2009 models obtained similar RMSEs of about 0.38 m. In all cases, these values were comparable to the average GSD of the aerial images. Regarding the 2019 survey, the model accuracy was assessed by 10 CPs, resulting in a RMSE error of 0.17 m, comparable to three times the GSD. This was due to the low quality of the camera employed. Nevertheless, as the GSD was on the order of magnitude of the centimeter, the model accuracy was still higher than that of the older flights.
Once camera EO was performed by aerial triangulation, georeferenced dense point clouds (PCs) were computed (a downscale factor of 2 was set to make the PCs more manageable) and used as starting point for glacier analyses. The number of points in each PC and the density of each dense cloud are summarized in
Table 2.
While the PC size was strictly related to the survey coverage, the PC average density was directly related to the GSD of the original photogrammetric survey, indicating the capability of resolving smaller details.
5. Glacier Analyses
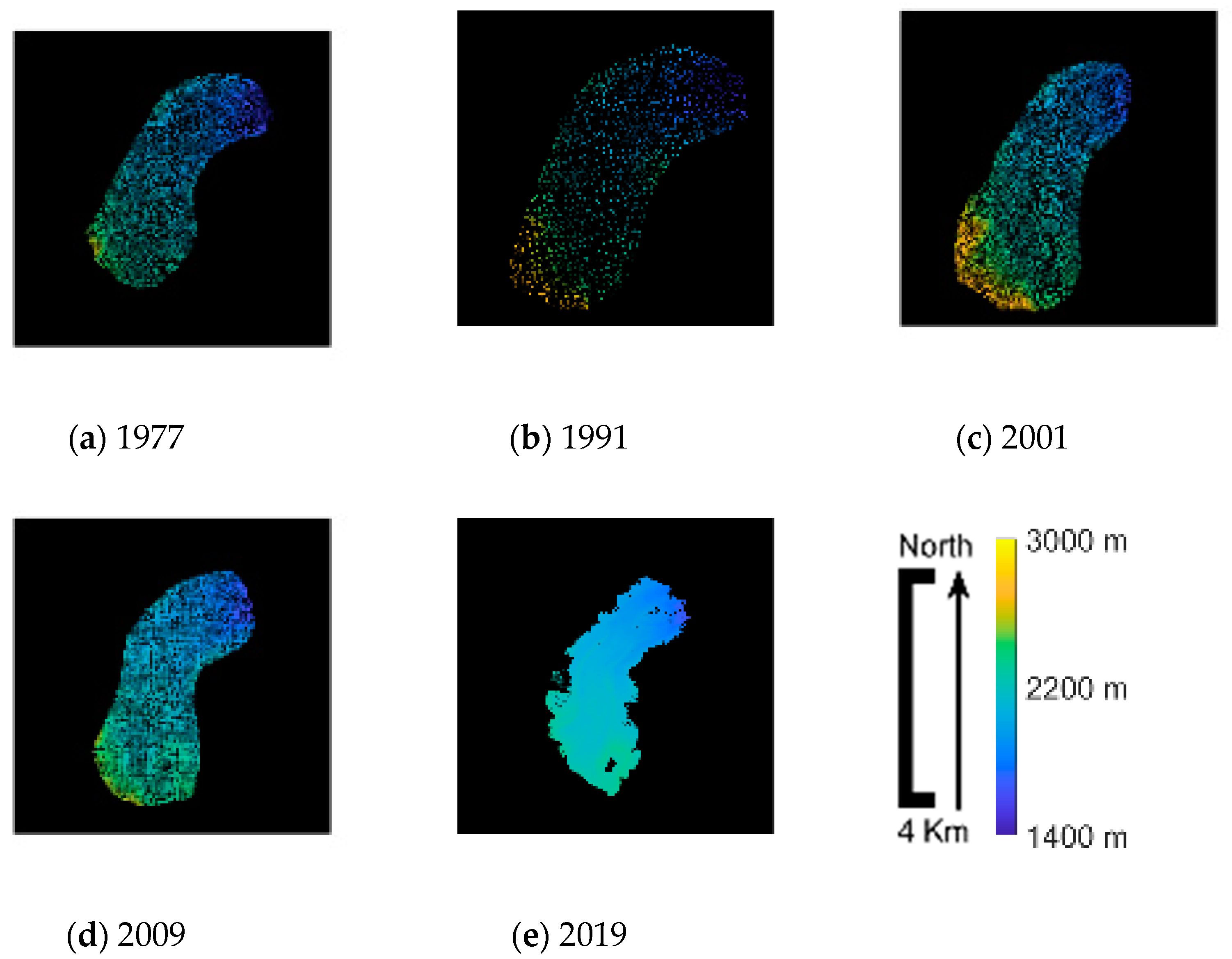
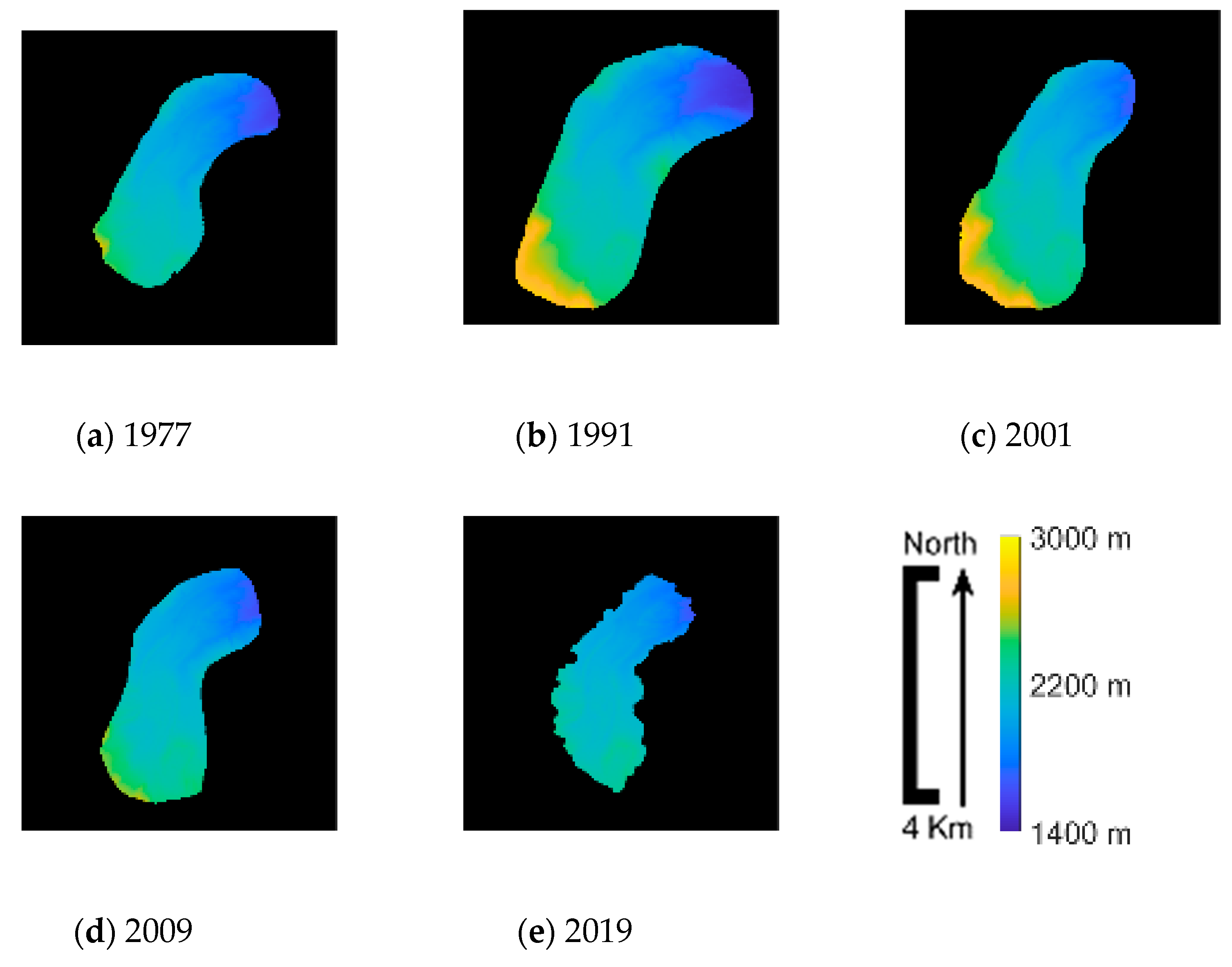
The final masked DSMs allowed spatial analyses of the glacier surface by comparing the measured altitude variations. Information on dynamics, evolution and volume ablation/accumulation could quantified during the considered timespan, from 1977 to 2019. First, the DSMs were analyzed in absolute terms, i.e., in terms of their altitude variability range and the spatial distribution of areas classified on the basis of their measured altitude.
Table 4 shows the surveyed minimum and maximum altitudes. The minimum values were more or less similar, within 5 m of variability, the while maximum values ranged between about 2339 and 2385 m. The stability of the minimum values can be justified by the area masking. Minimum altitudes likely occurred in the vicinity of the glacier terminus, and the mask buffering could have comprised points surveyed at the terminus foot, where transported rock deposits and debris were present in different positions along the valley. On the other hand, the variability of the maximum values can be justified by reversing the analyses. Higher altitudes likely occurred closer to mountainous peaks along the surveyed glacier accumulation area, located in the SW region of the mask, where mass balance can benefit from events such as avalanches or particular meteorological conditions immediately before the epoch of the surveys.
Other information was extrapolated by analyzing the spatial distribution of the measured altitudes. In this sense, the evolution in time of the glacier contours provided immediate feedback on the glacier’s surface dynamics.
Figure 15 presents glacier contour altitudes between 1800 and 2400 m, so as to comprise the maximum altitude range measured by the five surveys with a contour interval of 50m. With respect to the 1977 DSM (
Figure 15a), 1991 DSM cells classified in the range 2200–2400 m remained almost unchanged while the following contour lines gradually moved toward a valley, clearly indicating a mass accumulation (
Figure 15b). The following 2001 survey showed a continuation in these areas of the trend of increasing altitude toward the glacier terminus, but an altitude decrease was observed in the SW cells of the accumulation area (note the extension of the altitude class 2200–2250 m in
Figure 15c), and cells of the highest altitude class were practically absent (see
Table 4). The 2009 DSM showed totally different behavior (
Figure 15d). Lower contour lines retreated toward peaks, approximately in the same location as in 1977, while the 2150–2200 m range greatly retreated and covered a large part of the glacier toward the accumulation area. The most recent 2019 DSM (
Figure 15e) again showed a general retreat trend of lower contour lines, with no sharp transition in the range of 2100–2200 m (probably due to high surface ablation phenomena) and no great variation in the remaining areas in the range of 2200–2350 m.
In order to quantify the different effects of accumulation and ablation processes on Belvedere Glacier during time, relative comparisons were conducted. As previously clarified, because the different DSMs were georeferenced and made consistent in terms of spatial resolution, volume variations could be computed by considering DSM altitude variations and cell size. Cumulate volume variations were obtained, taking the 1977 DSM as reference, while average annual volume losses/gains were obtained in the considered periods.
Table 5 reports these relative comparisons.
The numbers in
Table 5 confirm what was found by analyzing the glacier contours variations, but from a different perspective. In the period 1977–2001, the glacier’s volume increased by about +20.66 million m
3, and its rate of volume gain increased by about 50% in the period 1991–2001 (from +0.72 to +1.06 million m
3/year). The period 2001–2019 revealed an important reduction of glacier volume. In the period 2001–2009, the average yearly volume decrease was −5.97 million m
3/year, bringing the volume down to −27.12 million m
3 with respect to the initial volume recorded in 1977 despite the volume accumulation in the previous period. In the following period, between 2009 and 2019, the trend remained negative but was less severe (−2.72 million m
3/year), resulting in a total loss of −54.28 million m
3 in the considered 42 years, from 1977 to 2019. The reported volume gains or losses refer to the whole glacier surface, but it could be interesting to investigate local variations.
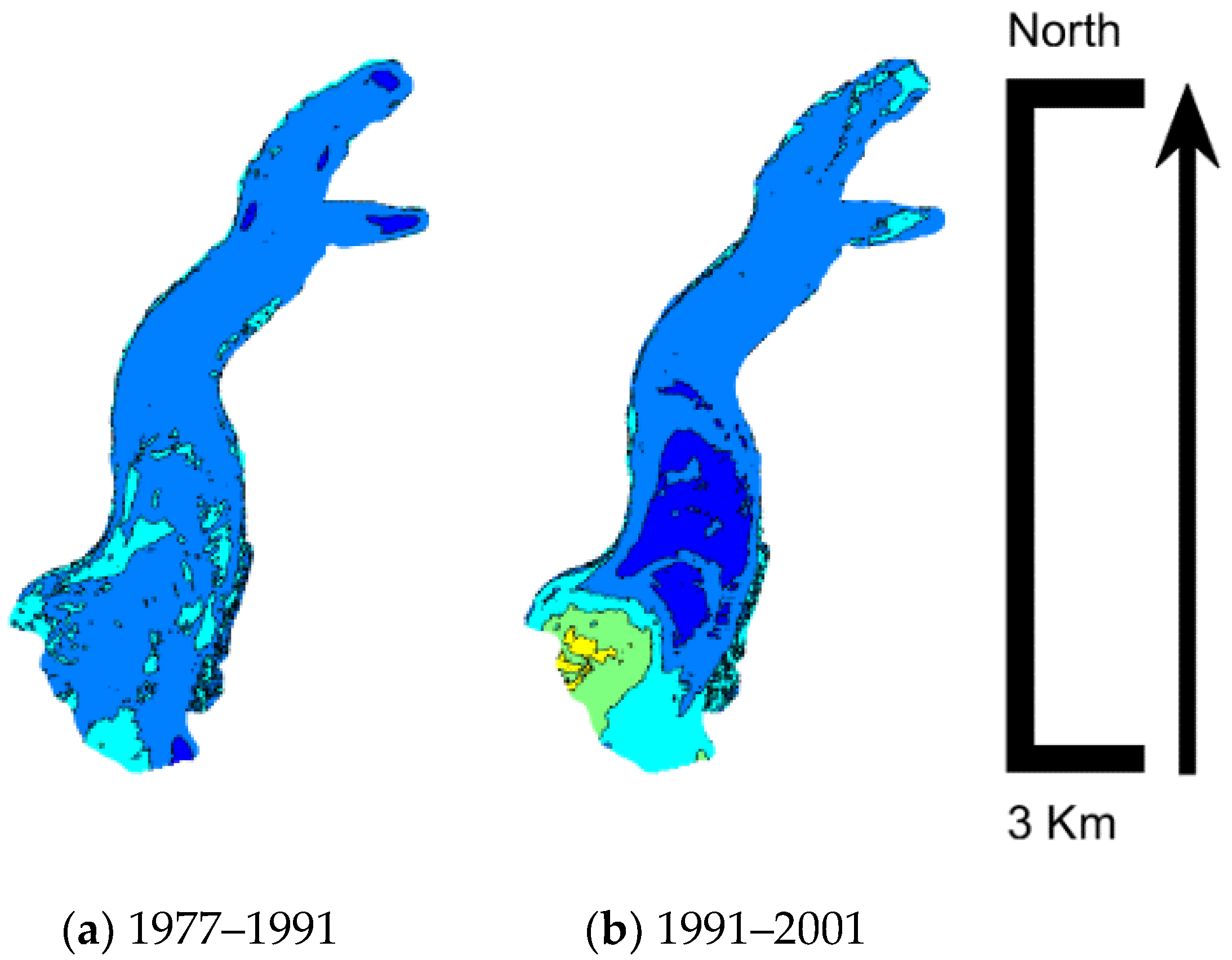
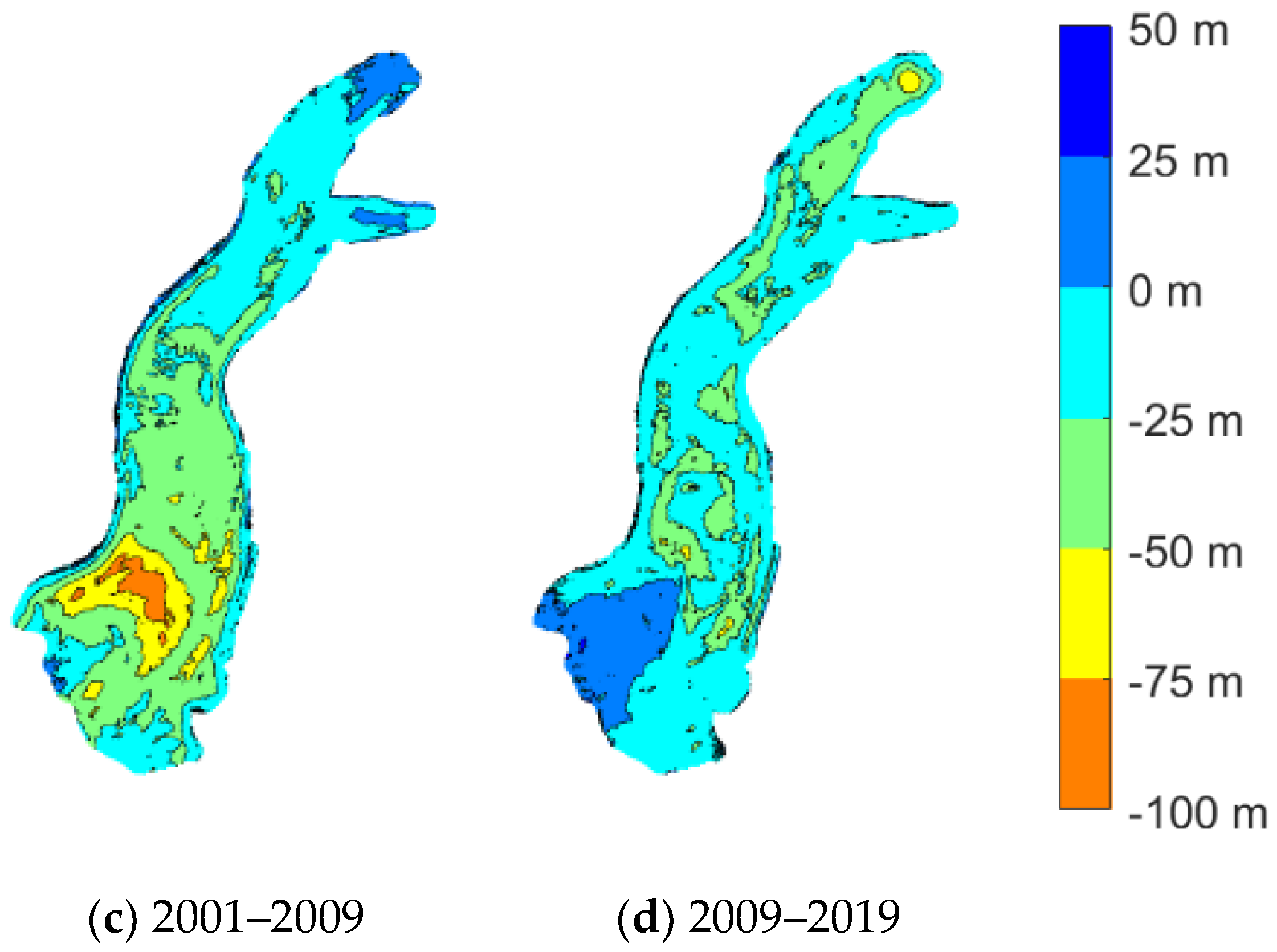
Figure 16 classifies glacier areas in terms of altitude variation, with contour intervals of 25 m. In the first considered period, from 1977 to 1991, the volume increase was quite distributed. Glacier terminus advancement was clearly visible, and volume decrease was measured in small portions at higher altitudes. The following period, 1991–2001, saw an important volume accumulation in the central part of the glacier, which was partially counterbalanced at higher altitudes. The following periods showed general volume loss, which was particularly important between 2001 and 2009 in the higher portion and was distributed until the terminus (see the northern one) in the period 2009–2019.
6. Conclusions
This work analyzed the evolution of the Belvedere Glacier by means of SfM techniques applied to digitalized historical aerial images combined with more recent digital surveys, either from aerial platforms or UAVs. This allowed the monitoring of the Belvedere Glacier with high resolution and geometrical accuracy over a long span of time, which is crucial for this application. Digital surface models of the area surrounding the glacier were produced on the basis of five different surveys conducted at the epochs 1977, 1991, 2001, 2009 and 2019 with different ground resolutions and accuracies, which for the most recent survey even reached the decimeter level. First, DSMs were made comparable by producing georeferenced raster images at equal spatial resolution (with common cell size of 0.5 m). Then, proper masks focusing on the glacier surface were determined by following a data-driven approach and exploiting common image processing techniques. This preprocessing led to the determination of glacier altitude and volume variations during the considered time span, sampled about every 10 years. Volume gains/losses were clearly identified and, more importantly, quantified. In the period 1977–2019, a loss of about 54 million m3 was computed, but the trend of these losses was far from linear. In the first half of the considered period, the glacier increased its volume and extent, accelerating this phenomenon in the second period. In the second half, a sudden glacier retreat began, particularly severe in the first decade of the current century, that almost totally compensated the volume increase of the previous 20 years. In the last period, the retreat continued, bringing us the current state of the glacier with thickness reduced by tenths of meters, particularly at higher altitudes. Without the use of historical aerial acquisitions, such long-term analyses would have suffered from a lack of data referring to less recent epochs that was suitable to be processed and made consistent with most recent technologies. This proved how the availability of such data is a remarkable heritage for glaciological studies.