Landslide Susceptibility Assessment Based on Different MaChine Learning Methods in Zhaoping County of Eastern Guangxi
Abstract
:1. Introduction
2. Study Areas and Materials
2.1. Study Areas
2.2. Data Sources and Landslide Inventory Data
2.3. Classification of Evaluation Factors
3. Methods
3.1. Support Vector Machine (SVM) Model
3.2. Particle Swarm Optimization Support Vector Machine (PSO-SVM)
3.3. Random Forest (RF) Model
3.4. Weighted PSO-RF
4. Results and Discussion
4.1. Evaluation Results
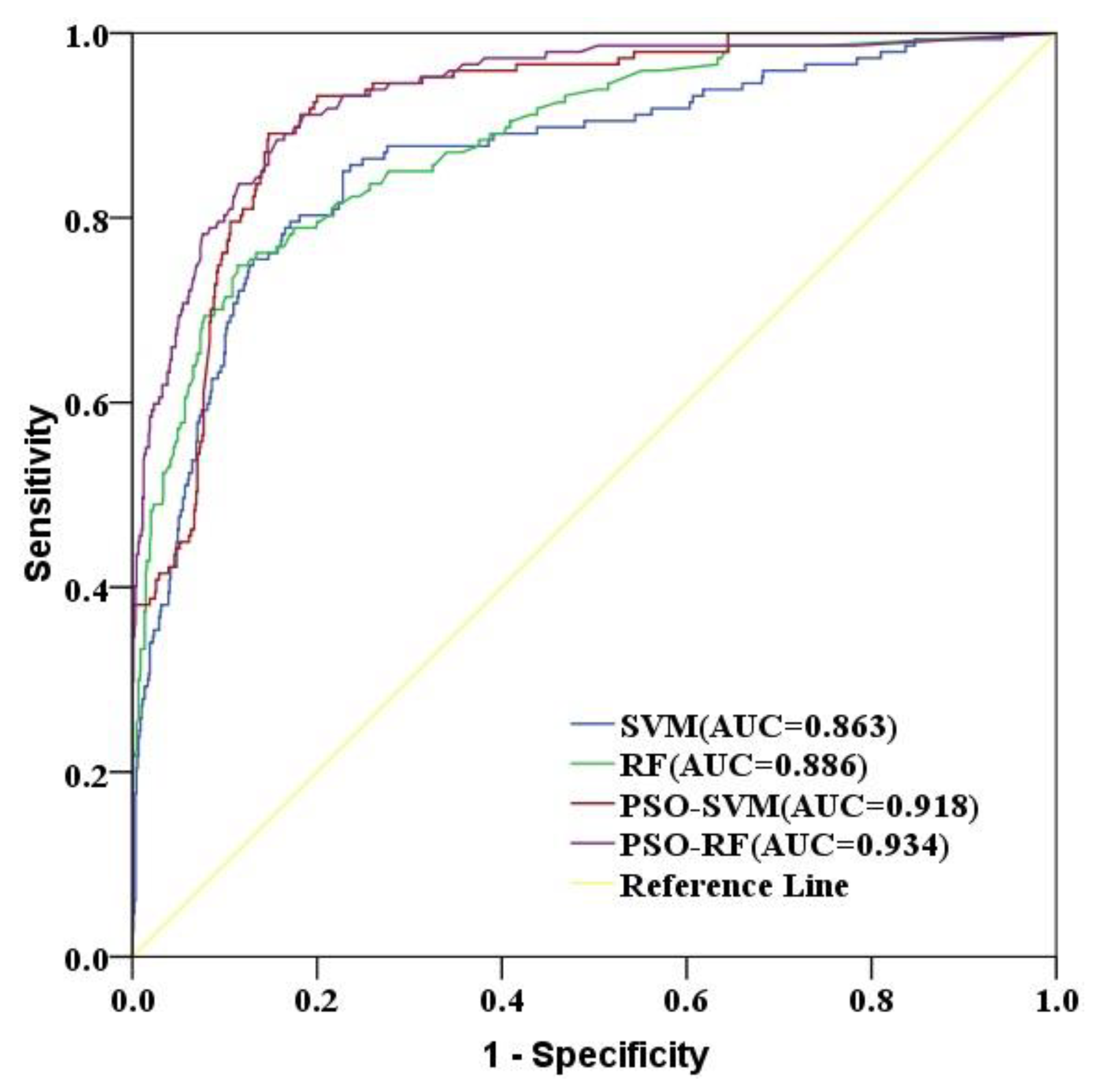
4.2. Evaluation Accuracy and Validation Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pourghasemi, H.R.; Mohammady, M.; Pradhan, B. Landslide susceptibility mapping using index of entropy and conditional probability models in GIS: Safarood Basin, Iran. Catena 2012, 97, 71–84. [Google Scholar] [CrossRef]
- Huang, Z.; He, W. The Field Investigation Report of the Geological Hazards Project by Guangxi Geological Survey Bureau; Guangxi Geological Survey Bureau Office: Nanning, China, 2018. [Google Scholar]
- Chen, Q.; Liu, G.; Ma, X.; Zhang, J.; Zhang, X. Conditional multiple-point geostatistical simulation for unevenly distributed sample data. Stoch. Environ. Res. Risk Assess. 2019, 33, 973–987. [Google Scholar] [CrossRef]
- Zhang, L.; Shi, S.; Liu, Q. spatial-temporal distribution characteristics and genetic analysis of geological disasters in Guangxi. Guangxi Water Resour. Hydropower Eng. 2016, 6, 64–67. [Google Scholar]
- Sezer, E.A.; Nefeslioglu, H.A.; Osna, T. An expert-based landslide susceptibility mapping (LSM) module developed for Netcad Architect Software. Comput. Geosci. 2017, 98, 26–37. [Google Scholar] [CrossRef]
- Myronidis, D.; Papageorgiou, C.; Theophanous, S. Landslide susceptibility mapping based on landslide history and analytic hierarchy process (AHP). Nat. Hazards 2016, 81, 245–263. [Google Scholar] [CrossRef]
- Sharma, S.; Mahajan, A.K. A comparative assessment of information value, frequency ratio and analytical hierarchy process models for landslide susceptibility mapping of a Himalayan watershed, India. Bull. Eng. Geol. Environ. 2019, 78, 2431–2448. [Google Scholar] [CrossRef]
- Ciurleo, M.; Mandaglio, M.C.; Moraci, N. Landslide susceptibility assessment by TRIGRS in a frequently affected shallow instability area. Landslides 2019, 16, 175–188. [Google Scholar] [CrossRef]
- Regmi, A.D.; Devkota, K.C.; Yoshida, K.; Pradhan, B.; Pourghasemi, H.R.; Kumamoto, T.; Akgun, A. Application of frequency ratio, statistical index, and weights-of-evidence models and their comparison in landslide susceptibility mapping in Central Nepal Himalaya. Arab. J. Geosci. 2014, 7, 725–742. [Google Scholar] [CrossRef]
- Sun, L.; Ren, N.; Li, Y. Risk Assessment on karst collapse of the highway subgrade based on weights of evidence method. Chin. J. Geol. Hazards Control. 2019, 30, 94–100. [Google Scholar]
- Aditian, A.; Kubota, T.; Shinohara, Y. Comparison of GIS-based landslide susceptibility models using frequency ratio, logistic regression, and artificial neural network in a tertiary region of Ambon, Indonesia. Geomorphology 2018, 318, 101–111. [Google Scholar] [CrossRef]
- Li, L.; Lan, H. Integration of spatial probability and size in slope-unit-based landslide susceptibility assessment: A case study. Int. J. Environ. Res. Public Health 2020, 17, 8055. [Google Scholar] [CrossRef]
- Li, Y.; Mei, H.; Ren, X.; Hu, X.; Li, M. Geological disaster susceptibility evaluation based on certainty factor and support vector machine. J. Geo-Inf. Sci. 2018, 20, 1699–1709. [Google Scholar]
- Yang, G.; Xu, P.; Cao, C.; Zhang, W.; Lan, Z.; Chen, J.; Dong, X. Assessment of regional landslide susceptibility based on combined model of certainty factor method. J. Eng. Geol. 2019, 27, 1153–1163. [Google Scholar]
- Kavzoglu, T.; Sahin, E.K.; Colkesen, I. Landslide susceptibility mapping using GIS-based multi-criteria decision analysis, support vector machines, and logistic regression. Landslides 2014, 11, 425–439. [Google Scholar] [CrossRef]
- Jean, N.; Luo, G.; Lamek, N.; Huang, X.; Cai, P. Landslide susceptibility assessment using spatial multi-criteria evaluation model in Rwanda. Int. J. Environ. Res. Public Health 2018, 15, 243. [Google Scholar]
- Huang, R.; Xu, X.; Tang, C.; Xiang, X. Geological Environmental Assessment and Geological Hazard Management; Science Press: Beijing, China, 2008. [Google Scholar]
- Marjanović, M.; Kovaǔević, M.; Bajat, B.; Voženílek, V. Landslide susceptibility assessment using SVM machine learning algorithm. Eng. Geol. 2011, 123, 225–234. [Google Scholar] [CrossRef]
- Bui, D.T.; Pradhan, B.; Lofman, O.; Revhaug, I. Landslide susceptibility assessment in vietnam using support vector machines, decision tree, and naïve bayes models. Math. Probl. Eng. 2012, 2012, 974638. [Google Scholar]
- Bui, D.T.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar]
- Zhou, C.; Yin, K.; Cao, Y.; Ahmed, B.; Li, Y.; Catani, F.; Pourghasemi, H.R. Landslide susceptibility modeling applying machine learning methods: A case study from Longju in the Three Gorges Reservoir area, China. Comput. Geosci. 2018, 112, 23–37. [Google Scholar] [CrossRef] [Green Version]
- Aktas, H.; San, B.T. Landslide susceptibility mapping using an automatic sampling algorithm based on two level random sampling. Comput. Geosci. 2019, 133, 104329. [Google Scholar] [CrossRef]
- Wang, N.; Guo, Y.; Liu, T.; Zhu, Q. Assessment of landslide susceptibility based on SVM-LR model: A case study of Lintong District. Sci. Technol. Eng. 2019, 19, 62–69. [Google Scholar]
- Nguyen, H.; Bui, X.N.; Choi, Y.; Lee, C.W.; Armaghani, D.J. A novel combination of whale optimization algorithm and support vector machine with different kernel functions for prediction of blasting-induced fly-rock in quarry mines. Nat. Resour. Res. 2021, 30, 191–207. [Google Scholar] [CrossRef]
- Li, X.; Cheng, X.; Chen, W. Identification of forested landslides using lidar data, object-based image analysis, and machine learning algorithms. Remote Sens. 2015, 7, 9705–9726. [Google Scholar] [CrossRef] [Green Version]
- Song, Y.; Gong, J.; Gao, S.; Wang, D.; Cui, T.; Li, Y.; Wei, B. Susceptibility assessment of earthquake-induced landslides using bayesian network: A case study in Beichuan, China. Comput. Geosci. 2012, 42, 189–199. [Google Scholar] [CrossRef]
- Pham, B.T.; Pradhan, B.; Tien Bui, D.; Prakash, I.; Dholakia, M.B. A comparative study of different machine learning methods for landslide susceptibility assessment: A case study of Uttarakhand area (India). Environ. Model. Softw. 2016, 84, 240–250. [Google Scholar] [CrossRef]
- Xu, K.; Guo, Q.; Li, Z.; Xiao, J.; Qin, Y.; Chen, D.; Kong, C. Landslide susceptibility evaluation based on BPNN and GIS: A case of Guojiaba in the three gorges reservoir area. Int. J. Geogr. Inf. Sci. 2015, 29, 1111–1124. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, Z.; Wang, M.; Peng, L.; Hong, H. Comparative study of landslide susceptibility mapping with different recurrent neural networks. Comput. Geosci. 2020, 138, 104445. [Google Scholar] [CrossRef]
- Pradhan, B. A comparative study on the predictive ability of the decision tree, support vector machine and neuro-fuzzy models in landslide susceptibility mapping using GIS. Comput. Geosci. 2013, 51, 350–365. [Google Scholar] [CrossRef]
- Ada, M.; San, B.T. Comparison of machine-learning techniques for landslide susceptibility mapping using two-level random sampling (2LRS) in Alakir catchment area, Antalya, Turkey. Nat. Hazards 2018, 90, 237–263. [Google Scholar] [CrossRef]
- Wang, Z.; Brenning, A. Active-learning approaches for landslide mapping using support vector machines. Remote Sens. 2021, 13, 2588. [Google Scholar] [CrossRef]
- Sevgen, E.; Kocaman, S.; Nefeslioglu, H.A.; Gokceoglu, C. A novel performance assessment approach using photogrammetric techniques for landslide susceptibility mapping with logistic regression, ANN and random forest. Sensors 2019, 19, 3940. [Google Scholar] [CrossRef] [Green Version]
- Trigila, A.; Iadanza, C.; Esposito, C.; Scarascia-Mugnozza, G. Comparison of logistic regression and random forests techniques for shallow landslide susceptibility assessment in giampilieri (NE Sicily, Italy). Geomorphology 2015, 249, 119–136. [Google Scholar] [CrossRef]
- Youssef, A.M.; Pourghasemi, H.R.; Pourtaghi, Z.S.; Al-Katheeri, M.M. Landslide susceptibility mapping using random forest, boosted regression tree, classification and regression tree, and general linear models and comparison of their performance at Wadi Tayyah Basin, Asir Region, Saudi Arabia. Landslides 2016, 13, 839–856. [Google Scholar] [CrossRef]
- Hong, H.; Liu, J.; Tien Bui, D.; Pradhan, B.; Acharya, T.D.; Pham, B.T.; Zhu, A.; Chen, W.; Ahma, B.B. Landslide susceptibility mapping using J48 Decision Tree with Adaboost, Bagging and Rotation Forest ensembles in the Guangchang area (China). Catena 2018, 163, 399–413. [Google Scholar] [CrossRef]
- Khosravi, K.; Pham, B.T.; Chapi, K.; Shirzadi, A.; Shahabi, H.; Revhaug, I.; Prakash, I.; Tien Bui, D. A comparative assessment of decision trees algorithms for flash flood susceptibility modeling at Haraz watershed, northern Iran. Sci. Total Environ. 2018, 627, 744–755. [Google Scholar] [CrossRef]
- Chen, W.; Li, X.; Wang, Y.; Chen, G.; Liu, S. Forested landslide detection using LiDAR data and the random forest algorithm: A case study of the Three Gorges, China. Remote Sens. Environ. 2014, 152, 291–301. [Google Scholar] [CrossRef]
- Chen, W.; Xie, X.; Wang, J.; Pradhan, B.; Hong, H.; Tien Bui, D.; Duan, Z.; Ma, J. A comparative study of logistic model tree, random forest, and classification and regression tree models for spatial prediction of landslide susceptibility. Catena 2017, 151, 147–160. [Google Scholar] [CrossRef] [Green Version]
- Deng, J.; Lei, C.; Cao, K.; Ma, L.; Wang, C.; Zhai, X. Random forest method for predicting coal spontaneous combustion in gob. J. China Coal Soc. 2018, 43, 2800–2808. [Google Scholar]
- Sun, D.; Wen, H.; Wang, D.; Xu, J. A random forest model of landslide susceptibility mapping based on hyper-parameter optimization using Bayes algorithm. Geomorphology 2020, 362, 107201. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, Y.; Peng, L.; Hong, H. Integration of convolutional neural network and conventional machine learning classifiers for landslide susceptibility mapping. Comput. Geosci. 2020, 139, 104470. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Tax, D.; Duin, E. Support vector domain description. Pattern Recogn. Lett. 1999, 20, 1191–1199. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.; Wu, X.; Niu, R.; Yang, K.; Zhao, L. The assessment of landslide susceptibility mapping using random forest and decision tree methods in the Three Gorges Reservoir Area, China. Environ. Earth Sci. 2017, 76, 405. [Google Scholar] [CrossRef]
- Frattini, P.; Crosta, G.; Carrara, A. Techniques for evaluating the performance of landslide susceptibility models. Eng. Geol. 2010, 111, 62–72. [Google Scholar] [CrossRef]
- Hanley, J.A.; Mc Neil, B.J. A method of comparing the areas under receiver operating characteristic curves derived from the same cases. Radiology 1983, 148, 839–843. [Google Scholar] [CrossRef] [Green Version]
- Fawcett, T. An Introduction to ROC analysis. Pattern Recogn. Lett. 2005, 27, 861–874. [Google Scholar] [CrossRef]
- Feng, F.; Wu, X.; Niu, R.; Xu, S.; Yu, X. Landslide susceptibility assessment based on PSO-BP neural network. Sci. Surv. Mapp. 2017, 42, 170–175. [Google Scholar]

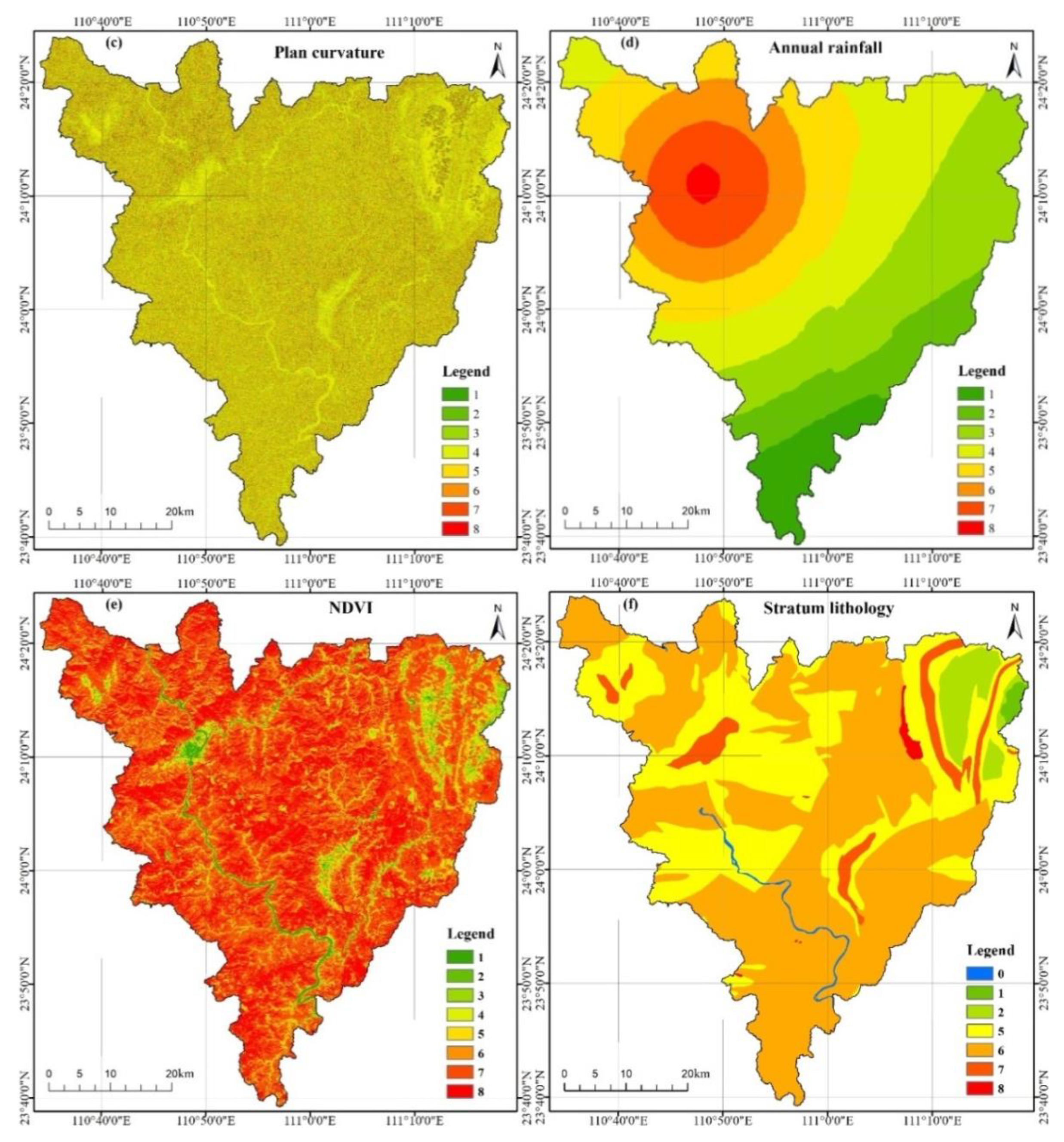
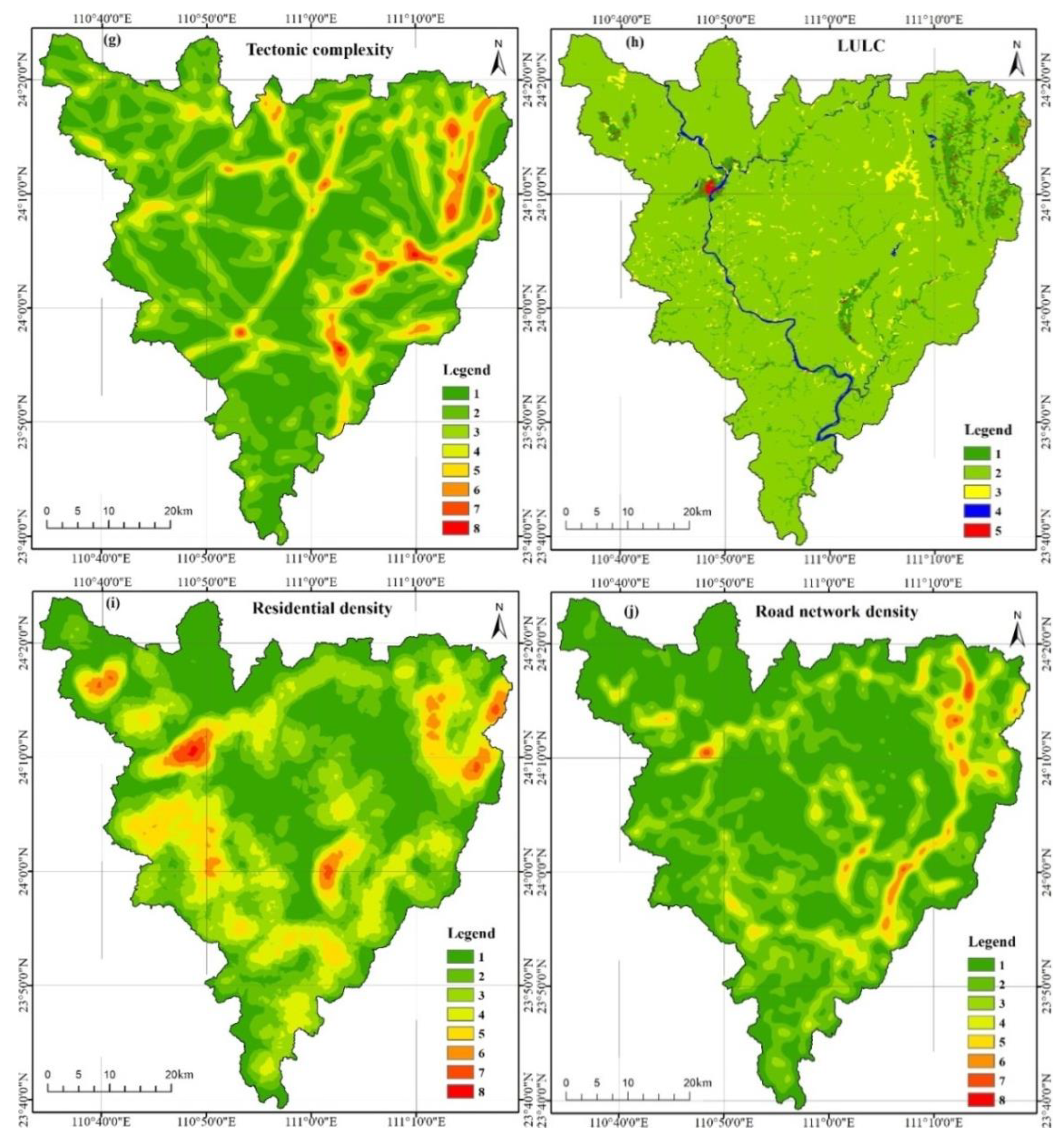

| No. | Evaluation Factor | Classification |
|---|---|---|
| (a) | Slope (°) | 1-[0,7); 2-[7,13); 3-[13,19); 4-[19,25); 5-[25,34); 6-[34,50); 7-[50,70); 8-[70,76) |
| (b) | Aspect (°) | 1-[337.5,22.5); 2-[22.5,67.5); 3-[67.5,112.5); 4-[112.5,157.5); 5-[157.5,202.5); 6-[205.2,247.5); 7-[247.5,292.5); 8-[292.5,337.5) |
| (c) | Plan curvature | 1-[-25,-5); 2-[-5,-2.5); 3-[-2.5,-1); 4-[-1,0); 5-[0,1); 6-[1,2.5); 7-[2.5,5); 8-[5,28.9) |
| (d) | Annual rainfall (mm) | 1-[0,1980); 2-[1980,2100); 3-[2100,2220); 4-[2220,2340); 5-[2340,2460); 6-[2460,2580); 7-[2580,2700); 8-[2700,2820) |
| (e) | Normalized differential vegetation index (NDVI) | 1-[0,0.01); 2-[0.01,0.09); 3-[0.09,0.17); 4-[0.17,0.25); 5-[0.25,0.33); 6-[0.33,0.4); 7-[0.4,0.5); 8-[0.5,0.71) |
| (f) | Stratum lithology | 0-River; 1-Quaternary; 2-carbonate rock; 5-clasolite intercalated with siliceous rocks; 6-clastic rock; 7-sandstone and shale; 8-granite or basal rocks |
| (g) | Tectonic complexity | 1-[0,1.4); 2-[1.4,2.7); 3-[2.7,3.8); 4-[3.8,4.9); 5-[4.9,6); 6-[6,7.3); 7-[7.3,8.9); 8-[8.9,9.4) |
| (h) | LULC | 1-cultivated land; 2-woodland; 3-grassland; 4-river and lake; 5-construction land |
| (i) | Residential density | 1-[0,1.2); 2-[1.2,2.7); 3-[2.7,4.5); 4-[4.5,6.9); 5-[6.9,10.1); 6-[10.1,14.2); 7-[14.2,19.7); 8-[19.7,25) |
| (j) | Road network density (km/km2) | 1-[0,3.2); 2-[3.2,4.7); 3-[4.7,6.1); 4-[6.1,7.8); 5-[7.8,9.7); 6-[9.7,11.7); 7-[11.7,13.9); 8-[13.9,14) |
| (1) Initialization: |
| The initial parameters of the PSO-SVM model are set, including species size, iteration times, learning factor, inertia weight, initial particle, and particle initial velocity. The particle vector represents a SVM model corresponding to different C and σ. |
| (2) Optimization: |
| In the process of particle optimization, each solution of the optimization problem is called a particle in the search space. The particle adaptation value (fi) is calculated according to the fitness function. Adaptive function is the measure basis of the selection individual, and the individual is evaluated by the fitness function. |
| (3) Replacement: |
| Based on the objective function, the adaptive value of each particle (fi), the population individual optimal solution fi(pbest), and the population global optimal solution fi(pgbest) were calculated and compared. If fi < fi(pbest), then the optimization solution of the previous round is replaced with the new adaptation value (fi), and the particles of the previous round is replaced with the new particles, and then the fi(pbest) of each particle is compared with the fi(pgbest) of all particles. If fi(pbest) < fi(pgbest), the optimal solution of each particle is used to replace the optimal solution of all the original particles, and the current state of the particles is saved at the same time. |
| (4) Determination: |
| If the fi of the individual in the population meets the requirements, or if the evolutionary algebra is terminated, then the calculation is ended, and the particle individual corresponds to the optimal C and σ combination, otherwise go to step (2) to continue the iteration. |
| (5) Set Up the PSO-SVM Model: |
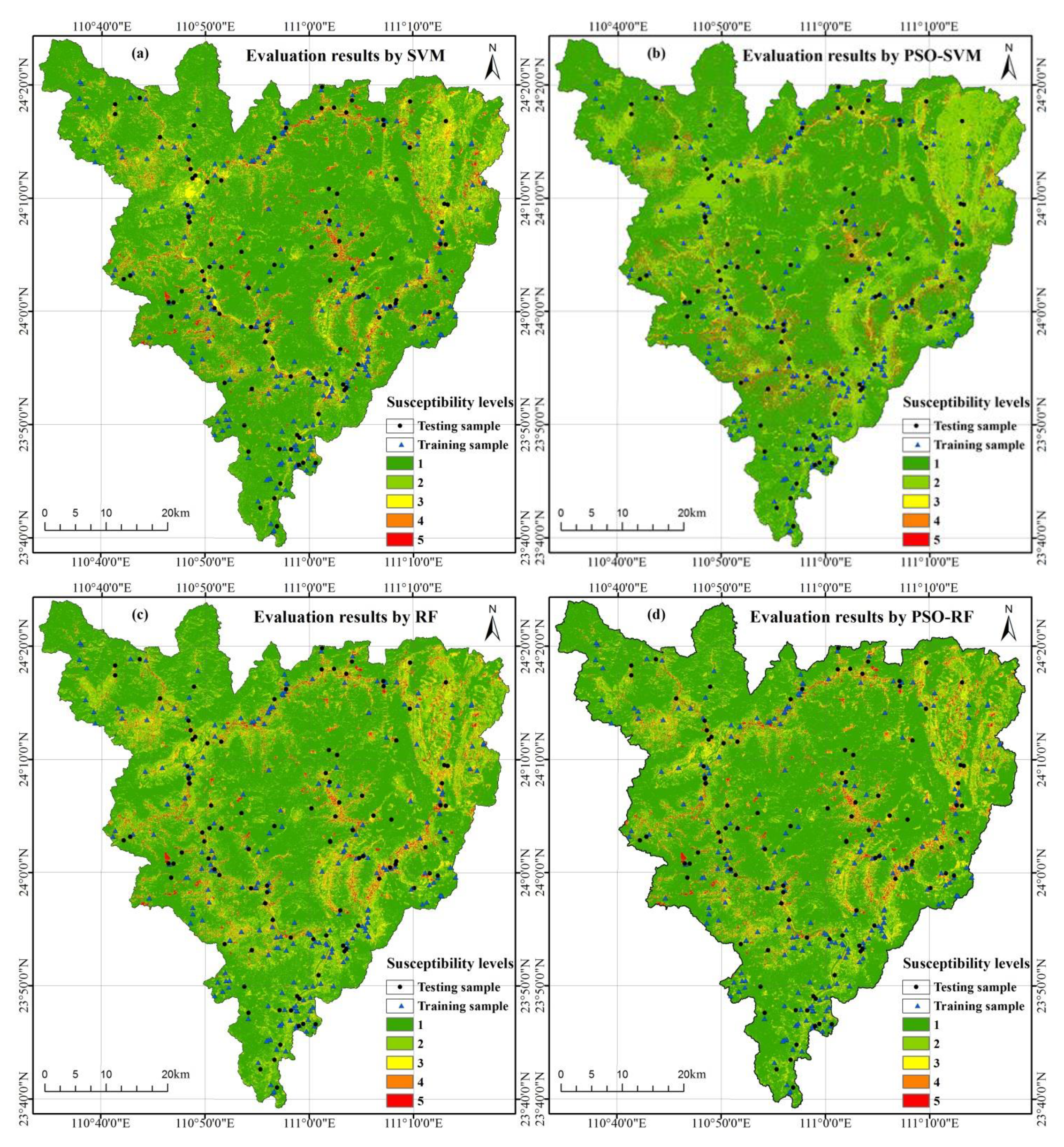
| The global optimal PSO-SVM model is obtained by using the optimal parameters of the SVM with the optimal C and σ combination to train the training samples. The susceptibility of landslides is quantitatively evaluated and divided into five levels: extremely high, high, medium, low, and extremely low areas Figure 4b. |
| (1) Initialization: |
| Suppose D is an original training dataset of landslide susceptibility assessment factors, which is composed of M prediction attributes (M = 10) and a classification attribute Y (Y = 5). There are n (n = 3,581,859) different examples in D. |
| (2) Get Multiple Training Datasets: |
| The K new training subsets of {D1, D2, …, DK} were obtained by K times random sampling with replay from the original training dataset D by using the Bagging algorithm. At the same time, each of the K training subsets contains n instances, in which there is repetition. |
| (3) Training to Generate Decision Tree: |
| For each training subset Di (1 ≤ I ≤ K), the decision tree without pruning is generated by the following procedure: Firstly, let the number of predictive attributes in the training sample be M, F (F < M) attributes are randomly chosen from M to compose a random characteristic subspace Xi, and those as the split attribute datasets of the present node of the decision tree. In the process of generating the RF model, the value of F remains unaltered; Secondly, the node was split according to the optimal split attribute of each node selecting from the random feature subspace Xi by the decision tree generation algorithm; Thirdly, every tree grows completely and has no pruning process. The corresponding decision tree hi(Di) is generated by each training dataset Di; Fourthly, the RF model of {h1(D1), h2(D2), …, hi(Di)} was generated by combining all the generated decision trees. And the corresponding classification result of {C1(X), C2(X), …, CK(X)} is obtained by using testing of each decision tree hi(Di) with test dataset sample X; Finally, according to the classification results of K decision trees, the final classification results corresponding to the test dataset sample X was determined by classification results with a large number of decision trees by voting method. |
| (4) Dividing Levels: |
| According to the above steps, the landslide susceptibility of Zhaoping is divided into 5 levels Figure 4c. |
| (1) Initialization: |
| The initial parameters of the PSO-RF model are set, including the number of decision trees R, pruning threshold ε, number of predicted test samples X, and initial value of random attributes m. |
| (2) Sampling: |
| Using the Bootstrap algorithm, R training datasets are randomly produced, and X pre-test samples are selected in each training dataset. |
| (3) Generating Decision Tree: |
| A total of R decision trees are generated by using the rest of the samples of each training dataset. In the process of generating decision trees, m attributes are selected from all attributes as the decision attributes of the present node before each attribute is selected. |
| (4) Determination: |
| When the number of samples included in the node is less than the threshold ε, the node is taken as the leaf node, and the mode of the target attributes is returned as the classification result of the decision tree. |
| (5) Setting Up the PSO-RFModel: |
| When all decision trees are produced, each decision tree is pre-tested and its weights are calculated by using the equation (7): |
| where is the classified correct number of samples of r decision trees, and X is the number of pre-tested samples. |
| (6) Calculation of the Classification Results: |
| The classification results of the model are calculated by Equation (8): |
| (7) Optimization: |
| Taking the classification results as the fitness values, the PSO algorithm is applied to optimize the parameters of Equation (6) iteratively and determine the parameters of the final RF model. |
| (8) Running |
| Finally, the optimized parameters are input into the model, and the output results of the model are obtained. According to the results, the susceptibility of landslides is divided into five levels Figure 4d. |
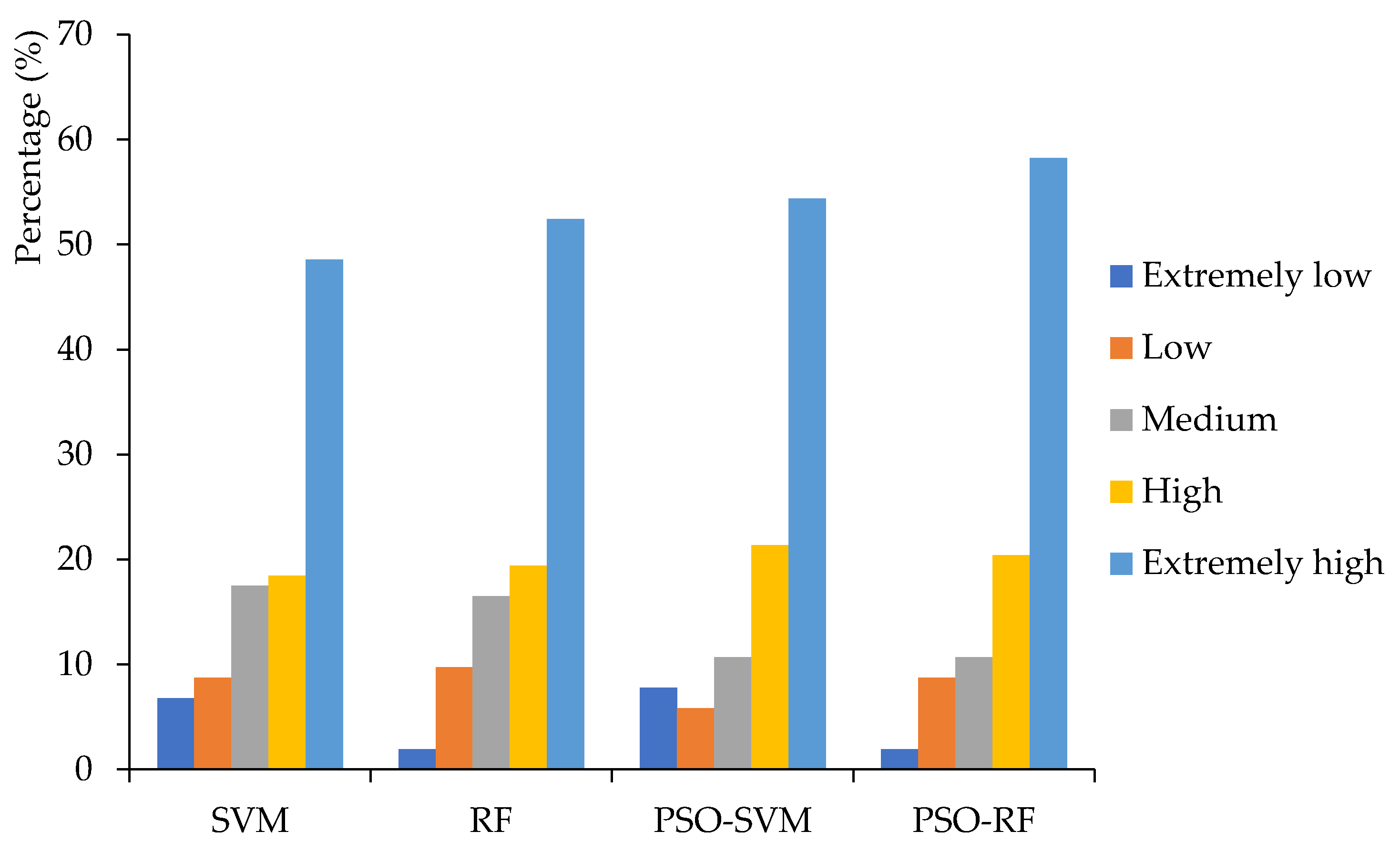
| Model | The Proportion of Different Susceptibility Levels (%) | ||||
|---|---|---|---|---|---|
| Extremely High | High | Medium | Low | Extremely Low | |
| SVM | 44.64 | 20.87 | 16.52 | 10.43 | 7.54 |
| RF | 50.43 | 19.13 | 18.26 | 9.57 | 2.61 |
| PSO-SVM | 53.33 | 21.16 | 7.83 | 6.38 | 11.30 |
| PSO-RF | 54.78 | 21.74 | 15.07 | 4.35 | 4.06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, C.; Tian, Y.; Ma, X.; Weng, Z.; Zhang, Z.; Xu, K. Landslide Susceptibility Assessment Based on Different MaChine Learning Methods in Zhaoping County of Eastern Guangxi. Remote Sens. 2021, 13, 3573. https://doi.org/10.3390/rs13183573
Kong C, Tian Y, Ma X, Weng Z, Zhang Z, Xu K. Landslide Susceptibility Assessment Based on Different MaChine Learning Methods in Zhaoping County of Eastern Guangxi. Remote Sensing. 2021; 13(18):3573. https://doi.org/10.3390/rs13183573
Chicago/Turabian StyleKong, Chunfang, Yiping Tian, Xiaogang Ma, Zhengping Weng, Zhiting Zhang, and Kai Xu. 2021. "Landslide Susceptibility Assessment Based on Different MaChine Learning Methods in Zhaoping County of Eastern Guangxi" Remote Sensing 13, no. 18: 3573. https://doi.org/10.3390/rs13183573
APA StyleKong, C., Tian, Y., Ma, X., Weng, Z., Zhang, Z., & Xu, K. (2021). Landslide Susceptibility Assessment Based on Different MaChine Learning Methods in Zhaoping County of Eastern Guangxi. Remote Sensing, 13(18), 3573. https://doi.org/10.3390/rs13183573







