Horizon Picking from SBP Images Using Physicals-Combined Deep Learning
Abstract
:1. Introduction
2. Materials and Methods
- Data preprocessing: convert SEG-Y data to SBP images;
- DL prediction: picking horizons (a crude result) from SBP images using the DL method;
- Multiple filtering: eliminate multiples from the picked horizons to obtain final horizons (a refined result). These three steps are elaborated below.
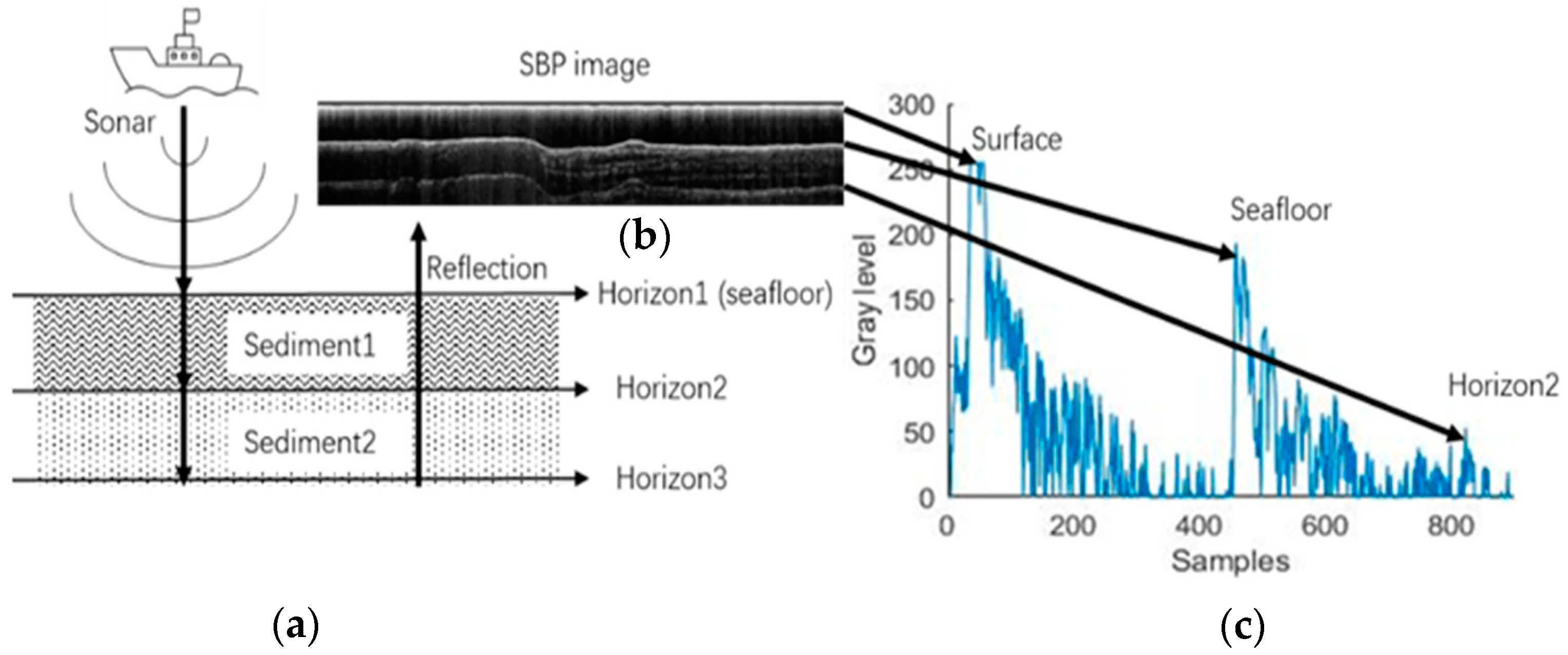
2.1. SBP Data Preprocessing
2.2. DL-Based Identification
- 4.
- Generate training dataset and validation dataset in a 3:1 ratio;
- 5.
- Design a neural network and then use the training dataset to train the network;
- 6.
- Select a well-trained network according to the training loss, validation loss, and accuracy;
- 7.
- Once the network is trained, it will output horizons for any observed SBP images.
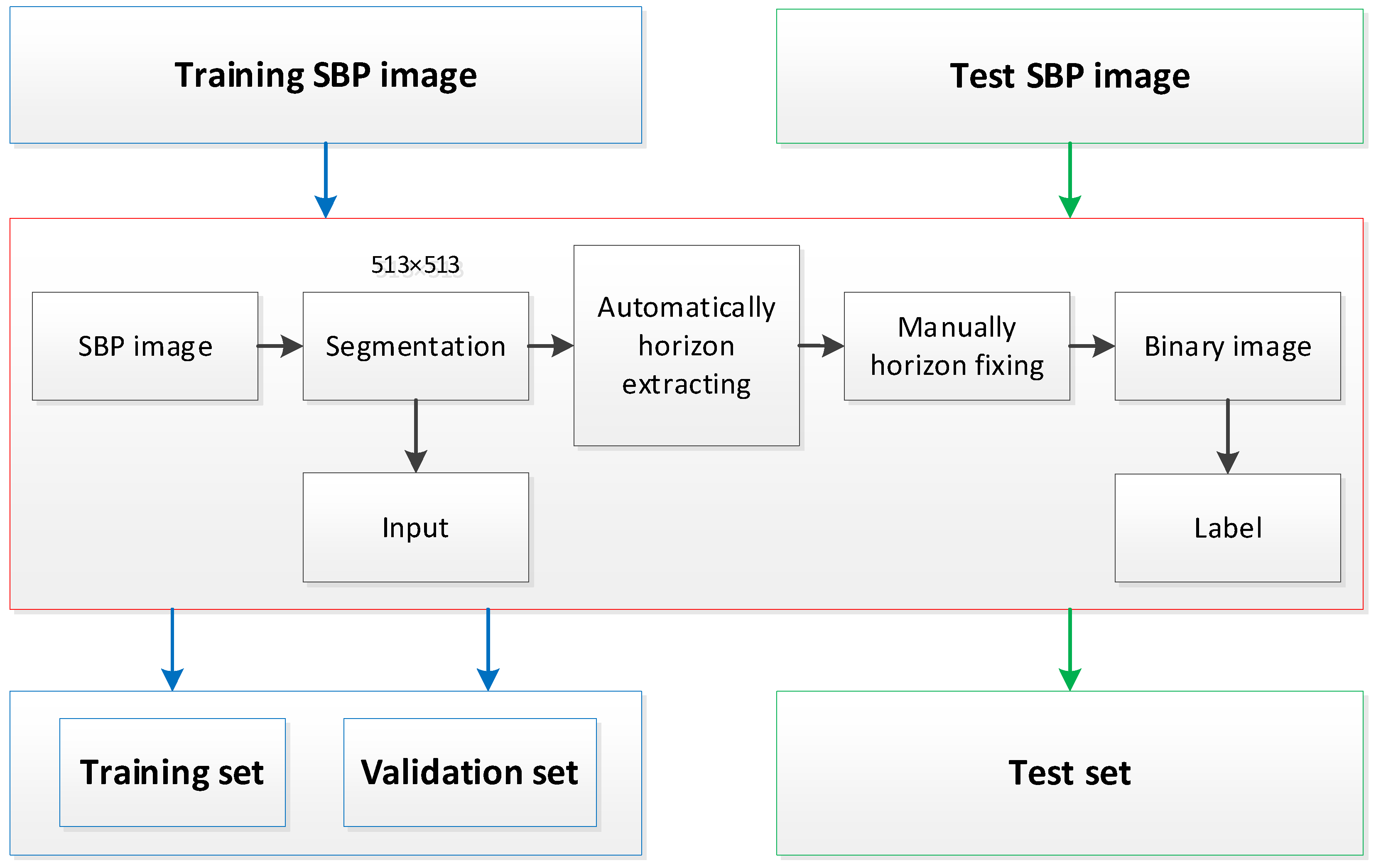
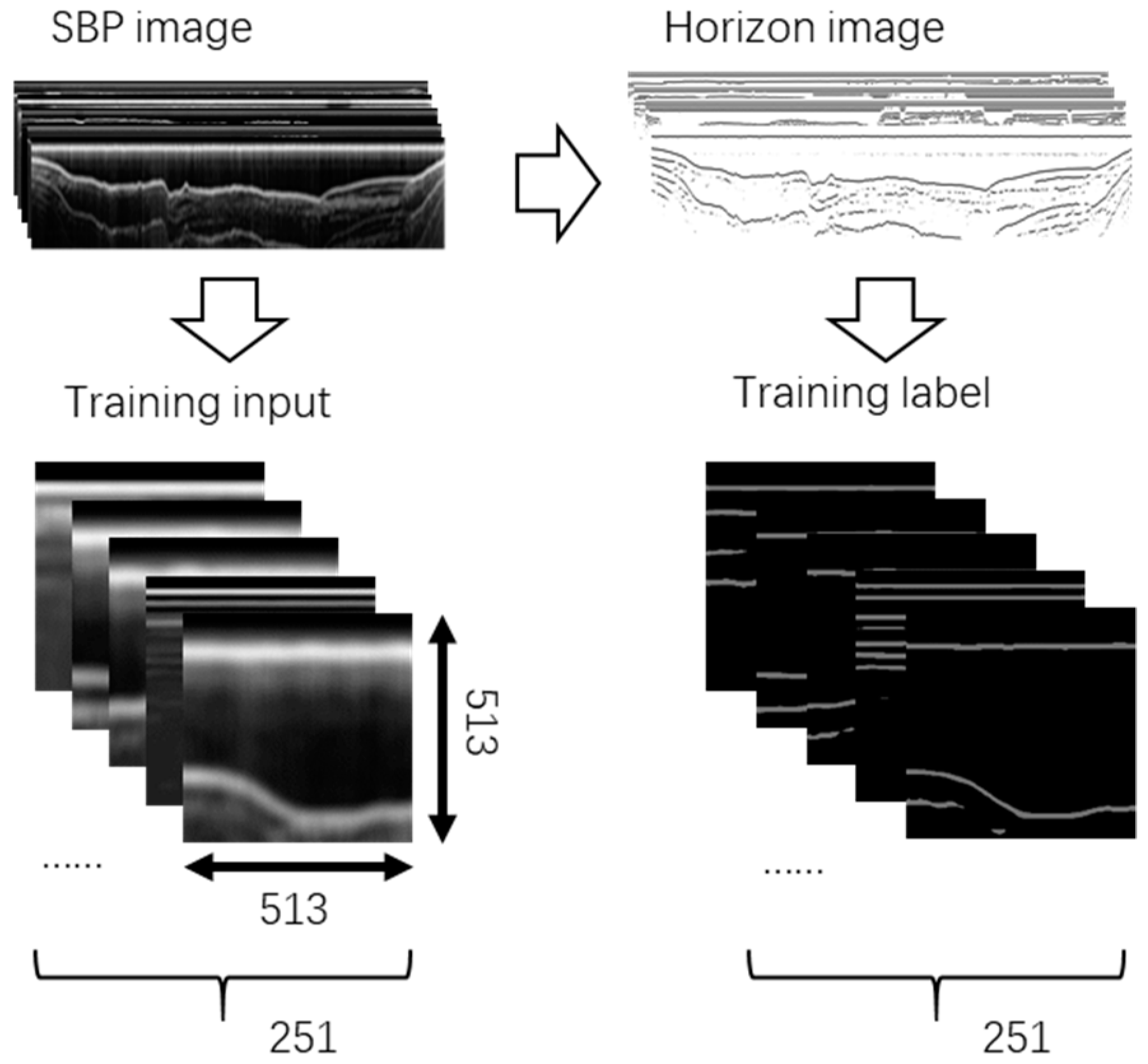
2.2.1. Training Dataset Generation
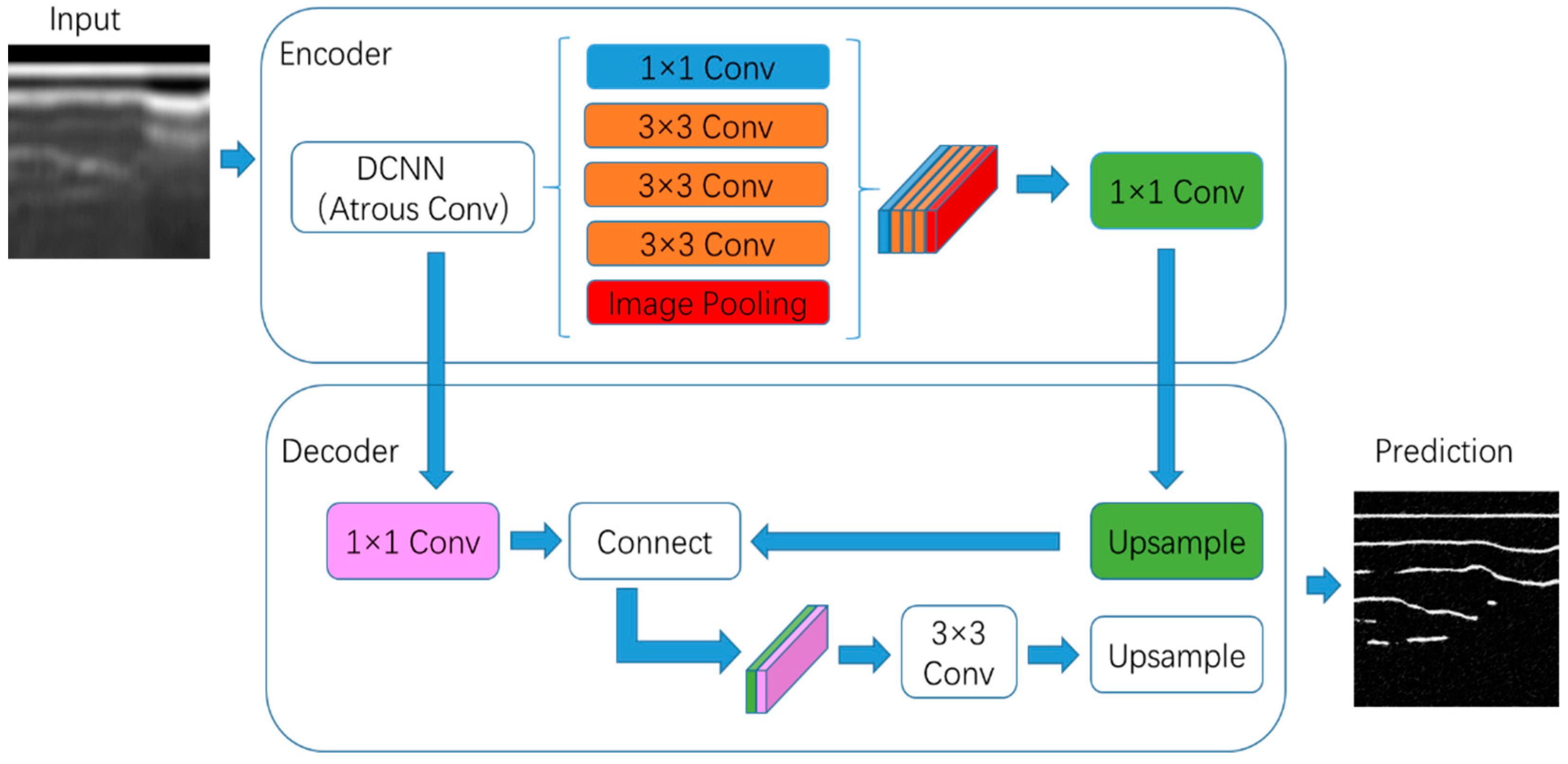
2.2.2. Network Architecture and Training
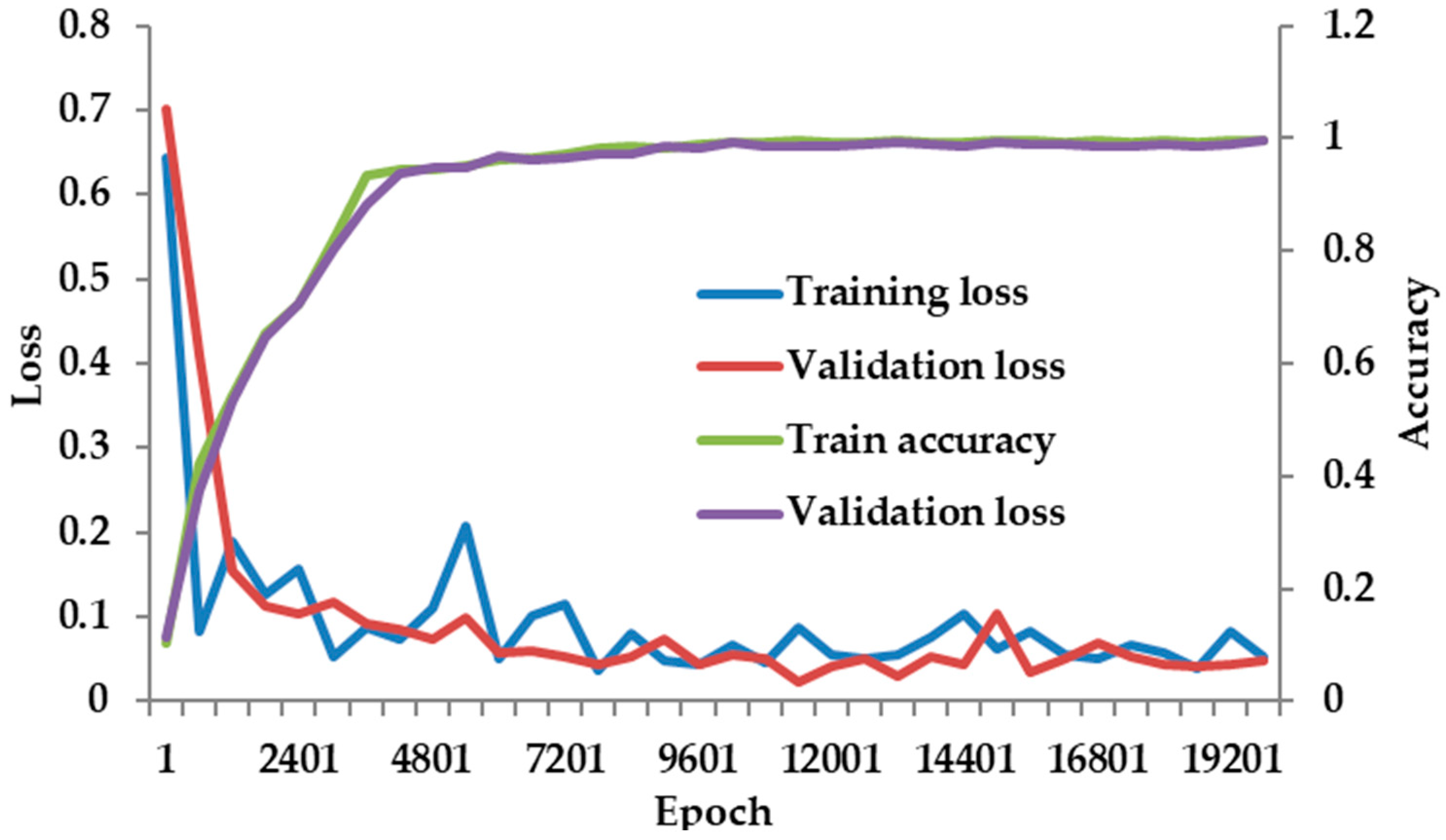
2.2.3. Evaluation
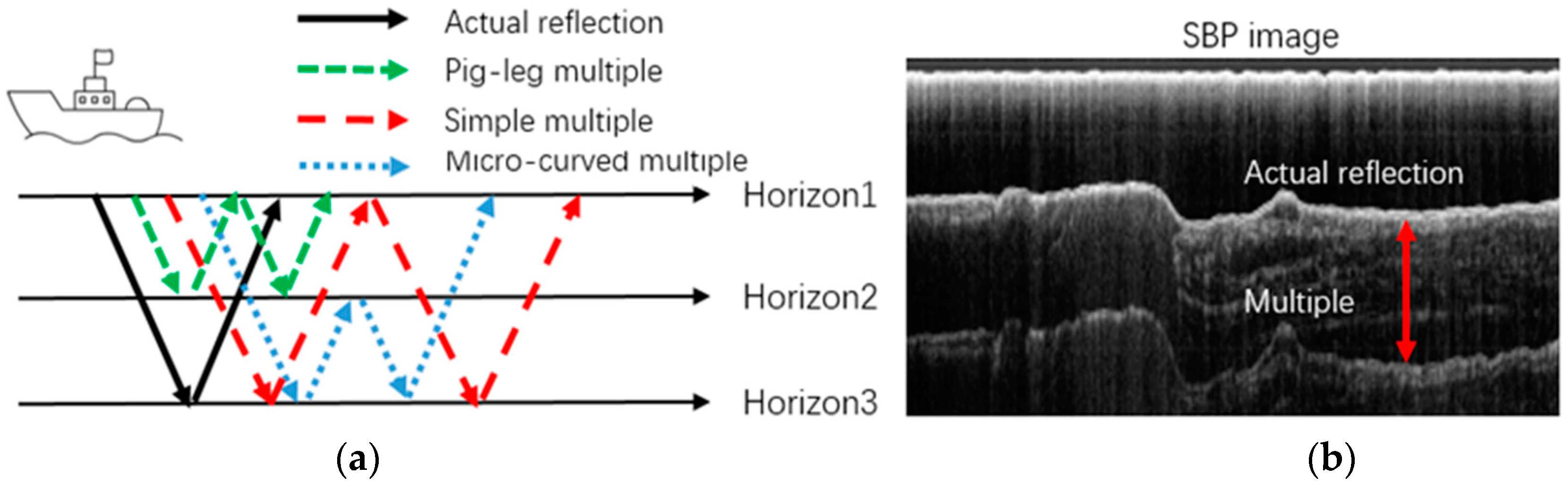
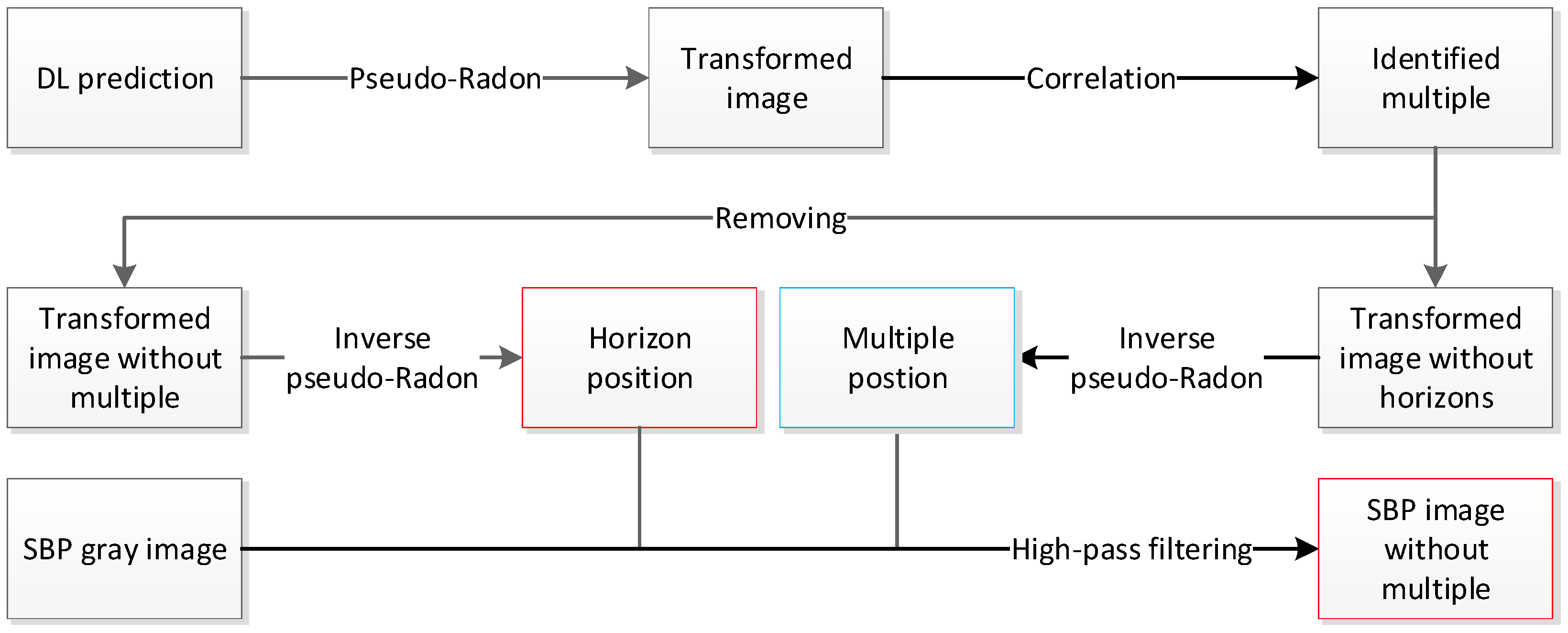
2.3. Multiples Suppression
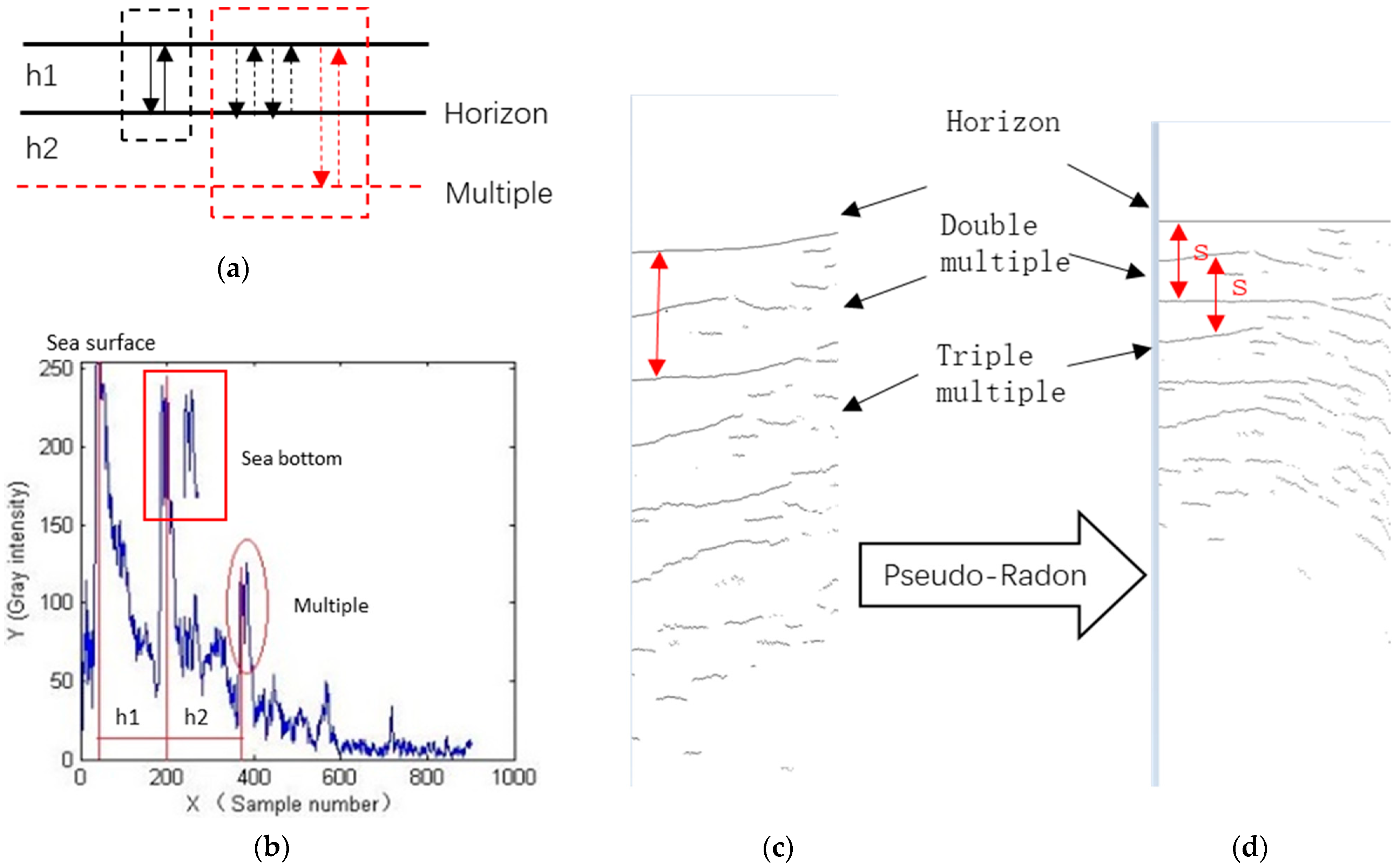
2.3.1. Pseudo-Radon Transform
- 8.
- Locate the sea surface and bottom. Because the sea surface and sea bottom are strong reflection interfaces and present two obvious continuous lines in the prediction result of the DL method, it is easy to obtain their accurate position.
- 9.
- Transform the prediction result by the pseudo-Radon transform. We design the pseudo-Radon transform rule as in Equation (5).
2.3.2. Correlation Analysis
2.3.3. Horizon Refinement
3. Results
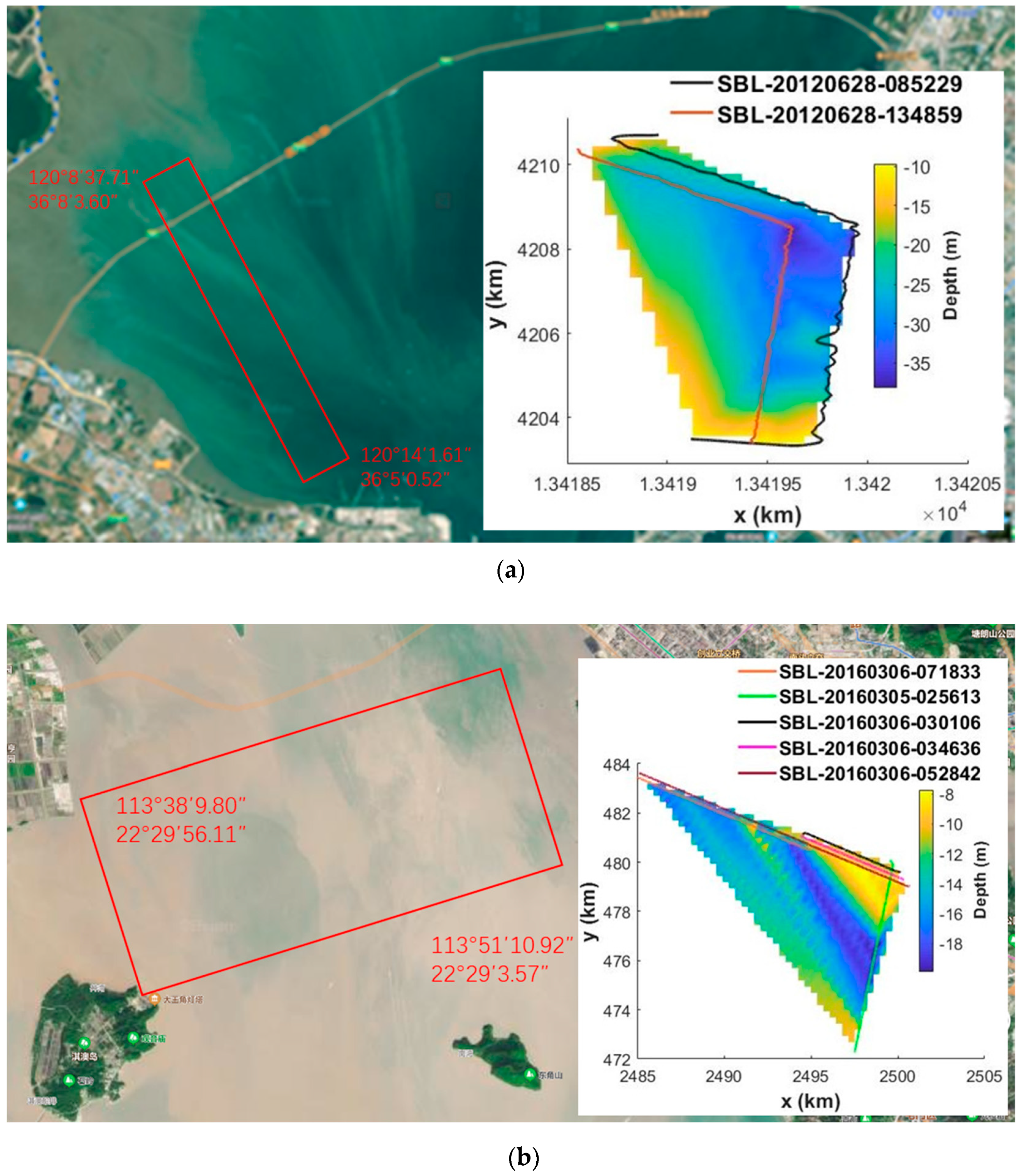
3.1. Data Collection
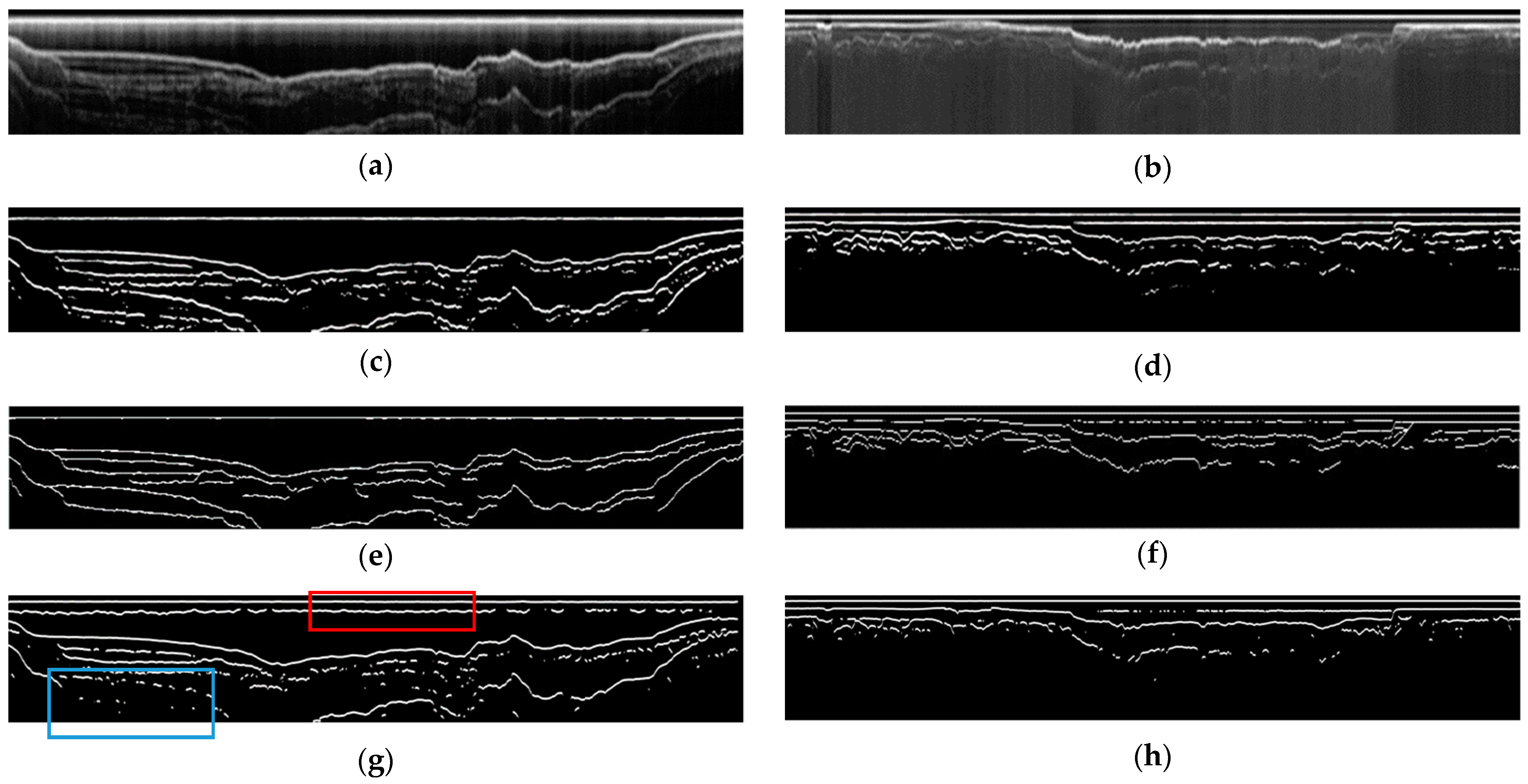
3.2. DL-Based Identification for Horizons and Multiples
3.2.1. Training Dataset
3.2.2. The Neural Network Training and the Prediction by the DL Method
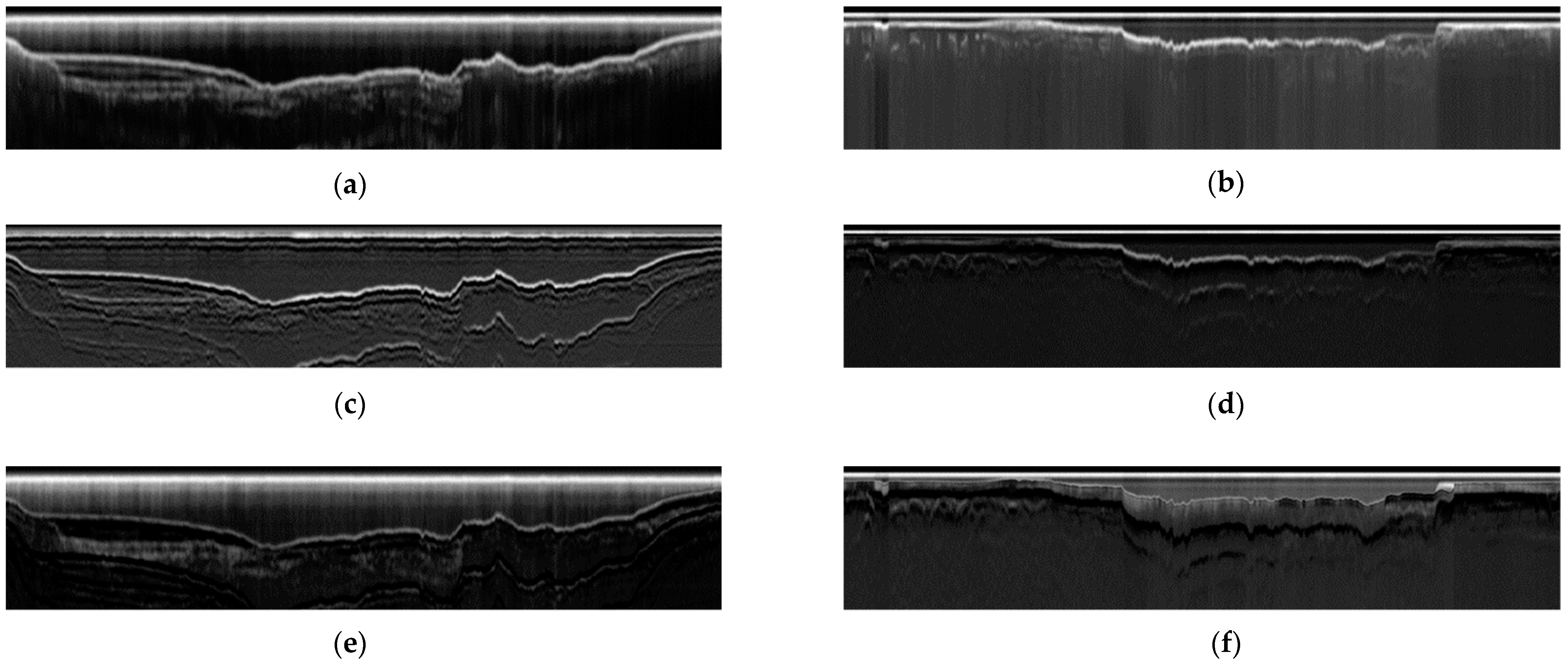
3.3. Multiples Suppression
3.3.1. Zhujiang and Jiaozhou Surveys
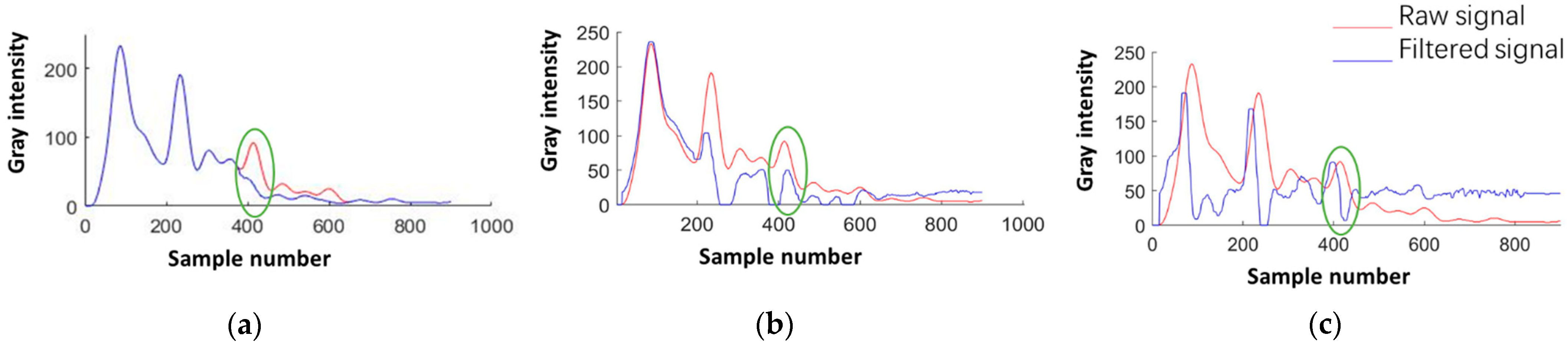
3.3.2. Methods Comparison
4. Discussion
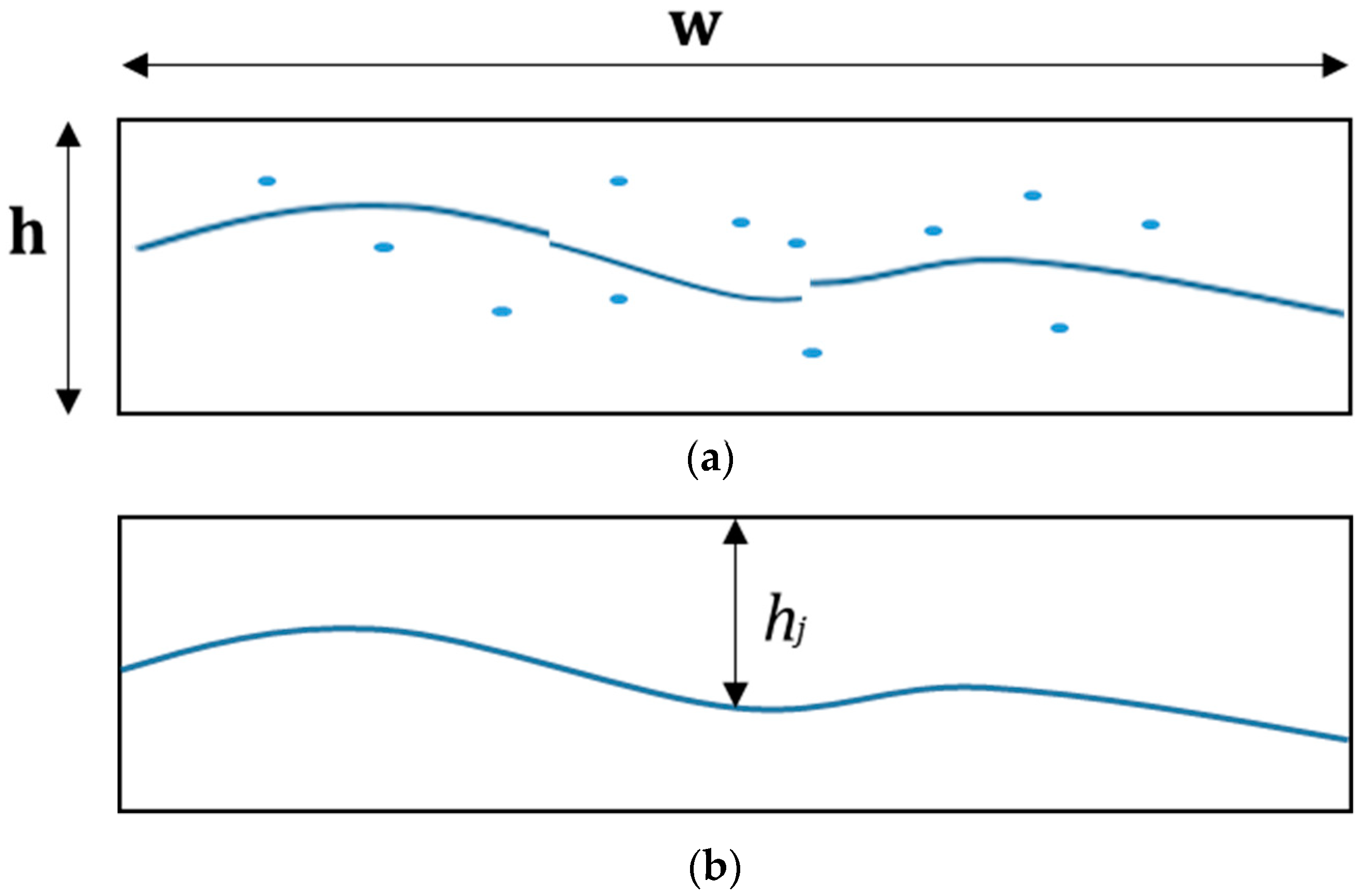
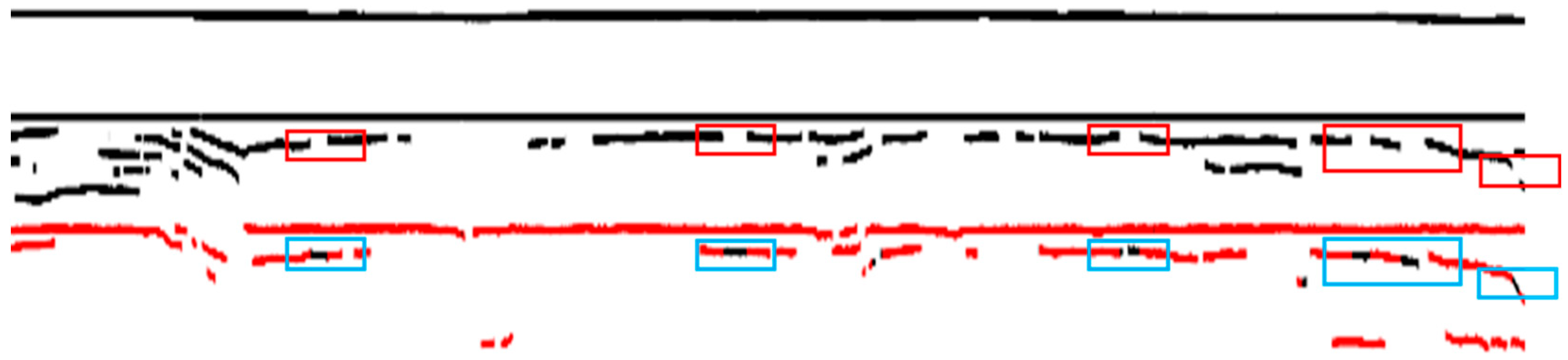
4.1. Obtaining Discontinuous Horizons Using Multiples
- 10.
- Recover the multiples discontinuity. Search the position of horizons connected with multiples and mark the horizons as multiples.
- 11.
- Recover the horizon discontinuity. Determine the position of horizon discontinuity according to the position of multiples discontinuity and recover the horizon discontinuity according to the shape of the recovered multiple.
4.2. The Specialty of the Proposed Method
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cukur, D.; Krastel, S.; Cagatay, M.N.; Damcı, E.; Meydan, A.F.; Kim, S.P. Evidence of extensive carbonate mounds and sublacustrine channels in shallow waters of Lake Van, eastern Turkey, based on high-resolution chirp subbottom profiler and multibeam echosounder data. Geo-Mar. Lett. 2015, 35, 329–340. [Google Scholar] [CrossRef]
- Li, S.J.; Chu, F.Y.; Fang, Y.X.; Wu, Z.Y. Associated interpretation of sub-bottom and single-channel seismic profiles from Shenhu Area in the north slope of South China Sea—characteristic of gas hydrate sediment. Adv. Mat. Res. 2011, 217, 1430–1437. [Google Scholar] [CrossRef]
- Kim, Y.J.; Koo, N.H.; Cheong, S.; Kim, J.K.; Chun, J.H.; Shin, S.R.; Riedel, M.; Lee, H.Y. A case study on pseudo 3-D Chirp sub-bottom profiler (SBP) survey for the detection of a fault trace in shallow sedimentary layers at gas hydrate site in the Ulleung Basin, East Sea. J. Appl. Phys. 2016, 133, 98–115. [Google Scholar] [CrossRef]
- Ding, W.F.; Luo, J.H.; LAI, X.H.; Gou, Z.K.; Fu, X.M. The research of interactive interpretation picking for sub-bottom profile. Mar. Sci. 2008, 32, 1–6. [Google Scholar]
- Tan, C.; Zhang, X.B.; Yang, P.X.; Sun, M. A Novel Sub-Bottom Profiler and Signal Processor. Sensors 2019, 19, 5052. [Google Scholar] [CrossRef] [Green Version]
- Plets, R.M.K.; Dix, J.K.; Adams, J.R.; Bull, J.M.; Henstock, T.J.; Gutowski, M.; Best, A.I. The use of a high-resolution 3D Chirp sub-bottom profiler for the reconstruction of the shallow water archaeological site of the Grace Dieu (1439), River Hamble, UK. J. Archaeol. Sci. 2009, 36, 408–418. [Google Scholar] [CrossRef]
- Nakamura, K.; Machida, S.; Okino, K.; Masaki, Y.; Iijima, K.; Suzuki, K.; Kato, Y. Acoustic characterization of pelagic sediments using sub-bottom profiler data: Implications for the distribution of REY-rich mud in the Minamitorishima EEZ, western Pacific. Geochem. J. 2016, 50, 605–619. [Google Scholar] [CrossRef] [Green Version]
- Cao, X.H.; Qu, Z.G.; Shen, B.J.; Zhang, H.Y. Illuminating centimeter-level resolution stratum via developed high-frequency sub-bottom profiler mounted on Deep-Sea Warrior deep-submergence vehicle. Mar. Georesour. Geotec. 2020. [Google Scholar] [CrossRef]
- Bondar, I. Seismic horizon detection using image processing algorithms. Geophys. Prospect. 1992, 40, 785–800. [Google Scholar] [CrossRef]
- Maroni, C.S.; Quinquis, A.; Vinson, S. Horizon Picking on Subbottom Profiles Using Multiresolution Analysis. Digit. Signal. Process. 2001, 11, 269–287. [Google Scholar] [CrossRef]
- Zhao, J.H.; Li, S.B.; Zhang, H.M.; Feng, J. Comprehensive Sediment Horizon Picking From Subbottom Profile Data. IEEE J. Ocean. Eng. 2018, 44, 524–534. [Google Scholar] [CrossRef]
- Fakiris, E.; Blondel, P.; Papatheodorou, G.; Christodoulou, D.; Dimas, X.; Georgiou, N.; Kordella, S.; Dimitriadis, C.; Rzhanov, Y.; Geraga, M.; et al. Multi-Frequency, Multi-Sonar Mapping of Shallow Habitats—Efficacy and Management Implications in the National Marine Park of Zakynthos, Greece. Remote Sens. 2019, 11, 461. [Google Scholar] [CrossRef] [Green Version]
- Dossi, M.; Forte, E.; Pipan, M. Automated reflection picking and polarity assessment through attribute analysis: Theory and application to synthetic and real ground-penetrating radar data. Geophysics 2015, 80, 23–35. [Google Scholar] [CrossRef]
- Forte, E.; Dossi, M.; Pipan, M.; Del Ben, A. Automated phase attribute-based picking applied to reflection seismics. Geophysics 2016, 81, 141–150. [Google Scholar] [CrossRef]
- Zhao, J.H.; Li, S.B.; Zhao, X.; Feng, J. A Comprehensive Horizon-Picking Method on Subbottom Profiles by Combining Envelope, Phase Attributes, and Texture Analysis. Earth Space Sci. 2020, 7, e2019EA000680. [Google Scholar] [CrossRef] [Green Version]
- Li, S.B.; Zhao, J.H.; Zhang, H.M.; Bi, Z.J.; Qu, S.H. A Novel Horizon Picking Method on Sub-Bottom Profiler Sonar Images. Remote Sens. 2020, 12, 3322. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berkhout, A.J.; Verschuur, D.J. Imaging of multiple reflections. Geophysics 2006, 71, SI209–SI220. [Google Scholar] [CrossRef]
- Muijs, R.; Robertsson, J.O.A.; Holliger, K. Prestack depth migration of primary and surface-related multiple reflections: Part I—Imaging. Geophysics 2007, 72, 59–69. [Google Scholar] [CrossRef]
- Slob, E.; Zhang, L.L. Unified elimination of 1D acoustic multiple reflection. Geophys. Prospect. 2021, 69, 327–348. [Google Scholar] [CrossRef]
- Wang, X.; Xia, C.L.; Liu, X.W. A case study: Imaging OBS multiples of South China Sea. Mar. Geophys. Res. 2012, 33, 89–95. [Google Scholar] [CrossRef]
- Verschuur, D.J. Seismic Multiple Removal Techniques—Past, Present and Future; EAGE Publications: Houten, The Netherlands, 2006; pp. 37–119. [Google Scholar]
- Imamverdiyev, Y.; Sukhostat, L. Lithological facies classification using deep convolutional neural network. J. Pet. Sci. Eng. 2019, 174, 216–228. [Google Scholar] [CrossRef]
- Feng, Q.; Miao, Y.; Xiao, Y.L.; Yao, J.W.; Cai, L.; Guang, M.H. Unsupervised seismic facies analysis via deep convolutional autoencoders. Geophysics 2018, 83, A39–A43. [Google Scholar]
- Maxwell, A.E.; Warner, T.A.; Guillén, L.A. Accuracy Assessment in Convolutional Neural Network-Based Deep Learning Remote Sensing Studies—Part 1: Literature Review. Remote Sens. 2021, 13, 2450. [Google Scholar] [CrossRef]
- Park, C.I.; Sohn, C.B. Data Augmentation for Human Keypoint Estimation Deep Learning based Sign Language Translation. Electronics 2020, 9, 1257. [Google Scholar] [CrossRef]
- Feldens, P.; Darr, A.; Feldens, A.; Tauber, F. Detection of Boulders in Side Scan Sonar Mosaics by a Neural Network. Geosciences 2019, 9, 159. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, H.T.; Lee, E.H.; Lee, S. Study on the Classification Performance of Underwater Sonar Image Classification Based on Convolutional Neural Networks for Detecting a Submerged Human Body. Sensors 2020, 20, 13. [Google Scholar] [CrossRef] [Green Version]
- Cheng, B.; Li, Z.; Xu, B.; Yao, X.; Ding, Z.; Qin, T. Structured Object-Level Relational Reasoning CNN-Based Target Detection Algorithm in a Remote Sensing Image. Remote Sens. 2021, 13, 281. [Google Scholar] [CrossRef]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-Decoder with Atrous Separable Convolution for Semantic Image Segmentation, In Proceedings of the European conference on computer vision (ECCV), Munich, Germany, 8–16 October 2018, 833–851.
- Shankar, U.; Singh, S.S.; Sain, K. Signal enhancement and multiple suppression using Radon transform: An application to marine multichannel seismic data. Mar. Geophys. Res. 2009, 30, 85–93. [Google Scholar] [CrossRef]
- Lurton, X. An Introduction to Underwater Acoustics: Principles and Applications, 2nd ed.; Springer: New York, NY, USA, 2010. [Google Scholar]
- Zheng, G.; Zhang, H.; Li, Y.; Zhao, J. A Universal Automatic Bottom Tracking Method of Side Scan Sonar Data Based on Se-mantic Segmentation. Remote Sens. 2021, 13, 1945. [Google Scholar] [CrossRef]
- Zhao, P.; Liu, K.; Zou, H.; Zhen, X. Multi-Stream Convolutional Neural Network for SAR Automatic Target Recognition. Remote Sens. 2018, 10, 1473. [Google Scholar] [CrossRef] [Green Version]







| Survey Area | Line Number | Image Height (pixel) | Image Width (pixel) |
|---|---|---|---|
| Jiaozhou Bay | SBL_20120628_085229 | 900 | 15,242 |
| SBL_20120628_134859 | 900 | 14,127 | |
| Zhujiang Estuary | SBL_20160305_025613 | 1000 | 15,496 |
| SBL_20160306_030106 | 1000 | 8177 | |
| SBL_20160306_034636 | 1000 | 11,752 | |
| SBL_20160306_052842 | 1000 | 19,639 | |
| SBL_20160306_071833 | 1000 | 17,687 |
| Accuracy | Method | Line 229 | Line 613 |
|---|---|---|---|
| MIoU | A&B | 0.9155 | 0.9458 |
| A&C | 0.6077 | 0.7483 | |
| SSIM | A&B | 0.9792 | 0.9447 |
| A&C | 0.6588 | 0.8637 |
| Accuracy | Method | Value |
|---|---|---|
| MIoU | ground truth & our method | 0.9563 |
| ground truth & predictive deconvolution | 0.7060 | |
| SSIM | ground truth & our method | 0.9849 |
| ground truth & predictive deconvolution | 0.9246 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, J.; Zhao, J.; Zheng, G.; Li, S. Horizon Picking from SBP Images Using Physicals-Combined Deep Learning. Remote Sens. 2021, 13, 3565. https://doi.org/10.3390/rs13183565
Feng J, Zhao J, Zheng G, Li S. Horizon Picking from SBP Images Using Physicals-Combined Deep Learning. Remote Sensing. 2021; 13(18):3565. https://doi.org/10.3390/rs13183565
Chicago/Turabian StyleFeng, Jie, Jianhu Zhao, Gen Zheng, and Shaobo Li. 2021. "Horizon Picking from SBP Images Using Physicals-Combined Deep Learning" Remote Sensing 13, no. 18: 3565. https://doi.org/10.3390/rs13183565
APA StyleFeng, J., Zhao, J., Zheng, G., & Li, S. (2021). Horizon Picking from SBP Images Using Physicals-Combined Deep Learning. Remote Sensing, 13(18), 3565. https://doi.org/10.3390/rs13183565








