2.1.1. B-Spline Surfaces for Deformation Analysis
The developed approach is based on approximating B-spline surfaces. The mathematical definition of a B-spline surface is given by the following [
22]:
According to Equation (
1), a three-dimensional surface point
in Cartesian coordinates is computed as the weighted average of
control points
. The B-spline basis functions
and
with degree
p and
q are the corresponding weights and can be computed recursively (cf. references [
23,
24]). The basis functions are functions of the surface parameters
u and
v, locating a surface point on the surface and defining the parameter space. Two knot vectors
and
split the B-splines’ domain into knot spans, leading to the B-splines’ property of ‘locality’, meaning that the shifting of a single control point changes the surface only locally.
B-spline surfaces allow for the flexible modelling of a variety of objects under investigation. Hence, they are used in several engineering geodetic applications, either for geometric state descriptions (cf. references [
25,
26,
27]) or in the context of monitoring tasks ([
28,
29]). In addition to their flexibility, B-spline surfaces have two other properties that qualify them for use within an areal deformation analysis:
Firstly, B-spline surfaces are invariant under common geometric transformations, such as the similarity transform: the application of a transformation to the control points
of a B-spline surface results in the same surface as the application of this transformation to the surface itself [
22]. As proven in [
20], the estimated control points of different B-spline surfaces can be used as corresponding points to estimate the parameters of a similarity transform, provided that a joint parameterisation is used when determining the best-fitting B-spline surfaces. However, not only can the control points be used for this purpose, but also surface points
, with the surface parameters
u and
v identifying the point correspondences. This property is demonstrated in
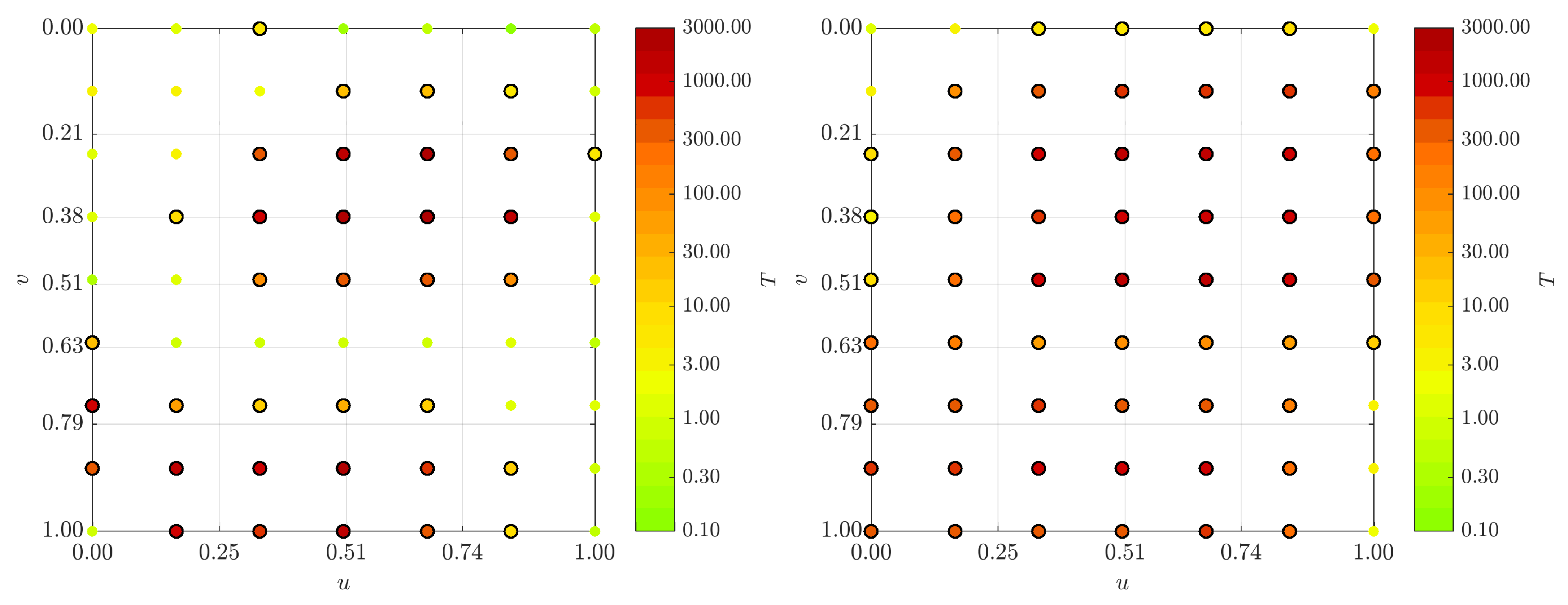
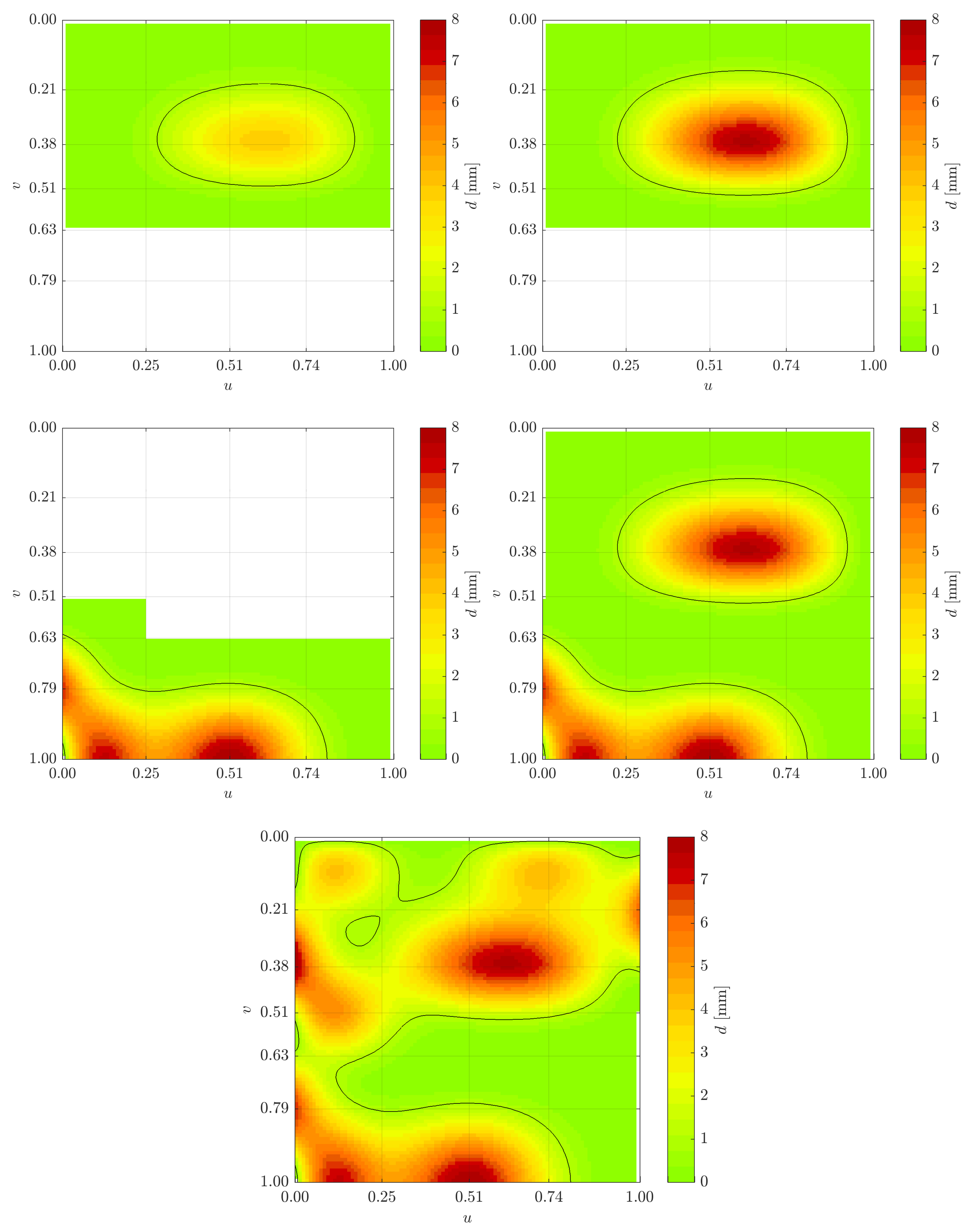
Figure 1, presenting two B-spline surfaces that differ from each other only by rotations and translations (left surface: epoch 1, right surface: epoch 2). As can be seen, parameter grids (green quadrangles) of the surface of epoch 1 that are individually transformed by means of the same transformation parameters as the surface are congruent with the respective grid quadrangles of the transformed surface.
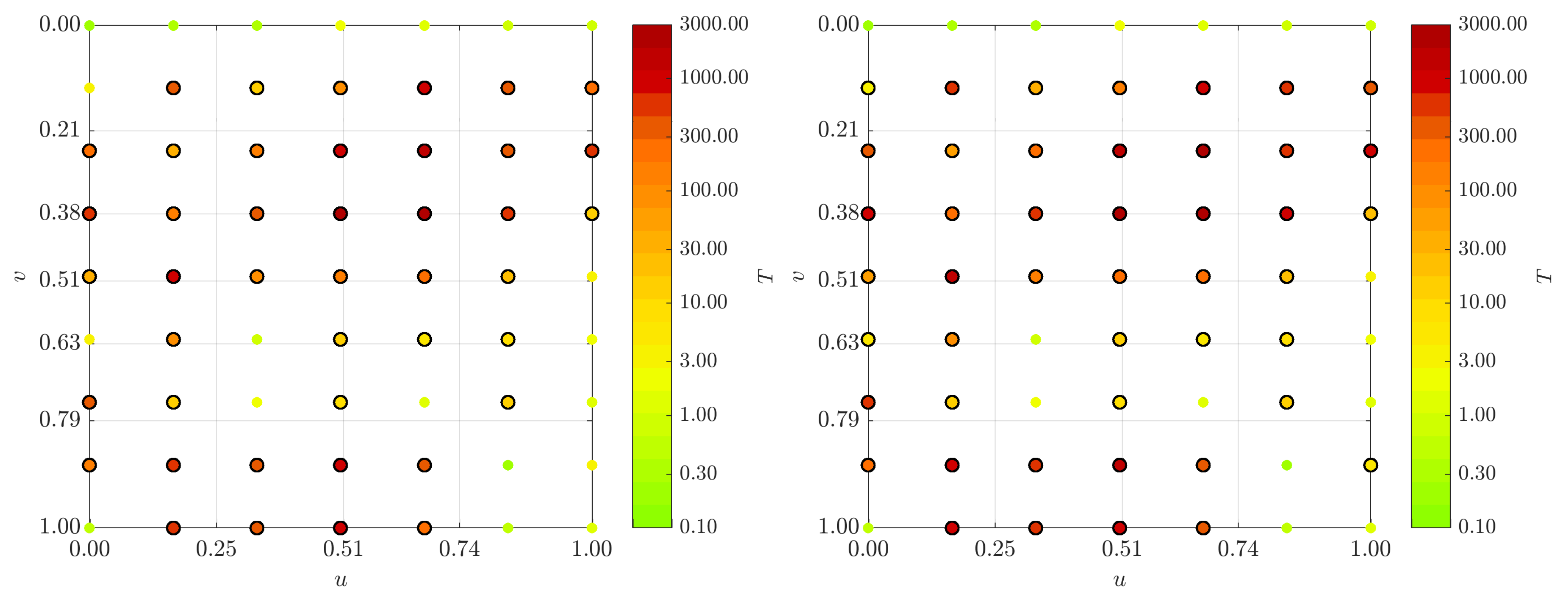
Secondly, the locality of the B-spline surfaces directly allows for the modelling and for the localisation of an object’s distortions. For example, when the rigid body movement of a B-spline surface is superimposed by distortions, non-distorted areas can be identified by means of the surface parameter grid as demonstrated in
Figure 2. The figure presents two B-spline surfaces that differ from each other by a rigid body movement and a superimposed local distortion (left surface: epoch 1, right surface: epoch 2). The transformation of the four parameter quadrangles (green quadrangles) of the surface of epoch 1, using the same transformation parameters as those for the rigid body movement of the surface, highlights that this local distortion only locally influences the parameter lines: only the red quadrangle in epoch 2—being the only one of the four example quadrangles located in the distorted area—is not congruent with the respective grid quadrangles of the surface of epoch 2.
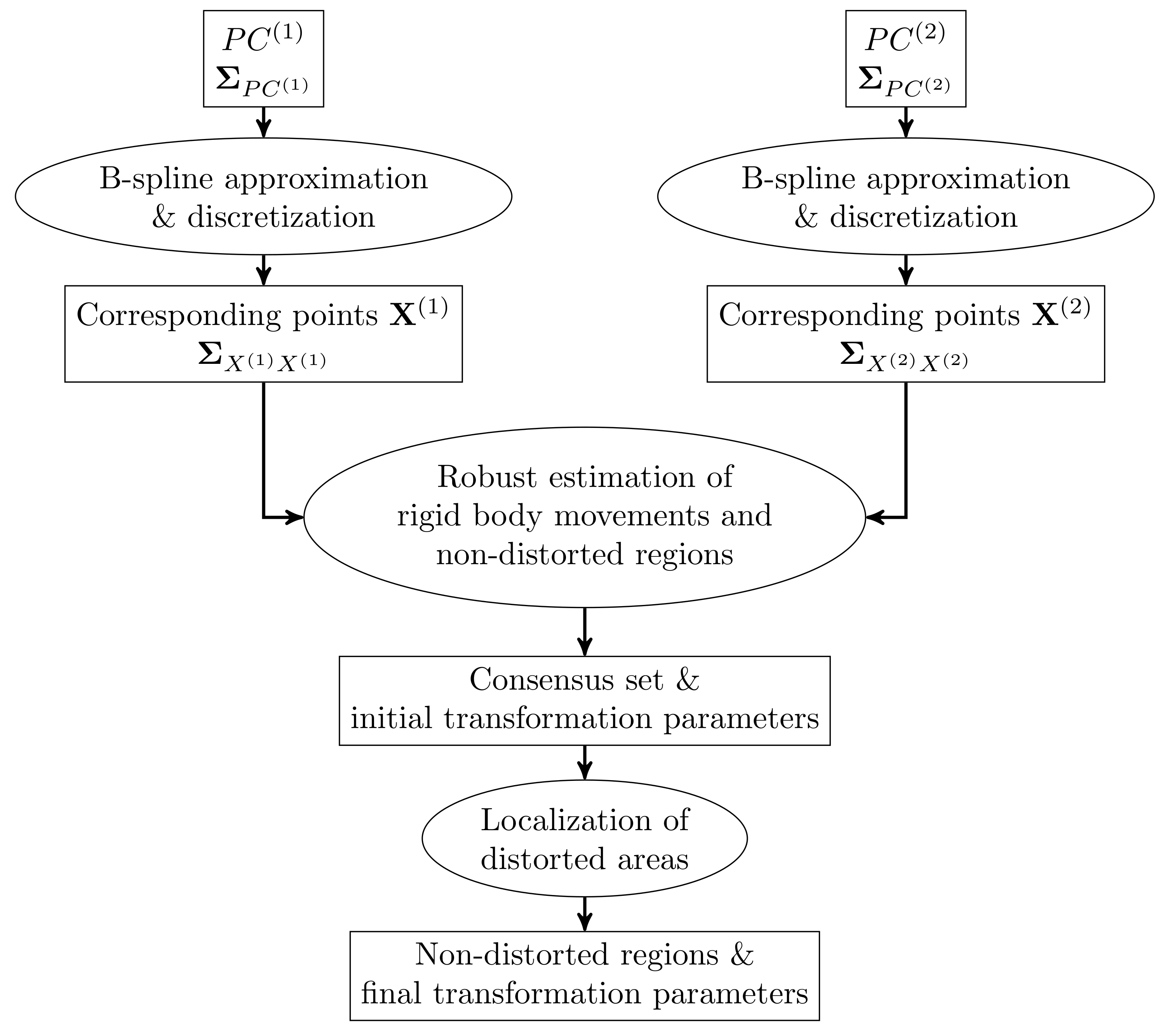
These two properties of B-spline surfaces form the cornerstones of the developed approach that is summarised in the flow chart in
Figure 3.
For the sake of simplicity, only two measuring epochs are considered; the extension by further epochs is straightforward.
Starting points are point clouds of an object acquired in two different measuring epochs ( and ), along with their variance covariance matrices (VCM) ( and ). Between these two epochs, the object may undergo rigid body movements, which additionally may be superimposed by distortions. It is assumed, however, that only parts of the object are subject to distortions. The resulting non-distorted regions of the object are necessary for successful application of the developed approach.
Both point clouds are initially approximated by means of best-fitting B-spline surfaces, taking into account the stochastic information of the available point clouds (
Section 2.1.2). Due to the use of joint parameterisation during this step, afterwards, the surface parameters can be used to defined point correspondences on the estimated B-spline surfaces. These corresponding points, resulting from discretisations of the B-spline surfaces (
Section 2.1.3), are then used to robustly estimate rigid body movements and to initially define non-distorted regions of the object (
Section 2.1.4 and
Section 2.1.5). Finally, the non-distorted regions are extended and their stability as well as their extents are statistically confirmed (
Section 2.1.6).
2.1.2. Point Cloud Modelling by Means of Best-Fitting B-Spline Surfaces
When using B-spline surfaces (cf. Equation (
1)) to model a point cloud
(
: indicating the measuring epoch), the
individual points of the point cloud are the observations
(
) that are used to determine the best-fitting B-spline surface
:
with the three-dimensional residual vectors
. As in Equation (
1), each observation
is a three-dimensional point expressed in Cartesian coordinates.
Usually, only the position of the control points
(cf. Equation (
1), for reasons of simplicity, the epochal affiliations indicated by the superscript
are not carried along) is estimated in a linear Gauß Markov model, according to the following [
31]:
In Equation (
3), the vector of unknowns
summarises the estimated positions of all
control points and is ordered coordinate-wise. The observation vector
is structured accordingly and contains the observed noisy surface points
. The stochastic behaviour of the observations is characterised by the corresponding cofactor matrix
, the inverse of which is used as a weighting matrix in the estimation and which differs from the corresponding VCM by the a priori variance factor
[
1]:
The design matrix
, describing the functional relationship between observations and unknowns, is determined by means of the B-spline basis functions [
31]:
with
being the 3 × 3 identity matrix. The vector of estimated control points
is completed by the corresponding VCM
, containing the stochastic information of the estimated control points [
1]:
and with the vector of estimated residuals
being computed according to the following:
A geometrical interpretation of the estimation
in Equation (
7) is that the original vector of observations
is orthogonally projected to the
-dimensional column space of the design matrix
[
32]. Thus, the vector of estimated observations
can be computed as a linear combination of the vector of estimated control points
. Due to
, linear dependencies between the estimated observations emerge. The corresponding VCM of the vector of estimated observations
thus, has a maximum rank of
and—assuming an overdetermined estimation problem—is singular.
The strategy described above requires appropriately determining the remaining parameter groups of the best-fitting B-spline surface separately from the adjustment of the optimal control points: The B-spline’s degrees
p and
q are usually specified a priori. Using cubic B-splines with
and
is a generally accepted choice [
22]. Strategies to determine the knot vectors are proposed in, for example, [
22,
31,
33]. The optimal number of control points to be estimated can be interpreted as a model selection problem and can either be solved by classical model selection strategies or by structural risk minimisation (cf. [
34,
35]). The latter strategy has the advantage that the degrees
p and
q can also be taken into account during model selection, rather than choosing them arbitrarily [
36]. Finally, appropriate surface parameters
u and
v have to be allocated to the observations (cf. e.g., [
37] for an iterative parameterisation approach for laser scanning point clouds). When B-spline surfaces are used as a basis for deformation analysis, however, an independent parameterisation of different point clouds is not expedient; rather, a joint parameterisation has to be implemented as demonstrated in [
35]. As simulated data sets are investigated in this initial study (cf.
Section 2.2), nominal values for degrees, knot vectors and surface parameters are available and, therefore, the appropriate determination of these parameter groups can be left aside during this initial study.
2.1.3. Constructing Identical Points on Approximating B-Spline Surfaces
Having estimated the best-fitting B-spline surfaces, they are used to construct
identical (id) points
in the two measuring epochs
and
. Provided that the surfaces are based on a joint parameterisation, the surface parameters
u and
v, discretising the estimated surfaces (cf. Equations (
1) and (
2)), can be used for this purpose:
Using the stochastic information of the estimated control points, the sampled surface points are completed by their VCMs
. Following the considerations in
Section 2.1.2, linear dependencies emerge between the discretised points as soon as
, resulting in rank defects of the corresponding VCMs
. More precisely, a rank defect occurs in at least one parameter direction of the B-spline surface when the number of discretised surface points exceeds the number of estimated control points. The rank defect linked to the
u-direction, therefore, can be computed according to the following [
30]:
and the rank defect linked to the
v-direction accordingly arises to the following:
The overall rank defect
is the sum of these two parts [
30]:
This singularity in the VCMs of the corresponding points represents an important difference to deformation models in which the observed data points are directly incorporated.
2.1.4. Estimation of Rigid Body Movements
The estimation of rigid body movements of an object of interest is based on
three-dimensional corresponding points
and
(
,
) in two measuring epochs, in this study on corresponding surface points (cf. Equation (
9)).
Assuming that the object undergoes solely rigid body movements, all corresponding points—just like the entire surface—are subject to translations (summarised in the translation vector
) and rotations (fully described by means of the rotation matrix
, containing the rotation angles
,
and
). Sometimes, a change of scale (indicated by the scale factor
s) is also included, resulting in the mathematical formulation of a three-dimensional similarity transform [
1]:
When estimating the parameters of the similarity transform
,
and
s based on the corresponding surface points, it must be taken into account that both the points
available in the start system and the points
available in the target system are defined by estimated B-spline surfaces and, thus, are subject to uncertainties. In order to include the stochastic information of both point groups into the estimation of the transformation parameters, two strategies, delivering identical results, exist [
38]: Either the transformation parameters are estimated in a Gauß–Helmert model, or the classical Gauß–Markov model, assuming the points in the start system to be deterministic, is extended. Because of the easier possibility to extend the approach to a robust one, the second variant is chosen here [
30].
Assuming that the data sets under investigation are acquired by means of the same laser scanner and, hence, neglecting the scale factor
s, the extended functional model to estimate the transformation parameters is then given by the following [
38]:
with
(
) being residual vectors. The first part of the model (Equation (
14)) describes the functional relationship between the identical points in the two epochs by means of the unknown transformation parameters. Equation (
15) simultaneously introduces the coordinates of the identical points in the start system as additional observations and, thus, allows for the consideration of their stochastic information. The link between Equations (
14) and (
15) is given by the estimated point coordinates available in the start system, which are introduced in both equations and are marked with an asterisk. Neglecting inter-epochal correlations, the extended stochastic model is composed of the VCMs
as well as
of the constructed surface points, resulting in the following [
38]:
Based on the functional model in Equations (
14) and (
15) as well as on the stochastic model in Equation (
16), the unknown transformation parameters can be estimated in a non-linear Gauß–Markov model (cf. [
38] for more information).
2.1.5. Robust Estimation of Rigid Body Movements
The derivations in
Section 2.1.4 are based on the assumption that the object under investigation is only subject to rigid body movements. However, rigid body movements are usually superimposed by additional distortions in reality. When taking into account points that are subject to both rigid body movements and distortions in the estimation of the rigid body movement, these points falsify the estimated transformation parameters. As a consequence, the determination of transformation parameters must necessarily be accompanied by an elimination of surface points in distorted areas. Otherwise, the required congruence of identical points is not given.
Considering points that are subject to both rigid body movements and distortion to be outliers in the context of the similarity transform is one possible strategy to cope with this challenge [
30]. In order to accurately estimate rigid body movements in this situation, a robust strategy based on the random sample consensus (RANSAC)-algorithm [
39] is proposed in this section. In general, RANSAC is an easy-to-implement method and is characterised by a high breakpoint (>50%). Furthermore, with respect to the presented problem, RANSAC allows for the robust estimation of rigid body movements while obtaining initial information about non-distorted regions.
The general idea of RANSAC is to initially determine the unknown parameters of a model describing
data points by the minimum number
of data points that is needed for this determination [
39]. These
data points are randomly drawn from the entire set of data points. After having computed the model parameters by means of these
points, the distances of the resulting preliminary model to the entirety of the data points are calculated. Points with distances that are within a predefined error tolerance
are considered to be consistent with the determined model parameters. These points form the consensus set
. The procedure is repeated iteratively until either the number of points in the consensus set equals a specified minimum number
or a maximum number of iterations
is performed. Finally, the points in the largest consensus set are used to estimate the optimal model parameters.
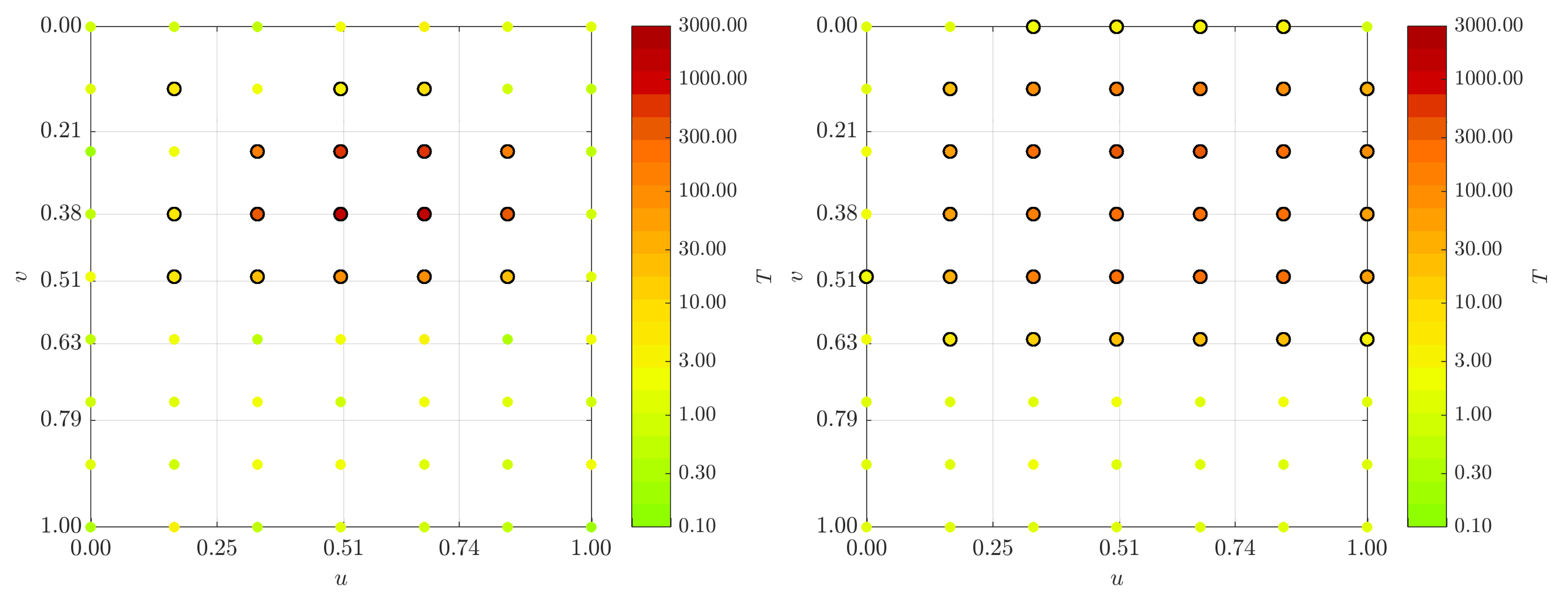
RANSAC can be directly applied to the robust estimation of rigid body movements that are superimposed by distortions (see
Figure 4 for a schematic sketch of the procedure): the six parameters of a three-dimensional similarity transform with neglected scale factor (cf. Equation (
14)) can principally be determined by means of two pairs of three-dimensional corresponding data points. However, the estimation of the transformation parameters described in
Section 2.1.4 is a non-linear estimation problem and, thus, requires approximate values. As these approximate values are determined by means of quaternions (see, for example, [
40]) in this study, a strategy that also yields the scale factor
s, the number of point pairs required is
. Hence, three pairs of sampled surface points are repeatedly and randomly drawn from the entirety of surface points and are afterwards used to determine approximate parameters
,
and
by means of a quaternion approach. (Strictly speaking, the modelled transformation is not a rigid body movement in this step. However, as the results are only approximate values for the final estimation of rigid body movements, this strategy is not to be regarded as critical.) Unlike the quaternion approach, the strategy presented in
Section 2.1.4 allows for the accuracies of the corresponding points to be taken into account when estimating rigid body movements. For this reason, the approximate parameters are improved in a second step as described above, yielding optimal translations
and optimal rotations
, describing the rigid body movements of the three chosen surface points. During this step, the scale factor is set to
[
30]. The entirety of computed surface points of the first measuring epoch
is afterwards transformed using the estimated transformation parameters as follows:
The Euclidean distance
between each transformed point
belonging to epoch
and its corresponding point
belonging to epoch
provides the basis for the decision of whether a surface point is included in the consensus set of model-conforming points. This distance is compared to the error tolerance as follows:
which is determined by the accuracy
of the computed distance
, arising from variance covariance propagation as well as a factor
, which needs to be chosen appropriately (see below). According to Equation (
19), the error tolerance is assessed for each point pair individually since the discretised surface points are not available with a homogeneous precision [
30]. When
is fulfilled, the corresponding point pair is assigned to the consensus set
.
This procedure is repeated either until the number
of points fulfilling Equation (
20) is larger than or equal the minimum size
of the consensus set or until the maximum number of iterations
is reached. It is worth noting that it is not possible to distinguish distortions from gross errors in the data during this step. For this reason, it is essential to successfully remove gross errors a priori using standard techniques, for example, when estimating best-fitting B-spline surfaces.
The successful application of the developed strategy requires the definition of three parameters:
The parameter
in Equation (
19) has to be chosen in such a way that only model-compliant points are included in
. When
is chosen too small, points will be erroneously identified as outliers, whereas when
is chosen too large, outliers may be included in the consensus set and, thus, the estimation result will become biased. The influence of the parameter
on the results is investigated in
Section 3.2.
The minimum number
of model-compliant points required to accept the current
is estimated from the expected amount of gross errors
(
) contained in the data set. When
is known, the optimal
can be determined according to the following [
41]:
The maximum number of iterations
is determined by the desired probability
P that a solution without outliers is found [
41]:
Finally, after the iteration is completed, the point pairs of the largest consensus set are used to estimate the transformation parameters
and
in the extended Gauß–Markov model (
14) and (
15).
With a final statistical global test, comparing the respective a priori variance factor
with the corresponding a posteriori variance factor
, the presence of outliers can be excluded with a confidence probability of
, with
being the error probability [
42]:
The corresponding test variable
is F-distributed with the degrees of freedom
f and
∞:
If
lies outside the associated quantile and, thus, the null hypothesis (
23) has to be rejected, a further RANSAC iteration should be performed [
30]. (It is worth noting that in this formulation of the global test the presence of errors in the stochastic model is excluded).
2.1.6. Statistically Based Localisation of Distortions
Having successfully conducted the steps described in the previous section, estimated parameters of the rigid body movement as well as a consensus set are available. The latter is a set of point pairs that is free from outliers w.r.t to the estimated rigid body movement with the confidence probability of the global test . Therefore, these points can already be assigned to the non-distorted region. However, depending on the parameter to be chosen, the consensus set does usually not cover the entire non-distorted region of the B-spline surface. Hence, no exact statement can be made about the position and the extent of the distorted regions. Therefore, the consensus set is stepwise and statistically ensured extended by individual point pairs. With the extended consensus set, the parameters of the rigid body movement can be estimated with a higher redundancy and, thus, more precisely.
The starting point of the localisation is the set of points to be tested, which includes all data points that are not assigned to the consensus set at the beginning. Using a forward strategy (see below for information about the order in which the points are considered), these points are then sequentially added to the group of points that is already detected as non-distorted. Based on this extended set, the parameters of the rigid body movement are re-estimated. Point pairs that are detected as outliers within this re-estimation are assigned to the distorted region of the surface, whereas points that do not significantly change the estimated transformation parameters are allocated to the set of non-distorted points, the extended consensus set .
In order to implement the outlier detection, the classical Gauß–Markov model is extended by an additional parameter vector
that allows for the estimation of possible outliers [
42]. This extension enables the simultaneous testing of several observations with regard to gross errors, a strategy that is desirable in the context of estimating rigid body movements, as a testing of single coordinates is not meaningful [
30].
The linearised Gauß–Markov model to estimate the parameters of the rigid body movement (cf. Equations (
14) and (
15)) is the null hypothesis of the statistical test performed [
42]:
Compared to Equations (
14) and (
15), the corresponding data points
and
are summarised in the observation vector
, and the transformation parameters
and
to be estimated are combined in the vector of unknowns
in Equation (
26). The design matrix
describes the functional relationship between observations and unknowns.
Using the additional parameter vector
, containing the outliers to be estimated, and the corresponding design matrix
, being a sparse matrix with numbers of ones at the entries of the suspected observations, the alternative hypothesis can be formulated as follows:
Due to the model extension, the parameter vector
of the rigid body movement as well as the residual vector
are modified (indicated by the apostrophe). The dimensions of
and
are determined by the number
of suspected observations. The null hypothesis (
26) corresponds to the equivalent null hypothesis
. Hence, it is examined whether the estimated gross errors differ significantly from zero. The test variable
used to investigate the validity of the null hypothesis, follows the F-distribution
, the degrees of freedom of which are determined by the number
of suspected observations as well as the redundancy
f of the initial estimation problem [
42]. The computation of
T requires the determination of the following quantities:
In the equations above, is the cofactor matrix of the vector of residuals , the cofactor matrix of the additional parameter vector and the corrected sum of squared residuals.
With the strategy described above, the stability of single point pairs with respect to distortions can be evaluated in a statistically ensured way (single point test).
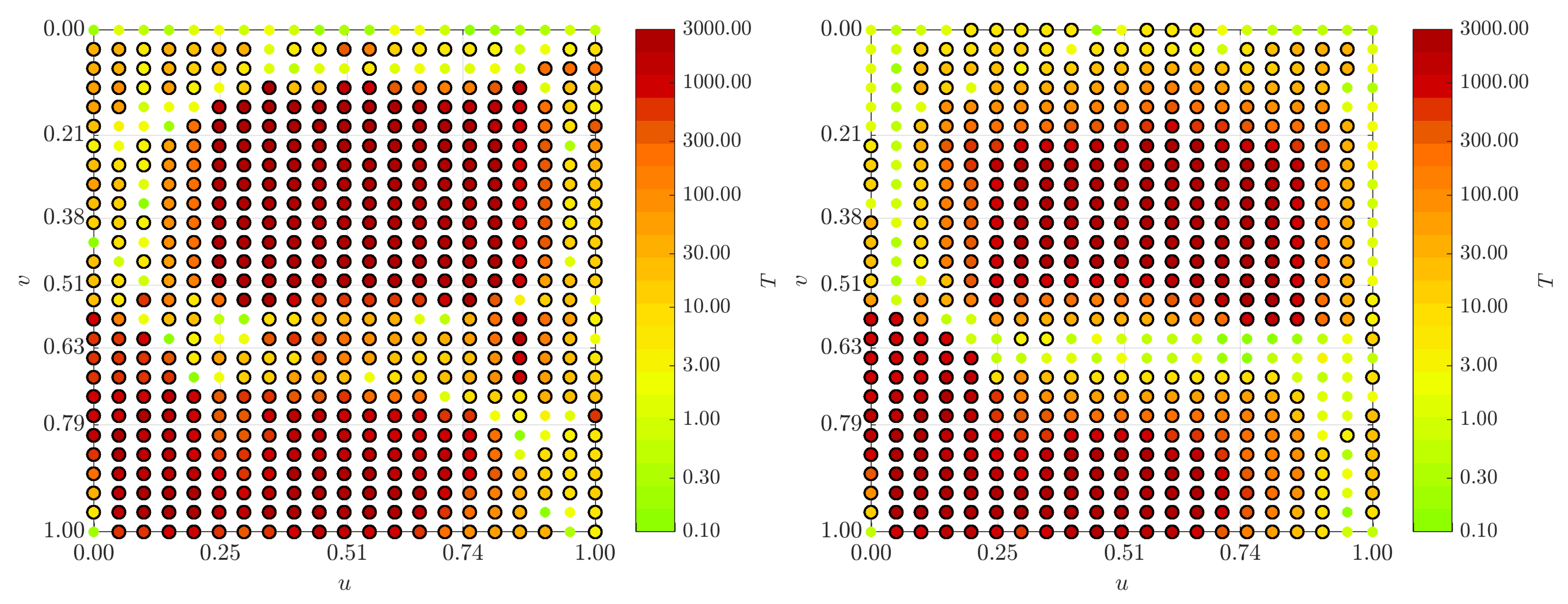
In order to obtain an areal character of the localisation, alternatively, a predefined domain of the surface can be included in the outlier detection. A straightforward way to define this domain is to use the parametric neighbourhood
of the investigated point pair
(see
Figure 5 for an example with
). The parameter
a to be chosen determines the size of the neighbourhood. Depending on the choice of
a,
observations are examined for gross errors [
30]. Naturally, Equation (
35) does only hold when
does not lie at the surface’s boundary. In that case,
reduces accordingly.
Having determined the neighbourhood of the point pair to be tested, all point pairs lying in the domain
are temporarily included in the extended consensus set
by adjusting the matrix
(cf. Equation (
24)) accordingly. (It is worth noting that previous test decisions on neighbouring points are not taken into account during this step: neighbouring points that have already been allocated either to the distorted or to the non-distorted regions as well as points that have not been under investigation yet are equally treated and, thus, are involved in the formation of the neighbourhood.) If the comparison of the resulting test variable
(cf. Equation (
28)) with the corresponding quantile of the Fisher distribution supports the null hypothesis, the existence of gross errors can be ruled out with the respective confidence probability
. As a consequence, the point pair under investigation is added to the extended consensus set and is considered non-distorted in the subsequent outlier tests. Otherwise, if the null hypothesis has to be rejected, a distortion of the surface in the domain that is under investigation must be assumed. In this case, the extended consensus set is not modified. With the removal of the point pair
from
, an iteration step of the procedure is completed and the next point pair is investigated. The procedure is continued until all point pairs are removed from
. At the end, the extended consensus set is used to estimate the final parameters of the rigid body movement. Additionally, a completing global test can be used to check the consistency of the detected non-distorted point pairs.
The order in which the point pairs are investigated by means of the strategy described above, is determined by their degree of consistency with the determined rigid body movement. For this purpose, all points
to be tested are transformed using the transformation parameters
and
, determined by means of the (extended) consensus set. The transformed points
are then compared with their correspondences
by computing the Euclidean distances
(cf. Equation (
18)). Since a small
indicates the consensus of the corresponding point pair with the estimated transformation model, of all the point pairs to be tested, the one with the smallest
is examined first [
30]. The strategy to localise the distortions is summarised in the schematic sketch in
Figure 6.