Water Extraction in SAR Images Using Features Analysis and Dual-Threshold Graph Cut Model
Abstract
:1. Introduction
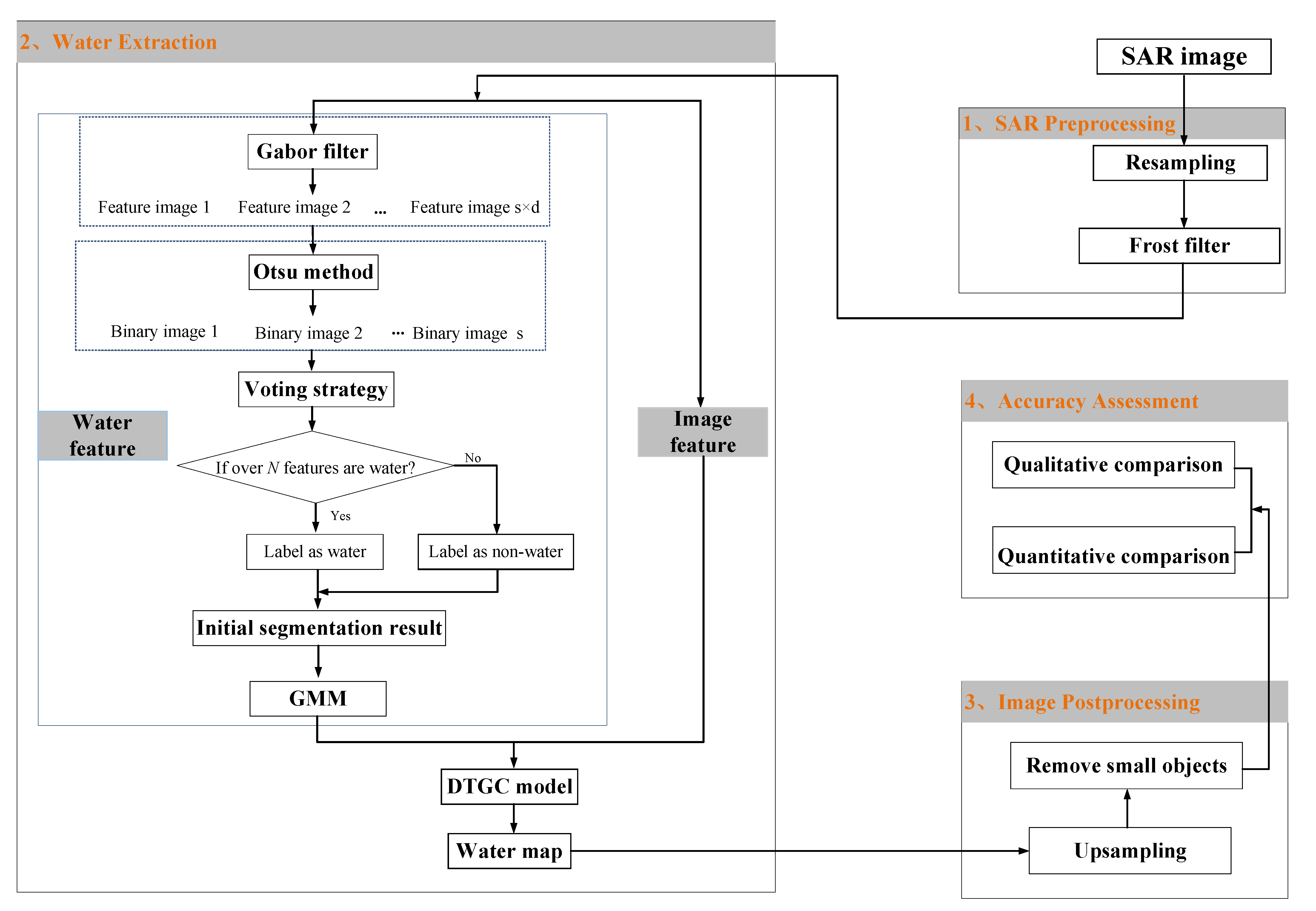
2. Materials and Methods
2.1. Image Preprocessing
2.1.1. Image Resampling
2.1.2. Frost Filter
2.2. Water Extraction
2.2.1. Water Feature
2.2.2. Image Feature
2.2.3. DTGC Model
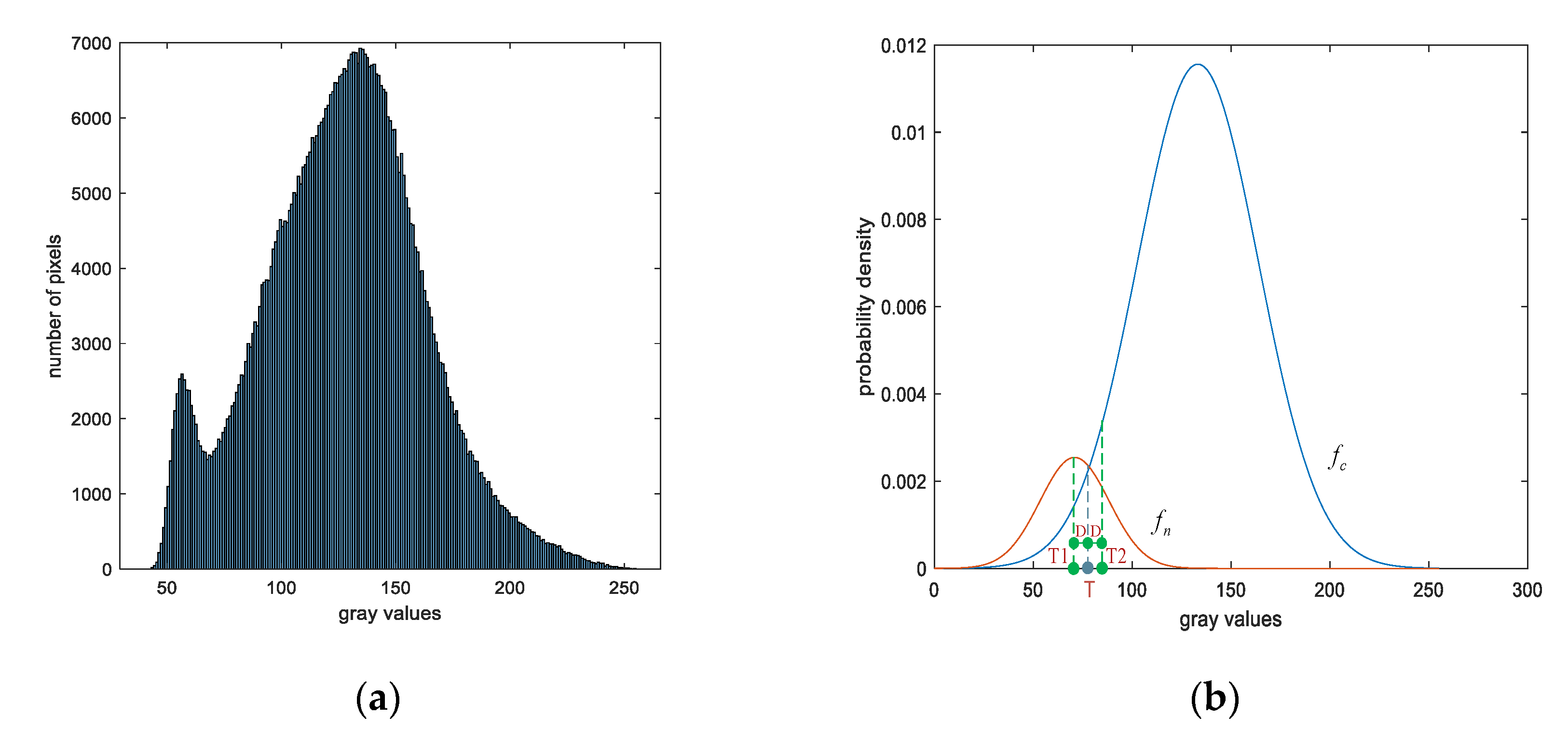
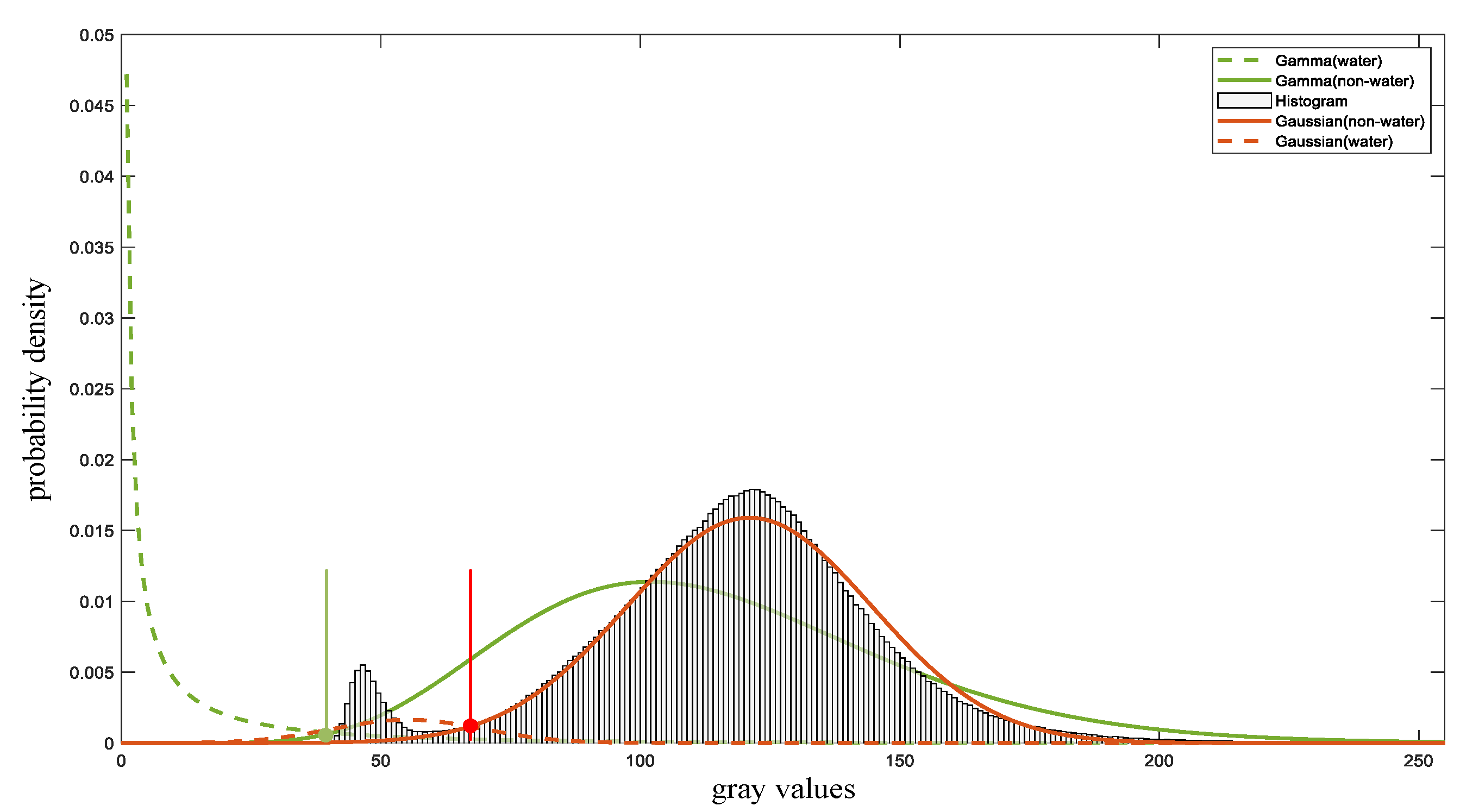
Dual-Threshold
Energy Function
Graph Construction
Weight Setting
- For , similar pixels should be assigned higher weights, whereas obviously different pixels are given lower weights [37].
- For , the edge weights are further restricted by the dual threshold. A detailed analysis of Figure 2b, when , the probability of the gray value on the curve surpasses more than 1 time of which on the , showing that the possibility of pixels belonging to the foreground is very low. Thus, to ensure that the minimum cut acts on the edge , the edge weights of pixels that meet the above given condition are assigned as 0. In a similar way, for the case of , the probability of pixels being water is slightly greater than that of non-water. Specifically, because of the water body generally of a low gray value, the pixels fulfilling the above conditions have a greater chance of being water; therefore, the weights of the edge are set to 0.
- For , supposing that the edge weights between the interval [,] and [,] are still serving as the Gaussian probability, the boundary of water and non-water sometimes would become blurred. Therefore, the weights are set to and allow the maximum flow to pass. The definition rule of is in Equation (19):
Energy Minimization
2.3. Postprocessing
2.4. Accuracy Assessment
3. Results
3.1. Study Area and Dataset Description
3.2. Experiment Results
3.2.1. Parameter Setting
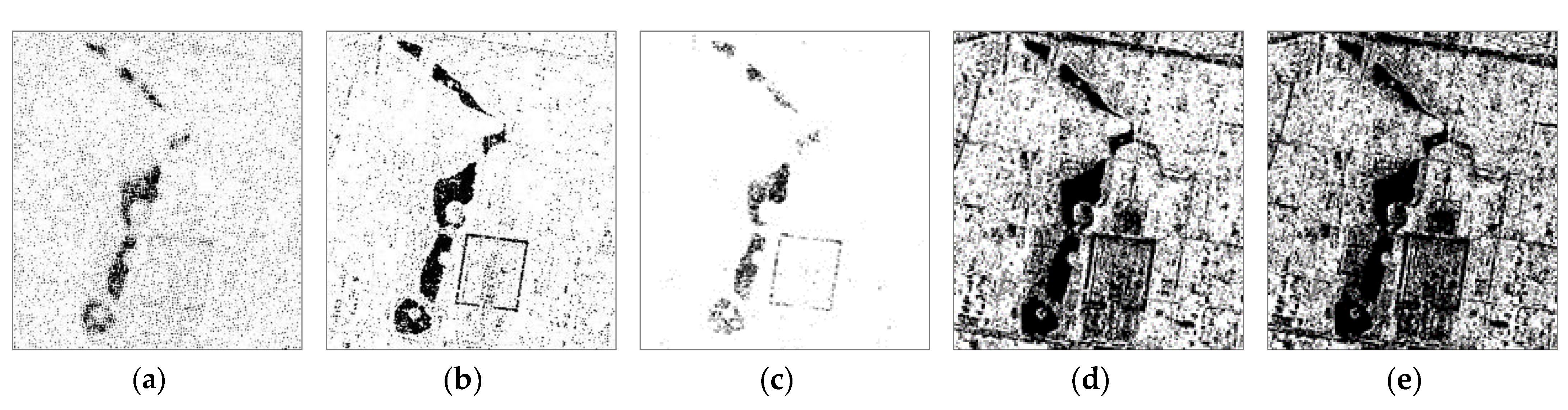
3.2.2. Feature Extraction Results
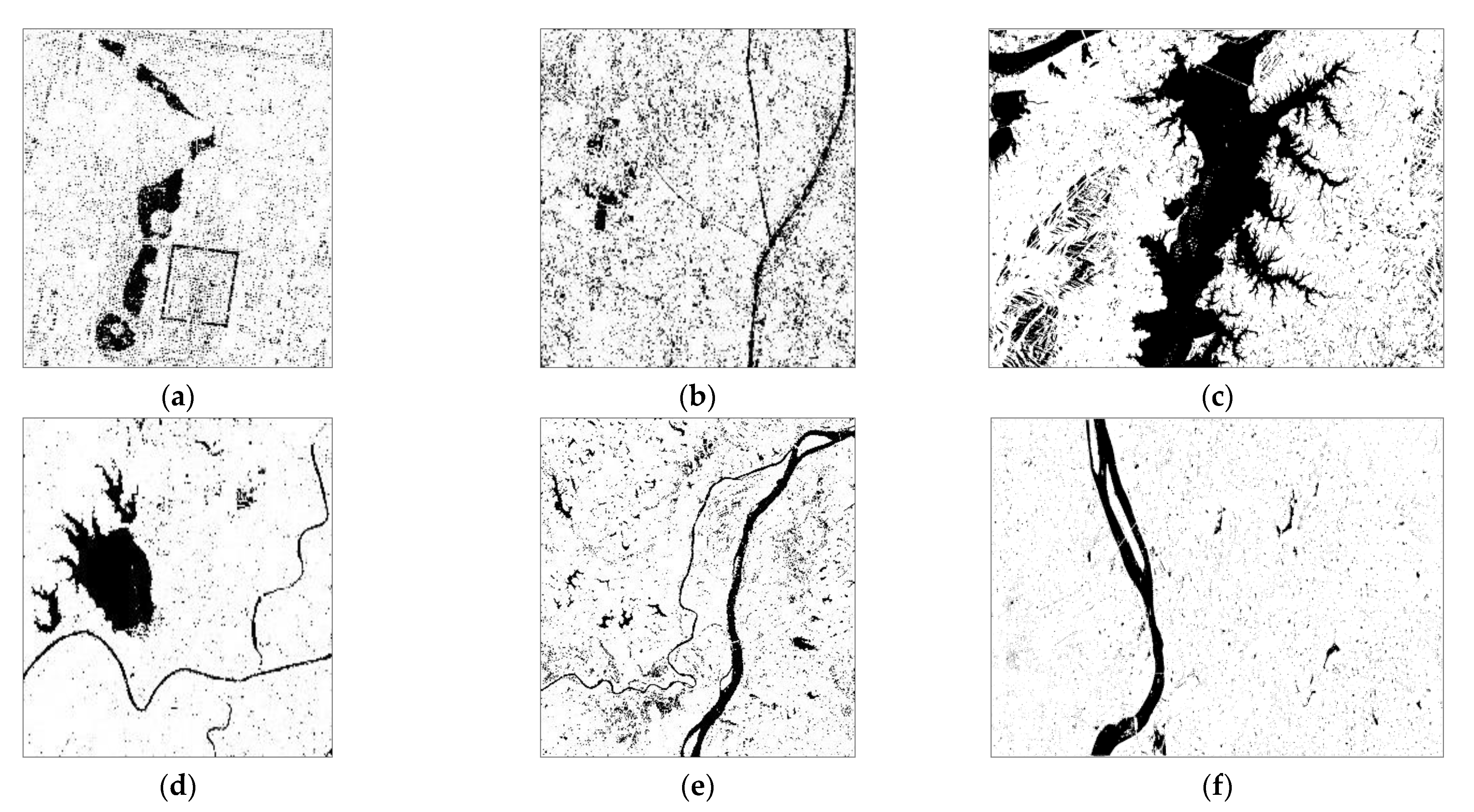
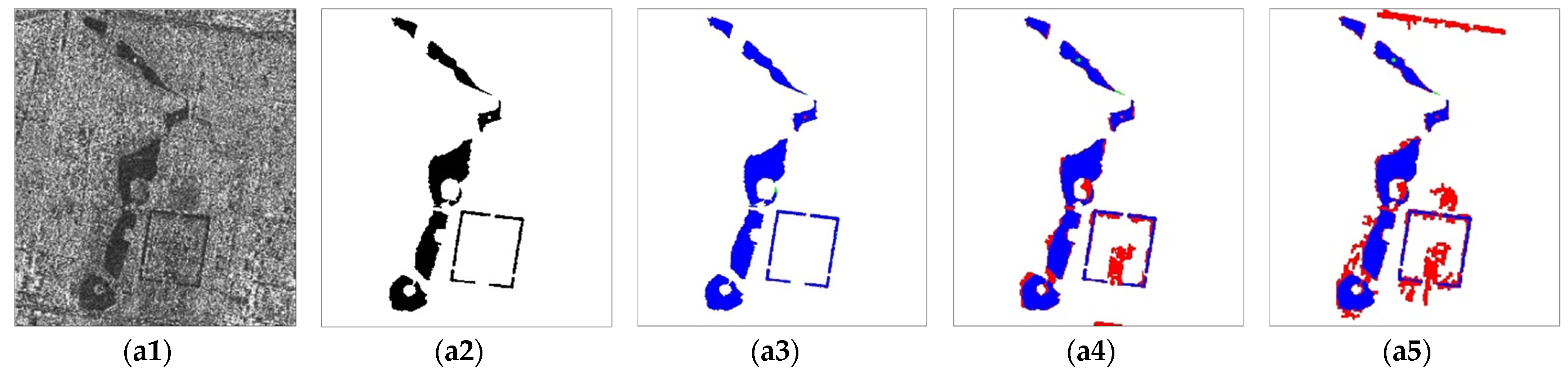
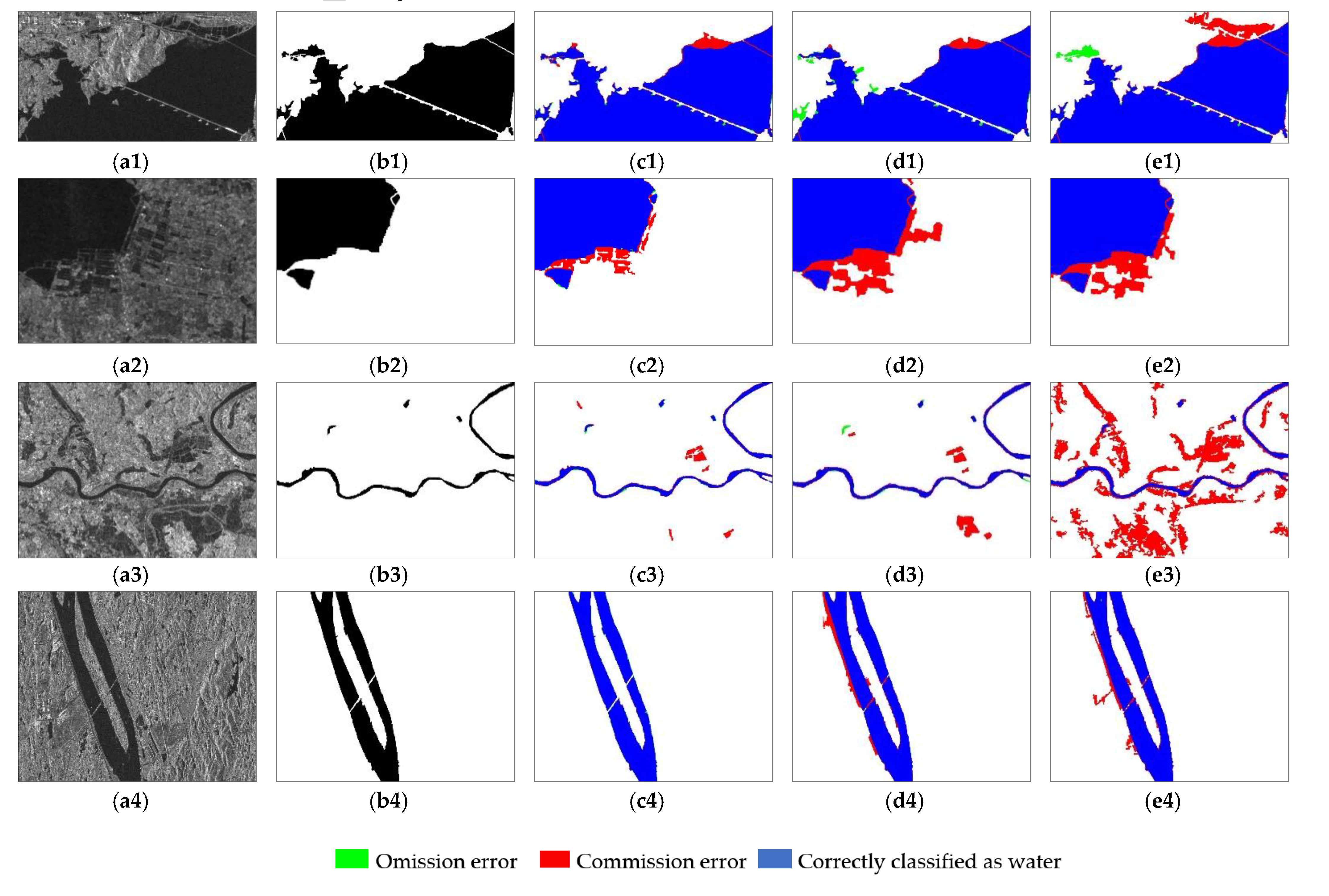
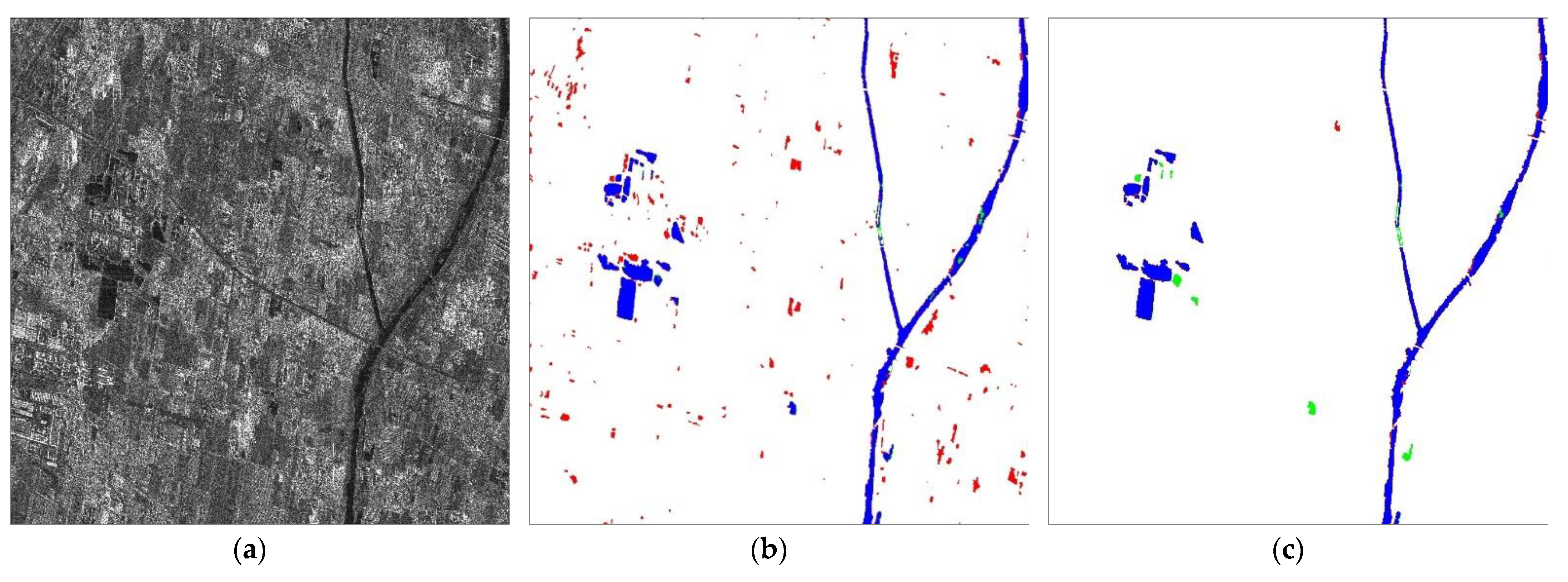
3.2.3. Proposed Method and Comparison Methods Results
4. Discussion
4.1. Qualitative Comparison for Different Water Types
4.2. Classification Accuracy Results of Three Methods
4.3. The Fitting Effect of Different Probability Distributions
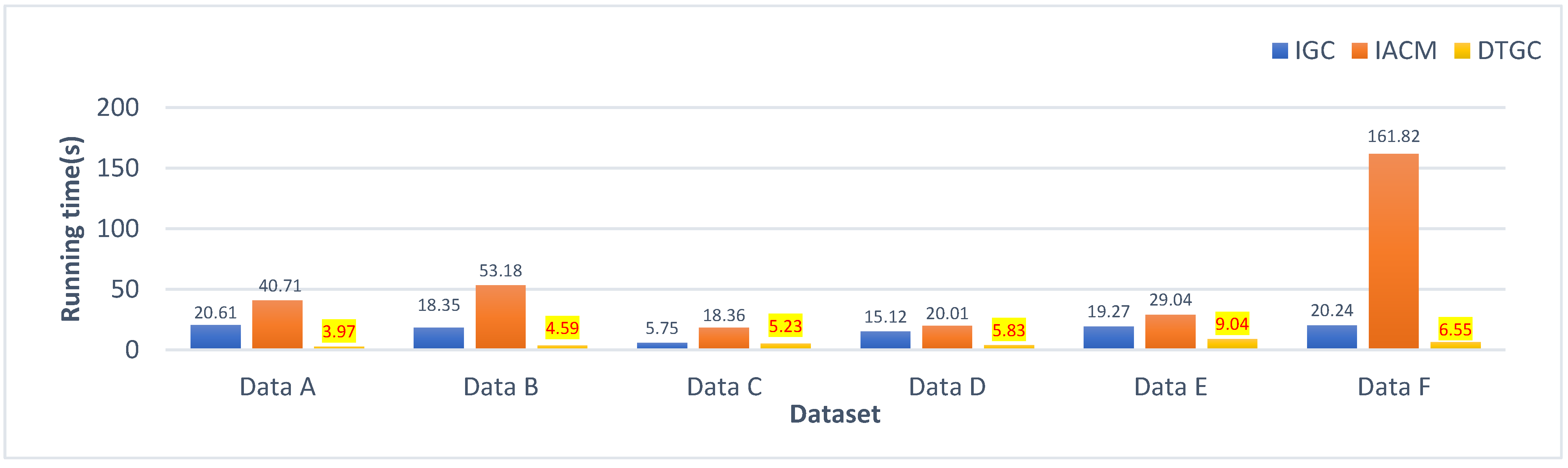
4.4. Algorithm Complexity
5. Conclusions
- Locating the optimal threshold range by introducing the dual threshold. The dual-threshold is a good approach to determine threshold automatically. The DTGC model provides better results, pinpointing the water body location.
- Expanding the types of water bodies extracted from SAR images. The proposed method performs reliably better across open lakes, rivers, and complex areas than other traditional methods, making it a compelling classification tool.
- Achieving rapid and automatic extraction of various water types without requiring manual screening of thresholds and other specific prior knowledge.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A


References
- Wang, Y.; Li, Z.; Zeng, C.; Xia, G.-S.; Shen, H. An Urban Water Extraction Method Combining Deep Learning and Google Earth Engine. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 769–782. [Google Scholar] [CrossRef]
- Zhuang, Y.; Wang, P.; Yang, Y.; Shi, H.; Chen, H.; Bi, F. Harbor Water Area Extraction from Pan-Sharpened Remotely Sensed Images Based on the Definition Circle Model. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1690–1694. [Google Scholar] [CrossRef]
- Yuan, J.; Lv, X.; Dou, F.; Yao, J. Change Analysis in Urban Areas Based on Statistical Features and Temporal Clustering Using TerraSAR-X Time-Series Images. Remote Sens. 2019, 11, 926. [Google Scholar] [CrossRef] [Green Version]
- Hoekstra, M.; Jiang, M.; Clausi, D.A.; Duguay, C. Lake Ice-Water Classification of RADARSAT-2 Images by Integrating IRGS Segmentation with Pixel-Based Random Forest Labeling. Remote Sens. 2020, 12, 1425. [Google Scholar] [CrossRef]
- Li, N.; Wang, R.; Deng, Y.; Chen, J.; Liu, Y.; Du, K.; Lu, P.; Zhang, Z.; Zhao, F. Waterline Mapping and Change Detection of Tangjiashan Dammed Lake After Wenchuan Earthquake from Multitemporal High-Resolution Airborne SAR Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3200–3209. [Google Scholar] [CrossRef]
- Bi, F.; Chen, J.; Wei, H.; Zhao, Y. A hierarchical method for accurate water region detection in SAR images. In Proceedings of the IET International Radar Conference 2015, Hangzhou, China, 14–16 October 2015; pp. 1–4. [Google Scholar]
- Zhou, Y.; Luo, J.; Shen, Z.; Hu, X.; Yang, H. Multiscale Water Body Extraction in Urban Environments from Satellite Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4301–4312. [Google Scholar] [CrossRef]
- Huang, X.; Xie, C.; Fang, X.; Zhang, L. Combining Pixel- and Object-Based Machine Learning for Identification of Water-Body Types from Urban High-Resolution Remote-Sensing Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2097–2110. [Google Scholar] [CrossRef]
- Guo, H.; He, G.; Jiang, W.; Yin, R.; Yan, L.; Leng, W. A Multi-Scale Water Extraction Convolutional Neural Network (MWEN) Method for GaoFen-1 Remote Sensing Images. ISPRS Int. J. Geoinf. 2020, 9, 189. [Google Scholar] [CrossRef] [Green Version]
- Katiyar, V.; Tamkuan, N.; Nagai, M. Near-Real-Time Flood Mapping Using Off-the-Shelf Models with SAR Imagery and Deep Learning. Remote Sens. 2021, 13, 2334. [Google Scholar] [CrossRef]
- Zhang, J.; Xing, M.; Sun, G. A Water Segmentation Algorithm for SAR Image Based on Dense Depthwise Separable Convolution. J. Radars 2019, 8, 400–412. [Google Scholar]
- Liu, Z.; Li, F.; Li, N.; Wang, R.; Zhang, H. A Novel Region-Merging Approach for Coastline Extraction From Sentinel-1A IW Mode SAR Imagery. IEEE Geosci. Remote Sens. Lett. 2016, 13, 324–328. [Google Scholar] [CrossRef]
- Du, Y.; Xu, J.; Liu, S. Water Self-extraction Algorithm From Remote Sensing Image Based on Improved Graph Cut. Comput. Eng. Design 2019, 40, 1413–1417. [Google Scholar]
- Leng, Y.; Liu, Z.; Zhang, H.; Wang, Y.; Li, N. Improved ACM Algorithm for Poyang Lake Monitoring. J. Electron. Inf. Technol. 2017, 39, 1064–1070. [Google Scholar]
- Ciecholewski, M. River channel segmentation in polarimetric SAR images: Watershed Transform Combined with Average Contrast Maximisation. Expert Syst. Appl. 2017, 82, 196–215. [Google Scholar] [CrossRef]
- Sghaier, M.O.; Foucher, S.; Lepage, R. River Extraction from High-Resolution SAR Images Combining a Structural Feature Set and Mathematical Morphology. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1025–1038. [Google Scholar] [CrossRef]
- Hu, S.; Qin, J.; Ren, J.; Zhao, H.; Ren, J.; Hong, H. Automatic Extraction of Water Inundation Areas Using Sentinel-1 Data for Large Plain Areas. Remote Sens. 2020, 12, 243. [Google Scholar] [CrossRef] [Green Version]
- Mao, C.; Wan, S. A Water/Land Segmentation Algorithm Based on an Improved Chan-Vese Model with Edge Constraints of Complex Wavelet Domain. Chin. J. Electron. 2015, 24, 361–365. [Google Scholar] [CrossRef]
- Zeng, L.; Schmitt, M.; Li, L.; Zhu, X.X. Analysing changes of the Poyang Lake water area using Sentinel-1 synthetic aperture radar imagery. Int. J. Remote Sens. 2017, 38, 7041–7069. [Google Scholar] [CrossRef] [Green Version]
- Ding, X.; Li, X. Monitoring of the water-area variations of Lake Dongting in China with ENVISAT ASAR images. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 894–901. [Google Scholar] [CrossRef]
- Xing, L.; Tang, X.; Wang, H.; Fan, W.; Wang, G. Monitoring monthly surface water dynamics of Dongting Lake using Sentinel-1 data at 10 m. PeerJ 2018, 6, e4992. [Google Scholar] [CrossRef] [PubMed]
- Niu, S.; Li, N.; Guo, Z.; Wang, R.; Guo, Y.; Wu, L.; Zhao, J. Robust boundary extraction of great lakes by blocking Active Contour Model using Chinese GF-3 SAR data: A case study of Danjiangkou reservoir, China. J. Eng. 2019, 2019, 6876–6879. [Google Scholar] [CrossRef]
- Ferrentino, E.; Nunziata, F.; Buono, A.; Urciuoli, A.; Migliaccio, M. Multi-polarization time-series of Sentinel-1 SAR imagery to analyze variations of reservoirs’ water-body. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 840–846. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Y.; Zhao, Q. Urban Riverway Extraction from High-Resolution SAR Image Based on Blocking Segmentation and Discontinuity Connection. Remote Sens. 2020, 12, 4014. [Google Scholar] [CrossRef]
- Mason, D.C.; Speck, R.; Devereux, B.; Schumann, G.J.P.; Neal, J.C.; Bates, P.D. Flood Detection in Urban Areas Using TerraSAR-X. IEEE Trans. Geosci. Remote Sens. 2010, 48, 882–894. [Google Scholar] [CrossRef] [Green Version]
- Zeng, C.; Wang, J.; Huang, X.; Bird, S.; Luce, J.J. Urban water body detection from the combination of high-resolution optical and SAR images. In Proceedings of the 2015 Joint Urban Remote Sensing Event (JURSE), Lausanne, Switzerland, 30 March–1 April 2015. [Google Scholar]
- Feyisa, G.L.; Meilby, H.; Fensholt, R.; Proud, S.R. Automated Water Extraction Index: A new technique for surface water mapping using Landsat imagery. Remote Sens. 2014, 140, 23–35. [Google Scholar] [CrossRef]
- Liang, J.; Liu, D. A local thresholding approach to flood water delineation using Sentinel-1 SAR imagery. ISPRS J. Photogramm. Remote Sens. 2020, 159, 53–62. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, Z.; Chen, Y.; Liu, S.; Song, Y. Frost Filtering Algorithm of SAR Images with Adaptive Windowing and Adaptive Tuning Factor. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1097–1101. [Google Scholar] [CrossRef]
- Greig, D.M.; Porteous, B.T.; Seheult, A.H. Exact Maximum A Posteriori Estimation for Binary Images. J. R. Stat. Soc. 1989, 51, 271–279. [Google Scholar] [CrossRef]
- Meng, Q.; Wen, X.; Yuan, L.; Xu, H. Factorization-Based Active Contour for Water-Land SAR Image Segmentation via the Fusion of Features. IEEE Access 2019, 7, 40347–40358. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef] [Green Version]
- Deng, Y.; Zhang, H.; Wang, C.; Liu, M. Object-oriented water extraction of PolSAR image based on target decomposition. In Proceedings of the 2015 IEEE 5th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Singapore, 1–4 September 2015; pp. 596–601. [Google Scholar]
- Dempster, A.P. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. 1977, 39, 1–38. [Google Scholar]
- Zhao, B.; Zhong, Y.; Ma, A.; Zhang, L. A Spatial Gaussian Mixture Model for Optical Remote Sensing Image Clustering. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 5748–5759. [Google Scholar] [CrossRef]
- Xiao, P.; Yuan, M.; Zhang, X.; Feng, X.; Guo, Y. Cosegmentation for Object-Based Building Change Detection from High-Resolution Remotely Sensed Images. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1587–1603. [Google Scholar] [CrossRef]
- Zhang, K.; Fu, X.; Lv, X.; Yuan, J. Unsupervised Multitemporal Building Change Detection Framework Based on Cosegmentation Using Time-Series SAR. Remote Sens. 2021, 13, 471. [Google Scholar] [CrossRef]
- Boykov, Y.; Kolmogorov, V. An experimental comparison of min-cut/max- flow algorithms for energy minimization in vision. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 1124–1137. [Google Scholar] [CrossRef] [Green Version]
- Chen, P.; Cai, X.; Zhao, D.; Liang, R.; Intelligence, M. Side scan sonar image speckle noise reduction based on adaptive BM3D. Opto-Electron. Eng. 2020, 47, 71–80. [Google Scholar]
- Giustarini, L.; Hostache, R.; Kavetski, D.; Chini, M.; Corato, G.; Schlaffer, S.; Matgen, P. Probabilistic Flood Mapping Using Synthetic Aperture Radar Data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6958–6969. [Google Scholar] [CrossRef]
- Giustarini, L.; Hostache, R.; Matgen, P.; Schumann, G.J.P.; Bates, P.D.; Mason, D.C. A Change Detection Approach to Flood Mapping in Urban Areas Using TerraSAR-X. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2417–2430. [Google Scholar] [CrossRef] [Green Version]


| Edge Type | Weight | Condition |
|---|---|---|
| 0 | ||
| 0 |
| Scheme | Satellite | Size | Location | Type | Polarization | Date |
|---|---|---|---|---|---|---|
| Data A | TerraSAR-X | 2404 × 2638 | Chaoyang District, Beijing | Urban water | HH | 9 May 2013 |
| Data B | GF-3 | 2444 × 2444 | Fangshan District, Beijing | Urban water | HH | 28 July 2017 |
| Data C | Sentinal-1 | 4669 × 3032 | Poyang Lake, Jiangxi | Lakes | VH | 8 July 2020 |
| Data D | Sentinal-1 | 2965 × 1735 | East Lake, Hunan | Lakes and rivers | VH | 25 September 2016 |
| Data E | Sentinal-1 | 2765 × 3007 | Poyang Lake, Jiangxi | Small tributary | VH | 8 July 2020 |
| Data F | TerraSAR-X | 6626 × 5273 | Xiangjiang, Hunan | Rivers | HH | 24 July 2020 |
| Parameter | Data A | Data B | Data C | Data D | Data E | Data F |
|---|---|---|---|---|---|---|
| 0.3 | 0.45 | 0.35 | 0.75 | 0.8 | 0.5 | |
| 0.2 | 0.25 | 0.2 | 0.45 | 0.2 | 0.2 | |
| 0.8 | 0.25 | 0.9 | 0.2 | 0.2 | 0.2 | |
| 10 | 10 | 5 | 10 | 20 | 20 |
| Image | Data A | Data B | Data C | Data D | Data E | Data F |
|---|---|---|---|---|---|---|
| Original | 12.71 | 9.55 | 5.66 | 10.40 | 11.94 | 17.60 |
| Denoised | 3.52 | 3.26 | 4.36 | 8.57 | 9.80 | 5.02 |
| Test data | Method | OA(%) | Pre(%) | Rec(%) | Kappa | F1-score | IoU |
|---|---|---|---|---|---|---|---|
| Data A | IGC | 90.91 | 72.48 | 99.31 | 0.826 | 0.838 | 0.721 |
| IACM | 95.27 | 55.69 | 99.09 | 0.689 | 0.713 | 0.554 | |
| DTGC | 99.70 | 96.26 | 98.82 | 0.972 | 0.975 | 0.952 | |
| Data B | IGC | 18.12 | 3.18 | 99.96 | 0.010 | 0.062 | 0.032 |
| IACM | 65.59 | 4.35 | 56.08 | 0.032 | 0.081 | 0.042 | |
| DTGC | 99.50 | 90.13 | 92.46 | 0.906 | 0.908 | 0.832 | |
| Data C | IGC | 99.03 | 98.34 | 97.08 | 0.971 | 0.977 | 0.955 |
| IACM | 98.92 | 95.99 | 99.09 | 0.968 | 0.975 | 0.952 | |
| DTGC | 99.16 | 96.91 | 99.22 | 0.975 | 0.981 | 0.962 | |
| Data D | IGC | 98.77 | 88.51 | 99.69 | 0.931 | 0.938 | 0.883 |
| IACM | 98.94 | 90.00 | 99.73 | 0.940 | 0.946 | 0.900 | |
| DTGC | 99.46 | 96.61 | 98.13 | 0.970 | 0.972 | 0.946 | |
| Data E | IGC | 99.04 | 87.62 | 96.28 | 0.912 | 0.917 | 0.847 |
| IACM | 92.16 | 41.13 | 97.40 | 0.547 | 0.580 | 0.408 | |
| DTGC | 99.24 | 90.64 | 96.32 | 0.929 | 0.934 | 0.876 | |
| Data F | IGC | 99.66 | 92.13 | 99.45 | 0.955 | 0.957 | 0.917 |
| IACM | 99.63 | 91.28 | 99.53 | 0.950 | 0.952 | 0.909 | |
| DTGC | 99.88 | 99.13 | 97.72 | 0.983 | 0.984 | 0.969 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, L.; Lv, X.; Yao, J. Water Extraction in SAR Images Using Features Analysis and Dual-Threshold Graph Cut Model. Remote Sens. 2021, 13, 3465. https://doi.org/10.3390/rs13173465
Bao L, Lv X, Yao J. Water Extraction in SAR Images Using Features Analysis and Dual-Threshold Graph Cut Model. Remote Sensing. 2021; 13(17):3465. https://doi.org/10.3390/rs13173465
Chicago/Turabian StyleBao, Linan, Xiaolei Lv, and Jingchuan Yao. 2021. "Water Extraction in SAR Images Using Features Analysis and Dual-Threshold Graph Cut Model" Remote Sensing 13, no. 17: 3465. https://doi.org/10.3390/rs13173465
APA StyleBao, L., Lv, X., & Yao, J. (2021). Water Extraction in SAR Images Using Features Analysis and Dual-Threshold Graph Cut Model. Remote Sensing, 13(17), 3465. https://doi.org/10.3390/rs13173465





