EddyGraph: The Tracking of Mesoscale Eddy Splitting and Merging Events in the Northwest Pacific Ocean
Abstract
:1. Introduction
2. Data and Methods
2.1. Data
2.2. Eddytree: Eddy Identification with Spatial Topological Relationship
2.2.1. Eddytree
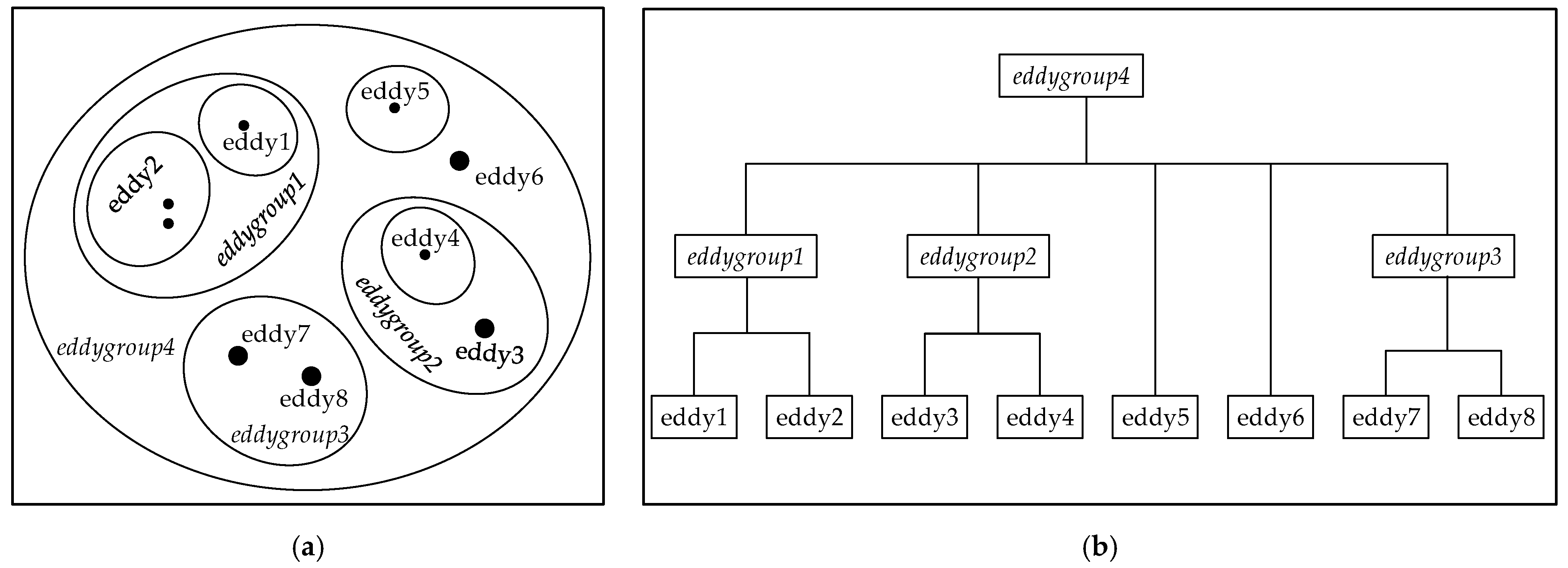
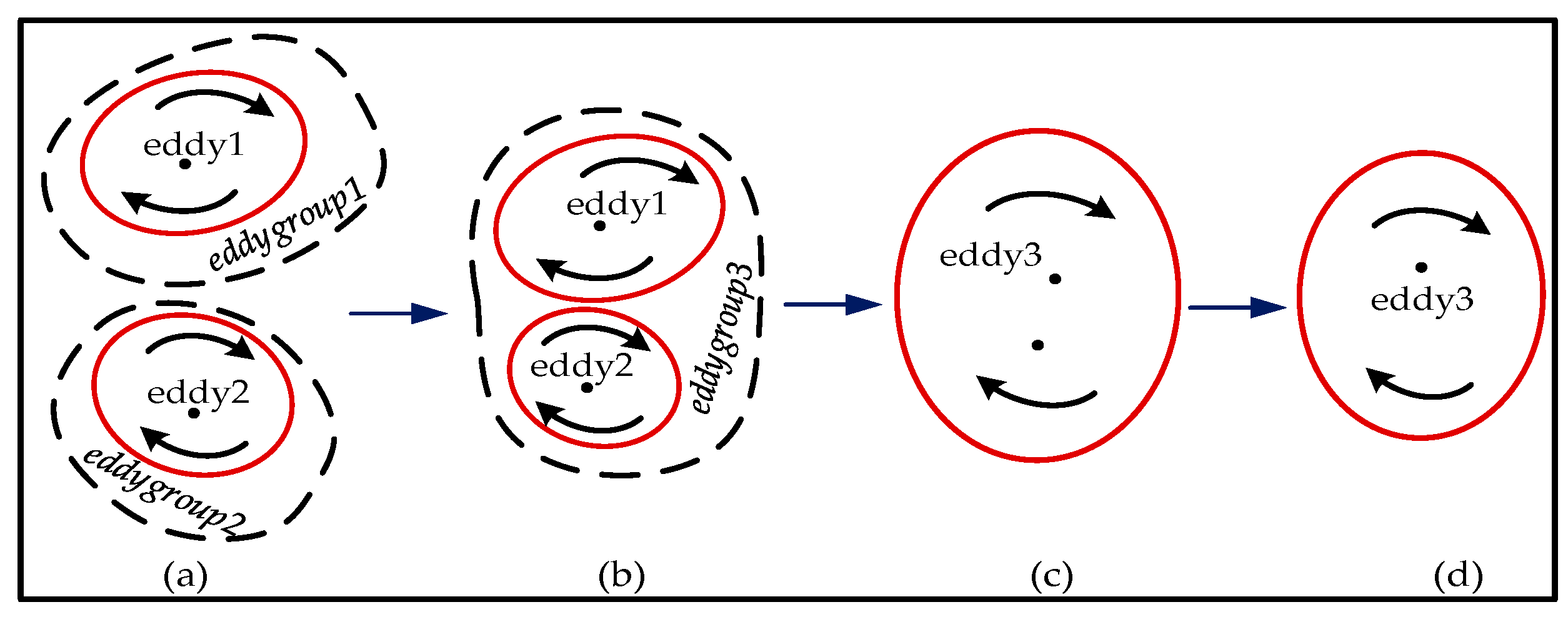
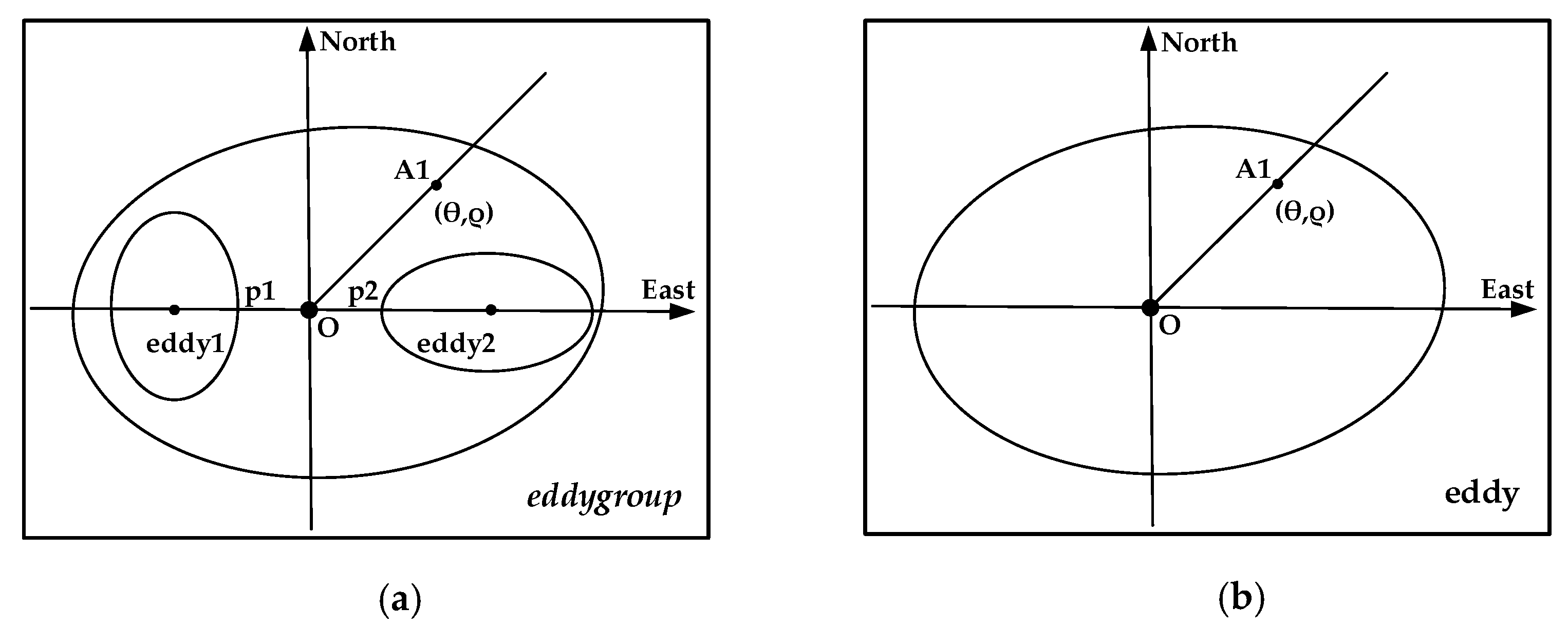
2.2.2. Eddygroup
2.2.3. Eddy Identification Criteria
- (i)
- Mononuclear eddy
- (1)
- Only one local SLA maxima/minima point is contained.
- (2)
- There are I pixels (0.25° × 0.25°), where 4 ≤ I < ≤ 2000.
- (3)
- The amplitude A ≥ 0.25 cm, where A = |h1 − h0|, h1 is the SLA value at the local maxima/minima point in the eddy and h0 is the SLA value on the outermost closed SLA contour that defines the eddy perimeter.
- (ii)
- Multicore eddyThe boundaries of multicore eddies should satisfy the following criteria:
- (1)
- Multiple local SLA maxima/minima points are contained.
- (2)
- Multicore eddies are independent of mononuclear eddies: multicore eddies do not contain any mononuclear eddies, which means that any local maxima/minima point within a multicore eddy cannot be identified as a mononuclear eddy.
- (3)
- The amplitude A ≥ 0.25 cm, where A =|hm − h0|, hm is the SLA value at the local maxima/minima point with the largest A among all the local maxima/minima points in the eddy and h0 is the SLA value on the outermost closed SLA contour that defines the eddy perimeter.
- (iii)
- Eddy seed
2.3. EddyGraph: Eddy Splitting and Merging Tracking
2.3.1. Criteria
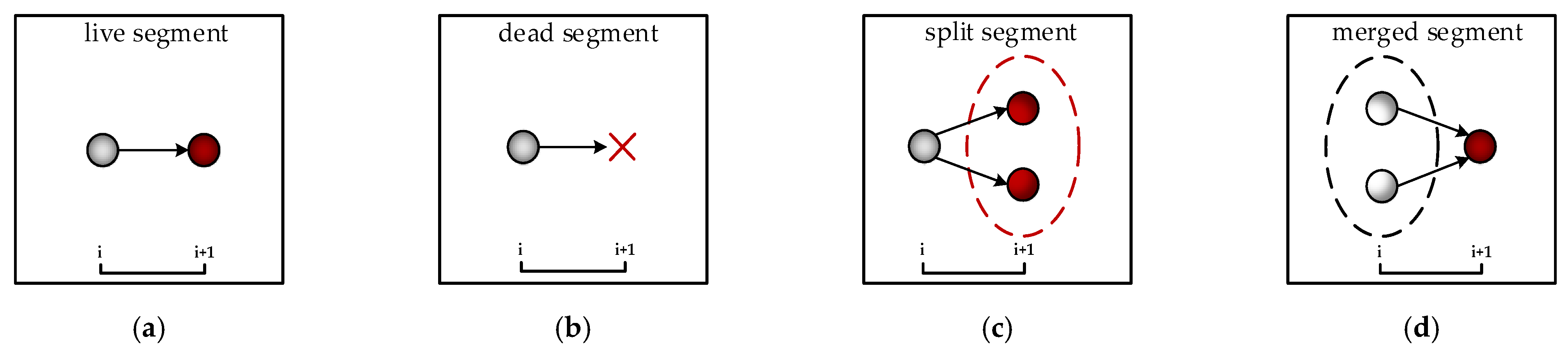
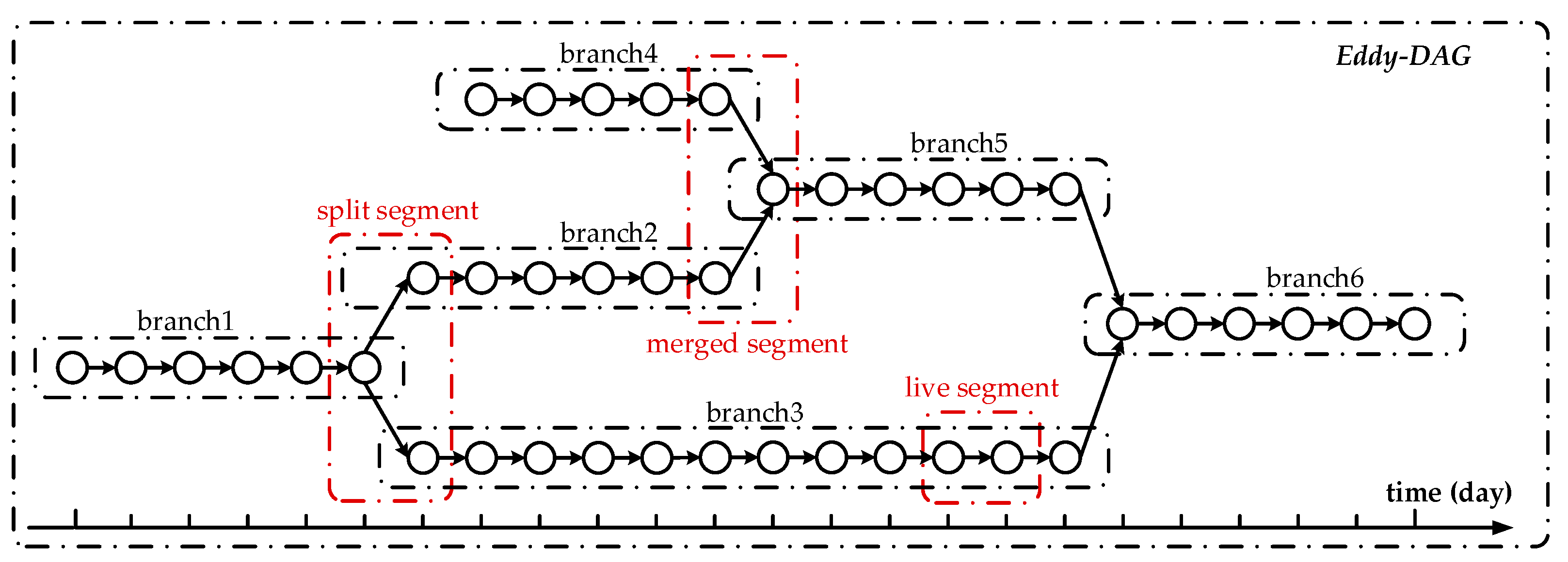
- (i)
- Segment
- (ii)
- Branch
- (iii)
- Eddy-DAG
2.3.2. Tracking for Eddy Splitting and Merging
- (i)
- Segment
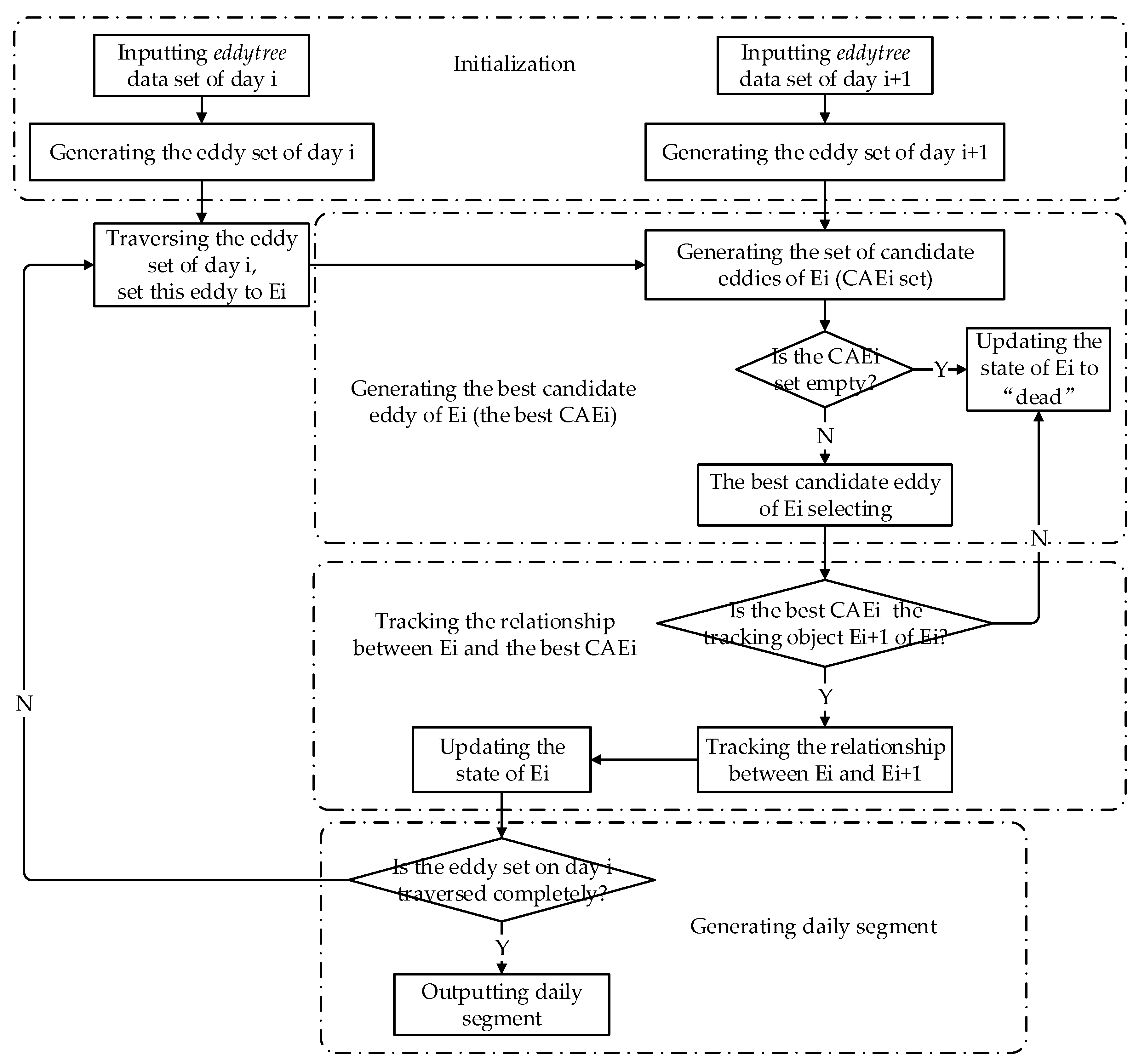
- (1)
- Initialization: First, the eddy sets for day i and day i + 1 are generated from the eddytree data set. Then, the eddy set on day i will be traversed (set this eddy to Ei).
- (2)
- Generating the best candidate eddy of Ei (the best CAEi): If Ei is not dead on day i + 1, the tracking object Ei + 1 of Ei should be within the search circle with a radius of 0.5° [27] and the eddy core of Ei as the center, based on which the set of candidate eddies of Ei (the CAEi set) is retrieved from the eddy set of day i + 1. If the CAEi set is empty, Ei is dead on day i + 1. If the CAEi set is a nonempty set, the best CAEi is selected based on the largest overlapping area principle and the nearest principle. When one of the best CAEi and Ei is an eddy seed and the other is a multicore eddy/mononuclear eddy, the best CAEi is the tracking object Ei + 1 of Ei only if eddy seed is within in the boundary of a multicore eddy/mononuclear eddy. For the other classification of the best CAEi and Ei, the best CAEi is the tracking object Ei + 1 of Ei.
- (3)
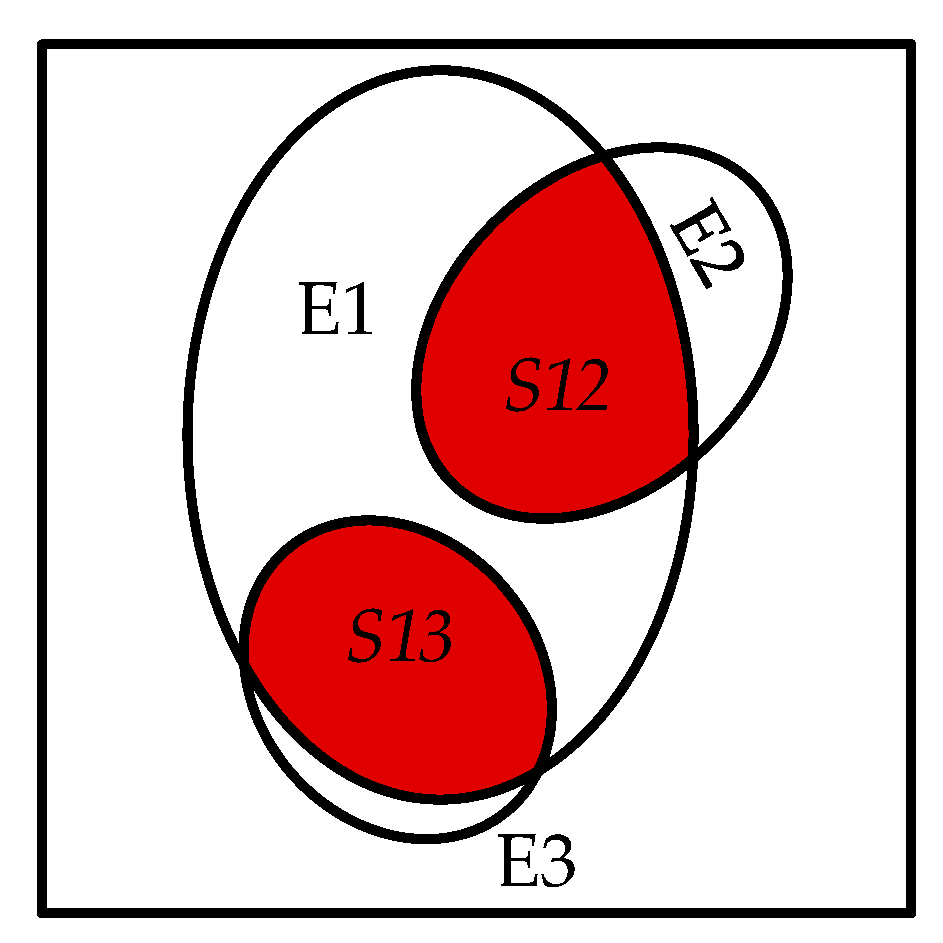
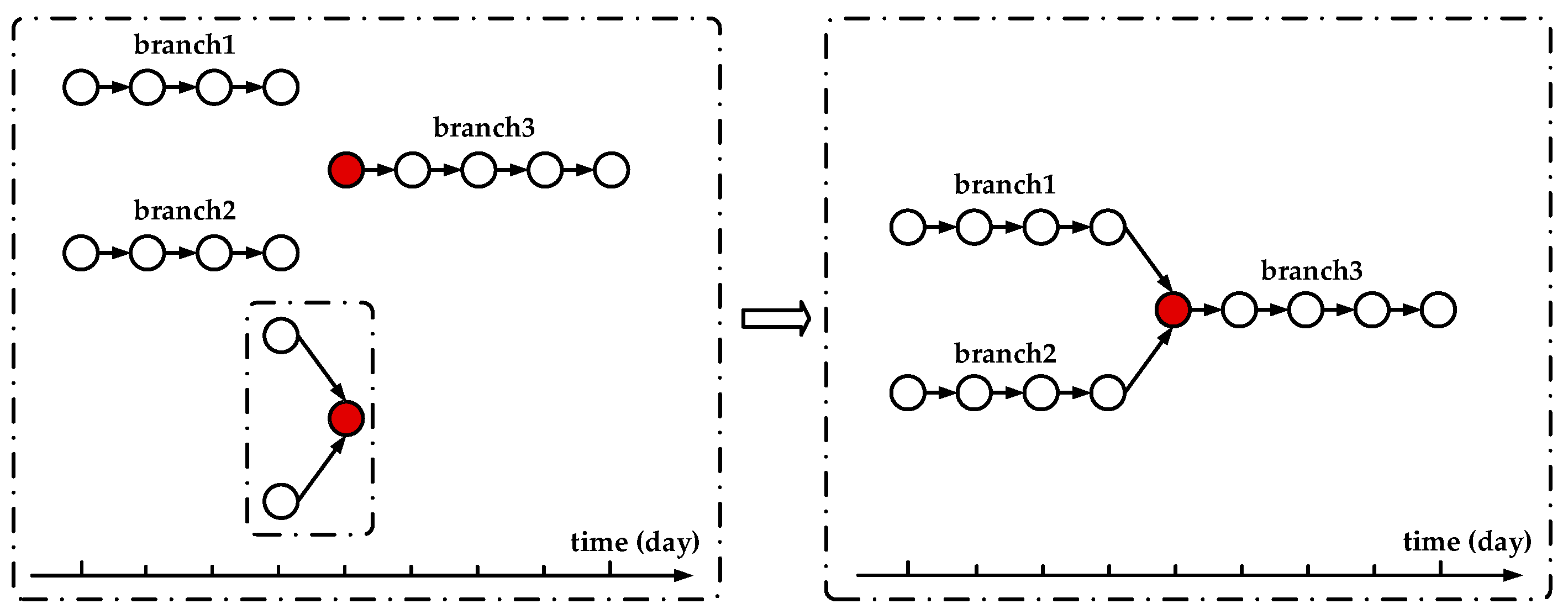
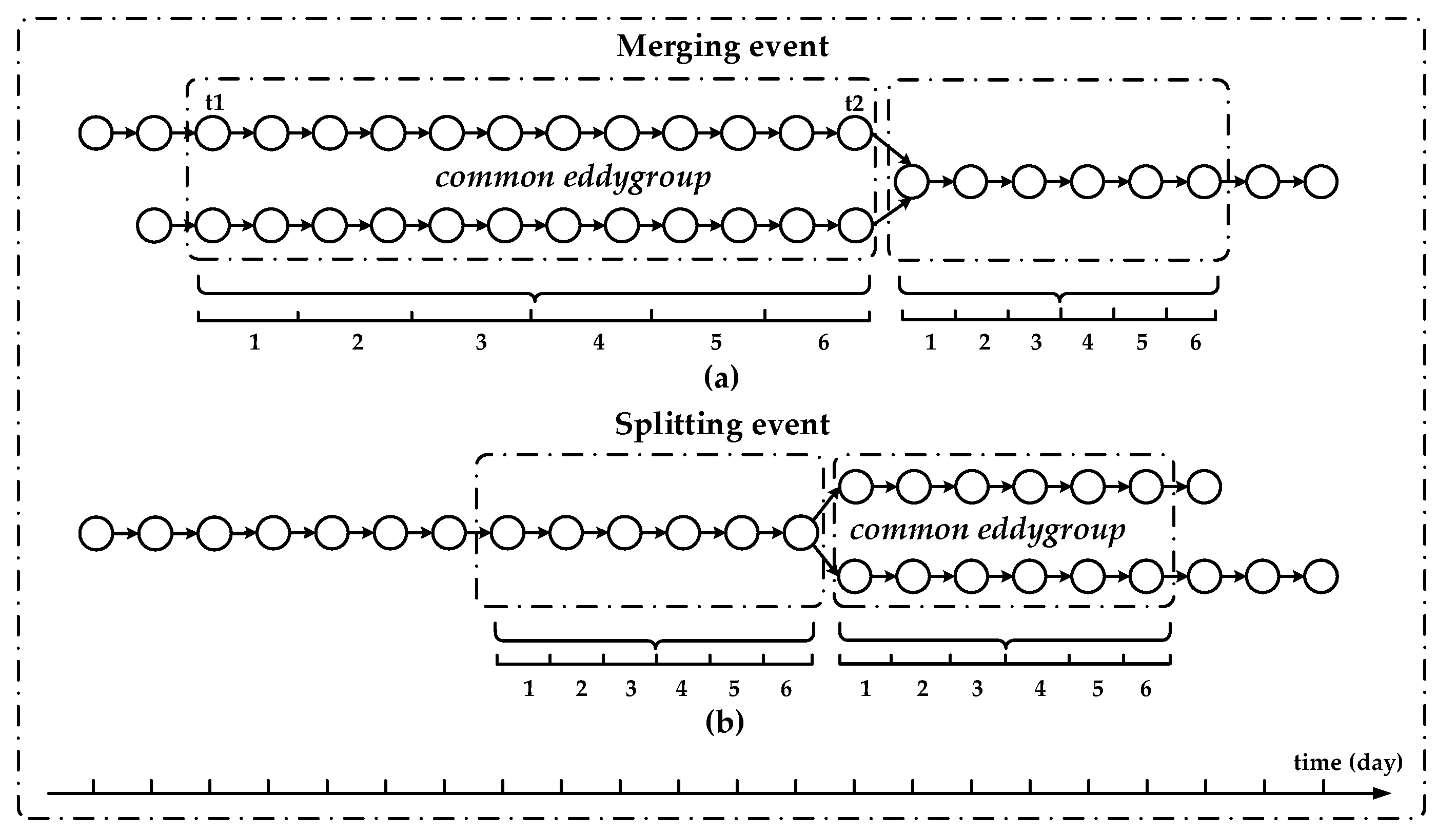
- Tracking the relationship between Ei and the best CAEi: If the best CAEi is not the tracking object Ei + 1 of Ei, Ei is dead on day i + 1. Otherwise, based on the common eddygroup, the splitting and merging relationships between Ei and Ei + 1 are tracked by the similarity method with the area overlap ratio as the similarity parameter [31]:where S1 is the area of eddy E1 and S2 is the area of eddy E2. Moreover, S12 is the area of overlap between E1 and E2. The area overlap ratio of eddy E1 with E2 can be represented by r1, whereas the area overlap ratio of eddy E2 with E1 is r2. E2 is the part from E1 when r2 ≥ 2/3 (Figure 7) [24]. (On the contrary, E1 is the part from E2 when r1 ≥ 2/3. In this paper, we take r2 ≥ 2/3 as an example.) In this study, r2 should be no less than 2/3 when eddy E2 is split from eddy E1. Similarly, r3 should also be no less than 2/3 when eddy E3 merges into eddy E1 (Figure 7). If no splitting or merging occurs between them, Ei + 1 is alive from Ei. Figure 4a,c,d show the possible relationships between Ei and Ei + 1. A sink eddy Ei + 1 generated from splitting is either an eddy seed within the boundary of Ei or a mononuclear eddy/multicore eddy with its area overlap ratio with Ei being no less than 2/3 and must be in the common eddygroup with its sibling eddy (Figure 4c). A source eddy Ei merging into Ei + 1 is either a mononuclear eddy/multicore eddy with its area overlap ratio with Ei + 1 being no less than 2/3 or an eddy seed within the boundary of Ei + 1 and must be in the common eddygroup with its sibling eddy (Figure 4d). Ei + 1 with no splitting or merging relationship with Ei is alive from Ei (Figure 4a).
- (4)
- Generating daily segment: Finally, when the traversal of the eddy set of day i terminates, the process of tracking the segments for the eddies on day i is finished.
- (ii)
- Branch
- (iii)
- Eddy-DAG
3. Results
3.1. Statistics of the Tracking Data Set
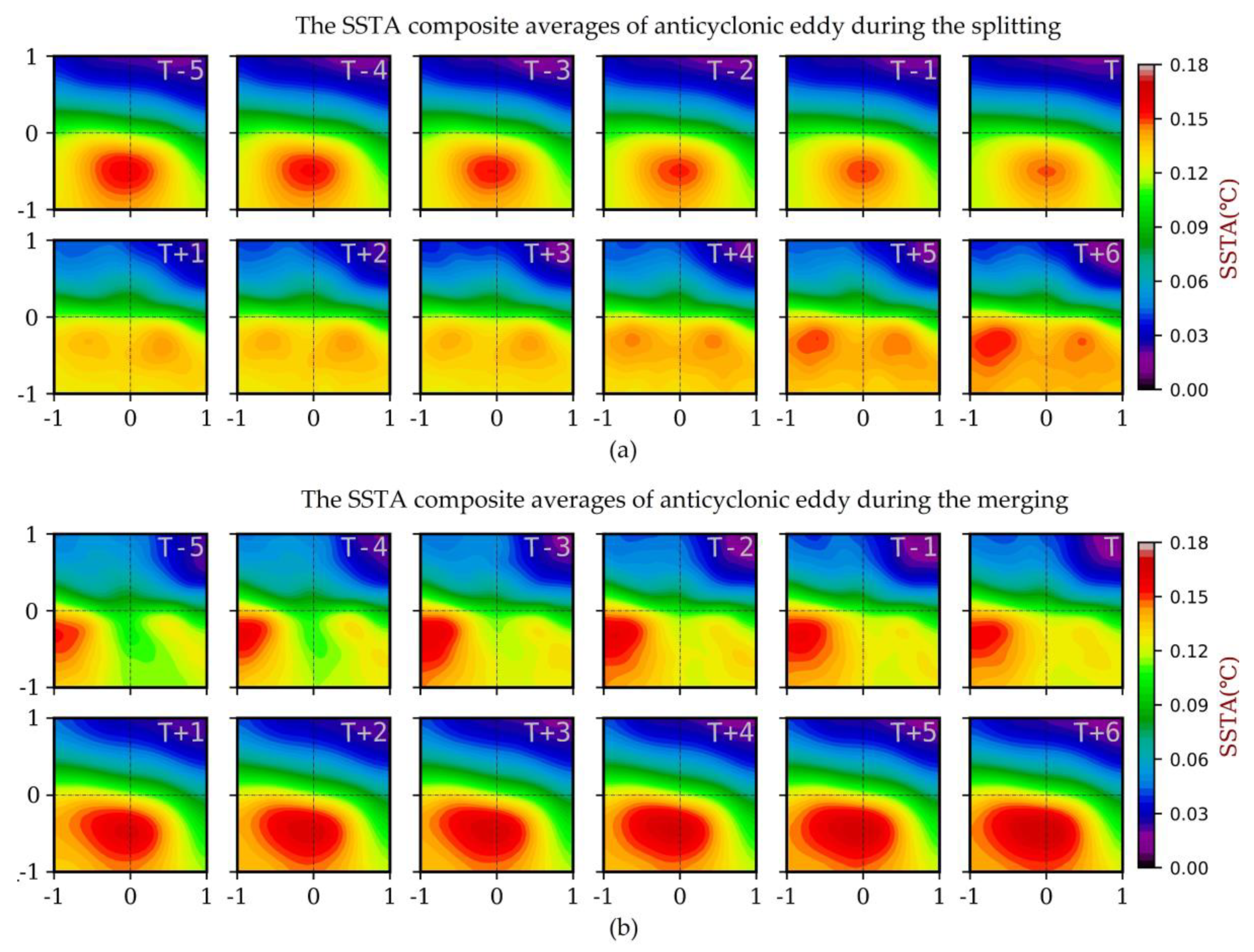
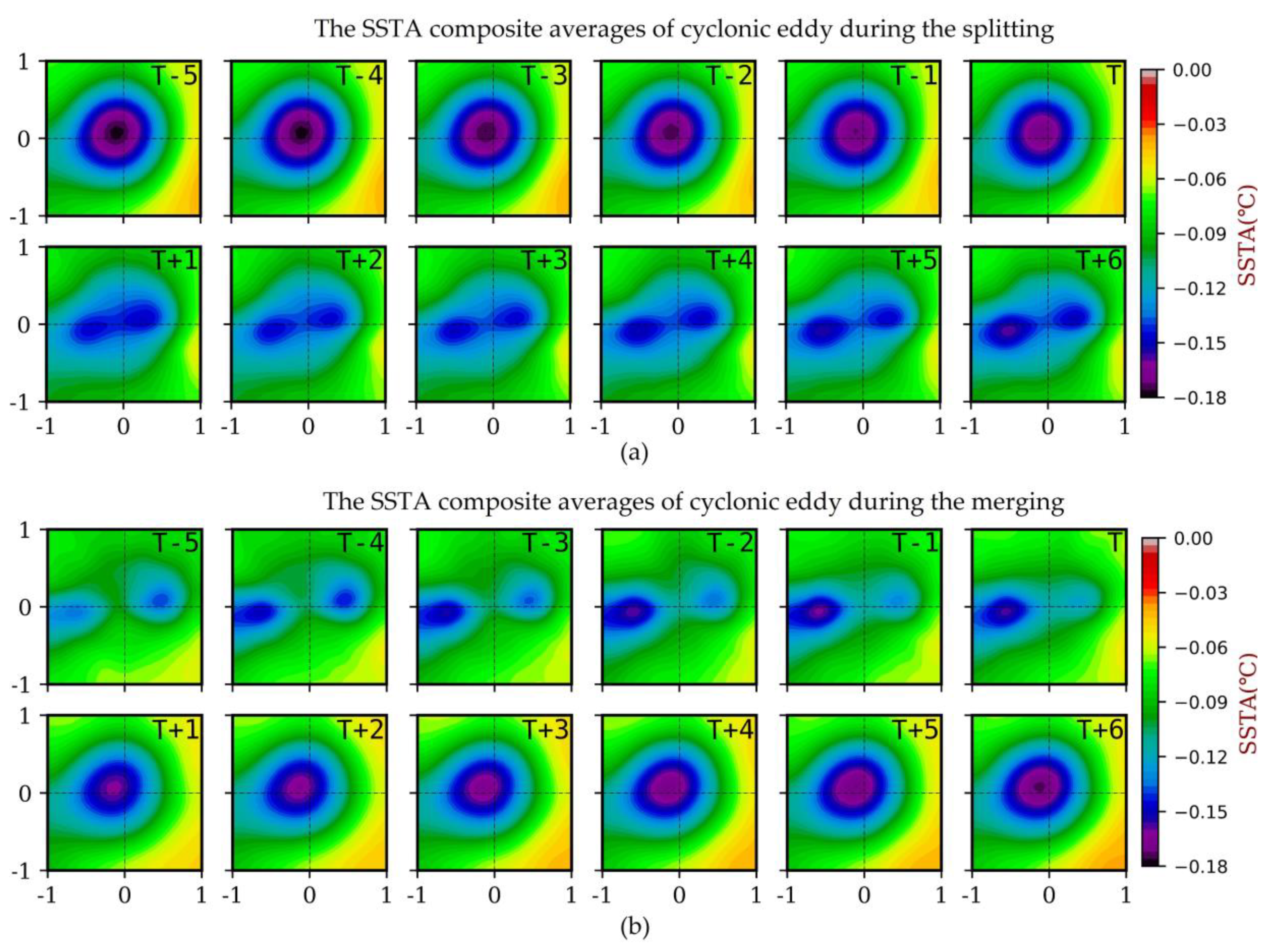
3.2. Extraction of Typical Events
4. Validation
4.1. Verification with Remote Sensing Observations
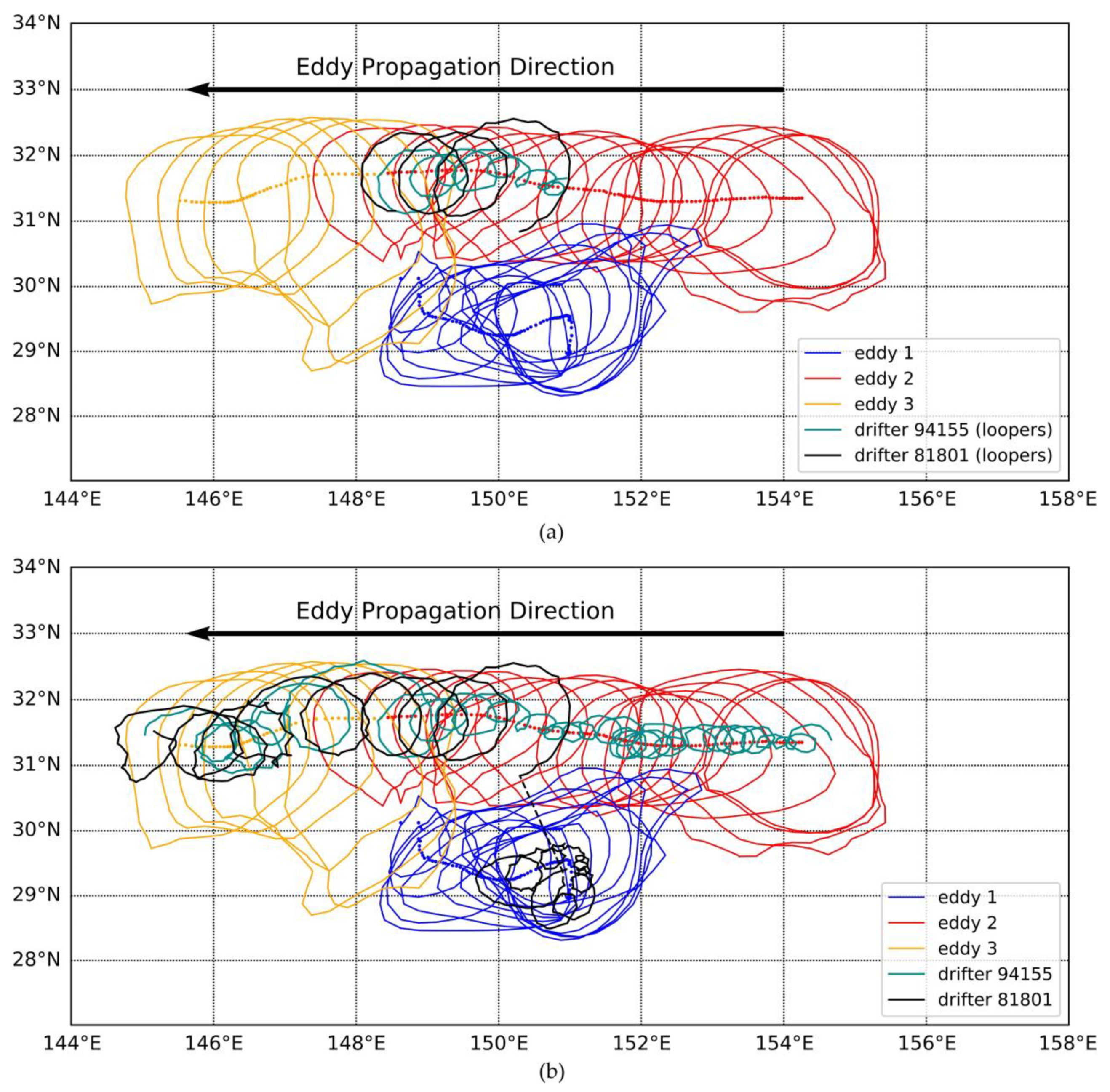
4.2. Verification with In Situ Data
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chelton, D.B.; Gaube, P.; Schlax, M.G.; Early, J.J.; Samelson, R.M. The Influence of Nonlinear Mesoscale Eddies on Near-Surface Oceanic Chlorophyll. Science 2011, 334, 328. [Google Scholar] [CrossRef] [PubMed]
- Volkov, D.L.; Tong, L.; Fu, L.L. Eddy-induced meridional heat transport in the ocean. Geophys. Res. Lett. 2008, 35, 295–296. [Google Scholar] [CrossRef] [Green Version]
- Wunsch, C. Where do ocean eddy heat fluxes matter? J. Geophys. Res. Ocean. 1999, 104, 13235–13249. [Google Scholar] [CrossRef]
- Roemmich, D.; Gilson, J. Eddy Transport of Heat and Thermocline Waters in the North Pacific: A Key to Interannual/Decadal Climate Variability? J. Phys. Oceanogr. 2001, 13, 675–688. [Google Scholar] [CrossRef]
- Hausmann, U.; Czaja, A. The observed signature of mesoscale eddies in sea surface temperature and the associated heat transport. Deep-Sea Res. Part. I Oceanogr. Res. Pap. 2012, 70, 60–72. [Google Scholar] [CrossRef]
- Morrow, R.; Traon, P. Recent advances in observing mesoscale ocean dynamics with satellite altimetry. Adv. Space Res. 2012, 50, 1062–1076. [Google Scholar] [CrossRef] [Green Version]
- Dong, C.; Mcwilliams, J.C.; Liu, J.; Chen, D. Global heat and salt transports by eddy movement. Nat. Commun. 2014, 5, 3294. [Google Scholar] [CrossRef] [Green Version]
- Amores, A.; Melnichenko, O.; Maximenko, N. Coherent mesoscale eddies in the North Atlantic subtropical gyre: 3-D structure and transport with application to the salinity maximum. J. Geophys. Res. Ocean. 2017, 122, 23–41. [Google Scholar] [CrossRef]
- Sun, B.; Liu, C.; Wang, F. Eddy induced SST variation and heat transport in the western North Pacific Ocean. J. Oceanol. Limnol. 2020, 38, 1–15. [Google Scholar] [CrossRef]
- Zhang, Z.; Wei, W.; Qiu, B. Oceanic mass transport by mesoscale eddies. Science 2014, 345, 322–324. [Google Scholar] [CrossRef]
- Sadarjoen, I.A.; Post, F.H. Detection, quantification, and tracking of vortices using streamline geometry. Comput. Graph. 2000, 24, 333–341. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M.; de Szoeke, R.A. Global observations of large oceanic eddies. Geophys. Res. Lett. 2007, 34, 87–101. [Google Scholar] [CrossRef]
- Henson, S.A.; Thomas, A.C. A census of oceanic anticyclonic eddies in the Gulf of Alaska. Deep-Sea Res. Part I 2008, 55, 163–176. [Google Scholar] [CrossRef]
- Chaigneau, A.; Gizolme, A.; Grados, C. Mesoscale eddies off peru in altimeter records: Identification algorithms and eddy spatio-temporal patterns. Prog. Oceanogr. 2008, 79, 106–119. [Google Scholar] [CrossRef]
- Isern-Fontanet, J.; Garcia-Ladona, E.; Font, J. Identification of Marine Eddies from Altimetric Maps. J. Atmos. Ocean. Technol. 2003, 20, 772–778. [Google Scholar] [CrossRef]
- Nencioli, F.; Dong, C.M.; Dickey, T.; Washburn, L.; McWilliams, J.C. A Vector Geometry-Based Eddy Detection Algorithm and Its Application to a High-Resolution Numerical Model Product and High-Frequency Radar Surface Velocities in the Southern California Bight. J. Atmos. Ocean. Technol. 2010, 27, 564–579. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M. Global observations of nonlinear mesoscale eddies. Prog. Oceanogr. 2011, 91, 167–216. [Google Scholar] [CrossRef]
- Faghmous, J.H.; Frenger, I.; Yao, Y.S.; Warmka, R.; Lindell, A.; Kumar, V. A daily global mesoscale ocean eddy dataset from satellite altimetry. Sci. Data 2015, 2, 150028. [Google Scholar] [CrossRef] [Green Version]
- Mason, E.; Pascual, A.; McWilliams, J.C. A New Sea Surface Height–Based Code for Oceanic Mesoscale Eddy Tracking. J. Atmos. Ocean. Technol. 2014, 31, 1181–1188. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Chen, G.; Sun, M.; Liu, S.; Tian, F. A Parallel SLA-Based Algorithm for Global Mesoscale Eddy Identification. J. Atmos. Ocean. Technol. 2016, 33, 2743–2754. [Google Scholar] [CrossRef]
- Penven, P.; Echevin, V.; Pasapera, J.; Colas, F.; Tam, J. Average circulation, seasonal cycle, and mesoscale dynamics of the Peru Current System: A modeling approach. J. Geophys. Res. Ocean. 2005, 110, C10021. [Google Scholar] [CrossRef]
- Halo, I.; Backeberg, B.; Penven, P.; Ansorge, I.; Reason, C.; Ullgren, J.E. Eddy properties in the Mozambique Channel: A comparison between observations and two numerical ocean circulation models. Deep-Sea Res. Part II 2014, 100, 38–53. [Google Scholar] [CrossRef]
- Le Vu, B.; Stegner, A.; Arsouze, T. Angular Momentum Eddy Detection and tracking Algorithm (AMEDA) and its application to coastal eddy formation. J. Atmos. Ocean. Technol. 2017, 35, 739–762. [Google Scholar] [CrossRef]
- Mkhinini, N.; Coimbra, A.; Stegner, A.; Arsouze, T.; Taupier-Letage, I.; Béranger, K. Long-lived mesoscale eddies in the eastern Mediterranean Sea: Analysis of 20 years of AVISO geostrophic velocities. J. Geophys. Res. Ocean. 2014, 119, 8603–8626. [Google Scholar] [CrossRef]
- Pessini, F.; Olita, A.; Cotroneo, Y.; Perilli, A. Mesoscale eddies in the Algerian Basin: Do they differ as a function of their formation site? Ocean. Sci. 2018, 14, 669–688. [Google Scholar] [CrossRef] [Green Version]
- Haller, G. An objective definition of a vortex. J. Fluid Mech. 2005, 525, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Sun, M.; Tian, F.; Liu, Y.; Chen, G. An Improved Automatic Algorithm for Global Eddy Tracking Using Satellite Altimeter Data. Remote Sens. 2017, 9, 206. [Google Scholar] [CrossRef] [Green Version]
- Tian, F.; Wu, D.; Yuan, L.; Chen, G. Impacts of the efficiencies of identification and tracking algorithms on the statistical properties of global mesoscale eddies using merged altimeter data. Int. J. Remote Sens. 2020, 41, 2835–2860. [Google Scholar] [CrossRef]
- Isern-Fontanet, J.; Lapeyre, G.; Klein, P.; Chapron, B.; Hecht, M.W. Three-dimensional reconstruction of oceanic mesoscale currents from surface information. J. Geophys. Res. Ocean. 2008, 113, C09005. [Google Scholar] [CrossRef] [Green Version]
- Fa, N.F.; Morrow, R. Evolution, movement and decay of warm-core Leeuwin Current eddies. Deep-Sea Res. Part II 2003, 50, 2245–2261. [Google Scholar]
- Zhai, X.; Johnson, H.L.; Marshall, D.P. Significant sink of ocean-eddy energy near western boundaries. Nat. Geosci. 2010, 3, 608–612. [Google Scholar] [CrossRef]
- Li, Q.Y.; Sun, L.; Lin, S.F. GEM: A Dynamic Tracking Model for Mesoscale Eddies in the Ocean. Ocean. Sci. Discuss. 2016, 12, 1–27. [Google Scholar] [CrossRef] [Green Version]
- Cui, W.; Wang, W.; Zhang, J.; Yang, J. Multicore structures and the splitting and merging of eddies in global oceans from satellite altimeter data. Ocean. Sci. 2019, 15, 413–430. [Google Scholar] [CrossRef] [Green Version]
- Lumpkin, R. Global characteristics of coherent vortices from surface drifter trajectories. J. Geophys. Res. Ocean. 2016, 121, 1306–1321. [Google Scholar] [CrossRef] [Green Version]
- Overman, E.A. Evolution and merger of isolated vortex structures. Phys. Fluids 1982, 25, 1297–1305. [Google Scholar] [CrossRef]
- Dritschel, D.G.; Waugh, D.W. Quantification of the inelastic interaction of unequal vortices in two-dimensional vortex dynamics. Phys. Fluids A 1992, 4, 1737–1744. [Google Scholar] [CrossRef] [Green Version]
- Cotroneo, Y.; Aulicino, G.; Ruiz, S.; Pascual, A.; Budillon, G.; Fusco, G.; Tintoré, J. Glider and satellite high resolution monitoring of a mesoscale eddy in the algerian basin: Effects on the mixed layer depth and biochemistry. J. Mar. Syst. 2016, 162, 73–88. [Google Scholar] [CrossRef] [Green Version]
- Ma, C.; Guo, X.; Zhang, H.; Di, J.; Chen, G. An Investigation of the Influences of SWOT Sampling and Errors on Ocean Eddy Observation. Remote Sens. 2020, 12, 2682. [Google Scholar] [CrossRef]

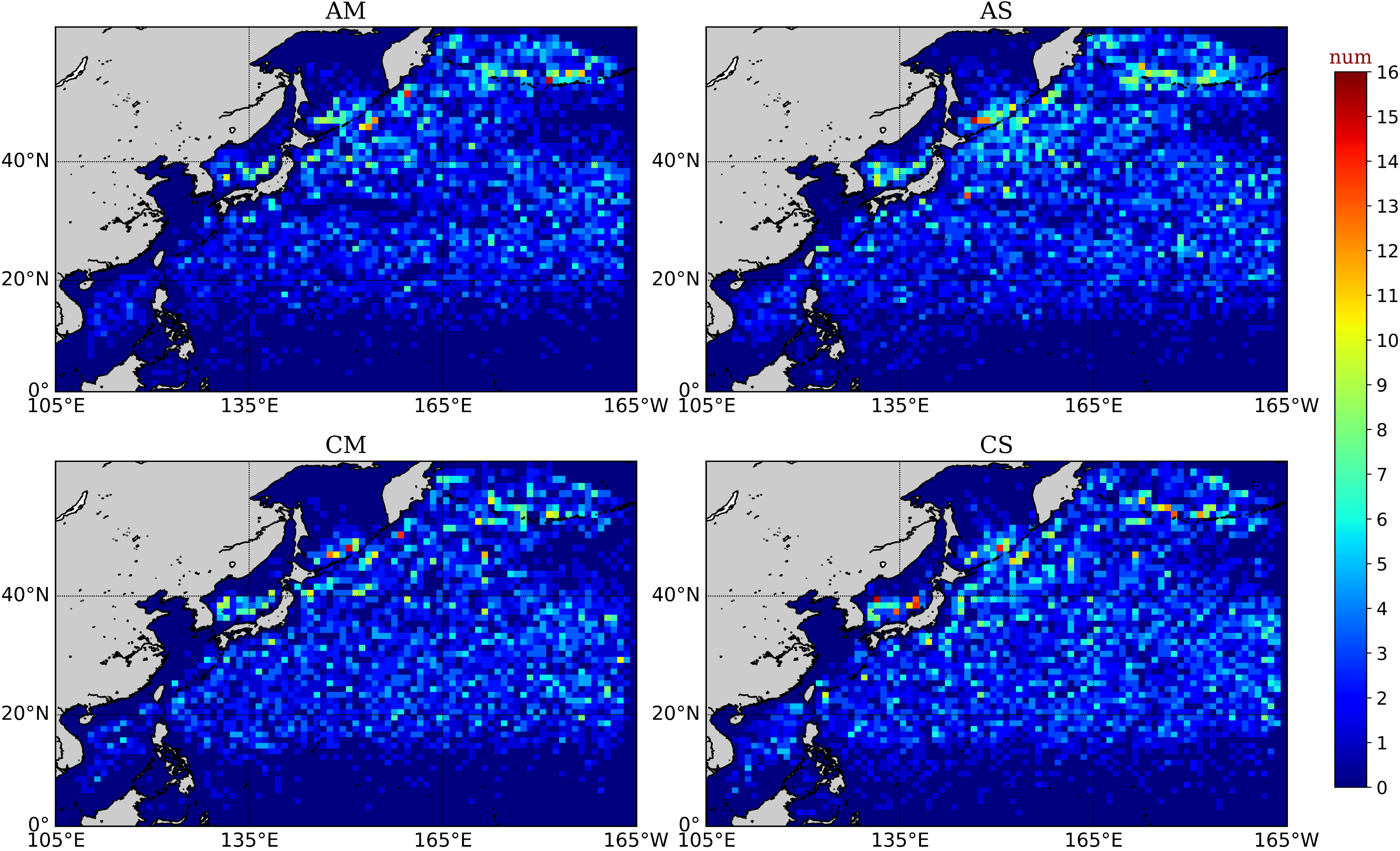
| Anticyclonic Eddy | Cyclonic Eddy | Total | |
|---|---|---|---|
| Branches | 497,339 | 526,374 | 1,023,713 |
| Eddy-DAG | 190,594 | 204,713 | 395,307 |
| Nonlinear Eddy-DAG | 490,34 | 541,86 | 103,220 |
| Linear Eddy-DAG | 141,560 | 150,527 | 292,087 |
| Splitting event | 72,224 | 74,198 | 146,422 |
| Merging event | 98,157 | 104,124 | 202,281 |
| Anticyclonic Eddy Splitting Event | Anticyclonic Eddy Merging Event | Cyclonic Eddy Splitting Event | Cyclonic Eddy Merging Event |
|---|---|---|---|
| 5500 | 4231 | 4584 | 3945 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, F.; Li, Z.; Yuan, Z.; Chen, G. EddyGraph: The Tracking of Mesoscale Eddy Splitting and Merging Events in the Northwest Pacific Ocean. Remote Sens. 2021, 13, 3435. https://doi.org/10.3390/rs13173435
Tian F, Li Z, Yuan Z, Chen G. EddyGraph: The Tracking of Mesoscale Eddy Splitting and Merging Events in the Northwest Pacific Ocean. Remote Sensing. 2021; 13(17):3435. https://doi.org/10.3390/rs13173435
Chicago/Turabian StyleTian, Fenglin, Zhijiao Li, Zhonghao Yuan, and Ge Chen. 2021. "EddyGraph: The Tracking of Mesoscale Eddy Splitting and Merging Events in the Northwest Pacific Ocean" Remote Sensing 13, no. 17: 3435. https://doi.org/10.3390/rs13173435
APA StyleTian, F., Li, Z., Yuan, Z., & Chen, G. (2021). EddyGraph: The Tracking of Mesoscale Eddy Splitting and Merging Events in the Northwest Pacific Ocean. Remote Sensing, 13(17), 3435. https://doi.org/10.3390/rs13173435







