Spatial Variations in Terrestrial Water Storage with Variable Forces across the Yellow River Basin
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data
2.3. Method
2.3.1. Mann–Kendall and Sen’s Slope
2.3.2. Pearson’s Correlation Analysis
2.3.3. Multiple Adaptive Regression Splines (MARS)
- (1)
- Constant term, i.e., intercept, which represents the possible intercept of other basic equations.
- (2)
- Hinge function in the form of max (0, x-knot), or max (0, knot-x), where MARS automatically selects the variable x and its corresponding node value (knot), where the knot point is a constant splitting the variable x into two sections in each of which MARS has a linear or non-linear form and joins at the node.
- (3)
- A product of two or more hinge functions indicating the interaction between two or more variables. In a two-variable case, the product represents the interaction between the variables.
2.3.4. Measures of Performance Assessment
3. Results
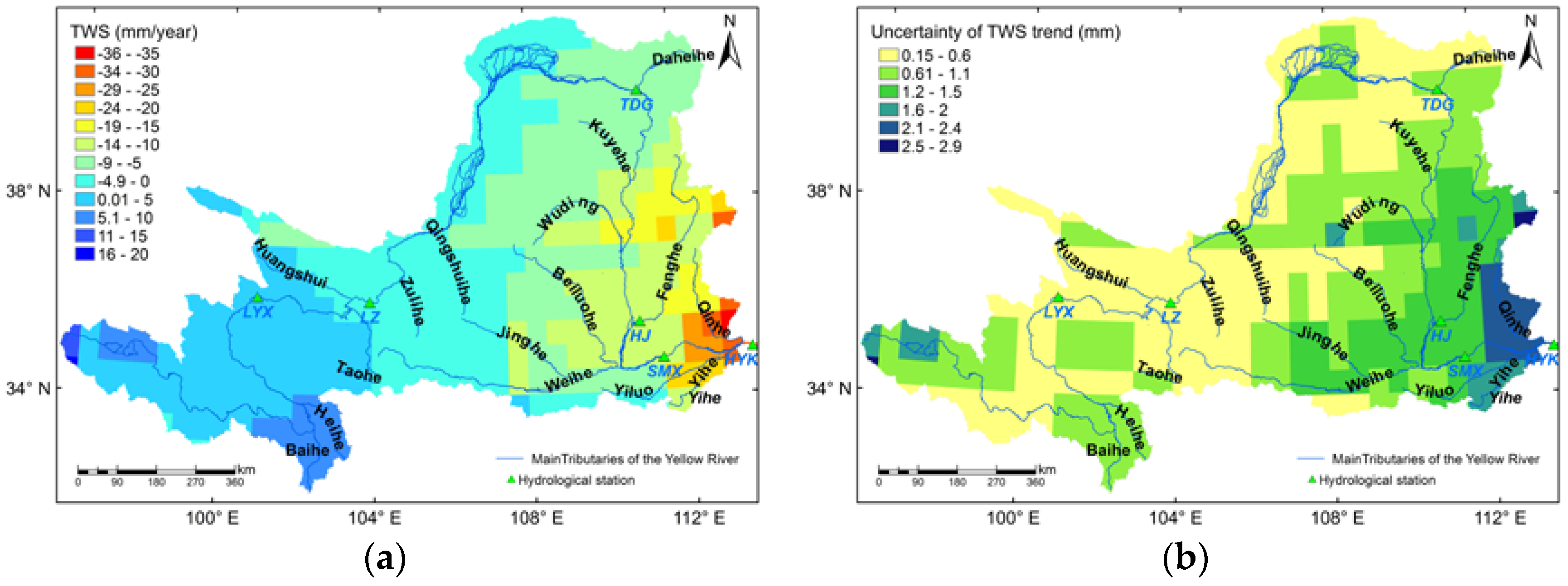
3.1. Spatial Variations in TWS Trend and Its Uncertainty
3.2. Spatial Trend Variations of Influencing Factors
3.3. Correlation between Variables
3.4. Variables and Their Interactions Identified by MARS
3.5. Assessment of MARS Model’s Performance
4. Discussion
4.1. Main Influencing Factors of TWS Spatiotemporal Variations
4.2. Impact of Factors’ Interaction on Spatiotemporal Variations in TWS
4.3. Uncertainty and Limitations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Guentner, A.; Stuck, J.; Werth, S.; Doell, P.; Verzano, K.; Merz, B. A Global Analysis of Temporal and Spatial Variations in Continental Water Storage. Water Resour. Res. 2007, 43, 687–6906. [Google Scholar] [CrossRef]
- Riegger, J. Quantification of Drainable Water Storage Volumes in Catchments in River Networks on Global Scales Using the GRACE and/or River Runoff. Hydrol. Earth Syst. Sci. Discuss. 2018, 1–27. [Google Scholar] [CrossRef]
- Joodakii, G.; Wahr, J.; Swenson, S. Estimating the Human Contribution to Groundwater Depletion in the Middle East, from GRACE Data, Land Surface Models, and Well Observations. Water Resour. Res. 2014, 50, 2679–2692. [Google Scholar] [CrossRef]
- Girotto, M.; Rodell, M. Terrestrial water storage. In Extreme Hydroclimatic Events and Multivariate Hazards in a Changing Environment; Elsevier: Amsterdam, The Netherlands, 2019; pp. 41–64. ISBN 978-0-12-814899-0. [Google Scholar]
- Ahmed, M.; Sultan, M.; Wahr, J.; Yan, E. The Use of GRACE Data to Monitor Natural and Anthropogenic Induced Variations in Water Availability across Africa. Earth-Sci. Rev. 2014, 136, 289–300. [Google Scholar] [CrossRef]
- Wahr, J.; Molenaar, M.; Bryan, F. Time Variability of the Earth’s Gravity Field: Hydrological and Oceanic Effects and Their Possible Detection Using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Wahr, J.; Swenson, S.; Zlotnicki, V.; Velicogna, I. Time-Variable Gravity from GRACE: First Results. Geophys. Res. Lett. 2004, 31, 293–317. [Google Scholar] [CrossRef] [Green Version]
- Swenson, S.; Yeh, P.J.-F.; Wahr, J.; Famiglietti, J. A Comparison of Terrestrial Water Storage Variations from GRACE with in Situ Measurements from Illinois. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
- Rodell, M.; Chen, J.; Kato, H.; Famiglietti, J.S.; Nigro, J.; Wilson, C.R. Estimating Groundwater Storage Changes in the Mississippi River Basin (USA) Using GRACE. Hydrogeol. J. 2007, 15, 159–166. [Google Scholar] [CrossRef] [Green Version]
- Grippa, M.; Kergoat, L.; Frappart, F.; Araud, Q.; Boone, A.; de Rosnay, P.; Lemoine, J.-M.; Gascoin, S.; Balsamo, G.; Ottlé, C.; et al. Land Water Storage Variability over West Africa Estimated by Gravity Recovery and Climate Experiment (GRACE) and Land Surface Models. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Nakaegawa, T.; Yamamoto, K.; Tanaka, T.Y.; Hasegawa, T.; Fukuda, Y. Investigation of Temporal Characteristics of Terrestrial Water Storage Changes and Its Comparison to Terrestrial Mass Changes. Hydrol. Process. 2012, 26, 2470–2481. [Google Scholar] [CrossRef]
- Yang, P.; Xia, J.; Zhan, C.; Qiao, Y.; Wang, Y. Monitoring the Spatio-Temporal Changes of Terrestrial Water Storage Using GRACE Data in the Tarim River Basin between 2002 and 2015. Sci. Total Environ. 2017, 595, 218–228. [Google Scholar] [CrossRef]
- Chen, H.; Liu, H.; Chen, X.; Qiao, Y. Analysis on Impacts of Hydro-Climatic Changes and Human Activities on Available Water Changes in Central Asia. Sci. Total Environ. 2020, 737, 139779. [Google Scholar] [CrossRef] [PubMed]
- Syed, T.H.; Famiglietti, J.S.; Chen, J.; Rodell, M.; Seneviratne, S.I.; Viterbo, P.; Wilson, C.R. Total Basin Discharge for the Amazon and Mississippi River Basins from GRACE and a Land-Atmosphere Water Balance. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Huang, J.; Li, J.; Rivera, A.; McKenney, D.W.; Sheffield, J. Assessment of Water Budget for Sixteen Large Drainage Basins in Canada. J. Hydrol. 2014, 512, 1–15. [Google Scholar] [CrossRef]
- Rodell, M. Basin Scale Estimates of Evapotranspiration Using GRACE and Other Observations. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef] [Green Version]
- Xiaoyu, S.; Caiping, J.; Bing, S.; Wenjuan, S.; Lingmei, H. Interaction between ecological environment construction and sustainable use of water resources in Northwest China. Agric. Res. Arid Areas 2004, 22, 127–131. [Google Scholar]
- Wada, Y.; van Beek, L.P.H.; van Kempen, C.M.; Reckman, J.W.T.M.; Vasak, S.; Bierkens, M.F.P. Global Depletion of Groundwater Resources. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef] [Green Version]
- Yin, Y.; Tang, Q.; Liu, X.; Zhang, X. Water Scarcity under Various Socio-Economic Pathways and Its Potential Effects on Food Production in the Yellow River Basin. Hydrol. Earth Syst. Sci. 2017, 21, 791–804. [Google Scholar] [CrossRef] [Green Version]
- Ya, L.; Shengtian, Y.; Xiaoyan, L.; Changming, L.; Wenlong, S.; Guotao, D.; Haigen, Z.; Hezhen, L. Land Use Change in the Reach from Hekouzhen to Tongguan of the Yellow River during 1998–2010. Acta Geogr. Sin. 2014, 69, 42–53. [Google Scholar]
- Guangqian, W.; Siyuan, W.; Zhixiang, C. Land-use/land-cover changes in the Yellow River basin. J. Tsinghua Univ. (Sci. Technol.) 2004, 44, 1218–1222. [Google Scholar]
- Kong, D.; Miao, C.; Borthwick, A.G.L.; Lei, X.; Li, H. Spatiotemporal Variations in Vegetation Cover on the Loess Plateau, China, between 1982 and 2013: Possible Causes and Potential Impacts. Environ. Sci. Pollut. Res. 2018, 25, 13633–13644. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dawen, Y.; Shulei, Z.; Xiangyu, X. Attribution analysis for runoff decline in Yellow River Basin during past fifty years based on Budyko hypothesis. Sci. Sin. 2015, 45, 1024–1034. [Google Scholar] [CrossRef] [Green Version]
- Zuo, D.; Xu, Z.; Yao, W.; Jin, S.; Xiao, P.; Ran, D. Assessing the Effects of Changes in Land Use and Climate on Runoff and Sediment Yields from a Watershed in the Loess Plateau of China. Sci. Total Environ. 2016, 544, 238–250. [Google Scholar] [CrossRef] [PubMed]
- Jia, X.; Shao, M.; Zhu, Y.; Luo, Y. Soil Moisture Decline Due to Afforestation across the Loess Plateau, China. J. Hydrol. 2017, 546, 113–122. [Google Scholar] [CrossRef]
- Zhang, K.; Xie, X.; Zhu, B.; Meng, S.; Yao, Y. Unexpected Groundwater Recovery with Decreasing Agricultural Irrigation in the Yellow River Basin. Agric. Water Manag. 2019, 213, 858–867. [Google Scholar] [CrossRef]
- Sun, W.; Jin, Y.; Yu, J.; Wang, G.; Xue, B.; Zhao, Y.; Fu, Y.; Shrestha, S. Integrating Satellite Observations and Human Water Use Data to Estimate Changes in Key Components of Terrestrial Water Storage in a Semi-Arid Region of North China. Sci. Total Environ. 2020, 698, 134171. [Google Scholar] [CrossRef]
- Lv, M.; Ma, Z.; Li, M.; Zheng, Z. Quantitative Analysis of Terrestrial Water Storage Changes Under the Grain for Green Program in the Yellow River Basin. J. Geophys. Res. Atmos. 2019, 124, 1336–1351. [Google Scholar] [CrossRef]
- Li, C.; Zhang, Y.; Shen, Y.; Yu, Q. Decadal Water Storage Decrease Driven by Vegetation Changes in the Yellow River Basin. Sci. Bull. 2020, 65, 1859–1861. [Google Scholar] [CrossRef]
- Xie, J.; Xu, Y.-P.; Wang, Y.; Gu, H.; Wang, F.; Pan, S. Influences of Climatic Variability and Human Activities on Terrestrial Water Storage Variations across the Yellow River Basin in the Recent Decade. J. Hydrol. 2019, 579, 124218. [Google Scholar] [CrossRef]
- Jing, W.; Yao, L.; Zhao, X.; Zhang, P.; Liu, Y.; Xia, X.; Song, J.; Yang, J.; Li, Y.; Zhou, C. Understanding Terrestrial Water Storage Declining Trends in the Yellow River Basin. J. Geophys. Res. Atmos. 2019, 124, 12963–12984. [Google Scholar] [CrossRef]
- Deng, H.; Pepin, N.C.; Liu, Q.; Chen, Y. Understanding the Spatial Differences in Terrestrial Water Storage Variations in the Tibetan Plateau from 2002 to 2016. Clim. Chang. 2018, 151, 379–393. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Chen, X.; Hu, Q.; Liu, J. Responses of Terrestrial Water Storage to Climate Variation in the Tibetan Plateau. J. Hydrol. 2020, 584, 124652. [Google Scholar] [CrossRef]
- Meng, F.; Su, F.; Li, Y.; Tong, K. Changes in Terrestrial Water Storage During 2003–2014 and Possible Causes in Tibetan Plateau. J. Geophys. Res. Atmos. 2019, 124, 2909–2931. [Google Scholar] [CrossRef]
- Chen, X.; Jiang, J.; Lei, T.; Yue, C. GRACE Satellite Monitoring and Driving Factors Analysis of Groundwater Storage under High-Intensity Coal Mining Conditions: A Case Study of Ordos, Northern Shaanxi and Shanxi, China. Hydrogeol. J. 2020, 28, 673–686. [Google Scholar] [CrossRef]
- Xie, X.; Xu, C.; Wen, Y.; Li, W. Monitoring Groundwater Storage Changes in the Loess Plateau Using GRACE Satellite Gravity Data, Hydrological Models and Coal Mining Data. Remote Sens. 2018, 10, 605. [Google Scholar] [CrossRef] [Green Version]
- Yi, S.; Song, C.; Wang, Q.; Wang, L.; Heki, K.; Sun, W. The Potential of GRACE Gravimetry to Detect the Heavy Rainfall-Induced Impoundment of a Small Reservoir in the Upper Yellow River. Water Resour. Res. 2017, 53, 6562–6578. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, J.; Shamsuddin, S.; Oyang, R.; Guan, T.; Xue, J.; Zhang, X. Impacts of Climate Variability and Changes on Domestic Water Use in the Yellow River Basin of China. Mitig. Adapt. Strat. Strateg. Glob. Chang. 2017, 22, 595–608. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, J.; Shahid, S.; Guan, E.; Wu, Y.; Gao, J.; He, R. Adaptation to Climate Change Impacts on Water Demand. Mitig. Adapt. Strateg. Glob. Chang. 2016, 21, 81–99. [Google Scholar] [CrossRef]
- Ellison, D.; Morris, C.E.; Locatelli, B.; Sheil, D.; Cohen, J.; Murdiyarso, D.; Gutierrez, V.; van Noordwijk, M.; Creed, I.F.; Pokorny, J.; et al. Trees, Forests and Water: Cool Insights for a Hot World. Glob. Environ. Chang. Hum. Policy Dimens. 2017, 43, 51–61. [Google Scholar] [CrossRef]
- Lin, M.; Biswas, A.; Bennett, E.M. Socio-Ecological Determinants on Spatio-Temporal Changes of Groundwater in the Yellow River Basin, China. Sci. Total Environ. 2020, 731, 138725. [Google Scholar] [CrossRef]
- Hasan, E.; Tarhule, A. GRACE: Gravity Recovery and Climate Experiment Long-Term Trend Investigation over the Nile River Basin: Spatial Variability Drivers. J. Hydrol. 2020, 586, 124870. [Google Scholar] [CrossRef]
- Lin, M.; Biswas, A.; Bennett, E.M. Spatio-Temporal Dynamics of Groundwater Storage Changes in the Yellow River Basin. J. Environ. Manag. 2019, 235, 84–95. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; He, B.; Guo, L.; Liu, J.; Xie, X. The Relative Contributions of Precipitation, Evapotranspiration, and Runoff to Terrestrial Water Storage Changes across 168 River Basins. J. Hydrol. 2019, 579, 124194. [Google Scholar] [CrossRef]
- Friedman, J.H. Multivariate Adaptive Regression Splines. Ann. Stat. 1991, 19, 1–141. [Google Scholar] [CrossRef]
- Shao, Q.; Traylen, A.; Zhang, L. Nonparametric Method for Estimating the Effects of Climatic and Catchment Characteristics on Mean Annual Evapotranspiration. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Xing, W.; Wang, W.; Shao, Q.; Yong, B. Identification of Dominant Interactions between Climatic Seasonality, Catchment Characteristics and Agricultural Activities on Budyko-Type Equation Parameter Estimation. J. Hydrol. 2018, 556, 585–599. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D.; Ries, J.C. Low Degree Gravitational Changes from GRACE: Validation and Interpretation. Geophys. Res. Lett. 2004, 31, L22607. [Google Scholar] [CrossRef]
- Save, H.; Bettadpur, S.; Tapley, B.D. Reducing Errors in the GRACE Gravity Solutions Using Regularization. J. Geod. 2012, 86, 695–711. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Zhang, Z.; Save, H.; Sun, A.Y.; Schmied, H.M.; van Beek, L.P.H.; Wiese, D.N.; Wada, Y.; Long, D.; Reedy, R.C.; et al. Global Models Underestimate Large Decadal Declining and Rising Water Storage Trends Relative to GRACE Satellite Data. Proc. Natl. Acad. Sci. USA 2018, 115, E1080–E1089. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, Z.; Yeh, P.J.-F.; Pan, Y.; Jiao, J.J.; Gong, H.; Li, X.; Güntner, A.; Zhu, Y.; Zhang, C.; Zheng, L. Detection of Large-Scale Groundwater Storage Variability over the Karstic Regions in Southwest China. J. Hydrol. 2019, 569, 409–422. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef] [Green Version]
- Huang, Z.; Hejazi, M.; Li, X.; Tang, Q.; Vernon, C.; Leng, G.; Liu, Y.; Doell, P.; Eisner, S.; Gerten, D.; et al. Reconstruction of global gridded monthly sectoral water withdrawals for 1971–2010 and analysis of their spatiotemporal patterns. Hydrol. Earth Syst. Sci. 2018, 22, 1–30. [Google Scholar] [CrossRef] [Green Version]
- Sun, W.; Wang, Y.; Fu, Y.H.; Xue, B.; Wang, G.; Yu, J.; Zuo, D.; Xu, Z. Spatial Heterogeneity of Changes in Vegetation Growth and Their Driving Forces Based on Satellite Observations of the Yarlung Zangbo River Basin in the Tibetan Plateau. J. Hydrol. 2019, 574, 324–332. [Google Scholar] [CrossRef]
- Piao, S.; Wang, X.; Ciais, P.; Zhu, B.; Wang, T.; Liu, J. Changes in Satellite-Derived Vegetation Growth Trend in Temperate and Boreal Eurasia from 1982 to 2006. Glob. Chang. Biol. 2011, 17, 3228–3239. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods. Brit. J. Psychol. 1990, 25, 86–91. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Sen, K.P. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Groemping, U. Relative Importance for Linear Regression in R: The Package Relaimpo. J. Stat. Softw. 2006, 17. [Google Scholar] [CrossRef] [Green Version]
- Yuan, R.-Q.; Chang, L.-L.; Gupta, H.; Niu, G.-Y. Climatic Forcing for Recent Significant Terrestrial Drying and Wetting. Adv. Water Resour 2019, 133, 1103425. [Google Scholar] [CrossRef]
- Jekabsons, G. ARESLab: Adaptive Regression Splines Toolbox for Matlab/Octave. 2016. Available online: http://www.cs.rtu.lv/jekabsons/regression.html (accessed on 25 August 2021).
- Jia, Y.-H.; Shao, M.-A. Dynamics of Deep Soil Moisture in Response to Vegetational Restoration on the Loess Plateau of China. J. Hydrol. 2014, 519, 523–531. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, B.; Liu, G.; Zhang, Y. Soil Water Depletion Depth by Planted Vegetation on the Loess Plateau. Sci. China Ser. D 2009, 52, 835–842. [Google Scholar] [CrossRef]
- Yang, L.; Wei, W.; Chen, L.; Chen, W.; Wang, J. Response of Temporal Variation of Soil Moisture to Vegetation Restoration in Semi-Arid Loess Plateau, China. Catena 2014, 115, 123–133. [Google Scholar] [CrossRef]
- Ma, S.; Zhang, W. Spatial and Temporal Development Pattern and Environmentally-friendly Development Path of Electricity Industry in the Yellow River Basin. Bull. Chin. Acad. Sci. 2020, 35, 86–98. [Google Scholar] [CrossRef]
- Zhang, L.; Karthikeyan, R.; Bai, Z.; Srinivasan, R. Analysis of Streamflow Responses to Climate Variability and Land Use Change in the Loess Plateau Region of China. Catena 2017, 154, 1–11. [Google Scholar] [CrossRef]

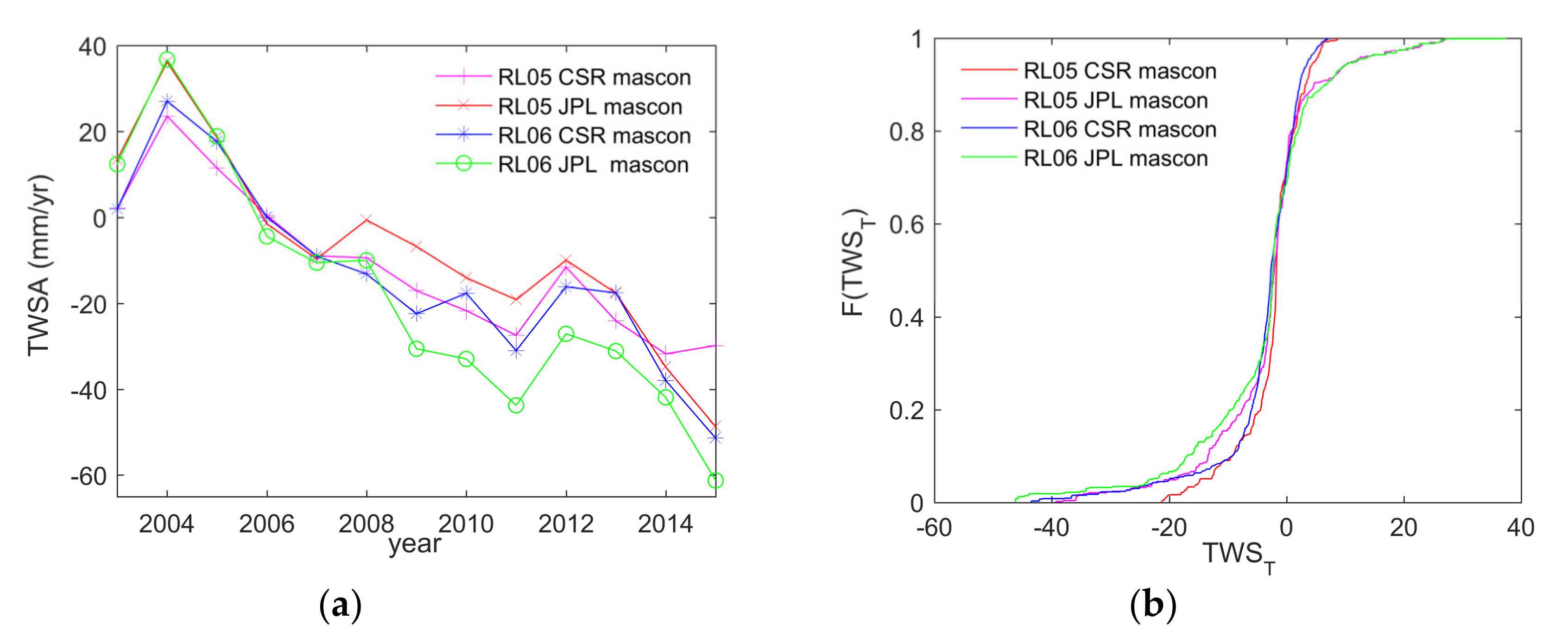



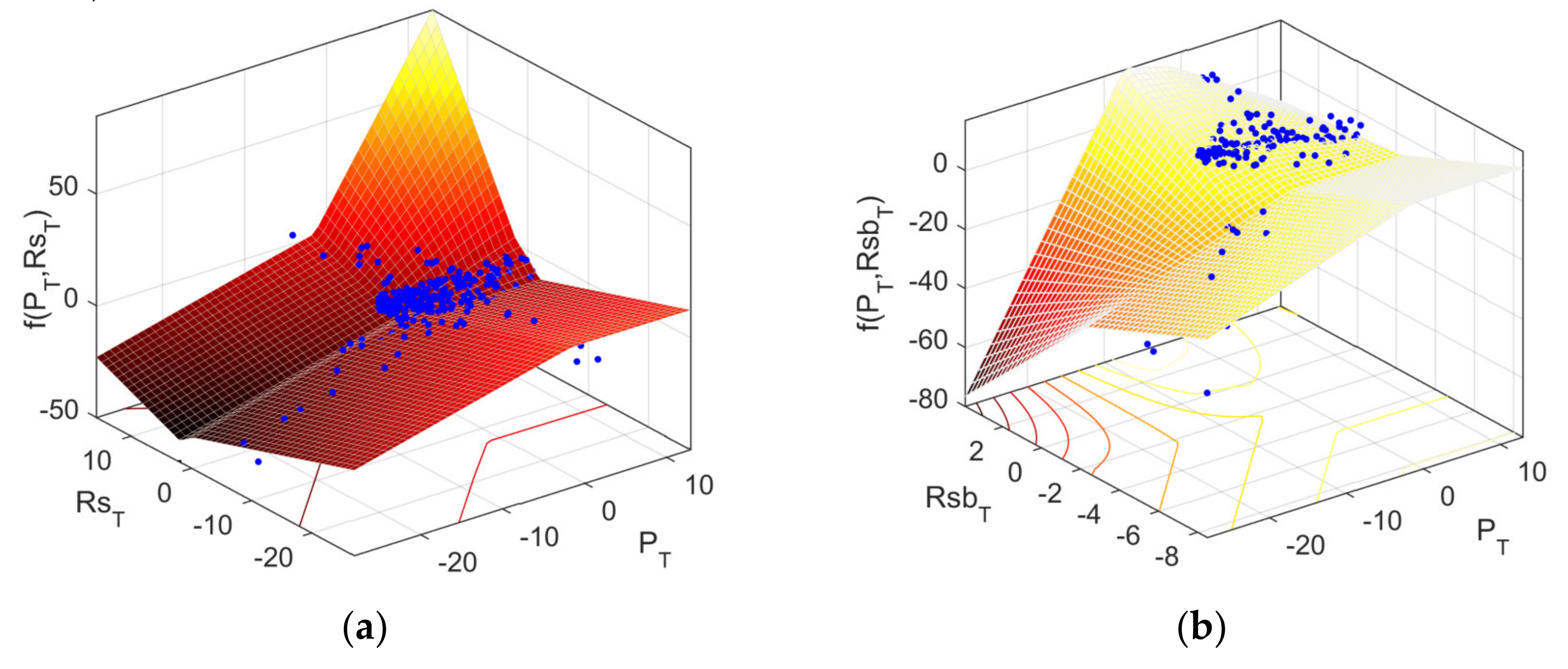


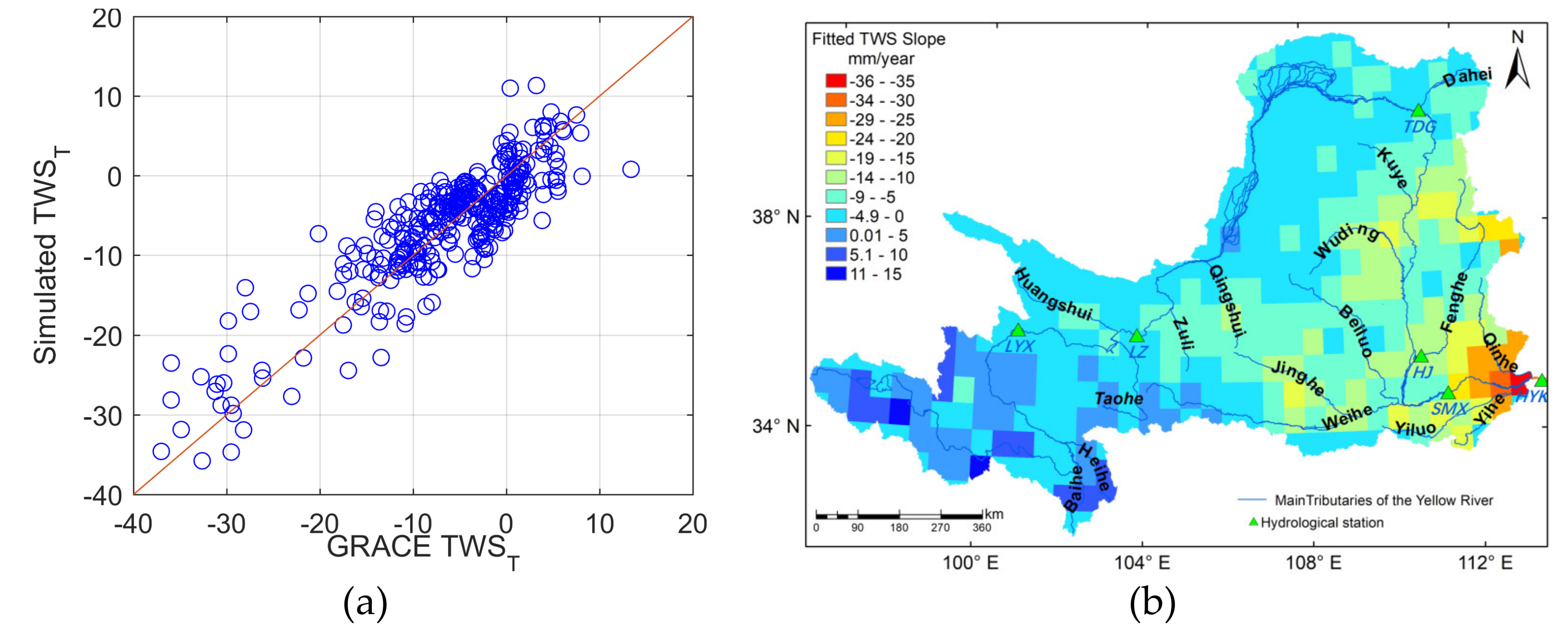
| Category | Variables | Resolution | Data Source |
|---|---|---|---|
| Climate | Precipitation | Daily, point-scale | China Meteorological Administration |
| Maximum temperature | |||
| Minimum temperature | |||
| Hydrology | Net radiation | Monthly, 0.25° | Rodell et al. (2004) |
| Evaporation | |||
| Runoff | |||
| Base runoff | |||
| Water withdrawal | Domestic | Monthly, 0.5° | Huang et al. (2018) |
| Electricity | |||
| Irrigation | |||
| Livestock | |||
| Manufacturing | |||
| Mining | |||
| GRACE terrestrial water storage | TWSA | Monthly, 0.5° | CSR Mascon JPL Mascon |
| Vegetation | NDVI | 15 Day, 1/12° | GIMMS NDVI3g.v1 |
| Basis | Coefficient | P | Rs | Rsb | NDVI | ElecW | Tmin |
|---|---|---|---|---|---|---|---|
| Function | |||||||
| 1 | −0.35 | 1(0) | |||||
| 2 | −0.48 | −1(0) | |||||
| 3 | −0.90 | −1(−1.47) | |||||
| 4 | 4.70 | 1(−2.32) | |||||
| 5 | 2.90 | −1(−2.32) | |||||
| 6 | −835.68 | 1(−0.000755) | |||||
| 7 | 0.51 | 1(1.95) | −1(0) | ||||
| 8 | 0.06 | −1(1.95) | −1(0) | ||||
| 9 | −770.94 | 1(−0.27) | 1(−0.000755) | ||||
| 10 | 243.01 | −1(−0.27) | 1(−0.000755) | ||||
| 11 | 0.32 | 1(−1.47) | 1(−1.89) | ||||
| 12 | −0.26 | 1(−7.30) | 1(−2.32) | ||||
| 13 | −0.58 | −1(−7.30) | 1(−2.32) | ||||
| 14 | −13.56 | −1(0) | 1(0.0145) | ||||
| 15 | −48.13 | −1(0) | −1(0.0145) |
| Category | Input Variables | R2 | MAE | AIC |
|---|---|---|---|---|
| 1 | P, ET, Rs, Rsb | 0.65 | 1.84 | 2381.94 |
| 2 | DomW, ElecW, MinW, LivW, IrrW, MfgW | 0.66 | 1.70 | 2371.30 |
| 3 | NDVI, Tmin, Tmax, NetRad | 0.56 | 1.88 | 2631.62 |
| 4 | All factors | 0.83 | 1.18 | 1702.66 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, M.; Wang, X.; Sun, L.; Luo, Y. Spatial Variations in Terrestrial Water Storage with Variable Forces across the Yellow River Basin. Remote Sens. 2021, 13, 3416. https://doi.org/10.3390/rs13173416
Zhou M, Wang X, Sun L, Luo Y. Spatial Variations in Terrestrial Water Storage with Variable Forces across the Yellow River Basin. Remote Sensing. 2021; 13(17):3416. https://doi.org/10.3390/rs13173416
Chicago/Turabian StyleZhou, Meilin, Xiaolei Wang, Lin Sun, and Yi Luo. 2021. "Spatial Variations in Terrestrial Water Storage with Variable Forces across the Yellow River Basin" Remote Sensing 13, no. 17: 3416. https://doi.org/10.3390/rs13173416
APA StyleZhou, M., Wang, X., Sun, L., & Luo, Y. (2021). Spatial Variations in Terrestrial Water Storage with Variable Forces across the Yellow River Basin. Remote Sensing, 13(17), 3416. https://doi.org/10.3390/rs13173416






