Abstract
The coastal mangrove forest bears important ecosystem functions and services, including the protection of shorelines and coastal communities. While coastal mangroves often suffer severe damage during storms, understanding the vulnerability and resistance of mangroves to the damage at a landscape scale is crucial for coastal mangrove management and conservation. In September 2017, two consecutive major hurricanes caused tremendous damage to the coastal mangroves in the Caribbean. By utilizing LiDAR data taken before and after the hurricanes in a basin mangrove forest in Northeast Puerto Rico, we analyzed the spatial variation of a canopy structure before the hurricanes and hurricane-induced canopy height reduction and explored possible drivers by means of spatial regressions. Regarding the canopy structure, we found that the pre-hurricane canopy height of the mangrove forest decreased with elevation and distance to the freshwater/sewage canals within the forest, and these two drivers explained 82% of variations in the mangrove canopy height. The model, thus, implies that freshwater and nutrient inputs brought by the canals tend to promote the canopy height, and mangrove trees at lower elevation are especially more advantageous. Similarly, tree densities decreased with the canopy height but increased with the elevation and the distance to the canals. We also found that this mangrove forest suffered on average a 53% canopy height reduction, reflecting mostly heavy crown defoliation and the rupture of branches. The regression, which explains 88% of spatial variation in the canopy height reduction, showed that mangroves with a higher canopy or lower density, or growing in lower elevation, or being closer to the canals suffered more damage. Our findings indicate that delivered freshwater/sewage by means of human-made canals has a strong impact on the canopy structure as well as its resistance to tropical storms. Freshwater and sewage tend to release the salinity stress and nutrient deficit and, thus, to promote the mangrove canopy height. However, the addition of freshwater and nutrients might also increase the risk of mangrove damage during the storms probably because of an altered allometry of assimilates.
1. Introduction
Mangrove forests were estimated to occupy 137,760 km2 of the global coast [1], and are homes of many fauna from invertebrate to vertebrate [2]. Mangrove forests grow in a salty and anaerobic environment with a great carbon sequestration capability due to a high carbon assimilation but low ecosystem respiration, and the extremely high water and nutrient use efficiencies of the mangrove trees [3]. The capability of fixing great amount of nutrients makes mangrove the best filter of toxicants in the coastal water [4,5]. Meanwhile, mangroves tend to stabilize the coastline because of their high capacity of vertical accretion to offset the coastal retrieve due to sea level rise [6].
Tropical and subtropical coasts are often the places of historical agriculture, tourism, and urban development, which compete with mangrove forests for land and other resources [7]. Although protected by international and national policies and regulations, mangrove forests in close distance to urban areas are connected to the urban communities via historical legacy, aerodynamics, hydrology, and nutrients [8]. For people living near the coast, the dense canopy and root system of mangroves provide essential protection during the tropical storms [9].
While protecting shorelines and coastal communities, mangroves often expericence severe damage during strong storms. In addition to defoliation, the rapture of branches and trunks, and windthrows by the storm winds, the surge of ocean and floods of rivers can inundate the mangrove system for weeks. A prolonged inundation submerges the aerial roots of mangroves, prevents trees from respirating, and causes a delayed mortality [10,11,12]. Due to the salinity and hypoxia stress, the recovery of a mangrove ecosystem may take decades [13,14,15].
Assessing and analyzing the damage of tropical storms to mangroves at landscape scales are crucial to understanding the resistance of coastal mangroves. An assessment by ground observation [16] is often limited by scale. Vegetation indices and moisture indices derived from multispectral remote sensing provide a continuous, spatiotemporal observation of the terrestrial ecosystem and have been used to assess the wide range damages of mangroves [15,17,18]. Compared to upland forests, coastal mangroves experience the greatest impact after major hurricanes in terms of the relative drop in the vegetation index [15]. However, changes in the vegetation index mostly reflect changes in green biomass or leaf area with a limited capacity to assess vertical structural damages of mangrove branches and trunks by hurricanes.
Space- or air-borne LiDAR (Light Detection and Ranging) is ideal to assess storm damages to the vertical structure of coastal mangroves [19]. High-intense infrared laser beams can penetrate canopy layers and return multiple signals reflecting the structure of the forest canopy. The laser can reach the ground and result in a last return from the ground if the canopy is not exceptionally dense or thick. LiDAR data can be used to derive a digital surface model (DSM), digital terrain model (DTM), and canopy height model (CHM). The spatial variation of canopy height can be used to derive planar cartesian coordinates of tree tops, the canopy area, and tree density in a forest [20,21].
The severity of damage to a forest structure by storm winds can be affected by various factors. Mitchell [22] gave a comprehensive review on the wind disturbance on forests: An emergent overstory and higher canopy may intercept more wind force and more momentum to damage the trees in a forest, and a big stem diameter tends to increase the shear modulus and, thus, resists the rapture of stems and branches. Larger spacing among tree stems (lower stem density) decreases the critical stem-rupture wind speed, implying that under given storm wind speed larger spacing might lead to more damage [23]. However, when the density is too high, trees allocate more materials for longer rather than larger-diameter stems, which makes the forest stand more vulnerable to strong winds. The windthrow of trees is also affected by root–soil anchorage. Wet, especially saturated, soil plus a shallow root system makes a forest more prone to windthrow [22]. In addition to the wind damage, the lengthy of flooding may cause delayed damage to the mangroves [10].
The Caribbean coasts, in between the Atlantic Ocean and Central America (Figure A1), are frequently disturbed by tropical cyclones [24]. For example, in 2017, Hurricane Irma of category five passed nearby the northeast of Puerto Rico, one of the Great Antilles islands in the Northeastern Caribbean (Figure A1), on Sep. 6. Two weeks later, another high-end category four hurricane, Hurricane Maria, made a landfall in the east of the island which swept Puerto Rico (Figure 1a) and created tremendous damages to the mangrove ecosystems [17,25]. An assessment and analysis of the hurricane damage at a landscape level are still in great need to understand the mechanism of the mangrove resistance to storms [15].
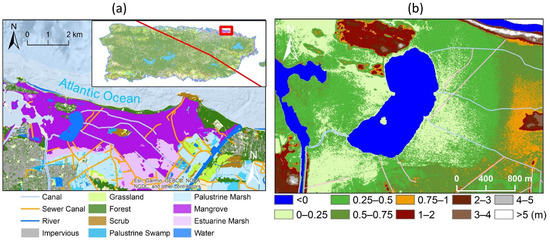
Figure 1.
(a) Piñones State Forest, the largest mangrove forest in Puerto Rico. Map of Puerto Rico is in the upper right with a red line indicating the path of Hurricane Maria on 20 September 2017. Land cover from the NOAA C-CAP Program for 2010 shows the distribution of mangroves, together with the rivers and canals. (b) Digital Elevation Model around the Piñones Lagoon, also with the canals.
The objectives of this study are to assess the hurricane damage to the largest mangrove forest in Northeast Puerto Rico and to determine key variables that explain the spatial variation of the canopy structure as well as that of the hurricane damage. Using the available LiDAR data sources in Spring 2017 and 2018, we started with analyzing the spatial patterns of LiDAR-derived canopy height and tree density and then attributed the spatial variation of mangrove structures to the environment such as topography and sewage/freshwater discharges to the forest. Assuming the changes in canopy height from Spring 2017 to 2018 were mostly caused by the hurricanes in September 2017, we then analyzed the spatial pattern of canopy height reduction by the hurricanes to identify key factors that regulate the damages during the hurricanes. We hypothesized that the spatial variation of canopy height and tree density of the basin mangroves can be mostly explained by the elevation profile and the distance to freshwater/sewage canals within the forest, as a freshwater and nutrients input may benefit the mangroves, and the benefit is especially prominent at a lower elevation. Specifically, the lower elevation or the closer distance to canal tends to be associated with a higher mangrove canopy. We also hypothesized that the reduction in canopy height by the hurricanes is severer at a lower elevation, or with closer distance to the freshwater/sewage canals, or with lower tree density, as mangroves at a lower elevation or with a closer distance to the canals may have a lower stem density and higher canopy which are vulnerable to both wind and flooding damage.
2. Methods
2.1. Study Area
Puerto Rico had about 11,000 ha of mangroves in 1800 which declined to about 6000 ha in 1960s due to the expansion of agriculture and urban development on the coast [26]. However, conservation of wetlands guided by international and national laws led to the recovery to about 8000 ha in large, aggregated patches [26,27,28,29]. The mangroves are found mostly in the northern coast with high wave energy, large fluvial plains, and abundant rainfall to dilute salinity stress. Northern coast is predominated by the riverine and basin mangroves, whereas fringes and over-washed mangroves are mostly distributed in the south of the island [30]. Mangrove forests at the coast of Puerto Rico are often connected to the urban areas with canals of sewage and freshwater due to historical coastal agriculture and current coastal development.
Our study area is the largest continuous mangrove forest in Puerto Rico (–65°56′, 18°26′30″) lying in the Northern Loíza municipality with a total area of 1660 hectares (from NOAA C-CAP map). Piñones State Forest was established here in 1918 around Piñones Lagoon which has slow exchange of water with the ocean. However, a stream from the southeast (Quebrada Blasina) and several canals, including those for sewage purposes in the east and south of the lagoon, provide freshwater and nutrients to the mangroves nearby (Figure 1a). Elevation (Figure 1b) around the lagoon varied from –0.5 to 4 m. However, the 5th and 95th percentiles of the 0.5 m DEM were 0.09 and 0.41 m, respectively. This State Forest hosts four major species of mangroves [31]. Red mangroves (Rhizophora mangle L.) with stilt roots live mostly near salty water or muddy environments. Black mangroves (Avicennia germinans L.) featuring long horizontal roots connecting numerous pneumatophores can grow in shallow water environment. Both red and black mangroves have high tolerance to salinity, while white mangroves (Laguncularia racemosa (L.) Gaerth.) and buttonwood mangroves (Conocarpus erectus L.) have moderate salinity tolerance [3]. These four species in general appear along an elevation gradient. Within the forest, red mangrove grows on the verge of the lagoon, black mangrove and white mangrove occupy the most area, and buttonwood mangrove is only found in spots with higher and drier conditions [32].
2.2. LiDAR Data Processing
To investigate spatial patterns of the mangrove structure and to assess the hurricanes’ damages, we used airborne LiDAR data provided by two flight campaigns before and after the hurricanes. In March 2017, the campaign of Goddard’s LiDAR, Hyperspectral and Thermal Imager (G-LiHT) [33] by National Aeronautics and Space Administration (NASA) covered two transects with tiles around the Piñones Lagoon: PR_17March2017_198 to the north and PR_15March2017_112_196 to the south (https://glihtdata.gsfc.nasa.gov/, accessed on 24 August 2021), which we hereafter refer to as North and South transects, respectively. Each transect consists of several tiles, and we used three tiles of the former and four tiles of the latter, which altogether covered 187.8 ha of mangroves and spanned approximately 3 km long from west to east. The normal point spacing of the point cloud was 0.24 m and the vertical and horizontal accuracies were within 1 m (https://glihtdata.gsfc.nasa.gov/, accessed on 24 August 2021). The other LiDAR campaign (USGS, https://nationalmap.gov/3DEP/, accessed on 24 August 2021) was conducted in 2018 for the whole island of Puerto Rico which could be used to assess the damage brought by the two major hurricanes. The vertical accuracy was within 0.1 m and the horizontal accuracy was within 1 m. The nominal point spacing was 0.35 m. Hereafter we will refer to the mangrove forest state in March 2017 as ‘pre-hurricane’ or ‘intact’, whereas that in 2018 as ‘post-hurricane’ or ‘disturbed’.
Each tile of LiDAR data before or after the hurricanes (point cloud in .las files) was clipped to our study area with a high-resolution map of mangroves of 2010 [34]. Using the ‘lidR’ package of R, we derived Canopy Height Models (CHM) at 1 m resolution before and after the hurricanes from the LiDAR data with ‘grid canopy’ function after z coordinate of LiDAR point cloud was normalized with ‘normalize height’ function [35]. We also derived a tree density from the LiDAR data before the hurricanes based on the local maximum algorithm. This detection of trees provided the coordinates of treetops. However, the algorithm may fail to detect small trees with crowns overlapping with adjacent big trees. Hence, the average density of derived trees in the two transects would be checked against an onsite inventory of trees with diameter greater than 2.5 cm.
Subtracting the intact CHM from the disturbed CHM, we could assess the impact of the hurricanes on canopy height. To further explain the spatial variations in canopy height and tree density as well as the reduction in canopy height by the hurricanes, we adopted a high-resolution DEM (0.5 m) and computed a map of the distance to the canals (including sewage canals) (ArcGIS 10, ESRI, Redlands, CA, USA).
2.3. Statistical Modeling
To test the hypotheses, we applied regression with spatial autocorrelation of error to quantify the dependence of mangrove structure and damages by hurricanes on the covariate variables. Spatial error model [36] considered the spatial autocorrelation of error of a linear regression model:
where y is the dependent variable represented as an n × 1 matrix (n, number of records), x is one or multiple (m) independent variables represented by an n× (m + 1) matrix, β is an (m + 1) × 1 coefficient matrix to be estimated, and u is an n × 1 spatial error matrix. W is an n × n weight matrix determined by the neighborhood structure, λ is the spatial autocorrelation coefficient, and ε is the normal i.i.d. (independent and identically distributed) residual.
We intended to regress the intact canopy height and tree density as well as the reduction in canopy on covariates, including the elevation and the distance to the canals. Before regression, all maps were aggregated to a grid of 40 m resolution. We normalized the variables so that they span within the range of 0 to 1. Selection of explanatory variables was performed in the regression to achieve the minimum Akaike Information Criterion (AIC). All the statistical analyses were performed in R [37].
3. Results
3.1. Spatial Variations in Canopy Height and Tree Density
The intact canopy (Figure 2a, Table 1) was higher in the south transect than in the north transect. The mean canopy height was 10.1 and 14.5 m for the north and south transects, respectively, whereas the pooled mean height was 12.9 m. The canopy height was greatly reduced by the hurricanes (Figure 2b) in both transects. However, there seemed not to be such a sharp comparison in the disturbed canopy height between the two transects, as we found that the mean disturbed canopy height was 6.2 and 5.4 m for the north and south transects, respectively. Figure 2 also showed that there were great spatial variations in canopy height within both transects.
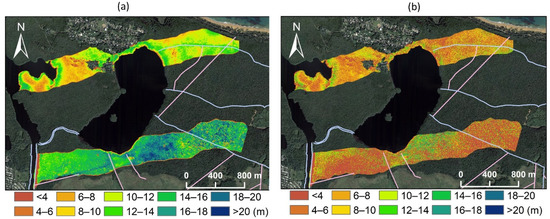
Figure 2.
The LiDAR-detected canopy height model for (a) intact (pre-hurricane) and (b) disturbed (post-hurricane) mangrove forest along the north and south transects. The changes in canopy height were illustrated in Figure 6a.

Table 1.
Summary of the comparison between the two transects. Numbers were computed based on 5 m resolution maps. We did not attempt to conduct statistical comparisons as these means are based on spatially dependent maps.
We checked the LiDAR-derived canopy height with an available in situ inventory study of the mangrove structure in Puerto Rico and the Caribbean [30,38], which placed four plots of 0.1 ha around the Piñones Lagoon. The ground measurement showed that the mean tree height of mangroves varied from 11.5 to 16 m with a mean of 13.6 m and a standard deviation of 1.9 m indicating the variation among plots. Although the mean canopy height was not the tree stem height and four small plots could not be compared with a 188 ha landscape, our LiDAR-detected intact canopy height with a mean of 12.9 m was likely to be true for the intact canopy height.
Canopy height averaged over the width of the transects also showed a distinct comparison of reduction by the hurricanes between the two transects with more reduction in the south than in the north (Figure 3). Within the north transect, the intact canopy height in the west was lower than that in the east, and the canopy height reduction in the west was less severe than that in the east.
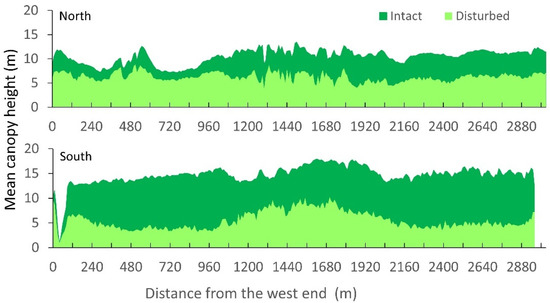
Figure 3.
Mean canopy height along the north and south transects before (intact) and after (disturbed) the hurricanes in September 2017.
The tree density before the hurricanes was expressed as the number of trees found within 5 m × 5 m grid cells (Figure 4). Converting to the number of trees per hectare, we found that the north transect had a mean density of 2579 trees ha−1, higher than the south transect which had a mean density of 1806 trees ha−1. The pooled mean density was 2174 trees ha−1, compared to the field finding of 2352 ± 831 ha−1 for trees with a diameter > 2.5 cm in the aforementioned four plots [30,38] in the area. There were also large spatial variations of tree density within the transects. We did not attempt to derive the post-hurricane (disturbed) tree density because the hurricane damage caused mangrove trees to greatly incline and the canopies were mixed (Figure A2: aerial photos taken before and after the hurricanes).
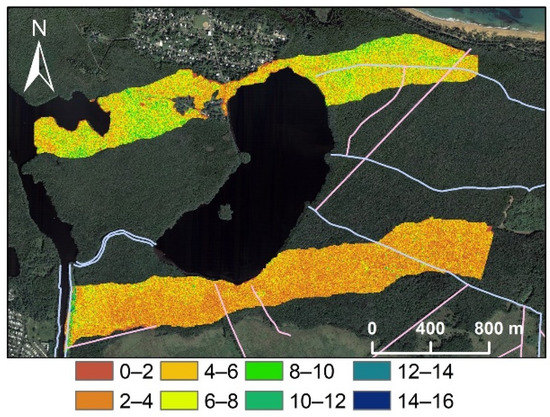
Figure 4.
The intact tree density expressed as the number of trees in 5 m by 5 m grid cells. The numbers in the legend can be converted to number of trees per ha by multiplying 400.
To explore the drivers that might cause the spatial variations of the canopy height, tree density, and canopy height reduction, we summarized the maps of DEM and distance to canals for the two transects with the available data (Table 1). We found that the north transect had a higher mean elevation (0.28 m) than the south transect (0.18 m), whereas the south transect had a closer mean distance to the canals (164.5 m) than the north transect (414.6 m). Table 1 shows a clear pattern: a higher elevation and farther distance to canals in the north transect were associated with a lower intact canopy height, a higher intact tree density, and a smaller canopy height reduction by the hurricanes, whereas the lower elevation and near distance to the canals in the south transect were associated with a higher intact canopy height, a lower intact tree density, and a greater reduction in canopy height. The large standard deviations in Table 1 implied a great within-transect variation. Whether the elevation and the distance to the canals actually explained the spatial variations of the canopy height, tree density, and canopy height reduction was further tested by the spatial modeling.
3.2. Spatial Regression of Intact Canopy Height and Tree Density
The spatial regression with autocorrelation among eight nearest neighboring grid cells showed that the normalized canopy height (h) before the hurricanes could be well explained by the normalized elevation (z) and the distance to the canals (s):
All the coefficients were significant with p-value ≤ 0.01. The regression estimated a significant λ (spatial autocorrelation coefficient) as 0.94. Using the original definition of r2 in ordinary linear regression, we computed r2 as 0.82, and the model-predicted canopy height aligned well with the LiDAR-detected canopy height (Figure 5a). The standard error of the residual was 0.011 compared to the range of h between 0 and 1. The regression result (Equation (2)) indicated that the intact canopy height decreased significantly, linearly with the distance to canals, and declined significantly with the elevation in a quadratic manner.
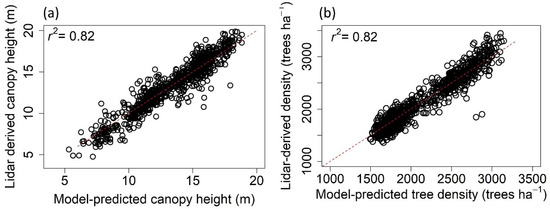
Figure 5.
Model-predicted intact canopy height versus LiDAR CHM (a), and model predicted intact tree density versus LiDAR-detected tree density (b).
The spatial regression of the intact tree density gave the following equation:
where D is the intact tree density in trees ha−1. All the coefficients were significant with p-value ≤ 0.01. The regression also had an r2 of 0.82 and the model-predicted tree density was in general aligned with the LiDAR-detected tree density (Figure 5b). The negative coefficient in front of the normalized canopy height (h) indicated that the tree density decreased significantly with canopy height, implying self-thinning. The positive coefficients in front of the elevation (z) and the distance to the canals (s) indicated that the intact tree density significantly increased with the elevation and the distance to the canals.
3.3. Spatial Regression of Canopy Height Reduction
Canopy height reduction was computed as the pre-hurricane canopy height minus the post-hurricane canopy height, which was the opposite of the canopy height change (Figure 6a). Considering the relationship between the canopy height and elevation (Equation (2)), we envisioned that the canopy height reduction was also correlated with the elevation and the distance to the canals. The relative canopy height reduction, that is, dividing the reduction in canopy height by the pre-hurricane canopy height, gave the mean ± standard deviation as 0.40 ± 0.22, 0.64 ± 0.23, and 0.53 ± 0.26 for the north, south, and pooled two transects, respectively.
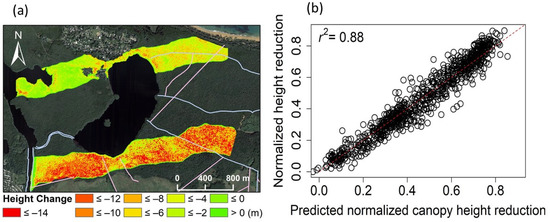
Figure 6.
Canopy height change by the hurricanes calculated as disturbed minus intact canopy height (a), and model-predicted versus LiDAR-derived normalized canopy height reduction (b).
The spatial regression of the mean canopy heigh reduction at a 40 m grid on the normalized elevation, canopy height, tree density, and distance to the canals gave the following equation:
where Δh is the normalized canopy height reduction, and d is the normalized intact tree density. All the coefficients were significant with p-value ≤ 0.05 except the coefficient before the distance to the canals (s) which had a p-value of 0.09. The r2 for this regression was 0.88 (Figure 6b). Hence, the canopy height reduction increased with the intact canopy height, but decreased with the intact tree density, the distance to the canals, and the elevation in a quadratic manner.
4. Discussion
Vertical structures of mangroves were highly regulated by the hydrology, salinity, and nutrient supply among others [3,39]. In this study, we found that an intact canopy height significantly depended on the elevation and distance to the freshwater/sewage canals (Equation (2)), which control the spatial patterns of the hydrology, salinity, and nutrients of the mangrove ecosystem. The lower elevation and closer distance to canals tended to give a higher intact canopy (Figure 2, Figure 3 and Figure 4, Table 1), whereas places with a higher elevation or further distance from the canals were associated with a lower canopy. Although mangroves flourish in the low salinity environments, the growth of mangrove trees is greatly suppressed by a high salinity [40,41]. Ample rainfall results in overland flow, and the canals carry freshwater and nutrients to the lower elevation. In addition to the verge of the lagoon, there exist local minimums in the elevation profile (Figure 1b). Freshwater and nutrients are likely to build up in these minimums to alleviate the salinity stress and to provide nutrients for better mangrove growth. Indeed, mangroves closer to the canals had a higher canopy, and the coefficient in front of the normalized distance to canals was in the same order of that for the normalized elevation (Equation (2)). When the elevation increases, the availability of freshwater declines, and salinity is likely to be high. However, when elevation becomes too high, soils will have less of a chance to receive salty water and the ample rainfall prevents a salinity built-up in the soil, so that the salinity may start to decrease with elevation [42].
We summarized the connections among the spatial variables in Figure 7: Not only did the elevation and the distance to the canals significantly contribute to the spatial patterns of the intact canopy height and tree density, which in term significantly contributed to the spatial pattern of canopy height reduction, but also they directly affected canopy height reduction, the signs in Figure 7 indicate the directions of the effects.
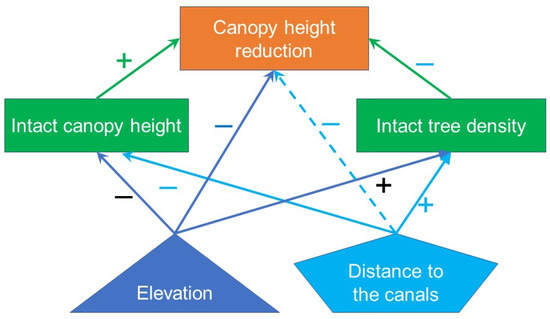
Figure 7.
Connection graph showing the roles of elevation and distance to canals in the spatial variations of intact canopy height, intact tree density, and canopy height reduction by the hurricanes. The dashed line between the distance to canals and the canopy height reduction considers the 0.09 p-value in Equation (4).
The spatial variation of the structural characteristics significantly modified the responses of the ecosystem to the major hurricanes. Specifically, the canopy height reduction was amplified with a higher intact canopy height (Equation (4)). A greater canopy height before a hurricane often implies more leaves to intercept greater wind drag forces during the hurricanes [43,44] and, thus, damage to the canopy. The maximum tree height was found important to explain the resistance of the tropical forest to hurricanes [45], and the emergent tree height in a forest has been used as a predictor of damages by tropical cyclones [46,47].
High tree density is also identified as a significant factor to resist canopy damage (Equation (4)), and spatial arrangement of trees is also important even for a forest with big trees [48]. Trees in a forest growing at a close distance, especially the mangrove trees with a height averaged around 10 m, tend to provide mutual support during wind disturbance [44,49]. Interactions via leaves and branches among trees during storms dissipate a portion of wind energy [50] and such interactions are enhanced by a high tree density. If a forest during hurricane winds can be viewed as a windbreak, an increased density of trees tends to reduce the average gap size and increase the effect of the windbreak. A forest with a low tree density is seen associated with more dead trees and bent trunks after a major hurricane [51]. ForestGales, a hybrid model to simulate the wind damage risk to a forest, uses predictor parameters, including spacing between trees, top tree height, mean DBH, gap size, soil types, and rooting depth [23,52]. The model computes a critical stem rupture wind speed which is inversely proportional to average spacing between trees so that a greater wind speed is needed to rupture stems with closer tree spacing. Tree spacing is the inverse of the density, and the model, thus, implies that a greater wind speed is needed to rupture trees with a high density. Gaps in the forest are mostly created by fallen trees or timber harvesting. However, gaps can also be the result of a low tree density. The recent variance-based sensitivity analysis on the risk of wind damage showed that tree height, mean diameter, and tree spacing are the mostly determinative factors, whereas the soil type and rooting depth are much less important [53].
The availability of a freshwater and nutrients input may also modify the response of the mangrove forest to hurricanes. Mangroves have a great morphological plasticity and change allometric growth upon altered salinity and nutrients balances via freshwater/sewage canals. The altered allometric growth is likely to modify the resistance of a mangrove forest to tropical storms. A reduced salinity by freshwater and an ample nutrients input tend to increase the shoot to root ratio [39,54,55,56], implying less root to support taller trees during hurricane winds. Trees living in a lower salinity and higher nutrient availability tend to grow more leaves [57,58,59], thus, to intercept more drag winds during storms [43]. On the other hand, trees with more nutrients tend to grow thinner leaves with a shorter average lifespan, which makes leaves easier to be torn by hurricane winds so as to cause more damage to the canopy [60,61]. These facts explained our results that mangroves with a close distance to the freshwater/sewage canals suffered more hurricane damage and had a lower canopy height remaining after the hurricanes (Figure 2 and Figure 3, Equation (4)).
An elevation profile was shown to be important in regulating canopy height before the hurricanes (Equation (2)) and differentiating the canopy height reduction (Equation (4)) in this study. Specifically, a lower elevation was associated with more canopy height reduction (Equations (2)–(4)). In addition to facilitating the accumulation of freshwater and nutrients, a lower elevation also implies more chances for inundation during the hurricanes [15]. The two hurricanes brought torrential rainfall to the island, and the lagoon with an extremely low exchange with ocean water made it very prone to prolonged inundation. The preliminary study showed that the low and moderate elevation in this area had been inundated for more than a week, which may have greatly damaged the black mangroves at a lower and moderate elevation after the hurricanes, such as immersing the pneumatophores and causing a delayed mortality. The soil under a mangrove forest is likely saturated. This is especially the reality for places with a low elevation where mangroves grow in muddy or submerging soil. The variation of elevation can also have an implication on soil–root anchorage. Muddy soil under a lower elevation has less anchorage for mangrove roots than soils at a higher elevation; thus, making the mangroves prone to soil–root failure during the hurricanes [62].
The LiDAR-detected canopy height was based on the return of a laser beam by tree leaves [63]. The canopy height is the height of tree crowns which consists of treetops, branches, and more importantly, tree leaves on tops of the crowns. The first return of LiDAR beam was often from leaves on the top of the tree crown. For trees with heavy leaves, trunks might have much less of a chance to be hit the first by LiDAR beams. The 53% canopy height reduction may have been mostly because of the defoliation and rupture of tree branches, but to a lesser extent, reflecting falling trunk or death of trees. Further efforts to separate the loss of leaves/branches from the loss of trunks will be promising to facilitate the assessment of the recovery of a forest structure. Our analysis showed that there were strong mechanistic connections among tree density, canopy height, elevation, and distance to the freshwater/sewage canals. Future research is necessitated to separate the effects of inundation and those of fertilization and desalinization by the freshwater/sewage canals at a low elevation. LiDAR detection combined with more frequent multispectral and hyperspectral images is suggested to further approach the problem of this kind. With the increased climate variability and warming [64,65], more frequent or/and intensified storms are expected at these coastal ecosystems. This research contributed to advancing the understanding of urban mangroves, especially the impact of human activities that modified the hydrology, salinity, and nutrients, such as canaling and sewage disposition, on the mangrove structure, and helped to elaborate the resistance of coastal mangroves to tropical storms.
5. Conclusions
This study used LiDAR data to analyze the structure of a basin mangrove near urban areas. We found that elevation and distance to the freshwater/sewage canals were significant explanators to the canopy height and tree density as well as the canopy height reduction during the hurricane season in 2017. The 188 ha mangroves suffered on average a 53% canopy height reduction. The canopy height reduction was found to increase with the canopy height before the hurricanes, but decrease with the elevation, the distance to the freshwater/sewage canals, and the tree density before the hurricanes. Adding freshwater/sewage to the forest made mangroves grow higher; however, it may also make the canopy more prone to hurricane damages.
Author Contributions
Conceptualization, Q.G. and M.Y.; methodology, Q.G. and M.Y.; formal analysis, Q.G. and M.Y.; writing—original draft preparation, Q.G.; writing—review and editing, Q.G. and M.Y. Both authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the NOAA Puerto Rico Sea Grant.
Acknowledgments
We acknowledge USGS for providing the LiDAR after the hurricanes, publicly available at the USGS 3D Elevation Program (3DEP) data portal (https://nationalmap.gov/3DEP/, accessed on 24 August 2021), and NASA for providing the LiDAR data before the hurricanes, publicly accessible at NASA G-LiHT (https://glihtdata.gsfc.nasa.gov/, accessed on 24 August 2021).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A
Figure A1.
Location of Puerto Rico in the Caribbean. The blue and red lines are the paths of Hurricane Irma and Hurricane Maria, respectively.

Figure A2.
Aerial photographs taken before and after the hurricanes at the southern Piñones lagoon (–65.96°, 18.43°, source: NASA G-LiHT https://glihtdata.gsfc.nasa.gov/puertorico/, accessed on 24 August 2021).
References
- Giri, C.; Ochieng, E.; Tieszen, L.L.; Zhu, Z.; Singh, A.; Loveland, T.; Masek, J.; Duke, N. Status and distribution of mangrove forests of the world using earth observation satellite data. Glob. Ecol. Biogeogr. 2011, 20, 154–159. [Google Scholar] [CrossRef]
- Field, C.; Osborn, J.; Hoffman, L.; Polsenberg, J.; Ackerly, D.; Berry, J.; BjÖRkman, O.; Held, A.; Matson, P.; Mooney, H. Mangrove biodiversity and ecosystem function. Glob. Ecol. Biogeogr. Lett. 1998, 7, 3–14. [Google Scholar] [CrossRef]
- Lovelock, C.E.; Krauss, K.W.; Osland, M.J.; Reef, R.; Ball, M.C. The Physiology of Mangrove Trees with Changing Climate. In Tropical Tree Physiology—Adaptations and Responses in a Changing Environment; Goldstein, G., Santiago, L.S., Eds.; Springer: Berlin, Germany, 2016; pp. 149–179. [Google Scholar]
- Alongi, D. Carbon sequestration in mangrove forests. Carbon Manag. 2014, 3, 313–322. [Google Scholar] [CrossRef]
- Kristensen, E.; Andersen, F.O.; Homboe, N.; Holmer, M. Carbon and nitrogen mineralization in sediments of the Bangrong mangrove area, Phuket, Thailand. Aquat. Microb. Ecol. 2000, 22, 199–213. [Google Scholar] [CrossRef]
- Gedan, K.B.; Kirwan, M.L.; Wolanski, E.; Barbier, E.B.; Silliman, B.R. The present and future role of coastal wetland vegetation in protecting shorelines: Answering recent challenges to the paradigm. Clim. Chang. 2011, 106, 7–29. [Google Scholar] [CrossRef]
- Doody, J.P. ‘Coastal squeeze’—An historical perspective. J. Coast. Conserv. 2004, 10, 129–138. [Google Scholar] [CrossRef]
- Branoff, B. Urban Mangrove Biology and Ecology: Emergent Patterns and Management Implications; University of Puerto Rico: San Juan, PR, USA, 2018. [Google Scholar]
- Lee, S.Y.; Primavera, J.H.; Dahdouh-Guebas, F.; McKee, K.; Bosire, J.O.; Cannicci, S.; Diele, K.; Fromard, F.; Koedam, N.; Marchand, C.; et al. Ecological role and services of tropical mangrove ecosystems: A reassessment. Glob. Ecol. Biogeogr. 2014, 23, 726–743. [Google Scholar] [CrossRef]
- Choy, S.C.; Booth, W.E. Prolonged inundation and ecological changes in an Avicennia mangrove: Implications for conservation and management. Hydrobiologia 1994, 285, 237–247. [Google Scholar] [CrossRef]
- Mbense, S.; Rajkaran, A.; Bolosha, U.; Adams, J. Rapid colonization of degraded mangrove habitat by succulent salt marsh. S. Afr. J. Bot. 2016, 107, 129–136. [Google Scholar] [CrossRef]
- Lovelock, C.E.; Feller, I.C.; Reef, R.; Hickey, S.; Ball, M.C. Mangrove dieback during fluctuating sea levels. Sci. Rep. 2017, 7, 1680. [Google Scholar] [CrossRef]
- Ward, G.A.; Smith, T., III. Predicting mangrove forest recovery on the southwest coast of Florida following the impact of Hurricane Wilma, Octobe 2005. In Science and the Storms: The USGS Response to the Hurricanes of 2005; Farris, G.S., Smith, G.J., Crane, M.P., Demas, C.R., Robbins, L.L., Lavoie, D.L., Eds.; U.S. Geological Survey Circular, John W. Powell National Center: Reston, VA, USA, 2005; 283p. [Google Scholar]
- Blankespoor, B.; Dasgupta, S.; Lange, G.-M. Mangroves as a protection from storm surges in a changing climate. Ambio 2017, 46, 478–491. [Google Scholar] [CrossRef]
- Yu, M.; Gao, Q. Topography, drainage capability, and legacy of drought differentiate tropical ecosystem response to and recovery from major hurricanes. Environ. Res. Lett. 2020, 15, 104046. [Google Scholar] [CrossRef]
- Branoff, B.; Cuevas, E.; Hernandez, E. Assessment of Urban Coastal Wetlands Vulnerability to Hurricanes in Puerto Rico; Department of Natural and Environmental Resources: San Juan, PR, USA, 2015. [Google Scholar]
- Taillie, P.J.; Roman-Cuesta, R.; Lagomasino, D.; Cifuentes-Jara, M.; Fatoyinbo, T.; Ott, L.E.; Poulter, B. Widespread mangrove damage resulting from the 2017 Atlantic mega hurricane season. Environ. Res. Lett. 2020, 15, 064010. [Google Scholar] [CrossRef]
- Zhang, K.; Thapa, B.; Ross, M.; Gann, D. Remote sensing of seasonal changes and disturbances in mangrove forest: A case study from South Florida. Ecosphere 2016, 7, e01366. [Google Scholar] [CrossRef] [Green Version]
- Huang, W.; Sun, G.; Dubayah, R.; Cook, B.; Montesano, P.; Ni, W.; Zhang, Z. Mapping biomass change after forest disturbance: Applying LiDAR footprint-derived models at key map scales. Remote Sens. Environ. 2013, 134, 319–332. [Google Scholar] [CrossRef]
- van Leeuwen, M.; Nieuwenhuis, M. Retrieval of forest structural parameters using LiDAR remote sensing. Eur. J. For. Res. 2010, 129, 749–770. [Google Scholar] [CrossRef]
- Gao, Q.; Yu, M. Canopy Density and Roughness Differentiate Resistance of a Tropical Dry Forest to Major Hurricane Damage. Remote Sens. 2021, 13, 2262. [Google Scholar] [CrossRef]
- Mitchell, S.J. Wind as a natural disturbance agent in forests: A synthesis. For. Int. J. For. Res. 2012, 86, 147–157. [Google Scholar] [CrossRef] [Green Version]
- Gardiner, B.; Byrne, K.; Hale, S.; Kamimura, K.; Mitchell, S.J.; Peltola, H.; Ruel, J.-C. A review of mechanistic modelling of wind damage risk to forests. For. Int. J. For. Res. 2008, 81, 447–463. [Google Scholar] [CrossRef] [Green Version]
- Krauss, K.W.; Osland, M.J. Tropical cyclones and the organization of mangrove forests: A review. Ann. Bot. 2019, 125, 213–234. [Google Scholar] [CrossRef]
- Cartier, K. Hurricanes Hit Puerto Rico’s Mangroves Harder Than Florida’s. EOS 2019. [Google Scholar] [CrossRef]
- Martinuzzi, S.; Gould, W.A.; Lugo, A.E.; Medina, E. Conversion and recovery of Puerto Rican mangroves: 200 years of change. For. Ecol. Manag. 2009, 257, 75–84. [Google Scholar] [CrossRef]
- Yu, M.; Rivera-Ocasio, E.; Heartsill-Scalley, T.; Davila-Casanova, D.; Rios-López, N.; Gao, Q. Landscape-Level Consequences of Rising Sea-Level on Coastal Wetlands: Saltwater Intrusion Drives Displacement and Mortality in the Twenty-First Century. Wetlands 2019, 39, 1343–1355. [Google Scholar] [CrossRef]
- Gao, Q.; Yu, M. Discerning Fragmentation Dynamics of Tropical Forest and Wetland during Reforestation, Urban Sprawl, and Policy Shifts. PLoS ONE 2014, 9, e113140. [Google Scholar] [CrossRef]
- Kennaway, T.; Helmer, E.H. The forest types and ages cleared for land development in Puerto Rico. Giscience Remote Sens. 2007, 44, 356–382. [Google Scholar] [CrossRef]
- Martinez, R.; Cintron, G.; Encarnacion, L.A. Mangroves in Puerto Rico: A Structural Inventory; Department of Natural Resources, Puerto Rico: San Juan, PR, USA, 1979. [Google Scholar]
- Lugo, A.E.; Medina, E. Mangrove Forests. In Encyclopedia of Natural Resources—Land; Wang, Y., Ed.; Taylor & Francis: New York, NY, USA, 2014; Volume 1. [Google Scholar]
- Puerto Rico Department of Natural and Environmental Resources. Bosque Estatal de Piñones; Puerto Rico Department of Natural and Environmental Resources: San Juan, PR, USA, 2008. [Google Scholar]
- Cook, B.; Corp, L.; Nelson, R.; Middleton, E.; Morton, D.; McCorkel, J.; Masek, J.; Ranson, K.; Ly, V.; Montesano, P. NASA Goddard’s LiDAR, Hyperspectral and Thermal (G-LiHT) Airborne Imager. Remote Sens. 2013, 5, 4045. [Google Scholar] [CrossRef] [Green Version]
- Office for Coastal Management. C-CAP Land Cover, Puerto Rico, 2010. 2020. Available online: https://www.fisheries.noaa.gov/inport/item/48301 (accessed on 24 August 2021).
- Roussel, J.-R.; Auty, D.; Boissieu, F.D.; Meador, A.S. Lidr: Airborne LiDAR Data Manipulation and Visualization for Forestry Applications. 2019. Available online: https://cran.r-project.org/package=lidR (accessed on 24 August 2021).
- Anselin, L.; Griffith, D.A. DO SPATIAL EFFECFS REALLY MATTER IN REGRESSION ANALYSIS? Pap. Reg. Sci. 1988, 65, 11–34. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Pool, D.; Snedaker, S.C.; Lugo, A.E. Structure of Mangrove Forests in Florida, Puerto Rico, Mexico, and Costa Rica. Biotropica 1977, 9, 195–212. [Google Scholar] [CrossRef] [Green Version]
- Krauss, K.W.; McKee, K.L.; Lovelock, C.E.; Cahoon, D.R.; Saintilan, N.; Reef, R.; Chen, L. How mangrove forests adjust to rising sea level. New Phytol. 2014, 202, 19–34. [Google Scholar] [CrossRef] [Green Version]
- Lugo, A.E.; Snedaker, S.C. The ecology of mangroves. Annu. Rev. Ecol. Syst. 1974, 5, 39–64. [Google Scholar] [CrossRef]
- Medina, E. Mangrove Physiology: The challenge of salt, heat, and light stress under recurrent flooding. In Ecosystemas de Manglar en America Tropical; Yanez-Arancibia, A., Lara-Dominquez, A.L., Eds.; Instituto de Ecologia A.C. Mexico: Xalapa, Mexico, 1999; pp. 109–126. [Google Scholar]
- Leong, R.C.; Friess, D.; Crase, B.; Lee, W.K.; Webb, E. High-resolution pattern of mangrove species distribution is controlled by surface elevation. Estuar. Coast. Shelf Sci. 2017, 202, 185–192. [Google Scholar] [CrossRef]
- Angelou, N.; Dellwik, E.; Mann, J. Wind load estimation on an open-grown European oak tree. For. Int. J. For. Res. 2019, 92, 381–392. [Google Scholar] [CrossRef]
- Peterson, C.J.; Ribeiro, G.H.P.d.M.; Negrón-Juárez, R.; Marra, D.M.; Chambers, J.Q.; Higuchi, N.; Lima, A.; Cannon, J.B. Critical wind speeds suggest wind could be an important disturbance agent in Amazonian forests. For. Int. J. For. Res. 2019, 92, 444–459. [Google Scholar] [CrossRef]
- Paz, H.; Vega-Ramos, F.; Arreola-Villa, F. Understanding hurricane resistance and resilience in tropical dry forest trees: A functional traits approach. For. Ecol. Manag. 2018, 426. [Google Scholar] [CrossRef]
- Renaud, J.-P.; Vega, C.; Durrieu, S.; Lisein, J.; Magnussen, S.; Lejeune, P.; Fournier, M. Stand-level wind damage can be assessed using diachronic photogrammetric canopy height models. Ann. For. Sci. 2017, 74, 74. [Google Scholar] [CrossRef] [Green Version]
- Hall, J.; Muscarella, R.; Quebbeman, A.; Arellano, G.; Thompson, J.; Zimmerman, J.K.; Uriarte, M. Hurricane-Induced Rainfall is a Stronger Predictor of Tropical Forest Damage in Puerto Rico Than Maximum Wind Speeds. Sci. Rep. 2020, 10, 4318. [Google Scholar] [CrossRef] [PubMed]
- Duryea, M.L.; Kamp, E. Wind and Trees: Lessons Learned from Hurricanes; School of Forest Resources and Conservation, University of Florida FAS Extension: Gainesville, FL, USA, 2017; Available online: http://edis.ifas.ufl.edu (accessed on 24 August 2021).
- Moore, J.; Lin, Y. Determining the extent and drivers of attrition losses from wind using long-term datasets and machine learning techniques. For. Int. J. For. Res. 2019, 92, 425–435. [Google Scholar] [CrossRef]
- Walter, B.; Gromke, C.; Lehning, M. The SLF boundary layer wind tunnel—An experimental facility for aerodynamical investigations of living plants. In Proceedings of the 2nd International Conference Wind Effects on Trees, Freiburg, Germany, 13–16 October 2009; pp. 31–38. [Google Scholar]
- Jimenez, D.L.; Alvarez-Añorve, M.; Pineda-Cortes, M.; Flores-Puerto, J.; Benitez-Malvido, J.; Oyama, K.; Avila Cabadilla, L. Structural and functional traits predict short term response of tropical dry forests to a high intensity hurricane. For. Ecol. Manag. 2018, 426. [Google Scholar] [CrossRef]
- Hale, S.; Gardiner, B.; Peace, A.; Nicoll, B.; Taylor, P.; Pizzirani, S. Comparison and validation of three versions of a forest wind risk model. Environ. Model. Softw. 2015, 68, 27–41. [Google Scholar] [CrossRef] [Green Version]
- Locatelli, T.; Tarantola, S.; Gardiner, B.; Patenaude, G. Variance-based sensitivity analysis of a wind risk model—Model behaviour and lessons for forest modelling. Environ. Model. Softw. 2017, 87, 84–109. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, H.T.; Stanton, D.E.; Schmitz, N.; Farquhar, G.D.; Ball, M.C. Growth responses of the mangrove Avicennia marina to salinity: Development and function of shoot hydraulic systems require saline conditions. Ann. Bot. 2015, 115, 397–407. [Google Scholar] [CrossRef]
- Chen, Y.; Ye, Y. Effects of Salinity and Nutrient Addition on Mangrove Excoecaria agallocha. PLoS ONE 2014, 9, e93337. [Google Scholar] [CrossRef]
- Peters, R.; Vovides, A.G.; Luna, S.; Gruters, U.; Berger, U. Changes in allometric relations of mangrove trees due to resource availability—A new mechanistic modelling approach. Ecol. Model. 2014, 283, 53–61. [Google Scholar] [CrossRef]
- Vovides, A.G.; Vogt, J.; Kollert, A.; Berger, U.; Grueters, U.; Peters, R.; Lara-Domínguez, A.L.; López-Portillo, J. Morphological plasticity in mangrove trees: Salinity-related changes in the allometry of Avicennia germinans. Trees 2014, 28, 1413–1425. [Google Scholar] [CrossRef]
- Whigham, D.F.; Verhoeven, J.T.A.; Samarkin, V.; Megonigal, P.J. Responses of Avicennia germinans (Black Mangrove) and the Soil Microbial Community to Nitrogen Addition in a Hypersaline Wetland. Estuaries Coasts 2009, 32, 926–936. [Google Scholar] [CrossRef] [Green Version]
- Kodikara, K.A.S.; Jayatissa, L.P.; Huxham, M.; Dahdouh-Guebas, F.; Koedam, N. The effects of salinity on growth and survival of mangrove seedlings changes with age. Acta Bot. Bras. 2017, 32. [Google Scholar] [CrossRef] [Green Version]
- Reich, P.B.; Walter, M.B.; Ellsworth, D.S. Leaf life-span in relation to leaf, plant, and stand characterisitics among diverse ecosystems. Ecol. Monogr. 1992, 62, 365–392. [Google Scholar] [CrossRef]
- Chapin, F.S.I.; Matson, P.; Vitousek, P.M. Principles of Terrestrial Ecosystem Ecology, 2nd ed.; Springer: New York, NY, USA, 2011. [Google Scholar]
- Lugo, A.E. Visible and invisible effects of hurricanes on forest ecosystems: An international review. Austral Ecol. 2008, 33, 368–398. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, H. Estimation of LAI with the LiDAR Technology: A Review. Remote Sens. 2020, 12, 3457. [Google Scholar] [CrossRef]
- Gao, Q.; Yu, M. Reforestation-induced changes of landscape composition and configuration modulate freshwater supply and flooding risk of tropical watersheds. PLoS ONE 2017, 12, e0181315. [Google Scholar] [CrossRef] [Green Version]
- Yu, M.; Gao, Q.; Gao, C.; Wang, C. Extent of Night Warming and Spatially Heterogeneous Cloudiness Differentiate Temporal Trend of Greenness in Mountainous Tropics in the New Century. Sci. Rep. 2017, 7, 41256. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).