Abstract
With the advent of very-high-resolution remote sensing images, semantic change detection (SCD) based on deep learning has become a research hotspot in recent years. SCD aims to observe the change in the Earth’s land surface and plays a vital role in monitoring the ecological environment, land use and land cover. Existing research mainly focus on single-task semantic change detection; the problem they face is that existing methods are incapable of identifying which change type has occurred in each multi-temporal image. In addition, few methods use the binary change region to help train a deep SCD-based network. Hence, we propose a dual-task semantic change detection network (GCF-SCD-Net) by using the generative change field (GCF) module to locate and segment the change region; what is more, the proposed network is end-to-end trainable. In the meantime, because of the influence of the imbalance label, we propose a separable loss function to alleviate the over-fitting problem. Extensive experiments are conducted in this work to validate the performance of our method. Finally, our work achieves a 69.9% mIoU and 17.9 Sek on the SECOND dataset. Compared with traditional networks, GCF-SCD-Net achieves the best results and promising performances.
1. Introduction
Change detection (CD) plays an important role in land-use planning, population estimation, natural disasters and city management [1,2,3]. Change detection is a technique for obtaining change regions of interest using remote sensing images in different time periods. There are more than thirty years of studies related to change detection [1], and many state-of-the-art techniques [4,5,6,7,8,9,10,11,12,13,14,15,16,17] have been proposed to automatically identify changes in a region in remote sensing images. However, most of these change detection methods [12,13,14,15,16,17] are binary change detection (BCD), which overlooks the pixel’s categories that are usually necessary for practical application.
Semantic change detection (SCD) can detect the change regions and identify the semantic labels simultaneously. However, SCD-based datasets that are openly available are still limited [18]. Hence, to validate the proposed methods, a large-scale semantic change detection dataset (HRSCD) was built by Daudt et al. [18], and a sequential training framework for semantic change detection was proposed. Based on semantic change detection, Mou et al. [19] proposed a recurrent convolutional neural network (ReCNN) network, and two data sets were built to validate their work, but the proposed datasets are not publicly available. Although, existing methods can achieve the semantic change detection with promising results, their studies face the problems of locating and identifying the area of change [20]. Consequently, Yang et al. [20] proposed an asymmetric Siamese network (ASN) for dual-task semantic change detection, and a large-scale semantic change detection dataset was built, named SECOND, to detect change regions between the same land-cover types.
Different from binary labels, semantic change labels contain multiple categories, and each period image corresponds to a semantic change label. However, existing change detection methods usually can only realize binary change detection (such as References [12,13,14,15,16,17,18]) or single task semantic change detection [19]. The SECOND dataset contains a pair of semantic change labels corresponding to two periods’ images. Consequently, conventional methods, such as FC-EF [15], FC-conc [15] and FC-diff [15], do not work well.
With the development of remote sensing and machine learning technology [21,22], change detection has achieved great progress. Change detection generally falls into two categories, one is binary change detection and the other is semantic change detection. Binary change detection mainly focuses on change regions yet overlook categories of pixels. Different from binary change detection, semantic change detection not only achieves the change regions detection, but also identifies the categories of each pixel of change regions.
In recent years, a lot of studies mainly pay attention to binary change detection [12,23,24,25,26,27]; most of the works focus on detecting change regions, labeling them with “0” and “1”, where “0” is no change and “1” represents a change region. Consequently, the binary change map can be obtained through extracting difference features from image pairs. The main purpose of change detection in remote sensing images is to obtain the change information from the bitemporal images; the change regions usually are highly important to analyze land-use and land-cover change. However, binary change detection usually fails to identify the ground truth of each pixel in change regions. Consequently, semantic change detection (SCD)-based methods have been developed for achieving semantic segmentation based on a change region. However, we found that the existing works have two shortcomings, as follows:
(1) Based on the above, since the existing methods are single-task-oriented change detection frameworks, they are inappropriate to achieve dual-task semantic change detection.
(2) Although, dual-task-based semantic change detection has been developed, its generality is not strong, and thus the model has space for improvement.
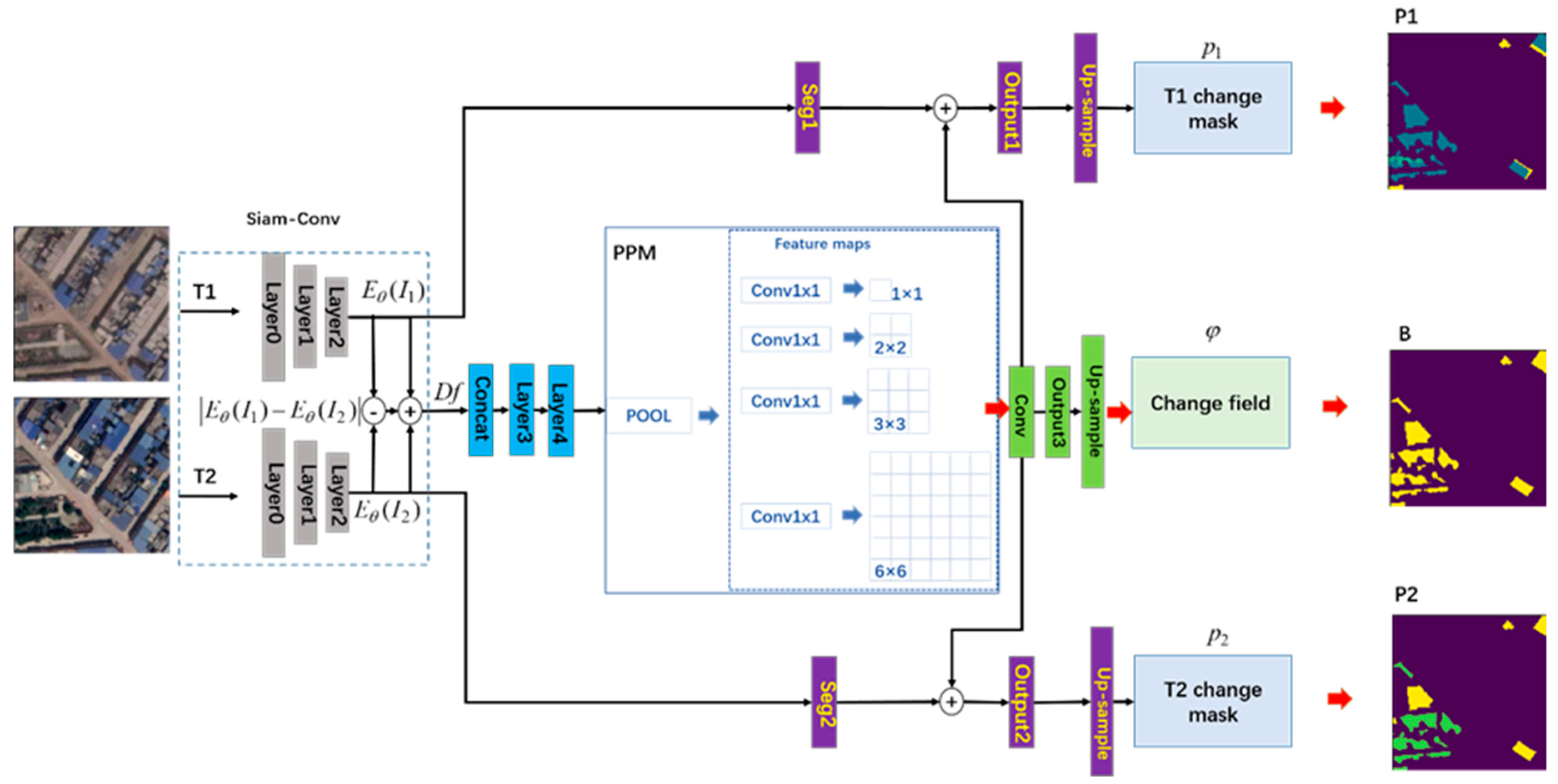
Based on the abovementioned problems, our work proposes a novel dual-task semantic change detection Siamese network using the generative change field module to help the prediction of change regions and segmentation. The proposed network uses a binary change detection branch to guide the two semantic segmentation networks to predict pixels’ categories. Since the semantic segmentation branch does not have the perception of the change information before the fusion of the change region information (generative change field) and semantic information, then only by fusing the change information can the two semantic segmentation branches realize the prediction of the change region. Therefore, the proposed network is called the Generative Change Field (GCF)-based dual-task Semantic Change Detection Network (GCF-SCD-Net), as shown in Figure 1. Although, in previous work [19], Mou et al. have proposed to use the binary change map to help model training, the proposed network exploits the convolutional neural network and recurrent neural network to achieve feature extraction and change detection, and obtains the binary change maps by using fully connected layers activated by the sigmoid function. Their method only used the auxiliary loss method to generate a sematic change map. For the SCD task, change features play an important role in helping the model predict semantic change labels. They can guide the generative semantic change map module to focus on different regions between bitemporal images. In addition, change regions can be generated using a change feature map. Fusing the binary change feature map and semantic change feature map is an effective method to improve the segmentation results. In this paper, the main contributions are as follows.
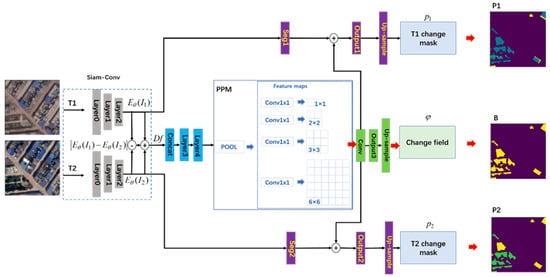
Figure 1.
Architecture of the proposed network.
(1) We propose a novel dual-task semantic change network to identify the change region in bitemporal images, and it achieves strong results using the SECOND dataset. The proposed SCD-based model effectively solves the dual-task semantic change detection problem.
(2) To the best of our knowledge, we are the first to exploit the generative change field method to guide two branch networks to achieve dual-task semantic change detection.
(3) In order to alleviate the influence of an imbalanced label between the change region and no-change region, we propose a robust separable loss function that enables to improve the performance of the network.
2. Materials and Methods
To simplify the mathematical modeling, Table 1 depicts the meanings of the abbreviated letters we used.

Table 1.
Descriptions of the abbreviations used.
2.1. Siamese Convolutional Network
Siam-Conv has been widely used to extract feature information in existing works [13,15,16,17,18], which shows the effectiveness of Siam-Conv for change detection. Therefore, we exploited Siam-Conv to extract the feature information from the image pairs, as shown in Figure 1.
Let and represent an input image pair, . Let be Siam-Conv (as shown the Siam-Conv module in Figure 1) for extracting the feature maps from the bitemporal images, and the learning parameters of the Siam-Conv. Then, the feature extraction can be formulated as follows:
where is the feature maps captured from the input image at time Ti, and .
In this work, we used seven residual blocks, which are from ResNet34 proposed by He et al. [28], to extract the shallow features. The details of Siam-Conv are listed in Table 2. Firstly, we use Layer0 (correspond to “Layer0” in Figure 1) to extract the salient features and reducing the size of the feature maps, which contains a convolutional layer (Conv) with a kernel size of 7 × 7, Batch Normalization layer (BN), Rectified Linear Unit (ReLU) and Maxpooling layer (Maxpool). Next, we used three residual blocks (“Layer1” in Figure 1) to extract the low-dimension features with a size of 64 × 64, and four residual blocks (“Layer2” in Figure 1) were used to capture the middle dimension features with a size of 32 × 32.

Table 2.
Configuration of Siam-Conv.
2.2. General Networks for Dual-Task Semantic Change Detection
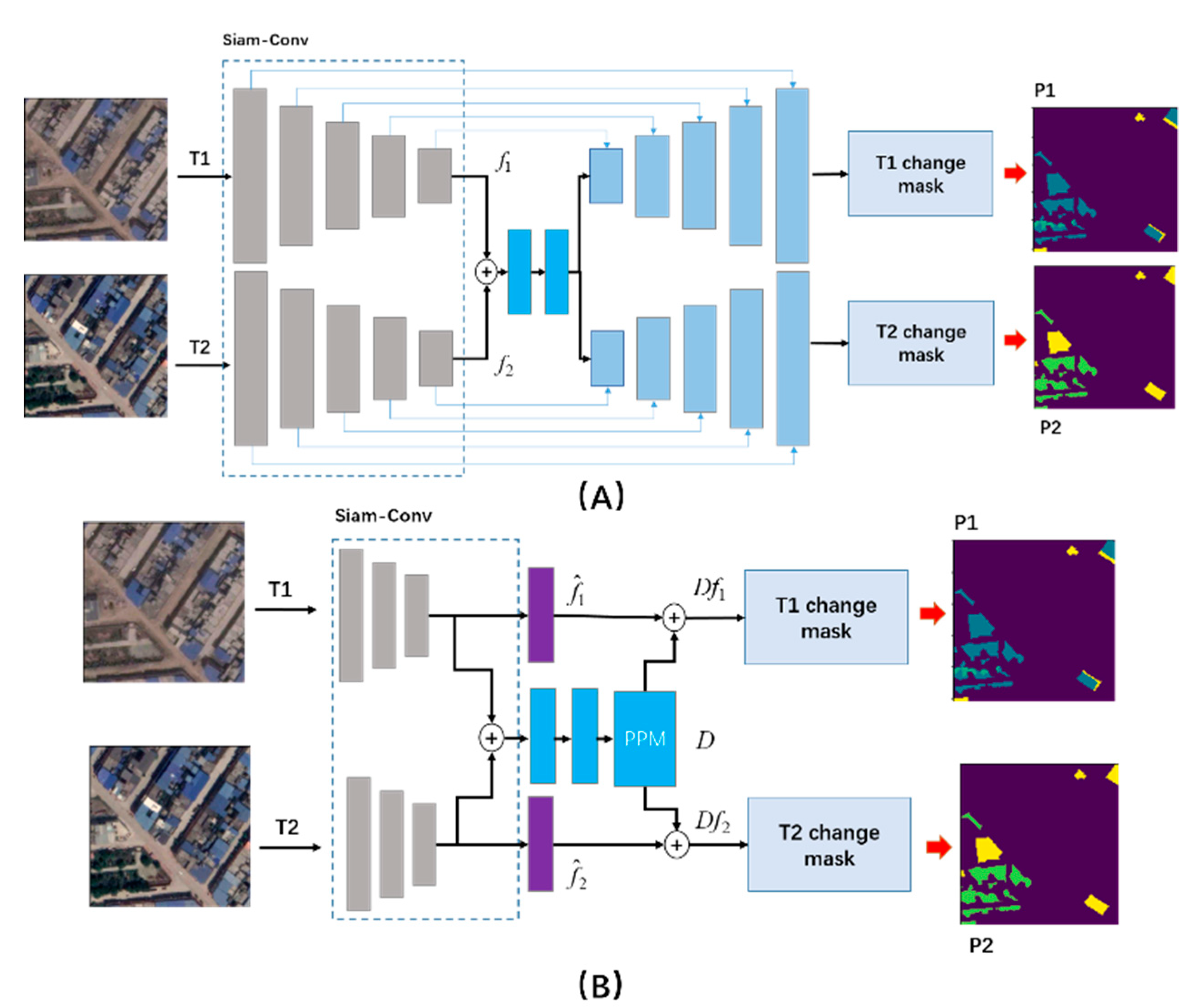
Traditional change detection methods cannot effectively achieve dual-task semantic change detection; the main reason is that the general networks are designed based on a single task, so it is impossible to achieve dual-task change detection. Hence, based on classical segmentation networks, such as UNet [29] and PSPNet [30], we built two dual-task semantic change detection networks, as shown in Figure 2.
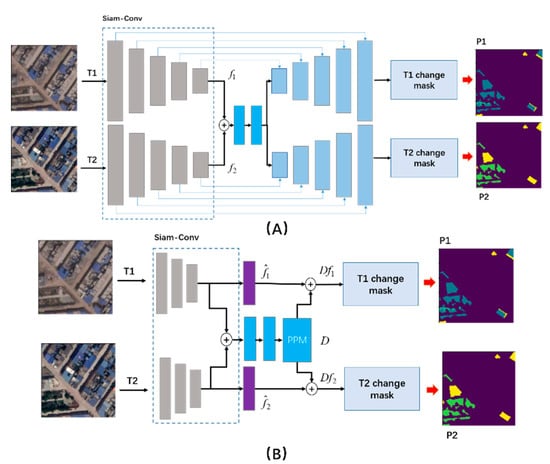
Figure 2.
General networks for SCD: (A) is the UNet-based SCD network, and (B) represents the PSPNet-based SCD network.
2.2.1. UNet-SCD
In the Siam-Conv module, we exploited ResNet34 to extract the feature representation from the bitemporal images, separately. Let and represent the feature maps captured from the image pairs at two different times, and . Next, the feature pairs were fused by a concatenation operation, which can be formulated by
where . In order to obtain the difference features, we used two convolutional groups (Conv + BN + ReLU) to refine the difference maps. The convolutional group was defined as follows:
Then, we used two upsampling branches and a skip connection strategy to guide each branch to generate the difference maps.
2.2.2. PSPNet-SCD
Different from the UNet-SCD network, the bitemporal images were downsampled by 1/8 in the Siam-Conv module. Then, we use the concatenation operation to fuse the bitemporal features. Meanwhile, we use the pyramid pooling module (PPM) [30] to capture features with different receptive fields. Finally, through reusing the bitemporal features outputted from the Siam-Conv module, we can achieve the dual-task semantic change maps. The fusion process can be defined as follows:
where means the difference features are taken from PPM, and represents the bitemporal feature maps. In order to extract the difference maps from , we use the two convolutional groups to generate the semantic change maps in the different time periods, separately.
2.3. Generative Change Field Network for Dual-Task Semantic Change Detection
Above, we established two types of dual-task semantic change detection networks. However, their results obtained on the SECOND dataset are mediocre. Hence, we developed a method (GCF-SCD-Net) that can achieve strong performance for dual-task SCD in this work.
We introduce a generative change field (GCF) module that only focuses on change regions based on difference maps. Since the details of the Siam-Conv module are given in Table 2, we only present the configuration of the GCF-based dual-task semantic change detection in Table 3. The process of generating a change field is as follows:

Table 3.
Configuration of the generative change field module.
Firstly, we can obtain the bitemporal features and . Let Df represents the fusion features, , which can be achieved through the concatenation operation
Then, using two Conv modules, we reduced the dimension of to obtain . Next, nine residual blocks were used to obtain the difference maps (correspond to “Layer3” and “Layer4” in Figure 1). To effectively capture the feature representation from , we used the PPM strategy, the PPM module shown in Figure 1, to extract the difference feature maps at different scales. In this work, we used four scales of the feature maps with bin sizes of 1 × 1, 2 × 2, 3 × 3 and 6 × 6, respectively. Finally, a convolutional group and output layer were used to generate the binary change maps, , which are marked with a green box in Figure 1.
The aim of the GCF-SCD-Net is to achieve dual-task semantic change detection; thus, we exploited two branches to generate bitemporal semantic change maps. A “Seg1” module contains two convolutional layers is used to increase the dimensions of from 128 to 512, therefore, we can obtain the feature maps at time of , . After that, we make use of difference feature maps generated by GCF module to guide branch-1 (top side of Figure 1) to predict the pixels’ categories of the T1 image (). Similarly, the semantic change map of T2 image () can be obtained in the same way; this is shown on the bottom of Figure 1.
The final binary change map and semantic change maps are generated by the softmax activation function, which can be formulated by
where is the softmax function and represents the maximum index of prediction, so we have
where represents the prediction of a pixel in the x-row and y-column of the c-th channel. S is the channels, which is equal to the total number of change types and no-change types. Through the abovementioned strategy, we can obtain the change region maps and semantic change segmentation maps simultaneously.
2.4. Dual-Task Semantic Change Detection Loss Function
Model training plays an important role in achieving surprising results. A suitable loss function is good for obtaining better performance and reducing training time. In this article, a loss function consists of generative change field loss (gcf_loss) and semantic change loss (sc_loss). The loss function can be written as
2.4.1. WCE_Loss
For our task, cross-entropy loss (CE_loss) is capable of measuring the similarity between prediction and ground truth, which is an appropriate choice for calculating the loss. The CE_loss can be formulated as follows:
where N is the number of training samples, and yi and pi are the ground truth and prediction of the i-th samples. However, the distribution of the target class is unbalanced. Hence, according to the statistics of the pixels for each class, we added a distribution weight based on the number of each category to the cross-entropy loss function (WCE_loss), so Equation (11) can be rewritten as
where w is the weight, .
2.4.2. Separable Loss
Due to the influence of the imbalance label, we propose a separable loss function that calculates the loss of the no-change regions and change regions, respectively. Let indicate the softmax function, where is the prediction of the 0th channel of activated by the softmax function, . We define the separable loss as follows:
where : E is the matrix with all the elements of one, and B is the ground truth of the binary change. and are the ground truth and prediction of the j-th sample at time Ti without the no-change type, , . We use the no-change loss to train the network through calculating the loss of the no-change channel. Meanwhile, change loss that ignores the no-change channel can contribute to the loss without the influence of the imbalance label between change and no change.
2.4.3. Union Loss
In this work, we make use of the WCE_loss and separable loss to punish the network based on the generative change field and semantic change prediction during the training process. Let and represent the prediction and ground truth, and b and B are the binary change prediction and ground truth; then, the loss can be formulated as
3. Results
In this section, we first introduce the experimental setup in Section 3.1. Next, we describe the dataset used in this work and the evaluation criteria of the models in Section 3.2 and Section 3.3. Further, in Section 3.4 and Section 3.5, we present the experimental results and analysis.
3.1. Implementation Details
To ensure a fair comparison, all experiments were conducted with the same training strategy, software environment and hardware platform. The details are as follows.
The total number of training epochs is 100 for all experiments. We use the stochastic gradient descent (SGD) algorithm [31] to train the networks; the momentum is set to 0.9, with a weight decay of 5 × 10−4. The initial learning rate was 0.005, which dynamically decreased every 30 epochs by 1/10 during training. The input size of the image pair was 256 × 256 pixels. Due to the limitation of GPU memory, the batch size was set as 16. All experiments were implemented in Ubuntu 18.04.1 LTS. Pytorch 1.6 and Python 3.6 were used to build the CNN-based networks. We implemented all experiments on a DELL platform, which was built with an Inter Xeon(R) Silver 4210 CPU, RTX 2080Ti 11-GB GPU and 256-GB of RAM.
3.2. Dataset
Currently, the public semantic change detection datasets are still limited. Most of the existing public benchmarks [32,33,34,35] mainly focus on binary change detection. Mou et al. [19] built a multi-class change detection benchmark for SCD, while the dataset is a single-task SCD and is not publicly available.
Hence, we used the dual-task SCD benchmark (SECOND) http://www.captain-whu.com/PROJECT/SCD/ (accessed on 8 March 2021) proposed by [20] to validate our methods. The dataset is a dual-task-based semantic change detection dataset. There are six categories in the SECOND dataset, including non-vegetated ground surface, tree, low vegetation, water, buildings and playgrounds. It contains 4662 pairs of aerial images, and each sample has size of 512 × 512, in three bands (red, green and blue).
3.3. Metrics
For change detection, the Over Accuracy (OA) and mean Intersection over Union (mIoU) are usually utilized for validating the performance of the methods [15,18,19,26,35]. Since the numbers of categories are unevenly distributed, Yang et al. [20] proposed a Separated Kappa (SeK) coefficient to alleviate the influence of an imbalance label.
In this article, we utilize three types of metrics, namely, OA, mIoU and SeK, to evaluate the performance of our methods. Then OA is defined as
where S represents the total number of change categories and no-change type (“I = 0”). indicates the total number of pixels correctly predicted by network, and represents the total number of pixels that are predicted for i-th change type, but in fact they belong to the j-th type. , where is used to evaluate the prediction in the no-change regions, and is used for validating the change regions.
The SeK can be formulated as follows:
where is the consistency between the prediction and the ground truth [20].
3.4. Effect of the GCF Module
Firstly, we evaluate the effect of the GCF module for dual-task semantic change detection on the SECOND dataset. For a fair comparison, all experiments were with the conventional cross-entropy loss function, to contribute to the loss during training process. As illustrated in Table 4, in terms of the SCD task, the conventional methods, such as FC-EF, FC-Siam-conv and FC-Siam-diff, cannot achieve competitive results. Compared with the FC-Siam-diff, the proposed dual-task-based PSPNet-SCD increases the performance of the semantic change detection considerably by 1.2% of IoU2, 0.8% of mIoU and 1.8 of SeK, respectively. More surprisingly, the GCF-based network can effectively improve the IoU2 and SeK by 2.6% and 2.7 compared with FC-Siam-diff, which demonstrates that the proposed GCF module is effective. We can also see in Table 4 that the GCF-based network shows higher performance compared with PSPNet-SCD, with the improvements in IoU2 and SeK achieved by GCF-SCD-Net being 1.4% and 0.9, respectively. Therefore, the use of the GCF module can effectively increase the performance of the models.

Table 4.
Comparison with the state-of-the-art methods on the SECOND dataset (% for all except seK).
3.5. Performance Analysis of Separable Loss
An imbalance label is a severe problem that causes difficulty in network training. In order to obtain strong results for the SCD task, this article introduce a separable loss to improve the performance of semantic segmentation in the change region. As shown in Table 5, it is obvious that the proposed separable loss can alleviate the imbalance label problem. Networks with separable loss outperform those with WCE_loss, such as PSPNet-SCD and GCF-SCD-Net achieving improvements in IoU2 by 1.9% and 1.7%, respectively. The increments in SeK obtained by PSPNet-SCD and GCF-SCD-Net are 1.4 and 1.5. Although the cost of improvement is that OA and IoU1 would be influenced or even slightly decreased, the segmentation results in the change region are greatly improved.

Table 5.
Comparison of the change detection networks with different loss functions (% for all except seK).
Lin et al. [36] proposed a focal loss function to alleviate the influence of sample imbalance. Consequently, to demonstrate the superiority of the separable loss, we report the results by using the focal loss in Table 5. Obviously, the proposed loss function performs with prominent superiority across all evaluation metrics.
The reason for this phenomenon is that separable loss calculates losses for the change region and the no-change region, separately, which guides the model to pay more attention to the loss of the change area, and alleviates the problem of over-confidence caused by the imbalance label. In particular, the improvements in the overall metrics obtained by GCF-SCD-Net further demonstrate the competitive performance of the proposed GCF module.
4. Discussion
To validate the performance of GCF-SCD-Net, we list the results obtained by [20] and our methods in Table 6. The proposed method achieves the best results on the SECOND dataset, 16.5 in SeK and 69.1% in mIoU. In the testing process, Yang et al. [20] improved the detection results by flip methods and a multiscale strategy. Since the proposed network did not use the multiscale strategy to optimize the parameters of the models, we only used the flip method to validate the performance of the networks. As shown in Table 6, although ASN-ATL outperforms GCF-SCD-Net slightly in mIoU, the proposed network achieves the best results in SeK by an improvement of 1.1.

Table 6.
Comparison with the state-of-the-art methods (% for all except seK).
Above, the proposed method stably improves the performance of the semantic change detection, which effectively demonstrates the superiority and robustness of GCF-SCD-Net.
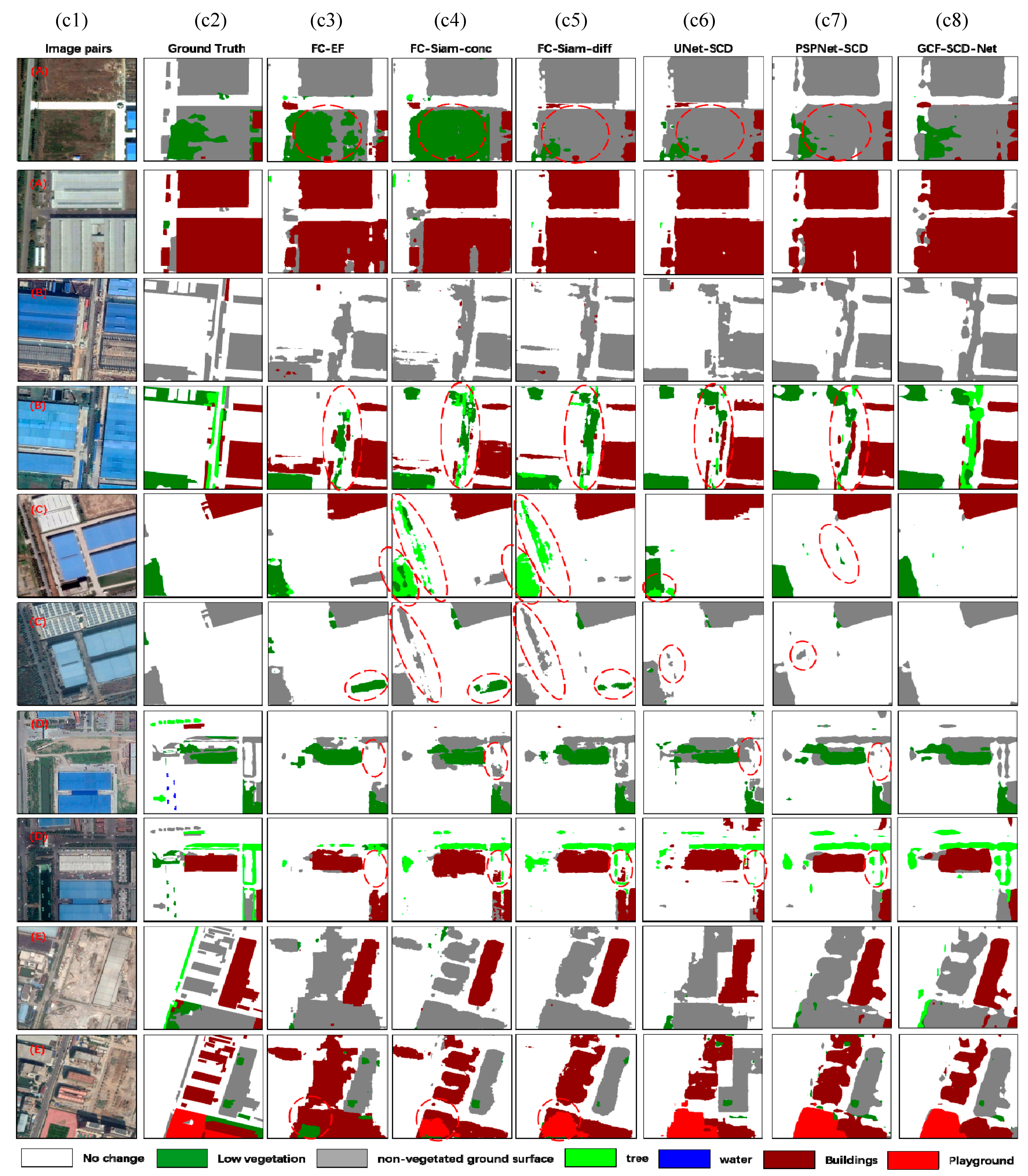
To present the change detection results intuitively, we visualized the segmentation results to demonstrate the performance of the proposed methods. Figure 3 shows the change detection results generated by FC-EF, FC-Siam-conv, FC-Siam-diff and the three types of dual-task semantic change detection networks proposed in this work.
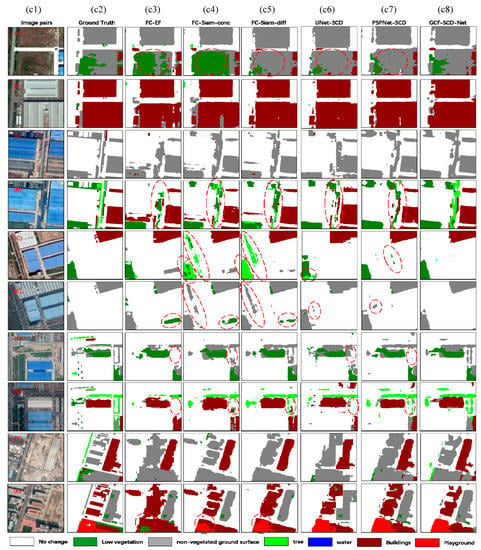
Figure 3.
Comparisons with state-of-the-art methods on the SECOND dataset. c1 and c2 represent image pairs and ground truth, respectively; from c3 to c8 are the semantic segmentation results obtained by various change detection methods. (A–E) are the image pairs.
According to semantic segmentation results in Samples A and B, we can note that the proposed GCF module enables to identify the change region accurately and the no-change region in complex scenarios. Since “tree” and “low vegetation” have a similar texture and color, most of the SCD networks have a poor detection performance, but this does not limit the segmentation results of GCF-SCD-Net, as shown in Sample B. In terms of sample C, conventional change detection methods cannot identify the pseudochange region well, but the proposed SCD-based UNet and PSPNet are capable of alleviating this problem, which demonstrates that existing change detection networks are improper for dual-task SCD. Generally, the trees on both sides of the road are elongated. According to Sample D, we note that the proposed GCF module performs well for the stripe scenario. Due to the small number of samples (such as “Playground”), it is difficult to accurately identify these change types; our method performs well under the abovementioned conditions.
Figure 4 depicts the visual results of the semantic prediction and binary prediction based on GCF-SCD-Net, where we can see that the GCF module can extract the change regions accurately. Consequently, the semantic change detection module can effectively classify the categories of each pixel based on the change field.

Figure 4.
Semantic change maps and binary change maps generated by GCF-SCD-Net. c1 is an image pair; c2 and c3 are the semantic label and prediction; images in c4 were obtained by fusing the raw images and semantic prediction masks; c-5,6,7 represent the binary change label, binary change prediction and binary fusion results.
Above, the visual results fully demonstrate that our method is effective and superior to the existing methods.
5. Conclusions
In this work, in order to address the problem that existing methods are incapable of obtaining a significant result for dual-task semantic change detection, we proposed a generative change field (GCF)-based dual-task semantic change detection network for remote sensing images. The proposed network consists of a Siamese convolutional neural network (Siam-Conv) module for extracting the feature representation from the raw image pairs, a generative change field module for obtaining the binary change map and two generative semantic change modules for generating the semantic segmentation maps of the bitemporal images. Moreover, it is an end-to-end SCD network. To alleviate the sample imbalance problem, we designed a separable loss for better training the deep models.
Extensive experiments were conducted in this work to demonstrate the competitive performance that can be achieved by GCF-SCD-Net, compared with existing methods as well as the proposed dual-task SCD networks (UNet-SCD and PSPNet-SCD). What is more, we validate the effectiveness of the proposed separable loss function; it is worth noting that the proposed separable loss is a general strategy to alleviate the sample imbalance problem. Therefore, it can be applied to other benchmark datasets that suffer from label imbalance.
At present, the SECOND dataset is the only public dataset for dual-task semantic change detection. In the meantime, we note that the proposed network and conventional networks perform poor regarding edge detection and contour extraction in the intersecting zone. Consequently, in future work, we intend to build a large-scale, very-high-resolution benchmark dataset for semantic change detection based on multi-source satellite data. To achieve better segmentation results, we intend to use the Markov Random Field (MRF) [37] method as well as boundary loss [38] to optimize the segmentation results.
Author Contributions
Conceptualization, S.X. and M.W.; methodology, S.X.; software, M.W.; validation, S.X., X.J., G.X. and Z.Z.; formal analysis, P.T. and X.J.; investigation, G.X. and P.T.; resources, X.J. and Z.Z.; data curation, M.W.; writing—original draft preparation, S.X., M.W. and P.T.; writing—review and editing, G.X., X.J. and Z.Z.; visualization, S.X.; supervision, M.W.; project administration, S.X. and M.W.; funding acquisition, M.W. All authors have read and agreed to the published version of the manuscript.
Funding
The study was supported by a grant from the National Natural Science Foundation of China under project 61825103, 91838303, and 91738302.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The authors would like to thank the Xia Guisong team for providing the data used in this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yang, J.; Weisberg, P.J.; Bristow, N.A. Landsat remote sensing approaches for monitoring long-term tree cover dynamics in semi-arid woodlands: Comparison of vegetation indices and spectral mixture analysis. Remote Sens. Environ. 2012, 119, 62–71. [Google Scholar] [CrossRef]
- Xian, G.; Homer, C. Updating the 2001 national land cover database impervious surface products to 2006 using landsat imagery change detection methods. Remote Sens. Environ. 2010, 114, 1676–1686. [Google Scholar] [CrossRef]
- Liang, B.; Weng, Q. Assessing urban environmental quality change of Indianapolis, United States, by the remote sensing and gis integration. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 43–55. [Google Scholar] [CrossRef]
- Wang, M.; Tan, K.; Jia, X.; Wang, X.; Chen, Y. A deep siamese network with hybrid convolutional feature extraction module for change detection based on multi-sensor remote sensing images. Remote Sens. 2020, 12, 205. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Chen, Y. Multi-feature object-based change detection using self-adaptive weight change vector analysis. Remote Sens. 2016, 8, 549. [Google Scholar] [CrossRef] [Green Version]
- Robin, A.; Moisan, L.; Le Hegarat-Mascle, S. An a-contrario approach for subpixel change detection in satellite imagery. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1977–1993. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lanza, A.; Di Stefano, L. Statistical change detection by the pool adjacent violators algorithm. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 1894–1910. [Google Scholar] [CrossRef] [PubMed]
- Lingg, A.J.; Zelnio, E.; Garber, F.; Rigling, B.D. A sequential framework for image change detection. IEEE Trans. Image Process. 2014, 23, 2405–2413. [Google Scholar] [CrossRef]
- Prendes, J.; Chabert, M.; Pascal, F.; Giros, A.; Tourneret, J.-Y. A new multivariate statistical model for change detection in images acquired by homogeneous and heterogeneous sensors. IEEE Trans. Image Process. 2015, 24, 799–812. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.-C.; Fu, C.-W.; Chang, S. Statistical change detection with moments under time-varying illumination. IEEE Trans. Image Process. 1998, 7, 1258–1268. [Google Scholar] [CrossRef]
- Chatelain, F.; Tourneret, J.-Y.; Inglada, J.; Ferrari, A. Bivariate gamma distributions for image registration and change detection. IEEE Trans. Image Process. 2007, 16, 1796–1806. [Google Scholar] [CrossRef] [Green Version]
- Huang, X.; Zhang, L.; Zhu, T. Building change detection from multitemporal high-resolution remotely sensed images based on a morphological building index. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 105–115. [Google Scholar] [CrossRef]
- Zhan, Y.; Fu, K.; Yan, M.; Sun, X.; Wang, H.; Qiu, X. Change detection based on deep siamese convolutional network for optical aerial images. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1845–1849. [Google Scholar] [CrossRef]
- Lv, Z.Y.; Shi, W.; Zhang, X.; Benediktsson, J.A. Landslide inventory mapping from bitemporal high-resolution remote sensing images using change detection and multiscale segmentation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1520–1532. [Google Scholar] [CrossRef]
- Daudt, R.C.; Le Saux, B.; Boulch, A. Fully convolutional siamese networks for change detection. In Proceedings of the 2018 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–8 October 2018; pp. 4063–4067. [Google Scholar]
- Liu, Y.; Pang, C.; Zhan, Z.; Zhang, X.; Yang, X. Building change detection for remote sensing images using a dual-task constrained deep siamese convolutional network model. IEEE Geosci. Remote Sens. Lett. 2021, 18, 811–815. [Google Scholar] [CrossRef]
- Chen, J.; Yuan, Z.; Peng, J.; Chen, L.; Huang, H.; Zhu, J.; Liu, Y.; Li, H. DASNet: Dual attentive fully convolutional siamese networks for change detection in high-resolution satellite images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 1194–1206. [Google Scholar] [CrossRef]
- Daudt, R.C.; Le Saux, B.; Boulch, A.; Gousseau, Y. Multitask learning for large-scale semantic change detection. Comput. Vis. Image Underst. 2019, 187, 102783. [Google Scholar] [CrossRef] [Green Version]
- Mou, L.; Bruzzone, L.; Zhu, X.X. Learning spectral-spatial-temporal features via a recurrent convolutional neural network for change detection in multispectral imagery. IEEE Trans. Geosci. Remote Sens. 2019, 57, 924–935. [Google Scholar] [CrossRef] [Green Version]
- Yang, K.; Xia, G.-S.; Liu, Z.; Du, B.; Yang, W.; Pelillo, M. Asymmetric Siamese Networks for Semantic Change Detection. arXiv 2020, arXiv:2010.05687. [Google Scholar]
- Yao, J.; Cao, X.; Zhao, Q.; Meng, D.; Xu, Z. Robust subspace clustering via penalized mixture of Gaussians. Neurocomputing 2018, 278, 4–11. [Google Scholar] [CrossRef]
- Hong, D.; Gao, L.; Yao, J.; Zhang, B.; Plaza, A.; Chanussot, J. Graph convolutional networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5966–5978. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, X.; Huang, J.; Wang, H.; Xin, Q. Fine-grained building change detection from very high-spatial-resolution remote sensing images based on deep multitask learning. IEEE Geosci. Remote Sens. Lett. 2020, 1–5. [Google Scholar] [CrossRef]
- Peng, D.; Bruzzone, L.; Zhang, Y.; Guan, H.; Ding, H.; Huang, X. SemiCDNet: A semisupervised convolutional neural network for change detection in high resolution remote-sensing images. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5891–5906. [Google Scholar] [CrossRef]
- Liu, J.; Gong, M.; Qin, K.; Zhang, P. A deep convolutional coupling network for change detection based on heterogeneous optical and radar images. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 545–559. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Wu, C.; Du, B.; Zhang, L.; Wang, L. Change detection in multisource VHR images via deep siamese convolutional multiple-layers recurrent neural network. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2848–2864. [Google Scholar] [CrossRef]
- Graves, A. Generating sequences with recurrent neural networks. arXiv 2014, arXiv:1308.0850. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Granada, Spain, 16–20 September 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid scene parsing network. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 630–645. [Google Scholar]
- Robbins, H.; Monro, S. A stochastic approximation method. In Herbert Robbins Selected Papers; Springer: New York, NY, USA, 1985; Volume 1, pp. 102–109. [Google Scholar] [CrossRef]
- Lopez-Fandino, J.; Garea, A.S.; Heras, D.B.; Arguello, F. Stacked autoencoders for multiclass change detection in hyperspectral images. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 1906–1909. [Google Scholar]
- Saha, S.; Bovolo, F.; Brurzone, L. Unsupervised multiple-change detection in VHR optical images using deep features. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 1902–1905. [Google Scholar]
- Benedek, C.; Sziranyi, T. Change detection in optical aerial images by a multilayer conditional mixed markov model. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3416–3430. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Shi, Z. A spatial-temporal attention-based method and a new dataset for remote sensing image change detection. Remote Sens. 2020, 12, 1662. [Google Scholar] [CrossRef]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2999–3007. [Google Scholar]
- Solberg, A.; Taxt, T.; Jain, A. A markov random field model for classification of multisource satellite imagery. IEEE Trans. Geosci. Remote Sens. 1996, 34, 100–113. [Google Scholar] [CrossRef]
- Li, A.; Jiao, L.; Zhu, H.; Li, L.; Liu, F. Multitask semantic boundary awareness network for remote sensing image segmentation. IEEE Trans. Geosci. Remote Sens. 2021, 1–14. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).