Parametric Decomposition of Pulsed Lidar Signals with Noise Corruption Using FRFT Spectrum Analysis
Abstract
1. Introduction
2. Related Work
2.1. Problem Formulation of Parametric Decomposition
2.2. Exploration of Typical JTFA Techniques
3. FRFT Representation of Pulsed Lidar Signals
3.1. FRFT of Gaussian Kernel Function
- (a)
- Time-shifting property:
- (b)
- Wigner distribution: The TF plane and all coordinates of the p-order FRFT are the results of rotating an angle relative to the original TF plane and the coordinates , which can be described as:
3.2. FRFT Spectrum of Pulsed Lidar Signal
- (a)
- When : monotonically increases with the increase of within and decreases with the increase of within . When , reaches the maximum, which is . On the other hand, monotonically decreases with the increase of within and increases with the increase of within . When , reaches the minimum, which is . In summary, possesses the maximum amplitude and the minimum pulse width when .
- (b)
- When : monotonically decreases with the increase of within and increases with the increase of within . When , reaches the minimum, which is . On the other hand, monotonically increases with the increase of within and decreases with the increase of within . When , reaches the maximum, which is . In summary, possesses the minimum amplitude and the maximum pulse width when .
- (c)
- When : and do not vary with ,and remains .
4. FRFT Spectrum Processing Solution
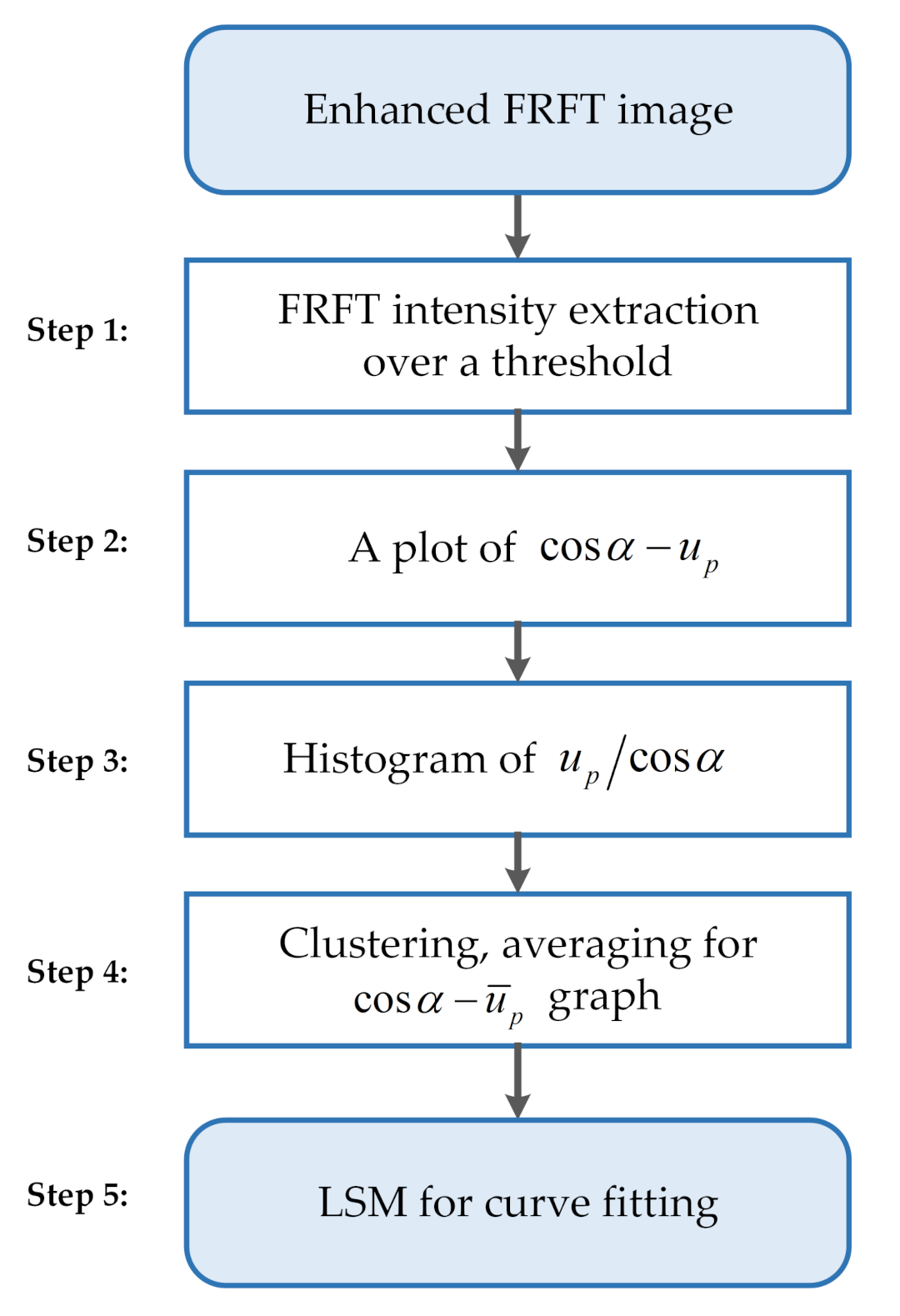
4.1. Enhancement of FRFT Spectrum
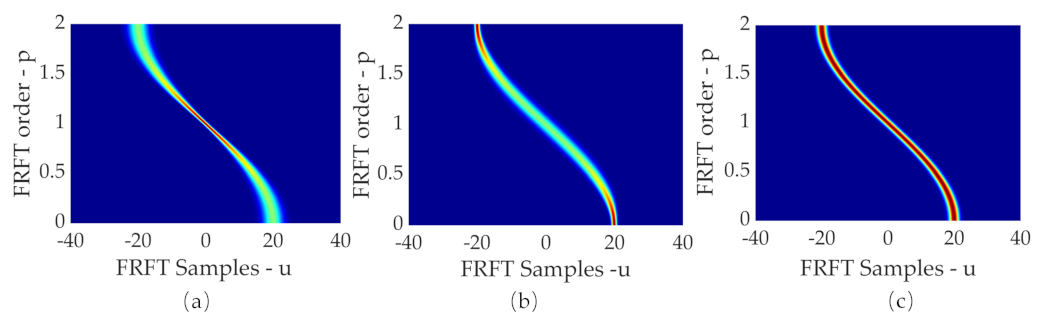
4.2. Clustering of Components and Extraction of ToFs
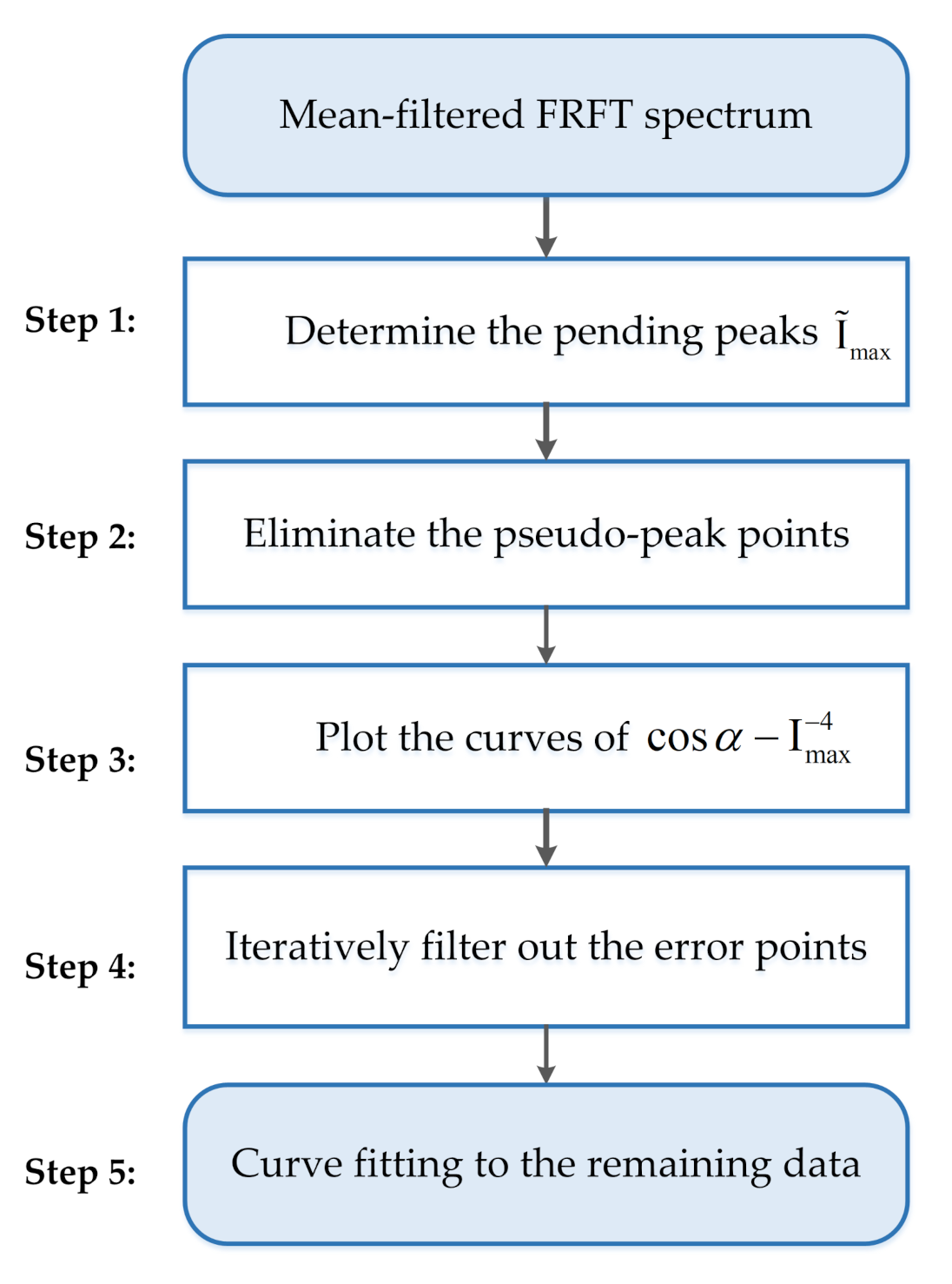
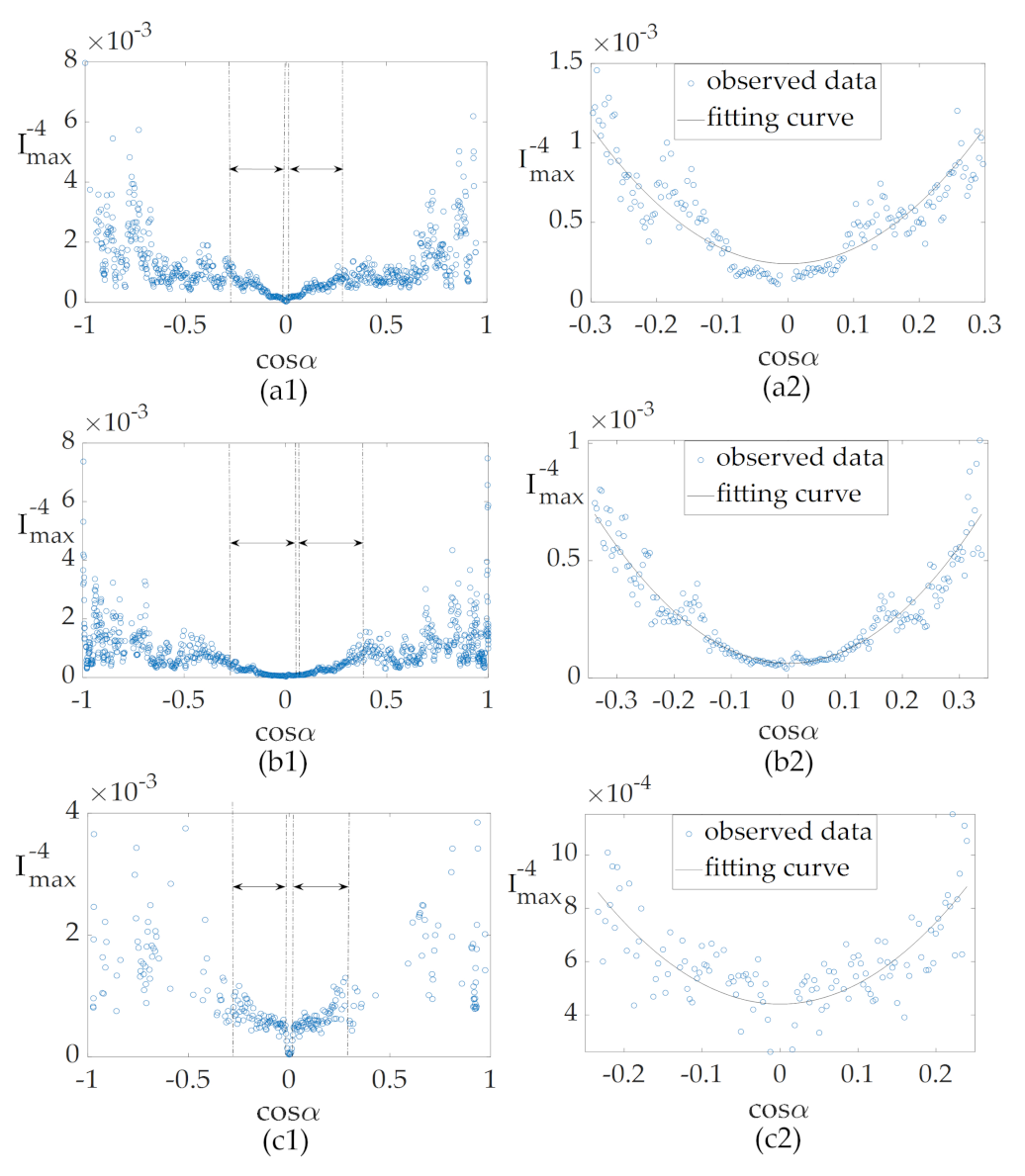
4.3. Extraction of Pulse Widths and Amplitudes
- (a)
- The data length of is assumed to be L,a shifting step is initiated to 0.
- (b)
- Remove -point data simultaneously from two sides of the observed data. The length of the remaining data is reduced to . By using Equations (24) and (25), and are calculated, and the fitting curve is thus derived. The root-mean-square error (RMSE) between the remaining data and the fitting-curve data is obtained.
- (c)
- When the RMSE is less than a prescribed level or , the iteration ends; the calculated and are used for and ; otherwise, , continue Step (b).
5. Experimental Results
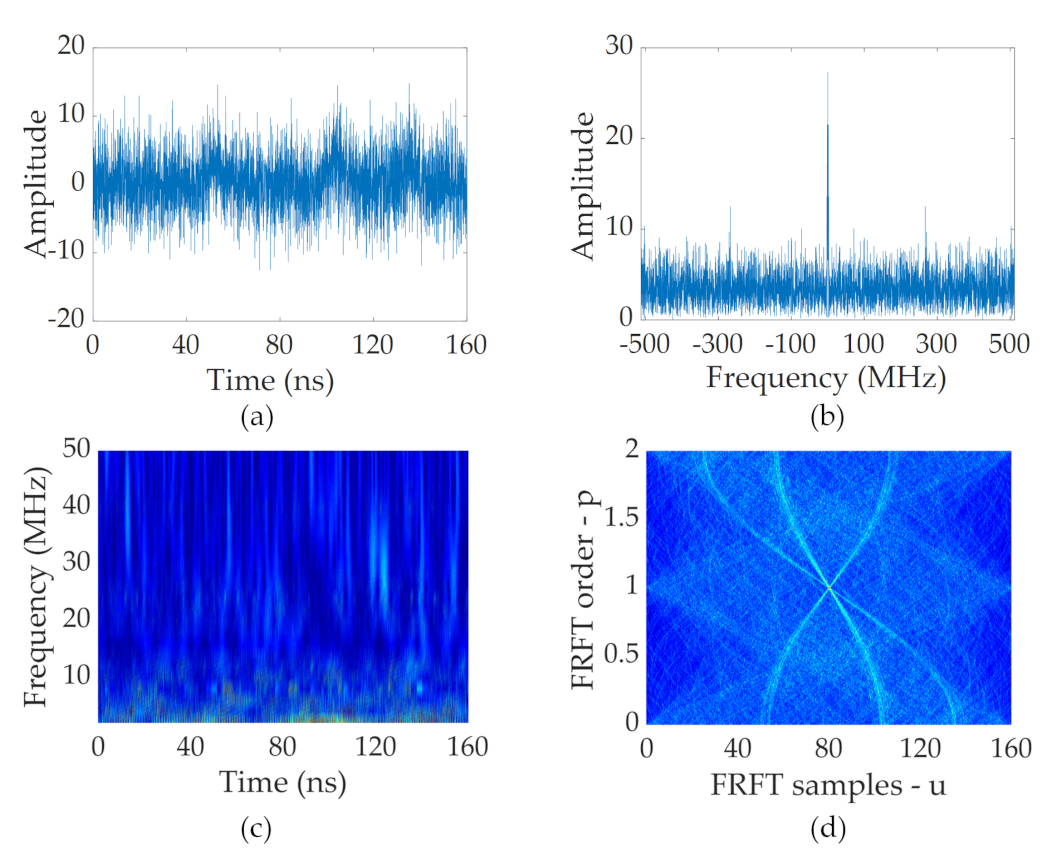
5.1. Data Acquisition
5.2. Performance of FRFT Spectrum Enhancement
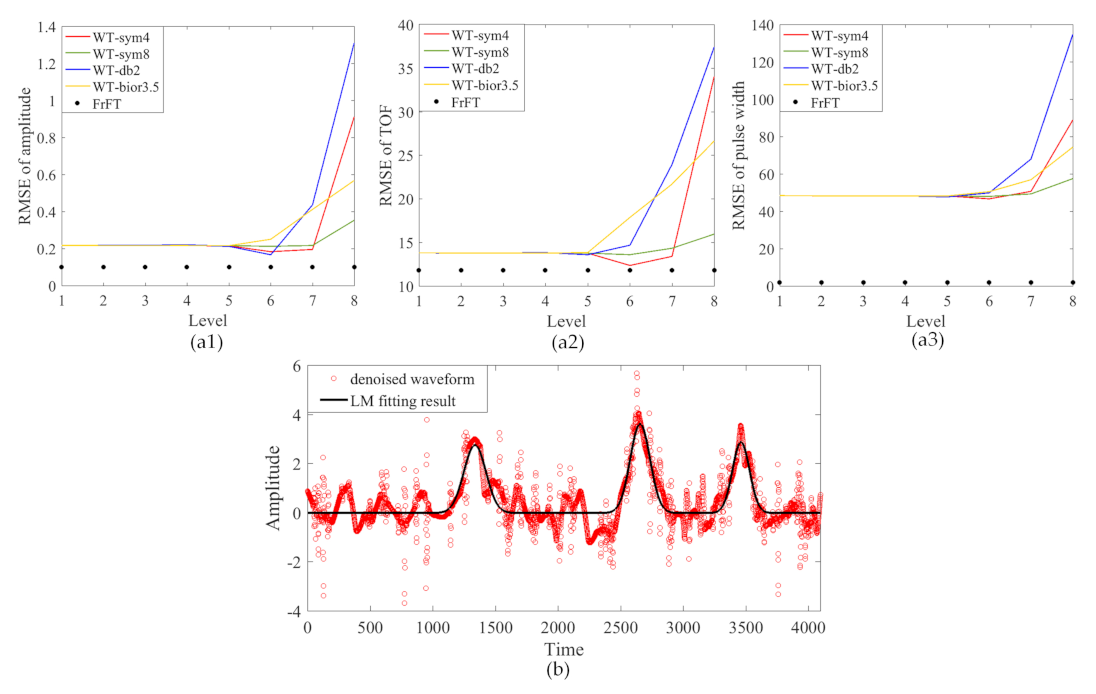
5.3. Performance of Parametric Decomposition
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Altmann, Y.; Wallace, A.; McLaughlin, S. Spectral unmixing of multispectral lidar signals. IEEE Trans. Signal Process. 2015, 63, 5525–5534. [Google Scholar] [CrossRef]
- Groll, L.; Kapp, A. Effect of fast motion on range images acquired by lidar scanners for automotive applications. IEEE Trans. Signal Process. 2007, 55, 2945–2953. [Google Scholar] [CrossRef][Green Version]
- Hofton, M.A.; Minster, J.B.; Blair, J.B. Decomposition of laser altimeter waveforms. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1989–1996. [Google Scholar] [CrossRef]
- Xu, F.; Li, F.; Wang, Y. Modified Levenberg–Marquardt-based optimization method for LiDAR waveform decomposition. IEEE Geosci. Remote Sens. Lett. 2016, 13, 530–534. [Google Scholar] [CrossRef]
- Qin, Y.; Li, B.; Niu, Z.; Huang, W.; Wang, C. Stepwise decomposition and relative radiometric normalization for small footprint LiDAR waveform. Sci. China Earth Sci. 2011, 54, 625–630. [Google Scholar] [CrossRef]
- Chauve, A.; Vega, C.; Durrieu, S.; Bretar, F.; Allouis, T.; Pierrot-Deseilligny, M.; Puech, W. Processing full-waveform lidar data in an alpine coniferous forest: Assessing terrain and tree height quality. Int. J. Remote Sens. 2009, 30, 5211–5228. [Google Scholar] [CrossRef]
- Reitberger, J.; Krzystek, P.; Stilla, U. Analysis of full waveform lidar data for tree species classification. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2006, 36, 228–233. [Google Scholar]
- Yan, S.; Yang, G.; Li, Q.; Wang, C. Waveform centroid discrimination of pulsed Lidar by combining EMD and intensity weighted method under low SNR conditions. Infrared Phys. Technol. 2020, 109, 103385. [Google Scholar] [CrossRef]
- Chang, J.; Zhu, L.; Li, H.; Xu, F.; Liu, B.; Yang, Z. Noise reduction in Lidar signal using correlation-based EMD combined with soft thresholding and roughness penalty. Opt. Commun. 2018, 407, 290–295. [Google Scholar] [CrossRef]
- Tian, P.; Cao, X.; Liang, J.; Zhang, L.; Yi, N.; Wang, L.; Cheng, X. Improved empirical mode decomposition based denoising method for lidar signals. Opt. Commun. 2014, 325, 54–59. [Google Scholar] [CrossRef]
- Shen, X.; Li, Q.Q.; Wu, G.; Zhu, J. Decomposition of LiDAR waveforms by B-spline-based modeling. ISPRS J. Photogramm. Remote Sens. 2017, 128, 182–191. [Google Scholar] [CrossRef]
- Zhou, Z.; Hua, D.; Wang, Y.; Yan, Q.; Li, S.; Li, Y.; Wang, H. Improvement of the signal to noise ratio of Lidar echo signal based on wavelet de-noising technique. Opt. Lasers Eng. 2013, 51, 961–966. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, X.; Hua, D.; Cui, Y.; Sui, L. An EMD-based denoising method for lidar signal. In Proceedings of the 2010 3rd International Congress on Image and Signal Processing, Yantai, China, 16–18 October 2010; Volume 8, pp. 4016–4019. [Google Scholar]
- Rocadenbosch, F.; Soriano, C.; Comerón, A.; Baldasano, J.M. Lidar inversion of atmospheric backscatter and extinction-to-backscatter ratios by use of a Kalman filter. Appl. Opt. 1999, 38, 3175–3189. [Google Scholar] [CrossRef] [PubMed]
- Sun, B.Y.; Huang, D.S.; Fang, H.T. Lidar signal denoising using least-squares support vector machine. IEEE Signal Process. Lett. 2005, 12, 101–104. [Google Scholar]
- Chen, V.C.; Ling, H. Joint time-frequency analysis for radar signal and image processing. IEEE Signal Process. Mag. 1999, 16, 81–93. [Google Scholar] [CrossRef]
- Kumar, R.; Zhao, W.; Singh, V. Joint time-frequency analysis of seismic signals: A critical review. Struct. Durab. Health Monit. 2018, 12, 65. [Google Scholar]
- Sharma, M.; Achuth, P.V.; Pachori, R.B.; Gadre, V.M. A parametrization technique to design joint time—Frequency optimized discrete-time biorthogonal wavelet bases. Signal Process. 2017, 135, 107–120. [Google Scholar] [CrossRef]
- Qian, S.; Chen, D. Joint time-frequency analysis. IEEE Signal Process. Mag. 1999, 16, 52–67. [Google Scholar] [CrossRef]
- Lao, G.; Yin, C.; Ye, W.; Sun, Y.; Li, G. A frequency domain extraction based adaptive joint time frequency decomposition method of the maneuvering target radar echo. Remote Sens. 2018, 10, 266. [Google Scholar] [CrossRef]
- Stanković, L.; Mandić, D.; Daković, M.; Brajović, M. Time-frequency decomposition of multivariate multicomponent signals. Signal Process. 2018, 142, 468–479. [Google Scholar] [CrossRef]
- Ahmad, A.A.; Lawan, S.; Ajiya, M.; Yusuf, Z.Y.; Bello, L.M. Extraction of the pulse width and pulse repetition period of linear FM radar signal using time-frequency analysis. J. Adv. Sci. Eng. 2020, 3, 1–8. [Google Scholar] [CrossRef]
- Daubechies, I. The wavelet transform, time-frequency localization and signal analysis. IEEE Trans. Inf. Theory 1990, 36, 961–1005. [Google Scholar] [CrossRef]
- Wang, P.; Gao, J.; Wang, Z. Time-frequency analysis of seismic data using synchrosqueezing transform. IEEE Geosci. Remote Sens. Lett. 2014, 11, 2042–2044. [Google Scholar] [CrossRef]
- Qian, S.; Chen, D. Decomposition of the Wigner-Ville distribution and time-frequency distribution series. IEEE Trans. Signal Process. 1994, 42, 2836–2842. [Google Scholar] [CrossRef]
- Almeida, L.B. The fractional Fourier transform and time-frequency representations. IEEE Trans. Signal Process. 1994, 42, 3084–3091. [Google Scholar] [CrossRef]
- Tant, K.M.; Mulholland, A.J.; Langer, M.; Gachagan, A. A fractional Fourier transform analysis of the scattering of ultrasonic waves. Proc. R. Soc. Math. Phys. Eng. Sci. 2015, 471, 20140958. [Google Scholar] [CrossRef] [PubMed]
- Weimann, S.; Perez-Leija, A.; Lebugle, M.; Keil, R.; Tichy, M.; Gräfe, M.; Heilmann, R.; Nolte, S.; Moya-Cessa, H.; Weihs, G. Implementation of quantum and classical discrete fractional Fourier transforms. Nat. Commun. 2016, 7, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Saxena, R.; Singh, K. Fractional Fourier transform: A novel tool for signal processing. J. Indian Inst. Sci. 2005, 85, 11. [Google Scholar]
- Herrera, R.H.; Han, J.; van der Baan, M. Applications of the synchrosqueezing transform in seismic time-frequency analysis. Geophysics 2014, 79, V55–V64. [Google Scholar] [CrossRef]
- Ahrabian, A.; Looney, D.; Stanković, L.; Mandic, D.P. Synchrosqueezing-based time-frequency analysis of multivariate data. Signal Process. 2015, 106, 331–341. [Google Scholar] [CrossRef]
- Li, C.; Liang, M. A generalized synchrosqueezing transform for enhancing signal time–frequency representation. Signal Process. 2012, 92, 2264–2274. [Google Scholar] [CrossRef]
- Liu, W.; Cao, S.; Chen, Y. Seismic time–frequency analysis via empirical wavelet transform. IEEE Geosci. Remote Sens. Lett. 2015, 13, 28–32. [Google Scholar] [CrossRef]
- Galati, G.; Pavan, G.; De Palo, F. Chirp signals and noisy waveforms for solid-state surveillance radars. Aerospace 2017, 4, 15. [Google Scholar] [CrossRef]
- Sun, H.B.; Liu, G.S.; Gu, H.; Su, W.M. Application of the fractional Fourier transform to moving target detection in airborne SAR. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 1416–1424. [Google Scholar]
- Daubechies, I.; Lu, J.; Wu, H.T. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool. Appl. Comput. Harmon. Anal. 2011, 30, 243–261. [Google Scholar] [CrossRef]
- Messioud, S.; Sbartai, B.; Dias, D. Harmonic seismic waves response of 3D rigid surface foundation on layer soil. Earthq. Struct. 2019, 16, 109–118. [Google Scholar]
- Mallet, C.; Bretar, F. Full-waveform topographic lidar: State-of-the-art. ISPRS J. Photogramm. Remote Sens. 2009, 64, 1–16. [Google Scholar] [CrossRef]
- Qin, Y.; Vu, T.T.; Ban, Y. Toward an optimal algorithm for LiDAR waveform decomposition. IEEE Geosci. Remote Sens. Lett. 2011, 9, 482–486. [Google Scholar] [CrossRef]
- Wagner, W.; Ullrich, A.; Ducic, V.; Melzer, T.; Studnicka, N. Gaussian decomposition and calibration of a novel small-footprint full-waveform digitising airborne laser scanner. ISPRS J. Photogramm. Remote Sens. 2006, 60, 100–112. [Google Scholar] [CrossRef]
- Qin, Y.; Vu, T.T.; Ban, Y.; Niu, Z. Range determination for generating point clouds from airborne small footprint LiDAR waveforms. Opt. Express 2012, 20, 25935–25947. [Google Scholar] [CrossRef] [PubMed]
- Steinvall, O.; Carlsson, T. Three-dimensional laser radar modeling. Proc. SPIE 2001, 4377, 23–34. [Google Scholar]
- Steinvall, O. Effects of target shape and reflection on laser radar cross sections. Appl. Opt. 2000, 39, 4381–4391. [Google Scholar] [CrossRef] [PubMed]
- Der, S.; Redman, B.; Chellappa, R. Simulation of error in optical radar range measurements. Appl. Opt. 1997, 36, 6869–6874. [Google Scholar] [CrossRef]
- Rioul, O.; Vetterli, M. Wavelets and signal processing. IEEE Signal Process. Mag. 1991, 8, 14–38. [Google Scholar] [CrossRef]
- Wang, S.; Chen, X.; Cai, G.; Chen, B.; Li, X.; He, Z. Matching demodulation transform and synchrosqueezing in time-frequency analysis. IEEE Trans. Signal Process. 2013, 62, 69–84. [Google Scholar] [CrossRef]
- Boashash, B.; Black, P. An efficient real-time implementation of the Wigner-Ville distribution. IEEE Trans. Acoust. Speech Signal Process. 1987, 35, 1611–1618. [Google Scholar] [CrossRef]
- Namias, V. The fractional order Fourier transform and its application to quantum mechanics. IMA J. Appl. Math. 1980, 25, 241–265. [Google Scholar] [CrossRef]
- Pei, S.C.; Ding, J.J. Fractional Fourier transform, Wigner distribution, and filter design for stationary and nonstationary random processes. IEEE Trans. Signal Process. 2010, 58, 4079–4092. [Google Scholar] [CrossRef]
- Lv, X.; Xing, M.; Zhang, S.; Bao, Z. Keystone transformation of the Wigner–Ville distribution for analysis of multicomponent LFM signals. Signal Process. 2009, 89, 791–806. [Google Scholar] [CrossRef]
- Barbarossa, S. Analysis of multicomponent LFM signals by a combined Wigner-Hough transform. IEEE Trans. Signal Process. 1995, 43, 1511–1515. [Google Scholar] [CrossRef]
- Alieva, T.; Bastiaans, M.J. On fractional Fourier transform moments. IEEE Signal Process. Lett. 2000, 7, 320–323. [Google Scholar] [CrossRef]
- Bastiaans, M.J.; Alieva, T.; Stankovic, L. On rotated time-frequency kernels. IEEE Signal Process. Lett. 2002, 9, 378–381. [Google Scholar] [CrossRef]
- Lohmann, A.W.; Soffer, B.H. Relationships between the Radon–Wigner and fractional Fourier transforms. JOSA A 1994, 11, 1798–1801. [Google Scholar] [CrossRef]
- Lohmann, A.W. Image rotation, Wigner rotation, and the fractional Fourier transform. JOSA A 1993, 10, 2181–2186. [Google Scholar] [CrossRef]
- Wu, H.R.; Yuen, M. A generalized block-edge impairment metric for video coding. IEEE Signal Process. Lett. 1997, 4, 317–320. [Google Scholar] [CrossRef]
- Zhou, W. Image quality assessment: From error measurement to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–613. [Google Scholar]
- Kundu, A.; Mitra, S.; Vaidyanathan, P. Application of two-dimensional generalized mean filtering for removal of impulse noises from images. IEEE Trans. Acoust. Speech Signal Process. 1984, 32, 600–609. [Google Scholar] [CrossRef]
- Donoho, D.L.; Johnstone, I.M. Threshold selection for wavelet shrinkage of noisy data. In Proceedings of the 16th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Baltimore, MD, USA, 3–6 November 1994; Volume 1, pp. A24–A25. [Google Scholar]
- Donoho, D.L. De-noising by soft-thresholding. IEEE Trans. Inf. Theory 1995, 41, 613–627. [Google Scholar] [CrossRef]
- Chappalli, M.B.; Bose, N.K. Simultaneous noise filtering and super-resolution with second-generation wavelets. IEEE Signal Process. Lett. 2005, 12, 772–775. [Google Scholar] [CrossRef]
- Tang, H.Y.; Zhuang, T.G. Realizations of Fast 2D/3D Image Filtering and Enhancement. J. Shanghai Jiaotong Univ. (Sci.) 1998, 3, 108–112. [Google Scholar]
- Dogra, A.; Bhalla, P. Image sharpening by gaussian and butterworth high pass filter. Biomed. Pharmacol. J. 2014, 7, 707–713. [Google Scholar] [CrossRef]
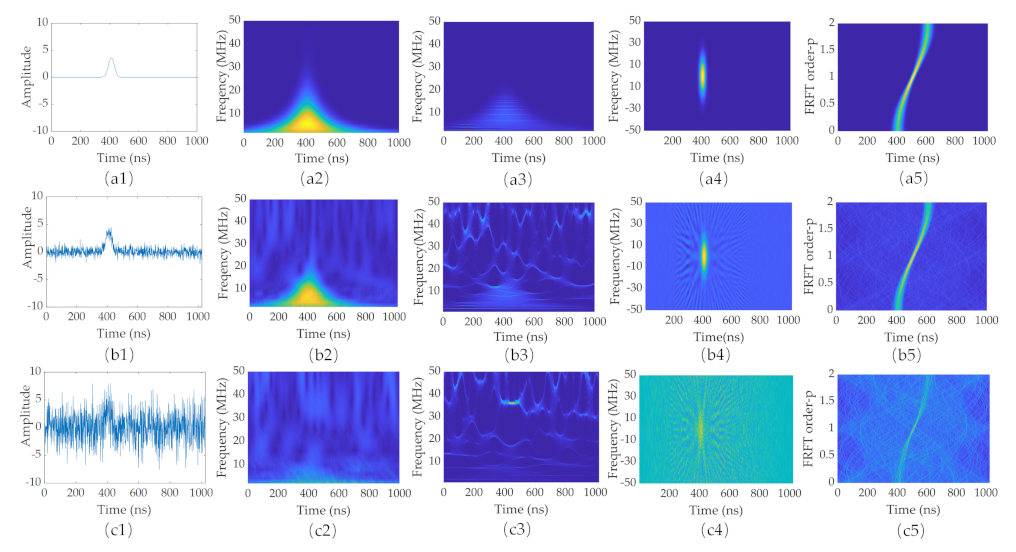

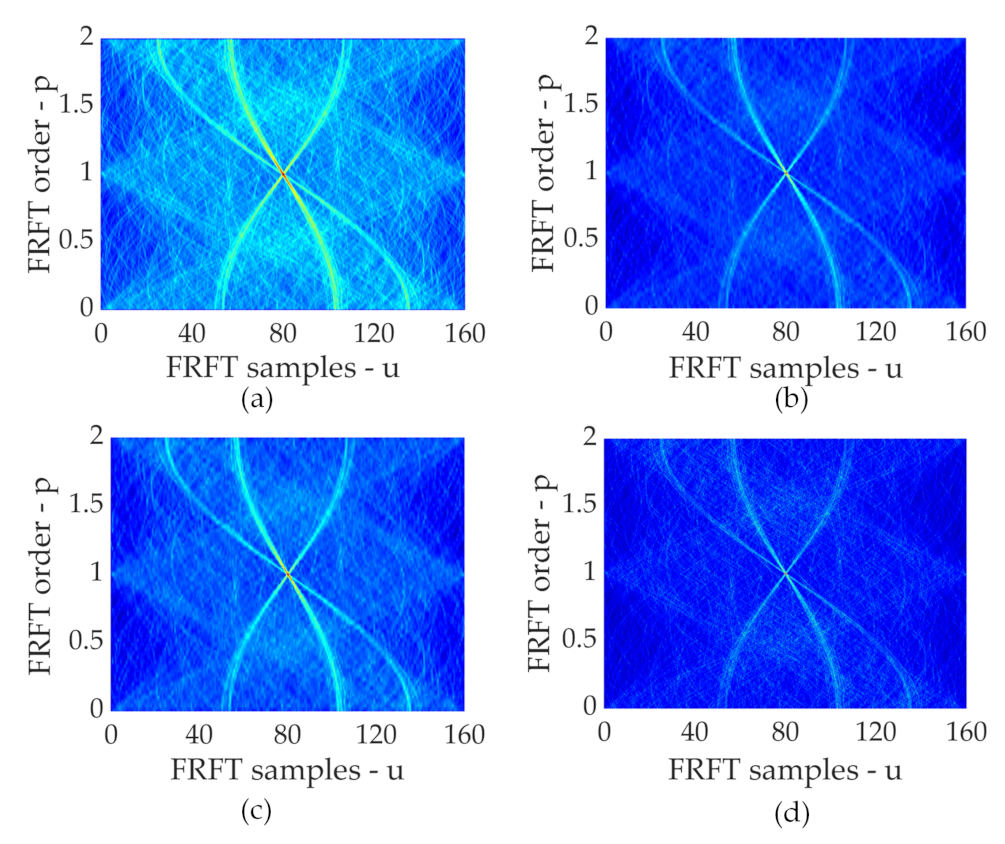
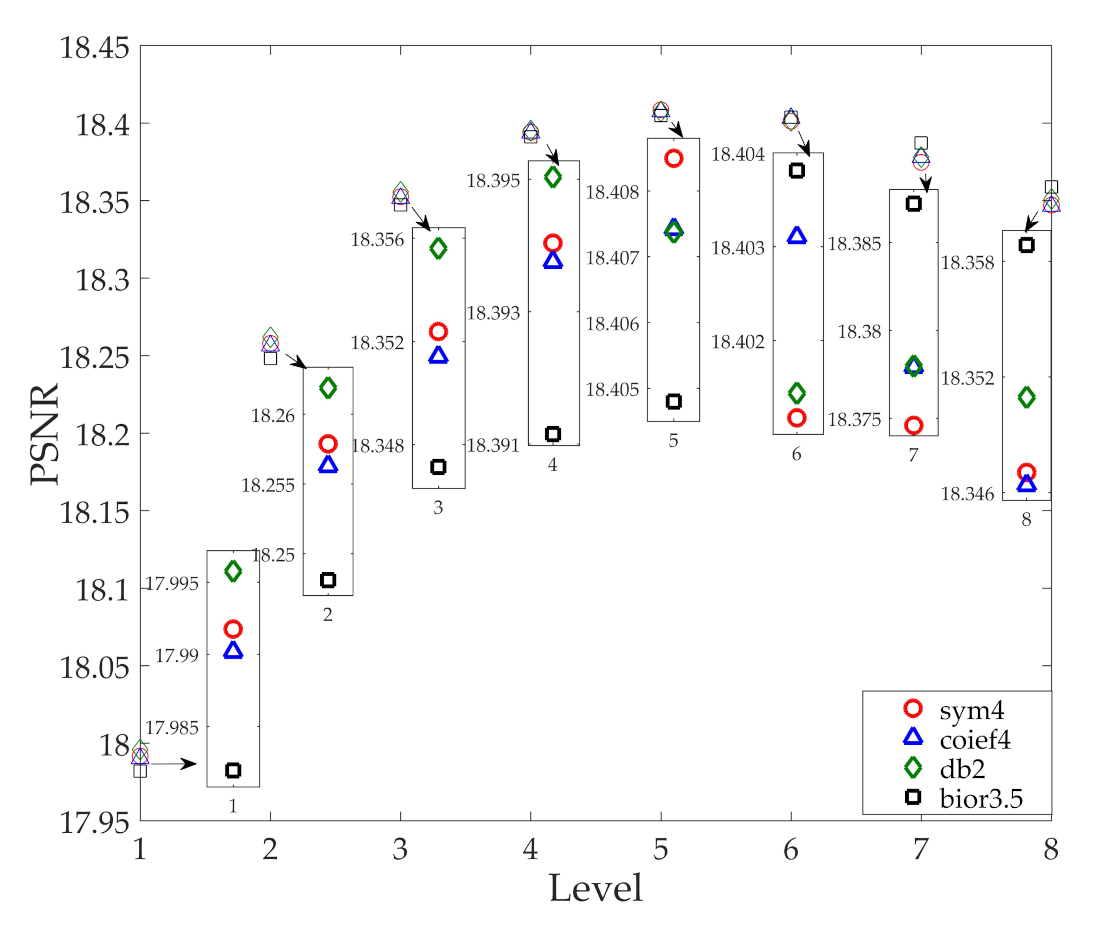



| Filter (s) | Mean | Wavelet | Mean & Wavelet | Mean & Wavelet & Butterworth |
|---|---|---|---|---|
| PSNR (dB) | 17.23 | 18.41 | 18.82 | 30.68 |
| Parameters | |||
|---|---|---|---|
| Cluster 1 | −705.69 | 2047.21 | 1341.44 ns |
| Cluster 2 | 604.16 | 2047.88 | 2651.90 ns |
| Cluster 3 | 141.99 | 2047.64 | 3467.52 ns |
| Parameters | ||||
|---|---|---|---|---|
| Cluster 1 | 0.0141 | 64.72 ns | 2.90 mV | |
| Cluster 2 | 0.0056 | 78.87 ns | 3.66 mV | |
| Cluster 3 | 0.0081 | 53.07 ns | 3.33 mV |
| SNR (dB) | Method | MD of Amplitude | MD of Time Offset | MD of Pulse Width |
|---|---|---|---|---|
| 10 | WT-LM | 0.648% | 0.072% | 41.535% |
| FRFT-S | 0.621% | 0.079% | 6.629% | |
| 8 | WT-LM | 1.007% | 0.060% | 42.299% |
| FRFT-S | 1.053% | 0.188% | 5.562% | |
| 6 | WT-LM | 2.750% | 0.107% | 42.162% |
| FRFT-S | 1.702% | 0.082% | 5.763% | |
| 4 | WT-LM | 1.243% | 0.101% | 43.293% |
| FRFT-S | 1.363% | 0.157% | 5.397% | |
| 2 | WT-LM | 2.189% | 0.022% | 39.201% |
| FRFT-S | 2.965% | 0.082% | 10.066% | |
| 0 | WT-LM | 2.112% | 0.050% | 49.043% |
| FRFT-S | 1.771% | 0.172% | 5.264% | |
| −2 | WT-LM | 1.298% | 0.164% | 40.974% |
| FRFT-S | 1.833% | 0.223% | 7.630% | |
| −4 | WT-LM | 2.189% | 0.151% | 51.580% |
| FRFT-S | 3.305% | 0.247% | 4.467% | |
| −6 | WT-LM | 5.141% | 0.433% | 42.926% |
| FRFT-S | 3.540% | 0.231% | 6.195% | |
| −8 | WT-LM | 6.287% | 0.691% | 44.258% |
| FRFT-S | 4.164% | 0.284% | 11.966% | |
| −10 | WT-LM | 12.758% | 0.778% | 62.747% |
| FRFT-S | 4.885% | 0.531% | 7.802% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, F.; Chen, J.; Liu, Y.; Wu, Q.; Zhang, X.; Shu, Z. Parametric Decomposition of Pulsed Lidar Signals with Noise Corruption Using FRFT Spectrum Analysis. Remote Sens. 2021, 13, 3296. https://doi.org/10.3390/rs13163296
Xu F, Chen J, Liu Y, Wu Q, Zhang X, Shu Z. Parametric Decomposition of Pulsed Lidar Signals with Noise Corruption Using FRFT Spectrum Analysis. Remote Sensing. 2021; 13(16):3296. https://doi.org/10.3390/rs13163296
Chicago/Turabian StyleXu, Fan, Jun Chen, Ya Liu, Qihui Wu, Xiaofei Zhang, and Zhengyang Shu. 2021. "Parametric Decomposition of Pulsed Lidar Signals with Noise Corruption Using FRFT Spectrum Analysis" Remote Sensing 13, no. 16: 3296. https://doi.org/10.3390/rs13163296
APA StyleXu, F., Chen, J., Liu, Y., Wu, Q., Zhang, X., & Shu, Z. (2021). Parametric Decomposition of Pulsed Lidar Signals with Noise Corruption Using FRFT Spectrum Analysis. Remote Sensing, 13(16), 3296. https://doi.org/10.3390/rs13163296








