Three-Dimensional Unique-Identifier-Based Automated Georeferencing and Coregistration of Point Clouds in Underground Mines
Abstract
:1. Introduction
2. Materials and Methods
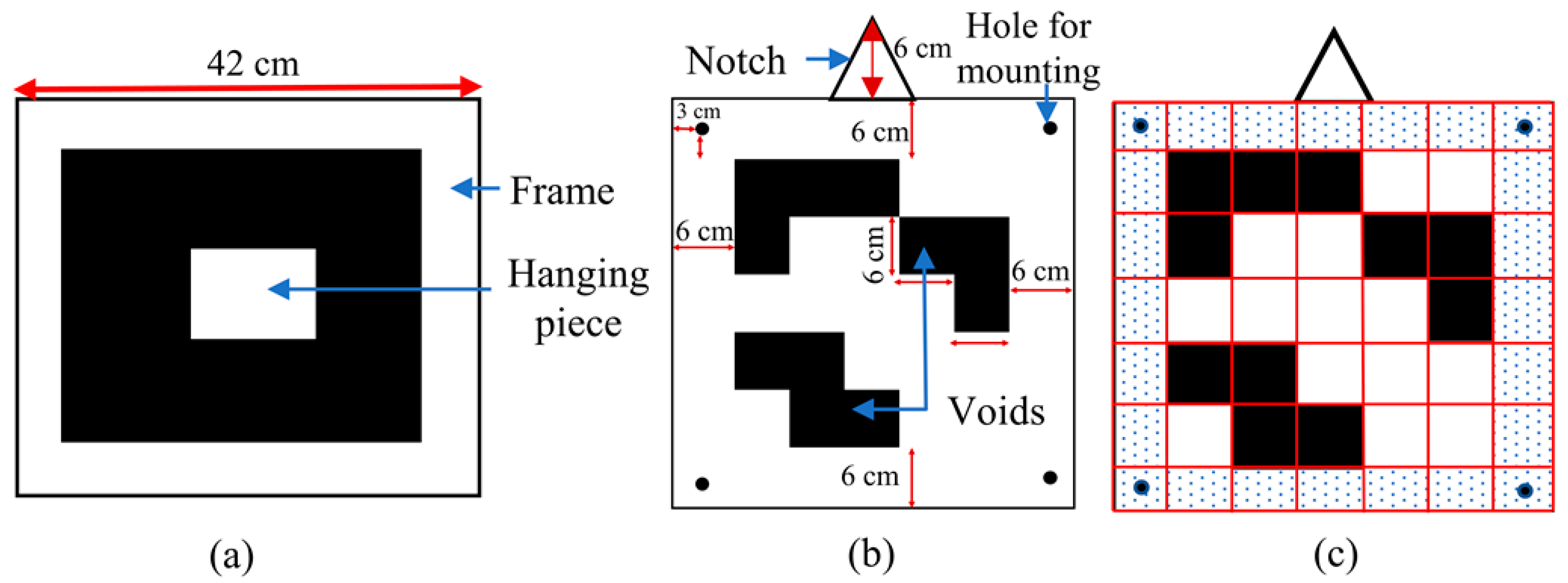
2.1. 3DUID Development
| Algorithm 1. 3DUID pattern generation. |
| Input: Window size (m × m) |
| Output: All the possible 3DUID patterns |
| 1: Generate a grid of m + 2 × m + 2, where the factor ‘2’ is grid associated with boundary frame |
| 2: Store 1 in the boundary grids, i.e., pad first row, last row, first column and last column with ‘1’ |
| 3: for i = 1 to m × m |
| 4: index = m × mCi |
| 5: Store 1 at given index location in m × m pattern and 0 elsewhere |
| 6: Check for hanging pieces using connected component (pattern of 1 not connected to edge in m + 2 × m + 2 pattern) |
| 7: if number of connected component > 1 |
| 8: ignore pattern and continue loop |
| 9: else |
| 10: store 3DUID pattern |
| 11: end if |
| 12: end for |
| 13: Scale pattern or modify dots per inch (dpi) to convert the pattern to world dimensions for 3D printing or laser cutting (optional) |
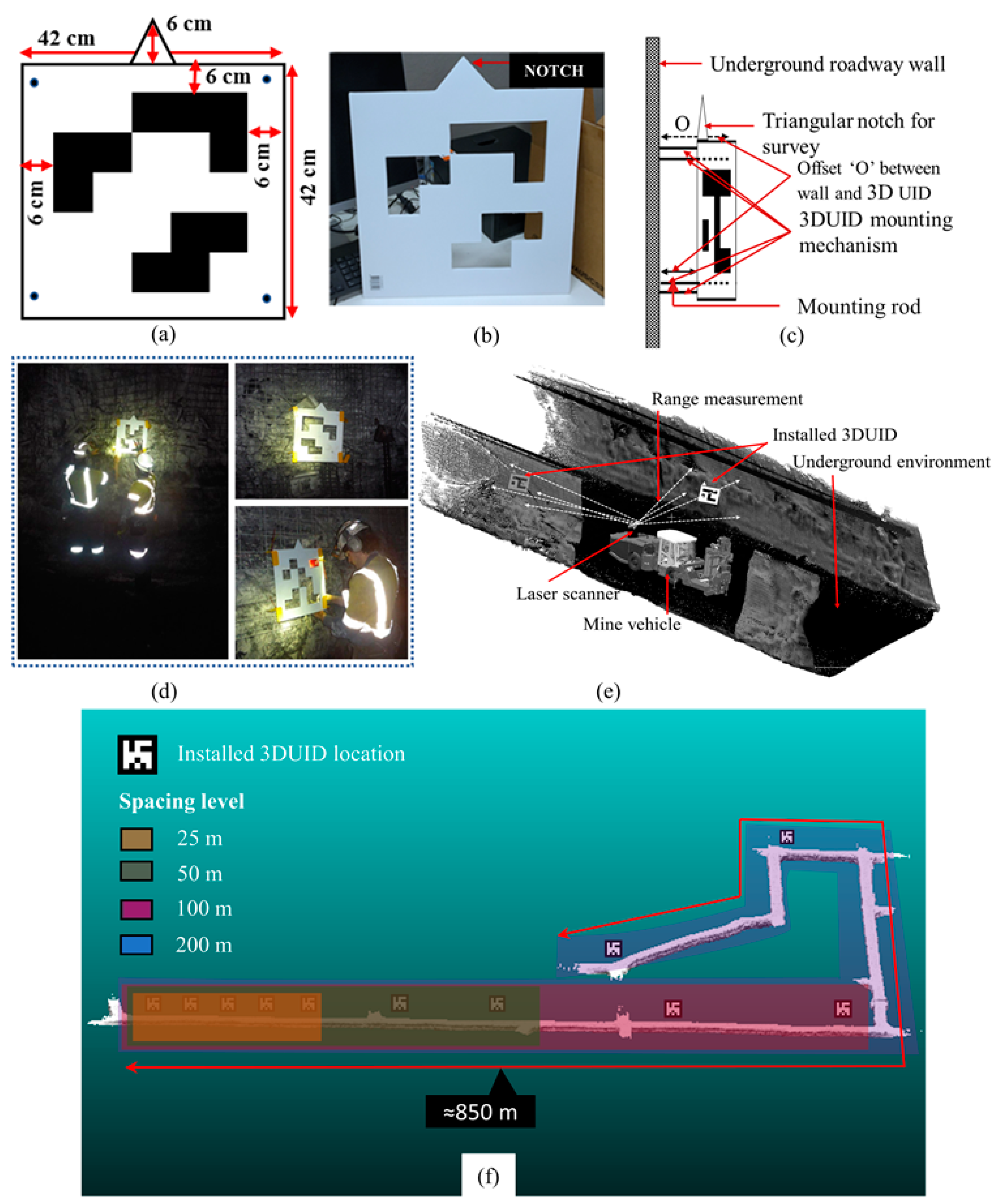
2.2. Study Area, 3DUID Installation and Laser Scanning
2.3. Methodology for 3DReG
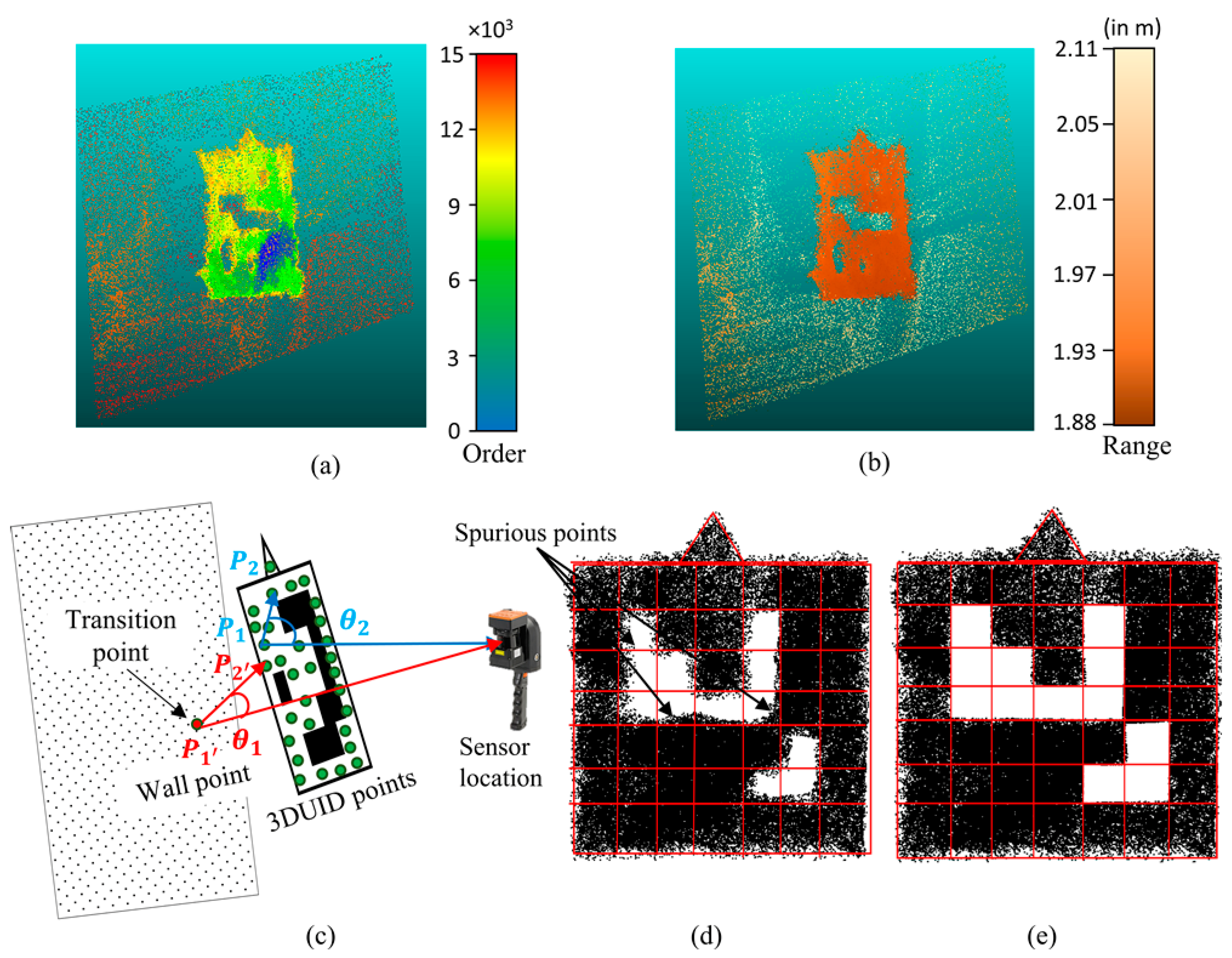
2.3.1. Filtering
2.3.2. Roof, Floor and Wall Segmentation
2.3.3. 3DUID Recognition and Decoding
2.3.4. Georeferencing, Coregistration and Accuracy Analysis
2.3.5. Extraction of Roadway Clearance
3. Results
3.1. 3DUID Recognition
3.2. Georeferencing
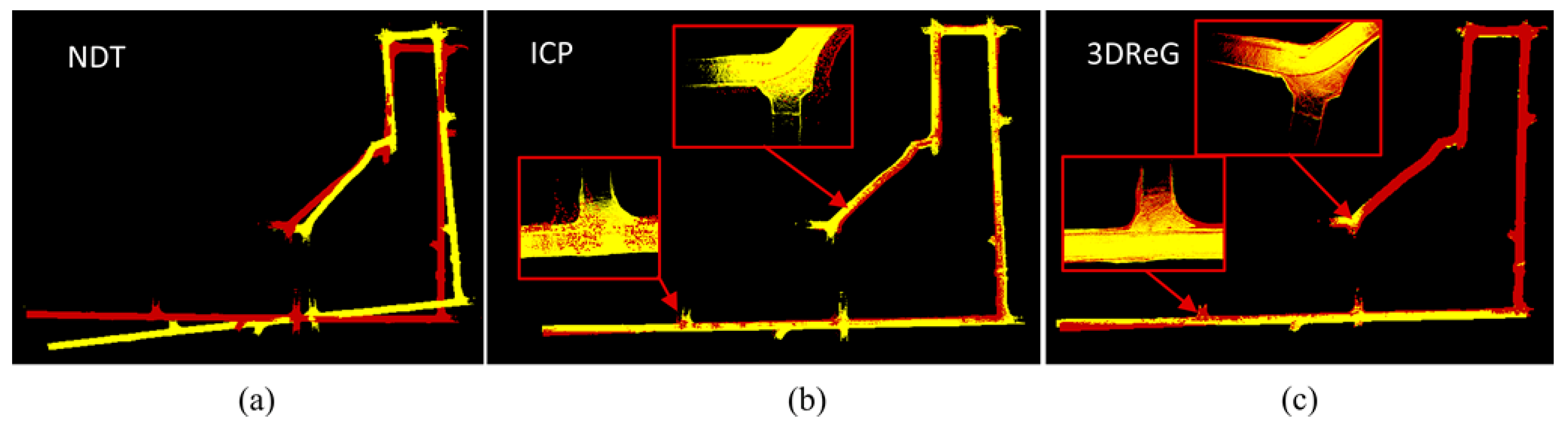
3.3. Coregistration
3.4. Roadway Profile Extraction
4. Discussion
4.1. 3DUID Recognition
4.2. Georeferencing and Coregistration
4.3. Improvement over the Conventional Approach
4.4. Potential Issues and Scope for Further Improvement
4.5. Future Application of 3DUID
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kukutsch, R.; Kajzar, V.; Konicek, P.; Waclawik, P.; Ptacek, J. Possibility of convergence measurement of gates in coal mining using terrestrial 3D laser scanner. J. Sustain. Min. 2015, 14, 30–37. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Q.; Zhong, S.; Pan, P.-Z.; Shi, Y.; Guo, H.; Kou, Y. Observe the temporal evolution of deep tunnel’s 3D deformation by 3D laser scanning in the Jinchuan No. 2 Mine. Tunn. Undergr. Space Technol. 2020, 97, 103237. [Google Scholar] [CrossRef]
- Gikas, V. Three-dimensional laser scanning for geometry documentation and construction management of highway tunnels during excavation. Sensors 2012, 12, 11249–11270. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baiden, G.; Bissiri, Y.; Luoma, S.; Henrich, G. Mapping Utility Infrastructure via Underground GPS Positioning with Autonomous Telerobotics. In Pipelines 2012; American Society of Civil Engineers: Reston, VA, USA, 2012; pp. 1377–1390. [Google Scholar]
- Dang, T.; Mascarich, F.; Khattak, S.; Nguyen, H.; Nguyen, H.; Hirsh, S.; Reinhart, R.; Papachristos, C.; Alexis, K. Autonomous Search for Underground Mine Rescue Using Aerial Robots. In Proceedings of the 2020 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2020; pp. 1–8. [Google Scholar]
- Fan, L.; Smethurst, J.A.; Atkinson, P.M.; Powrie, W. Error in target-based georeferencing and registration in terrestrial laser scanning. Comput. Geosci. 2015, 83, 54–64. [Google Scholar] [CrossRef] [Green Version]
- Riquelme, A.; Cano, M.; Tomás, R.; Abellán, A. Identification of Rock Slope Discontinuity Sets from Laser Scanner and Photogrammetric Point Clouds: A Comparative Analysis. In Proceedings of the ISRM European Rock Mechanics Symposium-EUROCK, Ostrava, Czech Republic, 20–22 June 2017; Elsevier Ltd.: Amsterdam, The Netherlands, 2017; Volume 191, pp. 838–845. [Google Scholar]
- Bae, K.H.; Lichti, D.D. A method for automated registration of unorganised point clouds. ISPRS J. Photogramm. Remote Sens. 2008, 63, 36–54. [Google Scholar] [CrossRef]
- Letortu, P.; Costa, S.; Maquaire, O.; Delacourt, C.; Augereau, E.; Davidson, R.; Suanez, S.; Nabucet, J. Retreat rates, modalities and agents responsible for erosion along the coastal chalk cliffs of Upper Normandy: The contribution of terrestrial laser scanning. Geomorphology 2015, 245, 3–14. [Google Scholar] [CrossRef]
- Abellán, A.; Calvet, J.; Vilaplana, J.M.; Blanchard, J. Detection and spatial prediction of rockfalls by means of terrestrial laser scanner monitoring. Geomorphology 2010, 119, 162–171. [Google Scholar] [CrossRef]
- Milan, D.J.; Heritage, G.L.; Hetherington, D. Application of a 3D laser scanner in the assessment of erosion and deposition volumes and channel change in a proglacial river. Earth Surf. Process. Landf. 2007, 32, 1657–1674. [Google Scholar] [CrossRef]
- Magnusson, M.; Lilienthal, A.; Duckett, T. Scan registration for autonomous mining vehicles using 3D-NDT. J. Field Robot. 2007, 24, 803–827. [Google Scholar] [CrossRef] [Green Version]
- Dong, Z.; Liang, F.; Yang, B.; Xu, Y.; Zang, Y.; Li, J.; Wang, Y.; Dai, W.; Fan, H.; Hyyppäb, J.; et al. Registration of large-scale terrestrial laser scanner point clouds: A review and benchmark. ISPRS J. Photogramm. Remote Sens. 2020, 163, 327–342. [Google Scholar] [CrossRef]
- Raval, S.; Banerjee, B.P.; Kumar Singh, S.; Canbulat, I. A Preliminary Investigation of Mobile Mapping Technology for Underground Mining. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Yokohama, Japan, 28 July–2 August 2019; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2019; pp. 6071–6074. [Google Scholar]
- Bueno, M.; González-Jorge, H.; Martínez-Sánchez, J.; Lorenzo, H. Automatic point cloud coarse registration using geometric keypoint descriptors for indoor scenes. Autom. Constr. 2017, 81, 134–148. [Google Scholar] [CrossRef]
- Vandapel, N.; Huber, D.F.; Kapuria, A.; Hebert, M. Natural terrain classification using 3-D ladar data. In Proceedings of the IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April–1 May 2004; pp. 5117–5122. [Google Scholar]
- Singh, S.K.; Raval, S.; Banerjee, B. Roof bolt identification in underground coal mines from 3D point cloud data using local point descriptors and artificial neural network. Int. J. Remote Sens. 2021, 42, 367–377. [Google Scholar] [CrossRef]
- Rusu, R.B.; Blodow, N.; Beetz, M. Fast Point Feature Histograms (FPFH) for 3D registration. In Proceedings of the IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3212–3217. [Google Scholar] [CrossRef]
- Marton, Z.C.; Pangercic, D.; Blodow, N.; Kleinehellefort, J.; Beetz, M. General 3D Modelling of Novel Objects from a Single View. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 3700–3705. [Google Scholar] [CrossRef] [Green Version]
- Zhao, G.; Yuan, J.; Dang, K. HeIght Gradient Histogram (HIGH) for 3D Scene Labeling. In Proceedings of the 2014 2nd International Conference on 3D Vision, Washington, DC, USA, 8 December 2014; pp. 569–576. [Google Scholar] [CrossRef]
- Eo, Y.D.; Pyeon, M.W.; Kim, S.W.; Kim, J.R.; Han, D.Y. Coregistration of terrestrial lidar points by adaptive scale-invariant feature transformation with constrained geometry. Autom. Constr. 2012, 25, 49–58. [Google Scholar] [CrossRef]
- Mishra, P.K.; Stewart, R.F.; Bolic, M.; Yagoub, M.C.E. RFID in underground-mining service applications. IEEE Pervasive Comput. 2014, 13, 72–79. [Google Scholar] [CrossRef]
- Muduli, L.; Mishra, D.P.; Jana, P.K. Application of wireless sensor network for environmental monitoring in underground coal mines: A systematic review. J. Netw. Comput. Appl. 2018, 106, 48–67. [Google Scholar] [CrossRef]
- Lavigne, N.J.; Marshall, J.A. A landmark-bounded method for large-scale underground mine mapping. J. Field. Robot. 2012, 29, 861–879. [Google Scholar] [CrossRef]
- Lavigne, N.J.; Marshall, J.A.; Artan, U. Towards Underground Mine Drift Mapping with RFID. In Proceedings of the Canadian Conference on Electrical and Computer Engineering, Calgary, Alberta, BC, Canada, 2–5 May 2010; pp. 1–6. [Google Scholar]
- Digiampaolo, E.; Martinelli, F. Mobile robot localization using the phase of passive UHF RFID signals. IEEE Trans. Ind. Electron. 2014, 61, 365–376. [Google Scholar] [CrossRef]
- Lemus, R.; Díaz, S.; Gutiérrez, C.; Rodríguez, D.; Escobar, F. SLAM-R algorithm of simultaneous localization and mapping using RFID for obstacle location and recognition. J. Appl. Res. Technol. 2014, 12, 551–559. [Google Scholar] [CrossRef] [Green Version]
- Motroni, A.; Buffi, A.; Nepa, P. A survey on Indoor Vehicle Localization through RFID Technology. IEEE Access 2021. [Google Scholar] [CrossRef]
- Ahmed, S.; Gagnon, J.D.; Makhdoom, M.; Naeem, R.; Wang, J. New Methods and Equipment for Three-Dimensional Laser Scanning, Mapping and Profiling Underground Mine Cavities. In Proceedings of the First International Conference on Underground Mining Technology, Sudbury, ON, Canada, 11–13 October2017; pp. 467–473. [Google Scholar]
- Pesci, A.; Teza, G. Terrestrial laser scanner and retro-reflective targets: An experiment for anomalous effects investigation. Int. J. Remote Sens. 2008, 29, 5749–5765. [Google Scholar] [CrossRef]
- Schaer, P.; Vallet, J. Trajectory Adjustment of Mobile Laser Scan Data in Gps Denied Environments. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XL-3/W4, 61–64. [Google Scholar] [CrossRef] [Green Version]
- Zhang, M. Accurate Sphere Marker-Based Registration System of 3D Point Cloud Data in Applications of Shipbuilding Blocks. J. Ind. Intell. Inf. 2015, 3, 318–323. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, H.; Zhang, Y.; Zhang, D. Automatic registration of laser point cloud using precisely located sphere targets. J. Appl. Remote Sens. 2014, 8, 083588. [Google Scholar] [CrossRef]
- Shi, G.; Tang, J.; Guan, Y.; Cheng, X. Target Selection and Development in 3D Laser Scanning Based on Sampling Interval. In Proceedings of the 2nd International Conference on Information Science and Engineering, Hangzhou, China, 3–5 December 2010; pp. 4110–4112. [Google Scholar]
- Yang, C.; Liu, L.; Luo, W.; Meng, Y.; Su, W. Identification of Barcode Beacon and Its Application in Underground Mining. In Proceedings of the ICACTE 2010 3rd International Conference on Advanced Computer Theory and Engineering, Chengdu, China, 20–22 August 2010; Volume 1. [Google Scholar]
- Li, Z.; Huang, J. Study on the use of Q-R Codes as Landmarks for Indoor Positioning: Preliminary Results. In Proceedings of the 2018 IEEE/ION Position, Location and Navigation Symposium, PLANS 2018, Monterey, CA, USA, 23–36 April 2018; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NY, USA, 2018; pp. 1270–1276. [Google Scholar]
- Lin, G.; Chen, X. A robot indoor position and orientation method based on 2D barcode landmark. J. Comput. 2011, 6, 1191–1197. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, C.; Yang, W.; Chen, C.Y. Localization and Navigation Using QR Code for Mobile Robot in Indoor Environment. In Proceedings of the 2015 IEEE International Conference on Robotics and Biomimetics, Zhuhai, China, 6–9 December 2015; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NY, USA, 2015; pp. 2501–2506. [Google Scholar]
- Simela, J.V.; Marshall, J.A.; Daneshmend, L.K. Automated Laser Scanner 2D Positioning and Orienting by Method of Triangulateration for Underground Mine Surveying. In Proceedings of the ISARC 2013 30th International Symposium on Automation and Robotics in Construction and Mining, Montreal, QB, Canada, 11–15 August 2013; Volume 30, pp. 708–717. [Google Scholar]
- GeoSLAM. ZEB-REVO User Manual. 2017. Available online: http://download.geoslam.com/docs/zeb-revo/ZEB-REVO User Guide V3.0.0.pdf (accessed on 25 August 2020).
- Tan, K.; Cheng, X. Specular Reflection Effects Elimination in Terrestrial Laser Scanning Intensity Data Using Phong Model. Remote Sens. 2017, 9, 853. [Google Scholar] [CrossRef] [Green Version]
- Baltsavias, E.P. Airborne laser scanning: Basic relations and formulas. ISPRS J. Photogramm. Remote Sens. 1999, 54, 199–214. [Google Scholar] [CrossRef]
- Soudarissanane, S.; Lindenbergh, R.; Menenti, M.; Teunissen, P. Scanning geometry: Influencing factor on the quality of terrestrial laser scanning points. ISPRS J. Photogramm. Remote Sens. 2011, 66, 389–399. [Google Scholar] [CrossRef]
- Rusu, R.B.; Cousins, S. 3D is here: Point Cloud Library (PCL). In Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011. [Google Scholar]
- Banerjee, B.P.; Raval, S.; Cullen, P.J.; Kumar Singh, S. Mapping of Complex Vegetation Communities and Species Using UAV-LIDAR Metrics and High-Resolution Optical Data. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Yokohama, Japan, 28 July–2 August 2019; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NY, USA, 2019; pp. 6110–6113. [Google Scholar]
- Singh, S.K.; Raval, S.; Banerjee, B.P. Automated structural discontinuity mapping in a rock face occluded by vegetation using mobile laser scanning. Eng. Geol. 2021, 106040. [Google Scholar] [CrossRef]
- Persad, R.A.; Armenakis, C. Automatic co-registration of 3D multi-sensor point clouds. ISPRS J. Photogramm. Remote Sens. 2017, 130, 162–186. [Google Scholar] [CrossRef]
- Breitkopf, P.; Naceur, H.; Rassineux, A.; Villon, P. Moving least squares response surface approximation: Formulation and metal forming applications. Comput. Struct. 2005, 83, 1411–1428. [Google Scholar] [CrossRef]
- Singh, S.K.; Raval, S.; Banerjee, B. A robust approach to identify roof bolts in 3D point cloud data captured from a mobile laser scanner. Int. J. Min. Sci. Technol. 2021. [Google Scholar] [CrossRef]
- Su, Y.-T.; Bethel, J.; Hu, S. Octree-based segmentation for terrestrial LiDAR point cloud data in industrial applications. ISPRS J. Photogramm. Remote Sens. 2016, 113, 59–74. [Google Scholar] [CrossRef]
- Li, L.; Yang, F.; Zhu, H.; Li, D.; Li, Y.; Tang, L. An improved RANSAC for 3D point cloud plane segmentation based on normal distribution transformation cells. Remote Sens. 2017, 9, 433. [Google Scholar] [CrossRef] [Green Version]
- Dong, Z.; Yang, B.; Liang, F.; Huang, R.; Scherer, S. Hierarchical registration of unordered TLS point clouds based on binary shape context descriptor. ISPRS J. Photogramm. Remote Sens. 2018, 144, 61–79. [Google Scholar] [CrossRef]
- Ankerst, M.; Breunig, M.M.; Kriegel, H.P.; Sander, J. OPTICS: Ordering Points to Identify the Clustering Structure. SIGMOD Rec. (ACM Spec. Interes. Gr. Manag. Data) 1999, 28, 49–60. [Google Scholar] [CrossRef]
- Kalita, H.K.; Bhattacharyya, D.K.; Kar, A. A new algorithm for Ordering of Points to Identify Clustering structure based on perimeter of triangle: OPTICS (BOPT). In Proceedings of the 15th International Conference on Advanced Computing and Communications, Guwahati, India, 18–21 December 2007; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NY, USA, 2007; pp. 523–528. [Google Scholar]
- Oomori, S.; Nishida, T.; Kurogi, S. Point cloud matching using singular value decomposition. Artif. Life Robot. 2016, 21, 149–154. [Google Scholar] [CrossRef]
- Horn, B.K.P. Closed-form solution of absolute orientation using unit quaternions. J. Opt. Soc. Am. A 1987, 4, 629. [Google Scholar] [CrossRef]
- Wang, J.; Huo, S.; Liu, Y.; Li, R.; Liu, Z. Research of fast point cloud registration method in construction error analysis of hull blocks. Int. J. Nav. Archit. Ocean. Eng. 2020, 12, 605–616. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, C.; Song, Z.; Wang, M. Efficient global point cloud registration by matching rotation invariant features through translation search. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; Volume 11216 LNCS, pp. 460–474. [Google Scholar]
- Besl, P.; McKay, N. A method for registration of 3D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Hong, H.; Lee, B.H. Probabilistic normal distributions transform representation for accurate 3D point cloud registration. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Vancouver, BC, Canada, 24–28 September 2017; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NY, USA, 2017; Volume 2017, pp. 3333–3338. [Google Scholar]
- Biber, P. The Normal Distributions Transform: A New Approach to Laser Scan Matching. In Proceedings of the IEEE International Conference on Intelligent Robots and Systemsm, Las Vegas, NV, USA, 27–31 October 2003; Volume 3, pp. 2743–2748. [Google Scholar]
- Magnusson, M.; Nüchter, A.; Lörken, C.; Lilienthal, A.J.; Hertzberg, J. Evaluation of 3D Registration Reliability and Speed-A Comparison of ICP and NDT. In Proceedings of the IEEE International Conference on Robotics and Automation, Kobe, Japan, 12 May 2009; pp. 3907–3912. [Google Scholar]
- Kaasalainen, S.; Ruotsalainen, L.; Kirkko-Jaakkola, M.; Nevalainen, O.; Hakala, T. Towards multispectral, multi-sensor indoor positioning and target identification. Electron. Lett. 2017, 53, 1008–1011. [Google Scholar] [CrossRef] [Green Version]
- Ruotsalainen, L.; Kirkko-Jaakkola, M.; Rantanen, J.; Mäkelä, M. Error modelling for multi-sensor measurements in infrastructure-free indoor navigation. Sensors 2018, 18, 590. [Google Scholar] [CrossRef] [Green Version]
- Hu, E.; Deng, Z.; Hu, M.; Yin, L.; Liu, W. Cooperative indoor positioning with factor graph based on FIM for wireless sensor network. Futur. Gener. Comput. Syst. 2018, 89, 126–136. [Google Scholar] [CrossRef]
- Peel, H.; Luo, S.; Cohn, A.G.; Fuentes, R. Localisation of a mobile robot for bridge bearing inspection. Autom. Constr. 2018, 94, 244–256. [Google Scholar] [CrossRef]
- Guo, J.; Tsai, M.J.; Han, J.Y. Automatic reconstruction of road surface features by using terrestrial mobile lidar. Autom. Constr. 2015, 58, 165–175. [Google Scholar] [CrossRef]
- Czerniawski, T.; Ma, J.W. Fernanda Leite Automated building change detection with amodal completion of point clouds. Autom. Constr. 2021, 124, 103568. [Google Scholar] [CrossRef]
- Hu, H.; Fernandez-Steeger, T.M.; Dong, M.; Azzam, R. Numerical modeling of LiDAR-based geological model for landslide analysis. Autom. Constr. 2012, 24, 184–193. [Google Scholar] [CrossRef]
- Forbes, B.; Vlachopoulos, N.; Diederichs, M.S.; Hyett, A.J.; Punkkinen, A. An in situ monitoring campaign of a hard rock pillar at great depth within a Canadian mine. J. Rock Mech. Geotech. Eng. 2020, 12, 427–448. [Google Scholar] [CrossRef]
- Gage, J.R.; Fratta, D.; Turner, A.L.; MacLaughlin, M.M.; Wang, H.F. Validation and implementation of a new method for monitoring in situ strain and temperature in rock masses using fiber-optically instrumented rock strain and temperature strips. Int. J. Rock Mech. Min. Sci. 2013, 61, 244–255. [Google Scholar] [CrossRef]
- Spearing, A.J.S.; Hyett, A. In situ monitoring of primary roofbolts at underground coal mines in the USA. J. South. African Inst. Min. Metall. 2014, 114, 791–800. [Google Scholar]
- Esterhuizen, G.S.; Gearhart, D.F.; Klemetti, T.; Dougherty, H.; van Dyke, M. Analysis of gateroad stability at two longwall mines based on field monitoring results and numerical model analysis. Int. J. Min. Sci. Technol. 2019, 29, 35–43. [Google Scholar] [CrossRef]
- Xing, Y.; Kulatilake, P.H.S.W.; Sandbak, L.A. Investigation of Rock Mass Stability Around the Tunnels in an Underground Mine in USA Using Three-Dimensional Numerical Modeling. Rock Mech. Rock Eng. 2017, 51, 579–597. [Google Scholar] [CrossRef]
- Cadena, C.; Carlone, L.; Carrillo, H.; Latif, Y.; Scaramuzza, D.; Neira, J.; Reid, I.; Leonard, J.J. Past, present, and future of simultaneous localization and mapping: Toward the robust-perception age. IEEE Trans. Robot. 2016, 32, 1309–1332. [Google Scholar] [CrossRef] [Green Version]
- Toth, C.; Jóźków, G. Remote sensing platforms and sensors: A survey. ISPRS J. Photogramm. Remote Sens. 2016, 115, 22–36. [Google Scholar] [CrossRef]
- Bimbraw, K. Autonomous Cars: Past, Present and Future: A Review of the Developments in the Last Century, the Present Scenario and The Expected Future of Autonomous Vehicle Technology. In Proceedings of the ICINCO 2015 12th International Conference on Informatics in Control, Automation and Robotics, Colmar, France, 21–23 July 2015; Volume 1, pp. 191–198. [Google Scholar]




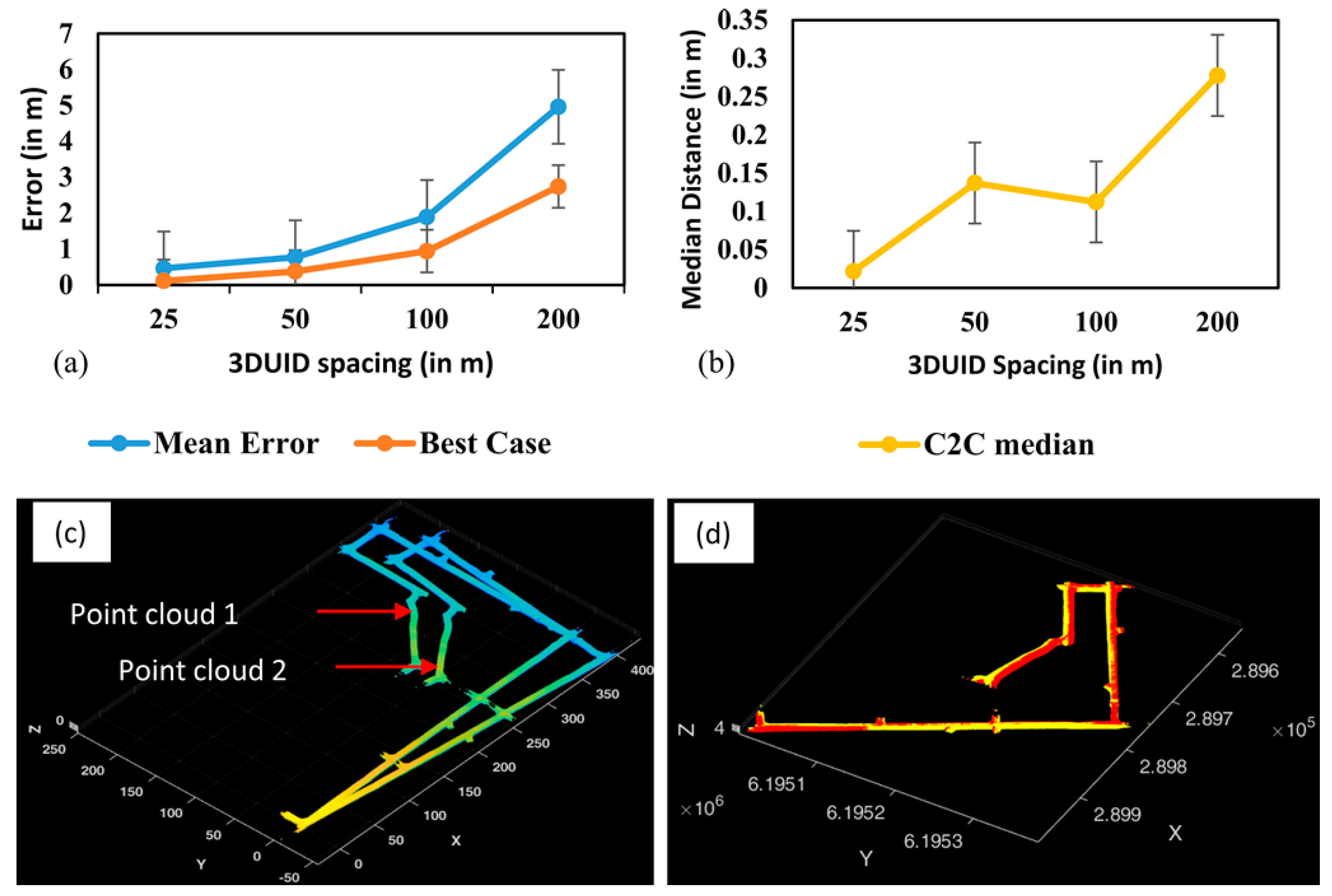

| 3DUID Spacing (in m) | MAE of LOOCV (in m) | Best Case Absolute Error in LOOCV (in m) | Median of C2C Distance between the Two Datasets (in m) |
|---|---|---|---|
| 25 | 0.46 | 0.11 | 0.02 |
| 50 | 0.78 | 0.38 | 0.14 |
| 100 | 1.89 | 0.94 | 0.11 |
| 200 | 4.96 | 2.74 | 0.28 |
| Georeferencing and Coregistration Method | Median C2C Distance (in m) | Time | Iterations | Sampling |
|---|---|---|---|---|
| Georeferencing Using Surveyed 3DUID | 0.50 | 5 s | 0 | - |
| ICP | 0.69 | 17.4 s | 100 | 1,000,000 |
| NDT | 6.93 | 32 min | 100 | 1,000,000 |
| 3DReG | 0.16 | 20 s | 100 | 1,000,000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, S.K.; Banerjee, B.P.; Raval, S. Three-Dimensional Unique-Identifier-Based Automated Georeferencing and Coregistration of Point Clouds in Underground Mines. Remote Sens. 2021, 13, 3145. https://doi.org/10.3390/rs13163145
Singh SK, Banerjee BP, Raval S. Three-Dimensional Unique-Identifier-Based Automated Georeferencing and Coregistration of Point Clouds in Underground Mines. Remote Sensing. 2021; 13(16):3145. https://doi.org/10.3390/rs13163145
Chicago/Turabian StyleSingh, Sarvesh Kumar, Bikram Pratap Banerjee, and Simit Raval. 2021. "Three-Dimensional Unique-Identifier-Based Automated Georeferencing and Coregistration of Point Clouds in Underground Mines" Remote Sensing 13, no. 16: 3145. https://doi.org/10.3390/rs13163145
APA StyleSingh, S. K., Banerjee, B. P., & Raval, S. (2021). Three-Dimensional Unique-Identifier-Based Automated Georeferencing and Coregistration of Point Clouds in Underground Mines. Remote Sensing, 13(16), 3145. https://doi.org/10.3390/rs13163145








