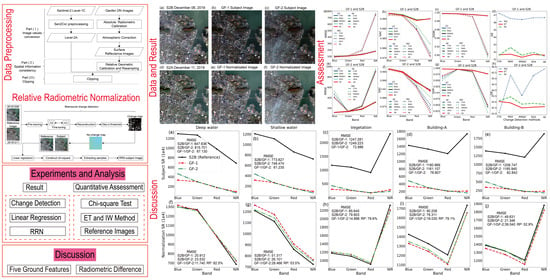
Radiometric Normalization for Cross-Sensor Optical Gaofen Images with Change Detection and Chi-Square Test
Abstract
:1. Introduction
2. Data and Preprocessing
2.1. Sentinel-2 and Gaofen Satellites
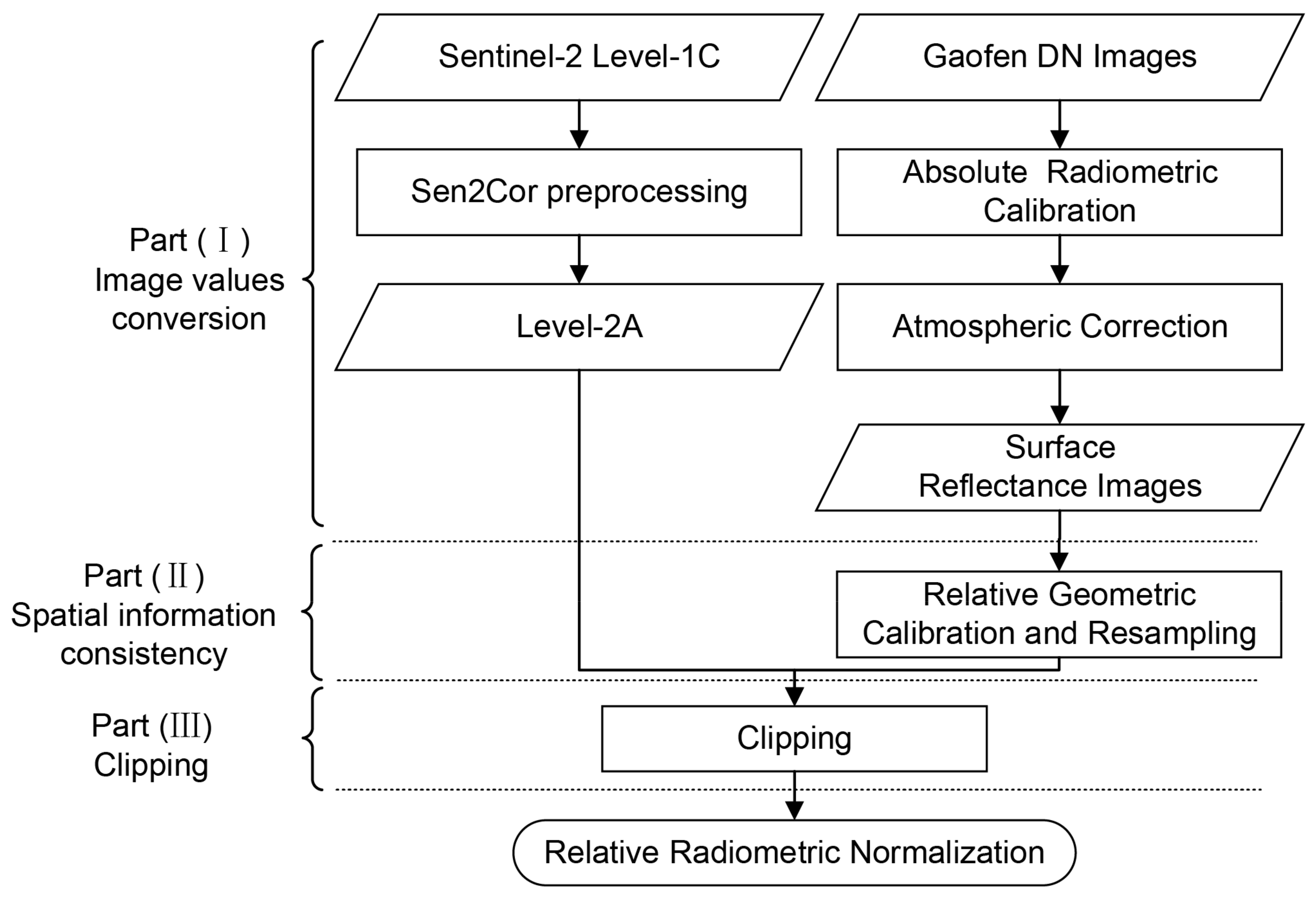
2.2. Images Preprocessing
3. Methodology
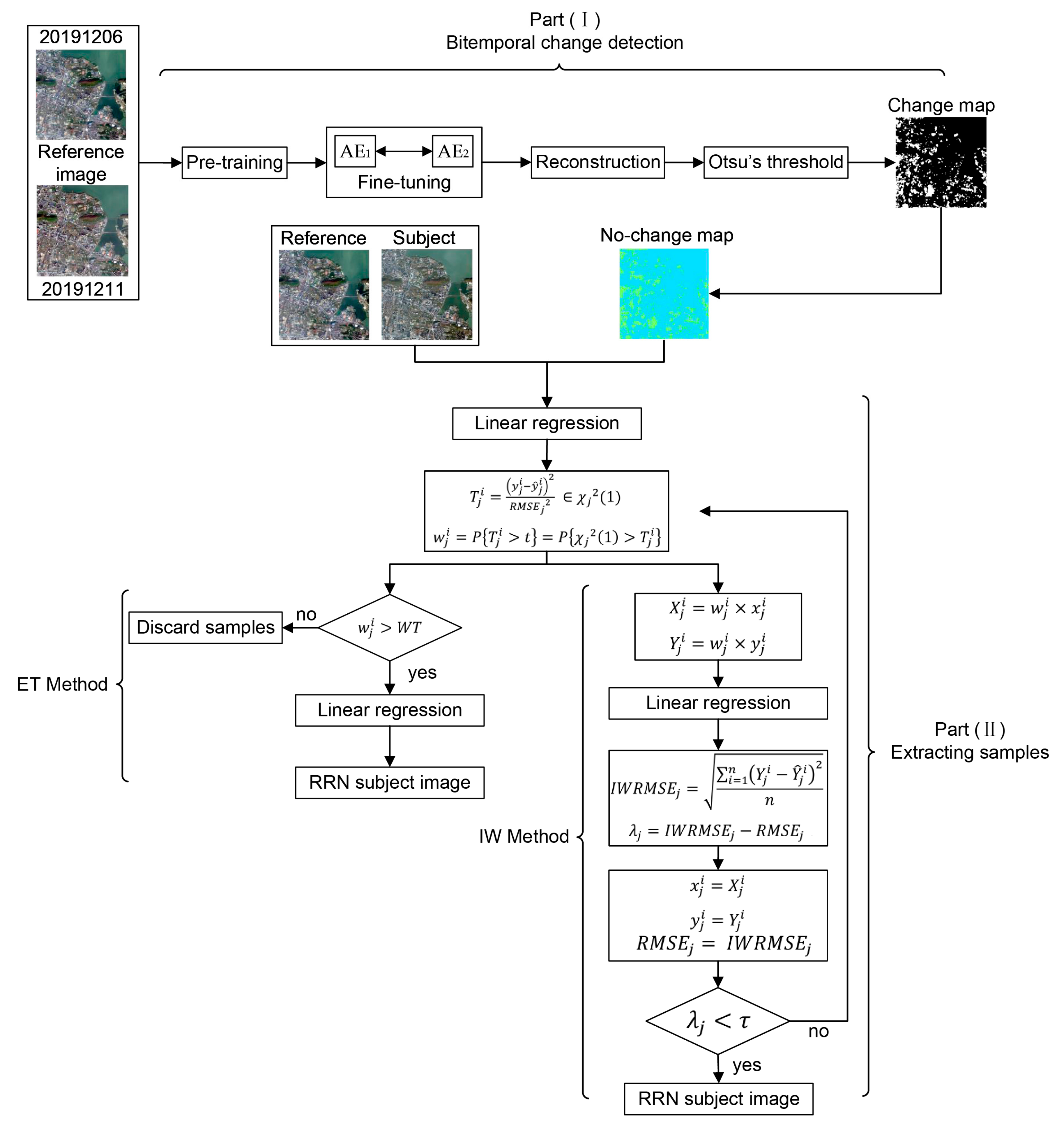
3.1. Proposed Workflow
3.1.1. Bitemporal Change Detection
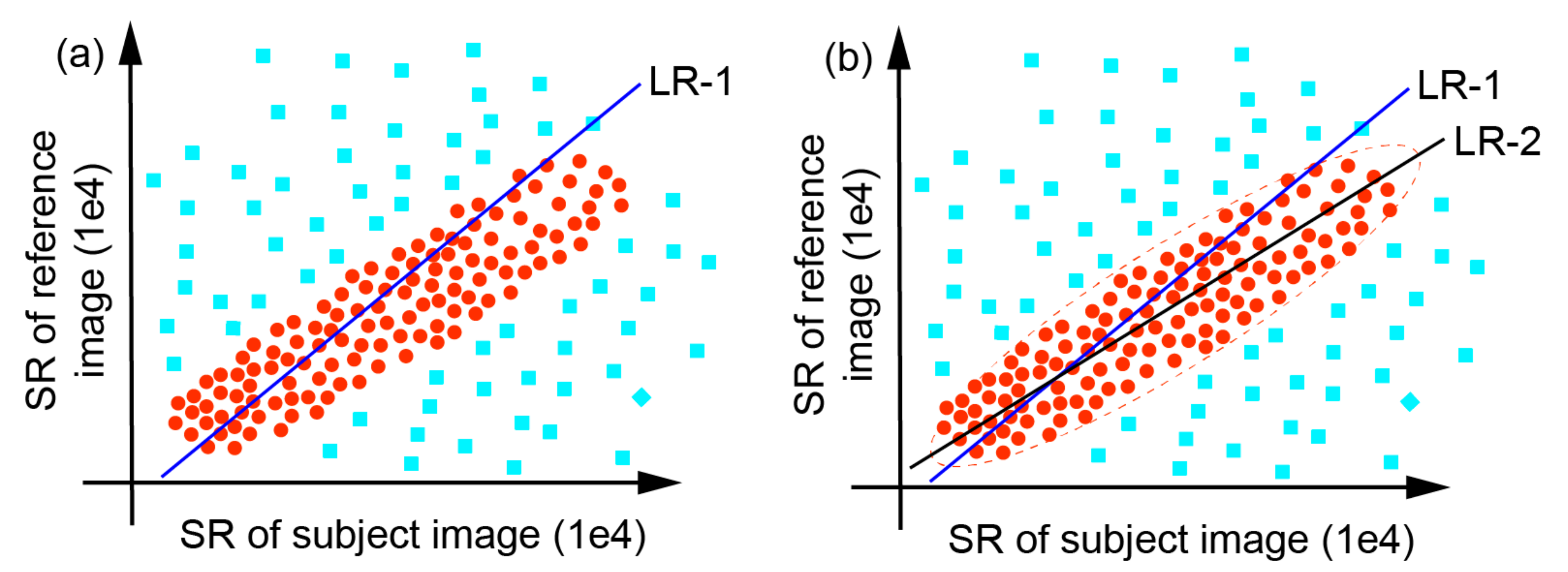
3.1.2. Extracting Samples
3.2. Quantitative Assessment
4. Experiments and Analysis
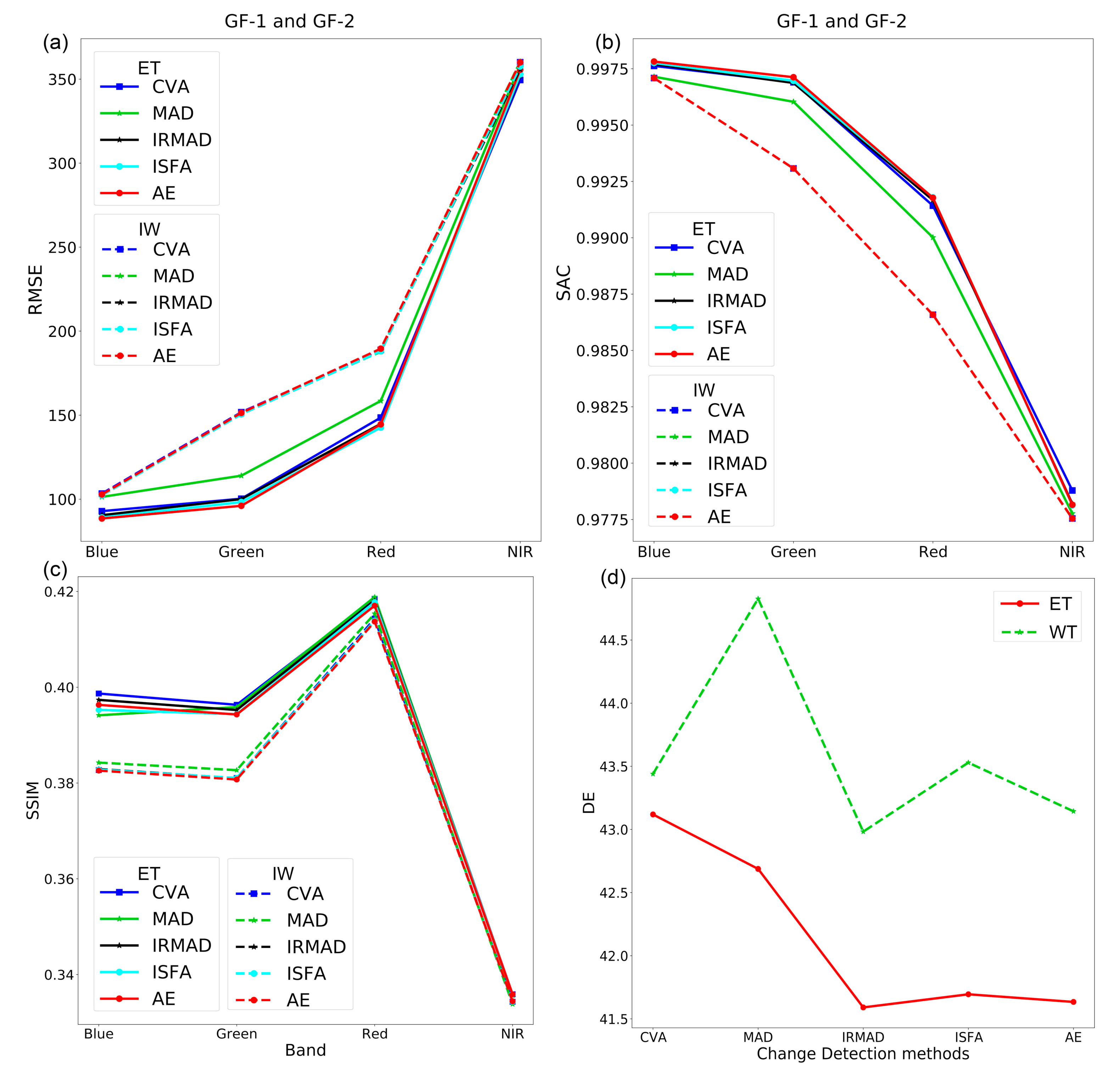
4.1. Effectiveness of AE and ET Method
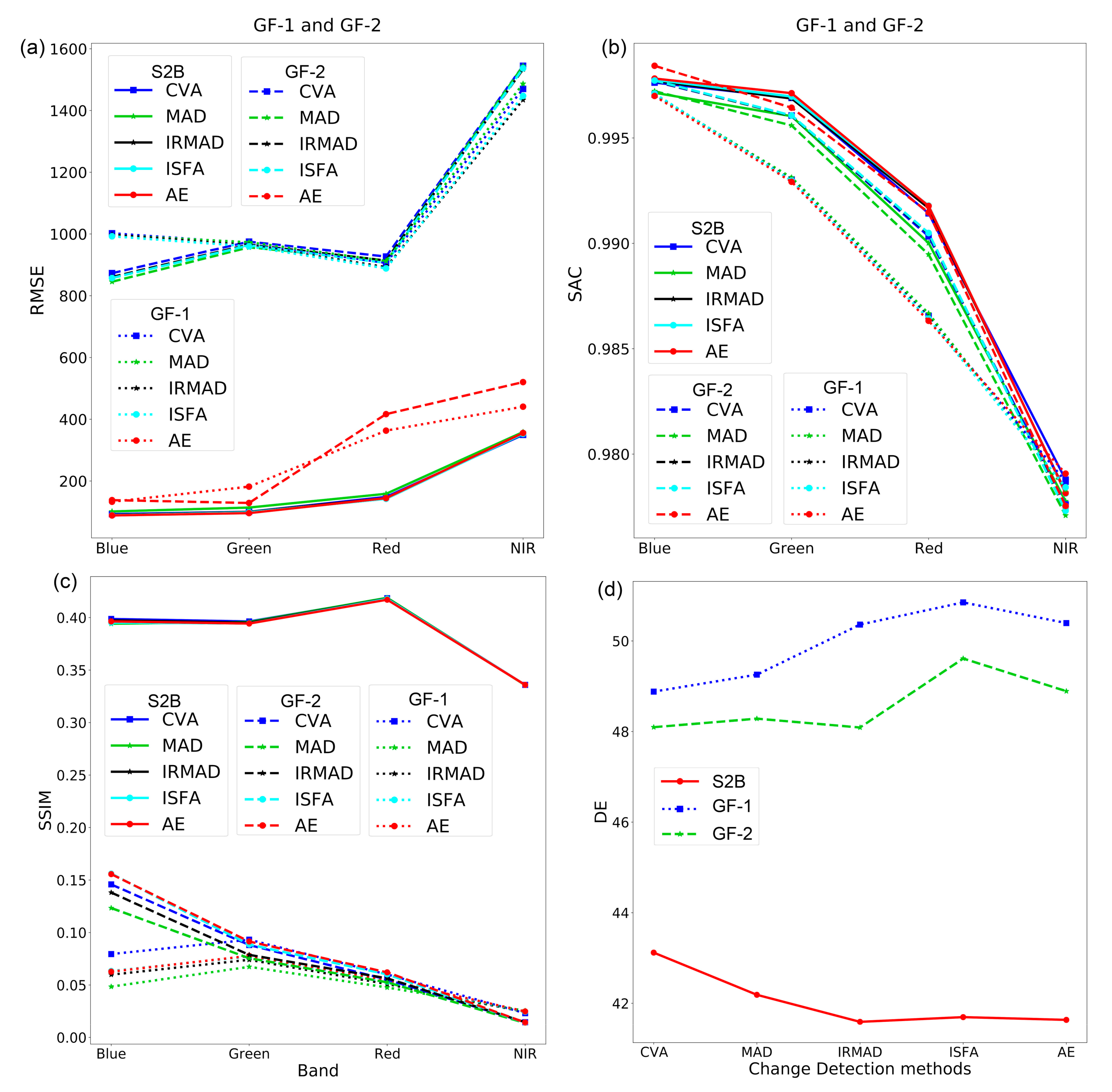
4.2. The Performance of Different Reference Images
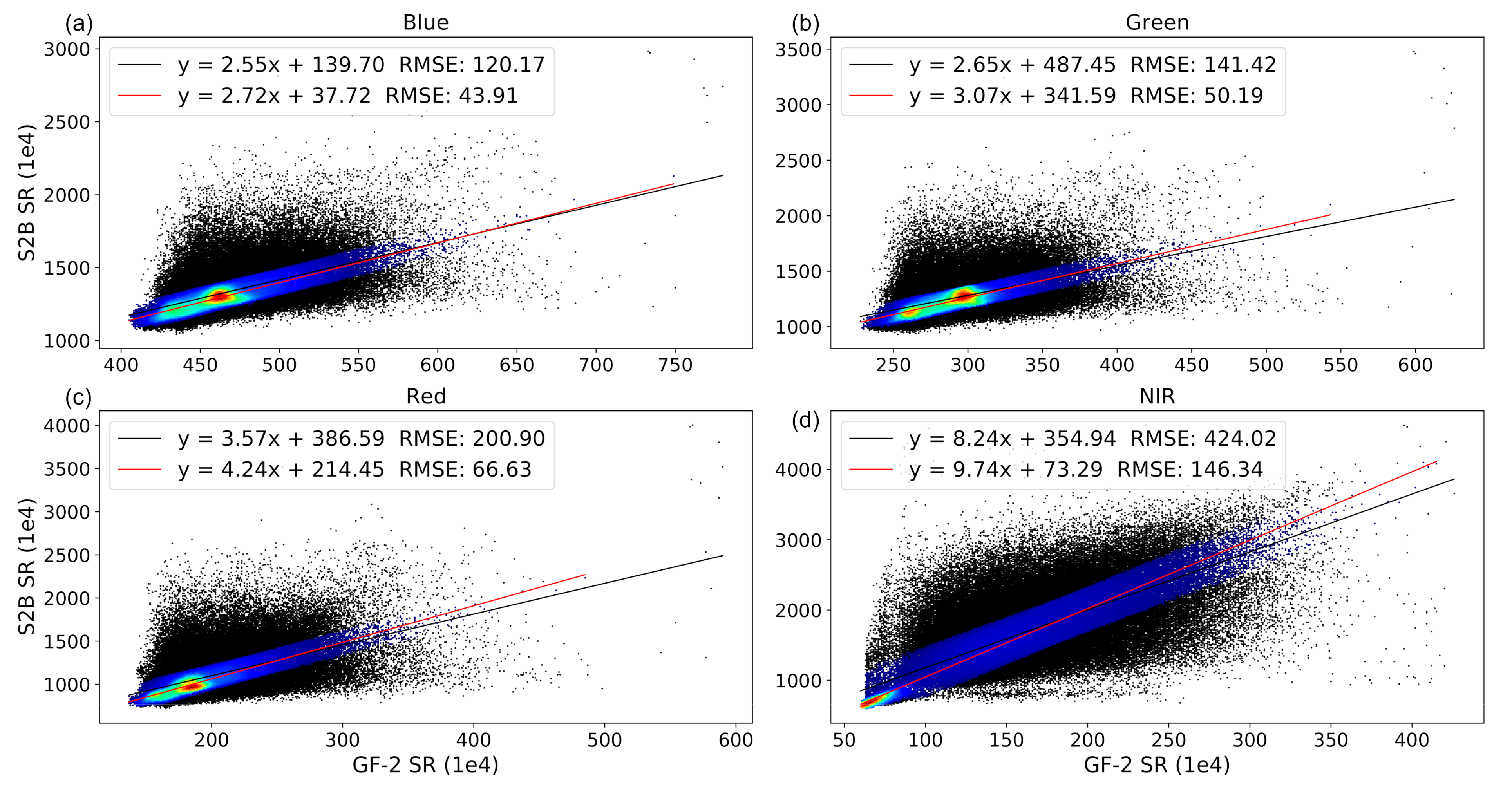
4.3. Radiometric Normalization Result
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, X.; Lo, C.P. Relative radiometric normalization performance for change detection from multi-date satellite images. Photogramm. Eng. Remote Sens. 2000, 66, 967–980. [Google Scholar]
- Zhang, L.; Wu, C.; Du, B. Automatic radiometric normalization for multitemporal remote sensing imagery with iterative slow feature analysis. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6141–6155. [Google Scholar] [CrossRef]
- Collins, J.B.; Woodcock, C.E. An assessment of several linear change detection techniques for mapping forest mortality using multitemporal landsat TM data. Remote Sens. Environ. 1996, 56, 66–77. [Google Scholar] [CrossRef]
- Song, C.; Woodcock, C.E.; Seto, K.C.; Lenney, M.P.; Macomber, S.A. Classification and change detection using Landsat TM Data: When and how to correct atmospheric effects? Remote Sens. Environ. 2001, 75, 230–244. [Google Scholar] [CrossRef]
- Teillet, P.M. Image correction for radiometric effects in remote sensing. Int. J. Remote Sens. 1986, 7, 1637–1651. [Google Scholar] [CrossRef]
- Moghimi, A.; Mohammadzadeh, A.; Celik, T.; Amani, M. A Novel radiometric control set sample selection strategy for relative radiometric normalization of multitemporal satellite images. IEEE Trans. Geosci. Remote Sens. 2020, 59, 2503–2519. [Google Scholar] [CrossRef]
- Seo, D.K.; Kim, Y.H.; Eo, Y.D.; Park, W.Y.; Park, H.C. Generation of radiometric, phenological normalized image based on random forest regression for change detection. Remote Sens. 2017, 9, 1163. [Google Scholar] [CrossRef] [Green Version]
- Friedl, M.A.; Sulla-Menashe, D.; Tan, B.; Schneider, A.; Ramankutty, N.; Sibley, A.; Huang, X. MODIS Collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sens. Environ. 2010, 114, 168–182. [Google Scholar] [CrossRef]
- Nazeer, M.; Wong, M.S.; Nichol, J.E. A new approach for the estimation of phytoplankton cell counts associated with algal blooms. Sci. Total. Environ. 2017, 590–591, 125–138. [Google Scholar] [CrossRef]
- Gens, R. Remote sensing of coastlines: Detection, extraction and monitoring. Int. J. Remote Sens. 2010, 31, 1819–1836. [Google Scholar] [CrossRef]
- Deng, C.; Zhu, Z. Continuous subpixel monitoring of urban impervious surface using Landsat time series. Remote Sens. Environ. 2020, 238, 110929. [Google Scholar] [CrossRef]
- Moghimi, A.; Sarmadian, A.; Mohammadzadeh, A.; Celik, T.; Amani, M.; Kusetogullari, H. Distortion robust relative radiometric normalization of multitemporal and multisensor remote sensing images using image features. IEEE Trans. Geosci. Remote Sens. 2021, 1–20. [Google Scholar] [CrossRef]
- Janzen, D.T.; Fredeen, A.L.; Wheate, R.D. Radiometric correction techniques and accuracy assessment for Landsat TM data in remote forested regions. Can. J. Remote Sens. 2006, 32, 330–340. [Google Scholar] [CrossRef]
- Sadeghi, V.; Ebadi, H.; Ahmadi, F.F. A new model for automatic normalization of multitemporal satellite images using Artificial Neural Network and mathematical methods. Appl. Math. Model. 2013, 37, 6437–6445. [Google Scholar] [CrossRef]
- Hong, G.; Zhang, Y. A comparative study on radiometric normalization using high resolution satellite images. Int. J. Remote Sens. 2008, 29, 425–438. [Google Scholar] [CrossRef]
- Rahman, M.M.; Hay, G.J.; Couloigner, I.; Hemachandran, B.; Bailin, J. An assessment of polynomial regression techniques for the relative radiometric normalization (RRN) of high-resolution multi-temporal airborne thermal infrared (TIR) imagery. Remote Sens. 2014, 6, 11810–11828. [Google Scholar] [CrossRef] [Green Version]
- Huang, L.T.; Jiao, W.L.; Long, T.F.; Kang, C.L. A radiometric normalization method of controlling no-changed set (cncs) for diverse landcover using multi-sensor data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, XLII-3/W10, 863–870. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Vierling, L.; Deering, D. A simple and effective radiometric correction method to improve landscape change detection across sensors and across time. Remote Sens. Environ. 2005, 98, 63–79. [Google Scholar] [CrossRef]
- El Hajj, M.; Bégué, A.; Lafrance, B.; Hagolle, O.; Dedieu, G.; Rumeau, M. Relative radiometric normalization and atmospheric correction of a SPOT 5 time series. Sensors 2008, 8, 2774–2791. [Google Scholar] [CrossRef] [Green Version]
- Zhong, C.; Xu, Q.; Li, B. Relative radiometric normalization for multitemporal remote sensing images by hierarchical regression. IEEE Geosci. Remote Sens. Lett. 2015, 13, 217–221. [Google Scholar] [CrossRef]
- Schott, J.R.; Salvaggio, C.; Volchok, W.J. Radiometric scene normalization using pseudoinvariant features. Remote Sens. Environ. 1988, 26, 15–16. [Google Scholar] [CrossRef]
- Philpot, W.; Ansty, T. Analytical description of pseudoinvariant features. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2016–2021. [Google Scholar] [CrossRef]
- Liu, S.; Marinelli, D.; Bruzzone, L.; Bovolo, F. A Review of change detection in multitemporal hyperspectral images: Current techniques, applications, and challenges. IEEE Geosci. Remote Sens. Mag. 2019, 7, 140–158. [Google Scholar] [CrossRef]
- Bovolo, F.; Bruzzone, L. A novel theoretical framework for unsupervised change detection based on CVA in polar domain. Int. Geosci. Remote. Sens. Symp. IGARSS 2006, 45, 379–382. [Google Scholar] [CrossRef]
- Shi, W.; Zhang, M.; Zhang, R.; Chen, S.; Zhan, Z. Change detection based on artificial intelligence: State-of-the-art and challenges. Remote Sens. 2020, 12, 1688. [Google Scholar] [CrossRef]
- Xian, G.; Homer, C.; Fry, J. Updating the 2001 National Land Cover Database land cover classification to 2006 by using Landsat imagery change detection methods. Remote Sens. Environ. 2009, 113, 1133–1147. [Google Scholar] [CrossRef] [Green Version]
- Deng, J.S.; Wang, K.; Deng, Y.H.; Qi, G.J. PCA-based land-use change detection and analysis using multitemporal and multisensor satellite data. Int. J. Remote Sens. 2008, 29, 4823–4838. [Google Scholar] [CrossRef]
- Wu, C.; Du, B.; Zhang, L. Slow feature analysis for change detection in multispectral imagery. IEEE Trans. Geosci. Remote Sens. 2013, 52, 2858–2874. [Google Scholar] [CrossRef]
- Nielsen, A.; Conradsen, K.; Simpson, J.J. Multivariate alteration detection (MAD) and MAF postprocessing in multispectral, bitemporal image data: New approaches to change detection studies. Remote Sens. Environ. 1998, 64, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Canty, M.J.; Nielsen, A.A. Automatic radiometric normalization of multitemporal satellite imagery with the iteratively re-weighted MAD transformation. Remote Sens. Environ. 2008, 112, 1025–1036. [Google Scholar] [CrossRef] [Green Version]
- Du, Y.; Cihlar, J.; Beaubien, J.; Latifovic, R. Radiometric normalization, compositing, and quality control for satellite high resolution image mosaics over large areas. IEEE Trans. Geosci. Remote Sens. 2001, 39, 623–634. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, L.; Sun, M.; Zhu, X. A Mixed Radiometric normalization method for mosaicking of high-resolution satellite imagery. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2972–2984. [Google Scholar] [CrossRef]
- Khelifi, L.; Mignotte, M. Deep learning for change detection in remote sensing images: Comprehensive review and meta-analysis. IEEE Access 2020, 8, 126385–126400. [Google Scholar] [CrossRef]
- Yuan, Q.; Shen, H.; Li, T.; Li, Z.; Li, S.; Jiang, Y.; Xu, H.; Tan, W.; Yang, Q.; Wang, J.; et al. Deep learning in environmental remote sensing: Achievements and challenges. Remote Sens. Environ. 2020, 241, 111716. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.-S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep learning in remote sensing: A comprehensive review and list of resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef] [Green Version]
- Mohamed, A.-R.; Dahl, G.E.; Hinton, G. Acoustic modeling using deep belief networks. IEEE Trans. Audio Speech Lang. Process. 2011, 20, 14–22. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Chelgani, S.C.; Shahbazi, B.; Hadavandi, E. Support vector regression modeling of coal flotation based on variable importance measurements by mutual information method. Measurements 2018, 114, 102–108. [Google Scholar] [CrossRef]
- Kalinicheva, E.; Ienco, D.; Sublime, J.; Trocan, M. Unsupervised change detection analysis in satellite image time series using deep learning combined with graph-based approaches. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1450–1466. [Google Scholar] [CrossRef]
- Kalinicheva, E.; Sublime, J.; Trocan, M. Change detection in satellite images using reconstruction errors of joint autoencoders. In Proceedings of the International Conference on Artificial Networks, Munich, Germany, 17–19 September 2019; pp. 637–648. [Google Scholar] [CrossRef]
- Copernicus. Copernicus Open Access Hub. Available online: https://Scihub.Copernicus.Eu/ (accessed on 24 October 2020).
- ESA Mueller-Wilm U. 2018 Sen2cor ESA Science Toolbox Exploitation Platform. Available online: http://Step.Esa.Int/Main/Third-Party-Plugins-2/Sen2cor/ (accessed on 11 April 2020).
- Lang, N.; Schindler, K.; Wegner, J.D. Country-wide high-resolution vegetation height mapping with Sentinel-2. Remote Sens. Environ. 2019, 233, 111347. [Google Scholar] [CrossRef] [Green Version]
- MultiSpectral Instrument (MSI) Overview. Available online: https://Sentinel.Esa.Int/Web/Sentinel/Technical-Guides/Sentinel-2-Msi/Msi-Instrument (accessed on 20 November 2020).
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s optical high-resolution mission for GMES operational services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Teillet, P.; Barker, J.; Markham, B.; Irish, R.; Fedosejevs, G.; Storey, J. Radiometric cross-calibration of the Landsat-7 ETM+ and Landsat-5 TM sensors based on tandem data sets. Remote Sens. Environ. 2001, 78, 39–54. [Google Scholar] [CrossRef] [Green Version]
- China Center for Resource Satellite Data and Applications. Available online: http://www.Cresda.Com/CN/ (accessed on 15 February 2021).
- Natural Resources Satellite Remote Sensing Cloud Service Platform. Available online: http://www.Sasclouds.Com/Chinese/Home/661 (accessed on 15 February 2021).
- Clewley, D.; Bunting, P.; Shepherd, J.; Gillingham, S.; Flood, N.; Dymond, J.; Lucas, R.; Armston, J.; Moghaddam, M. A Python-Based open source system for geographic object-based image analysis (GEOBIA) utilizing raster attribute tables. Remote Sens. 2014, 6, 6111–6135. [Google Scholar] [CrossRef] [Green Version]
- Wilson, R. Py6S: A Python interface to the 6S radiative transfer model. Comput. Geosci. 2013, 51, 166–171. [Google Scholar] [CrossRef] [Green Version]
- Muchsin, F.; Dirghayu, D.; Prasasti, I.; Rahayu, M.I.; Fibriawati, L.; Pradono, K.A.; Hendayani; Mahatmanto, B. Comparison of atmospheric correction models: FLAASH and 6S code and their impact on vegetation indices (case study: Paddy field in Subang District, West Java). IOP Conf. Series: Earth Environ. Sci. 2019, 280. [Google Scholar] [CrossRef] [Green Version]
- Tan, F. The Research on Radiometric Correction of Remote Sensing Image Combined with Sentinel-2 Data. Master’s Thesis, Wuhan University, Wuhan, China, 2020. (In Chinese with English Abstract). [Google Scholar]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern 1979, 9, 62–66. [Google Scholar] [CrossRef] [Green Version]
- Caselles, V.; García, M.J.L. An alternative simple approach to estimate atmospheric correction in multitemporal studies. Int. J. Remote Sens. 1989, 10, 1127–1134. [Google Scholar] [CrossRef]
- Yin, Z.; Zhang, M.; Yin, J. A method for correction of multitemporal satellite imagery. In Proceedings of the 2011 International Conference on Electronic and Mechanical Engineering and Information Technology Harbin, Heilongjiang, China, 12–14 August 2011. [Google Scholar]
- Wang, Z.; Bovik, A.; Sheikh, H.; Simoncelli, E. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Bovik, A.C.; Lu, L. Why is image quality assessment so difficult? Comput. Sci. 2002, 4, IV-3313–IV-3316. [Google Scholar] [CrossRef] [Green Version]
- Luo, M.R.; Cui, G.; Rigg, B. The development of the CIE 2000 colour-difference formula: CIEDE2000. Color Res. Appl. 2001, 26, 340–350. [Google Scholar] [CrossRef]
- Sharma, G.; Wu, W.; Dalal, E.N. The CIEDE2000 color-difference formula: Implementation notes, supplementary test data, and mathematical observations. Color Res. Appl. 2004, 30, 21–30. [Google Scholar] [CrossRef]
- Rodríguez-Esparragón, D.; Marcello, J.; Gonzalo-Martín, C.; Garcia-Pedrero, A.; Eugenio, F. Assessment of the spectral quality of fused images using the CIEDE2000 distance. Computing 2018, 100, 1175–1188. [Google Scholar] [CrossRef]
- Wiskott, L. Slow Feature Analysis. Encycl. Comput. Neurosci. 2014, 1, 1–2. [Google Scholar] [CrossRef]
- Du, B.; Ru, L.; Wu, C.; Zhang, L. Unsupervised deep slow feature analysis for change detection in multi-temporal remote sensing images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9976–9992. [Google Scholar] [CrossRef] [Green Version]
- Chai, D.; Newsam, S.; Zhang, H.K.; Qiu, Y.; Huang, J. Cloud and cloud shadow detection in Landsat imagery based on deep convolutional neural networks. Remote Sens. Environ. 2019, 225, 307–316. [Google Scholar] [CrossRef]
- Lin, C.-H.; Lin, B.-Y.; Lee, K.-Y.; Chen, Y.-C. Radiometric normalization and cloud detection of optical satellite images using invariant pixels. ISPRS J. Photogramm. Remote Sens. 2015, 106, 107–117. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, S.; Woodcock, C.E. Improvement and expansion of the Fmask algorithm: Cloud, cloud shadow, and snow detection for Landsats 4–7, 8, and Sentinel 2 images. Remote Sens. Environ. 2015, 159, 269–277. [Google Scholar] [CrossRef]
- Niu, Y.; Zhang, Y.; Li, Y. Influence on spectral band selection for satellite optical remote sensor. Spacecr. Recovery Remote Sens. 2004, 25, 29–35, (In Chinese with English Abstract). [Google Scholar]
- Goetz, A.F.; Vane, G.; Solomon, J.E.; Rock, B.N. Imaging spectrometry for earth remote sensing. Science 1985, 228, 1147–1153. [Google Scholar] [CrossRef]
- Peiman, R. Pre-classification and post-classification change-detection techniques to monitor land-cover and land-use change using multi-temporal Landsat imagery: A case study on Pisa Province in Italy. Int. J. Remote Sens. 2011, 32, 4365–4381. [Google Scholar] [CrossRef]
- DeFries, R.S.; Townshend, J.R.G. NDVI-derived land cover classifications at a global scale. Int. J. Remote Sens. 1994, 15, 3567–3586. [Google Scholar] [CrossRef]
- Sun, G.; Huang, H.; Weng, Q.; Zhang, A.; Jia, X.; Ren, J.; Sun, L.; Chen, X. Combinational shadow index for building shadow extraction in urban areas from Sentinel-2A MSI imagery. Int. J. Appl. Earth Obs. Geoinf. 2019, 78, 53–65. [Google Scholar] [CrossRef]
- Wang, Y.; Li, M. Urban impervious surface detection from remote sensing images: A review of the methods and challenges. IEEE Geosci. Remote Sens. Mag. 2019, 7, 64–93. [Google Scholar] [CrossRef]
- Denaro, L.G.; Lin, C.H. Nonlinear relative radiometric normalization for Landsat 7 and Landsat 8 imagery. IEEE Int. Geosci. Remote. Sens. Symp. (IGARSS) 2019, 1, 1967–1969. [Google Scholar] [CrossRef]




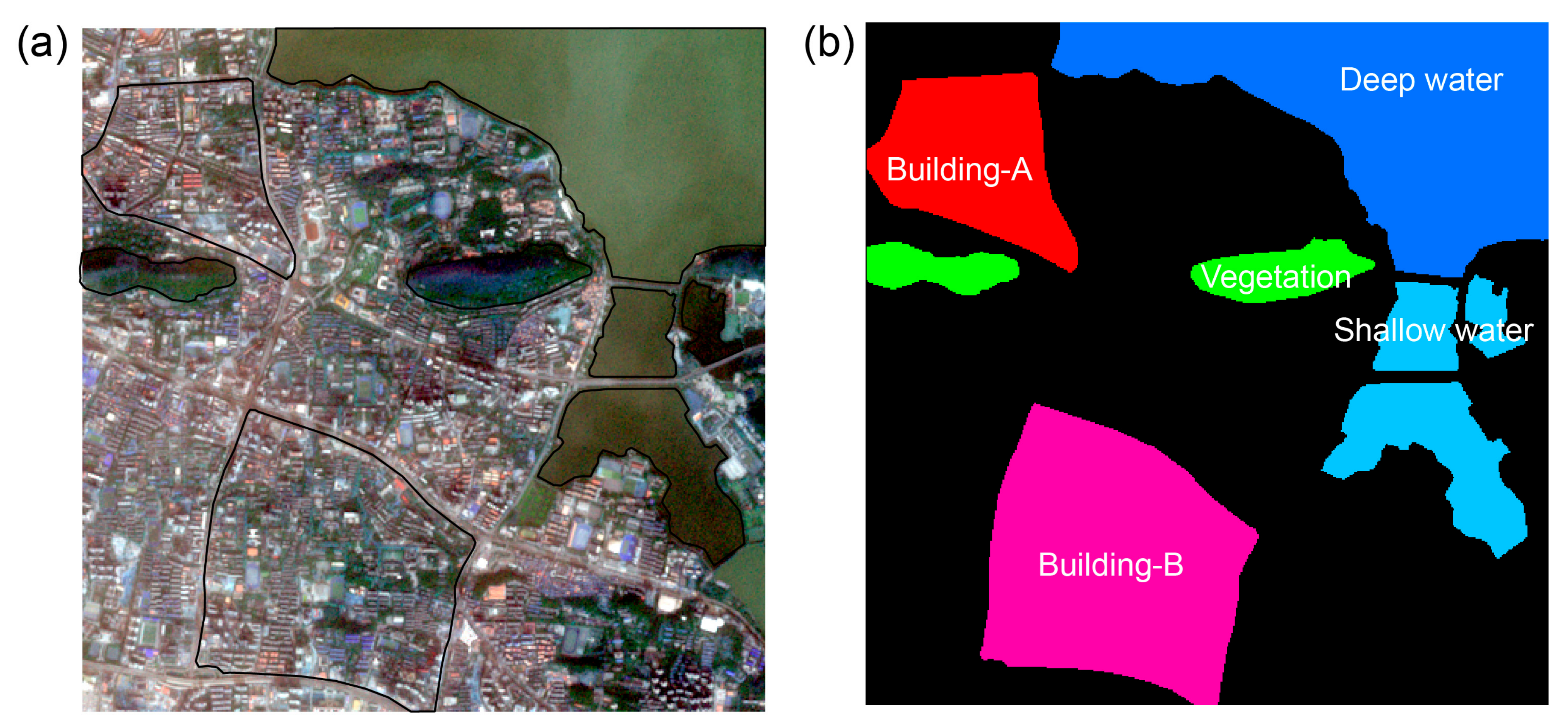
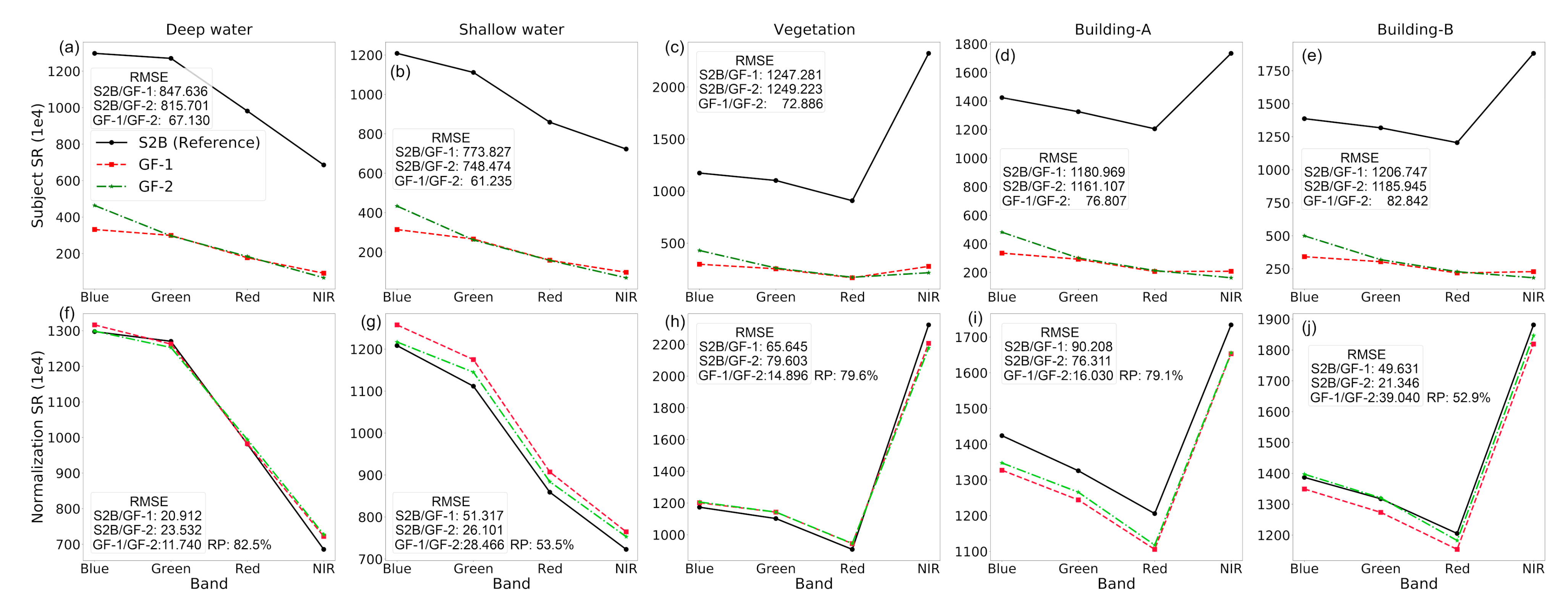

| S2A | S2B | ||||
|---|---|---|---|---|---|
| Band | Central Wavelength (nm) | Bandwidth (nm) | Central Wavelength (nm) | Bandwidth (nm) | Spatial Resolution (m) |
| B1 | 442.7 | 21 | 442.3 | 21 | 60 |
| B2 | 492.4 | 66 | 492.1 | 66 | 10 |
| B3 | 559.8 | 36 | 559.0 | 36 | 10 |
| B4 | 664.6 | 31 | 665.0 | 31 | 10 |
| B5 | 704.1 | 15 | 703.8 | 16 | 20 |
| B6 | 740.5 | 15 | 739.1 | 15 | 20 |
| B7 | 782.8 | 20 | 779.7 | 20 | 20 |
| B8 | 832.8 | 106 | 833.0 | 106 | 10 |
| B8a | 864.7 | 21 | 864.0 | 22 | 20 |
| B9 | 945.1 | 20 | 943.2 | 21 | 60 |
| B10 | 1373.5 | 31 | 1376.9 | 30 | 60 |
| B11 | 1613.7 | 91 | 1610.4 | 94 | 20 |
| B12 | 2202.4 | 175 | 2185.7 | 185 | 20 |
| Satellite Sensor | Blue (nm) | Green (nm) | Red (nm) | Near-Infrared (nm) | Spatial Resolution (m) | Revisit Time (Day) |
|---|---|---|---|---|---|---|
| GF-1 PMS2 | 450–520 | 520–590 | 630–690 | 770–890 | 8 | 3–5 |
| GF-2 PMS1 | 450–520 | 520–590 | 630–690 | 770–890 | 4 | 5 |
| Satellite Sensor | Blue | Green | Red | NIR | ||||
|---|---|---|---|---|---|---|---|---|
| Gain | Bias | Gain | Bias | Gain | Bias | Gain | Bias | |
| GF-1 PMS2 | 0.1490 | 0 | 0.1328 | 0 | 0.1311 | 0 | 0.1217 | 0 |
| GF-2 PMS1 | 0.1453 | 0 | 0.1826 | 0 | 0.1727 | 0 | 0.1908 | 0 |
| Satellite Images | Geography Offset | Spatial Resolution (m) | Acquisitions Date | Image Size | |
|---|---|---|---|---|---|
| Reference | S2B | 2.6 m | 10 | 12/06/2019 | 450 × 450 |
| S2A | 2.6 m | 10 | 12/11/2019 | 450 × 450 | |
| Subject | GF-1 | 3.8 m | 10 | 12/11/2019 | 450 × 450 |
| GF-2 | 3.3 m | 10 | 12/02/2019 | 450 × 450 | |
| Reference | Band | Five Change-Detection Methods Mean Value | ||
|---|---|---|---|---|
| RMSE | SAC | SSIM | ||
| S2B | Blue | 92.451 | 0.9976 | 0.3964 |
| Green | 101.721 | 0.9968 | 0.3952 | |
| Red | 147.805 | 0.9913 | 0.4181 | |
| NIR | 353.739 | 0.9782 | 0.3358 | |
| GF-1 | Blue | 824.447 | 0.9971 | 0.0628 |
| Green | 810.102 | 0.9930 | 0.0779 | |
| Red | 792.677 | 0.9865 | 0.0533 | |
| NIR | 1255.810 | 0.9785 | 0.0245 | |
| GF-2 | Blue | 715.083 | 0.9977 | 0.1438 |
| Green | 798.030 | 0.9960 | 0.0845 | |
| Red | 815.662 | 0.9904 | 0.0573 | |
| NIR | 1335.977 | 0.9773 | 0.0143 | |
| Satellites | Band | RMSE | SAC | SSIM | ||||
|---|---|---|---|---|---|---|---|---|
| Before | After | Rates | Before | After | Before | After | ||
| GF-1 | Blue | 1035.675 | 97.562 | 90.58% | 0.9979 | 0.9977 | 0.5630 | 0.9977 |
| Green | 1007.617 | 99.335 | 90.15% | 0.9968 | 0.9969 | 0.5498 | 0.9970 | |
| Red | 965.953 | 134.187 | 86.11% | 0.9942 | 0.9943 | 0.5128 | 0.9950 | |
| NIR | 1541.707 | 178.702 | 88.41% | 0.9951 | 0.9950 | 0.3806 | 0.9924 | |
| GF-2 | Blue | 900.479 | 118.529 | 86.84% | 0.9967 | 0.9967 | 0.6862 | 0.9966 |
| Green | 1010.343 | 139.199 | 86.22% | 0.9951 | 0.9948 | 0.5497 | 0.9952 | |
| Red | 969.920 | 185.729 | 80.85% | 0.9894 | 0.9889 | 0.5127 | 0.9909 | |
| NIR | 1594.127 | 315.005 | 80.24% | 0.9838 | 0.9844 | 0.3364 | 0.9766 | |
| Ground Features | Satellites | DE | ||
|---|---|---|---|---|
| Before | After | Difference | ||
| Deep water | GF-1 | 25.5975 | 19.7521 | 5.8454 |
| GF-2 | 21.6382 | 12.7635 | 8.8747 | |
| Shallow water | GF-1 | 38.7180 | 24.7531 | 13.9649 |
| GF-2 | 29.5386 | 19.4215 | 10.1171 | |
| Vegetation | GF-1 | 54.5283 | 28.5795 | 25.9488 |
| GF-2 | 38.1057 | 28.2407 | 9.8650 | |
| Building-A | GF-1 | 49.7646 | 45.6616 | 4.1030 |
| GF-2 | 50.4641 | 45.4170 | 5.0471 | |
| Building-B | GF-1 | 48.6006 | 39.4771 | 9.1235 |
| GF-2 | 49.0103 | 47.9965 | 1.0138 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, L.; Yang, J.; Zhang, Y.; Zhao, A.; Li, X. Radiometric Normalization for Cross-Sensor Optical Gaofen Images with Change Detection and Chi-Square Test. Remote Sens. 2021, 13, 3125. https://doi.org/10.3390/rs13163125
Yan L, Yang J, Zhang Y, Zhao A, Li X. Radiometric Normalization for Cross-Sensor Optical Gaofen Images with Change Detection and Chi-Square Test. Remote Sensing. 2021; 13(16):3125. https://doi.org/10.3390/rs13163125
Chicago/Turabian StyleYan, Li, Jianbing Yang, Yi Zhang, Anqi Zhao, and Xi Li. 2021. "Radiometric Normalization for Cross-Sensor Optical Gaofen Images with Change Detection and Chi-Square Test" Remote Sensing 13, no. 16: 3125. https://doi.org/10.3390/rs13163125
APA StyleYan, L., Yang, J., Zhang, Y., Zhao, A., & Li, X. (2021). Radiometric Normalization for Cross-Sensor Optical Gaofen Images with Change Detection and Chi-Square Test. Remote Sensing, 13(16), 3125. https://doi.org/10.3390/rs13163125