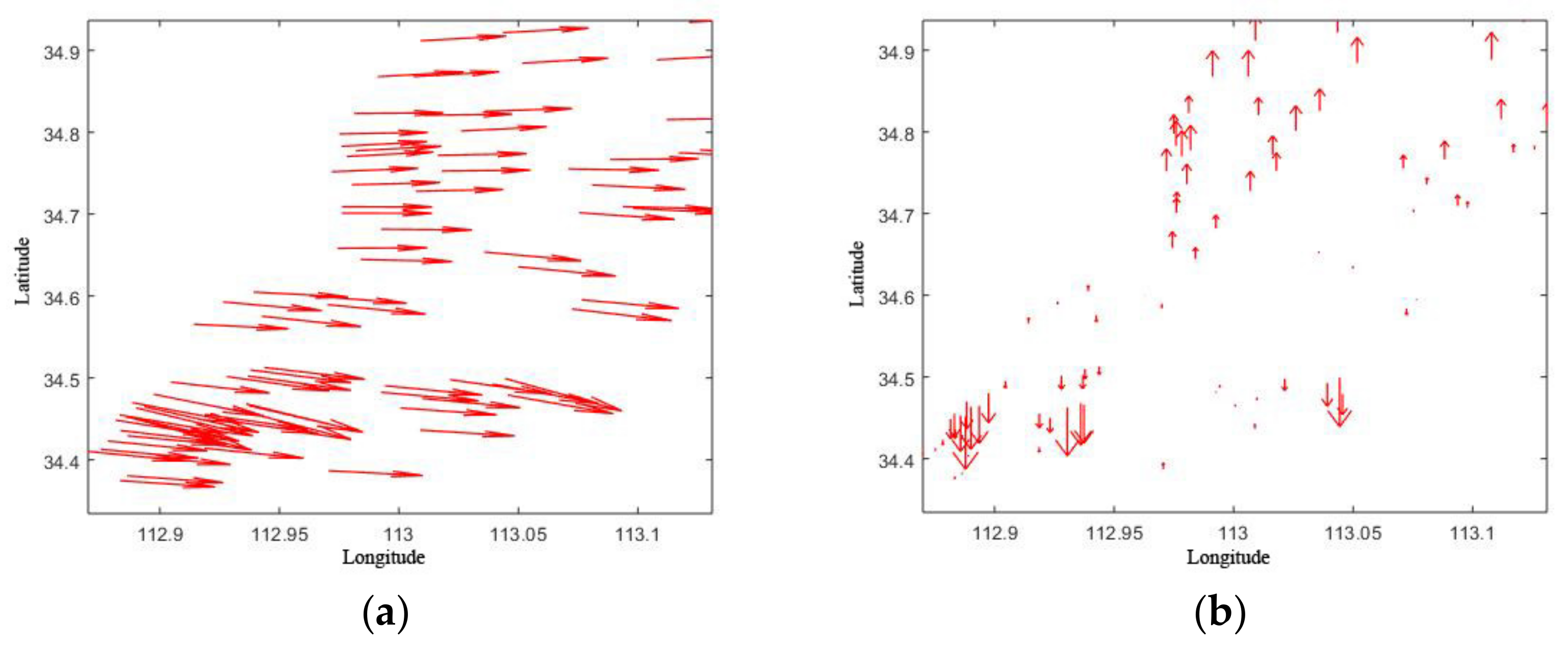
1. Introduction
Optical satellites are an important means for global and regional remote sensing, surveying, and mapping. The larger the imaging swath of satellite-borne sensors, the higher the imagery overlapping ratio and the shorter the satellite revisiting period. However, due to limitations of the sensor manufacturing level, obtaining high-resolution imagery with a large field view can be difficult using a single imaging chip. The satellite payload development department combines several small optical imaging chips, such as the linear charge couple device (CCD), complementary metal-oxide-semiconductor (CMOS), and time delay integration CCD (TDI CCD), into a larger spliced chip in order to image a larger ground area in one shot. Currently, the use of spliced satellite optical cameras has become mainstream. For example, IKONOS, WorldView-2, and Pleiades 1A/1B satellites are all equipped with such types of cameras. The stitching accuracy of this camera type is a critical factor and should be carefully considered during the engineering design. However, due to the influence of the processing technology and various factors in satellite on-orbit operations, the camera’s actual stitching accuracy often decreases, directly degrading the subsequent image product accuracy. When the image resolution is low and the image geometric positioning accuracy is ordinary, the influence of stitching errors is not obvious. However, due to improvements in remote sensing technology, the spatial resolution of numerous stereo optical surveying and mapping cameras (e.g., Gaofen-7 and Gaofen-14) has reached sub-meter level. This means that the impact of mosaic errors can no longer be ignored. Moreover, subsequent data processing necessitates stricter requirements on the stitching precision, making it more difficult and costly in actual satellite projects, which has become the main bottleneck of current remote sensing technology.
Geometric calibration of the satellite images is crucial in guaranteeing high image geometric quality and positioning accuracy. A number of studies have been conducted to improve satellite image geometric calibration. Jacobsen [
1] adopted 15 additional parameters in a series of on-orbit geometric calibration investigations for the Indian IRS-1C satellite. For the German MOMS-2P camera, optimization and refinement for geometric calibration parameters were achieved through the self-calibration block adjustment technique with additional parameters [
2]. The French Space Agency performed static and dynamic parameter geometric calibration on the SPOT-5 satellite camera and achieved high positioning precision with worldwide distributed field calibration sites [
3]. The IKONOS satellite achieved the 12 m planar positioning accuracy and 10 m vertical positioning accuracy by refining the camera geometric parameters [
4,
5]. Detailed studies were also conducted on OrbView-3′s geometric model and geometric calibration process [
6,
7]. Satisfactory geometric positioning was achieved for the Japanese ALOS/PRISM camera by on-orbit geometric calibration with multiple field calibration sites [
8,
9,
10]. A detailed description was given for the PRISM sensor geometric calibration work over the first 2.5 years of on-orbit operations, and the generated DSM accuracies were consistent with sensor configurations [
11].
Zhang Yan and Wang Tao made thorough investigations into self-calibration block adjustment for Mapping Satellite-1 (TH-1) three-linear CCD images [
12,
13]. Their experimental results showed that after self-calibration, the direct geopositioning accuracy of TH-1 is greatly enhanced, and scare controls can help realize high-accuracy geopositioning for island imagery. The uncontrolled positioning accuracy of TH-1 satellite images was improved from 170 m to 11.8 m by utilizing the Equivalent Frame Photo geometric calibration model [
14]. The stereo intersection constraint of the ZY-3 three-line CCD optical camera can reduce the dense planar dependence and vertical dependence during the geometric calibration process [
15]. The principle of on-orbit calibration and production processes for the ZY-3 sensor was also fully investigated [
16]. The study showed that ZY-3 could be used to generate cartographic maps at the 1:50,000 scale and for revisions and updates of 1:25,000 scale maps after geometric calibration. A geometric calibration method has been proposed utilizing the corresponding elevation constraints between two overlapped images and sparse ground control points (GCPs). The results showed that geometric calibration of XY-3 nadir images could be achieved without calibration sites [
17]. A piece point with a weight polynomial trajectory model was proposed for ZY-3 sensor geometric calibration. The experimental results proved that the model could reduce the correlation of the parameters and improve the solved accuracy [
18]. While these geometric calibration methods have achieved remarkable progress, all the investigations used stitched satellite images, which means that the geometric relationship between the original multi-chip images had not been considered in the geometric calibration process.
This knowledge gap can result in image accuracy loss in image positioning and subsequent data products. Studies on SPOT 5, QuickBird, ALOS/PRISM, and other satellite images have confirmed the existence of residual systematic errors in the ALOS/PRISM image positioning results [
19,
20]. They found that low accuracy in multi-chip stitching decreases the accuracy of the generated DEM for IKONOS stereo pairs [
21]. Only the sub-pixel level stitching of multi-chip images can guarantee the accuracy of DEM production [
22]. For the Indian IRS-1C satellite panchromatic camera stitched by three linear array CCDs, a simple translation method was used for image mosaic, and its highest accuracy was 0.2–0.5 pixel [
23,
24]. For ZY-3 imagery, Zhang et al. [
25] proposed a geometric calibration method that can correct sensor misalignment angles and CCD array alignment errors. A total of 19 strips of ZY-3 TLC data were used in the geometric calibration process. The results demonstrated that the CCD array alignment errors for the nadir view were greater than for the forward and backward views and could not be neglected. Using the imaging mode of the spliced satellite TDI CCD camera, Tang et al. [
26] carried out a systematic analysis of various factors affecting the horizontal overlap and vertical misalignment between adjacent TDI CCD chips. They then divided the multi-chip mosaic algorithms into image space and ground object space and proposed various mosaic schemes. The image space mosaic algorithm can only realize local stitching and fitting, which destroys the integral geometric imaging relationship. In contrast, the ground object space mosaic algorithm can fully realize the strict geometric mosaic of adjacent chips, with the corresponding points in adjacent chips strictly meeting the same set of ground coordinates. High-precision satellite geometric calibration processing based on the inter-chip geometric relationship can be used to obtain high-precision multi-chip mosaics from the ground object space. The above methods merely deal with the internal distortion errors of each chip independently and fail to consider inter-chip geometry constraints during the geometric calibration process.
To address the current methodological limitations, we put forward a novel geometric calibration method for the spliced satellite optical cameras based on inter-chip geometry constraints. We first analyzed the imaging characteristics and main error sources of two typical spliced cameras and built an integral rigorous geometric imaging model for spliced satellite cameras. We then proposed an integral geometric calibration model based on inter-chip geometry constraints for spliced satellite cameras, including the corresponding external geometric calibration model and the internal geometric calibration model, and designed the detailed geometric calibration scheme and implementation method. Finally, images of the typical optical butting satellite ZY-3 and mechanical interleaving satellite TH-1 were selected for the experiments.
The rest of this article is organized as follows.
Section 2 discusses the imaging characteristics and main error sources of two typical spliced cameras and presents the integral rigorous geometric imaging model.
Section 3 puts forward the integral geometric calibration model based on inter-chip geometry constraints for spliced satellite cameras and builds the corresponding external and internal geometric calibration models.
Section 4 presents the experiments on the images of the typical optical butting satellite ZY-3 and mechanical interleaving satellite TH-1, and
Section 5 summarizes the study’s conclusions based on detailed analysis.
2. Integral Imaging Model of Spliced Satellite Optical Camera
According to the current stitching scheme, spliced satellite optical cameras can be divided into four categories: optical butting, mechanical interleaving stitching, prism stitching, and special configuration stitching. This paper focuses on optical butting and mechanical interleaving stitching, which are more popular than the other two categories. We first analyze their imaging properties and geometric error characteristics and then establish the integral geometric imaging model for the spliced satellite optical camera.
2.1. Imaging Properties
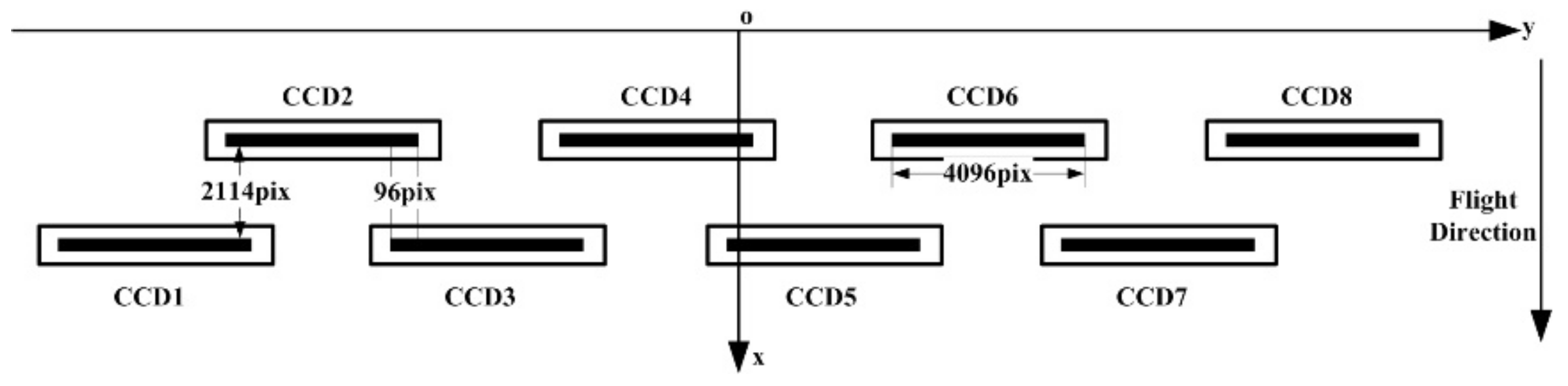
The optical butting scheme arranges multiple chips as an equivalent, long-line CCD array through an optical mirror. Ideally, the misalignment of each chip along the orbit direction is zero allowing the formation of a continuous straight line on the focal plane, which results in few difficulties in the subsequent mosaic process. The main disadvantages of this include light energy reduction and chromatic aberration from prism splitting and limitations of the stitching length due to the prism material and manufacturing technology. One typical example is the three-line array camera in the ZY-3 satellite, whose nadir-view camera is stitched by three TDI CCD chips, and the front-view and backward-view cameras are stitched by four TDI CCD chips, as shown in
Figure 1. Through use of the optical mirror, the optical butting scheme divides the imaging space into the transmission area and the reflectance area, which are separate in space. In the ZY-3 nadir-view camera, TDI CCD chips CCD1 and CCD3 are arranged in the transmission area. TDI CCD chip CCD2 is arranged in the reflectance area. In the ZY-3 front-view and backward-view cameras, TDI CCD chips CCD1 and CCD3 are arranged in the transmission area. TDI CCD chip CCD2 is arranged in the reflectance area in both cameras. The TDI CCD chips in both the transmission area and the reflectance area form an equivalent, long-line CCD array on the focal plane through the optical mirror.
The mechanical interleaving scheme installs multiple CCD, CMOS, or TDI CCD chips into two staggered row configurations on the stitching plate mechanically. The advantage of this is that no additional chromatic aberrations are introduced in imaging, while the disadvantage is that a continuous straight line cannot be formed on the focal plane. The larger the mechanical misalignment, the greater the imaging time delay and the greater the difficulties involved in the subsequent geometric processing. IKONOS, QuickBird, LandSat-8, WorldView-2, French SPOT 6/7, and Chinese TH-1 have all adopted this kind of splicing scheme.
Figure 2 shows the focal plane assembly diagram of a 2 m high-resolution (HR) camera in TH-1, which has eight multi-chip CCDs. In
Figure 2, each chip contains 4096 photosensitive detector units. The number of overlapping units between adjacent CCDs is constant: 96 overlapping units. For example, the number of overlapping units between CCD1 and CCD2 is 96 units, that of CCD2 and CCD3 is also 96 units, and it is the same for CCD3 and CCD4, CCD5 and CCD6, and CCD7 and CCD8. Along the orbit flight direction the staggering misalignment between two rows is 2114 pixels.
2.2. Geometric Error Characteristics
Systematic errors of spliced satellite optical cameras can be categorized as either external or internal. External errors mainly include errors in satellite attitude measurement, satellite position measurement, camera installation angle, GPS antenna eccentricity, and time synchronization. While the camera installation matrix, the star sensor installation matrix, and the GPS antenna eccentricity are all calibrated in the laboratory before launch, these parameters may deviate considerably during on-orbit operations.
Internal errors mainly include lens error and CCD array error. The sources for lens error consist primarily of the principal point offset, focal length deviation, and optical distortions. The CCD array error sources are composed of the CCD array translation, scaling, and rotation. Internal errors for each chip are generally independent of each other.
2.3. Geometric Imaging Model
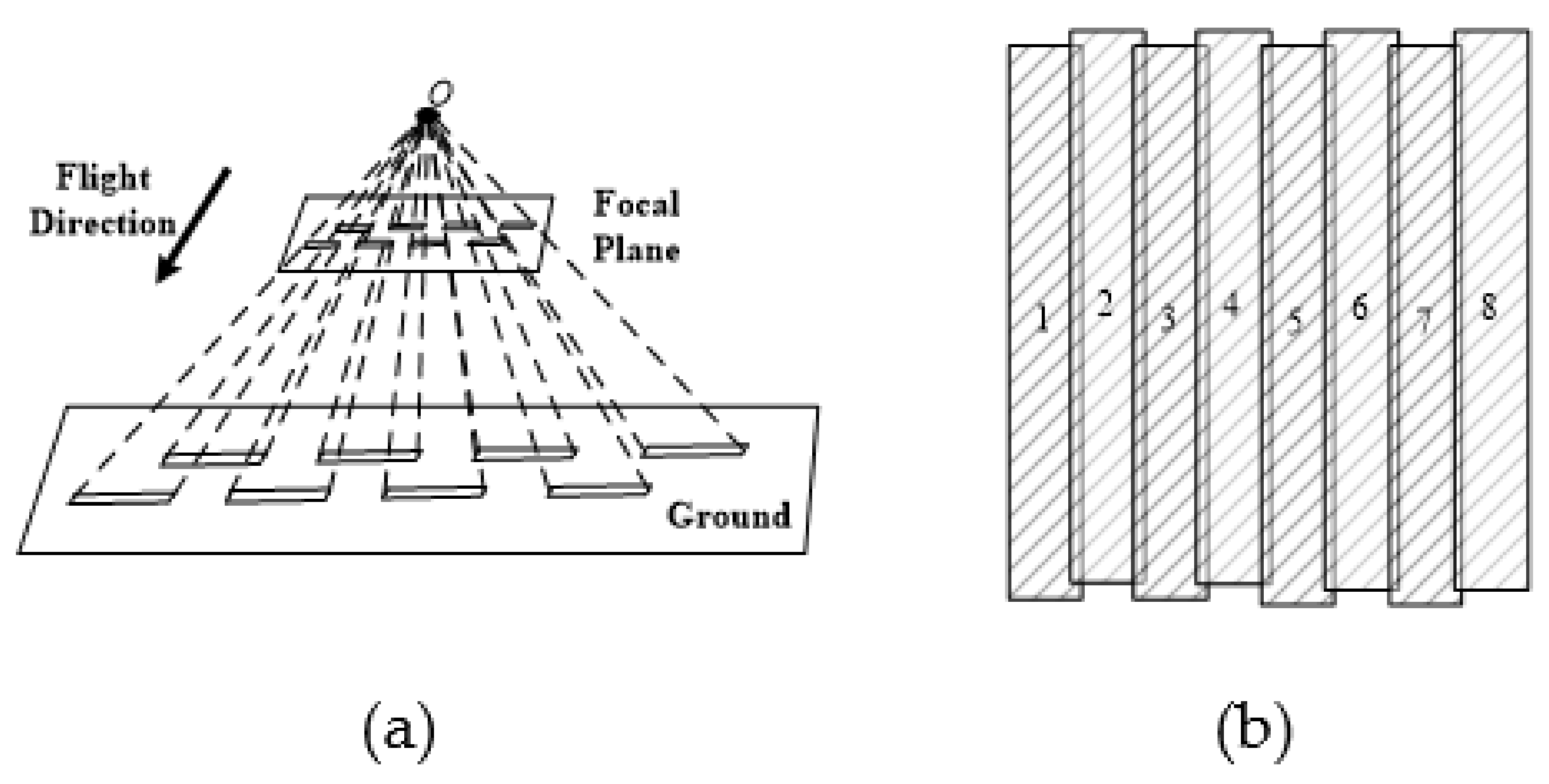
Due to the multi-chip placement position difference on the focal plane, the spliced satellite optical camera does not instantaneously generate a continuous straight line on the ground but instead obtains multiple discontinuous “short scanning lines”, as shown in
Figure 3a. The alignment difference in the discontinuous short scan lines along the orbit flight direction depends on the degree of multi-chip misalignment on the focal plane. Each chip acquires push broom images separately along the satellite platform flight and forms multiple-segmented narrow strip images with certain horizontal overlap and vertical misalignment, as in
Figure 3b.
For the image point
p in the spliced satellite optical image and the ground object point
P(
X,
Y,
Z), the rigorous geometric imaging model is set up as follows: the coordinates of image point
p in the camera system are
:
where
P(
X,
Y,
Z) represents the ground object point coordinates in the WGS84 coordinate system;
indicates the installation matrix from the camera system to the satellite body system, predetermined in the laboratory;
is the rotation matrix from the satellite body system to space conventional inertial system (
J2000) calculated using satellite attitude data;
indicates the rotation matrix from the
J2000 system to the WGS84 coordinate system;
are the GPS antenna phase center coordinates obtained from the satellite position measurement data;
is the image space coordinates represented by the probe pointing angle
. The initial value of
is calculated from the preliminary installation angle of each imaging view and the CCD detector unit size. (
BX,
BY,
BZ) expresses the GPS antenna eccentricity error, which defines the offset vector of the camera projection center relative to the GPS antenna phase center in the satellite body coordinate system. The multi-chip images of the spliced satellite optical camera share one set of satellite orbit and attitude measurement data in a unified camera system. The GPS position and attitude data corresponding to each line in the separate chip can be interpolated from the satellite orbit and attitude data according to the time stamp.
The external geometric calibration is responsible for the accurate determination of the position of the camera’s projection center and the direction of its principal optical axis at the imaging instance. In order to overcome the correlation among the external orientation parameters, the GPS antenna eccentricity (
BX,
BY,
BZ) can be ignored, and its influence is absorbed into the camera alignment angle
, such that
is the pitch angle,
is the roll angle, and
is the yaw angle. The parameters
indicate the misalignment matrix
, as shown in Equation (2).
The misalignment matrix includes systematic errors in the satellite orbit and attitude measurement data, the camera installation angle error, and the GPS antenna eccentricity. The main goal of external geometric calibration is to determine the camera alignment angle .
Absorbing the misalignment matrix
into Equation (1), the rigorous imaging model with the camera alignment angle is obtained as follows
The multi-chip images of the same view correspond to one misalignment matrix. If the camera is a three-line array stereo CCD camera, such as the TH-1 and ZY-3 optical cameras, three groups of are utilized to represent the external error in each view.
Internal geometric calibration aims to determine the geometric sight vector for every detector unit in each chip in the camera system and estimate the camera’s intrinsic errors. This process includes the conversion from image point coordinates in the image system to the spatial coordinates in the camera system.
- (1)
Calculating the chip number
i. According to the column
c of the image point
in the original image system, calculate the point imaged on the
i-th chip using Equation (4), where
n is the total number of chips in different views,
fix indicates the truncating operation, and
Ns is the length of a single chip in detector units.
- (2)
Converting the original image system
o-
rc to the single-chip system
oci-
xciyci. Calculate the image point coordinates (
xci,
yci) in the single-chip system based on chip number, where
ps is the size of the detector unit in millimeters.
In
Figure 4,
oci-
xciyci is the single-chip system in the focal plane. Each single-chip system takes the center of the left detector unit as the origin, the orbit flight direction as the
xci axis, and the scanning direction as the
yci axis.
oc-
xcyczc represents the camera system, and
o-
xy represents the focal plane system.
- (3)
Transforming from the single-chip system
oci-
xciyci to the camera system
oc-
xcyczc. Complete the conversion of the single-chip system to the focal plane system
o-
xy using the placement parameters of each chip in the focal plane, as shown in Equation (6).
Taking the focal length into consideration, the image point coordinates in the camera system can then be determined, which is also the direction of the optical axis.
The optical axis vector
in Equation (7) is consistent with
in the rigorous geometric imaging model (Equation (3)). The optical axis vector can also be normalized into the unit vector
,
,
, as shown in
Figure 4.
The camera internal geometric calibration calibrates the probe pointing angle of each detector unit in the camera system. The internal geometric calibration model can take the physical or general model. Currently, the general probe pointing angle is more widely used in airborne and spaceborne linear array camera calibration [
27,
28,
29]. The general internal geometric calibration model is the cubic or high-order polynomial of the column number
on each chip.
where
c0,
c1,
c2,
c3 are the interior calibration parameters along
x axis for each chip, and
r0,
r1,
r2,
r3 are the interior calibration parameters along
y axis for each chip.
Equations (3) and (8) establish the integral rigorous geometric imaging model for the spliced satellite optical camera. The multi-chip images in each view share the same set of external geometric calibration parameters except for one independent set of interior geometric calibration parameters for various intrinsic errors. The integral rigorous geometric imaging model is the basis for the subsequent external and internal geometric calibration processes.
3. Proposed Integral Geometric Calibration Method Investigation Based on Inter-Chip Geometry Constraints
For a spliced satellite optical camera, the overlapped area of adjacent chips comprises the same ground coverage, which means that one ground point has two corresponding image points in the adjacent overlapped chip area. This supposes that the ground point
P(
X,
Y,
Z) forms image point
p1(
xp1,
yp1) on the left chip and the corresponding image point
p2(
xp2,
yp2) on the right chip. For image points
p1 and
p2, the rigorous geometric imaging models are generated using Equations (9) and (10), where the multiple rotation matrices in Equation (3) can then be combined into Equation (11).
where (
XS1,
YS1,
ZS1) and (
XS2,
YS2,
ZS2) are the GPS antenna centers corresponding to the left and right chips, respectively. Combining Equations (9) and (10), the geometry constraint model between adjacent chips can be constructed, as presented in Equation (12).
The inter-chip geometry constraint model reflects the geometric restricting relationship of the corresponding points in the overlapping chip area. Theoretically, the corresponding image points on the left and right chips coincide on the same ground point. When Equation (12) is met, the corresponding image points on the left and right CCD chips correspond to the same ground point, resulting in seamless stitching of the original multi-chip images and generating continuous and consistent mosaic images without geometric deformation. However, the misalignment error of the adjacent chips, the external error in the imaging process, and the internal error of different chips undermine the geometry constraint (Equation (12)), resulting in geometric mosaic misalignment and reduced positioning accuracy. Therefore, an integral geometric calibration model that considers external and internal errors must be established based on Equation (12). After linearization and expanding the formula using first-order Taylor series, the integral geometric calibration model based on inter-chip geometry constraints is obtained.
where
and
are the camera alignment angles for the left and right chips, respectively, and,
A1 and
A2 are the corresponding coefficient matrices. Since all chips of the forward/nadir/backward view share the same set of attitude observation equipment, all chips in each view take one set of camera alignment angles to describe the external error
.
is obtained from the interior calibration parameters of the left chip and is the image point coordinate error for
on the left chip.
is calculated by the interior calibration parameters of the right chip and is the image point coordinate error of
on the right chip. The interior calibration parameters for each chip differ from each other. Equation (13) can then be simplified to the expression
Equation (14) presents the integral geometric calibration model for spliced satellite optical cameras based on inter-chip geometry constraints proposed in this paper. The geometric calibration operation is performed on spliced optical cameras, which can calibrate the alignment angles and interior calibration parameters for each chip and generate seamless image mosaics and high-precision direct geopositioning. Given the strong correlation between exterior and interior parameters, the external and internal geometric calibration processes need to be implemented separately and iteratively.
The external and internal calibration models can be derived based on the inter-chip geometry constraints. The external calibration model only considers the external errors, i.e., the alignment angles of each view, and assumes the interior calibration parameters to be unchanged. The external geometric calibration model is as follows
where
The alignment angles
can be acquired using least squares or linear optimization algorithms. After determining the external calibration parameters and keeping them fixed, the internal geometric calibration model based on inter-chip geometry constraints is established
If the image point coordinates are represented by the normalized probe pointing angle form, the following model is obtained
where
The two items on the left side of Equation (17) can then be expanded to
Substituting Equations (18) and (19) into Equation (17), the interior calibration parameters for the left chip and for the right chip can be obtained using least squares adjustment. The internal geometric calibration process is accomplished by establishing Equations (17)–(19) for all chips of each view.
An integral geometric calibration implementation scheme for the spliced satellite optical camera can then be developed according to the inter-chip geometry constraints. The workflow diagram is shown in
Figure 5. In order to improve the seamless stitching accuracy for multi-chip images, the internal calibration processing is divided into two steps: conventional processing and refined processing.
Image matching is implemented on each chip and every high-resolution digital orthophoto map (DOM) to automatically obtain DOM GCPs. Image matching is implemented on the multi-chip images to obtain the corresponding image points in the overlap areas of adjacent chips [
27,
28,
30].
- (2)
External geometric calibration process
The integral rigorous geometric imaging model is built following Equation (3). Using the corresponding image points, the external calibration model based on inter-chip geometry constraints is formed following Equation (15). The geometric calibration values of the alignment angles are obtained by linearizing and adjusting these two equations together.
- (3)
Conventional internal geometric calibration processing
The external calibration parameters are statically fixed, and conventional internal geometric calibration is performed using DOM GCPs and the corresponding image points. For DOM GCPs, the linearized internal calibration equations can be obtained from Equation (3). For the corresponding image points, the internal calibration equations are derived from Equation (17). Conventional geometric calibration is implemented, and the interior calibration parameters for each chip are obtained by adjusting these two equations.
- (4)
Refined internal geometric calibration processing
Refined internal geometric calibration is performed by utilizing only corresponding image points to establish the internal calibration error equations based on Equation (17). This step optimizes the interior calibration parameters for each chip and improves the geometric stitching accuracy.
Steps 2 to 4 are repeated iteratively until the generated values for the alignment angles and interior geometric calibration parameters are less than the predefined threshold.