Abstract
This paper proposes the use of terrestrial laser scanning (TLS) measurements together with finite element method (FEM) numerical modeling to assess the current technical condition. The main aim of the paper was to evaluate the effect of point cloud size reduction on the quality of the geometric model and the ability to represent the corrosion level in assessing its load-carrying capacity. In this study, a standard scanning was performed on a historical object and a point cloud of a selected corroded element was generated. In order to further process the data, gradual reductions were made in the number of points from which meshes representing the geometry of the selected beam were created. Inaccuracy analyses of the meshes generated on the reduced point clouds were performed. Numerical analysis was then conducted for the selected mesh generated from the reduced point cloud. The results identified the locations of maximum stresses. The presented analysis showed that by developing the presented measurement and computational technique, laser scanning can be used to determine the degree of corrosion of hard-to-reach steel elements.
1. Introduction
Modern remote sensing is not only oriented at remote acquisition, processing and interpretation of qualitative information about objects, but also focused on the effects and processes occurring on their surfaces. In a combination with computer-aided engineering, it is increasingly applied both in construction design [1] and inventory of existing objects [2]. The process of developing geometric models of new designed structures is widely described in the literature [3], and the first attempts to automatically reproduce the geometry of a building in virtual form took place as early as 1992 using information and communications technology (ICT) tools [4]. However, it is still problematic to prepare models of existing buildings as well as structural elements with adequate mapping accuracy. In previous years, geometric models based on remote sensing data were developed primarily for administrative purposes, spatial analysis of land surfaces and promotion of individuals or entire regions [5]. The rapid development of BIM technology has meant that three-dimensional models have now become the basis for design, cost analysis, management and operation of buildings. In the case of newly designed objects, 3D modeling takes place already at the design stage, but in the case of existing objects, it is necessary to obtain applicable data that allow for accurate representation of the geometry of the objects. One of the methods of collecting such data is 3D scanning, which is widely used in civil engineering. The consequence of the development of 3D scanning technology appears to be the use of these data to conduct advanced strength analysis, taking into account the interactions between the various structural elements. It should be noted that the complexity of the analyzed structures goes far beyond the isolated structural elements. Analyses with nonlinear material characteristics, large deformations or explicit dynamics are becoming standard when working on complex projects.
There have been studies that analyzed data acquisition methods in terms of automation of identification processes of structural elements and indicated the high quality of laser scanning data [6,7]. In parallel, point cloud reduction methods are being developed to improve performance of hardware and save storage space [8]. Analogically, the increase in demand for large-scale analyses of structures—often historic structures—has been imprinted in recent years on the development of remote sensing practices themselves. Conducting modern surveys increasingly compels surveyors to use computer algorithms. There are already known applications of neural networks in estimating errors of a surface model described with shape functions [9].
Due to its high resolution, a point cloud obtained by 3D scanning is in itself a good set of data describing the mutual position of elements, an example of which would be Figure 1. Essentially, laser scanning enables the acquisition of data on the shape of the object under measurement. The device uses the phenomenon of electromagnetic waves to determine the distance of a given point from the measuring sensor. The position of the point is described in an assumed coordinate system. The result of the survey work is a group of points representing a quasicontinuous model of the surface in the form of a so-called point cloud.

Figure 1.
Example of TLS data usage: (a) AGH University of Science and Technology building point cloud; (b) conversion to an architectural drawing.
The widespread use of laser scanning has been made possible by the parallel development of different measurement methods. Four leading methods of data collection can be distinguished:
- Terrestrial laser scanning (TLS) is a method using ground-based equipment. The scanner usually performs an even rotation around two perpendicular axes. Using a laser for a few to tens of minutes acquires up to several hundred million points. The resulting point cloud is presented in grayscale (intensity of beam reflection) or with assigned real colors. Due to the size and price of the service, TLS is widely used not only in the sciences involved in engineering, but also in art, history and forestry [10].
- Airborne laser scanning (ALS) is the idea can be summed up by the principle of laser distance measurement from the deck of a flying craft, such as an airplane, a helicopter or, more recently, a drone. The measurement system works with GPS to determine the position of the machine in space. Additionally, the position of the measurement platform is monitored by the inertial navigation system (INS). As a result of the measurement, a spatial model of the surface is generated [11].
- Mobile laser scanning (MLS) is a method that brings a measuring device on board a vehicle. A car, truck or train can be adapted to MLS. There are also systems carried by humans. This type of measurement allows for efficient reconstruction of the interiors of industrial halls, urban layout of a city, landscape, facades of buildings or the arrangement and assessment of the condition of roads and rails [12].
- Satellite laser scanning (SLS) is the first satellite working in the Geoscience Laser Altimeter System program was ICESat. The device works from orbit, about 600 km from the surface of the earth. The beam diameter falling on the ground is about 70 m. The spacing of the research grid is about 172 m. The satellite began its work with a view to observing polar regions [13].
The characteristics of the data generated allow the analysis of objects that are geometrically complex [14]. However, because of the size of data files and the associated hardware requirements, handling such files becomes burdensome and impractical. An interdisciplinary research problem is to try to automate the processing of point cloud data without loss of quality. This can be of great importance in the case of analyses whose aim is to assess the current technical condition of structural objects with particular emphasis on the stress level of structural elements [15].
Construction diagnostics are increasingly turning to sophisticated reverse engineering tools [16]. From the perspective of geometric model development, the method of acquiring data about the existing structure is highly important. The designer at an early stage of preparing the opinion must decide on the precision of the geometric model and at the same time the required accuracy of the TLS data, an example of which is shown in Figure 2. The basic division indicates the possibility of using linear, surface or volumetric elements. In case of the existing structure, which is repeatedly exposed to long-term, time-varying loads, each time the potential influence of imperfections on the expected calculation result has to be assessed. Lack of such analyses may lead to construction failure [17,18]. Therefore, it is necessary to make compromise assumptions as to the accuracy of data acquisition methods used in the light of their subsequent use in technical analysis.
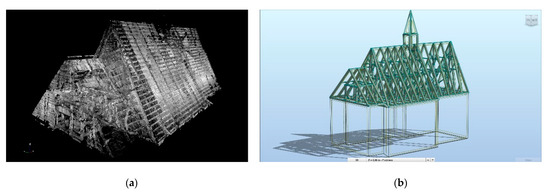
Figure 2.
Example of using TLS data: (a) point cloud of a wooden roof truss; (b) conversion to a geometric numerical model.
Issue such as TLS in diagnostic studies of various historic structures at both the detail scale [6] and large-scale wooden objects [19], masonry such as walls [20] or pillars [21] and determination of bridge displacements under load [22] has been already discussed in the literature. On a laboratory level, preliminary testing of post-fire concrete elements [23] or moisture in masonry elements [24] seems interesting.
In the field of structural steel diagnosis, we can identify two main factors that influence the assessment of the current load-bearing capacity: the level of corrosion and geometric imperfections [25]. The aim of this paper is to present the possibilities of using remote sensing data from laser scanning for numerical analyses. Selected structural elements of a historic steel object were tested in terms of assessing its current load capacity and the influence of successive point reduction and meshing processes on the accuracy of the mapped geometry, and thus on the results of calculations of its load capacity.
2. Materials and Methods
2.1. Analyzed Object
Due to the presented research problem and the size of the analyzed object, the authors decided to use the TLS method of remote sensing data acquisition. In this study, a historic site that is part of the Jan Pazdura “EKOMUZEUM” located in Starachowice, Poland, was analyzed. The object of interest was the steel frame structure of the blast furnace. Its height is about 18 m. At the time of construction, it had a capacity of 180 m3, but after modifications in 1922–1931, its capacity was increased to 250 m3. The outline of the furnace can be described using two cones. The bottom cone, or pit, is supported by the pot, which is supported by the frame. The space at the common base has a diameter of 5 m, and it is the widest part of the blast furnace. In the higher part, called the throat, which ends in the charging plane, there is a system whose task was to charge the blast furnace charge (ore, coke, fluxes, limestone). Within the widest part of the blast furnace, box coolers were built. The upper edge of the brick-lined furnace rim is finished with a charging pan with a Langen-type charging device. The object is equipped with an internal lift mounted outside the contour of the structure, leading to the upper platform. The steel structure from the level of the furnace foundation to the first working level consists of six steel columns of closed rectangular cross-section topped with a steel “circular” beam of rectangular cross-section. Steel brackets supporting the circular beam are attached to the columns. The footings of the steel columns are set at an angle in the foundation and have connections between them in the form of tie rods made of flat bars. The supporting structure of the platforms includes four pillars made of pipes RO 700 × 10 mm, to which the main beams of technological platforms in the form of hot-rolled sections and plate girders are attached at the corner joints. The columns have external cross bracing made of steel rods passing through two levels. The overview is presented in Figure 3a.

Figure 3.
Steel structure of the blast furnace in Starachowice: (a) location of the analyzed beam; (b) view of the test site; (c) point cloud of the whole structure; (d) clipped point cloud of the analyzed beam.
2.2. Terrestrial Laser Scanning
One of the beams supporting the basic working level was selected for testing. The beam is marked with a red circle in Figure 3a. On the basis of historical data and macroscopic observations, it was determined that the section used for the beam corresponds to the present rolled profile IPN 400. A FARO Focus S150 scanner was used in the data acquisition process. The obtained point clouds of the analyzed object and the tested beam are presented in Figure 3c,d.
Due to the need to demonstrate the technical feasibility of using the TLS method to acquire an adequate amount of remote sensing data, the work carried out attempted to reflect the conditions of standard measurements as accurately as possible. However, it should be emphasized that access to the selected structural element was significantly limited. The number of structural elements and the platform and their arrangement necessitated performing 10 high-resolution scans with the device. Each scanning position was approximately 3.0 m from the selected element; the distance between scanning positions was approximately 1.0 m. All scans were made from the ground level. No additional structures (such as scaffolding or ladder) were used to reach the covered elements. In order to support the automatic process of joining the individual scans, monochromatic markers supplied by the software manufacturer were placed on the element and other objects in the measurement field (Figure 3b).
2.3. Ultrasonic Corrosion Testing
In order to verify the obtained results of the analysis, additional in situ tests of the corrosion progression were performed using an ultrasonic thickness gauge SONATEST type T-GAGE V DLW equipped with a DK-537 head (Figure 4). According to the test procedure, the device was calibrated on a VW-ML calibration tile. The result of the test was the actual thickness of the profile wall. The coupling medium included in the kit was used, and the test surface itself was prepared by grinding off the existing corrosion products. Ultrasonic measurement of the thickness of the walls of the tested steel element was carried out using the echo method. Standard PN-EN-14127 “Non-destructive testing—Ultrasonic thickness measurements” [26] was adopted as the basic procedure. For the assessment of corrosion by this method building documentation is needed. By comparing the measured profile thickness with the profile producer′s data, the degree of corrosion was obtained.

Figure 4.
Corrosion tests of steel elements of the blast furnace.
2.4. Processing
Conducted laser scanning made it possible to obtain data that represent the object in normal conditions of work with point clouds. Current experience with such data characteristics indicates that it is necessary to use mostly programs supplied by manufacturers of equipment in the basic scope, sometimes enriched with minor additional programs (often under a free license). For the merging of individual measurements, the program FARO Scene 2018 was used. The algorithm merged the point cloud automatically using the cloud-to-cloud method, with subsampling of 50 mm. The merging process used instruments built into the scanner in the form of an inclinometer and a compass. Additionally, an automatic algorithm was used to detect monochromatic markers stuck on the object. In order to perform a detailed analysis of the selected structural element, a part containing points of the analyzed beam with a length of 1.3 m was cut out of the point cloud (ClippingBox).
The separated dataset containing geometric information of the analyzed element was reduced in CloudCompare software. The method of minimum distance between points was used. The points from the separated data set (point cloud) were reduced in successive steps so that the distance between them was at least 1, 2.5, 5, 7.5, 10, 12.5 and 15 mm.
The next step in data processing was to mesh the reduced point clouds for each level of reduction. For this purpose, the Mesh module of VG Studio MAX 3.4 was used. The meshing process was performed automatically, and the mesh continuity option was chosen as the size parameter of a single triangular element. Geometric representations of the analyzed steel beam prepared in this way were the basis for further strength analysis and evaluation of their corrosion level. A schematic is shown in Figure 5.
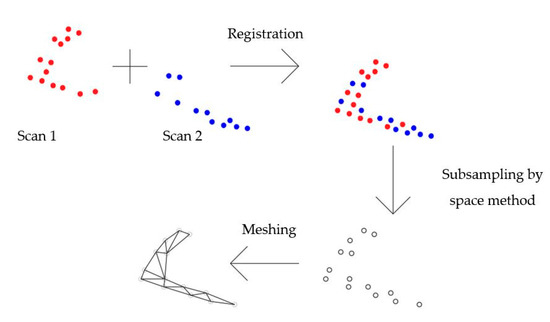
Figure 5.
Data processing scheme.
2.5. FEM
Modern numerical methods require the input of a geometric model into the computational environment. Sources point out the widespread use of point cloud to represent the geometry of chambers in mines [27] and laboratory testing of beam deformation [28]. A similar workflow to that proposed by the authors is observed. The individual scans are combined, the number of points is reduced and the meshing process and visual inspection follow.
Two 1.3 m long beam models were prepared for this test. The geometry of the first beam was based on an IPN 400 simple extrude (CAD model). The second beam was described by a mesh geometry generated on a point cloud. Standard 3D finite elements (tetrahedron) with sides to be determined in the course of analysis were used. Due to the curvature of the planes connecting the web to the flanges, a parabolic interpolation was used in the section-based model. Young′s modulus of 210 GPa was applied. It was assumed that both beams were supported by a 20 mm wide plane. Displacement in dX, dY and dZ directions and rotations rZ and rX were blocked. A distributed load of 25 kN over a length of 100 mm was assigned at the center of the span. A schematic of the numerical model is shown in Figure 6. It is important to point out the problem of load assignability for a model based on a reduced triangle mesh. In the case of geometry based on simple extraction (CAD model), the indication of support or load ranges is a directly applicable task. In the case of mesh-based geometry, it must be taken into account that the triangular elements in the developed model do not align in a single plane, and that the introduction of straights to explicitly describe the boundary conditions requires changes at the stage of building the entire geometry.
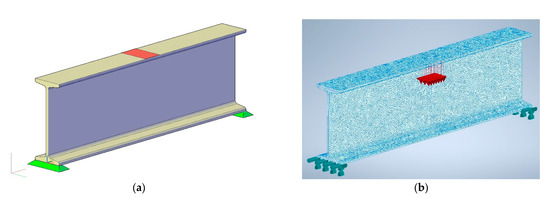
Figure 6.
Models of the analyzed beam: (a) 3D CAD model; (b) 3D FEM model.
Therefore, a code was developed to load the beam using a gradient function on the boundary triangles. The end result was a load whose equivalent concentrated force was placed at the same location as the CAD profile loads. The fields of influence were equal in magnitude.
3. Results
3.1. Corrosion Degree Measurement
The study resulted in measurements of the actual thickness of the individual sections of the analyzed beam. The results are presented in Table 1 and compared with the catalog section dimensions. On this basis, a higher level of corrosion loss was found in the bottom flange (11.94%) in relation to the web (6.53%) of the tested beam. This is probably due to the flow of water along the web to the bottom flange and the accumulation of water on its surface, which acts destructively in the long time perspective.

Table 1.
Comparison of point cloud mesh to CAD model—cumulated absolute.
3.2. Process Results
The processing resulted in meshes with varying numbers of points and triangular elements. The output value generated from TLS was over 15 million points, for which meshing resulted in over 5 million triangular elements. For the maximum point cloud reduction considered (15.0 mm), slightly less than 7000 points and over 13,000 triangles were obtained. Geometric deviation analysis was performed on all meshes. Information on the size reduction and the number of triangles of the obtained mesh is presented in Table 2.

Table 2.
Processing result.
3.3. Nominal Mesh Analysis
The main objective of the analysis was to determine the effect of point cloud reduction on the quality of the subsequent mesh of the represented beam element and to evaluate its load capacity compared to a simple CAD model using the finite element method. A three-dimensional CAD model was generated using the simple extrude tool. The same model was also used for the FEM numerical simulation. Due to the lack of access to the top flange and part of the bottom flange, the nominal mesh created during the automation process had discontinuities. Figure 7a shows the results of comparison of the nominal mesh in the selected cross-section to the CAD model of the section. The analysis was performed on the entire 3D surface of the element, and the selected cross-section is presented in order to visualize examples of geometric deviations of the nominal mesh from the CAD model. The applied method allowed the selection of any cross-section of the beam. The colored lines in the analyzed cross-section indicate the differences found in the dimensions in relation to the CAD model. The influence of ranging accuracy of applied TLS and possible noise of the raw point cloud should be emphasized. However, the use of high-quality scanning, maximum resolution and a small distance between the stations reduces the influence of these factors on the results. According to the authors of this manuscript, the differences have two reasons. In the process of joining the individual scans, small displacements of the analyzed surfaces (the bottom part of the section) could have occurred, which, among other factors, led to the appearance of a double end of the bottom flange. Additionally, when working with the steel structure of a historical object, the fact of corrosion should be taken into account. The local inspection revealed pitting and delamination, which caused the protective coating applied in the past to swell.
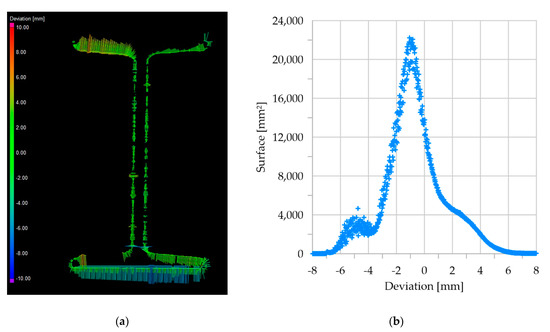
Figure 7.
Results of the comparative analysis of the nominal mesh and the CAD model: (a) graphical visualization in the selected cross-section (cold colors correspond to the reduction in the cross-section compared with the CAD model, warm colors correspond to the expansion of the cross-section with respect to the CAD model); (b) distribution of the deviations of the sum of the areas of the triangular elements for the whole analyzed beam.
Positive values obtained in Figure 7b should be interpreted as the sum of areas of triangular elements where the generated nominal mesh is larger than the CAD model surface (spalling), and negative values should be interpreted as places where the nominal mesh surface is inside the CAD model (pitting corrosion). On both sides of the zero value, an irregular decrease in the value on the graph can be observed, which can be interpreted as corrosion of the analyzed surface.
3.4. Comparative Analysis of Reduced Meshes
Similar comparative analyses were performed for the mesh reduced in the processing. Figure 8 shows an example cross-section of the analyzed beam developed from successive point cloud reductions compared to the CAD model. The first reduction in Figure 8a (space method = 1 mm) led to a slight improvement in the alignment of the meshed model with the CAD model. At the same time, there were local disturbances in places—part of the web and the top flange—where the deviations turned out to be much larger. The model consisted of almost three million small triangular planes. The second reduction (space = 2.5 mm method) reduced the number of mesh elements by almost 12 times compared to the model based on the nominal cloud. The reduction was not followed by a significant change in the course of the planes. In the cross-section of Figure 8c, the reduction of the 5 mm space is visible. There is a noticeable change in the course of the lower surface plane. The shift distance of the defective measurement was smaller than the distance set during the reduction. This resulted in the generation of one bottom flange finial, with the surface being irregular. Significant improvement was observed in the 7.5 and 10 mm space filtering. The planes have adjusted their trajectory to that initially expected. In these cases, it is possible to use the resulting mesh as geometry representation for finite element method. In the next reductions, the problem turned out to be the beam web. Its edges were located in insufficient distance. The course in the meshed model was reduced to a single repeatedly angled surface extending between the actual edges. Distribution of deviations of the sum of the areas of the triangular elements for the whole analyzed beam at mesh reduction compared to the CAD model show Figure 9.
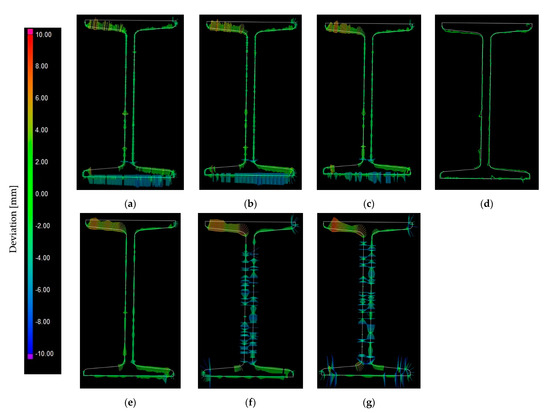
Figure 8.
Results of comparing reduced meshes to a 3D CAD model in a selected section: (a) 1.0 mm; (b) 2.5 mm; (c) 5.0 mm; (d) 7.5 mm; (e) 10.0 mm; (f) 12.5 mm; (g) 15.0 mm.
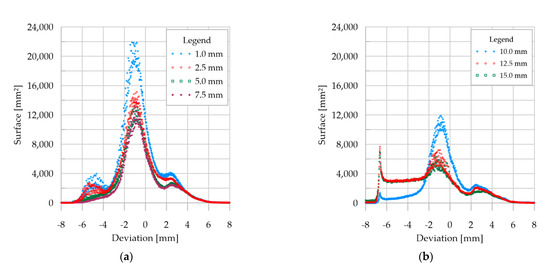
Figure 9.
Distribution of deviations of the sum of the areas of the triangular elements for the whole analyzed beam at mesh reduction compared to the CAD model: (a) 1–7.5 mm; (b) 10–15 mm.
The analysis performed shows the positive effect of using space subsampling when comparing to a CAD model. The first noticeable advantage is the reduction in file size. Working on a smaller number of points allows faster mesh generation, simpler model processing and more efficient use of system resources. In addition, proper selection of the parameter allows reducing misalignment errors created in the process of automatic registration of files from individual measurements. Table 3 show the cumulated absolute distance of the generated mesh to the CAD model for 90%, 95% and 98% convergence. Reducing to 1 and 2.5 mm space had no significant effect on the differences in deviations. Further subsampling of 5 and 7.5 mm space led to a reduction in error and a reduction in dimensional deviations. The results for the second group show additional decreases in accuracy in geometry representation.

Table 3.
Comparison of point cloud mesh to CAD model—cumulated absolute.
In addition to the comparison to the CAD object, the convergence of the mesh formed on the reduced cloud to the mesh formed on the nominal cloud is an important parameter. Figure 10 shows the following comparisons. Visually, the meshes spanned on the reduced point clouds reproduce the original geometry in a accurate way. Similar to the previous comparisons, at the 5 mm space, one can notice the removal of the duplicated bottom shelf finial. Further reductions result in a smoother bottom surface. With 12.5 and 15 mm space, the generated web significantly differs from the initial one.
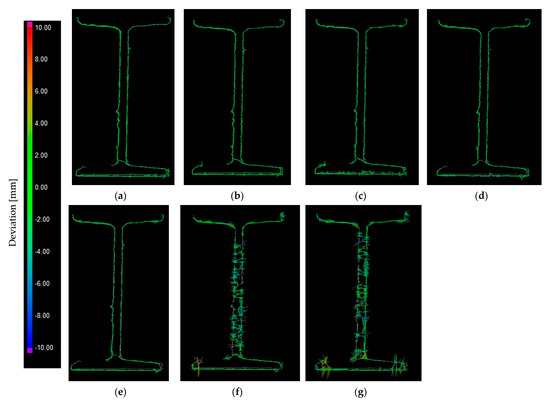
Figure 10.
Results of comparing reduced meshes to nominal mesh in a selected section: (a) 1.0 mm; (b) 2.5 mm; (c) 5.0 mm; (d) 7.5 mm; (e) 10.0 mm; (f) 12.5 mm; (g) 15.0 mm.
A deviation histogram of differences between nominal and reduced mesh is presented in Figure 11. Case 11a shows a low influence of reduction in points by space method on reconstruction accuracy. When the thickness of the thinnest component (in this case, the web) exceeds a certain value, an increase in the number of elements distant by 0.5–4 mm is observed.
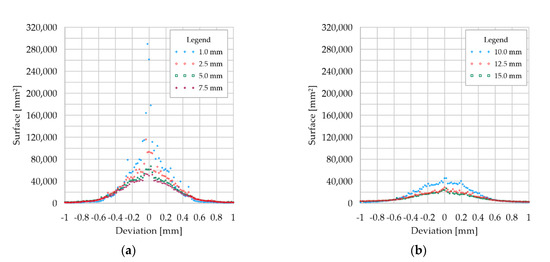
Figure 11.
Distribution of deviations of the sum of the areas of the triangular elements for the whole analyzed beam at mesh reduction compared to the nominal mesh: (a) 1–7.5 mm; (b) 10–15 mm.
Table 4 shows the evolution of the mesh accuracy level compared to the nominal mesh. Up to the 7.5 mm space reduction, 95% of the surfaces are less than 1 mm away from the nominal object. Between reductions of 1 mm space and 7.5 mm space, this value does not change significantly (from the modeling point of view). After the reduction of 10 mm space, a decrease in accuracy is noticeable for 95% of surfaces. The last two reductions cause significant accuracy drops for 90% of the surface. However, the distance of maximum deviation for 98% of the surface increases in a quasilinear manner for all levels of reduction.

Table 4.
Comparison of subsampled point cloud mesh to nominal point cloud mesh—cumulated absolute.
3.5. Using a Reduced Mesh for FEA Calculations
Due to the obtained results of comparative analyses of reduced meshes, numerical calculations were performed for a mesh based on a cloud reduced by the space = 7.5 mm method. The results presented show the stresses according to the Huber–Mises–Hencky yield criterion. The HMH yield criterion has a history of more than 100 years and is widely used in the calibration of FEM models to evaluate the stress level of steel members [29]. The relationship is described by the formula [30]:
The 3D results are presented in the XZ plane. The visualization is based on a distorted mesh with a deformation multiplier of ×1000.
Figure 12 shows a beam for which geometry was based on a section extrude of IPN 400. The stress range was from near 0 to 27.25 MPa. However, the main concentrations were found at the load application point and at the supports. The outline of the stress concentration responsible for the transmission of the vertical force from the center of the span to the supports is captured in the view. The geometric idealization adopted favored the symmetry conditions.

Figure 12.
HMH equivalent stress distribution in the analyzed beam—geometry model based on simple extrude CAD model.
In the case of the second beam, the geometry of which was described by a processed point cloud, the stresses ranged from nearly 0 to 24.5 MPa (Figure 13). In this case, the concentration also occurred at the location of support and force application. As expected, a higher web stress was obtained, the thickness of which was slightly smaller than that of the CAD model because of corrosion processes.

Figure 13.
HMH equivalent stress distribution in the analyzed beam—geometry model based on meshed TLS data and 7.5 mm point cloud reduction.
4. Discussion
The geometric representation of the analyzed beam based on TLS data differs from the prepared 3D CAD model. In the analyzed beam section, especially in the lower and upper flanges, differences on the level of 6.0–8.0 mm were obtained in relation to the CAD model. On the web itself, smaller differences at the level of 1.0 mm were obtained. Globally, the greatest number of triangular elements generated describing the surface of the tested beam are located inside the compared CAD model, which is illustrated by the largest sum of triangular element areas in Figure 7b. Therefore, it can be concluded that the obtained deviation of −1.0 mm is a measure of the average level of corrosion. The irregularity of the graph at a deviation level of 2.0 mm can be interpreted as a summed increase in deviation due to local corrosion effects in the form of spalling. However, it should be emphasized that the significant increase in deviation at −5.0 mm in the analyzed case can be interpreted by an incorrect registration of individual scans. The deviation results obtained from the analysis performed on the TLS data are consistent with the ultrasonic thickness tests performed on the component. The average thickness change of the web was 6.53%, and that of the flanges was 11.94%. It should be noted that the thickness change was 1.0 mm for the web and −2.5 mm for the flanges. Therefore, taking into account the share of individual surfaces of the web and flanges in the total surface of the tested beam, the obtained deviation of nominal grid at the level of –1.0 mm as a measure of the average level of corrosion is consistent with the results of in situ tests.
Comparative analysis of the reduced meshes with the 3D CAD model showed that the point cloud reduction level in the range of 1.0–7.5 mm did not negatively influence the quality of the geometric model, as shown in Figure 14. For the reduction level of 7.5 mm, 90% of all triangular element surfaces are within 3.41 mm of the 3D CAD model surface. Considering the merging error of the bottom flange scans, which was about 2.0 mm, the point cloud reduction performed in the range of 2.5–7.5 mm positively affected the top of the bottom flange by generating a more convergent surface to the CAD model.
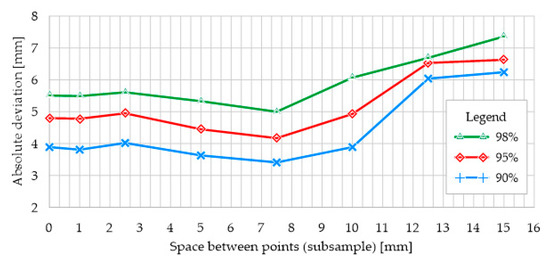
Figure 14.
Comparison of meshes based on TLS data to 3D CAD model. Absolute deviation.
A further increase in point cloud reduction showed an increase in deviation caused mainly by incorrect web surface trajectory.
In the case of comparative analysis of meshes based on reduced point cloud for 90% and 95% of all triangular element surfaces, reduction in the range of 1.0–7.5 mm gave similar results to the nominal mesh (Figure 15). For this range of reduction, 95% of all triangular surfaces are within 1.0 mm of the nominal mesh surface. Similarly to the comparison of the reduced mesh with the 3D CAD model, further reduction in the point cloud results in lower accuracy. It should be noted that each successive point cloud reduction for nearly 5% of all triangular element surfaces resulted in an almost linear decrease in accuracy.
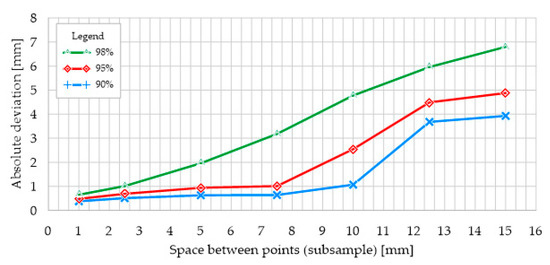
Figure 15.
Comparison of reduced meshes based on TLS data to nominal mesh. Absolute deviation.
The conducted numerical calculations showed the relation between the obtained results and the way of representation of the model geometry. Although higher values of maximum stresses were obtained for the numerical model based on 3D CAD geometry, they must be linked to the local load effects and the way the beam is supported. The model based on the straight section pull-out geometry at the end of the beam has sharp edges where stress concentrations were directly obtained. When analyzing the stress state of the web for the reduced point cloud meshed model, zones with higher stress values are visible in comparison to the CAD model, for which a symmetrical stress state image was obtained. The reduced point cloud model is characterized by the occurrence of asymmetric zones with increased stress levels between the support and the load application point (left side of the beam). This is due to the more accurate representation of the geometry in the analyzed zones, which take into account the level of corrosion of the web surface. Although the calculations are purely theoretical and illustrative, it must be pointed out that the numerical solution shows a significant influence of shear on the stress distributions obtained [31]. Similar relationships between the average corrosion level and the results of experiments and numerical calculations were given by [25]. It should be noted that the work discussed above did not take into account the local corrosion effects in the tested components.
With reference to the accuracy of the representation of the geometry itself, it should be noted that the differences in the results obtained for the maximum stresses in the web excluding the zones of local stress concentration are within 5%. These are significantly larger differences than those in similar analyses performed by [32]. It should be noted that the analysis in this study focused on elements in which geometric changes were made, primarily to architectural details, and to a lesser extent directly to the main load-bearing elements. On the other side, the presented results of the analysis fit well with the presented tendencies in [33], in which differences in reaction forces were obtained for the analyzed object as a result of a 4% reduction in the FEM mesh.
Calculations have shown that when a historic structure is being tested to determine where corrosion may have occurred, especially with a local impact area, using a section without reduction or averaging the corrosion level can result in a dangerous failure condition.
5. Conclusions
The determination of the current technical condition of historic buildings is extremely important both in terms of safety of use and preservation of cultural heritage. In the case of such objects, the performance of invasive tests is unacceptable, and therefore, it is necessary to use nondestructive measuring and testing methods.
This paper proposes the use of TLS measurements together with FEM numerical modeling to determine the current condition. The purpose of the paper was to evaluate the effect of point cloud size reduction on the quality of the geometric model and the ability to represent the corrosion level in assessing its load-carrying capacity. It should be emphasized that the quality of the performed 3D scanning has a significant influence on the accuracy of the obtained geometric models, as demonstrated by [34]. This becomes highly important in the context of historic buildings, both in terms of assessing their technical condition and preparing object documentation. The possibility of representation of the exact geometry of the object also allows popularizing the building information modeling (BIM) technology and overcoming further barriers in the implementation of the technology [35].
It seems reasonable to conclude that by developing the presented measurement and calculation technique, laser scanning combined with as-built documentation can be used to determine the degree of corrosion of hard-to-reach steel components. However, this procedure requires a wider range of calibration and is limited only to the evaluation of the size of corrosion pits.
Author Contributions
Conceptualization, D.W. and G.P.K.; methodology, D.W. and G.P.K.; software, D.W. and G.P.K.; validation, D.W. and G.P.K.; formal analysis, D.W. and G.P.K.; investigation, D.W. and G.P.K.; writing—original draft preparation, G.P.K.; writing—review and editing, D.W.; visualization, D.W. and G.P.K. Both authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fenves, S.J. Computer-Aided Design in Civil Engineering. Proc. IEEE 1981, 69, 1240–1248. [Google Scholar] [CrossRef]
- Janowski, A.; Renigier-Biłozor, M.; Walacik, M.; Chmielewska, A. Remote measurement of building usable floor area—Algorithms fusion. Land Use Policy 2021, 100. [Google Scholar] [CrossRef]
- Um, D. Rendering Theory in Solid Modeling and Applications; Springer: Cham, Switzerland, 2018; pp. 173–191. [Google Scholar]
- Gimenez, L.; Hippolyte, J.L.; Robert, S.; Suard, F.; Zreik, K. Review: Reconstruction of 3D building information models from 2D scanned plans. J. Build. Eng. 2015, 2, 24–35. [Google Scholar] [CrossRef]
- Miller, R.B.; Small, C. Cities from space: Potential applications of remote sensing in urban environmental research and policy. Environ. Sci. Policy 2003, 6, 129–137. [Google Scholar] [CrossRef]
- Adamopoulos, E.; Rinaudo, F.; Ardissono, L. A Critical Comparison of 3D Digitization Techniques for Heritage Objects. ISPRS Int. J. Geo Inf. 2020, 10, 10. [Google Scholar] [CrossRef]
- Daneshmand, M.; Helmi, A.; Avots, E.; Noroozi, F.; Alisinanoglu, F.; Arslan, H.S.; Gorbova, J.; Haamer, R.E.; Ozcinar, C.; Anbarjafari, G. 3D scanning: A comprehensive survey. arXiv 2018, arXiv:1801.08863. [Google Scholar]
- Li, M.; Nan, L. Feature-preserving 3D mesh simplification for urban buildings. ISPRS J. Photogramm. Remote Sens. 2021, 173, 135–150. [Google Scholar] [CrossRef]
- Mrówczyńska, M. Neural networks and neuro-fuzzy systems applied to the analysis of selected problems of geodesy. Comput. Assist. Mech. Eng. Sci. 2011, 18, 161–173. [Google Scholar]
- Aryan, A.; Bosché, F.; Tang, P. Planning for terrestrial laser scanning in construction: A review. Autom. Constr. 2021, 125. [Google Scholar] [CrossRef]
- Sabatini, R.; Richardson, M.A.; Gardi, A.; Ramasamy, S. Airborne laser sensors and integrated systems. Prog. Aerosp. Sci. 2015, 79, 15–63. [Google Scholar] [CrossRef]
- Wang, C.; Wen, C.; Dai, Y.; Yu, S.; Liu, M. Urban 3D modeling with mobile laser scanning: A review. Virtual Real. Intell. Hardw. 2020, 2, 175–212. [Google Scholar] [CrossRef]
- Zhou, H.; Chen, Y.; Hyyppä, J.; Li, S. An overview of the laser ranging method of space laser altimeter. Infrared Phys. Technol. 2017, 86, 147–158. [Google Scholar] [CrossRef]
- Oleniacz, G.; Skrzypczak, I.; Ślęczka, L.; Świętoń, T.; Rymar, M. Survey of the Urban Bell in the Belfry of St. Trinity Church in Krosno. Rep. Geod. Geoinform. 2017, 103, 38–45. [Google Scholar] [CrossRef]
- Panah, R.S.; Kioumarsi, M. Application of building information modelling (BIM) in the health monitoring and maintenance process: A systematic review. Sensors 2021, 21, 837. [Google Scholar] [CrossRef]
- Ding, Z.; Liu, S.; Liao, L.; Zhang, L. A digital construction framework integrating building information modeling and reverse engineering technologies for renovation projects. Autom. Constr. 2019, 102, 45–58. [Google Scholar] [CrossRef]
- Wałach, D.; Dybeł, P.; Cała, M.; Jaskowska-Lemańska, J. Evaluation of Load Capacity of Shaft Collar Subject to Unintended Exceptional Loads. Arch. Min. Sci. 2015, 60, 613–624. [Google Scholar] [CrossRef]
- Piątkowski, M. Impact of truss girder geometrical imperfections on roof bracing load. MATEC Web Conf. 2019, 262, 09008. [Google Scholar]
- Brinken, D.; Kogut, T. Development of architectural and construction documentation and the study of roof distortion based on terrestrial laser scanning data (in Polish). Arch. Fotogram. Kartogr. Teledetekcji 2018, 30, 43–53. [Google Scholar]
- Suchocki, C.; Błaszczak-Bak, W.; Damiecka-Suchocka, M.; Jagoda, M.; Masiero, A. On the use of the OptD method for building diagnostics. Remote Sens. 2020, 12, 1806. [Google Scholar] [CrossRef]
- Markiewicz, J.; Łapiński, S.; Kot, P.; Tobiasz, A.; Muradov, M.; Nikel, J.; Shaw, A.; Al-Shamma’a, A. The Quality Assessment of Different Geolocalisation Methods for a Sensor System to Monitor Structural Health of Monumental Objects. Sensors 2020, 20, 2915. [Google Scholar] [CrossRef] [PubMed]
- Kermarrec, G.; Kargoll, B.; Alkhatib, H. Deformation analysis using B-spline surface with correlated terrestrial laser scanner observations-a bridge under load. Remote Sens. 2020, 12, 829. [Google Scholar] [CrossRef]
- Mukupa, W.; Roberts, G.W.; Hancock, C.M.; Al-Manasir, K. A non-destructive technique for health assessment of fire-damaged concrete elements using terrestrial laser scanning. J. Civ. Struct. Heal. Monit. 2016, 6, 665–679. [Google Scholar] [CrossRef]
- Suchocki, C.; Katzer, J.; Rapiński, J. Terrestrial laser scanner as a tool for assessment of saturation and moisture movement in building materials. Period. Polytech. Civ. Eng. 2018, 62, 1–6. [Google Scholar] [CrossRef]
- Fiolek, P.; Jakubowski, J. Local buckling of highly corroded hot-rolled box-section beams. J. Constr. Steel Res. 2019, 157, 359–370. [Google Scholar] [CrossRef]
- PN-EN 14127. Non-Destructive Testing—Ultrasonic Thickness Measurements; European Committee for Standardization: Bruxelles, Belgium, 2011. [Google Scholar]
- Cała, M.; Stopkowicz, A.; Kowalski, M.; Blajer, M.; Cyran, K.; D’Obyrn, K. Stability analysis of underground mining openings with complex geometry. Stud. Geotech. Mech. 2016, 38, 25–32. [Google Scholar] [CrossRef][Green Version]
- Yang, H.; Xu, X.; Neumann, I. The benefit of 3D laser scanning technology in the generation and calibration of FEM models for health assessment of concrete structures. Sensors 2014, 14, 21889–21904. [Google Scholar] [CrossRef]
- Karnati, S.; Hoerchler, J.; Flood, A.; Liou, F. Incorporation of automated ball indentation methodology for studying powder bed fabricated 304L stainless steel. Solid Freeform Fabrication 2018. In Proceedings of the 29th Annual International Solid Freeform Fabrication Symposium—An Additive Manufacturing Conference SFF 2018, Austin, TX, USA, 13–15 August 2018; pp. 1349–1365. [Google Scholar]
- Autodesk Support “Equivalent Stress in a Nonlinear Analysis with Autodesk Nastran”. Available online: https://knowledge.autodesk.com/support/fusion-360/troubleshooting/caas/sfdcarticles/sfdcarticles/Equivalent-stress-in-a-nonlinear-analysis-with-Autodesk-Nastran.html (accessed on 12 February 2021).
- Kuchta, K.; Tylek, I. Design models of girders intermediate stiffeners in post-buckling range (in Polish). J. Civ. Eng. Environ. Archit. 2015, 62, 243–261. [Google Scholar] [CrossRef]
- Giaccone, D.; Fanelli, P.; Santamaria, U. Influence of the geometric model on the structural analysis of architectural heritage. J. Cult. Herit. 2020, 43, 144–152. [Google Scholar] [CrossRef]
- Bartoli, G.; Betti, M.; Bonora, V.; Conti, A.; Fiorini, L.; Kovacevic, V.C.; Tesi, V.; Tucci, G. From TLS data to FE model: A workflow for studying the dynamic behavior of the Pulpit by Giovanni Pisano in Pistoia (Italy). Procedia Struct. Integr. 2020, 29, 55–62. [Google Scholar] [CrossRef]
- Soudarissanane, S.; Lindenbergh, R.; Gorte, B. Reducing the error in terrestrial laser scanning by optimizing the measurement set-up. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, XXXVII, 615–620. [Google Scholar]
- Leśniak, A.; Górka, M.; Skrzypczak, I. Barriers to BIM Implementation in Architecture, Construction, and Engineering Projects—The Polish Study. Energies 2021, 14, 2090. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).