Simulating Heat Stress of Coal Gangue Spontaneous Combustion on Vegetation Using Alfalfa Leaf Water Content Spectral Features as Indicators
Abstract
:1. Introduction
2. Materials and Methods
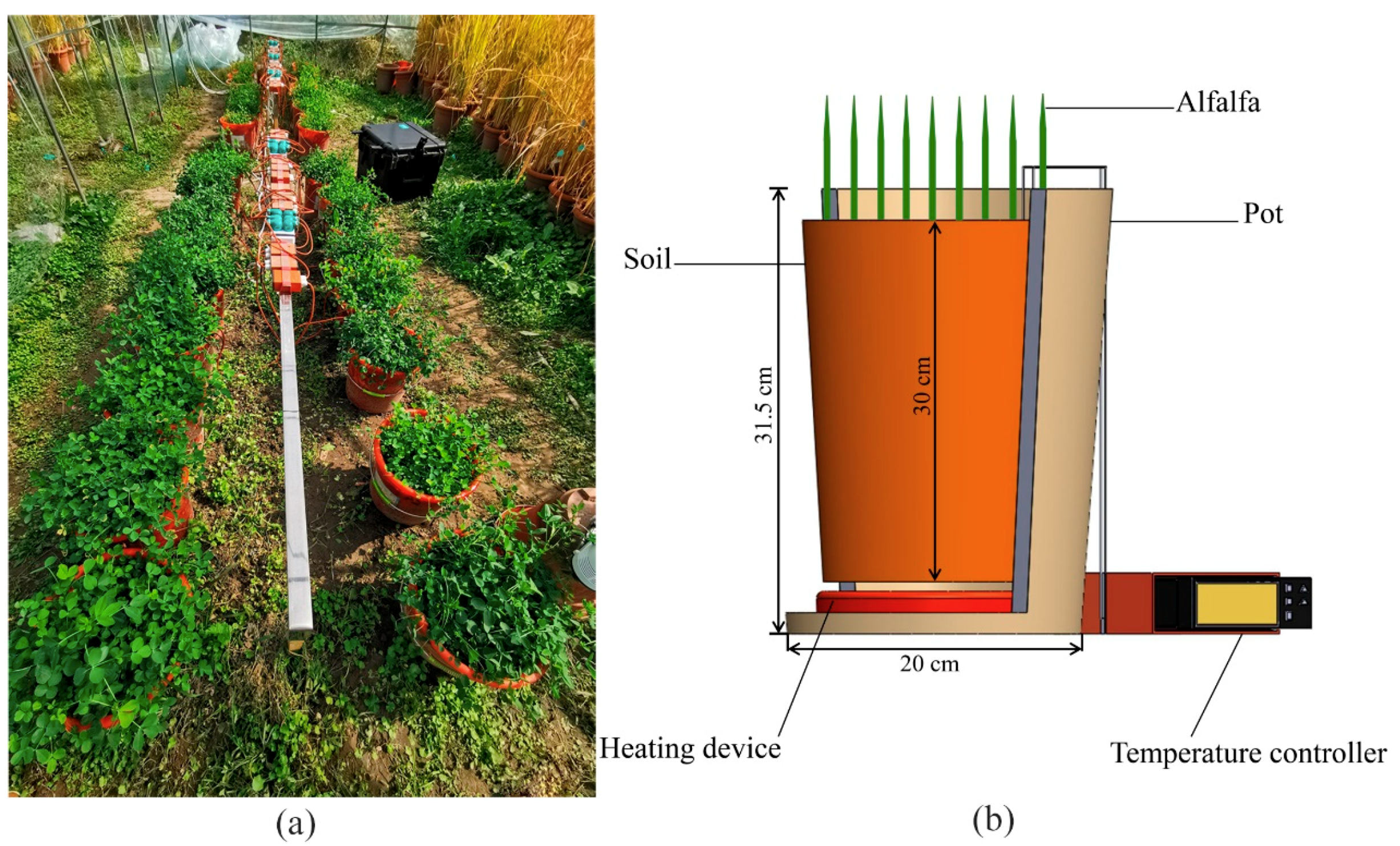
2.1. Experimental Design
2.2. Data Acquisition
2.2.1. Spectral Data
2.2.2. Leaf Water Content
2.3. Methods
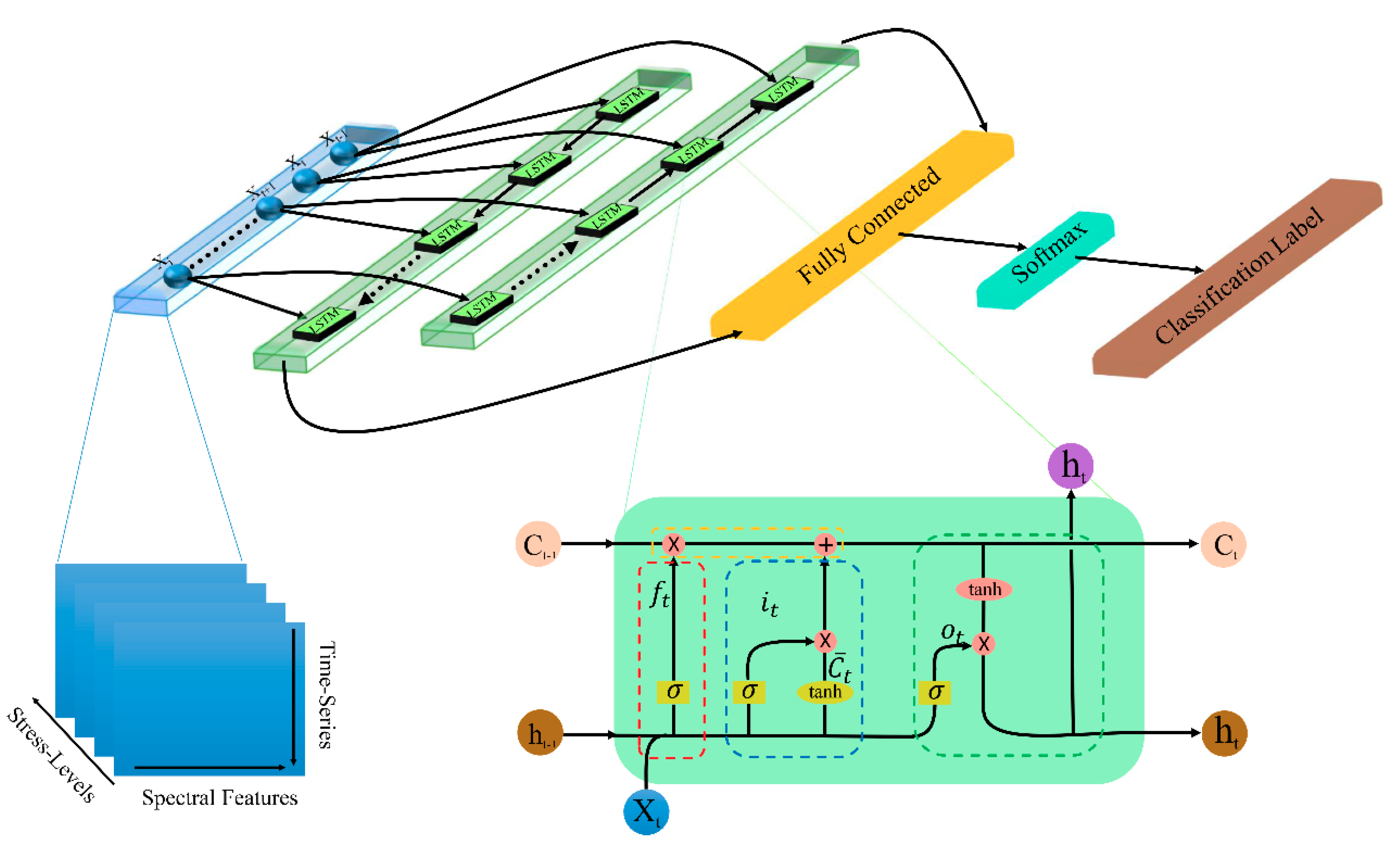
2.3.1. Spectral Feature Construction
2.3.2. Spectral Feature Selection
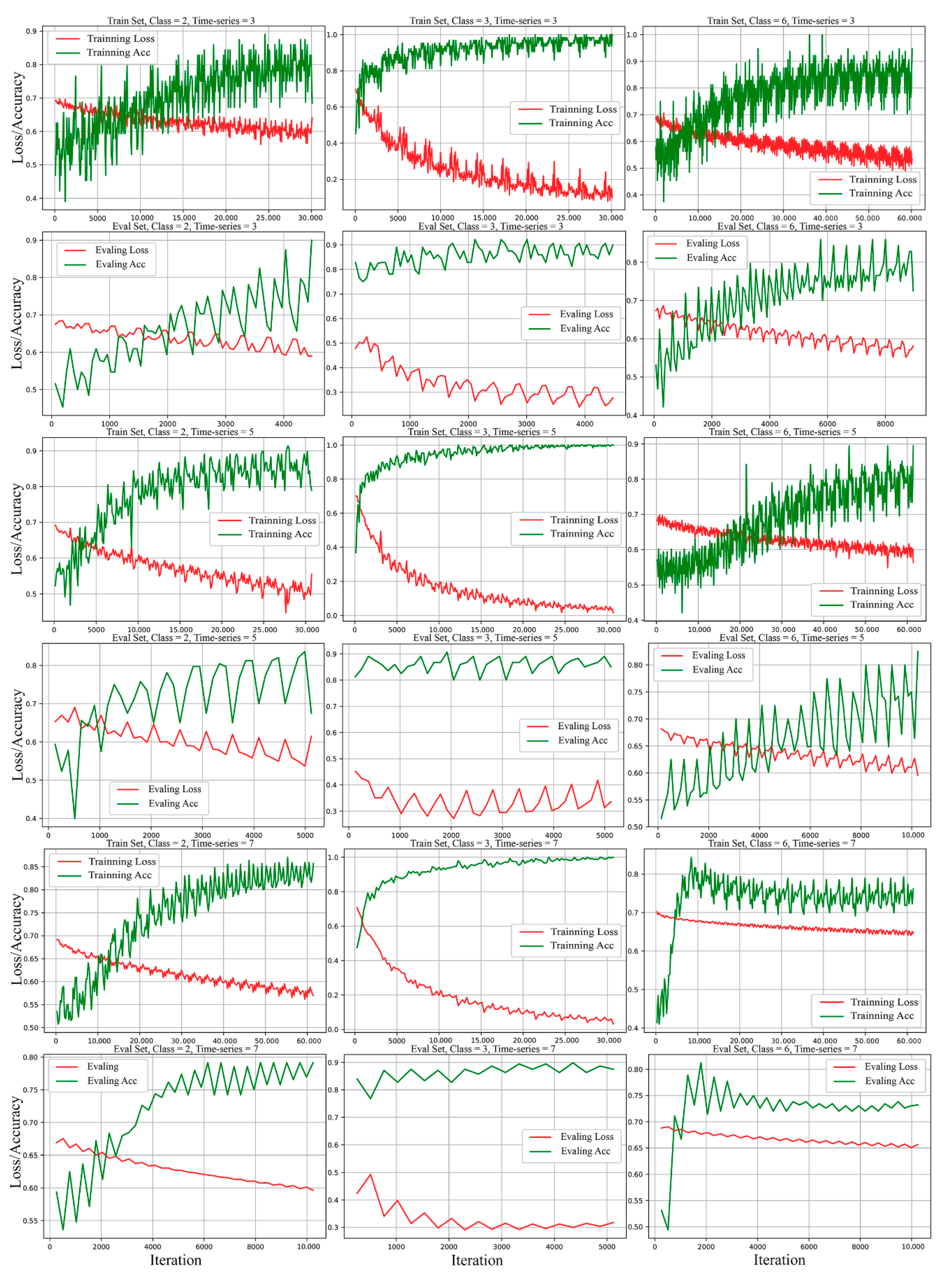
2.3.3. Assessment of Heat Stress by SF-LSTM
2.3.4. Validation
3. Results
3.1. LFMC, EWT, and RWC Time Series Analysis
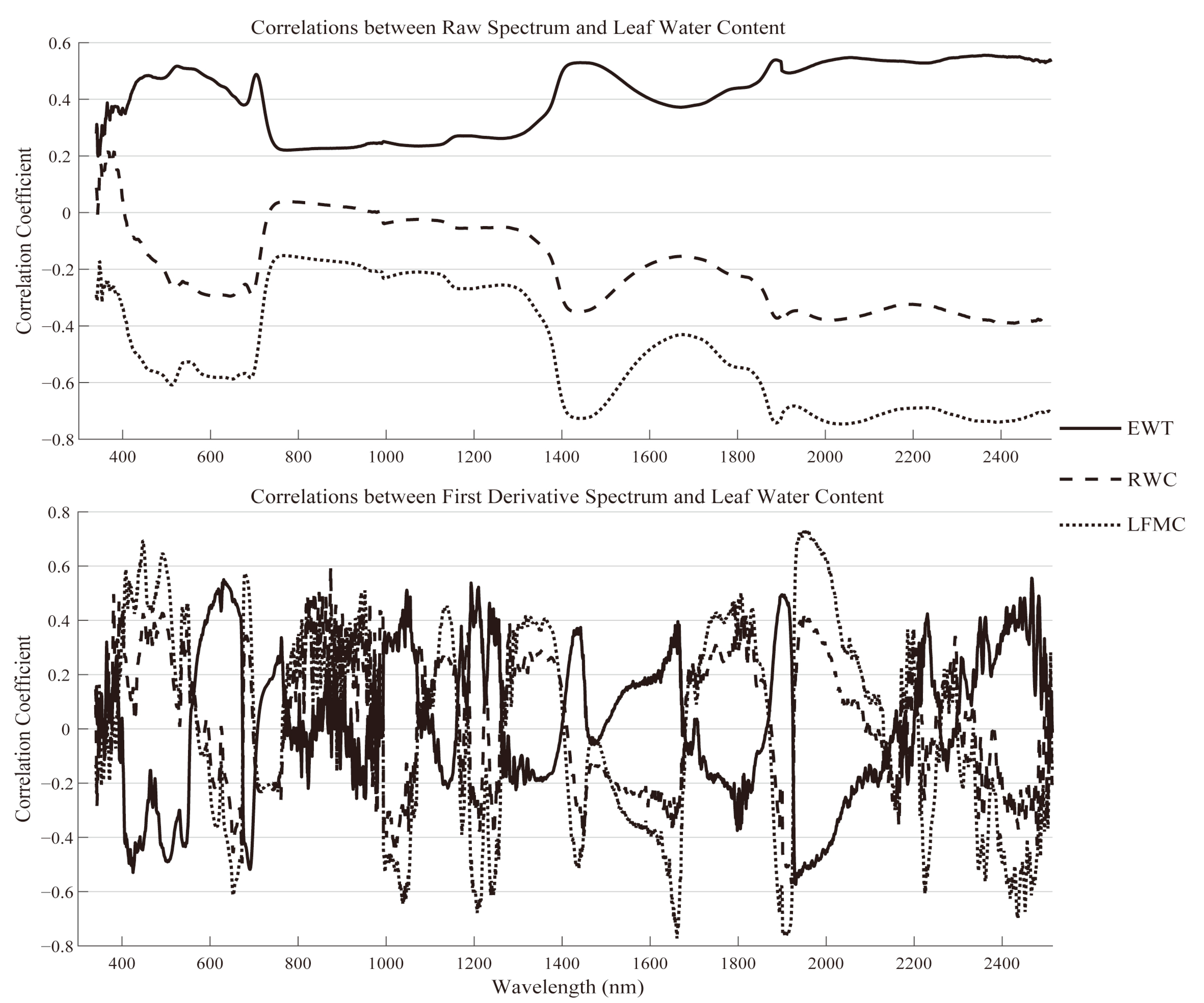
3.2. Correlation Analysis of Spectral Features and Leaf Water Content
3.2.1. Correlations between Raw Spectrum, Derivative Spectrum, and Leaf Water Content Data
3.2.2. Correlation between Spectral Reflectance Indices and Leaf Water Content
3.3. Optimal Spectral Features
3.4. SF-LSTM Estimation of Heat-Stress Level
4. Discussion
4.1. Leaf Water Content
4.2. Spectral Features
4.3. Heat Stress Estimation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Onifade, M.; Genc, B. Spontaneous combustion liability of coal and coal-shale: A review of prediction methods. Int. J. Coal Sci. Technol. 2019, 6, 151–168. [Google Scholar] [CrossRef] [Green Version]
- Alekseenko, V.A.; Bech, J.; Alekseenko, A.V.; Shvydkaya, N.V.; Roca, N. Environmental impact of disposal of coal mining wastes on soils and plants in Rostov Oblast, Russia. J. Geochem. Explor. 2018, 184, 261–270. [Google Scholar] [CrossRef]
- Wu, Y.; Yu, X.; Hu, S.; Shao, H.; Liao, Q.; Fan, Y. Experimental study of the effects of stacking modes on the spontaneous combustion of coal gangue. Process Saf. Environ. 2019, 123, 39–47. [Google Scholar] [CrossRef]
- Li, J.; Wang, J. Comprehensive utilization and environmental risks of coal gangue: A review. J. Clean. Prod. 2019, 239, 117946. [Google Scholar] [CrossRef]
- Nie, X.; Zhao, T.; Su, Y. Fossil fuel carbon contamination impacts soil organic carbon estimation in cropland. Catena 2021, 196, 104889. [Google Scholar] [CrossRef]
- Wang, H.; Tan, B.; Zhang, X. Research on the technology of detection and risk assessment of fire areas in gangue hills. Environ. Sci. Pollut. R. 2020, 27, 38776–38787. [Google Scholar] [CrossRef] [PubMed]
- Xing, Y.; Feng, J.; Rong, X. Discussion on causes of combustion and explosion and of coal gangue at the No. 4 mine of Pingdingshan coal Mine and countermeasures. Chin. J. Geol. Hazard. Control 2007, 18, 145–150. [Google Scholar]
- Sloss, L.L. Assessing and Managing Spontaneous Combustion of Coal; IEA Clean Coal Centre: Washington, DC, USA, 2015. [Google Scholar]
- Querol, X.; Zhuang, X.; Font, O.; Izquierdo, M.; Alastuey, A.; Castro, I.; Van Drooge, B.L.; Moreno, T.; Grimalt, J.O.; Elvira, J. Influence of soil cover on reducing the environmental impact of spontaneous coal combustion in coal waste gobs: A review and new experimental data. Int. J. Coal Geol. 2011, 85, 2–22. [Google Scholar] [CrossRef]
- Xiaoshuai, W.; Yuegang, T.; Wang, S.; Schobert, H.H. Clean coal geology in China: Research advance and its future. Int. J. Coal Sci. Technol. 2020, 7, 299–310. [Google Scholar]
- Roy, P.; Guha, A.; Kumar, K.V. An approach of surface coal fire detection from ASTER and Landsat-8 thermal data: Jharia coal field, India. Int. J. Appl. Earth Obs. 2015, 39, 120–127. [Google Scholar] [CrossRef]
- Hu, Z.; Xia, Q. An integrated methodology for monitoring spontaneous combustion of coal waste dumps based on surface temperature detection. Appl. Therm. Eng. 2017, 122, 27–38. [Google Scholar] [CrossRef]
- Pandey, J.; Kumar, D.; Mishra, R.K.; Mohalik, N.K.; Khalkho, A.; Singh, V.K. Application of thermography technique for assessment and monitoring of coal mine fire: A special reference to Jharia Coal Field, Jharkhand, India. Int. J. Adv. Remote Sens. GIS 2013, 2, 138–147. [Google Scholar]
- Mishra, R.K.; Pandey, J.K.; Pandey, J.; Kumar, S.; Roy, P.N.S. Detection and analysis of coal fire in Jharia Coalfield (JCF) using Landsat remote sensing data. J. Indian Soc. Remote 2020, 48, 181–195. [Google Scholar] [CrossRef]
- Mishra, R.K.; Roy, P.; Singh, V.K.; Pandey, J.K. Detection and delineation of coal mine fire in Jharia coal field, India using geophysical approach: A case study. J. Earth Syst. Sci. 2018, 127, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Misz-Kennan, M.; Tabor, A. The thermal history of selected coal waste dumps in the Upper Silesian Coal Basin (Poland). Coal Peat Fires A Glob. Perspect. 2011, 3, 431–474. [Google Scholar]
- Nádudvari, A.; Abramowicz, A.; Fabiańska, M.; Misz-Kennan, M.; Ciesielczuk, J. Classification of fires in coal waste dumps based on Landsat, Aster thermal bands and thermal camera in Polish and Ukrainian mining regions. Int. J. Coal Sci. Technol. 2020. [Google Scholar] [CrossRef]
- Rossi, S.; Burgess, P.; Jespersen, D.; Huang, B. Heat-induced leaf senescence associated with chlorophyll metabolism in Bentgrass lines differing in heat tolerance. Crop Sci. 2017, 57, 169–178. [Google Scholar] [CrossRef]
- Iqbal, N.; Umar, S.; Khan, N.A.; Corpas, F.J. Crosstalk between abscisic acid and nitric oxide under heat stress: Exploring new vantage points. Plant Cell Rep. 2021, 1–22. [Google Scholar] [CrossRef]
- Zhang, F.; Zhou, G. Estimation of canopy water content by means of hyperspectral indices based on drought stress gradient experiments of maize in the north plain China. Remote Sens. 2015, 7, 15203–15223. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Huang, J.; Wei, C.; Wang, X.; Mansaray, L.R.; Han, J.; Zhang, D.; Chen, Y. Mapping water-logging damage on winter wheat at parcel level using high spatial resolution satellite data. ISPRS J. Photogramm. Remote. Sens. 2018, 142, 243–256. [Google Scholar] [CrossRef]
- Song, Y.; Wu, C. Examining human heat stress with remote sensing technology. Gisci. Remote Sens. 2018, 55, 19–37. [Google Scholar] [CrossRef]
- Ma, B.; Pu, R.; Zhang, S.; Wu, L. Spectral identification of stress types for maize seedlings under single and combined stresses. IEEE Access 2018, 6, 13773–13782. [Google Scholar] [CrossRef]
- Zhou, X.; Sun, J.; Tian, Y.; Lu, B.; Hang, Y.; Chen, Q. Development of deep learning method for lead content prediction of lettuce leaf using hyperspectral images. Int. J. Remote Sens. 2020, 41, 2263–2276. [Google Scholar] [CrossRef]
- Caballero, D.; Calvini, R.; Amigo, J.M. Hyperspectral imaging in crop fields: Precision agriculture. In Data Handling in Science and Technology; Elsevier: Amsterdam, The Netherlands, 2020; Volume 32, pp. 453–473. [Google Scholar]
- Cao, Z.; Wang, Q.; Zheng, C. Best hyperspectral indices for tracing leaf water status as determined from leaf dehydration experiments. Ecol. Indic. 2015, 54, 96–107. [Google Scholar] [CrossRef]
- Nigam, R.; Vyas, S.S.; Bhattacharya, B.K.; Oza, M.P.; Manjunath, K.R. Retrieval of regional LAI over agricultural land from an Indian geostationary satellite and its application for crop yield estimation. J. Spat. Sci. 2017, 62, 103–125. [Google Scholar] [CrossRef]
- Kong, W.; Huang, W.; Liu, J.; Chen, P.; Qin, Q.; Ye, H.; Peng, D.; Dong, Y.; Mortimer, A.H. Estimation of canopy carotenoid content of winter wheat using multi-angle hyperspectral data. Adv. Space Res. 2017, 60, 1988–2000. [Google Scholar] [CrossRef]
- Sperdouli, I.; Moustakas, M. Spatio-temporal heterogeneity in Arabidopsis thaliana leaves under drought stress. Plant Biol. 2012, 14, 118–128. [Google Scholar] [CrossRef]
- Zhang, F.; Zhou, G. Estimation of vegetation water content using hyperspectral vegetation indices: A comparison of crop water indicators in response to water stress treatments for summer maize. BMC Ecol. 2019, 19, 18. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Sun, P.; Liu, S. A review of plant spectral reflectance response to water physiological changes. Chin. J. Plant Ecol. 2016, 40, 80. [Google Scholar]
- Yebra, M.; Dennison, P.E.; Chuvieco, E.; Riano, D.; Zylstra, P.; Hunt Jr, E.R.; Danson, F.M.; Qi, Y.; Jurdao, S. A global review of remote sensing of live fuel moisture content for fire danger assessment: Moving towards operational products. Remote Sens. Environ. 2013, 136, 455–468. [Google Scholar] [CrossRef]
- Peñuelas, J.; Filella, I.; Biel, C.; Serrano, L.; Save, R. The reflectance at the 950–970 nm region as an indicator of plant water status. Int. J. Remote Sens. 1993, 14, 1887–1905. [Google Scholar] [CrossRef]
- Berger, K.; Atzberger, C.; Danner, M.; Urso, G.D.; Mauser, W.; Vuolo, F.; Hank, T. Evaluation of the PROSAIL model capabilities for future hyperspectral model environments: A review study. Remote Sens. 2018, 10, 85. [Google Scholar] [CrossRef] [Green Version]
- Boren, E.J.; Boschetti, L. Landsat-8 and Sentinel-2 Canopy Water Content Estimation in Croplands through Radiative Transfer Model Inversion. Remote Sens. 2020, 12, 2803. [Google Scholar] [CrossRef]
- Rodríguez-Pérez, J.R.; Ordó Ez, C.; González-Fernández, A.B.; Sanz-Ablanedo, E.; Valenciano, J.B.; Marcelo, V. Leaf water content estimation by functional linear regression of field spectroscopy data. Biosyst. Eng. 2018, 165, 36–46. [Google Scholar] [CrossRef]
- Ge, Y.; Bai, G.; Stoerger, V.; Schnable, J.C. Temporal dynamics of maize plant growth, water use, and leaf water content using automated high throughput RGB and hyperspectral imaging. Comput. Electron. Agric. 2016, 127, 625–632. [Google Scholar] [CrossRef] [Green Version]
- Virnodkar, S.S.; Pachghare, V.K.; Patil, V.C.; Jha, S.K. Remote sensing and machine learning for crop water stress determination in various crops: A critical review. Precis. Agric. 2020, 21, 1121–1155. [Google Scholar] [CrossRef]
- Yebra, M.; Quan, X.; Riaño, D.; Larraondo, P.R.; van Dijk, A.I.; Cary, G.J. A fuel moisture content and flammability monitoring methodology for continental Australia based on optical remote sensing. Remote Sens. Environ. 2018, 212, 260–272. [Google Scholar] [CrossRef]
- Yi, Q.; Bao, A.; Wang, Q.; Zhao, J. Estimation of leaf water content in cotton by means of hyperspectral indices. Comput. Electron. Agric. 2013, 90, 144–151. [Google Scholar] [CrossRef]
- Krishna, G.; Sahoo, R.N.; Singh, P.; Bajpai, V.; Patra, H.; Kumar, S.; Dandapani, R.; Gupta, V.K.; Viswanathan, C.; Ahmad, T. Comparison of various modelling approaches for water deficit stress monitoring in rice crop through hyperspectral remote sensing. Agric. Water Manag. 2019, 213, 231–244. [Google Scholar] [CrossRef]
- Xiong, X.; Liu, N.; Wei, Y.; Bi, Y.; Luo, J.; Xu, R.; Zhou, J.; Zhang, Y. Effects of non-uniform root zone salinity on growth, ion regulation, and antioxidant defense system in two alfalfa cultivars. Plant Physiol. Biochem. 2018, 132, 434–444. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Li, X.; Bai, Z.; Huang, L. The effects of coal gangue and fly ash on the hydraulic properties and water content distribution in reconstructed soil profiles of coal-mined land with a high groundwater table. Hydrol. Process 2017, 31, 687–697. [Google Scholar] [CrossRef]
- Thorp, K.R.; Wang, G.; Bronson, K.F.; Badaruddin, M.; Mon, J. Hyperspectral data mining to identify relevant canopy spectral features for estimating durum wheat growth, nitrogen status, and grain yield. Comput. Electron. Agric. 2017, 136, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Atzberger, C.; Darvishzadeh, R.; Immitzer, M.; Schlerf, M.; Skidmore, A.; Maire, G.L. Comparative analysis of different retrieval methods for mapping grassland leaf area index using airborne imaging spectroscopy. Int. J. Appl. Earth Obs. Geoinf. 2015, 43, 19–31. [Google Scholar] [CrossRef] [Green Version]
- Caturegli, L.; Matteoli, S.; Gaetani, M.; Grossi, N.; Magni, S.; Minelli, A.; Corsini, G.; Remorini, D.; Volterrani, M. Effects of water stress on spectral reflectance of bermudagrass. Sci. Rep. 2020, 10, 1–12. [Google Scholar] [CrossRef]
- Seelig, H.D.; Hoehn, A.; Stodieck, L.S.; Klaus, D.M.; Adams, W.W.; Emery, W.J. Plant water parameters and the remote sensing R 1300/R 1450 leaf water index: Controlled condition dynamics during the development of water deficit stress. Irrig. Sci. 2009, 27, 357–365. [Google Scholar] [CrossRef]
- Ihuoma, S.O.; Madramootoo, C.A. Recent advances in crop water stress detection. Comput. Electron. Agric. 2017, 141, 267–275. [Google Scholar] [CrossRef]
- Wolf, A.F. Using WorldView-2 Vis-NIR multispectral imagery to support land mapping and feature extraction using normalized difference index ratios. In Algorithms and Technologies for Multispectral, Hyperspectral and Ultraspectral Imagery XVIII; International Society for Optics and Photonics: Baltimore, MD, USA, 2012; Volume 8390. [Google Scholar]
- Maimaitiyiming, M.; Ghulam, A.; Bozzolo, A.; Wilkins, J.L.; Kwasniewski, M.T. Early detection of plant physiological responses to different levels of water stress using reflectance spectroscopy. Remote Sens. 2017, 9, 745. [Google Scholar] [CrossRef] [Green Version]
- Joiner, J.; Yoshida, Y.; Anderson, M.; Holmes, T.; Hain, C.; Reichle, R.; Koster, R.; Middleton, E.; Zeng, F. Global relationships among traditional reflectance vegetation indices (NDVI and NDII), evapotranspiration (ET), and soil moisture variability on weekly timescales. Remote Sens. Environ. 2018, 219, 339–352. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peng, D.; Zhang, H.; Yu, L.; Wu, M.; Wang, F.; Huang, W.; Liu, L.; Sun, R.; Li, C.; Wang, D. Assessing spectral indices to estimate the fraction of photosynthetically active radiation absorbed by the vegetation canopy. Int. J. Remote Sens. 2018, 39, 8022–8040. [Google Scholar] [CrossRef]
- Sukhova, E.; Sukhov, V. Connection of the photochemical reflectance index (PRI) with the photosystem II quantum yield and nonphotochemical quenching can be dependent on variations of photosynthetic parameters among investigated plants: A meta-analysis. Remote Sens. 2018, 10, 771. [Google Scholar] [CrossRef] [Green Version]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Kim, J. Estimating classification error rate: Repeated cross-validation, repeated hold-out and bootstrap. Comput. Stat. Data Anal. 2009, 53, 3735–3745. [Google Scholar] [CrossRef]
- Anderson, S.A.; Anderson, W.R. Ignition and fire spread thresholds in gorse (Ulex europaeus). Int. J. Wildland Fire 2010, 19, 589–598. [Google Scholar] [CrossRef]
- Zhang, W.; Li, X.; Zhao, L. A fast hyperspectral feature selection method based on band correlation analysis. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1750–1754. [Google Scholar] [CrossRef]
- Pramanik, P.; Chakrabarti, B.; Bhatia, A.; Singh, S.D.; Maity, A.; Aggarwal, P.; Krishnan, P. Effect of elevated temperature on soil hydrothermal regimes and growth of wheat crop. Environ. Monit. Assess. 2018, 190, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Khalil, U.; Ali, S.; Rizwan, M.; Rahman, K.U.; Ata-Ul-Karim, S.T.; Najeeb, U.; Ahmad, M.N.; Adrees, M.; Sarwar, M.; Hussain, S.M. Role of mineral nutrients in plant growth under extreme temperatures. In Plant Nutrients and Abiotic Stress Tolerance; Springer: Berlin/Heidelberg, Germany, 2018; pp. 499–524. [Google Scholar]
- Smart, C.M.; Scofield, S.R.; Bevan, M.W.; Dyer, T.A. Delayed leaf senescence in tobacco plants transformed with tmr, a gene for cytokinin production in Agrobacterium. Plant Cell 1991, 3, 647–656. [Google Scholar] [CrossRef]
- Liu, X.; Huang, B. Root physiological factors involved in cool-season grass response to high soil temperature. Environ. Exp. Bot. 2005, 53, 233–245. [Google Scholar] [CrossRef]
- Xu, Q.; Huang, B. Growth and physiological responses of creeping bentgrass to changes in air and soil temperatures. Crop Sci. 2000, 40, 1363–1368. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, Z.; Zhang, G.; Meng, Y.; Chen, B.; Wang, Y. Monitoring the leaf water content and specific leaf weight of cotton (Gossypium hirsutum L.) in saline soil using leaf spectral reflectance. Eur. J. Agron. 2012, 41, 103–117. [Google Scholar] [CrossRef]
- Wu, J.; Chen, T.S.; Pan, L.X. Spectrum Variance Analysis of Tree Leaves under the Condition of Different Leaf water Content. Guang Pu Xue Yu Guang Pu Fen Xi = Guang Pu 2015, 35, 1961–1966. [Google Scholar]
- Cheng, T.; Rivard, B.; Sanchez-Azofeifa, A. Spectroscopic determination of leaf water content using continuous wavelet analysis. Remote Sens. Environ. 2011, 115, 659–670. [Google Scholar] [CrossRef]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Marquéz, J.R.G.; Gruber, B.; Lafourcade, B.; Leitao, P.J. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography 2013, 36, 27–46. [Google Scholar] [CrossRef]
- De Castro Filho, H.C.; De Carvalho Júnior, O.A.; De Carvalho, O.L.F.; De Bem, P.P.; Dos Santos De Moura, R.; De Albuquerque, A.O.; Rosa Silva, C.; Guimarães Ferreira, P.H.; Fontes Guimarães, R.; Trancoso Gomes, R.A. Rice crop detection using LSTM, Bi-LSTM, and machine learning models from Sentinel-1 time series. Remote Sens. 2020, 12, 2655. [Google Scholar] [CrossRef]
- Karim, F.; Majumdar, S.; Darabi, H.; Chen, S. LSTM fully convolutional networks for time series classification. IEEE Access 2017, 6, 1662–1669. [Google Scholar] [CrossRef]



| Water-SRIs | Acronym | Equation 1 | Reference |
| Water index | WI (900, 970) | [46] | |
| Water index | WI (1300, 1450) | [47] | |
| Normalized difference water index | NDWI | [48] | |
| Moisture stress index | MSI | [49] | |
| Vegetation-SRIs | Acronym | Equation 1 | Reference |
| Normalized difference vegetation index | NDVI | [50] | |
| Normalized difference infrared index | NDII | [51] | |
| Simple ratio vegetation index | SR | [52] | |
| Photochemical reflectance index | PRI | [53] |
| Water-SRIs | r | Vegetation-SRIs | r | ||||
|---|---|---|---|---|---|---|---|
| EWT | RWC | LFMC | EWT | RWC | LFMC | ||
| WI (900,970) | 0.34 | −0.39 | −0.64 * | SR | −0.37 | −0.33 | −0.57 * |
| WI (1300,1450) | 0.44 | −0.39 | −0.7 * | NDVI | 0.39 | −0.33 | −0.57 * |
| NDWI | 0.22 | −0.57 * | −0.59 * | NDII | 0.33 | −0.44 | −0.63 * |
| MSI | −0.35 | 0.42 | 0.64 * | PRI | −0.44 | 0.31 | −0.5 |
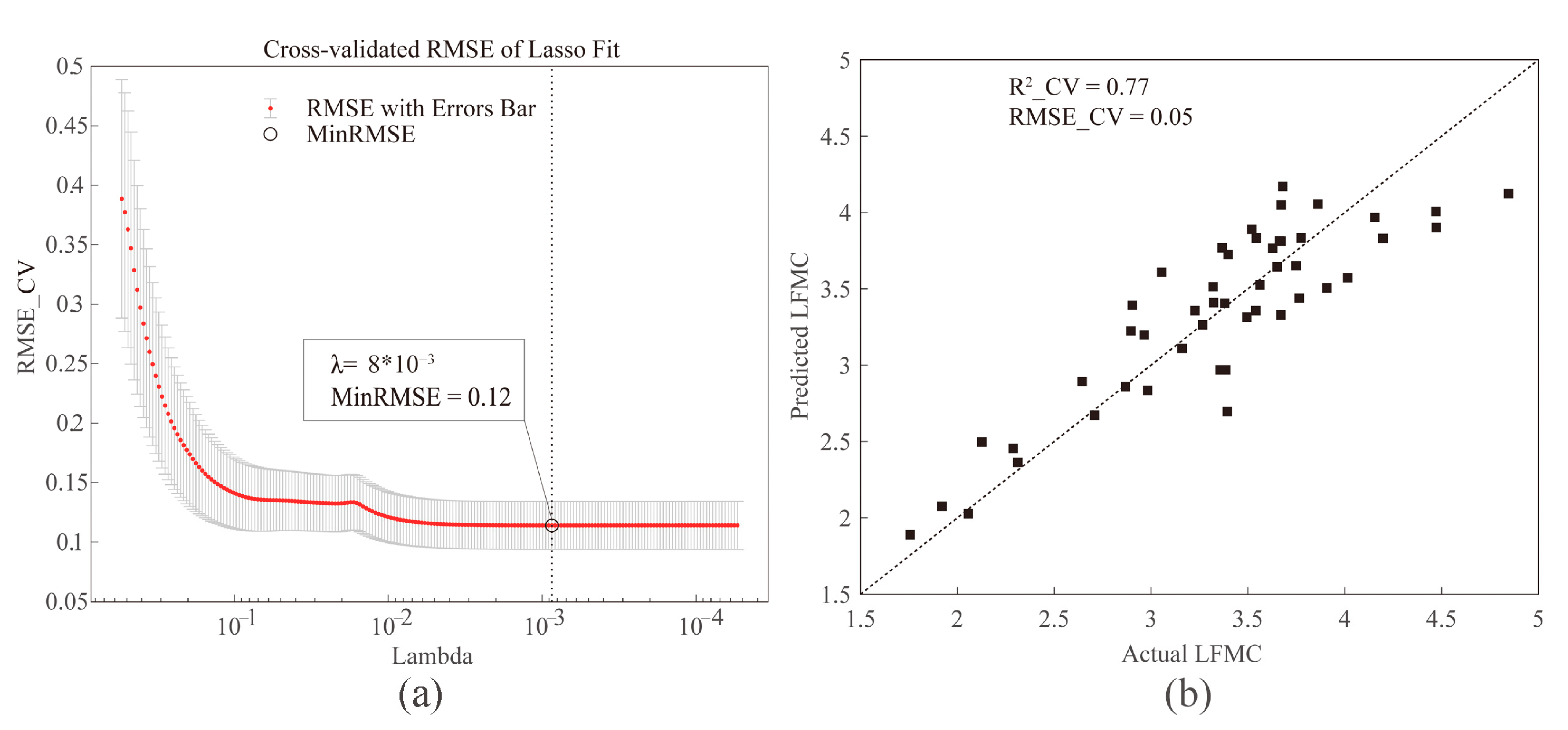
| Lasso Regression | Regression Coefficients | R2_CV | RMSE_CV | |
|---|---|---|---|---|
| Spectral Parameters | ||||
| RS (1889) | 0 | 0.77 | 0.05 | |
| FDS (1661) | 29 | |||
| RVI (1525,1771) | 30.93 | |||
| DVI (1412,740) | 0.19 | |||
| NDVI (1447,1803) | −2.76 | |||
| Equation 1 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Zhao, Y.; Yang, F.; Liu, T.; Xiao, W.; Sun, H. Simulating Heat Stress of Coal Gangue Spontaneous Combustion on Vegetation Using Alfalfa Leaf Water Content Spectral Features as Indicators. Remote Sens. 2021, 13, 2634. https://doi.org/10.3390/rs13132634
Wang Q, Zhao Y, Yang F, Liu T, Xiao W, Sun H. Simulating Heat Stress of Coal Gangue Spontaneous Combustion on Vegetation Using Alfalfa Leaf Water Content Spectral Features as Indicators. Remote Sensing. 2021; 13(13):2634. https://doi.org/10.3390/rs13132634
Chicago/Turabian StyleWang, Qiyuan, Yanling Zhao, Feifei Yang, Tao Liu, Wu Xiao, and Haiyuan Sun. 2021. "Simulating Heat Stress of Coal Gangue Spontaneous Combustion on Vegetation Using Alfalfa Leaf Water Content Spectral Features as Indicators" Remote Sensing 13, no. 13: 2634. https://doi.org/10.3390/rs13132634
APA StyleWang, Q., Zhao, Y., Yang, F., Liu, T., Xiao, W., & Sun, H. (2021). Simulating Heat Stress of Coal Gangue Spontaneous Combustion on Vegetation Using Alfalfa Leaf Water Content Spectral Features as Indicators. Remote Sensing, 13(13), 2634. https://doi.org/10.3390/rs13132634