Hyperspectral Remote Sensing Images Deep Feature Extraction Based on Mixed Feature and Convolutional Neural Networks
Abstract
:1. Introduction
2. Proposed Pixel Frequency Spectrum Feature and Feature Mixing
2.1. Proposed Pixel Frequency Spectrum Feature
2.2. Proposed Spectral and Frequency Spectrum Mixed Feature
3. Proposed Multi-Branch CNN Models, 3-D CNN-PCA Model, and Training Strategy
3.1. Basic CNN
3.2. Proposed Multi-Branch CNNs
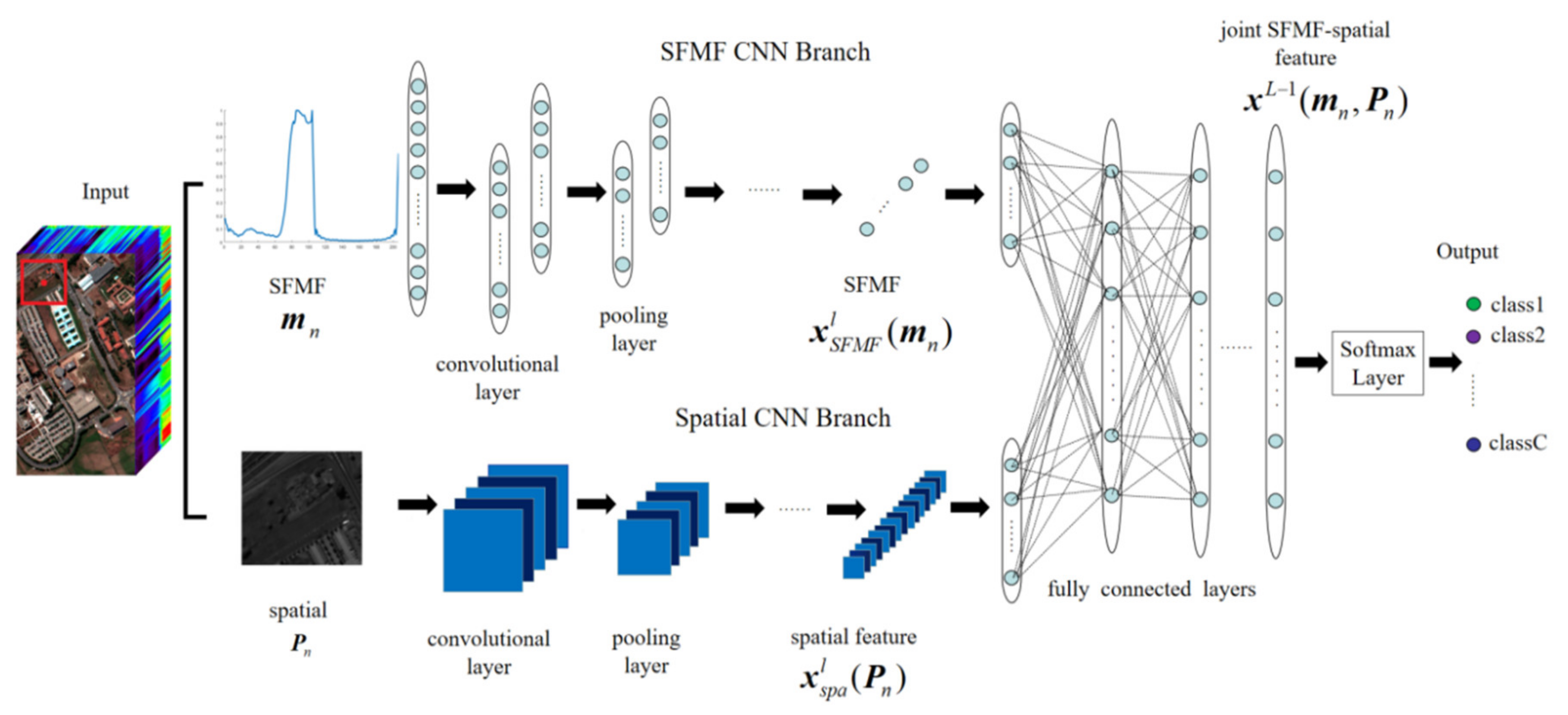
3.2.1. Proposed Two-Branch CNNs
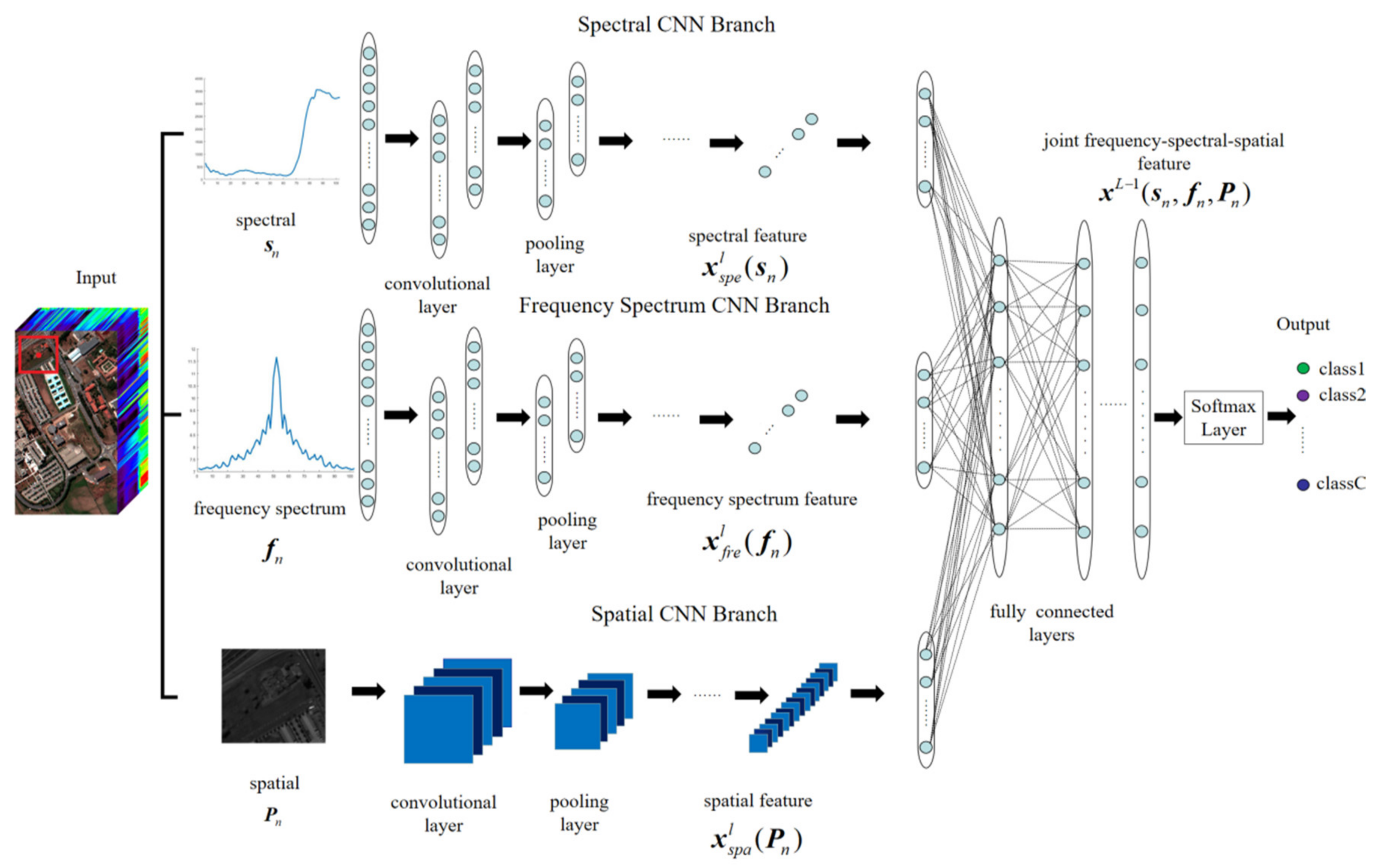
3.2.2. Proposed Three-Branch CNN
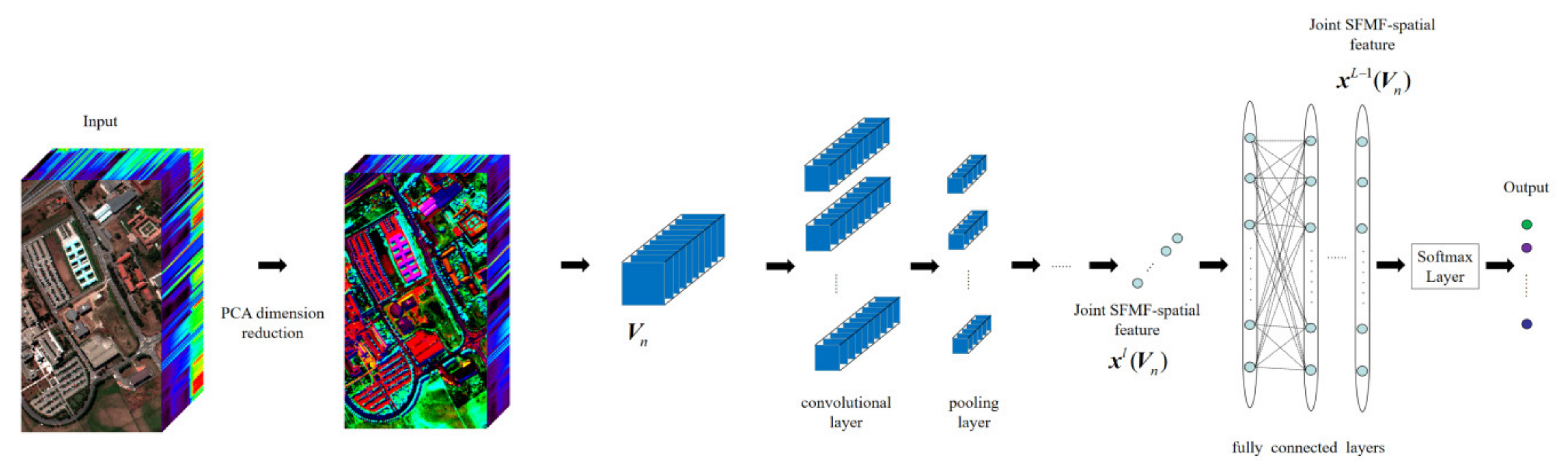
3.3. 3-D CNN-PCA
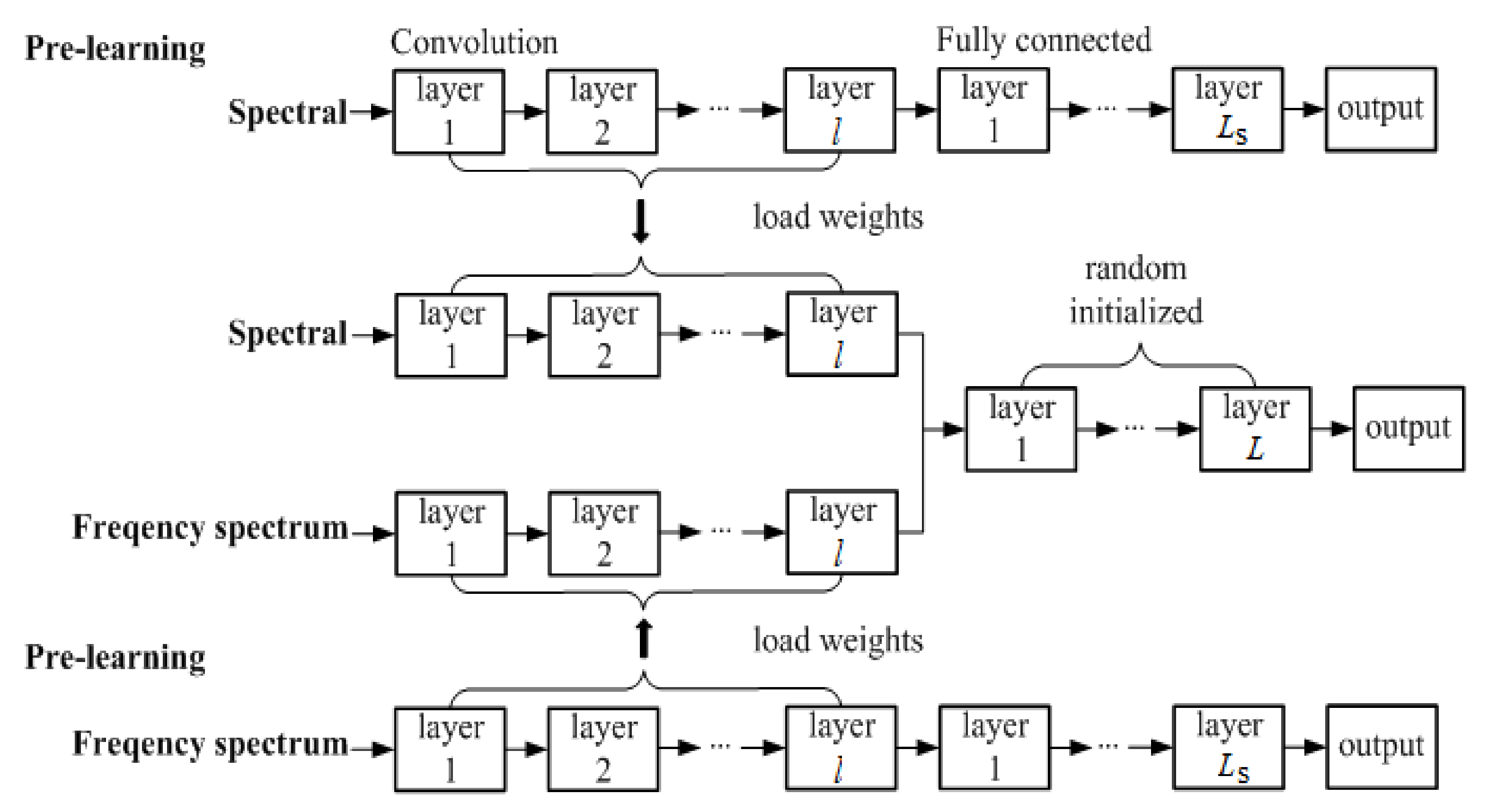
3.4. Proposed Pre-Learning Strategy
4. Experiment Results
4.1. Experiment Datasets
4.2. CNNs Structure Design and Parameter Setting
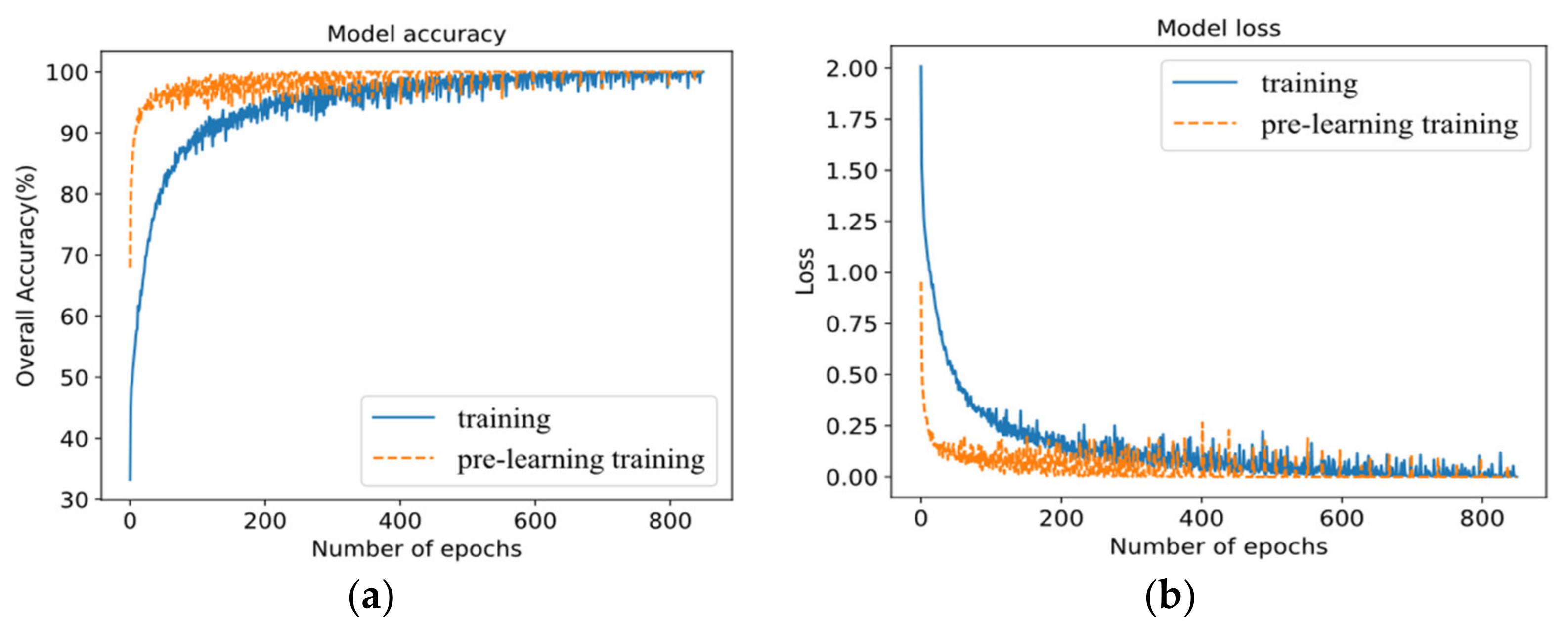
4.3. Effectiveness Analysis of Proposed Pre-Learning Training Strategy
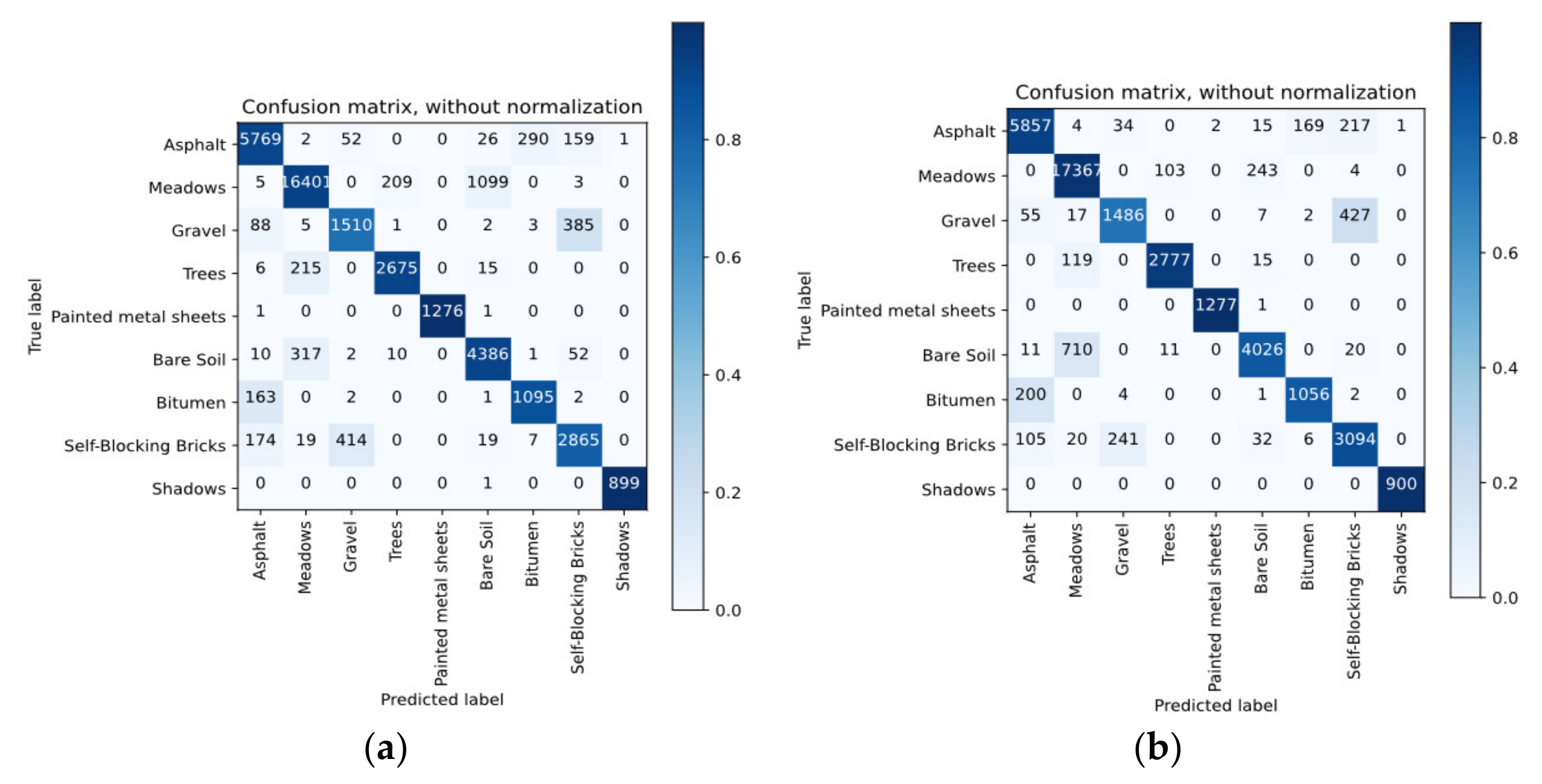
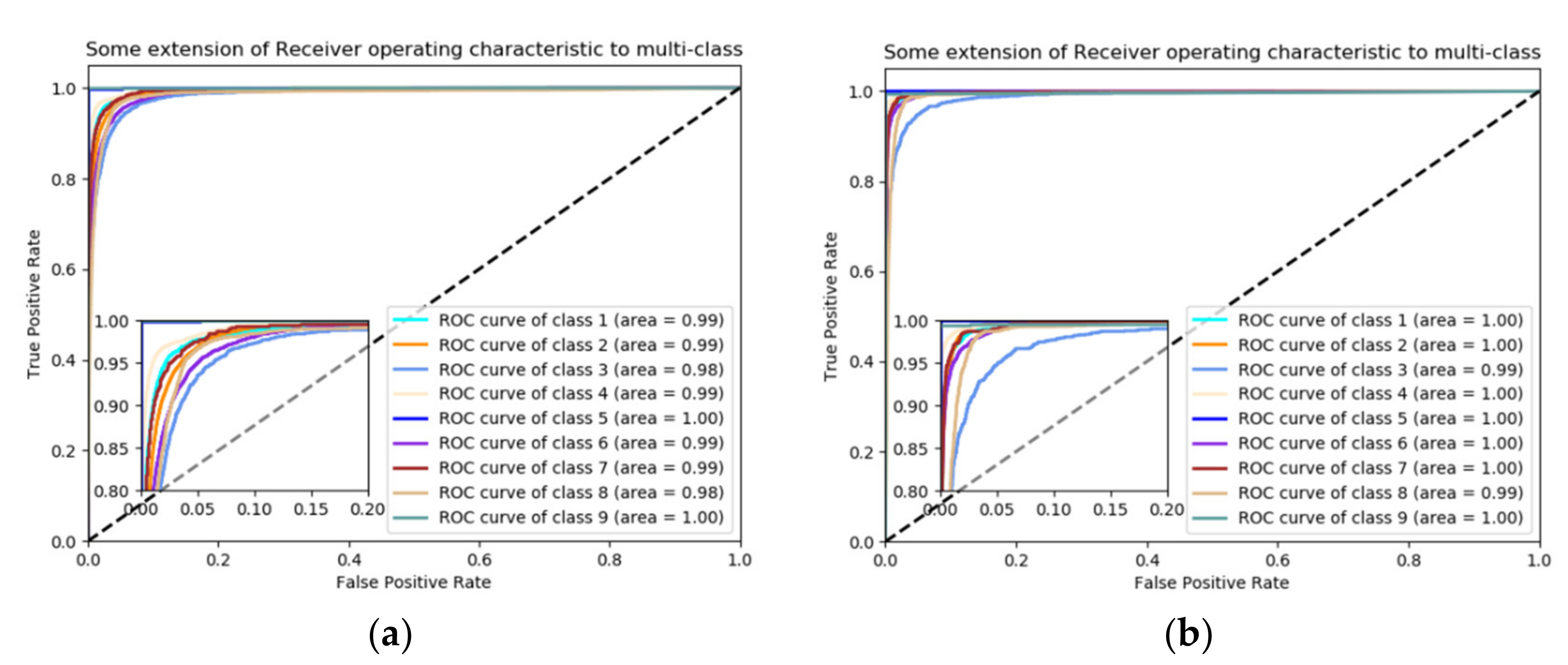
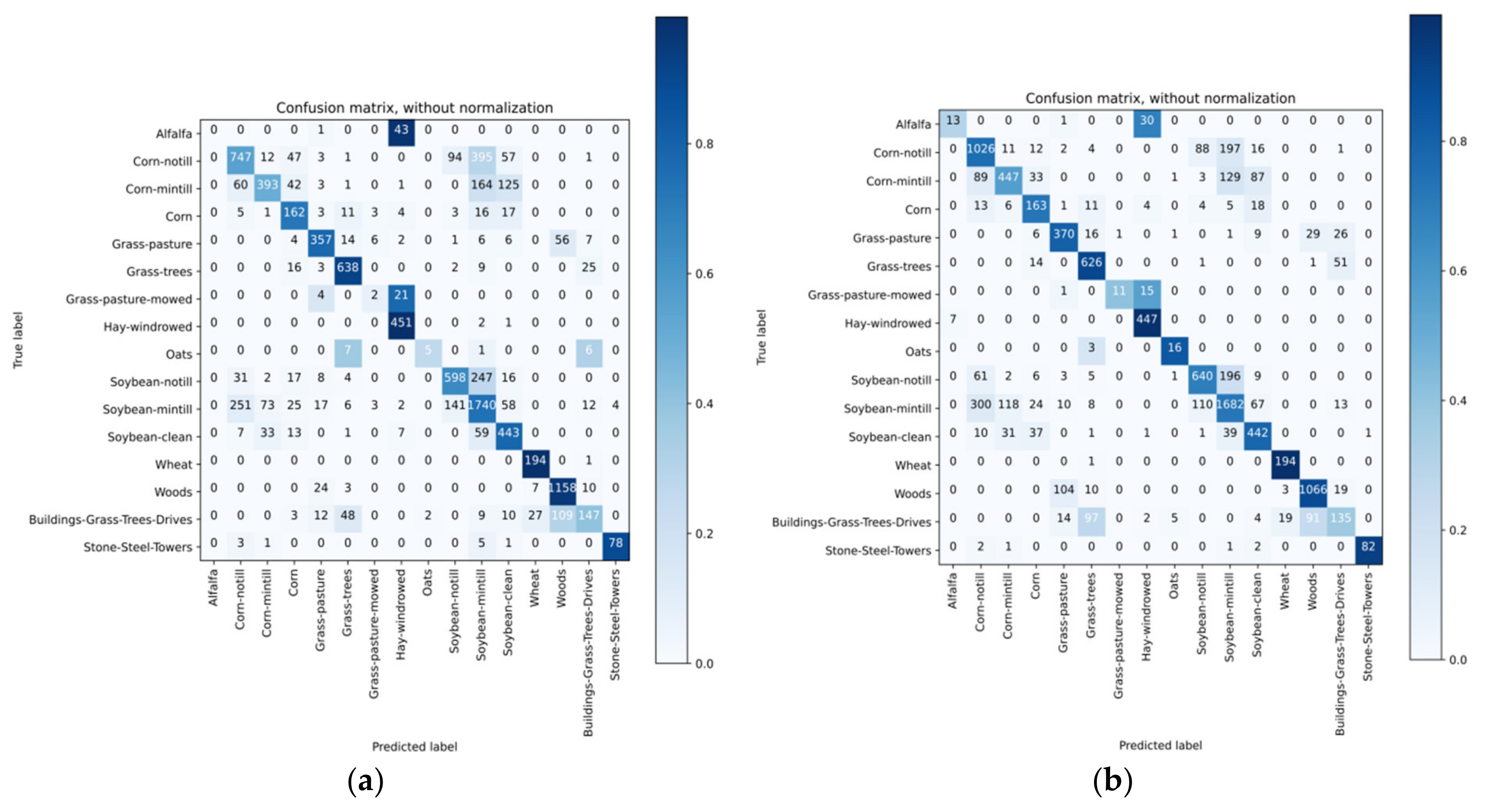
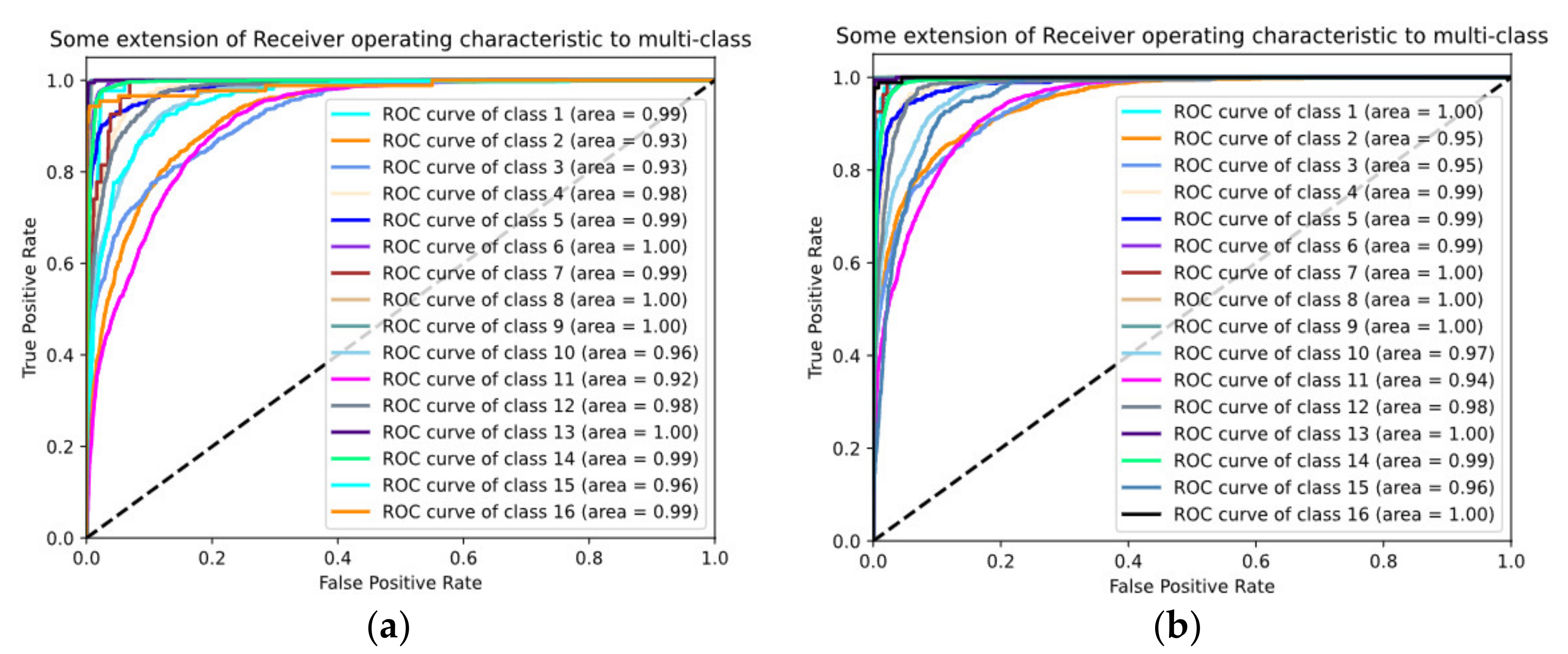
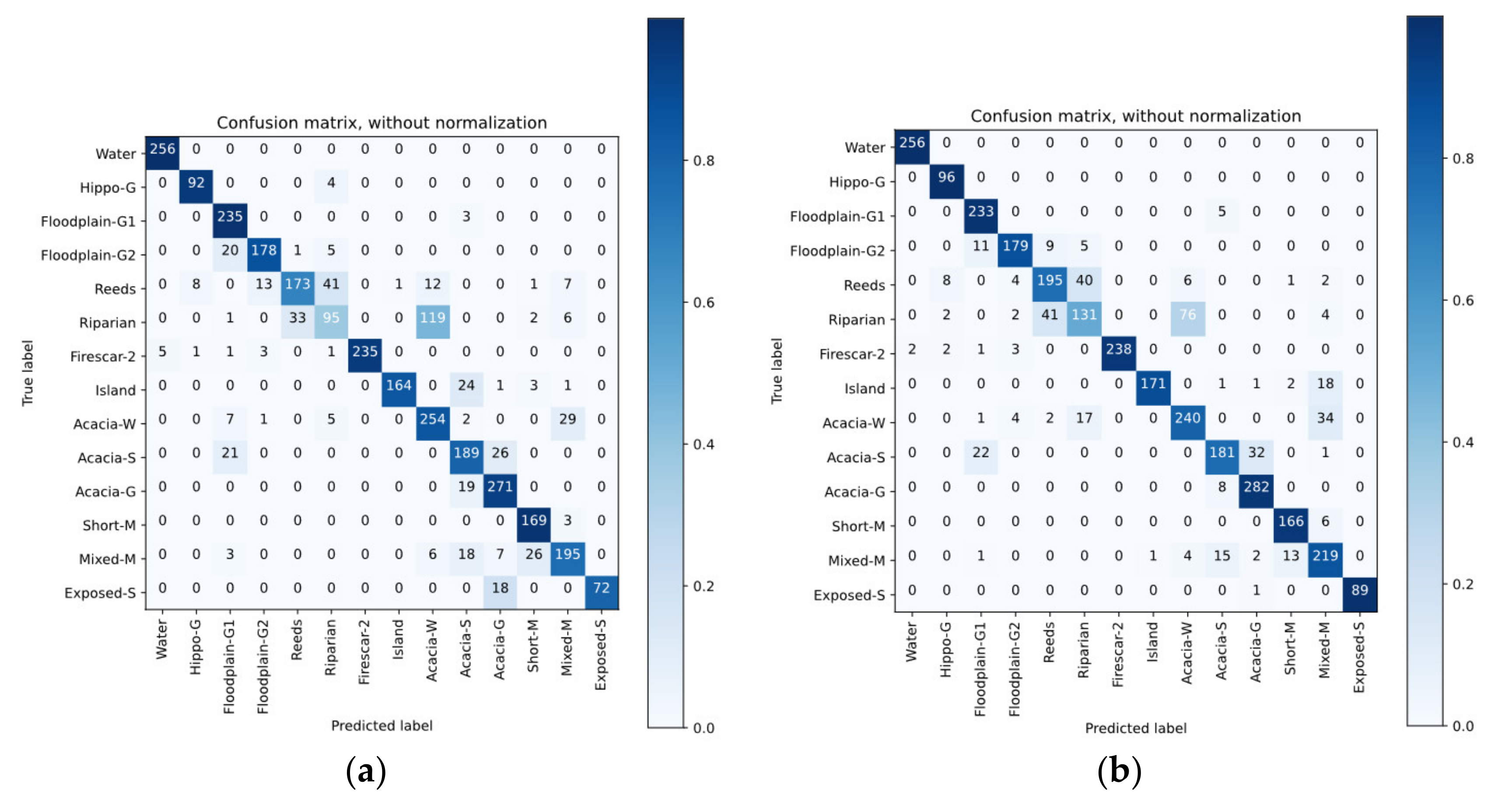
4.4. Classification Results
4.5. Discussion of Classification Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tong, Q.; Xue, Y.; Zhang, L. Progress in Hyperspectral Remote Sensing Science and Technology in China over the Past Three Decades. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 70–91. [Google Scholar] [CrossRef]
- Zeng, S.; Wang, Z.; Gao, C.; Kang, Z. Hyperspectral Image Classification With Global–Local Discriminant Analysis and Spatial–Spectral Context. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 11, 5005–5018. [Google Scholar] [CrossRef]
- Liu, J.; Guo, X.; Liu, Y. Hyperspectral remote sensing image feature extraction based on spectral clustering and subclass discriminant analysis. Remote Sens. Lett. 2020, 11, 166–175. [Google Scholar] [CrossRef]
- Sakarya, U. Hyperspectral dimension reduction using global and local information based linear discriminant analysis. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, II-7, 61–66. [Google Scholar] [CrossRef] [Green Version]
- Cui, X.; Zheng, K.; Gao, L.; Zhang, B. Multiscale Spatial-Spectral Convolutional Network with Image-Based Framework for Hyperspectral Imagery Classification. Remote Sens. 2019, 11, 2220. [Google Scholar] [CrossRef] [Green Version]
- Guo, H.; Bai, H.; Zhou, Y.; Li, W. DF-SSD: A deep convolutional neural network-based embedded lightweight object detection frame work for remote sensing imagery. J. Appl. Remote Sens. 2020, 14, 014521. [Google Scholar] [CrossRef]
- Fricker, G.; Ventura, J.; Wolf, J.; North, M.; Davis, F.; Franklin, J. A Convolutional Neural Network Classifier Identifies Tree Species in Mixed-Conifer Forest from Hyperspectral Imagery. Remote Sens. 2019, 11, 2326. [Google Scholar] [CrossRef] [Green Version]
- Hu, W.; Huang, Y.; Li, W.; Li, H. Deep Convolutional Neural Networks for Hyperspectral Image Classification. J. Sens. 2015, 2015, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Yue, J.; Zhao, W.; Mao, S.; Liu, H. Spectral–spatial classifification of hyperspectral images using deep convolutional neural networks. Remote Sens. Lett. 2015, 6, 468–477. [Google Scholar] [CrossRef]
- Zhao, W.; Du, S. Spectral–Spatial Feature Extraction for Hyperspectral Image Classification: A Dimension Reduction and Deep Learning Approach. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4544–4554. [Google Scholar] [CrossRef]
- Neagoe, V.; Diaconescu, P. CNN Hyperspectral Image Classification Using Training Sample Augmentation with Generative Adversarial Networks. In Proceedings of the 2020 13th International Conference on Communications (COMM), Bucharest, Romania, 18–20 June 2020; pp. 515–519. [Google Scholar]
- Feng, J.; Wu, X.; Chen, J.; Zhang, X.; Tang, X.; Li, D. Joint Multilayer Spatial-Spectral Classification of Hyperspectral Images Based on CNN and Convlstm. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 588–591. [Google Scholar]
- Yang, J.; Zhao, Y.; Chan, J. Learning and Transferring Deep Joint Spectral–Spatial Features for Hyperspectral Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4729–4742. [Google Scholar] [CrossRef]
- Ahmad, M. A fast 3D CNN for hyperspectral image classifification. arXiv 2020, arXiv:2004.14152. [Google Scholar]
- Chen, Y.; Jiang, H.; Li, C.; Ghamisi, P. Deep Feature Extraction and Classification of Hyperspectral Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef] [Green Version]
- Sellami, A.; Abbes, A.; Barra, V.; Farah, R. Fused 3-D spectral-spatial deep neural networks and spectral clustering for hyperspectral image classification. Pattern Recognit. Lett. 2020, 138, 594–600. [Google Scholar] [CrossRef]
- Yu, C.; Han, R.; Song, M.; Liu, C.; Chang, C. A Simplified 2D-3D CNN Architecture for Hyperspectral Image Classification Based on Spatial–Spectral Fusion. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2020, 13, 2485–2501. [Google Scholar] [CrossRef]
- Sellami, A.; Farah, M.; Farah, I.; Solaiman, B. Hyperspectral imagery classification based on semi-supervised 3-D deep neural network and adaptive band selection. Expert Syst. Appl. 2019, 129, 246–259. [Google Scholar] [CrossRef]
- Gao, H.; Yao, D.; Yang, Y.; Li, C.; Liu, H.; Hua, Z. Multiscale 3-D-CNN based on spatial–spectral joint feature extraction for hyperspectral remote sensing images classification. J. Electron. Imaging 2020, 29, 013007. [Google Scholar] [CrossRef]
- Li, F.; Wang, J.; Lan, R.; Liu, Z. Hyperspectral image classification using multi-feature fusion. Opt. Laser Technol. 2019, 110, 176–183. [Google Scholar] [CrossRef]
- Carranza-García, M.; García-Gutiérrez, J.; Riquelme, J.C. A Framework for Evaluating Land Use and Land Cover Classification Using Convolutional Neural Networks. Remote Sens. 2019, 11, 274. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Huang, C.; Tao, J.; Luo, J. Interpreting deep convolutional neural network classification results indirectly through the preprocessing feature fusion method in ship image classification. J. Appl. Remote Sens. 2020, 14, 016510. [Google Scholar] [CrossRef]
- Feng, J.; Chen, J.; Liu, L.; Cao, X. CNN-Based Multilayer Spatial–Spectral Feature Fusion and Sample Augmentation with Local and Nonlocal Constraints for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1299–1313. [Google Scholar] [CrossRef]
- Wang, L.; Liu, M.; Liu, X.; Wu, L. Pretrained convolutional neural network for classifying rice-cropping systems based on spatial and spectral trajectories of Sentinel-2 time series. J. Appl. Remote Sens. 2020, 14, 014506. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, M.; Chen, T.; Sun, Z.; Ma, Y.; Yu, B. Recent advances in convolutional neural network acceleration. Neurocomputing 2019, 323, 37–51. [Google Scholar] [CrossRef] [Green Version]
- Zeiler, M.; Taylor, G.; Fergus, R. Adaptive deconvolutional networks for mid and high level feature learning. In Proceedings of the IEEE International Conference on Computer Vision, ICCV 2011, Barcelona, Spain, 6–13 November 2011; pp. 2018–2025. [Google Scholar]
- Shen, D.; Wu, G.; Suk, H. Deep Learning in Medical Image Analysis. Annu. Rev. Biomed. Eng. 2017, 19, 221–248. [Google Scholar] [CrossRef] [Green Version]
- Che, Z.; Purushotham, S.; Cho, K.; Songtag, D.; Liu, Y. Recurrent Neural Networks for Multivariate Time Series with Missing Values. Sci. Rep. 2018, 8, 6085. [Google Scholar] [CrossRef] [Green Version]


| Layer Name | I1 | C2 S3 | C4 S5 | C6 S7 | C8 S9 | C10 S11 | F12 | F13 | O14 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Kernel Size | Pavia | Spectral/ SFMF | 1 × 103/ 1 × 206 | 1 × 8 1 × 2 | 1 × 7 1 × 2 | 1 × 8 1 × 2 | - | - | F | F | 1 × 9 |
| Spatial | 21 × 21 | 3 × 3 2 × 2 | 3 × 3 2 × 2 | - | - | - | 1 × 9 | ||||
| Fre. spectrum | 1 × 103 | 1 × 103 | - | - | - | - | 1 × 9 | ||||
| SFMF-Spa. | 21 × 21 × 80 | 3 × 3 × 3 2 × 2 × 2 | 3 × 3 × 3 2 × 2 × 2 | - | - | - | 1 × 9 | ||||
| Spectral-Spa. | 21 × 21 × 40 | 3 × 3 × 3 2 × 2 × 2 | 3 × 3 × 3 2 × 2 × 2 | - | - | - | 1 × 9 | ||||
| Indian | Spectral/ SFMF | 1 × 220/ 1 × 440 | 1 × 5 1 × 2 | 1 × 5 1 × 2 | 1 × 4 1 × 2 | 1 × 5 1 × 2 | 1 × 4 1 × 2 | 1 × 16 | |||
| Spatial | 21 × 21 | 3 × 3 2 × 2 | 3 × 3 2 × 2 | - | - | - | 1 × 16 | ||||
| Fre. spectrum | 1 × 220 | 1 × 220 | - | - | - | - | 1 × 16 | ||||
| SFMF-Spa. | 21 × 21 × 175 | 3 × 3 × 3 2 × 2 × 2 | 3 × 3 × 3 2 × 2 × 2 | - | - | - | 1 × 16 | ||||
| Spectral-Spa. | 21 × 21 × 100 | 3 × 3 × 3 2 × 2 × 2 | 3 × 3 × 3 2 × 2 × 2 | - | - | - | 1 × 16 | ||||
| Bot | Spectral/ SFMF | 1 × 145/ 1 × 290 | 1 × 8 1 × 2 | 1 × 7 1 × 2 | 1 × 8 1 × 2 | - | - | 1 × 14 | |||
| Spatial | 21 × 21 | 3 × 3 2 × 2 | 3 × 3 2 × 2 | - | - | - | 1 × 14 | ||||
| Fre. spectrum | 1 × 145 | 1 × 145 | - | - | - | - | 1 × 14 | ||||
| SFMF-Spa. | 21 × 21 × 30 | 3 × 3 × 3 2 × 2 × 2 | 3 × 3 × 3 2 × 2 × 2 | - | - | - | 1 × 14 | ||||
| Spectral-Spa. | 21 × 21 × 90 | 3 × 3 × 3 2 × 2 × 2 | 3 × 3 × 3 2 × 2 × 2 | - | - | - | 1 × 14 | ||||
| FeatureMap | Pavia | Spectral/ SFMF | 1 | 6 | 12 | 24 | - | - | 256 | - | 9 |
| Spatial | 1 | 30 | 30 | - | - | - | 400 | 400 | 9 | ||
| Fre. spectrum | 1 | 103 | - | - | - | - | 256 | - | 9 | ||
| SFMF-Spa. | 1 | 6 | 12 | - | - | - | 256 | - | 9 | ||
| Spectral-Spa. | 1 | 6 | 12 | - | - | - | 256 | - | 9 | ||
| Indian | Spectral/ SFMF | 1 | 6 | 12 | 24 | 48 | 96 | 256 | - | 16 | |
| Spatial | 1 | 30 | 30 | - | - | - | 256 | 256 | 16 | ||
| Fre. spectrum | 1 | 220 | - | - | - | - | 256 | - | 16 | ||
| SFMF-Spa. | 1 | 6 | 12 | - | - | - | 256 | - | 16 | ||
| Spectral-Spa. | 1 | 6 | 12 | - | - | - | 256 | - | 16 | ||
| Bot | Spectral/ SFMF | 1 | 6 | 12 | 24 | - | - | 256 | - | 14 | |
| Spatial | 1 | 6 | 12 | - | - | - | 256 | - | 14 | ||
| Fre. spectrum | 1 | 145 | - | - | - | - | 256 | - | 14 | ||
| SFMF-Spa. | 1 | 6 | 12 | - | - | - | 256 | - | 14 | ||
| Spectral-Spa. | 1 | 6 | 12 | - | - | - | 256 | - | 14 | ||
| Ratio of Training Samples | 5% | 10% | 20% | Computational Cost |
|---|---|---|---|---|
| AOA(%) ± SD(%) | AOA(%) ± SD(%) | AOA(%) ± SD(%) | ||
| CNNfre | 89.62 ± 0.42 | 91.73 ± 0.34 | 92.41 ± 0.29 | 2.19 M |
| CNNspe | 91.32 ± 1.32 | 93.06 ± 0.61 | 93.98 ± 0.50 | 5.74 M |
| CNNSFMF | 92.83 ± 0.70 | 94.07 ± 0.36 | 94.65 ± 0.36 | 22.32 M |
| Two-CNNfre-spe | 93.65 ± 0.03 | 94.99 ± 0.03 | 95.74 ± 0.03 | 21.39 M |
| Two-CNNspe-spa | 93.24 ± 0.30 | 96.36 ± 0.71 | 98.54 ± 0.34 | 111.44 M |
| Two-CNNSFMF-spa | 93.41 ± 0.13 | 96.73 ± 0.20 | 98.67 ± 0.05 | 228.41 M |
| Three-CNN | 93.39 ± 0.16 | 96.62 ± 0.18 | 98.55 ± 0.22 | 122.63 M |
| 3-D CNN-PCAspe-spa | 98.37 ± 0.20 | 98.74 ± 1.13 | 99.77 ± 0.06 | 910.15 M |
| 3-D CNN-PCASFMF-spa | 98.51 ± 0.20 | 99.12 ± 0.14 | 99.78 ± 0.05 | 3695.57 M |
| Ratio of Training Samples | 5% | 10% | 20% | Computational Cost |
|---|---|---|---|---|
| AOA(%) ± SD(%) | AOA(%) ± SD(%) | AOA(%) ± SD(%) | ||
| CNNfre | 63.39 ± 0.21 | 70.31 ± 0.39 | 76.84 ± 0.57 | 21.30 M |
| CNNspe | 74.44 ± 1.28 | 81.22 ± 2.30 | 85.75 ± 1.46 | 18.44 M |
| CNNSFMF | 77.06 ± 1.64 | 83.15 ± 1.36 | 86.11 ± 0.82 | 68.71 M |
| Two-CNNfre-spe | 78.28 ± 0.24 | 83.42 ± 0.22 | 87.56 ± 0.31 | 125.48 M |
| Two-CNNspe-spa | 64.50 ± 1.16 | 85.91 ± 0.33 | 95.52 ± 0.35 | 238.18 M |
| Two-CNNSFMF-spa | 68.25 ± 0.20 | 87.87 ± 0.74 | 95.55 ± 0.29 | 502.88 M |
| Three-CNN | 64.77 ± 1.19 | 86.01 ± 0.85 | 95.63 ± 0.14 | 345.22 M |
| 3-D CNN-PCAspe-spa | 93.16 ± 0.42 | 97.37 ± 0.11 | 99.00 ± 0.17 | 5790.30 M |
| 3-D CNN-PCASFMF-spa | 94.67 ± 0.42 | 97.63 ± 0.25 | 99.07 ± 0.16 | 17,811.00 M |
| Ratio of Training Samples | 5% | 10% | 20% | Computational Cost |
|---|---|---|---|---|
| AOA(%) ± SD(%) | AOA(%) ± SD(%) | AOA(%) ± SD(%) | ||
| CNNfre | 83.19 ± 0.29 | 89.09 ± 0.71 | 91.93 ± 0.17 | 6.10 M |
| CNNspe | 85.88 ± 1.47 | 89.39 ± 1.28 | 93.35 ± 0.62 | 11.28 M |
| CNNSFMF | 87.08 ± 0.41 | 91.37 ± 0.47 | 93.74 ± 0.75 | 43.40 M |
| Two-CNNfre-spe | 86.98 ± 0.29 | 91.43 ± 0.47 | 94.63 ± 0.26 | 42.14 M |
| Two-CNNspe-spa | 63.84 ± 0.71 | 84.59 ± 0.62 | 91.50 ± 0.37 | 40.21 M |
| Two-CNNSFMF-spa | 65.07 ± 0.75 | 84.87 ± 1.07 | 92.21 ± 0.29 | 100.59 M |
| Three-CNN | 72.47 ± 1.42 | 85.17 ± 0.70 | 93.19 ± 0.28 | 71.06 M |
| 3-D CNN-PCAspe-spa | 90.84 ± 0.87 | 98.15 ± 0.48 | 99.68 ± 0.20 | 4684.49 M |
| 3-D CNN-PCASFMF-spa | 93.41 ± 0.87 | 98.63 ± 0.44 | 99.70 ± 0.11 | 506.36 M |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Yang, Z.; Liu, Y.; Mu, C. Hyperspectral Remote Sensing Images Deep Feature Extraction Based on Mixed Feature and Convolutional Neural Networks. Remote Sens. 2021, 13, 2599. https://doi.org/10.3390/rs13132599
Liu J, Yang Z, Liu Y, Mu C. Hyperspectral Remote Sensing Images Deep Feature Extraction Based on Mixed Feature and Convolutional Neural Networks. Remote Sensing. 2021; 13(13):2599. https://doi.org/10.3390/rs13132599
Chicago/Turabian StyleLiu, Jing, Zhe Yang, Yi Liu, and Caihong Mu. 2021. "Hyperspectral Remote Sensing Images Deep Feature Extraction Based on Mixed Feature and Convolutional Neural Networks" Remote Sensing 13, no. 13: 2599. https://doi.org/10.3390/rs13132599
APA StyleLiu, J., Yang, Z., Liu, Y., & Mu, C. (2021). Hyperspectral Remote Sensing Images Deep Feature Extraction Based on Mixed Feature and Convolutional Neural Networks. Remote Sensing, 13(13), 2599. https://doi.org/10.3390/rs13132599






