Simulation of Earth’s Outward Radiative Flux and Its Radiance in Moon-Based View
Abstract
:1. Introduction
2. Materials and Methods
2.1. The ERA5 Reanalysis
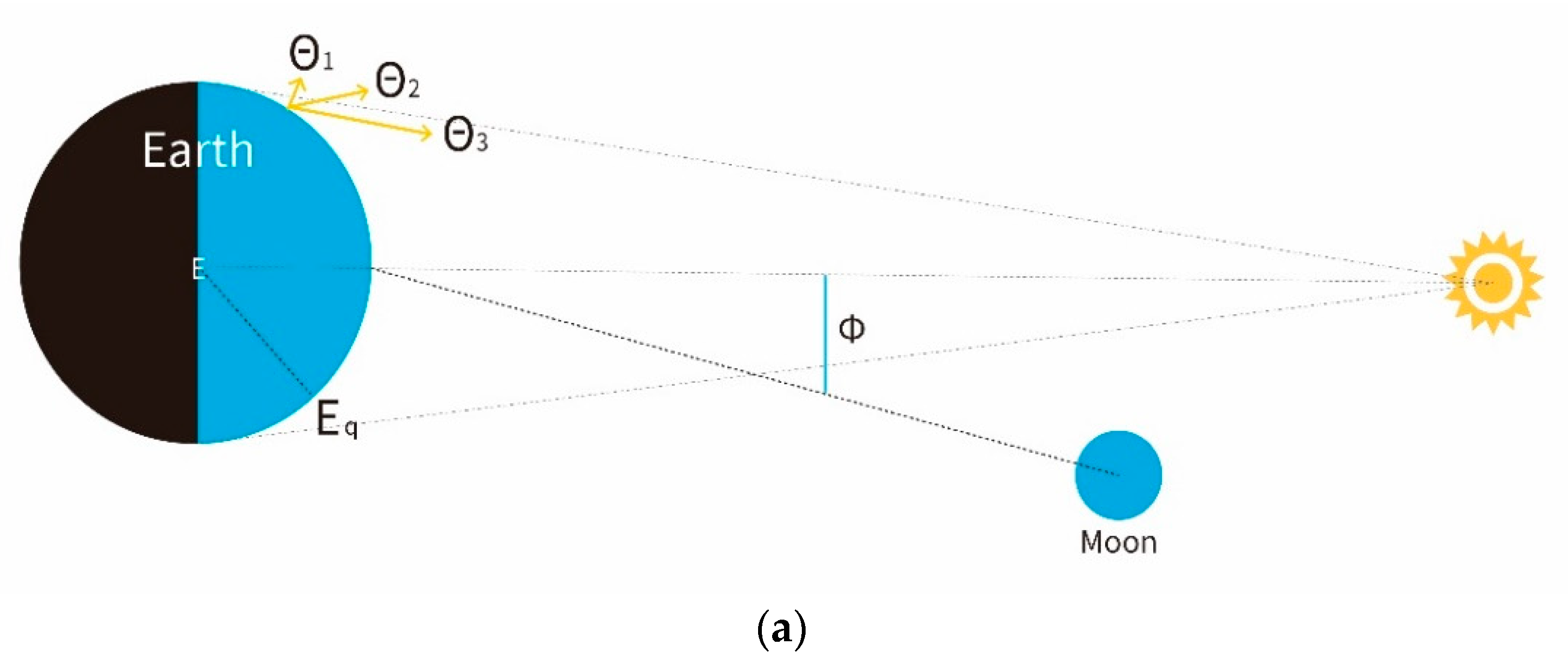
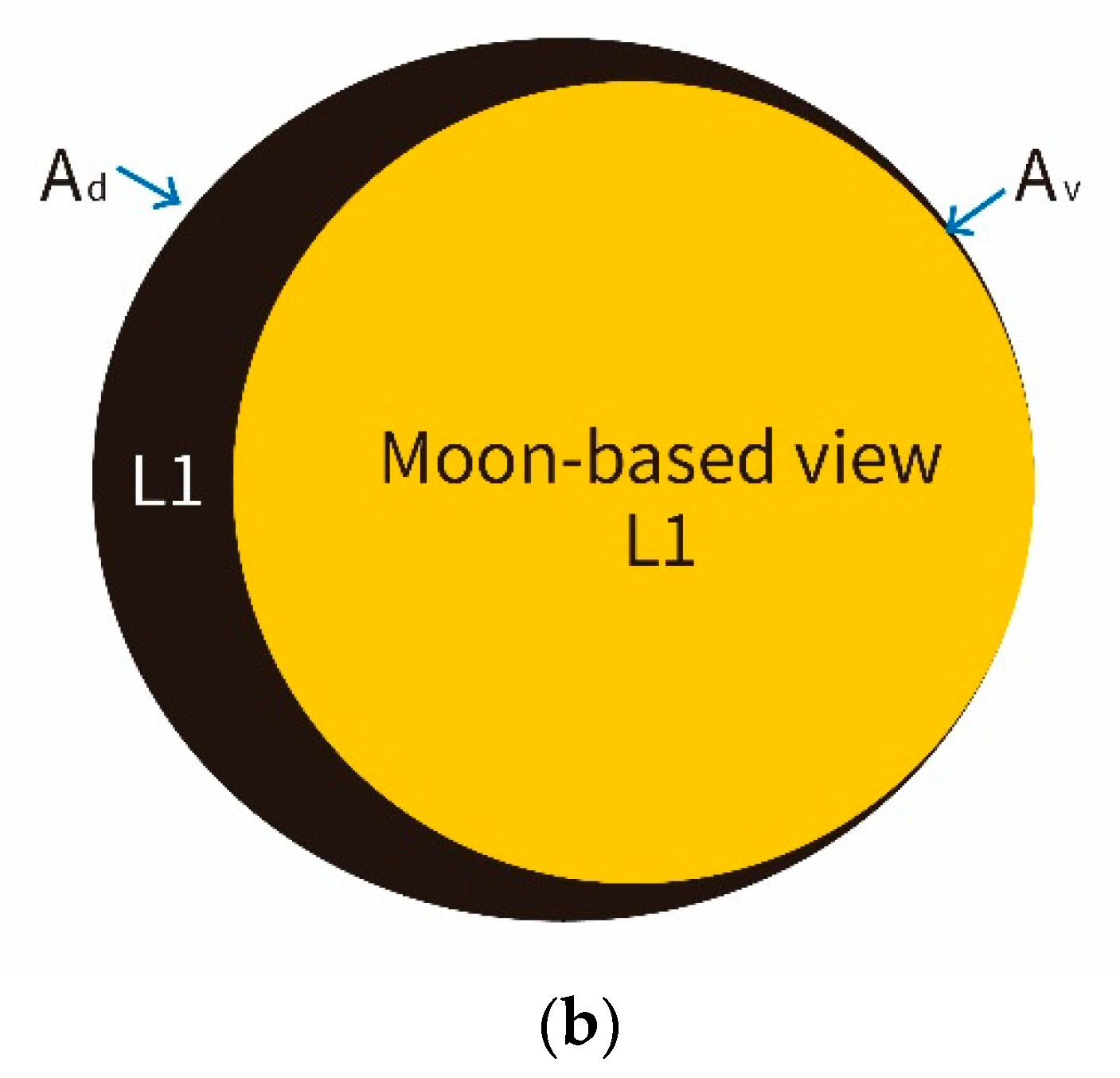
2.2. CERES ADM Model to Simulate Regional Radiance
2.3. Global ADM Model
2.4. The Parameters Identify the Scene Type of CERES/TRMM ADMs
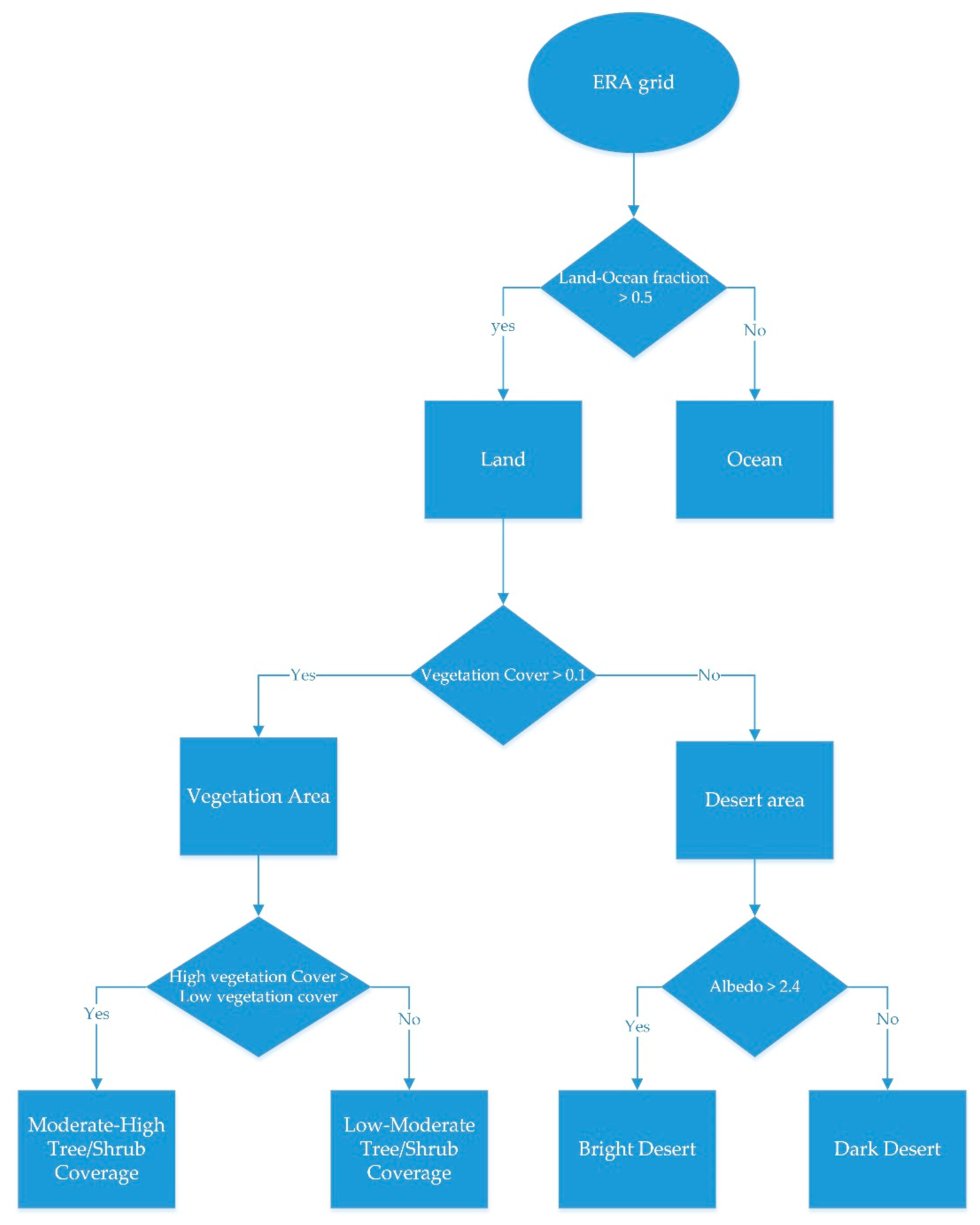
2.4.1. Surface Type
2.4.2. Cloud Category
2.4.3. Cloud Optical Depth
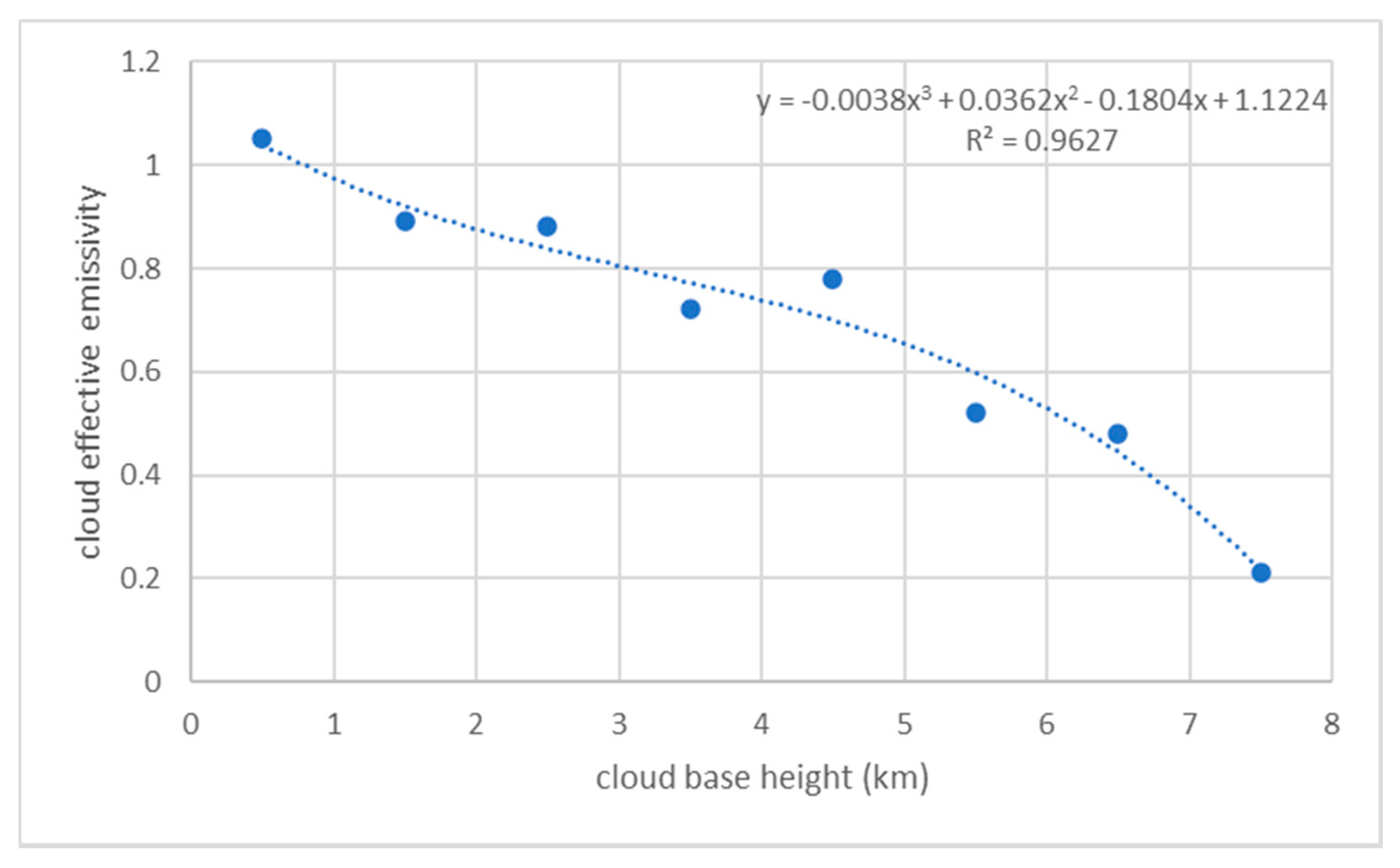
2.4.4. Vertical Temperature Change and Cloud Effective Emissivity
3. Results
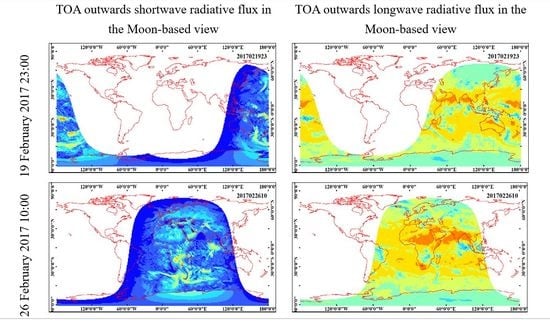
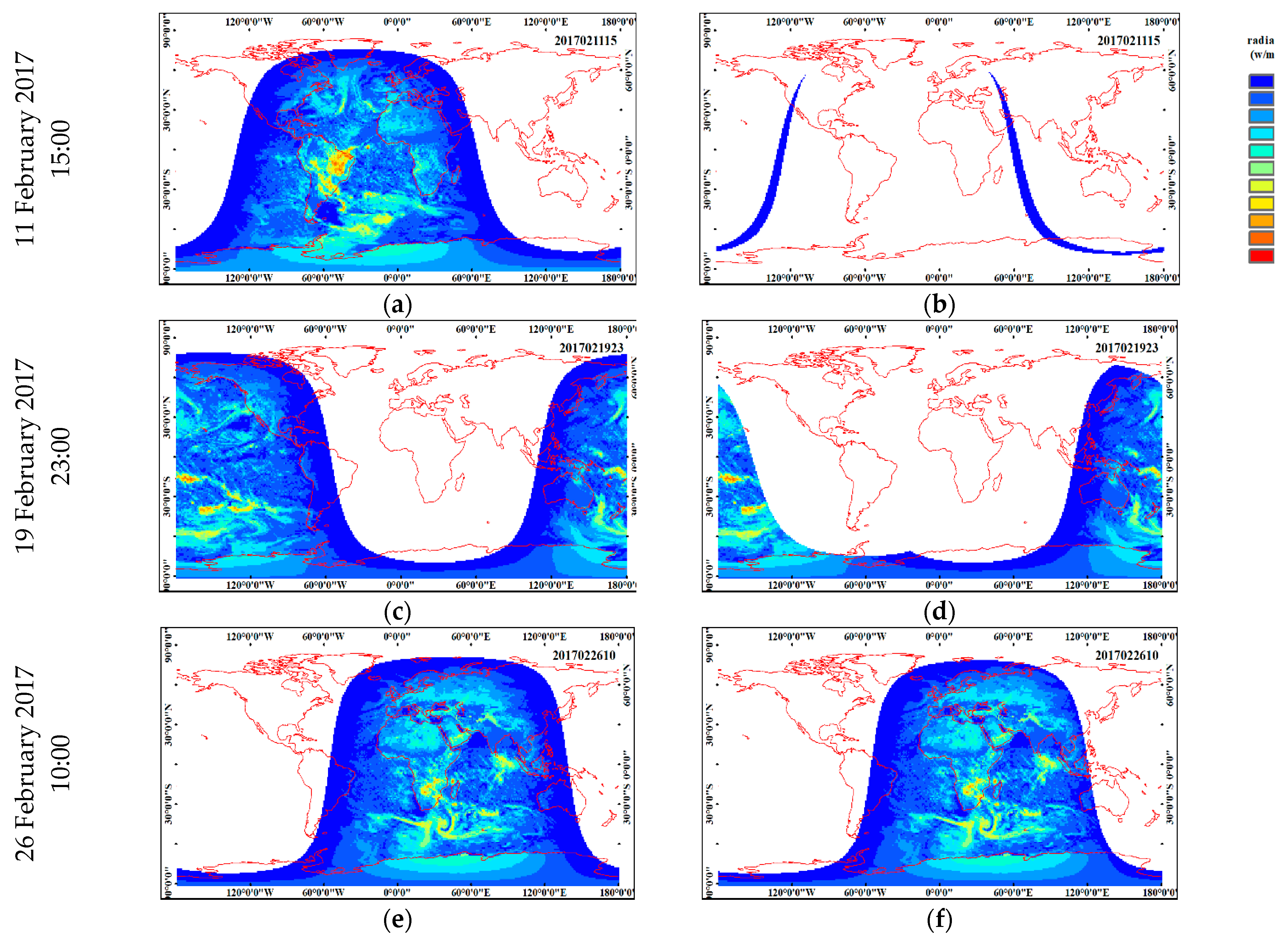
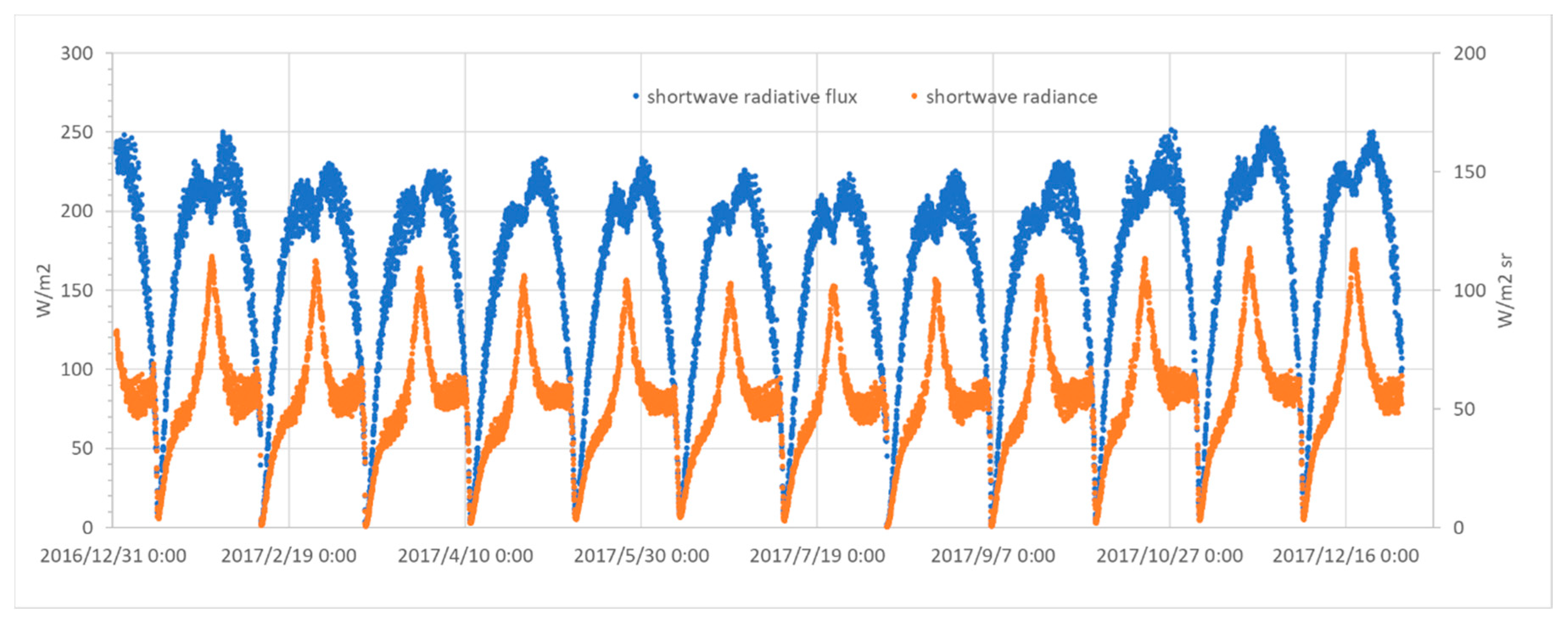
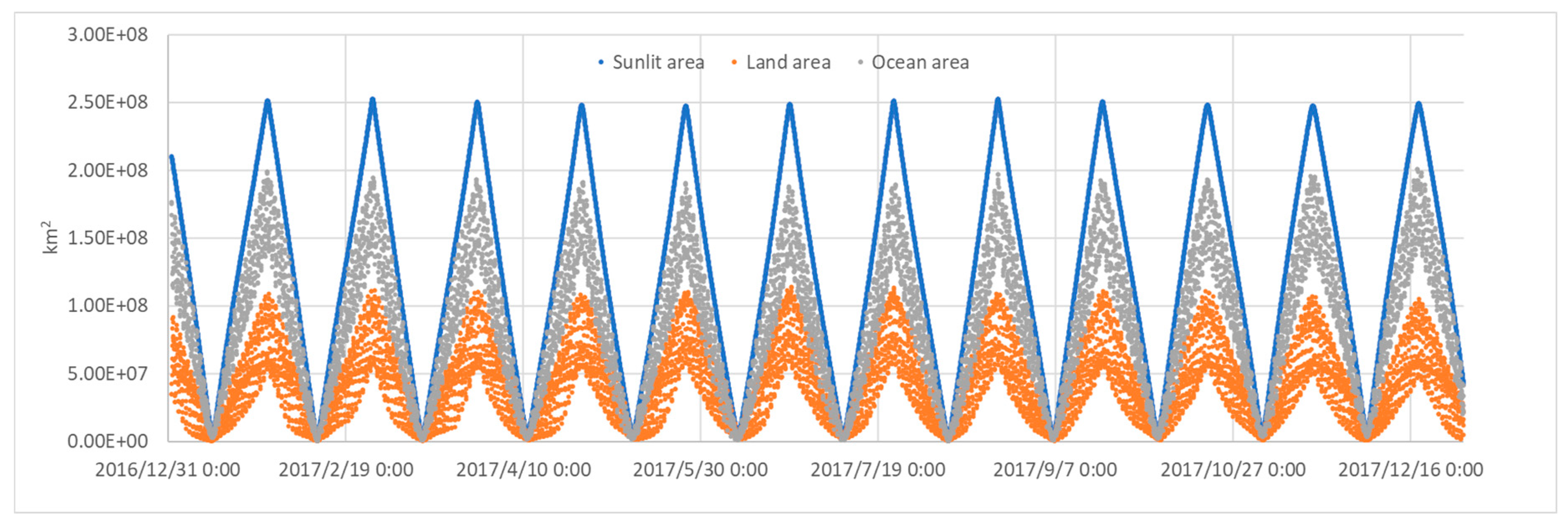
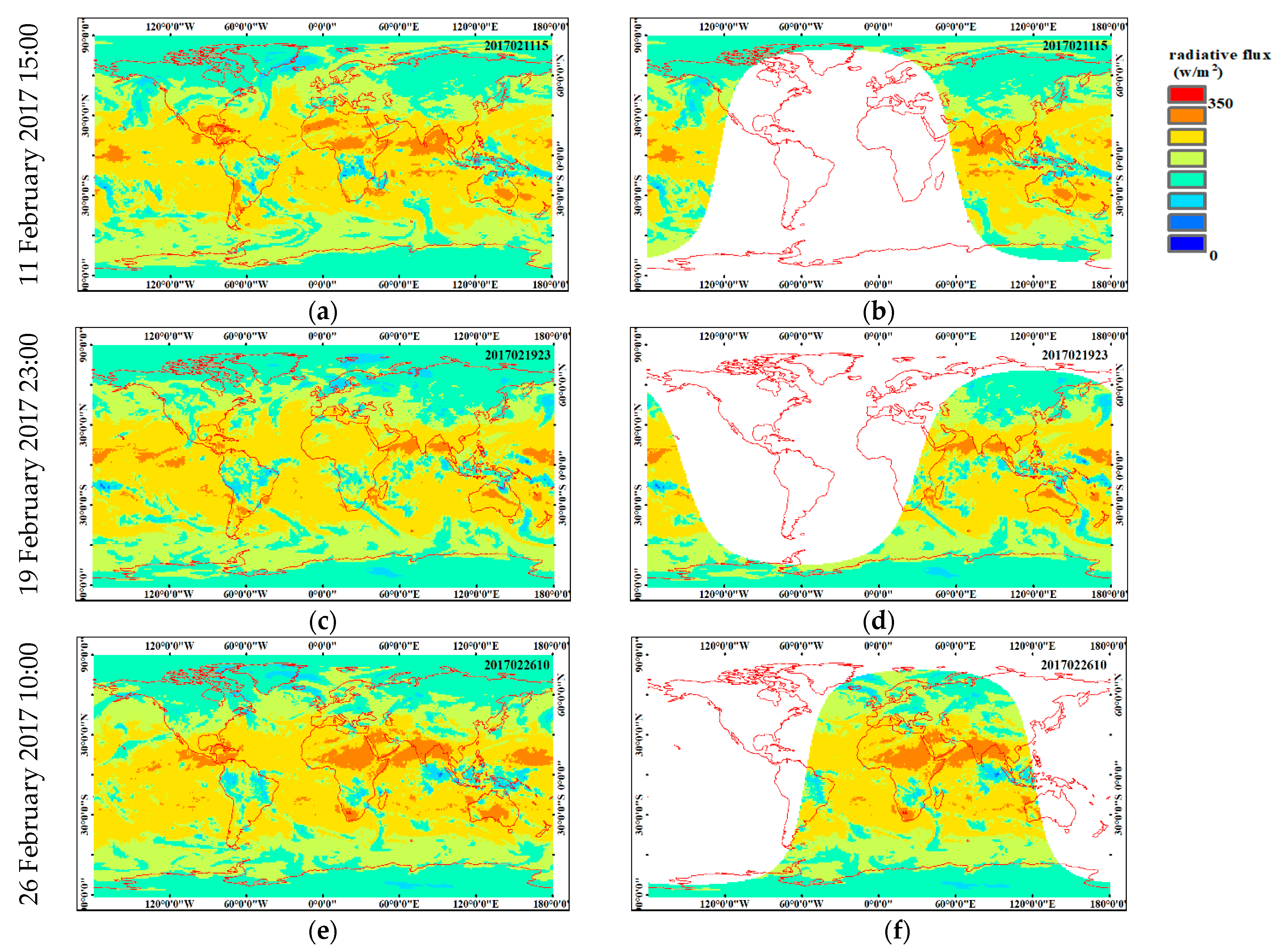
3.1. Global Mean Outward Shortwave Radiative Flux and Its Radiance of Earth in the Moon-Based View
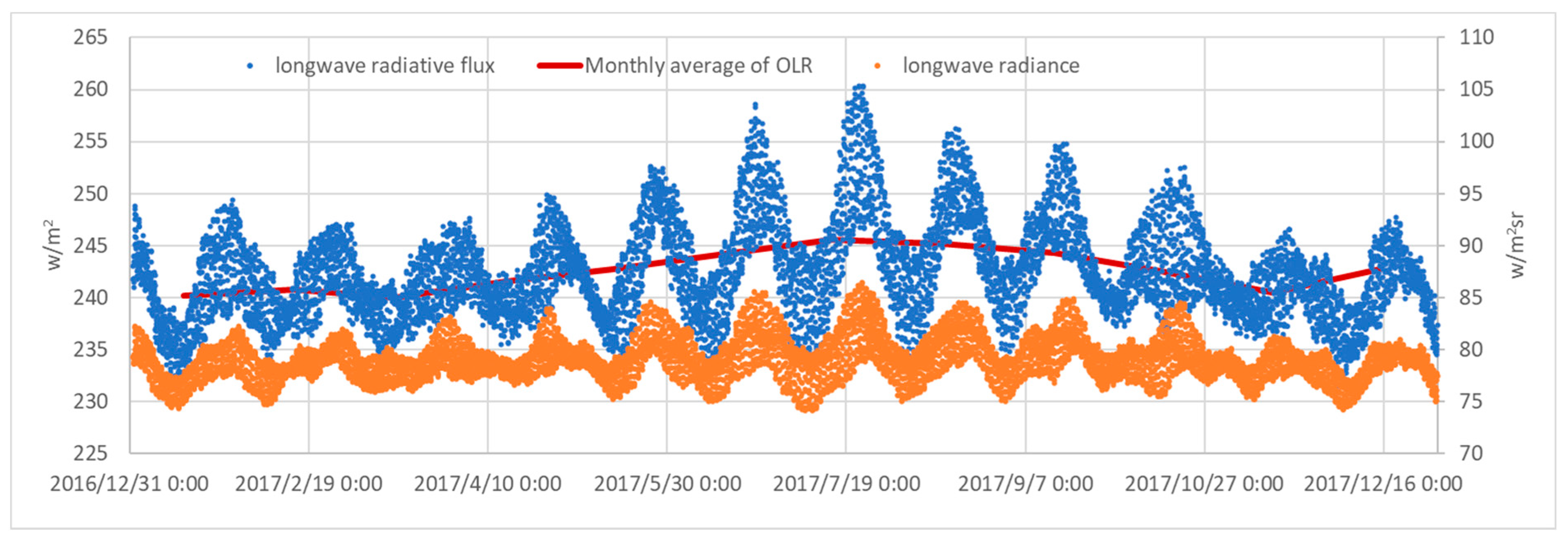
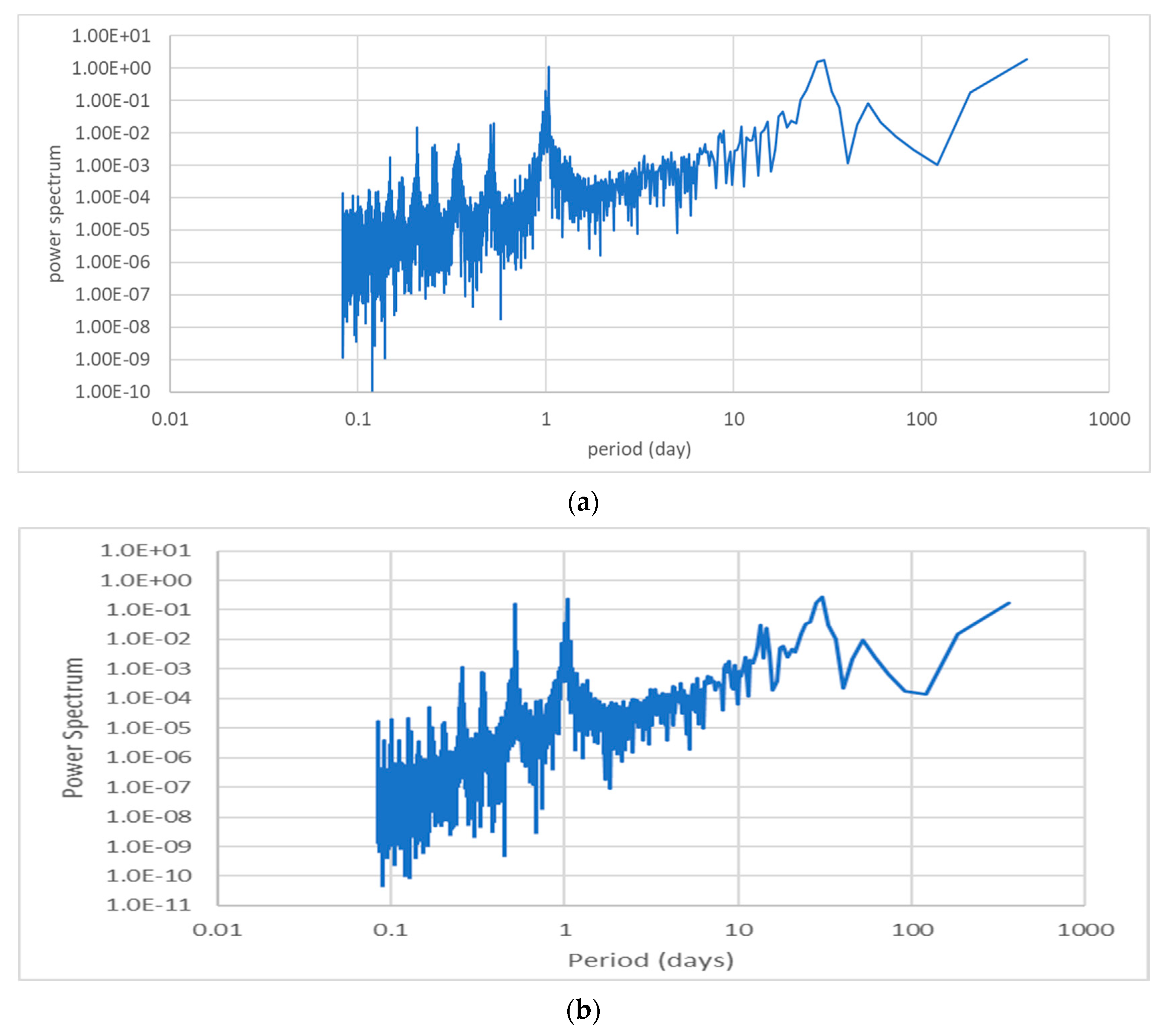
3.2. Global Mean Outward Longwave Radiative Flux and Its Radiance of Earth in the Moon-Based View
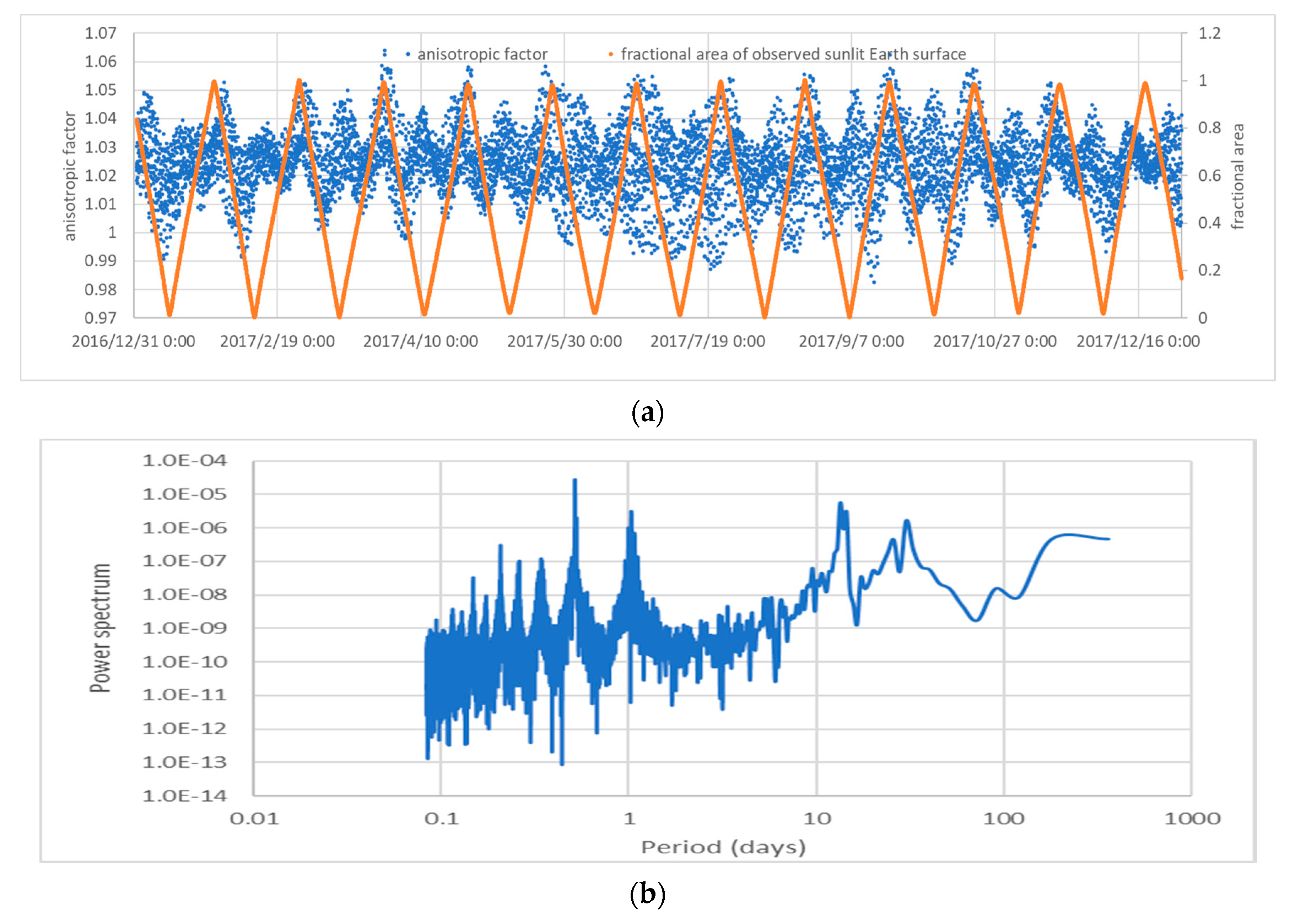
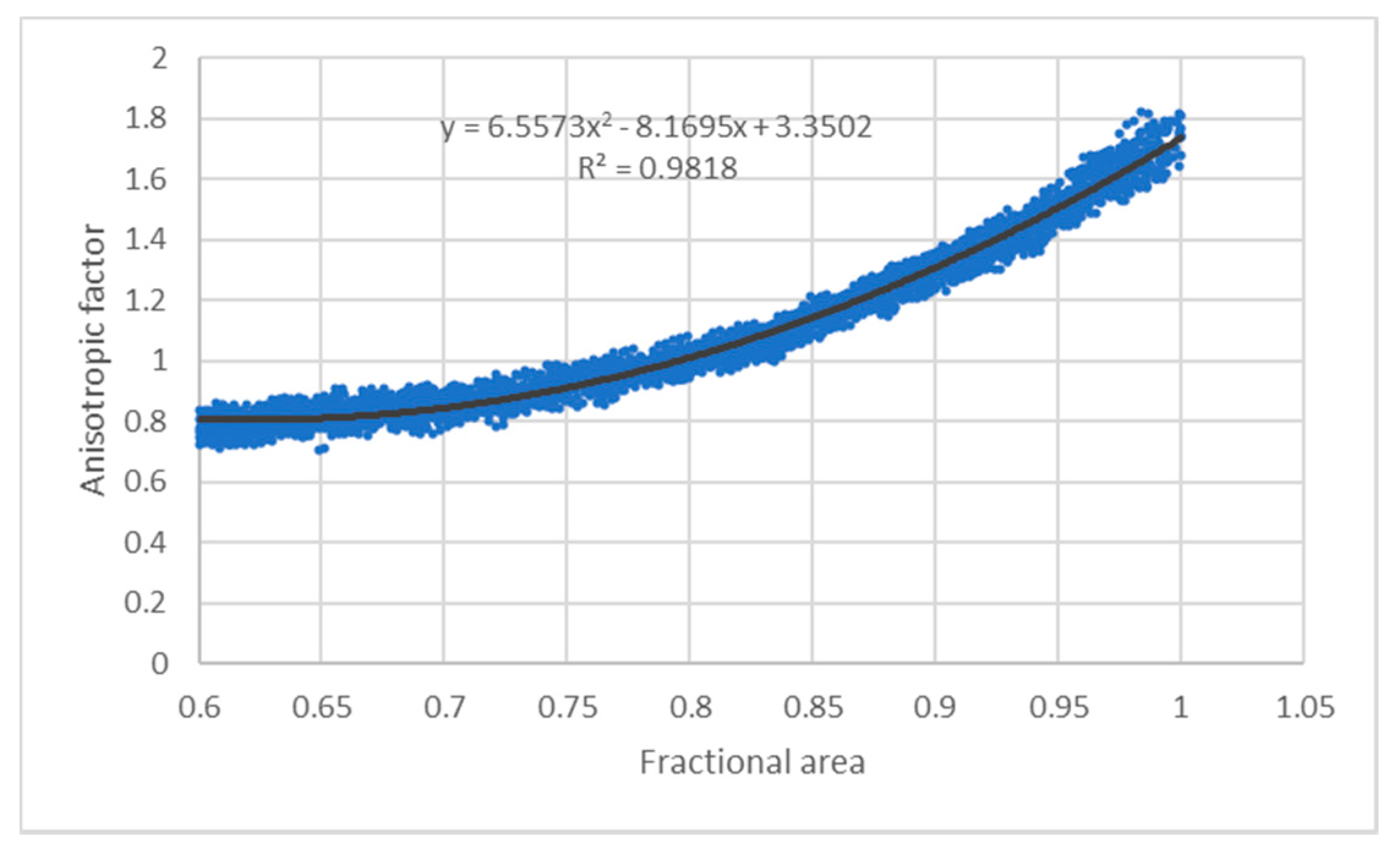
3.3. Anisotropic Factor of the Global ADM
4. Discussion
4.1. Impact of Earth Climate on the Radiance of the Earth Surface in the Moon-Based View
4.2. Implication for Exoplanet Studies from Moon-Based Radiatiance Observations
4.3. Error Analysis for the Simulations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Stephens, G.L.; Li, J.; Wild, M.; Clayson, C.A.; Loeb, N.; Kato, S.; L’ecuyer, T.; Stackhouse, P.W.; Lebsock, M.; Andrews, T. An update on earth’s energy balance in light of the latest global observations. Nat. Geosci. 2012, 5, 691–696. [Google Scholar] [CrossRef]
- Von Schuckmann, K.; Palmer, M.; Trenberth, K.E.; Cazenave, A.; Chambers, D.; Champollion, N.; Hansen, J.; Josey, S.; Loeb, N.; Mathieu, P.-P. An imperative to monitor earth’s energy imbalance. Nat. Clim. Chang. 2016, 6, 138–144. [Google Scholar] [CrossRef] [Green Version]
- House, F.B.; Gruber, A.; Hunt, G.E.; Mecherikunnel, A.T. History of satellite missions and measurements of the earth radiation budget (1957–1984). Rev. Geophys. 1986, 24, 357–377. [Google Scholar] [CrossRef]
- Carlson, B.; Lacis, A.; Colose, C.; Marshak, A.; Su, W.; Lorentz, S. Spectral signature of the biosphere: Nistar finds it in our solar system from the lagrangian l-1 point. Geophys. Res. Lett. 2019, 46, 10679–10686. [Google Scholar] [CrossRef]
- Jiang, J.H.; Zhai, A.J.; Herman, J.; Zhai, C.; Hu, R.; Su, H.; Natraj, V.; Li, J.; Xu, F.; Yung, Y.L. Using deep space climate observatory measurements to study the earth as an exoplanet. Astron. J. 2018, 156, 26. [Google Scholar] [CrossRef]
- Schwieterman, E.W.; Kiang, N.Y.; Parenteau, M.N.; Harman, C.E.; DasSarma, S.; Fisher, T.M.; Arney, G.N.; Hartnett, H.E.; Reinhard, C.T.; Olson, S.L. Exoplanet biosignatures: A review of remotely detectable signs of life. Astrobiology 2018, 18, 663–708. [Google Scholar] [CrossRef]
- Barkstrom, B.R. The earth radiation budget experiment (erbe). Bull. Am. Meteorol. Soc. 1984, 65, 1170–1185. [Google Scholar] [CrossRef]
- Kandel, R.; Viollier, M.; Raberanto, P.; Duvel, J.P.; Pakhomov, L.; Golovko, V.; Trishchenko, A.; Mueller, J.; Raschke, E.; Stuhlmann, R. The scarab earth radiation budget dataset. Bull. Am. Meteorol. Soc. 1998, 79, 765–784. [Google Scholar] [CrossRef] [Green Version]
- Wielicki, B.A.; Barkstrom, B.R.; Harrison, E.F.; Lee, R.B., III; Smith, G.L.; Cooper, J.E. Clouds and the earth’s radiant energy system (ceres): An earth observing system experiment. Bull. Am. Meteorol. Soc. 1996, 77, 853–868. [Google Scholar] [CrossRef] [Green Version]
- Doelling, D.R.; Loeb, N.G.; Keyes, D.F.; Nordeen, M.L.; Morstad, D.; Nguyen, C.; Wielicki, B.A.; Young, D.F.; Sun, M. Geostationary enhanced temporal interpolation for ceres flux products. J. Atmos. Ocean. Technol. 2013, 30, 1072–1090. [Google Scholar] [CrossRef]
- Su, W.; Liang, L.; Doelling, D.R.; Minnis, P.; Duda, D.P.; Khlopenkov, K.; Thieman, M.M.; Loeb, N.G.; Kato, S.; Valero, F.P. Determining the shortwave radiative flux from earth polychromatic imaging camera. J. Geophys. Res. Atmos. 2018, 123, 11479–411491. [Google Scholar] [CrossRef]
- Su, W.; Minnis, P.; Liang, L.; Duda, D.P.; Khlopenkov, K.; Thieman, M.M.; Yu, Y.; Smith, A.; Lorentz, S.; Feldman, D. Determining the daytime earth radiative flux from national institute of standards and technology advanced radiometer (nistar) measurements. Atmos. Meas. Tech. 2020, 13, 429–443. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Marshak, A.; Várnai, T.; Knyazikhin, Y. Epic spectral observations of variability in earth’s global reflectance. Remote Sens. 2018, 10, 254. [Google Scholar] [CrossRef] [Green Version]
- Ding, Y.; Guo, H.; Liu, G.; Han, C.; Shang, H.; Ruan, Z.; Lv, M. Constructing a high-accuracy geometric model for moon-based earth observation. Remote Sens. 2019, 11, 2611. [Google Scholar] [CrossRef] [Green Version]
- Guo, H.; Ding, Y.; Liu, G.; Zhang, D.; Fu, W.; Zhang, L. Conceptual study of lunar-based sar for global change monitoring. Sci. China Earth Sci. 2014, 57, 1771–1779. [Google Scholar] [CrossRef]
- Guo, H.; Liu, G.; Ding, Y. Moon-based earth observation: Scientific concept and potential applications. Int. J. Digit. Earth 2018, 11, 546–557. [Google Scholar] [CrossRef]
- Guo, H.; Ren, Y.; Liu, G.; Ye, H. The angular characteristics of moon-based earth observations. Int. J. Digit. Earth 2020, 13, 339–354. [Google Scholar] [CrossRef]
- Pallé, E.; Goode, P. The lunar terrestrial observatory: Observing the earth using photometers on the moon’s surface. Adv. Space Res. 2009, 43, 1083–1089. [Google Scholar] [CrossRef]
- Klindžić, D.; Stam, D.M.; Snik, F.; Keller, C.; Hoeijmakers, H.; van Dam, D.; Willebrands, M.; Karalidi, T.; Pallichadath, V.; van Dijk, C. Loupe: Observing earth from the moon to prepare for detecting life on earth-like exoplanets. Philos. Trans. R. Soc. A 2021, 379, 20190577. [Google Scholar] [CrossRef]
- Shang, H.; Jia, L.; Menenti, M. Modeling and reconstruction of time series of passive microwave data by discrete fourier transform guided filtering and harmonic analysis. Remote Sens. 2016, 8, 970. [Google Scholar] [CrossRef] [Green Version]
- Loeb, N.G.; Manalo-Smith, N.; Kato, S.; Miller, W.F.; Gupta, S.K.; Minnis, P.; Wielicki, B.A. Angular distribution models for top-of-atmosphere radiative flux estimation from the clouds and the earth’s radiant energy system instrument on the tropical rainfall measuring mission satellite. Part I: Methodology. J. Appl. Meteorol. 2003, 42, 240–265. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D. The era5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Sianturi, Y.; Marjuki; Sartika, K. Evaluation of era5 and merra2 reanalyses to estimate solar irradiance using ground observations over indonesia Region. In Proceedings of the AIP Conference Proceedings, Yogyakarta, Indonesia, 30–31 October 2019; AIP Publishing LLC: Melville, NY, USA, 2020; p. 020002. [Google Scholar]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I. Era5 hourly data on single levels from 1979 to present. Copernicus climate change service (c3s) climate data store (cds). 2018. [Google Scholar]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I. Era5 hourly data on pressure levels from 1979 to present. Copernicus climate change service (c3s) climate data store (cds). 2018. [Google Scholar]
- Su, W.; Corbett, J.; Eitzen, Z.; Liang, L. Next-generation angular distribution models for top-of-atmosphere radiative flux calculation from ceres instruments: Methodology. Atmos. Meas. Tech. 2015, 8, 611–632. [Google Scholar] [CrossRef] [Green Version]
- Hurk, B.J.J.v.d.; Viterbo, P.; Beljaars, A.; Betts, A. Offline validation of the era40 surface scheme. In ECMWF Technical Memoranda; ECMWF: Shinfield Park, Reading, UK, 2000. [Google Scholar]
- Lucht, W.; Hyman, A.H.; Strahler, A.H.; Barnsley, M.J.; Hobson, P.; Muller, J.-P. A comparison of satellite-derived spectral albedos to ground-based broadband albedo measurements modeled to satellite spatial scale for a semidesert landscape. Remote Sens. Environ. 2000, 74, 85–98. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, T.; Wu, Y.; Niu, Z.; Wang, Q. Cloud effective emissivity retrievals using combined ground-based infrared cloud measuring instrument and ceilometer observations. Remote Sens. 2018, 10, 2033. [Google Scholar] [CrossRef] [Green Version]
- Koll, D.D.; Cronin, T.W. Earth’s outgoing longwave radiation linear due to h2o greenhouse effect. Proc. Natl. Acad. Sci. USA 2018, 115, 10293–10298. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Y.; Jeevanjee, N.; Fueglistaler, S. Linearity of outgoing longwave radiation: From an atmospheric column to global climate models. Geophys. Res. Lett. 2020, 47, e2020GL089235. [Google Scholar] [CrossRef]
- Feulner, G.; Rahmstorf, S.; Levermann, A.; Volkwardt, S. On the origin of the surface air temperature difference between the hemispheres in earth’s present-day climate. J. Clim. 2013, 26, 7136–7150. [Google Scholar] [CrossRef]
- Kang, S.M.; Seager, R.; Frierson, D.M.; Liu, X. Croll revisited: Why is the northern hemisphere warmer than the southern hemisphere? Clim. Dyn. 2015, 44, 1457–1472. [Google Scholar] [CrossRef]
- Li, Q.; Ma, M.; Wu, X.; Yang, H. Snow cover and vegetation-induced decrease in global albedo from 2002 to 2016. J. Geophys. Res. Atmos. 2018, 123, 124–138. [Google Scholar] [CrossRef] [Green Version]
- Stephens, G.L.; O’Brien, D.; Webster, P.J.; Pilewski, P.; Kato, S.; Li, J.l. The albedo of earth. Rev. Geophys. 2015, 53, 141–163. [Google Scholar] [CrossRef] [Green Version]
- Myhre, G.; Samset, B.H.; Hodnebrog, Ø.; Andrews, T.; Boucher, O.; Faluvegi, G.; Fläschner, D.; Forster, P.; Kasoar, M.; Kharin, V. Sensible heat has significantly affected the global hydrological cycle over the historical period. Nat. Commun. 2018, 9, 1–9. [Google Scholar] [CrossRef]
- Karalidi, T.; Stam, D.; Snik, F.; Bagnulo, S.; Sparks, W.; Keller, C. Observing the earth as an exoplanet with loupe, the lunar observatory for unresolved polarimetry of earth. Planet. Space Sci. 2012, 74, 202–207. [Google Scholar] [CrossRef] [Green Version]
- Sagan, C.; Pollack, J.B. Anisotropic nonconservative scattering and the clouds of venus. J. Geophys. Res. 1967, 72, 469–477. [Google Scholar] [CrossRef]
- Babar, B.; Graversen, R.; Boström, T. Solar radiation estimation at high latitudes: Assessment of the cmsaf databases, asr and era5. Solar Energy 2019, 182, 397–411. [Google Scholar] [CrossRef]
- Loeb, N.G.; Loukachine, K.; Manalo-Smith, N.; Wielicki, B.A.; Young, D.F. Angular distribution models for top-of-atmosphere radiative flux estimation from the clouds and the earth’s radiant energy system instrument on the tropical rainfall measuring mission satellite. Part II: Validation. J. Appl. Meteorol. 2003, 42, 1748–1769. [Google Scholar] [CrossRef]



| Variables | Unit | Spatial Coverage | Spatial Resolution (°) | Temporal Resolution |
|---|---|---|---|---|
| TOA incident solar radiation data (radiant exposure) | J·m−2 | global | 1 | hourly |
| Top net solar radiation data (radiant exposure) | J·m−2 | global | 1 | hourly |
| Top net thermal radiation data (radiant exposure) | J·m−2 | global | 1 | hourly |
| Wavelength | Parameters | Definition | ERA5 Data |
|---|---|---|---|
| Shortwave | Surface type | Ocean | Land–ocean mask, high vegetation cover, low vegetation cover, albedo |
| Bright desert | |||
| Dark desert | |||
| Moderate–high tree/shrub coverage | |||
| Low–moderate tree/shrub coverage | |||
| Cloud category | Clear sky | Total cloud cover, total column cloud ice water, total column cloud liquid water | |
| Ice cloud | |||
| Liquid cloud | |||
| Cloud fraction | Percentage of cloud cover | total cloud cover | |
| Cloud Optical depth | Cloud visible optical depth | TOA incident solar radiation, total sky direct solar radiation at surface | |
| Wind speed | Surface wind speed only for ocean under clear sky | 10 m u-component of wind, 10 m v-component of wind | |
| Longwave | Surface type | Land | Land–ocean mask, high vegetation cover, low vegetation cover |
| Desert | |||
| Ocean | |||
| Cloud category | Clear sky (cloud fraction < 0.01%) | Low cloud cover | |
| Broken cloud (0.01% < cloud fraction < 99.9%) | |||
| Overcast (cloud fraction > 99.9%) | |||
| Cloud fraction | Percentage of cloud cover | Total cloud cover | |
| Precipitable water | Water vapor burden from surface to TOA | Total column water | |
| Vertical temperature change | Indicator of the lapse rate under clear sky | Skin temperature, air temperature at 700 hpa, cloud base height | |
| Indicator of cloud base height | |||
| Cloud effective emissivity | Cloud effective emissivity at VIRS 11-μm, an indicator for mean emissivity of cloud at longwave | Cloud base height |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, H.; Ding, Y.; Guo, H.; Liu, G.; Liu, X.; Wu, J.; Liang, L.; Jiang, H.; Chen, G. Simulation of Earth’s Outward Radiative Flux and Its Radiance in Moon-Based View. Remote Sens. 2021, 13, 2535. https://doi.org/10.3390/rs13132535
Shang H, Ding Y, Guo H, Liu G, Liu X, Wu J, Liang L, Jiang H, Chen G. Simulation of Earth’s Outward Radiative Flux and Its Radiance in Moon-Based View. Remote Sensing. 2021; 13(13):2535. https://doi.org/10.3390/rs13132535
Chicago/Turabian StyleShang, Haolu, Yixing Ding, Huadong Guo, Guang Liu, Xiaoyu Liu, Jie Wu, Lei Liang, Hao Jiang, and Guoqiang Chen. 2021. "Simulation of Earth’s Outward Radiative Flux and Its Radiance in Moon-Based View" Remote Sensing 13, no. 13: 2535. https://doi.org/10.3390/rs13132535
APA StyleShang, H., Ding, Y., Guo, H., Liu, G., Liu, X., Wu, J., Liang, L., Jiang, H., & Chen, G. (2021). Simulation of Earth’s Outward Radiative Flux and Its Radiance in Moon-Based View. Remote Sensing, 13(13), 2535. https://doi.org/10.3390/rs13132535