Optimization of Aerosol Model Selection for TROPOMI/S5P
Abstract
:1. Introduction
2. Methodology
- is a Gaussian random vector with zero mean and covariance matrix , where is the measurement error variance and a normalized measurement error covariance matrix;
- is a Gaussian random vector with zero mean and covariance matrix , where is the aerosol model error variance and the identity matrix; and
- and are independent random vectors,
3. Aerosol Models
- non-absorbing (NONABS) aerosols, generated from fossil fuel combustion in urban-industrial areas;
- moderately absorbing (MODABS) aerosols;
- absorbing (ABS) aerosols, generated from biomass burning; and
- desert dust (DUST), originated from desert and transported by wind.
- weakly absorbing (WA),
- biomass burning (BB),
- desert dust (DD),
- marine (MA), and
- volcanic (VO).
4. Tests with Synthetic Data
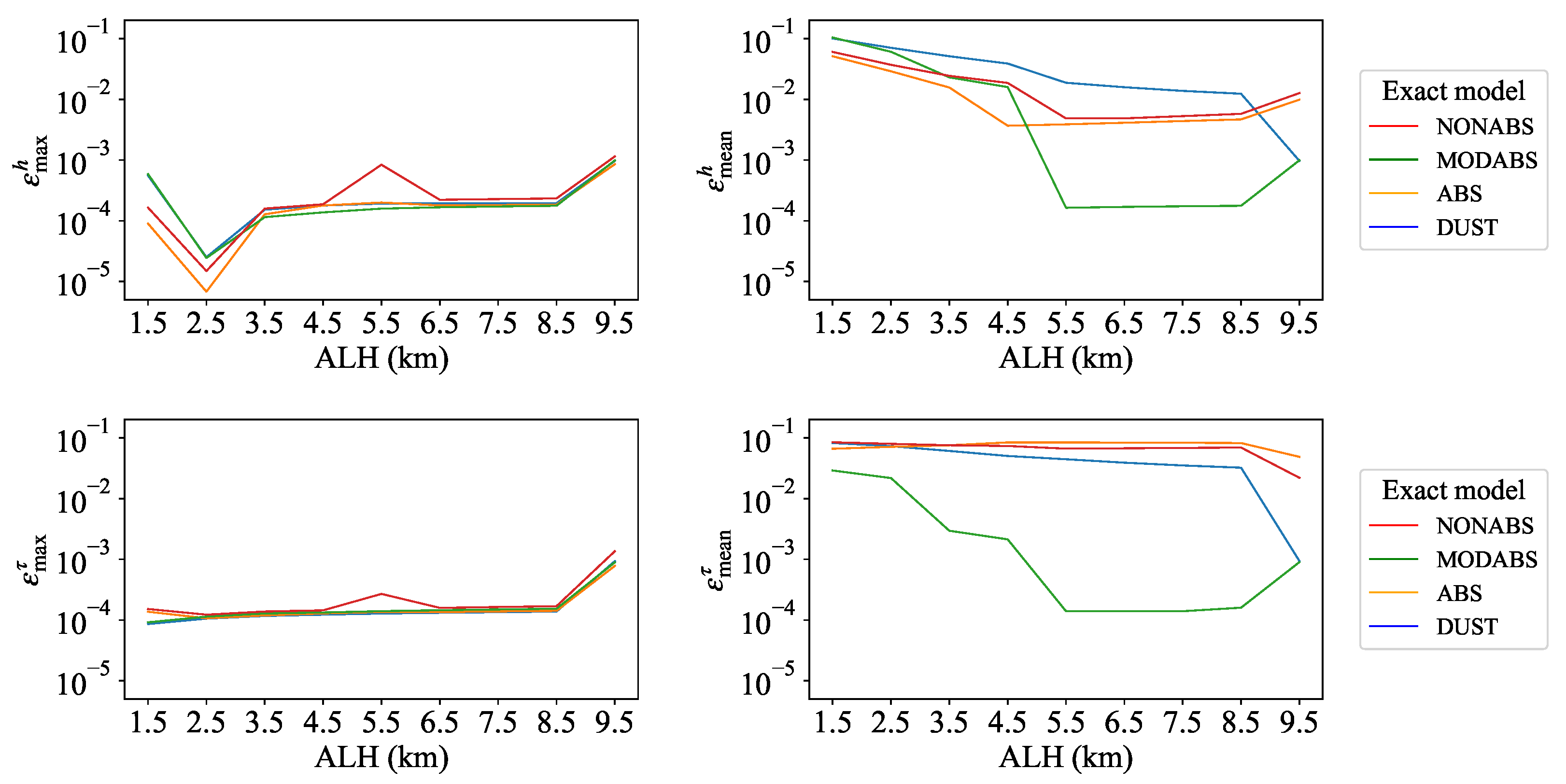
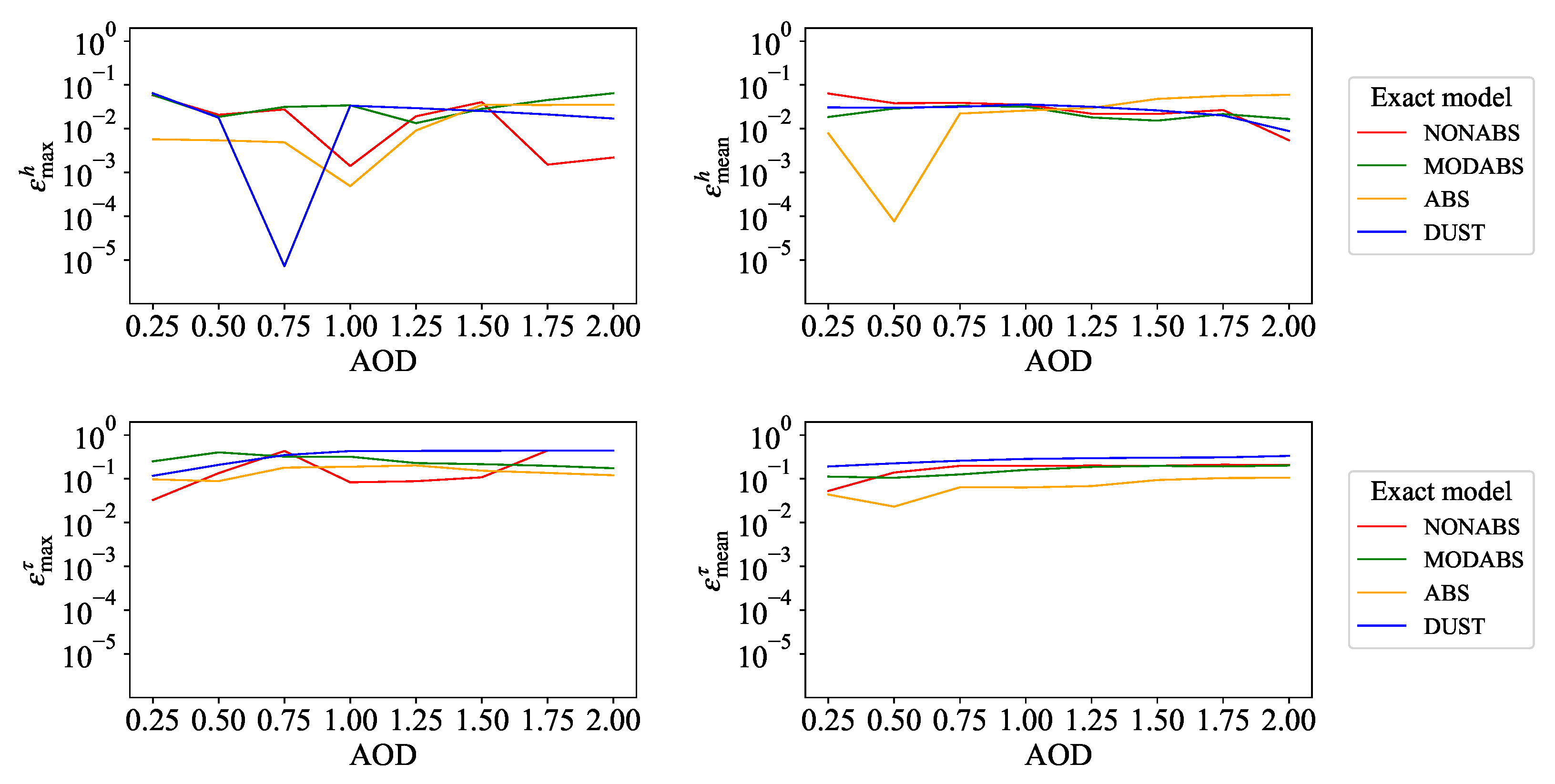
4.1. Test 1
- The relative errors corresponding to the maximum solution estimate ( and ) are considered to be acceptable according to the scientific requirements defined in the pre-launch characterization tests and significantly smaller than those corresponding to the mean solution estimate ( and ). Thus, the retrieval algorithm can recognize correctly the exact aerosol model.
- For the maximum solution estimate, the retrieved aerosol optical depth achieves a higher accuracy than the retrieved aerosol layer height.
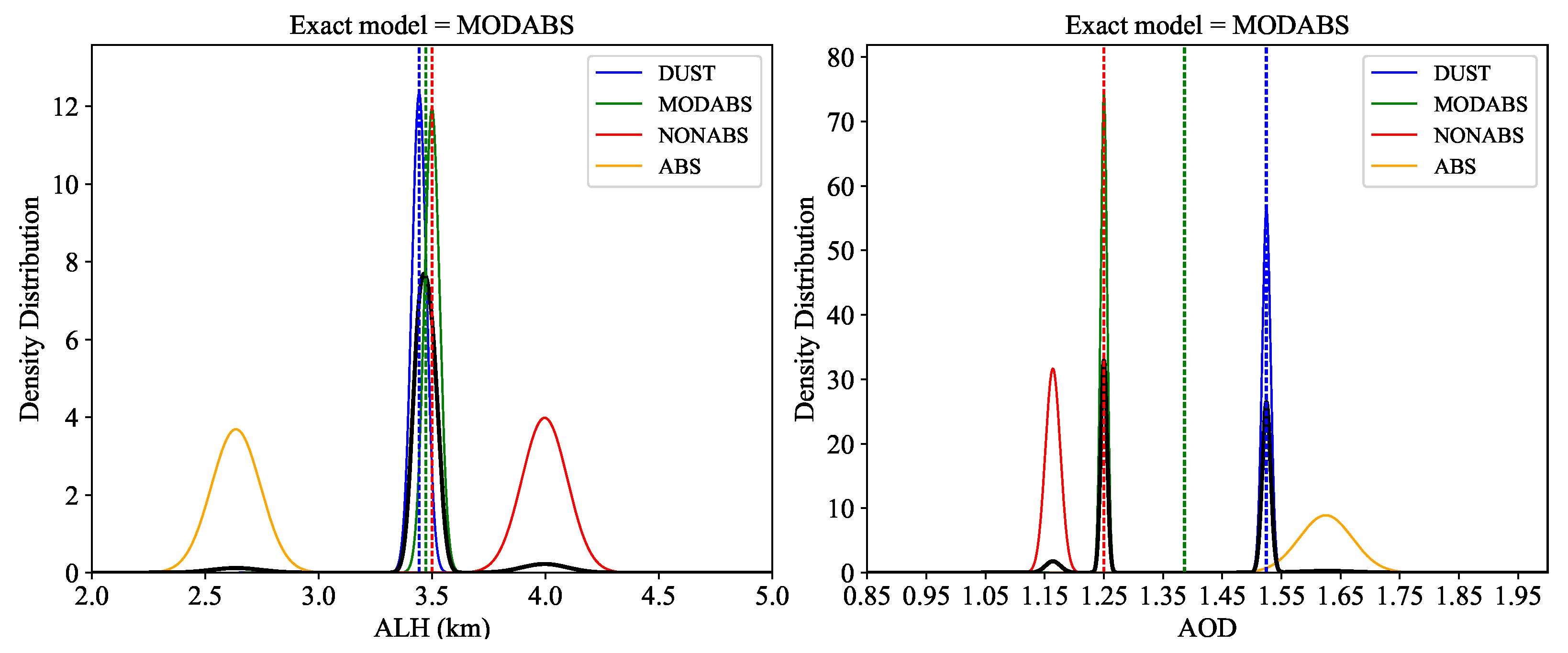
- Different aerosol models could have similar a posteriori densities as the inversion process is not ideally perfect. An inappropriate aerosol model may occasionally be identified, which can result in unexpected errors ().
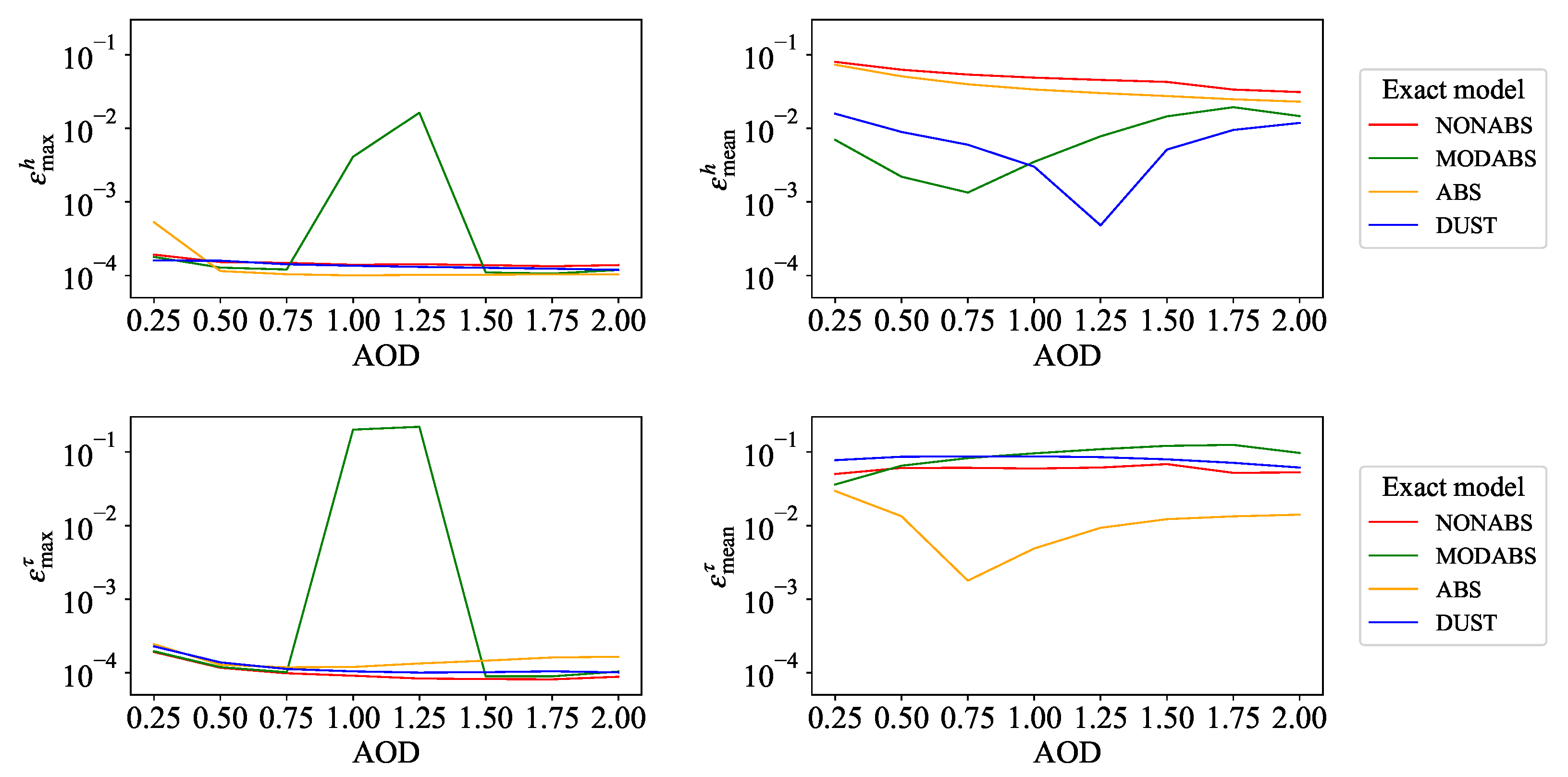
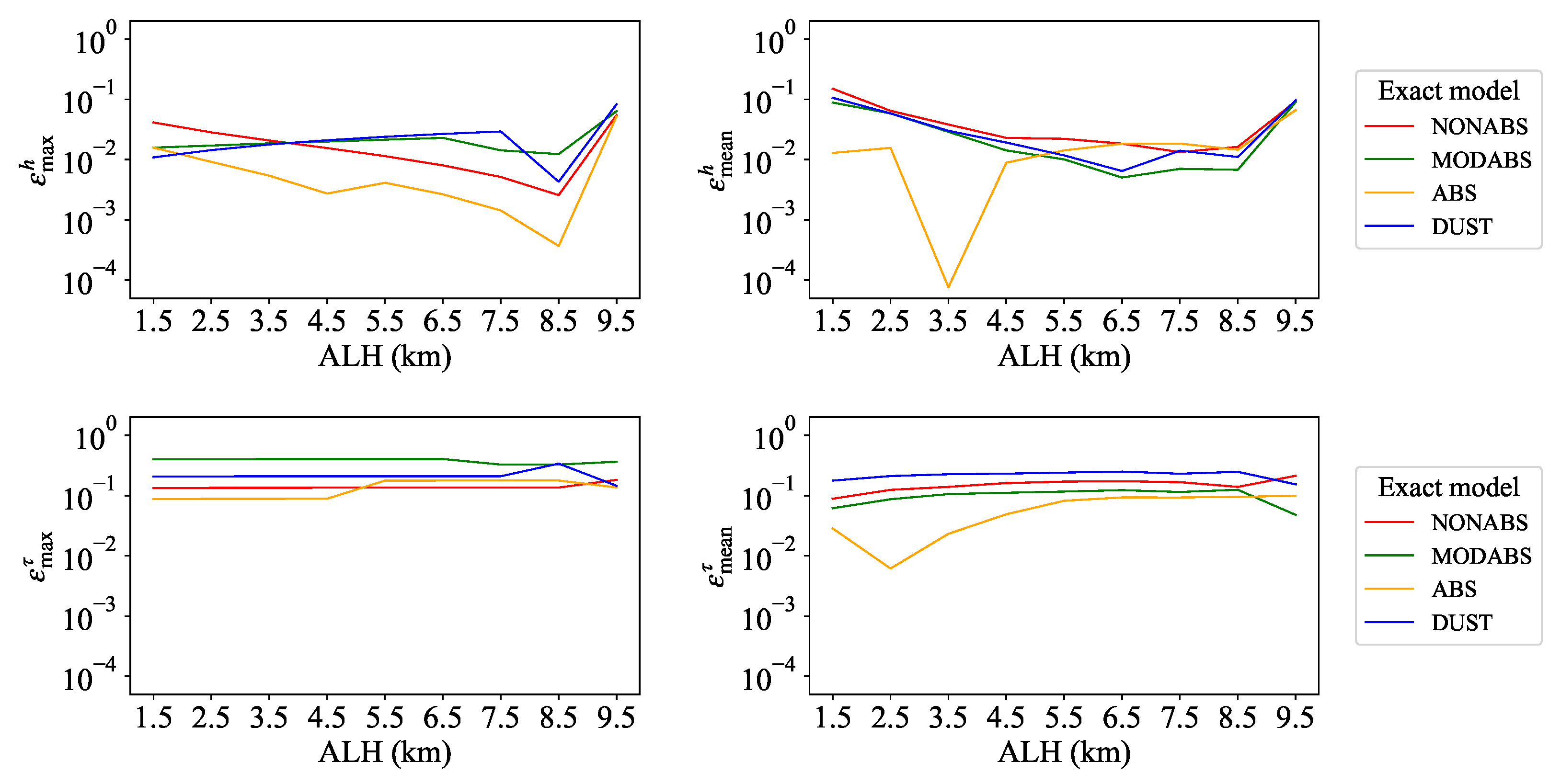
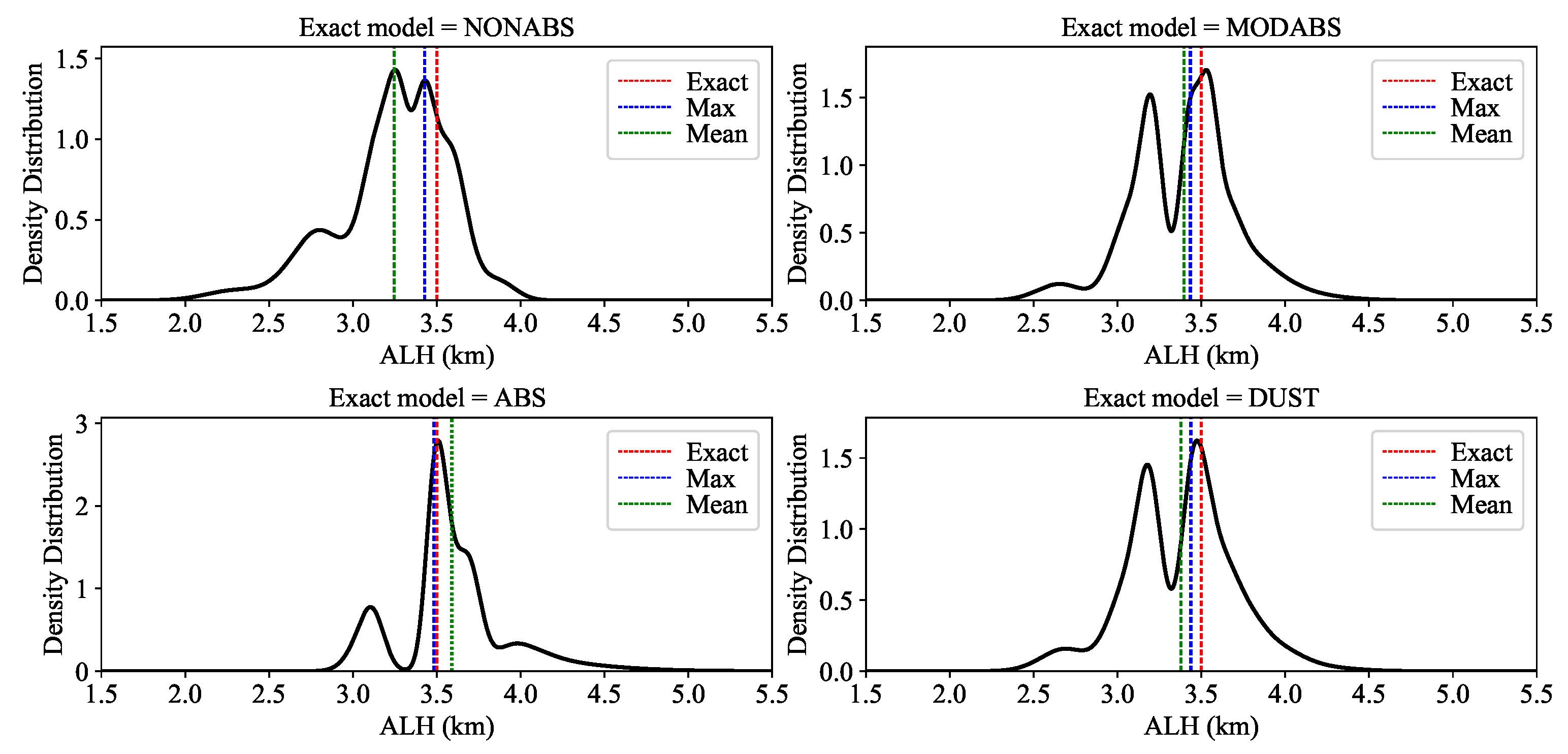
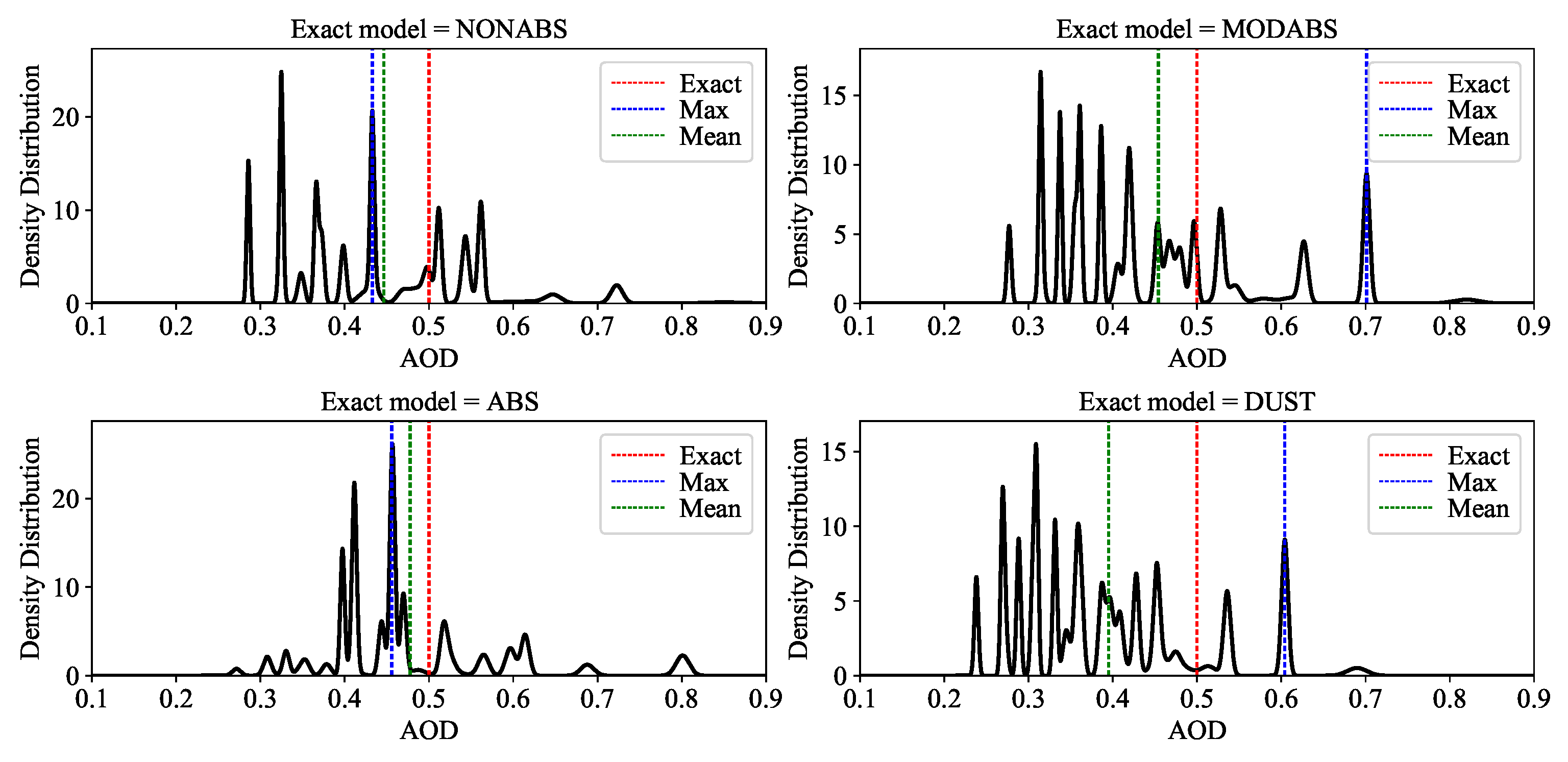
4.2. Test 2
- the relative errors are larger than those in the first test example,
- the relative errors corresponding to the maximum solution estimate ( and ) and the mean solution estimate ( and ) are comparable, and
- on average, the retrieved aerosol layer height obtains a higher accuracy than the retrieved aerosol optical depth.
- and are both not too far from ; thus, for aerosol layer height retrieval, the maximum solution estimate and the mean solution estimate ( and ) have similar accuracies;
- is relatively closer to than ; thus, for aerosol optical depth retrieval, the mean solution estimate performs better than the maximum solution estimate;
- aerosol layer height retrievals have wide a posteriori densities that cover the exact layer height; and
- aerosol optical depth retrievals have multi-peaked densities, in which the exact optical depth does not have the highest probability.
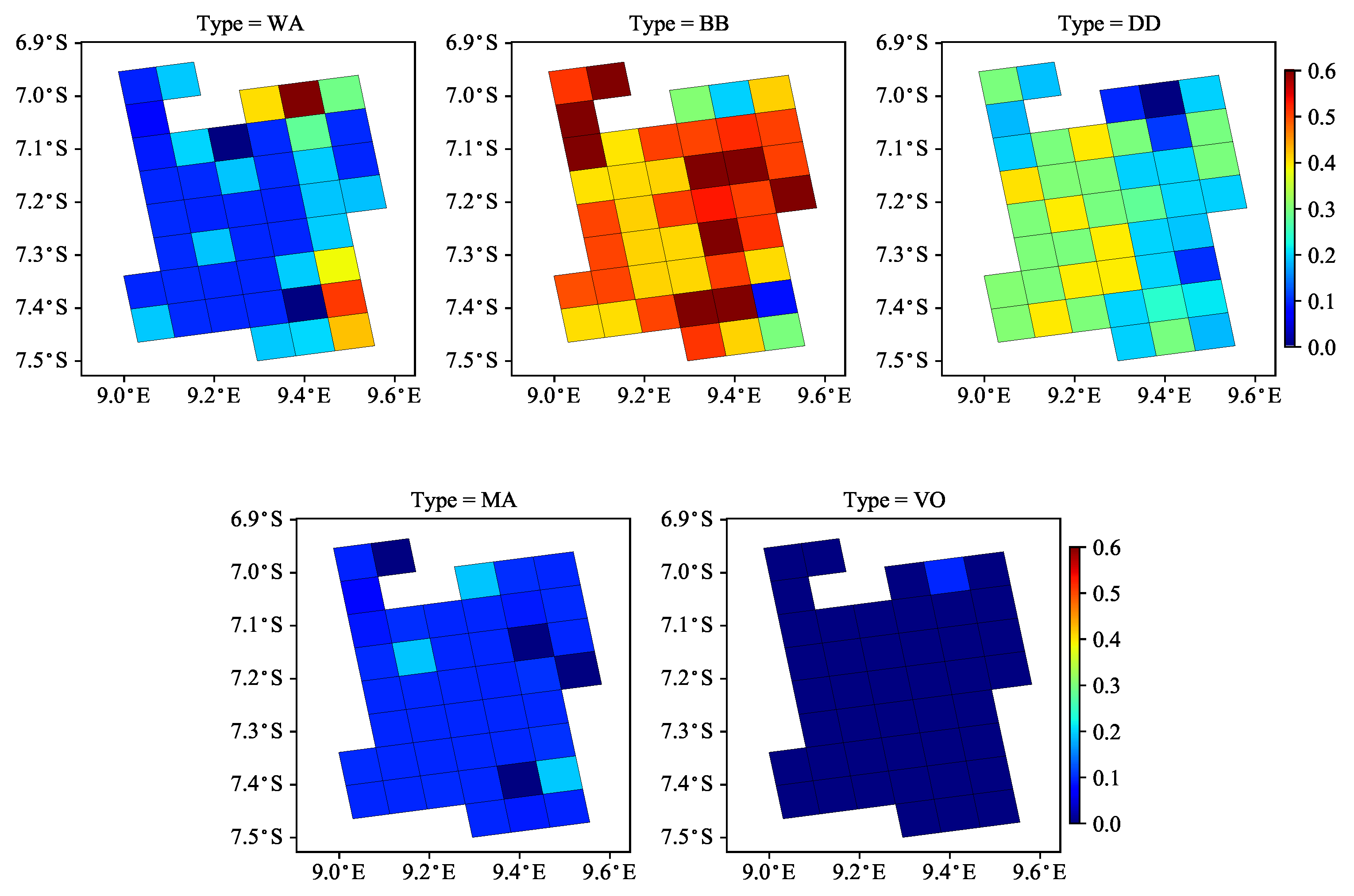
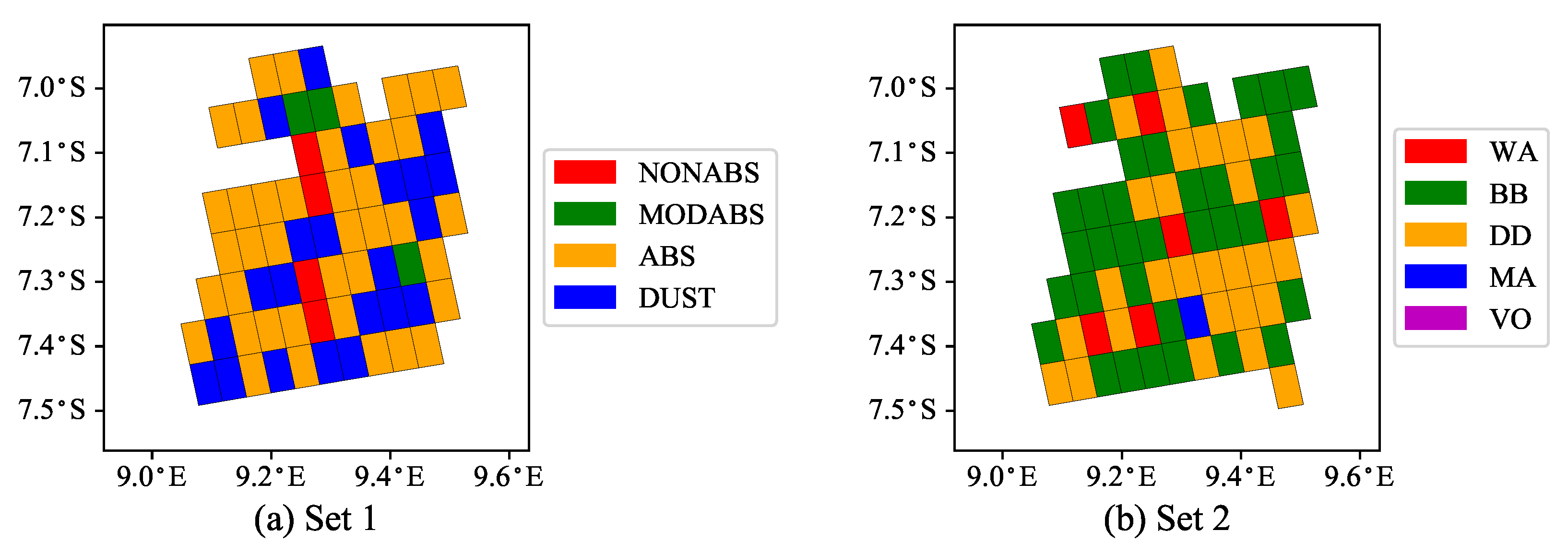
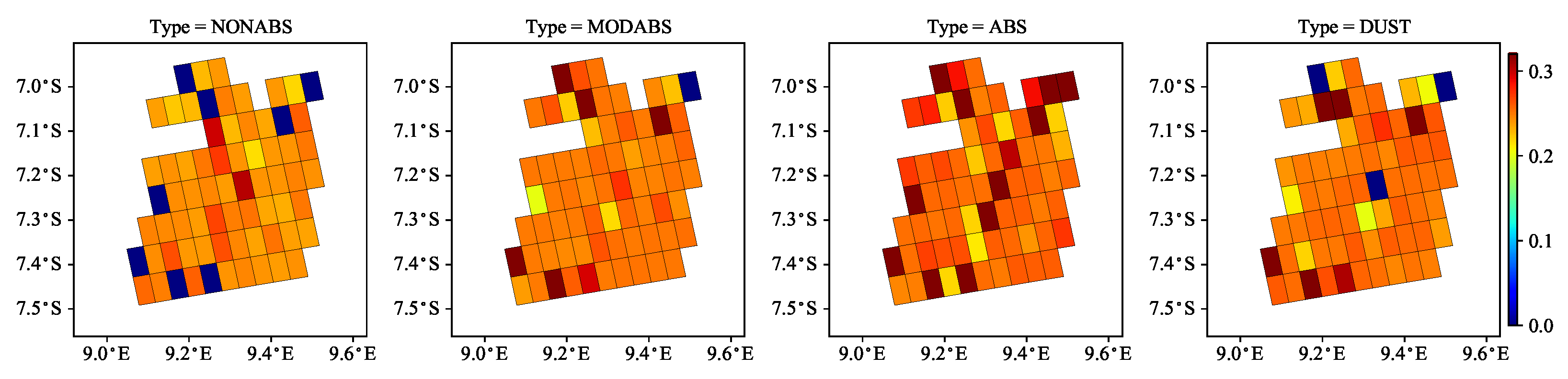
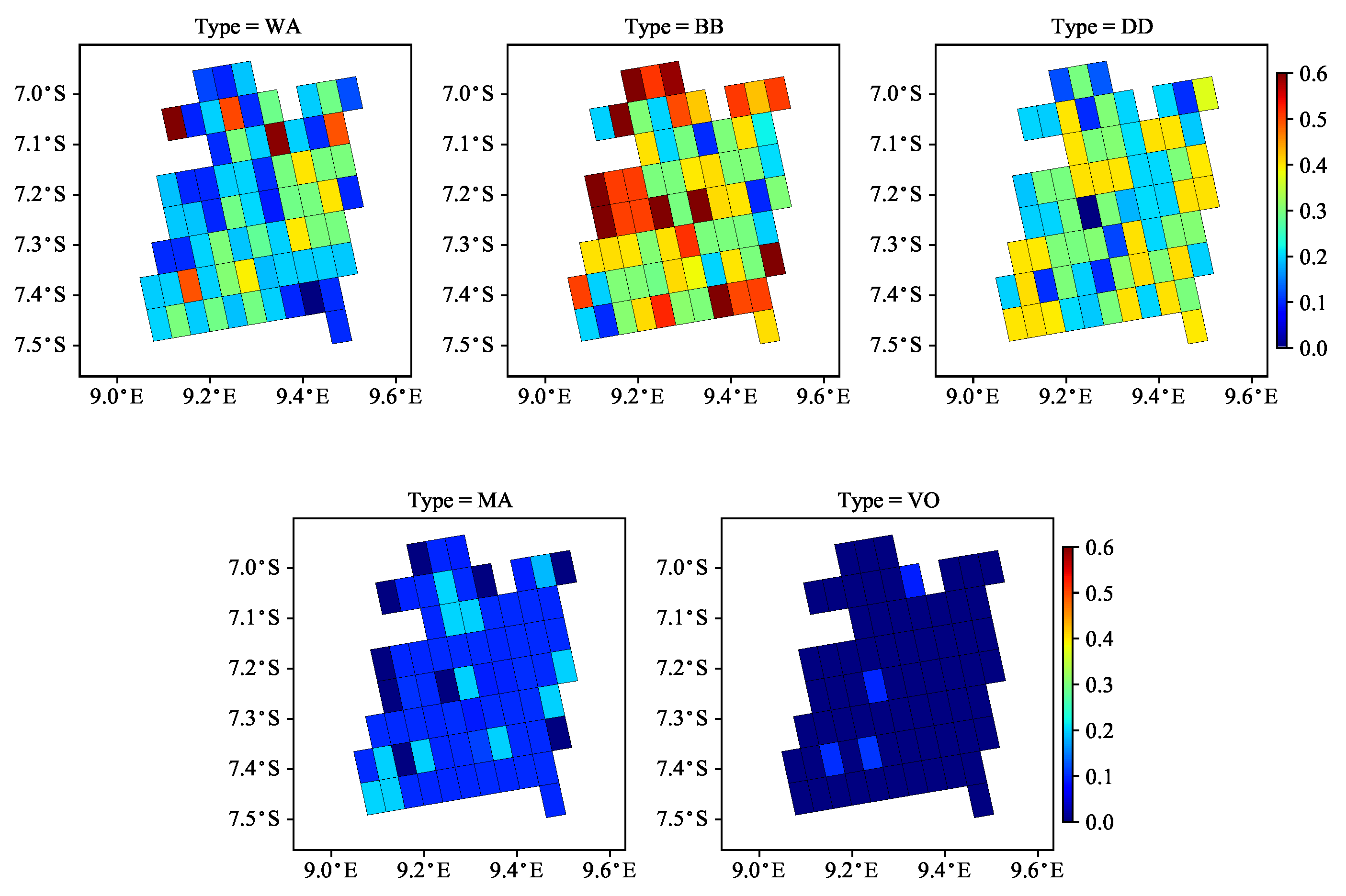
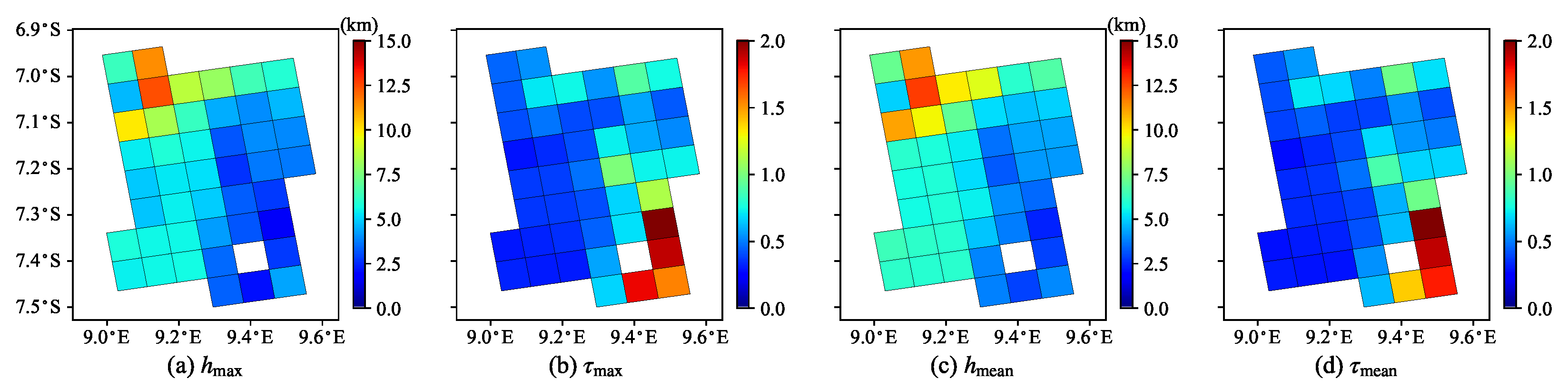
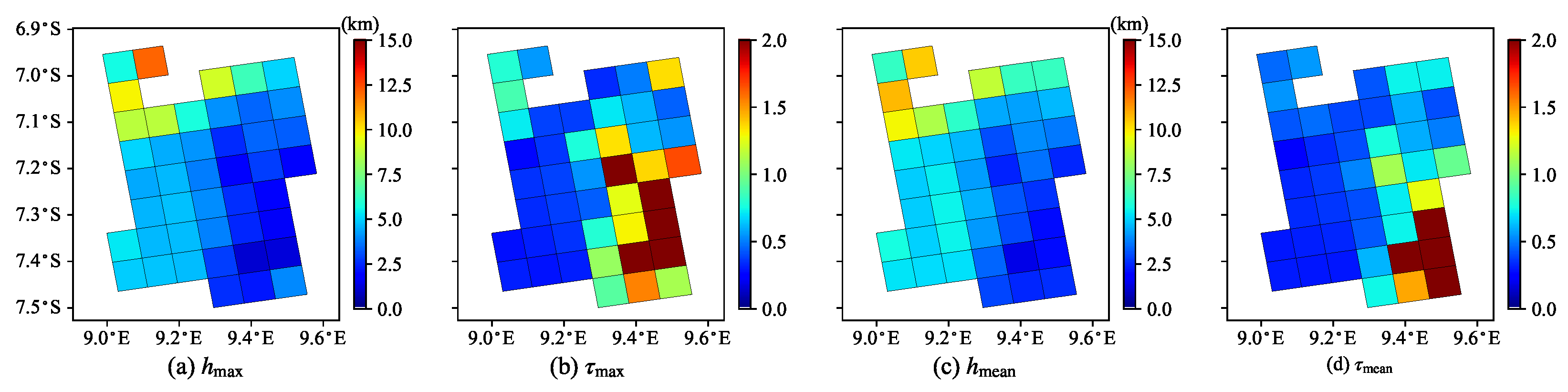
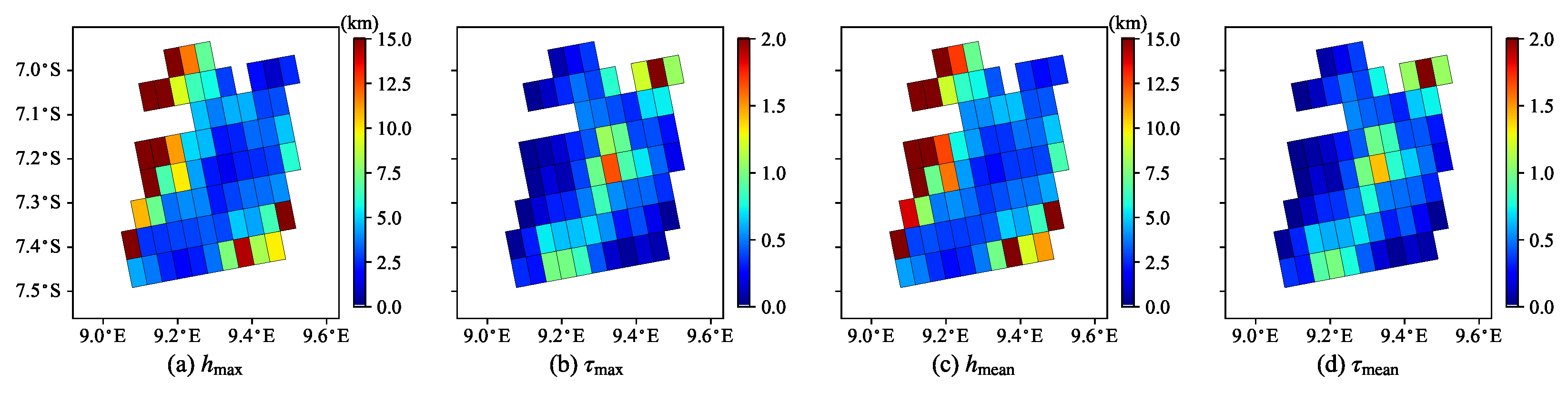
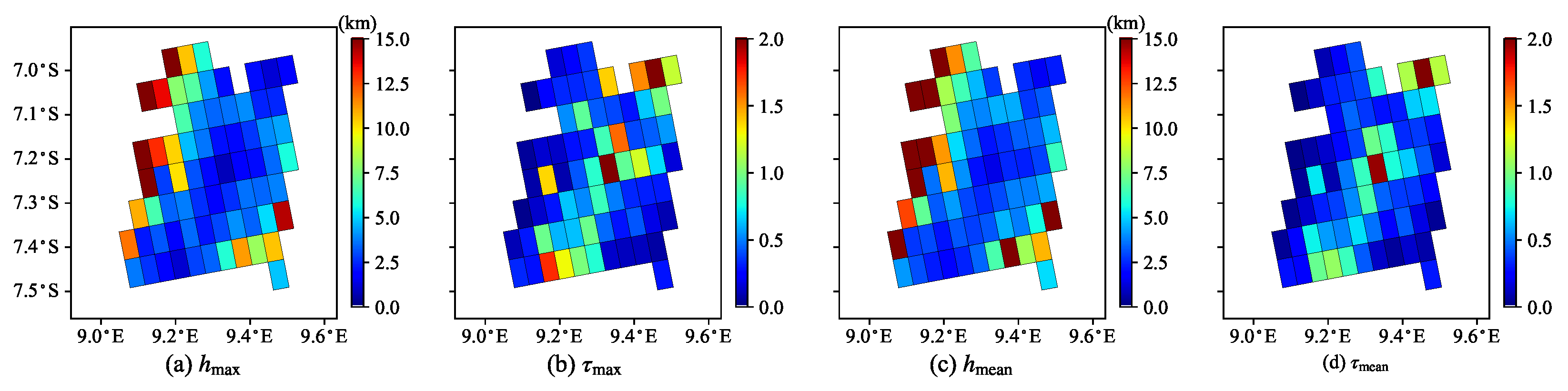
5. Case Study with TROPOMI Data
- the mean solution estimates show a slightly smoother spatial pattern than the maximum solution estimates, and
- despite the differences in the micro-physical properties of the aerosol models from Sets 1 and 2, the spatial distributions of the mean retrieval results are comparable.
6. Conclusions
- When the exact aerosol model, for which synthetic data are generated, is included in the set of candidate models, the relative errors corresponding to the maximum solution estimate are relatively small. When this is not the case, it is likely that several aerosol models are able to fit the data equally well. In such situations, the mean solution estimate has a smaller bias than the maximum solution estimate.
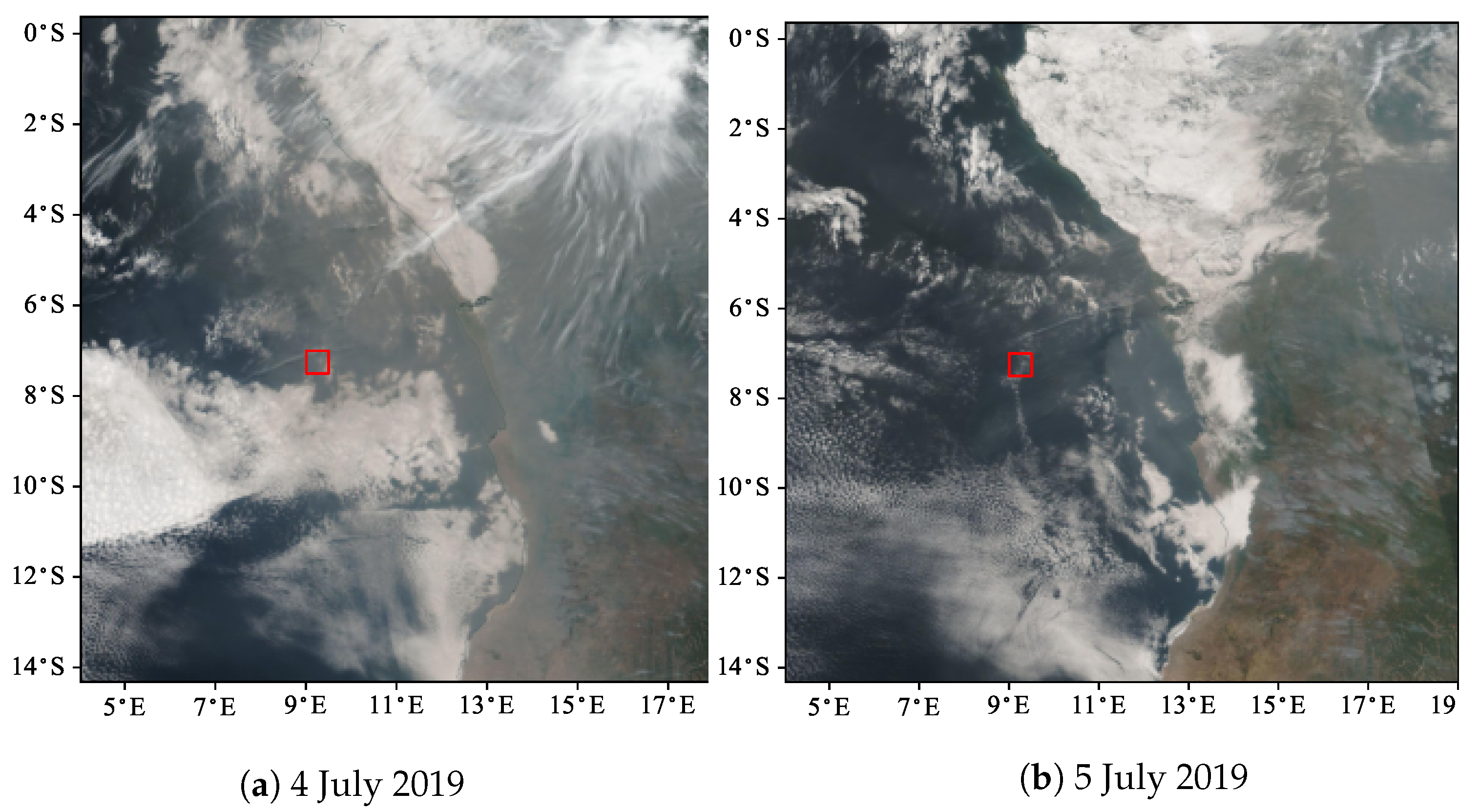
- For the real measurements on 4 July 2019, the absorbing aerosol model from Set 1 and the biomass burning aerosol type from Set 2 are found to be the most plausible. This result is in agreement with the thick smoke observed in the true-color image. For the thinner smoke scenario on 5 July 2019, the above models together with the dust aerosol model are found to be the most probable aerosol models. Actually, no dominant aerosol model, but rather a less absorbing mixture of different aerosol types, is identified in this case. The mean and maximum solution estimates have a similar spatial distribution, but the mean solution estimates have a more continuous spatial pattern.
- The two TROPOMI cases on 6 June 2020 and 10 February 2020 for desert dust and urban aerosols, respectively, have demonstrated the promising performance of the proposed algorithm under various aerosol loading scenarios.
- A definite choice between Sets 1 and 2 for possible candidate models may not exist and a suitable one could be problem dependent.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ALH | Aerosol Layer Height |
| AOD | Aerosol Optical Depth |
| GE_LER | Geometry-dependent Effective Lambertian Equivalent Reflectivity |
| MODIS | Moderate-resolution Imaging Spectroradiometer |
| NIR | Near-infrared |
| OMI | Ozone Monitoring Instrument |
| OMAERO | OMI Multi-wavelength |
| S5P | Sentinel-5 Precursor |
| TROPOMI | Tropospheric Monitoring Instrument |
| ABS | Absorbing (Set 1) |
| DUST | Desert dust (Set 1) |
| MODABS | Moderately absorbing (Set 1) |
| NONABS | Non-absorbing (Set 1) |
| BB | Biomass Burning (Set 2) |
| DD | Desert Dust (Set 2) |
| MA | Marine (Set 2) |
| VO | Volcanic (Set 2) |
| WA | Weakly absorbing (Set 2) |
References
- Holben, B.; Vermote, E.; Kaufman, Y.J.; Tanré, D.; Kalb, V. Aerosol retrieval over land from AVHRR data-application for atmospheric correction. IEEE Trans. Geosci. Remote Sens. 1992, 30, 212–222. [Google Scholar] [CrossRef]
- Levy, R.; Mattoo, S.; Munchak, L.; Remer, L.; Sayer, A.; Patadia, F.; Hsu, N. The Collection 6 MODIS aerosol products over land and ocean. Atmos. Meas. Tech. 2013, 6, 2989–3034. [Google Scholar] [CrossRef] [Green Version]
- Jackson, J.M.; Liu, H.; Laszlo, I.; Kondragunta, S.; Remer, L.A.; Huang, J.; Huang, H.C. Suomi-NPP VIIRS aerosol algorithms and data products. J. Geophys. Res. Atmos. 2013, 118, 12673–12689. [Google Scholar] [CrossRef]
- Wei, J.; Li, Z.; Sun, L.; Peng, Y.; Zhang, Z.; Li, Z.; Su, T.; Feng, L.; Cai, Z.; Wu, H. Evaluation and uncertainty estimate of next-generation geostationary meteorological Himawari-8/AHI aerosol products. Sci. Total Environ. 2019, 692, 879–891. [Google Scholar] [CrossRef] [PubMed]
- Kahn, R.A.; Li, W.H.; Moroney, C.; Diner, D.J.; Martonchik, J.V.; Fishbein, E. Aerosol source plume physical characteristics from space-based multiangle imaging. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Virtanen, T.; Kolmonen, P.; Rodríguez, E.; Sogacheva, L.; Sundström, A.M.; de Leeuw, G. Ash plume top height estimation using AATSR. Atmos. Meas. Tech. 2014, 7, 2437–2456. [Google Scholar] [CrossRef] [Green Version]
- Dubovik, O.; Herman, M.; Holdak, A.; Lapyonok, T.; Tanré, D.; Deuzé, J.; Ducos, F.; Sinyuk, A.; Lopatin, A. Statistically optimized inversion algorithm for enhanced retrieval of aerosol properties from spectral multi-angle polarimetric satellite observations. Atmos. Meas. Tech. 2011, 4, 975–1018. [Google Scholar] [CrossRef] [Green Version]
- Nanda, S.; Graaf, M.d.; Veefkind, J.P.; Sneep, M.; Linden, M.t.; Sun, J.; Levelt, P.F. A first comparison of TROPOMI aerosol layer height (ALH) to CALIOP data. Atmos. Meas. Tech. 2020, 13, 3043–3059. [Google Scholar] [CrossRef]
- Kokhanovsky, A.; Davis, A.; Cairns, B.; Dubovik, O.; Hasekamp, O.; Sano, I.; Mukai, S.; Rozanov, V.; Litvinov, P.; Lapyonok, T.; et al. Space-based remote sensing of atmospheric aerosols: The multi-angle spectro-polarimetric frontier. Earth Sci. Rev. 2015, 145, 85–116. [Google Scholar] [CrossRef]
- Hess, M.; Koepke, P.; Schult, I. Optical properties of aerosols and clouds: The software package OPAC. Bull. Am. Meteorol. Soc. 1998, 79, 831–844. [Google Scholar] [CrossRef]
- Levy, R.C.; Remer, L.A.; Dubovik, O. Global aerosol optical properties and application to Moderate Resolution Imaging Spectroradiometer aerosol retrieval over land. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef] [Green Version]
- Torres, O.; Tanskanen, A.; Veihelmann, B.; Ahn, C.; Braak, R.; Bhartia, P.K.; Veefkind, P.; Levelt, P. Aerosols and surface UV products from Ozone Monitoring Instrument observations: An overview. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef] [Green Version]
- Chin, M.; Ginoux, P.; Kinne, S.; Torres, O.; Holben, B.N.; Duncan, B.N.; Martin, R.V.; Logan, J.A.; Higurashi, A.; Nakajima, T. Tropospheric aerosol optical thickness from the GOCART model and comparisons with satellite and Sun photometer measurements. J. Atmos. Sci. 2002, 59, 461–483. [Google Scholar] [CrossRef]
- Taylor, M.; Kazadzis, S.; Amiridis, V.; Kahn, R. Global aerosol mixtures and their multiyear and seasonal characteristics. Atmos. Environ. 2015, 116, 112–129. [Google Scholar] [CrossRef]
- Martonchik, J.; Diner, D.; Kahn, R.; Ackerman, T.; Verstraete, M.; Pinty, B.; Gordon, H. Techniques for the retrieval of aerosol properties over land and ocean using multiangle imaging. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1212–1227. [Google Scholar] [CrossRef] [Green Version]
- Bellouin, N.; Boucher, O.; Tanré, D.; Dubovik, O. Aerosol absorption over the clear-sky oceans deduced from POLDER-1 and AERONET observations. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Lee, J.; Lee, H.C.; Higurashi, A.; Takemura, T.; Song, C.H. Consistency of the aerosol type classification from satellite remote sensing during the Atmospheric Brown Cloud–East Asia Regional Experiment campaign. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Penning de Vries, M.J.M.; Beirle, S.; Hörmann, C.; Kaiser, J.W.; Stammes, P.; Tilstra, L.G.; Tuinder, O.N.E.; Wagner, T. A global aerosol classification algorithm incorporating multiple satellite data sets of aerosol and trace gas abundances. Atmos. Chem. Phys. 2015, 15, 10597–10618. [Google Scholar] [CrossRef] [Green Version]
- Kumar, K.R.; Kang, N.; Yin, Y. Classification of key aerosol types and their frequency distributions based on satellite remote sensing data at an industrially polluted city in the Yangtze River Delta, China. Int. J. Climatol. 2018, 38, 320–336. [Google Scholar] [CrossRef]
- Hoeting, J.A.; Madigan, D.; Raftery, A.E.; Volinsky, C.T. Bayesian model averaging: A tutorial. Stat. Sci. 1999, 14, 382–401. [Google Scholar]
- Määttä, A.; Laine, M.; Tamminen, J.; Veefkind, J. Quantification of uncertainty in aerosol optical thickness retrieval arising from aerosol microphysical model and other sources, applied to Ozone Monitoring Instrument (OMI) measurements. Atmos. Meas. Tech. 2014, 7, 1185–1199. [Google Scholar] [CrossRef]
- Kauppi, A.; Kolmonen, P.; Laine, M.; Tamminen, J. Aerosol-type retrieval and uncertainty quantification from OMI data. Atmos. Meas. Tech. 2017, 10. [Google Scholar] [CrossRef] [Green Version]
- Sasi, S.; Natraj, V.; Molina García, V.; Efremenko, D.S.; Loyola, D.; Doicu, A. Model Selection in Atmospheric Remote Sensing with an Application to Aerosol Retrieval from DSCOVR/EPIC, Part 1: Theory. Remote Sens. 2020, 12, 3724. [Google Scholar] [CrossRef]
- Sasi, S.; Natraj, V.; Molina García, V.; Efremenko, D.S.; Loyola, D.; Doicu, A. Model Selection in Atmospheric Remote Sensing with Application to Aerosol Retrieval from DSCOVR/EPIC. Part 2: Numerical Analysis. Remote Sens. 2020, 12, 3656. [Google Scholar] [CrossRef]
- Marshak, A.; Herman, J.; Adam, S.; Karin, B.; Carn, S.; Cede, A.; Geogdzhayev, I.; Huang, D.; Huang, L.K.; Knyazikhin, Y.; et al. Earth observations from DSCOVR EPIC instrument. Bull. Am. Meteorol. Soc. 2018, 99, 1829–1850. [Google Scholar] [CrossRef]
- Veefkind, J.; Aben, I.; McMullan, K.; Förster, H.; de Vries, J.; Otter, G.; Claas, J.; Eskes, H.; de Haan, J.; Kleipool, Q.; et al. TROPOMI on the ESA Sentinel-5 Precursor: A GMES mission for global observations of the atmospheric composition for climate, air quality and ozone layer applications. Remote Sens. Environ. 2012, 120, 70–83. [Google Scholar] [CrossRef]
- Spurr, R. LIDORT and VLIDORT. Linearized pseudo-spherical scalar and vector discrete ordinate radiative transfer models for use in remote sensing retrieval problems. In Light Scattering Reviews; Kokhanovsky, A., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 3, pp. 229–271. [Google Scholar]
- Efremenko, D.; Doicu, A.; Loyola, D.; Trautmann, T. Acceleration techniques for the discrete ordinate method. J. Quant. Spectrosc. Radiat. Transf. 2013, 114, 73–81. [Google Scholar] [CrossRef]
- Goody, R.; West, R.; Chen, L.; Crisp, D. The correlated-k method for radiation calculations in nonhomogeneous atmospheres. J. Quant. Spectrosc. Radiat. Transf. 1989, 42, 437–651. [Google Scholar] [CrossRef]
- Natraj, V.; Shia, R.L.; Huang, X.; Margolis, J.S.; Yung, Y.L. Application of principal component analysis to high spectral resolution radiative transfer: A case study of the O2 A band. J. Quant. Spectrosc. Radiat. Transf. 2005, 95, 539–556. [Google Scholar] [CrossRef]
- Natraj, V.; Shia, R.L.; Yung, Y.L. On the use of principal component analysis to speed up radiative transfer calculations. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 810–816. [Google Scholar] [CrossRef]
- Xu, J.; Schreier, F.; Doicu, A.; Trautmann, T. Assessment of Tikhonov-type regularization methods for solving atmospheric inverse problems. J. Quant. Spectrosc. Radiat. Transf. 2016, 184, 274–286. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Rao, L.; Schreier, F.; Efremenko, D.S.; Doicu, A.; Trautmann, T. Insight into Construction of Tikhonov-Type Regularization for Atmospheric Retrievals. Atmosphere 2020, 11, 1052. [Google Scholar] [CrossRef]
- Rao, L.; Xu, J.; Efremenko, D.S.; Loyola, D.G.; Doicu, A. Hyperspectral Satellite Remote Sensing of Aerosol Parameters. In preparation.
- Molina García, V.; Sasi, S.; Efremenko, D.S.; Doicu, A.; Loyola, D. Radiative transfer models for retrieval of cloud parameters from EPIC/DSCOVR measurements. J. Quant. Spectrosc. Radiat. Transf. 2018, 213, 228–240. [Google Scholar] [CrossRef] [Green Version]
- Molina García, V.; Sasi, S.; Efremenko, D.S.; Doicu, A.; Loyola, D. Linearized radiative transfer models for retrieval of cloud parameters from EPIC/DSCOVR measurements. J. Quant. Spectrosc. Radiat. Transf. 2018, 213, 241–251. [Google Scholar] [CrossRef] [Green Version]
- Patterson, H.D.; Thompson, R. Recovery of inter-block information when block sizes are unequal. Biometrika 1971, 58, 545–554. [Google Scholar] [CrossRef]
- Smyth, G.K.; Verbyla, A.P. A conditional likelihood approach to residual maximum likelihood estimation in generalized linear models. J. R. Stat. Soc. Ser. B Methodol. 1996, 58, 565–572. [Google Scholar] [CrossRef]
- Stuart, A.; Ord, K.; Arnold, S. Kendall’s Advanced Theory of Statistics. Volume 2A: Classical Inference and the Linear Model; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2000. [Google Scholar]
- Wahba, G. Practical approximate solutions to linear operator equations when the data are noisy. SIAM J. Numer. Anal. 1977, 14, 651–667. [Google Scholar] [CrossRef]
- Wahba, G. Spline Models for Observational Data; SIAM: Philadelphia, PA, USA, 1990. [Google Scholar]
- Meng, Z.; Yang, P.; Kattawar, G.W.; Bi, L.; Liou, K.; Laszlo, I. Single-scattering properties of tri-axial ellipsoidal mineral dust aerosols: A database for application to radiative transfer calculations. J. Aerosol Sci. 2010, 41, 501–512. [Google Scholar] [CrossRef]
- Alados-Arboledas, L.; Müller, D.; Guerrero-Rascado, J.L.; Navas-Guzmán, F.; Pérez-Ramírez, D.; Olmo, F.J. Optical and microphysical properties of fresh biomass burning aerosol retrieved by Raman lidar, and star-and sun-photometry. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Waquet, F.; Cornet, C.; Deuzé, J.L.; Dubovik, O.; Ducos, F.; Goloub, P.; Herman, M.; Lapyonok, T.; Labonnote, L.C.; Riedi, J.; et al. Retrieval of aerosol microphysical and optical properties above liquid clouds from POLDER/PARASOL polarization measurements. Atmos. Meas. Tech. 2013, 6, 991–1016. [Google Scholar] [CrossRef] [Green Version]
- Yu, X.; Shi, C.; Ma, J.; Zhu, B.; Li, M.; Wang, J.; Yang, S.; Kang, N. Aerosol optical properties during firework, biomass burning and dust episodes in Beijing. Atmos. Environ. 2013, 81, 475–484. [Google Scholar] [CrossRef]
- Loyola, D.G.; Xu, J.; Heue, K.P.; Zimmer, W. Applying FP_ILM to the retrieval of geometry-dependent effective Lambertian equivalent reflectivity (GE_LER) daily maps from UVN satellite measurements. Atmos. Meas. Tech. 2020, 13, 985–999. [Google Scholar] [CrossRef] [Green Version]


| Model | Mode | (μm) | m = (Re(m), Im(m)) | ||
|---|---|---|---|---|---|
| NONABS | fine | (1.42, ) | |||
| coarse | |||||
| MODABS | fine | (1.43, ) | |||
| coarse | |||||
| ABS | fine | (1.51, 0.02) | |||
| coarse | |||||
| DUST | fine | (, ) | |||
| coarse | 2.2 |
| Type | Model | Fine Mode | Coarse Mode | m = (Re, Im) | |||
|---|---|---|---|---|---|---|---|
| WA | WA1101 | 0.078 | 1.499 | 0.497 | 2.160 | ||
| WA1102 | 0.088 | 1.499 | 0.509 | 2.160 | |||
| WA1103 | 0.137 | 1.499 | 0.567 | 2.160 | |||
| WA1104 | 0.030 | 2.030 | 0.240 | 2.030 | |||
| WA1201 | 0.078 | 1.499 | 0.497 | 2.160 | |||
| WA1202 | 0.088 | 1.499 | 0.509 | 2.160 | |||
| WA1203 | 0.137 | 1.499 | 0.567 | 2.160 | |||
| WA1301 | 0.078 | 1.499 | 0.497 | 2.160 | |||
| WA1302 | 0.088 | 1.499 | 0.509 | 2.160 | |||
| WA1303 | 0.137 | 1.499 | 0.567 | 2.160 | |||
| BB | BB2101 | 0.074 | 1.537 | 0.511 | 2.203 | ||
| BB2102 | 0.087 | 1.537 | 0.567 | 2.203 | |||
| BB2103 | 0.124 | 1.537 | 0.719 | 2.203 | |||
| BB2201 | 0.074 | 1.537 | 0.511 | 2.203 | |||
| BB2202 | 0.087 | 1.537 | 0.509 | 2.203 | |||
| BB2203 | 0.124 | 1.537 | 0.719 | 2.203 | |||
| BB2102 | 0.087 | 1.537 | 0.509 | 2.203 | |||
| BB2103 | 0.124 | 1.537 | 0.719 | 2.203 | |||
| DD | BB2101 | 0.074 | 1.537 | 0.511 | 2.203 | ||
| DD3101 | 0.042 | 1.697 | 0.670 | 1.806 | |||
| DD3102 | 0.052 | 1.697 | 0.670 | 1.806 | |||
| DD3201 | 0.042 | 1.697 | 0.670 | 1.806 | |||
| DD3202 | 0.052 | 1.697 | 0.670 | 1.806 | |||
| MA | MA mod. abs. | 0.030 | 2.030 | 0.240 | 2.030 | ||
| MA abs. | 0.030 | 2.030 | 0.240 | 2.030 | |||
| VO | VO4101 | 0.230 | 0.800 | 0.240 | 2.030 | 0.5 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rao, L.; Xu, J.; Efremenko, D.S.; Loyola, D.G.; Doicu, A. Optimization of Aerosol Model Selection for TROPOMI/S5P. Remote Sens. 2021, 13, 2489. https://doi.org/10.3390/rs13132489
Rao L, Xu J, Efremenko DS, Loyola DG, Doicu A. Optimization of Aerosol Model Selection for TROPOMI/S5P. Remote Sensing. 2021; 13(13):2489. https://doi.org/10.3390/rs13132489
Chicago/Turabian StyleRao, Lanlan, Jian Xu, Dmitry S. Efremenko, Diego G. Loyola, and Adrian Doicu. 2021. "Optimization of Aerosol Model Selection for TROPOMI/S5P" Remote Sensing 13, no. 13: 2489. https://doi.org/10.3390/rs13132489
APA StyleRao, L., Xu, J., Efremenko, D. S., Loyola, D. G., & Doicu, A. (2021). Optimization of Aerosol Model Selection for TROPOMI/S5P. Remote Sensing, 13(13), 2489. https://doi.org/10.3390/rs13132489








