1. Introduction
Due to the limitation of technology, a single sensor cannot simultaneously obtain remote sensing images with high resolution in both the spectral and spatial domains. Currently, high-resolution panchromatic (PAN) components and low-resolution spectral components are usually used instead [
1]. However, a single information component cannot match the effect of remote sensing images with high-resolution spectral domains and spatial domains in many fields. Therefore, in practical applications, it is better to combine the spectral and spatial components [
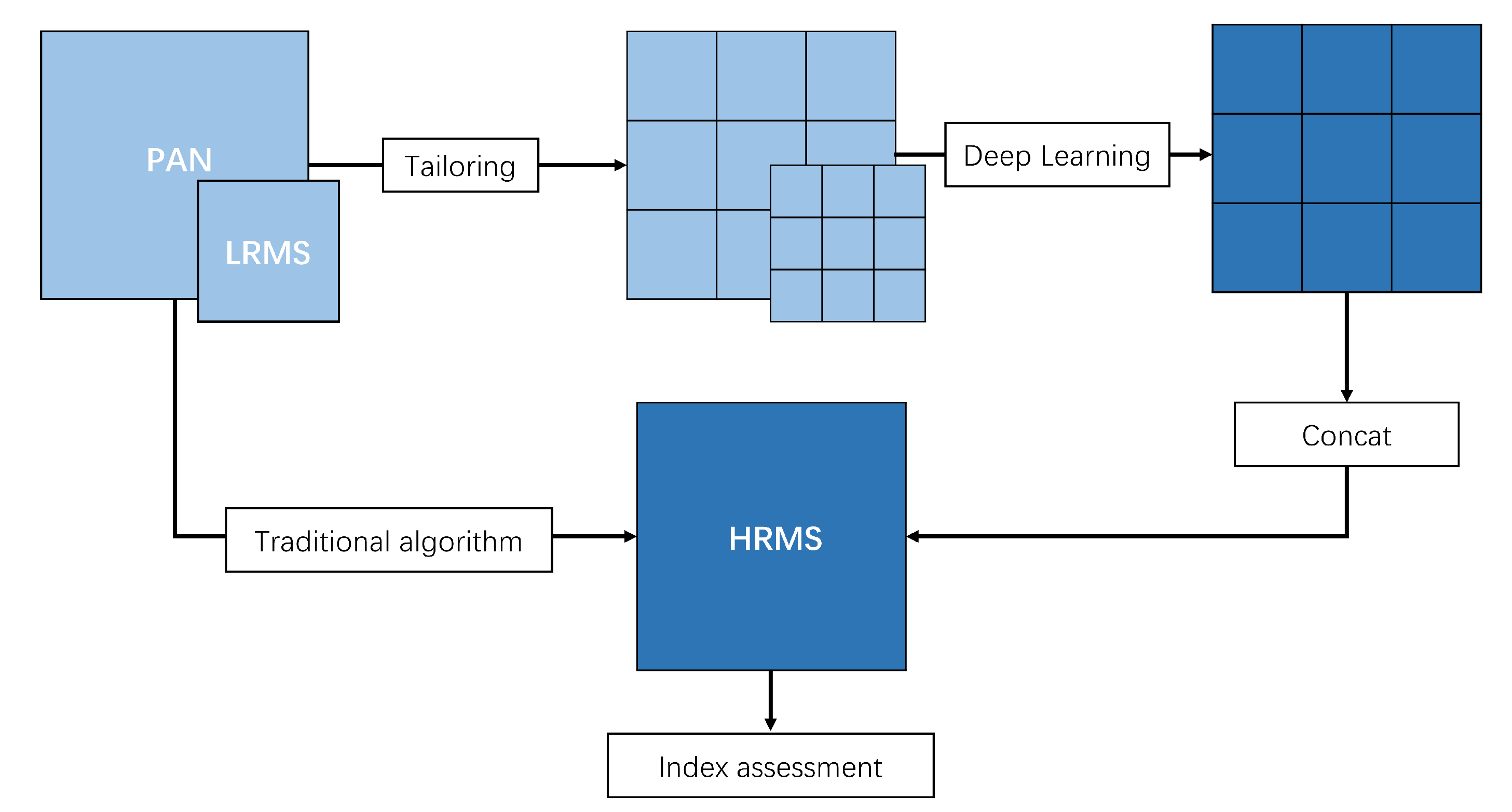
2], that is, to obtain high-resolution spectrograms by fusing low-resolution spectrograms and high-resolution PAN images [
3].
A classic and simple pansharpening method is to perform component replacement [
4]. It is mainly divided into two categories. The first category is to transform the multispectral (MS) image in the appropriate domain and use the high-resolution PAN image to replace the components in the domain (e.g., principal component analysis (PCA) [
5], the intensity-hue-saturation (IHS) transform [
6], and the band-dependent spatial-detail (BDSD) algorithm [
7]). This type of method usually has the characteristics of high spectral distortion because the PAN image and the MS image overlap only in a part of the spectral range. The second category extracts the spatial details of the PAN image and injects the extracted information into the upsampled MS image (e.g., the “a’-Trous” wavelet transform (ATWT) [
8], Laplacian pyramid (LP) [
9] and MTF-Generalized LP (MTF-GLP) [
10]). The second type of component replacement method retains the spectral information better than the first type but still has the problem of insufficient spatial information extraction.
To solve the problem that the MS image spectral information and PAN spatial information cannot be fully utilized, more related methods have been proposed (e.g., a hybrid algorithm that combines the IHS transform and curvelet transform algorithms [
11], a variational model solved using a convex optimization difference solution framework [
12], and a method based on compressed sensing with sparse prior information [
13]). However, these methods still have some problems. The combined algorithm does not significantly improve the overall quality of the fusion image, the model solution hyperparameters are difficult to set [
14], and the sparse expression brings about the problem of increased costs due to dictionary construction.
Deep learning has been widely used in various computer vision tasks. As a result, researchers have begun to explore the application of deep learning in pansharpening and achieved remarkable results. These methods are implemented based on a convolutional neural network (CNN), which is used to extract the spectral features from low-resolution MS (LRMS) images and spatial features from PAN images and uses these features to reconstruct high-resolution MS (HRMS) images. For example, the pansharpening by CNNs (PCNN) method, which is the first algorithm to use a CNN for pansharpening [
15]). The PCNN is modified from the three-layer architecture of the super-resolution CNN (SRCNN) [
16]; it is unable to learn the complex mapping relationship, and the obtained fusion effect is not good. For this, PanNet [
17] introduced a residual neural network (ResNet) [
18], combined with domain knowledge, to improve the output effect of pansharpening. A high-pass-filtered PAN image and an upsampled LRMS image are input into the network, and a long connection is used for the corresponding spectral information. Compared with PCNNs, PanNet has made some progress in both the spectral and spatial domain performance. However, PanNet’s learning in the low-pass domain is still insufficient. The generative adversarial network (GAN) for remote sensing image pansharpening (PSGAN) generative adversarial network for remote sensing image pansharpening [
19] is the first algorithm to use a GAN in pansharpening [
20]. It designs a dual-stream CNN architecture for shallow feature extraction. The L1 loss (Mean Absolute Error) of the image pixels and the loss of the GAN are combined to optimize the image. It effectively avoids partial blur and improves the overall quality of the image. However, the PSGAN has the problems of insufficient retention of PAN structural information and insufficient spectral compensation. Moreover, it lacks a well-designed optimization target and integration rules for overall structure maintenance. We have tried to improve the problems of the PSGAN, combining a GAN and a variational model to propose a pansharpening method [
21]. This method improves some of the problems of the PSGAN to a certain extent, but it still fails to achieve the ideal fusion effect.
Therefore, to solve the problems of the PSGAN, this paper proposes a pansharpening GAN with multilevel structure enhancement and a multistream fusion architecture. The main contributions of this paper are as follows.
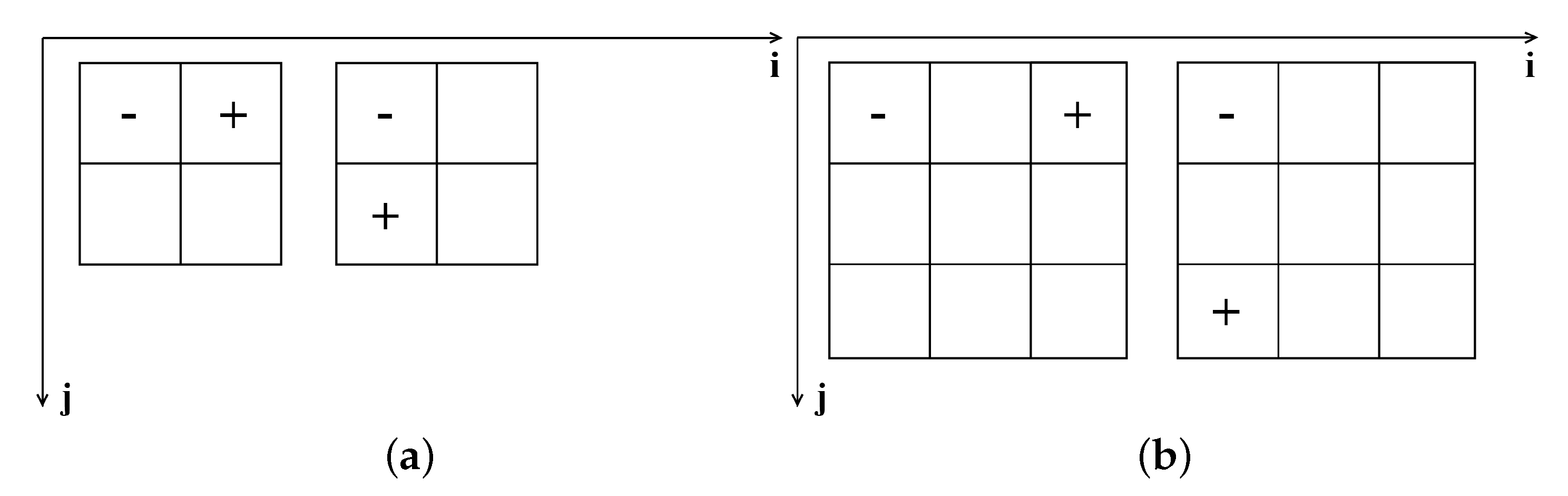
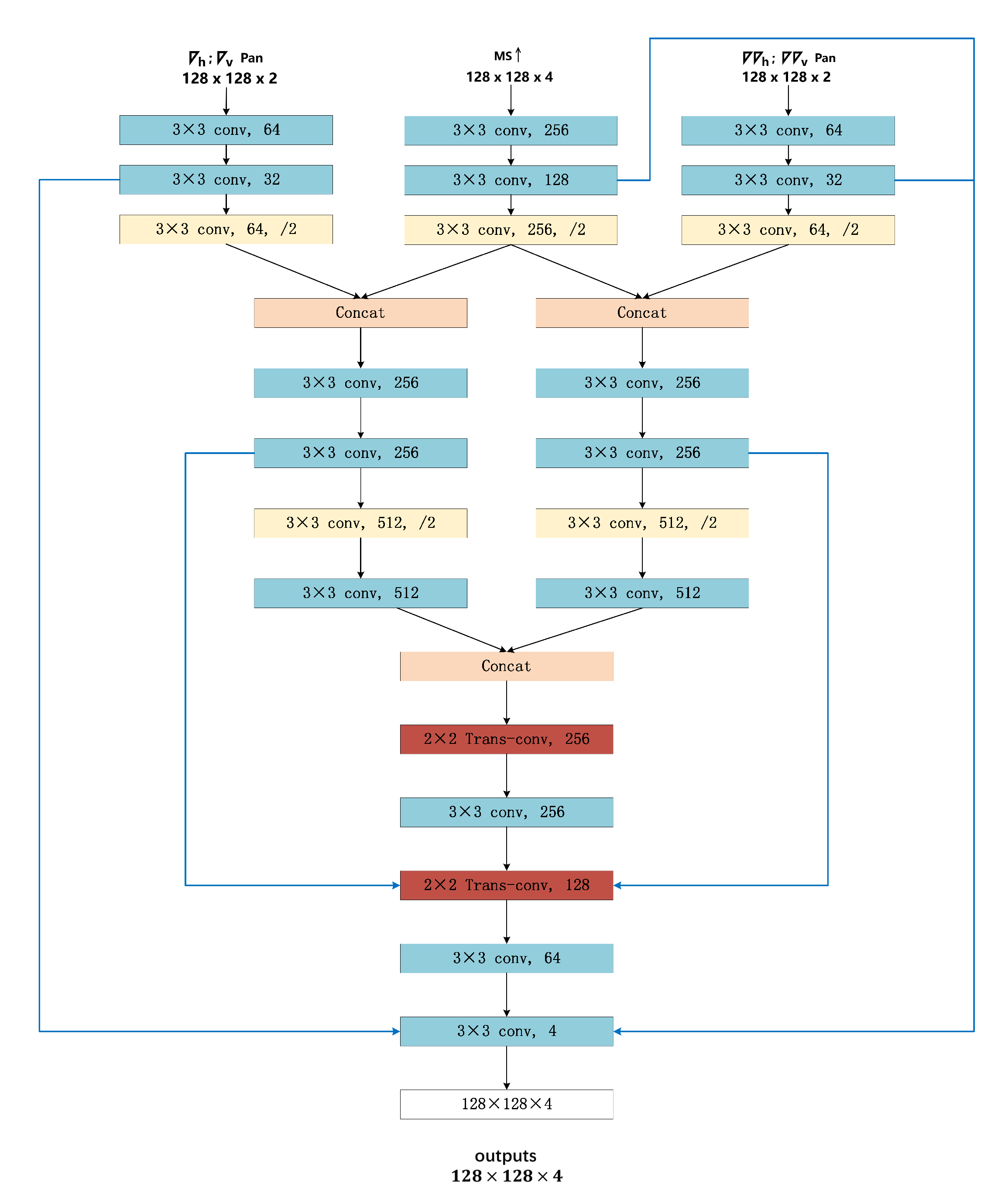
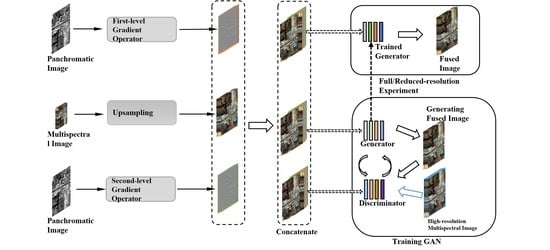
(1) We use multi-level differential operators to extract the spatial features of the panchromatic image, and fully integrate the spatial features of different levels with the spectral features. So that the spatial information of the fusion image can be fully expressed. Specifically, we used two types of gradient operators in the paper, the first-level gradient operator and the second-level gradient operator.
(2) In order to better combine the spatial information extracted by the multi-level gradient operator, we use the multi-stream fusion CNN architecture as the GAN generator. The multi-stream fusion architecture consists of three inputs and two sub-networks. Different types of structural information are input into specific subnets to better maintain structural and spectral information.
(3) We designed a comprehensive loss function. The loss function comprehensively considers the spectral loss, multi-level structure loss and adversarial loss. Among them, the multi-level structure loss combines two types of gradient operators to better give the optimization direction of network training, so that the extraction of structure information is more sufficient.
(4) To make it easier for the discriminator to distinguish real and fake images, we provide as much spectral and structural information as possible.
The remainder of the paper is organized as follows.
Section 2 introduces the related work.
Section 3 describes the method proposed in this paper.
Section 4 presents the experiment and discussion.
Section 5 is the conclusions.
2. Related Work
As pan-sharpening has attracted much attention, deep learning methods have been widely used in it. Researchers have proposed a lot of pan-sharpening methods based on deep learning according to different strategy modes, which have shown excellent nonlinear expression ability. Some methods choose simple shallow convolutional network as the architecture of training network, and extract the features from the input data using different techniques and strategies. For example, PCNN uses a simple three-layer convolutional network, and manually extracts important features such as the normalized water index (NDWI) as the input of the network [
15]. Some methods choose to introduce excellent modules or architectures that are widely used in other fields of deep learning. For example, PANNET introduces residual network and uses high-pass filtering to extract the features of high-pass filtering domain from the input images, so that the network only needs to recover high-frequency information and can migrate between satellites with different numerical imaging ranges [
17]. In [
22], the author introduced Densely connected convolutional networks [
23], which improved the ability to express spectral and spatial characteristics. In [
24], the author proposed a multi-scale channel attention mechanism for panchromatic sharpening based on the channel attention mechanism originally applied to image classification work. This method considers the interdependence between channels and uses the attention mechanism to recalibrate, so as to perform feature representation more accurately. In both PSGAN and Pan-GAN [
25], the author introduces generative confrontation network as the main architecture. PSGAN proposes to use dual-stream input to allow image feature-level fusion instead of pixel-level fusion. Pan-GAN adopts a method of establishing confrontational games between the generator and the spectral discriminator and the spatial discriminator, so as to retain the rich spectral information of the multi-spectral image and the spatial information of the panchromatic image. Some other methods use strategies to improve the loss function to optimize the training direction of the network. For example, in [
26], the author proposed a perceptual loss function and further optimized the model based on advanced features in the near-infrared space. In general, the purpose of panchromatic sharpening is to obtain high-resolution multispectral images through fusion, and to preserve the spectral information of the multispectral images and the spatial information of the panchromatic images to the greatest extent. The methods mentioned above focus on the improvement of a certain aspect, or the simple application of a certain technology. These methods lack comprehensive leverage of image preprocessing, feature extraction, attention module, and loss function improvement. It is critical that how to use more than two technologies in one pansharpening method reasonably. This idea inspired our work.