Abstract
The existing inverse synthetic aperture radar (ISAR) imaging algorithms for ship targets with complex three-dimensional (3D) rotational motion are not applicable because of continuous change of image projection plane (IPP), especially under low signal-to-noise-ratio (SNR) condition. To overcome this obstacle, an efficient approach based on generalized Radon Fourier transform (GRFT) and gradient-based descent optimal is proposed in this paper. First, the geometry and signal model for nonstationary IPP of ship targets with complex 3-D rotational motion is established. Furthermore, the two-dimensional (2D) spatial-variant phase errors caused by complex 3-D rotational motion which can seriously blur the imaging performance are derived. Second, to improve the computational efficiency for 2-D spatial-variant phase errors compensation, the coarse motion parameters of ship targets are estimated via the GRFT method. In addition, using the gradient-based descent optimal method, the global optimum solution is iteratively estimated. Meanwhile, to solve the local extremum for cost surface obtained via conventional image entropy, the image entropy combined with subarray averaging is applied to accelerate the global optimal convergence. The main contributions of the proposed method are: (1) the geometry and signal model for ship targets with a complex 3-D rotational motion under nonstationary IPP are established; (2) the image entropy conjunct with subarray averaging operation is proposed to accelerate the global optimal convergence; (3) the proposed method can ensure the imaging accuracy even with high imaging efficiency thanks to the sole optimal solution generated by using the subarray averaging and image entropy. Several experiments using simulated and electromagnetic data are performed to validate the effectiveness of the proposed approach.
1. Introduction
Inverse synthetic aperture radar (ISAR) is an applicable technique to obtain high-resolution ISAR images for targets because the structure, size, and shape can be reconstructed using the echoes reflected from it under all-day and all-weather condition. Therefore, it can be widely utilized in military and civilian fields [1,2,3].
Compared with cooperative targets, e.g., on-orbit satellite and airplane, non-cooperative targets such as ship targets have complex three-dimensional (3D) rotational motions, e.g., roll, pitch and yaw, and translational motions. Typically, the translational motions can be accurately compensated via a standard compensation algorithm [4]. However, according to the analysis presented in [5,6], the components of 3D rotational motions are time-varying in amplitude and direction vectors. As a result, the image projection plane (IPP) of the targets with complex 3-D rotational motion presents nonstationary characteristics, which would violate the assumption that the IPP is fixed during coherent processing interval (CPI), and followed by the inapplicable of existing ISAR imaging approach for non-cooperative targets.
Several imaging algorithms for maneuvering targets with complex motion have been proposed in recent years [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21]. They can be roughly divided into parametric-based and non-parametric methods. For the parametric-based method, the typical methods are modeling the signals of a specific range bin as quadratic phase signals or cubic phase signals [7,8,9,10,11,12,13]. By using parameters estimation methods, e.g., cubic phase function (CPF) [8,9], non-uniform sampled CPF [10], integrated generalized cubic phase function (IGCPF) [11], scaled Fourier transform (SCFT)-based algorithm [12], generalized decoupling technique (GDT)-based algorithm [13], et al., the coefficients of those phase signal can be accurately estimated. However, the operation for selecting a specific range bin to estimate the coefficients is computationally extensive and infeasible under low SNR conditions. For non-parametric-based methods, the typical methods are time-frequency distribution (TFD) [14] based or polynomial-phase transform (PPT) based [15], which include short-time Fourier transform (STFT) [16], continuous wavelet transform (CWT) [17], Wigner-Ville distribution (WVD) et al. Those methods can reduce the order of signals by using a nonlinear transform operation. Nevertheless, the cross-term interference will be generated while processing multicomponent chirps signals. Besides, the resolution is low, which would also affect the application in the real world. To improve the robustness and effectiveness for ISAR imaging of ship targets, the autofocus algorithm based on data-driven is proposed in [18]. The approach can be divided into two kinds, e.g., estimating and compensating phase errors from the image domain or from the signal domain. The essence of the first one is that the phase errors are modeled as three orders or higher orders polynomial. With the evaluation indicators in the image domain, the phase errors can be estimated and compensated via existing optimum approaches. In [19], the phase gradient autofocus (PGA) is presented. However, the number of iteration and the width of the data window are troublesome problems. The key of the second one is accurately extracting phase errors from the signal domain. In [20], the phase errors between consecutive two pulses are estimated. However, the accumulation of phase errors will inevitably occur while processing multiple pulses. Additionally, the ship target images can be reconstructed using at least two times GRFT [21], where the GRFT method is used for coarse and fine estimation for motion parameters, which is time-consuming because the estimation accuracy is determined by the search step of the motion parameters.
In addition, the methods based on optimum coherent processing interval (CPI) selection are developed for ISAR imaging of ship targets with complex 3-D motion. By coarsely reconstructing the images and extracting the features from which, the maneuvering severity of ship targets is determined and followed by the selection of optimum CPIs [22,23]. However, it suffers from serious efficiency problems. Further, the methods of analyzing Doppler frequency from prominent scatterers are proposed to estimate the characteristics of target motion [24,25]. However, these algorithms either need to detect strong scatterers or have high computational complexity, thus the application in practice has limitations.
To obtain well-focused ISAR images for ship targets with a complex 3-D rotational motion under low SNR, a ship ISAR imaging algorithm based on the GRFT and gradient-based descent optimal is proposed in this paper. Considering the nonstationary characteristic of IPP during CPI, the radar LOS is modeled as the function in terms of slow time, which can accurately describe the motion characteristic for ship targets with complex 3-D rotational motion. Meanwhile, the 2-D spatial-variant phase errors caused by the 3-D rotational motion are derived. Additionally, the GRFT-based is introduced to a rough estimate of the motion parameters. Furthermore, the accurate motion parameters are estimated using the gradient-based descent optimal method. Considering the local convergence of cost surface obtained using conventional image entropy, the approach of image entropy combined with subarray averaging operation is used to improve the convergence efficiency for the global optimal solution. Accordingly, the 2-D spatial-variant phase errors can be precisely estimated and followed by the well-focused ISAR images. Simulated data and electromagnetic data are utilized to verify the effectiveness of the proposed approach. Compared with the existing imaging algorithm for ship targets, the main contribution is as follows: (1) the signal model for ship target with nonstationary IPP is derived, which can accurately describe the motion characteristic of ship targets with complex 3-D rotational motion; (2) the GRFT combined with gradient-based optimal estimation is proposed to improve the processing efficiency for motion parameters estimation; (3) the image entropy based on subarray averaging operation is applied to accelerate the global convergence for the optimum solution.
The rest of this work is organized as follows. In Section 2, the geometric and signal model for ship target with complex 3-D rotational motion are introduced, and 2-D spatial-variant phase errors with nonstationary IPP are also provided. An efficient parameters estimation approach based on the GRFT method and gradient descent approach is proposed in Section 3, where GRFT is adopted to a rough estimate of the motion parameters, and the gradient-based optimal combined with subarray averaging operation is proposed to exactly estimate the motion parameters. At the same time, some considerations in practical application are presented in this part. The experimental results and corresponding analysis with simulated and electromagnetic data are described in Section 4, and some conclusions are summarized in Section 5.
2. ISAR Imaging for Ship Targets
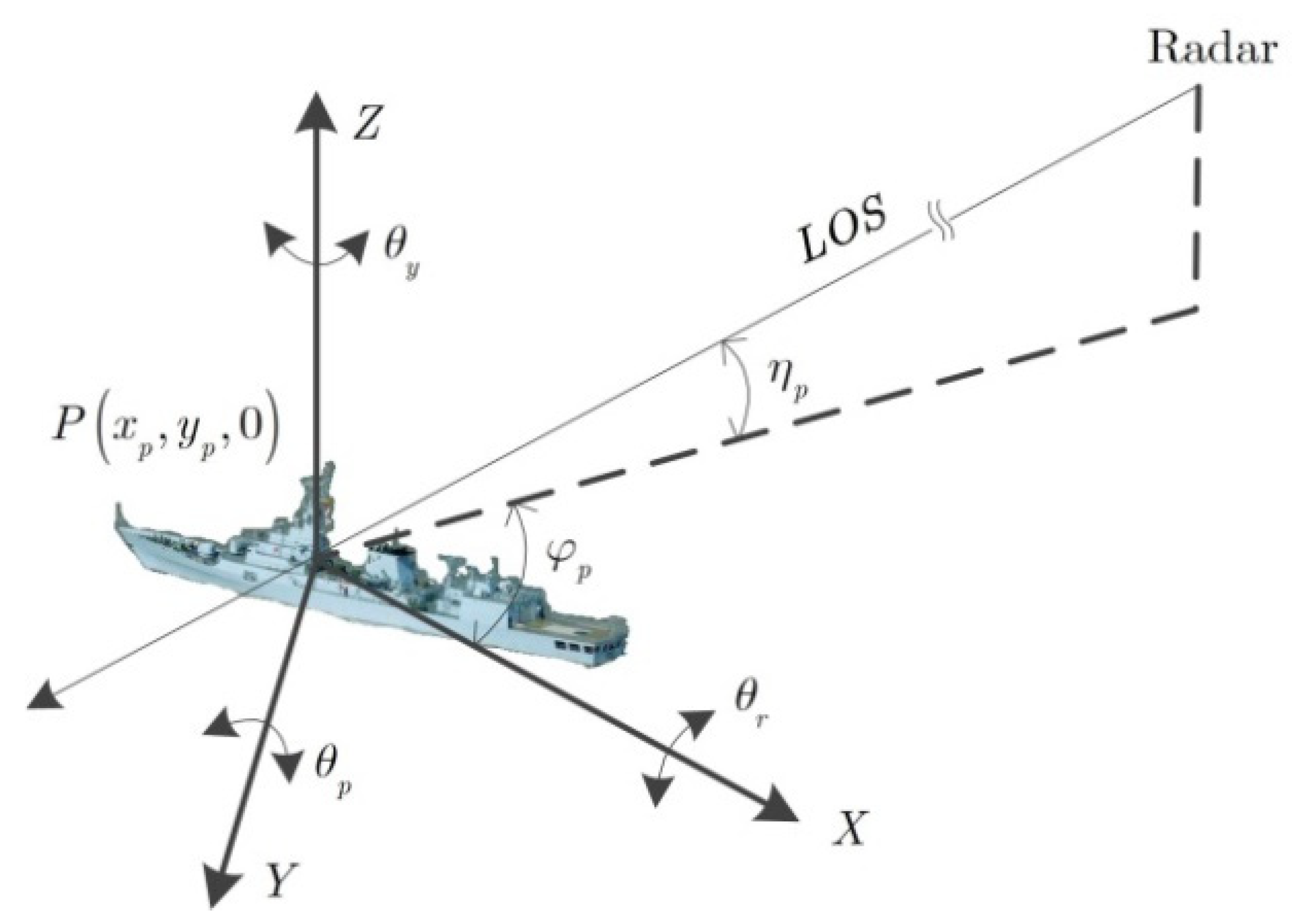
In this section, the geometry model and three-dimensional (3D) rotational motion model are given in Figure 1, where the Cartesian coordinate is established in the target body, and origin is the rotation center, and denote the elevation angle and azimuth angle of the radar line-of-sight (LOS), respectively. , , and , respectively, represent the angular motion yaw, roll, and pitch, which are rotating around , , and axes, respectively.
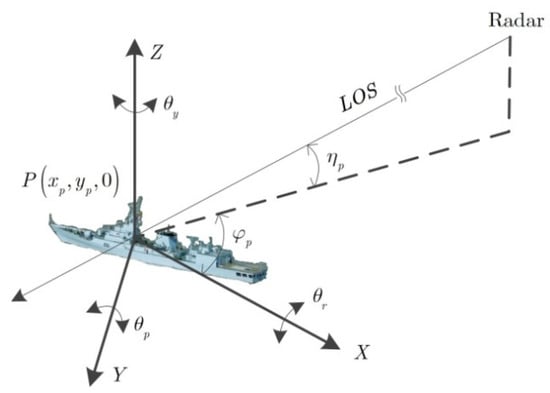
Figure 1.
Geometry model for ship target with complex motion.
2.1. Signal Model for Ship Targets
Now, we suppose the linear-frequency-modulated (LFM) signals are transmitted in the radar system, and it can be written as
where , denote the fast time, slow time, carrier frequency, frequency modulation rate, and pulse width, respectively, , stands for the full time, and is the total number of the received pulses. As shown in Figure 1, arbitrary scatterer P is located on the target body, whose coordinate is .
The echoes of the scatterer P after demodulation are given by
where denote the reflected coefficients, speed of light, coherent integration time, and instantaneous slant range from radar to scatterer P, respectively.
Conducting Fourier transform (FT) along with and range compression to (2), one obtains
where denotes the frequency window function.
Generally speaking, the instantaneous slant range of the target can be decomposed into translational motions part and rotational motions part , given by
The translational motion part should be compensated for because all of the scatterers in the target body share the same part that has no contribution to ISAR imaging. The rotational motions can be calculated as [26]
where , , and , respectively, are the coordinate of the scatterer P, rotational matrix, and radar LOS, denotes the transposition. It should be noted that, from (5), the rotational motion is related to and during the CPI. Obviously, the structure of the targets is projected to the 2-D image plane, e.g., IPP. The range dimension is defined as the direction of LOS, while the cross-range dimension is defined as the cross-product of the radar LOS direction and the effective vector. Therefore, the definition of IPP is related to the radar LOS and effective rotational vector. In general, is a constant during the CPI if the motions of targets are moderate. However, when the targets are involved in complex 3-D rotational motion, are varied by the azimuth time, which will cause the change of IPP. Therefore, to accurately describe the motion characteristic of maneuvering targets, in this work, the and can be modeled as the function of slow time , which form the unit vector for the direction of , given by
where
Further, based on second-order Taylor series expression, we have
Thus, substituting (7)–(10) into (6), is as , where
where
In addition, the form of [27] in (5) can be written as
where
where can also be expressed as
where represent the constant rotation velocity of roll, yaw, and pitch, the rotation acceleration of roll, yaw, and pitch, respectively.
Therefore, can be written as
Therefore, can be re-expressed as
where
According to the analysis above, and can be written as
Furthermore, can be expressed as the function of and , given by
Thus, can be re-written as
Therefore, the echoes of targets can be re-expressed as
2.2. Signal Analysis for Targets with Complex Motion
Rewriting (31), and given by
What is noteworthy is that, from (32), the first phase term is the range compression term. The second one is a linear phase term that is related to the Doppler frequency. The third one is a constant independent to ISAR imaging. The fourth one and the last one are, respectively, the range migration term and the 2-D spatial-variant phase error term [28]. It is quite obvious by now that the well-focused ISAR images can be obtained via compensating the range migration term and 2-D spatial-variant phase error term. The standard compensation algorithm can be applied to compensate for the range migration term, while the 2-D spatial-variant phase error terms that are different from scatterer to scatterer should be compensated for in every pixel because of the range and azimuth spatial-variant features, which increases the difficulty of phase error compensation for.
As described in [28], the analytical expression of the polluted signal consists of a focused ISAR imagery and azimuth phase history data, given by
where is the focused ISAR imagery, and it is
Performing inverse Fourier transform (IFT) for (33) in terms of , it can be writing a discrete form as
where denotes the range indices and denotes the number of samples in range dimension, denotes the azimuth index in synthetic aperture time and denotes the number of azimuth dimension, and are the discrete forms of and , respectively.
It should be noted that unless the azimuth phase history data is perfect compensated for, or we cannot obtain a well-focused ISAR imagery, given by
Suppose the parameters are exactly estimated, then the well-focused ISAR images can be obtained via an inverse discrete Fourier transform (IDFT) along with azimuth dimension, and it is
Once the 2-D spatial-variant phase error terms are accurately compensated for, the well-focused ISAR images can be obtained. Thus, we suppose the 2-D spatial-variant phase error terms are perfectly compensated for, and conduct IFT and FT along with and , respectively, to (33), the well-focused ISAR imagery can be expressed as
where and denote the IFT and FT operator to and , respectively. Obviously, based on the resolution relationship in range dimension and cross-range dimension, and can also be expressed as
Substituting (39) and (40) to (37), it can be re-written as
It is noticeable that once the 2-D spatial-variant phase error terms are precisely compensated for, the well-focused ISAR images can be obtained. Furthermore, the 2-D spatial-variant phase errors are determined by two unknown parameters . Therefore, many existing optimization algorithms such as gradient-based Newton algorithms or extended algorithms can be utilized to estimate those parameters. However, those methods need a large processing cost. In addition, the selection of initial values largely determines the imaging efficiency and accuracy of those algorithms. As a result, a fast parameters estimation method is still needed to improve computational efficiency.
2.3. Proposed Approach Description
In this section, to improve the ISAR imaging efficiency, the Generalized Radon-Fourier transform (GRFT) is firstly utilized to coarsely estimate the two unknown parameters for a suitable initial value to fine global optimal estimation. Following the coarse estimation operation, the fine search operation via gradient-based descent algorithm, e.g., Broyden–Fletcher–Goldfarb–Shanno (BFGS) method, is conducted. Additionally, the image entropy based on subarray averaging operation is generated to accelerate the global optimal convergence.
2.3.1. Coarse Parameters Estimation with GRFT
In general, the GRFT [29] can be defined as
where is the observation time, , are the definition domains of parameters , and are the maximum and minimum values of , respectively. denotes the coherent peak of GRFT. The analytical expression of can be written as
It should be noted that, after GRFT processing, the signal of (36) are now projected to the parameters domain, where the sole coherent peak value is obtained once the real value is around the estimated value , given by
where is the pulse repetition frequency (PRF).
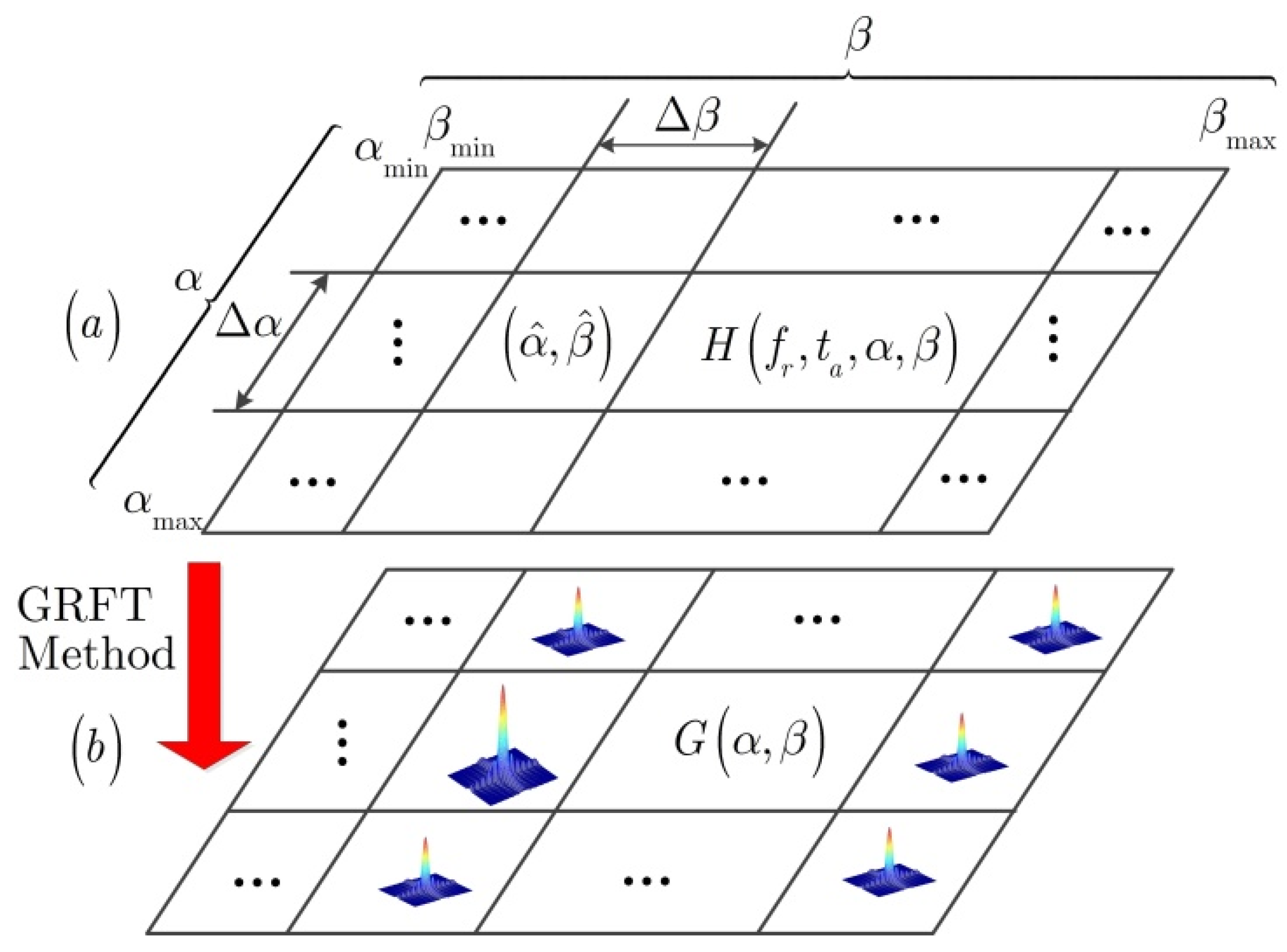
To further describe the principle of GRFT, the sketch map is shown in Figure 2. For the sake of simplicity, it is assumed that the component sets that calculated using different and are presented in Figure 2a, where with step , and with step . The mapping results with the GRFT method are provided in Figure 2b. Therefore, if the real values are around , the coherent peak that larger than others can be detected, shown in Figure 2b.
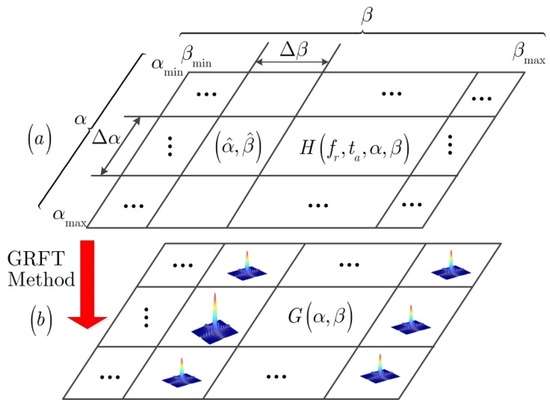
Figure 2.
Principle schematic GRFT.
Therefore, according to the position and value of the maximal coherent peak, the true value is thought to be around it and the general range of can be estimated as
where denotes the estimated parameters around the true one. Besides, the GRFT method can be repeatedly utilized to narrow down the range of the parameters to be estimated.
2.3.2. Fine Parameters Estimation with Gradient-Based Optimal
Image Entropy Combined with Subarray Averaging Operation
The entropy refers to the degree of chaos in the system, and the entropy of a well-focused ISAR image is littler than that of the unfocused one. Hence, the littler the image entropy is, the clearer the images will become. Therefore, for existing parameters estimation methods based on optimization technique, image entropy [30] is widely utilized as an image quality indicator to evaluate the ISAR imaging performance, which is an effective method to signify the definition of ISAR image. However, the cost surface obtained via conventional image entropy contains many local optimal and global optima solutions, which increase the difficulty for the search of the global optimum solution because the convergence of optimal solution cannot be guaranteed. To overcome the barrier above, many optimization methods, such as evolutionary computation (EC), simulated annealing (SA), ant colony optimization, are utilized to find the global optimum solution. However, those methods require a large processing time, which is inapplicable in practical applications [31]. Additionally, their solutions are extremely susceptible to the number of search spaces. Taking the difficulty above into consideration, in this work, the subarray averaging combined with image entropy [32,33] is proposed to eliminate the local optimal solution.
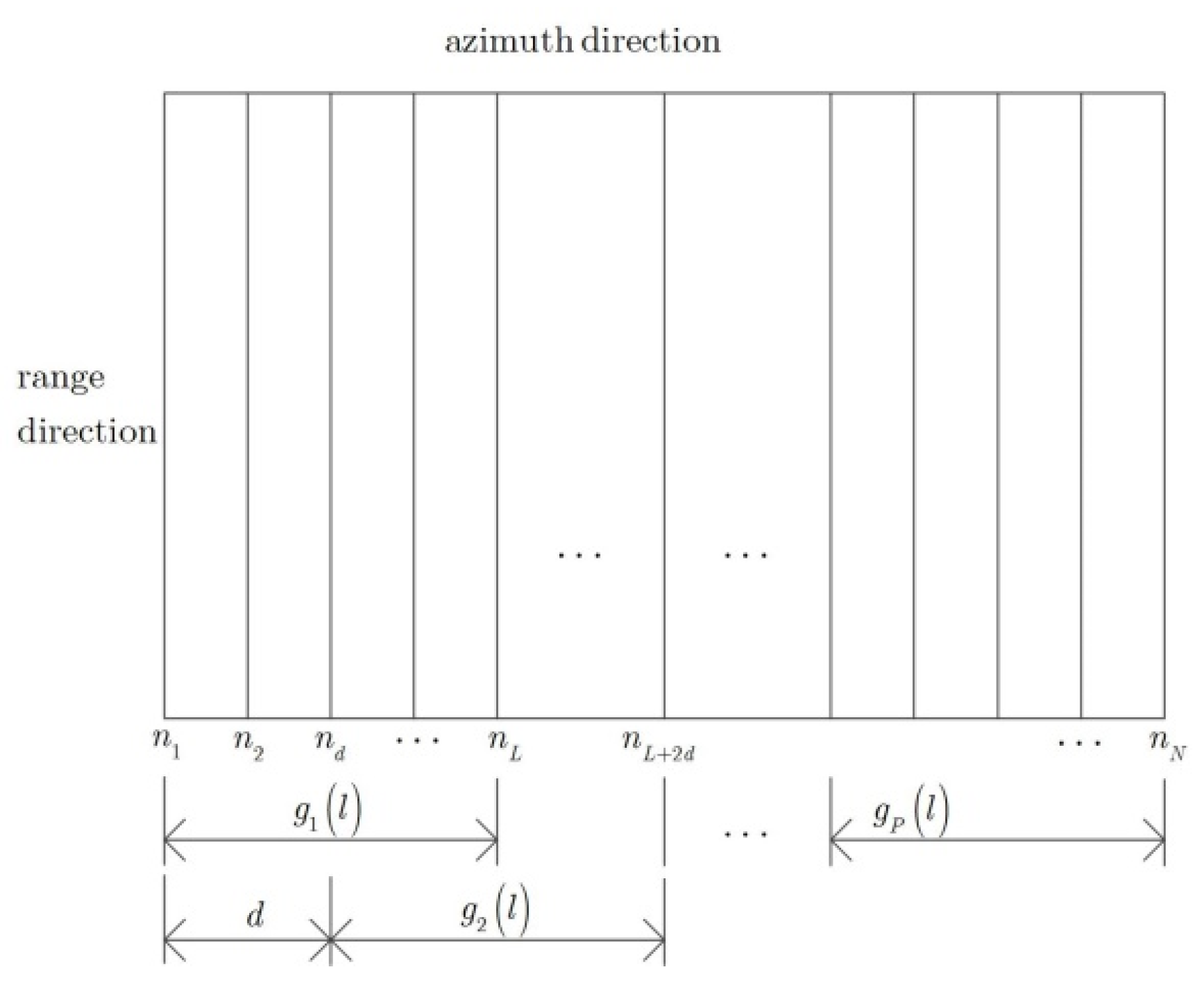
Subsequently, the image entropy combined with subarray averaging is defined as
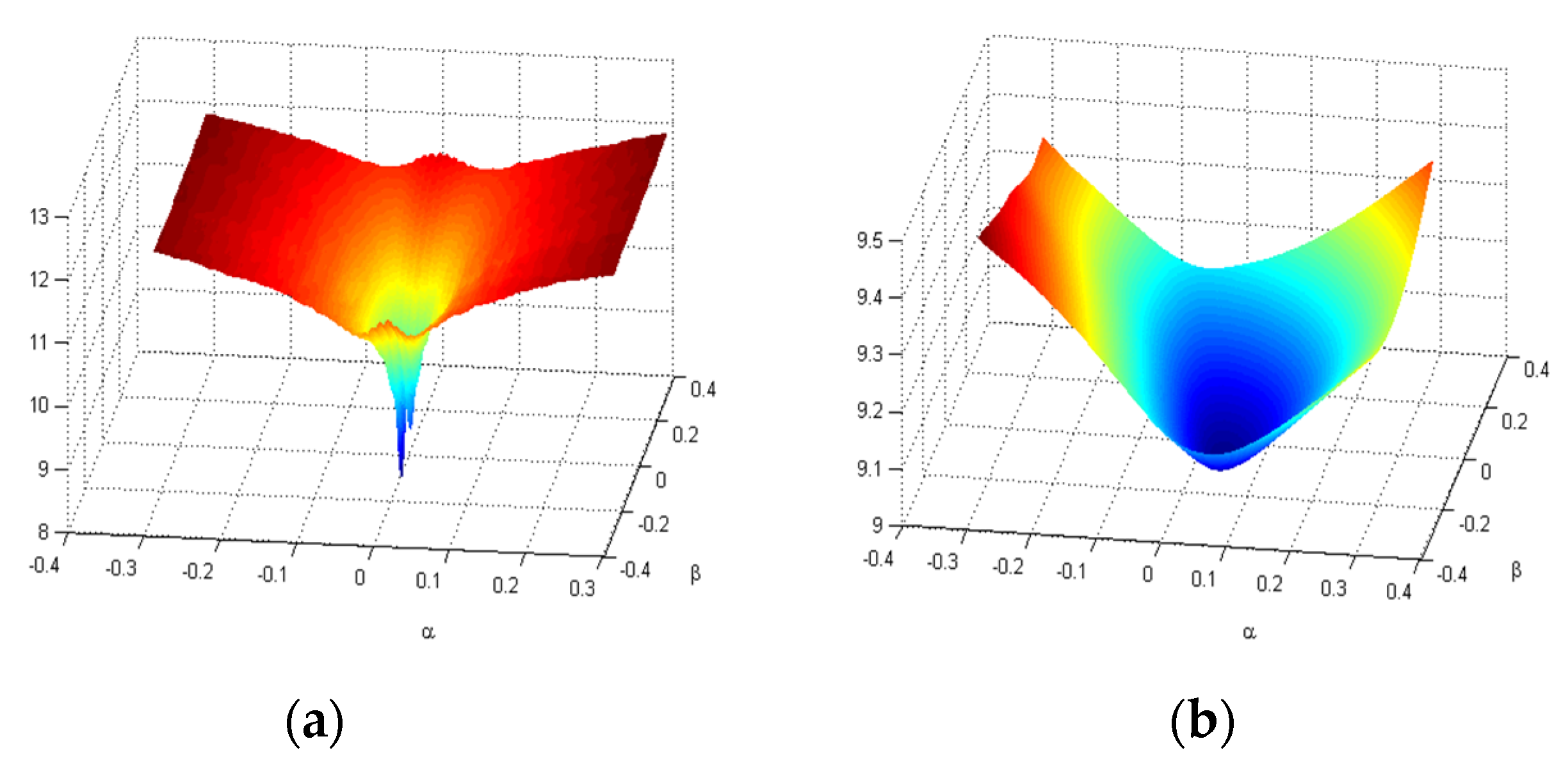
where is subarray image in (47), and denote the length and total number of the subarray sub-image, respectively, denotes the summation of squared sub-image for subarrays, normalized by total energy calculated in -squared sub-image. Therefore, can be applied as a new sub-image obtained via the subarray averaging technique proposed in this work. As shown in Figure 3, the sketch map of the subarray averaging is provided, where the ISAR image is divided into many overlapped subarrays sub-images with length along with azimuth dimension, the interval of consecutive subarrays is , shown in Figure 3. Besides, the cost surface using conventional image entropy and subarray averaging combined with image entropy are provided in Figure 4a,b, respectively, where the simulated parameters are the same as provided in Section 3.1. A notable feature, from Figure 4, is that the global minimum solution and local minimum solution coexist in the cost surface calculated using conventional image entropy compared with that of the image entropy combined with subarray averaging, shown in Figure 4a,b, respectively. Thus, the global optimal solution cannot be guaranteed while the local extremum solutions existed in the cost surface. Therefore, the image entropy combined with subarray averaging is generated as the cost surface for optimal searching, which would significantly improve the ISAR imaging efficiency.
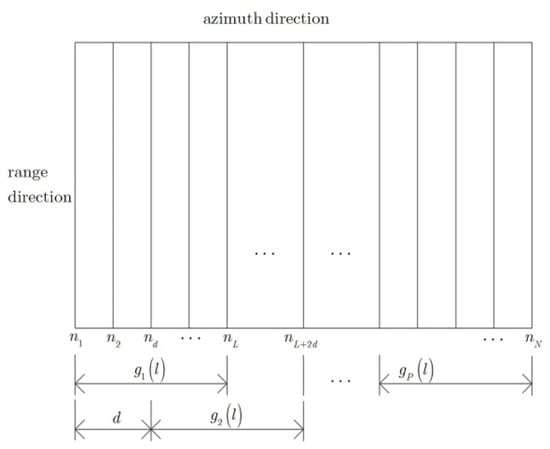
Figure 3.
Subarray averaging technique schematic diagram.
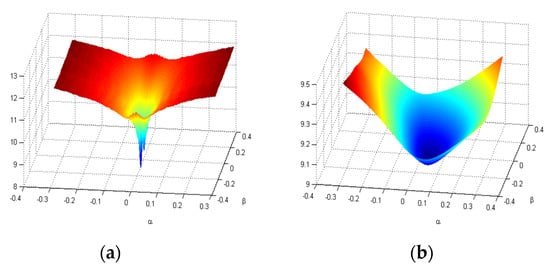
Figure 4.
Cost surface of image entropy. (a) Cost surface via conventional image entropy. (b) Cost surface via image entropy combined with subarray averaging.
Parameters Estimation Based on Gradient Descent Method
In Section 3.1, the approximate solution of the parameters is estimated. As a result, an effective method should be adopted to further accurately estimate parameters . Thanks to the smooth cost surface shown in Figure 4b, the global optimal solution can be quickly detected along the gradient descent direction of which. Therefore, for the existing method, gradient-based algorithms, e.g., Newton, are a valid approach to iteratively search the global optimal solutions. However, both the Newton method and the damped Newton method are time-consuming because the Hesse matrix should be calculated. Thanks to the Hesse matrix can be increasingly approximated by using the gradient information in each iteration, the quasi-Newton method [34] is effective for solving the unconstrained optimization problems. Therefore, in this work, the quasi-Newton method based on the BFGS algorithm [35,36] is adopted to search for the global optimal solutions.
Based on (46) and (47), the Formula for the partial derivative of to is derived as
where can be expressed as
where can be written as
where denotes the real parts. can be written as
Similar to the derivation of , the partial derivative of to can also be derived. The sole difference of is as
Thus, the gradient of entropy to can be expressed as
Furthermore, the detailed implementation procedure of BFGS is as
- Set the initial parameter , initial matrix , and the precision of error as , unit matrix, and , respectively.
- Calculate the gradient . If , then stop the calculation and the optimal parameter is . Otherwise, conduct the next step.
- Set , and conduct the next step.
- Perform a one-dimensional search to obtain such that is satisfied. Set and conduct the next step.
- Calculate , if , then stop the calculation, and set the optimal parameter as . Otherwise, conduct the next step.
- If , then and conduct Step 3. Otherwise, conduct the next step.
- Calculatewhere , denotes the transposition of , and , and repeat to step 4.
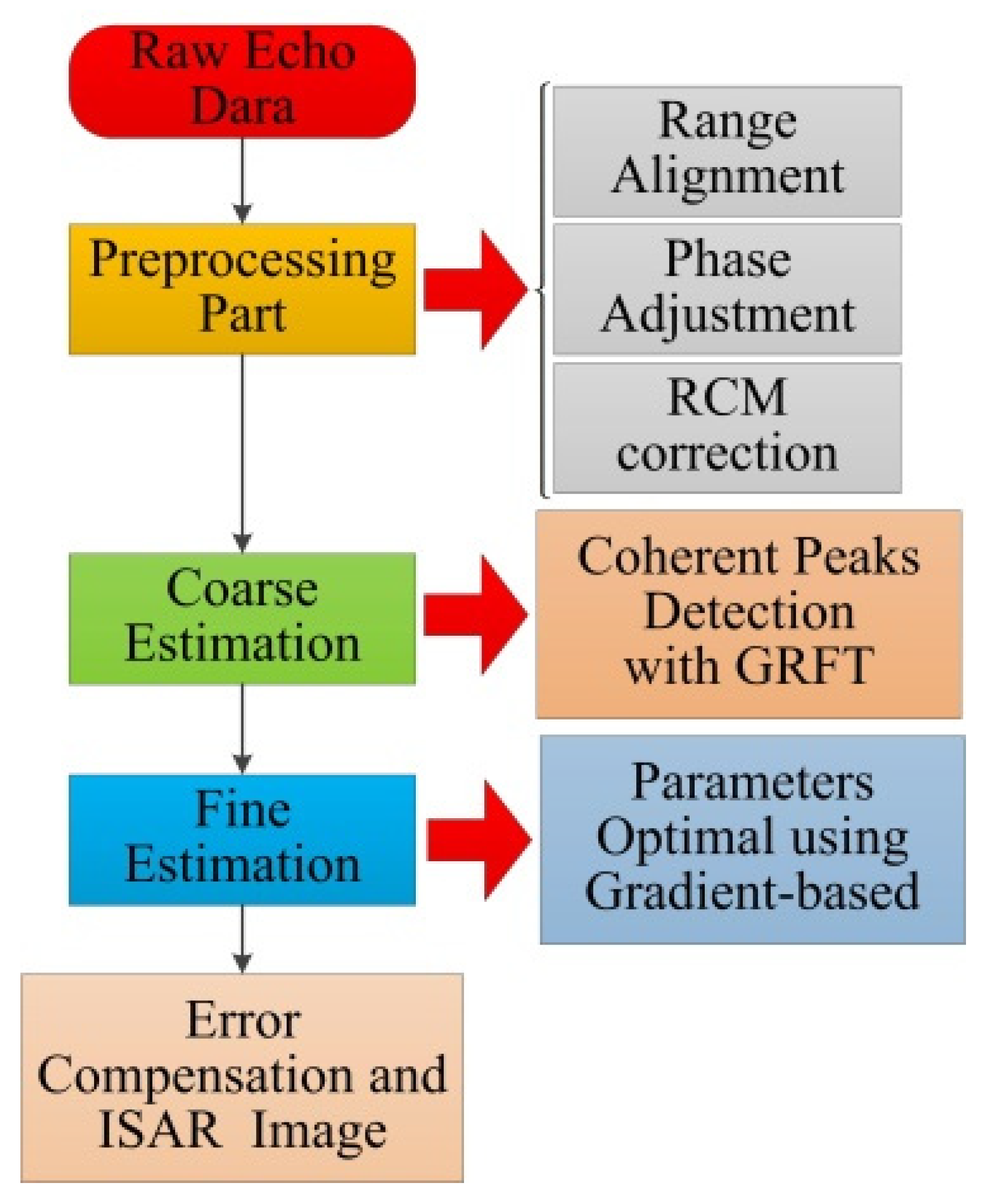
Finally, the whole ISAR imaging procedure of our proposed method is as follows, and the flowchart of the proposed method is provided in Figure 5.
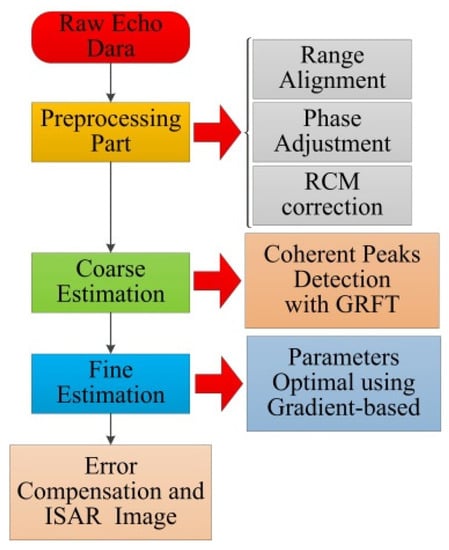
Figure 5.
Flowchart of the proposed method.
- Obtain the raw echoes, and conduct preprocessing part, e.g., range alignment, phase adjustment, and RCM correction.
- Coarsely search the range of true parameters via detecting the coherent peak with GRFT.
- Finely estimate the optimal parameters by using the gradient descent method.
- Finishing the compensation of 2D spatial-variant phase errors and obtain the well-focused ISAR image.
2.4. Some Considerations for the Proposed Method in Applications
2.4.1. Computational Complexity Analysis
In this section, the computational complexity of our proposed method is compared with that of the PGA [37] method, STFT. Without loss of generality, the operations with less time cost are omitted. Generally, we suppose floating-point operations (FLOPs) are required to compute -point FT or IFT, and FLOPs are needed to compute -point data center shifting operation, FLOPs are required to calculate the image entropy for ISAR image with size , and FLOPs are needed for the STFT of -point data, and FLOPs are needed to calculate gradient for ISAR image with size . Let represent the samples in range dimension and azimuth dimension, the search number for the search space , respectively.
The realization procedure of the PGA algorithm consists of five steps [36], which are coarsely RD imaging, center shifting operation, windowing operation, phase gradient estimation, and iterative phase error correction. The computational complexity of coarsely RD imaging that is composed of range compression and azimuth compression is . The computational cost of center shifting operation, windowing operation, phase gradient estimation, and iterative phase error correction are ,,, respectively. Thus, the total computational complexity of the PGA algorithm is
According to [16], the signal after pulse compression is processed by the STFT method. Hence, the procedure consists of range compression, and iteratively STFT processing along with azimuth dimensional in each range cell. In this paper, the length of the frequency smoothing window of STFT is . Thus, the computational cost of time-frequency processing for points data is . Therefore, the total computational complexity of STFT is
Based on the imaging procedure shown in Figure 5, the computational cost of range compression is . Suppose the number of subarray sub-image is , and the size of the subarray image is , and the iterative time of the BFGS procedure is . Considering the algorithm based on image entropy combined with subarray averaging operation, the computation of the gradient in (30) consumes . The considerable time-consuming procedure is the decision of the step size using GRFT in each iteration, which needs FLOPs complex multiplications and FLOPs FT operations. Suppose the number of conducting GRFT method is . Thus, the all computational load of the proposed method is
According to the analysis above, the computational complexity of our proposed method is larger than that of the PGA. In addition, due to time-frequency processing in all range-cell, the computational complexity of the STFT method is the largest. Though the computational complexity of PGA is superior to that of our proposed method, the imaging quality of the PGA’s is poor, which have limitation in a real application. Considering the tradeoff between imaging quality and imaging efficiency, the proposed method has superiority in contrast to that of the PGA and STFT methods.
2.4.2. Doppler Frequency Spectrum Analysis
In this section, the time-varying Doppler frequency spectrum is analyzed. To illustrate the Doppler spectrum, suppose targets have yaw motion only, e.g.,. Thus, the rotation matrix becomes
Substituting (59) into (5), then the rotational motion part can be written as
Thus, the phase of the returned signal from targets can be re-written as
Conducting the derivation of in terms of , the Doppler frequency spectrum of the targets can be derived as
where
where denote the derivation of .
Similarly, if the radar LOS is a constant during CPI, then the Doppler frequency becomes
where
where .
Accordingly, the Doppler frequency spectrum for targets with roll or pitch only has the same expression form. Additionally, comparing with the assumption that the radar LOS is a constant, from (62)–(65), the Doppler frequency has a higher-order phase term which is determined by the higher-order coefficients of the radar LOS that would affect the Doppler frequency spectrum. Therefore, the Doppler frequency spectrum calculated using time-varying radar LOS can accurately present the non-stationary IPP.
2.4.3. Sampling Rate and PRF
According to (61), the Doppler frequency of targets can be written as
Based on the Nyquist sampling theorem, the pulse repetition frequency (PRF) must satisfy , where is the maximum of the Doppler frequency, and it is
where denotes the maximum value related to the maximum size of the targets.
2.4.4. Phase Error Analysis
For the instantaneous slant range , given by
The approximation of second-order Taylor series expression will cause the phase error , and it can be written as
where and , respectively, denote the instantaneous slant range before and after Taylor series expression, and it can be written as
Substituting (70) and (71) into (69), the phase error can be written as
In general, the phase errors caused by the motion can be neglected if it is confined within , given by
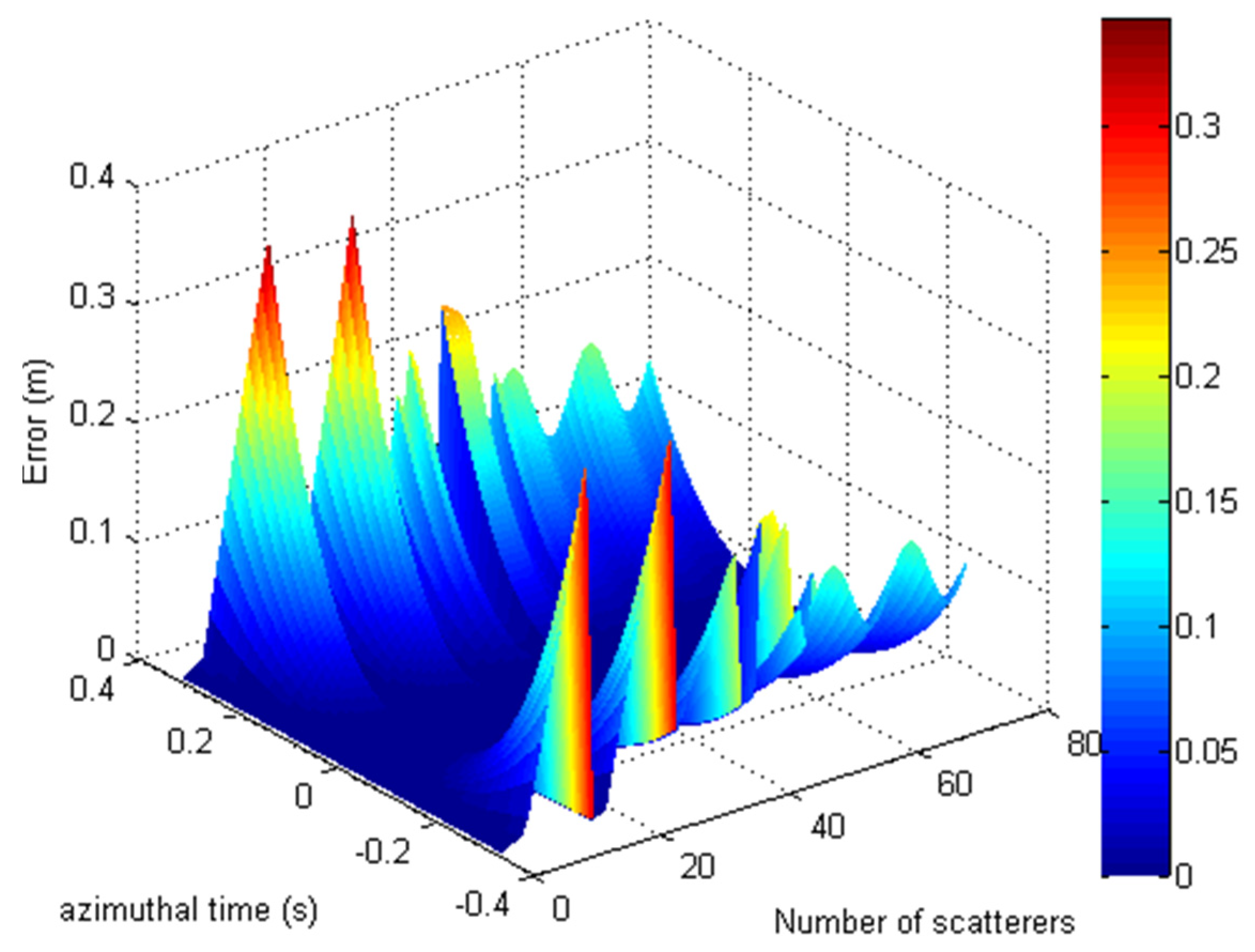
To further present the phase error caused by the operation of approximation, the simulated result based on (72) is shown in Figure 6, where the simulated parameters are the same as Section 3.1. It is worthy to be noted that the phase errors of approximation are confined with , shown in Figure 6.
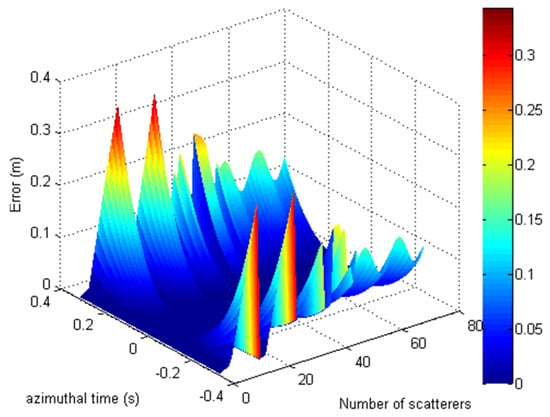
Figure 6.
The phase error of approximation operation.
3. Experimental Results and Analysis
In this section, several experiments and corresponding analyses using simulated data and electromagnetic data are presented to verify the availability and robustness of our proposed approach.
3.1. Simulation Results
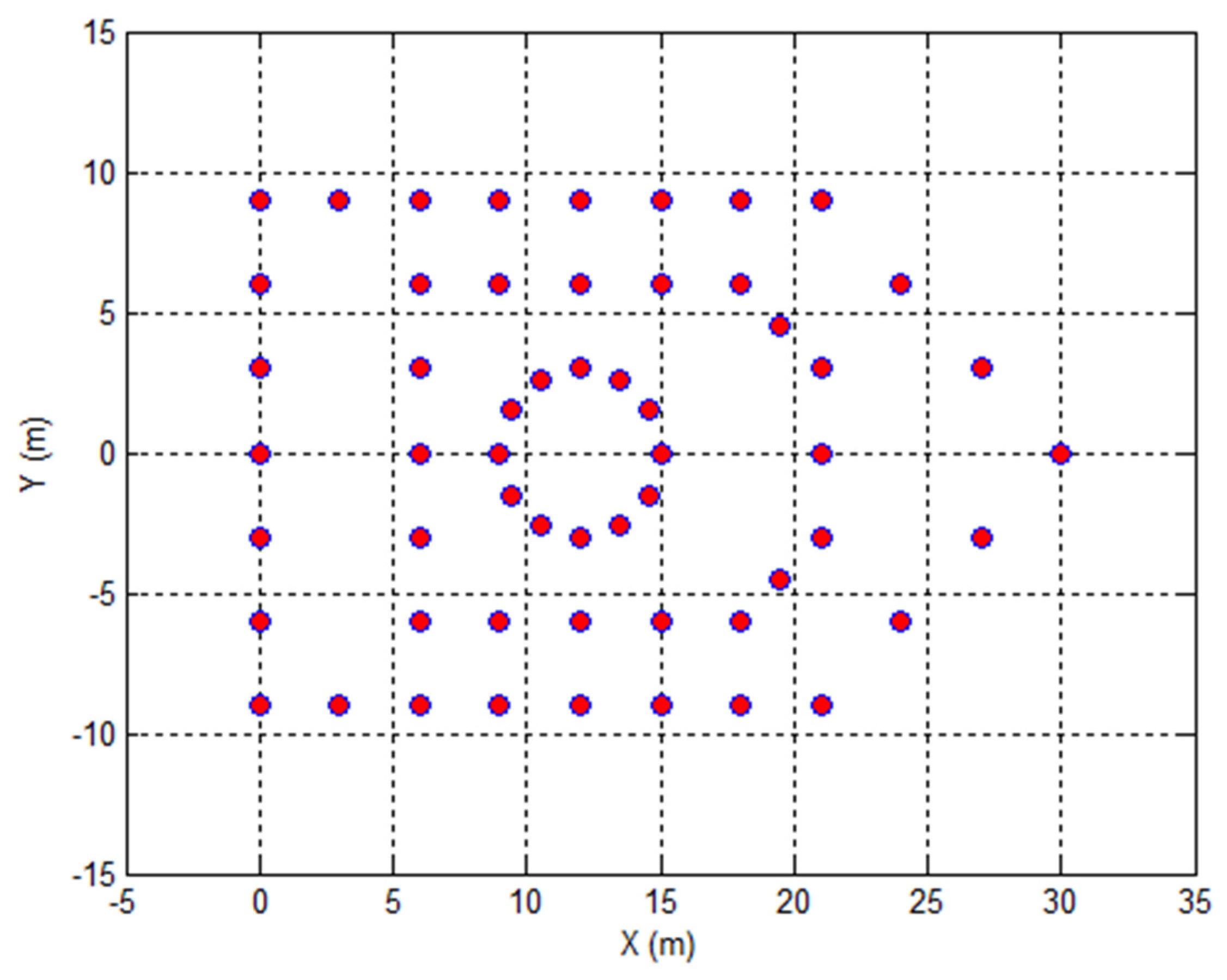
In this part, some experimental results based on simulated echoes are presented to validate the effectiveness of our proposed method. The simplified ship model is shown in Figure 7, where the model consists of 73 scatterers located on the surface of the target. Suppose the linear frequency modulation (LFM) signal is transmitted, whose carrier frequency, bandwidth, pulse width, and pulse repetition frequency are 5 GHz, 500 MHz, 4us, and 1000 Hz, respectively. For the sake of simplicity, the amplitudes of echoes are all ones. The target motion parameters and radar LOS parameters are given in Table 1. The number of pulses utilized for ISAR imaging is 640, and each pulse contains 3000 samples. All experiments are conducted on the platform of MATLAB 2014a on an Intel(R) Core(TM) i5-8400 CPU @ 2.8 GHz, 2808 MHz, RAM 8 GB, and Microsoft Window 10 operating system.
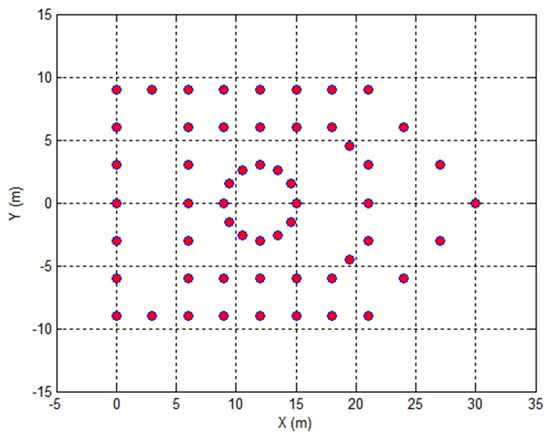
Figure 7.
Scatterers model of a ship target.

Table 1.
Motion parameters of the targets and radar LOS parameters.
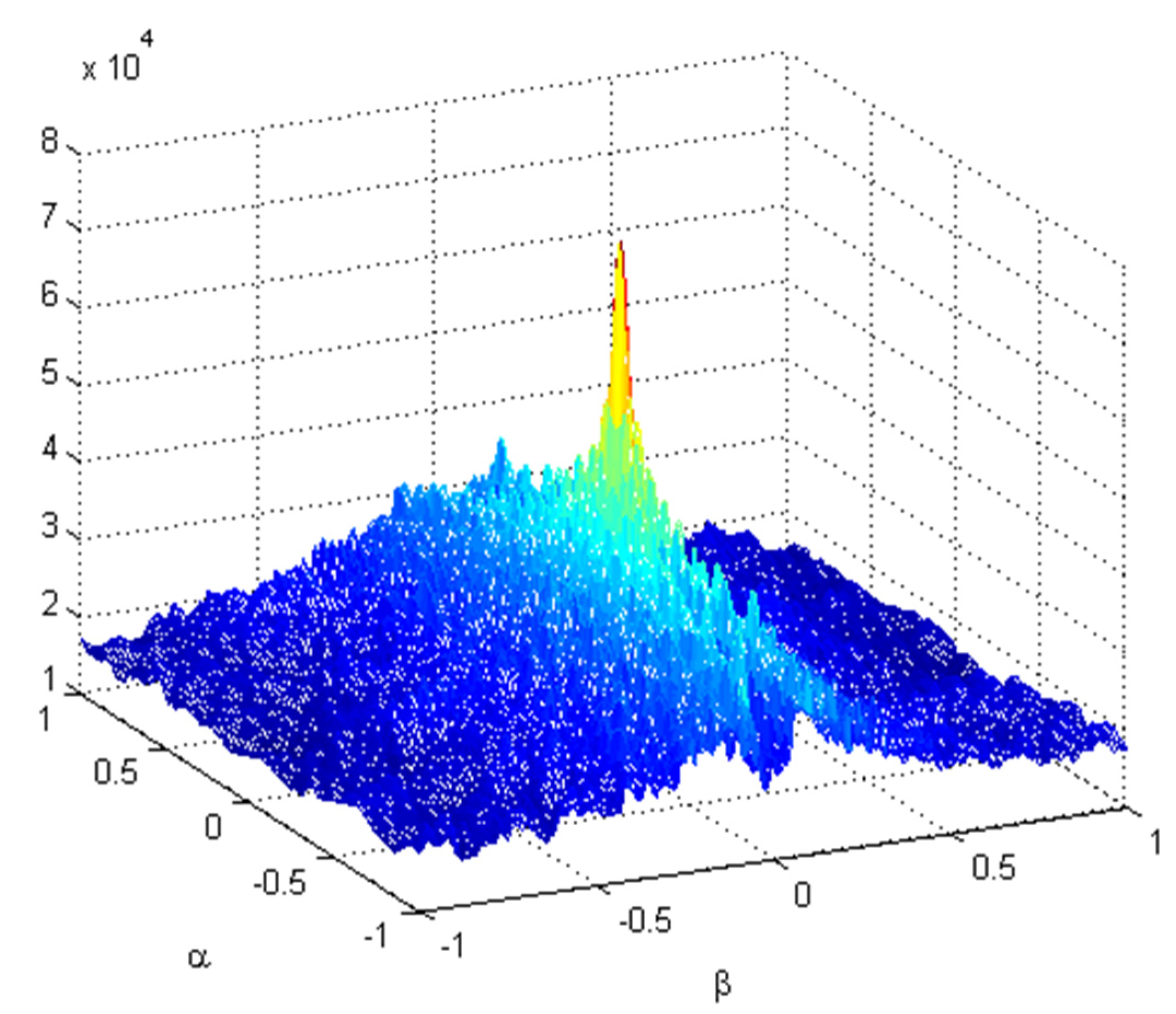
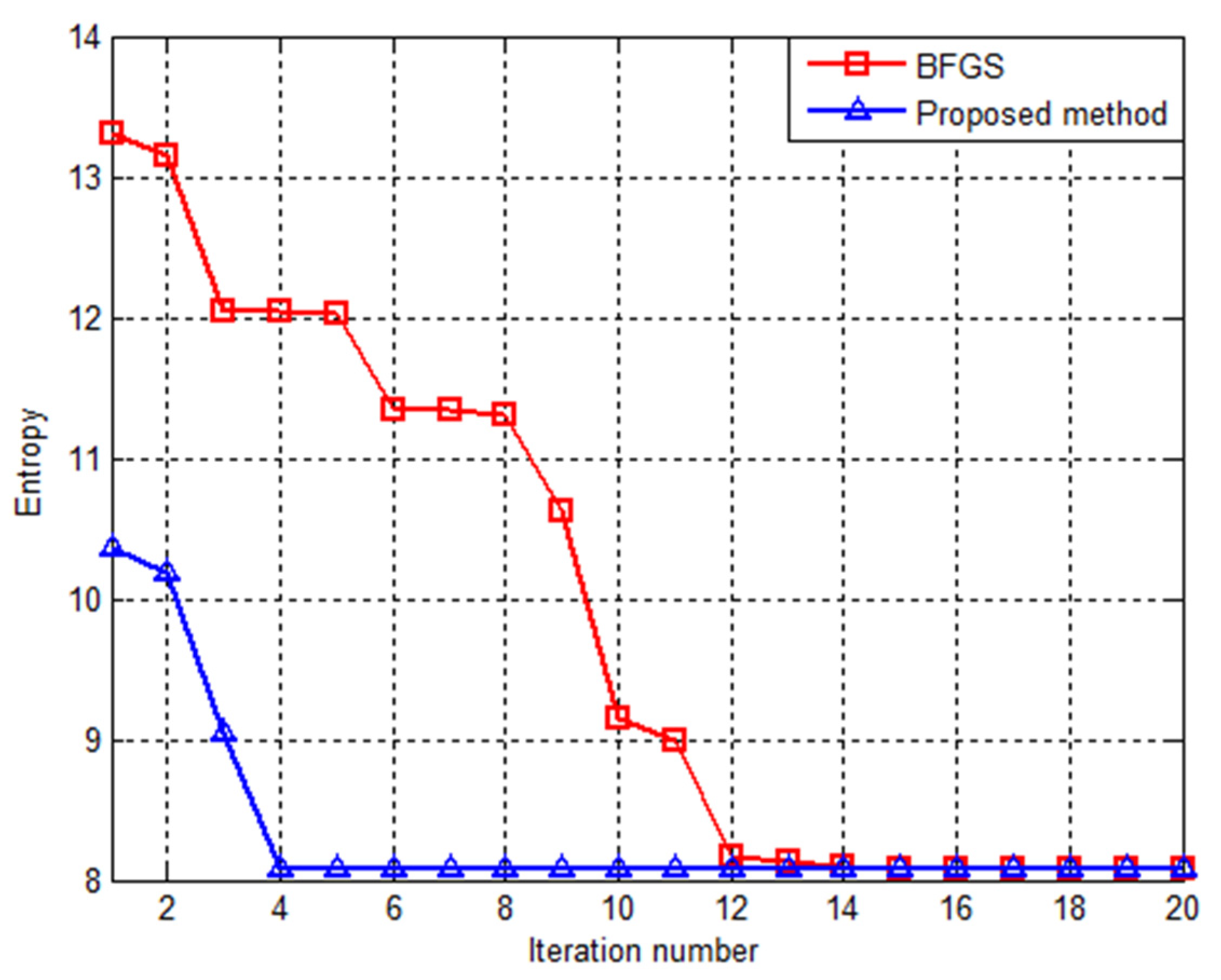
Based on the realization procedure of our proposed method, the GRFT is utilized to coarsely estimate the range of true parameters. In general, we can roughly calculate the range of and according to the extreme motion condition of the ship targets. By doing so, in this work, the coarse result with the GRFT method is shown in Figure 8. Noticeably, the sole coherent peak is obtained from Figure 8, which means that the true parameters are around it. Thus, the coarse parameters can be obtained by detecting the coordinates of the sole coherent peak. Additionally, the fine parameters are estimated by using the BFGS method, and the convergence process of fine parameters estimation operation is provided in Figure 9, where the convergence of image entropy in terms of iteration number with BFGS method is compared with that of the proposed method. The initial value using the BFGS method is set as (1, 1), and the cost function is obtained with conventional image entropy. The search range of coarse estimation using the GRFT approach is (−1, 1) with step 0.25, and the cost function is calculated using the image entropy combined with subarray averaging. It is worthy to be pointed out that the convergence of iteration number with the proposed method and BFGS, respectively, are 4-time and 12-time. Our proposed method converges faster than that of the BFGS method. Thus, our proposed method can improve the convergent efficiency for global convergence.
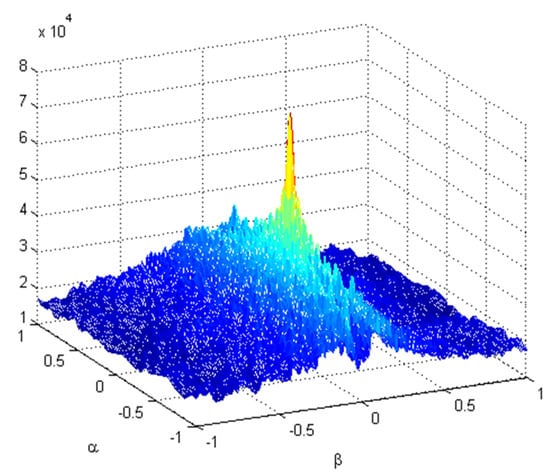
Figure 8.
Coarse estimation results with the GRFT method.
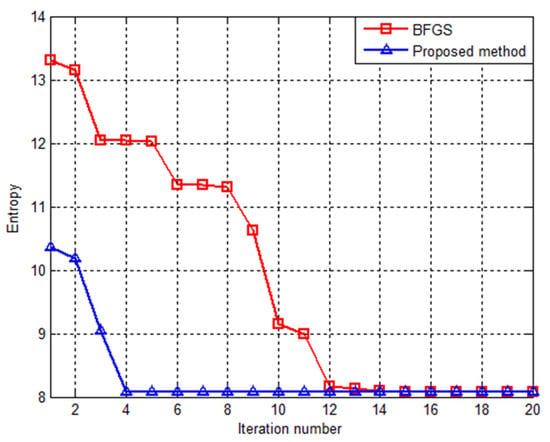
Figure 9.
Comparison of image Entropy versus iteration number using different methods.
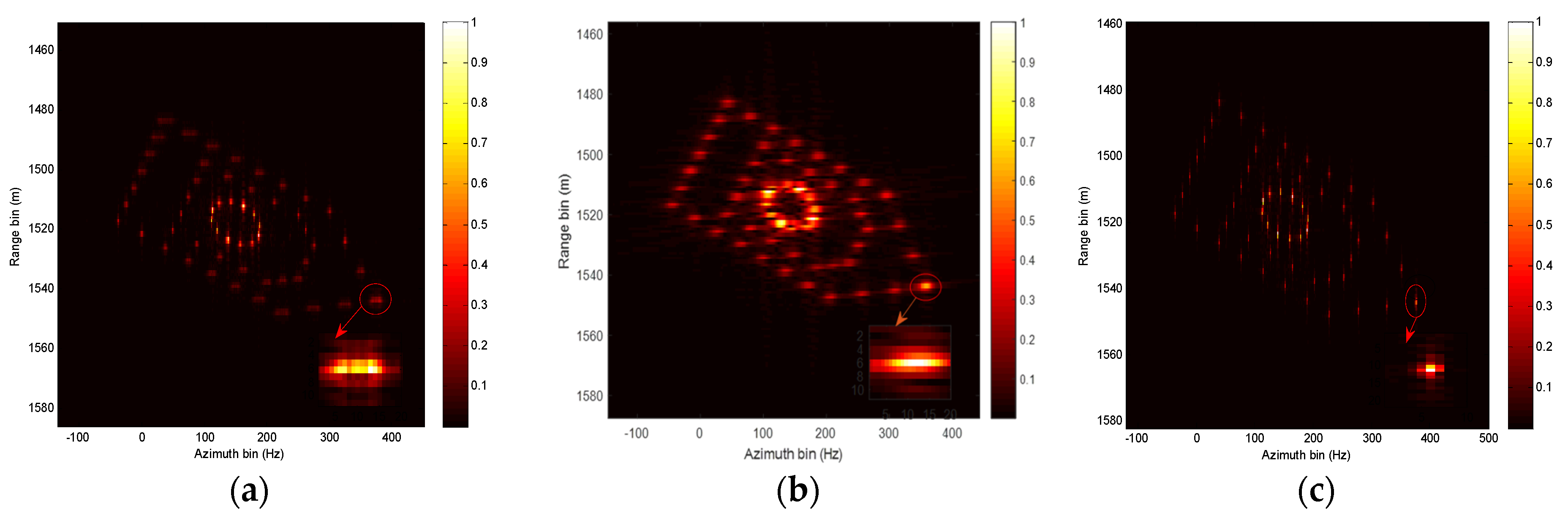
And then, we are focusing on the imaging performance of PGA, STFT, and our proposed method. The ISAR imaging results using PGA, STFT, and our proposed method are provided in Figure 10a–c, respectively. In addition, the image entropy of different imaging methods is provided in Table 2, where the image entropy of the imaging result with the proposed approach is littler than that of the PGA and STFT methods. To further demonstrate the focal performance, a scatterer marked with a circular is partially enlarged. Notably, the imaging performance of our proposed method is superior to that of the PGA and STFT methods.
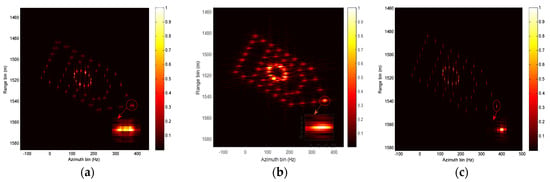
Figure 10.
ISAR imaging results with different approaches. (a) PGA imaging results. (b) STFT imaging results. (c) Our proposed method.

Table 2.
Image entropy of corresponding imaging method.
3.2. Imaging Result under Different SNRs
In this section, different zero-mean complex Gaussian noises are added to the range-compressed echoes to verify the anti-noise performance of our proposed method, and the signal-to-noise ratio (SNR) is defined as
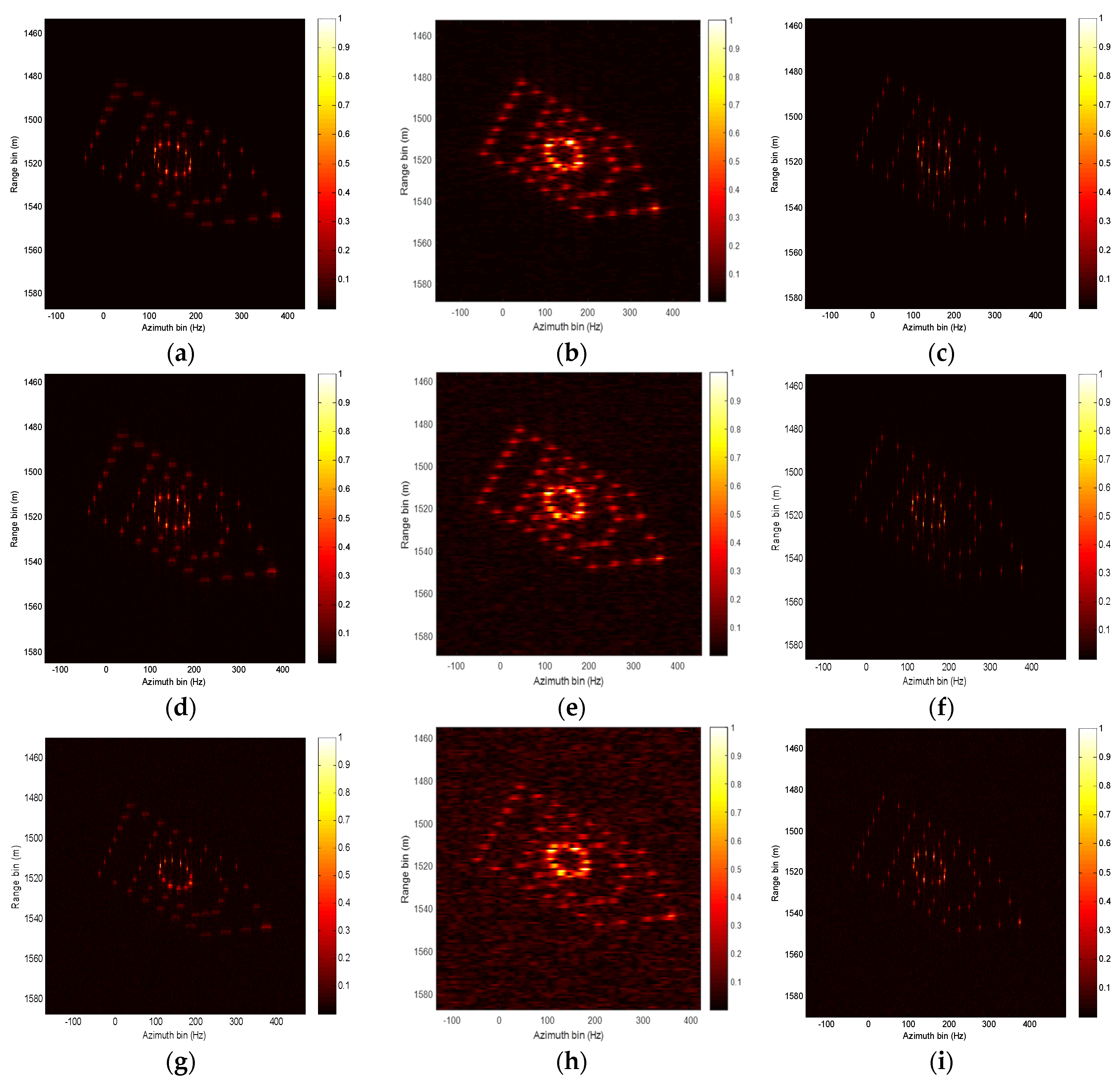
The imaging results under different SNRs from 0 to −14 dB are provided in Figure 11, where Figure 11a–c, Figure 11d–f, Figure 11g–i are the imaging results via PGA, STFT, and our proposed method under SNR = 0 dB, SNR = −7 dB, SNR = −14 dB, respectively. It should be observed that, from Figure 11, the anti-noise performance of our proposed method is better than that of the RD, PGA method, especially at low SNR conditions.
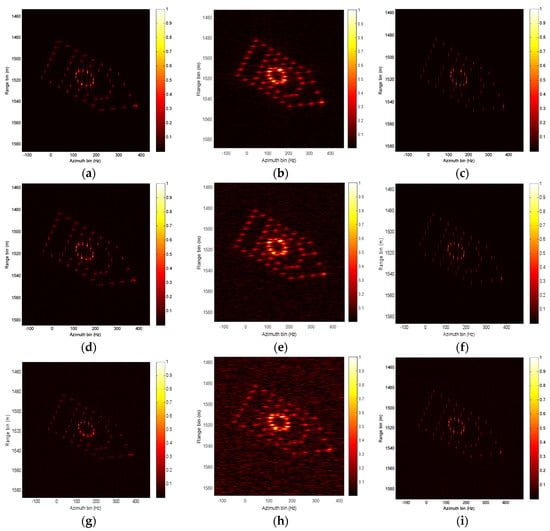
Figure 11.
ISAR imaging results with different complex white Gaussian noise. (a–c) Imaging results of PGA, STFT, and proposed method under SNR is 0 dB. (d–f) Imaging results of PGA, STFT, and proposed method under SNR is −7 dB. (g–i) Imaging results of PGA, STFT, and proposed method under SNR is −14 dB.
Additionally, the conventional image entropy [30] is utilized as a quality indicator for imaging performance, and the image entropy is defined as
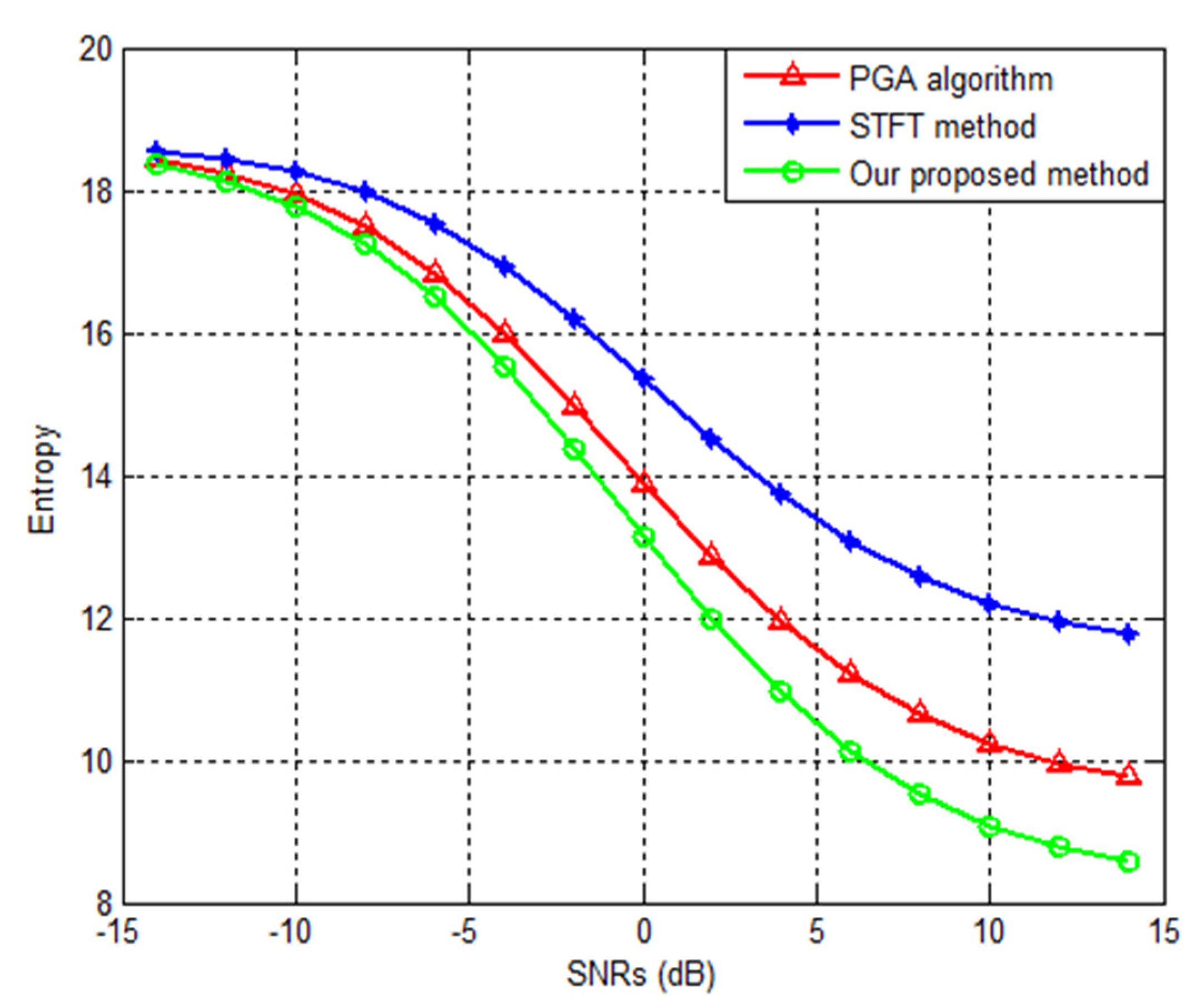
where , and is the ISAR image. 50-time Monte Carlo experiments are performed to obtain the average value of image entropy, provided in Figure 12, where the SNRs are from −14 dB to 14 dB. It is seen from Figure 12, that the image entropy of our imaging results is lower than that of the PGA and STFT method, which means that the anti-noise performance of our proposed method is more obvious as the decrease of SNRs, as demonstrated in Figure 12.
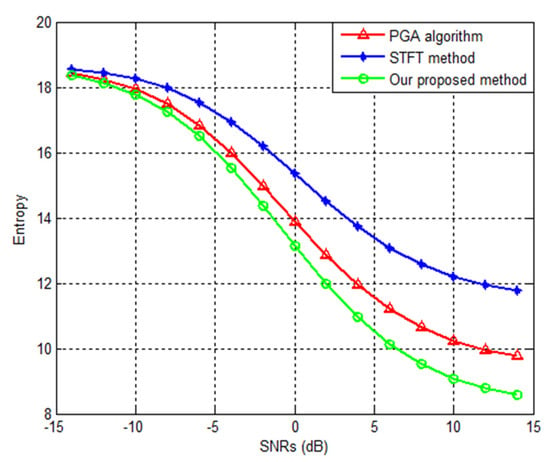
Figure 12.
Image Entropy against different SNRs.
3.3. Electromagnetic Data
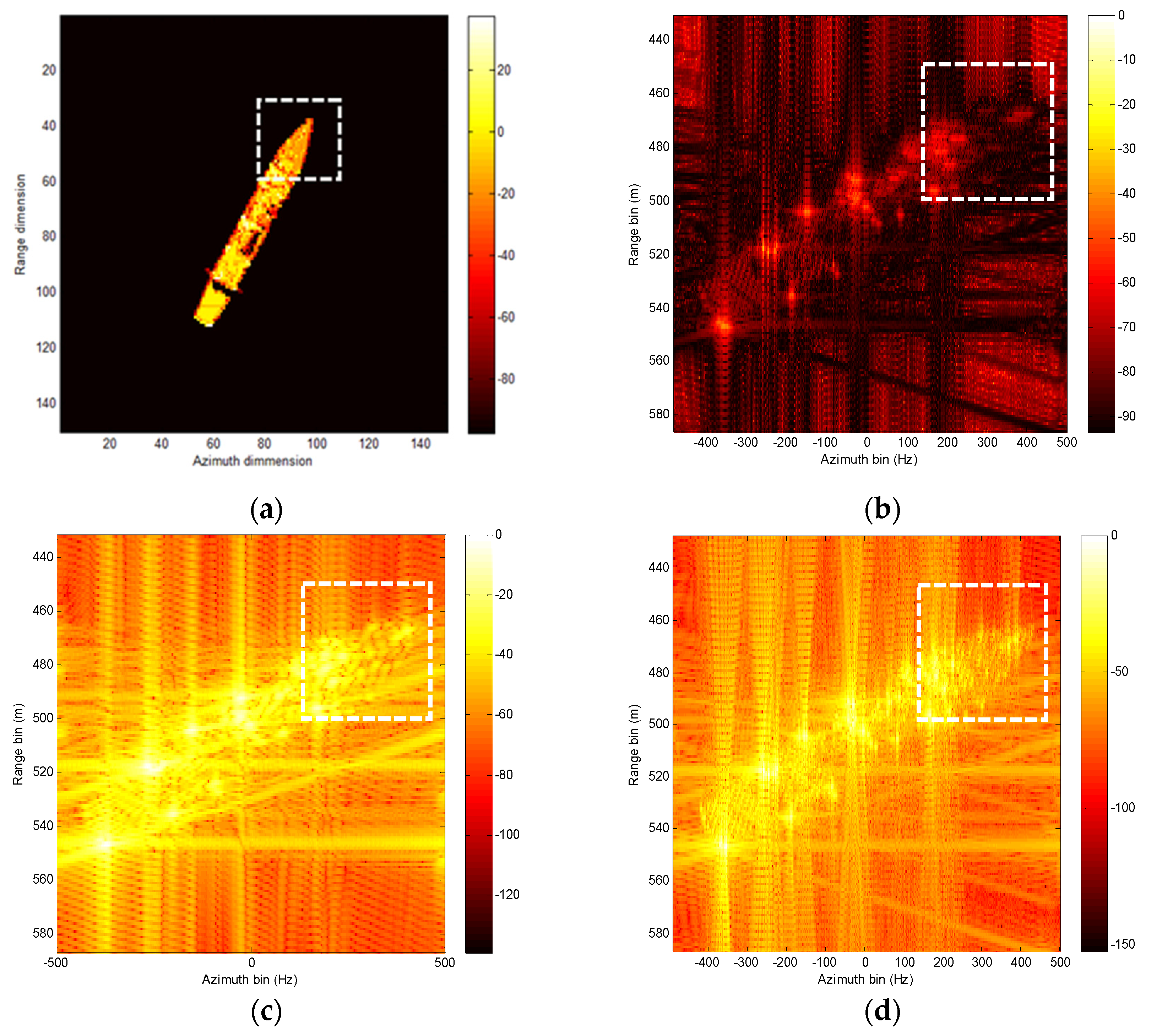
To verify the performance of the proposed method in a more realistic environment, in this section, the radar cross-section (RCS) data are produced using an electromagnetic (EM) scattering prediction technique, which is an effective and economical way to obtain the radar echoes from ship target due to the practical difficulties in measuring real-world radar data. The well-known physical optical (PO) [38] technique which is one of the widely adopted techniques for high-frequency EM computation is utilized to generate the RCS data for ship targets. As shown in Figure 13, the scene contains a destroyer, where the entity and 3-D computer-aided design (CAD) is presented in Figure 13a,b, respectively. In addition, the model of original RCS data is provided in Figure 14a. For comparison, the imaging results using PGA, STFT, and our proposed method are provided in Figure 14b–d, respectively. Obviously, although three algorithms can roughly reconstruct the outline of the destroyer, the result of our proposed method is closer to the real outline in Figure 14a, especially for the head of the target which is labeled using a white box. Meanwhile, to further quantitative analysis for the imaging results, the conventional image entropy in (47) is utilized to evaluate the imaging results, provided in Table 3. Notably, from Table 3, the image entropy of our proposed method is obviously littler than that of the PGA and STFT approach, which is consistent with the imaging results presented in Figure 14b–d.

Figure 13.
Destroyer model. (a) Photograph of the destroyer. (b) 3-D CAD model of the destroyer.
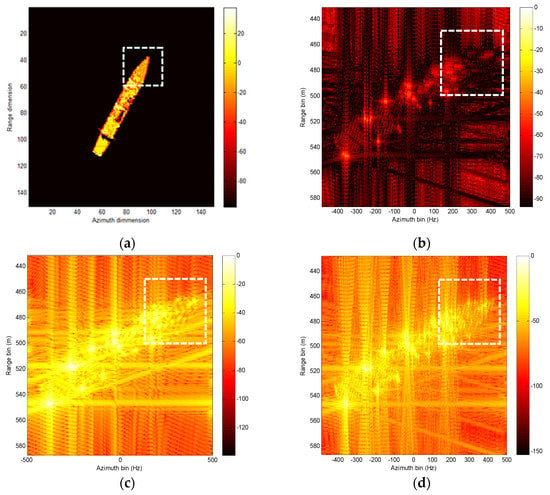
Figure 14.
Imaging results for the destroyer. (a) RCS model of the destroyer. (b) Imaging results with RD algorithm. (c) Imaging results with the PGA method. (d) Imaging results with our proposed method.

Table 3.
Image entropy of corresponding imaging method.
4. Discussion
Inverse synthetic aperture radar (ISAR) plays an important role in target detection and recognition thanks to the all-weather, all-day, high-resolution. During imaging for ship targets with moderate motion characteristics, the IPP is modeled as a constant, which is accurate. However, if the ship targets are combined with a highly maneuvering motion, the assumption that the IPP is stationary during CPI is invalid and followed by the disabling of the existing imaging approach. Therefore, to accurately present the motion characteristic, in this work, the nonstationary IPP is introduced by using the time-varying instantaneous slant range where the radar LOS is modeled as a function about slow time. In addition, the 2-D spatial-variant phase errors which can severely blur ISAR images are derived. By exploring the relationship that the coordinate of scatterer can be described via the resolution in range dimension and azimuth dimension, the 2-D spatial-variant phase errors are estimated using two parameters that corresponding to the velocity of targets. Furthermore, the GRFT method and gradient-based optimal are proposed to coarsely and finely estimate those two parameters, respectively. Besides, the approach of image entropy combined with subarray averaging operation is generated to accelerate the global optimal convergence. In conclusion, thanks to the coarse estimation operation of the parameters via the GRFT method, the global convergence can be finished quickly, which can effectively improve the imaging efficiency. Meanwhile, the subarray averaging operation can eliminate the local optimal, which can not only improve the imaging efficiency but also ensures the accuracy of parameters estimation. The imaging results of our proposed method are compared with that of the PGA method and STFT method. The experimental results using simulations and electromagnetic data demonstrate that the proposed method has a tradeoff between imaging efficiency and imaging quality.
5. Conclusions
To reconstruct the ISAR images for ship targets with nonstationary IPP under complex 3-D rotation motion, an efficient imaging approach based on GRFT and gradient-based optimal is proposed in this work. First, the geometry and signal model for ship targets with nonstationary IPP is established. The 2-D spatial-variant phase errors caused by complex 3-D rotation motion are derived because they can seriously blur the ISAR images. Second, for the accuracy and effectiveness of compensating the 2-D spatial-variant phase errors, the GRFT in conjunction with gradient-based optimal is utilized to coarsely and finely estimate the motion parameters, respectively. Considering the local convergence of cost surface obtained with conventional image entropy, the image entropy combined with subarray averaging is introduced to improve the convergence efficiency for the global optimal solution. Finally, the 2-D spatial-variant phase errors can be precisely estimated followed by the well-focused ISAR images. Simulated data and EM data are adopted to verify the effectiveness of our proposed approach. In conclusion, the proposed method can take a tradeoff between imaging performance and computational efficiency under a low noisy environment.
Author Contributions
Z.Y. and X.T. proposed the method, designed the experiments, and conceived, and analyzed the data; Z.Y. performed the experiments and wrote the paper; D.L. and G.L. analyzed the data, and H.L. and Y.L. revised the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China (Grant No. 61571069, 51877015, and 61971075), in part by the graduate research and innovation foundation of Chongqing, China (grant No. CYB18068), in part by The Key Project of Application and Development of Chongqing (cstc2019jscx-fxydX0049) in part by the Joint Research Fund in Astronomy through a Cooperative Agreement between the National Natural Science Foundation of China (NSFC) (grant No. U1831117), in part by the Guangxi Key Laboratory of Wireless Wideband Communication and Signal Processing (grant no. GXKL06200205).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank all the anonymous reviewers and editors for their useful comments and suggestions that greatly improved this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fu, J.; Xing, M.; Sun, G. Time-Frequency Reversion-Based Spectrum Analysis Method and Its Applications in Radar Imaging. Remote Sens. 2021, 13, 600. [Google Scholar] [CrossRef]
- Prickect, M.J.; Chen, C.C. Principle of inverse synthetic aperture radar (ISAR) imaging. In Proceedings of the EASCON’80; Electronics and Aerospace Systems Conference, Arlington, VA, USA, 29 September–1 October 1980; pp. 340–345. [Google Scholar]
- Tan, X.; Yang, Z.; Li, D.; Liu, H.; Liao, G.; Wu, Y.; Liu, Y. An Efficient Range-Doppler Domain ISAR Imaging Approach for Rapidly Spinning Targets. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2670–2681. [Google Scholar] [CrossRef]
- Li, D.; Zhan, M.; Liu, H.; Liao, Y.; Liao, G. A Robust Translational Motion Compensation Method for ISAR Imaging Based on Keystone Transform and Fractional Fourier Transform Under Low SNR Environment. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2140–2156. [Google Scholar] [CrossRef]
- Berizzi, F.; Diani, M. ISAR imaging of rolling, pitching and yawing targets. In Proceedings of the International Radar Conference, Edinburgh, UK, 15–17 October 2002; pp. 346–349. [Google Scholar]
- Liu, Z.; Jiang, Y. A Novel Doppler Frequency Model and Imaging Procedure Analysis for Bistatic ISAR Configuration with Shorebase Transmitter and Shipborne Receiver. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2989–3000. [Google Scholar] [CrossRef]
- Li, D.; Zhan, M.; Su, J.; Liu, H.; Liao, G. Performances analysis of coherently integrated cubic phase function for LFM signal and its application to ground moving target imaging. IEEE Trans. Geosci. Remote Sens. 2017, 11, 6402–6419. [Google Scholar] [CrossRef]
- O’Shea, P.J. A new technique for instantaneous frequency rate estimation. IEEE Signal Process. Lett. 2002, 9, 251–252. [Google Scholar] [CrossRef]
- O’Shea, P.J. A Fast Algorithm for Estimating the Parameters of a Quadratic FM Signal. IEEE Trans. Signal Process. 2004, 52, 385–393. [Google Scholar] [CrossRef]
- Simeunovi´c, M.; Djurovi´c, I. Non-uniform sampled cubic phase function. Signal Process. 2014, 101, 99–103. [Google Scholar] [CrossRef]
- Wang, Y.; Lin, Y. ISAR Imaging of Non-Uniformly Rotating Target via Range-Instantaneous-Doppler-Derivatives Algorithm. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 7, 167–176. [Google Scholar] [CrossRef]
- Bai, X.; Tao, R.; Wang, Z.; Wang, Y. ISAR Imaging of a Ship Target Based on Parameter Estimation of Multicomponent Quadratic Frequency-Modulated Signals. IEEE Trans. Geosci. Remote Sens. 2013, 52, 1418–1429. [Google Scholar] [CrossRef]
- Zheng, J.; Liu, H.; Liao, G.; Su, T.; Liu, Z.; Liu, Q.H. ISAR Imaging of Nonuniformly Rotating Targets Based on Generalized Decoupling Technique. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 520–532. [Google Scholar] [CrossRef]
- Chen, V.; Ling, H. Time-Frequency Transform for Radar Imaging and Signal Analysis; Artech House: Boston, MA, USA, 2002. [Google Scholar]
- Peleg, S.; Friedlander, B. The discrete polynomial-phase transform. IEEE Trans. Signal Process. 1995, 43, 1901–1914. [Google Scholar] [CrossRef]
- Cohen, L. Time-Frequency Analysis; Englewood Cliffs, Prentice-Hall: Bergen, NJ, USA, 1996. [Google Scholar]
- Kim, K.-T.; Choi, I.-S.; Kim, H.-T. Efficient radar target classification using adaptive joint time-frequency processing. IEEE Trans. Antennas Propag. 2000, 48, 1789–1801. [Google Scholar] [CrossRef]
- Berizzi, F.; Corsini, G. Autofocusing of inverse synthetic aperture radar images using contrast optimization. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 1185–1191. [Google Scholar] [CrossRef]
- Eichel, P.H.; Ghiglia, D.C.; Jakowatz, C.V. Speckle processing method for synthetic-aperture-radar phase correction. Opt. Lett. 1989, 14, 1–3. [Google Scholar] [CrossRef]
- Zhu, Z.; Qiu, X.; She, Z. ISAR motion compensation using modified Doppler centroid tracking method. In Proceedings of the IEEE 1996 National Aerospace and Electronics Conference, Dayton, OH, USA, 20–22 May 1966. [Google Scholar]
- Ding, Z.; Zhang, T.; Li, Y.; Li, G.; Dong, X.; Zeng, T.; Ke, M. A Ship ISAR Imaging Algorithm Based on Generalized Radon-Fourier Transform with Low SNR. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6385–6396. [Google Scholar] [CrossRef]
- Martorella, M.; Berizzi, F. Time windowing for highly focused ISAR image reconstruction. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 992–1007. [Google Scholar] [CrossRef]
- Zhou, P.; Zhang, X.; Dai, Y.S.; Sun, W.F.; Wan, Y. Time window selection algorithm for ISAR ship imaging based on in-stantaneous Doppler frequency estimation of multiple scatterers. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 10, 3799–3812. [Google Scholar] [CrossRef]
- Kang, B.-S.; Ryu, B.-H.; Kim, K.-T. Efficient Determination of Frame Time and Length for ISAR Imaging of Targets in Complex 3-D Motion Using Phase Nonlinearity and Discrete Polynomial Phase Transform. IEEE Sensors J. 2018, 18, 5739–5752. [Google Scholar] [CrossRef]
- Zhang, S.; Sun, S.; Zhang, W.; Zong, Z.; Yeo, T.S. High-Resolution Bistatic ISAR Image Formation for High-Speed and Complex-Motion Targets. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1–12. [Google Scholar] [CrossRef]
- Chen, V.C.; Miceli, W.J. Time-varying spectral analysis for radar imaging of maneuvering targets. IEEE Proc.-Radar Sonar Navigat. 1998, 145, 262–268. [Google Scholar] [CrossRef]
- Li, J.; Ling, H.; Chen, V. An Algorithm to Detect the Presence of 3D Target Motion from ISAR Data. Multidimens. Syst. Signal Process. 2003, 14, 223–240. [Google Scholar] [CrossRef]
- Feng, C.Q.; Tong, N.N.; Huang, D.R.; Guo, Y.D. 2D spatial-variant phase errors compensation for ISAR imagery based on contrast maximization. Electron. Lett. 2016, 52, 1480–1482. [Google Scholar]
- Xu, J.; Yu, J.; Peng, Y.-N.; Xia, X.-G. Radon-Fourier Transform for Radar Target Detection, I: Generalized Doppler Filter Bank. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1186–1202. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, Y.; Li, X. Fast Entropy Minimization Based Autofocusing Technique for ISAR Imaging. IEEE Trans. Signal Process. 2015, 63, 3425–3434. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in Fortran: The Art of Scientific Computing. Math. Comput. 1994, 62, 433. [Google Scholar] [CrossRef]
- Kim, K.T. Reconstruction of high range resolution profiles of moving targets using stepped frequency waveforms. IET Radar Sonar Navig. 2010, 4, 564–575. [Google Scholar] [CrossRef]
- Jeong, H.-R.; Kim, H.-T.; Kim, K.-T. Application of Subarray Averaging and Entropy Minimization Algorithm to Stepped-Frequency ISAR Autofocus. IEEE Trans. Antennas Propag. 2008, 56, 1144–1154. [Google Scholar] [CrossRef]
- Mokhtari, A.; Ribeiro, A. Stochastic Quasi-Newton Methods. Proc. IEEE 2020, 108, 1906–1922. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Marston, T.M.; Plotnick, D.S. Semiparametric statistical strip-map synthetic aperture autofocusing. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2086–2095. [Google Scholar] [CrossRef]
- Wahl, D.E.; Eichel, P.H.; Ghiglia, D.C.; Jakowatz, C.V. Phase gradient autofocus-a robust tool for high resolution SAR phase correction. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 827–835. [Google Scholar] [CrossRef]
- Kouyoumjian, R. Asymptotic high-frequency methods. Proc. IEEE 1965, 53, 864–876. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).