Long-Term Observations of Microwave Brightness Temperatures over a Metropolitan Area: Comparison of Radiometric Data and Spectra Simulated with the Use of Radiosonde Measurements
Abstract
1. Introduction
2. Materials and Methods
2.1. Observations
2.2. Radiative Transfer Model
2.3. Absorption Models
- They are a self-consistent set (i.e., one cannot just change only first- or only second-order coefficients as they are all calculated from the relaxation matrix).
2.4. Data Filtering
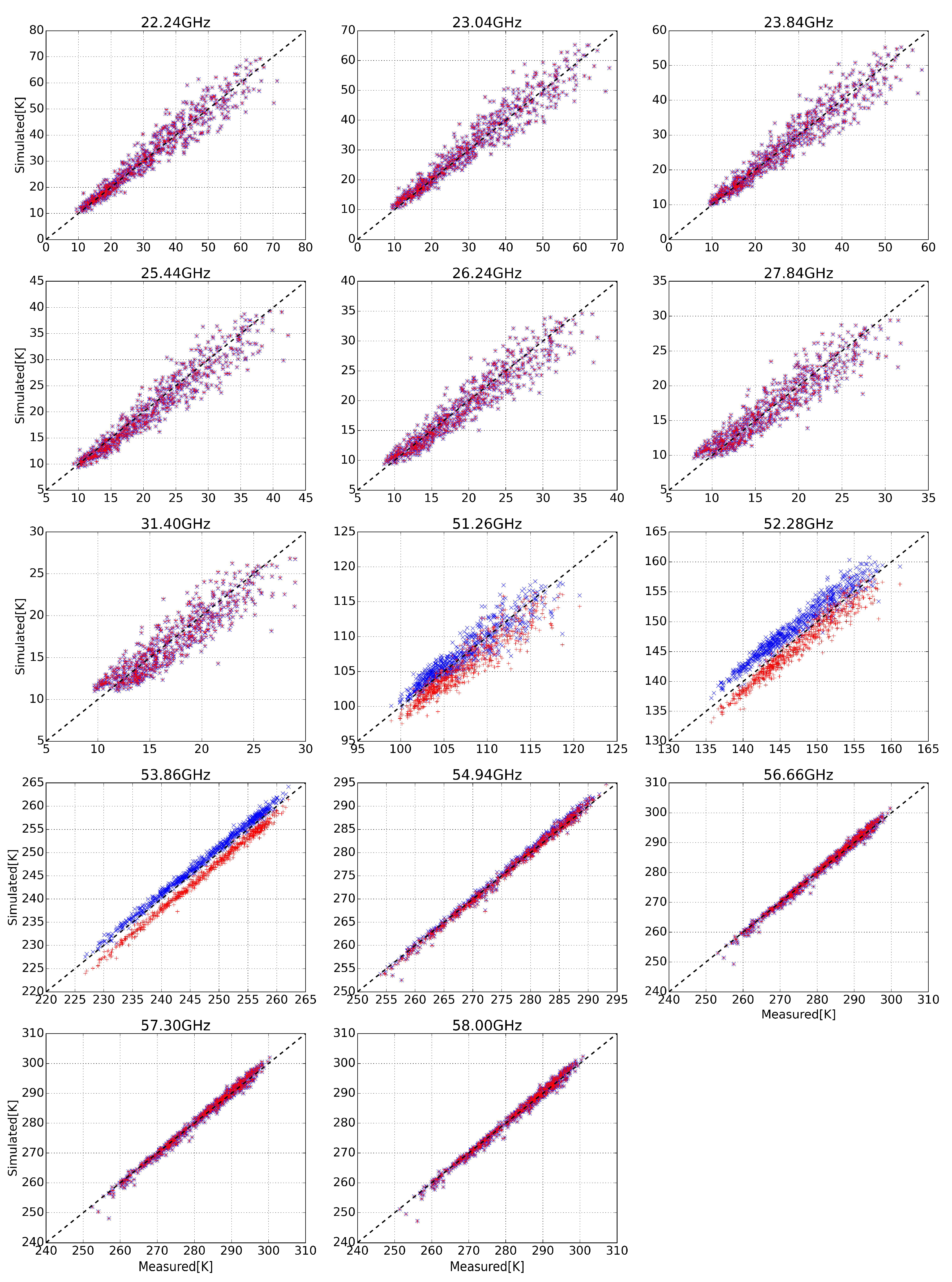
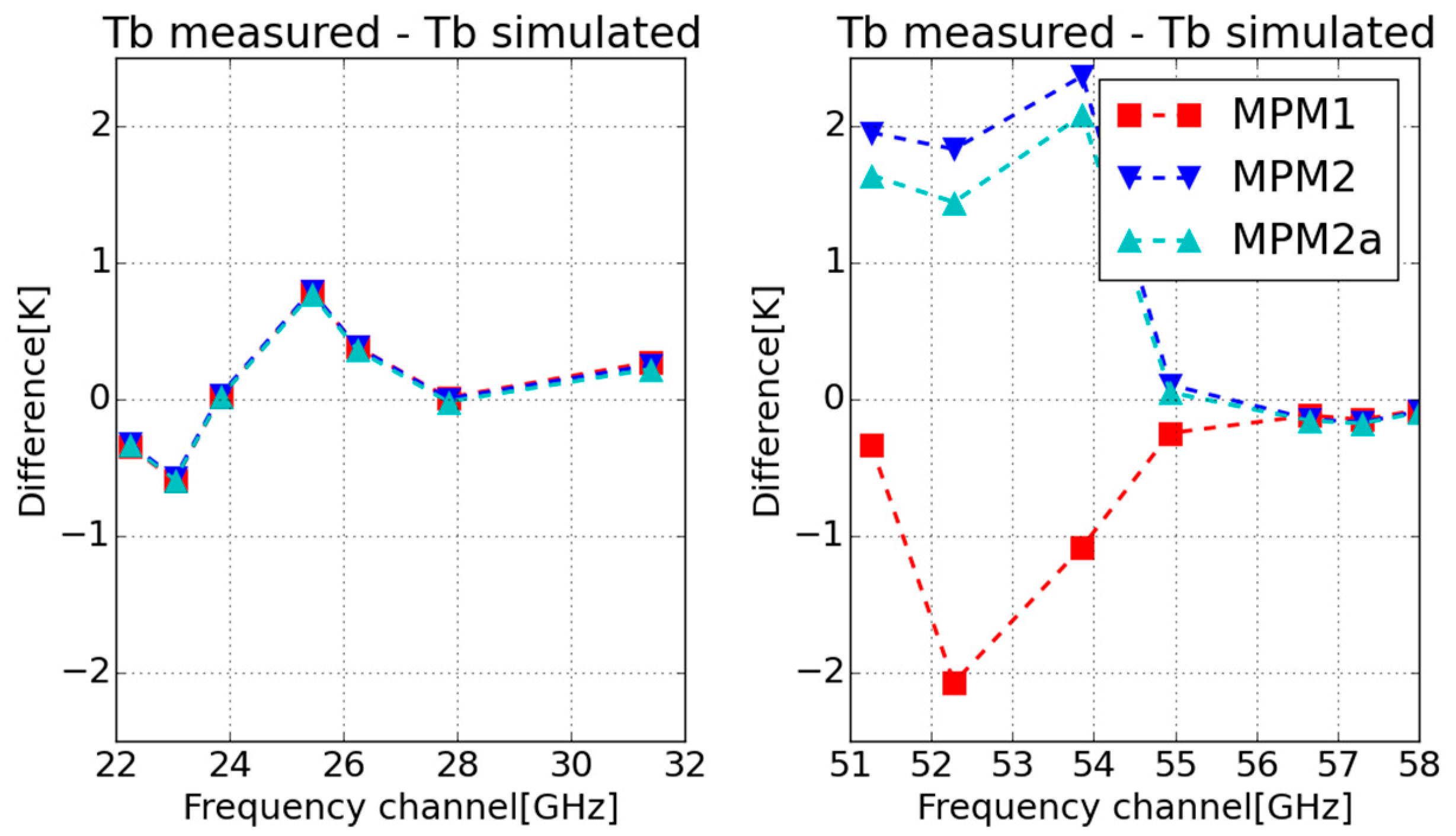
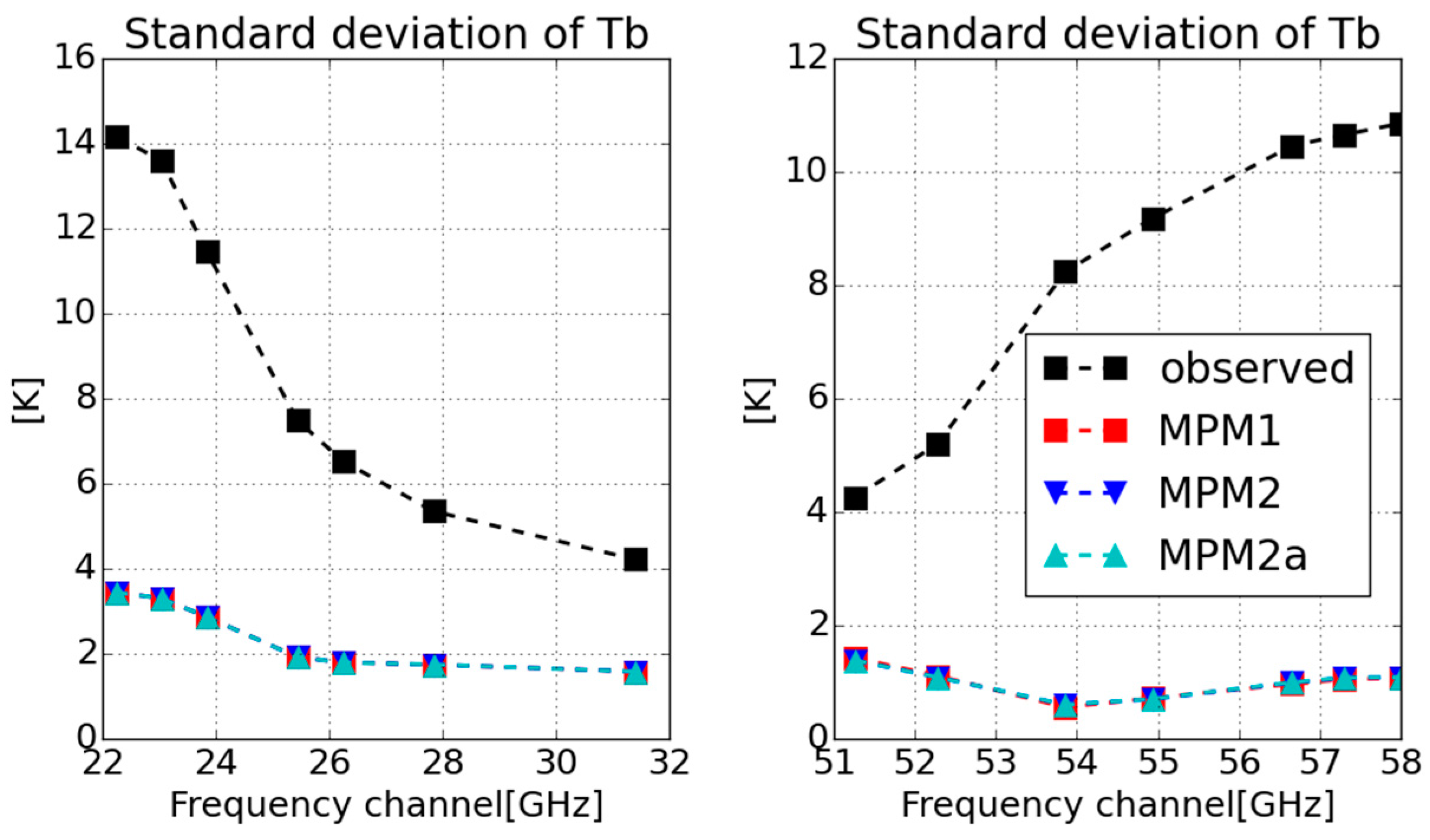
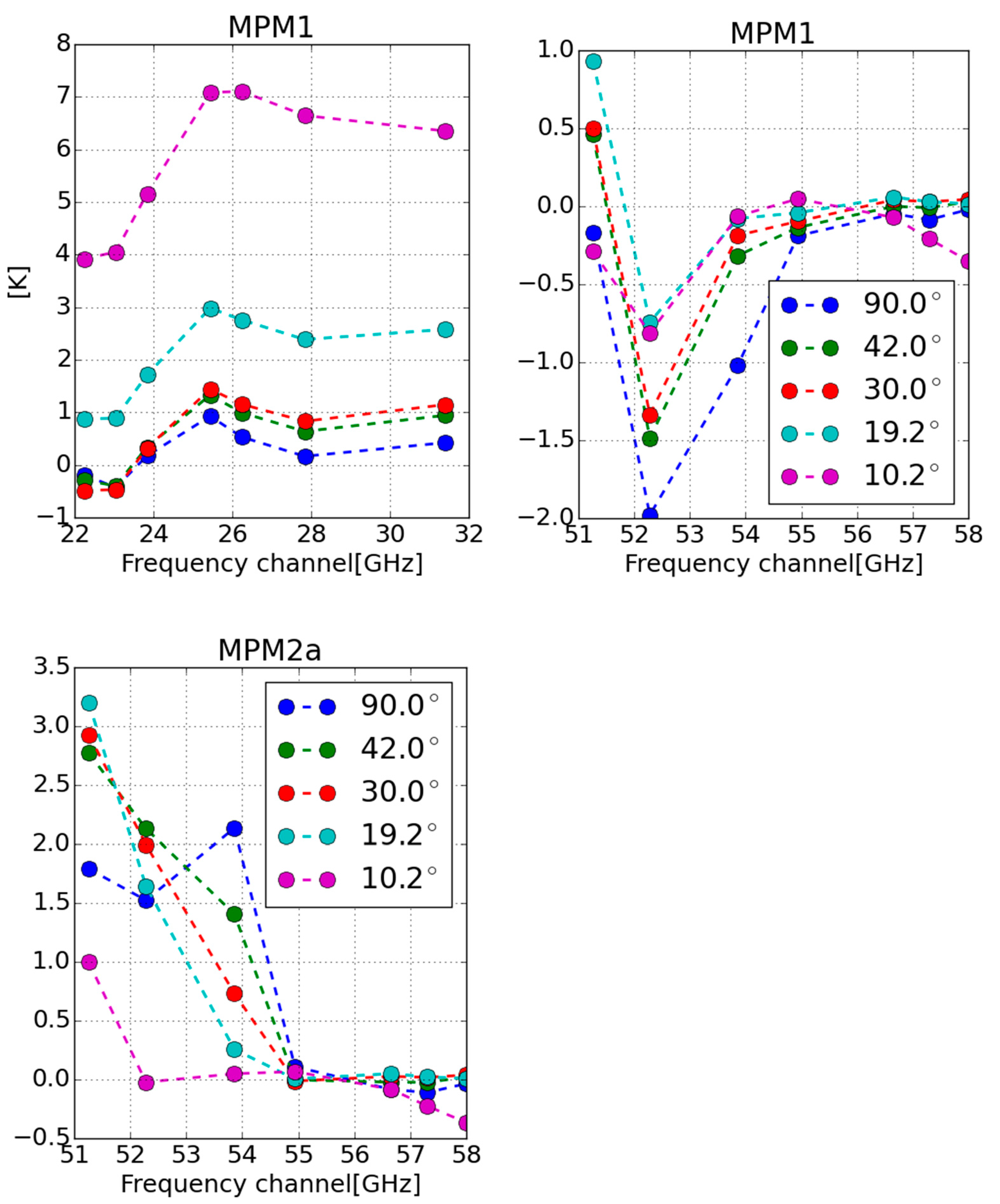
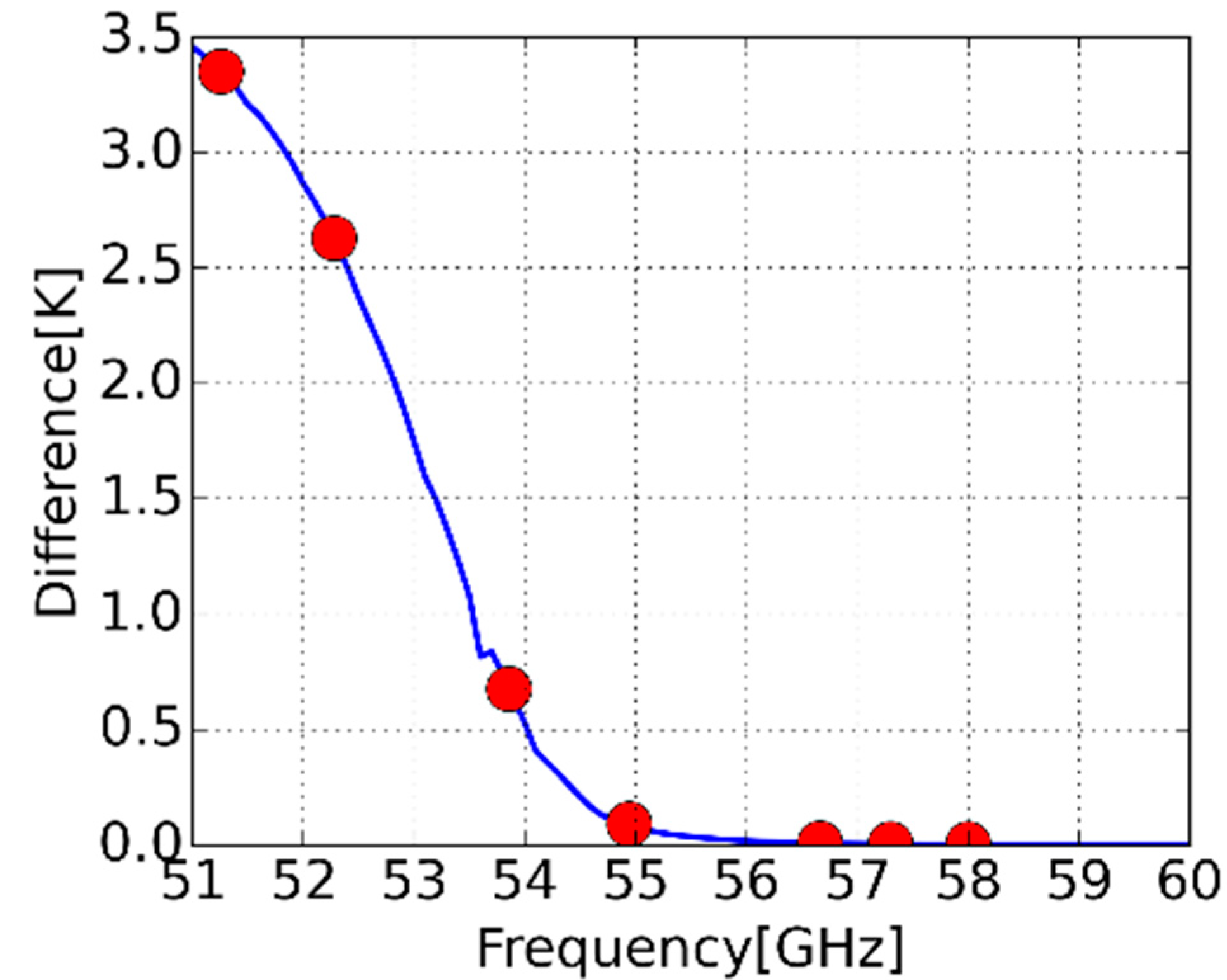
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- National Research Council. Observing Weather and Climate from the Ground Up: A Nationwide Network of Networks; The National Academies Press: Washington, DC, USA, 2009; 250p. [Google Scholar] [CrossRef]
- National Research Council. When Weather Matters: Science and Services to Meet Critical Societal Needs; The National Academies Press: Washington, DC, USA, 2010; 198p. [Google Scholar] [CrossRef]
- Troitsky, A.V.; Gajkovich, K.P.; Gromov, V.D.; Kadygrov, E.N.; Kosov, A.S. Thermal sounding of the atmospheric boundary layer in the oxygen absorption band center at 60 GHz. IEEE Trans. Geosci. Remote Sens. 1993, 31, 116–120. [Google Scholar] [CrossRef]
- Ware, R.; Carpenter, R.; Güldner, J.; Liljegren, J.; Nehrkorn, T.; Solheim, F.; Vandenberghe, F. A multichannel radiometric profiler of temperature, humidity, and cloud liquid. Radio Sci. 2003, 38, 8079. [Google Scholar] [CrossRef]
- Rose, T.; Crewell, S.; Löhnert, U.; Simmer, C. A network suitable microwave radiometer for operational monitoring of the cloudy atmosphere. Atmos. Res. 2005, 75, 183–200. [Google Scholar] [CrossRef]
- Navas-Guzmán, F.; Kämpfer, N.; Haefele, A. Validation of brightness and physical temperature from two scanning microwave radiometers in the 60 GHz O2 band using radiosonde measurements. Atmos. Meas. Tech. 2016, 9, 4587–4600. [Google Scholar] [CrossRef]
- Shvetsov, A.A.; Ryskin, V.G.; Kulikov, M.Y.; Kukin, L.M.; Fedoseev, L.I.; Schitov, A.M.; Feigin, A.M. Ground-based microwave spectroradiometer for thermal sounding of the troposphere. Instrum. Exp. Tech. 2016, 59, 433–436. [Google Scholar] [CrossRef]
- Shvetsov, A.A.; Belikovich, M.V.; Krasilnikov, A.A.; Kulikov, M.Y.; Kukin, L.M.; Ryskin, V.G.; Bolshakov, O.S.; Lesnov, I.V.; Shitov, A.M.; Feigin, A.M.; et al. A 5-mm Wavelength-Range Spectroradiometer for Studying the Atmosphere and Underlying Surface. Instrum. Exp. Tech. 2020, 63, 885–889. [Google Scholar] [CrossRef]
- Güldner, J. A model-based approach to adjust microwave observations for operational applications: Results of a campaign at Munich Airport in winter 2011/2012. Atmos. Meas. Tech. 2013, 6, 2879–2891. [Google Scholar] [CrossRef]
- Cimini, D.; Rizi, V.; Di Girolamo, P.; Marzano, F.S.; Macke, A.; Pappalardo, G.; Richter, A. Overview: Tropospheric profiling: State of the art and future challenges—Introduction to the AMT special issue. Atmos. Meas. Tech. 2014, 7, 2981–2986. [Google Scholar] [CrossRef]
- Rodgers, C.D. Inverse Methods for Atmospheric Sounding: Theory and Practice; World Scientific: Singapore, 2000; p. 240. [Google Scholar]
- Ware, R.; Cimini, D.; Campos, E.; Giuliani, G.; Albers, S.; Nelson, M.; Koch, S.E.; Joe, P.; Cober, S. Thermodynamic and liquid profiling during the 2010 Winter Olympics. Atmos. Res. 2013, 132–133, 278–290. [Google Scholar] [CrossRef]
- Chan, P.W. Performance and application of a multiwavelength, ground-based microwave radiometer in intense convective weather. Meteorol. Z. 2009, 18, 253–265. [Google Scholar] [CrossRef]
- Chan, P.W.; Hon, K.K. Application of ground-based, multichannel microwave radiometer in the nowcasting of intense convective weather through instability indices of the atmosphere. Meteorol. Z. 2011, 20, 431–440. [Google Scholar] [CrossRef]
- Madhulatha, A.; Rajeevan, M.; Venkat Ratnam, M.; Bhate, J.; Naidu, C.V. Nowcasting severe convective activity over southeast India using ground-based microwave radiometer observations. J. Geophys. Res. Atmos. 2013, 118, 1–13. [Google Scholar] [CrossRef]
- Venkat Ratnam, M.; Durga Santhi, Y.; Rajeevan, M.; Vijaya Bhaskara Rao, S. Diurnal variability of stability indices observed using radiosonde observations over a tropical station: Comparison with microwave radiometer measurements. Atmos. Res. 2013, 124, 21–33. [Google Scholar] [CrossRef]
- Cimini, D.; Nelson, M.; Güldner, J.; Ware, R. Forecast indices from a ground-based microwave radiometer for operational meteorology. Atmos. Meas. Tech. 2015, 8, 315–333. [Google Scholar] [CrossRef]
- Kulikov, M.Y.; Belikovich, M.V.; Skalyga, N.K.; Shatalina, M.V.; Dementyeva, S.O.; Ryskin, V.G.; Shvetsov, A.A.; Krasil’nikov, A.A.; Serov, E.A.; Feigin, A.M. Skills of Thunderstorm Prediction by Convective Indices over a Metropolitan Area: Comparison of Microwave and Radiosonde Data. Remote Sens. 2020, 12, 604. [Google Scholar] [CrossRef]
- Martinet, P.; Dabas, A.; Donier, J.-M.; Douffet, T.; Garrouste, O.; Guillot, R. 1D-Var Temperature retrievals from Microwave Radiometer and convective scale Model. Tellus A Dyn. Meteorol. Oceanogr. 2015, 67, 27925. [Google Scholar] [CrossRef]
- Caumont, O.; Cimini, D.; Löhnert, U.; Alados-Arboledas, L.; Bleisch, R.; Buffa, F.; Ferrario, M.E.; Haefele, A.; Huet, T.; Madonna, F.; et al. Assimilation of humidity and temperature observations retrieved from ground-based microwave radiometers into a convective-scale NWP model. Q. J. R. Meteorol. Soc. 2016, 142, 2692–2704. [Google Scholar] [CrossRef]
- Liljegren, J.C.; Boukabara, S.A.; Cady-Pereira, K.; Clough, S.A. The effect of the half-width of the 22 GHz water vapor line on retrievals of temperature and water vapor profiles with a twelve-channel microwave radiometer. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1102–1108. [Google Scholar] [CrossRef]
- Hewison, T.J.; Cimini, D.; Martin, L.; Gaffard, C.; Nash, J. Validating clear air absorption model using ground-based microwave radiometers and vice-versa. Meteorol. Z. 2006, 15, 27–36. [Google Scholar] [CrossRef]
- Martinet, P.; Cimini, D.; De Angelis, F.; Canut, G.; Unger, V.; Guillot, R.; Tzanos, D.; Paci, A. Combining ground-based microwave radiometer and the AROME convective scale model through 1DVAR retrievals in complex terrain: An Alpine valley case study. Atmos. Meas. Tech. 2017, 10, 3385–3402. [Google Scholar] [CrossRef]
- De Angelis, F.; Cimini, D.; Löhnert, U.; Caumont, O.; Haefele, A.; Pospichal, B.; Martinet, P.; Navas-Guzmán, F.; Klein-Baltink, H.; Dupont, J.-C.; et al. Long-term observations minus background monitoring of ground-based brightness temperatures from a microwave radiometer network. Atmos. Meas. Tech. 2017, 10, 3947–3961. [Google Scholar] [CrossRef]
- Cimini, D.; Rosenkranz, P.W.; Tretyakov, M.Y.; Koshelev, M.A.; Romano, F. Uncertainty of atmospheric microwave absorption model: Impact on ground-based radiometer simulations and retrievals. Atmos. Chem. Phys. 2018, 18, 15231–15259. [Google Scholar] [CrossRef]
- Instrument Operation and Software Guide. Available online: http://www.radiometer-physics.de/download/PDF/Radiometers/HATPRO/RPG_MWR_STD_Software_Manual%20G5.pdf (accessed on 31 March 2021).
- Technical Instrument Manual. Available online: http://www.radiometer-physics.de//downloadftp/pub/PDF/Radiometers/General_documents/Manuals/2015/RPG_MWR_STD_Technical_Manual_2015.pdf (accessed on 31 March 2021).
- OOO «Aэpoпpибop» (PLC “Aeropribor”). Available online: http://zondr.ru/development-product/10-ak-2.html (accessed on 1 May 2021).
- Rosenkranz, P.W. Absorption of microwaves by atmospheric gases. In Atmospheric Remote Sensing by Microwave Radiometry; Janssen, M.A., Ed.; John Wiley & Sons: New York, NY, USA, 1993; pp. 37–90. [Google Scholar]
- Liebe, H.J.; Rosenkranz, P.W.; Hufford, G.A. Atmospheric 60-GHz oxygen spectrum: New laboratory measurement and line parameters. J. Quant. Spectrosc. Rad. Transf. 1992, 48, 629–643. [Google Scholar] [CrossRef]
- Tretyakov, M.Y.; Koshelev, M.A.; Dorovskikh, V.V.; Makarov, D.S.; Rosenkranz, P.W. 60-GHz oxygen band: Precise broadening and central frequencies of fine structure lines, absolute absorption profile at atmospheric pressure, revision of mixing coefficients. J. Molec. Spectrosc. 2005, 231, 1–14. [Google Scholar] [CrossRef]
- Rosenkranz, P.W. Line-by-Line Microwave Radiative Transfer (Non-Scattering), Remote Sens. Code Library. Available online: http://cetemps.aquila.infn.it/mwrnet/lblmrt_ns.html (accessed on 8 April 2021).
- Picone, J.M.; Hedin, A.E.; Drob, D.P.; Aikin, A.C. NRLMSISE-00 empirical model of the atmosphere: Statistical comparisons and scientific issues. J. Geophys. Res. 2002, 107, 1468. [Google Scholar] [CrossRef]
- Rosenkranz, P.W. Shape of the 5 mm oxygen band in the atmosphere. IEEE Trans Antennas Propag. 1975, 23, 498–506. [Google Scholar] [CrossRef]
- Lam, K.S. Application of pressure broadening theory to the calculation of atmospheric oxygen and water vapor microwave absorption. J. Quant. Spectrosc. Rad. Transfer. 1977, 17, 351–383. [Google Scholar] [CrossRef]
- Makarov, D.S.; Tretyakov, M.Y.; Boulet, C. Line mixing in the 60-GHz atmospheric oxygen band: Comparison of the MPM and ECS model. J. Quant. Spectrosc. Rad. Transf. 2013, 124, 1–10. [Google Scholar] [CrossRef]
- Rosenkranz, P.W. Interference coefficients for overlapping oxygen lines in air. J. Quant. Spectrosc. Rad. Transf. 1988, 39, 281–297. [Google Scholar] [CrossRef]
- Twomey, S. On the numerical solution of Fredholm integral equations of the first kind by the inversion of the linear system produced by quadrature. J. Assoc. Comput. Mach. 1963, 10, 97–101. [Google Scholar] [CrossRef]
- Tikhonov, A.N. On the solution of incorrectly stated problems and a method of regularization. Dokl. Akad. Nauk. SSSR 1963, 151, 501–504. [Google Scholar]
- Gordon, R.G. Semiclassical theory of spectra and relaxation in molecular gases. J. Chem. Phys. 1966, 45, 1649–1655. [Google Scholar] [CrossRef]
- Smith, E.W. Absorption and dispersion in the O2 microwave spectrum at atmospheric pressures. J. Chem. Phys. 1981, 74, 6658–6673. [Google Scholar] [CrossRef]
- Van Vleck, J.H.; Weisskopf, V.F. On the shape of collision-broadened lines. Rev. Mod. Phys. 1945, 17, 227–236. [Google Scholar] [CrossRef]
- Van Vleck, J.H. The Absorption of Microwaves by Oxygen. Phys. Rev. 1947, 71, 413–424. [Google Scholar] [CrossRef]
- Makarov, D.S.; Tretyakov, M.Y.; Rosenkranz, P.W. 60-Ghz oxygen band: Precise experimental profiles and extended absorption modeling in a wide temperature range. J. Quant. Spectrosc. Rad. Transf. 2011, 112, 1420–1428. [Google Scholar] [CrossRef]
- Koshelev, M.A.; Vilkov, I.N.; Tretyakov, M.Y. Collisional broadening of oxygen fine structure lines: The impact of temperature. J. Quant. Spectrosc. Rad. Transf. 2016, 169, 91–95. [Google Scholar] [CrossRef]
- Makarov, D.S.; Tretyakov, M.Y.; Rosenkranz, P.W. Revision of the 60-GHz atmospheric oxygen absorption band models for practical use. J. Quant. Spectrosc. Rad. Transf. 2020, 243, 106798. [Google Scholar] [CrossRef]
- Turner, D.D.; Clough, S.A.; Liljegren, J.C.; Clothiaux, E.E.; Cady-Pereira, K.E.; Gaustad, K.L. Retrieving Liquid Water Path and Precipitable Water Vapor From the Atmospheric Radiation Measurement (ARM) Microwave Radiometers. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3680–3690. [Google Scholar] [CrossRef]
- Moors, J.J.A. The meaning of kurtosis: Darlington reexamined. Am. Stat. 1986, 40, 283–284. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis, 2nd ed.; Springer Series in Statistics; Springer: New York, NY, USA, 2002; p. 497. [Google Scholar]
- Meunier, V.; Löhnert, U.; Kollias, P.; Crewell, S. Biases caused by the instrument bandwidth and beam width on simulated brightness temperature measurements from scanning microwave radiometers. Atmos. Meas. Tech. 2013, 6, 1171–1187. [Google Scholar] [CrossRef]

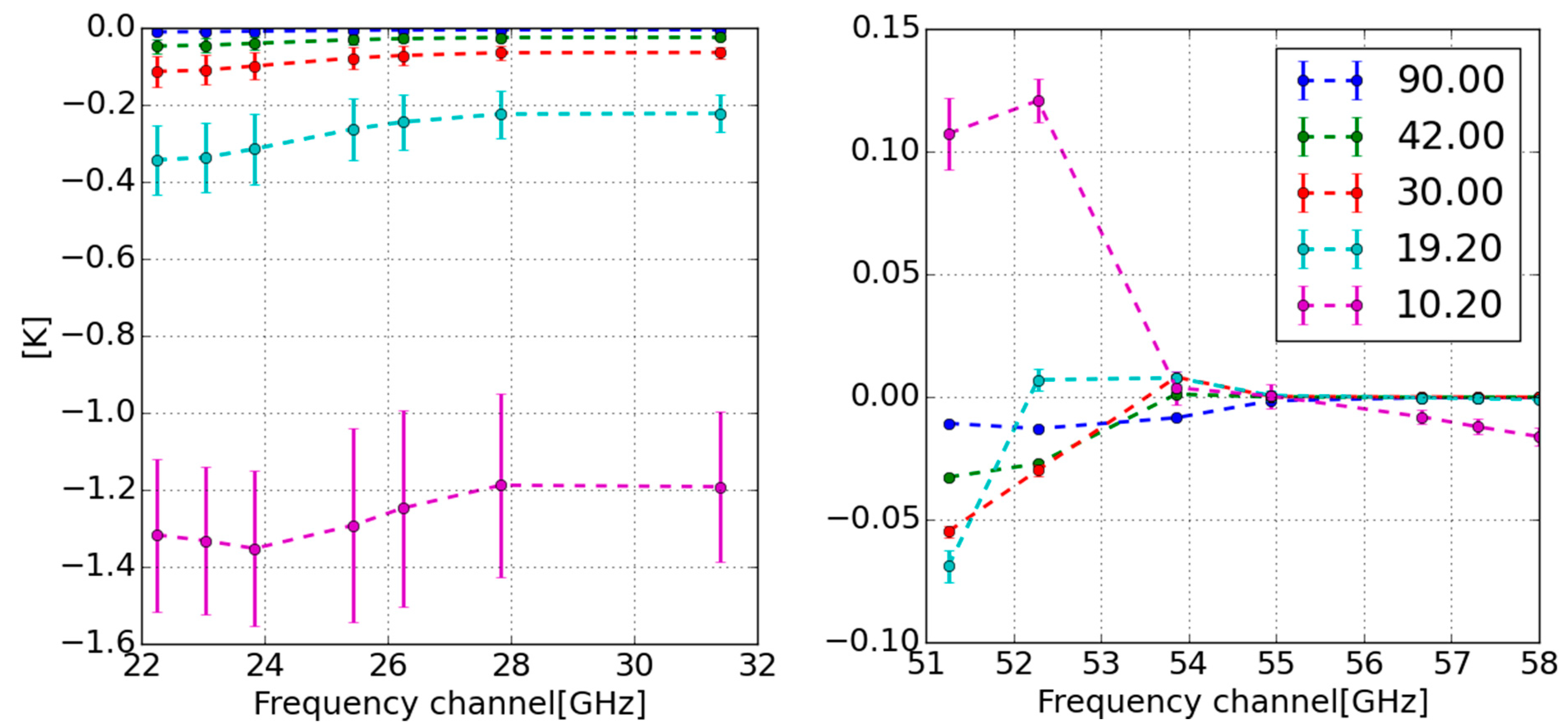
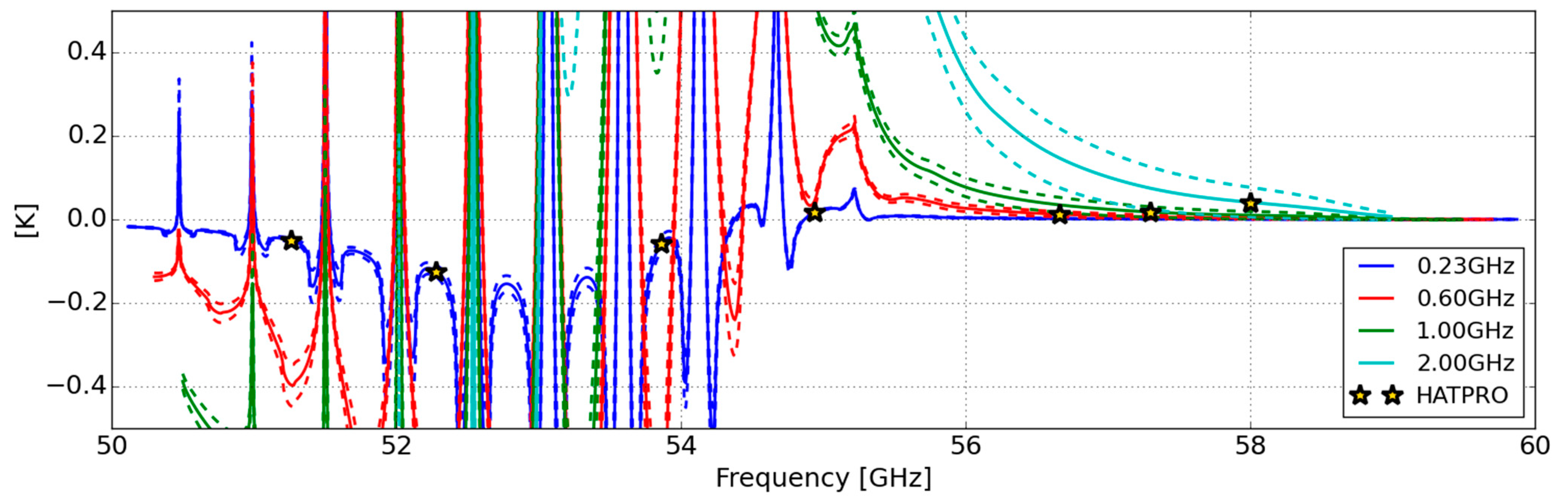
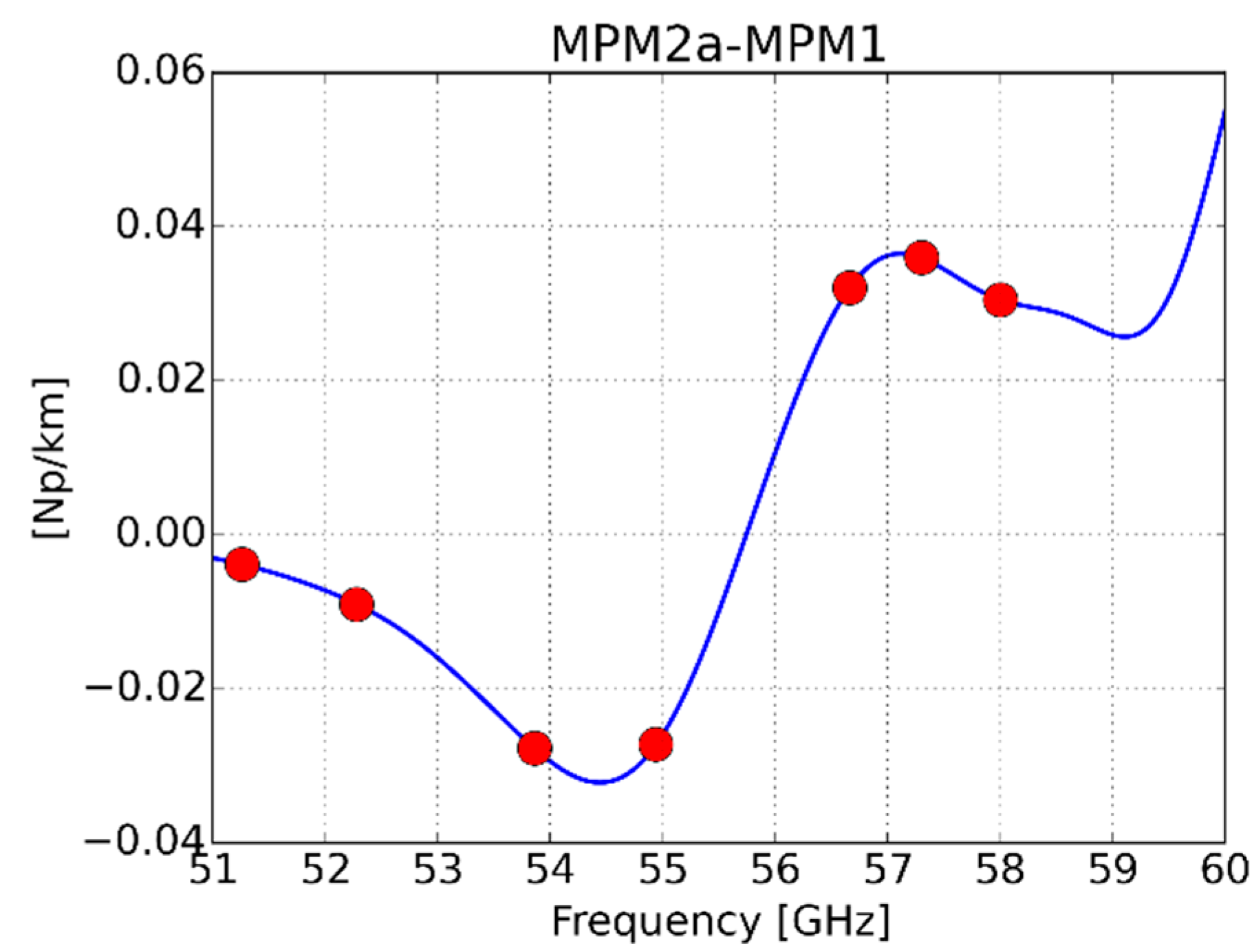
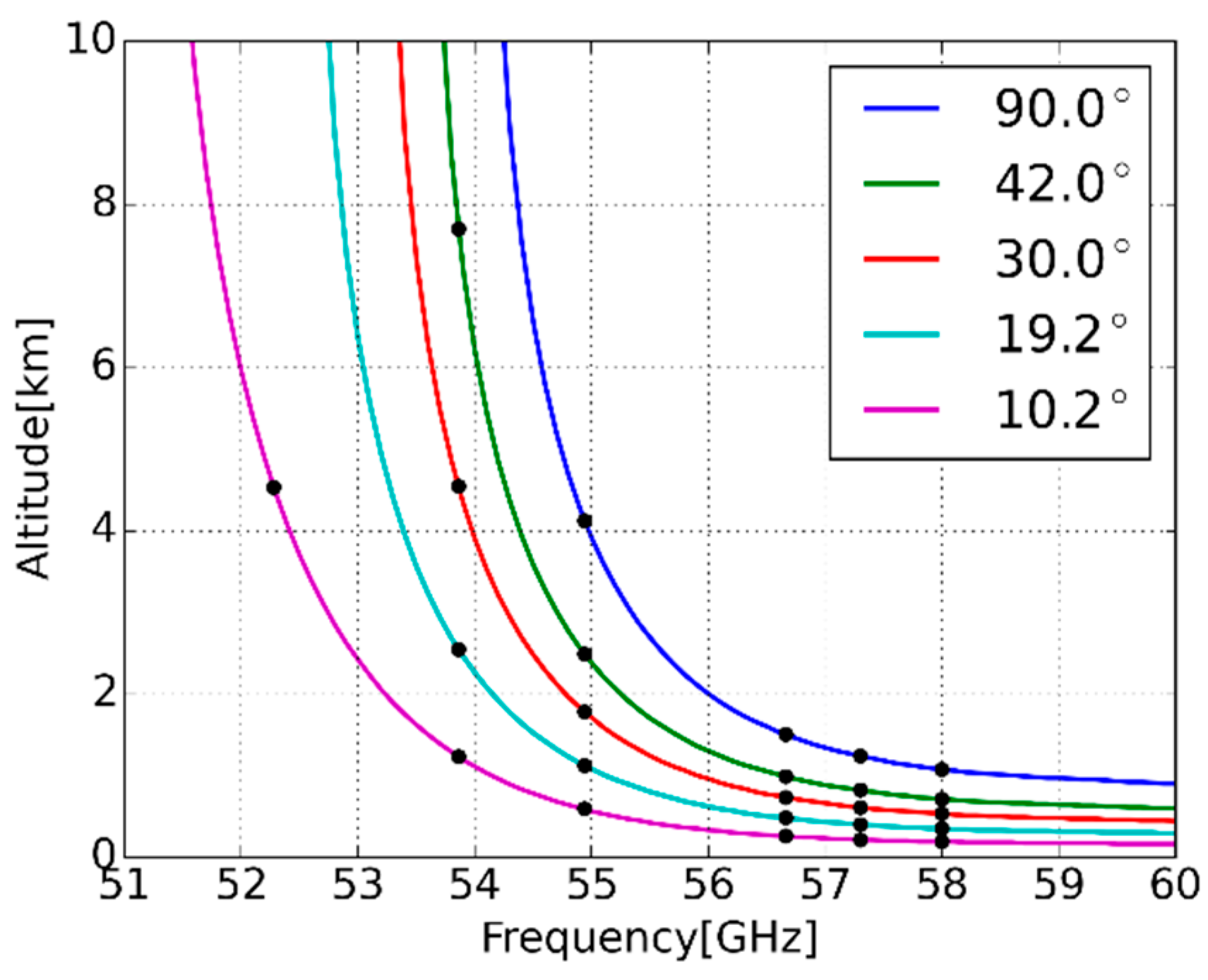
| Channel (GHz) | 22.24 | 23.04 | 23.84 | 25.44 | 26.24 | 27.84 | 31.4 |
| Kurtosis | 0.62 | 0.7 | 0.59 | 0.55 | 0.35 | −0.15 | −0.41 |
| Skewness | −0.15 | −0.13 | −0.21 | −0.15 | −0.22 | −0.1 | 0.07 |
| Channel (GHz) | 51.26 | 52.28 | 53.86 | 54.94 | 56.66 | 57.3 | 58 |
| Kurtosis | 0.39 | 0.22 | −0.06 | 0.12 | 0.23 | 0.21 | 0.29 |
| Skewness | −0.29 | −0.05 | 0.1 | −0.01 | −0.17 | −0.21 | −0.26 |
| Index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Singular values [K/°C] | 0.43 | 0.14 | 0.04 | 0.01 | 4.41 × 10−3 | 6.87 × 10−4 | 1.6 × 10−4 |
| MPM1 difference in the basis of left-singular vectors [K] | 0.63 | −1.21 | −0.86 | −0.087 | −1.61 | 0.58 | 0.39 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belikovich, M.V.; Kulikov, M.Y.; Makarov, D.S.; Skalyga, N.K.; Ryskin, V.G.; Shvetsov, A.A.; Krasil’nikov, A.A.; Dementyeva, S.O.; Serov, E.A.; Feigin, A.M. Long-Term Observations of Microwave Brightness Temperatures over a Metropolitan Area: Comparison of Radiometric Data and Spectra Simulated with the Use of Radiosonde Measurements. Remote Sens. 2021, 13, 2061. https://doi.org/10.3390/rs13112061
Belikovich MV, Kulikov MY, Makarov DS, Skalyga NK, Ryskin VG, Shvetsov AA, Krasil’nikov AA, Dementyeva SO, Serov EA, Feigin AM. Long-Term Observations of Microwave Brightness Temperatures over a Metropolitan Area: Comparison of Radiometric Data and Spectra Simulated with the Use of Radiosonde Measurements. Remote Sensing. 2021; 13(11):2061. https://doi.org/10.3390/rs13112061
Chicago/Turabian StyleBelikovich, Mikhail V., Mikhail Yu. Kulikov, Dmitry S. Makarov, Natalya K. Skalyga, Vitaly G. Ryskin, Alexander A. Shvetsov, Alexander A. Krasil’nikov, Svetlana O. Dementyeva, Evgeny A. Serov, and Alexander M. Feigin. 2021. "Long-Term Observations of Microwave Brightness Temperatures over a Metropolitan Area: Comparison of Radiometric Data and Spectra Simulated with the Use of Radiosonde Measurements" Remote Sensing 13, no. 11: 2061. https://doi.org/10.3390/rs13112061
APA StyleBelikovich, M. V., Kulikov, M. Y., Makarov, D. S., Skalyga, N. K., Ryskin, V. G., Shvetsov, A. A., Krasil’nikov, A. A., Dementyeva, S. O., Serov, E. A., & Feigin, A. M. (2021). Long-Term Observations of Microwave Brightness Temperatures over a Metropolitan Area: Comparison of Radiometric Data and Spectra Simulated with the Use of Radiosonde Measurements. Remote Sensing, 13(11), 2061. https://doi.org/10.3390/rs13112061







