Next Article in Journal
Spherically Optimized RANSAC Aided by an IMU for Fisheye Image Matching
Next Article in Special Issue
Predicting Table Beet Root Yield with Multispectral UAS Imagery
Previous Article in Journal
Performance Improvement of Spaceborne Carbon Dioxide Detection IPDA LIDAR Using Linearty Optimized Amplifier of Photo-Detector
Previous Article in Special Issue
Spatiotemporal Changes of Winter Wheat Planted and Harvested Areas, Photosynthesis and Grain Production in the Contiguous United States from 2008–2018
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 13
Issue 10
10.3390/rs13102016
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Crop Yield Prediction Based on Agrometeorological Indexes and Remote Sensing Data

by
Xiufang Zhu
1,
Rui Guo
2,*,
Tingting Liu
3 and
Kun Xu
3
1
State Key Laboratory of Remote Sensing Science, Jointly Sponsored by Beijing Normal University and Institute of Remote Sensing and Digital Earth of Chinese Academy of Sciences, Beijing 100875, China
2
Key Laboratory of Environmental Change and Natural Disaster, Ministry of Education, Beijing Normal University, Beijing 100875, China
3
Institute of Remote Sensing Science and Engineering, Faculty of Geographical Science, Beijing Normal University, Beijing 100875, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2021, 13(10), 2016; https://doi.org/10.3390/rs13102016
Submission received: 29 March 2021 / Revised: 30 April 2021 / Accepted: 14 May 2021 / Published: 20 May 2021
(This article belongs to the Special Issue Advances in Remote Sensing for Crop Monitoring and Yield Estimation)
Browse Figures
Versions Notes

Abstract

:
Timely and reliable estimations of crop yield are essential for crop management and successful food trade. In previous studies, remote sensing data or climate data are often used alone in statistical yield estimation models. In this study, we synthetically used agrometeorological indicators and remote sensing vegetation parameters to estimate maize yield in Jilin and Liaoning Provinces of China. We applied two methods to select input variables, used the random forest method to establish yield estimation models, and verified the accuracy of the models in three disaster years (1997, 2000, and 2001). The results show that the R2 values of the eight yield estimation models established in the two provinces were all above 0.7, Lin’s concordance correlation coefficients were all above 0.84, and the mean absolute relative errors were all below 0.14. The mean absolute relative error of the yield estimations in the three disaster years was 0.12 in Jilin Province and 0.13 in Liaoning Province. A model built using variables selected by a two-stage importance evaluation method can obtain a better accuracy with fewer variables. The final yield estimation model of Jilin province adopts eight independent variables, and the final yield estimation model of Liaoning Province adopts nine independent variables. Among the 11 adopted variables in two provinces, ATT (accumulated temperature above 10 °C) variables accounted for the highest proportion (54.54%). In addition, the GPP (gross primary production) anomaly in August, NDVI (Normalized Difference Vegetation Index) anomaly in August, and standardized precipitation index with a two-month scale in July were selected as important modeling variables by all methods in the two provinces. This study provides a reference method for the selection of modeling variables, and the results are helpful for understanding the impact of climate on potential yield.

1. Introduction

Agriculture is fundamental for the progression and stability of human society. Agricultural production data is vital for addressing societal, economic, agricultural, and policy concerns [1,2]. A reliable and timely estimate of crop yield prior to harvest is crucial for crop management, food trade, food security, and policy making.
Crop yield prediction methods can be summarized into three categories: a sampling survey method [3], a mechanism model [4,5,6,7], and a data modelling method [8,9,10]. The sampling survey method requires a certain number of samples, and yield surveying is then performed within the selected sample locations; then, the crop yield of the whole investigation area is estimated. It is time consuming and laborious, and it cannot obtain the spatial continuous yield data in the survey area. The mechanism model includes a production efficiency model and a crop growth model. The production efficiency model assumes that crop yields under nonstressed conditions correlate linearly with the amount of absorbed photosynthetically active radiation. This method first estimates the amount of crop aboveground dry matter using remotely sensed data and then converts it into crop yield. The crop growth model simulates physical crop growth processes and finally estimates the resulting yield. It is complex and requires a large amount of input data, such as soil, farmland management, and climate parameters. The uncertainty of the mechanism model is difficult to analyze [11]. The response of crops to extreme climate is not well reflected in the mechanism models [12,13,14,15,16,17]. The data modelling method includes a statistical modelling and a machine learning method. The statistical model establishes a function relation between yield predictors and the resulting yield. It is often based on a series of assumptions, such as linear regression model assumptions. The machine learning method constructs an analysis system through data learning, which does not rely on explicit construction rules. It cannot give explicit expressions of the functional relationships between yield predictors and the resulting yield.
From the perspective of data sources, the modelling method can be further divided into remote sensing data-based, meteorological data-based, and other data-based yield estimation models. The other data used in the modelling include soil characteristic parameters, production inputs (such as chemical fertilizer, agricultural machinery, etc.), production conditions (such as irrigation), etc. [18,19,20,21].
In yield estimation models based on remote sensing data, NDVI(Normalized Difference Vegetation Index) is the most commonly used remote sensing data, including the original NDVI, average or cumulative NDVI over a growth period [22], average or cumulative NDVI over the key growing stages [23,24], etc. In addition to NDVI, other vegetation-based indexes (VIs), such as the leaf area index (LAI) [25], enhanced vegetation index (EVI) [26], perpendicular vegetation index (PVI) [9], green area index (GAI) [27], vegetation condition index (VCI) [28,29], fraction of photosynthetically active radiation (FPAR) [30], and wide dynamic range vegetation index (WDRVI) [31,32], have also been used as independent variables to build a regression model considering yield [33].
In meteorological data-based yield estimation models, input variables can be original meteorological factors (such as precipitation, temperature, solar radiation, etc.) or agrometeorological indexes calculated by original meteorological factors (such as various drought indexes) [34,35,36]. For example, Seffrin, et al. [34] used average air temperature, rainfall, solar radiation, etc., as input variables to build spatial regression models for predicting corn yield in Brazil from 2012 to 2014. Mathieu, et al. [35] compared the correlations of fifty-eight agro-climatic indexes and corn yield anomalies in the United States and noted that temperature and the standardized precipitation evapotranspiration index (SPEI) obtained in July are the two best yield predictors.
A large number of studies have reported the impact of adverse weather conditions on crop yield. For example, Zhang [37] established a quadratic equation to explain maize yield losses on the Songliao Plain of China. Ming, et al. [38] analyzed the regression relationship between the detrended maize yield and the standardized precipitation evapotranspiration index (SPEI) in the North China Plain (NCP) and found that the three-month SPEIs in August, which reflect water conditions during June and July, had the best relationship with the detrended maize yield. Xu, et al. [39] built a multivariate regression model between the detrended winter wheat yield and the SPEI in Jiangsu Province, China. Wang, et al. [40] established seven aggregate drought indexes to quantify the relationships between them and the anomalies of the climatic yields (or standardized climatic yields) of wheat by using two statistical regression models applied in the NCP. Chen, et al. [41] set up a logistic function that related a drought hazard index to the yield loss rate for maize in China. A previous study noted that agrometeorological indexes can help improve yield prediction accuracy in the presence of adverse weather conditions [42].
In this paper, remote sensing data and meteorological data are used together to develop a yield estimation model utilizing the random forest (RF) method with two different variable selection methods, and experiments are conducted in Liaoning and Jilin provinces in Northeast China. Our main objectives include (1) to verify the accuracy of yield estimations models built in this study; (2) to compare the differences of the two variable selection methods; (3) to compare the importance of different variables on yield estimation; and (4) to compare the differences in modeling between the two provinces.

2. Study Area and Data

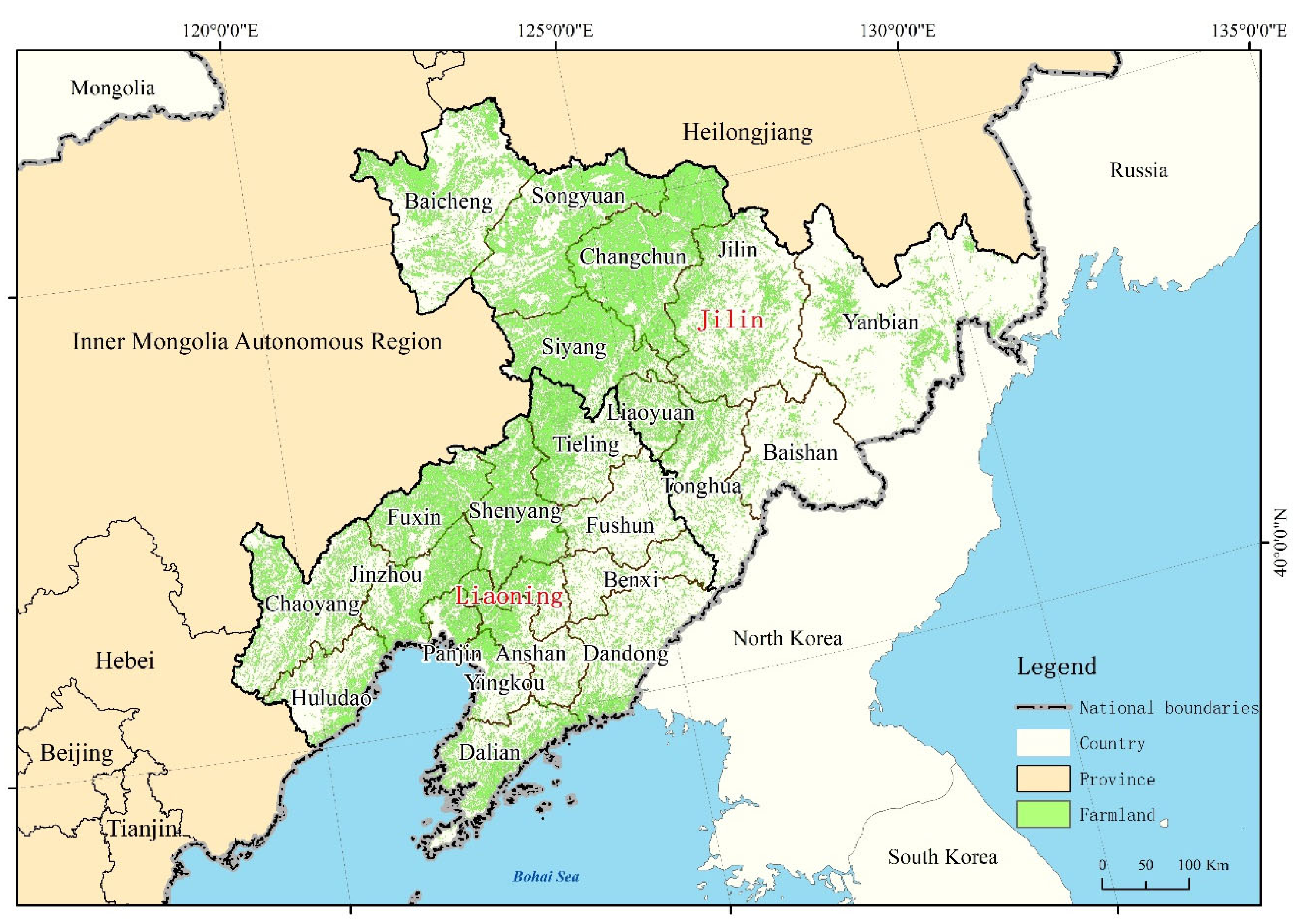
2.1. Study Area

The study area includes Jilin Province and Liaoning Province in Northeast China (Figure 1). It is located in a high latitude area of China (38.5° N-46.5° N and 118.5° E-131.5° E) and belongs to the temperate continental monsoon climate. It has low temperature and dry conditions in winter, and warm and humid conditions in summer, thus exhibiting obvious seasonal characteristics. The terrain of this area is low in the northwest and high in the southeast, which includes three farming areas: the coastal area of Eastern Liaoning, the Changbai Mountain Area, and the southern Songliao Plain area. The main planting system in the study is one crop per year, and the maize planting area accounts for 40% of the total grain planting area. It is one of main maize producing areas in China. The agricultural cultivation in Jilin Province and Liaoning Province is mainly dependent on rainfall [43]. The temperature rise in this area is significant, and the degree of drought has increased over the last 30 years [44,45]. The frequency of extreme climate events is higher than that in other regions of China [46,47]. These climatic factors are important factors driving crop yield fluctuations in the region. Therefore, the establishment of a yield estimation model driven by climate factors would be useful for predicting the impact of climate change factors on agricultural production in the region.

2.2. Data

The data used in this study mainly include meteorological reanalysis data, remote sensing data, and statistical data (Table 1). The meteorological reanalysis data were taken from the ERA5 dataset of the European Center for Medium-Term Weather Forecast (ECMWF 2017). The total precipitation of ERA5 monthly averaged data and the 2 m temperature of ERA5 hourly data were used in this study. The spatial resolution of the data is 0.25°, and the time series covers the period from 1979 to 2018 [48]. The GPP (gross primary production) data were obtained from the National Science and Technology Basic Conditions Platform-National Earth System Science Data Sharing Service Platform [49], which provides GPP data with a resolution of 0.05° from 1982 to 2018 with a temporal resolution of 8 d. This data set was estimated by the EC-LUE model [50], and the verification results of the data set showed that its simulation capability exceeded that of the MODIS-GPP product. The NDVI data, which has a spatial resolution of 0.05° from 1981 to 2018 on a time scale of 1 d, were obtained from the long time series AVH13C1 dataset of the LTDR project [51]. The Chinese land use and land cover data at a 1 km resolution were provided by the Resource and Environmental Science Data Center of the Chinese Academy of Sciences (http://www.resdc.cn). This dataset was used to extract the range of cultivated land. The statistical data mainly included the time series maize yield at the municipal level (1996–2018 in Jilin Province and 1997–2018 in Liaoning Province) and agricultural disaster statistics from 1990 to 2016 provided by the China Bureau of Statistics, as well as crop phenological calendar from the planting management department of the Ministry of Agriculture.

3. Methodology

3.1. Input Variable Calculation

3.1.1. Calculation of Technical Yield

Grain yield is affected by many factors, including natural factors and nonnatural factors. Climate is the most important natural factor, as it is constantly fluctuating. Nonnatural factors such as cultivation techniques and field management strategies have improved over time. Therefore, the annual crop yield per unit area ( Y ), which is defined as the average amount of agricultural products harvested per unit of land area, can be divided into two parts: climatic yield ( Y w ) and trend yield ( Y t ) (Equation (1)). Climatic yield is determined by short-term climate variations, while the trend yield, which is also referred to as the technical yield, is influenced by long-term factors.
Y = Y t + Y w
There are many methods used to calculate the technical yield [52]. The most commonly used methods include the moving average method, HP filtering method [53], and exponential smoothing method [54]. We used these three methods to separate the technical yield from the historical actual yield and then used the historical actual yield minus the technical yield to calculate the climate yield. We calculated the correlation between the climate yield derived from the three methods and the area of cultivated land suffered by disaster. The climate yield with the highest correlation and the corresponding technical yield were selected as the final calculation results. The correlation here was calculated using the gray correlation analysis. Gray correlation analysis judges the correlation degree between variables according to the degree of geometric similarity of the time series curve, focuses on the consistency of the change trends among variables and is not limited by the size and distribution of samples [55]. Through the above method, based on municipal-level corn yield data of Jilin Province from 1996 to 2018 and Liaoning Province from 1997 to 2018, the technical yield and climate yield of the corresponding period were obtained.

3.1.2. Calculation of Agrometeorological Index

As a crop with high water requirements, maize is sensitive to water deficiency, and the effects of drought during different growth stages on maize production differ [56]. Eighty-five percent of the corn planting areas in the study area are rain fed [43,57,58,59], and drought occurs frequently during the maize growth period [60,61,62]. The standardized precipitation index (SPI) [63] is a commonly used drought monitoring index and has the advantage of multitemporal characteristics. The growth period of maize in the study area lasts from April to September. To reflect the effects of drought on maize growth at different times, SPI indexes with a two-month scale in May (SPI2-5), July (SPI2-7) and September (SPI2-9) were selected to represent drought conditions during the early, middle, and late growth stages of maize, respectively. For each study year, we first calculated the SPI2-5, SPI2-7, and SPI2-9 values iteratively for each grid; then, for each SPI index, we calculated its average value within the cultivated land area of each municipal administrative region and used it as a candidate independent variable to participate in the construction of the subsequent production estimation model.
Temperature is also an important climatic factor affecting maize production. The suitable growth temperature of maize ranges from 10 to 30 °C [64]. During the growth period, with increasing temperature, the yield of maize will increase; however, when the temperature exceeds a certain threshold, temperature will have an obvious negative effect on maize production [65,66,67,68]. Therefore, we calculated the extreme degree-day (EDD) and accumulated temperature above 10 °C (AAT) to reflect the impact of temperature on maize production. EDD was calculated as follows:
E D D = ∑ h = 1 N D D h / 24
D D h = 0 T h − T o p t     i f i f     T h < T o p t T h ≥ T o p t
In Equations (2) and (3), N is the number of hours within a certain period of time, T h is the actual temperature at h-th hour, and T o p t is the high temperature threshold. We chose 30 °C as the threshold.
For each study year, we first calculated the EDD and AAT for each grid throughout the whole growing season (from April to September) and each for month in the whole growing season. The EDD from April to September was recorded as EDD4, EDD5, EDD6, EDD7, EDD8, and EDD9, and the EDD of the whole growing season was recorded as EDD4-9. Similarly, the AAT from April to September was recorded as AAT4, AAT5, AAT6, AAT7, AAT8, and AAT9, and the AAT of the whole growing season was recorded as AAT4-9. Then, for each EDD (AAT) index, we calculated its average value in the cultivated land area of each municipal administrative region and used it as a candidate independent variable to participate in the construction of the subsequent yield estimation model.

3.1.3. Calculation of NDVI and GPP Anomalies

In this study, the AVH13C1 daily scale NDVI from 1990 to 2018 was merged into a monthly NDVI dataset by using the maximum composite method (MVC), and then the residual noise in the time series was removed by S-G filtering to obtain high-quality NDVI data [69]. After that, NDVI anomalies were obtained according to the method proposed by Papagiannopoulou et al. [70].
First, the overall trend of NDVI values in each pixel over the study years was removed, meaning that the time series was taken as the independent variable t , and the NDVI value of the corresponding pixel in the time series was taken as the dependent variable y k for linear fitting (Equation (4)). The difference between the NDVI value y and the NDVI fitted value y k was the detrended NDVI value y d k (Equation (5)).
y k = β + α t
y d k = y − y k
Second, the seasonal component of the NDVI values after detrending was calculated. Assuming that the data were evenly distributed in the time series, the monthly mean value of NDVI in each pixel was taken as the NDVI value in the seasonal period ( y c i r ).
Third, the NDVI anomaly y a b was calculated by taking the detrended NDVI value y d k minus the NDVI value in the seasonal period ( y c i r ).
y a b = y d k − y c i r
For the monthly NDVI data collected from 1981 to 2018, the corresponding monthly NDVI anomaly (NDVIa) was calculated for each grid using the method mentioned above. Then, for each study year, we calculated the average NDVIa value in the cultivated land area of each municipal administrative region for the whole growing season (from April to September) and for each month in the whole growing season. The average NDVIa from April to September was recorded as NDVIa4, NDVIa5, NDVIa6, NDVIa7, NDVIa8, and NDVIa9, and the average NDVIa of the whole growing season was recorded as NDVIa4-9. Using the same method, we calculated the monthly GPP anomaly (GPPa) for each grid and then further calculated the average value of GPPa in the cultivated land area of each municipal administrative region for the whole growing season (from April to September) and for each month during the whole growing season. The average GPPa from April to September was recorded as GPPa4, GPPa5, GPPa6, GPPa7, GPPa8, and GPPa9, and the average GPPa of the whole growing season was recorded as GPPa4-9.

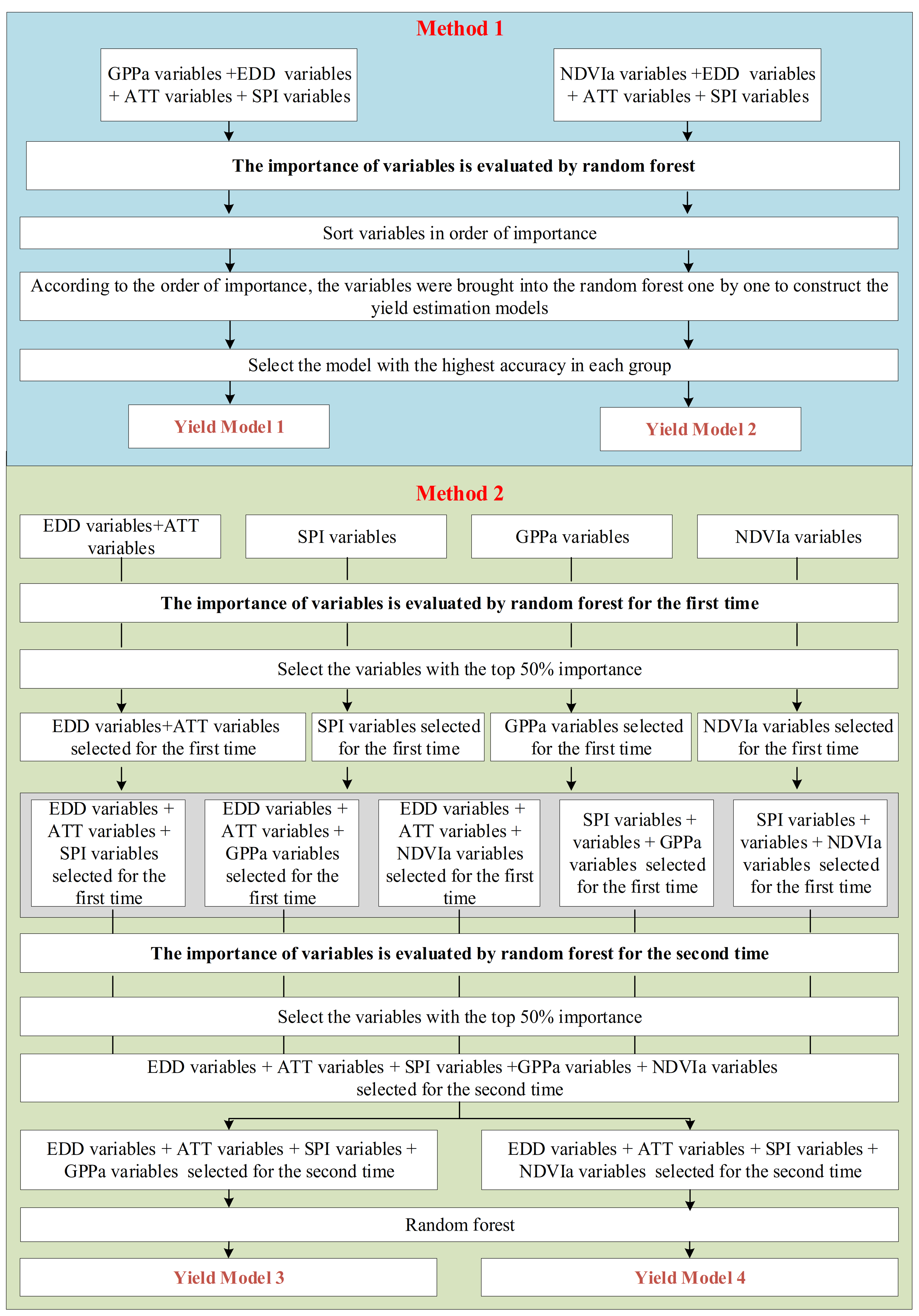
3.2. Model Building Process

Taking the municipal level corn yield data of Jilin Province from 1996 to 2018 and Liaoning Province from 1997 to 2018 as a dependent variable, the technical yield Y t of the corresponding years in each municipal administrative region as a fixed independent variable, and GPPa variables, NDVIa variables, SPI variables, EDD variables, and AAT variables as candidate independent variables, two methods were used to select the independent variables of the input model from the candidate independent variables, and then the yield estimation models were established by the RF with the fixed independent variable and selected candidate independent variables as input. The accuracy of the yield estimation model established by the two variable selection methods was compared, and the differences in the selected variables were analyzed. It should be emphasized here that the fixed variable ( Y t ) acted as an input variable in each modeling process. GPPa variables included GPPa4, GPPa5, GPPa6, GPPa7, GPPa8, GPPa9, and GPPa4-9. NDVIa variables included NDVIa4, NDVIa5, NDVIa6, NDVIa7, NDVIa8, NDVIa9, and NDVIa4-9. SPI variables included SPI2-5, SPI2-7, and SPI2-9. EDD variables included EDD4, EDD5, EDD6, EDD7, EDD8, EDD9, and EDD4-9. AAT variables included AAT4, AAT5, AAT6, AAT7, AAT8, AAT9, and AAT4-9. Therefore, there were 31 candidate independent variables in total. The random forest regression under scikit learn in Python is used to train the model. In the process of RF construction, the number of regression trees ‘n_estimators’ and the number of randomly selected features per decision tree ‘max_feature’ are important parameters affecting the prediction ability of the RF model, and max_feature should be less than the number of variables in the model (n_features). The optimal parameters of the RF model were selected using the grid search method in which max_feature ranged from 1 to n_features with a step size of 2, and n_estimators ranged from 80 to 200 with a step size of 10. By comparing the out-of-bag data errors of the models with different combinations of parameters, the max_feature and n_estimators values corresponding to the minimum out-of-bag data errors were defined as the optimal parameters. Eighty percent of the complete dataset was randomly selected to train each model, and the remaining data were used to validate the model. The specific processes of the two variable selection methods are shown in Figure 2.
In the first method, the importance of the candidate independent variables was evaluated by the random forest method. We first divided the candidate variables into two groups: the GPP group and the NDVI group. The GPP group included GPPa variables, EDD variables, ATT variables, and SPI variables; the NDVI group included NDVIa variables, EDD variables, ATT variables, and SPI variables. Each group had 24 variables. According to the importance of variables ranked by the random forest method, the variables were iteratively added to establish the best yield estimation model. The most important variable was added first, and then the next important variable was added until all variables were added to the model. In this way, for each group of variables, we established 24 yield estimation models, verified the accuracy of each production estimation model, and selected the model with the highest accuracy as the final yield estimation model corresponding to this group of variables. To facilitate the subsequent analysis, we defined the final yield estimation model for the GPP group as Yield Model 1 and the final yield estimation model for the NDVI group as Yield Model 2.
In the second method, modeling variables were selected by a two-stage importance evaluation method. We first divided the candidate variables into four groups: a temperature group (including EDD variables and ATT variables), an SPI group (including SPI variables), a GPPa group (including GPPa variables), and a NDVIa group (including NDVIa variables). For each group, we evaluated the importance of the candidate variables using the random forest method and selected the variables constituting the top 50% importance from each group to form new variable groups. Then, the new temperature group (including EDD variables and ATT variables), SPI group, GPPa group, and NDVIa group were combined in pairs to form 5 groups: temperature group variables + SPI variables; temperature group variables + GPPa variables; temperature group variables + NDVIa variables; SPI variables + GPPa variables; and SPI variables + NDVIa variables. For each group, we reevaluated the importance of the candidate variables by the random forest method and selected the variables constituting the top 50% importance from each group to obtain the final candidate independent variables. Then, we divided the final candidate independent variables into two groups: the GPP group and the NDVI group. The GPP group included temperature group variables, SPI variables, and GPPa variables selected for the second time; the NDVI group included temperature group variables, SPI variables, and NDVIa variables selected for the second time. Finally, we built two yield estimation models (referred to as Yield Models 3 and 4) based on the two group variables using the random forest method.

3.3. Model Validation

The performances of the yield estimation models were evaluated by using three validation measurements: the mean absolute relative deviation (MARE), coefficient of determination (R2) and the Lin’s concordance correlation coefficient (CCC):
M A R E = 1 n ∑ i = 1 n r i − R i r i
R 2 = ∑ i = 1 n r i − r ¯ R i − R ¯ ∑ i = 1 n ( r i − r ¯ ) 2 ∑ i = 1 n ( R i − R ¯ ) 2 2
CCC = 2 S R r R ¯ − r ¯ 2 + V r + V R
where r i and R i refer to the reported and estimated maize yield in year i ; r ¯ and R ¯ are the mean values of the reported and estimated values of maize yield; V r and V R are the variance of the reported and estimated values of maize yield; n is the number of samples, S R r is the covariance between the reported and estimated values of maize yield. MARE reflects the credibility of an estimation. The CCC measures the agreement between two variables. The model results become increasingly more accurate as R2 and CCC approach 1 and MARE approaches 0.

4. Results

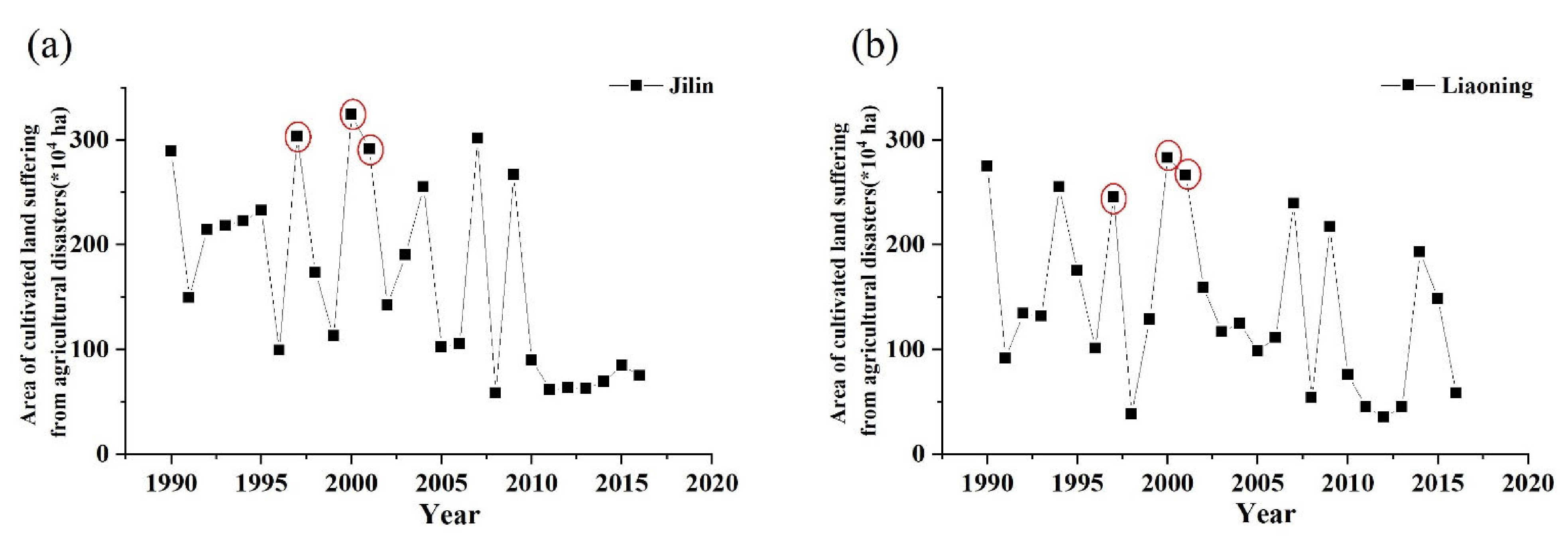
4.1. Trend Yield

The correlation between climate yield and agricultural disaster data obtained by the moving average method, HP filtering method and exponential smoothing method was analyzed by using the gray correlation degree. The results are shown in Figure 3. As shown in the figure, compared with the other methods, the climate yield obtained by the moving average method in most municipalities of Jilin Province and Liaoning Province shows a better degree of correlation with the agricultural disaster area, with the average value of the correlation degree reaching 0.9181 and 0.9038, respectively. Among them, the gray correlation degree of six municipalities in Jilin Province exceeded 0.9500, that of four municipalities in Liaoning Province exceeded 0.9400 and that of another seven cities exceeded 0.9000. Therefore, the trend yield obtained by the moving average method was used in subsequent analysis and modeling.

4.2. Yield Estimations Models Built in Jilin and Liaoning Provinces

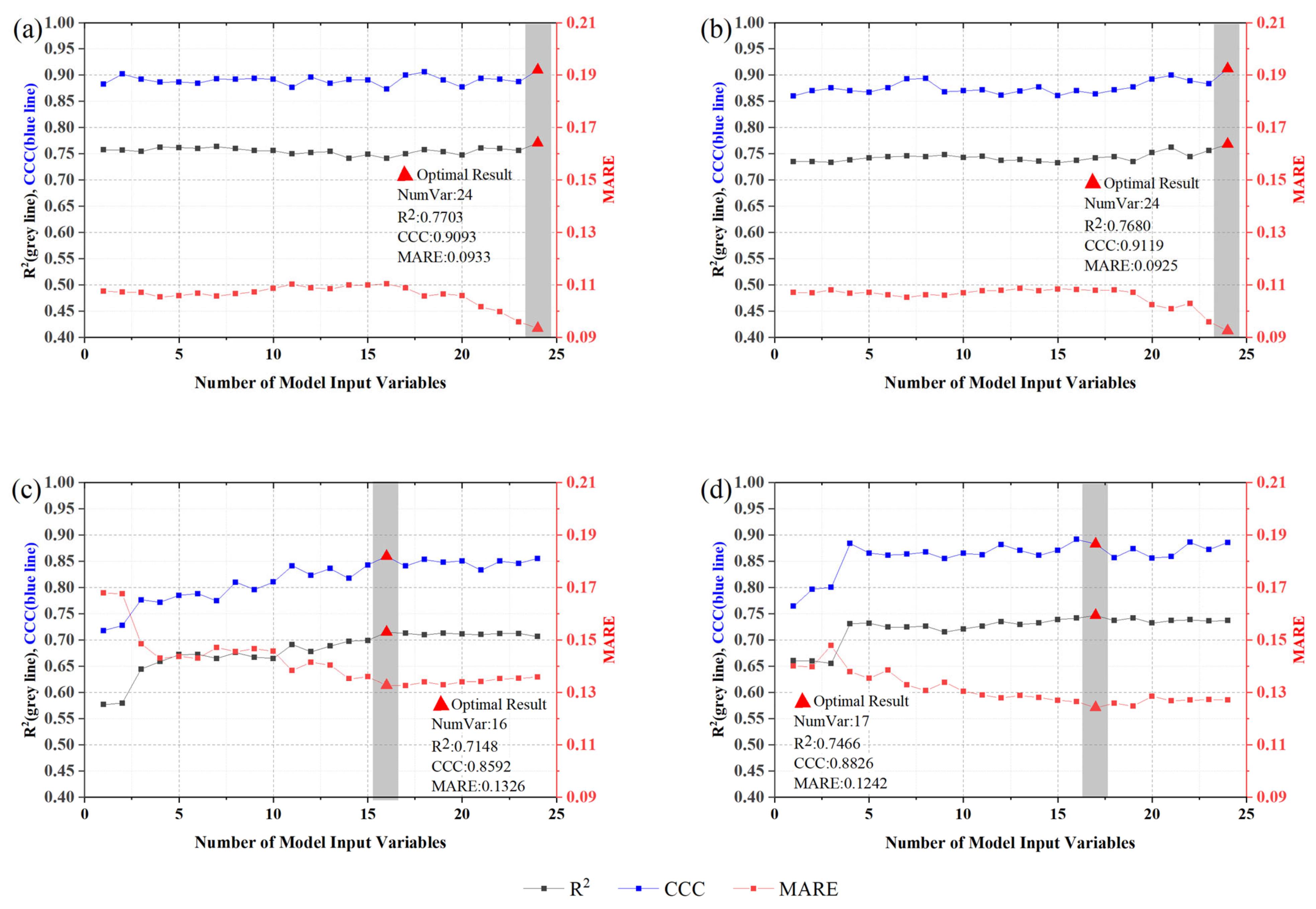
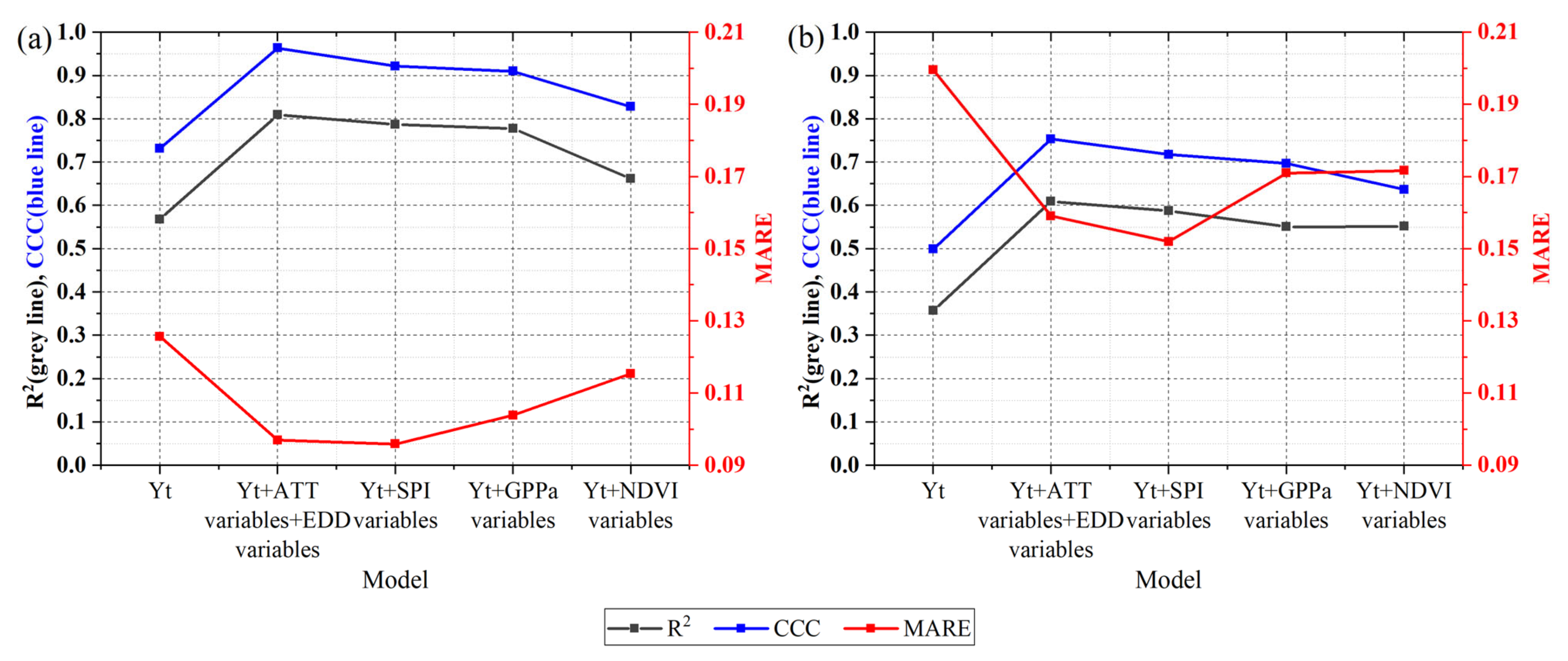
4.2.1. Models Built Using Variables Selected by Random Forest

Based on the first method described in Section 3.2, for each variable group and each province, 24 yield estimation models were established and validated (Figure 4). In Jilin Province, the accuracy of the model established by the GPP variable group fluctuated continuously. The increase in independent variables does not significantly improve the overall accuracy of the yield estimation models in Jilin Province. For the GPP variable group, the MARE values of the 24 models ranged from 0.0993 to 0.1104, the R2 values ranged from 0.7410 to 0.7703, and the CCC values ranged 0.8730 to 0.9093, respectively (Figure 4a). For the NDVI variable group, the MARE values of the 24 models ranged from 0.0925 to 0.1086, the R2 values ranged from 0.7410 to 0.7703, and the CCC values ranged from 0.8730 to 0.9093, respectively (Figure 4b). Overall, taking all three validation measurements (MARE, R2, and CCC) into account, when the number of independent variables was 24, the accuracy of the model reached the highest for each variable group in Jilin Province.
In Liaoning Province, the accuracy of the yield estimation models increases with increases in the number of independent variables. For the GPP variable group, the MARE values of the 24 models ranged from 0.1326 to 0.1679, the R2 values ranged from 0.5766 to 0.7148, and the CCC values ranged from 0.7176 to 0.8592, respectively (Figure 4c). For the NDVI variable group, the MARE values of the 24 models ranged from 0.1242 to 0.1480, the R2 values ranged from 0.6552 to 0.7466, and the CCC values ranged from 0.7641 to 0.8918, respectively (Figure 4d). The accuracy of the GPP variable group reached its highest when the number of independent variables was 16, and the accuracy of the NDVI variable group reached its highest when the number of independent variables was 17.

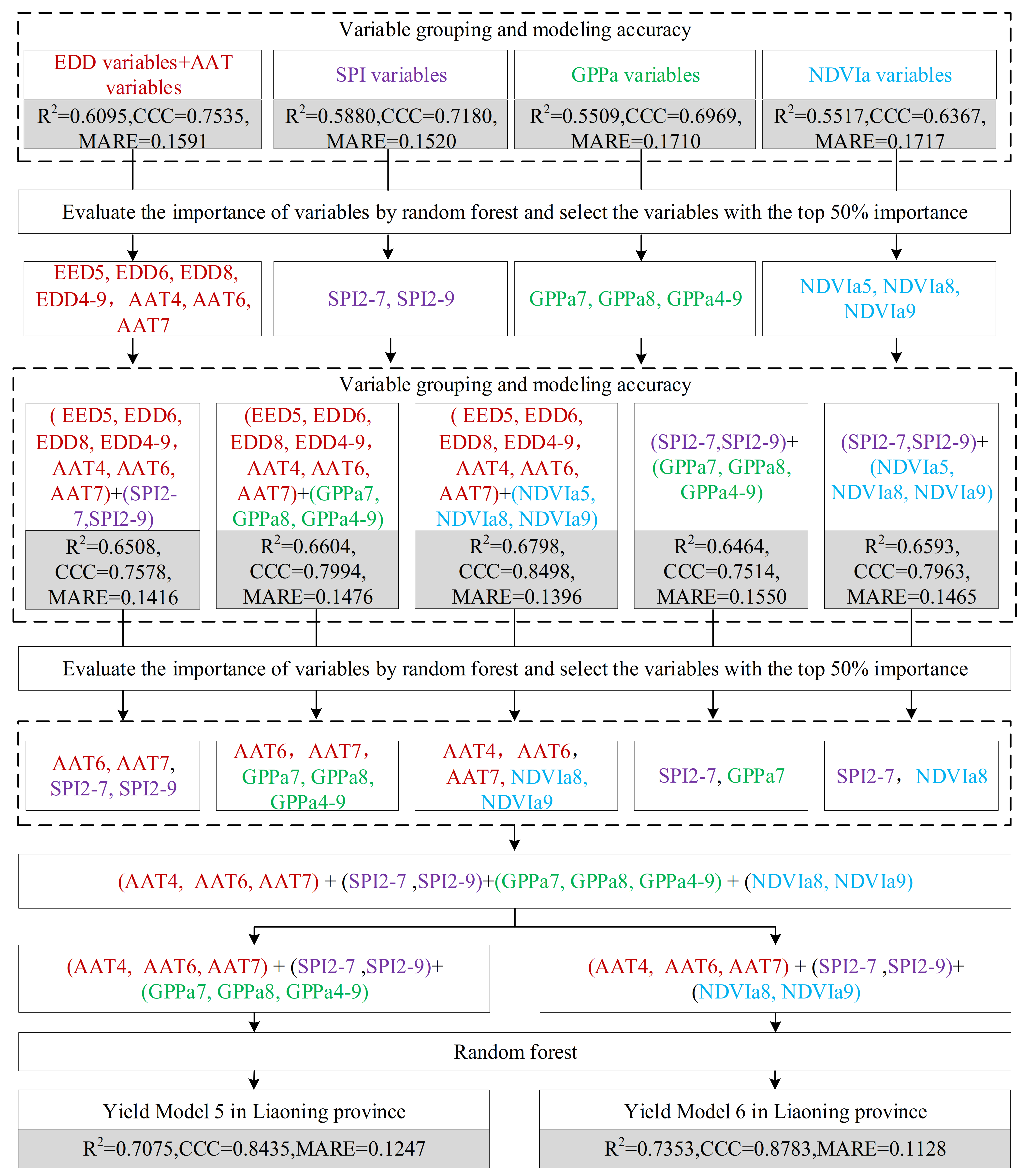
4.2.2. Model Built Using Variables Selected by a Two-Stage Importance Evaluation Method

Figure 5 and Figure 6 show the modeling process according to the second method described in Section 3.2 in Jilin and Liaoning provinces, respectively. In Jilin Province, the R2, CCC, and MARE of the yield estimation model (Yield Model 3) built with the variables from the GPP group were 0.8201, 0.9761, and 0.0943, respectively. The R2, CCC, and MARE of the yield estimation model (Yield Model 4) built with variables from the NDVI group were 0.8019, 0.9599, and 0.0961, respectively. The modeling accuracy using only the remote sensing variables was lower than that using only the agrometeorological indexes. The model built using only NDVIa variables had the lowest accuracy (R2 = 0.6622; CCC = 0.8282; MARE = 0.1154). In Liaoning Province, the R2, CCC, and MARE of the yield estimation model (Yield Model 3) built with variables from the GPP group were 0.7075, 0.8435, and 0.1247, respectively. The R2, CCC, and MARE of the yield estimation model (Yield Model 4) built with variables from the NDVI group were 0.7353, 0.8783, and 0.1128, respectively. The accuracy of models using EDD variables, AAT variables, SPI variables, and GPPa (NDVIa) variables together was higher than that of using any one of them alone (Table 2). The model built using only GPPa variables had the lowest accuracy (R2 = 0.5509; CCC = 0.6969; MARE = 0.1710).

4.2.3. Determination and Verification of the Final Yield Estimation Model

Table 2 summarizes the input variables and accuracy levels of models 1 to 4 established by the three methods in the two provinces. Based on the table, we finally chose Yield Model 3 for Jilin Province and Yield Model 4 for Liaoning Province as their best yield estimation models. According to agricultural disaster statistics from 1997 to 2016 in China, Liaoning and Jilin suffered severe agricultural disasters in 1997, 2000, and 2001 (Figure 7). For the disaster year of 1997 in Jilin Province, we rebuilt a yield estimation model with data on the input variables of Yield Model 3 by removing data from 1997. We then estimated the maize yield in 1997 using the newly built model and evaluated the accuracy of the yield estimation for that disaster year. Using the same method, the model performance was also evaluated in the other two disaster years in Jilin Province and the three disaster years in Liaoning Province. The accuracy evaluation is shown in Figure 8. The MARE values for all municipal administrative units in Jilin Province was 0.1379 in 1997, 0.1163 in 2000, and 0.0919 in 2001. The MARE value for all municipal administrative units in Liaoning Province was 0.1508 in 1997, 0.1170 in 2000, and 0.1186 in 2001. The model accuracy of Jilin Province is higher than that of Liaoning Province.

4.3. Comparision of Two Variable Selection Methods

The modeling variables selected by the two variable selection methods were obviously different. In Jilin Province, the number of input variables of models 1 to 4 were 24, 24, 8, and 7, respectively. In Liaoning Province, the number of input variables of models 1 to 4 were 16, 17, 8, and 7, respectively. The difference in the input variables were caused the accuracy differences among the different yield estimation models built by the random forest method. In general, the second method had the highest modeling accuracy and used the least input variables. A possible reason is that the second method reduced the correlation between the selected variables, thus reducing information redundancy. There was a strong correlation between input variables (Figure 9). The first methods did not consider correlations between the input variables. Therefore, the selected variables were redundant to some extent. For example, the correlation coefficient between EDD7 and SPI2-7 is -0.5410, which is significant at the 0.01 level. Both were selected by method 1 and used as the input variables of Model 1 and Model 2 in Jilin Province (Table 2). In the second method, we used a two-stage variable selection method. In the first stage, 31 candidate independent variables were divided into four groups (temperature group, SPI group, GPPa group, and NDVIa group), and then the variables constituting the top 50% importance from each group were selected. In addition, GPPa and NDVIa were often highly correlated, and the selected GPPa and NDVIa variables were used in different models (Yield Model 3 and 4). The above processing reduced the number of selected variables and the correlations among them.

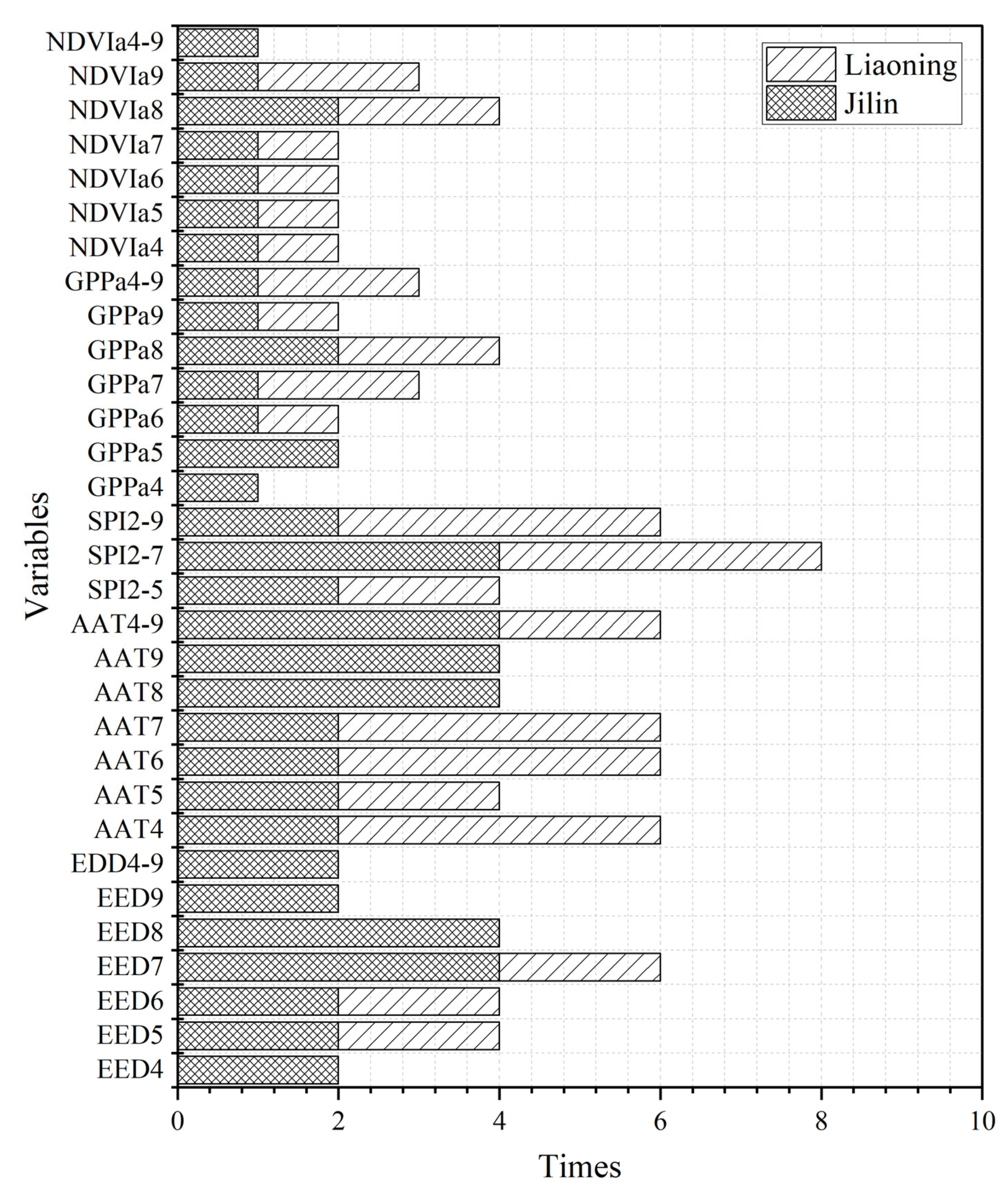
4.4. Comparison of the Importance of Different Variables

Overall, the contribution of the agrometeorological indexes to improving the modeling accuracy in the two provinces was greater than that of the remote sensing parameters (Figure 10). The contribution of the temperature indexes (AAT variables and EDD variables) to improving the modeling accuracy in the two provinces was greater than that of the SPI variables (Figure 10). The contribution of the GPPa and NDVIa variables to the modeling accuracy in the two provinces was inconsistent. In Jilin Province, the GPPa variables performed better than the NDVIa variables, but in Liaoning Province, the opposite was true (Figure 10). In general, under the same method, the modeling accuracy difference between the GPP variable group and the NDVI variable group was not large, the R2 difference was within 0.04, the CCC difference was within 0.04, and the MARE difference was within 0.02 (Table 1). NDVI is a basic remote sensing variable, which can be calculated only by using the reflectance of near infrared and red bands. However, the GPP calculation process is complex and requires a large amount of input data; the calculation itself introduces a certain amount of error [71]. Therefore, we recommend the use of NDVI in the establishment of a yield estimation model.
There were 31 candidate variables in this study. For a given candidate variable in each province, we counted the cumulative number of times that it was selected as one of the input variables for building models 1–4. The maximum cumulative number of times was four for the ATT, EDD, and SPI variables, while the maximum cumulative number of times was two for the GPPa and NDVIa variables. The results are shown in Figure 11. From the figure, we can see that EDD7, AAT4-9, EDD8, AAT8, AAT9, and SPI2-7 were the most important variables in Jilin Province. ATT4, ATT6, ATT7, SPI2-9, and SPI2-7 were the most important variables in Liaoning Province. Among the 11 most important variables in two provinces, the ATT variables accounted for 6, constituting for the highest proportion (54.54%). SPI2-7 was used as the input variable in all models, which indicates that drought in the middle period of maize growth (June and July) has a great impact on maize yield in both Jilin and Liaoning Provinces. From June to July, maize is in the transitional period between three leaves and silking, and its water demand is high [72,73,74]. The critical period of water supply lasts from 10 days before tasseling to 20 days after tasseling. The ear differentiation and flowering stages are sensitive to water deficiencies [75]. Drought conditions lasting for more than half a month will cause "neck drought" in maize, which results in poor development of young ears, small ears, and few grains. In addition, GPPa and NDVIa in August were important modeling variables for both provinces. This is probably because the GPP and NDVI values usually peak in August. A large number of studies have shown that the peak NDVI value is highly correlated with crop yield, so it is often selected as an input variable for remote sensing statistical yield estimation models [76,77]. NDVIa (GPPa) represents NDVI (GPP) anomaly; thus, the NDVIa observed in August can well reflect the yield fluctuation [69,78,79].

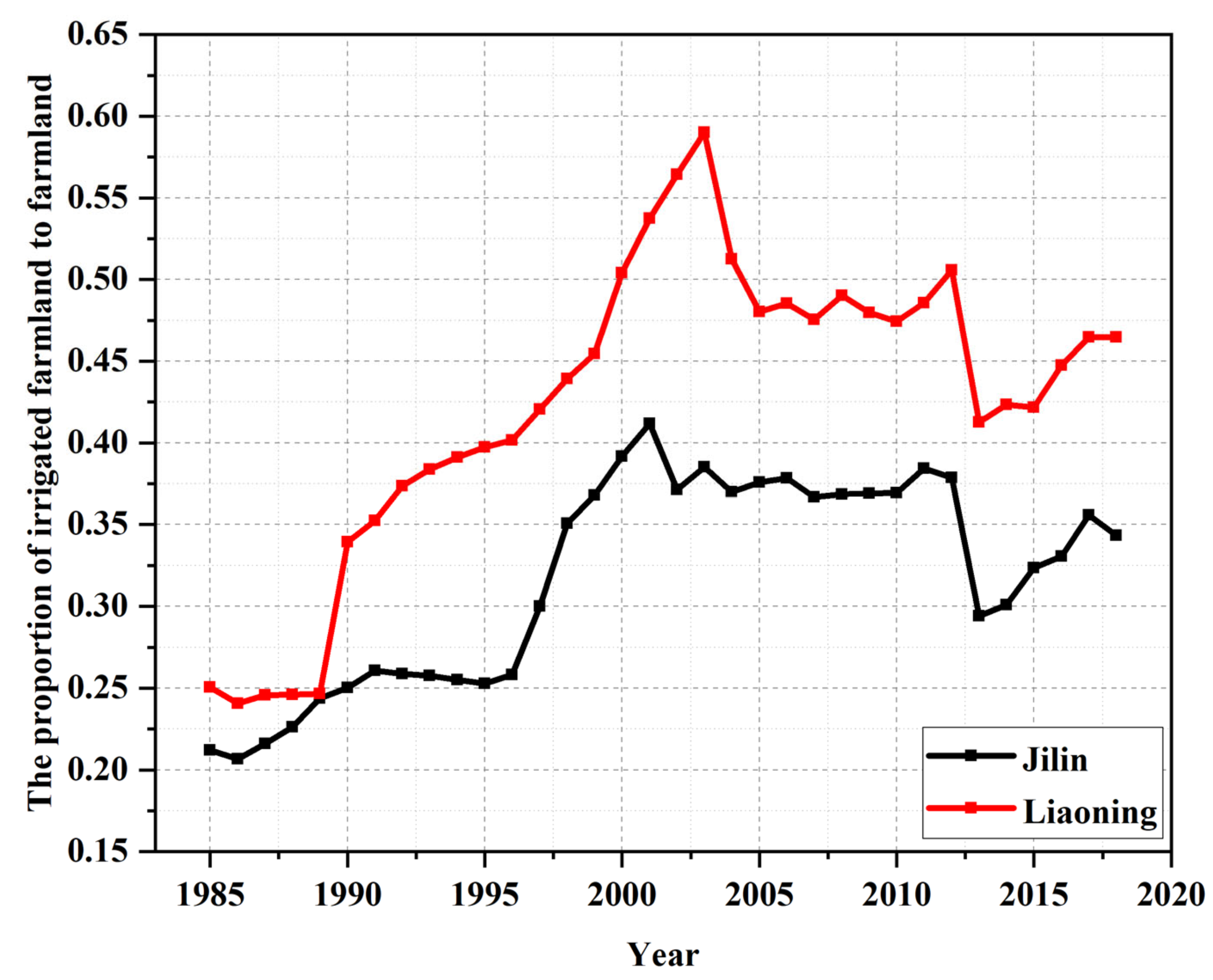
4.5. Comparision of Two Studied Provinces

The modeling accuracy of Jilin Province is higher than that of Liaoning Province. The R2 of the four yield estimation models in Jilin Province ranged between 0.7680 and 0.8201, the CCC value ranged between 0.9093 and 0.9761, and the MARE value ranged between 0.0925 and 0.0961. The R2 of the four yield estimation models in Liaoning Province ranged between 0.7075 and 0.7466, the CCC value ranged between 0.8435 and 0.8918 and the MARE values ranged between 0.1128 and 0.1326. This is likely because the stability of the technical yield in Jilin Province is conducive to ensuring the modeling accuracy. The contribution of the technical yield to the total yield is usually greater than that of the climatic yield. A good prediction of the technical yield can ensure the accuracy of yield estimations. In our study, the stability of the technical yield in Jilin Province is higher than that in Liaoning Province (Figure 12). If we only use the technical yield as the input variable to build the yield estimation model, the R2, CCC, and MARE are 0.5679, 0.7319, and 0.1257 in Jilin Province and 0.3570, 0.4990, and 0.1996 in Liaoning Province, respectively.
The contribution of agrometeorological indexes and remote sensing parameters to improving yield estimation accuracy in Liaoning Province is greater than that in Jilin Province (Figure 10). In Jilin Province, after adding agrometeorological indexes and remote sensing parameters, the accuracy of modeling is not significantly improved; R2 increases between 0.0944 and 0.2522, CCC increases between 0.0964 and 0.2442, and MARE decreases between 0.0103 and 0.0314. In Liaoning Province, after adding agrometeorological indexes and remote sensing parameters, the accuracy of modeling is significantly improved; R2 increases between 0.1948 and 0.3784, CCC increases between 0.1378 and 0.3794, and MARE decreases between 0.0279 and 0.0749. The above results show that for areas with a low technical yield stability (i.e., large fluctuations in the climate yield), adding agricultural climate factors has great benefits in improving the modeling.

5. Discussion

RF is a very efficient machine learning algorithm. Compared with traditional regression model, random forests modeling method has good stability and high accuracy and does not need to check whether the interaction of the variables is significant. It has high tolerance to the outliers and noises, and does not easily appear over fitting phenomenon. Although machine learning modeling methods perform well in yield prediction [80,81,82], the modeling process of them is a "black box", and the yield estimation model constructed cannot be directly expressed by the functional relationship between input variables and yield. However, compared with other machine learning modeling methods, RF has a prominent advantage; that is, it can estimate the importance of variables. Therefore, it can be used to identify variables that are more important for crop yield estimation and analyze and explain the factors affecting crop yield according to the differences of variables. However, the ability of RF simulation to explain crop physiology is still limited. The crop growth model can simulate the physiological growth process of crops, and has a better mechanism [7,83]. The combination of machine learning and the crop growth model could be a new direction for crop yield estimation [84].
We proposed a new strategy for the yield estimation model development in which remote sensing indexes, agrometeorological indexes, and technical yield are used together, and modeling variables are selected by a two-stage importance evaluation method. The new strategy was tested in two different provinces: Jilin and Liaoning. Although both provinces are the main maize producing provinces, and located in Northeast China, there are some differences between them. First, technical yield is the dominant component of yield. It is also the most important modelling variable. The average coefficient of variation of maize technical yield during the study period was 8.94% in Jilin Province and 10.86% in Liaoning Province (Figure 12), indicating the stability of the technical yield in Jilin Province is higher than that in Liaoning Province. This makes the overall modelling accuracy in Jilin Province higher than that in Liaoning Province. Second, rainfed cropland is the main cropland type in both Liaoning and Jilin Provinces. The average proportion of irrigated farmland area to farmland area is 0.32 in Jilin Province and 0.42 in Liaoning Province, respectively (Figure 13). The crop yield in rainfed cropland is easily affected by meteorological conditions. The climate yield is defined as the difference between technical yield and yield and determined by short-term climate variations. The range, standard deviation, and mean deviation of climate yield during our study period are 2893.13 kg/ha, 661.96 kg/ha, and 522.75.96 kg/ha in Jilin Province, and they are 3641.34 kg/ha, 800.46 kg/ha, and 603.42 kg/ha in Liaoning province, respectively (Figure 14). The climate yield fluctuation of Liaoning Province is larger than that of Jilin Province. Thus, the agrometeorological indexes play a greater role in improving the yield estimation accuracy in Liaoning Province than in Jilin Province. Third, the altitude and latitude of Jilin Province are higher than those of Liaoning Province (Figure 1), and the growth period of maize is later than that of Liaoning Province. Therefore, the months of the selected modelling variables are different, and the months of the important temperature indicators affecting the yield in Jilin are delayed. For example, the ATT8 and ATT9 were important variables in Jilin Province, while ATT6 and ATT7 were the most important variables in Liaoning Province. The validation results at the municipal level in these two provinces show that the MARE of the established models is lower than 0.15 (including disaster years), which indicates that our method has good application prospects. Our method can select the best modeling variable for each province. It is applicable to yield estimation in both normal and disaster years.
Our research has some limitations. First, the maize yield at municipal level was used for modeling because the time series yield data at county level is missing. Technical yield is one of the input variables of our modeling, and it has the greatest contribution to the accuracy of modeling. In order to calculate the technical yield, the yield data of long time series, usually longer than 30 years, is required. County level yield data can only be obtained for recent years, and there is an insufficiently long enough time series. However, our modeling strategy is also applicable to regions with long time series county scale data. Second, among the remote sensing parameters, we only tested NDVI and GPP. On the one hand, it is limited by article space. On the other hand, the vegetation indexes are highly correlated, and there is a certain degree of information redundancy among them. NDVI is the most widely used remote sensing parameter for yield estimation. Many other remote sensing parameters have been developed on the basis of NDVI. GPP is highly correlated with aboveground biomass and has a strong biophysics mechanism. Therefore, we chose NDVI and GPP to test. Our test results show that there is little difference between NDVI and GPP in the modeling accuracy. Finally, we recommend the use of NDVI in the establishment of a yield estimation model because it is easy to calculate. Third, technical yield is one of the input variables of modeling. The accuracy of the technical yield calculation has a certain influence on the accuracy of the subsequent yield estimation model. In order to reduce the uncertainty of the technical yield calculation results, we used three of the most popular methods to separate the technical yield from the historical actual yield. Corresponding to the three methods, we obtained three technical yield time series. Then, we chose the best result by calculating the correlation between the climate yield, which is the historical actual yield minus the technical yield, and the area of cultivated land suffered by disaster. Adverse climate conditions will lead to yield reduction, while favorable climate conditions will increase yield. There should be a good correlation between climate yield and the area of cultivated land suffered by disaster. Therefore, the climate yield with the highest correlation and the corresponding technical yield were regarded as the best calculation results. Although we chose the best technical yield calculation results by comparing the moving average method, HP filtering method, and exponential smoothing method, there are many other methods that can be used to calculate technical yield, and these methods can be tested in the future. Fourth, the agrometeorological indexes and remote sensing vegetation parameters used for model building in this study are monthly scale data and calculated in a fixed time period (April to September). However, maize phenology varies among different regions and require different climate conditions at different growth phases. Dividing the growth season of maize into multiple phases and calculating agrometeorological indexes and remote sensing vegetation parameters for each phase can better capture the impact of climate conditions of different growth phases on maize yield. Fifth, a large quantity of remote sensing data, meteorological data, and statistical data with a long time series were used in this study. Collecting and preprocessing these data consume a great amount of computer storage and computation time. At present, some earth science data and analysis cloud computing platforms such as GEE provide a large number of high resolution remote sensing data, meteorological data, advanced computing functions, and flexible user interfaces. If the experimental process of this study were transferred to the cloud computing platform, the time cost and computer storage cost would be greatly reduced. Meanwhile, the applicability of this research method in other study areas could be tested with highly efficiency because the model constructed in this study has explorability, simplicity, and convenience. Therefore, the wide use of the cloud computing platforms for data calculation and processing is a new trend which will assist greatly in yield estimation with big data processing.

6. Conclusions

In this paper, we combined technical yields, agrometeorological indexes, and remote sensing vegetation parameters together to build maize yield estimation models for Liaoning and Jilin Provinces. We validated the accuracy of yield estimations models built in this study, compared the differences of the two variable selection methods and discussed the importance of different variables on yield estimation. The main conclusions are as follows:
First, the validation results show that the models built in this study have good application potential and are suitable for both normal and disaster years. R2, CCC, and MARE of yield estimation model built in Jilin Province were 0.8201, 0.9761, and 0.0942, and they were 0.7353, 0.8783 and 0.1128 in Liaoning Province, respectively. The average error of yield estimation for the three disaster years was 0.12 in Jilin Province and 0.13 in Liaoning Province.
Second, the accuracy of the two-stage importance evaluation method was better than, or equivalent to, that of the other method, but it used the fewest variables. It is better to group the variables according to their physical meaning, and to select important variables from each group, than to input all variables at one time and select important variables to build the model.
Third, the contribution of the agrometeorological indexes to the improvement of the overall modeling accuracy in the two provinces was greater than that of the remote sensing parameters. The ATT variables were more important than the EDD variables. SPI2 in July has a great impact on maize yield in both Jilin and Liaoning Provinces. GPPa (NDVIa) in August is more important than the GPPa (NDVIa) variables in the other months.
Our study can not only be used as yield estimation tool for the related users, but also guide the relevant researchers to establish similar yield estimation models in other regions. In future, we can build such models using the cloud computing platform, which will greatly reduce the time cost and computer storage cost.

Author Contributions

Conceptualization, X.Z.; Data curation, X.Z., R.G., T.L. and K.X.; Formal analysis, R.G.; Funding acquisition, X.Z.; Investigation, R.G.; Methodology, X.Z.; Software, R.G.; Validation, R.G.; Visualization, X.Z. and R.G.; Writing—original draft, X.Z.; Writing—review and editing, X.Z., R.G., T.L. and K.X. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Key R&D Program of China (Grant No. 2019YFA0606900) and the National Natural Science Foundation of China (Grant No. 42077436).

Data Availability Statement

Data is available upon request.

Acknowledgments

We thank the journal’s editors and reviewers for their kind comments and valuable suggestions to improve the quality of this paper.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Van Ittersum, M.K.; Cassman, K.G.; Grassini, P.; Wolf, J.; Tittonell, P.; Hochman, Z. Yield gap analysis with local to global relevance–A review. Field Crops Res. 2013, 143, 4–17. [Google Scholar] [CrossRef] [Green Version]
  2. Lobell, D.B.; Cassman, K.G.; Field, C.B. Crop yield gaps: Their importance, magnitudes, and causes. Annu. Rev. Environ. Resour. 2009, 34, 179–204. [Google Scholar] [CrossRef] [Green Version]
  3. Murthy, C.S.; Thiruvengadachari, S.; Raji, P.V.; Jonna, S. Improved ground sampling and crop yield estimation using satellite data. Int. J. Remote Sens. 1996, 17, 945–956. [Google Scholar] [CrossRef]
  4. Kasampalis, D.A.; Alexandridis, T.K.; Deva, C.; Challinor, A.; Moshou, D.; Zalidis, G. Contribution of remote sensing on crop models: A review. J. Imaging 2018, 4, 52. [Google Scholar] [CrossRef] [Green Version]
  5. Moulin, S.; Bondeau, A.; Delecolle, R. Combining agricultural crop models and satellite observations: From field to regional scales. Int. J. Remote Sens. 1998, 19, 1021–1036. [Google Scholar] [CrossRef]
  6. Yao, F.; Tang, Y.; Wang, P.; Zhang, J. Estimation of maize yield by using a process-based model and remote sensing data in the Northeast China Plain. Phys. Chem. Earth 2015, 87–88, 142–152. [Google Scholar] [CrossRef]
  7. Huang, J.; Sedano, F.; Huang, Y.; Ma, H.; Li, X.; Liang, S.; Tian, L.; Zhang, X.; Fan, J.; Wu, W. Assimilating a synthetic Kalman filter leaf area index series into the WOFOST model to improve regional winter wheat yield estimation. Agric. For. Meteorol. 2016, 216, 188–202. [Google Scholar] [CrossRef]
  8. Shanahan, J.F.; Schepers, J.S.; Francis, D.D.; Varvel, G.E.; Wilhelm, W.W.; Tringe, J.M.; Schlemmer, M.R.; Major, D.J. Use of remote-sensing imagery to estimate corn grain yield. Agron. J. 2001, 93, 583–589. [Google Scholar] [CrossRef] [Green Version]
  9. Panda, S.S.; Ames, D.P.; Panigrahi, S. Application of vegetation indices for agricultural crop yield prediction using neural network techniques. Remote Sens. 2010, 2, 673–696. [Google Scholar] [CrossRef] [Green Version]
  10. Becker-Reshef, I.; Vermote, E.; Lindeman, M.; Justice, C. A generalized regression-based model for forecasting winter wheat yields in Kansas and Ukraine using MODIS data. Remote Sens. Environ. 2010, 114, 1312–1323. [Google Scholar] [CrossRef]
  11. Palosuo, T.; Kersebaum, K.C.; Angulo, C.; Hlavinka, P.; Moriondo, M.; Olesen, J.E.; Patil, R.H.; Ruget, F.; Rumbaur, C.; Takac, J.; et al. Simulation of winter wheat yield and its variability in different climates of Europe: A comparison of eight crop growth models. Eur. J. Agron. 2011, 35, 103–114. [Google Scholar] [CrossRef] [Green Version]
  12. Eitzinger, J.; Thaler, S.; Schmid, E.; Strauss, F.; Ferrise, R.; Moriondo, M.; Bindi, M.; Palosuo, T.; Rotter, R.; Kersebaum, K.C.; et al. Sensitivities of crop models to extreme weather conditions during flowering period demonstrated for maize and winter wheat in Austria. J. Agric. Sci. 2013, 151, 813–835. [Google Scholar] [CrossRef]
  13. Asseng, S.; Ewert, F.; Martre, P.; Roetter, R.P.; Lobell, D.B.; Cammarano, D.; Kimball, B.A.; Ottman, M.J.; Wall, G.W.; White, J.W.; et al. Rising temperatures reduce global wheat production. Nat. Clim. Chang. 2015, 5, 143–147. [Google Scholar] [CrossRef]
  14. Barlow, K.M.; Christy, B.P.; O’Leary, G.J.; Riffkin, P.A.; Nuttall, J.G. Simulating the impact of extreme heat and frost events on wheat crop production: A review. Field Crops Res. 2015, 171, 109–119. [Google Scholar] [CrossRef] [Green Version]
  15. Glotter, M.J.; Moyer, E.J.; Ruane, A.C.; Elliott, J.W. Evaluating the sensitivity of agricultural model performance to different climate inputs. J. Appl. Meteorol. Climatol. 2016, 55, 579–594. [Google Scholar] [CrossRef]
  16. Rotter, R.P.; Palosuo, T.; Kersebaum, K.C.; Angulo, C.; Bindi, M.; Ewert, F.; Ferrise, R.; Hlavinka, P.; Moriondo, M.; Nendel, C.; et al. Simulation of spring barley yield in different climatic zones of Northern and Central Europe: A comparison of nine crop models. Field Crops Res. 2012, 133, 23–36. [Google Scholar] [CrossRef]
  17. van der Velde, M.; Tubiello, F.N.; Vrieling, A.; Bouraoui, F. Impacts of extreme weather on wheat and maize in France: Evaluating regional crop simulations against observed data. Clim. Chang. 2012, 113, 751–765. [Google Scholar] [CrossRef] [Green Version]
  18. Mladenova, I.E.; Bolten, J.D.; Crow, W.T.; Anderson, M.C.; Hain, C.R.; Johnson, D.M.; Mueller, R. Intercomparison of soil moisture, evaporative stress, and vegetation indices for estimating corn and soybean yields over the US. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1328–1343. [Google Scholar] [CrossRef]
  19. Sepaskhah, A.R.; Fahandezh-Saadi, S.; Zand-Parsa, S. Logistic model application for prediction of maize yield under water and nitrogen management. Agric. Water Manag. 2011, 99, 51–57. [Google Scholar] [CrossRef]
  20. Geetha, M.C.S.; Shanthi, I.E. Predicting the soil profile through modified regression by discretisation algorithm for the crop yield in Trichy district, India. Int. J. Grid Util. Comput. 2018, 9, 235–242. [Google Scholar] [CrossRef]
  21. Tittonell, P.; Shepherd, K.D.; Vanlauwe, B.; Giller, K.E. Unravelling the effects of soil and crop management on maize productivity in smallholder agricultural systems of western Kenya—An application of classification and regression tree analysis. Agric. Ecosyst. Environ. 2008, 123, 137–150. [Google Scholar] [CrossRef] [Green Version]
  22. Bognar, P.; Kern, A.; Pasztor, S.; Lichtenberger, J.; Koronczay, D.; Ferencz, C. Yield estimation and forecasting for winter wheat in Hungary using time series of MODIS data. Int. J. Remote Sens. 2017, 38, 3394–3414. [Google Scholar] [CrossRef] [Green Version]
  23. Huang, J.; Wang, H.; Dai, Q.; Han, D. Analysis of NDVI Data for Crop Identification and Yield Estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4374–4384. [Google Scholar] [CrossRef]
  24. Ren, J.; Chen, Z.; Zhou, Q.; Tang, H. Regional yield estimation for winter wheat with MODIS-NDVI data in Shandong, China. Int. J. Appl. Earth Obs. Geoinf. 2008, 10, 403–413. [Google Scholar] [CrossRef]
  25. Zhang, P.; Anderson, B.; Tan, B.; Huang, D.; Myneni, R. Potential monitoring of crop production using a satellite-based Climate-Variability Impact Index. Agric. For. Meteorol. 2005, 132, 344–358. [Google Scholar] [CrossRef]
  26. Son, N.T.; Chen, C.F.; Chen, C.R.; Chang, L.Y.; Duc, H.N.; Nguyen, L.D. Prediction of rice crop yield using MODIS EVI-LAI data in the Mekong Delta, Vietnam. Int. J. Remote Sens. 2013, 34, 7275–7292. [Google Scholar] [CrossRef]
  27. Kouadio, L.; Duveiller, G.; Djaby, B.; El Jarroudi, M.; Defourny, P.; Tychon, B. Estimating regional wheat yield from the shape of decreasing curves of green area index temporal profiles retrieved from MODIS data. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 111–118. [Google Scholar] [CrossRef] [Green Version]
  28. Domenikiotis, C.; Spiliotopoulos, M.; Tsiros, E.; Dalezios, N.R. Early cotton yield assessment by the use of the NOAA/AVHRR derived Vegetation Condition Index (VCI) in Greece. Int. J. Remote Sens. 2004, 25, 2807–2819. [Google Scholar] [CrossRef]
  29. Salazar, L.; Kogan, F.; Roytman, L. Use of remote sensing data for estimation of winter wheat yield in the United States. Int. J. Remote Sens. 2007, 28, 3795–3811. [Google Scholar] [CrossRef]
  30. Meroni, M.; Marinho, E.; Sghaier, N.; Verstrate, M.M.; Leo, O. Remote sensing based yield estimation in a stochastic framework—Case study of durum wheat in tunisia. Remote Sens. 2013, 5, 539–557. [Google Scholar] [CrossRef] [Green Version]
  31. Sakamoto, T.; Gitelson, A.A.; Arkebauer, T.J. MODIS-based corn grain yield estimation model incorporating crop phenology information. Remote Sens. Environ. 2013, 131, 215–231. [Google Scholar] [CrossRef]
  32. Sakamoto, T.; Gitelson, A.A.; Arkebauer, T.J. Near real-time prediction of US corn yields based on time-series MODIS data. Remote Sens. Environ. 2014, 147, 219–231. [Google Scholar] [CrossRef]
  33. Bala, S.K.; Islam, A.S. Correlation between potato yield and MODIS-derived vegetation indices. Int. J. Remote Sens. 2009, 30, 2491–2507. [Google Scholar] [CrossRef]
  34. Seffrin, R.; de Araujo, E.C.; Bazzi, C.L. Regression models for prediction of corn yield in the state of Parana (Brazil) from 2012 to 2014. Acta Sci. Agron. 2018, 40, e36494. [Google Scholar] [CrossRef]
  35. Mathieu, J.A.; Aires, F. Assessment of the agro-climatic indices to improve crop yield forecasting. Agric. For. Meteorol. 2018, 253, 15–30. [Google Scholar] [CrossRef]
  36. Holzman, M.E.; Carmona, F.; Rivas, R.; Niclos, R. Early assessment of crop yield from remotely sensed water stress and solar radiation data. ISPRS J. Photogramm. Remote Sens. 2018, 145, 297–308. [Google Scholar] [CrossRef]
  37. Zhang, J.Q. Risk assessment of drought disaster in the maize-growing region of Songliao Plain, China. Agric. Ecosyst. Environ. 2004, 102, 133–153. [Google Scholar] [CrossRef]
  38. Ming, B.; Guo, Y.; Tao, H.; Liu, G.; Li, S.; Wang, P. SPEIPM-based research on drought impact on maize yield in North China Plain. J. Integr. Agric. 2015, 14, 660–669. [Google Scholar] [CrossRef]
  39. Xu, X.; Gao, P.; Zhu, X.; Guo, W.; Ding, J.; Li, C. Estimating the responses of winter wheat yields to moisture variations in the past 35 years in Jiangsu Province of China. PLoS ONE 2018, 13, e0191217. [Google Scholar] [CrossRef]
  40. Wang, S.; Mo, X.; Hu, S.; Liu, S.; Liu, Z. Assessment of droughts and wheat yield loss on the North China Plain with an aggregate drought index (ADI) approach. Ecol. Indic. 2018, 87, 107–116. [Google Scholar] [CrossRef]
  41. Chen, F.; Jia, H.; Pan, D. Risk assessment of maize drought in china based on physical vulnerability. J. Food Qual. 2019, 2019, 9392769. [Google Scholar] [CrossRef]
  42. Lalic, B.; Eitzinger, J.; Thaler, S.; Vucetic, V.; Nejedlik, P.; Eckersten, H.; Jacimovic, G.; Nikolic-Djoric, E. can agrometeorological indices of adverse weather conditions help to improve yield prediction by crop models? Atmosphere 2014, 5, 1020–1041. [Google Scholar] [CrossRef] [Green Version]
  43. Shumin, L. Comprehensive evaluation on the drought risk of rain-fed agriculture in China based on GIS. J. Arid Land Resour. Environ. 2011, 25, 39–44. [Google Scholar] [CrossRef]
  44. Chavas, D.R.; Izaurralde, R.C.; Thomson, A.M.; Gao, X. Long-term climate change impacts on agricultural productivity in eastern China. Agric. For. Meteorol. 2009, 149, 1118–1128. [Google Scholar] [CrossRef]
  45. Zhou, B.; Xu, Y.; Wu, J.; Dong, S.; Shi, Y. Changes in temperature and precipitation extreme indices over China: Analysis of a high-resolution grid dataset. Int. J. Climatol. 2016, 36, 1051–1066. [Google Scholar] [CrossRef]
  46. Wu, H.; Hou, W.; Qian, Z.-H.; Hu, J.-G. The research on the sensitivity of climate change in China in recent 50 years based on composite index. Acta Phys. Sin. 2012, 61, 149205. [Google Scholar] [CrossRef]
  47. Gao, G.; Huang, C.Y. Climate change and its impact on water resources in North China. Adv. Atmos. Sci. 2001, 18, 718–732. [Google Scholar] [CrossRef]
  48. Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
  49. National Earth System Science Data Center. National Science & Technology Infrastructure of China. Available online: http://www.geodata.cn/ (accessed on 7 June 2020).
  50. Yuan, W.; Liu, S.; Yu, G.; Bonnefond, J.M.; Chen, J.; Davis, K.; Desai, A.R.; Goldstein, A.H.; Gianelle, D.; Rossi, F. Global estimates of evapotranspiration and gross primary production based on MODIS and global meteorology data. Remote Sens. Environ. 2010, 114, 1416–1431. [Google Scholar] [CrossRef] [Green Version]
  51. Land Long Term Data Record. Available online: https://ltdr.modaps.eosdis.nasa.gov/cgi-bin/ltdr/ltdrPage.cgi (accessed on 8 June 2020).
  52. Gooijer, J.G.D.; Hyndman, R.J. 25 years of time series forecasting. Int. J. Forecast. 2005, 22, 443–473. [Google Scholar] [CrossRef] [Green Version]
  53. Ravn, M.O.; Uhlig, H. On Adjusting the Hodrick-Prescott filter for the frequency of observations. Rev. Econ. Stats 2002, 84, 371–375. [Google Scholar] [CrossRef] [Green Version]
  54. Gardner, E.S. Forecasting the failure of component parts in computer systems: A case study. Int. J. Forecast. 1993, 9, 245–253. [Google Scholar] [CrossRef]
  55. Dong, W.; Liu, S.; Fang, Z. On modeling mechanisms and applicable ranges of grey incidence analysis models. Grey Syst. Theory Appl. 2018, 8, 448–461. [Google Scholar] [CrossRef]
  56. Junfu, X.; Zhandong, L.I.U.; Yumin, C. Study on the water requirement and water requirement regulation of maize in china. Maize Sci. 2008, 16, 21–25. [Google Scholar]
  57. Cao, X.; Wang, Y.; Wu, P.; Zhao, X.; Wang, J. An evaluation of the water utilization and grain production of irrigated and rain-fed croplands in China. Sci. Total Environ. 2015, 529, 10–20. [Google Scholar] [CrossRef]
  58. Sun, F.; Yang, X.; Lin, E.; Ju, H.; Xiong, W. Study on the sensitivity and vulnerability of wheat to climate change in china. Sci. Agric. Sin. 2005, 38, 692–696. [Google Scholar]
  59. Wang, J.; Yang, X.; Lu, S.; Liu, Z.; Li, K.; Xun, X.; Liu, Y.; Wang, E. Spatial-temporal characteristics of potential yields and yield gaps of spring maize in Heilongjiang province. Sci. Agric. Sin. 2012, 45, 1914–1925. [Google Scholar] [CrossRef]
  60. Leng, G.Y.; Hall, J. Crop yield sensitivity of global major agricultural countries to droughts and the projected changes in the future. Sci. Total Environ. 2019, 654, 811–821. [Google Scholar] [CrossRef]
  61. Yu, X.; He, X.; Zheng, H.; Guo, R.; Ren, Z.; Zhang, D.; Lin, J. Spatial and temporal analysis of drought risk during the crop-growing season over northeast China. Nat. Hazards 2014, 71, 275–289. [Google Scholar] [CrossRef]
  62. Zhang, Z.; Chen, Y.; Wang, P.; Zhang, S.; Tao, F.; Liu, X. Spatial and temporal changes of agro-meteorological disasters affecting maize production in China since 1990. Nat. Hazards 2014, 71, 2087–2100. [Google Scholar] [CrossRef]
  63. McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration of time scales. In Proceedings of the Eight Conference on Apllied Climatology, American Meteorological Society, Anaheim, CA, USA, 17–23 January 1993; pp. 179–186. [Google Scholar]
  64. Sanchez, B.; Rasmussen, A.; Porter, J.R. Temperatures and the growth and development of maize and rice: A review. Glob. Chang. Biol. 2014, 20, 408–417. [Google Scholar] [CrossRef] [PubMed]
  65. Hawkins, E.; Fricker, T.E.; Challinor, A.J.; Ferro, C.A.T.; Ho, C.K.; Osborne, T.M. Increasing influence of heat stress on French maize yields from the 1960s to the 2030s. Glob. Chang. Biol. 2013, 19, 937–947. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  66. Lobell, D.B.; Hammer, G.L.; McLean, G.; Messina, C.; Roberts, M.J.; Schlenker, W. The critical role of extreme heat for maize production in the United States. Nat. Clim. Chang. 2013, 3, 497–501. [Google Scholar] [CrossRef]
  67. Lobell, D.B.; Sibley, A.; Ivan Ortiz-Monasterio, J. Extreme heat effects on wheat senescence in India. Nat. Clim. Chang. 2012, 2, 186–189. [Google Scholar] [CrossRef]
  68. Schlenker, W.; Roberts, M.J. Nonlinear temperature effects indicate severe damages to US crop yields under climate change. Proc. Natl. Acad. Sci. USA 2009, 106, 15594–15598. [Google Scholar] [CrossRef] [Green Version]
  69. Chen, J.; Jonsson, P.; Tamura, M.; Gu, Z.H.; Matsushita, B.; Eklundh, L. A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky-Golay filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
  70. Papagiannopoulou, C.; Miralles, D.G.; Decubber, S.; Demuzere, M.; Verhoest, N.E.C.; Dorigo, W.A.; Waegeman, W. A non-linear Granger-causality framework to investigate climate-vegetation dynamics. Geosci. Model. Dev. 2017, 10, 1945–1960. [Google Scholar] [CrossRef] [Green Version]
  71. Schaefer, K.; Schwalm, C.R.; Williams, C.; Arain, M.A.; Barr, A.; Chen, J.M.; Davis, K.J.; Dimitrov, D.; Hilton, T.W.; Hollinger, D.Y.; et al. A model-data comparison of gross primary productivity: Results from the North American Carbon Program site synthesis. J. Geophys. Res. Biogeosci. 2012, 117, 15. [Google Scholar] [CrossRef] [Green Version]
  72. Wang, Y.; Tang, P.; Li, S.; Tian, Y.; Li, J. The water demand and optimal irrigation schedule of maize in drought years at eastern area of Inner Mongolia. Agric. Res. Arid Areas 2018, 36, 108–114. [Google Scholar]
  73. Gao, X.; Wang, C.; Zhang, J.; Xue, X. Crop water requirement and temporal-spatial variation of drought and flood disaster during growth stages for maize in Northeast during past 50 years. Trans. Chin. Soc. Agric. Eng. 2012, 28, 101–109. [Google Scholar]
  74. Cao, Y.; Yu, Z.; Zhao, T. Study of water demand and consumption rules in summer maize. Acta Agric. Boreali-Sin. 2003, 18, 47–50. [Google Scholar]
  75. Song, L.; Jin, J.; He, J. Effects of Severe Water Stress on Maize Growth Processes in the Field. Sustainability 2019, 11, 5086. [Google Scholar] [CrossRef] [Green Version]
  76. Aktas, A.F.; Ustundag, B.B. Phenology Based NDVI Time-series Compensation for Yield Estimation Analysis. In Proceedings of the 6th International Conference on Agro-Geoinformatics, Fairfax, VA, USA, 7–10 August 2017; pp. 1–5. [Google Scholar]
  77. Govedarica, M.; Jovanovic, D.; Sabo, F.; Borisov, M.; Vrtunski, M.; Alargic, I. Comparison of MODIS 250 m products for early corn yield predictions: A case study in Vojvodina, Serbia. Open Geosci. 2016, 8, 747–759. [Google Scholar] [CrossRef] [Green Version]
  78. Moriondo, M.; Maselli, F.; Bindi, M. A simple model of regional wheat yield based on NDVI data. Eur. J. Agron. 2007, 26, 266–274. [Google Scholar] [CrossRef]
  79. Mkhabela, M.S.; Mkhabela, M.S.; Mashinini, N.N. Early maize yield forecasting in the four agro-ecological regions of Swaziland using NDVI data derived from NOAAs-AVHRR. Agric. For. Meteorol. 2005, 129, 1–9. [Google Scholar] [CrossRef]
  80. Liu, J.; He, X.; Wang, P.; Huang, J. Early prediction of winter wheat yield with long time series meteorological data and random forest method. Trans. Chin. Soc. Agric. Eng. 2019, 35, 158–166. [Google Scholar] [CrossRef]
  81. Mutanga, O.; Adam, E.; Cho, M.A. High density biomass estimation for wetland vegetation using WorldView-2 imagery and random forest regression algorithm. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 399–406. [Google Scholar] [CrossRef]
  82. Cai, Y.; Guan, K.; Lobell, D.; Potgieter, A.B.; Wang, S.; Peng, J.; Xu, T.; Asseng, S.; Zhang, Y.; You, L.; et al. Integrating satellite and climate data to predict wheat yield in Australia using machine learning approaches. Agric. For. Meteorol. 2019, 274, 144–159. [Google Scholar] [CrossRef]
  83. Huang, J.; Ma, H.; Liu, J.; Zhu, D.; Zhang, X. Regional winter wheat yield estimation by assimilating MODIS ET and LAI products into SWAP model. In Proceedings of the Second International Conference on Agro-Geoinformatics, Fairfax, VA, USA, 12–16 August 2013; pp. 452–457. [Google Scholar]
  84. Feng, P.; Wang, B.; Liu, D.L.; Waters, C.; Yu, Q. Incorporating machine learning with biophysical model can improve the evaluation of climate extremes impacts on wheat yield in south-eastern Australia. Agric. For. Meteorol. 2019, 275, 100–113. [Google Scholar] [CrossRef]
Remotesensing 13 02016 g001 550
Figure 1. Location of the study area.
Figure 1. Location of the study area.
Remotesensing 13 02016 g001
Remotesensing 13 02016 g002 550
Figure 2. Technical flowchart of the study.
Figure 2. Technical flowchart of the study.
Remotesensing 13 02016 g002
Remotesensing 13 02016 g003 550
Figure 3. Gray correlation degree between the climate yield and the agricultural disaster data in Jilin (a) and Liaoning (b).
Figure 3. Gray correlation degree between the climate yield and the agricultural disaster data in Jilin (a) and Liaoning (b).
Remotesensing 13 02016 g003
Remotesensing 13 02016 g004 550
Figure 4. The accuracy of yield estimation models built using variables selected by random forest ((a) GPP group in Jilin Province, (b) NDVI group in Jilin Province, (c) GPP group in Liaoning Province, and (d) NDVI group in Liaoning Province).
Figure 4. The accuracy of yield estimation models built using variables selected by random forest ((a) GPP group in Jilin Province, (b) NDVI group in Jilin Province, (c) GPP group in Liaoning Province, and (d) NDVI group in Liaoning Province).
Remotesensing 13 02016 g004
Remotesensing 13 02016 g005 550
Figure 5. The modeling process according to the two-stage importance evaluation method in Jilin Province.
Figure 5. The modeling process according to the two-stage importance evaluation method in Jilin Province.
Remotesensing 13 02016 g005
Remotesensing 13 02016 g006 550
Figure 6. The modeling process according to the two-stage importance evaluation method in Liaoning Province.
Figure 6. The modeling process according to the two-stage importance evaluation method in Liaoning Province.
Remotesensing 13 02016 g006
Remotesensing 13 02016 g007 550
Figure 7. Area of cultivated land suffering agricultural disasters in Jilin (a) and Liaoning (b) Provinces.
Figure 7. Area of cultivated land suffering agricultural disasters in Jilin (a) and Liaoning (b) Provinces.
Remotesensing 13 02016 g007
Remotesensing 13 02016 g008 550
Figure 8. The modeling accuracy in three severe disaster years in Jilin (a) and Liaoning (b) Provinces.
Figure 8. The modeling accuracy in three severe disaster years in Jilin (a) and Liaoning (b) Provinces.
Remotesensing 13 02016 g008
Remotesensing 13 02016 g009 550
Figure 9. Correlation coefficients of the candidate input variables in Jilin (a) and Liaoning (b) Provinces.
Figure 9. Correlation coefficients of the candidate input variables in Jilin (a) and Liaoning (b) Provinces.
Remotesensing 13 02016 g009
Remotesensing 13 02016 g010 550
Figure 10. The resulting modeling accuracy using only the technical yield and by adding different variable groups on the basis of the technical yield in Jilin (a) and Liaoning (b) Provinces.
Figure 10. The resulting modeling accuracy using only the technical yield and by adding different variable groups on the basis of the technical yield in Jilin (a) and Liaoning (b) Provinces.
Remotesensing 13 02016 g010
Remotesensing 13 02016 g011 550
Figure 11. The cumulative number of times that variables were selected as one of the input variables for building models 1–4.
Figure 11. The cumulative number of times that variables were selected as one of the input variables for building models 1–4.
Remotesensing 13 02016 g011
Remotesensing 13 02016 g012 550
Figure 12. Variance in the technical yield in Jilin (a) and Liaoning (b) Provinces.
Figure 12. Variance in the technical yield in Jilin (a) and Liaoning (b) Provinces.
Remotesensing 13 02016 g012
Remotesensing 13 02016 g013 550
Figure 13. The proportion of irrigated farmland to farmland.
Figure 13. The proportion of irrigated farmland to farmland.
Remotesensing 13 02016 g013
Remotesensing 13 02016 g014 550
Figure 14. The climate yield in Jilin and Liaoning Provinces during the study period.
Figure 14. The climate yield in Jilin and Liaoning Provinces during the study period.
Remotesensing 13 02016 g014
Table
Table 1. Data sources and characteristics.
Table 1. Data sources and characteristics.
DataData SourceSpatial ResolutionTemporal Resolution
Meteorological reanalysis dataTotal
precipitation		ERA5 dataset of the European Center for Medium-Term Weather Forecast
(ECMWF 2017)		0.25°Monthly
2 m
temperature		ECMWF 20170.25°Hourly
Remote sensing dataGross primary productionNational Science and Technology Basic Conditions Platform-National Earth System Science Data Sharing Service Platform0.05°8 d
NDVIAVH13C1 dataset of the LTDR project0.05°1 d
Land use and land cover dataResource and Environmental Science Data Center of the Chinese Academy of Sciences1 km-
Statistical dataMaize yieldChina Bureau of StatisticsMunicipalityYearly
Agricultural disaster
statistics		China Bureau of StatisticsProvinceYearly
Table
Table 2. The input variables and accuracy of models 1 to 4 established by two methods in two provinces.
Table 2. The input variables and accuracy of models 1 to 4 established by two methods in two provinces.
ProvinceModelThe Number of Input VariablesInput VariablesR2CCCMARE
JilinYield Model 124SPI2-7, AAT9, GPPa8, AAT8, EDD8, GPPa7, AAT4-9, SPI2-5, AAT5, GPPa4-9, GPPa6, EDD6, EDD4-9, GPPa5, AAT7, SPI2-9, EDD7, AAT4, GPPa4, AAT6, EDD5, GPPa9, EDD9, EDD40.77030.90930.0933
Yield Model 224SPI2-7, AAT9, NDVIa4, NDVIa8, AAT8, EDD8, AAT4-9, SPI2-5, NDVIa7, AAT5, EDD6, EDD4-9, NDVIa5, AAT7, SPI2-9, EDD7, AAT4, NDVIa6, AAT6, EDD5, NDVIa4-9, NDVIa9, EDD9, EDD40.76800.91190.0925
Yield Model 38SPI2-7, AAT9, GPP8, EDD8, AAT4-9, GPPa5, AAT8, EDD70.82010.97610.0943
Yield Model 47SPI2-7, AAT9, EDD8, AAT4-9, NDVIa8, AAT8, EDD70.80190.95990.0961
LiaoningYield Model 116GPPa7, SPI2-5, SPI2-7, GPP4-9, GPPa8, AAT7, SPI2-9, GPPa9, EDD5, AAT6, AAT4, GPPa6, EDD6, AAT5, EDD7, AAT4-90.71480.85920.1326
Yield Model 217NDVIa8, SPI2-5, SPI2-7, AAT7, SPI2-9, NDVIa9, NDVIa5, EDD5, AAT6, AAT4, EDD6, NDVIa6, AAT5, EDD7, NDVIa4, NDVIa7, AAT4-90.74660.89180.1241
Yield Model 38GPPa7, AAT6, SPI2-7, AAT7, GPPa4-9, GPPa8, SPI2-9, AAT40.70750.84350.1247
Yield Model 47NDVIa8, SPI2-7, AAT7, AAT4, SPI2-9, NDVIa9, AAT60.73530.87830.1128
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Zhu, X.; Guo, R.; Liu, T.; Xu, K. Crop Yield Prediction Based on Agrometeorological Indexes and Remote Sensing Data. Remote Sens. 2021, 13, 2016. https://doi.org/10.3390/rs13102016

AMA Style

Zhu X, Guo R, Liu T, Xu K. Crop Yield Prediction Based on Agrometeorological Indexes and Remote Sensing Data. Remote Sensing. 2021; 13(10):2016. https://doi.org/10.3390/rs13102016

Chicago/Turabian Style

Zhu, Xiufang, Rui Guo, Tingting Liu, and Kun Xu. 2021. "Crop Yield Prediction Based on Agrometeorological Indexes and Remote Sensing Data" Remote Sensing 13, no. 10: 2016. https://doi.org/10.3390/rs13102016

APA Style

Zhu, X., Guo, R., Liu, T., & Xu, K. (2021). Crop Yield Prediction Based on Agrometeorological Indexes and Remote Sensing Data. Remote Sensing, 13(10), 2016. https://doi.org/10.3390/rs13102016

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop