Improving the Image Quality of Moving Ships for GF-3NG Based on Simultaneous AIS Information

Abstract

The synthetic aperture radar (SAR) is an important means of ship surveillance, but the motion of the ship leads to azimuth position offset, false targets, and azimuth defocusing for the spaceborne high-resolution and wide-swath (HRWS) SAR system, causing the degradation of imaging quality. The automatic identification system (AIS) can provide real-time information of the ships, which is an important auxiliary method for ship surveillance. Up to now, the traditional fusion of SAR and AIS mainly has focused on location matching and auxiliary recognition, and the next generation of GaoFen-3 (GF-3NG) satellite is equipped with both a SAR sensor and an AIS sensor to obtain the SAR images and simultaneous AIS information of ships. Consequently, this paper proposes a novel scheme to improve the imaging quality of moving ships for GF-3NG using AIS information. In this paper, through introducing the virtual stationary target, the slant range derivation (SRD) algorithm is proposed to estimate the radial velocity (RV) and the radial acceleration (RA) between the ship and the SAR platform relative to the stationary scene. According to the calculated RV, the azimuth position offset can be estimated and the ship can be repositioned on the image. After that, the traditional method is conducted to suppress the false targets. Finally, the method of using the RA to refocus ship slices is proposed. Additionally, the experiment results based on real data illustrate the effectiveness of the proposed methods.

1. Introduction

With the continuous improvement of the resolution and surveying width of the spaceborne synthetic aperture radar (SAR), the spaceborne SAR has gradually become an important means of ship surveillance [1,2,3,4]. However, due to the characteristics of SAR itself, there are still some deficiencies in ship monitoring. First, the Doppler effect between the SAR and target is the key to achieve high azimuth resolution, but the motion of the ship on the sea surface introduces an extra Doppler frequency shift, which results in the azimuth position offset and azimuth defocus of the ship after imaging [5,6,7]. Besides, there are false targets along the azimuth in multichannel mode. All of these damage the quality of the SAR image, which is not conducive to ship surveillance. Hence, scholars have proposed a large number of algorithms to estimate the motion of the ship in order to improve the SAR image quality, which can be mainly divided into two categories [8]: motion parameters estimation based on the wake [9,10,11] and the Doppler parameters estimation algorithm. However, the wakes of many ships are invisible on the SAR images and at larger incidence angles, the wakes are less visible [12]. Additionally, most of the existing time-frequency analysis algorithms, such as the Wigner Ville distribution method [13] and fractional Fourier transform (FrFT) method [14,15], are based on single-channel SAR, and there are few time-frequency analysis algorithms for high-resolution and wide-swath (HRWS) SAR. Consequently, other supplementary information is necessary for making up for the defects of the SAR. The automatic identification system (AIS) is a new type of auxiliary navigation system based on very high-frequency (VHF) technology with a global positioning system (GPS). It can obtain static information such as the ship name, maritime mobile service identify (MMSI), and ship type and length, as well as dynamic information such as the course, speed, latitude, and longitude [16]. According to AIS, we can analyze and predict the motion of the ship. Additionally, with the ability to work all day and in all weather conditions, AIS has also become an important technical means for marine monitoring [17,18]. However, AIS data are not always reliable because there is inevitably some uncertainty when sending signals [19].

The fusion of AIS and SAR images can make up for the deficiencies caused by a single monitoring means. Therefore, many SAR satellites that have been launched or is launched are equipped with both SAR payload and AIS payload, in order to obtain the SAR image and AIS information of the ship simultaneously. GaoFen-3 (GF-3) is a SAR satellite launched by China in August 2016 with the most abundant imaging modes in the world [20]. Additionally, the next generation of GF-3 (GF-3NG) that China plans to launch in the future will also carry AIS payloads to achieve the simultaneous monitoring of the ship by AIS and SAR.

At present, the traditional fusion of SAR and AIS mainly focuses on position matching. A general method of matching the SAR-detected vessels to their AIS messages is described and optimized with tailored weights for each vessel class in [21]. After the target is matched, the AIS information is applied to improve the recognition ability of SAR image ships as auxiliary information, for example, literature [22] improves ship classification in SAR images by transferring AIS knowledge and [17] uses large datasets of medium-resolution SAR images and AIS data as ground truths to evaluate the efficiency of different ship detectors based on adaptive threshold algorithms. There are also studies using AIS information to estimate the radial velocity (RV) of the ship on the SAR image. For instance, literature [23] projects the speed provided by the AIS data to get the relative RV. According to the heading and speed information reported by AIS, the speed can be projected to the line of sight (LOS) of the radar beam, and the RV can be estimated. However, this method turns the velocity of the ship to the two-dimensional velocity in the Mercator coordinate system, ignoring the velocity of the ship in the height direction, and it cannot estimate the azimuth velocity. Up to now, using AIS data to improve the SAR image quality has not been studied or published. In this paper, we further study how to use simultaneous AIS information to improve the imaging quality of moving ships on the basis of position matching.

Based on the imaging mode of GF-3NG, a novel scheme to improve the imaging quality of moving ships is proposed. This article innovatively proposes the slant range derivation (SRD) method to estimate RV and radial acceleration (RA) based on AIS data by introducing a virtual target, and proposes the method of using AIS data to improve the imaging quality of moving ships for the first time. According to the trajectory of the SAR platform reported by GPS and the trajectory of the ship reported by the AIS, the slant range between the ship and the SAR platform can be obtained. Then, the position of the ship at the moment of the shortest slant range is regarded as that of the virtual stationary target. Moreover, the relative RV and RA can be estimated by the SRD algorithm. Additionally, on the basis of the calculated RV, the azimuth position offset is estimated, and the ship is repositioned on the SAR image. Furthermore, the compensation method in [24] is used to suppress the false targets according to the RV. Finally, the method of using the RA to refocus ship slices is proposed. The GF-3 SAR image and the simultaneous AIS data offered by the commercial website [25] are adopted for experimental verification.

The remaining of the paper is organized as follows. In Section 2, the imaging geometry model of GF-3 is described, and the signal echo model of the moving ship is analyzed. Then, the methods of AIS data preprocessing, the RV and RA estimation, and the azimuth refocusing are explained in Section 3. Additionally, experimental results based on GF-3 real data are presented in Section 4. Moreover, Section 5 makes the discussion of the experiments and analyzes the algorithm performance. Finally, Section 6 makes the conclusions and points out the future directions of research.

2. Geometry Model and Signal Mode

A detailed analysis of the moving target signal model in GF-3 dual-channel mode is given in [24], and this article conducts further research on the basis of it. GF-3NG, like GF-3, includes azimuth dual-channel receive (DRC) mode and single-channel receive mode. For the single-channel mode, the motion of the target causes azimuth position offset and azimuth defocusing, whereas for the DRC mode, in addition to the above problems, there are also false targets in the azimuth resulting from under-sampling [26]. Without loss of generality, the DRC mode is taken as an example for modeling and analysis in this article.

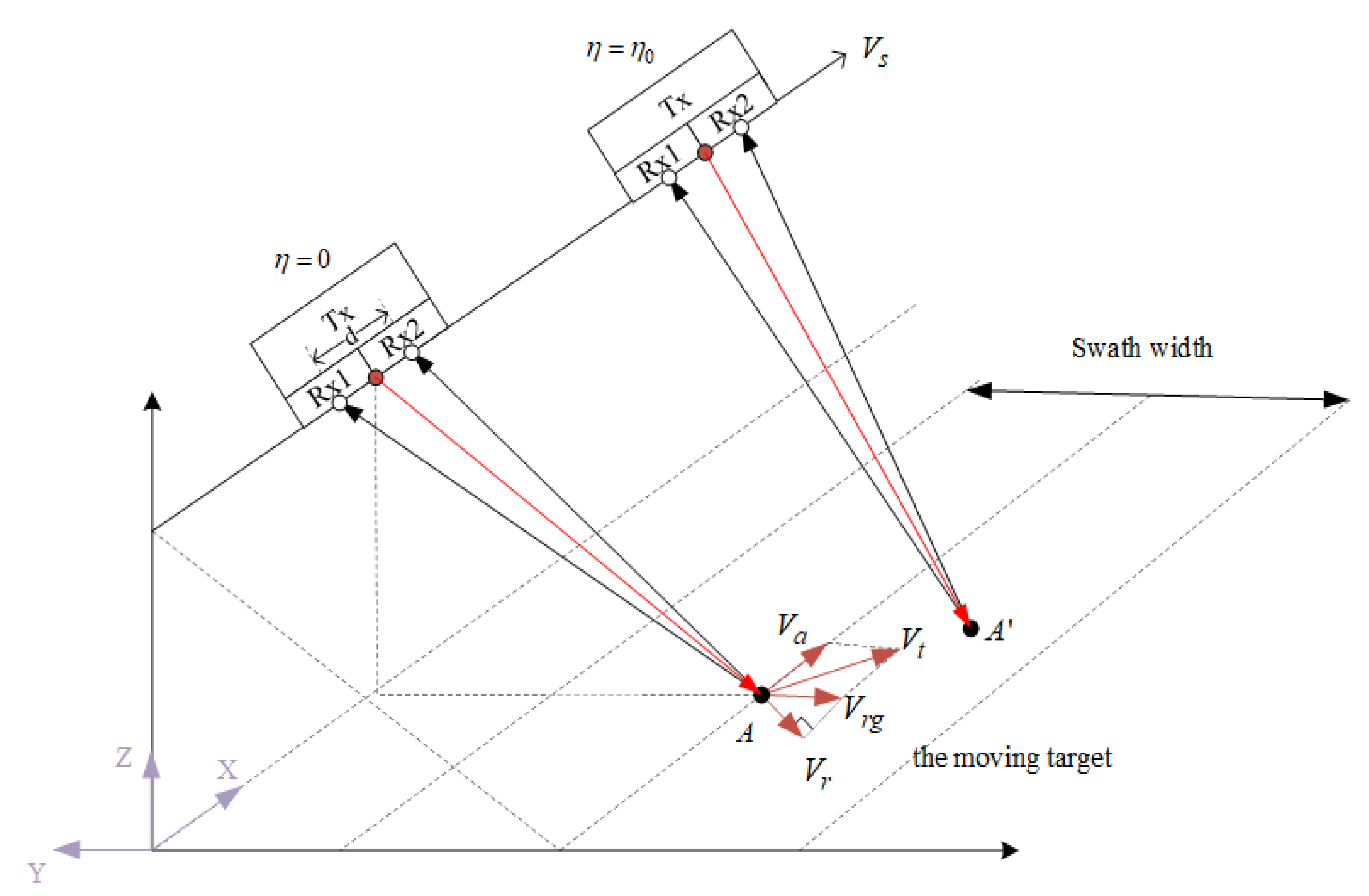
The geometry of the GF-3 DRC model is depicted in Figure 1. The x-axis points to the direction of the SAR platform velocity $V_s$, and the z-axis points away from the earth’s center; the three axes satisfy the orthogonal right-hand rule, and $\eta$represents the azimuth time.

The full area of the antenna$\mathrm{Tx}$ is used to transmit the chirp signal, where the solid red circle represents the phase center of the $\mathrm{Tx}$. It is divided into two channels in the azimuth receiving echoes simultaneously, denoted as $\mathrm{Rx}1$ and $\mathrm{Rx}2,$ respectively. The white circle represents the effective phase center (EPC), and the distance between the two phase centers is $d$.

There is a moving target modeled as an ideal point target in the scene where the shortest slant range is $R_0$ and the incidence is $\theta$, and its speed over ground (SOG) $V_t$ is projected into two directions, respectively: cross-track velocity $V_{rg}$ and along-track velocity $V_a$. The radial velocity $V_r$ is the projection of $V_{rg}$ on the slant range direction. Additionally, ${\eta }_0$ represents the radar observation time duration. When $\eta =0$, the position of the target is denoted as $A$, and when ${\eta =\eta }_0$, it moves uniformly in a straight line to the position marked as $A^{\prime }$.

Based on the geometry model described above, the slant range between the n-th EPC and the moving target denoted as $R_n\left(\eta \right)$ can be written as:

$$R_n\left(\eta \right)=\sqrt{{\left(R_0{+V}_r\eta \right)}^2+{\left(\left(V_s{-V}_a\right){\eta +x}_{n\_e}\right)}^2}\approx R_0{+V}_r\eta +\frac{{\left(\left(V_s{-V}_a\right){\eta +x}_{n\_e}\right)}^2}{{2R}_0},$$

(1)

where $x_{n\_e}$ represents the displacement length from the n-th EPC to the array center in the along-track direction and can be written as:

$$x_{n\_e}=\left(n-\frac{N+1}{2}\right)\frac{d}{2},n=1,2,$$

(2)

where $n$ represents the number of receivers in the azimuth direction, and in the model of this article, $N=2$. Then, the ideal received echo of the n-th channel can be expressed as Equation (4), where the $rect\{\cdot \}$stands for the unit rectangular function, the $\tau$ is the range time, and $T_p$ and $K_r$ are the pulse width and chirp rate of the transmitted signal, respectively. Additionally, $T_s$ is synthetic aperture time, $R_n\left({\eta -\eta }_c\right)$ is the instantaneous slant range of the moving target at azimuth position $X_0$, and ${\eta }_c$ is defined as follows.

$${\eta }_c=\frac{X_0}{V_s-V_a},$$

(3)

$$S_n\left(\tau ,h\right)=A_0\cdot rect\left\{\frac{\tau - \frac{2R_n\left(\eta -{\eta }_c\right)}{c}}{T_p}\right\}\cdot rect\left(\frac{\eta -{\eta }_c}{T_s}\right)\cdot exp\left\{j\pi K_r{\left(\tau -\frac{2R_n\left(\eta -{\eta }_c\right)}{c}\right)}^2\right\}\cdot exp\left\{-j\frac{4\pi R_n\left(\eta -{\eta }_c\right)}{\lambda }\right\}.$$

(4)

With reference to Equation (4), the azimuth Doppler frequency can be calculated as:

$$f_{\eta }=-\frac{2}{\lambda }\cdot \frac{\partial R_n\left(\eta \right)}{\partial \eta }.$$

(5)

Additionally, the Doppler rate can be obtained by deriving the Doppler frequency as follows:

$$K_a=\frac{\partial f_{\eta }}{\partial \eta }=-\frac{2}{\lambda }\cdot \frac{{\partial }^2{R}_n\left(\eta \right)}{{\eta }^2},$$

(6)

Substituting Equation (1) into Equation (5), the azimuth Doppler frequency of the moving target can be expressed as:

$${\widehat{f}}_n=-\left(\frac{2V_r}{\lambda }+\frac{2\left(V_s-V_a\right)x_{n\_e}}{\lambda R_0}\right)-\frac{2{\left(V_s-V_a\right)}^2}{\lambda R_0}\eta .$$

(7)

Let $\eta =0$, and the Doppler centroid of the n-th channel is

$${\widehat{f}}_{n\_dc}=-\left(\frac{2V_r}{\lambda }+\frac{2\left(V_s-V_a\right)x_{n\_e}}{\lambda R_0}\right).$$

(8)

Based on Equation (6), the Doppler rate of the moving target can be written as:

$${\widehat{K}}_a=-\frac{2{\left(V_s-V_a\right)}^2}{\lambda R_0},$$

(9)

where, for a stationary target, $V_r$ and $V_a$ are both equal to 0, then the azimuth Doppler frequency can be expressed as:

$$f_{\eta }=-\frac{{2V}_s{x}_{n\_e}}{{\lambda R}_0}-\frac{{2V}_s{}^2}{{\lambda R}_0}\eta .$$

(10)

Additionally, the Doppler centroid of the n-th channel and the Doppler rate can be written as Equations (11) and (12), respectively:

$$f_{n\_dc}=-\frac{{2V}_s{x}_{n\_e}}{{\lambda R}_0},$$

(11)

$$K_a=-\frac{{2V}_s^2}{{\lambda R}_0}.$$

(12)

According to Equations (8) and (11), the Doppler centroid shift introduced by the moving target can be written as:

$$\Delta f_{dc}={\widehat{f}}_{n\_dc}-f_{n\_dc}=-\frac{2V_r}{\lambda }+\frac{2V_a{x}_{n\_e}}{\lambda R_0}.$$

(13)

In the case of spaceborne SAR, the azimuth velocity $V_a$ is relatively small, so its impact on the center can be ignored; thus, Equation (13) can be rewritten as:

$${\Delta f}_{\mathrm{dc}}\approx -\frac{{2V}_r}{\lambda }.$$

(14)

As analyzed above, the existence of the RV results in an offset of the Doppler frequency. Besides, the echo spliced by each channel of HSWR SAR is nonuniformly sampled in azimuth, so it is necessary to reconstruct it to recover the uniformly sampled signal. Additionally, the traditional method is to reconstruct the signal spectrum with the reconstruction filter bank [26,27,28]. While reconstructing the spectrum of the moving target with the filter bank for the stationary target, there is a step phase that leads to the false targets in pairs in azimuth after imaging. The azimuth position of false targets can be written as:

$$X_n=\left(\frac{2V_r}{\lambda }-n{f}_p\right)\cdot \frac{V_s}{K_a},\hspace{1em}\hspace{1em}n=-N\sim N,$$

(15)

where $f_p$ is the pulse repetition frequency for each channel, and only when $n=0$ corresponds to the real target, and the others correspond to the false targets. According to Equations (14) and (15), the azimuth offset of the moving target relative to the static scene can be expressed as:

$${\Delta X}_n=\frac{{2V}_r}{\lambda }\cdot \frac{V_s}{K_a}=-\frac{V_r{R}_0}{V_s}.$$

(16)

As suggested by Equations (9) and (12), the azimuth velocity $V_a$ introduced by the moving target causes the azimuth Doppler rate of the moving target echo to be inconsistent with that of stationary scene echo. Then in practice, the matching filter suitable for the stationary target is used to process the echo of the moving target. Therefore, for the moving target, the residual Doppler rate is not compensated, which leads to the azimuth defocusing, and the residual Doppler rate error is shown in Equation (17).

$$\Delta K_a={\widehat{K}}_a-K_a=-\frac{4V_s{V}_a-2V_a^2}{\lambda R_0}.$$

(17)

According to the analysis above, in GF-3 DRC mode, the existence of the target motion results in the azimuth position offset, defocusing, and false targets on the SAR image.

3. Processing Method

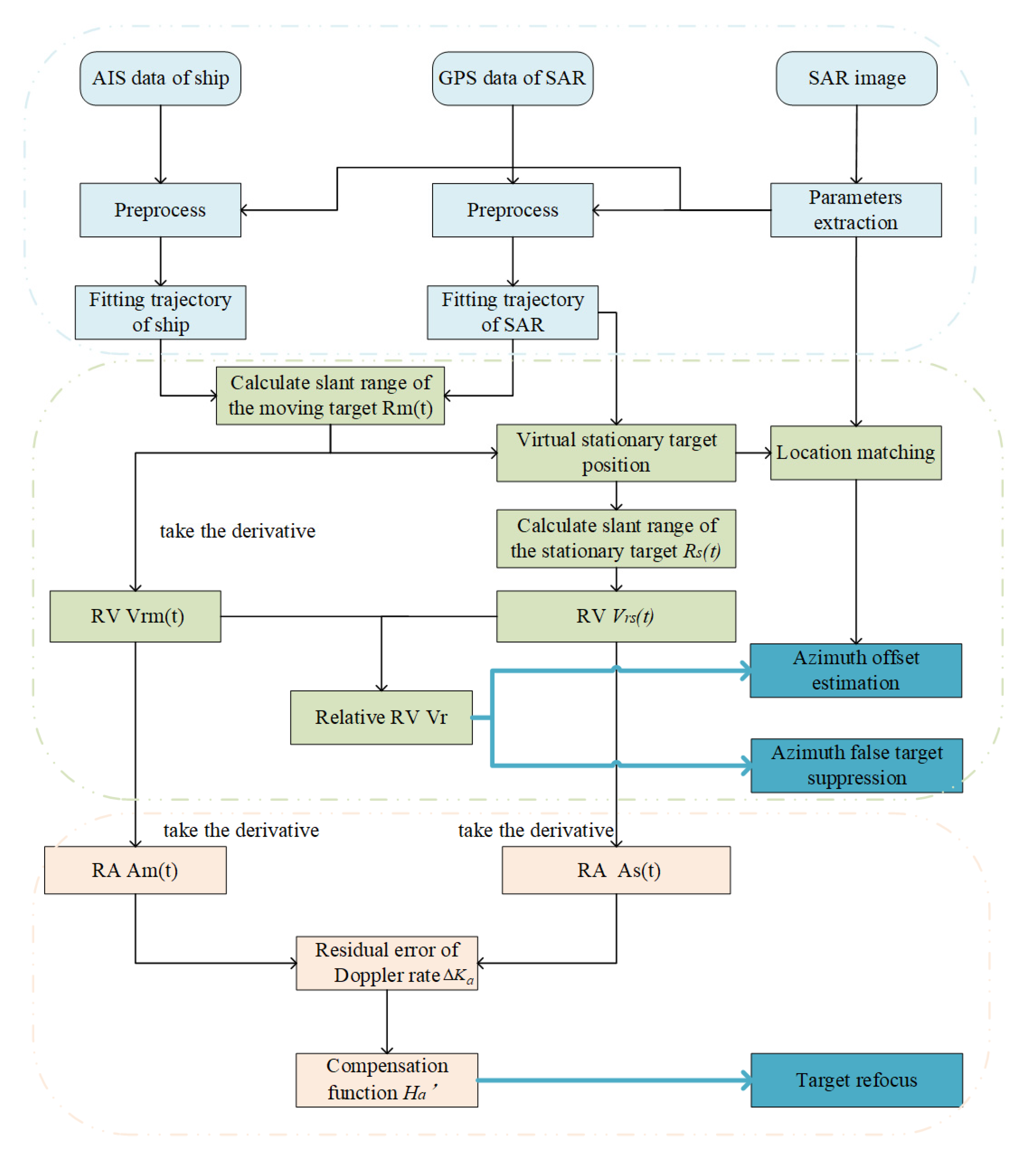
In this section, we describe a scheme of using AIS to improve the imaging quality of the moving ships. Additionally, the main processing flow is shown in Figure 2. First, we introduced the preprocessing of data. Then, the SRD algorithm for calculating the relative RV is presented and how to use the RV to calculate the azimuth offset is deduced. Finally, the calculation of the relative RA and the method of compensating the residual Doppler rate error to achieve refocusing are proposed.

3.1. The Preprocessing of Data

The AIS data record the voyage message of the ship, including dynamic information such as speed, heading, and position, as well as static information such as MMSI and ship length and width, is of great help to ship monitoring. However, the AIS data are not always reliable. The final file of the AIS data may contain duplicated data of the same ship at a certain moment. Besides, AIS information may be missing at some moments. Additionally, the latitude and longitude reported by AIS may deviate from its true value. Due to these anomalies, we have to preprocess AIS data before using it to improve ship imaging quality.

The preprocessing consists of three steps. First, according to the imaging area and time of the SAR image, the AIS data of the ships corresponding to the SAR image are extracted. Since the AIS data are discrete, and we expect to obtain the continuous motion function of the ship with respect to time, the data after preprocessing need to be fitted at the end. The specific fitting method is introduced later. Generally, the movement of a ship in a short time is relatively stable, so for the accuracy of the final fitting, only the data within 30 min around the imaging time are selected for the next step. Then, the selected AIS data need to be deduplicated. According to the time stamp, the data of the same ship at the same time is removed. If the position of several consecutive data does not change, but the speed of the ship is not zero, it is considered that these data are abnormal, and only the first data in this group are retained, and the rest of the data are eliminated. Finally, the data processed after the first two steps are fitted to overcome the sparsity of AIS data. After several tests, it is found that the accuracy of fitting with a third-order polynomial is sufficient. We use the time-stamp as an independent variable, and latitude and longitude as dependent variables for fitting to obtain the ship’s motion curve.

The positions of the SAR satellite are expressed in the WGS-84 coordinate system, whereas the positions in the AIS data are represented by latitude (lat) and longitude (lon). Thus, the lat and lon in the AIS data need to be converted to the WGS-84 coordinate system, so as to unify the coordinate system. The method to convert the position represented by $\left[lon,lat\right]$ to the WGS-84 coordinate system is as follows:

$$\{\begin{array}{l}x=\left(R+H\right)\cdot cos\left(lat\right)\cdot cos\left(lon\right)\hfill \\ y=\left(R+H\right)\cdot cos\left(lat\right)\cdot sin\left(lon\right)\hfill \\ z=\left(R+H\right)\cdot sin\left(lat\right)\hfill \end{array},$$

(18)

where$R$ is the approximate radius of the earth, $R\approx 6371.393 \mathrm{km},$ and $H$ is the altitude of the target. In practice, the altitude of the ship on the sea is generally considered to be zero; thus, $H=0$. As suggested by Equation (18), the coordinates of the ship in the WGS-84 coordinates system, denoted as $\left(x_{ship}\left(t\right){,y}_{ship}\left(t\right){,z}_{ship}\left(t\right)\right)$, can be known.

The spatial position of the SAR platform in the WGS-84 coordinates system can be obtained from the GPS. Similarly, only the data within 30 min around the imaging time are selected, and the three-dimensional coordinates are respectively fitted with the third-order polynomial to functions of time. Thus, the spatial position of the SAR platform can be expressed as $\left(x_{\mathit{sar}}\left(t\right){,y}_{\mathit{sar}}\left(t\right){,z}_{\mathit{sar}}\left(t\right)\right)$.

3.2. Relative RV Calculation

When the coordinates of the SAR platform and ship are determined, the slant range between them can be calculated as:

$$\{\begin{array}{c}{\Delta X}_m\left(t\right){=x}_{\mathit{sar}}\left(t\right)-x_{ship}\left(t\right)\\ {\Delta Y}_m\left(t\right){=y}_{\mathit{sar}}\left(t\right)-y_{ship}\left(t\right)\\ {\Delta Z}_m\left(t\right){=z}_{\mathit{sar}}\left(t\right)-z_{ship}\left(t\right)\end{array},$$

(19)

$$R_m\left(t\right)=\sqrt{{\Delta X}_m{\left(t\right)}^2{+\Delta Y}_m{\left(t\right)}^2{+\Delta Z}_m{\left(t\right)}^2}.$$

(20)

Additionally, by deriving $R_m\left(t\right)$, the RV of the moving ship relative to the satellite can be obtained.

$$V_{\mathit{rm}}\left(t\right)=\frac{{\mathit{dR}}_m\left(t\right)}{\mathit{dt}}.$$

(21)

Generally, the imaging scene of SAR is considered to be stationary relative to the earth. Therefore, the parameters of azimuth-matched filter, such as Doppler centroid and Doppler rate, are designed for stationary scenes. Additionally, according to the analysis of the signal model in Section 2, it is not the movement of the moving ship relative to the SAR platform, but the movement of the moving ship relative to the stationary scene, that causes the azimuth offset, the false targets, and the azimuth defocus. However, the velocity calculated according to Equation (21) is the RV of the moving ship relative to the SAR platform, rather than the RV relative to the ground stationary scene, and it cannot be used directly for azimuth offset correction and azimuth refocusing. If the RV of the stationary scene relative to the SAR platform is also known, the difference between the two velocities can be regarded as the RV of the moving ship relative to the stationary scene. As analyzed in Section 2, the Doppler centroid frequency reflects the RV of the target relative to the satellite platform, and the Doppler rate demonstrates the acceleration of the target relative to the satellite platform. However, even if they reflect the relative motion between the satellite platform and the target, the Doppler parameters used in imaging are calculated based on the satellite attitude and orbit parameters. Additionally, the measurement errors of both the attitude and orbit are inevitable, resulting in azimuth target location error. The measurement errors of the yaw angle, pitch angle, and roll angle cause the measured beam center pointing to be inconsistent with its real pointing, which is shown in Figure 3, leading to the calculation error of the Doppler centroid. Therefore, the Doppler parameters used in imaging cannot be directly regarded as the real Doppler parameters of the stationary scene relative to the satellite platform. Below, we introduce our method of solving the Doppler parameters of the stationary scene relative to the SAR platform.

According to the AIS data and the SAR platform’s GPS information, the slant range between the moving target and the SAR platform $R_m\left(t\right)$ can be obtained. The moment when$R_m\left(t\right)$ reaches the minimum value is regarded as the target imaging center moment, denoted as $t_c$. Assuming that there is a stationary target at the ship position corresponding to $t_c$, with reference to Equations (19) and (20), the slant range between the stationary target and the satellite platform can be obtained by the same method. The slant range between this virtual stationary target and the SAR platform can be expressed as:

$$\{\begin{array}{c}{\Delta X}_s\left(t\right){=x}_{\mathit{sar}}\left(t\right)-x_{ship}\left(t_c\right)\\ {\Delta Y}_s\left(t\right){=y}_{\mathit{sar}}\left(t\right)-y_{ship}\left(t_c\right)\\ {\Delta Z}_s\left(t\right){=z}_{\mathit{sar}}\left(t\right)-z_{ship}\left(t_c\right)\end{array},$$

(22)

$$R_s\left(t\right)=\sqrt{{\Delta X}_s{\left(t\right)}^2{+\Delta Y}_s{\left(t\right)}^2{+\Delta Z}_s{\left(t\right)}^2}.$$

(23)

Taking the derivative of $R_s\left(t\right)$ as Equation (24), the RV of this stationary point relative to the SAR platform can be obtained.

$$V_{\mathit{rs}}\left(t\right)=\frac{{\mathit{dR}}_s\left(t\right)}{\mathit{dt}}.$$

(24)

Additionally, the relative RV between the moving target and the SAR platform introduced in the stationary scene can be calculated as:

$$V_r{=V}_{\mathit{rm}}\left(t_c\right)-V_{\mathit{rs}}\left(t_c\right).$$

(25)

According to Equations (25) and (16), the azimuth offset of the moving target after imaging can be calculated.

In summary, the calculation of RV can be achieved by the SRD algorithm, and the azimuth offset of the moving ship on the SAR image can also be obtained. The methods of azimuth position offset correction and multichannel false target suppression of the moving target are introduced in detail in [24]. This article does not repeat it, but does give a detailed method of azimuth defocusing compensation.

3.3. Calculation of RA and Compensation

The Doppler centroid shift of the moving ship relative to the stationary scene can be obtained by deriving the slant range $R_s\left(t\right)$ and $R_m\left(t\right)$, and by the same method, the relative RA introduced by the moving ship can also be known, and it can be used to calculate the residual Doppler rate error. Additionally, the relative RA of the moving target and the virtual stationary target can be calculated as below:

$$A_m\left(t\right)=\frac{{\mathit{dV}}_{\mathit{rm}}\left(t\right)}{\mathit{dt}},$$

(26)

$$A_s\left(t\right)=\frac{{\mathit{dV}}_{\mathit{rs}}\left(t\right)}{\mathit{dt}}.$$

(27)

According to Equation (6), the Doppler rate error caused by ship motion can be written as:

$${\Delta K}_a=-\frac{2\left(A_m\left(t_c\right)-A_s\left(t_c\right)\right)}{\lambda }.$$

(28)

Generally speaking, the azimuth defocusing of moving target mainly results from the mismatch between the parameters of the filter and the actual echo. Taking the RD imaging algorithm as an example, the azimuth matched filter can be written as:

$$H_a=\exp \left(-j\pi \frac{f_a^2}{K_a}\right),$$

(29)

where $K_a$is the Doppler rate used in the imaging process. However, the real Doppler rate of the moving target is

$$K_{\mathit{at}}{=K}_a{+\Delta K}_a.$$

(30)

To compensate for the Doppler rate error to achieve refocusing, firstly, the ship slice needs to be transformed into the range-Doppler domain by the azimuth fast Fourier transform (FFT) method, and then multiplied with the compensation function in Equation (31).

$$H_a^{\prime }=\exp \left(j\pi ·\frac{K_{\mathit{at}}-K_a}{K_{\mathit{at}}·K_a}{f}_a^2\right)=\exp \left(j\pi ·\frac{{\Delta K}_a}{K_{\mathit{at}}·K_a}{f}_a^2\right).$$

(31)

After compensating $H_a^{\prime }$ in the range-Doppler domain, and conducting the azimuth inverse fast Fourier transform (IFFT) method, the well-focused moving ship slice can be obtained.

4. Experimental Results

In this section, we verify the above methods with real data. The SAR images near Kyushu Island in Japan acquired by GF-3 in DRC mode were adopted for experiments. The location and acquisition time of the SAR image are shown in

Table 1. SAR image information.

Satellite	Orbit ID	Imaging Mode	Center (Longitude/Latitude)	Scene Date (UTC)
GF-3	11725	UFS	129.127942/33.455959	2018-11-01 17:27:41

. The SAR image area is depicted in Figure 4a, and Figure 4b shows the SAR image. Additionally Figure 4c is the slice of the real target in Figure 4b, where the ship’s trajectory obtained from AIS data is marked with yellow dots, and the actual photo of the ship is also attached. Additionally, the AIS data for the experiment are provided by the commercial company [25]. The message type and some description of the AIS data are listed in

Table 2. The description of AIS data.

Message Type	Description
Static information	Maritime Mobile Service Identify (MMSI) number, Ship type, International Maritime Organization (IMO) number, Ship name, Ship length, Ship width, Draught, etc.
Dynamic information	Turn rate, Latitude, Longitude, Speed, Course, True heading of ship, Position accuracy, Time-stamp, etc.
Navigation information	Destination, Cargo type, etc.

.

First, the relative RV and RA were calculated. The relative RV obtained by SRD was compared with the results of other algorithms, and the error was analyzed. Then, the RV was used to suppress false targets. The results after suppression were compared with those before suppression. At last, according to the obtained RA, the azimuth phase compensation was carried out to achieve the refocusing of ship slices. At the same time, the conventional autofocus method was also conducted to process the slices, and the results of the two methods were compared and analyzed.

4.1. Relative RV and RA Estimation

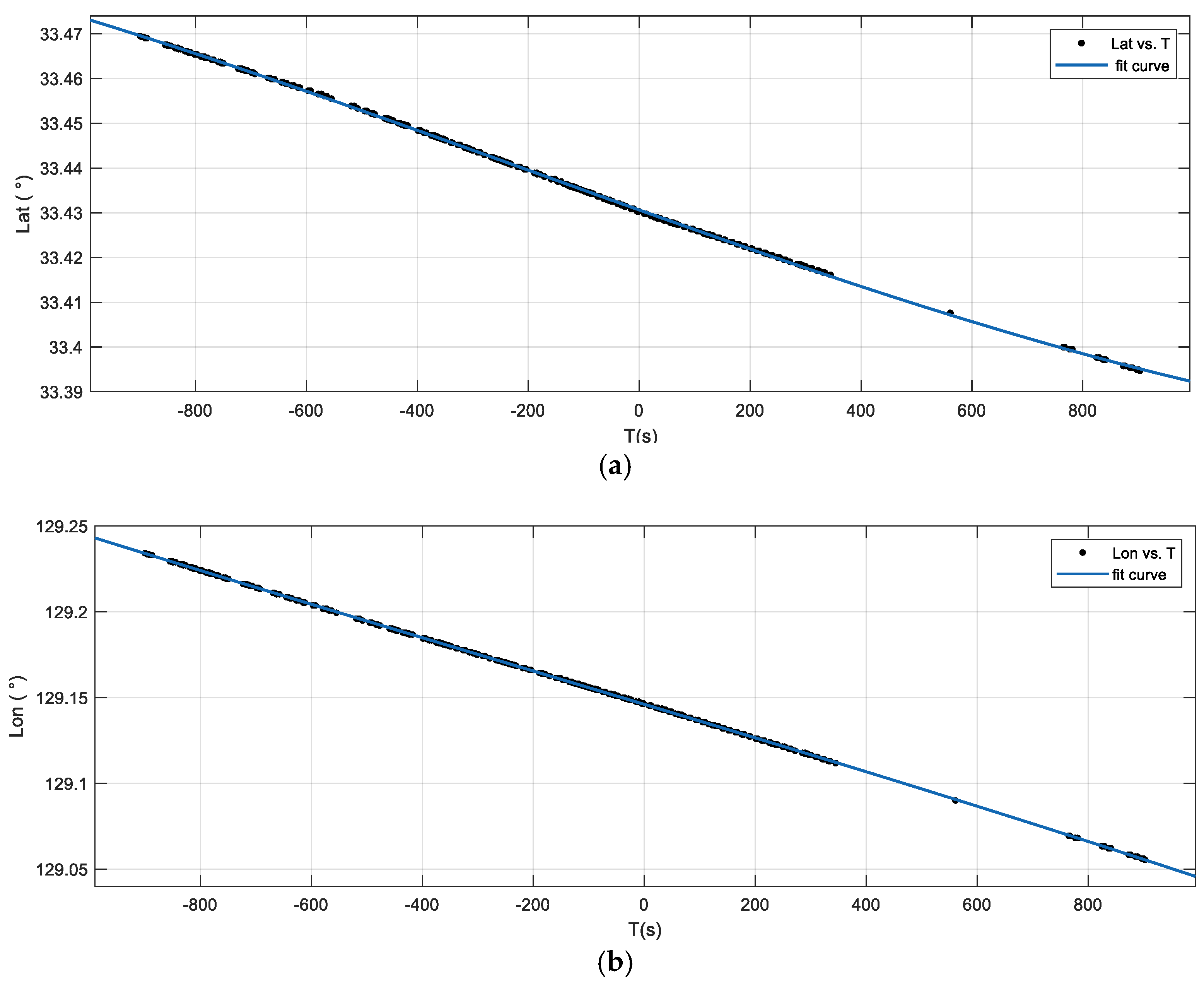
Firstly, the spatial position of the GF-3 SAR platform in the WGS-84 coordinate around the imaging time can be obtained from the metafile of the SAR image product. Additionally, the AIS data corresponding to the ship on the SAR image were processed by the method mentioned in Section 3.1 to obtain the ship’s position information. Then, the lat and the lon of the ship were respectively fitted with a third-order polynomial, as shown in Figure 5, where the moment T = 0 represents the starting moment of imaging, and T < 0 represents the moment before imaging. Additionally, the goodness of fit is shown in

Table 3. Goodness of fit results.

Data	Fit Type	SSE	R-Square	RMSE
Lat vs. T	Polynomial 3	$1.12101{\times 10}^{-5}$	0.999865121	$2.15227{\times 10}^{-4}$
Lon vs. T	Polynomial 3	$1.72693{\times 10}^{-5}$	0.999960823	$2.67135{\times 10}^{-4}$

. From the fitting results, the sum of squares due to error (SSE) and root-mean-squared error (RMSE) were very close to 0, and the coefficient of determination (R-square) was approximately equal to 1, meaning that the accuracy of fit is extremely high.

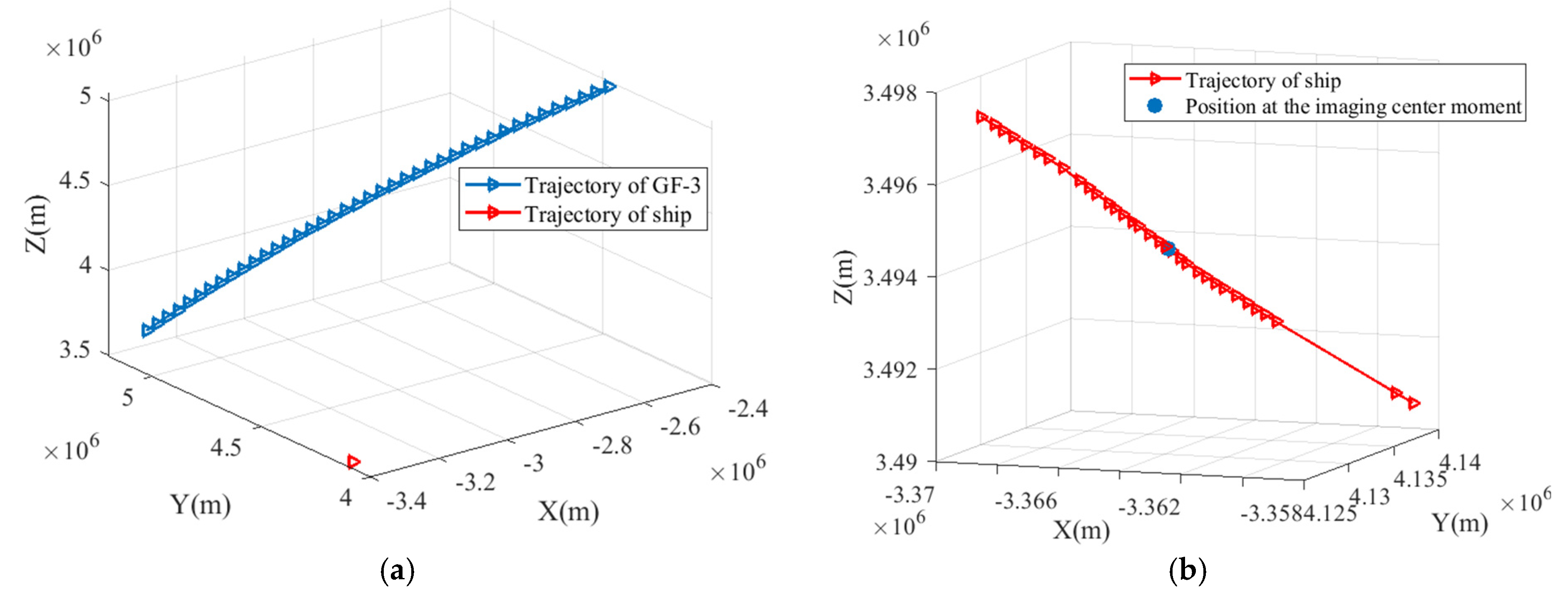
After fitting, the positions of the ship were converted to the WGS-84 coordinate system as suggested by Equation (18). The spatial positions of the GF-3 SAR platform and the ship in the WGS-84 coordinate system are shown in Figure 6a. Since the speed of the satellite is much higher than the speed of the ship, the ship is approximately stationary relative to the satellite in a short time. Thus, it is difficult to see the specific trajectory of the ship in Figure 6a. Additionally Figure 6b is an enlarged view of the ship trajectory in Figure 6a, where the blue point represents the position of the ship at the imaging center moment, that is, the position of the virtual stationary target.

Based on the methods mentioned in Section 3.2 and Section 3.3, the relative RV and relative RA at the imaging center moment were calculated, and the results were −6.39 m/s and 0.0496 m/s², respectively (the direction along the slant range direction was positive). Figure 7 shows the slant range, RV, and RA of the moving target and the virtual stationary target relative to the SAR platform, respectively.

The conventional method of estimating the RV based on AIS data is velocity projection (VP), which projects the SOG $V_t$ provided by the AIS data to the direction of the LOS to estimate the RV. Additionally, the relative RV can be calculated as:

$$V_r=\chi \cdot V_t\cdot cos\varphi \cdot sin\theta .$$

(32)

where $\varphi =\frac{\pi }{2}-\chi \left({\mathit{COG}}_{\mathit{proj}}-\mathit{LH}\right)$, ${\mathit{COG}}_{\mathit{proj}}$ indicates the angle between the course over ground (COG) of the ship and the SAR azimuth, $\mathit{LH}$ is the angle between the center of the beam and the zero Doppler line, and the $\theta$ represents the incidence of the radar beam. The $\chi$ is the indication coefficient. If the satellite is in orbit descending operation, $\chi =-1$, otherwise, $\chi =1$.

In Reference [24], the time-domain correlation (TDC) algorithm and maximum likelihood (ML)-based algorithm are compared in estimating the RV from dual-channel echoes. In this paper, we use SRD, VP, TDC, and ML-based algorithms to estimate the RV. The results and their corresponding relocation coordinates calculated by Equation (16) are shown in

Table 4. Results of RV estimation and relocation.

Algorithm	RV (m/s)	Position (x, y)
SRD	−6.39	(10,048, 9559)
VP	−6.31	(10,048, 9553)
TDC	−5.78	(10,048, 9515)
ML-based	−5.82	(10,048, 9517)

. It can be seen that the difference of RV between SRD and VP, which were calculated based on AIS data, was only 0.08 m/s. Additionally, the two results of TDC and ML-based algorithms, which were calculated from SAR raw data echo, were also very close, and the difference between them was only 0.04 m/s. However, there was a velocity error of about 0.5 m/s between the two different methods, which resulted in an error of about 36 pixels in azimuth. The relocation positions in Table 4 are depicted in Figure 8.

The position of the ship regarded as a stationary target at the imaging center moment on the SAR image was (10,048, 9092), that is, the position of the blue point in Figure 8. As suggested by the annotation of Figure 8, the position results of SRD and VP were closer to the ship than that of TDC and ML-based, which means that the RV estimation results of SRD and VP are more accurate. However, the VP algorithm only uses the AIS data of the ship at the imaging time, without considering the radial component of the flight velocity of the SAR platform, and it does not have the ability to calculate the RA either.

In terms of accuracy and stability, the SRD method is a better choice for estimating the relative RV.

4.2. False Target Suppression

The RV obtained by the SRD algorithm in Table 4 is used to compensate for the original echo, and the compensation method refers to [24]. The compensated echo is imaged again, and the results of false target suppression are shown in Figure 9.

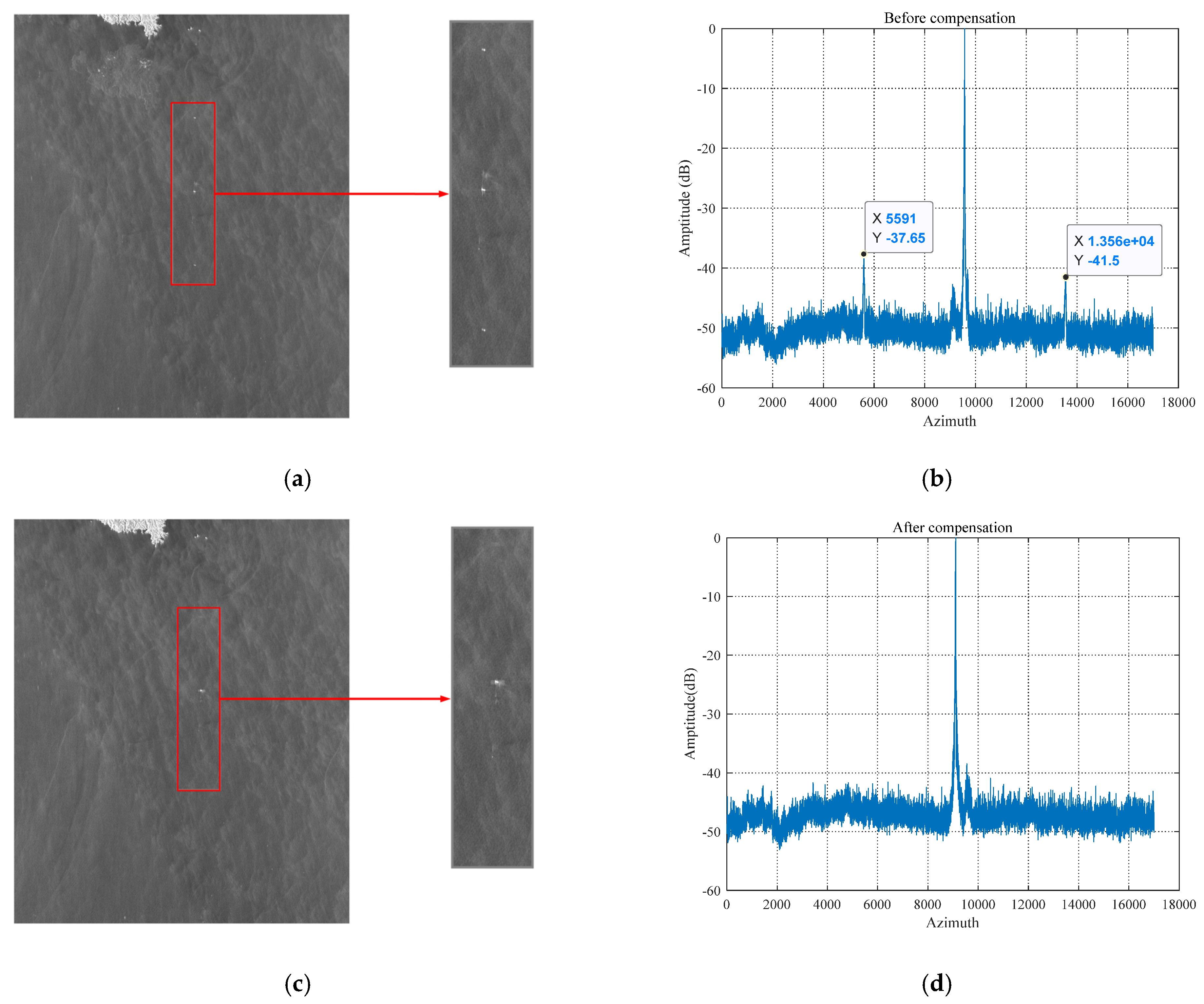
Generally, compared with the main target, the false target can be ignored when its intensity is lower than −40 dB [29]. Before the suppression, the ship target in the image has a pair of obvious false targets, as shown in Figure 9a. Perform statistical analysis on the image area marked by the red rectangle: take the maximum value of each row along the azimuth direction of the slice, and normalized. The image before compensation is shown in Figure 9b. It can be seen that there are two obvious side peaks caused by false targets. After compensation, as shown in Figure 9c, the false targets are invisible, and the real target is corrected to the actual azimuth position corresponding to the wake. Additionally the red rectangle in Figure 9c is analyzed in the same way, and the result is shown in Figure 9d. After compensation, the false targets are successfully suppressed at the same level as sea clutter and are much lower than −40 dB.

By compensating the echo according to the RV, the false targets are successfully suppressed, and the real target is also corrected to the true azimuth position. The results of false target suppression and azimuth offset correction also prove that the estimate of the RV is accurate, thus proving the reliability of the SRD algorithm.

4.3. RA Estimation and Azimuth Refocusing

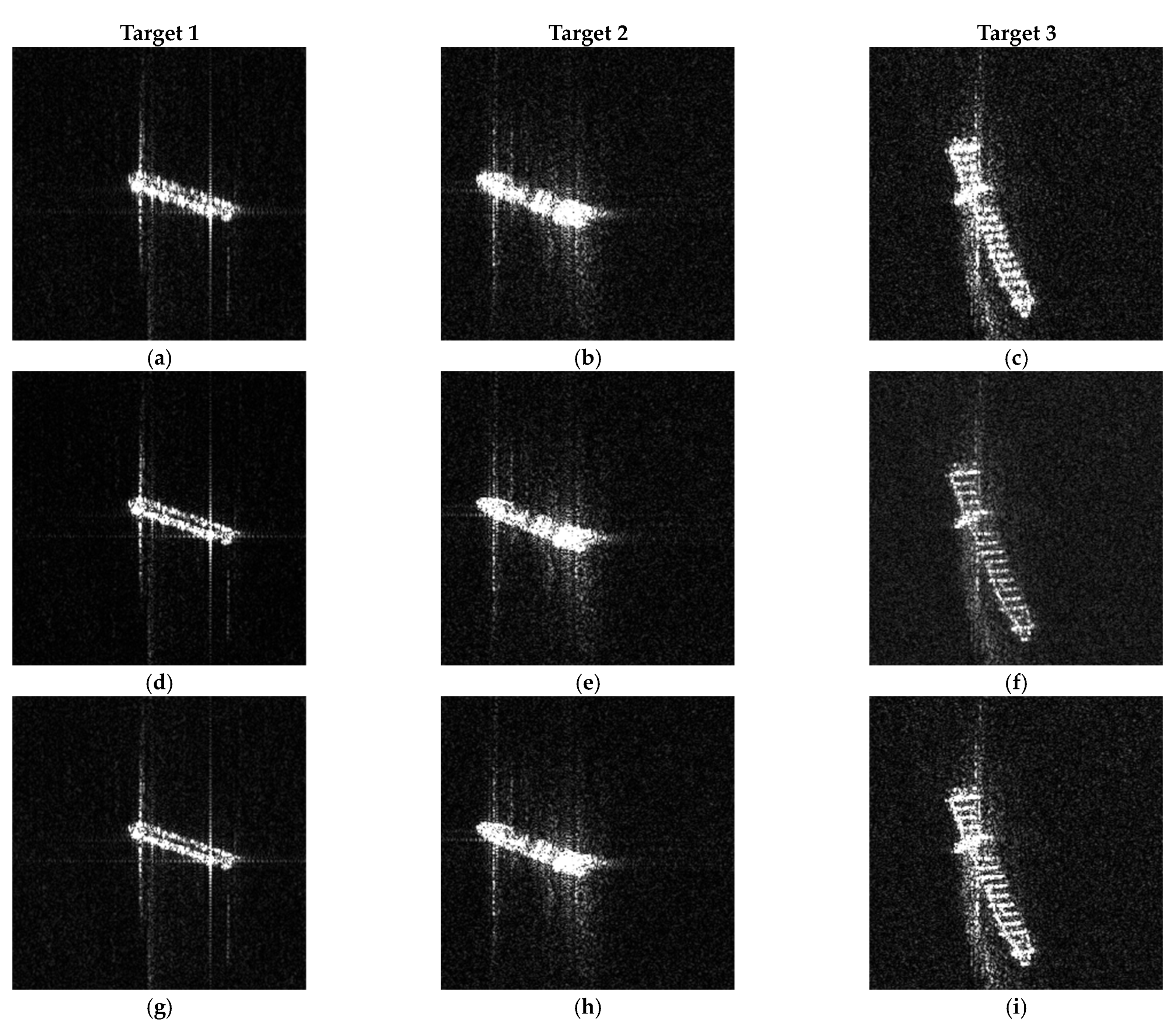
As the RA of the moving target and the stationary target are obtained, respectively, the Doppler rate error can be estimated according to Equation (28), and then the compensating Doppler rate error (CDRE) as suggested by Equation (31) can achieve refocusing. In addition to the ship mentioned above, named Target 1, there are two other ships in another UFS mode image with the same orbit number, named Target 2 and Target 3, respectively, also used for azimuth refocusing. The original slices, the results of CDRE, and the conventional autofocus method in [24] are compared in Figure 10.

Entropy is an essential criterion for measuring the quality of image focus, and the peak signal-to-noise ratio (PSNR) is the most common objective measurement to evaluate image quality. Here, the entropy and the PSNR of the slice are regarded as evaluation indicators to compare the focusing effects of the two methods. If the defocused image is focused, the entropy decreases, and the PSNR increases. The results of CDRE are compared with the autofocus method in

Table 5. The analysis of the Figure 10.

Target	Number	PSNR(dB)	Entropy
Target 1	(a)	57.2958	0.31602
	(d)	59.1419	0.24085
	(g)	58.8588	0.25446
Target 2	(b)	51.9702	0.78291
	(e)	51.2988	0.73133
	(h)	52.0951	0.71665
Target 3	(c)	38.2393	2.2692
	(f)	39.5554	2.0946
	(i)	39.9511	2.0912

. According to the experimental results, it can be seen that the method in this article can achieve the same or better effect compared with the autofocus method. Besides, the computational complexity of the CDRE method is far lower than the autofocus method. The central processing unit (CPU) used in this experiment is Intel(R) Core (TM) i5-9300H and the software used is MATLAB. With the RA known, it only takes 0.080503 s to refocus target 1 with the CDRE method, whereas the autofocus method takes 0.339980 s under the premise of setting the required parameters. Moreover, the CDRE method is more robust. The autofocus method may decrease the overall image amplitude value causing the image to darken, as shown in Figure 10, but the CDRE method does not have such a problem.

In summary, the compensation method in this paper can indeed achieve refocusing, and in the case of uncomplicated sea conditions, both the method proposed in this paper and the traditional autofocus method can achieve good results, but our method is more efficient.

5. Discussion

In Section 4, a comprehensive experiment is conducted to illustrate the effectiveness of the proposed SRD algorithm. In the RV estimation, the difference between the results of the SRD algorithm and the other three methods was within 0.61 m/s, and from the relocation results of Figure 8, the SRD algorithm and VP algorithm were more accurate than the ML-based and TDC algorithm with lower computational complexity. Besides, the SRD algorithm uses the AIS position information for a long period, whereas the VP algorithm only uses the velocity and heading information at the imaging center moment, and the VP algorithm only considers the motion of the ship without considering the radial component of the flight velocity of the SAR platform. Thus, the SRD algorithm is more robust than the VP algorithm.

From the experimental results in Figure 9, it can be seen that according to the RV calculated by the SRD algorithm, the false targets were suppressed to the clutter level and were invisible on the image after compensating the echo. This also confirms the accuracy of the SRD algorithm and the feasibility of using AIS information to suppress false targets.

In Section 4.3, the RA can be obtained by the SRD algorithm, and then the residual phase errors are calculated. The traditional autofocus method and CDRE algorithm were conducted to refocus the three ship slices, respectively. As suggested by Figure 10, the method in this article can achieve the same or better effect compared with the traditional autofocus method. Moreover, the CDRE algorithm does not change the image amplitude, and the computational complexity is much lower than that of the traditional method.

In terms of effectiveness and computational complexity, the methods proposed in this article are superior to the traditional methods, and if the ship is not obvious on the SAR image due to its size beingtoo small, it can be detected by positioning with AIS data, and the image quality of it can be improved with the scheme in the article, which is also an advantage over the traditional ship detection method. However, the scheme proposed in this paper is not suitable for the ship’s shaking caused by strong wind and sea waves, and the stability of AIS data has a great influence on the experiment. Even if the AIS data are preprocessed, only individual abnormal data can be eliminated. Only when most of the AIS data are stable can the reliability of the results be guaranteed. In the case of a dense ship, such as a port, the AIS data between ships may collide or interfere. In this situation, further processing of the AIS data is needed, but the AIS data processing is not the focus of this article, and it is not discussed too much here. The scheme proposed in this paper can not only improve the imaging quality of moving ships, but also improve the matching accuracy of the ship and AIS data, which can be used to make data sets for ship detection and identification. Further research will be conducted in the future.

6. Conclusions

A novel scheme is proposed in this paper to improve the imaging quality of the moving ship based on simultaneous AIS information for the first time. The main impact of the moving ship is to cause Doppler spectrum different from that of the static target, leading to the azimuth position offset, false targets, and defocus. This article innovatively proposes the SRD algorithm in Section 3 to calculate the RV and RA of the moving ship by introducing the virtual stationary target. The RV can be used to correct the azimuth position offset and suppress the false targets. In the same way, the RA between the ship and the stationary target is calculated and the residual error of the azimuth Doppler rate can also be obtained, and the CDRE algorithm is proposed to solve azimuth defocusing resulting from the target motion in Section 3.3. The real data are adopted to illustrate the effectiveness of the proposed methods in Section 4. Compared with the classical methods, the proposed scheme can achieve better image quality improvement with lower computational complexity.