Industrial Plume Properties Retrieved by Optimal Estimation Using Combined Hyperspectral and Sentinel-2 Data
Abstract
1. Introduction
2. Methods
2.1. Theory
2.2. Definition of the Optimal Estimation Method
2.3. Forward Model Definition and State Vectors
2.4. Forward Model Initialization: First Guess
2.5. Sensitivity Analysis
3. Data
3.1. Airborne Hyperspectral Data
3.2. Sentinel-2 Products
4. Results
4.1. Atmospheric Correction
4.2. Image Classification
4.3. Surface Reflectance
4.4. Plume Segmentation Using CTMF
4.5. Plume Properties’ Initialisation
4.6. Results of the Optimal Estimation Method
5. Discussion
5.1. Retrieved Modal Radius
5.2. Ground Reflectance Estimation and OEM
5.3. Model Assumptions and Uncertainties
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- World Health Organization. Health Risks of Particulate Matter from Long-Range Transboundary Air Pollution; World Health Organization: Geneva, Switzerland, 2006. [Google Scholar]
- Burnett, R.; Chen, H.; Szyszkowicz, M.; Fann, N.; Hubbell, B.; Pope, C.A.; Apte, J.S.; Brauer, M.; Cohen, A.; Weichenthal, S.; et al. Global Estimates of Mortality Associated with Long-term Exposure to Outdoor Fine Particulate Matter. Proc. Natl. Acad. Sci. USA 2018, 115, 9592–9597. [Google Scholar] [CrossRef]
- National Emissions Reported to the Convention on Long-Range Transboundary Air Pollution (LRTAP Convention)—European Environment Agency. Available online: https://www.eea.europa.eu/data-and-maps/data/national-emissions-reported-to-the-convention-on-long-range-transboundary-air-pollution-lrtap-convention-14 (accessed on 14 December 2020).
- European Environment Agency. EMEP/EEA Air Pollutant Emission Inventory Guidebook 2019: Technical Guidance to Prepare National Emission Inventories; European Environment Agency: Copenhagen, Denmark, 2019.
- Andre, J.M.; Barrault, S.; Bongrand, G.; Bort, R.; Cuniasse, B.; Druart, A.; Durand, A.; Feutren, E.; Gavel, A.; Glass, T.; et al. Rapport Ominea, 16th ed.; Technical Report; 2019. Available online: https://www.citepa.org/fr/ominea/ (accessed on 8 May 2021).
- Amaral, S.; de Carvalho, J.; Costa, M.; Pinheiro, C. An Overview of Particulate Matter Measurement Instruments. Atmosphere 2015, 6, 1327–1345. [Google Scholar] [CrossRef]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Atmospheric and Oceanographic Sciences Library; Springer: Dordrecht, The Netherlands, 1988. [Google Scholar] [CrossRef]
- Gordon, M.; Makar, P.A.; Staebler, R.M.; Zhang, J.; Akingunola, A.; Gong, W.; Li, S.M. A Comparison of Plume Rise Algorithms to Stack Plume Measurements in the Athabasca Oil Sands. Atmos. Chem. Phys. 2018, 18, 14695–14714. [Google Scholar] [CrossRef]
- Alakian, A.; Marion, R.; Briottet, X. Retrieval of Microphysical and Optical Properties in Aerosol Plumes with Hyperspectral Imagery: L-APOM Method. Remote Sens. Environ. 2009, 113, 781–793. [Google Scholar] [CrossRef]
- Philippets, Y.; Foucher, P.Y.; Marion, R.; Briottet, X. Anthropogenic Aerosol Emissions Mapping and Characterization by Imaging Spectroscopy–Application to a Metallurgical Industry and a Petrochemical Complex. Int. J. Remote Sens. 2018, 40, 364–406. [Google Scholar] [CrossRef]
- Foucher, P.Y.; Deliot, P.; Poutier, L.; Duclaux, O.; Raffort, V.; Roustan, Y.; Temime-Roussel, B.; Durand, A.; Wortham, H. Aerosol Plume Characterization from Multitemporal Hyperspectral Analysis. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2429–2438. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Sendra, C. Algorithm for Automatic Atmospheric Corrections to Visible and Near-IR Satellite Imagery. Int. J. Remote Sens. 1988, 9, 1357–1381. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Tanré, D.; Gordon, H.R.; Nakajima, T.; Lenoble, J.; Frouin, R.; Grassl, H.; Herman, B.M.; King, M.D.; Teillet, P.M. Passive Remote Sensing of Tropospheric Aerosol and Atmospheric Correction for the Aerosol Effect. J. Geophys. Res. Atmos. 1997, 102, 16815–16830. [Google Scholar] [CrossRef]
- Levy, R.C.; Remer, L.A.; Kleidman, R.G.; Mattoo, S.; Ichoku, C.; Kahn, R.; Eck, T.F. Global Evaluation of the Collection 5 MODIS Dark-target Aerosol Products Over Land. Atmos. Chem. Phys. 2010, 10, 10399–10420. [Google Scholar] [CrossRef]
- Remer, L.A.; Levy, R.C.; Mattoo, S.; Tanré, D.; Gupta, P.; Shi, Y.; Sawyer, V.; Munchak, L.A.; Zhou, Y.; Kim, M.; et al. The Dark Target Algorithm for Observing the Global Aerosol System: Past, Present, and Future. Remote Sens. 2020, 12, 2900. [Google Scholar] [CrossRef]
- Hsu, N.; Tsay, S.C.; King, M.; Herman, J. Aerosol Properties Over Bright-Reflecting Source Regions. IEEE Trans. Geosci. Remote Sens. 2004, 42, 557–569. [Google Scholar] [CrossRef]
- Hsu, N.; Tsay, S.C.; King, M.; Herman, J. Deep Blue Retrievals of Asian Aerosol Properties during ACE-asia. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3180–3195. [Google Scholar] [CrossRef]
- Sayer, A.M.; Hsu, N.C.; Lee, J.; Kim, W.V.; Dutcher, S.T. Validation, Stability, and Consistency of MODIS Collection 6.1 and VIIRS Version 1 Deep Blue Aerosol Data Over Land. J. Geophys. Res. Atmos. 2019, 124, 4658–4688. [Google Scholar] [CrossRef]
- Thomas, G.E.; Poulsen, C.A.; Sayer, A.M.; Marsh, S.H.; Dean, S.M.; Carboni, E.; Siddans, R.; Grainger, R.G.; Lawrence, B.N. The GRAPE Aerosol Retrieval Algorithm. Atmos. Meas. Tech. 2009, 2, 679–701. [Google Scholar] [CrossRef]
- Dubovik, O.; Herman, M.; Holdak, A.; Lapyonok, T.; Tanré, D.; Deuzé, J.L.; Ducos, F.; Sinyuk, A.; Lopatin, A. Statistically Optimized Inversion Algorithm for Enhanced Retrieval of Aerosol Properties from Spectral Multi-Angle Polarimetric Satellite Observations. Atmos. Meas. Tech. 2011, 4, 975–1018. [Google Scholar] [CrossRef]
- Wurl, D.; Grainger, R.G.; McDonald, A.J.; Deshler, T. Optimal Estimation Retrieval of Aerosol Microphysical Properties from SAGE~II Satellite Observations in the Volcanically Unperturbed Lower Stratosphere. Atmos. Chem. Phys. 2010, 10, 4295–4317. [Google Scholar] [CrossRef]
- Zheng, F.; Hou, W.; Sun, X.; Li, Z.; Hong, J.; Ma, Y.; Li, L.; Li, K.; Fan, Y.; Qiao, Y. Optimal Estimation Retrieval of Aerosol Fine-Mode Fraction from Ground-Based Sky Light Measurements. Atmosphere 2019, 10, 196. [Google Scholar] [CrossRef]
- Govaerts, Y.M.; Wagner, S.; Lattanzio, A.; Watts, P. Joint retrieval of surface reflectance and aerosol optical depth from MSG/SEVIRI observations with an optimal estimation approach: 1. Theory. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Thompson, D.R.; Natraj, V.; Green, R.O.; Helmlinger, M.C.; Gao, B.C.; Eastwood, M.L. Optimal Estimation for Imaging Spectrometer Atmospheric Correction. Remote Sens. Environ. 2018, 216, 355–373. [Google Scholar] [CrossRef]
- Thompson, D.R.; Babu, K.; Braverman, A.J.; Eastwood, M.L.; Green, R.O.; Hobbs, J.M.; Jewell, J.B.; Kindel, B.; Massie, S.; Mishra, M.; et al. Optimal Estimation of Spectral Surface Reflectance in Challenging Atmospheres. Remote Sens. Environ. 2019, 232, 111258. [Google Scholar] [CrossRef]
- Hou, W.; Wang, J.; Xu, X.; Reid, J.S.; Han, D. An Algorithm for Hyperspectral Remote Sensing of Aerosols: 1. Development of Theoretical Framework. J. Quant. Spectrosc. Radiat. Transf. 2016, 178, 400–415. [Google Scholar] [CrossRef]
- Hou, W.; Wang, J.; Xu, X.; Reid, J.S. An Algorithm for Hyperspectral Remote Sensing of Aerosols: 2. Information Content Analysis for Aerosol Parameters and Principal Components of Surface Spectra. J. Quant. Spectrosc. Radiat. Transf. 2017, 192, 14–29. [Google Scholar] [CrossRef]
- Rodgers, C.D. Inverse Methods for Atmospheric Sounding; World Scientific: Singapore, 2000. [Google Scholar] [CrossRef]
- Kangah, K.G.Y. Measurement of Nitrous Oxide (N2O) from Space. Ph.D. Thesis, Université Paul Sabatier-Toulouse III, Toulouse, France, 2017. [Google Scholar]
- Hurtmans, D.; Coheur, P.F.; Wespes, C.; Clarisse, L.; Scharf, O.; Clerbaux, C.; Hadji-Lazaro, J.; George, M.; Turquety, S. FORLI Radiative Transfer and Retrieval Code for IASI. J. Quant. Spectrosc. Radiat. Transf. 2012, 113, 1391–1408. [Google Scholar] [CrossRef]
- Barret, B.; Flochmoen, E.L.; Sauvage, B.; Pavelin, E.; Matricardi, M.; Cammas, J.P. The Detection of Post-monsoon Tropospheric Ozone Variability Over South Asia Using IASI Data. Atmos. Chem. Phys. 2011, 11, 9533–9548. [Google Scholar] [CrossRef]
- Yoshida, Y.; Ota, Y.; Eguchi, N.; Kikuchi, N.; Nobuta, K.; Tran, H.; Morino, I.; Yokota, T. Retrieval Algorithm for CO2 and CH4 Column Abundances from Short-wavelength Infrared Spectral Observations by the Greenhouse Gases Observing Satellite. Atmos. Meas. Tech. 2011, 4, 717–734. [Google Scholar] [CrossRef]
- Hagolle, O.; Huc, M.; Desjardins, C.; Auer, S.; Richter, R. Maja Algorithm Theoretical Basis Document. 2017. Available online: https://doi.org/10.5281/ZENODO.1209633 (accessed on 8 May 2021).
- Dubovik, O.; Lapyonok, T.; Litvinov, P.; Herman, M.; Fuertes, D.; Ducos, F.; Torres, B.; Derimian, Y.; Huang, X.; Lopatin, A.; et al. GRASP: A Versatile Algorithm for Characterizing the Atmosphere. SPIE Newsroom 2014. [Google Scholar] [CrossRef]
- Qu, Z.; Kindel, B.; Goetz, A. The High Accuracy Atmospheric Correction for Hyperspectral Data (hatch) Model. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1223–1231. [Google Scholar] [CrossRef]
- Adler-Golden, S.M.; Matthew, M.W.; Bernstein, L.S.; Levine, R.Y.; Berk, A.; Richtsmeier, S.C.; Acharya, P.K.; Anderson, G.P.; Felde, J.W.; Gardner, J.A.; et al. Atmospheric Correction for Shortwave Spectral Imagery Based on MODTRAN4; Descour, M.R., Shen, S.S., Eds.; Imaging Spectrometry V; SPIE: Bellingham, WA, USA, 1999. [Google Scholar] [CrossRef]
- Staenz, K.; Szeredi, T.; Schwarz, J. ISDAS—A System for Processing/analyzing Hyperspectral Data. Can. J. Remote Sens. 1998, 24, 99–113. [Google Scholar] [CrossRef]
- Richter, R. Atmospheric Correction of DAIS Hyperspectral Image Data. Comput. Geosci. 1996, 22, 785–793. [Google Scholar] [CrossRef]
- Richter, R. Correction of Satellite Imagery Over Mountainous Terrain. Appl. Opt. 1998, 37, 4004. [Google Scholar] [CrossRef]
- Richter, R.; Schläpfer, D. Geo-atmospheric Processing of Airborne Imaging Spectrometry Data. Part 2: Atmospheric/topographic Correction. Int. J. Remote Sens. 2002, 23, 2631–2649. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Radiative Transfer; Dover Publications: New York, NY, USA, 1960. [Google Scholar]
- Alakian, A.; Marion, R.; Briottet, X. Remote Sensing of Aerosol Plumes: A Semianalytical Model. Appl. Opt. 2008, 47, 1851. [Google Scholar] [CrossRef]
- Poutier, L.; Miesch, C.; Lenot, X.; Achard, V.; Boucher, Y. COMANCHE and COCHISE: Two reciprocal atmospheric codes for hyperspectral remote sensing. In Proceedings of the 2002 AVIRIS Earth Science and Applications Workshop Proceedings, Pasadena, CA, USA, 5–8 March 2002. [Google Scholar]
- Berk, A.; Conforti, P.; Kennett, R.; Perkins, T.; Hawes, F.; van den Bosch, J. MODTRAN® 6: A Major Upgrade of the MODTRAN® Radiative Transfer Code. In Proceedings of the 2014 6th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Lausanne, Switzerland, 24–27 June 2014. [Google Scholar] [CrossRef]
- Ångström, A. On the Atmospheric Transmission of Sun Radiation and on Dust in the Air. Geogr. Ann. 1929, 11, 156–166. [Google Scholar] [CrossRef]
- QGIS Development Team. QGIS Geographic Information System. Open Source Geospatial Foundation. 2020. Available online: http://qgis.osgeo.org (accessed on 12 March 2021).
- Eismann, M.T.; Hardie, R.C. Resolution enhancement of hyperspectral imagery using coincident panchromatic imagery and a stochastic mixing model. In Proceedings of the IEEE Workshop on Advances in Techniques for Analysis of Remotely Sensed Data, Greenbelt, MD, USA, 27–28 October 2003; pp. 282–289. [Google Scholar] [CrossRef]
- Lanaras, C.; Baltsavias, E.; Schindler, K. Hyperspectral Super-resolution by Coupled Spectral Unmixing. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015. [Google Scholar] [CrossRef]
- Simoes, M.; Bioucas-Dias, J.; Almeida, L.B.; Chanussot, J. A Convex Formulation for Hyperspectral Image Superresolution Via Subspace-based Regularization. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3373–3388. [Google Scholar] [CrossRef]
- Wei, Q.; Dobigeon, N.; Tourneret, J.Y. Fast Fusion of Multi-band Images Based on Solving a Sylvester Equation. IEEE Trans. Image Process. 2015, 24, 4109–4121. [Google Scholar] [CrossRef]
- Yokoya, N.; Yairi, T.; Iwasaki, A. Coupled Nonnegative Matrix Factorization Unmixing for Hyperspectral and Multispectral Data Fusion. IEEE Trans. Geosci. Remote Sens. 2012, 50, 528–537. [Google Scholar] [CrossRef]
- Nascimento, J.; Dias, J. Vertex Component Analysis: A Fast Algorithm to Unmix Hyperspectral Data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 898–910. [Google Scholar] [CrossRef]
- Liu, X.; Xia, W.; Wang, B.; Zhang, L. An Approach Based on Constrained Nonnegative Matrix Factorization to Unmix Hyperspectral Data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 757–772. [Google Scholar] [CrossRef]
- Lee, D.D.; Seung, H.S. Learning the Parts of Objects by Non-negative Matrix Factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef]
- Funk, C.C.; Theiler, J.; Roberts, D.A.; Borel, C.C. Clustering to Improve Matched Filter Detection of Weak Gas Plumes in Hyperspectral Thermal Imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1410–1420. [Google Scholar] [CrossRef]
- Thorpe, A.K.; Roberts, D.A.; Dennison, P.E.; Bradley, E.S.; Funk, C.C. Point Source Emissions Mapping Using the Airborne Visible/infrared Imaging Spectrometer (AVIRIS). In Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XVIII; Shen, S.S., Lewis, P.E., Eds.; SPIE: Bellingham, WA, USA, 2012. [Google Scholar] [CrossRef]
- Thorpe, A.; Frankenberg, C.; Aubrey, A.; Roberts, D.; Nottrott, A.; Rahn, T.; Sauer, J.; Dubey, M.; Costigan, K.; Arata, C.; et al. Mapping Methane Concentrations from a Controlled Release Experiment Using the Next Generation Airborne Visible/infrared Imaging Spectrometer (AVIRIS-NG). Remote Sens. Environ. 2016, 179, 104–115. [Google Scholar] [CrossRef]
- Dennison, P.E.; Thorpe, A.K.; Pardyjak, E.R.; Roberts, D.A.; Qi, Y.; Green, R.O.; Bradley, E.S.; Funk, C.C. High Spatial Resolution Mapping of Elevated Atmospheric Carbon Dioxide Using Airborne Imaging Spectroscopy: Radiative Transfer Modeling and Power Plant Plume Detection. Remote Sens. Environ. 2013, 139, 116–129. [Google Scholar] [CrossRef]
- Institut Géographique National. Géoservices|Pourquoi #ChoisirGéoportail? Available online: https://geoservices.ign.fr/documentation/ (accessed on 16 December 2020).
- Brigot, G.; Colin-Koeniguer, E.; Plyer, A.; Janez, F. Adaptation and Evaluation of an Optical Flow Method Applied to Coregistration of Forest Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2923–2939. [Google Scholar] [CrossRef]
- Plyer, A.; Colin-Koeniguer, E.; Weissgerber, F. A New Coregistration Algorithm for Recent Applications on Urban SAR Images. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2198–2202. [Google Scholar] [CrossRef]
- Hagolle, O.; Huc, M.; Pascual, D.V.; Dedieu, G. A Multi-temporal and Multi-spectral Method to Estimate Aerosol Optical Thickness Over Land, for the Atmospheric Correction of FormoSat-2, LandSat, VENμs and Sentinel-2 Images. Remote Sens. 2015, 7, 2668–2691. [Google Scholar] [CrossRef]
- THEIA-LAND. Available online: https://www.theia-land.fr/pole-theia-2/infrastructure-de-donnees-et-de-services-ids/muscate-2/ (accessed on 16 March 2021).
- Kruse, F.; Lefkoff, A.; Boardman, J.; Heidebrecht, K.; Shapiro, A.; Barloon, P.; Goetz, A. The spectral image processing system (SIPS)—interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
- Leoni, C.; Hovorka, J.; Dočekalová, V.; Cajthaml, T.; Marvanová, S. Source Impact Determination Using Airborne and Ground Measurements of Industrial Plumes. Environ. Sci. Technol. 2016, 50, 9881–9888. [Google Scholar] [CrossRef]
- Deschamps, A. Industrial Plume Characterization Using Hyperspectral Imagery. Ph.D. Thesis, Université Pierre et Marie Curie-Paris VI, Paris, France, 2012. [Google Scholar]
- Marris, H.; Deboudt, K.; Augustin, P.; Flament, P.; Blond, F.; Fiani, E.; Fourmentin, M.; Delbarre, H. Fast changes in chemical composition and size distribution of fine particles during the near-field transport of industrial plumes. Sci. Total Environ. 2012, 427–428, 126–138. [Google Scholar] [CrossRef]
- Ehrlich, C.; Noll, G.; Kalkoff, W.; Baumbach, G.; Dreiseidler, A. PM10, PM2.5 and PM1.0—Emissions from industrial plants—Results from measurement programmes in Germany. Atmos. Environ. 2007, 41, 6236–6254. [Google Scholar] [CrossRef]
- Pignatti, S.; Palombo, A.; Pascucci, S.; Romano, F.; Santini, F.; Simoniello, T.; Umberto, A.; Vincenzo, C.; Acito, N.; Diani, M.; et al. The PRISMA hyperspectral mission: Science activities and opportunities for agriculture and land monitoring. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium-IGARSS, Melbourne, Australia, 21–26 July 2013; pp. 4558–4561. [Google Scholar] [CrossRef]

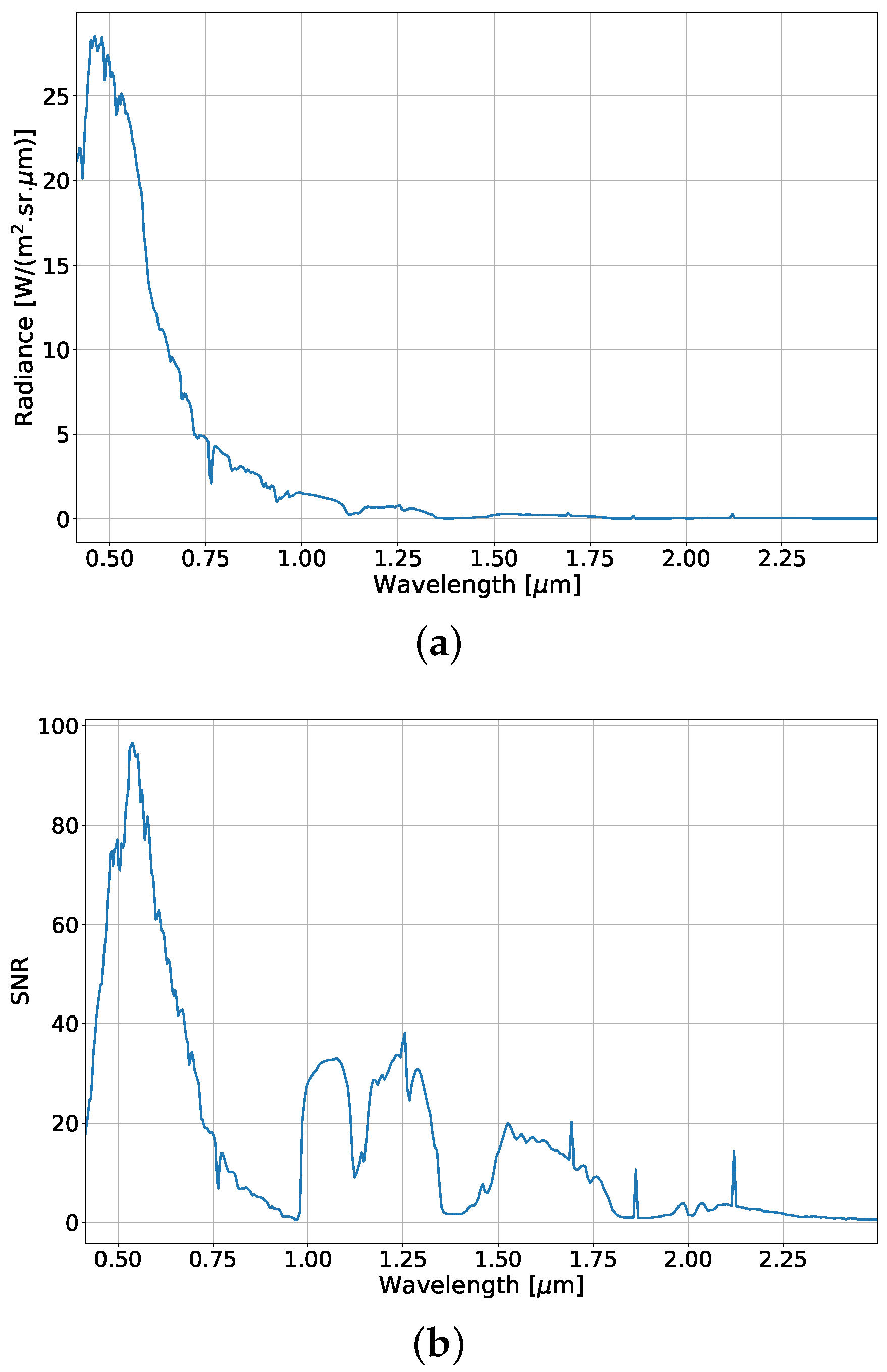




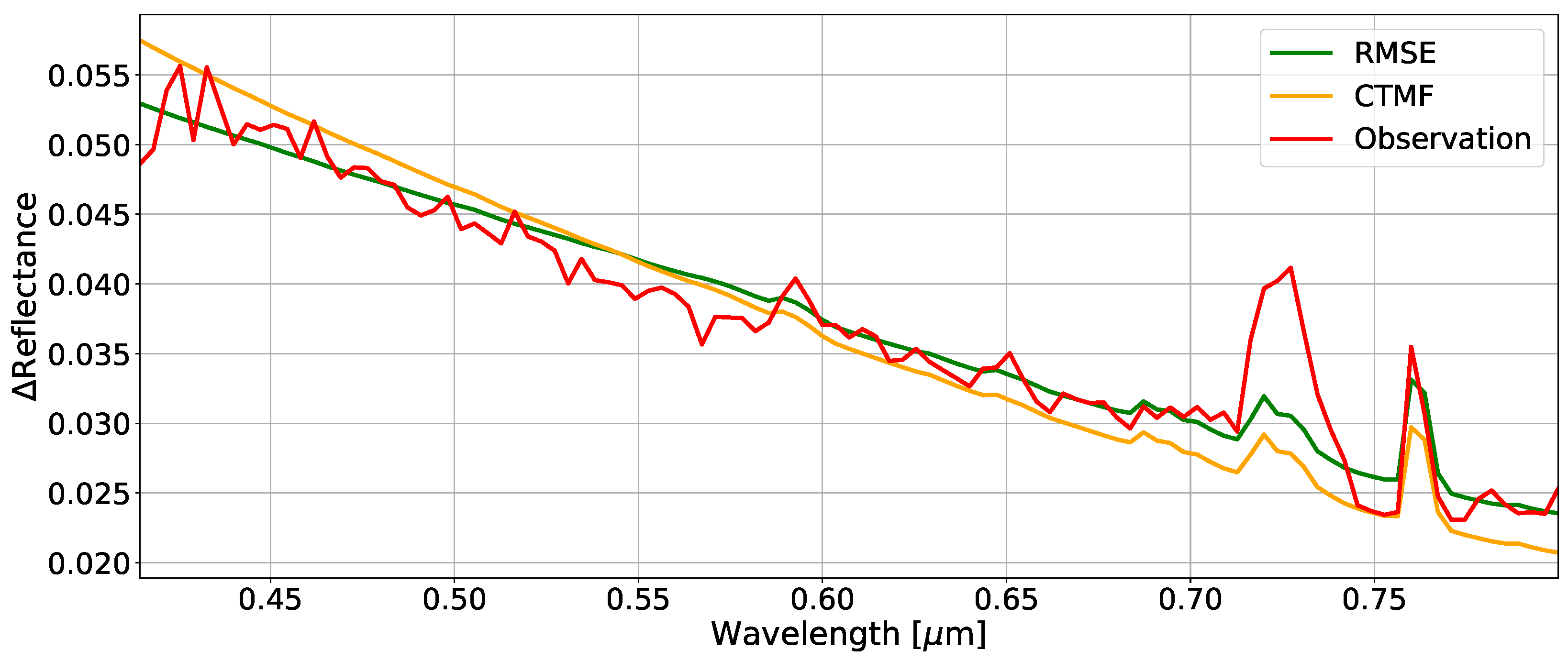
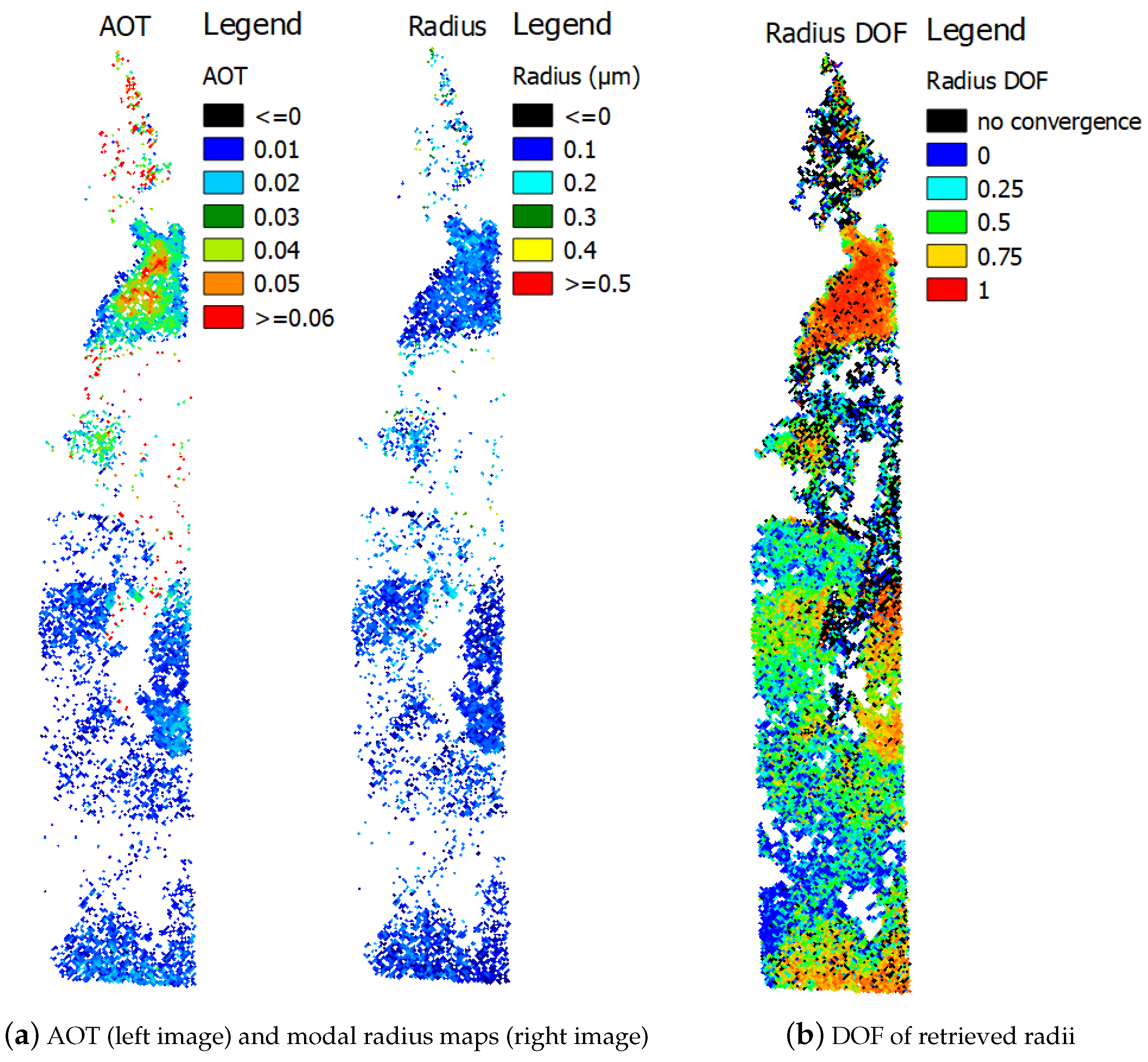

| Type | Real Part | Imag. Part |
|---|---|---|
| Brown carbon | 1.55 | |
| Sulphate | 1.52 | |
| Soot | 1.83 | 0.74 |
| Å | HO | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 5 km | 10% | 5% | 1.0 | 0.2 | 5% | 10% | 10% | 0.01 | |
| 0.0035 | 0.0044 | 0.0003 | 0.0066 | 0.0012 | 0.0082 | 0.0036 | 0.0038 | 0.012 | |
| 0.0011 | 0.0122 | 0.0226 | 0.0114 | 0.0008 | 0.0147 | 0.0450 | 0.0070 | 0.014 |
| Classes | HYSPEX Alone | HYSPEX + MSI | ||
|---|---|---|---|---|
| RMSE | SAM | RMSE | SAM | |
| Water | 0.0054 | 6.68 | 0.0057 | 6.10 |
| Sparse vegetation | 0.0426 | 14.06 | 0.0304 | 9.13 |
| Dense vegetation | 0.0414 | 7.55 | 0.0393 | 7.79 |
| Concrete soils | 0.0711 | 10.94 | 0.0473 | 7.60 |
| Dark soils | 0.0337 | 19.51 | 0.0267 | 14.28 |
| Bright soils | 0.1139 | 9.93 | 0.1040 | 7.53 |
| Classes | AOT | Radius (m) | ||
|---|---|---|---|---|
| CTMF | RMSE | CTMF | RMSE | |
| Water | 0.012 | 0.011 | 0.488 | 0.112 |
| Dense vegetation | 0.028 | 0.027 | 0.296 | 0.268 |
| Sparse vegetation | 0.029 | 0.026 | 0.346 | 0.357 |
| Concrete soils | 0.046 | 0.039 | 0.354 | 0.285 |
| Dark soils | 0.023 | 0.021 | 0.217 | 0.182 |
| Bright soils | 0.095 | 0.072 | 0.510 | 0.286 |
| Classes | Radius (m) | |
|---|---|---|
| OEM | Initial Guess | |
| Water | 0.118 | 0.137 |
| Dense vegetation | 0.151 | 0.197 |
| Sparse vegetation | 0.231 | 0.285 |
| Concrete soils | 0.184 | 0.341 |
| Dark soils | 0.158 | 0.208 |
| Bright soils | 0.263 | 0.423 |
| Classes | AOT | Radius (m) | ||||
|---|---|---|---|---|---|---|
| Water | 0.003 | 0.003 | 0.001 | 0.049 | 0.038 | 0.031 |
| Dense vegetation | 0.004 | 0.003 | 0.003 | 0.064 | 0.037 | 0.052 |
| Sparse vegetation | 0.005 | 0.003 | 0.004 | 0.051 | 0.030 | 0.042 |
| Concrete soils | 0.007 | 0.003 | 0.006 | 0.048 | 0.019 | 0.044 |
| Dark soils | 0.005 | 0.002 | 0.004 | 0.053 | 0.030 | 0.041 |
| Bright soils | 0.013 | 0.006 | 0.011 | 0.057 | 0.022 | 0.054 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Calassou, G.; Foucher, P.-Y.; Léon, J.-F. Industrial Plume Properties Retrieved by Optimal Estimation Using Combined Hyperspectral and Sentinel-2 Data. Remote Sens. 2021, 13, 1865. https://doi.org/10.3390/rs13101865
Calassou G, Foucher P-Y, Léon J-F. Industrial Plume Properties Retrieved by Optimal Estimation Using Combined Hyperspectral and Sentinel-2 Data. Remote Sensing. 2021; 13(10):1865. https://doi.org/10.3390/rs13101865
Chicago/Turabian StyleCalassou, Gabriel, Pierre-Yves Foucher, and Jean-François Léon. 2021. "Industrial Plume Properties Retrieved by Optimal Estimation Using Combined Hyperspectral and Sentinel-2 Data" Remote Sensing 13, no. 10: 1865. https://doi.org/10.3390/rs13101865
APA StyleCalassou, G., Foucher, P.-Y., & Léon, J.-F. (2021). Industrial Plume Properties Retrieved by Optimal Estimation Using Combined Hyperspectral and Sentinel-2 Data. Remote Sensing, 13(10), 1865. https://doi.org/10.3390/rs13101865







