Abstract
The Lunar Penetrating Radar (LPR) onboard the Yutu-2 rover from China’s Chang’E-4 (CE-4) mission is used to probe the subsurface structure and the near-surface stratigraphic structure of the lunar regolith on the farside of the Moon. Structural analysis of regolith could provide abundant information on the formation and evolution of the Moon, in which the rock location and property analysis are the key procedures during the interpretation of LPR data. The subsurface velocity of electromagnetic waves is a vital parameter for stratigraphic division, rock location estimates, and calculating the rock properties in the interpretation of LPR data. In this paper, we propose a procedure that combines the regolith rock extraction technique based on local correlation between the two sets of LPR high-frequency channel data and the common offset semblance analysis to determine the velocity from LPR diffraction hyperbola. We consider the heterogeneity of the regolith and derive the relative permittivity distribution based on the rock extraction and semblance analysis. The numerical simulation results show that the procedure is able to obtain the high-precision position and properties of the rock. Furthermore, we apply this procedure to CE-4 LPR data and obtain preferable estimations of the rock locations and the properties of the lunar subsurface regolith.
1. Introduction
The surface of the Moon is covered by regolith, which records at least a 4-billion-year history of meteoroid impacts and implantation of solar wind. The thickness of the regolith varies from about 2 m beneath the lunar maria to more than 10 m beneath the lunar highland, respectively, which is correlated with the age of the lunar surface [1]. The estimation of regolith thickness usually uses indirect measurements including seismic experiments [2], microwave remote sensing [3], and impact crater morphology and frequency distribution of the crater diameters [4]. Unlike the Apollo Lunar Sounder Experiment [5] and Lunar Radar Sounder [6], Chang’E-3 conducted the first in situ Lunar Penetrating Radar (LPR) exploration with a wide frequency band and high spatial resolution in the Imbrium basin, showing the detailed structure of lunar regolith [7,8]. In addition, Chang’E-4 (CE-4) is conducting the first in situ exploration on the farside of the Moon in the Von Kármán crater at the South Pole-Aitken (SPA) basin [9,10].
The LPR aboard on the Yutu-2 Rover of CE-4 is a nanosecond imaging radar which is carrier-free and operates in the time domain [11], and has two channels (CH-1 and CH-2) with center frequencies at 60 and 500 MHz, respectively [10]. CH-1 is used to map the structure of the shallow lunar crust with meter-level resolution and the CH-2 is used to detect the structure of regolith with a depth resolution of 0.3 m, which contains one transmitting antenna and two receiving antennas of different offsets—namely, CH-2A and CH-2B [12]. The LPR measurements suggest an underestimation of the global lunar regolith thickness by other methods and reveal a vast volume from the last volcanic eruption [8]. Yutu-2 has obtained a 425 m LPR profile along the rover tracks in the first 16 lunar days, displaying clear and complex subsurface structures of the landing area, which would help us to reveal the fine structure of lunar regolith.
The subsurface velocity of electromagnetic waves is a vital parameter for stratigraphic division, rock location estimates, and calculating rock properties including relative permittivity, density, and content of FeO and TiO2 during the interpretation of LPR data. Meanwhile, the location of rocks in regolith can cause diffractions in LPR data, and the vertex position of the diffractions can help estimate the possible location of rocks. This is different from the main reflections from the layers, which are useful in stratigraphic analysis. Analysis of the rock location and the properties of the lunar regolith can help to reveal the formation and evolution history of the landing site. Previous studies on geological stratification and parameter inversion of the lunar regolith were mainly based on the CH-2B data only [3,8,12]. For example, Feng et al. proposed a hyperbola fitting method for radar velocity analysis in the CH-2B radar-gram [12]. Dong et al. calculated the parameters of the regolith by relative reflection amplitudes [13]. Lai et al. acquired the radar velocity based on the two-way delay method [14]. Hu et al. proposed an adaptive rock extraction method based on local similarity constraints to achieve the rock location and quantitative analysis for regolith [15]. Dong et al. analyzed the regolith properties from the LPR data of Chang’E-4 based on the 3D velocity spectrum [16]. However, a complex subsurface structure and interference of noise always result in incomplete, interlaced, and amplitude-varying hyperbolas which cause the inaccurate velocity analysis of field LPR data [16], and the previous studies cannot reach a satisfied accuracy. In addition, the determination of the rock location or the vertex position of the diffractions is the key procedure to obtain a high-precision diffraction velocity analysis spectrum. Although Zhang et al. used two sets of CH-2A and CH-2B data to estimate the electrical parameters and the iron–titanium content of regolith [17], the subsurface velocity estimation is not as accurate as expected due to the limitation of their method.
In this paper, two sets of CH-2A and CH-2B data are used to estimate velocity and the relative permittivity; thus, the other properties of lunar regolith including density and content of FeO and TiO2 can be calculated based on the relative permittivity. Firstly, we consider the measurement similarity [18,19] between the two sets of CH-2A and CH-2B data based on the local correlation, and develop an extraction method to determine the vertex position of the diffractions and estimate the rock location. Secondly, we apply the normalized velocity spectrum based on the semblance analysis to estimate the subsurface velocity of the lunar regolith [20]. Finally, we utilize the interpolation method to obtain the velocity of the subsurface structure and derive the distribution of the relative permittivity.
2. Materials and Methods
2.1. LPR Data Processing
The CE-4 LPR is a dual-frequency ground penetrating radar (GPR) system, operating at 60 MHz (low-frequency) with a frequency band of 40~80 MHz and 500 MHz (high-frequency) with frequency band of 250~750 MHz [11,21]. The CH-2 radar data were collected during the first 16 lunar days along the Yutu-2′s traverse of about 425 m, as shown in Figure 1, which is consistent with the results acquired by Lin et al. [22].

Figure 1.
The location of Chang’E-4 landing site and the traverse of Yutu-2 rover for the first 16 lunar days. The lunar background was obtained using the imagery by the Lunar Reconnaissance Orbiter Camera.
To reveal the near-surface structure of the regolith, we processed and interpreted the high-frequency LPR data (CH-2A and CH-2B) by excluding the effects of the electromagnetic coupling with the rover’s metallic body. The CH-2 antenna is mounted at the bottom of the lunar rover about 0.3 m away from the ground, and the space between two adjacent antenna elements (one transmitting antenna and two receiving antennae) is about 0.16 m [23]. The receiving antenna for CH-2A data is closer to the transmitting antenna than that of CH-2B, and thus has a lower signal-to-noise ratio. Therefore, we developed a series of procedures to process the CH-2A and CH-2B data as follows: (1) data deleting; (2) time delay removal; (3) band-pass filter application; (4) removal of DC bias; (5) background removal; (6) mean spatial filter application. Then, we could obtain the high-resolution CH-2A and CH-2B data with 1958 samples with 0.3125 ns time intervals and 11,661 traces of 0.0365 m spatial intervals, as shown in Figure 2.
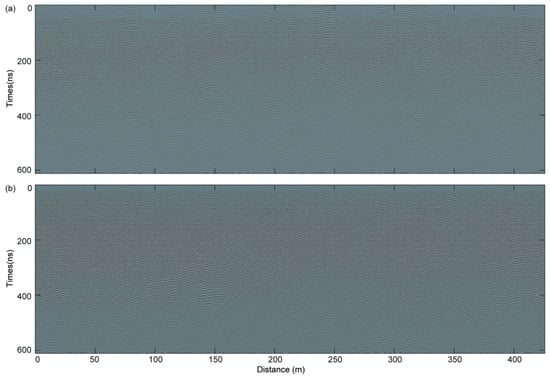
Figure 2.
High-frequency LPR profile along the track of rover Yutu-2 after the series of data processing. (a) The CH-2A data; (b) the CH-2B data.
2.2. Local Correlation
The processed LPR CH-2A and CH-2B data are always affected by noise significantly, and the strong coherence of the noise may cause local maximums [15]. Here, we introduce local correlation [18] to determine the rock position in order to take advantage of both LPR CH-2A and CH-2B data simultaneously.
The global correlation coefficient between two discrete signals, and , can be defined as [18]:
which can be represented as two least-squares inverse based on a linear algebra notation:
where N is the length of a signal, and are vector notions for and . Localizing Equations (3) and (4) were used to add regularization to inversion. Using shaping regularization, the scalars can turn into vectors [18]—i.e., scalars and turn into vectors and , defined as:
where and are scaling controls, and are two diagonal operators composed of the elements of and , and is a shaping operator, such as Gaussian smoothing, with an adjustable radius.
The componentwise of vectors and defines the local correlation as , whose elements are given by . The local correlation is a measure of the similarity between two signals [15,19].
2.3. Semblance Analysis
The high-frequency electromagnetic wave will be reflected, diffracted, and refracted simultaneously when propagating the interface with discontinuous dielectric properties, such as boulders, voids, and soil inhomogeneities [24]. The LPR CH-2A and CH-2B data represent the common offset profiles, and the responses analyzed in semblance analysis are diffraction hyperbola instead of reflection hyperbola in the common midpoint data. The normal moveout equation was reconfigured for diffraction trajectories in the common offset profile, thus the traveltime was approximated as:
where is the position along the common offset profile, is surface position vertically above the diffracting target, is the two-way traveltime to the target when the antenna is positioned at [25], and is the stacking velocity that is similar to the root-mean-square velocity. Velocity analysis is a reliable way to estimate stacking velocity and the accuracy depends on the signal-to-noise ratio of data, which influences the quality of picking. The semblance analysis was performed along the rover’s traverse, which corresponds to the diffraction hyperbola in the LPR profile.
The calculated stacking velocity by semblance analysis could be transferred to interval velocity through Dix inversion [26] as:
where is the interval velocity of n-th layer and is the root-mean-square velocity.
Semblance analysis provides a measure of the coherency of energy along trial trajectories defined by the substitution of trial pairs of and , which was conducted over an aperture of L traces and 2M + 1 samples as:
where L is 11,661 in LPR data, i and j are time sample indices, k is a trace number and is the amplitude of the j-th sample of the k-th trace [27]. The selection of M would not influence the peak location of contours for semblance analysis. A proper selection of M would gain a better tradeoff between resolution (traveltime and velocity) and noise compression. Our sensitivity analysis indicates that a value of M = 3 would give a reasonable resolution and less noise level, so here we set M = 3.
2.4. Property Calculation
The relative permittivity without considering the electric conductivity and magnetic permeability can be approximated by the propagating velocity as [8]:
where is the speed of light in vacuum, which is 0.3 m/ns. The relation between the relative permittivity and density of lunar regolith [28] is:
where is the bulk density with the unit of (g/cm3). Laboratory measurements show that the loss tangent represents the ratio of the imaginary part of the relative permittivity to its real part, which depends on bulk density. The (FeO+TiO2) abundance of lunar regolith could be estimated based on the loss tangent and bulk density, which is beyond the scope of this study.
3. Results
3.1. Simulation Data Results
We verify the effectiveness of the proposed method in a synthetic model using the finite difference time domain (FDTD) method [29], as shown in Figure 3a. The synthetic model consists of a heterogeneous background and several anomalous rocks with random relative permittivities less than 5.0 [24]. The dominant frequency of a Ricker wavelet is 500 MHz, the time windows and the sampling interval are 120 and 0.02 ns, respectively, and the trace interval is 0.005 m.
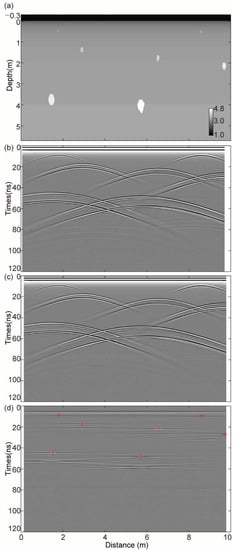
Figure 3.
(a) The synthetic regolith model; (b) forward result with offset of 0.16 m; (c) forward result with offset of 0.32 m; (d) the local correlation defined in Section 2.2 for the two filtered data. The red-cross indicates the vertex position of the diffractions and the white color indicates the maximum value of local correlation.
The forward simulation results of CH-2A with the offset of 0.16 m and CH-2B with the offset of 0.32 m are illustrated in Figure 3b,c, respectively. The double diffraction hyperbolas were generated due to the upper and bottom surfaces of the rocks [16]. We focused on the upper diffraction hyperbola to reduce the error of velocity estimation. Furthermore, we demonstrate the results by applying the local correlation based on the frequency wavenumber (FK) fan filtered data in Figure 3d, where the red-cross indicates the vertex position of the diffractions. Dong et al. determined the vertex positions of the diffractions by directly applying a 3D velocity spectrum for the whole data [16], which would cause a relatively large error because the maximum value position of semblance analysis would be significantly influenced by the noise. The vertex position of the diffraction determinations based on local correlation would have higher accuracy than the direct 3D velocity spectrum. Accurate determination of vertex positions of the diffractions is the basis of high-precision semblance analysis for the velocity.
Based on the picking positions in Figure 3d, we could scan the stacking velocity within the local scope of the simulation data. We display the contours from the semblance analysis for the velocity ranges from 0.1 to 0.3 m/ns within a 4 ns time window in Figure 4. The vertex positions of the diffractions are shown in the upper right corner of the graph. The stacking velocity and the calculated depth of each rock are listed in Table 1.
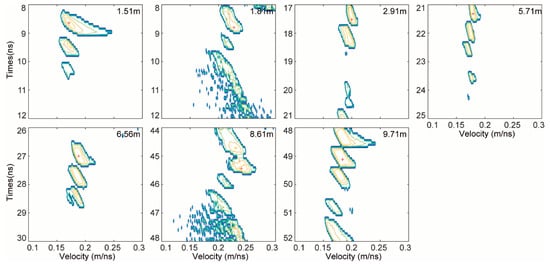
Figure 4.
Semblance analysis contours of selected diffraction hyperbolas for the simulation model, where the normalized stacked amplitude threshold of 0.6 was used. The red-cross indicates the maximum value 1 of the semblance analysis.

Table 1.
The estimated results of velocity and depth for the simulation model.
The scanning positions are well consistent with the actual positions of rocks except the two rocks in the shallow layer (Figure 5). The inconsistency may be due to the high velocity in the shallow layers which results in flat diffraction hyperbola, thus the accuracy of semblance analysis for velocity is insufficient. Thus, the simulation shows that our proposed procedures based on local correlation and semblance analysis is effective to obtain the subsurface parameters.
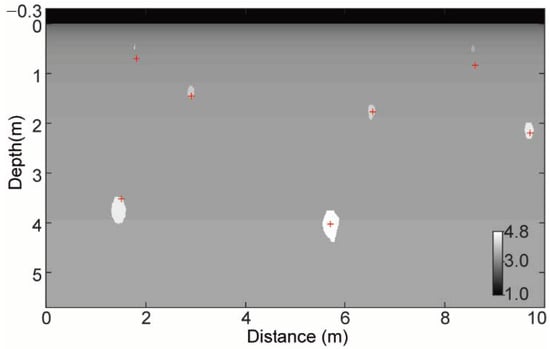
Figure 5.
The scanning location of the rocks in the synthetic model. The red-cross indicates the scanning location of the diffractions.
3.2. LPR Data Results
The amplitude of echoes in the first ~150 ns (length N = 501 with 0.3125 ns time interval), with a depth of about 10 m for the LPR CH-2A and CH-2B data, is displayed in Figure 6a,b, respectively. The local correlation for the filtered CH-2A and CH-2B data is shown in Figure 6c, where the red-cross indicates the vertex position of the diffractions after selection.
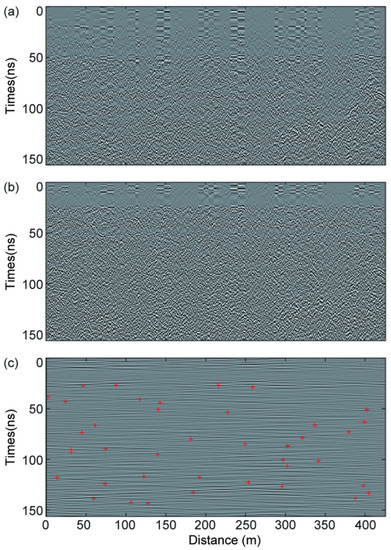
Figure 6.
The profile of lunar penetrating radar (LPR) data within the region of 0~150 ns. (a) The CH-2A data; (b) the CH-2B data; (c) the local correlation defined in Section 2.2 for the filtered CH-2A and CH-2B data. The red-cross indicates the vertex position of the diffractions and the white color indicates the maximum value of local correlation.
The semblance analysis contour of diffraction hyperbolas for the LPR CH-2B data was based on the rock location extraction by applying the local correlation, and the results are shown in Figure 7. The red-cross in the contour maps represents the maximum value of the semblance analysis. The stacking velocity for the rocks was obtained by picking the maximum value of the semblance analysis, and the calculated depths are listed in Table 2.
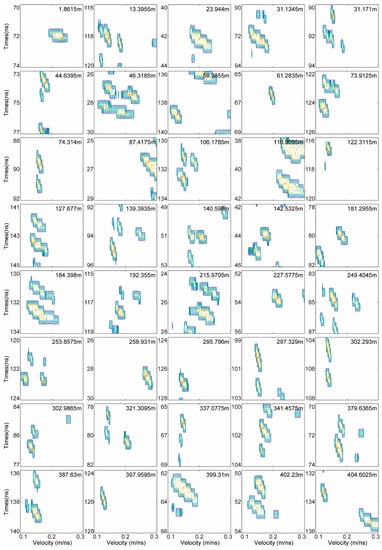
Figure 7.
Semblance analysis contour of diffraction hyperbolas after screening the LPR CH-2B data, where the normalized stacked amplitude threshold of 0.6 was used. The red-cross indicates the maximum value of 1 for the semblance analysis.

Table 2.
The estimated results of velocity and depth for the LPR data.
Meanwhile, we compared the diffraction hyperbola for No.30 and No.34 rocks with the CH-2B data. As shown in Figure 8, the white dotted lines represent the diffraction hyperbola at 302.2930 m and 106.5625 ns for the stacking velocity of 0.142 m/ns (Figure 8a) and at 341.3845 m and 101.5625 ns for the stacking velocity of 0.165 m/ns (Figure 8b), respectively. The trend of the hyperbola shows great consistency with the CH-2B data, which indicates the semblance analysis procedure can obtain the stacking velocity with high precision.
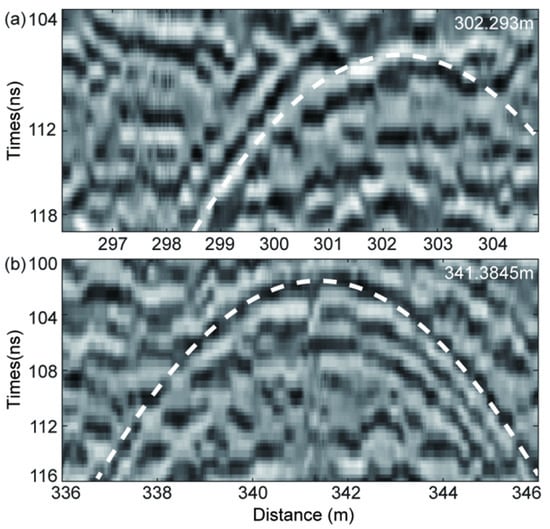
Figure 8.
The comparison between the diffraction hyperbola and the CH-2B data within the local region. (a) The white dotted lines represent the diffraction hyperbola at 302.2930 m and 106.5625 ns for the stacking velocity of 0.142 m/ns; (b) the white dotted lines represent the diffraction hyperbola at 341.3845 m and 101.5625 ns for the stacking velocity of 0.165 m/ns.
We applied the spline image interpolation method based on the 40 selected rocks to obtain the stacking velocity of the substructures. The stacking velocity and the root-mean-square velocity approach to the same when the source-receiver offset approaches zero for the isotropic layered model. The interval velocity can be calculated using the Dix formula as shown in Figure 9a. Subsequently, the estimated relative permittivity of the subsurface structure along the Yutu-2 rover’s traverse, as shown in Figure 9b, could be obtained based on the interval velocity distribution. The subsurface velocity and the relative permittivity are important parameters for calculating other physical properties. Based on the relative permittivity of the subsurface structure without considering the echo power attenuation, we could acquire the subsurface properties of lunar regolith, which are important for geological interpretation.
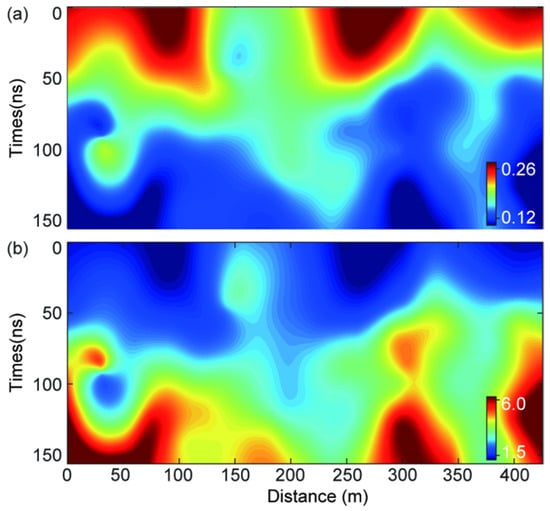
Figure 9.
The estimated subsurface velocity and relative permittivity distribution along the Yutu-2 rover route. (a) The subsurface velocity distribution; (b) the subsurface relative permittivity distribution.
4. Discussion
The noise interference and incomplete hyperbola will produce errors in semblance analysis. Additionally, the region selection of the data will influence the determination of the vertex position of the diffractions, which will affect the accuracy of semblance analysis. The determination of rock locations (i.e., the vertex position of the diffractions) is the most important procedure to obtain reliable semblance analysis results. Our analysis indicates that the semblance analysis in the shallow layers of the simulation model always has a larger bias than that in the deep layers. One possible reason is that the flat diffraction hyperbola would influence the accuracy of semblance analysis. Thus, a high-precision semblance analysis method such as the weighted AB semblance [30] or new migration methods [31] should be developed to improve the accuracy in the future studies. Additionally, LPR data processing should consider the local attributes to separate the data with higher accuracies.
We display the forward result with small Gaussian noise (mean is 0 and variance is 0.005) added and the corresponding local correlation results in Figure 10 to evaluate the validity of the combined method with noise. The results show that small noise has little influence on the local correlation results, and the combined method is valid to derive accurate velocity, permittivity, and bulk density distribution.
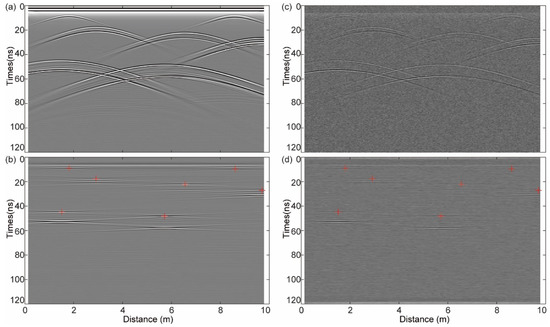
Figure 10.
(a) Forward result; (b) the local correlation results; (c) forward result with Gaussian noise added; (d) the local correlation results with Gaussian noise added. The red-cross indicates the vertex position of the diffractions and the white color indicates the maximum value of local correlation.
The local correlation and semblance analysis were combined to estimate the velocity structure, which can provide a good estimation of abnormal rock location and relative permittivity. The future multiple-input multiple-output radar onboard the lander from China’s Chang’E-5 (CE-5) mission can help the detection of the regolith structure and the position of the underlying abnormal rocks in the landing site. The combined method by using local correlation and semblance analysis could be helpful for further processing on the CE-5 radar data. Furthermore, the method can be used in the site selection of the International Lunar Research Station (ILRS) [32] and similar missions in the future.
5. Conclusions
We derived the similarity between filtered LPR CH-2A and CH-2B data based on the local correlation, which would help to reveal the rock location distribution in the lunar regolith. Subsequently, we applied the semblance analysis method for the diffraction hyperbola to obtain the subsurface velocity structure and the relative permittivity distribution. The other properties of lunar regolith including bulk density and FeO and TiO2 abundance can be calculated based on the relative permittivity. A procedure that combined the local correlation and semblance analysis has an advantage over traditional methods [12,13,14,15,16] in terms of accuracy and robustness in the interpretation of the high-frequency LPR data.
The velocity structure and the properties of the subsurface were derived from diffraction hyperbolas in the high-frequency LPR data, which could provide a good structural constraint for understanding the formation and evolution of the lunar regolith at the landing site. The combined procedure is an excellent choice for estimating the subsurface velocity and the other properties of the lunar regolith. Compared with the methods by analyzing Apollo’s samples [1] and by the microwave remote sensing techniques [3] to derive the physical parameters of lunar regolith, the application of LPR has great advantages both in terms of the range and the accuracy. Therefore, it is very important to develop parameter estimation methods based on the LPR data, especially its high-frequency data. The procedure combined with the local correlation and semblance analysis, proposed in this paper, is of great significance in the interpretation of LPR high-frequency data.
Author Contributions
Conceptualization, H.S. and J.Z.; methodology, H.S.; software, H.S. and C.L.; validation, H.S. and X.W.; formal analysis, Y.Z.; investigation, H.S., X.W. and C.L.; resources, Y.L. and Y.Z.; data curation, H.S., J.Z. and C.L.; writing—original draft preparation, H.S.; writing—review and editing, J.Z. and Y.L.; visualization, H.S.; supervision, J.Z. and Y.L.; project administration, H.S. and Y.L.; funding acquisition, H.S., J.Z. and Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program of China (grant number: 2020YFE0202100), the National Natural Science Foundation of China (grant number: 11941001), the pre-research project on Civil Aerospace Technologies funded by Chinese National Space Administration (CNSA) (grant number: D020201 and D020203) and the Beijing Municipal Science and Technology Commission (grant number: Z191100004319001 and Z181100002918003). J.Z. was supported by the National Natural Science Foundation of China (grant number: 41941002). Y.L. was supported by the pre-research project on Civil Aerospace Technologies funded by Chinese National Space Administration (CNSA) (grant number: D020101 and D020102) and the Strategic Priority Research Program of Chinese Academy of Sciences (grant number: XDB 41000000).
Acknowledgments
We thank Lin H.L. for his assistance with the manuscript. We would like to thank the editor and reviewers for their reviews that improved the content of this paper. The data reported in this work are archived at http://moon.bao.ac.cn/searchOrder_pdsData.search.
Conflicts of Interest
The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- McKay, D.S.; Heiken, G.; Basu, A.; Blanford, G.; Simon, S.; Reedy, R.; French, B.M.; Papike, J. The lunar regolith. In Lunar Source-Book: A User’s Guide to the Moon; Heiken, G., Ed.; Cambridge University Press: New York, NY, USA, 1991; Volume 7, pp. 285–357. [Google Scholar]
- Nakamura, Y.; Latham, G.V.; Dorman, H.J. Apollo Lunar Seismic Experiment—Final summary. J. Geophys. Res. Space Phys. 1982, 87, A117–A123. [Google Scholar] [CrossRef]
- Fa, W.; Jin, Y. A primary analysis of microwave brightness temperature of lunar surface from Chang-E 1 multi-channel radiometer observation and inversion of regolith layer thickness. Icarus 2010, 207, 605–615. [Google Scholar] [CrossRef]
- Neish, C.D.; Barnes, J.W.; Sotin, C.; MacKenzie, S.; Soderblom, J.M.; Le Mouélic, S.; Kirk, R.L.; Stiles, B.W.; Malaska, M.J.; Le Gall, A.; et al. Spectral properties of titan’s impact craters imply chemical weathering of its surface. Geophys. Res. Lett. 2015, 42, 3746–3754. [Google Scholar] [CrossRef] [PubMed]
- Porcello, L.; Jordan, R.; Zelenka, J.; Adams, G.; Phillips, R.; Brown, W.; Ward, S.; Jackson, P. The Apollo lunar sounder radar system. Proc. IEEE 1974, 62, 769–783. [Google Scholar] [CrossRef]
- Ono, T.; Kumamoto, A.; Kasahara, Y.; Yamaguchi, Y.; Yamaji, A.; Kobayashi, T.; Oshigami, S.; Nakagawa, H.; Goto, Y.; Hashimoto, K.; et al. The Lunar Radar Sounder (LRS) Onboard the KAGUYA (SELENE) Spacecraft. Space Sci. Rev. 2010, 154, 145–192. [Google Scholar] [CrossRef]
- Xiao, L.; Zhu, P.; Fang, G.; Xiao, Z.; Zou, Y.; Zhao, J.; Zhao, N.; Yuan, Y.; Qiao, L.; Zhang, X.; et al. A young multilayered terrane of the northern Mare Imbrium revealed by Chang’E-3 mission. Science 2015, 347, 1226–1229. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, W.; Hu, S.; Lin, Y.; Fang, G.; Li, C.; Peng, W.; Zhu, S.; He, Z.; Zhou, B.; et al. Volcanic history of the Imbrium basin: A close-up view from the lunar rover Yutu. Proc. Natl. Acad. Sci. USA 2015, 112, 5342–5347. [Google Scholar] [CrossRef]
- Li, C.; Su, Y.; Pettinelli, E.; Xing, S.; Ding, C.; Liu, J.; Ren, X.; Lauro, S.E.; Soldovieri, F.; Zeng, X.; et al. The Moon’s farside shallow subsurface structure unveiled by Chang’E-4 Lunar Penetrating Radar. Sci. Adv. 2020, 6, eaay6898. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, B.; Lin, Y.; Zhu, M.; Song, H.; Dong, Z.; Gao, Y.; Di, K.; Yang, W.; Lin, H.; et al. Lunar regolith and substructure at Chang’E-4 landing site in South Pole-Aitken basin. Nat. Astron. 2020, 1–6. [Google Scholar] [CrossRef]
- Fang, G.; Zhou, B.; Ji, Y.; Zhang, Q.; Shen, S.; Li, Y.; Guan, H.; Tang, C.; Gao, Y.; Lu, W.; et al. Lunar Penetrating Radar onboard the Chang’e-3 mission. Res. Astron. Astrophys. 2014, 14, 1607–1622. [Google Scholar] [CrossRef]
- Feng, J.; Su, Y.; Ding, C.; Xing, S.; Dai, S.; Zou, Y. Dielectric properties estimation of the lunar regolith at CE-3 landing site using lunar penetrating radar data. Icarus 2017, 284, 424–430. [Google Scholar] [CrossRef]
- Dong, Z.; Fang, G.; Ji, Y.; Gao, Y.; Wu, C.; Zhang, X. Parameters and structure of lunar regolith in Chang’E-3 landing area from lunar penetrating radar (LPR) data. Icarus 2017, 282, 40–46. [Google Scholar] [CrossRef]
- Lai, J.; Xu, Y.; Zhang, X.; Tang, Z. Structural analysis of lunar subsurface with Chang׳E-3 lunar penetrating radar. Planet. Space Sci. 2016, 120, 96–102. [Google Scholar] [CrossRef]
- Hu, B.; Wang, D.; Zhang, L.; Zeng, Z. Rock Location and Quantitative Analysis of Regolith at the Chang’e 3 Landing Site Based on Local Similarity Constraint. Remote Sens. 2019, 11, 530. [Google Scholar] [CrossRef]
- Dong, Z.; Feng, X.; Zhou, H.; Liu, C.; Zeng, Z.; Li, J.; Liang, W. Properties Analysis of Lunar Regolith at Chang’E-4 Landing Site Based on 3D Velocity Spectrum of Lunar Penetrating Radar. Remote Sens. 2020, 12, 629. [Google Scholar] [CrossRef]
- Zhang, L.; Zeng, Z.; Li, J.; Huo, Z.; Wang, K.; Zhang, J.; Huang, L. Parameter Estimation of Lunar Regolith from Lunar Penetrating Radar Data. Sensors 2018, 18, 2907. [Google Scholar] [CrossRef]
- Fomel, S. Local seismic attributes. Geophysics 2007, 72, 29–33. [Google Scholar] [CrossRef]
- Liu, G.; Fomel, S.; Jin, L.; Chen, X. Stacking seismic data using local correlation. Geophysics 2009, 74, V43–V48. [Google Scholar] [CrossRef]
- Fisher, E.; McMechan, G.A.; Annan, A.P. Acquisition and processing of wide-aperture ground-penetrating radar data. Geophysics 1992, 57, 495–504. [Google Scholar] [CrossRef]
- Su, Y.; Fang, G.; Feng, J.; Xing, S.; Ji, Y.; Zhou, B.; Gao, Y.; Li, H.; Dai, S.; Xiao, Y.; et al. Data processing and initial results of Chang’e-3 lunar penetrating radar. Res. Astron. Astrophys. 2014, 14, 1623–1632. [Google Scholar] [CrossRef]
- Lin, H.; Lin, Y.; Yang, W.; He, Z.; Hu, S.; Wei, Y.; Xu, R.; Zhang, J.; Liu, X.; Yang, J.; et al. New Insight Into Lunar Regolith-Forming Processes by the Lunar Rover Yutu-2. Geophys. Res. Lett. 2020, 47, e2020GL087949. [Google Scholar] [CrossRef]
- Angelopoulos, M.; Redman, D.; Pollard, W.H.; Haltigin, T.W.; Dietrich, P. Lunar ground penetrating radar: Minimizing po-tential data artifacts caused by signal interaction with a rover body. Adv. Space Res. 2014, 54, 2059–2072. [Google Scholar] [CrossRef]
- Lv, W.; Li, C.; Song, H.; Zhang, J.; Lin, Y. Comparative analysis of reflection characteristics of lunar penetrating radar data using nu-merical simulations. Icarus 2020, 350, 113896. [Google Scholar] [CrossRef]
- Ristic, A.V.; Petrovački, D.; Govedarica, M. A new method to simultaneously estimate the radius of a cylindrical object and the wave propagation velocity from GPR data. Comput. Geosci. 2009, 35, 1620–1630. [Google Scholar] [CrossRef]
- Dix, C.H. Seismic velocities from surface measurements. Geophysics 1955, 20, 68–86. [Google Scholar] [CrossRef]
- Neidell, N.S.; Taner, M.T. Sembalnce and other coherency measures for multichannel data. Geophysics 1971, 34, 859–891. [Google Scholar] [CrossRef]
- Carrier, W.D.; Olhoeft, G.R.; Mendell, W. Physical properties of the lunar surface. In Lunar Source-Book: A User’s Guide to the Moon; Heiken, G., Ed.; Cambridge University Press: New York, NY, USA, 1991; Volume 9, pp. 475–594. [Google Scholar]
- Irving, J.; Knight, R. Numerical modeling of ground-penetrating radar in 2-D using MATLAB. Comput. Geosci. 2006, 32, 1247–1258. [Google Scholar] [CrossRef]
- Ebrahimi, S.; Kahoo, A.R.; Chen, Y.; Porsani, M. A high-resolution weighted AB semblance for dealing with ampli-tude-variation-with-offset phenomenon. Geophysics 2017, 82, V85–V93. [Google Scholar] [CrossRef]
- Sun, H.; Gao, C.; Zhang, Z.; Liao, X.; Wang, X.; Yang, J. High-Resolution Anisotropic Prestack Kirchhoff Dynamic Focused Beam Migration. IEEE Sens. J. 2019, 20, 11753–11760. [Google Scholar] [CrossRef]
- Pei, Z.; Liu, J.; Wang, Q.; Kang, Y.; Zou, Y.; Zhang, H.; Zhang, Y.; He, H.; Wang, Q.; Yang, R. Overview of lunar exploration and International Lunar Research Station. Chin. Sci. Bull. 2020, 65, 2577–2586. (In Chinese) [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).