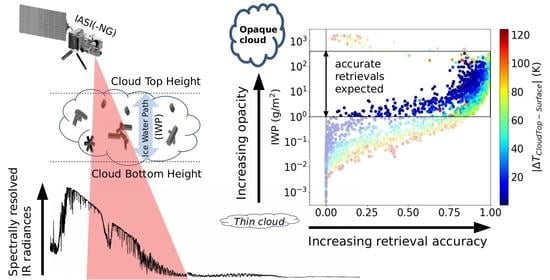
Potential of Hyperspectral Thermal Infrared Spaceborne Measurements to Retrieve Ice Cloud Physical Properties: Case Study of IASI and IASI-NG
Abstract
1. Introduction
2. Framework
2.1. IASI and IASI-NG Instruments
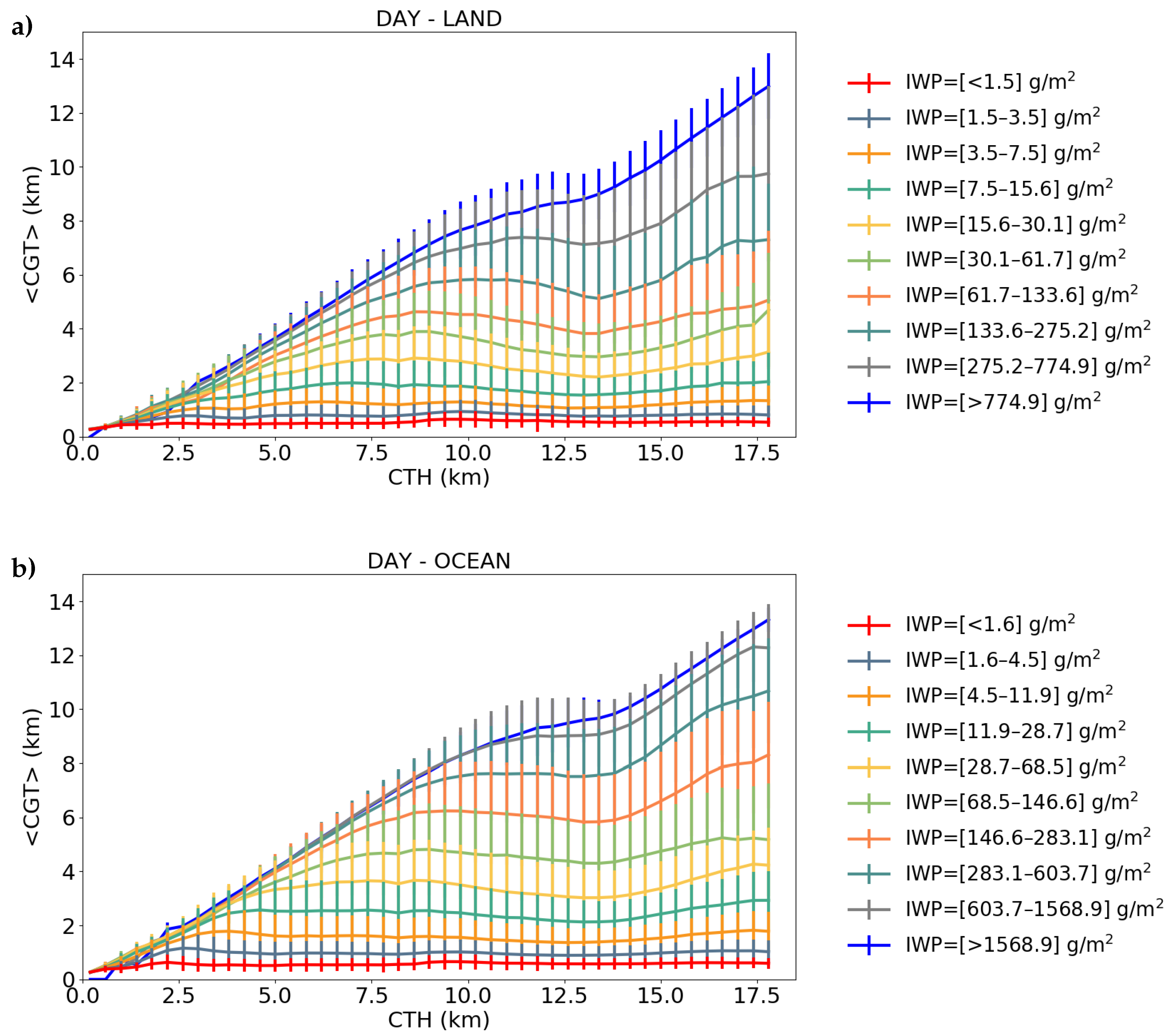
2.2. Microphysical Model
2.3. Forward Model
2.4. Retrieval Method and State Vector
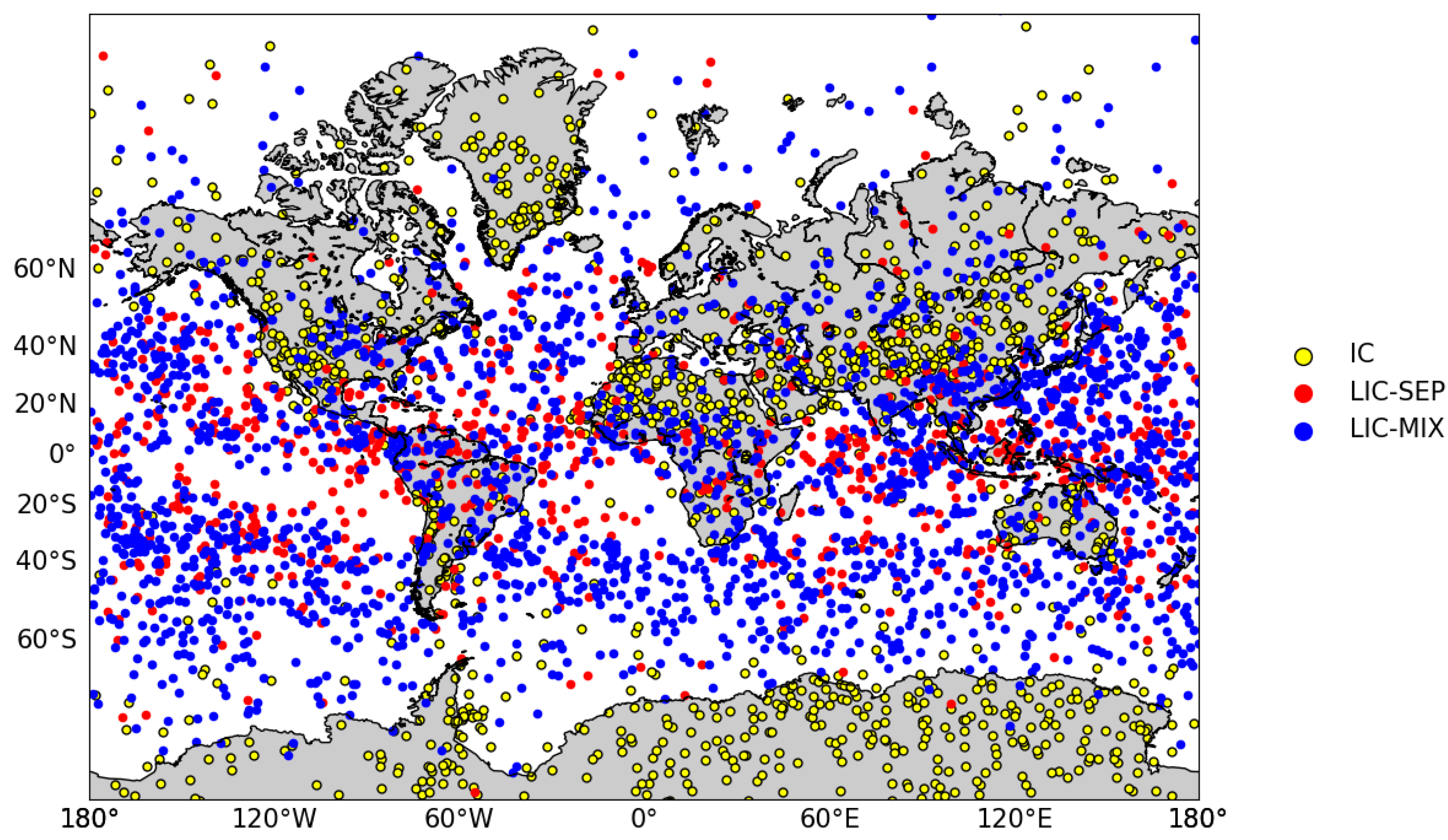
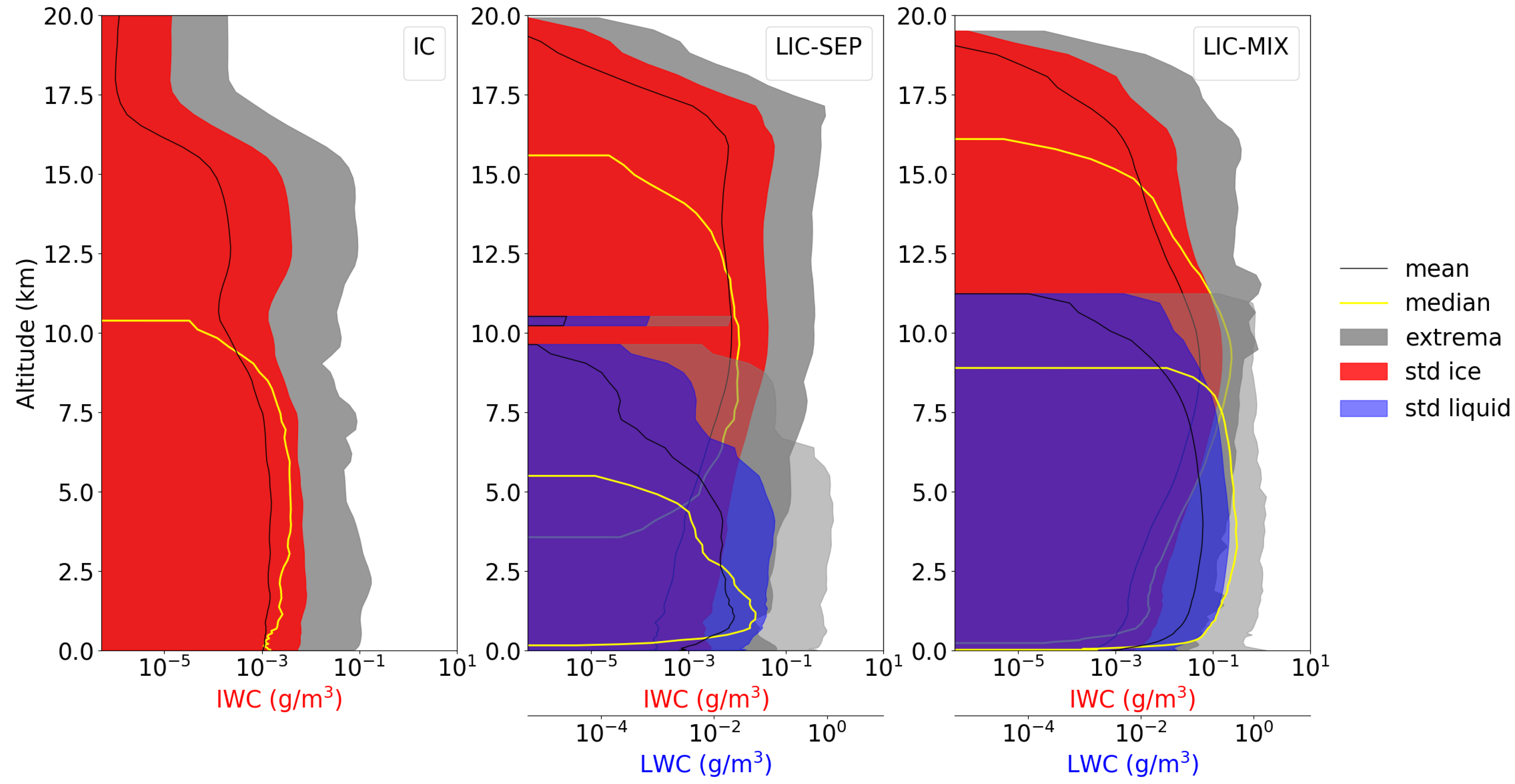
2.5. NWP Database and the Measurement Vector
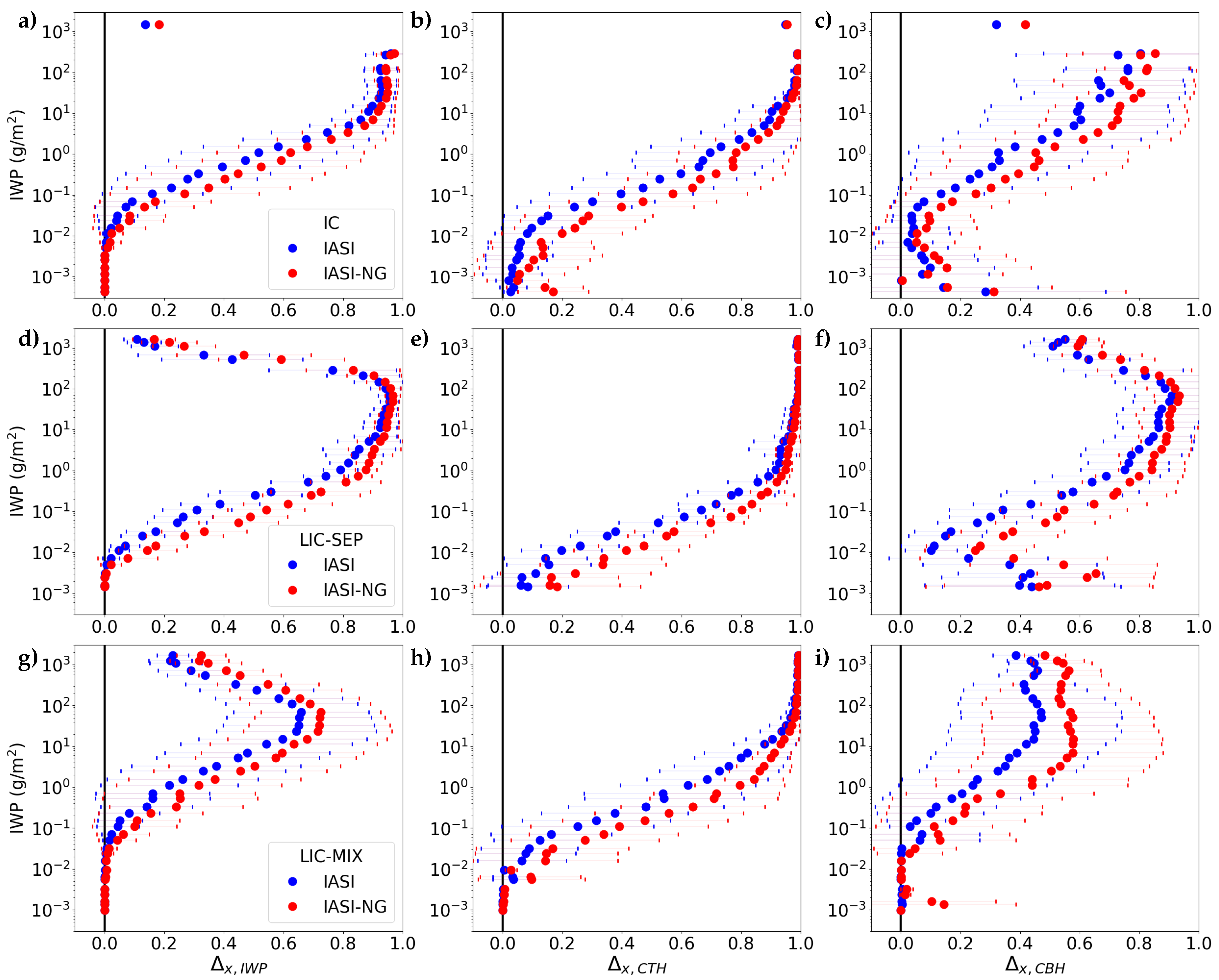
3. Information Content Analysis
3.1. A Priori Error Departure
- ,
- –
- Let be the vector that contains all the non-retrieved parameters (i.e., water vapor, ozone, temperature and liquid water content profile, as well as surface temperature and emissivity). Their covariance matrix, , which is considered a diagonal matrix, has been built by assuming a 10% error for the gas concentration profile, 5% for surface emissivity, 50% for liquid cloud altitude, vertical extent and column water content, and 1K for both surface and atmospheric profile temperatures. Those values are chosen as the target performances or maximum error of the IASI L2 products and the emissivity atlases, and arbitrarily for ozone profile and liquid cloud properties. Finally, is the Jacobian matrix of the vector;
- –
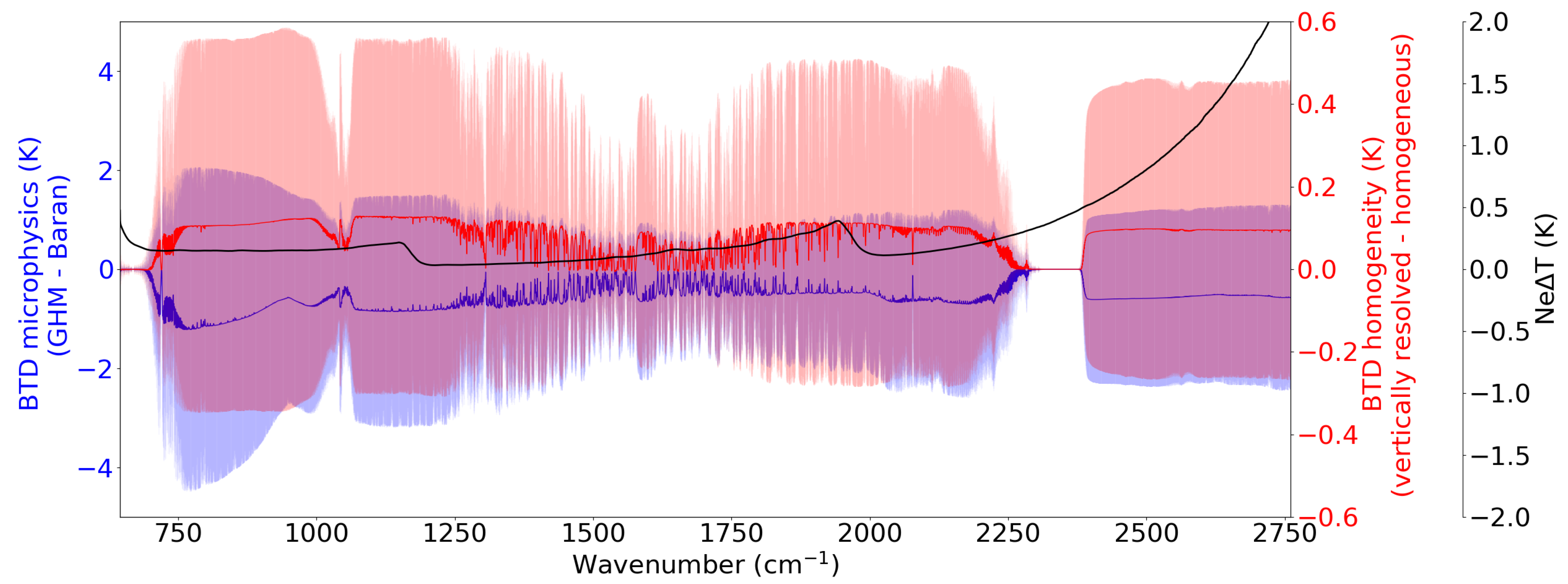
- , which is considered a diagonal matrix, has been built from the standard deviation of the radiance calculated from two different microphysical models, namely the Baran et al. (2014) [50] model described in Section 2.2 and the General Habit Mixture (GHM) model of Baum et al. (2007) [48]. The Baum et al. (2007) [48] model depends on the effective diameter of the ice crystals. We inferred this quantity from and cloud temperature using the Wyser (1998) parameterization [66,67]. This covariance matrix is introduced in order to take into account the error due to the microphysical diversity in the two models. Figure 3 illustrates the IASI Brightness Temperature Difference (BTD) calculated from the two models averaged over all the IC profiles. As one can see, this BTD is important compared to the radiometric noise of the instruments, particularly in the atmospheric window, showing the necessity of taking into account the error from the microphysics;
- –
- , which is considered a diagonal matrix, has been built from the difference between the radiance calculated from the vertically inhomogeneous and homogeneous ice water content profiles. We have introduced this covariance matrix in order to take into account the error due to the simplest assumption of vertically homogeneous cloud made in the forward model for the retrieval. The top and bottom heights of the homogeneous clouds are set to the first layer that brings more than 7% of the . This percentage has been found by minimizing the radiance difference between simulations with homogeneous and vertically resolved ice water content profiles. The is then distributed over the layers enclosed by and . Figure 3 illustrates the corresponding IASI BTD averaged over all the IC profiles. This figure shows that the vertical homogeneity assumption is reasonable as the mean brightness temperature difference is below 0.2 . Still, the error due to this simplification has to be accounted for as is of the same order of magnitude as the radiometric noise of the instruments;
- has been generated from the radiometric noise of each instrument according to the value given in Clerbaux et al. (2009) [40] for IASI and halved for IASI-NG. Five off-diagonal terms due to the apodization are accounted for. Details on the IASI instrument noise specification can be found in Serio et al. (2020) [68]. The IASI radiometric noise converted to noise equivalent temperature difference () for a reference temperature of 280 K is shown in Figure 3. As one can see, the radiometric noise is below 0.2 K from 650 to around 2200 apart from the wavenumbers between 1800 and 2000 where it reaches 0.3 K. For higher wavenumbers (above 2200 ), due to the lower emission of the Earth, the radiometric noise increases to 3 K.
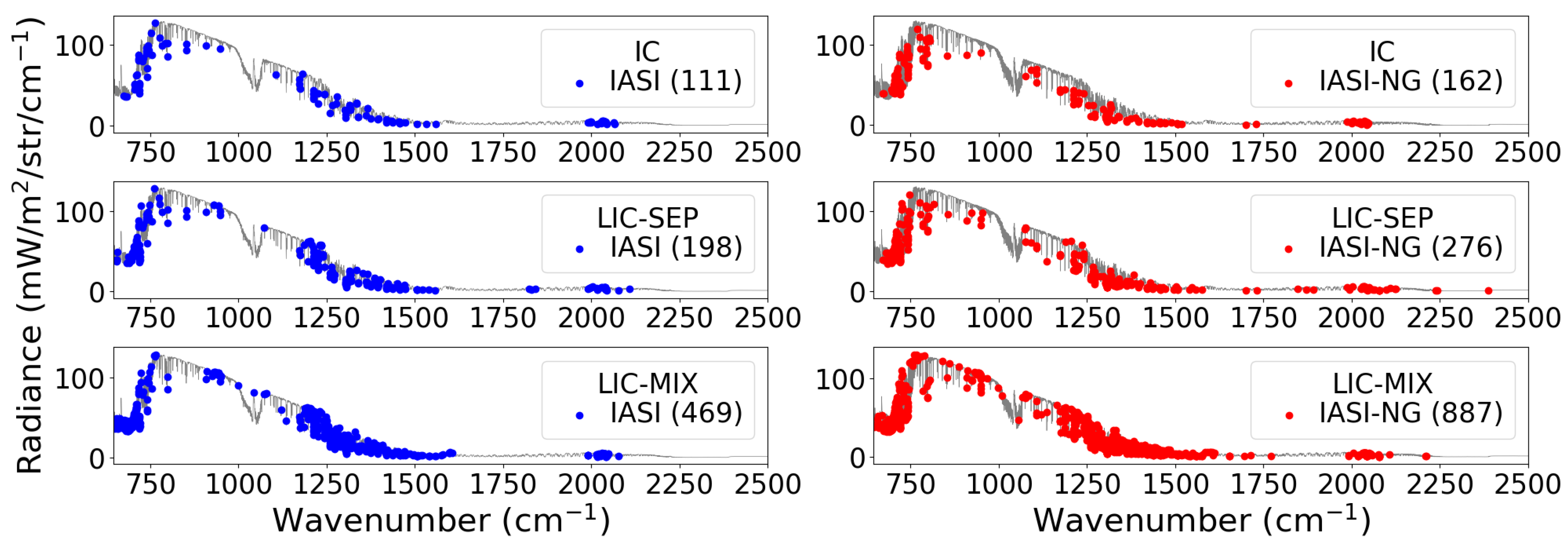
3.2. Channel Selection
4. Retrieval
4.1. Climatological Constraint
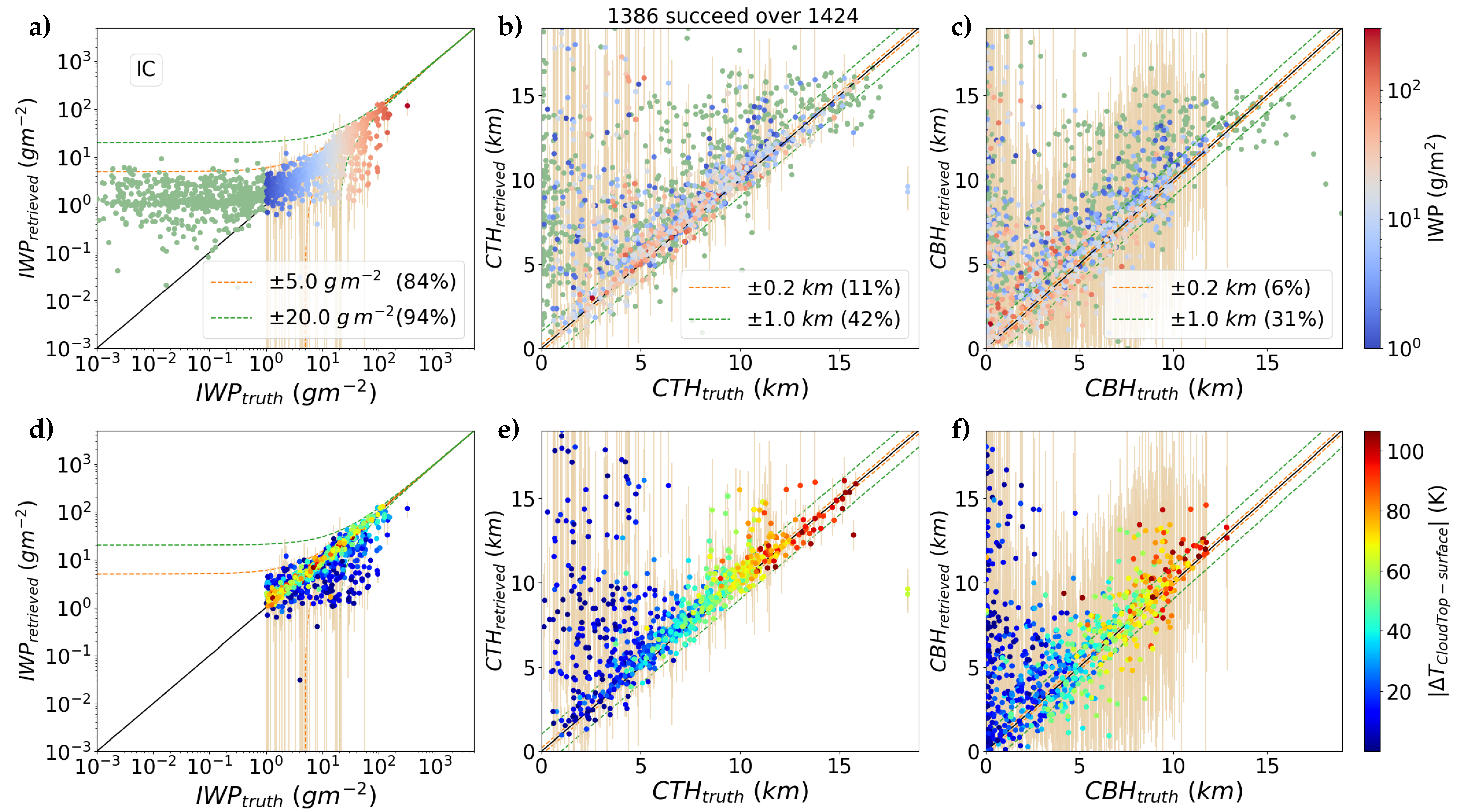
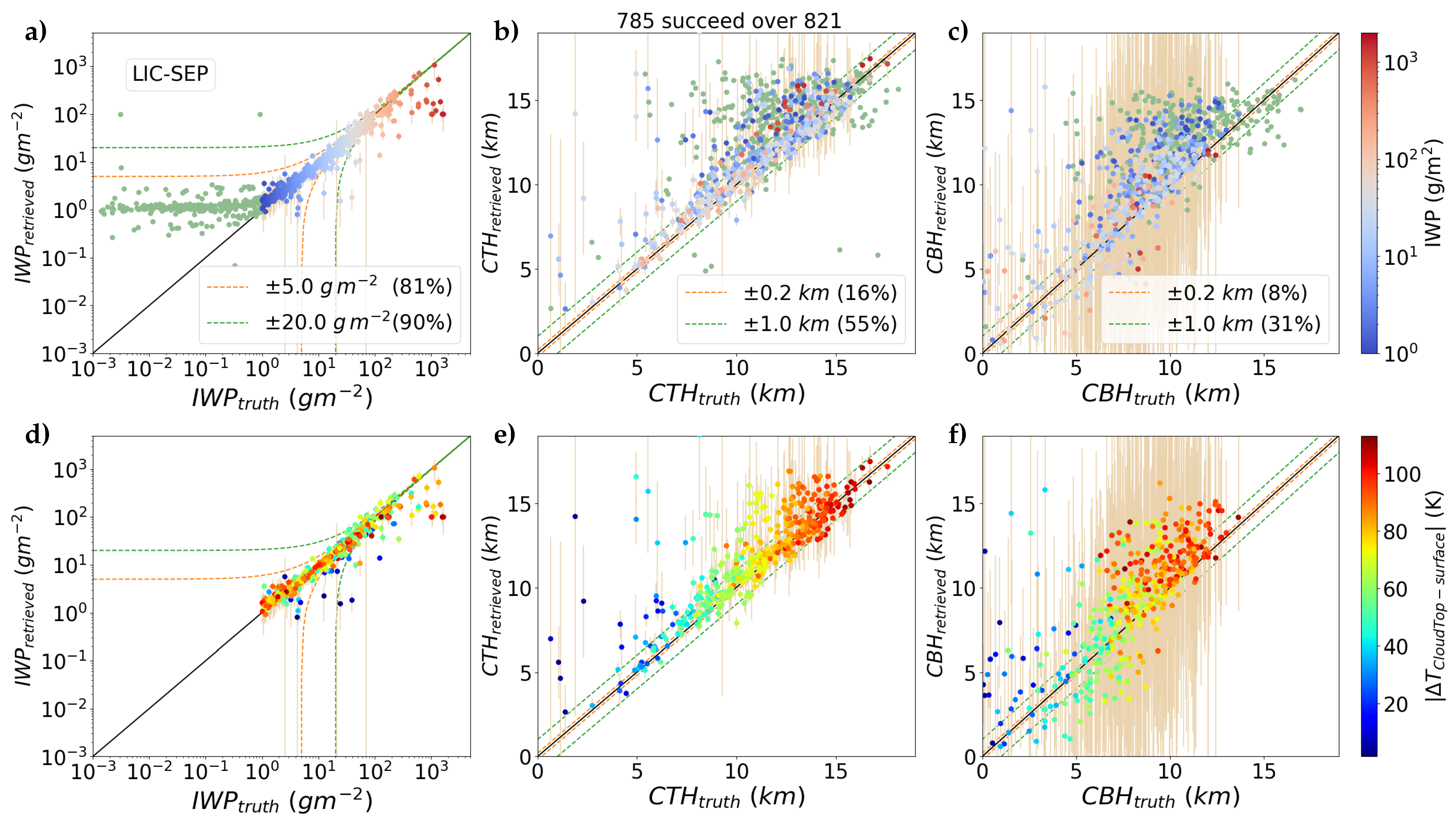
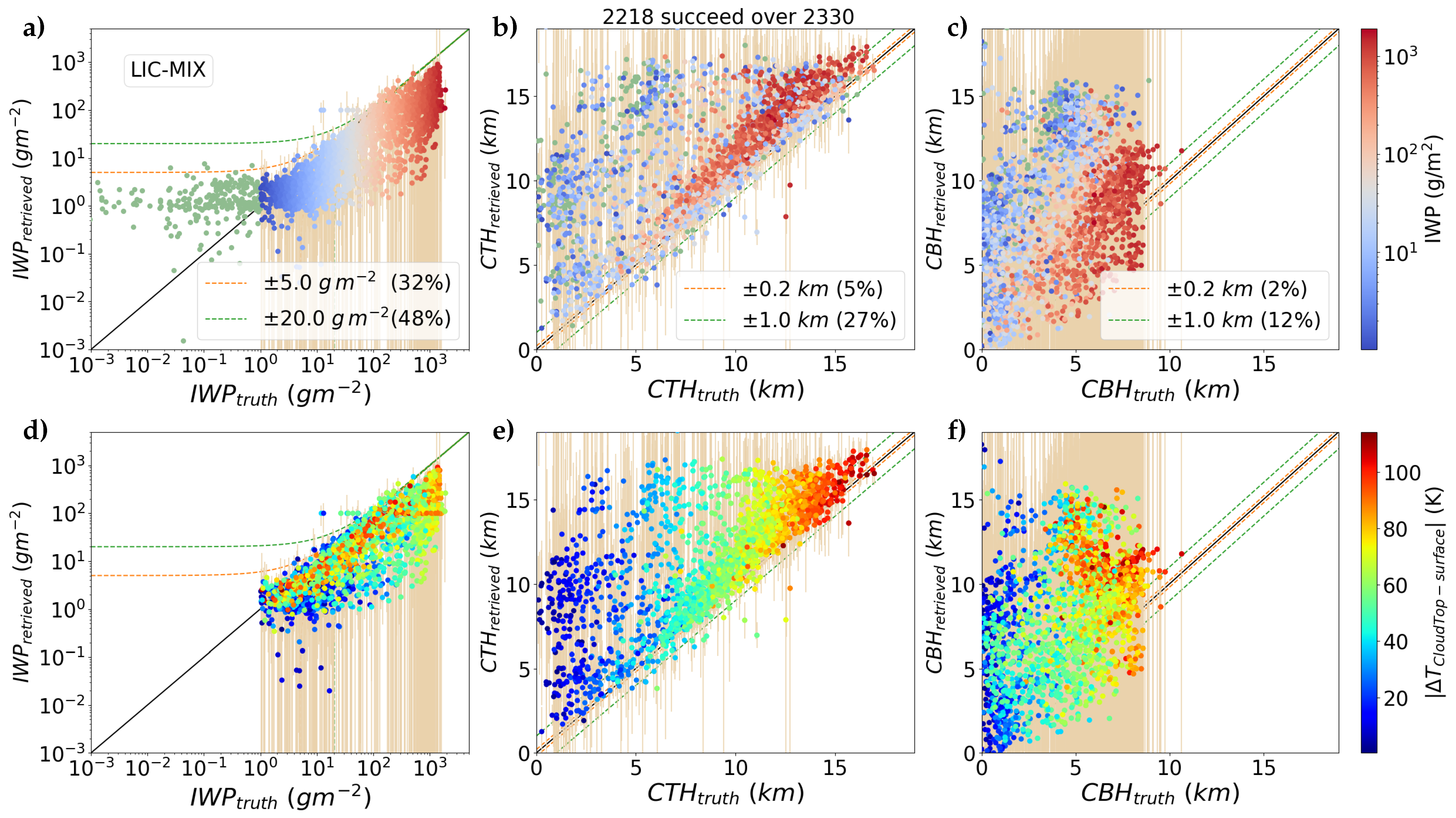
4.2. Retrieval Results from Synthetic Radiances
5. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Stocker, T.F.; Qin, D.; Plattner, G.K.; Tignor, M.; Allen, S.K.; Boschung, J.; Nauelsand, A.; Xia, Y.; Bex, V.; Midgley, P.M.E. IPCC, 2013: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; p. 1535. [Google Scholar]
- Zhang, Y.; Macke, A.; Albers, F. Effect of crystal size spectrum and crystal shape on stratiform cirrus radiative forcing. Atmos. Res. 1999, 52, 59–75. [Google Scholar] [CrossRef]
- Delanoë, J.; Hogan, R.J. A variational scheme for retrieving ice cloud properties from combined radar, lidar, and infrared radiometer. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Deng, M.; Mace, G.G.; Wang, Z.; Okamoto, H. Tropical Composition, Cloud and Climate Coupling Experiment validation for cirrus cloud profiling retrieval using CloudSat radar and CALIPSO lidar. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Deng, M.; Mace, G.G.; Wang, Z.; Lawson, R.P. Evaluation of several A-Train ice cloud retrieval products with in situ measurements collected during the SPARTICUS campaign. J. Appl. Meteorol. Climatol. 2013, 52, 1014–1030. [Google Scholar] [CrossRef]
- Sourdeval, O.; Gryspeerdt, E.; Krämer, M.; Goren, T.; Delanoë, J.; Afchine, A.; Hemmer, F.; Quaas, J. Ice crystal number concentration estimates from lidar–radar satellite remote sensing–Part 1: Method and evaluation. Atmos. Chem. Phys. 2018, 18, 14327–14350. [Google Scholar] [CrossRef]
- Hong, Y.; Liu, G. The characteristics of ice cloud properties derived from CloudSat and CALIPSO measurements. J. Clim. 2015, 28, 3880–3901. [Google Scholar] [CrossRef]
- Hong, Y.; Liu, G.; Li, J.L. Assessing the radiative effects of global ice clouds based on CloudSat and CALIPSO measurements. J. Clim. 2016, 29, 7651–7674. [Google Scholar] [CrossRef]
- Platnick, S.; Meyer, K.G.; King, M.D.; Wind, G.; Amarasinghe, N.; Marchant, B.; Arnold, G.T.; Zhang, Z.; Hubanks, P.A.; Holz, R.E.; et al. The MODIS cloud optical and microphysical products: Collection 6 updates and examples from Terra and Aqua. IEEE Trans. Geosci. Remote Sens. 2016, 55, 502–525. [Google Scholar] [CrossRef]
- Hong, G.; Yang, P.; Gao, B.C.; Baum, B.A.; Hu, Y.X.; King, M.D.; Platnick, S. High cloud properties from three years of MODIS Terra and Aqua collection-4 data over the tropics. J. Appl. Meteorol. Climatol. 2007, 46, 1840–1856. [Google Scholar] [CrossRef]
- Yang, P.; Zhang, L.; Hong, G.; Nasiri, S.L.; Baum, B.A.; Huang, H.L.; King, M.D.; Platnick, S. Differences between collection 4 and 5 MODIS ice cloud optical/microphysical products and their impact on radiative forcing simulations. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2886–2899. [Google Scholar] [CrossRef]
- Sourdeval, O.; C.-Labonnote, L.; Baran, A.J.; Brogniez, G. A methodology for simultaneous retrieval of ice and liquid water cloud properties. Part I: Information content and case study. Q. J. R. Meteorol. Soc. 2015, 141, 870–882. [Google Scholar] [CrossRef]
- Sourdeval, O.; C.-Labonnote, L.; Baran, A.J.; Mülmenstädt, J.; Brogniez, G. A methodology for simultaneous retrieval of ice and liquid water cloud properties. Part 2: Near-global retrievals and evaluation against A-Train products. Q. J. R. Meteorol. Soc. 2016, 142, 3063–3081. [Google Scholar] [CrossRef]
- Kelly, G.; Thépaut, J.N. Evaluation of the impact of the space component of the Global Observing System through Observing System Experiments. ECMWF Newsl. 2007, 113, 16–28. [Google Scholar]
- Collard, A.D.; McNally, A.P. The assimilation of infrared atmospheric sounding interferometer radiances at ECMWF. Q. J. R. Meteorol. Soc. 2009, 135, 1044–1058. [Google Scholar] [CrossRef]
- Guidard, V.; Fourrié, N.; Brousseau, P.; Rabier, F. Impact of IASI assimilation at global and convective scales and challenges for the assimilation of cloudy scenes. Q. J. R. Meteorol. Soc. 2011, 137, 1975–1987. [Google Scholar] [CrossRef]
- Siméoni, D.; Singer, C.; Chalon, G. Infrared atmospheric sounding interferometer. Acta Astronaut. 1997, 40, 113–118. [Google Scholar] [CrossRef]
- McNally, A.P. A note on the occurrence of cloud in meteorologically sensitive areas and the implications for advanced infrared sounders. Q. J. R. Meteorol. Soc. 2002, 128, 2551–2556. [Google Scholar] [CrossRef]
- Pavelin, E.G.; English, S.J.; Eyre, J.R. The assimilation of cloud-affected infrared satellite radiances for numerical weather prediction. Q. J. R. Meteorol. Soc. 2008, 134, 737–749. [Google Scholar] [CrossRef]
- McNally, A.P. The direct assimilation of cloud-affected satellite infrared radiances in the ECMWF 4D-Var. Q. J. R. Meteorol. Soc. 2009, 135, 1214–1229. [Google Scholar] [CrossRef]
- Martinet, P.; Fourrié, N.; Guidard, V.; Rabier, F.; Montmerle, T.; Brunel, P. Towards the use of microphysical variables for the assimilation of cloud-affected infrared radiances. Q. J. R. Meteorol. Soc. 2013, 139, 1402–1416. [Google Scholar] [CrossRef]
- Zhou, D.K.; Smith, W.L., Sr.; Liu, X.; Larar, A.M.; Huang, H.L.A.; Li, J.; McGill, M.J.; Mango, S.A. Thermodynamic and cloud parameter retrieval using infrared spectral data. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Zhou, D.K.; Smith, W.L., Sr.; Liu, X.; Larar, A.M.; Mango, S.A.; Huang, H.L. Physically retrieving cloud and thermodynamic parameters from ultraspectral IR measurements. J. Atmos. Sci. 2007, 64, 969–982. [Google Scholar] [CrossRef]
- Liu, X.; Zhou, D.K.; Larar, A.M.; Smith, W.L.; Schluessel, P.; Newman, S.M.; Taylor, J.P.; Wu, W. Retrieval of atmospheric profiles and cloud properties from IASI spectra using super-channels. Atmos. Chem. Phys. 2009, 9, 9121–9142. [Google Scholar] [CrossRef]
- Lavanant, L.; Fourrié, N.; Gambacorta, A.; Grieco, G.; Heilliette, S.; Hilton, F.I.; Kim, M.J.; McNally, A.P.; Nishihata, H.; Pavelin, E.G.; et al. Comparison of cloud products within IASI footprints for the assimilation of cloudy radiances. Q. J. R. Meteorol. Soc. 2011, 137, 1988–2003. [Google Scholar] [CrossRef]
- Martinet, P.; Fourrié, N.; Bouteloup, Y.; Bazile, E.; Rabier, F. Toward the improvement of short-range forecasts by the analysis of cloud variables from IASI radiances. Atmos. Sci. Lett. 2014, 15, 342–347. [Google Scholar] [CrossRef]
- Martinet, P.; Lavanant, L.; Fourrié, N.; Rabier, F.; Gambacorta, A. Evaluation of a revised IASI channel selection for cloudy retrievals with a focus on the Mediterranean basin. Q. J. R. Meteorol. Soc. 2014, 140, 1563–1577. [Google Scholar] [CrossRef]
- Stubenrauch, C.J.; Holz, R.; Chédin, A.; Mitchell, D.L.; Baran, A.J. Retrieval of cirrus ice crystal sizes from 8.3 and 11.1 m emissivities determined by the improved initialization inversion of TIROS-N Operational Vertical Sounder observations. J. Geophys. Res. Atmos. 1999, 104, 31793–31808. [Google Scholar] [CrossRef]
- Rädel, G.; Stubenrauch, C.J.; Holz, R.; Mitchell, D.L. Retrieval of effective ice crystal size in the infrared: Sensitivity study and global measurements from TIROS-N Operational Vertical Sounder. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Kahn, B.H.; Eldering, A.; Clough, S.A.; Fetzer, E.J.; Fishbein, E.; Gunson, M.R.; Lee, S.Y.; Lester, P.F.; Realmuto, V.J. Near micron-sized cirrus cloud particles in high-resolution infrared spectra: An orographic case study. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- August, T.; Klaes, D.; Schlüssel, P.; Hultberg, T.; Crapeau, M.; Arriaga, A.; O’Carroll, A.; Coppens, D.; Munro, R.; Calbet, X. IASI on Metop-A: Operational Level 2 retrievals after five years in orbit. J. Quant. Spectrosc. Radiat. Transf. 2012, 113, 1340–1371. [Google Scholar] [CrossRef]
- Huang, X.L.; Yung, Y.L.; Margolis, J.S. Use of high-resolution measurements for the retrieval of temperature and gas-concentration profiles from outgoing infrared spectra in the presence of cirrus clouds. Appl. Opt. 2003, 42, 2155–2165. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.L.; Yang, P.; Wei, H.; Baum, B.A.; Hu, Y.; Antonelli, P.; Ackerman, S.A. Inference of ice cloud properties from high spectral resolution infrared observations. IEEE Trans. Geosci. Remote. Sens. 2004, 42, 842–853. [Google Scholar] [CrossRef]
- Wei, H.; Yang, P.; Li, J.; Baum, B.A.; Huang, H.L.; Platnick, S.; Hu, Y.; Strow, L. Retrieval of semitransparent ice cloud optical thickness from Atmospheric Infrared Sounder (AIRS) measurements. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2254–2267. [Google Scholar] [CrossRef]
- Wang, C.; Yang, P.; Platnick, S.; Heidinger, A.K.; Baum, B.A.; Greenwald, T.; Zhang, Z.; Holz, R.E. Retrieval of ice cloud properties from AIRS and MODIS observations based on a fast high-spectral-resolution radiative transfer model. J. Appl. Meteorol. Climatol. 2013, 52, 710–726. [Google Scholar] [CrossRef]
- Wu, W.; Liu, X.; Zhou, D.K.; Larar, A.M.; Yang, Q.; Kizer, S.H.; Liu, Q. The application of PCRTM physical retrieval methodology for IASI cloudy scene analysis. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5042–5056. [Google Scholar] [CrossRef]
- Crevoisier, C.; Clerbaux, C.; Guidard, V.; Phulpin, T.; Armante, R.; Barret, B.; Camy-Peyret, C.; Chaboureau, J.-P.; Coheur, P.-F.; Crépeau, L.; et al. Towards IASI-New Generation (IASI-NG): Impact of improved spectral resolution and radiometric noise on the retrieval of thermodynamic, chemistry and climate variables. Atmos. Meas. Tech. 2014, 7, 4367–4385. [Google Scholar] [CrossRef]
- Hilton, F.; Armante, R.; August, T.; Barnet, C.; Bouchard, A.; Camy-Peyret, C.; Capelle, V.; Clarisse, L.; Clerbaux, C.; Coheur, P.F.; et al. Hyperspectral Earth observation from IASI: Five years of accomplishments. Bull. Am. Meteorol. Soc. 2012, 93, 347–370. [Google Scholar] [CrossRef]
- Prunet, P.; Thépaut, J.N.; Cassé, V. The information content of clear sky IASI radiances and their potential for numerical weather prediction. Q. J. R. Meteorol. Soc. 1998, 124, 211–241. [Google Scholar] [CrossRef]
- Clerbaux, C.; Boynard, A.; Clarisse, L.; George, M.; Hadji-Lazaro, J.; Herbin, H.; Hurtmans, D.; Pommier, M.; Razavi, A.; Turquety, S.; et al. Monitoring of atmospheric composition using the thermal infrared IASI/MetOp sounder. Atmos. Chem. Phys. 2009, 9, 6041–6054. [Google Scholar] [CrossRef]
- Baran, A.J. The dependence of cirrus infrared radiative properties on ice crystal geometry and shape of the size-distribution function. Q. J. R. Meteorol. Soc. 2005, 131, 1129–1142. [Google Scholar] [CrossRef]
- Hong, G.; Yang, P.; Huang, H.L.; Baum, B.A.; Hu, Y.; Platnick, S. The sensitivity of ice cloud optical and microphysical passive satellite retrievals to cloud geometrical thickness. IEEE Trans. Geosci. Remote. Sens. 2007, 45, 1315–1323. [Google Scholar] [CrossRef]
- Dubuisson, P.; Giraud, V.; Pelon, J.; Cadet, B.; Yang, P. Sensitivity of thermal infrared radiation at the top of the atmosphere and the surface to ice cloud microphysics. J. Appl. Meteorol. Climatol. 2008, 47, 2545–2560. [Google Scholar] [CrossRef]
- Heymsfield, A.J.; Knollenberg, R.G. Properties of cirrus generating cells. J. Atmos. Sci. 1972, 29, 1358–1366. [Google Scholar] [CrossRef][Green Version]
- Baran, A.J. A review of the light scattering properties of cirrus. J. Quant. Spectrosc. Radiat. Transf. 2009, 110, 1239–1260. [Google Scholar] [CrossRef]
- Heymsfield, A.J.; Platt, C.M.R. A parameterization of the particle size spectrum of ice clouds in terms of the ambient temperature and the ice water content. J. Atmos. Sci. 1984, 41, 846–855. [Google Scholar] [CrossRef]
- Baum, B.A.; Heymsfield, A.J.; Yang, P.; Bedka, S.T. Bulk scattering properties for the remote sensing of ice clouds. Part I: Microphysical data and models. J. Appl. Meteorol. Climatol. 2005, 44, 1885–1895. [Google Scholar] [CrossRef]
- Baum, B.A.; Yang, P.; Nasiri, S.; Heidinger, A.K.; Heymsfield, A.; Li, J. Bulk scattering properties for the remote sensing of ice clouds. Part III: High-resolution spectral models from 100 to 3250 cm-1. J. Appl. Meteorol. Climatol. 2007, 46, 423–434. [Google Scholar] [CrossRef]
- Field, P.R.; Heymsfield, A.J.; Bansemer, A. Snow size distribution parameterization for midlatitude and tropical ice clouds. J. Atmos. Sci. 2007, 64, 4346–4365. [Google Scholar] [CrossRef]
- Baran, A.J.; Cotton, R.; Furtado, K.; Havemann, S.; C.-Labonnote, L.; Marenco, F.; Smith, A.; Thelen, J.C. A self-consistent scattering model for cirrus. II: The high and low frequencies. Q. J. R. Meteorol. Soc. 2014, 140, 1039–1057. [Google Scholar] [CrossRef]
- Vidot, J.; Baran, A.J.; Brunel, P. A new ice cloud parameterization for infrared radiative transfer simulation of cloudy radiances: Evaluation and optimization with IIR observations and ice cloud profile retrieval products. J. Geophys. Res. Atmos. 2015, 120, 6937–6951. [Google Scholar] [CrossRef]
- Baran, A.J.; Connolly, P.J.; Heymsfield, A.J.; Bansemer, A. Using in situ estimates of ice water content, volume extinction coefficient, and the total solar optical depth obtained during the tropical ACTIVE campaign to test an ensemble model of cirrus ice crystals. Q. J. R. Meteorol. Soc. 2011, 137, 199–218. [Google Scholar] [CrossRef]
- Furtado, K.; Field, P.R.; Cotton, R.; Baran, A.J. The sensitivity of simulated high clouds to ice crystal fall speed, shape and size distribution. Q. J. R. Meteorol. Soc. 2015, 141, 1546–1559. [Google Scholar] [CrossRef]
- Baran, A.J.; C.-Labonnote, L. A self-consistent scattering model for cirrus. I: The solar region. Q. J. R. Meteorol. Soc. 2007, 133, 1899–1912. [Google Scholar] [CrossRef]
- Matricardi, M. An assessment of the accuracy of the RTTOV fast radiative transfer model using IASI data. Atmos. Chem. Phys. 2009, 9, 6899–6913. [Google Scholar] [CrossRef]
- Saunders, R.; Hocking, J.; Turner, E.; Rayer, P.; Rundle, D.; Brunel, P.; Vidot, J.; Roquet, P.; Matricardi, M.; Geer, A.; et al. An update on the RTTOV fast radiative transfer model (currently at version 12). Geosci. Model Dev. 2018, 11, 2717–2737. [Google Scholar] [CrossRef]
- Chou, M.D.; Lee, K.T.; Tsay, S.C.; Fu, Q. Parameterization for cloud longwave scattering for use in atmospheric models. J. Clim. 1999, 12, 159–169. [Google Scholar] [CrossRef]
- Vidot, J.; C.-Labonnote, L.; Baran, A.; Matricardi, M.; Brunel, P. Evaluation of the RTTOV scattering parameterization with LIDORT for hyperspectral IR cloudy brightness temperature and jacobians. Remote Sens. 2021. in preparation. [Google Scholar]
- Rodgers, C.D. Inverse Methods for Atmospheric Sounding: Theory and Practice, 2nd ed.; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2000. [Google Scholar]
- Smith, W.L.; Frey, R. On cloud altitude determinations from high resolution interferometer sounder (HIS) observations. J. Appl. Meteorol. Climatol. 1990, 29, 658–662. [Google Scholar] [CrossRef]
- Cooper, S.J.; L’Ecuyer, T.S.; Gabriel, P.; Baran, A.J.; Stephens, G.L. Objective assessment of the information content of visible and infrared radiance measurements for cloud microphysical property retrievals over the global oceans. Part II: Ice clouds. J. Appl. Meteorol. Climatol. 2006, 45, 42–62. [Google Scholar] [CrossRef]
- Garnier, A.; Pelon, J.; Dubuisson, P.; Yang, P.; Faivre, M.; Chomette, O.; Pascal, N.; Lucker, P.; Murray, T. Retrieval of cloud properties using CALIPSO Imaging Infrared Radiometer. Part II: Effective diameter and ice water path. J. Appl. Meteorol. Climatol. 2013, 52, 2582–2599. [Google Scholar] [CrossRef]
- Dubovik, O.; King, M.D. A flexible inversion algorithm for retrieval of aerosol optical properties from Sun and sky radiance measurements. J. Geophys. Res. Atmos. 2000, 105, 20673–20696. [Google Scholar] [CrossRef]
- Eresmaa, R.; McNally, A.P. Diverse Profile Datasets from the ECMWF 137-Level Short-Range Forecasts; Document No. NWPSAF-EC-TR-017, Version 1.0; EUMETSAT Satellite Application Facility (NWP SAF): Darmstadt, Germany, 2014. [Google Scholar]
- Rodgers, C.D. Information Content and Optimisation of High Spectral Resolution Remote Measurements. Adv. Space Res. 1998, 21, 361–367. [Google Scholar] [CrossRef]
- Wyser, K. The effective radius in ice clouds. J. Clim. 1998, 11, 1793–1802. [Google Scholar] [CrossRef]
- Iacobellis, S.F.; McFarquhar, G.M.; Mitchell, D.L.; Somerville, R.C.J. The sensitivity of radiative fluxes to parameterized cloud microphysics. J. Clim. 2003, 16, 2979–2996. [Google Scholar] [CrossRef][Green Version]
- Serio, C.; Masiello, G.; Mastro, P.; Tobin, D.C. Characterization of the Observational Covariance Matrix of Hyper-Spectral Infrared Satellite Sensors Directly from Measured Earth Views. Sensors 2020, 20, 1492. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- L’Ecuyer, T.S.; Gabriel, P.; Leesman, K.; Cooper, S.J.; Stephens, G.L. Objective assessment of the information content of visible and infrared radiance measurements for cloud microphysical property retrievals over the global oceans. Part I: Liquid clouds. J. Appl. Meteorol. Climatol. 2006, 45, 20–41. [Google Scholar] [CrossRef]
- Winker, D.M.; Pelon, J.R.; McCormick, M.P. CALIPSO mission: Spaceborne lidar for observation of aerosols and clouds. In Lidar Remote Sensing for Industry and Environment Monitoring III; International Society for Optics and Photonics: Bellingham, Washington, 2003; Volume 4893, pp. 1–11. [Google Scholar] [CrossRef]
- Stephens, G.L.; Vane, D.G.; Boain, R.J.; Mace, G.G.; Sassen, K.; Wang, Z.; Illingworth, A.J.; O’connor, E.J.; Rossow, W.B.; Durden, S.L.; et al. The CloudSat mission and the A-Train: A new dimension of space-based observations of clouds and precipitation. Bull. Am. Meteorol. Soc. 2002, 83, 1771–1790. [Google Scholar] [CrossRef]
- Intrieri, J.M.; Stephens, G.L.; Eberhard, W.L.; Uttal, T. A method for determining cirrus cloud particle sizes using lidar and radar backscatter technique. J. Appl. Meteorol. Climatol. 1993, 32, 1074–1082. [Google Scholar] [CrossRef][Green Version]
- Wang, Z.; Sassen, K. Cirrus cloud microphysical property retrieval using lidar and radar measurements. Part I: Algorithm description and comparison with in situ data. J. Appl. Meteorol. Climatol. 2002, 41, 218–229. [Google Scholar] [CrossRef]
- Tinel, C.; Testud, J.; Pelon, J.; Hogan, R.J.; Protat, A.; Delanoë, J.; Bouniol, D. The retrieval of ice-cloud properties from cloud radar and lidar synergy. J. Appl. Meteorol. Climatol. 2005, 44, 860–875. [Google Scholar] [CrossRef]
- Delanoë, J.; Hogan, R.J. Combined CloudSat-CALIPSO-MODIS retrievals of the properties of ice clouds. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leonarski, L.; C.-Labonnote, L.; Compiègne, M.; Vidot, J.; Baran, A.J.; Dubuisson, P. Potential of Hyperspectral Thermal Infrared Spaceborne Measurements to Retrieve Ice Cloud Physical Properties: Case Study of IASI and IASI-NG. Remote Sens. 2021, 13, 116. https://doi.org/10.3390/rs13010116
Leonarski L, C.-Labonnote L, Compiègne M, Vidot J, Baran AJ, Dubuisson P. Potential of Hyperspectral Thermal Infrared Spaceborne Measurements to Retrieve Ice Cloud Physical Properties: Case Study of IASI and IASI-NG. Remote Sensing. 2021; 13(1):116. https://doi.org/10.3390/rs13010116
Chicago/Turabian StyleLeonarski, Lucie, Laurent C.-Labonnote, Mathieu Compiègne, Jérôme Vidot, Anthony J. Baran, and Philippe Dubuisson. 2021. "Potential of Hyperspectral Thermal Infrared Spaceborne Measurements to Retrieve Ice Cloud Physical Properties: Case Study of IASI and IASI-NG" Remote Sensing 13, no. 1: 116. https://doi.org/10.3390/rs13010116
APA StyleLeonarski, L., C.-Labonnote, L., Compiègne, M., Vidot, J., Baran, A. J., & Dubuisson, P. (2021). Potential of Hyperspectral Thermal Infrared Spaceborne Measurements to Retrieve Ice Cloud Physical Properties: Case Study of IASI and IASI-NG. Remote Sensing, 13(1), 116. https://doi.org/10.3390/rs13010116