Spatial Downscaling of MODIS Chlorophyll-a with Genetic Programming in South Korea
Abstract
1. Introduction
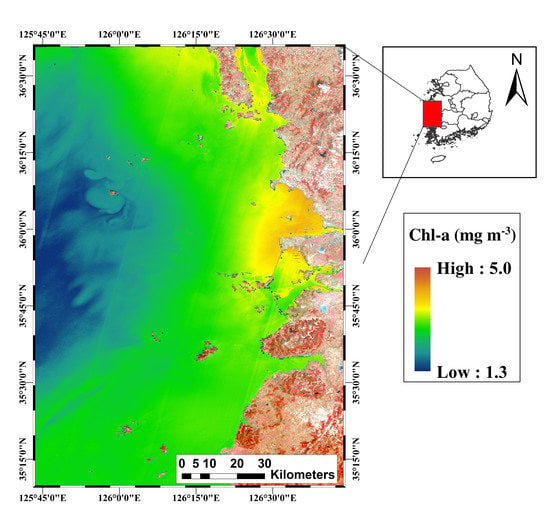
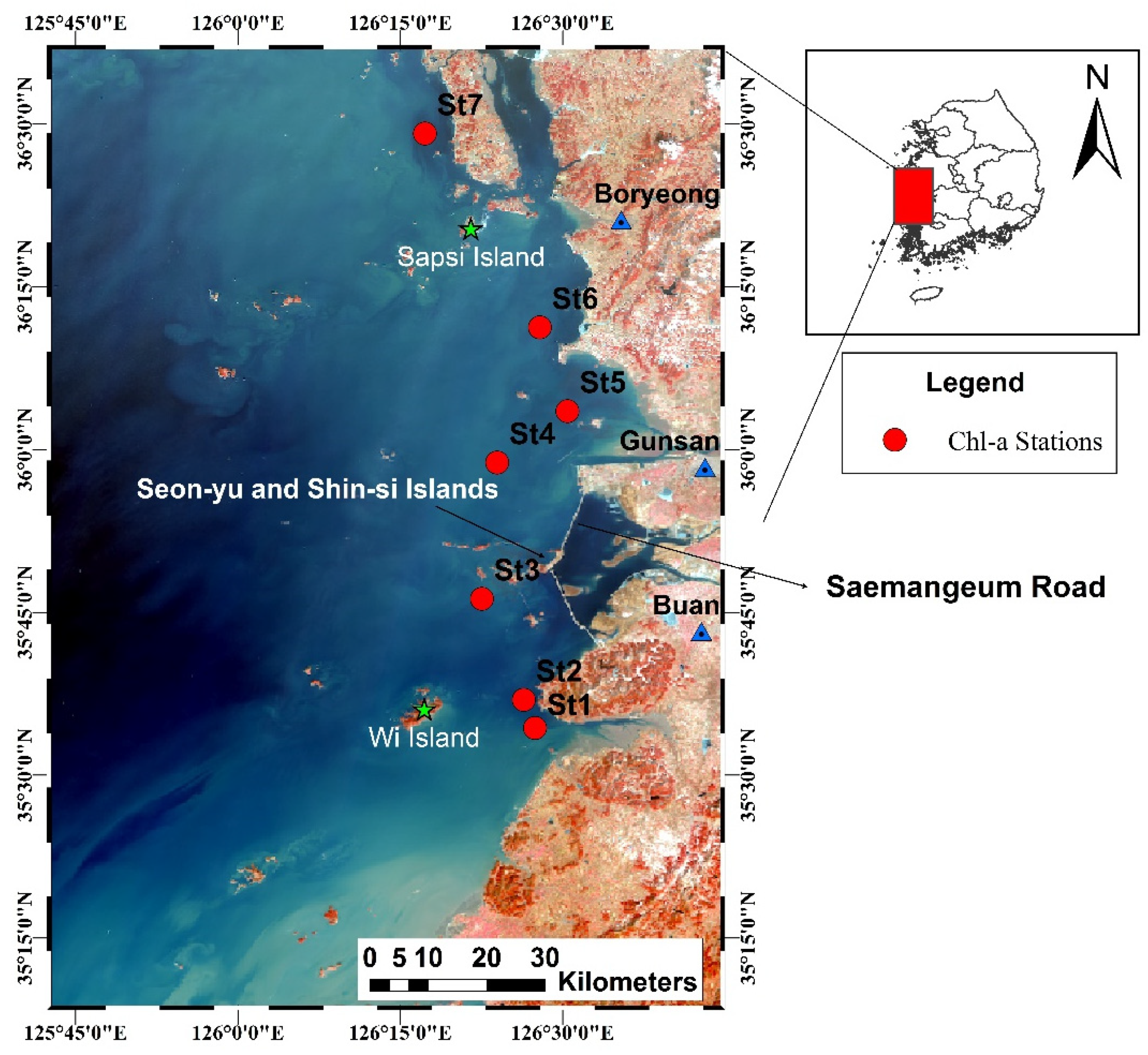
2. Study Area
3. Materials and Methods
3.1. Data Description
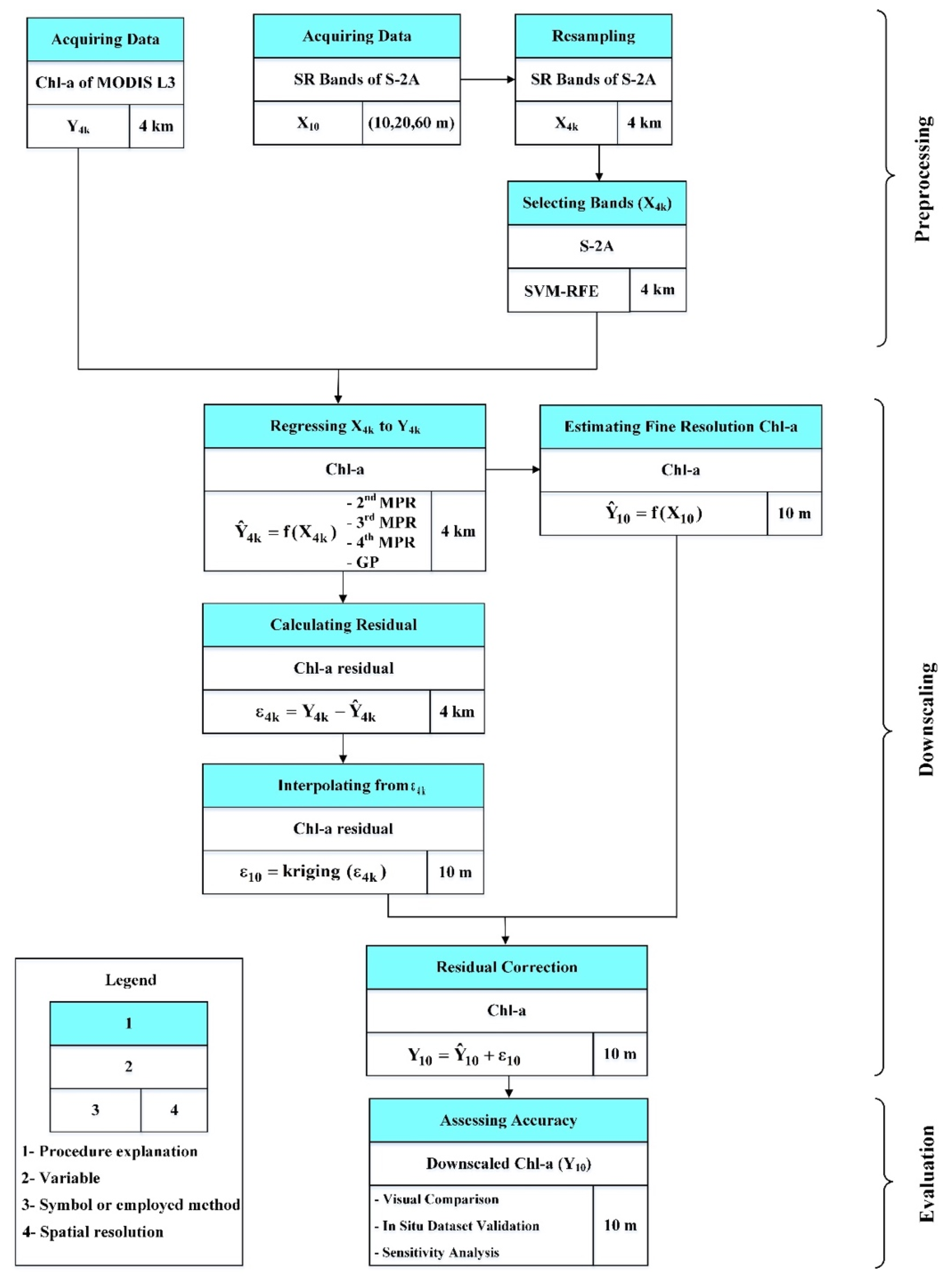
3.2. Preprocessing
3.3. Downscaling
3.4. Sensitivity Analysis
3.5. Mathematical Background
3.5.1. Multiple Polynomial Regression
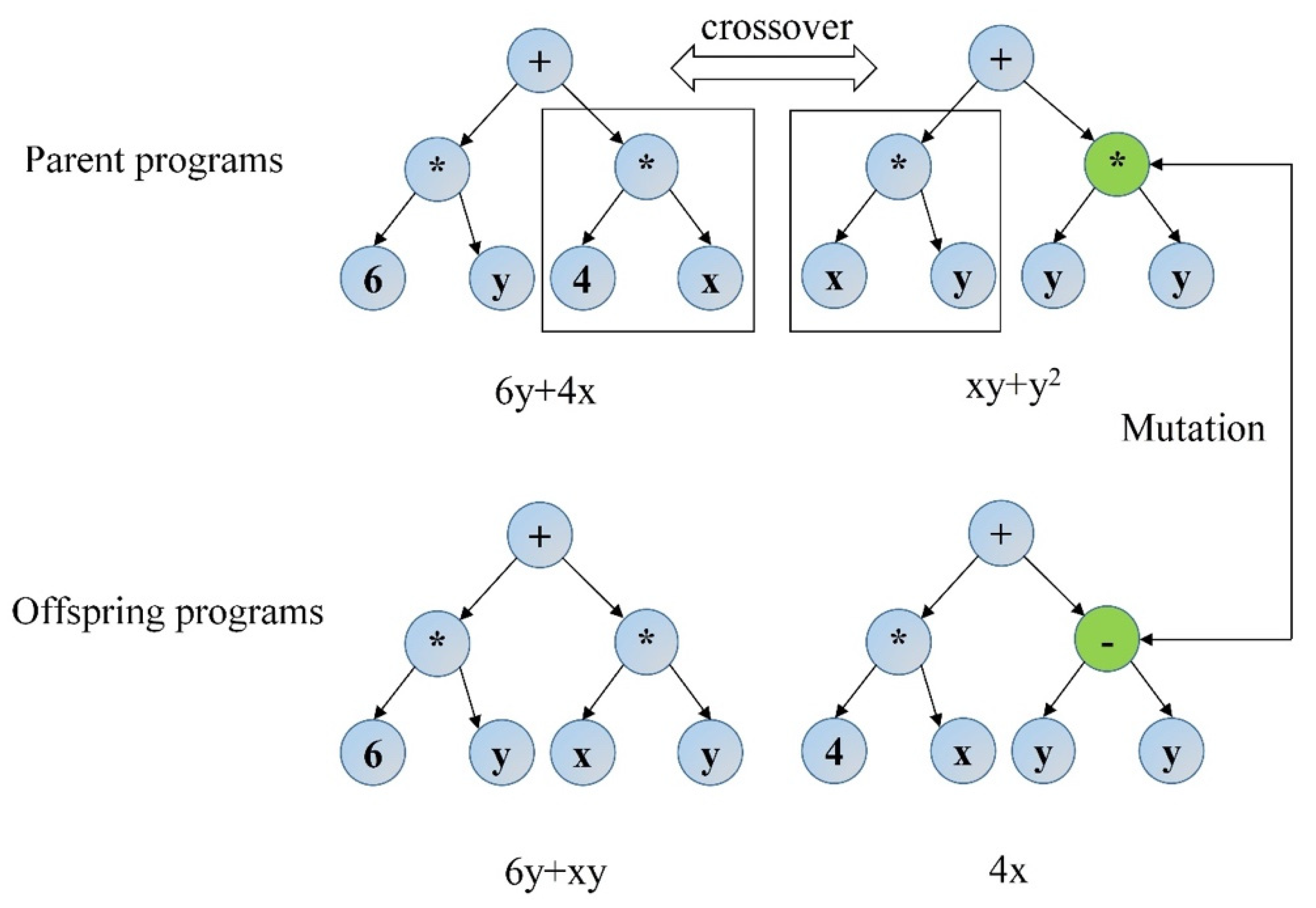
3.5.2. Genetic Programming
4. Results
4.1. Preprocessing
4.2. Downscaling Results
4.3. Model Evaluation
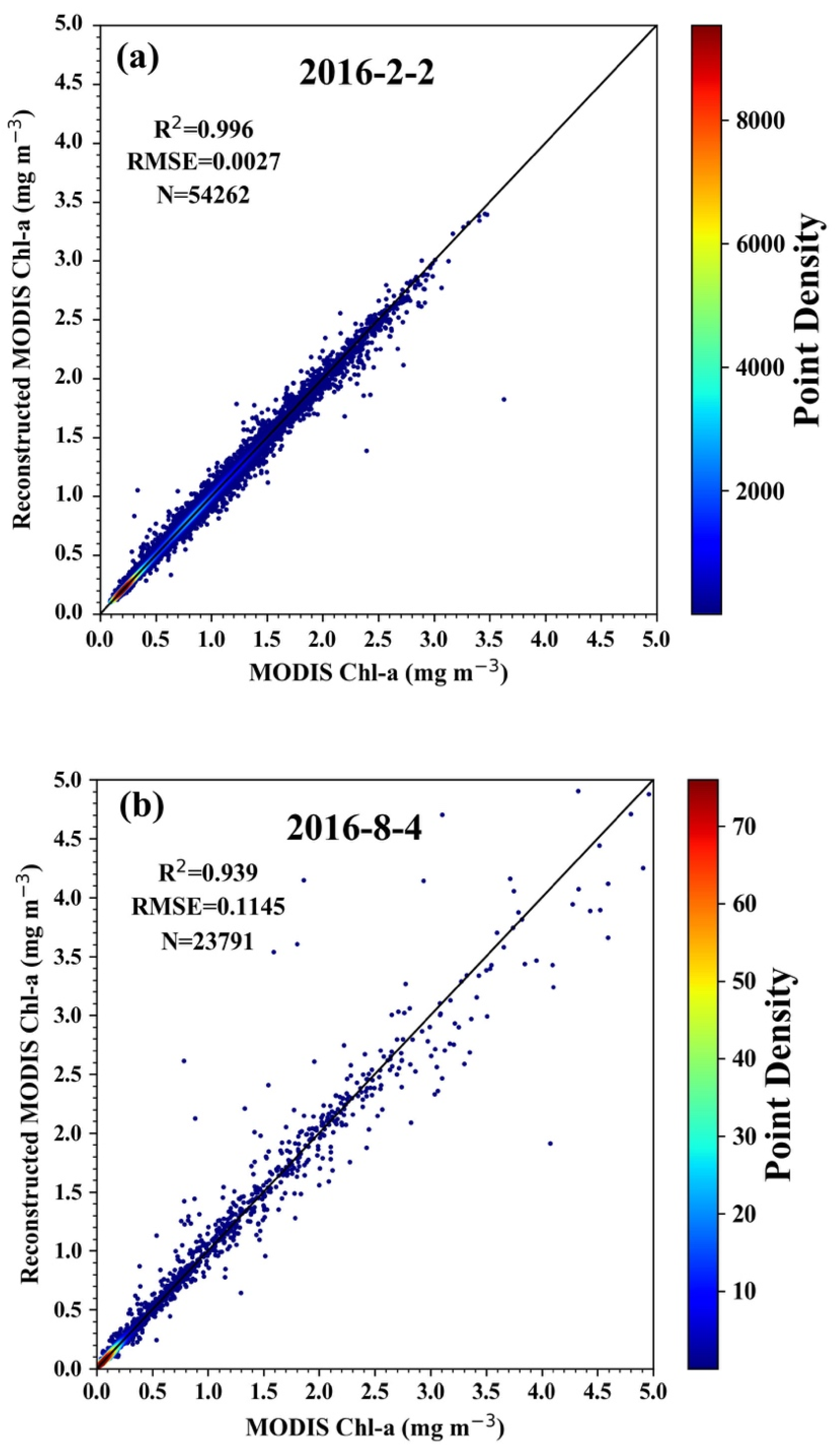
4.3.1. Visual Comparison
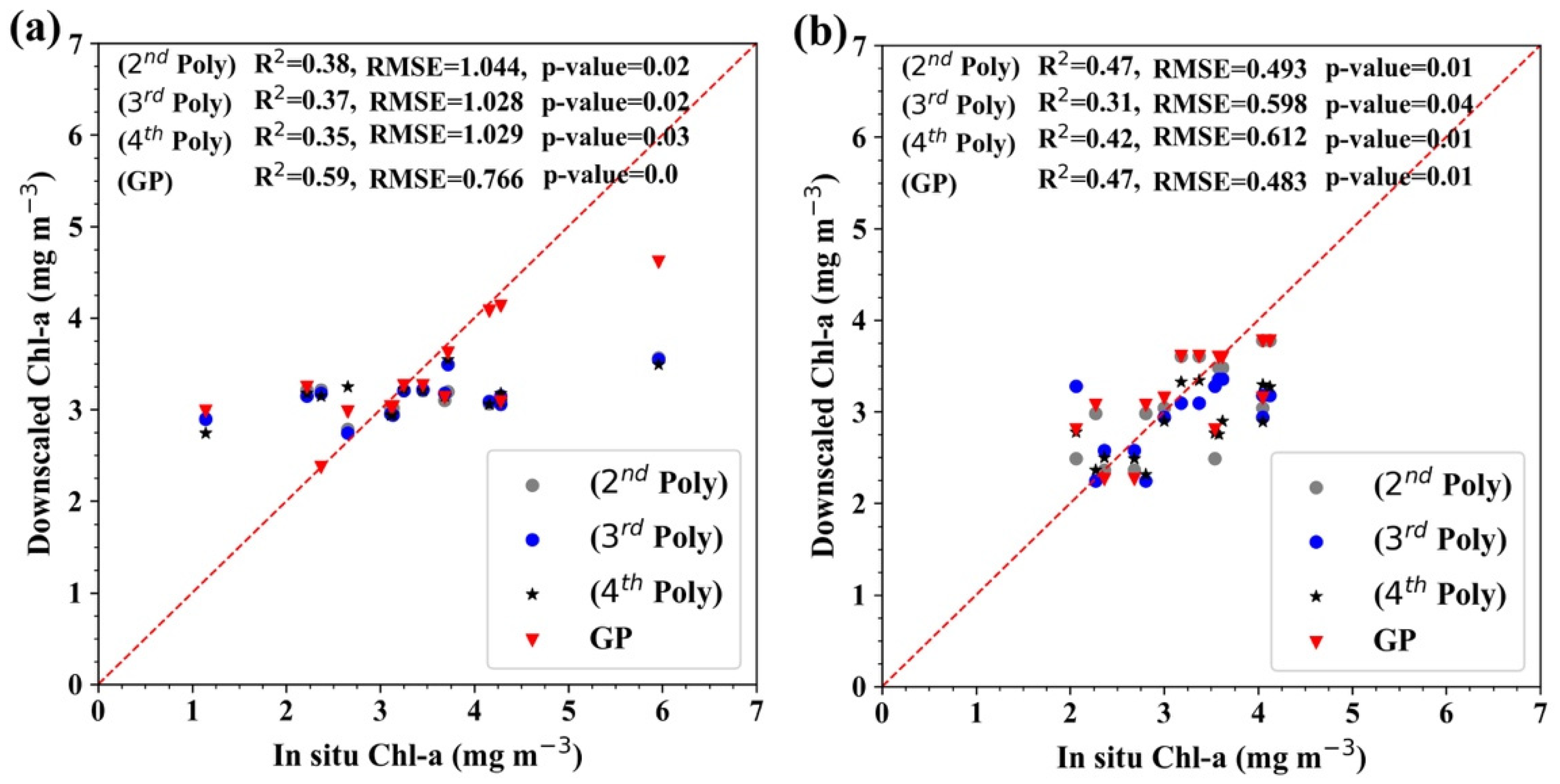
4.3.2. In Situ Validation
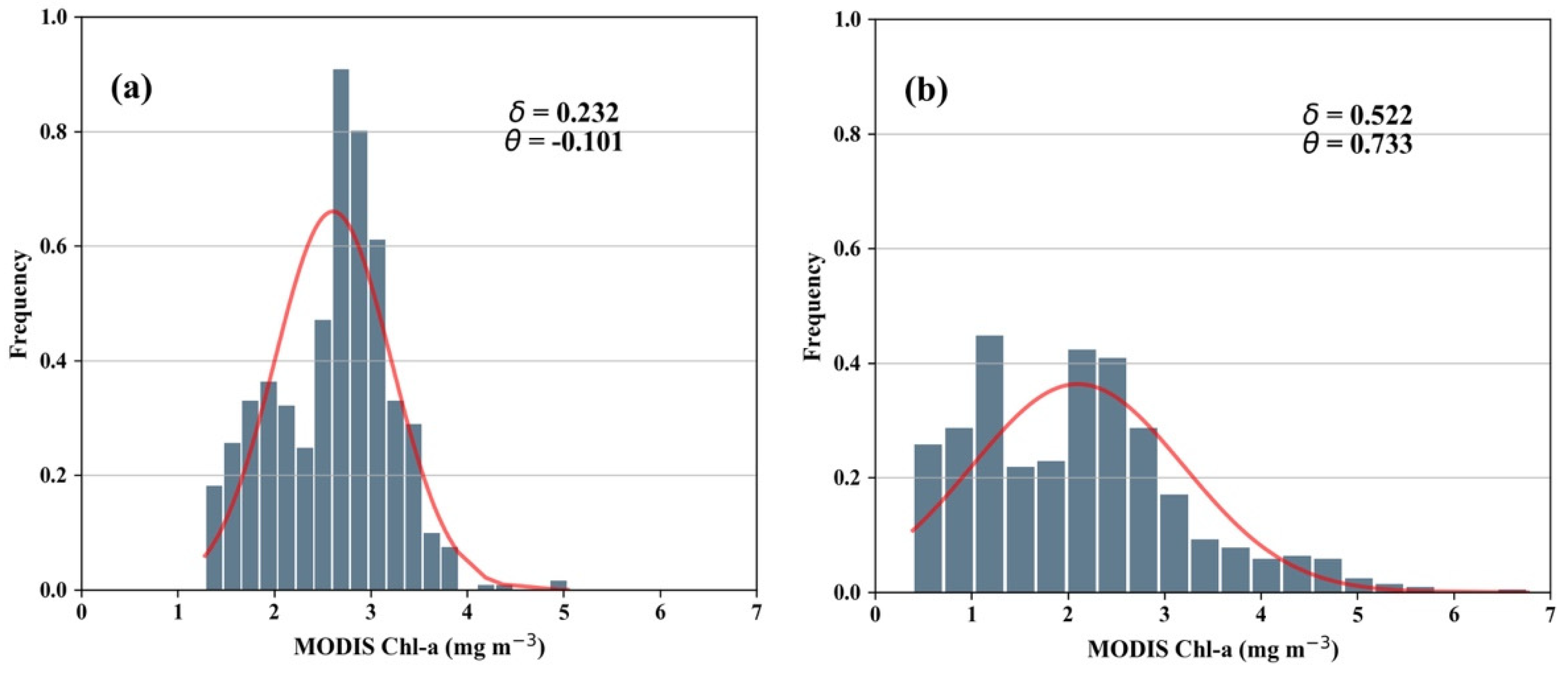
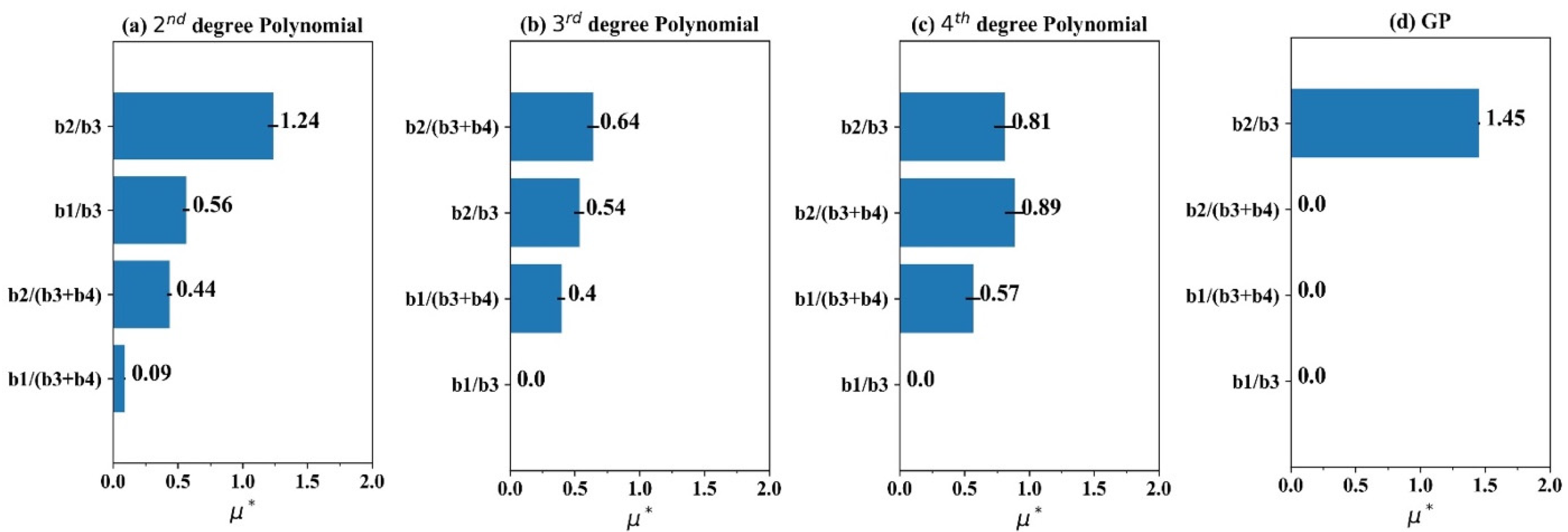
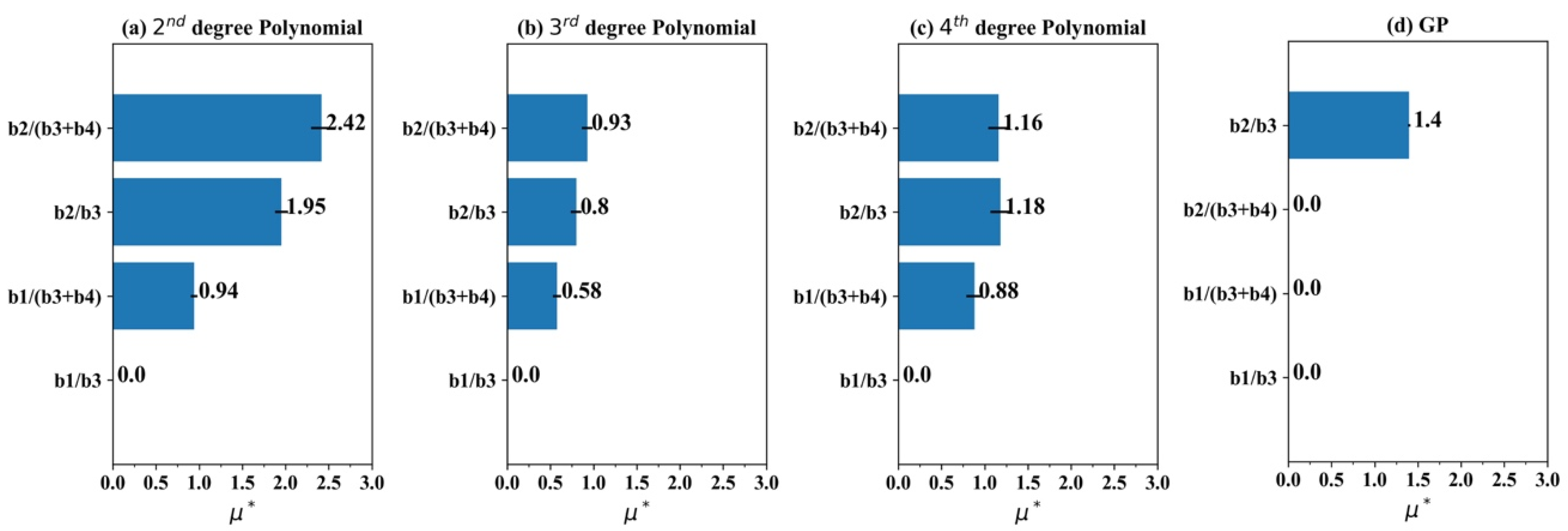
4.3.3. Sensitivity Analysis
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bierman, P.; Lewis, M.; Ostendorf, B.; Tanner, J. A review of methods for analysing spatial and temporal patterns in coastal water quality. Ecol. Indic. 2011, 11, 103–114. [Google Scholar] [CrossRef]
- Blondeau-Patissier, D.; Gower, J.F.; Dekker, A.; Phinn, S.; Brando, V. A review of ocean color remote sensing methods and statistical techniques for the detection, mapping and analysis of phytoplankton blooms in coastal and open oceans. Prog. Oceanogr. 2014, 123, 123–144. [Google Scholar] [CrossRef]
- Cullen, J.J. The deep chlorophyll maximum: Comparing vertical profiles of chlorophyll a. Can. J. Fish. Aquat. Sci. 1982, 39, 791–803. [Google Scholar] [CrossRef]
- Guan, X.; Li, J.; Booty, W.G. Monitoring lake simcoe water clarity using Landsat-5 TM images. Water Resour. Manag. 2011, 25, 2015–2033. [Google Scholar] [CrossRef]
- Carpenter, S.R.; Caraco, N.F.; Correll, D.L.; Howarth, R.W.; Sharpley, A.N.; Smith, V.H. Nonpoint pollution of surface waters with phosphorus and nitrogen. Ecol. Appl. 1998, 8, 559–568. [Google Scholar] [CrossRef]
- Smith, V.H. Cultural eutrophication of inland, estuarine, and coastal waters. In Successes, Limitations, and Frontiers in Ecosystem Science; Springer: New York, NY, USA, 1998; pp. 7–49. [Google Scholar]
- Kar, D. Epizootic Ulcerative Fish Disease Syndrome; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Bacher, C.; Grant, J.; Hawkins, A.J.; Fang, J.; Zhu, M.; Besnard, M. Modelling the effect of food depletion on scallop growth in Sungo Bay (China). Aquat. Living Resour. 2003, 16, 10–24. [Google Scholar] [CrossRef]
- Huot, Y.; Babín, M.; Bruyant, F.; Grob, C.; Twardowski, M.S.; Claustre, H. Does chlorophyll a provide the best index of phytoplankton biomass for primary productivity studies? Biogeosci. Discuss. 2007, 4, 707–745. [Google Scholar] [CrossRef]
- Goetz, S.J.; Gardiner, E.P.; Viers, J.H. Monitoring freshwater, estuarine and near-shore benthic ecosystems with multi-sensor remote sensing: An introduction to the special issue. Remote Sens. Environ. 2008, 112, 3993–3995. [Google Scholar] [CrossRef]
- Kutser, T. Passive optical remote sensing of cyanobacteria and other intense phytoplankton blooms in coastal and inland waters. Int. J. Remote Sens. 2009, 30, 4401–4425. [Google Scholar] [CrossRef]
- Schaeffer, B.A.; Schaeffer, K.G.; Keith, D.; Lunetta, R.S.; Conmy, R.; Gould, R.W. Barriers to adopting satellite remote sensing for water quality management. Int. J. Remote Sens. 2013, 34, 7534–7544. [Google Scholar] [CrossRef]
- Merico, A.; Brown, C.W.; Groom, S.B.; Miller, P.; Tyrrell, T. Analysis of satellite imagery forEmiliania huxleyiblooms in the Bering Sea before 1997. Geophys. Res. Lett. 2003, 30, 30. [Google Scholar] [CrossRef]
- Gower, J. Productivity and plankton blooms observed with Seawifs and in-situ sensors. In Proceedings of the IGARSS 2001, Scanning the Present and Resolving the Future, Proceedings, IEEE 2001 International Geoscience and Remote Sensing Symposium (Cat. No.01CH37217), Sydney, NSW, Australia, 9–13 July 2001; pp. 2181–2183. [Google Scholar]
- Lavender, S.; Groom, S.B. The detection and mapping of algal blooms from space. Int. J. Remote Sens. 2001, 22, 197–201. [Google Scholar] [CrossRef]
- Siegel, D.; Behrenfeld, M.J.; Maritorena, S.; McClain, C.; Antoine, D.; Bailey, S.W.; Bontempi, P.; Boss, E.; Dierssen, H.; Doney, S.C.; et al. Regional to global assessments of phytoplankton dynamics from the SeaWiFS mission. Remote Sens. Environ. 2013, 135, 77–91. [Google Scholar] [CrossRef]
- Hu, C.; Muller-Karger, F.E.; Taylor, C.J.; Carder, K.L.; Kelble, C.; Johns, E.; Heil, C.A. Red tide detection and tracing using MODIS fluorescence data: A regional example in SW Florida coastal waters. Remote Sens. Environ. 2005, 97, 311–321. [Google Scholar] [CrossRef]
- Gower, J.; King, S.; Yan, W.; Borstad, G.; Brown, L. Use of the 709 nm band of MERIS to detect intense plankton blooms and other conditions in coastal waters. In Proceedings of the MERIS User Workshop, Frascati, Italy, 10–13 November 2003. [Google Scholar]
- Hu, C. A novel ocean color index to detect floating algae in the global oceans. Remote Sens. Environ. 2009, 113, 2118–2129. [Google Scholar] [CrossRef]
- Claustre, H.; Babin, M.; Merien, D.; Ras, J.; Prieur, L.; Dallot, S.; Prášil, O.; Dousova, H.; Moutin, T. Toward a taxon-specific parameterization of bio-optical models of primary production: A case study in the North Atlantic. J. Geophys. Res. Space Phys. 2005, 110, 110. [Google Scholar] [CrossRef]
- Sathyendranath, S.; Watts, L.; Devred, E.; Platt, T.; Caverhill, C.; Maass, H. Discrimination of diatoms from other phytoplankton using ocean-colour data. Mar. Ecol. Prog. Ser. 2004, 272, 59–68. [Google Scholar] [CrossRef]
- Shang, S.; Dong, Q.; Lee, Z.; Li, Y.; Xie, Y.; Behrenfeld, M. MODIS observed phytoplankton dynamics in the Taiwan Strait: An absorption-based analysis. Biogeosciences 2011, 8, 841–850. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Arnone, R.A. Deriving inherent optical properties from water color: A multiband quasi-analytical algorithm for optically deep waters. Appl. Opt. 2002, 41, 5755–5772. [Google Scholar] [CrossRef]
- Addesso, P.; Longo, M.; Maltese, A.; Restaino, R.; Vivone, G. Batch methods for resolution enhancement of TIR image sequences. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3372–3385. [Google Scholar] [CrossRef]
- Bechtel, B.; Zakšek, K.; Hoshyaripour, G. Downscaling land surface temperature in an urban area: A case study for Hamburg, Germany. Remote Sens. 2012, 4, 3184–3200. [Google Scholar] [CrossRef]
- Liu, D.; Pu, R. Downscaling thermal infrared radiance for subpixel land surface temperature retrieval. Sensors 2008, 8, 2695–2706. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Zhao, S.; Duan, Z.; Qin, Z. An improved spatial downscaling procedure for TRMM 3B43 precipitation product using geographically weighted regression. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4592–4604. [Google Scholar] [CrossRef]
- Fang, J.; Du, J.; Xu, W.; Shi, P.; Li, M.; Ming, X. Spatial downscaling of TRMM precipitation data based on the orographical effect and meteorological conditions in a mountainous area. Adv. Water Resour. 2013, 61, 42–50. [Google Scholar] [CrossRef]
- Immerzeel, W.; Rutten, M.; Droogers, P. Spatial downscaling of TRMM precipitation using vegetative response on the Iberian Peninsula. Remote Sens. Environ. 2009, 113, 362–370. [Google Scholar] [CrossRef]
- Zhang, T.; Li, B.; Yuan, Y.; Gao, X.; Sun, Q.; Xu, L.; Jiang, Y. Spatial downscaling of TRMM precipitation data considering the impacts of macro-geographical factors and local elevation in the Three-River Headwaters Region. Remote Sens. Environ. 2018, 215, 109–127. [Google Scholar] [CrossRef]
- Kaheil, Y.H.; Gill, M.K.; Bastidas, L.A.; Rosero, E.; McKee, M. Downscaling and assimilation of surface soil moisture using ground truth measurements. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1375–1384. [Google Scholar] [CrossRef]
- Shi, J.; Jiang, L.; Zhang, L.; Chen, K.; Wigneron, J.-P.; Chanzy, A.; Jackson, T. Physically based estimation of bare-surface soil moisture with the passive radiometers. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3145–3153. [Google Scholar] [CrossRef]
- Fu, Y.; Xu, S.; Zhang, C.; Sun, Y. Spatial downscaling of MODIS Chlorophyll-a using Landsat 8 images for complex coastal water monitoring. Estuar. Coast. Shelf Sci. 2018, 209, 149–159. [Google Scholar] [CrossRef]
- Gao, F.; Kustas, W.; Anderson, M.C. A data mining approach for sharpening thermal satellite imagery over land. Remote Sens. 2012, 4, 3287–3319. [Google Scholar] [CrossRef]
- Ghosh, A.; Joshi, P. Hyperspectral imagery for disaggregation of land surface temperature with selected regression algorithms over different land use land cover scenes. ISPRS J. Photogramm. Remote Sens. 2014, 96, 76–93. [Google Scholar] [CrossRef]
- Hutengs, C.; Vohland, M. Downscaling land surface temperatures at regional scales with random forest regression. Remote Sens. Environ. 2016, 178, 127–141. [Google Scholar] [CrossRef]
- Mehr, A.D.; Nourani, V.; Kahya, E.; Hrnjica, B.; Sattar, A.M.A.; Yaseen, Z.M. Genetic programming in water resources engineering: A state-of-the-art review. J. Hydrol. 2018, 566, 643–667. [Google Scholar] [CrossRef]
- Koh, C.-H.; Khim, J.S. The Korean tidal flat of the Yellow Sea: Physical setting, ecosystem and management. Ocean Coast. Manag. 2014, 102, 398–414. [Google Scholar] [CrossRef]
- Park, K.-A.; Lee, E.-Y.; Chang, E.; Hong, S. Spatial and temporal variability of sea surface temperature and warming trends in the Yellow Sea. J. Mar. Syst. 2015, 143, 24–38. [Google Scholar] [CrossRef]
- Zhang, C.I.; Lim, J.-H.; Kwon, Y.; Kang, H.J.; Kim, H.; Seo, Y.I. The current status of west sea fisheries resources and utilization in the context of fishery management of Korea. Ocean Coast. Manag. 2014, 102, 493–505. [Google Scholar] [CrossRef]
- Zhang, C.; Kim, S. Living marine resources of the Yellow Sea ecosystem in Korean waters: Status and perspectives. In Large Marine Ecosystems of the Pacific Rim; Wiley, Blackwell Science: Cambridge, MA, USA, 1999; pp. 163–178. [Google Scholar]
- Ye, H.; Li, J.; Li, T.; Shen, Q.; Zhu, J.; Wang, X.; Zhang, F.; Zhang, J.; Zhang, B. Spectral classification of the Yellow Sea and implications for coastal ocean color remote sensing. Remote Sens. 2016, 8, 321. [Google Scholar] [CrossRef]
- Cho, Y.-K.; Kim, M.-O.; Kim, B.-C. Sea fog around the Korean Peninsula. J. Appl. Meteorol. 2000, 39, 2473–2479. [Google Scholar] [CrossRef]
- Letelier, R.M. An analysis of chlorophyll fluorescence algorithms for the moderate resolution imaging spectrometer (MODIS). Remote Sens. Environ. 1996, 58, 215–223. [Google Scholar] [CrossRef]
- Sarthyendranath, S. Remote Sensing of Ocean Colour in Coastal, and Other Optically-Complex, Waters; International Ocean Colour Coordinating Group (IOCCG): Dartmouth, NS, Canada, 2000. [Google Scholar]
- Hu, C.; Lee, Z.; Franz, B. Chlorophyll aalgorithms for oligotrophic oceans: A novel approach based on three-band reflectance difference. J. Geophys. Res. Ocean. 2012, 117. [Google Scholar] [CrossRef]
- Pahlevan, N.; Schott, J.R. Leveraging EO-1 to evaluate capability of new generation of landsat sensors for coastal/inland water studies. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 360–374. [Google Scholar] [CrossRef]
- Pahlevan, N.; Lee, Z.; Wei, J.; Schaaf, C.; Schott, J.R.; Berk, A. On-orbit radiometric characterization of OLI (Landsat-8) for applications in aquatic remote sensing. Remote Sens. Environ. 2014, 154, 272–284. [Google Scholar] [CrossRef]
- Gower, J.; King, S.; Borstad, G.; Brown, L. Detection of intense plankton blooms using the 709 nm band of the MERIS imaging spectrometer. Int. J. Remote Sens. 2005, 26, 2005–2012. [Google Scholar] [CrossRef]
- Gower, J.; King, S.; Borstad, G.; Brown, L. The importance of a band at 709 nm for interpreting water-leaving spectral radiance. Can. J. Remote Sens. 2008, 34, 287–295. [Google Scholar]
- Moses, W.J.; Gitelson, A.; Berdnikov, S.; Povazhnyy, V. Satellite estimation of chlorophyll-a concentration using the red and NIR bands of MERIS—The Azov Sea case study. IEEE Geosci. Remote Sens. Lett. 2009, 6, 845–849. [Google Scholar] [CrossRef]
- Pahlevan, N.; Chittimalli, S.K.; Balasubramanian, S.V.; Vellucci, V. Sentinel-2/Landsat-8 product consistency and implications for monitoring aquatic systems. Remote Sens. Environ. 2019, 220, 19–29. [Google Scholar] [CrossRef]
- Dawson, A. (2018, April 23). ajdawson/gridfill: Version 1.0.1 (Version v1.0.1). Zenodo.
- Gao, H.; Birkett, C.; Lettenmaier, D.P. Global monitoring of large reservoir storage from satellite remote sensing. Water Resour. Res. 2012, 48, 48. [Google Scholar] [CrossRef]
- McFeeters, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Mohebzadeh, H.; Fallah, M. Quantitative analysis of water balance components in Lake Urmia, Iran using remote sensing technology. Remote Sens. Appl. Soc. Environ. 2019, 13, 389–400. [Google Scholar] [CrossRef]
- Sima, S.; Ahmadalipour, A.; Tajrishy, M. Mapping surface temperature in a hyper-saline lake and investigating the effect of temperature distribution on the lake evaporation. Remote Sens. Environ. 2013, 136, 374–385. [Google Scholar] [CrossRef]
- Mohebzadeh, H. Extracting A-L relationship for Urmia Lake, Iran using MODIS NDVI/NDWI indices. J. Hydrogeol. Hydrol. Eng. 2018, 7, 1. [Google Scholar] [CrossRef]
- Lee, T.; Singh, V.P. Statistical Downscaling for Hydrological and Environmental Applications; CRC Press: Boca Raton, FL, USA, 2018; Volume 1, p. 165. [Google Scholar]
- Tuia, D.; Pacifici, F.; Kanevski, M.; Emery, W.J. Classification of very high spatial resolution imagery using mathematical morphology and support vector machines. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3866–3879. [Google Scholar] [CrossRef]
- Zheng, Z.; Zeng, Y.; Li, S.; Huang, W. A new burn severity index based on land surface temperature and enhanced vegetation index. Int. J. Appl. Earth Obs. Geoinf. 2016, 45, 84–94. [Google Scholar] [CrossRef]
- Ebrahimy, H.; Azadbakht, M. Downscaling MODIS land surface temperature over a heterogeneous area: An investigation of machine learning techniques, feature selection, and impacts of mixed pixels. Comput. Geosci. 2019, 124, 93–102. [Google Scholar] [CrossRef]
- Rossi, R.E.; Dungan, J.L.; Beck, L.R. Kriging in the shadows: Geostatistical interpolation for remote sensing. Remote Sens. Environ. 1994, 49, 32–40. [Google Scholar] [CrossRef]
- Karl, J. Spatial predictions of cover attributes of rangeland ecosystems using regression kriging and remote sensing. Rangel. Ecol. Manag. 2010, 63, 335–349. [Google Scholar] [CrossRef]
- Petropoulos, G.; Srivastava, P.K. Sensitivity Analysis in Earth Observation Modelling; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Morris, M.D. Factorial sampling plans for preliminary computational experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef]
- Rao, C.R.; Toutenburg, H.; Shalabh, H.C.; Schomaker, M. Linear models and generalizations. In Least Squares and Alternatives, 3rd ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2008. [Google Scholar]
- Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA; London, UK, 1992; Volume 1. [Google Scholar]
- Stephens, T. Gplearn Model, Genetic Programming; Copyright, 2015. [Google Scholar]
- Geem, Z.W.; Kim, J.H.; Loganathan, G. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Nazeer, M.; Nichol, J. Development and application of a remote sensing-based Chlorophyll-a concentration prediction model for complex coastal waters of Hong Kong. J. Hydrol. 2016, 532, 80–89. [Google Scholar] [CrossRef]

| Band Name | Central Wavelength (µm) | Spatial Resolution (m) |
|---|---|---|
| B1-Coastal aerosol | 0.443 | 60 |
| B2-Blue | 0.490 | 10 |
| B3-Green | 0.560 | 10 |
| B4-Red | 0.665 | 10 |
| B5-Vegetation red edge | 0.705 | 20 |
| B6-Vegetation red edge | 0.740 | 20 |
| B7-Vegetation red edge | 0.783 | 20 |
| B8-NIR | 0.842 | 10 |
| B8A-Narrow NIR | 0.865 | 20 |
| B9-Water vapor | 0.940 | 60 |
| B10-SWIR-Cirrus | 1.375 | 60 |
| B11-SWIR | 1.610 | 20 |
| B12-SWIR | 2.190 | 20 |
| MODIS | Sentinel-2A MSI | Chl-a Measurements |
|---|---|---|
| 2016.2.2 | 2016.2.2 | 2016.2.1 |
| 2016.8.4 | 2016.8.4 | 2016.8.1 |
| Date | Performance Statistics | Model | |||
|---|---|---|---|---|---|
| 2nd Degree MPR | 3rd Degree MPR | 4th Degree MPR | GP | ||
| 2016.2.2 | MAE | 0.108 | 0.144 | 0.150 | 0.108 |
| (Winter) | MBE | −0.014 | −0.012 | −0.020 | 0.011 |
| RMSE | 0.168 | 0.207 | 0.219 | 0.164 | |
| R2 | 0.922 | 0.886 | 0.872 | 0.927 | |
| 2016.8.4 | MAE | 0.360 | 0.383 | 0.409 | 0.341 |
| (Summer) | MBE | −0.056 | −0.044 | −0.068 | −0.030 |
| RMSE | 0.562 | 0.542 | 0.595 | 0.527 | |
| R2 | 0.732 | 0.753 | 0.704 | 0.763 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohebzadeh, H.; Yeom, J.; Lee, T. Spatial Downscaling of MODIS Chlorophyll-a with Genetic Programming in South Korea. Remote Sens. 2020, 12, 1412. https://doi.org/10.3390/rs12091412
Mohebzadeh H, Yeom J, Lee T. Spatial Downscaling of MODIS Chlorophyll-a with Genetic Programming in South Korea. Remote Sensing. 2020; 12(9):1412. https://doi.org/10.3390/rs12091412
Chicago/Turabian StyleMohebzadeh, Hamid, Junho Yeom, and Taesam Lee. 2020. "Spatial Downscaling of MODIS Chlorophyll-a with Genetic Programming in South Korea" Remote Sensing 12, no. 9: 1412. https://doi.org/10.3390/rs12091412
APA StyleMohebzadeh, H., Yeom, J., & Lee, T. (2020). Spatial Downscaling of MODIS Chlorophyll-a with Genetic Programming in South Korea. Remote Sensing, 12(9), 1412. https://doi.org/10.3390/rs12091412