The Capability of Integrating Optical and Microwave Data for Detecting Soil Moisture in an Oasis Region

Abstract

In the earth ecosystem, surface soil moisture is an important factor in the process of energy exchange between land and atmosphere, which has a strong control effect on land surface evapotranspiration, water migration, and carbon cycle. Soil moisture is particularly important in an oasis region because of its fragile ecological environment. Accordingly, a soil moisture retrieval model was conducted based on Dubois model and ratio model. Based on the Dubois model, the in situ soil roughness was used to simulate the backscattering coefficient of bare soil, and the empirical relationship was established with the measured soil moisture. The ratio model was used to eliminate the backscattering contribution of vegetation, in which three vegetation indices were used to characterize vegetation growth. The results were as follows: (1) the Dubois model was used to calibrate the unknown parameters of the ratio model and verified the feasibility of the ratio model to simulate the backscattering coefficient. (2) All three vegetation indices (Normalized Difference Vegetation Index (NDVI), Vegetation Water Content (VWC), and Enhanced Vegetation Index (EVI)) can represent the scattering characteristics of vegetation in an oasis region, but the VWC vegetation index is more suitable than the others. (3) Based on the Dubois model and ratio model, the soil moisture retrieval model was conducted, and the in situ soil moisture was used to analyze the accuracy of the simulated soil moisture, which found that the soil moisture retrieval accuracy is the highest under VWC vegetation index, and the coefficient of determination is 0.76. The results show that the soil moisture retrieval model conducted on the Dubois model and ratio model is feasible.

1. Introduction

Oases are important parts of the ecosystem that constitute arid and semi-arid regions; they are the “source of life” throughout the arid and semi-arid regions. China’s oases are mainly distributed in the five northwestern provinces, especially in the Xinjiang Uygur Autonomous Region (hereinafter referred to as “Xinjiang”). The Xinjiang oases covers 8% of the total area, but bears more than 90% of the cultivated land, population, and Gross Domestic Product (GDP) of Xinjiang. Meanwhile, the inner ecological environments of oases are fragile; once they are affected or destroyed by human or natural causes, it is difficult for them to restore to normal.

Soil moisture is an important parameter in meteorological, agro-environmental, and hydrological studies [1]. In meteorological research, accurate detection of surface soil moisture is important and can be applied in a variety of hydrological and climate models (e.g., rainfall mapping, drought monitoring, vegetation water requirement analysis, etc.). In agricultural research, the most important thing is to estimate the crop yields; in addition, the surface soil moisture can be introduced into the basin hydrological model as a priori knowledge (which can predict the deep soil moisture content in order to study vegetation water stress, etc.). Finally, soil moisture can help predict natural disasters, such as debris flows, landslides, etc.; meanwhile, surface soil moisture mapping plays a crucial role in improving local and even global climate predictions [2]. Moreover, soil moisture is an important indicator for monitoring land degradation and drought [3], an indispensable key factor in the land water cycle [4,5,6], and the basic guarantee for vegetation growth and development. It has guiding significance in estimating crop yield and drought monitoring [7,8].

In arid and semi-arid regions, the spatial and temporal soil moisture retrieval can be used to better understand the changes of soil moisture migration, to further understand the ecological effects of vegetation and, simultaneously, improve soil moisture holding capacity and vegetation water use efficiency (and, accordingly, play an important role in the sustainable development of an oasis ecology). Therefore, the importance of soil moisture for the sustainable development of an oasis is self-evident, and real-time monitoring of large-scale soil moisture is of great significance [9].

At present, high-precision retrieval of spatial and temporal distribution of soil moisture is an urgent problem to be solved [10,11], to which the hotspots and difficulties lies in the soil moisture retrieval under vegetation coverage. At present, the soil moisture monitoring method is based on the soil moisture monitoring site, which is time-consuming and labor-intensive, and the observation site is limited and unevenly distributed. On the other hand, with the rapid development of remote sensing technology, more and more people use remote sensing methods to monitor soil moisture. After several decades development of remote sensing technology, the data sources of soil moisture retrieval mainly include optical, microwave and thermal infrared [12]. Optical remote sensing has developed rapidly and has become a high time resolution, high spectral resolution, and high spatial resolution data [13,14], but it is susceptible to the external environment, such as atmosphere, clouds, fog, etc. It is susceptible to leaves and stems under vegetation-covered areas; with its strong penetrating ability, microwave remote sensing can realize all-day observation under various meteorological conditions, and most importantly, it is sensitive to soil moisture changes, making microwave remote sensing widely used in large-scale mapping of soil moisture in arid and semi-arid regions [15].

The microwave remote sensing has two kinds of observing systems, active and passive missions. The passive mission provides global soil moisture products with a high temporal resolution (2–3 days) and high retrieval accuracy [16], but with a poor spatial resolution. The active mission provide a high spatial resolution data, but can be influenced by the soil and radar’s system. Taking the study area into account, it was not fit for the passive remote sensing soil moisture derive, so the active mission was selected as the data source. Over the past few decades, active microwave remote sensing data have been successfully used for estimating soil moisture due to a finer spatial resolution [17]. Several soil moisture retrieval algorithms have been developed and tested for multiple Synthetic Aperture Radar (SAR) satellites operated at the L/C/X-bands [18], such as Advanced Land Observing Satellite-2 (ALOS-2) [16,19], Radarsat-2 [20,21], Advanced Synthetic Aperture Radar (ASAR) [22], Sentinel-1 [23,24,25,26,27], and Multi-temporal X-band SAR (TerraSAR-X) [28,29]; studies that have used these data to estimate bare soil moisture have achieved promising results. Based on this, several soil moisture models have been proposed to the bare land, including the statistical models (Oh model [30] and Dubois model [31]) and physical models (the integral equation model (IEM) [32] and advanced IEM (AIEM) [33,34,35,36,37]). Combined with the vegetation scattering model [38,39], which can be used to quantify vegetation attenuation of radar signals in radiative transfer function models [40], the bare soil scattering model can adapt to the vegetation areas. To eliminate the effect of vegetation, some studies [39,41,42,43,44] have attempted to use additional vegetation information provided by optical remote sensing, which has been widely used to derive information of vegetation properties. Furthermore, other studies [43,45,46,47] have suggested that the accuracy of soil moisture estimates was significantly improved when considering synergy between radar and optical data as compared to estimates from SAR data only.

The aim of this paper is to verify the feasibility of the soil moisture retrieval model based on bare surface scattering models and vegetation scattering models in an oasis region, in order to accurately derive soil moisture in the oasis of the arid region, which can better understand the response of the surface parameters and the canopy to backscatter. Based on this purpose, the Ugan-Kuqa River Delta Oasis in the Aksu region of Xinjiang was selected as our target area, with microwave data as the main and supplemented by optical data. We analyzed the relationship between backscattering coefficient and soil moisture based on microwave and optical data; therefore, a surface soil moisture retrieval model was conducted. The basic of this work is, coupled, the Dubois model and ratio model, using the surface roughness, soil moisture, and radar system parameters to simulate the backscattering coefficient of the bare soil to remove the backscatter contribution of vegetation and conduct a surface soil moisture retrieval model. This method can provide a theoretical support for the sustainable development of oases.

2. Materials and Methods

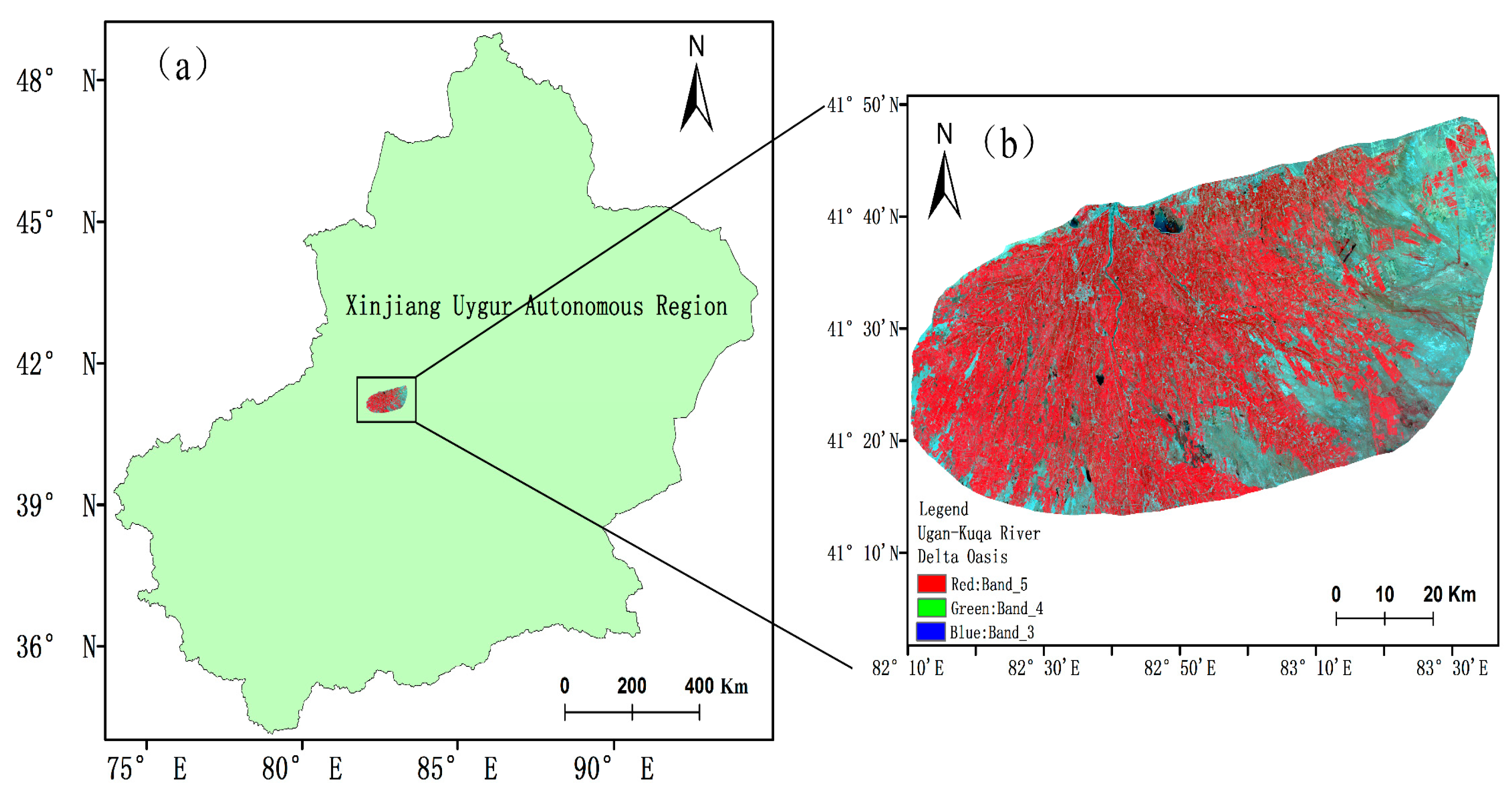
2.1. Overview of the Study Region

Currently, the ecological degradation problem in the lower reaches of the Tarim River Basin is serious; the upper reaches of the Tarim River Basin (Ugan-Kuqa River Delta Oasis) was selected as the study area. The main reason we selected this area is that the use of water resources is closely related to the ecological problems and this area an important food production base in Xinjiang. In this oasis region, vegetation coverage will affect the soil moisture retrieval accuracy based on optical remote sensing, and microwave remote sensing can provide a promising method of soil moisture derive.

The Ugan-Kuqa River Delta Oasis(latitude 41°00′ N–41°50′ N, longitude 82°10′ E–83°30′ E (hereinafter referred to as “this area”) is located on the northern edge of the Tarim Basin in Xinjiang. Luntai County lies to the east, Baicheng County lies to the west, the north bank of the Tarim River lies to the south, and the Qiulitage Mountain in the southern foothills of the Tianshan Mountains lies to the north (Figure 1). It is a typical fan-shaped plain oasis in China. This oasis has a temperate continental arid climate with abundant light and heat resources. The climate is very dry with a deficiency of rainfall. To be specific, the annual total radiation is 6.11 × 10⁵ J cm², the annual sunshine hours are approximately 2.85 × 10³ h, the sunshine rate is 65%, the annual average temperature is 11.3 °C, the potential evaporation is 2356 mm, the average annual precipitation is 55.45 mm, and the drying index is 42 [27]. This oasis agriculture is mainly based on planting. Artificial vegetation mainly includes cotton, corn, and winter wheat, while natural vegetation is halophyte, which mainly includes Kalidium foliatum, Halocnemum strabilaceum, Halostachys capsica, Alhagi sparsifolia, Populus euphratica, Tamarix spp, Phragmites communis.

The land cover use of the study area is shown in Figure 2. As shown in Figure 2, there are six types of land cover, which include built-up, agriculture, natural vegetation, bare land, water, salinized. The artificial vegetation is mainly planted in the center of this oasis; meanwhile, the natural vegetation is mainly in the oasis-desert ecotone region where the soil salinization is serious.

2.2. Observation Data

2.2.1. Soil Moisture, Texture, and Bulk

The soil samples were collected at a depth of 10 cm in July 2017, which used a random clustered sampling technique to allocate 69 samples in the Ugan-Kuqa River Delta Oasis. Each sample should be representative of the soil surrounding a larger area (which had a minimum distance of 2 km to the next site to avoid autocorrelation). The samples were selected away from the trails and consisted of homogenous land use types (

Table 1. Features of the land cover classes.

Class	Sites	Description
Agriculture	21	Planting crops
Natural vegetation	19	Almost all vegetation is shrubs with a high vegetation coverage
Bare land	10	No vegetation cover
Water	5	Rivers, reservoirs
Salinized	14	No vegetation cover, but there are salt shells on the surface

). Throughout the in situ soil sampling, the weather is clear and cloudless with no rainfall. The landscape in this region includes agriculture, natural vegetation, bare land, water, salinized. Soil data process were as follows:

• The soil sample of each site was uniformly mixed and placed into an aluminum box, which was weighed and recorded, then transported back to the laboratory for drying until the soil was completely dehydrated, cooled to room temperature, and weighed in a cool place. The soil moisture was calculated. The range of measured soil moisture value was 0.00 to 47.59%, and the average was 24.17%.
• The collected soil samples were transported to the laboratory, the plant and gravel impurities were removed after air drying, the soil was ground and sieved with a 0.5 mm aperture sieve; physical and chemical analyses were then conducted to measure soil texture and soil bulk density.

2.2.2. Soil Roughness

At present, there are two methods to obtain soil roughness: the probe method and laser scanning method. In this study, the probe method was used to obtain the surface roughness, which is a section panel with a centimeter grid (Figure 3a). The specific steps of soil roughness data process were divided into four steps:

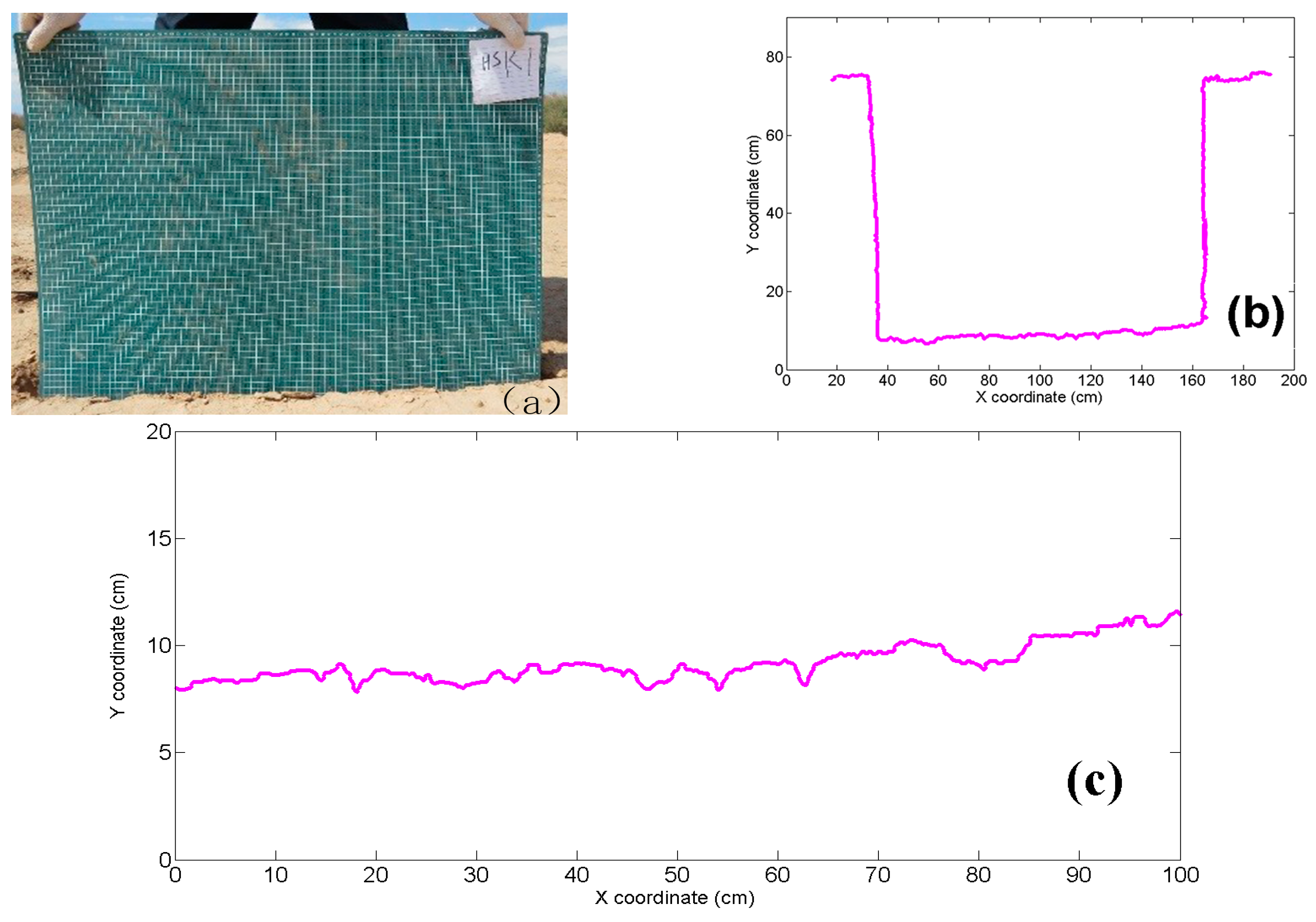
• Using a camera, the soil roughness was captured, ensuring that the samples board was perpendicular to the ground and that the camera was parallel to the soil surface.
• The captured photos of soil roughness were vectorized in MATLAB (Figure 3b), and then a manual correction processing was performed to get a vector picture of the soil roughness (Figure 3c).
• The discrete height value of each point was extracted by every 1 cm of the vectorized data, and data were saved in Excel for the next step.
• The data of the discrete height value were analyzed according to the equations of root mean square height and related length; therefore, the correlation length and the root mean square height was obtained. The range of the correlation length value was 13.73 cm to 42.16 cm, and the average was 24.09 cm. The range of the root mean square height value was 0.32 cm to 3.69 cm, and the average was 1.68 cm.

2.3. Satellite Data

2.3.1. Sentinel-1 Data

Sentinel-1 is an imaging radar mission providing continuous all weather, day-and-night imagery at C-band, which launched on April 3, 2014. This SAR instrument carries two satellites (Sentinel-1A and Sentinel-1B), and may acquire data in four exclusive modes: Stripmap (SM), Interferometric Wide swath (IW), Extra Wide swath (EW), Wave (WV).

The microwave data source used in this study was single polarization, which included VV (vertical transmit and receive) and HH (horizontal transmit and receive) polarization modes. The data were acquired on July 15, 2017, coinciding with the soil sample acquisition times that were used. The data used in this study were the so-called interferometric wide swath mode at a spatial resolution of 20 by 20 m, and the azimuth width was 250 km. These data were downloaded from https://scihub.copernicus.eu/dhus/#/home.

The Sentinel-1 image was an ellipsoid geocoded Ground Range Detected (GRDH), preprocessed by the SARscape 5.2.1^® module developed by SARmap in ENVI 5.3^® software. Following these procedures, the processed SAR data with a 30 m spatial resolution were projected onto World Geodetic System (WGS) 1984 Universal Transverse Mercator (UTM) coordinates. The preprocessing of Sentinel-1 data are as follows:

• Filtering and denoising processing (refined-Lee filtering, 3 pixels by 3 pixels window) was performed to eliminate speckle noise.
• Geocoding was performed, using digital elevation maps for geometric fine correction.
• Radiation calibration was conducted to obtain the backscattering coefficient in the multipolarization mode of the target region.

2.3.2. Landsat-8 OLI Data

Landsat-8, which was launched in February 2013 by National Aeronautics and Space Administration (NASA), carries two sensors, the OLI Land Imager and the Thermal Infrared Sensor (TIRS). For this study, OLI data from July 14, 2017, were downloaded from https://earthexplorer.usgs.gov/. The preprocessing of Landsat-8 OLI data includes radiation correction and atmospheric correction, which were conducted using the ENVI 5.3^® software (Exelis Visual Information Solutions, Broomfield, CO, United States). Following these procedures, the processed OLI data with a 30 m spatial resolution were also projected onto WGS 1984 UTM coordinates.

The three indices ((Normalized Difference Vegetation Index (NDVI), Vegetation Water Content (VWC), and Enhanced Vegetation Index (EVI)) were selected as the vegetation index, and the equation is as follows:

NDVI = (b5 − b4) / (b5 + b4)

(1)

VWC = (b5 − b6) / (b5 + b6) × 2.15 + 0.32

(2)

EVI = 2.5 × (b5 − b4) / (b5 + b4 − 7.5 × b2 + 1)

(3)

In the equation, b2 represents the value of band 2; b4 represents the value of band 4; b5 represents the value of band 5; b6 represents the value of band 6.

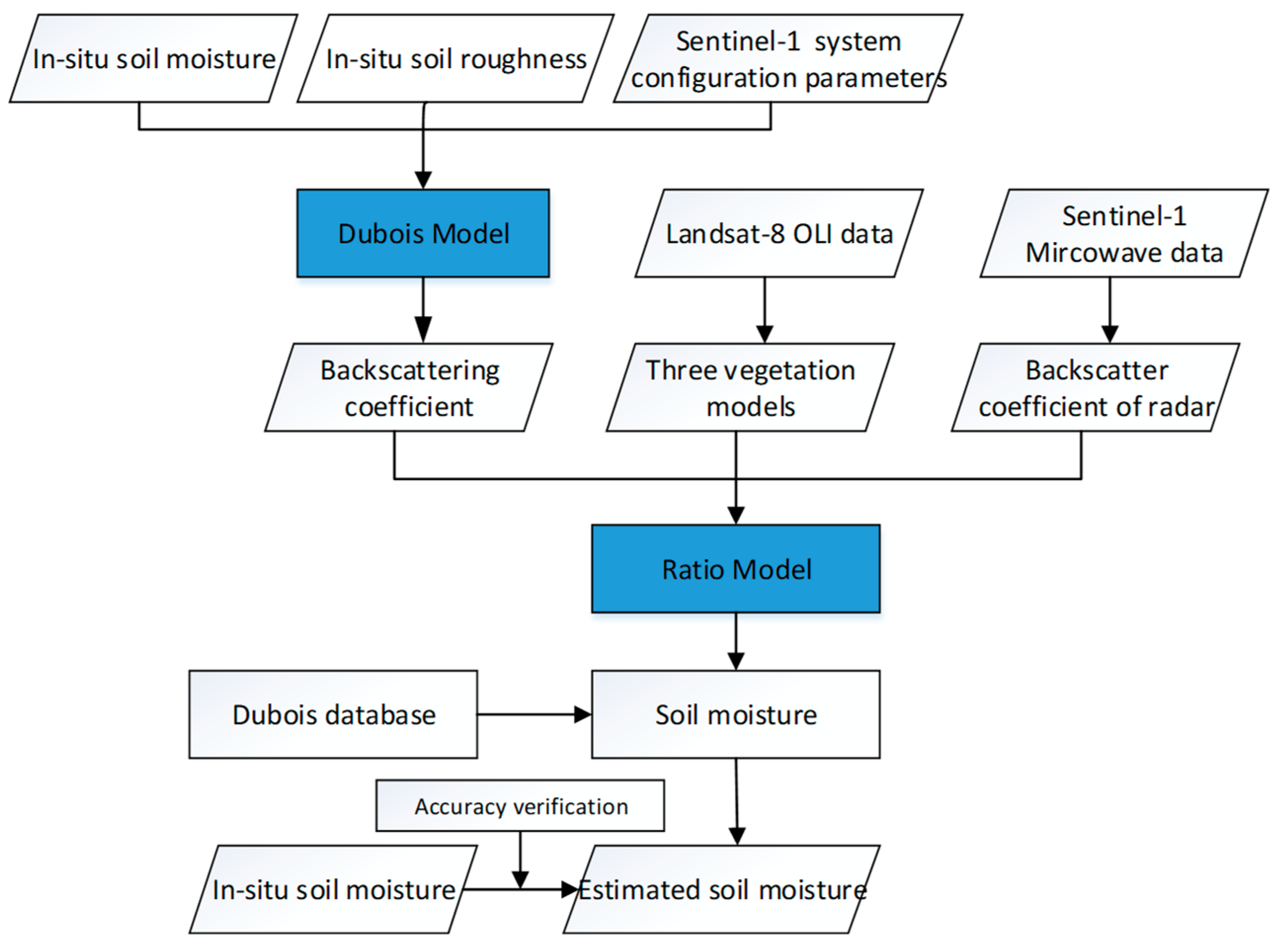
2.4. Methodology

SAR is the main way to detect the surface soil moisture by active microwave remote sensing. The basic principle is that the backscattering coefficient obtained by microwave remote sensing has a good correlation with the soil dielectric constant property, and the dielectric constant of the soil is mainly controlled by soil moisture. Therefore, based on this, the surface soil moisture can be effectively derived [48].

In this paper, the Dubois Model and the Ratio Model were used to derive soil moisture in the Ugan-Kuqa River Delta Oasis. The Ratio Model is used to simulate the vegetation backscattering, and the Dubois is used to simulate the bare soil backscattering. The implementation of the two models’ soil moisture retrieval can be seen in Figure 4, and detailed descriptions of the two models are introduced in the following sections.

Step 1: based on the Dubois model, the in situ surface roughness, and the other parameters, such as the in situ soil moisture, related length, and system configuration of the Sentinel-1 data were used to simulate the bare soil-backscattering coefficient under two polarizations.

Step 2: the backscattering coefficient of bare soil simulated by the Dubois model, the total backscattering coefficient of the Sentinel-1 image, and three optical vegetation indices (VWC, NDVI, and EVI) were introduced into the ratio model, and the unknown coefficient in the ratio model was calculated using the least squares algorithm.

Step 3: based on the in situ soil moisture and the backscattering coefficient of the bare soil simulated by the ration model, the empirical equations for the two polarizations were established (Equation (4)).

$$d{\sigma }_{ppsoil}^o+e=m_v$$

(4)

In the equation, d and e represents the unknown coefficient, $m_v$ represents the soil moisture, and $pp$ represents the polarization mode.

Step 4: based on the ratio model, because the radar-backscattering coefficient is known, the soil-backscattering coefficient can be obtained. Combined with Equation (4), the soil moisture was derived under two polarizations. Using Equation (5), the soil moisture was derived.

$$m_v=\left(m_v^{vv}+m_v^{hh}\right)/2$$

(5)

2.4.1. Dubois Model

In 1995, an empirical model was conducted based on microwave scatterometry data (including multiple frequencies, multi-polarization, multi-angle) under different rough conditions [31].

This model can be used in the following range:

$${30}^{\circ }<\theta <{65}^{\circ }$$

(6)

$$0.3\mathrm{cm}<S<3.0\mathrm{cm}$$

(7)

$$1.5\mathrm{GHz}<f<11\mathrm{GHz}$$

(8)

In the equation, $\theta$ represents the radar incident angle, $S$ represents the root mean square height, $f$ represents the radar frequency. Under this condition, the simulated scatter coefficient has good accuracy, but under a tough soil roughness, it is not suitable to use this model to simulate.

The equation of the Dubois model is:

$${\sigma }_{hh}^0={10}^{-2.75}\frac{{\cos }^{1.5}\theta }{{\sin }^5\theta }{10}^{0.028\epsilon \tan \theta }{(ks\sin \theta )}^{1.4}{\lambda }^{0.7}$$

(9)

$${\sigma }_{vv}^0={10}^{-2.35}\frac{{\cos }^3\theta }{{\sin }^3\theta }{10}^{0.046\epsilon \tan \theta }{(ks\sin \theta )}^{1.1}{\lambda }^{0.7}$$

(10)

In the equation, ${\sigma }_{hh}^0$ represents the backscattering coefficient of the HH polarization mode, ${\sigma }_{vv}^0$ represents the backscattering coefficient of the VV polarization mode, $k$ represents the radar wave number, $\lambda$ represents the wavelength, s represents the root mean square height, and $\theta$ represents the radar incident angle.

Based on a complex electromagnetic scattering model, the theoretical model was established, which has a certain physical basis. It can be widely applied to different SAR sensors and has good adaptability. Compared with the theoretical model, the empirical model has advantages, which can simulate the backscattering coefficient of the soil beyond the threshold range of the theoretical model, and the model has a better precision under a low vegetation coverage. Despite the above advantages, the model still has the condition that the soil moisture is underestimated [49,50], and the model ignores the influence of the correlation length on the backscattering coefficient [51], so the universality of the constructed model needs to be improved.

2.4.2. Topp Model

In 1980, an empirical relationship between soil water content and soil dielectric constant was conducted [52], based on the in situ data, which does not consider the effects of soil texture and temperature on soil moisture, and also ignores the influence of soil imaginary part on soil moisture. The empirical model relational equation is as follows:

$${\epsilon }^{\prime }=3.03+9.3m_v+146.0m_v^2-76.7m_v^3$$

(11)

$$m_v=-5.3\times {10}^{-2}+2.92\times {10}^{-2}{\epsilon }^{\prime }-5.5\times {10}^{-4}{\left({\epsilon }^{\prime }\right)}^2+4.3\times {10}^{-6}{\left({\epsilon }^{\prime }\right)}^3$$

(12)

In the equation, $m_v$ represents the soil water content, and ${\epsilon }^{\prime }$ represents the real part of the soil dielectric constant.

According to the above equation, it can be seen that the soil moisture can be obtained only when the real part of the soil dielectric constant is required. The model has simple expression and simple calculation, which is suitable for soil under lighter soil roughness, and in an oasis region, the imaginary part of the dielectric constant is negligible.

2.4.3. Ratio Model

In 2008, Joseph et al. used a microwave scatterometer to monitor the growth of corn throughout its growth cycle; the ratio model was conducted [53]. The model assumes that the ratio of the backscattering coefficient of the soil to the backscattering coefficient of the radar is only related to the vegetation indices under certain conditions of the microwave sensor. Therefore, the ratio model can be used to eliminate the influence of vegetation canopy on radar backscattering coefficient. Based on this, under vegetation coverage, this model can be used to establish the empirical relationship between the backscattering coefficient and soil moisture, and then derive the soil moisture. The ratio model replaces the surface backscattering, secondary scattering, and multiple scattering of vegetation by the total backscattering of the vegetation canopy. The ratio model can be simplified as follow:

$$\frac{{\sigma }_{ppsoil}^o}{{\sigma }_{pp}^o}=f\left(vegetation,antenna configuration\right)$$

(13)

In the equation, ${\sigma }_{ppsoil}^o$ represents the backscattering coefficient of bare soil, ${\sigma }_{pp}^o$ represents the total backscattering coefficient of the radar, and $pp$ represents the polarization mode. When the radar system parameters are certain, the ratio model is simplified as follows:

$$\frac{{\sigma }_{ppsoil}^o}{{\sigma }_{pp}^o}=f\left(vegetation\right)$$

(14)

In order to better separate the scattering contribution of vegetation, many researchers have proposed different optimal models (such as linear models, nonlinear models, etc.) to characterize the scattering contribution of vegetation. Joseph use quadratic and exponential equations to characterize vegetation coverage, in which the ratio model was modified [53].

$$a{V}^2+\exp \left(-bV\right)=f\left(vegetation\right)$$

(15)

In 2010, a constant term was added to the model by Joseph, which have a better usage under sparse vegetation coverage or the primary stage of vegetation growth [54].

$$a{V}^2+\exp \left(-bV\right)+c=f\left(vegetation\right)$$

(16)

In 2012, Prakash et al. [55] used a polynomial function to characterize the scattering component of vegetation.

$$a{V}^2+bV+c=f\left(vegetation\right)$$

(17)

Combined with the specific situation of the study area, where the inner oasis is mostly covered by low-lying crops and the oasis-desert ecotone region is under sparse vegetation coverage, we intend to use a combination of linear and power exponential functions to characterize vegetation scattering contributions. The equation is as follows:

$$a{V}^2+b{V}^c=f\left(vegetation\right)$$

(18)

In the equation, a, b, and c all represent unknown coefficients, and V represents optical vegetation indices. There is no uniform standard for the best choice of optical vegetation indices.

In 2011, Lievens et al. [38] selected three vegetation indexes, including LAI, VWC, and NDVI, which were used to initialize the water cloud model (WCM) model, and the soil moisture was derived. After precision analysis, it was found that the accuracy of using LAI to derive the soil moisture was much higher than the other two vegetation indices, which proved that the leaves of vegetation affected vegetation scattering, and affected the interaction between radar signals and vegetation canopy. In 2015, Kweon et al. [56] modified the water-cloud model by adding new parameters (the average and standard deviation of leaf angle distribution) to accurately estimate the backscattering coefficients with the angular effect of scattering particles in a vegetation canopy. It proved that vegetation water content affects the penetration depth of radar, and further affects the interaction between radar signal and vegetation canopy. In 2012, Mattar et al. [42] chose the NDVI index, obtained from optical measurements, for removing the vegetation effect, and concluded with positive results.

Therefore, three different vegetation indices are used in the ratio model, respectively, VWC, NDVI, and EVI. The three vegetation indices are used to estimate the scattering contribution of vegetation to better derive soil moisture.

2.4.4. Minimum-Maximum (Min-Max) Normalization Approach

The Min-Max normalization is a linear transformation of the original data, so that the result falls in the interval [0,1], the equation used is:

$$S_{normalization }=\frac{S-Min}{Max-Min}$$

(19)

where $S_{normalization }$ is normalized value of soil moisture, $S$ is derived value of soil moisture, $Max$ is maximum value of soil moisture data,$Min$ is minimum value of soil moisture data.

2.4.5. Accuracy Assessment

The correlation coefficient (R) is as follows:

$$\mathrm{R}\left(\mathrm{X},\mathrm{Y}\right)=\frac{Cov\left(X,Y\right)}{\sqrt{Var\left[X\right]Var\left[Y\right]}}$$

(20)

In the equation, $Cov\left(X,Y\right)$ represents the covariance of X and Y, $Var\left[X\right]$ represents the variance of X, and $Var\left[Y\right]$ represents the variance of Y.

The root mean square error (RMSE) is as follows:

$$\mathrm{RMSE}=\sqrt{\frac{1}{n}{{\displaystyle \sum }}_{=1}^n{\left(y_i-\widehat{y_i}\right)}^2}$$

(21)

In the equation, n represents the number of samples,$y_i$ represents the value of the i-th sample, $\widehat{y_i}$ represents the mean value of the sample.

3. Results

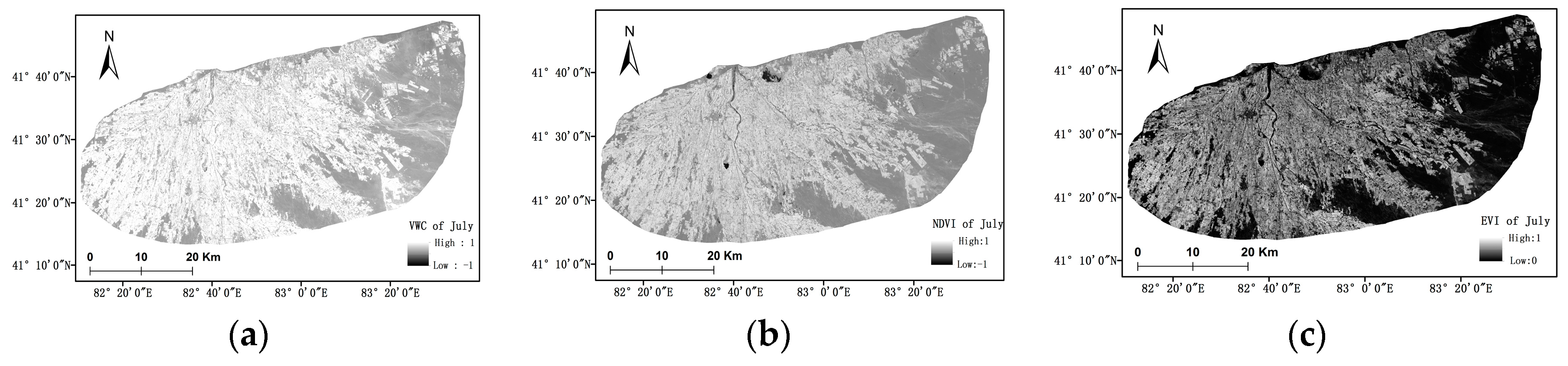
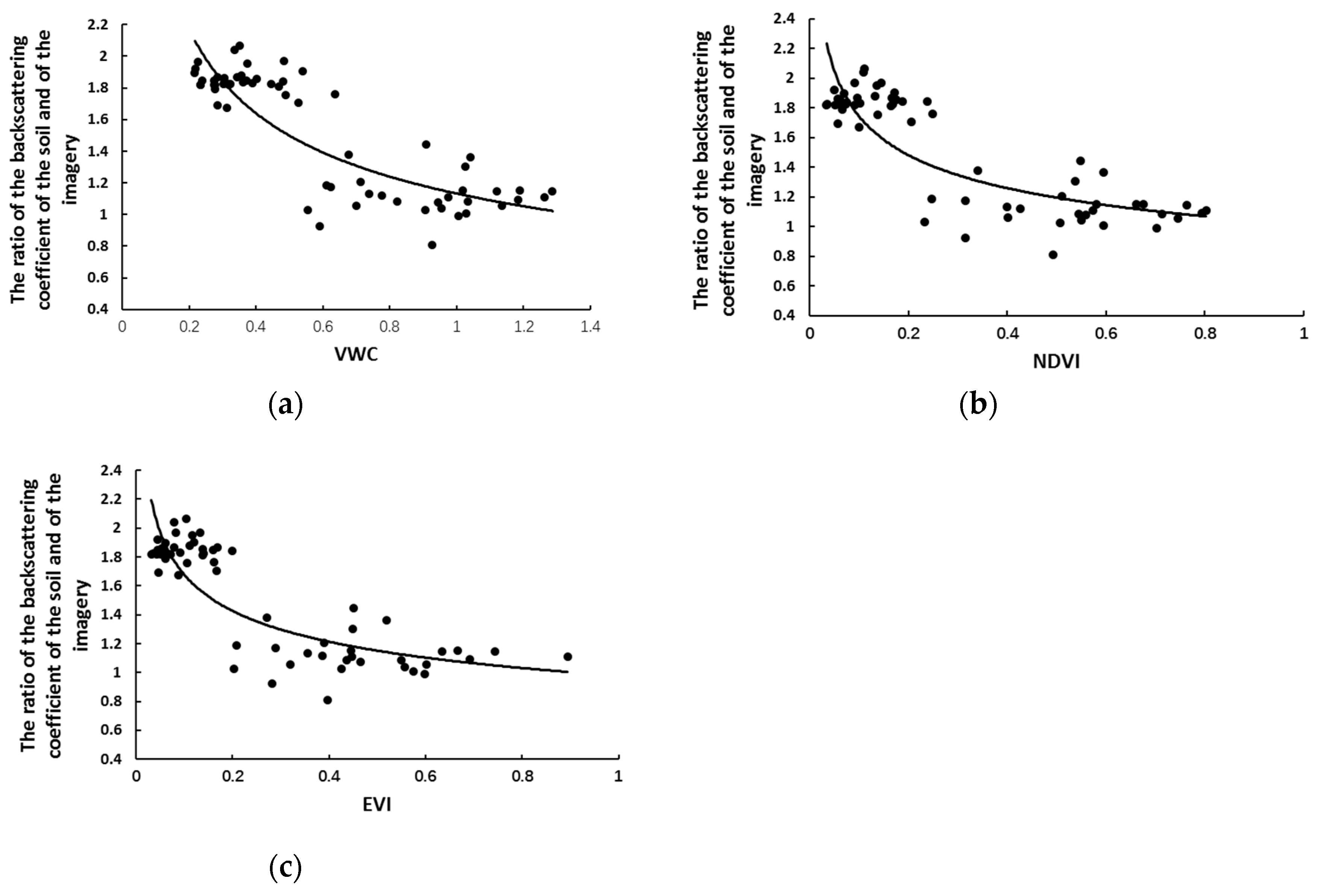
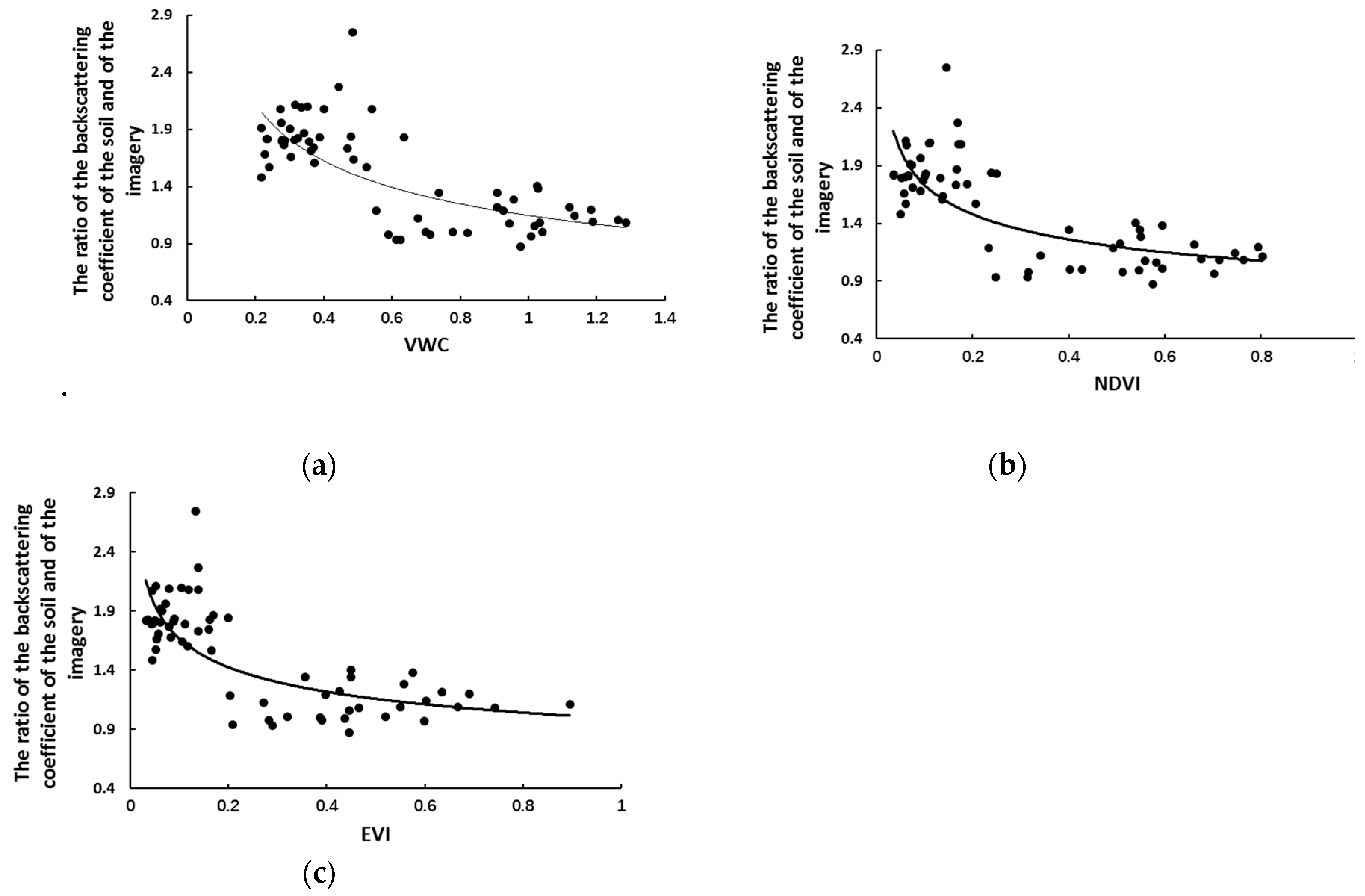
3.1. Removing the Vegetation Effect

In this study, the ratio model was used to eliminate the backscatter contribution of vegetation, in which the growth of vegetation is characterized by three vegetation indices of VWC, NDVI, and EVI, and the three vegetation indices were derived by optical data. The linear and power function were used to characterize the ratio model, which was the ratio of the backscattering coefficient of the soil and of the imagery, and the function also use the least square method to solve the unknown parameters in the ratio model.

Figure 5, Figure 6 and Figure 7 show the process of removing the vegetation effect in July. Figure 5 shows the retrieval of the three vegetation indices. Figure 5a shows the VWC vegetation index, Figure 5b shows the NDVI vegetation index, and Figure 5c shows the EVI vegetation index. Figure 6 shows the ratio scatter plots of ${\sigma }_{hhsoil}^o/{\sigma }_{hh}^o$ to vegetation indices. Figure 6a shows the ratio scatter plot under VWC vegetation index, Figure 6b shows the ratio scatter plot under NDVI vegetation index, and Figure 6c shows the ratio scatter plot under EVI vegetation index. Figure 7 shows the ratio scatter plots of ${\sigma }_{vvsoil}^o/{\sigma }_{vv}^o$ to vegetation indices. Figure 7a shows the ratio scatter plot under VWC vegetation index, Figure 7b shows the ratio scatter plot under NDVI vegetation index, and Figure 7c shows the ratio scatter plot under EVI vegetation index.

As shown in Figure 5, Figure 6 and Figure 7, the ratio of the backscattering coefficient has a negative correlation with the vegetation indices, and the comprehensive function can well characterize the relationship between the two models. When the vegetation indices are small, the ratio of backscattering coefficient decreases rapidly with the increase of vegetation indices. When it reaches the critical point, the ratio of backscattering coefficient decreases slowly and the saturation tends to be gentle. This rule is most pronounced when the vegetation index is NDVI.

After analysis, we can conclude that the ratio of the backscattering coefficient shows a rapid decrease when the vegetation indices are small (the main reason being the influence of vegetation and soil roughness on the backscattering coefficient). The main reason for the saturation is that the attenuation of vegetation and soil roughness to backscatter coefficient tends to be saturated, which is the same as Joseph et al.’s research [53,54].

The unknown coefficients in the ratio equations of three different vegetation indices were obtained by the least square method (

Table 2. The fitting result of the unknown coefficient of the ratio equation.

Vegetation Indices	HH Polarization			VV Polarization
	a	b	c	a	b	c
VWC	−0.23	1.15	−0.38	−0.26	1.13	−0.40
	$f=-0.23V^2+1.15V^{-0.38}$			$f=-0.26V^2+1.13V^{-0.40}$
NDVI	−0.16	1.02	−0.02	−0.15	1.01	−0.24
	$f=-0.16V^2+1.02V^{-0.02}$			$f=-0.15V^2+1.01V^{-0.24}$
EVI	−0.09	0.99	−0.23	−0.10	0.98	−0.24
	$f=-0.09V^2+0.99V^{-0.23}$			$f=-0.10V^2+0.98V^{-0.24}$

). So the regression equation of two polarizations under three vegetation indices were obtained. As shown in the regression equation, it can be found that coefficients a and c are negative values; coefficient b is positive value.

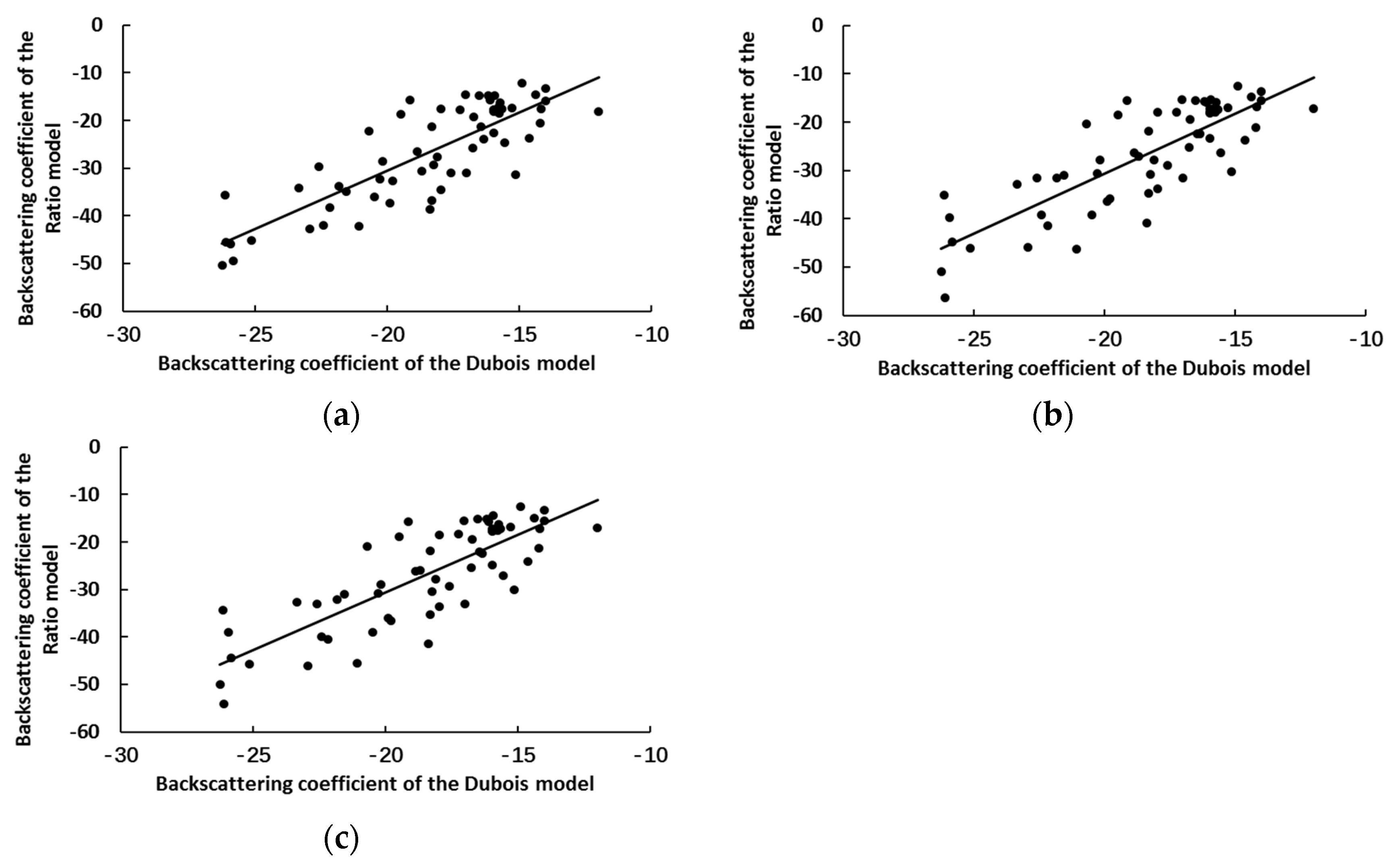
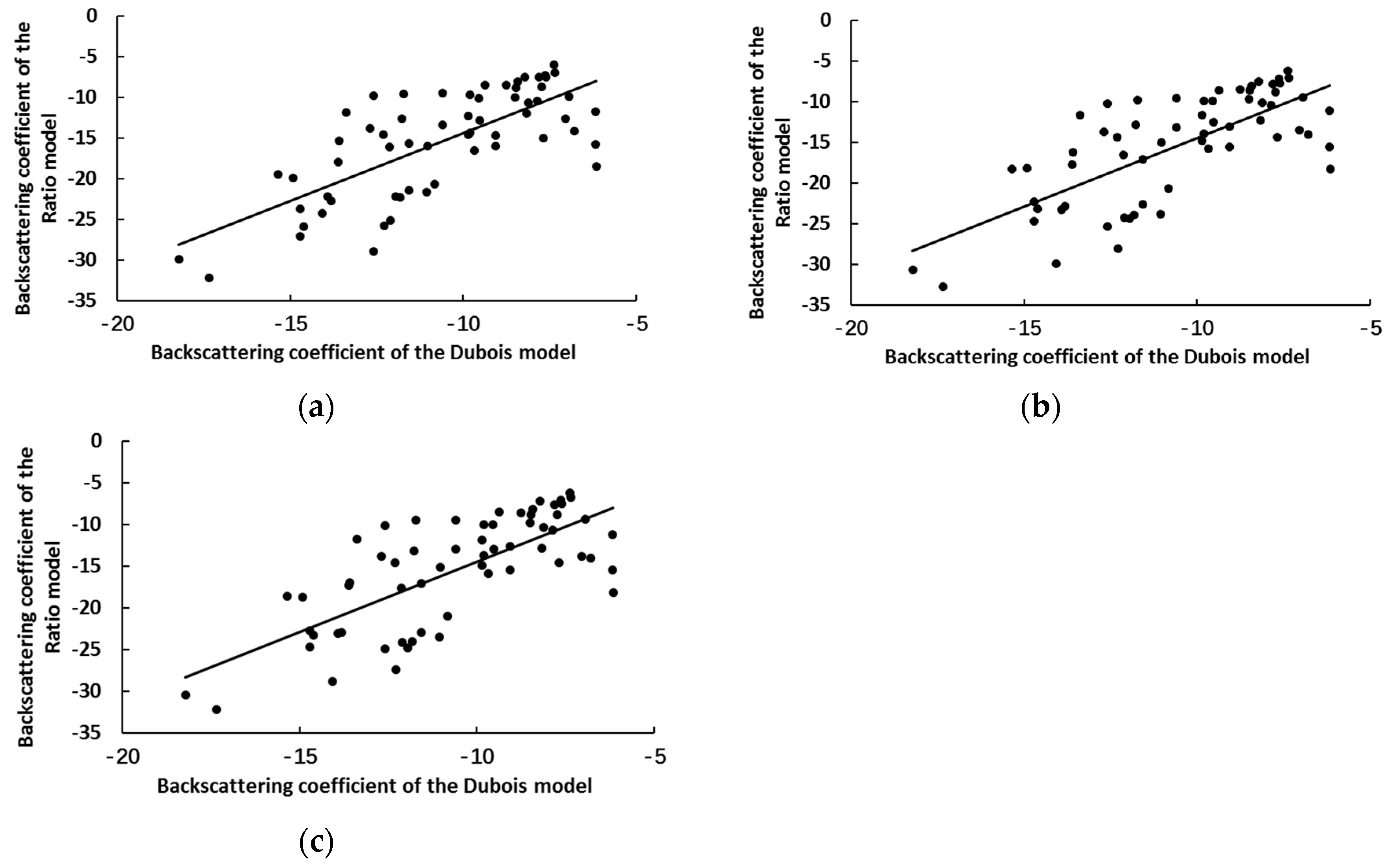
3.2. Constructing the Soil Moisture Retrieval Model

In order to evaluate the effectiveness of the ratio model of the soil moisture retrieval in this oasis, the relationship between the soil-backscattering coefficient of the ratio model and bare soil- backscattering coefficient of the Dubois model was established. Figure 8 shows the function of the backscattering coefficient of three vegetation indices under HH polarization mode. Figure 9 shows the function of the backscattering coefficient of three vegetation indices under VV polarization mode.

Table 3. Fitting result of backscattering coefficient.

SAR	Vegetation Index	HH Polarization		VV Polarization
		R	RMSE	R	RMSE
Sentinel-1	VWC	0.83	3.02	0.73	3.65
	NDVI	0.81	3.26	0.72	3.79
	EVI	0.81	3.30	0.72	3.84

shows R and RMSE between the simulated values of the backscattering coefficient.

As shown in Figure 8 and Figure 9, it can be found that the backscattering coefficient simulated by the Dubois model and the ratio model have a fine linear relationship, and the scatter plots are basically clustered near the 1:1 line, which shows that the backscattering coefficient simulated by ratio model is feasible. As shown in Table 3, the quantitative analysis of the fitting results of the backscattering coefficient shows that when the vegetation index is VWC, the backscattering coefficient has the highest correlation, the root mean square error has the smallest, and the modeling effect is the best.

There are two functions of the Dubois model in this research. One is to simulate the backscattering coefficient of bare soil and solve the unknown coefficient in the ratio model. The other is to simulate the backscattering coefficient of bare soil and establish the empirical relationship of soil moisture. Therefore, according to the Dubois model, it can be concluded that when the soil roughness is certain, the backscattering coefficient of bare soil is controlled by soil moisture. Based on this, the Dubois model is used to establish the relationship between soil backscattering coefficient and soil moisture. Moreover, 80% of the in situ soil data (55 soil samples) were used to build the empirical relationship between the in situ soil moisture and backscattering coefficient. Figure 10 shows the scatter plot of the backscattering coefficient of the Dubois model and in situ soil moisture under HH and VV polarization modes.

Figure 10 shows that there is a linear relationship between the backscattering coefficient simulated by the Dubois model and the in situ soil moisture. Therefore, we used a linear regression model to represent the functional relationship between the backscattering coefficient and soil moisture, which as shown in following Equation (4). The unknown coefficient of the equation was solved and the results are shown in

Table 4. The unknown coefficient of empirical model.

	d	e	R	RMSE
HH polarization	0.96	30.18	0.75	4.56
VV polarization	0.92	23.72	0.72	3.27

. The coefficient d represents the slope and the coefficient e represents the intercept. From Table 4, the regression equation can be concluded. The regression equation is $m_v=0.96\ast {\sigma }_{hhsoil}^o+30.18$ under HH polarization, the regression equation is $m_v=0.92\ast {\sigma }_{vvsoil}^o+23.72$ under VV polarization. As shown in Table 4, it can be found that the empirical relationship between the two polarizations and soil moisture are basically the same.

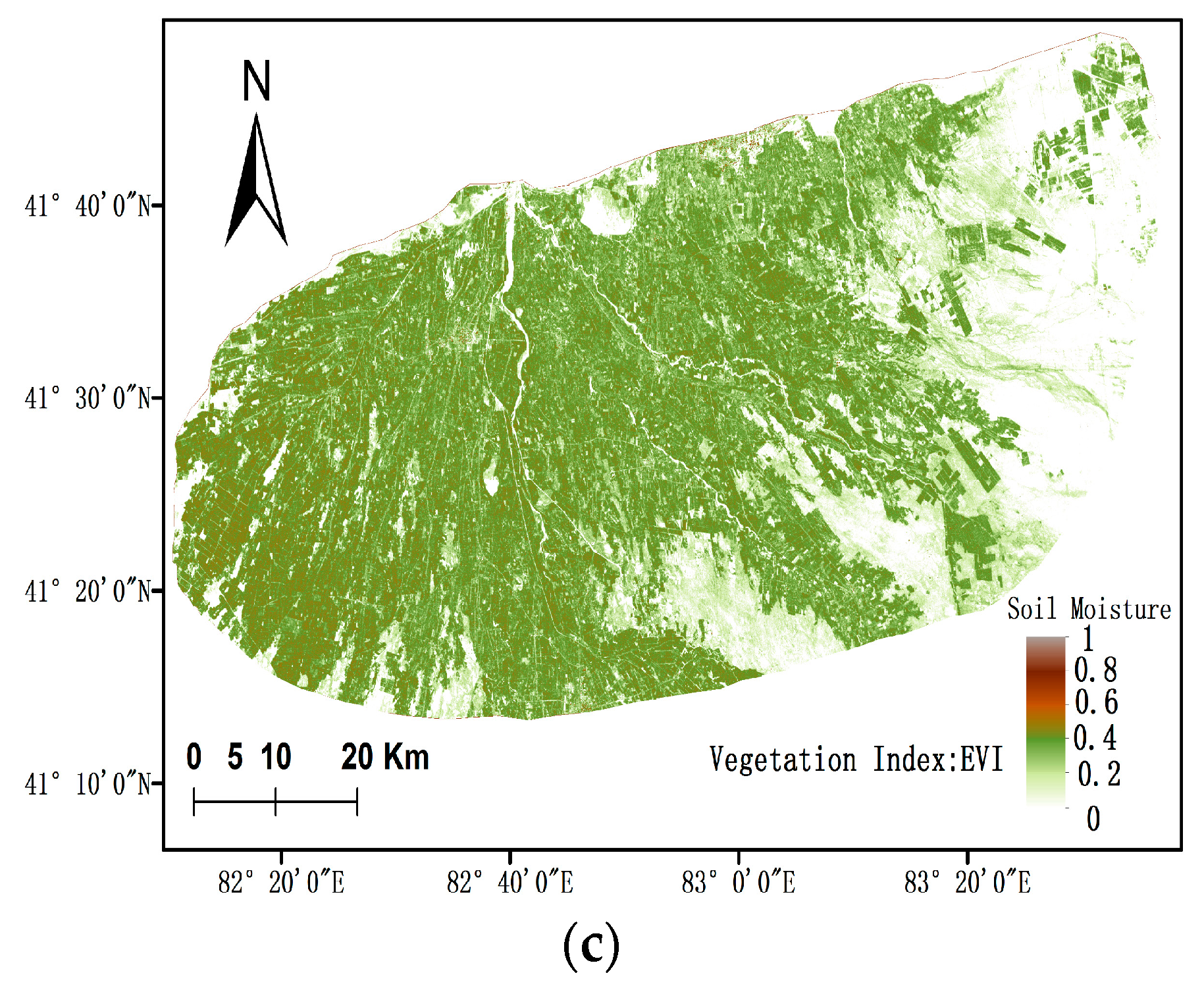
3.3. Soil Moisture Retrieval

The backscattering coefficient of the soil was obtained by using the ratio model; meanwhile, the empirical model (Equation (4)) was used to derive soil moisture based on the Sentinel-1 microwave data. In order to distinguish the changes of soil moisture, the results of surface soil moisture were normalized to [0,1] using a Min-Max normalization approach (Figure 11).

As shown in Figure 11, the soil moisture in the oasis-desert ecotone region (southeast) is low (below 0.2). In the oasis region (middle and north), it is moderate (about 0.3); this part has the largest proportion. In the oasis region (west), it is high (above 0.3). The soil moisture in the inner oasis is much higher than that in the oasis-desert ecotone region.

In order to see the difference between the soil moisture retrieval distribution, the pixel number of each interval was computed, and the percentage was computed. The results are listed in

Table 5. Pixel number of each interval of soil moisture map.

	VWC	NDVI	EVI
0–0.2	1,509,041 (24.36%)	1,577,622 (25.47%)	1,662,995 (26.85%)
0.2–0.4	3,853,753 (62.22%)	3,749,477 (60.53%)	3,703,183 (59.79%)
0.4–0.6	818,423 (13.21%)	841,098 (13.58%)	799,751 (12.91%)
0.6–0.8	12,282 (0.20%)	25,158 (0.41%)	27,313 (0.44%)
0.8–1	151 (0.01%)	295 (0.01%)	408 (0.01%)
Count	6,193,650	6,193,650	6,193,650

. In Table 5, it can be seen that the percentage remains highest when the soil moisture is between 0.2 and 0.4. When the soil moisture is between 0 and 0.2, the percentage is about 25%. When the soil moisture is higher than 0.4, the pixel number has a small percentage.

There were differences in the soil moisture retrieval under the three vegetation indices, which proved that the model conducted was suitable for deriving soil moisture in this oasis region. All of these findings can be seen in Figure 11.

Moreover, 20% of the in situ soil data (14 soil samples) were used to verify the accuracy of the soil moisture model constructed in this paper. The soil moisture simulated by the Dubois model were correlated with the in situ soil moisture under three vegetation indices. The results are shown in Figure 12, and their error metrics, i.e., bias, RMSE, are listed in

Table 6. Statistical metrics between in situ and simulation soil moisture.

Model	Coefficient of Determination (R2)	RMSE (vol. %)	Bias
VWC	0.76	2.04	0.86
NDVI	0.73	2.43	1.09
EVI	0.74	2.39	1.14

.

Figure 12 shows that the correlation coefficient between the simulation soil moisture and in situ soil moisture under three different vegetation indices. The soil moisture retrieval accuracy is the highest under the VWC vegetation index, and the coefficient of determination reached 0.76, which was significantly correlated. When NDVI and EVI vegetation indices are used to eliminate vegetation scattering contribution, the soil moisture retrieval accuracy is not much different, and the coefficient of determination is about 0.73, which is slightly weaker than the result under the VWC vegetation index.

As shown in Table 6, the error metrics were calculated under three vegetation indices. A positive bias indicates that the retrieved soil moisture is systematically overestimated compared with the in situ measurements. The RMSE represents the absolute errors between the observations and simulations. In general, the accuracy of the soil moisture estimation is promising; the model built using VWC vegetation index works best. The inner oasis is the most impacted by the choice of the vegetation indices, and the land cover is agriculture.

4. Discussion

According to the analyses of the soil moisture retrieval accuracy, which is not high, there are uncertain factors in the retrieval process. The main aspects are as follows: (1) it is difficult to maintain the same time for field survey data, microwave data, and the optical data. During this period, it is assumed that the vegetation index remain unchanged, but July is a period of vigorous vegetation growth, which will lead to a miscalculation of vegetation scattering. (2) The parameter error of soil moisture is caused by the nonstandard sampling and the uncertainty of data processing in the laboratory. (3) There are systematic errors in the model itself, such as the backscattering coefficients simulated by the Dubois model and the ratio model, which will affect the accuracy of the soil moisture retrieval. Nevertheless, this method is still feasible if the purpose is to obtain the soil moisture in an oasis region.

Note that two models have equal importance to the soil moisture derived. The Dubois model can establish an empirical relationship and the ratio model can eliminate the vegetation scattering contribution. Among them, the ratio model is suitable for low shrubs, crops, and is not fit for arbor. However, when it comes to the soil moisture derived under forest coverage, the continuous Michigan Microwave Canopy Scattering (MIMICS) model is commonly used to simulate the scattering characteristics of forests, which is suitable for arbor. In this situation, different vegetation coverage could influence the detection results. Therefore, this method may not be suitable for temperate forests or tropical forests.

5. Conclusions

The soil moisture retrieval model was conducted based on the Topp dielectric constant model, the Dubois model and ratio method; then, the Sentinel-1 data were used to derive the soil moisture in an oasis region, and the feasibility of this method was verified by using the in situ soil moisture. Based on the findings of this study, the following conclusions can be drawn:

• Based on the Dubois model, in situ soil roughness, the soil moisture, and radar system configuration parameters were used to simulate the backscattering coefficient of bare soil, which solved the unknown coefficient of the ratio model, on one hand, and verified the feasibility of the ratio model on the other hand.
• The VWC, NDVI, and EVI were the three vegetation parameters that were selected to characterize the scattering contribution of vegetation; based on the ratio model, the least squares method was used to calibrate the unknown coefficient. Based on this model, the unknown coefficient was certain; the backscattering coefficient of bare soil was simulated and fitted with the backscattering coefficient, simulated by the Dubois model, which found that the ratio model could effectively simulate the scattering characteristics of bare soil.
• The Dubois model was used to simulate the backscattering coefficient of the soil; an empirical relationship between it and the in situ soil moisture was established. Based on the model we conducted, the spatial soil moisture was successfully derived.
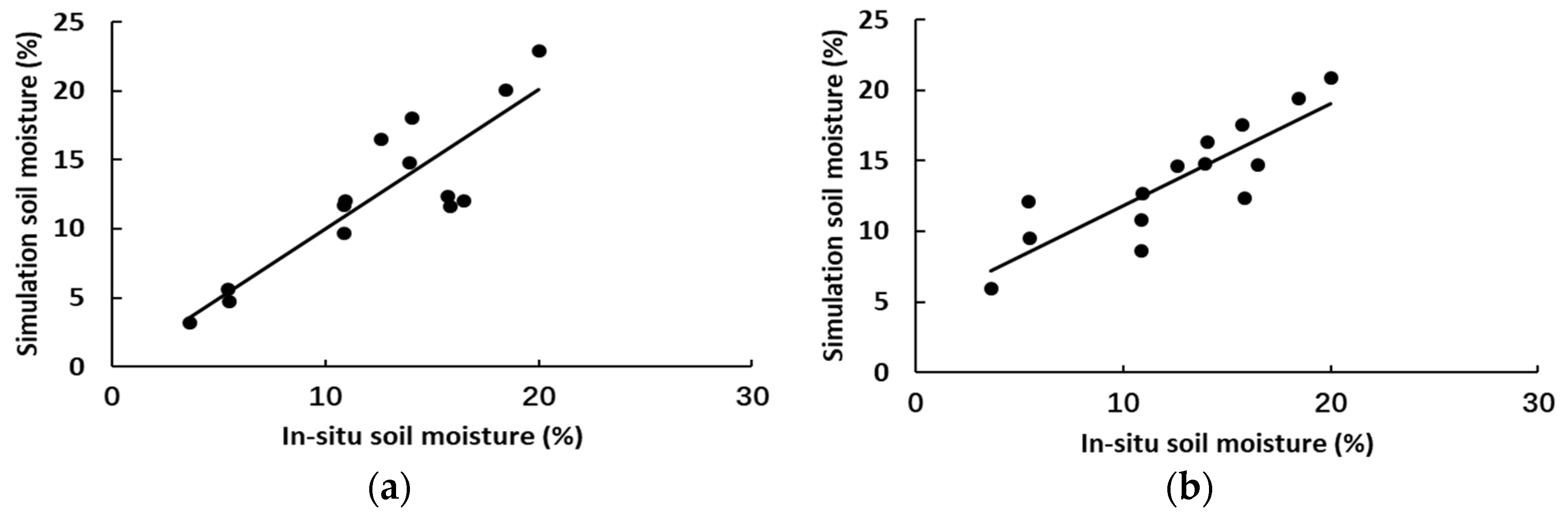
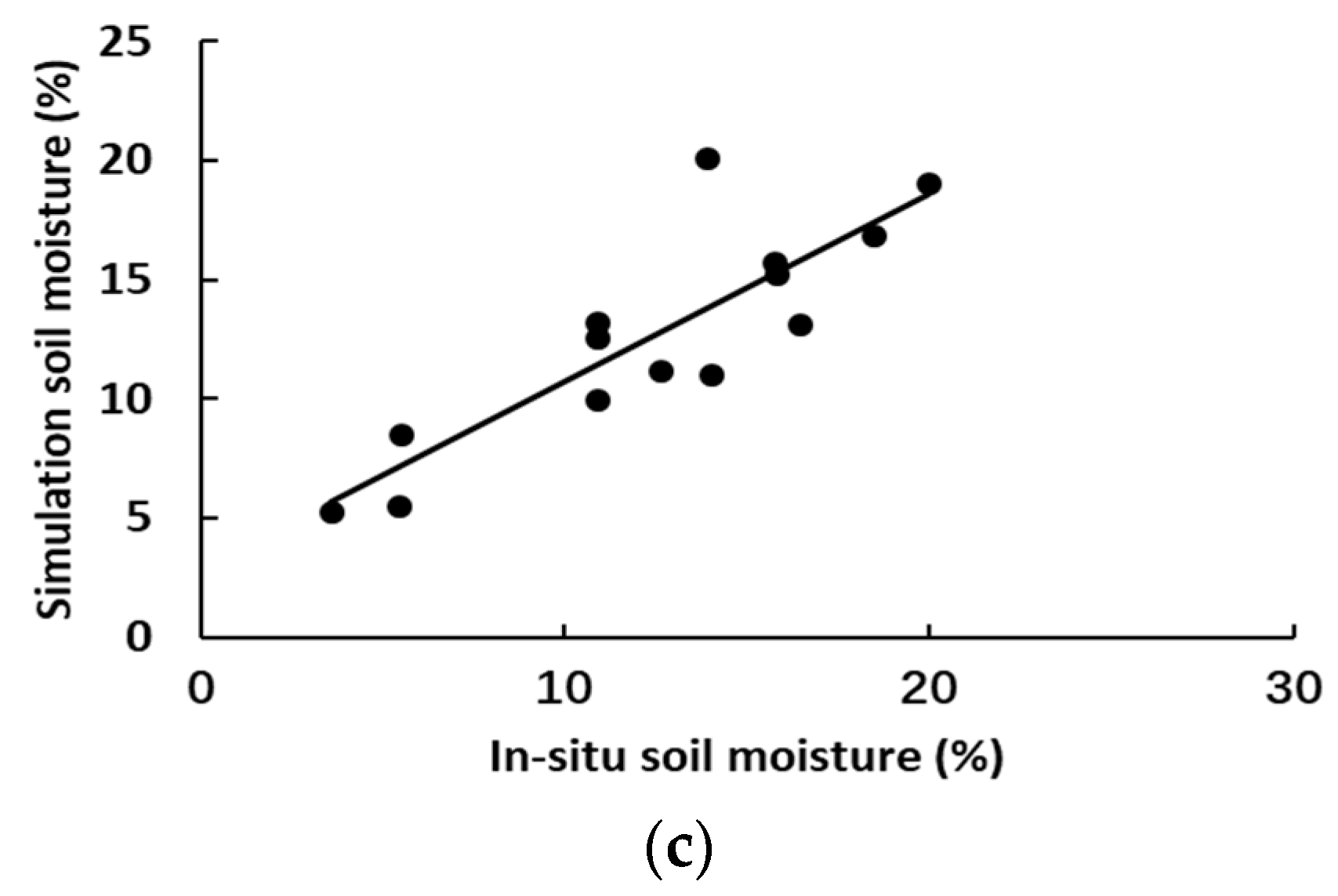
• The in situ soil moisture was used to analyze the accuracy of the soil moisture derived in this oasis under three vegetation indices. The results show that the soil moisture retrieval accuracy was the highest under the VWC vegetation index, and the soil moisture retrieval accuracy was not much different under NDVI and EVI vegetation indices. The results show that the soil moisture model conducted on the Dubois model and ratio model is feasible.