Comparison of Machine Learning Methods for Estimating Mangrove Above-Ground Biomass Using Multiple Source Remote Sensing Data in the Red River Delta Biosphere Reserve, Vietnam
Abstract
1. Introduction
2. Materials and Methods
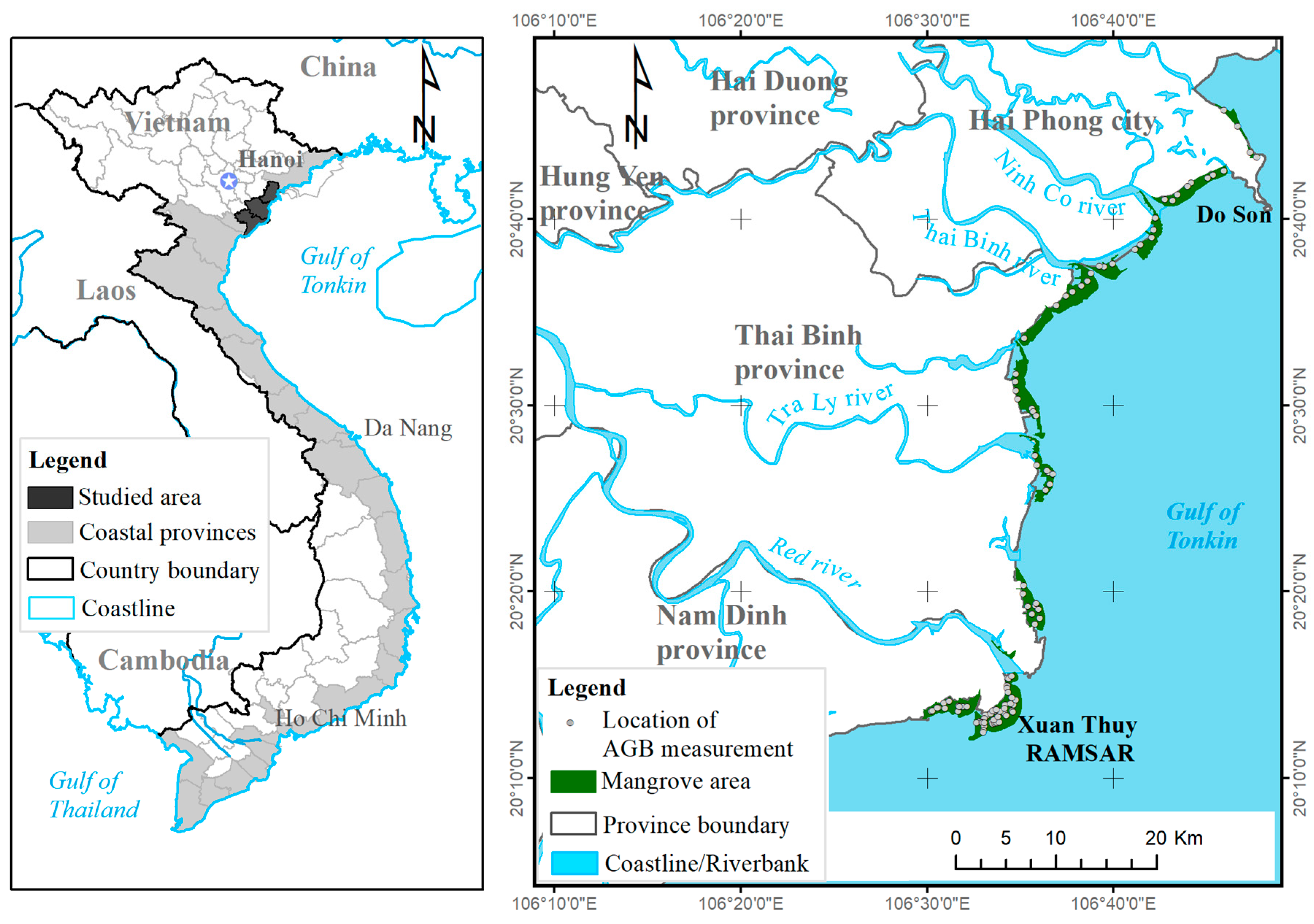
2.1. Study Site
2.2. EO and Field Survey Data Collection
2.2.1. Satellite Remotely Sensed Data
2.2.2. Data Collection from the Mangrove Inventory
3. Methods
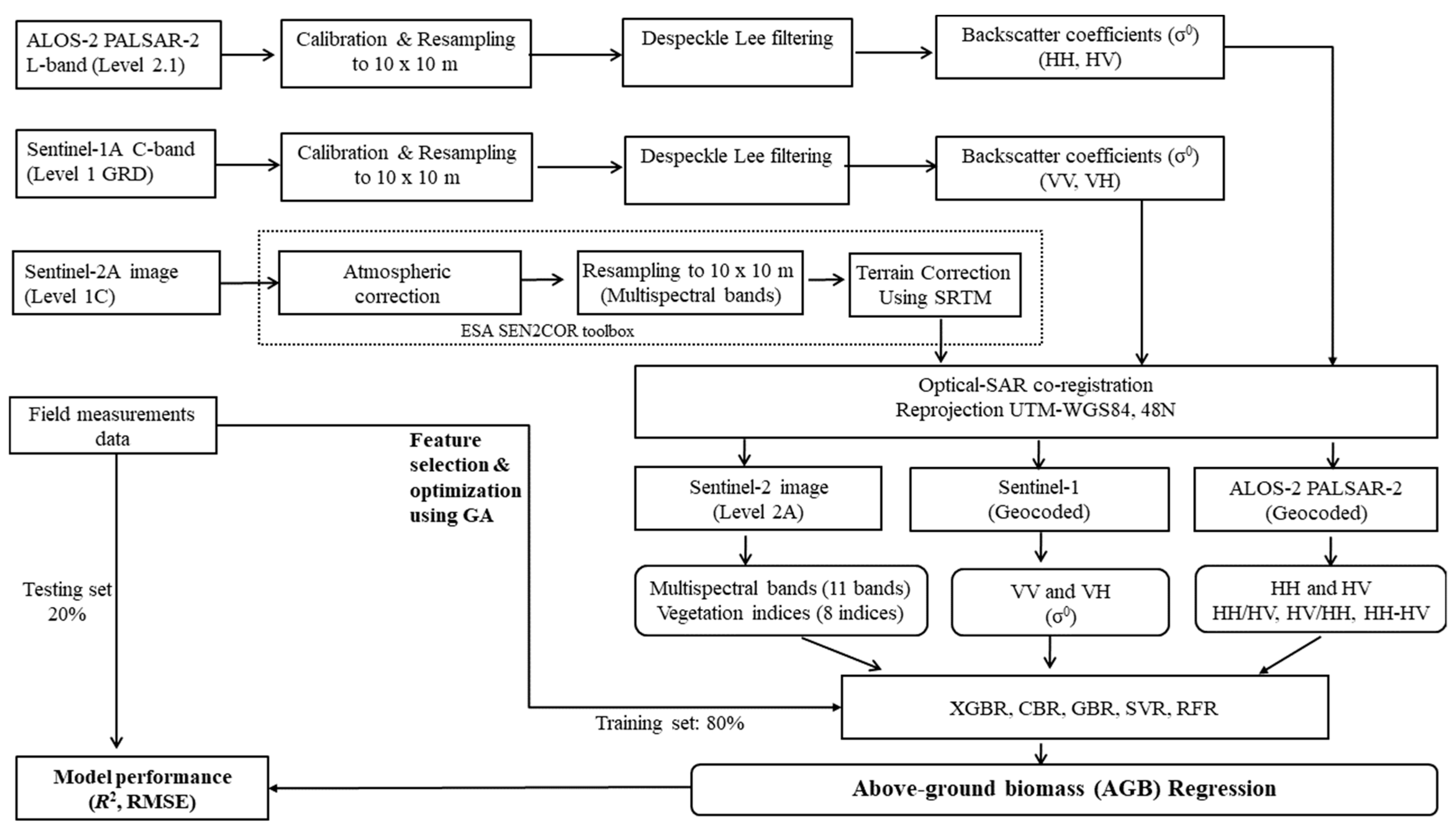
3.1. Satellite Image Processing
3.2. Image Transformation of the S-2 Multispectral and ALOS-2 PALSAR-2 Imagery
3.3. Machine Learning Models Used
3.3.1. Gradient Boosting Decision Tree (GBDT) Algorithms
3.3.2. Support Vector Regression (SVR)
3.3.3. Random Forest Regression (RFR)
3.4. Model Configuration, Implementation, and Assessment
3.4.1. Model Configuration and Training
3.4.2. Hyperparameter Tuning of XGBR, CBR, GBRT, RFR, and SVR.
3.4.3. GA for Feature Selection
3.4.4. Model Evaluation
4. Results
4.1. Mangrove Tree Characteristics in the RRDBR
4.2. Modeling Results, Assessment, and Comparison
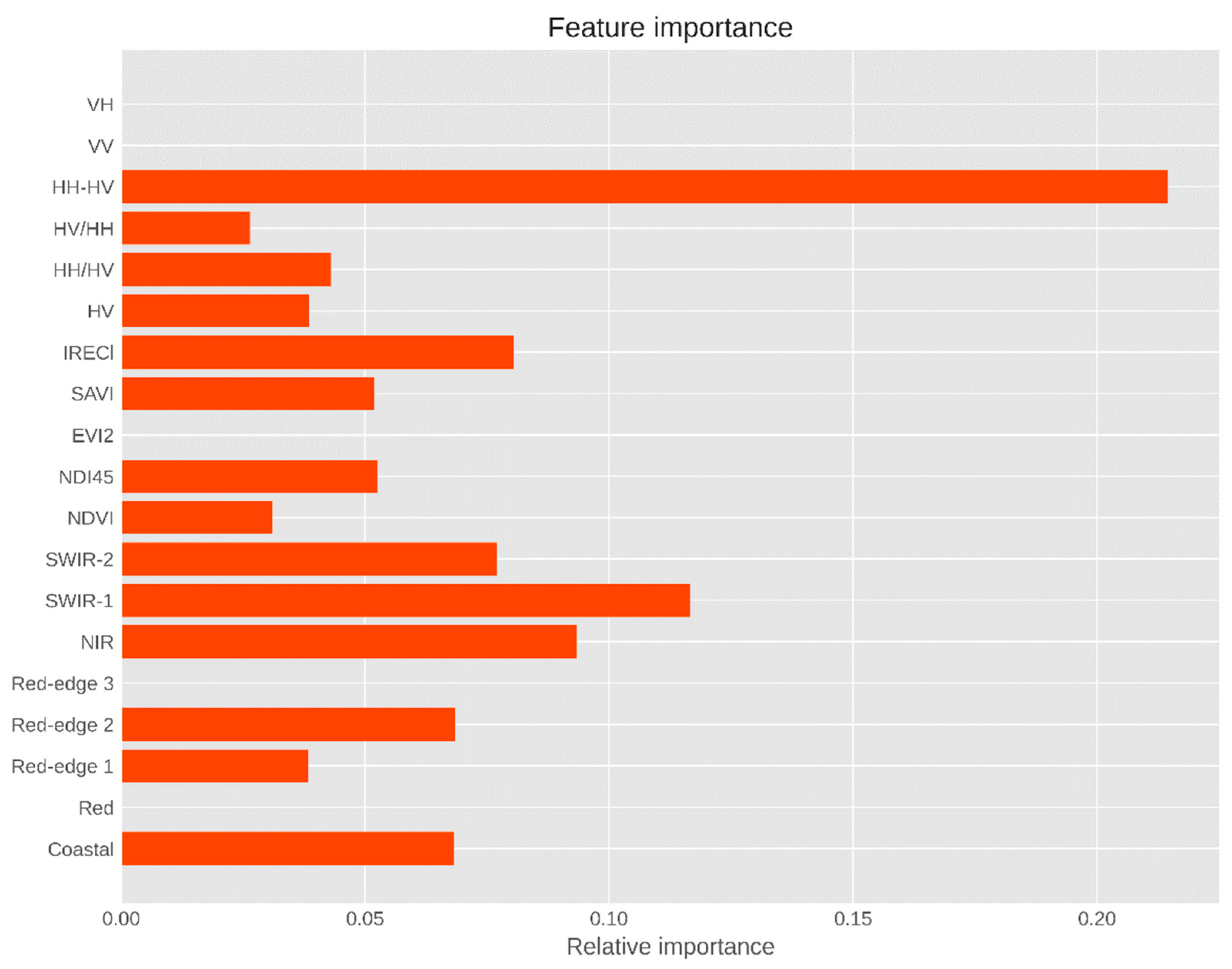
4.3. Variable Importance
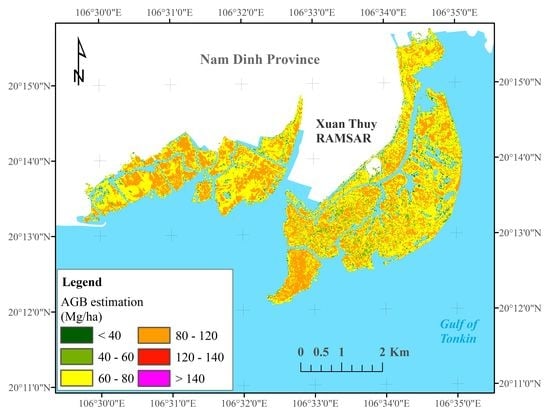
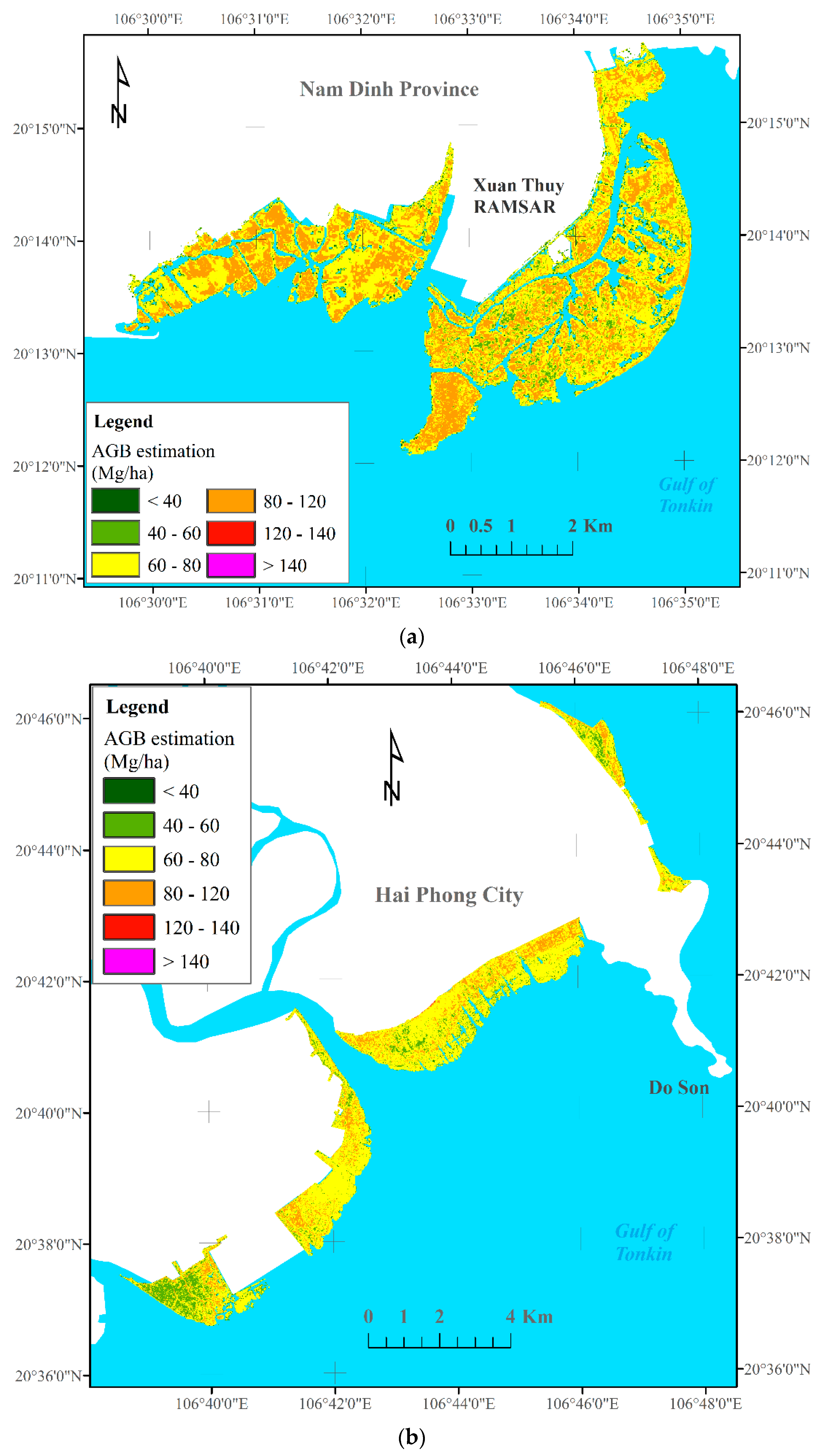
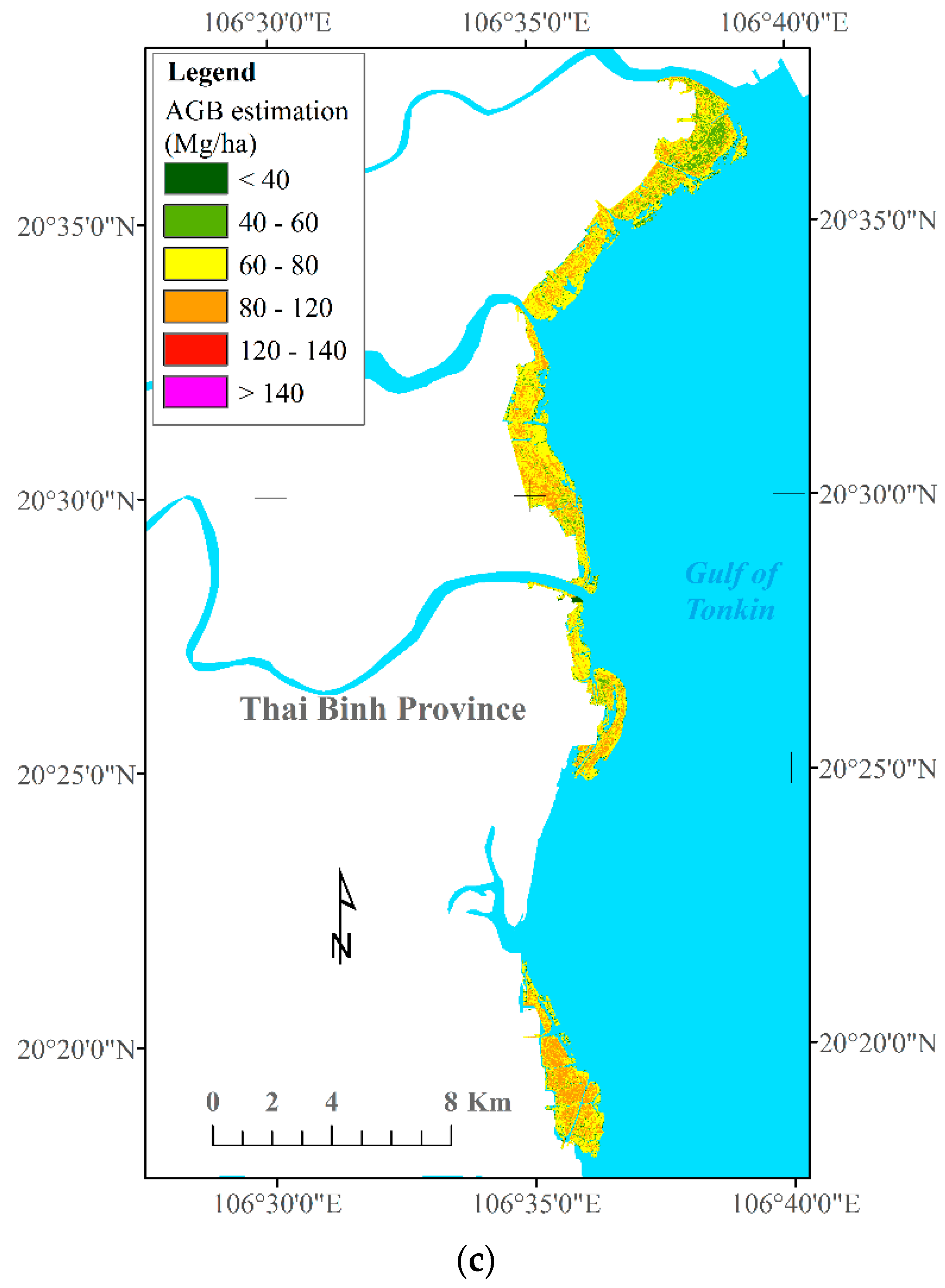
4.4. Generation of Mangrove AGB Maps in the Study Area
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Alongi, D.M. Carbon sequestration in mangrove forests. Carbon Manag. 2012, 3, 313–322. [Google Scholar] [CrossRef]
- Lee, S.Y.; Primavera, J.H.; Dahdouh-Guebas, F.; McKee, K.; Bosire, J.O.; Cannicci, S.; Diele, K.; Fromard, F.; Koedam, N.; Marchand, C.; et al. Ecological role and services of tropical mangrove ecosystems: A reassessment. Glob. Ecol. Biogeogr. 2014, 23, 726–743. [Google Scholar] [CrossRef]
- Friess, D.A.; Rogers, K.; Lovelock, C.E.; Krauss, K.W.; Hamilton, S.E.; Lee, S.Y.; Lucas, R.; Primavera, J.; Rajkaran, A.; Shi, S. The State of the World’s Mangrove Forests: Past, Present, and Future. Annu. Rev. Environ. Resour. 2019, 44, 89–115. [Google Scholar] [CrossRef]
- Richards, D.R.; Friess, D.A. Rates and drivers of mangrove deforestation in Southeast Asia, 2000–2012. Proc. Natl. Acad. Sci. USA 2016, 113, 344–349. [Google Scholar] [CrossRef]
- Hamilton, S.E.; Friess, D.A. Global carbon stocks and potential emissions due to mangrove deforestation from 2000 to 2012. Nat. Clim. Chang. 2018, 8, 240–244. [Google Scholar] [CrossRef]
- Ahmed, N.; Glaser, M. Coastal aquaculture, mangrove deforestation and blue carbon emissions: Is REDD+ a solution? Mar. Policy 2016, 66, 58–66. [Google Scholar] [CrossRef]
- Castillo, J.A.A.; Apan, A.A.; Maraseni, T.N.; Salmo, S.G. Estimation and mapping of above-ground biomass of mangrove forests and their replacement land uses in the Philippines using Sentinel imagery. ISPRS J. Photogramm. Remote Sens. 2017, 134, 70–85. [Google Scholar] [CrossRef]
- Pham, T.D.; Yoshino, K.; Le, N.; Bui, D. Estimating Aboveground Biomass of a Mangrove Plantation on the Northern coast of Vietnam using machine learning techniques with an integration of ALOS-2 PALSAR-2 and Sentinel-2A data. Int. J. Remote Sens. 2018, 39, 7761–7788. [Google Scholar] [CrossRef]
- Kauffman, J.B.; Donato, D.C. Protocols for the Measurement, Monitoring and Reporting of Structure, Biomass, and Carbon Stocks in Mangrove Forests; CIFOR: Bogor, Indonesia, 2012. [Google Scholar]
- Maeda, Y.; Fukushima, A.; Imai, Y.; Tanahashi, Y.; Nakama, E.; Ohta, S.; Kawazoe, K.; Akune, N. Estimating carbon stock changes of mangrove forests using satellite imagery and airborne lidar data in the south sumatra state, indonesia. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 705–709. [Google Scholar] [CrossRef]
- Navarro, J.A.; Algeet, N.; Fernández-Landa, A.; Esteban, J.; Rodríguez-Noriega, P.; Guillén-Climent, M.L. Integration of UAV, Sentinel-1, and Sentinel-2 Data for Mangrove Plantation Aboveground Biomass Monitoring in Senegal. Remote Sens. 2019, 11, 77. [Google Scholar] [CrossRef]
- Fatoyinbo, T.; Feliciano, E.A.; Lagomasino, D.; Lee, S.K.; Trettin, C. Estimating mangrove aboveground biomass from airborne LiDAR data: A case study from the Zambezi River delta. Environ. Res. Lett. 2018, 13, 025012. [Google Scholar] [CrossRef]
- Hamilton, S.E.; Castellanos-Galindo, G.A.; Millones-Mayer, M.; Chen, M. Remote Sensing of Mangrove Forests: Current Techniques and Existing Databases. In Threats to Mangrove Forests: Hazards, Vulnerability, and Management; Makowski, C., Finkl, C.W., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 497–520. [Google Scholar] [CrossRef]
- Pham, T.D.; Xia, J.; Ha, N.T.; Bui, D.T.; Le, N.N.; Takeuchi, W. A Review of Remote Sensing Approaches for Monitoring Blue Carbon Ecosystems: Mangroves, Seagrasses and Salt Marshes during 2010–2018. Sensors 2019, 19, 1933. [Google Scholar] [CrossRef]
- Curnick, D.; Pettorelli, N.; Amir, A.; Balke, T.; Barbier, E.; Crooks, S.; Dahdouh-Guebas, F.; Duncan, C.; Endsor, C.; Friess, D. The value of small mangrove patches. Science 2019, 363, 239. [Google Scholar]
- Wang, D.; Wan, B.; Liu, J.; Su, Y.; Guo, Q.; Qiu, P.; Wu, X. Estimating aboveground biomass of the mangrove forests on northeast Hainan Island in China using an upscaling method from field plots, UAV-LiDAR data and Sentinel-2 imagery. Int. J. Appl. Earth Obs. Geoinf. 2020, 85, 101986. [Google Scholar] [CrossRef]
- Pandey, P.C.; Anand, A.; Srivastava, P.K. Spatial distribution of mangrove forest species and biomass assessment using field inventory and earth observation hyperspectral data. Biodivers. Conserv. 2019, 28, 2143–2162. [Google Scholar] [CrossRef]
- Pham, T.D.; Yoshino, K. Aboveground biomass estimation of mangrove species using ALOS-2 PALSAR imagery in Hai Phong City, Vietnam. J. Appl. Remote Sens. 2017, 11, 026010. [Google Scholar] [CrossRef]
- Hamdan, O.; Khali Aziz, H.; Mohd Hasmadi, I. L-band ALOS PALSAR for biomass estimation of Matang Mangroves, Malaysia. Remote Sens. Environ. 2014, 155, 69–78. [Google Scholar] [CrossRef]
- Jachowski, N.R.A.; Quak, M.S.Y.; Friess, D.A.; Duangnamon, D.; Webb, E.L.; Ziegler, A.D. Mangrove biomass estimation in Southwest Thailand using machine learning. Appl. Geogr. 2013, 45, 311–321. [Google Scholar] [CrossRef]
- Pham, T.D.; Yoshino, K.; Bui, D.T. Biomass estimation of Sonneratia caseolaris (l.) Engler at a coastal area of Hai Phong city (Vietnam) using ALOS-2 PALSAR imagery and GIS-based multi-layer perceptron neural networks. GISci. Remote Sens. 2017, 54, 329–353. [Google Scholar] [CrossRef]
- Pham, L.T.H.; Brabyn, L. Monitoring mangrove biomass change in Vietnam using SPOT images and an object-based approach combined with machine learning algorithms. ISPRS J. Photogramm. Remote Sens. 2017, 128, 86–97. [Google Scholar] [CrossRef]
- Wang, L.; Silván-Cárdenas, J.L.; Sousa, W.P. Neural Network Classification of Mangrove Species from Multi-seasonal Ikonos Imagery. Photogramm. Eng. Remote Sens. 2008, 74, 921–927. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, L.; Wang, L. Evaluation of Morphological Texture Features for Mangrove Forest Mapping and Species Discrimination Using Multispectral IKONOS Imagery. IEEE Geosci. Remote Sens. Lett. 2009, 6, 393–397. [Google Scholar] [CrossRef]
- Heumann, B.W. Satellite remote sensing of mangrove forests: Recent advances and future opportunities. Prog. Phys. Geogr. 2011, 35, 87–108. [Google Scholar] [CrossRef]
- Wu, C.; Shen, H.; Shen, A.; Deng, J.; Gan, M.; Zhu, J.; Xu, H.; Wang, K. Comparison of machine-learning methods for above-ground biomass estimation based on Landsat imagery. J. Appl. Remote Sens. 2016, 10, 035010. [Google Scholar] [CrossRef]
- López-Serrano, P.M.; López-Sánchez, C.A.; Álvarez-González, J.G.; García-Gutiérrez, J. A Comparison of Machine Learning Techniques Applied to Landsat-5 TM Spectral Data for Biomass Estimation. Can. J. Remote Sens. 2016, 42, 690–705. [Google Scholar] [CrossRef]
- Wei, Z.; Meng, Y.; Zhang, W.; Peng, J.; Meng, L. Downscaling SMAP soil moisture estimation with gradient boosting decision tree regression over the Tibetan Plateau. Remote Sens. Environ. 2019, 225, 30–44. [Google Scholar] [CrossRef]
- Ghosh, S.M.; Behera, M.D. Aboveground biomass estimation using multi-sensor data synergy and machine learning algorithms in a dense tropical forest. Appl. Geogr. 2018, 96, 29–40. [Google Scholar] [CrossRef]
- Gao, Y.; Li, Q.; Wang, S.; Gao, J. Adaptive neural network based on segmented particle swarm optimization for remote-sensing estimations of vegetation biomass. Remote Sens. Environ. 2018, 211, 248–260. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Song, Y.; Jiao, X.; Yang, S.; Zhang, S.; Qiao, Y.; Liu, Z.; Zhang, L. Combining Multiple Factors of LightGBM and XGBoost Algorithms to Predict the Morbidity of Double-High Disease. In International Conference of Pioneering Computer Scientists, Engineers and Educators; Springer: Singapore, 2019; pp. 635–644. [Google Scholar]
- Li, P.; Zhang, J.-S. A New Hybrid Method for China’s Energy Supply Security Forecasting Based on ARIMA and XGBoost. Energies 2018, 11, 1687. [Google Scholar] [CrossRef]
- Dev, V.A.; Eden, M.R. Gradient Boosted Decision Trees for Lithology Classification. In Computer Aided Chemical Engineering; Muñoz, S.G., Laird, C.D., Realff, M.J., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; Volume 47, pp. 113–118. [Google Scholar]
- Leslie, M.; Nguyen, S.T.; Nguyen, T.K.D.; Pham, T.T.; Cao, T.T.N.; Le, T.Q.; Dang, T.T.; Nguyen, T.H.T.; Nguyen, T.B.N.; Le, H.N.; et al. Bringing social and cultural considerations into environmental management for vulnerable coastal communities: Responses to environmental change in Xuan Thuy National Park, Nam Dinh Province, Vietnam. Ocean Coast. Manag. 2018, 158, 32–44. [Google Scholar] [CrossRef]
- Li, Z.; Saito, Y.; Matsumoto, E.; Wang, Y.; Tanabe, S.; Lan Vu, Q. Climate change and human impact on the Song Hong (Red River) Delta, Vietnam, during the Holocene. Quat. Int. 2006, 144, 4–28. [Google Scholar] [CrossRef]
- Hong, P.N.; San, H.T. Mangroves of Vietnam; IUCN: Bangkok, Thailand, 1993; p. 173. [Google Scholar]
- Hong, P.N. Mangrove Ecosystem in the Red River Coastal Zone: Biodiversity, Ecology, Socio-Economic, Management and Education; Agricultural Publishing House: Hanoi, Vietnam, 2004; p. 509. [Google Scholar]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Clough, B.F.; Scott, K. Allometric relationships for estimating above-ground biomass in six mangrove species. For. Ecol. Manag. 1989, 27, 117–127. [Google Scholar] [CrossRef]
- Komiyama, A.; Poungparn, S.; Kato, S. Common allometric equations for estimating the tree weight of mangroves. J. Trop. Ecol. 2005, 21, 471–477. [Google Scholar] [CrossRef]
- Fu, W.; Wu, Y. Estimation of aboveground biomass of different mangrove trees based on canopy diameter and tree height. Procedia Environ. Sci. 2011, 10, 2189–2194. [Google Scholar] [CrossRef]
- Shimada, M.; Isoguchi, O.; Tadono, T.; Isono, K. PALSAR Radiometric and Geometric Calibration. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3915–3932. [Google Scholar] [CrossRef]
- Louis, J.; Debaecker, V.; Pflug, B.; Main-Knorn, M.; Bieniarz, J.; Mueller-Wilm, U.; Cadau, E.; Gascon, F. Sentinel-2 sen2cor: L2a processor for users. In Proceedings of the Living Planet Symposium, Prague, Czech Republic, 9–13 May 2016; pp. 9–13. [Google Scholar]
- Filipponi, F. Sentinel-1 GRD Preprocessing Workflow. Proceedings 2019, 18, 11. [Google Scholar] [CrossRef]
- Patil, V.; Singh, A.; Naik, N.; Unnikrishnan, S. Estimation of Mangrove Carbon Stocks by Applying Remote Sensing and GIS Techniques. Wetlands 2015, 35, 695–707. [Google Scholar] [CrossRef]
- Vafaei, S.; Soosani, J.; Adeli, K.; Fadaei, H.; Naghavi, H.; Pham, T.D.; Tien Bui, D. Improving Accuracy Estimation of Forest Aboveground Biomass Based on Incorporation of ALOS-2 PALSAR-2 and Sentinel-2A Imagery and Machine Learning: A Case Study of the Hyrcanian Forest Area (Iran). Remote Sens. 2018, 10, 172. [Google Scholar] [CrossRef]
- Bannari, A.; Morin, D.; Bonn, F.; Huete, A.R. A review of vegetation indices. Remote Sens. Rev. 1995, 13, 95–120. [Google Scholar] [CrossRef]
- Vaglio Laurin, G.; Pirotti, F.; Callegari, M.; Chen, Q.; Cuozzo, G.; Lingua, E.; Notarnicola, C.; Papale, D. Potential of ALOS2 and NDVI to Estimate Forest Above-Ground Biomass, and Comparison with Lidar-Derived Estimates. Remote Sens. 2017, 9, 18. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Manna, S.; Nandy, S.; Chanda, A.; Akhand, A.; Hazra, S.; Dadhwal, V.K. Estimating aboveground biomass in Avicennia marina plantation in Indian Sundarbans using high-resolution satellite data. J. Appl. Remote Sens. 2014, 8, 083638. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Baret, F.; Guyot, G. Potentials and limits of vegetation indices for LAI and APAR assessment. Remote Sens. Environ. 1991, 35, 161–173. [Google Scholar] [CrossRef]
- Frampton, W.J.; Dash, J.; Watmough, G.; Milton, E.J. Evaluating the capabilities of Sentinel-2 for quantitative estimation of biophysical variables in vegetation. ISPRS J. Photogramm. Remote Sens. 2013, 82, 83–92. [Google Scholar] [CrossRef]
- Pham, T.D.; Le, N.N.; Ha, N.T.; Nguyen, L.V.; Xia, J.; Yokoya, N.; To, T.T.; Trinh, H.X.; Kieu, L.Q.; Takeuchi, W. Estimating Mangrove Above-Ground Biomass Using Extreme Gradient Boosting Decision Trees Algorithm with Fused Sentinel-2 and ALOS-2 PALSAR-2 Data in Can Gio Biosphere Reserve, Vietnam. Remote Sens. 2020, 12, 777. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Rouse, J.W., Jr.; Haas, R.; Schell, J.; Deering, D. Monitoring vegetation systems in the Great Plains with ERTS. NASA Spec. Publ. 1974, 351, 309. [Google Scholar]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Jiang, Z.; Huete, A.R.; Didan, K.; Miura, T. Development of a two-band enhanced vegetation index without a blue band. Remote Sens. Environ. 2008, 112, 3833–3845. [Google Scholar] [CrossRef]
- Delegido, J.; Verrelst, J.; Alonso, L.; Moreno, J. Evaluation of Sentinel-2 Red-Edge Bands for Empirical Estimation of Green LAI and Chlorophyll Content. Sensors 2011, 11, 7063–7081. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Daughtry, C.S.T.; Walthall, C.L.; Kim, M.S.; De Colstoun, E.B.; McMurtrey, J.E. Estimating Corn Leaf Chlorophyll Concentration from Leaf and Canopy Reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Sun, X.; Liu, M.; Sima, Z. A novel cryptocurrency price trend forecasting model based on LightGBM. Financ. Res. Lett. 2018. [Google Scholar] [CrossRef]
- Ma, X.; Sha, J.; Wang, D.; Yu, Y.; Yang, Q.; Niu, X. Study on a prediction of P2P network loan default based on the machine learning LightGBM and XGboost algorithms according to different high dimensional data cleaning. Electron. Commer. Res. Appl. 2018, 31, 24–39. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 1189–1232. [Google Scholar] [CrossRef]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Rao, H.; Shi, X.; Rodrigue, A.K.; Feng, J.; Xia, Y.; Elhoseny, M.; Yuan, X.; Gu, L. Feature selection based on artificial bee colony and gradient boosting decision tree. Appl. Soft Comput. 2019, 74, 634–642. [Google Scholar] [CrossRef]
- Nielsen, D. Tree Boosting with XGBoost-Why Does XGBoost Win “Every” Machine Learning Competition? Master’s Thesis, NTNU, Trondheim, Norway, 2016. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer Science & Business Media: Berlin, Germany, 2009. [Google Scholar]
- Dorogush, A.V.; Ershov, V.; Gulin, A. CatBoost: Gradient boosting with categorical features support. arXiv 2018, arXiv:1810.11363. [Google Scholar]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. In Proceedings of the Advances in Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018; pp. 6638–6648. [Google Scholar]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Silveira, E.M.O.; Silva, S.H.G.; Acerbi-Junior, F.W.; Carvalho, M.C.; Carvalho, L.M.T.; Scolforo, J.R.S.; Wulder, M.A. Object-based random forest modelling of aboveground forest biomass outperforms a pixel-based approach in a heterogeneous and mountain tropical environment. Int. J. Appl. Earth Obs. Geoinf. 2019, 78, 175–188. [Google Scholar] [CrossRef]
- Jones, E.; Oliphant, T.; Peterson, P. SciPy: Open Source Scientific Tools for Python; 2001; Available online: https://www.scienceopen.com/document?vid=ab12905a-8a5b-43d8-a2bb-defc771410b9 (accessed on 5 November 2019).
- Davis, L. Handbook of Genetic Algorithms; Van Nostrand Reinhold: New York, NY, USA, 1991. [Google Scholar]
- Kadiyala, A.; Kumar, A. Applications of python to evaluate the performance of decision tree-based boosting algorithms. Environ. Prog. Sustain. Energy 2018, 37, 618–623. [Google Scholar] [CrossRef]
- Darmawan, S.; Sari, D.K.; Takeuchi, W.; Wikantika, K.; Hernawati, R. Development of aboveground mangrove forests’ biomass dataset for Southeast Asia based on ALOS-PALSAR 25-m mosaic. J. Appl. Remote Sens. 2019, 13, 044519. [Google Scholar] [CrossRef]
- Hirata, Y.; Tabuchi, R.; Patanaponpaiboon, P.; Poungparn, S.; Yoneda, R.; Fujioka, Y. Estimation of aboveground biomass in mangrove forests using high-resolution satellite data. J. For. Res. 2014, 19, 34–41. [Google Scholar] [CrossRef]
- Pham, T.D.; Yokoya, N.; Bui, D.T.; Yoshino, K.; Friess, D.A. Remote Sensing Approaches for Monitoring Mangrove Species, Structure, and Biomass: Opportunities and Challenges. Remote Sens. 2019, 11, 230. [Google Scholar] [CrossRef]
- Nam, V.N.; Sasmito, S.D.; Murdiyarso, D.; Purbopuspito, J.; MacKenzie, R.A. Carbon stocks in artificially and naturally regenerated mangrove ecosystems in the Mekong Delta. Wetl. Ecol. Manag. 2016, 24, 231–244. [Google Scholar] [CrossRef]
- Proisy, C.; Mougin, E.; Fromard, F.; Karam, M.A. Interpretation of Polarimetric Radar Signatures of Mangrove Forests. Remote Sens. Environ. 2000, 71, 56–66. [Google Scholar] [CrossRef]
- Gao, Y.; Lu, D.; Li, G.; Wang, G.; Chen, Q.; Liu, L.; Li, D. Comparative Analysis of Modeling Algorithms for Forest Aboveground Biomass Estimation in a Subtropical Region. Remote Sens. 2018, 10, 627. [Google Scholar] [CrossRef]
- Feng, Y.; Lu, D.; Chen, Q.; Keller, M.; Moran, E.; Dos-Santos, M.N.; Bolfe, E.L.; Batistella, M. Examining effective use of data sources and modeling algorithms for improving biomass estimation in a moist tropical forest of the Brazilian Amazon. Int. J. Digit. Earth 2017, 10, 996–1016. [Google Scholar] [CrossRef]
- Zhao, P.; Lu, D.; Wang, G.; Liu, L.; Li, D.; Zhu, J.; Yu, S. Forest aboveground biomass estimation in Zhejiang Province using the integration of Landsat TM and ALOS PALSAR data. Int. J. Appl. Earth Obs. Geoinf. 2016, 53, 1–15. [Google Scholar] [CrossRef]
- Lu, D.; Batistella, M. Exploring TM image texture and its relationships with biomass estimation in Rondônia, Brazilian Amazon. Acta Amazonica 2005, 35, 249–257. [Google Scholar] [CrossRef]
- Le Toan, T.; Quegan, S.; Woodward, I.; Lomas, M.; Delbart, N.; Picard, G. Relating Radar Remote Sensing of Biomass to Modelling of Forest Carbon Budgets. Clim. Chang. 2004, 67, 379–402. [Google Scholar] [CrossRef]
- Wang, D.; Wan, B.; Qiu, P.; Zuo, Z.; Wang, R.; Wu, X. Mapping Height and Aboveground Biomass of Mangrove Forests on Hainan Island Using UAV-LiDAR Sampling. Remote Sens. 2019, 11, 2156. [Google Scholar] [CrossRef]
- Liu, H.; Ren, H.; Hui, D.; Wang, W.; Liao, B.; Cao, Q. Carbon stocks and potential carbon storage in the mangrove forests of China. J. Environ. Manag. 2014, 133, 86–93. [Google Scholar] [CrossRef]
- Jia, M.; Wang, Z.; Wang, C.; Mao, D.; Zhang, Y. A New Vegetation Index to Detect Periodically Submerged Mangrove Forest Using Single-Tide Sentinel-2 Imagery. Remote Sens. 2019, 11, 2043. [Google Scholar] [CrossRef]



| EO Sensor | Scene ID | Acquisition Date (Year/Month/Day) | Processing Level | Spatial Resolution (m) | Spectral/Polarizations Used |
|---|---|---|---|---|---|
| S-2 MSI | S2A_MSI_T48QXH | 2018/11/02 | Level-1C | 10–20 | 11 multispectral bands |
| S-1 SAR | S1A-IW_02AE1F | 2018/11/05 | Level-1 GRD | 20 | C-band (VV and VH polarizations) |
| ALOS-2 PALSAR-2 | ALOS2206940200 | 2018/10/18 | Level 2.1 | 6 | L-band (HH and HV polarizations) |
| ALOS2206940190 |
| No. | Mangrove Species | Biomass Allometric Equation | Parameter | Reference |
|---|---|---|---|---|
| 1 | Sonneratia caseolaris | Biomass (kg) = 0.251× ρ ×DBH2.46 (R2 = 0.98) Biomass root (kg) = 0.199 × ρ × 0.899 × DBH2.22 | DBH, H | [41] |
| 2 | Bruguiera gymnorrhiza | Biomass (kg) = 0.168 × DBH2.31 (R2 = 0.99) | DBH, H | [40] |
| 3 | Kandelia obovata | Biomass (kg) = 2.5904 × CD2 × H (R2 = 0.89) Biomass (kg) = 0.251 × ρ × DBH2.46 (R2 = 0.98) | Canopy diameter, H (DBH < 5 cm) DBH, H (DBH > 5 cm) | [42] [41] |
| 4 | Avicennia marina | Biomass (kg) = 1.8247× CD2 × H (R2 = 0.97) | Canopy diameter, H | [42] |
| 5 | Aegiceras corniculatum | Biomass (kg) = 3.1253 × CD2 × H (R2 = 0.99) | Canopy diameter, H | [42] |
| 6 | Rhizophora stylosa | Biomass (kg) = 0.168 × D2.42 + Biomass stilt (kg) = 0.0209 × D2.55 (R2 = 0.99) | D30, H | [40] |
| Vegetation Index | Acronyms | S-2 Band Wavelengths Used | References |
|---|---|---|---|
| Ratio Vegetation Index | RVI | [56] | |
| Normalized Difference Vegetation Index | NDVI | [57] | |
| Green Normalized Difference Vegetation Index | GNDVI | [58] | |
| Enhanced Vegetation Index-2 | EVI-2 | [59] | |
| Normalized Difference Index using Bands 4 & 5 of S-2 | NDI45 | [60] | |
| Soil-Adjusted Vegetation Index | SAVI | L = 0.5 in most conditions | [61] |
| Inverted Red-Edge Chlorophyll Index | IRECl | [54] | |
| Modified Chlorophyll Absorption in Reflectance Index | MCARI | [(RE1 − Red) − 0.2 × (RE1 − Green)] × (RE1 − NIR) | [62] |
| Algorithm | Learning_Rate/Epsilon (ἑ) | Min_Samples_Leaf Min_Child_Weight | Gamma | Max_Depth/Max Feature | n_Estimators/ n_Iterations or C Value |
|---|---|---|---|---|---|
| RFR | NA | 5 | NA | 15 | 100 |
| SVR | 0.5 | NA | 1000 | NA | 1000 |
| GBRT | 0.2 | 5 | NA | 3, 3 | 100 |
| XGBR | 0.7 | 6 | 0 | 2 | 100 |
| CBR | 0.7 | NA | NA | 2 | 100 |
| Tree Density (stems ha−1) | Stem DBH (cm) | Stem H (m) | AGB min (Mg·ha−1) | AGB max (Mg·ha−1) | Mean (Mg·ha−1) | Standard Deviation (Mg·ha−1) | |
|---|---|---|---|---|---|---|---|
| Nam Dinh (n = 55) | 315–8285 | 2.2–11.5 | 0.6–7.5 | 2.71 | 157.41 | 51.58 | 34.06 |
| Thai Binh (n = 30) | 265–6434 | 2.7–15.5 | 1.1–9.8 | 11.41 | 157.45 | 79.90 | 39.64 |
| Hai Phong (n = 20) | 198–5596 | 3.5–23.8 | 1.5–14.8 | 9.57 | 257.08 | 72.31 | 44.04 |
| No. | ML Model | R2 Testing (20%) | RMSE (Mg·ha−1) |
|---|---|---|---|
| 1 | CatBoost regression (CBR) | 0.492 | 31.75 |
| 2 | Extreme boosting regression (XGBR) | 0.622 * | 27.39 * |
| 3 | Gradient boosted regression tree (GBRT) | 0.563 | 29.44 |
| 4 | Random forest regression (RFR) | 0.426 | 33.75 |
| 5 | Support vector regression (SVR) | 0.596 | 28.31 |
| Scenario (SC) | Number of Input Variables | R2 Testing (20%) | RMSE (Mg·ha−1) |
|---|---|---|---|
| SC1 | 7 features from ALOS-2 PALSAR-2 and S-1 | 0.302 | 37.20 |
| SC2 | 11 features from the MS bands of S-2 | 0.301 | 34.14 |
| SC3 | 13 features from the MS bands of S-2 and S-1 | 0.487 | 27.10 |
| SC4 | 19 features from the MS bands and VIs from S-2 | 0.378 | 48.24 |
| SC5 | 19 optimal features from feature selection using GA (8 MS bands, 5 VIs, 4 bands from ALOS-2 PALSAR-2, and 2 bands from S-1) | 0.683 * | 25.08 * |
| SC6 | 26 features (11 MS bands, 8 VIs, 5 bands from ALOS-2 PALSAR-2, and 2 bands from S-1) | 0.622 | 27.39 |
| No. | ML Model | R2 Testing (20%) | RMSE (Mg·ha−1) |
|---|---|---|---|
| 1 | CatBoost regression (CBR) | 0.587 | 28.62 |
| 2 | Extreme boosting regression (XGBR) | 0.683 * | 25.08 * |
| 3 | Gradient boosted regression trees (GBRT) | 0.596 | 28.30 |
| 4 | Random forest regression (RFR) | 0.529 | 30.58 |
| 5 | Support vector regression (SVR) | 0.488 | 31.86 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pham, T.D.; Yokoya, N.; Xia, J.; Ha, N.T.; Le, N.N.; Nguyen, T.T.T.; Dao, T.H.; Vu, T.T.P.; Pham, T.D.; Takeuchi, W. Comparison of Machine Learning Methods for Estimating Mangrove Above-Ground Biomass Using Multiple Source Remote Sensing Data in the Red River Delta Biosphere Reserve, Vietnam. Remote Sens. 2020, 12, 1334. https://doi.org/10.3390/rs12081334
Pham TD, Yokoya N, Xia J, Ha NT, Le NN, Nguyen TTT, Dao TH, Vu TTP, Pham TD, Takeuchi W. Comparison of Machine Learning Methods for Estimating Mangrove Above-Ground Biomass Using Multiple Source Remote Sensing Data in the Red River Delta Biosphere Reserve, Vietnam. Remote Sensing. 2020; 12(8):1334. https://doi.org/10.3390/rs12081334
Chicago/Turabian StylePham, Tien Dat, Naoto Yokoya, Junshi Xia, Nam Thang Ha, Nga Nhu Le, Thi Thu Trang Nguyen, Thi Huong Dao, Thuy Thi Phuong Vu, Tien Duc Pham, and Wataru Takeuchi. 2020. "Comparison of Machine Learning Methods for Estimating Mangrove Above-Ground Biomass Using Multiple Source Remote Sensing Data in the Red River Delta Biosphere Reserve, Vietnam" Remote Sensing 12, no. 8: 1334. https://doi.org/10.3390/rs12081334
APA StylePham, T. D., Yokoya, N., Xia, J., Ha, N. T., Le, N. N., Nguyen, T. T. T., Dao, T. H., Vu, T. T. P., Pham, T. D., & Takeuchi, W. (2020). Comparison of Machine Learning Methods for Estimating Mangrove Above-Ground Biomass Using Multiple Source Remote Sensing Data in the Red River Delta Biosphere Reserve, Vietnam. Remote Sensing, 12(8), 1334. https://doi.org/10.3390/rs12081334