Machine Learning Based On-Line Prediction of Soil Organic Carbon after Removal of Soil Moisture Effect
Abstract
1. Introduction
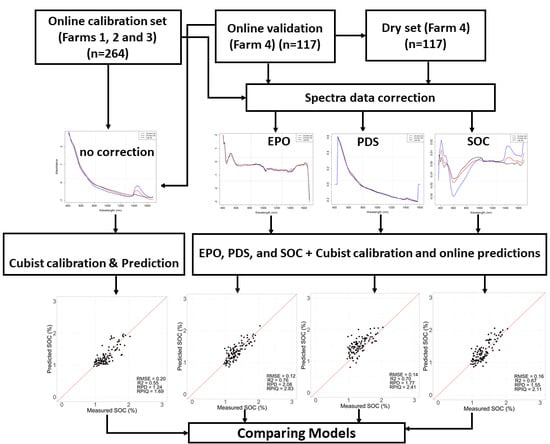
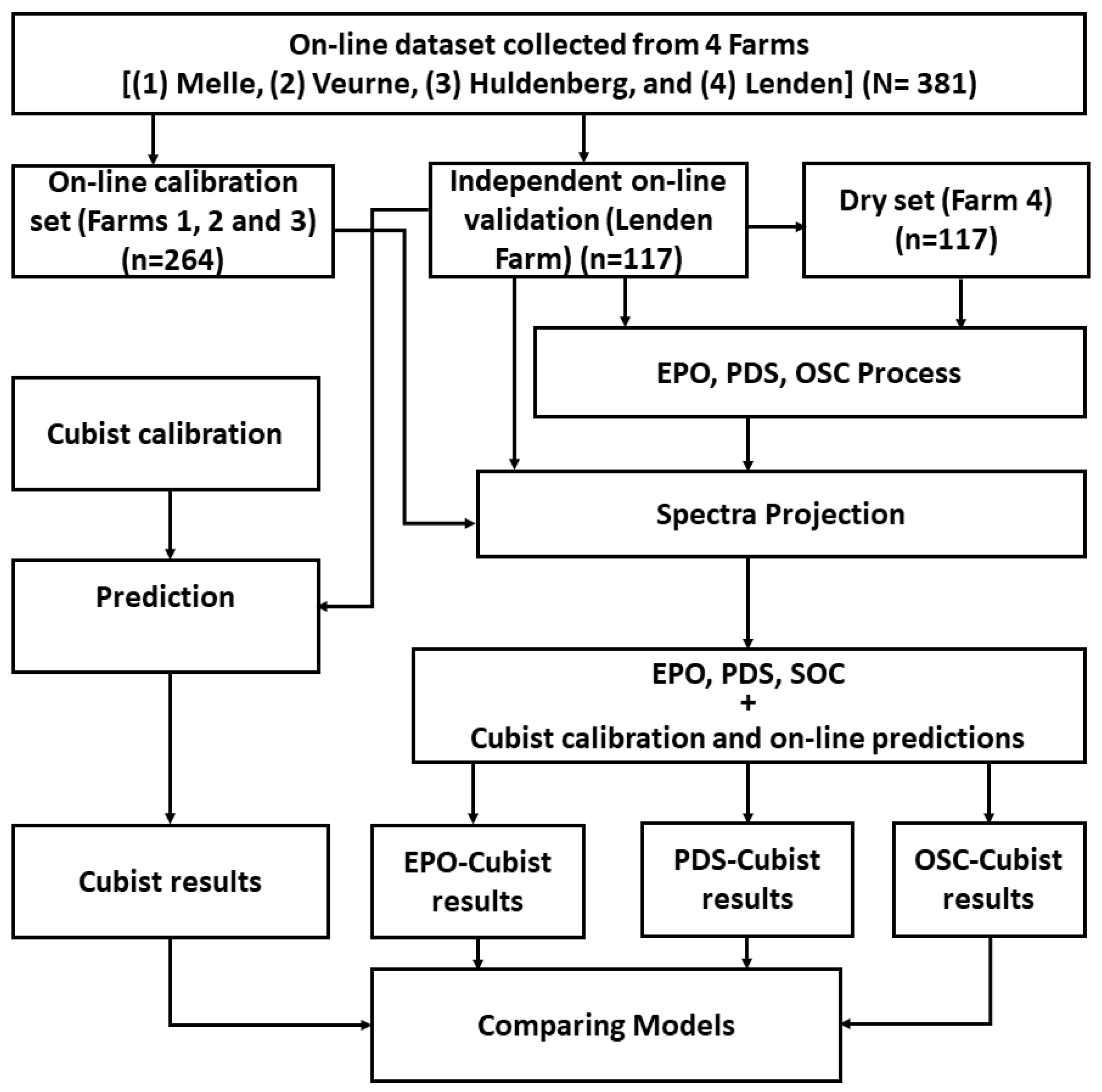
2. Materials and Methods
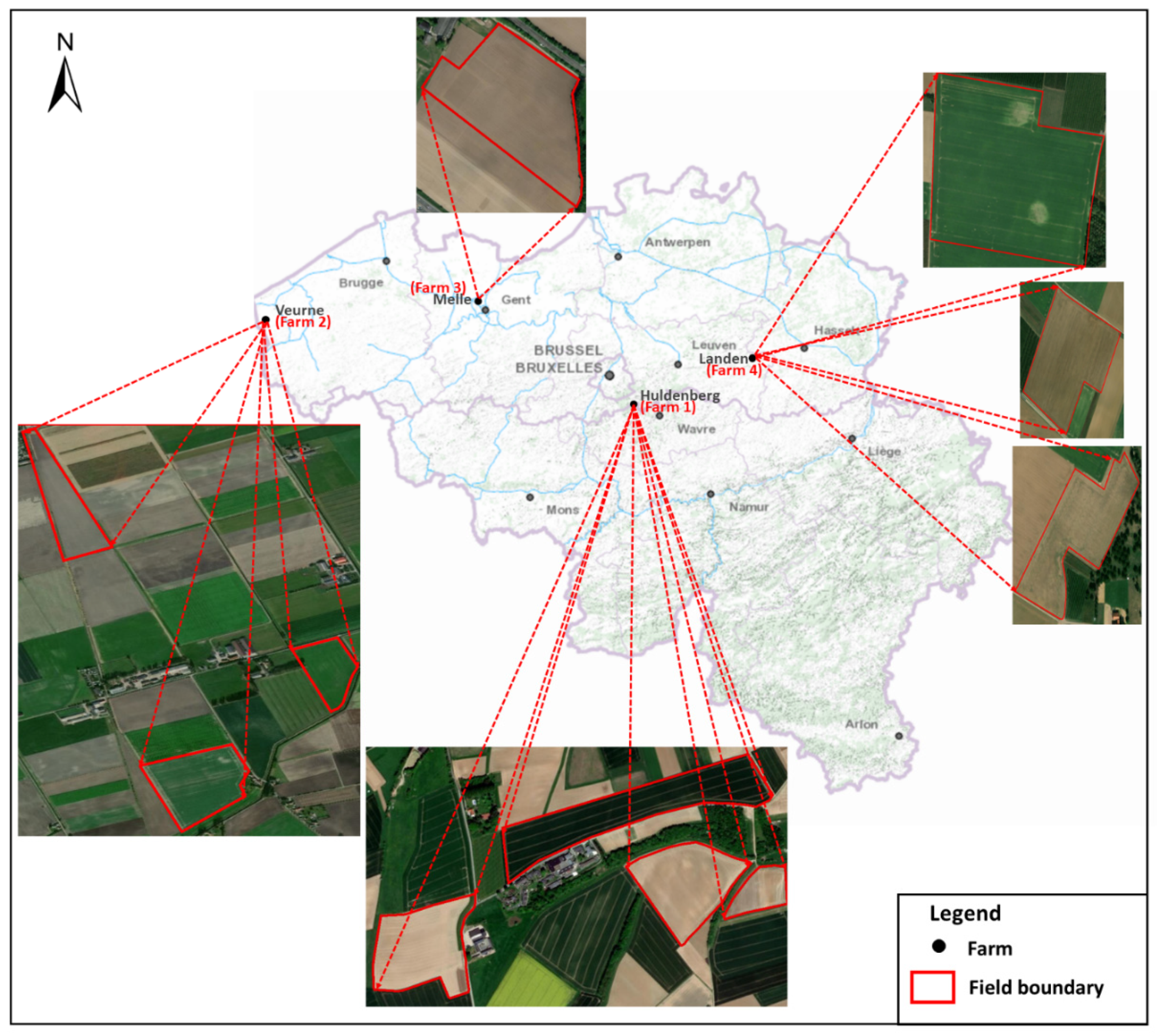
2.1. Study Area
2.2. On-line Vis-NIR Measurements and Soil Sampling
2.3. Soil Samples and the Experiment
2.4. Spectra Pretreatments
2.5. Algorithms to Eliminate the Effect of Soil Moisture Content from the Spectra
2.5.1. External Parameter Orthogonalization (EPO)
2.5.2. The Piecewise Direct Standardization Algorithm (PDS)
2.5.3. Orthogonal Signal Correction (OSC)
2.6. Principal Component Analysis (PCA)
2.7. Modeling with Cubist
3. Results
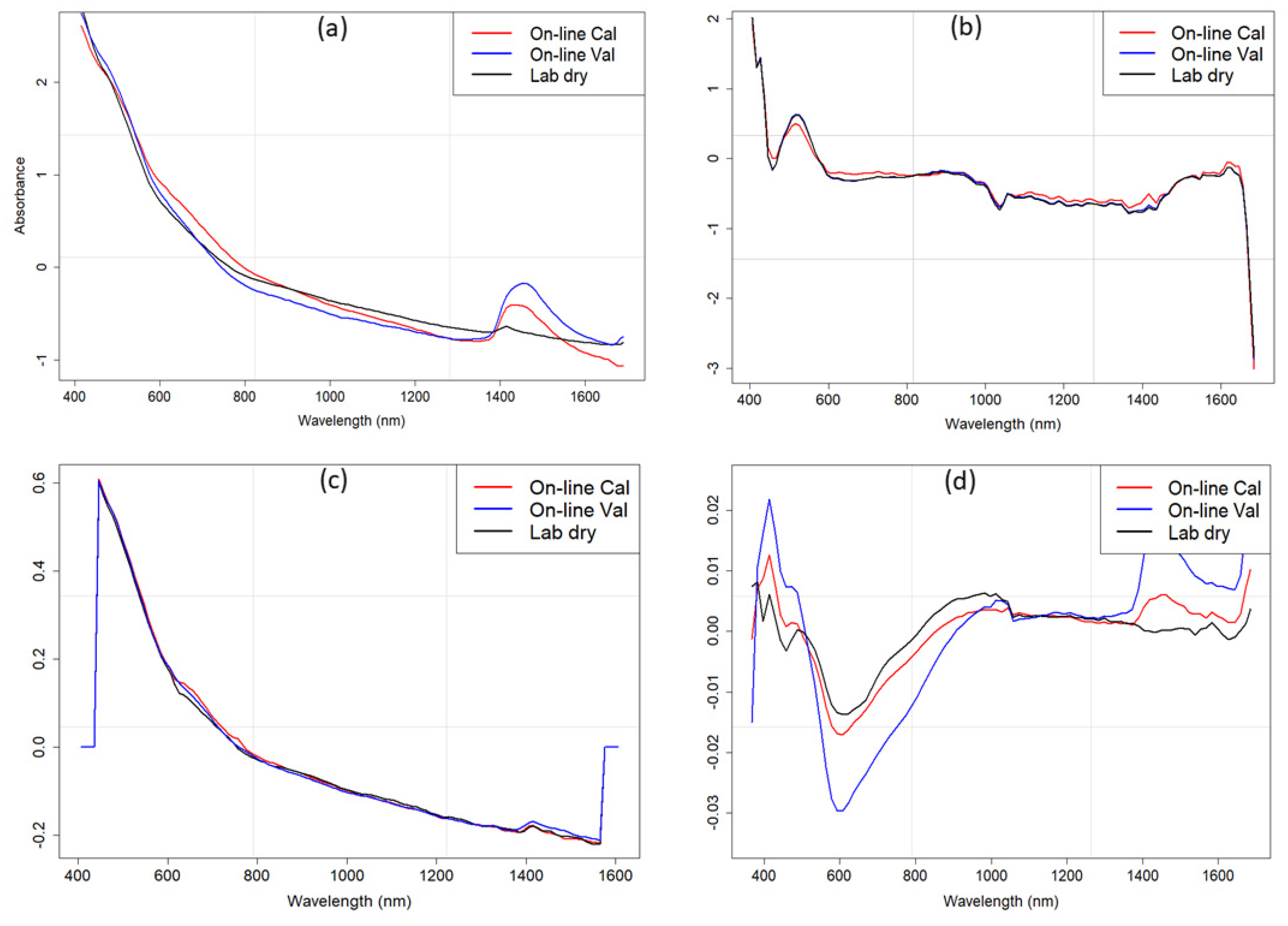
3.1. Spectral Data and Correction Methods
3.2. Principal Component Space of EPO, PDS, and OSC Datasets
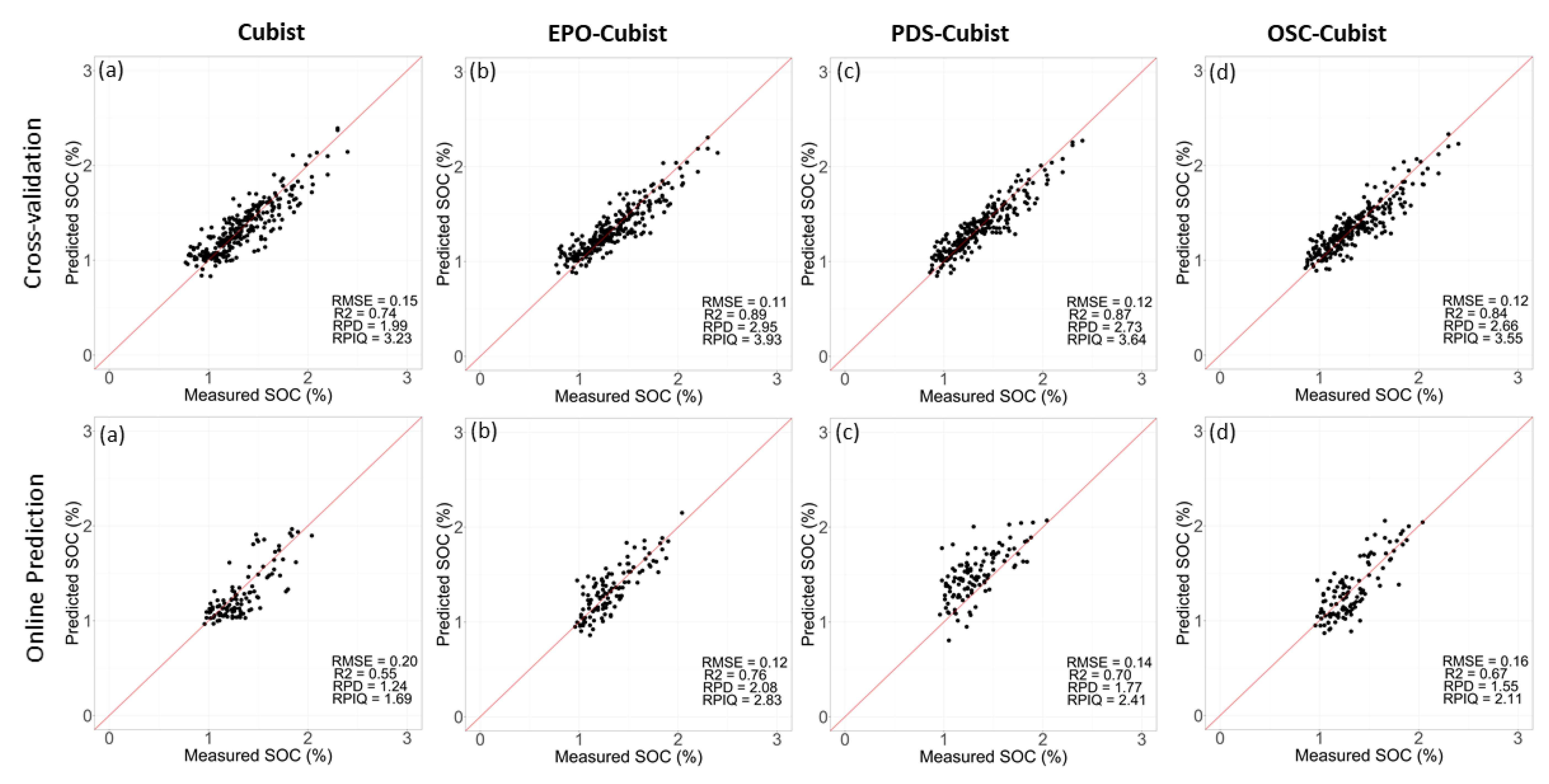
3.3. Cubist Modeling Results
3.3.1. Cubist Modeling without Spectral Correction
3.3.2. Cubist Modeling after Spectral Correction
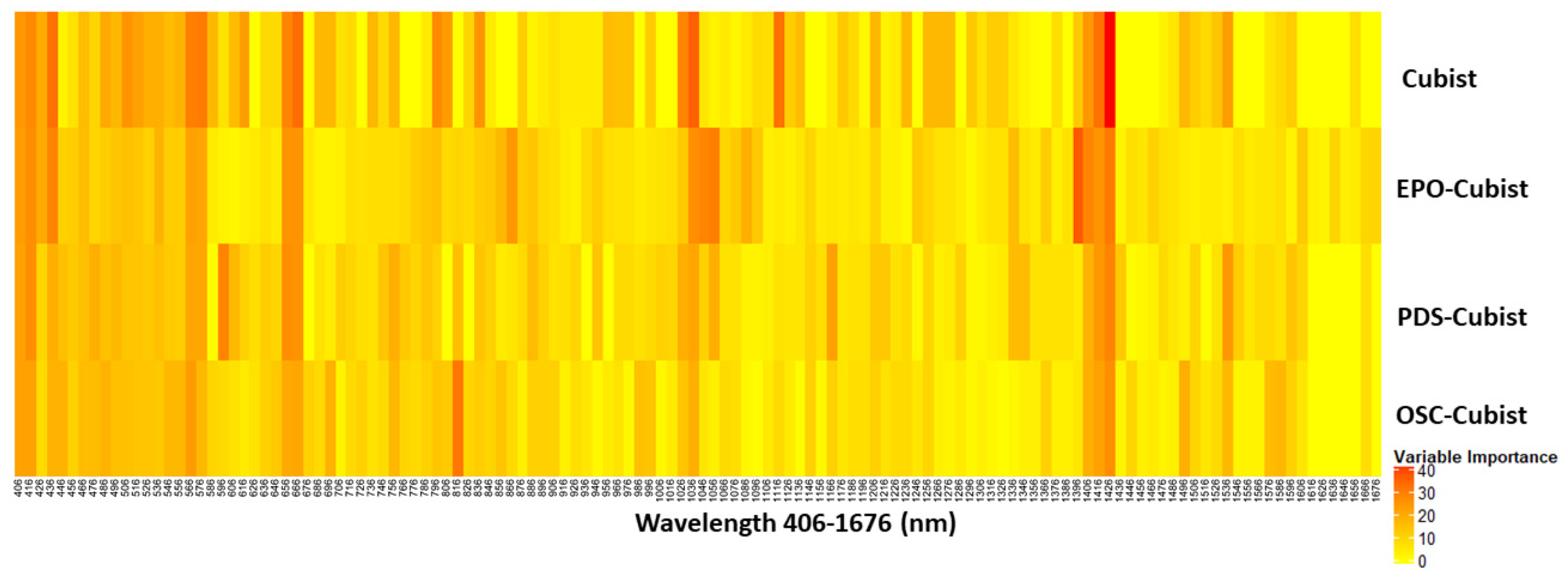
3.4. Variable Importance before and after Spectra Correction
4. Discussion
4.1. Soil and Spectral Data Analysis
4.2. The Performance of EPO, PDS, and OSC for Spectral Correction
4.3. Performance of Cubist Models before Moisture Correction
4.4. Performance of the Cubist Models after Correction for Moisture
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hoyle, F.C.; Baldock, J.A.; Murphy, D.V. Soil Organic Carbon—Role in Rainfed Farming Systems. In Rainfed Farming Systems; Springer: Dordrecht, The Netherlands, 2011; pp. 339–361. [Google Scholar]
- Bresson, L.M.; Koch, C.; Le Bissonnais, Y.; Barriuso, E.; Lecomte, V. Soil Surface Structure Stabilization by Municipal Waste Compost Application. Soil Sci. Soc. Am. J. 2001, 65, 1804–1811. [Google Scholar] [CrossRef]
- Wang, G.; Huang, Y.; Wang, E.; Yu, Y.; Zhang, W. Modeling Soil Organic Carbon Change across Australian Wheat Growing Areas, 1960–2010. PLoS ONE 2013, 8, e63324. [Google Scholar] [CrossRef] [PubMed]
- Kuang, B.; Mahmood, H.S.; Quraishi, M.Z.; Hoogmoed, W.B.; Mouazen, A.M.; van Henten, E.J. Sensing Soil Properties in the Laboratory, In Situ, and On-Line. Adv. Agron. 2012, 114, 155–223. [Google Scholar]
- Nawar, S.; Mouazen, A.M.M. On-line vis-NIR spectroscopy prediction of soil organic carbon using machine learning. Soil Tillage Res. 2019, 190, 120–127. [Google Scholar] [CrossRef]
- Stenberg, B.; Viscarra Rossel, R.A.; Mouazen, A.M.; Wetterlind, J. Visible and Near Infrared Spectroscopy in Soil Science. In Advances in Agronomy; Sparks, D.L., Ed.; Academic Press: Burlington, NJ, USA, 2010; Volume 107, pp. 163–215. [Google Scholar] [CrossRef]
- Mouazen, A.M.; Maleki, M.R.; De Baerdemaeker, J.; Ramon, H. On-line measurement of some selected soil properties using a VIS-NIR sensor. Soil Tillage Res. 2007, 93, 13–27. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; Walvoort, D.J.; McBratney, A.B.; Janik, L.J.; Skjemstad, J.O. Visible, near infrared, mid infrared or combined diffuse reflectance spectroscopy for simultaneous assessment of various soil properties. Geoderma 2006, 131, 59–75. [Google Scholar] [CrossRef]
- Nawar, S.; Mouazen, A.M. Comparison between random forests, artificial neural networks and gradient boosted machines methods of on-line Vis-NIR spectroscopy measurements of soil total nitrogen and total carbon. Sensors 2017, 17, 2428. [Google Scholar] [CrossRef]
- Bricklemyer, R.S.; Brown, D.J. On-the-go VisNIR: Potential and limitations for mapping soil clay and organic carbon. Comput. Electron. Agric. 2010, 70, 209–216. [Google Scholar] [CrossRef]
- Christy, C.D. Real-time measurement of soil attributes using on-the-go near infrared reflectance spectroscopy. Comput. Electron. Agric. 2008, 61, 10–19. [Google Scholar] [CrossRef]
- Tekin, Y.; Tumsavas, Z.; Mouazen, A.M. Effect of Moisture Content on Prediction of Organic Carbon and pH Using Visible and Near-Infrared Spectroscopy. Soil Sci. Soc. Am. J. 2012, 76, 188–198. [Google Scholar] [CrossRef]
- Mouazen, A.M.; De Baerdemaeker, J.; Ramon, H. Effect of wavelength range on the measurement accuracy of some selected soil constituents using visual-near infrared spectroscopy. J. Near Infrared Spectrosc. 2006, 14, 189–199. [Google Scholar] [CrossRef]
- Bogrekci, I.; Lee, W.S. Spectral Soil Signatures and sensing Phosphorus. Biosyst. Eng. 2005, 92, 527–533. [Google Scholar] [CrossRef]
- Minasny, B.; Mcbratney, A.B.; Bellon-Maurel, V.; Roger, J.M.; Gobrecht, A.; Ferrand, L.; Joalland, S. Removing the effect of soil moisture from NIR diffuse reflectance spectra for the prediction of soil organic carbon. Geoderma 2011, 167–168, 118–124. [Google Scholar] [CrossRef]
- Ackerson, J.P.; Morgan, C.L.S.; Ge, Y. Penetrometer-mounted VisNIR spectroscopy: Application of EPO-PLS to in situ VisNIR spectra. Geoderma 2017, 286, 131–138. [Google Scholar] [CrossRef]
- Morgan, C.L.S.; Waiser, T.H.; Brown, D.J.; Hallmark, C.T. Simulated in situ characterization of soil organic and inorganic carbon with visible near-infrared diffuse reflectance spectroscopy. Geoderma 2009, 151, 249–256. [Google Scholar] [CrossRef]
- Wijewardane, N.K.; Ge, Y.; Morgan, C.L.S.S. Geoderma Moisture insensitive prediction of soil properties from VNIR reflectance spectra based on external parameter orthogonalization. Geoderma 2016, 267, 92–101. [Google Scholar] [CrossRef]
- Roger, J.M.; Chauchard, F.; Bellon-Maurel, V. EPO-PLS external parameter orthogonalisation of PLS application to temperature-independent measurement of sugar content of intact fruits. Chemom. Intell. Lab. Syst. 2003, 66, 191–204. [Google Scholar] [CrossRef]
- Chakraborty, S.; Li, B.; Weindorf, D.C.; Morgan, C.L.S. External parameter orthogonalisation of Eastern European VisNIR-DRS soil spectra. Geoderma 2019, 337, 65–75. [Google Scholar] [CrossRef]
- Wang, Y.; Veltkamp, D.J.; Kowalski, B.R. Multivariate Instrument Standardization. Anal. Chem. 1991, 63, 2750–2756. [Google Scholar] [CrossRef]
- Ji, W.; Viscarra Rossel, R.A.; Shi, Z. Accounting for the effects of water and the environment on proximally sensed vis-NIR soil spectra and their calibrations. Eur. J. Soil Sci. 2015, 66, 555–565. [Google Scholar] [CrossRef]
- Wold, S.; Antti, H.; Lindgren, F.; Öhman, J. Orthogonal signal correction of near-infrared spectra. Chemom. Intell. Lab. Syst. 1998, 44, 175–185. [Google Scholar] [CrossRef]
- Woody, N.A.; Feudale, R.N.; Myles, A.J.; Brown, S.D. Transfer of Multivariate Calibrations between Four Near-Infrared Spectrometers Using Orthogonal Signal Correction. Anal. Chem. 2004, 76, 2595–2600. [Google Scholar] [CrossRef] [PubMed]
- Stevens, A.; Nocita, M.; Tóth, G.; Montanarella, L.; van Wesemael, B. Prediction of Soil Organic Carbon at the European Scale by Visible and Near InfraRed Reflectance Spectroscopy. PLoS ONE 2013, 8, e66409. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; Behrens, T. Using data mining to model and interpret soil diffuse reflectance spectra. Geoderma 2010, 158, 46–54. [Google Scholar] [CrossRef]
- Jaconi, A.; Don, A.; Freibauer, A. Prediction of soil organic carbon at the country scale: Stratification strategies for near-infrared data. Eur. J. Soil Sci. 2017, 68, 919–929. [Google Scholar] [CrossRef]
- Kuang, B.; Tekin, Y.; Mouazen, A.M. Comparison between artificial neural network and partial least squares for on-line visible and near infrared spectroscopy measurement of soil organic carbon, pH and clay content. Soil Tillage Res. 2015, 146, 243–252. [Google Scholar] [CrossRef]
- Liu, S.; Shen, H.; Chen, S.; Zhao, X.; Biswas, A.; Jia, X.; Shi, Z.; Fang, J. Estimating forest soil organic carbon content using vis-NIR spectroscopy: Implications for large-scale soil carbon spectroscopic assessment. Geoderma 2019, 348, 37–44. [Google Scholar] [CrossRef]
- Quinlan, J.R. Combining Instance-Based and Model-Based Learning. In Machine Learning Proceedings 1993; Morgan Kaufmann Publishers: San Francisco, FL, USA, 2014; pp. 236–243. [Google Scholar]
- Appelhans, T.; Mwangomo, E.; Hardy, D.R.; Hemp, A.; Nauss, T. Evaluating machine learning approaches for the interpolation of monthly air temperature at Mt. Kilimanjaro, Tanzania. Spat. Stat. 2015, 14, 91–113. [Google Scholar] [CrossRef]
- Walton, J.T. Subpixel urban land cover estimation: Comparing cubist, random forests, and support vector regression. Photogramm. Eng. Remote Sensing 2008, 74, 1213–1222. [Google Scholar] [CrossRef]
- Sorenson, P.T.; Underwood, A.; Sorenson, P.T.; Small, C.; Tappert, M.C.; Quideau, S.A.; Drozdowski, B.; Underwood, A.; Janz, A. Monitoring organic carbon, total nitrogen and pH for field reclaimed soils using reflectance spectroscopy. Can. J. Soil Sci. 2017, 97, 241–248. [Google Scholar] [CrossRef]
- Peng, Y.; Xiong, X.; Adhikari, K.; Knadel, M.; Grunwald, S.; Greve, M.H. Modeling soil organic carbon at regional scale by combining multi-spectral images with laboratory spectra. PLoS ONE 2015, 10. [Google Scholar] [CrossRef] [PubMed]
- Filippi, P.; Cattle, S.R.; Bishop, T.F.A.; Jones, E.J.; Minasny, B. Combining ancillary soil data with VisNIR spectra to improve predictions of organic and inorganic carbon content of soils. MethodsX 2018, 5, 551–560. [Google Scholar] [CrossRef] [PubMed]
- Morellos, A.; Pantazi, X.-E.E.; Moshou, D.; Alexandridis, T.; Whetton, R.; Tziotzios, G.; Wiebensohn, J.; Bill, R.; Mouazen, A.M. Machine learning based prediction of soil total nitrogen, organic carbon and moisture content by using VIS-NIR spectroscopy. Biosyst. Eng. 2016, 152, 104–116. [Google Scholar] [CrossRef]
- Mouazen, A.M. Soil sensing device. In International publication, Published under the Patent Cooperation Treaty (PCT); World Intellectual Property Organization, International Bureau: Brussels, Belgium, International Publication Number; W02006/015463; PCT/ BE 2005/000129; IPC: G01N21/00; GO1N21/00; 2006. [Google Scholar]
- Savitzky, A.; Golay, M.J.E. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Barnes, R.J.; Dhanoa, M.S.; Lister, S.J. Standard normal variate transformation and de-trending of near-infrared diffuse reflectance spectra. Appl. Spectrosc. 1989, 43, 772–777. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Boulet, J.C.; Roger, J.M. Pretreatments by means of orthogonal projections. Chemom. Intell. Lab. Syst. 2012, 117, 61–69. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; Webster, R. Predicting soil properties from the Australian soil visible-near infrared spectroscopic database. Eur. J. Soil Sci. 2012, 63, 848–860. [Google Scholar] [CrossRef]
- Kuhn, M. Building predictive models in R using the caret package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Bellon-Maurel, V.; Fernandez-Ahumada, E.; Palagos, B.; Roger, J.M.; McBratney, A. Critical review of chemometric indicators commonly used for assessing the quality of the prediction of soil attributes by NIR spectroscopy. TrAC Trends Anal. Chem. 2010, 29, 1073–1081. [Google Scholar] [CrossRef]
- Mevik, B.-H.; Wehrens, R.; Liland, K.H. Partial Least Squares and Principal Component Regression [R Package pls Version 2.7-1]. Available online: https://cran.r-project.org/web/packages/pls/index.html (accessed on 2 March 2020).
- Stevens, A.; Ramirez Lopez, L.; Lopez, L.R. Package ‘prospectr’: Miscellaneous Functions for Processing and Sample Selection of Spectroscopic Data. Available online: https://cran.r-project.org/web/packages/prospectr/prospectr.pdf (accessed on 16 March 2020).
- Viscarra Rossel, R.A.; Cattle, S.R.; Ortega, A.; Fouad, Y. In situ measurements of soil colour, mineral composition and clay content by vis-NIR spectroscopy. Geoderma 2009, 150, 253–266. [Google Scholar] [CrossRef]
- Kuang, B.; Mouazen, A.M. Calibration of visible and near infrared spectroscopy for soil analysis at the field scale on three European farms. Eur. J. Soil Sci. 2011, 62, 629–636. [Google Scholar] [CrossRef]
- Mouazen, A.M.; De Baerdemaeker, J.; Ramon, H.; Mounem, A.; De Baerdemaeker, J.; Ramon, H. Towards development of on-line soil moisture content sensor using a fibre-type NIR spectrophotometer. Soil Tillage Res. 2005, 80, 171–183. [Google Scholar] [CrossRef]
- Lobell, D.B.; Asner, G.P. Moisture Effects on Soil Reflectance. Soil Sci. Soc. Am. J. 2002, 66, 722. [Google Scholar] [CrossRef]
- Mouazen, A.M.; Ramon, H. Expanding implementation of an on-line measurement system of topsoil compaction in loamy sand, loam, silt loam and silt soils. Soil Tillage Res. 2009, 103, 98–104. [Google Scholar] [CrossRef]
- Poggio, M.; Brown, D.J.; Bricklemyer, R.S. Laboratory-based evaluation of optical performance for a new soil penetrometer visible and near-infrared (VisNIR) foreoptic. Comput. Electron. Agric. 2015, 115, 12–20. [Google Scholar] [CrossRef]
- Schirrmann, M.; Gebbers, R.; Kramer, E. Performance of Automated Near-Infrared Reflectance Spectrometry for Continuous in Situ Mapping of Soil Fertility at Field Scale. Vadose Zo. J. 2013, 12, 1–14. [Google Scholar] [CrossRef]
- Rodionov, A.; Pätzold, S.; Welp, G.; Pallares, R.C.; Damerow, L.; Amelung, W. Sensing of Soil Organic Carbon Using Visible and Near-Infrared Spectroscopy at Variable Moisture and Surface Roughness. Soil Sci. Soc. Am. J. 2014, 78, 949–957. [Google Scholar] [CrossRef]
- Kuang, B.; Mouazen, A.M. Effect of spiking strategy and ratio on calibration of on-line visible and near infrared soil sensor for measurement in European farms. Soil Tillage Res. 2013, 128, 125–136. [Google Scholar] [CrossRef]
- Ge, Y.; Morgan, C.L.S.; Ackerson, J.P. VisNIR spectra of dried ground soils predict properties of soils scanned moist and intact. Geoderma 2014, 221–222, 61–69. [Google Scholar] [CrossRef]
- Summers, D.; Lewis, M.; Ostendorf, B.; Chittleborough, D. Visible near-infrared reflectance spectroscopy as a predictive indicator of soil properties. Ecol. Indic. 2011, 11, 123–131. [Google Scholar] [CrossRef]
- Fontán, J.M.; Calvache, S.; López-Bellido, R.J.; López-Bellido, L. Soil carbon measurement in clods and sieved samples in a Mediterranean Vertisol by Visible and Near-Infrared Reflectance Spectroscopy. Geoderma 2010, 156, 93–98. [Google Scholar] [CrossRef]
- Gao, Y.; Cui, L.; Lei, B.; Zhai, Y.; Shi, T.; Wang, J.; Chen, Y.; He, H.; Wu, G. Estimating soil organic carbon content with visible-near infrared (Vis-NIR) spectroscopy. Appl. Spectrosc. 2015, 68, 712–722. [Google Scholar] [CrossRef] [PubMed]
- Sudduth, K.A.; Hummel, J.W. Portable, near-infrared spectrophotometer for rapid soil analysis. Trans. Am. Soc. Agric. Eng. 1993, 36, 185–194. [Google Scholar] [CrossRef]
- Ackerson, J.P.; Demattê, J.A.M.; Morgan, C.L.S. Predicting clay content on field-moist intact tropical soils using a dried, ground VisNIR library with external parameter orthogonalization. Geoderma 2015, 259–260, 196–204. [Google Scholar] [CrossRef]
- Wijewardane, N.K.; Hetrick, S.; Ackerson, J.; Morgan, C.L.S.; Ge, Y. VisNIR integrated multi-sensing penetrometer for in situ high-resolution vertical soil sensing. Soil Tillage Res. 2020, 199, 104604. [Google Scholar] [CrossRef]

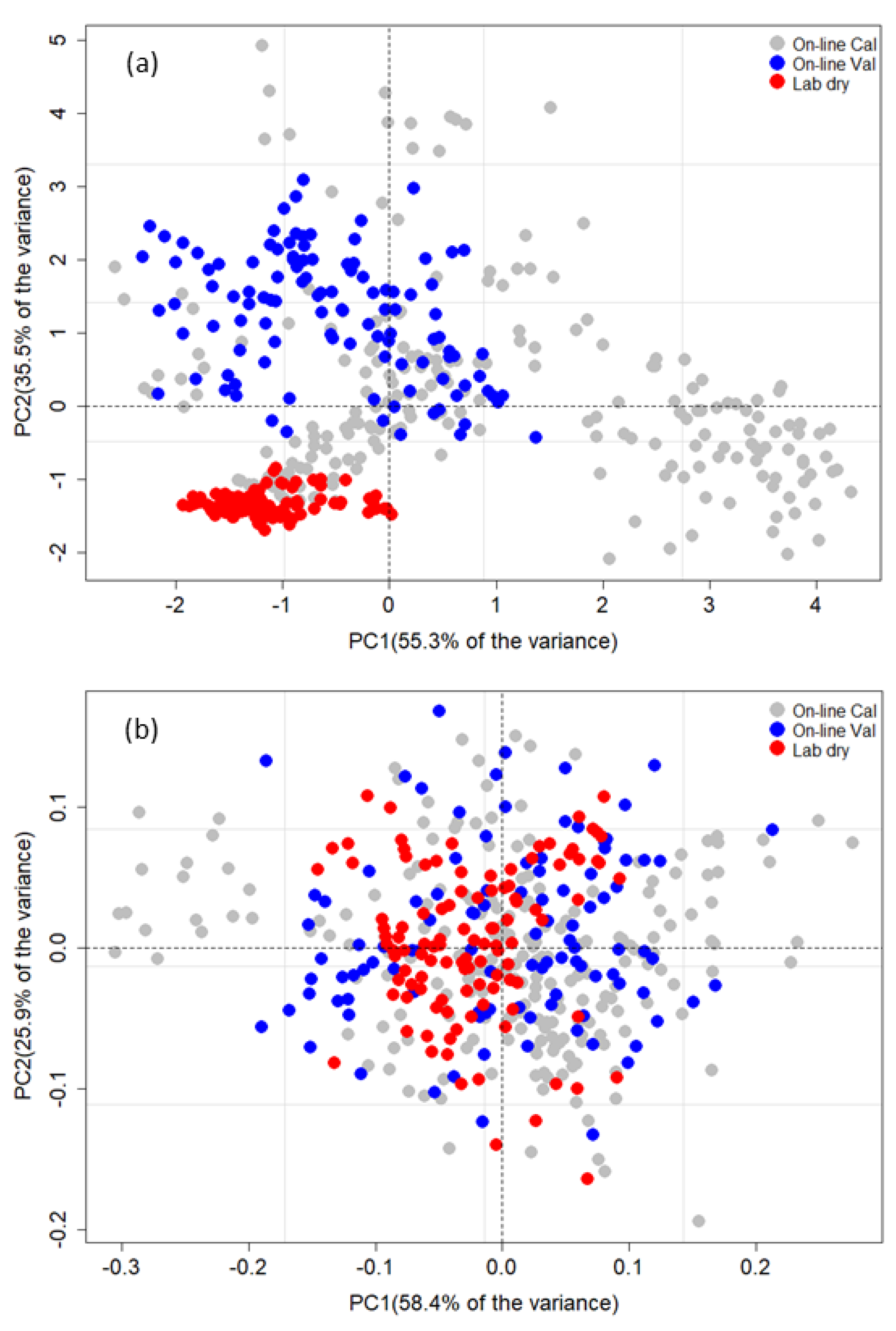

| Farm | Property (%) | No | Min. | 1Q | Med. | Mean | 3Q | Max. | SD |
|---|---|---|---|---|---|---|---|---|---|
| Huldenberg | SOC | 155 | 0.86 | 1.02 | 1.24 | 1.31 | 1.50 | 2.40 | 0.37 |
| SMC | 155 | 2.20 | 4.64 | 6.95 | 7.56 | 9.40 | 19.0 | 3.25 | |
| Veurne | SOC | 84 | 0.85 | 1.15 | 1.24 | 1.31 | 1.44 | 2.40 | 0.29 |
| SMC | 84 | 12.29 | 16.42 | 18.90 | 18.64 | 20.88 | 24.59 | 2.80 | |
| Melle | SOC | 25 | 1.20 | 1.50 | 1.64 | 1.61 | 1.72 | 1.90 | 0.17 |
| SMC | 25 | 11.27 | 13.03 | 15.05 | 14.64 | 15.92 | 17.64 | 1.91 | |
| Landen | SOC | 117 | 0.96 | 1.15 | 1.27 | 1.33 | 1.49 | 2.04 | 0.25 |
| SMC | 117 | 11.27 | 16.62 | 20.29 | 19.40 | 21.79 | 25.03 | 3.25 |
| No | Min. | 1Q | Med. | Mean | 3Q | Max. | SD | ||
|---|---|---|---|---|---|---|---|---|---|
| SOC (%) | Cal set (on-line fresh) | 264 | 0.86 | 1.09 | 1.28 | 1.34 | 1.53 | 2.40 | 0.33 |
| Val set (dry and on-line fresh) | 117 | 0.96 | 1.15 | 1.27 | 1.33 | 1.49 | 2.04 | 0.25 | |
| SMC (%) | Cal set (on-line fresh) | 264 | 2.28 | 6.92 | 13.03 | 12.28 | 17.06 | 24.59 | 6.01 |
| Val set (on-line set fresh) | 117 | 11.27 | 16.62 | 20.29 | 19.40 | 21.79 | 25.03 | 3.25 |
| Cross-Validation | On-Line Prediction | |||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | R2 | RPD | RPIQ | RMSEP | R2 | RPD | RPIQ | |
| (%) | (%) | |||||||
| Cubist | 0.151 | 0.74 | 1.99 | 3.23 | 0.203 | 0.55 | 1.24 | 1.69 |
| EPO-Cubist | 0.112 | 0.89 | 2.95 | 3.93 | 0.120 | 0.76 | 2.08 | 2.83 |
| PDS-Cubist | 0.121 | 0.87 | 2.73 | 3.64 | 0.141 | 0.70 | 1.77 | 2.41 |
| OSC-Cubist | 0.124 | 0.84 | 2.66 | 3.55 | 0.161 | 0.67 | 1.55 | 2.11 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nawar, S.; Abdul Munnaf, M.; Mouazen, A.M. Machine Learning Based On-Line Prediction of Soil Organic Carbon after Removal of Soil Moisture Effect. Remote Sens. 2020, 12, 1308. https://doi.org/10.3390/rs12081308
Nawar S, Abdul Munnaf M, Mouazen AM. Machine Learning Based On-Line Prediction of Soil Organic Carbon after Removal of Soil Moisture Effect. Remote Sensing. 2020; 12(8):1308. https://doi.org/10.3390/rs12081308
Chicago/Turabian StyleNawar, Said, Muhammad Abdul Munnaf, and Abdul Mounem Mouazen. 2020. "Machine Learning Based On-Line Prediction of Soil Organic Carbon after Removal of Soil Moisture Effect" Remote Sensing 12, no. 8: 1308. https://doi.org/10.3390/rs12081308
APA StyleNawar, S., Abdul Munnaf, M., & Mouazen, A. M. (2020). Machine Learning Based On-Line Prediction of Soil Organic Carbon after Removal of Soil Moisture Effect. Remote Sensing, 12(8), 1308. https://doi.org/10.3390/rs12081308