A New Soil Moisture Retrieval Algorithm from the L-Band Passive Microwave Brightness Temperature Based on the Change Detection Principle
Abstract
1. Introduction
2. Data and Methods
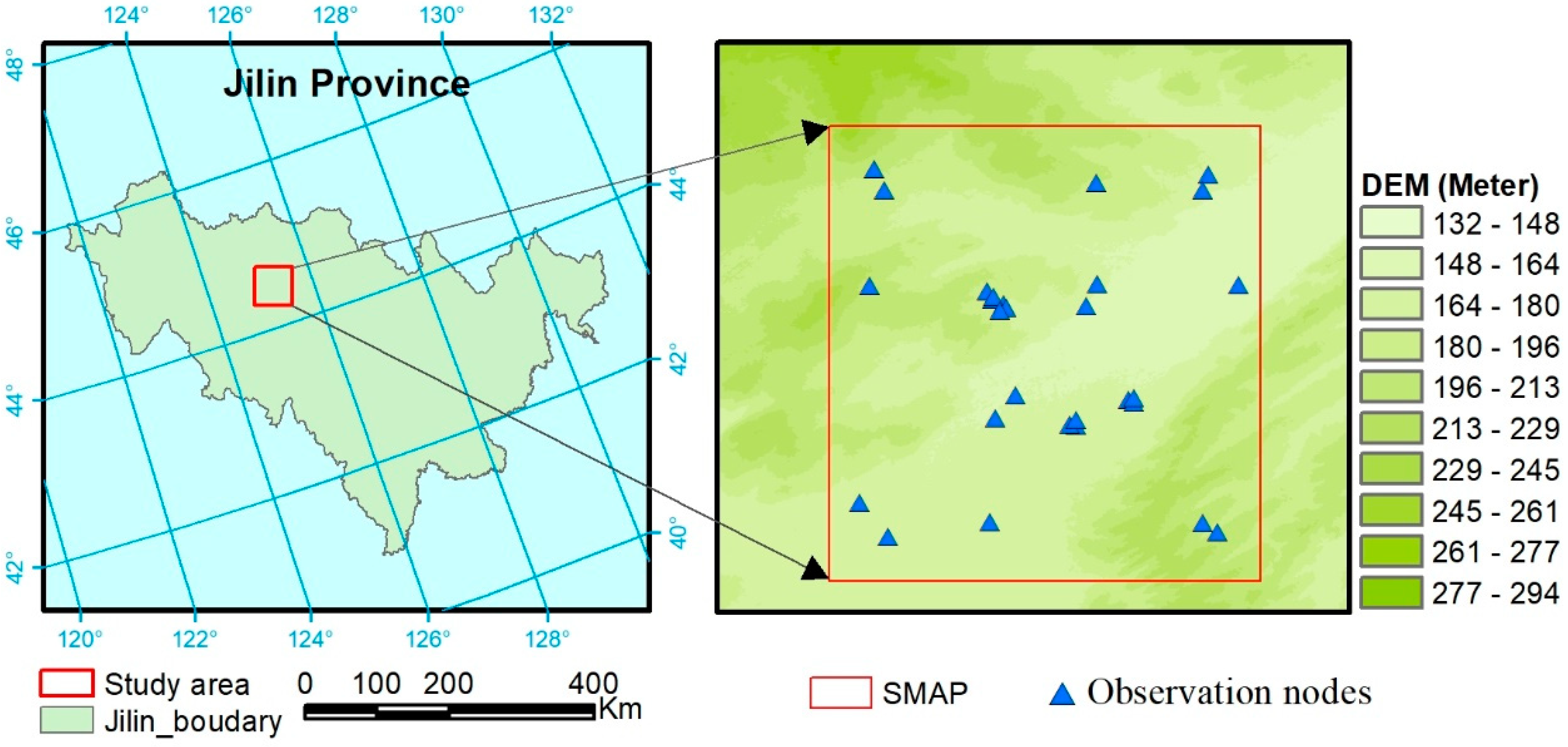
2.1. Study Area and in Situ SSM
2.2. SMAP L3 SSM Dataset
2.3. Change Detection Algorithm
2.3.1. Microwave Emission Model
2.3.2. Change Detection Algorithm Derivation
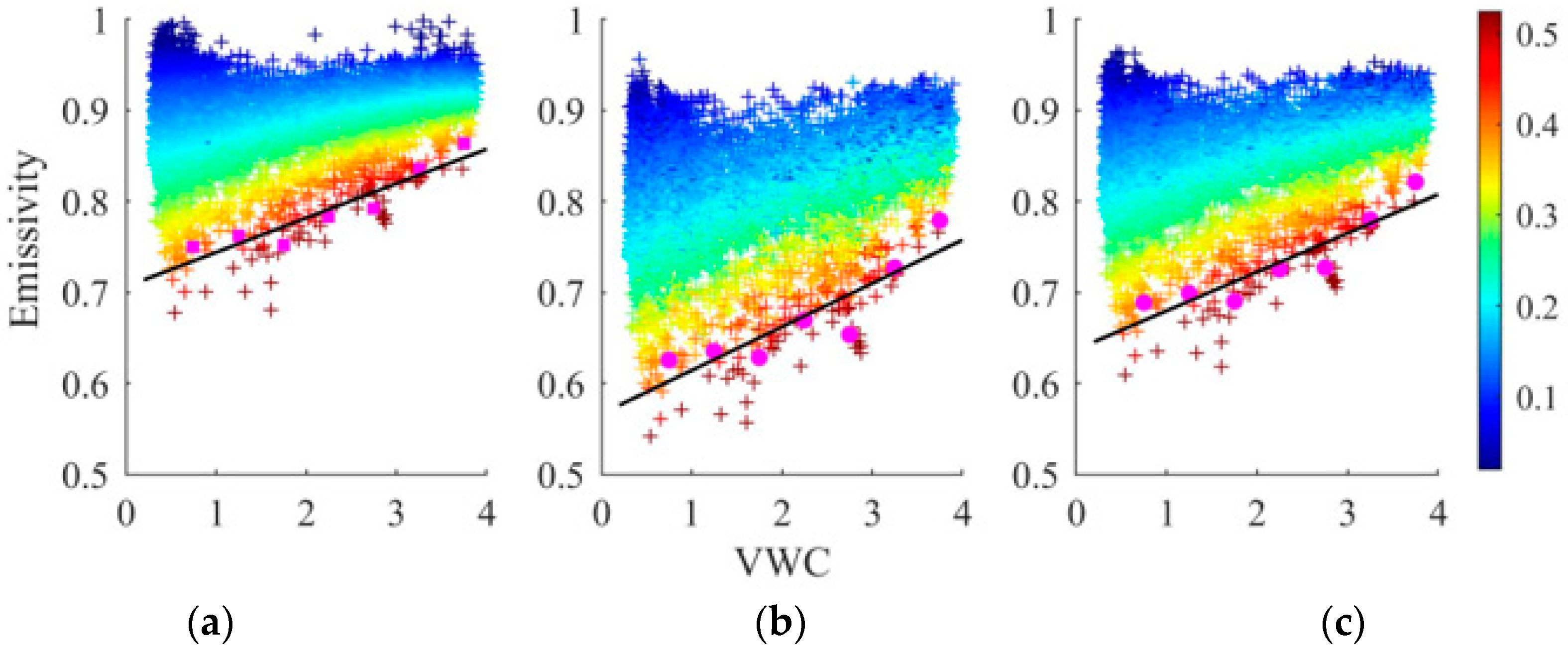
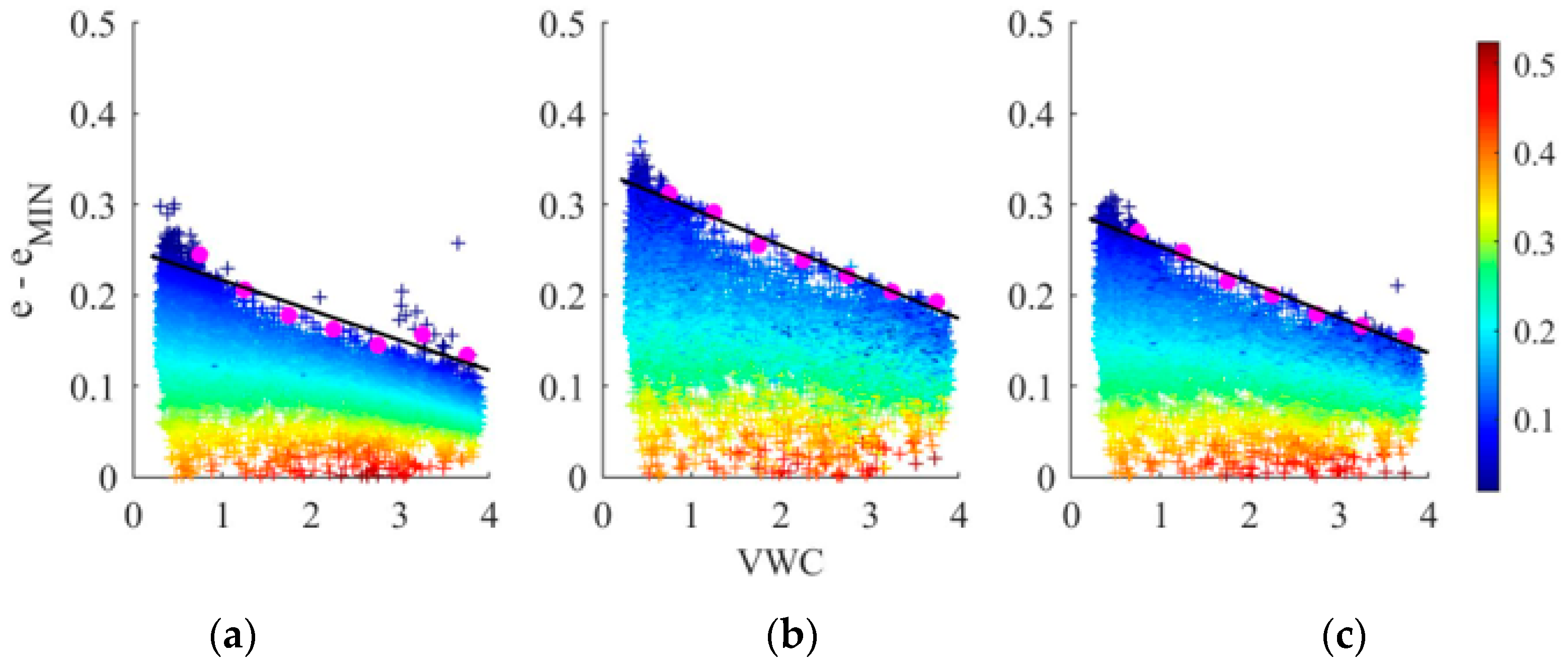
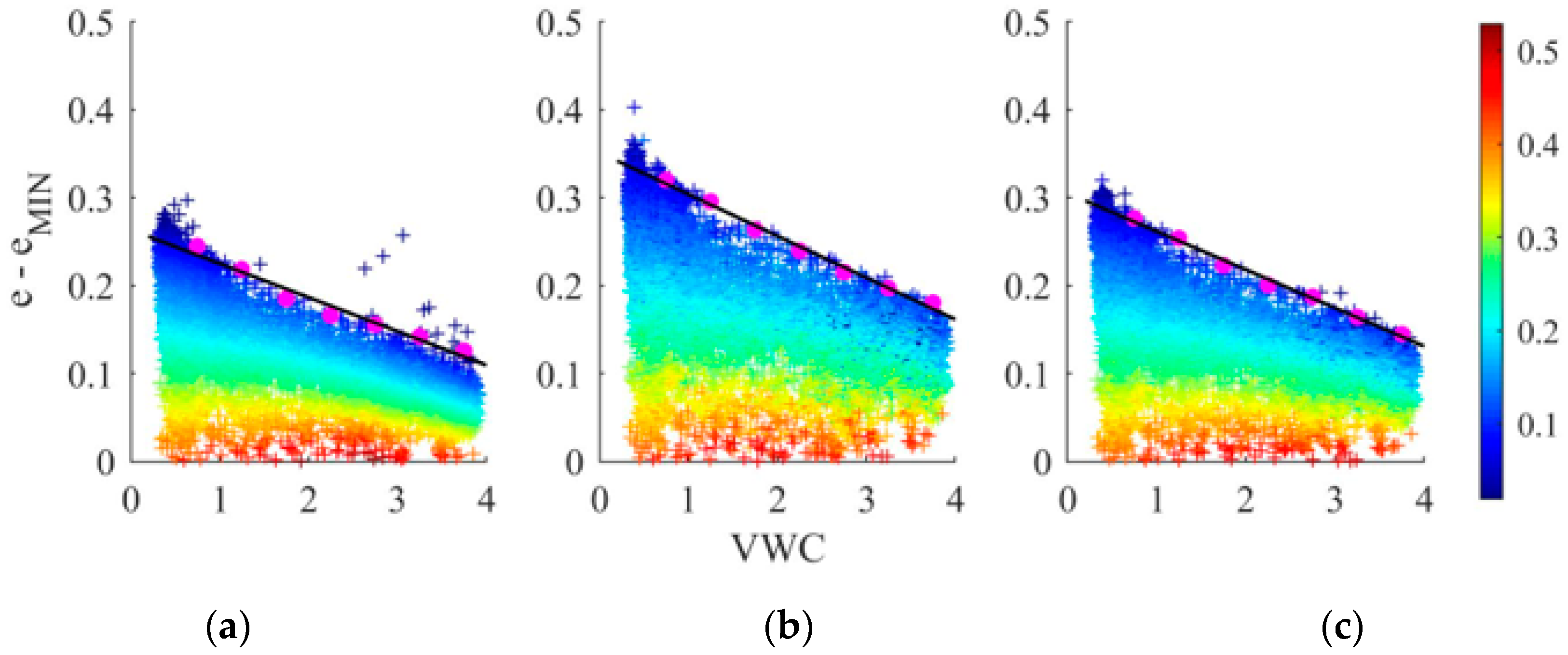
2.3.3. Determining Maximum and Minimum Surface Emissivity
3. Results
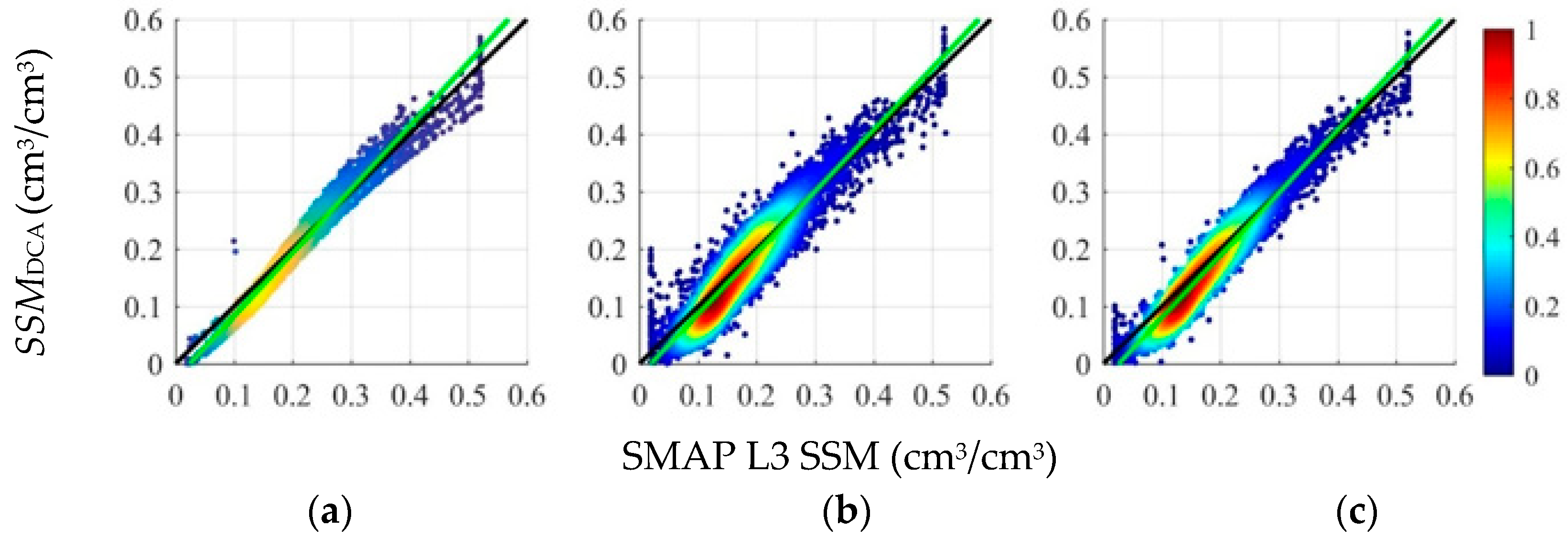
3.1. Comparison of SSM Derived from Change Detection Algorithm and SMAP L3 SSM
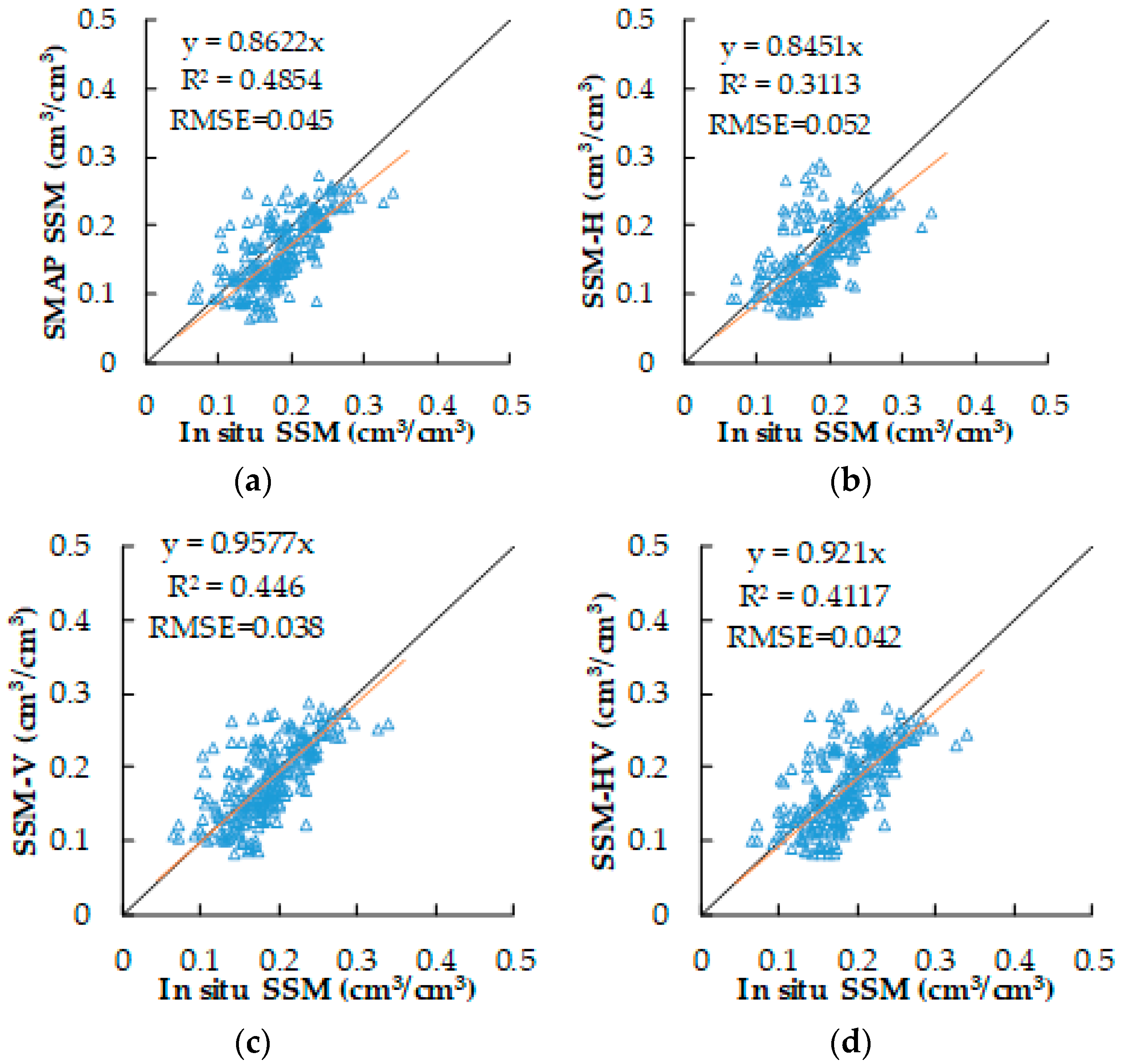
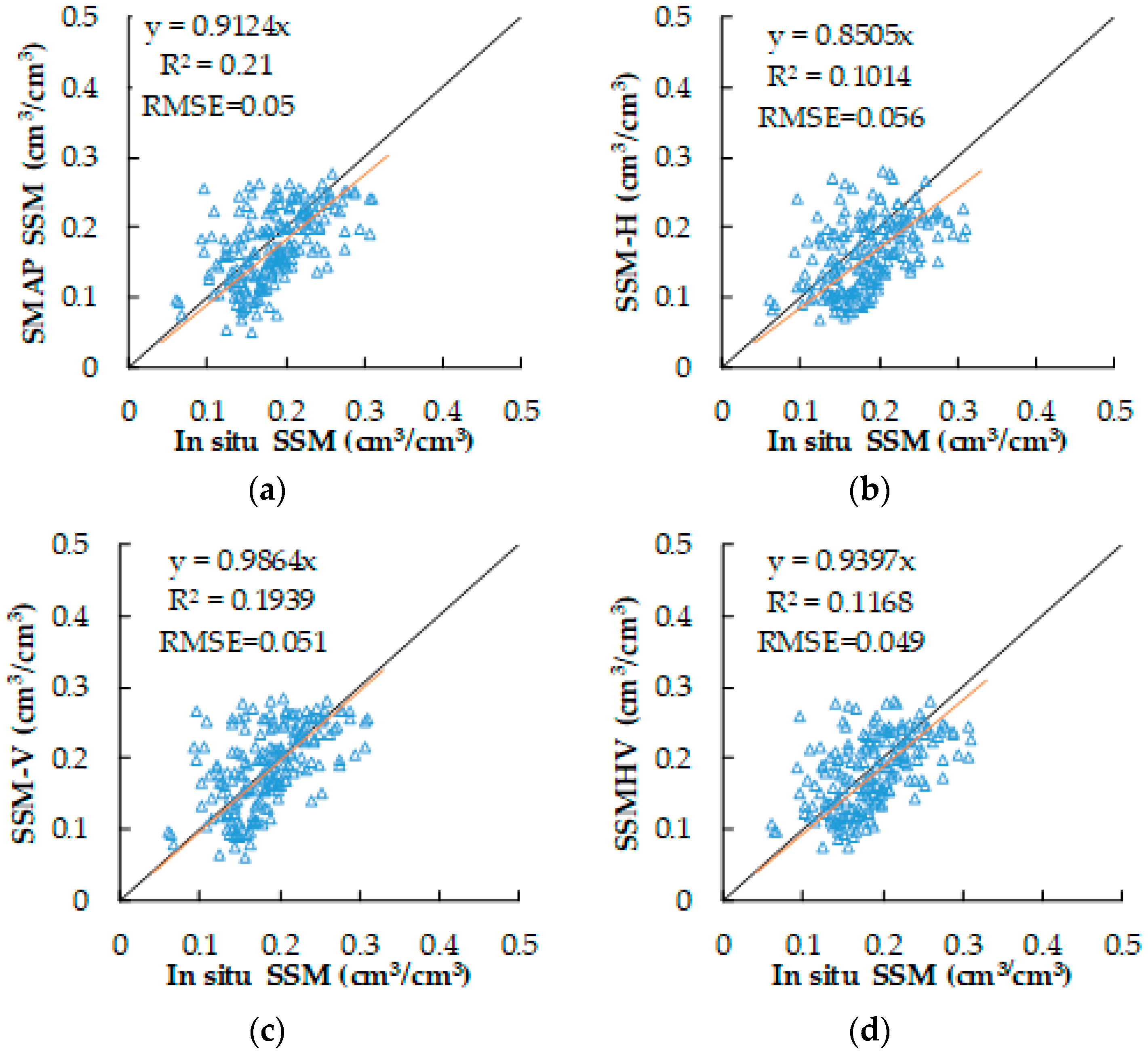
3.2. Comparison of SSM Derived From Change Detection Algorithm and In Situ SSM
4. Discussion
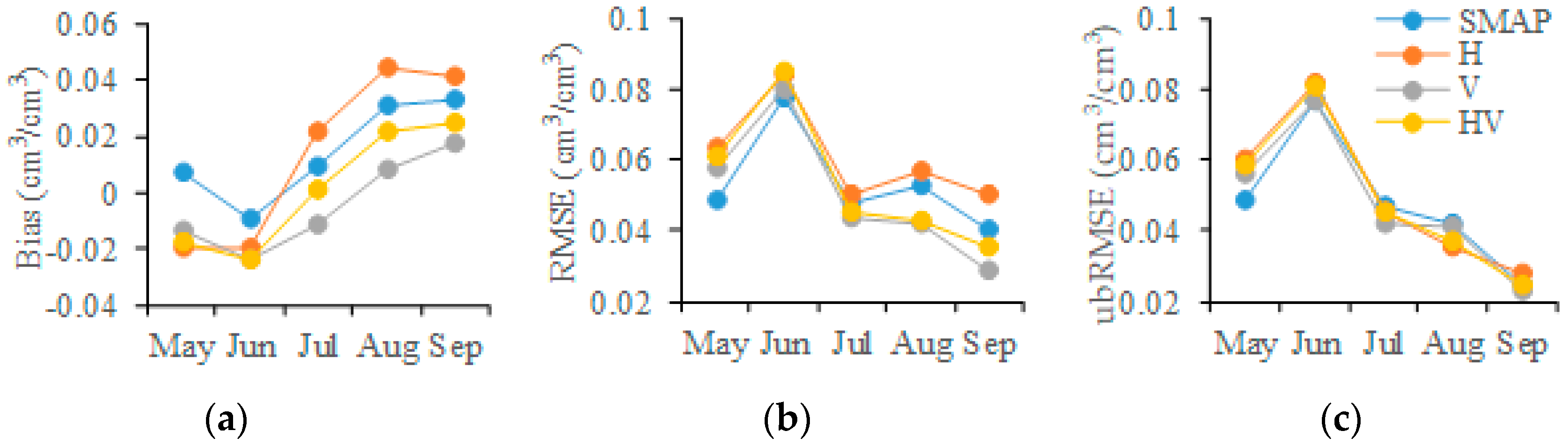
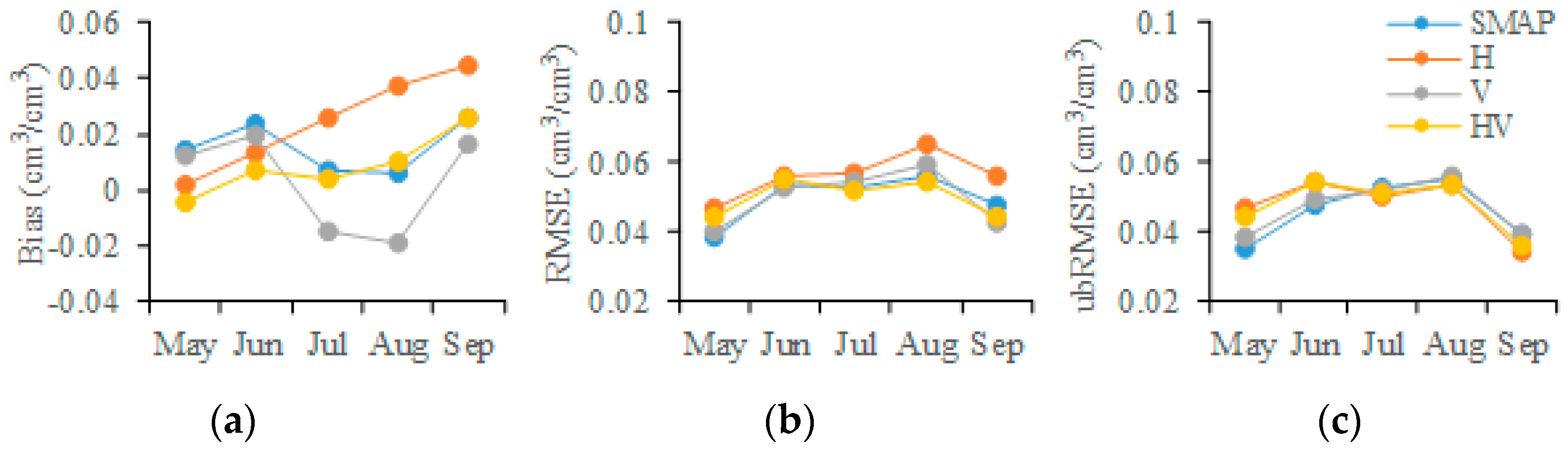
4.1. Temporal Distribution of SSM Error
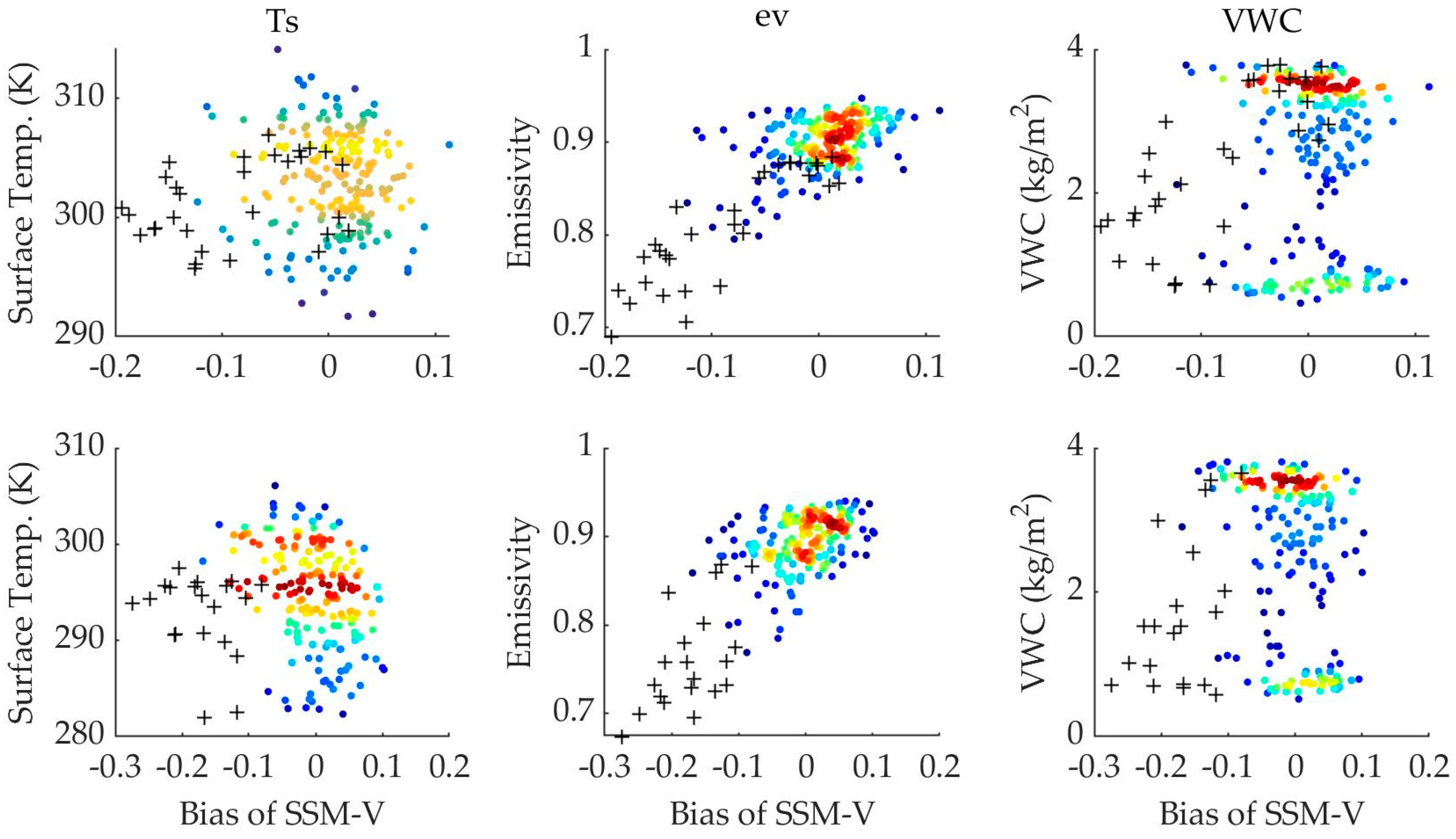
4.2. Dependence of Bias on SSM Algorithm Input Parameters
4.3. Limitations, Advantages, and Potential for SSM Estimation Using the Change Detection Algorithm
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Magagi, R.; Berg, A.A.; Goita, K.; Belair, S.; Jackson, T.J.; Toth, B.; Walker, A.; Mcnairn, H.; O’Neill, P.E.; Moghaddam, M. Canadian Experiment for Soil Moisture in 2010 (CanEx-SM10): Overview and Preliminary Results. IEEE Trans. Geosci. Remote Sens. 2012, 51, 347–363. [Google Scholar] [CrossRef]
- Shi, J.C.; Yang, D.; Du, J.Y.; Jiang, L.M.; Chai, L.N.; Mao, K.B.; Peng, X.; Ni, W.J.; Xiong, C.; Qiang, L. Progresses on microwave remote sensing of land surface parameters. J. Sci. China Earth Sci. 2012, 55, 1052–1078. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The Soil Moisture Active Passive (SMAP) Mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS Mission: New Tool for Monitoring Key Elements ofthe Global Water Cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef]
- Bazzi, H.; Baghdadi, N.; El Hajj, M.; Zribi, M.; Belhouchette, H. A Comparison of Two Soil Moisture Products S2MP and Copernicus-SSM over Southern France. J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3366–3375. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.P.; Martinuzzi, J.; Font, J.; Berger, M. Soil moisture retrieval from space: The Soil Moisture and Ocean Salinity (SMOS) mission. IEEE Trans. Geosci. Remote Sens. 2002, 39, 1729–1735. [Google Scholar] [CrossRef]
- Wigneron, J.-P.; Jackson, T.J.; O’Neill, P.; De Lannoy, G.; Rosnay, P.; Walker, J.P.; Ferrazzoli, P.; Mironov, V.; Bircher, S.; Grant, J.P.; et al. Modelling the passive microwave signature from land surfaces: A review of recent results and application to the L-band SMOS & SMAP soil moisture retrieval algorithms. Remote Sens. Environ. 2017, 192, 238–262. [Google Scholar]
- Wagner, W.; Lemoine, G.; Borgeaud, M.; Rott, H. A study of vegetation cover effects on ERS scatterometer data. IEEE Trans. Geosci. Remote Sens. 1999, 37, 938–948. [Google Scholar] [CrossRef]
- Srivastava, H.S.; Patel, P.; Sharma, Y. Large-area soil moisture estimation using multi-incidence-angle RADARSAT-1 SAR data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2528–2535. [Google Scholar] [CrossRef]
- Baghdadi, N.; Aubert, M.; Cerdan, O.; Franchistéguy, L.; Viel, C.; Eric, M.; Zribi, M.; Desprats, J.F. Operational Mapping of Soil Moisture Using Synthetic Aperture Radar Data: Application to the Touch Basin (France). Sensors 2007, 7, 2458–2483. [Google Scholar] [CrossRef]
- Zheng, X.M.; Bai, Y.; Jiang, T.; Zhao, X.W.; Yang, J.W. Evaluation of SMAP Passive Soil Moisture Products using in-situ data from a dense observation network over Agricultural Area in Northeast China. IEEE Int. Geosci. Remote Sens. Symp. 2018, 3779–3882. [Google Scholar] [CrossRef]
- Colliander, A.; Jackson, T.J.; Bindlish, J.R.; Chan, S.; Das, N.; Kim, S.B.; Cosh, M.H.; Dunbar, R.S.; Dang, L.; Pashaian, L.; et al. Validation of SMAP surface soil moisture products with core validation sites. Remote Sens. Environ. 2017, 191, 215–231. [Google Scholar] [CrossRef]
- O’Neill, P.E.; Chan, S.; Njoku, E.G.; Jackson, T.; Bindlish, R. SMAP L3 Radiometer Global Daily 36 km EASE-Grid Soil Moisture, Version 6. Boulder, Colorado USA. NASA National Snow and Ice Data Center Distributed Active Archive Center. In Proceedings of the 2019 Photonics & Electromagnetics Research Symposium—Fall (PIERS—Fall), Xiamen, China, 17–20 December 2019. [Google Scholar] [CrossRef]
- O’Neill, P.E.; Bindlish, R.; Chan, S.; Chaubell, J.; Njoku, E.G.; Jackson, T. Algorithm Theoretical Basis Document Level 2 & 3 Soil Moisture (Passive) Data Products, Revision E, 2019b, JPL D-66480. Available online: https://nsidc.org/sites/nsidc.org/files/technical-references/L2_SM_P_ATBD_rev_E_Aug2019.pdf (accessed on 18 April 2020).
- Le Vine, D.M.; Karam, M.A. Dependence of attenuation in a vegetation canopy on frequency and plant water content. IEEE Trans. Geosci. Remote Sens. 1996, 34, 1090–1096. [Google Scholar] [CrossRef]
- Loew, A. Impact of surface heterogeneity on surface soil moisture retrievals from passive microwave data at the regional scale: The Upper Danube case. Remote Sens. Environ. 2008, 112, 231–248. [Google Scholar] [CrossRef]
- Wigneron, J.P.; Calvet, J.C.; De Rosnay, P.; Kerr, Y.; Waldteufel, P.; Saleh, K.; Escorihuela, M.J.; Kruszewski, A. Soil moisture retrievals from biangular L-band passive microwave observations. IEEE Geosci. Remote Sens. Lett. 2004, 1, 277–281. [Google Scholar] [CrossRef]
- Wigneron, J.P.; Kerr, Y.; Waldteufel, P.; Saleh, K.; Escorihuela, M.J.; Richaume, P.; Ferrazzoli, P.; De Rosnay, P.; Gurney, R.; Calvet, J.C.; et al. L-band microwave emission of the biosphere (L-MEB) model: Description and calibration against experimental data sets over crop fields. Remote Sens. Environ. 2007, 107, 639–655. [Google Scholar] [CrossRef]
- Van de Griend, A.A.; Wigneron, J.P.; Waldteufel, P. Consequences of surface heterogeneity for parameter retrieval from 1.4-GHz multiangle SMOS observations. IEEE Trans. Geosci. Remote Sens. 2003, 41, 803–811. [Google Scholar] [CrossRef]
- Wigneron, J.P.; Laguerre, L.; Kerr, Y.H. A simple parameterization of the L-band microwave emission from rough agricultural soils. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1697–1707. [Google Scholar] [CrossRef]
- Li, D.; Jin, R.; Che, T.; Walker, J.; Gao, Y.; Ye, N.; Wang, S. Soil moisture retrieval from airborne PLMR and MODIS products in the Zhangye oasis of middle stream of the Heihe River Basin, China. J. Adv. Earth Sci. 2014, 29, 295–305. [Google Scholar] [CrossRef]
- Jiang, T.; Zhao, K.; Zheng, X.M.; Chen, S.; Wan, X.K. Dynamic bp in the L Band and Its Role in Improving the Accuracy of Soil Moisture Retrieval. J. Chin. Geogr. Sci. 2019, 29, 283–292. [Google Scholar] [CrossRef]
- Attarzadeh, R.; Amini, J.; Notarnicola, C.; Greifeneder, F. Synergetic Use of Sentinel-1 and Sentinel-2 Data for Soil Moisture Mapping at Plot Scale. Remote Sens. 2018, 10, 1285. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Long, D.G. Microwave Radar and Radiometric Remote Sensing; University Michigan Press: Ann Arbor, MI, USA, 2014; p. 252. ISBN 978-0-472-11935-6. [Google Scholar]
- Mironov, V.; Savin, I. A temperature-dependent multi-relaxation spectroscopic dielectric model for thawed and frozen organic soil at 0.05–15 GHz. Phys. Chem. Earth 2015, 83–84, 57–64. [Google Scholar] [CrossRef]
- Zheng, X.M.; Ding, Y.L.; Zhao, X.W.; Bai, Y.; Li, X.F.; Zhao, K.; Jiang, T. Uncertainty evaluation at three spatial scales for the NDVI-based VWC estimation method used in the SMAP algorithm. Remote Sens. Lett. 2019, 10, 563–572. [Google Scholar] [CrossRef]



| Orbit | Pol. | eMIN | eMAX-eMIN | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Slope | Intercept | R2 | RMSE | Slope | Intercept | R2 | RMSE | ||
| A | ev | 0.03784 | 0.7062 | 0.87 | 0.019 | −0.03316 | 0.2501 | 0.86 | 0.015 |
| eh | 0.0478 | 0.5665 | 0.79 | 0.029 | −0.04048 | 0.3363 | 0.97 | 0.008 | |
| 0.5(eh + ev) | 0.04265 | 0.6372 | 0.84 | 0.021 | −0.03894 | 0.2925 | 0.97 | 0.007 | |
| D | ev | 0.04524 | 0.6842 | 0.97 | 0.008 | −0.03854 | 0.2637 | 0.96 | 0.009 |
| eh | 0.05509 | 0.5454 | 0.88 | 0.024 | −0.04746 | 0.3514 | 0.99 | 0.005 | |
| 0.5(eh + ev) | 0.04842 | 0.6208 | 0.94 | 0.014 | −0.04359 | 0.3054 | 0.99 | 0.004 | |
| Orbit | Polarization | a | b | R2 | RMSE |
|---|---|---|---|---|---|
| A | ev | 1.102 | −0.02666 | 0.96 | 0.016 |
| eh | 1.071 | −0.02079 | 0.89 | 0.031 | |
| 0.5(eh + ev) | 1.089 | −0.02842 | 0.93 | 0.023 | |
| D | ev | 1.116 | −0.04217 | 0.97 | 0.015 |
| eh | 1.074 | −0.03591 | 0.92 | 0.027 | |
| 0.5(eh + ev) | 1.088 | −0.03662 | 0.96 | 0.019 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, X.; Feng, Z.; Xu, H.; Sun, Y.; Li, L.; Li, B.; Jiang, T.; Li, X.; Li, X. A New Soil Moisture Retrieval Algorithm from the L-Band Passive Microwave Brightness Temperature Based on the Change Detection Principle. Remote Sens. 2020, 12, 1303. https://doi.org/10.3390/rs12081303
Zheng X, Feng Z, Xu H, Sun Y, Li L, Li B, Jiang T, Li X, Li X. A New Soil Moisture Retrieval Algorithm from the L-Band Passive Microwave Brightness Temperature Based on the Change Detection Principle. Remote Sensing. 2020; 12(8):1303. https://doi.org/10.3390/rs12081303
Chicago/Turabian StyleZheng, Xingming, Zhuangzhuang Feng, Hongxin Xu, Yanlong Sun, Lei Li, Bingze Li, Tao Jiang, Xiaojie Li, and Xiaofeng Li. 2020. "A New Soil Moisture Retrieval Algorithm from the L-Band Passive Microwave Brightness Temperature Based on the Change Detection Principle" Remote Sensing 12, no. 8: 1303. https://doi.org/10.3390/rs12081303
APA StyleZheng, X., Feng, Z., Xu, H., Sun, Y., Li, L., Li, B., Jiang, T., Li, X., & Li, X. (2020). A New Soil Moisture Retrieval Algorithm from the L-Band Passive Microwave Brightness Temperature Based on the Change Detection Principle. Remote Sensing, 12(8), 1303. https://doi.org/10.3390/rs12081303







