Improved SRGAN for Remote Sensing Image Super-Resolution Across Locations and Sensors
Abstract
1. Introduction
- We propose the improved SRGAN (ISRGAN), which stabilizes the model training and enhances the generalization ability across locations and sensors;
- We test the performance of the ISRGAN from two sensors (Landsat 8 OLI and Chinese GF 1) at different locations (Guangdong and Xinjiang in China). Specifically, for the cross-location test, the model training in Guangdong with the Chinese GF 1 data was tested with the GF 1 data in Xinjiang. For the cross-sensor test, the same model training in Guangdong with GF 1 was tested with the Landsat 8 OLI data in Xinjiang;
- The proposed method is compared to the neighbor-embedding (NE), sparse representation (SCSR), and the original SRGAN methods, and the results show that the ISRGAN achieved the best performance;
- The model provided in this study shows a good generalization ability across locations and sensors. This model can be further applied to other satellite sensors and different locations for image super-resolution to achieve the goal of “training once, apply to everywhere and different sensors.”
2. Methods
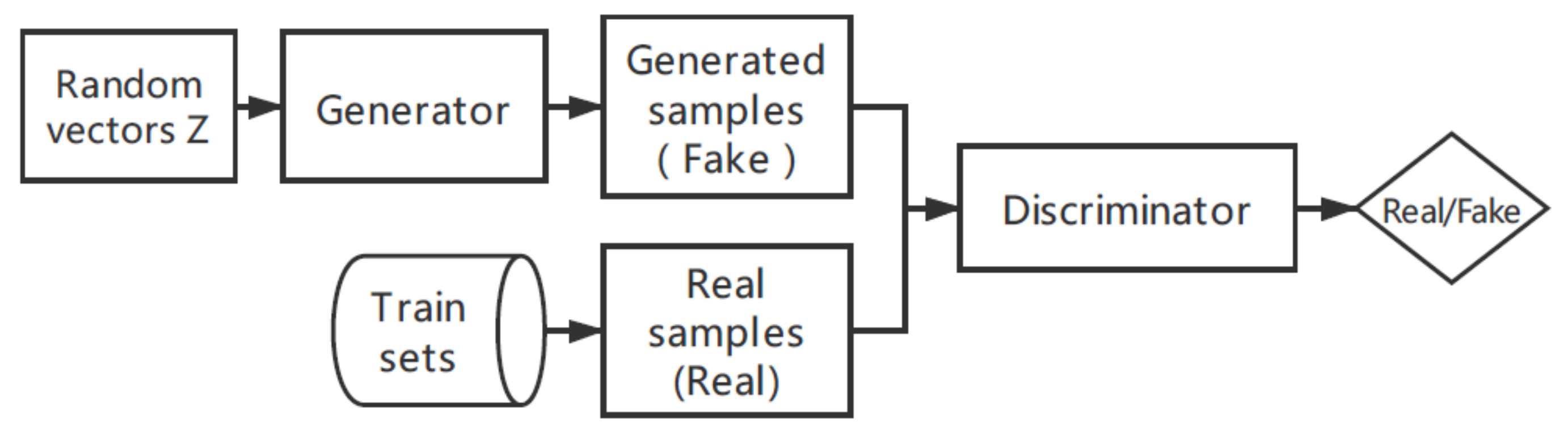
2.1. Workflow
2.2. SRGAN Review
2.3. The Improved SRGAN
2.3.1. Problems in SRGAN
2.3.2. Improved SRGAN
- (1)
- Sigmoid was removed from the last layer of the discriminator to transform the classification problem into a regression problem;
- (2)
- The loss functions of the generator and discriminator were not logarithmic;
- (3)
- During the training process, after updating the discriminator parameters, its absolute value was truncated to no more than a fixed constant;
- (4)
- The convolution kernel of the last layer of the generator was changed from 1 × 1 to 9 × 9.
3. Experiments
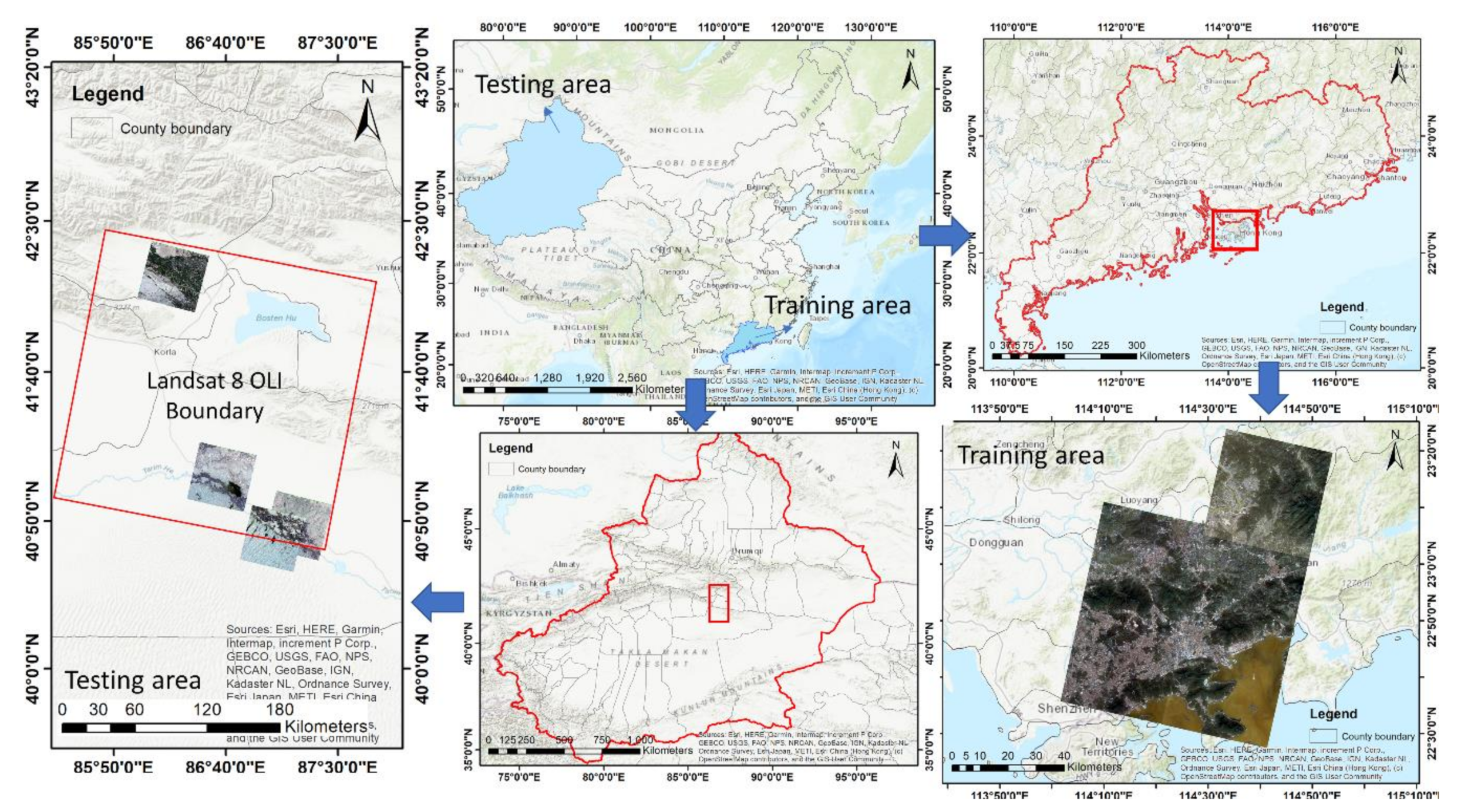
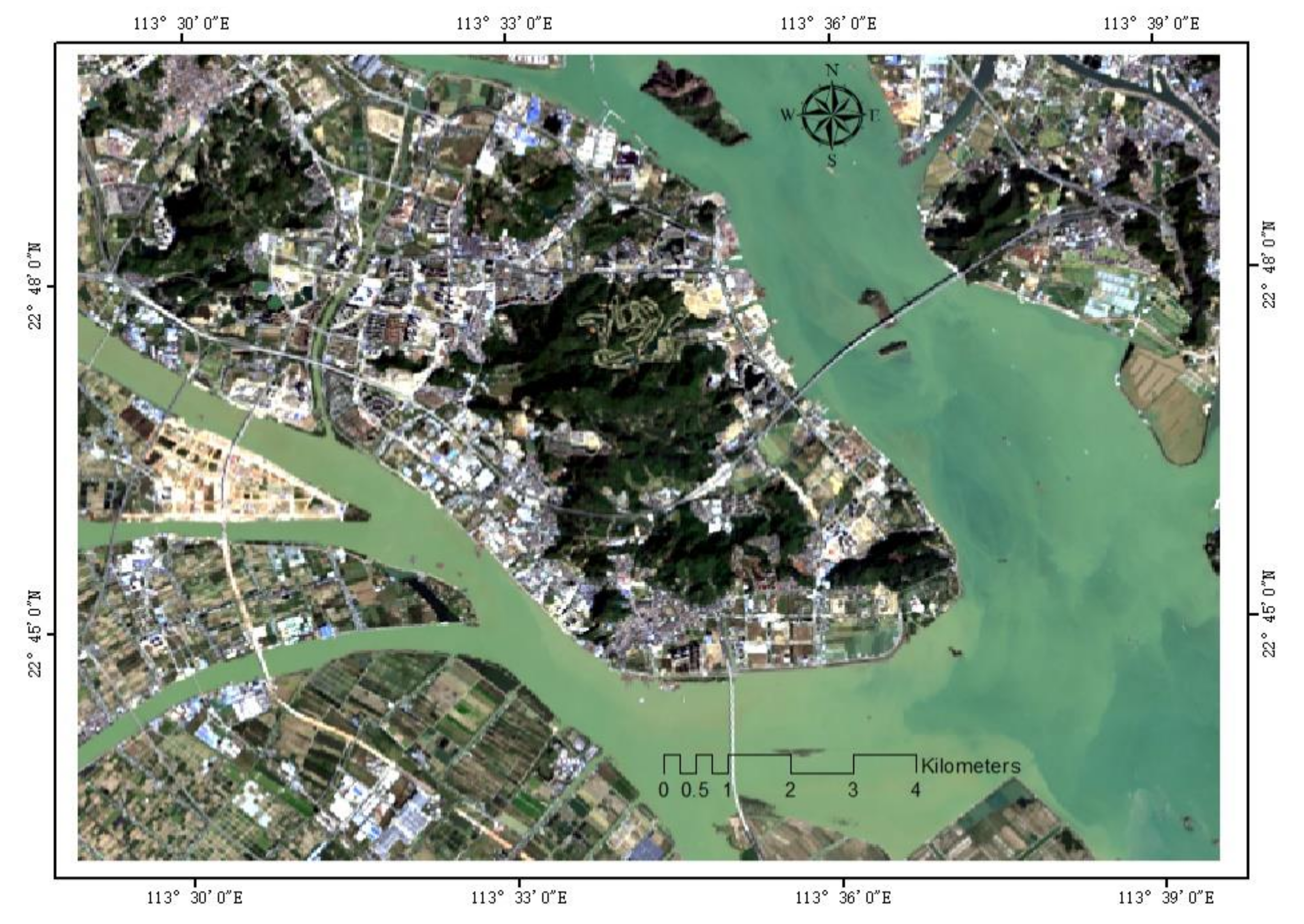
3.1. Study Area
3.2. Data and Datasets
3.3. Network Parameter Setting and Training
3.4. Assessment
4. Results
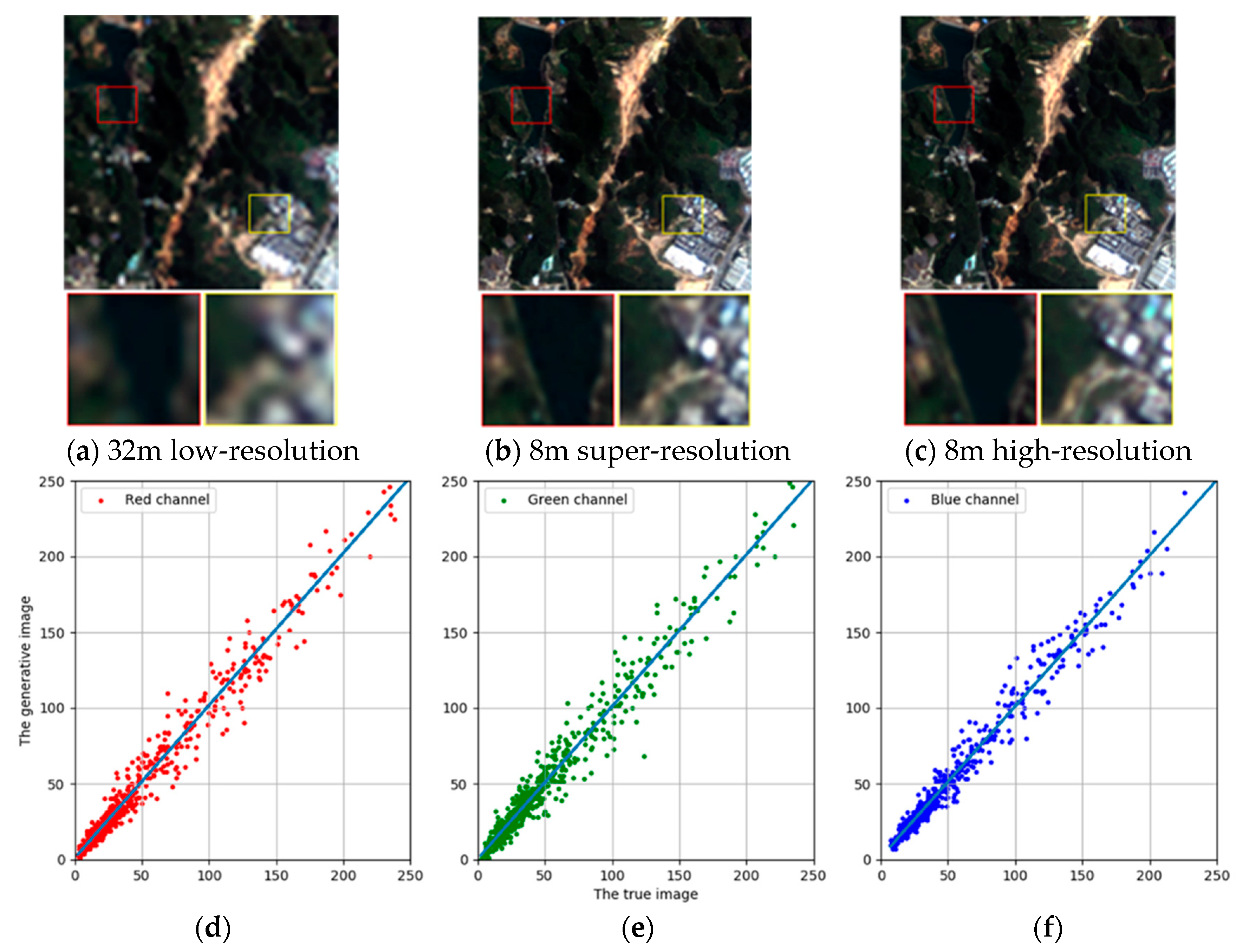
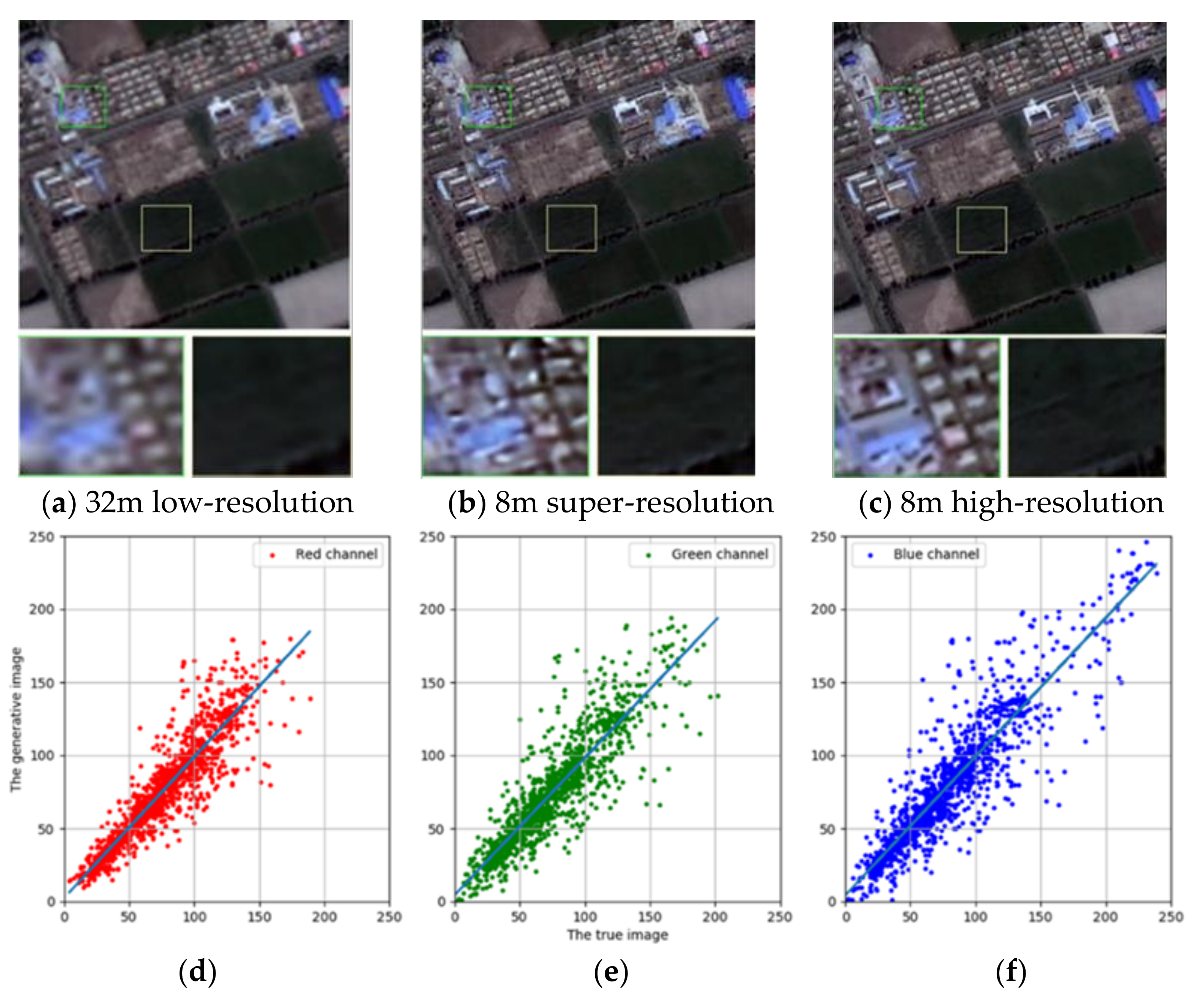
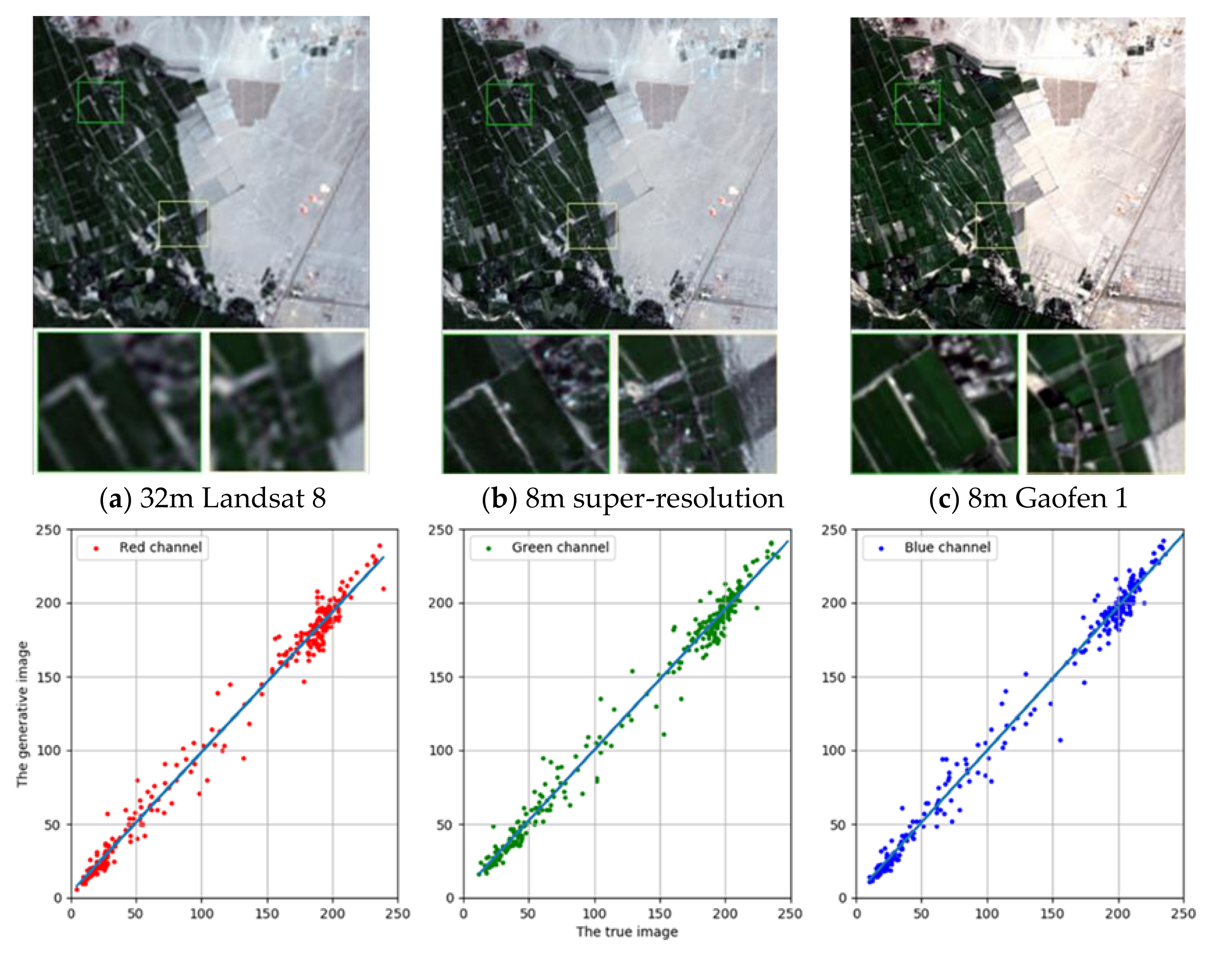
4.1. High Spatial Resolution Image of ISRGAN across Locations and Sensors
4.2. Compare ISRGAN with NE, SCSR, and SRGAN
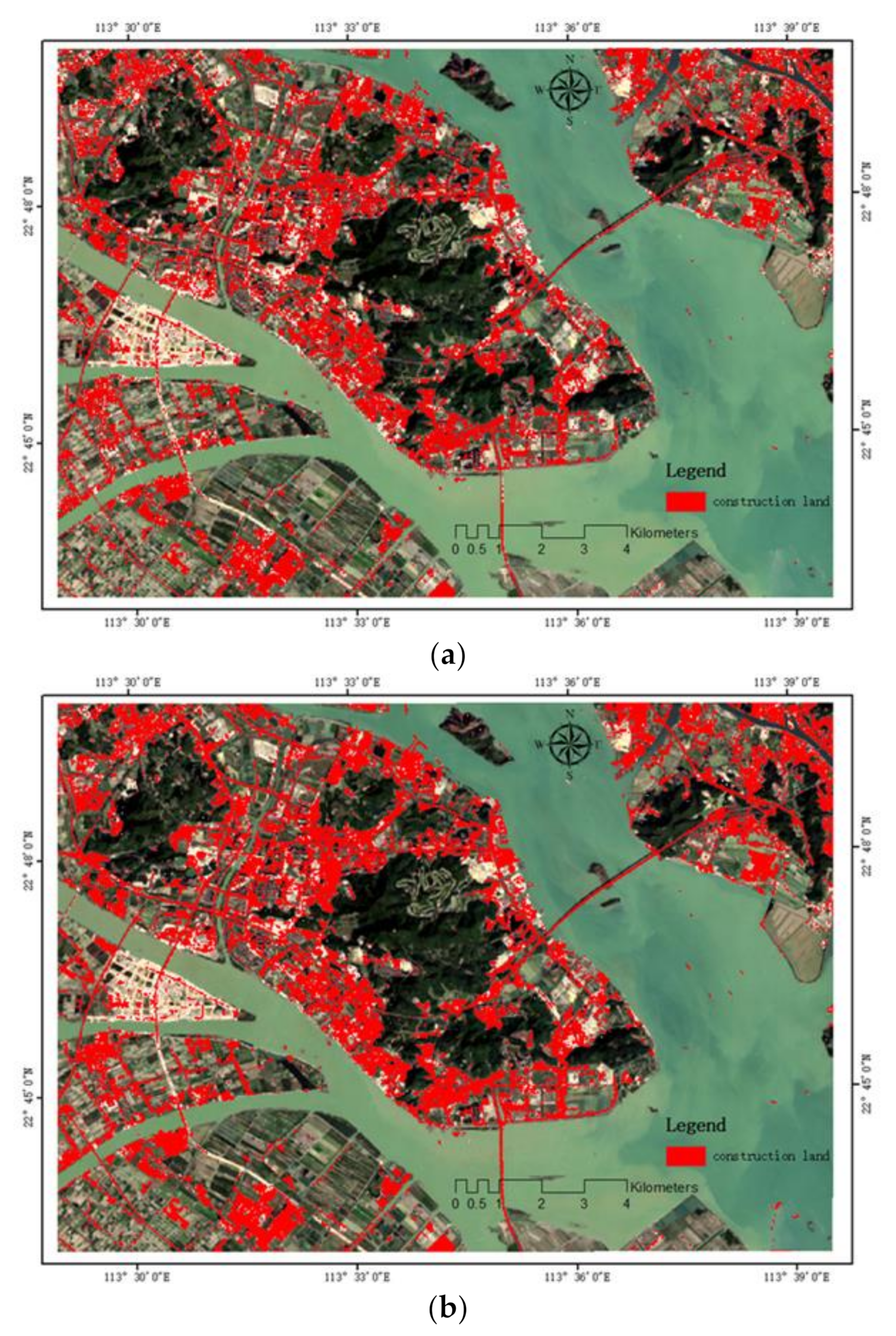
4.3. The Improvement of Land Cover Classification after ISRGAN Super-Resolution
5. Discussion
6. Conclusions
- (1)
- The ISRGAN super-resolution network proposed in this paper is applied to the super-resolution of remote sensing images, and the results obtained are better than other super-resolution methods, such as the neighbor-embedding method, the sparse representation method, and the SRGAN;
- (2)
- In order to realize the one-time training and repeated use of the super-resolution model, we directly applied the model trained with the Guangdong GF 1 image data to the Xinjiang GF 1 image data and conducted a t-test on the evaluation indexes of the super-resolution results of the two datasets, which verified the generalization ability of the super-resolution model across locations;
- (3)
- In order to combine the advantages of the domestic GF 1 image data and the Landsat 8 data, the super-resolution model trained on the GF 1 data was directly applied to the Landsat 8 data, and a t-test was performed on the evaluation indexes of the super-resolution results, verifying the generalization ability of the super-resolution model across sensors;
- (4)
- Taking the land use classification and ground-object extraction as examples, we compared the classification and extraction accuracy of the images before and after super-resolution. The K-means clustering algorithm was adopted for the land use classification, and the SVM algorithm was used for the ground-object extraction. The results show that the visual effect and accuracy of the images after super-resolution are improved in the classification and ground-object extraction, indicating that the super-resolution of remote sensing images is of great application value in resource development, environmental monitoring, disaster research, and global change analysis.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lim, H.S.; MatJafri, M.Z.; Abdullah, K. High spatial resolution land cover mapping using remotely sensed image. Modern Appl. Sci. 2009, 3, 82–91. [Google Scholar] [CrossRef][Green Version]
- Mou, L.; Zhu, X.; Vakalopoulou, M.; Karantzalos, K.; Paragios, N.; Le Saux, B.; Moser, G.; Tuia, D. Multitemporal Very High Resolution From Space: Outcome of the 2016 IEEE GRSS Data Fusion Contest. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3435–3447. [Google Scholar] [CrossRef]
- Schmitt, M.; Zhu, X.X. Data Fusion and Remote Sensing: An ever-growing relationship. IEEE Geosci. Remote Sens. Mag. 2016, 4, 6–23. [Google Scholar] [CrossRef]
- Yang, D.Q.; Li, Z.M.; Xia, Y.T.; Chen, Z.Z. Remote Sensing Image Super-resolution: Challenges and Approaches. In Proceedings of the 2015 IEEE International Conference on Digital Signal Processing (DSP), Singapore, 21–24 July 2015; pp. 196–200. [Google Scholar]
- Luo, Q.; Shao, X.; Peng, L.; Wang, Y.; Wang, L. Super-resolution imaging in remote sensing. Satell. Data Compress. Commun. Process. XI 2015, 9501, 950108. [Google Scholar]
- Zhang, X.G. A new kind of super-resolution reconstruction algorithm based on the ICM and the nearest neighbor interpolation. Adv. Sci. Through Comput. 2008, 344–346. [Google Scholar]
- Zhang, X.G. A New Kind of Super-Resolution Reconstruction Algorithm Based on the ICM and the Bilinear Interpolation. In Proceedings of the 2008 International Seminar on Future BioMedical Information Engineering, Wuhan, China, 18 December 2008; pp. 183–186. [Google Scholar]
- Zhang, X.G. A New Kind of Super-Resolution Reconstruction Algorithm Based on the ICM and the Bicubic Interpolation. In Proceedings of the 2008 International Symposium on Intelligent Information Technology Application Workshops, Shanghai, China, 21–22 December 2008; pp. 817–820. [Google Scholar]
- Hardie, R.C.; Barnard, K.J.; Armstrong, E.E. Joint MAP registration and high-resolution image estimation using a sequence of undersampled images. IEEE Trans. Image Process. 1997, 6, 1621–1633. [Google Scholar] [CrossRef]
- Tian, J.; Ma, K.K. Stochastic super-resolution image reconstruction. J. Vis. Commun. Image Represent. 2010, 21, 232–244. [Google Scholar] [CrossRef]
- Kim, K.I.; Kwon, Y. Single-image super-resolution using sparse regression and natural image prior. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1127–1133. [Google Scholar]
- Kursun, O.; Favorov, O. Super-resolution by unsupervised learning of high level features in natural images. In Proceedings of the 6th World Multi-Conference on Systemics, Cybernetics and Informatics (SCI 2002)/8th International Conference on Information Systems Analysis and Synthesis (ISAS 2002), Orlando, FL, USA, 14–18 July 2002; pp. 178–183. [Google Scholar]
- Begin, I.; Ferrie, F.P. Blind super-resolution using a learning-based approach. In Proceedings of the 17th International Conference on Pattern Recognition, Cambridge, UK, 23–26 August 2004; Volume 2, pp. 85–89. [Google Scholar]
- Joshi, M.V.; Chaudhuri, S.; Panuganti, R. A learning-based method for image super-resolution from zoomed observations. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2005, 35, 527–537. [Google Scholar] [CrossRef]
- Chan, T.M.; Zhang, J.P. An improved super-resolution with manifold learning and histogram matching. In International Conference on Biometrics; Springer: Berlin/Heidelberg, Germany, 2006; pp. 756–762. [Google Scholar]
- Rajaram, S.; Das Gupta, M.; Petrovic, N.; Huang, T.S. Learning-based nonparametric image super-resolution. EURASIP J. Appl. Signal Process. 2006, 51306. [Google Scholar] [CrossRef]
- Kim, C.; Choi, K.; Ra, J.B. Improvement on Learning-Based Super-Resolution by Adopting Residual Information and Patch Reliability. In Proceedings of the 2009 16th IEEE International Conference on Image Processing, Cairo, Egypt, 7–10 November 2009; pp. 1197–1200. [Google Scholar]
- Yang, M.C.; Chu, C.T.; Wang, Y.C.F. Learning Sparse Image Representation with Support Vector Regression for Single-Image Super-Resolution. In Proceedings of the 2010 IEEE International Conference on Image Processing, Hong Kong, China, 26–29 September 2010; pp. 1973–1976. [Google Scholar]
- Zhang, J.; Zhao, C.; Xiong, R.Q.; Ma, S.W.; Zhao, D.B. Image Super-Resolution Via Dual-Dictionary Learning and Sparse Representation. In Proceedings of the 2012 IEEE International Symposium on Circuits and Systems (ISCAS), Seoul, Korea, 20–23 May 2012; pp. 1688–1691. [Google Scholar]
- Dong, C.; Loy CC, G.; He, K.M.; Tang, X.O. Learning a Deep Convolutional Network for Image Super-Resolution. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2014; pp. 184–199. [Google Scholar]
- Chang, H.; Yeung, D.Y.; Xiong, Y. Super-resolution through neighbor embedding. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 27 June–2 July 2004; Volume 1, pp. 275–282. [Google Scholar]
- Yang, J.; Wright, J.; Huang, T.S.; Ma, Y. Image super-resolution via sparse representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [CrossRef] [PubMed]
- Miskin, J.; MacKay, D.C. Ensemble Learning for Blind Image Separation and Deconvolution. In Advances in Independent Component Analysis; Springer: London, UK, 2000; pp. 123–141. [Google Scholar]
- Guo, S.; Sun, B.; Zhang, H.K.; Liu, J.; Chen, J.; Wang, J.; Jiang, X.; Yang, Y. MODIS ocean color product downscaling via spatio-temporal fusion and regression: The case of chlorophyll-a in coastal waters. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 340–361. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K. Image Super-Resolution Using Deep Convolutional Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 295–307. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Qin, X.S. A coupled K-nearest neighbour and Bayesian neural network model for daily rainfall downscaling. Int. J. Climatol. 2014, 34, 3221–3236. [Google Scholar] [CrossRef]
- Takeda, H.; Farsiu, S.; Milanfar, P. Kernel regression for image processing and reconstruction. IEEE Trans. Image Process. 2007, 16, 349–366. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Huang, B. Support vector regression-based downscaling for intercalibration of multiresolution satellite images. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1114–1123. [Google Scholar] [CrossRef]
- Ledig, C.; Theis, L.; Huszar, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.H.; et al. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 105–114. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Proceedings of the NIPS’14: 27th International Conference on Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2014; pp. 2672–2680. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein GAN. arXiv 2017, arXiv:1701.07875. [Google Scholar]
- Steele, R. Peak Signal-to-Noise Ratio Formulas for Multistage Delta Modulation with Rc-Shaped Gaussian Input Signals. Bell Syst. Tech. J. 1982, 61, 347–362. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Coulter, L.L.; Stow, D.A. Monitoring habitat preserves in southern California using high spatial resolution multispectral imagery. Environ. Monit. Assess. 2009, 152, 343–356. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.W.; Shi, C.H.; Liew, S.C.; Kwoh, L.K. Land Cover Classification of Very High Spatial Resolution Satelite Imagery. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium—IGARSS, Melbourne, Australia, 21–26 July 2013; pp. 2685–2687. [Google Scholar]
- Lu, D.; Hetrick, S.; Moran, E.; Li, G. Detection of urban expansion in an urban-rural landscape with multitemporal QuickBird images. J. Appl. Remote Sens. 2010, 4, 041880. [Google Scholar] [CrossRef] [PubMed]
- Coppin, P.; Jonckheere, I.; Nackaerts, K.; Muys, B.; Lambin, E. Digital change detection methods in ecosystem monitoring: A review. Int. J. Remote Sens. 2004, 25, 1565–1596. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the Blending of the Landsat and MODIS Surface Reflectance: Predicting Daily Landsat Surface Reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar]
- Zhu, X.; Chen, J.; Gao, F.; Chen, X.; Masek, J.G. An enhanced spatial and temporal adaptive reflectance fusion model for complex heterogeneous regions. Remote Sens. Environ. 2010, 114, 2610–2623. [Google Scholar] [CrossRef]
- Huang, B.; Zhang, H. Spatio-temporal reflectance fusion via unmixing: Accounting for both phenological and land-cover changes. Int. J. Remote Sens. 2014, 35, 6213–6233. [Google Scholar] [CrossRef]
- Li, M.; Lin, J.; Ding, Y.; Liu, Z.; Zhu, J.Y.; Han, S. GAN Compression: Efficient Architectures for Interactive Conditional GANs. arXiv 2020, arXiv:2003.08936. [Google Scholar]
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-to-Image Translation with Conditional Adversarial Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5967–5976. [Google Scholar]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks Jun-Yan. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2223–2232. [Google Scholar]
- Park, T.; Liu, M.Y.; Wang, T.C.; Zhu, J.Y. Semantic image synthesis with spatially-adaptive normalization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 2332–2341. [Google Scholar]



| Types of Method | Basic Hypothesis | Representative Models | Advantages | Disadvantage |
|---|---|---|---|---|
| Interpolation-based methods | The value of the current pixel can be represented by the nearby pixels | The nearest neighbor interpolation [6] | low complexity and high efficiency | No image texture detail can be predicted and usually makes the image smoother looking |
| The bilinear interpolation [7] | ||||
| The bicubic interpolation [8] | ||||
| Refactoring-based methods | The physical properties and features can be recovered by image reconstruction (RE) technology, and these rules of the point spread function (PSF) can be further applying for the detail recovering | Joint MAP registration [9] | The different information on the same scene is fused to obtain high-quality reconstruction results | Requires pre-registration and a large amount of calculation |
| Sparse regression and natural image prior [11] | ||||
| Kernel regression | ||||
| PSF deconvolution [23] | ||||
| Learning-based methods | The point spread function can be created by learning from a large number of image samples [24] | Neighbor-embedding (NE) [21] | Getting better performance when training samples are more like the target image, and can achieve a higher PSNR when a large number of samples are involved | Highly time consuming, requiring big training datasets and usually limited model generalization ability across datasets |
| Convolutional neural network (SRCNN) [25] | ||||
| Bayesian networks [26] | ||||
| Kernel-based methods [27] | ||||
| SVM-based methods [28] | ||||
| Sparse representation (SCSR) [22] | ||||
| Super-resolution GAN(SRGAN) [29] |
| Parameters | 2m-PAN Sensor/8m-MS Sensor | 16m-MS Sensor | |
|---|---|---|---|
| Spectral range | Panchromatic | 0.45-0.90um | |
| Multispectral | 0.45-0.52um | 0.45-0.52um | |
| 0.52-0.59um | 0.52-0.59um | ||
| 0.63-0.69um | 0.63-0.69um | ||
| 0.77-0.89um | 0.77-0.89um | ||
| Spatial resolution | Panchromatic | 2m | 16m |
| Multispectral | 8m | ||
| Scale range | 60km (2 cameras) | 800km (4 cameras) | |
| Revisit cycle (side swing) | 4 days | ||
| Revisit cycle (non-side swing) | 41 days | 4 days | |
| Sensor | Band | Spectral Range/um | Spatial Resolution/m |
|---|---|---|---|
| OLI | 1-COASTAL | 0.43-0.45 | 30 |
| 2-Blue | 0.45-0.51 | 30 | |
| 3-Green | 0.53-0.59 | 30 | |
| 4-Red | 0.64-0.67 | 30 | |
| 5-NIR | 0.85-0.88 | 30 | |
| 6-SWIR1 | 1.57-1.65 | 30 | |
| 7-SWIR2 | 2.11-2.29 | 30 | |
| 8-PAN | 0.50-0.68 | 15 | |
| 9-Cirrus | 1.36-1.38 | 30 | |
| TIRS | 10-TIR | 10.60-11.19 | 100 |
| 11-TIR | 11.50-12.51 | 100 |
| Location | Sensor | Latitude and Longitude | Time | Filename |
|---|---|---|---|---|
| Guangdong | GF1-PMS1 | E114.2, N22.7 | 20171211 | GF1_PMS1_E114.2_N22.7_20171211_L1A0002840075 |
| Guangdong | GF1-PMS1 | E114.3, N23.0 | 20171211 | GF1_PMS1_E114.3_N23.0_20171211_L1A0002840076 |
| Guangdong | GF1-PMS2 | E114.6, N22.7 | 20171211 | GF1_PMS2_E114.6_N22.7_20171211_L1A0002840310 |
| Guangdong | GF1-PMS2 | E114.6, N22.9 | 20171211 | GF1_PMS2_E114.6_N22.9_20171211_L1A0002840309 |
| Guangdong | GF1-PMS2 | E114.7, N23.2 | 20171211 | GF1_PMS2_E114.7_N23.2_20171211_L1A0002840307 |
| Xinjiang | GF1-PMS1 | E86.3, N42.2 | 20180901 | GF1_PMS1_E86.3_N42.2_20180901_L1A0003427463 |
| Xinjiang | GF1-PMS1 | E86.6, N41.1 | 20171028 | GF1_PMS1_E86.6_N41.1_20171028_L1A0002715402 |
| Xinjiang | GF1-PMS1 | E87.2, N40.8 | 20171130 | GF1_PMS1_E87.2_N40.8_20171130_L1A0002807153 |
| Xinjiang | GF1-PMS2 | E87.0, N40.7 | 20170917 | GF1_PMS2_E87.0_N40.7_20170917_L1A0002605364 |
| Xinjiang | Landsat-8 OLI | E86.2, N41.7 | 20171229 | LC08_L1TP_143031_20171229_20180103_01_T1 |
| Levene Test of Variance | T-Test of the Mean | ||
|---|---|---|---|
| Sig | Sig(2-tailed) | ||
| SSIM | Variances are equal | 0.510 | 1.000 |
| Variances are not equal | 1.000 | ||
| PSNR | Variances are equal | 0.033 | 0.621 |
| Variances are not equal | 0.625 | ||
| Levene Test of Variance | T-Test of the Mean | ||
|---|---|---|---|
| Sig | Sig(2-tailed) | ||
| SSIM | Variances are equal | 0.011 | 0.824 |
| Variances are not equal | 0.826 | ||
| PSNR | Variances are equal | 0.197 | 0.000 |
| Variances are not equal | 0.000 | ||
| Data Sets | Index | NE | Super-Resolution Algorithms | ||
|---|---|---|---|---|---|
| SCSR | SRGAN | Ours | |||
| Guangdong (GF 1) | PSNR | 33.6349 | 31.1207 | 32.1658 | 36.3744 |
| SSIM | 0.9600 | 0.8854 | 0.9375 | 0.9884 | |
| Xinjiang (GF 1) | PSNR | 32.0343 | 30.1631 | 31.3782 | 35.8160 |
| SSIM | 0.9608 | 0.9001 | 0.9524 | 0.9885 | |
| Xinjiang (Landsat 8) | PSNR | 35.0010 | 33.639 | 32.8203 | 38.0922 |
| SSIM | 0.9818 | 0.9654 | 0.9488 | 0.9879 | |
| Class | Impervious Surface | Others |
|---|---|---|
| Impervious Surface | 61.48% | 15.28% |
| Others | 38.52% | 84.71% |
| Class | Impervious Surface | Others |
|---|---|---|
| Impervious Surface | 79.51% | 2.78% |
| Others | 20.49% | 97.22% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, Y.; Guo, S.; Chen, J.; Deng, X.; Sun, L.; Zheng, X.; Xu, W. Improved SRGAN for Remote Sensing Image Super-Resolution Across Locations and Sensors. Remote Sens. 2020, 12, 1263. https://doi.org/10.3390/rs12081263
Xiong Y, Guo S, Chen J, Deng X, Sun L, Zheng X, Xu W. Improved SRGAN for Remote Sensing Image Super-Resolution Across Locations and Sensors. Remote Sensing. 2020; 12(8):1263. https://doi.org/10.3390/rs12081263
Chicago/Turabian StyleXiong, Yingfei, Shanxin Guo, Jinsong Chen, Xinping Deng, Luyi Sun, Xiaorou Zheng, and Wenna Xu. 2020. "Improved SRGAN for Remote Sensing Image Super-Resolution Across Locations and Sensors" Remote Sensing 12, no. 8: 1263. https://doi.org/10.3390/rs12081263
APA StyleXiong, Y., Guo, S., Chen, J., Deng, X., Sun, L., Zheng, X., & Xu, W. (2020). Improved SRGAN for Remote Sensing Image Super-Resolution Across Locations and Sensors. Remote Sensing, 12(8), 1263. https://doi.org/10.3390/rs12081263








