A New GPU Implementation of Support Vector Machines for Fast Hyperspectral Image Classification

Abstract

The storage and processing of remotely sensed hyperspectral images (HSIs) is facing important challenges due to the computational requirements involved in the analysis of these images, characterized by continuous and narrow spectral channels. Although HSIs offer many opportunities for accurately modeling and mapping the surface of the Earth in a wide range of applications, they comprise massive data cubes. These huge amounts of data impose important requirements from the storage and processing points of view. The support vector machine (SVM) has been one of the most powerful machine learning classifiers, able to process HSI data without applying previous feature extraction steps, exhibiting a robust behaviour with high dimensional data and obtaining high classification accuracies. Nevertheless, the training and prediction stages of this supervised classifier are very time-consuming, especially for large and complex problems that require an intensive use of memory and computational resources. This paper develops a new, highly efficient implementation of SVMs that exploits the high computational power of graphics processing units (GPUs) to reduce the execution time by massively parallelizing the operations of the algorithm while performing efficient memory management during data-reading and writing instructions. Our experiments, conducted over different HSI benchmarks, demonstrate the efficiency of our GPU implementation.

1. Introduction

Recent advances in computer technology allowed for the development of powerful instruments for remote sensed data acquisition, lowering both the cost of their production and the cost of launching new Earth Observation (EO) missions. In particular, imaging spectroscopy (also known as hyperspectral imaging) [1] has attracted the attention of many researchers because of the great potential of hyperspectral images (HSIs) in characterizing the surface of the Earth by covering the visible, near-infrared and shortwave infrared regions of the electromagnetic spectrum. To exploit these data, multiple EO missions are now using imaging spectrometers, such as the Environmental Mapping and Analysis Programme (EnMAP) [2,3], or the Hyperspectral Precursor of the Application Mission (PRISMA) [4]. In this context, a high-dimensional stream of remotely sensed HSI data is now being generated, which can be applied to multiple tasks after being properly processed, such as managing of natural and environmental resources, urban planning and monitoring of agricultural fields, risk prevention and natural/human disaster management, among others.

However, HSI data processing faces important memory and computational requirements, due the large amount of information provided by EO airborne/satellite instruments. In fact, imaging spectrometers are able to collect hundreds of images over large areas along the Earth’s surface, gathering hundreds of narrow and continuous spectral bands along different wavelengths. As a result, each pixel in a HSI cube measures the reflection and absorption of electromagnetic radiation from ground objects into several spectral channels, creating a unique spectral signature for each material optically detected by the spectrometer [5]. This allows for a very accurate characterization of land cover surface, which is useful for the modeling and mapping of materials of interest but presents significant computational requirements. In particular, spectral-based classification algorithms need to process large amounts of spectral information in order to correctly assign a label (which corresponds to a fixed land cover class) to each pixel in the HSI scene, facing heavy computation burdens [6]. In this sense, the development of parallel implementations of traditional classification algorithms for fast and accurate processing is a requirement in order to efficiently process large HSI data repositories through proper management of computational resources.

With this aim, high performance computing (HPC) has become an efficient tool, not only for managing and analyzing the increasing amount of remotely sensed data that are currently being collected [7,8,9,10], but also for efficiently dealing with the high dimensionality of HSI data cubes [11,12]. From a computational point of view, most spectral-based HSI data classification algorithms exhibit inherent parallelism at three different levels [13]:

• through HSI pixel vectors (coarse-grained pixel level parallelism),
• through spectral-band information (fine-grained spectral level parallelism), and
• through tasks (task-level parallelism).

HSI classification algorithms generally map nicely on HPC systems [14], with several HPC approaches (from coarse-grained and fine-grained parallelism techniques to complex distributed environments) already successfully implemented. For instance, distributed approaches based on commodity (homogeneous and heterogeneous) clusters [15,16], grid computing [17,18], and cloud computing techniques [19,20,21,22] provided good results in terms of reducing execution times, enabling an efficient processing of massive data sets on the ground segment. However, dedicated resources such as massively parallel clusters and networks of computers are generally expensive and hard to maintain, being cloud computing a more appropriate and cheaper approach (in addition to a fully distributed solution) due to its “service-oriented” computing and “pay-per-use” model [23]. Neither cluster nor cloud computing models allow on-board processing.

On the other hand, parallel solutions based on multicore CPUs [10,24,25], graphics processing units (GPUs) [14,26,27,28,29], and field programmable gate arrays (FPGAs) [30,31,32,33,34] were also successful, leading to near real-time performance in many HSI applications [35]. These platforms generally provide a cheaper solution when compared to large-scale distributed systems. Also, these approaches consume much less energy in comparison with cluster-based or distributed systems, being GPU systems (in particular, those with low-power consumption [36]) and FPGAs the ones currently offering the best performance/consumption ratio. Nevertheless, although both kinds of devices are appealing for on-board processing, FPGAs (despite their reconfigurability) are still more difficult to program than GPUs. In fact, GPUs are massively parallel programmable systems that can satisfy the extremely high computational requirements by HSI-based applications at low cost, with very good programmability. As a result, many HSI data processing algorithms were implemented on GPUs, including target and anomaly detection methods [37,38], and techniques for image compression [39], scene classification [40], and spectral unmixing [41].

In this paper, we develop a new GPU implementation of the traditional support vector machine (SVM) algorithm [42]. Traditionally considered to be a powerful classifier in a wide variety of fields, such as medical computing or text and image processing (among others), the SVM has been succefully adopted in HSI classification problems. It separates two classes of samples with the maximal margin by exploiting an optimal decision boundary [43]. As a result, SVMs have often been found to provide higher classification accuracies than other widely used pattern recognition techniques, such as the maximum likelihood, the random forest (RF) or the multi-layer perceptron (MLP) classifiers. Furthermore, SVMs appear to be particularly advantageous in heterogeneous environments, for which only a few training samples are available per class. The SVM has demonstrated its success in HSI data classification in a multitude of scientific works within the remote sensing field [44] due to its robust behaviour when dealing with high-dimensional data and its great ability to generalize to unseen data. However, SVMs exhibit a high computational cost, which strongly discourages its use when facing large-scale, real-time HSI classification problems.

To mitigate the aforementioned problem, several techniques were adopted to reduce the execution time of SVMs. For instance, in [45], Osuna et al. presented a decomposition algorithm by addressing sub-problems iteratively to enable tackling larger problems. In [46], Platt proposed the sequential minimal optimization (SMO) algorithm by decomposing the quadratic programming (QP) problem into a series of smaller QP subproblems that can be solved analytically, without the need for a time-consuming QP optimization. Ease of implementation is a typical feature of the SMO algorithm. In [47], Fan et al. developed a series of working set selection (WSS) heuristics, based on second order information, to achieve a faster convergence of the SMO. Recently, some researchers used the portability and excellent computing performance of GPUs to address the computational requirements of SVMs. In particular, Tan et al. [48] proposed a novel two-level parallel computing framework based on NVIDIA’s compute device unified architecture (CUDA) and OpenMP to accelerate SVM-based classification, while Li et al. [49] used GPU devices to improve the speed performance of SVM training and prediction stages.

In this work, we present a novel GPU implementation of SVMs that does not only reduces the execution time by massively parallelizing the operations of the algorithm on the GPU, but also performing efficient memory management during data-reading and writing operations [50]. We empirically evaluate the efficiency of our method considering different HSI real scenes, which comprise urban and agricultural land-cover information, and observed that it is able to maintain the precision in the results while significantly improving the computational performance.

The remainder of the paper is organized as follows. Section 2 presents the fundamentals of the SVM method adapted to HSI data. Section 3 describes the GPU implementation of the considered classifier. Section 4 validates the GPU implementation by comparing it with other existing implementations. Finally, Section 5 concludes the paper with some remarks and hints at plausible future research lines.

2. Support Vector Machines (SVMs): A Review

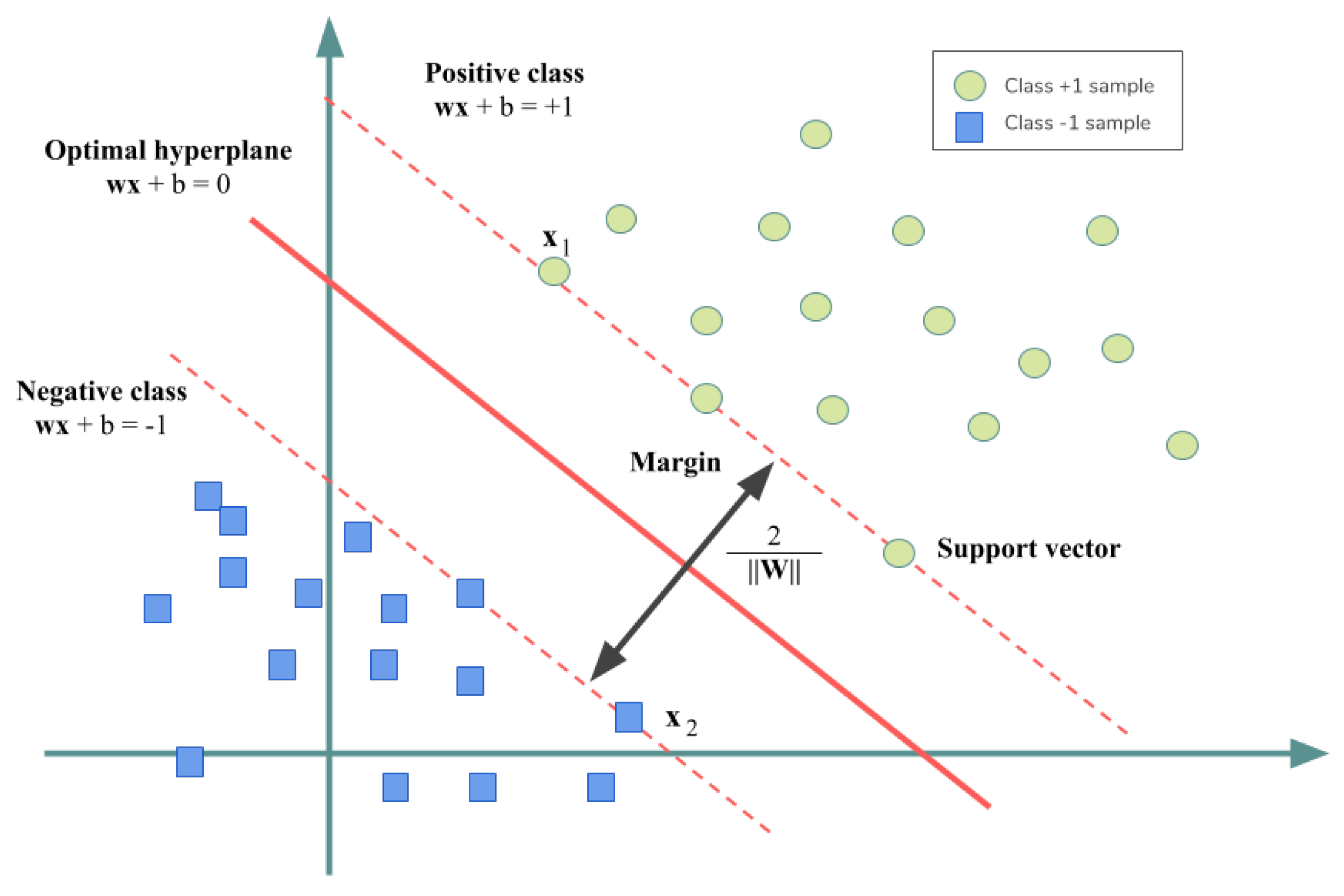
2.1. Linear SVM

Any HSI classification method $y=f\left(\mathbf{x}\right)$ can be described as the mapping function $f:{\mathbb{N}}^{n_b}\to \mathbb{N}$, where the domain is composed by those spectral pixels ${\mathbf{x}}_i\in {\mathbb{N}}^{n_b}=[x_{i1},x_{i2},\cdots ,x_{i{n}_b}]$ that encode the reflectance values of the HSI cube $\mathbf{X}\in {\mathbb{N}}^{n_h\times n_w\times n_b}$, which is composed by $n_h·n_w$ pixels (note that $i=\{1,\cdots ,n_h·n_w\}$) with $n_b$ spectral bands, while the co-domain is composed by the corresponding label-vectors $y_i\in [1,2,\cdots ,n_c]$, being $n_c$ the number of different land cover categories. The final goal is to obtain the sample-label pairs for each HSI image element, ${\{{\mathbf{x}}_i,y_i\}}_{i=1}^{n_h·n_w}$, obtaining as a result the final classification map $\mathbf{Y}\in {\mathbb{N}}^{n_h\times n_w}$.

In this context, the original SVM method [51] was proposed for binary classification problems, i.e., $n_c=2$ so $y_i\in \{1,-1\},\forall i\in \{1,\cdots ,n_h·n_w\}$, where the two considered classes are linearly separable, with at least one hyperplane separating them (see Figure 1). This hyperplane is defined by its normal vector$\mathbf{w}\in {\mathbb{R}}^{n_b}$ and the bias$b\in \mathbb{R}$ that defines the distance between the samples and the hyperplane. In this regard, the classifier can be defined as the discriminant function:

$$f\left(\mathbf{x}\right)=\mathbf{w}\mathbf{x}+b,$$

(1)

where $f\left(\mathbf{x}\right)=0$ is the hyperplane and the samples lie on the planes $f\left(\mathbf{x}\right)=\pm 1$ depending on the class they belong to. Both parameters $\mathbf{w}$ and b are estimated by the SVM during the training stage in order to maximize the distance between the closest sample and the hyperplane, i.e., with the aim of maximizing the margin $m=2/\left|\right|\mathbf{w}\left|\right|$ [42]. This maximization problem should be conveniently replaced by the equivalent minimization problem $\frac{1}{2}{\left|\right|\mathbf{w}\left|\right|}^2$. In the end, the SVM finds the optimal hyperplane along the space of samples by minimizing the quadratic optimization problem given by Equation (2):

$$\underset{\mathbf{w},b}{min}\frac{1}{2}{\left|\right|\mathbf{w}\left|\right|}^2,\mathrm{subject} \mathrm{to}{y}_i\left(\mathbf{w}·{\mathbf{x}}_i+b\right)-1\ge 0\forall i\in \{1,\cdots ,n_t\}$$

(2)

where $n_t$ is the number of training samples, ${\mathbf{x}}_i$ is the i-th sample, and $y_i$ is the correct output provided by the SVM, i.e., +1 for positive samples and -1 for negative ones. Considering the Lagrangian formulation [52], Equation (2) can be simplified by replacing the inequality ≥through a dual problem. In particular, employing the Lagrange multipliers ${\alpha }_i\ge 0\forall i\in \{1,\cdots ,n_t\}$, we define the optimization problem given by Equation (3), which only depends on the set of Lagrange multipliers $\alpha =\{{\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_{n_t}\}$:

$$\underset{\alpha }{min}\frac{1}{2}\sum _{i=1}^{n_t}\sum _{j=1}^{n_t}{y}_i{y}_j\left({\mathbf{x}}_i·{\mathbf{x}}_j\right){\alpha }_i{\alpha }_j-\sum _{i=1}^{n_t}{\alpha }_i,\mathrm{subject} \mathrm{to} {\alpha }_i\ge 0\mathrm{and}\sum _{i=1}^{n_t}{y}_i{\alpha }_i=0\forall i\in \{1,\cdots ,n_t\},$$

(3)

where ${\mathbf{x}}_i$ and ${\mathbf{x}}_j$ are two samples of the training set with labels $y_i$ and $y_j$ and Lagrange multipliers ${\alpha }_i$ and ${\alpha }_j$, respectively. Equation (3) can be computed using QP methods, such as the SMO [53], which breaks the problem into a series of smallest and equivalent QP problems, solving each one analytically.

With this problem representation, the normal vector $\mathbf{w}$ can be derived as the sum of all the samples that belong to the training set and modified by their corresponding Lagrange multiplier together with the associated class of the sample, ${\displaystyle \mathbf{w}=\sum _{i=1}^{n_t}{\alpha }_i{y}_i{\mathbf{x}}_i}$, while the bias is obtained for some multiplier ${\alpha }_j>0$ as $b=\mathbf{w}{\mathbf{x}}_j-y_j$. Moreover, the discriminant function $f\left(\mathbf{x}\right)$ provided by Equation (1) can be solely described in terms of Lagrange multipliers and samples as:

$${\displaystyle f\left(\mathbf{x}\right)=\sum _{i=1}^{n_t}{\alpha }_i{y}_i({\mathbf{x}}_i·\mathbf{x})+b}$$

(4)

It is worth noting that each Lagrange multiplier ${\alpha }_i$ measures the relevance of the sample ${\mathbf{x}}_i$ when calculating the hyperplane and classifying the data, so that samples with ${\alpha }_i=0$ will be ignored, while samples with ${\alpha }_i>0$ will be considered to be support vectors. Also, from Equation (4), we can observe that, to perform the classification of any sample $\mathbf{x}$, a significant volume of memory will be required, consuming also a large amount of computational resources to compute the dot products needed.

2.2. Linear SVM for Linearly Nonseparable Data Classification

The linear SVM has a limitation: with linearly nonseparable data classification there may not be a hyperplane, so the solution becomes infinite. To overcome this drawback, the linear soft-margin SVM implements a new cost function, which takes into account the original margin maximization and including a loss term that penalizes misclassified data, as it can be observed in Equation (5):

$$\underset{\mathbf{w},b}{min}\frac{1}{2}{\left|\right|\mathbf{w}\left|\right|}^2+C\sum _{i=1}^{n_t}{\delta }_i,\mathrm{subject} \mathrm{to}{y}_i\left(\mathbf{w}·{\mathbf{x}}_i+b\right)-1+{\delta }_i\ge 0\mathrm{and}{\delta }_i\ge 0,$$

(5)

where ${\delta }_i\ge 0$ are some slack variables that are introduced into the inequality restriction $y_i\left(\mathbf{w}·{\mathbf{x}}_i+b\right)-1+{\delta }_i\ge 0$ to relax the condition that all the samples that belongs to the same class lie on the same side of the hyperplane. Thus, ${\displaystyle \sum _{i=1}^{n_t}{\delta }_i}$ can be interpreted as some measure of the amount of misclassifications. Also, a regularization constant $C\in [0,\infty )$ is included to control the weight of minimizing $\frac{1}{2}{\left|\right|\mathbf{w}\left|\right|}^2$ while penalizing solutions with very large ${\delta }_i$. In fact, C can be considered to be a parameter that adjusts the robustness or flexibility of the model, depending its value.

Once more, the Lagrangian formulation can be applied to translate the primal problem defined by Equation (5) into the dual problem of Equation (3), by simply introducing the box constraint $C\ge {\alpha }_i\ge 0$. The slack variables ${\delta }_i$ do not affect the optimization problem.

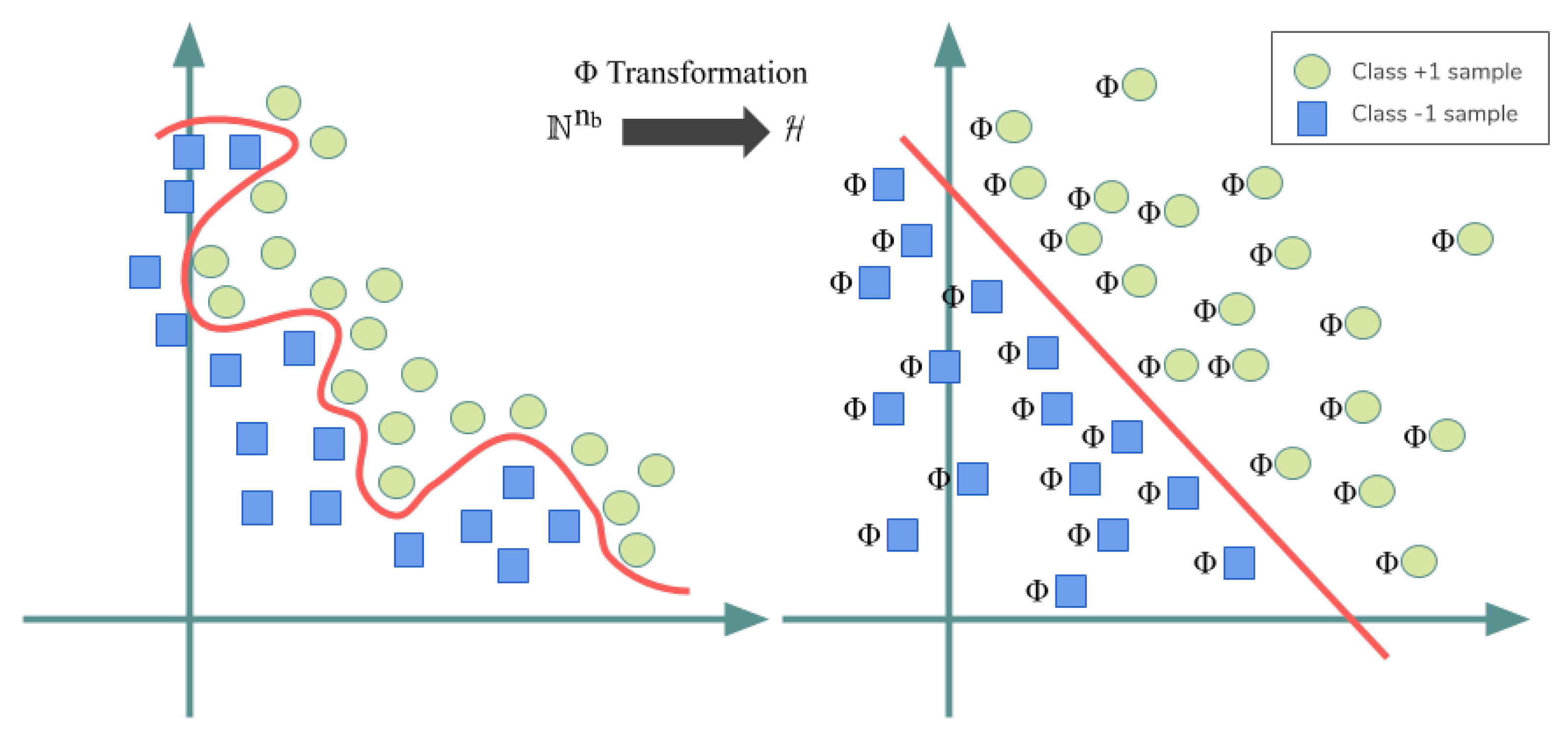
2.3. Kernel SVM for Non-Linear Data Classification

As an alternative to the soft-margin implementation, the SVM method can be adapted to perform non-linear classification by including a kernel [54,55] within the classifier. The main idea is to map the original feature vectors ${\mathbf{x}}_i\in {\mathbb{N}}^{n_b}$ into a higher dimensional Euclidean space, denoted as $\mathcal{H}$, by using a non-linear vector function $\mathsf{\Phi }:{\mathbb{N}}^{n_b}\to \mathcal{H}$, as we can observe in Figure 2. In this context, the optimal margin problem can be posed in the space $\mathcal{H}$ by replacing the original inner product between the samples ${\mathbf{x}}_i·\mathbf{x}$ with the transformed vectors $\mathsf{\Phi }\left({\mathbf{x}}_i\right)·\mathsf{\Phi }\left(\mathbf{x}\right)$, so the discriminant function will be defined as:

$$\begin{array}{c}\hfill {\displaystyle f\left(\mathbf{x}\right)=\sum _{i=1}^{n_t}{\alpha }_i{y}_i\left(\mathsf{\Phi }\left({\mathbf{x}}_i\right)·\mathsf{\Phi }\left(\mathbf{x}\right)\right)+b}\\ \hfill {\displaystyle \mathrm{Replacing}K({\mathbf{x}}_i,\mathbf{x})=\mathsf{\Phi }\left({\mathbf{x}}_i\right)·\mathsf{\Phi }\left(\mathbf{x}\right)\to f\left(\mathbf{x}\right)=\sum _{i=1}^{n_t}{\alpha }_i{y}_{i}K({\mathbf{x}}_i,\mathbf{x})+b}\end{array}$$

(6)

Equation (6) can be easily simplified by assuming there is such a kernel function that $K({\mathbf{x}}_i,\mathbf{x})=\mathsf{\Phi }\left({\mathbf{x}}_i\right)·\mathsf{\Phi }\left(\mathbf{x}\right)$. This assumption allows avoiding the computation of the inner product between transformed vectors, significantly reducing the computational consumption of the algorithm. To ensure the existence of the underlying map $\mathsf{\Phi }$, the kernel function is positively defined [51] by satisfying Mercer’s conditions [56].

Finally, the solution of the dual problem can be also meaningfully simplified as:

$$\underset{\alpha }{min}\frac{1}{2}\sum _{i=1}^{n_t}\sum _{j=1}^{n_t}{y}_i{y}_{j}K\left({\mathbf{x}}_i{\mathbf{x}}_j\right){\alpha }_i{\alpha }_j-\sum _{i=1}^{n_t}{\alpha }_i,\mathrm{subject} \mathrm{to}C\ge {\alpha }_i\ge 0 \mathrm{and}\sum _{i=1}^{n_t}{y}_i{\alpha }_i=0$$

(7)

In fact, the kernel function usually measures the distance between the input sample ${\mathbf{x}}_i$ and the other training samples ${\mathbf{x}}_j$.

Table 1. Most common kernels in the SVM method, where ${\mathbf{x}}_i$ and ${\mathbf{x}}_j$ are two samples of dataset $\mathbf{X}$.

Linear	$\langle {\mathbf{x}}_i,{\mathbf{x}}_j\rangle$
Polynomial	${(\gamma \langle {\mathbf{x}}_i,{\mathbf{x}}_j\rangle +c)}^n$
Gaussian	$exp(-\gamma ||{\mathbf{x}}_i-{\mathbf{x}}_j|{|}^2)\gamma$
Sigmoid	$tanh{(\gamma \langle {\mathbf{x}}_i,{\mathbf{x}}_j\rangle +c)}^n$
Radial basis function (RBF)	$exp\left(-\frac{\left|\right|{\mathbf{x}}_i-{\mathbf{x}}_j{\left|\right|}^2}{2{\sigma }^2}\right)$

shows some of the most widely used kernels. In particular, the RBF kernel has quite interesting properties. It can be simplified as $exp\left(-\gamma \left|\right|{\mathbf{x}}_i-{\mathbf{x}}_j{\left|\right|}^2\right)$, where $\gamma$ controls the model’s performance, in the sense that a small value of $\gamma$ will provide classification solutions with low bias and high variance, while a high value of $\gamma$ will give solutions with high bias and low variance.

2.4. Multi-Class SVM

The aforementioned SVM implementations can be generalized to develop multi-class classification by combining several binary classifiers [42]. In this regard, there are two main strategies that can be adopted to perform multi-class classification [57]: (i) constructing and combining several binary classifiers, and (ii) considering all data in one optimization formulation.

Regarding the first approach, it is usual to find one-against-all, one-against-one and decision directed acyclic graph (DDAG)-based approaches for multi-class SVM in the available literature [58,59,60]. The first approach constructs $n_c$ pairwise classifiers, where the k-th model is trained with those samples that belong to the k-th class by assigning them a positive label (while the rest of the samples are paired with negative labels). The classification procedure applies the $n_c$ SVM models to each sample ${\mathbf{x}}_i$, selecting the label of the classifier $f_k\left(\mathbf{x}\right)$ with the largest margin:

$$y_i=arg\underset{k}{max}{f}_k\left({\mathbf{x}}_i\right)$$

(8)

As a result, $n_c$$n_t$-variable QP-problems have to be solved, which implies that training time scales linearly with $n_c$. Instead of developing $n_c$ classifiers, the one-against-one approach adopts a pairwise decomposition strategy, implementing $n_c(n_c-1)/2$ binary models on all pairs of training data. Each model $f_{kt}$ is trained on data that belong to two different classes, k and t, ignoring all the other classes. In this way, those samples that belong to class k are labeled as positive, while the samples that belong to class t correspond to the negative label (note that $f_{tk}=-f_{kt}$). The final label is selected by majority voting strategy:

$$y_i=arg\underset{k}{max}\left(\sum _t{f}_{kt}\left({\mathbf{x}}_i\right)\right)$$

(9)

It is noteworthy that the one-against-one approach exhibits a much more robust behaviour when classifying imbalanced datasets; however, it is also more computationally expensive than the one-against-all for simpler problems, such as those with fewer classes.

Finally, the DDAGSVM also solves $n_c(n_c-1)/2$ binary models during the training stage, implementing a rooted binary directed acyclic graph with also $n_c(n_c-1)/2$ internal nodes (each one is a binary SVM) and $n_c$ leaves (i.e., the predicted class) during the testing stage.

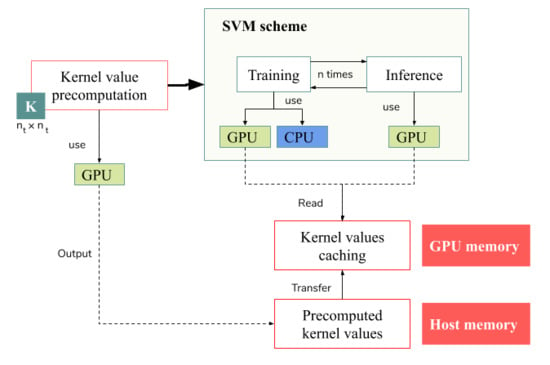
3. GPU-Accelerated SVM for HSI Data Classification

3.1. Previous Works and Proposal Overview

Despite obtaining great accuracy results, the training and prediction steps of the SVM algorithm are very expensive from a computational point of view, especially for large and complex problems. Furthermore, it is noteworthy that kernel-based techniques can greatly simplify the computations, thus reducing the execution times. However, these methods need to use all the data to properly calculate the kernel, which generally requires large memory consumption [61]. In particular, HSI data offers a great challenge to the SVM classifier, mainly due to (both) the large spectral dimensionality and volume of data to be processed. As noted in Section 1, there were some previous works in the literature focused on optimizing and parallelizing the execution of the SVM. However, there are few efforts in the recent literature oriented at the exploitation of GPU-based implementations for HSI data classification. From the current state-of-the-art in the literature, we can highlight two works. Tan et al. [48] combined the NVIDIA Compute Unified Device Architecture (CUDA) [50] and OpenMP [62] to optimize the classification problem, and implemented as a multi-class SVM following one-against-one strategy. In this sense, they were able to run the one-against-one strategy in parallel by implementing an OpenMP-based approach, while each single WSS-based binary SVM classifier was parallelized into GPUs. In addition, the calculation of every kernel element $K({\mathbf{x}}_i,{\mathbf{x}}_j)$ was done by the GPU, being the constant values stored into the shared memory of the GPU device, following column-major order, and sent (when needed) through a broadcasting mechanism. Also, Wu et al. [63] developed a GPU-parallelized SVM method based on composite kernels (SVMCK) [64] and able to integrate spatial and spectral information, with the aim of improving the accuracy in HSI data classification tasks. In this context, they carried the calculations of the composite kernel matrix in the GPU. The resulting $K({\mathbf{x}}_i,{\mathbf{x}}_j)$ were copied to the host (CPU), and then stored in the available memory of the host. The rest of the computations were carried out in the CPU.

In this context, we propose a new parallel version of the SVM algorithm for high dimensionality data. Our proposal can be efficiently generalized to be applied in other fields, being our parallel SVM adapted to the specific case of remote sensing HSI data classification. In particular, we propose a parallel implementation of a multi-class SVM, following one-against-one strategy, with the RBF kernel. It must be noted that each single binary SVM has been solved through the SMO method. Furthermore, the SMO solver (during the training stage) and the full inference stage were paralleled into a general purpose GPU (GPGPU) framework, employing the NVIDIA CUDA platform. Our goal is not only to achieve a good speed up ratio in comparison with other traditional SVM implementations, but also to develop a scalable implementation with regards to both the amount of data and the spectral dimensionality of the data. In this regard, the implemented approach performs the algorithmic parallelization of the SVM operations during the training and inference stages, implementing at the same time a series of optimizations in the memory read and write operations, with the aim of reducing the number of communications between the host and the device, and to reduce the memory latency. Also, it should be noted that a data-oriented parallelization strategy has been adopted, parallelizing the operations related to data management and reusing as much information as possible between different iterations. Regarding to this, a batch-based approach has been implemented within the SMO with the aim of solving multiple sub-problems in parallel. Particular attention has been paid to the calculation of the kernel matrix, as it consumes a massive amount of computational and storage resources. In the following sections we will provide details about our new implementation.

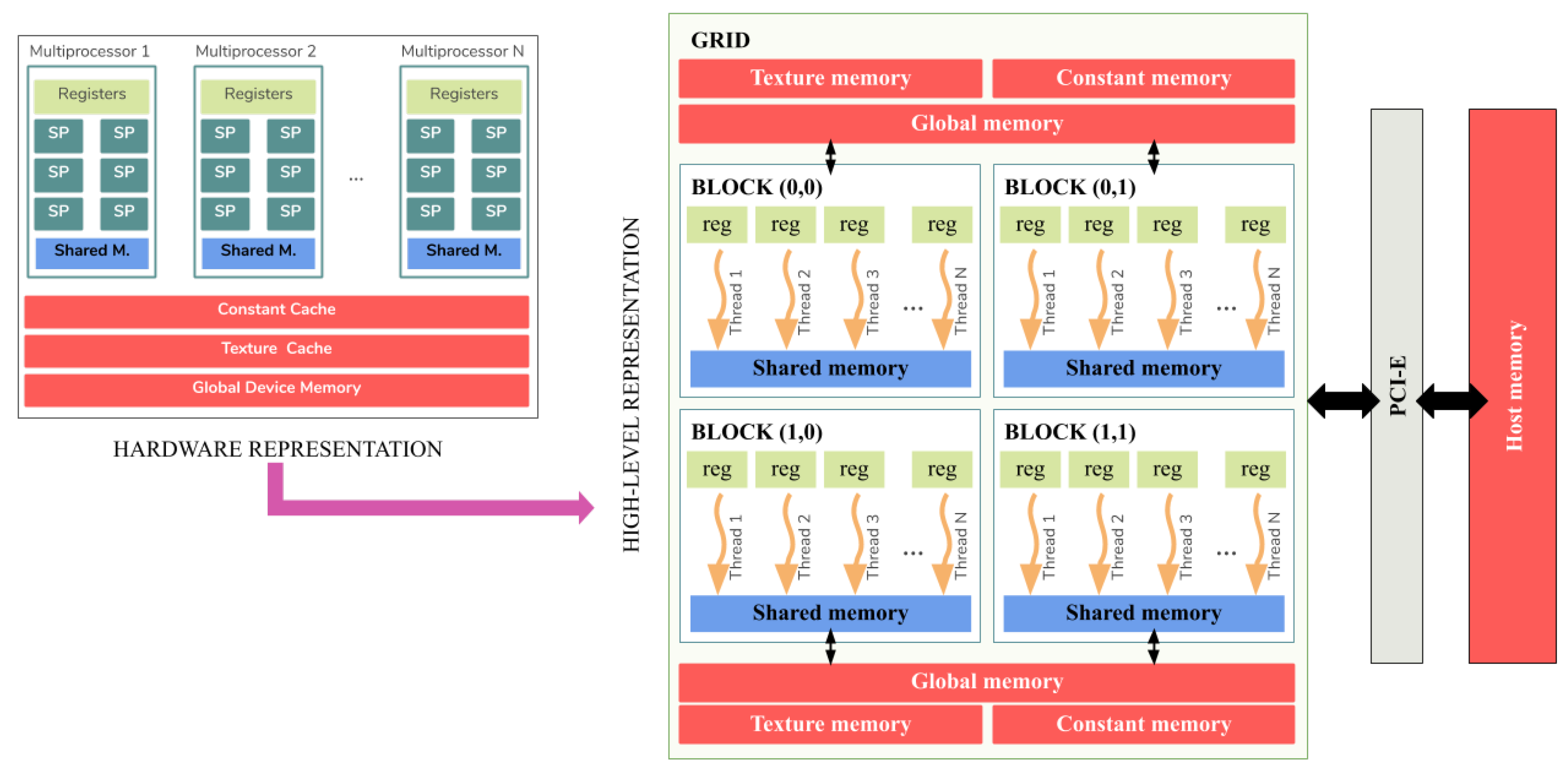
3.2. CUDA Platform

To obtain an accelerated version of the SVM for HSI data classification, a GPGPU-based implementation has been employed using NVIDIA CUDA platform [50]. The main goal is to exploit the full computing power of GPU devices (using the general-purpose parallel computing platform and the programming model offered by CUDA) to solve many complex computational problems in a more efficient way. Specifically, we solve $n_c$ binary SVM instances (with the RBF kernel) that compose our multi-class SVM algorithm for remote sensing HSI data classification. In this context, we consider the GPU device as a set of stream multiprocessors, composed by several cores with a 3-level hierarchical memory system: (i) several fast registers that are accessible by each stream processor, (ii) a multiprocessor-level memory that is shared between all the cores that compose the multiprocessor, and (iii) a global memory shared between all the multiprocessors.

As we can observe in Figure 3, CUDA maintains the hierarchy of memories at the same time that provides a programming model which abstracts the system of cores and multiprocessors into a three-level logical representation of threads, blocks and grids, where the thread is the minimum processing unit (that can be grouped into 1D/2D/3D blocks of warps), and the blocks can be organized into a 1D/2D grid environment. In this sense, the programmer determines the logical representation by organizing the structure of the threads in the grid that best fits the data structure handled by the problem to be parallelized. Underneath, CUDA maps this representation to the actual hardware resources. This distinction between physical and logical representations allows CUDA-based algorithms to be ported to any NVIDIA GPU platform, improving their scalability and computing performance as new and higher-capacity GPUs are released to the market. In addition, it should be highlighted that each thread has access to three different memory spaces: its local memory, the memory shared by all the threads of the same block, and the global memory shared by all the threads of the grid. Therefore the correct handling of the threads and their accesses to memory are fundamental for the correct and optimal parallelization of the problem.

Through the organization and synchronization of the threads, we can develop the parallel processing of the operations carried out by the SVM method. In particular, we can differentiate between those operations performed during the training stage of the SVM and those operations performed during the inference step.

3.3. Parallel SMO during the Training Stage

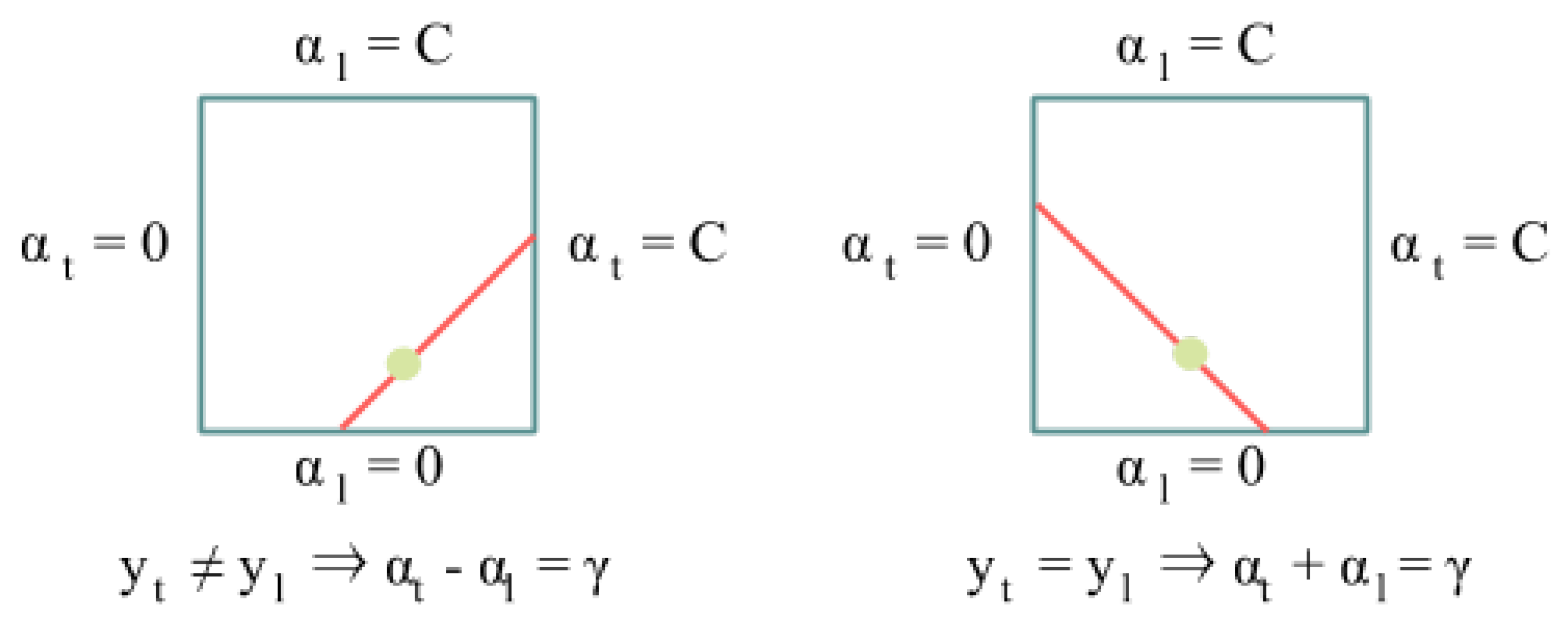
3.3.1. Previous Concepts about the SMO Algorithm

As pointed out before, we adopted the one-against-one approach for the multi-class SVM to perform remote sensing HSI data classification. Therefore $n_c(n_c-1)/2$ binary models must be properly trained to extract the support vectors and derive the corresponding Lagrange multipliers for each classifier. In particular, the binary models were trained using a decomposition method to solve the convex optimization problem defined by Equation (7). It is noticeable that the main difficulty when solving Equation (7) is how to calculate the kernel matrix $\mathbf{K}\in {\mathbb{R}}^{n_t\times n_t}$ that stores the kernel values $K({\mathbf{x}}_i,{\mathbf{x}}_j)$, $\forall i\in [1,n_t]$ and $\forall j\in [1,n_t]$, as:

$$\mathbf{K}=\left(\begin{array}{cccc}K({\mathbf{x}}_1,{\mathbf{x}}_1)& K({\mathbf{x}}_1,{\mathbf{x}}_2)& \cdots & K({\mathbf{x}}_1,{\mathbf{x}}_{n_t})\\ K({\mathbf{x}}_2,{\mathbf{x}}_1)& K({\mathbf{x}}_2,{\mathbf{x}}_2)& \cdots & K({\mathbf{x}}_2,{\mathbf{x}}_{n_t})\\ ⋮& ⋮& \ddots & ⋮\\ K({\mathbf{x}}_{n_t},{\mathbf{x}}_1)& K({\mathbf{x}}_{n_t},{\mathbf{x}}_2)& \cdots & K({\mathbf{x}}_{n_t},{\mathbf{x}}_{n_t})\end{array}\right)$$

Usually, $\mathbf{K}$ is a dense matrix and may be too difficult to be efficiently stored and handled if $n_t$ is too large. To deal with this limitation, some decomposition methods were designed [46,47,65,66,67,68,69,70,71,72,73,74] to break down the problem into several smaller and easier to handle sub-problems, where small subsets of Lagrange variables $\alpha$ are modified by employing some columns of $\mathbf{K}$ instead of the entire matrix. In particular, the SMO [46] algorithm has been considered in this work.

The SMO is a simple and iterative algorithm that allows for the quick and effective resolution of very large QP problems (such as those involved in the SVM calculations) by decomposing such overall QP problem into smaller QP sub-problems [45], which are solved analytically without the need for numerical optimization. It solves the optimization problem described by Equations (3) and (7), by solving the smallest possible optimization problem at every step until the optimal condition of the SVM classifier is reached. As the linear equality constraint ${\displaystyle \sum _{i=1}^{n_t}{y}_i{\alpha }_i=0}$ involves the Lagrange multipliers ${\alpha }_i$, the smallest possible optimization problem will involve two such multipliers, in the sense that, if we change one ${\alpha }_t$ by an amount in either direction, then the same change must be applied to another ${\alpha }_l$ in the opposite direction. That is, ${\alpha }_t$ and ${\alpha }_l$ should be on the same line in order to maintain the constraint (see Figure 4):

$$y_t{\alpha }_t+y_l{\alpha }_l=y_t{\widehat{\alpha }}_t+y_l{\widehat{\alpha }}_l,\mathrm{subject} \mathrm{to}{\alpha }_t\ge 0\mathrm{and}{\alpha }_l\ge C$$

(10)

In this way, the SMO algorithm comprises two main components: (i) a heuristic for selecting the pair of Lagrange multipliers to be optimized, and (ii) an analytic method for solving those multipliers. In this sense, in each iteration the SMO algorithm heuristically chooses two Lagrange multipliers ${\alpha }_t$ and ${\alpha }_l$ at every step to jointly optimize, then it analytically obtains the new optimal values ${\widehat{\alpha }}_t$ and ${\widehat{\alpha }}_l$, and finally it updates the SVM to reflect the new values.

Focusing on the heuristic procedure, the SMO applies two heuristic searches, one for each Lagrange multiplier. The first multiplier ${\alpha }_t$ is chosen by iterating over the entire training set, looking for those samples that violate the Karush-Kuhn-Tucker (KKT) conditions [75] that help to find an optimal separating hyperplane. In particular, the KKT conditions for Equation (7) are:

$$\begin{array}{c}\hfill {\alpha }_i=0\iff y_i(\mathbf{w}{\mathbf{x}}_i+b)\ge 1,\\ \hfill C>{\alpha }_i<0\iff y_i(\mathbf{w}{\mathbf{x}}_i+b)=1,\\ \hfill {\alpha }_i=C\iff y_i(\mathbf{w}{\mathbf{x}}_i+b)\le 1\end{array}$$

(11)

where $y_i$ is the correct SVM output and $(\mathbf{w}{\mathbf{x}}_i+b)$ is the current output of the SVM for the i-th sample ${\mathbf{x}}_i$, $\forall i\in [1,n_t]$. Any ${\alpha }_i$ that satisfies the KKT conditions will be an optimal solution for the QP optimization problem defined by Equation (7). On the contrary, any ${\alpha }_i$ that violates the KKT conditions will be eligible for optimization, so the SMO’s goal is to iterate until all these conditions are satisfied within a tolerance threshold (in our case, this tolerance has been set to 0.001). Once the first ${\alpha }_t$ has been chosen, the second Lagrange multiplier ${\alpha }_l$ is selected in order to maximize the size of the step taken during joint optimization. To do this, the SMO method implements an optimality indicator vector$\mathbf{E}=[E_1,E_2,\cdots ,E_{n_t}]$, where each $E_j$ is the optimality indicator of the j-th training sample, i.e., the classification errors on the j-th sample:

$$E_j=f\left({\mathbf{x}}_j\right)-y_j=\left({\displaystyle \sum _{i=1}^{n_t}{\alpha }_i{y}_{i}K({\mathbf{x}}_i,{\mathbf{x}}_j)+b}\right)-y_j$$

(12)

Related to this, ${\alpha }_t$ and ${\alpha }_l$ can be selected by looking for those samples ${\mathbf{x}}_t$ and ${\mathbf{x}}_l$ that have the maximum and minimum optimality indicators that maximize $|E_t-E_l|$, so if $E_t$ is positive, the SMO will choose a sample with minimum $E_l$, while if $E_t$ is negative, the SMO will select a sample with maximum $E_l$. The desired indexes t and l can be directly obtained by computing Equation (13) [67]:

$$\begin{array}{c}\hfill t=arg\underset{i}{min}\left\{E_i\right|{\mathbf{x}}_i\in {\mathcal{X}}_{upper}\}\\ \hfill l=arg\underset{i}{max}\left\{\frac{{(E_t-E_i)}^2}{{\mu }_i}|E_t<E_i,{\mathbf{x}}_i\in {\mathcal{X}}_{lower}\right\}\end{array}$$

(13)

where ${\mu }_i=K({\mathbf{x}}_t,{\mathbf{x}}_t)+K({\mathbf{x}}_i,{\mathbf{x}}_i)-2K({\mathbf{x}}_t,{\mathbf{x}}_i)$, $E_t$ and $E_i$ are the optimality indicator of samples ${\mathbf{x}}_t$ and ${\mathbf{x}}_i$, respectively, and ${\mathcal{X}}_{upper}={\mathcal{X}}_1\cup {\mathcal{X}}_2\cup {\mathcal{X}}_3$ and ${\mathcal{X}}_{lower}={\mathcal{X}}_1\cup {\mathcal{X}}_4\cup {\mathcal{X}}_5$ are two data subsets, where each ${\mathcal{X}}_{\ast }$ is composed by the following training samples:

$$\begin{array}{c}\hfill {\mathcal{X}}_1=\left\{{\mathbf{x}}_i\right|{\mathbf{x}}_i\in \mathbf{X},0<{\alpha }_i<C\}\\ \hfill {\mathcal{X}}_2=\left\{{\mathbf{x}}_i\right|{\mathbf{x}}_i\in \mathbf{X},y_i=+1,{\alpha }_i=0\}\\ \hfill {\mathcal{X}}_3=\left\{{\mathbf{x}}_i\right|{\mathbf{x}}_i\in \mathbf{X},y_i=-1,{\alpha }_i=C\}\\ \hfill {\mathcal{X}}_4=\left\{{\mathbf{x}}_i\right|{\mathbf{x}}_i\in \mathbf{X},y_i=+1,{\alpha }_i=C\}\\ \hfill {\mathcal{X}}_5=\left\{{\mathbf{x}}_i\right|{\mathbf{x}}_i\in \mathbf{X},y_i=-1,{\alpha }_i=0\}\end{array}$$

Once both Lagrange multipliers have been obtained, the SMO method will compute their optimal values ${\widehat{\alpha }}_t$ and ${\widehat{\alpha }}_l$ with the aim of obtaining the optimal class-separating hyperplane. In particular, it begins by calculating ${\widehat{\alpha }}_l$, whose feasible values are framed into the constraint $U\le {\widehat{\alpha }}_l\le V$ to meet the original $C\ge {\alpha }_l\ge 0$, being U and V two boundaries defined as:

$$If{y}_t\ne y_l\left\{\begin{array}{c}U=max\{0,{\alpha }_l-{\alpha }_t\}\hfill \\ V=min\{C,C-{\alpha }_t+{\alpha }_l\}\hfill \end{array}\right.$$

(14)

$$If{y}_t=y_l\left\{\begin{array}{c}U=max\{0,{\alpha }_t+{\alpha }_l-C\}\hfill \\ V=min\{C,{\alpha }_t+{\alpha }_l\}\hfill \end{array}\right.$$

(15)

Besides, the optimal $\widehat{{\alpha }_l}$ value within the range $[U,V]$ will be obtained as:

$${\widehat{\alpha }}_l=\left\{\begin{array}{cc}V,\hfill & \mathrm{if}{\tilde{\alpha }}_l>V\hfill \\ {\tilde{\alpha }}_j,\hfill & \mathrm{if}V\ge {\tilde{\alpha }}_l\ge U\hfill \\ U,\hfill & \mathrm{if}{\tilde{\alpha }}_l<U\hfill \end{array}\right.\mathrm{being}{\tilde{\alpha }}_l={\alpha }_l+\frac{y_l(E_t-E_l)}{\mu }$$

(16)

where $\mu =K({\mathbf{x}}_t,{\mathbf{x}}_t)+K({\mathbf{x}}_l,{\mathbf{x}}_l)-2K({\mathbf{x}}_t,{\mathbf{x}}_l)$ and $E_t$ and $E_l$ are the classification errors on the t-th and l-th training samples respectively. Once ${\widehat{\alpha }}_l$ has been obtained, an optimal ${\widehat{\alpha }}_t$ is easily calculated as:

$${\widehat{\alpha }}_t={\alpha }_t+y_t{y}_l\left({\alpha }_l-{\widehat{\alpha }}_l\right)$$

(17)

Once ${\widehat{\alpha }}_t$ and ${\widehat{\alpha }}_l$ have been obtained, the SMO updates the bias threshold b such that the KKT conditions are satisfied for the t-th and l-th samples. In this sense, three cases can occur, as we can observe in Equation (18):

$$\widehat{b}=\left\{\begin{array}{cc}{\widehat{b}}_1\hfill & \mathrm{if}C>{\alpha }_t>0\hfill \\ {\widehat{b}}_2\hfill & \mathrm{if}C>{\alpha }_l>0\hfill \\ \frac{({\widehat{b}}_1+{\widehat{b}}_2)}{2}\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(18)

where ${\widehat{b}}_1$ and ${\widehat{b}}_2$ are defined as follows:

$$\begin{array}{c}\hfill {\widehat{b}}_1=b-E_t-y_t({\widehat{\alpha }}_t-{\alpha }_t)K({\mathbf{x}}_t,{\mathbf{x}}_t)-y_l({\widehat{\alpha }}_l-{\alpha }_l)K({\mathbf{x}}_t,{\mathbf{x}}_l)\\ \hfill {\widehat{b}}_2=b-E_l-y_t({\widehat{\alpha }}_t-{\alpha }_t)K({\mathbf{x}}_t,{\mathbf{x}}_l)-y_l({\widehat{\alpha }}_l-{\alpha }_l)K({\mathbf{x}}_l,{\mathbf{x}}_l)\end{array}$$

Finally, the SMO updates the SVM. For each training sample ${\mathbf{x}}_i$, the SMO updates its $E_i$ using the following Equation (19):

$$E_i=E_i+({\widehat{\alpha }}_t-{\alpha }_t)y_{t}K({\mathbf{x}}_t,{\mathbf{x}}_i)+\left({\widehat{\alpha }}_l\right)y_{l}K({\mathbf{x}}_l,{\mathbf{x}}_i)$$

(19)

The full procedure is repeated until the optimal condition is reached, i.e., $E_t\ge E_{max}$, where $E_{max}$ acts as a threshold, $E_{max}=max\left\{E_i\right|{\mathbf{x}}_i\in {\mathcal{X}}_{lower}\}$.

3.3.2. CUDA Optimization of SMO Algorithm

The SVM starts by dividing the HSI scene into training and inference subsets. We can consider the training set as a collection of instances and their associated labels, i.e., ${\mathcal{D}}_{train}=\{\mathbf{X},\mathbf{Y}\}$. The training instances are represented by a 2D-matrix $\mathbf{X}\in {\mathbb{N}}^{n_t\times n_b}$ composed by $n_t$ training vectors, where each ${\mathbf{x}}_i\in {\mathbb{N}}^{n_b}=[x_{i,1},x_{i,2},\cdots ,x_{i,n_b}]$ comprises $n_b$ spectral bands, while the training labels are stored into the matrix $\mathbf{Y}\in {\mathbb{N}}^{n_t\times n_c}$, being ${\mathbf{y}}_i=[y_{i,1},y_{i,2},\cdots ,y_{i,n_c}]$ the corresponding label of sample ${\mathbf{x}}_i$ in one-hot encoding, where $n_c$ indicates the number of different land cover classes. The training stage starts by creating the different single binary SVMs in a sequential way, confronting each class i to each different class j, $\forall i,j\in [1,n_c]$. Each binary SVM was optimized by employing a parallel SMO solver.

The parallel SMO solver begins by creating its working set B. Traditionally, B is of size two; however, our proposal implements a bigger working set to solve in parallel multiple subproblems of SMO in a batch. Moreover, the proposed implementation precomputes all the kernel values for the current working set, storing them as a data buffer on the device’s global memory, in order to reduce the high latency memory accesses and also to avoid a large number of small read/write operations in the CPU memory. This implies that in each iteration of the SMO algorithm, the current working batch B will be updated, being $n_B$ Lagrange multipliers optimized. This allows us to compute (at once) $n_B$ rows of the kernel matrix $\mathbf{K}$, performing a more efficient use of the GPU by reducing the number of accesses to the device’s global memory (which is much slower than the shared memory) and enabling the re-use of kernel information (which in turn, reduces repeated kernel value computations). Taking this into account, our parallel SMO solver can be divided into three different steps.

During the step 1, the parallel SMO solver looks for the $n_B$ extreme training instances which can potentially improve the SVM the most according to Equation (9). This is parallelized by applying consecutive parallel reductions [76] over the training samples. For each working set, the optimality indicators of the training samples are sorted in ascending order, selecting the first $n_B/2$ and the last $n_B/2$ training samples to optimize the corresponding $n_B$ Lagrangre multipliers. During the reduction, one thread per sample takes the data from the global device memory to the block shared memory (in a coalesced way) to perform a fast execution. It must be noted that shared memory is around 7 times faster than global memory. Once synchronized, the threads operates over the data, where each one takes and compares the optimality indicators of the samples from the batch, choosing the smaller or the larger one depending on the desired Lagrange multiplier through the application of the corresponding heuristics given by Equation (13).

Once the $n_B$ Lagrange multipliers have been selected, the improvements of the Lagrangian multiplier pair ${\alpha }_t$ and ${\alpha }_l$ are sequentially obtained by one GPU thread per pair (step 2). It is worth noting from previous Equations (13), (16) and (19) that, during training stage, the same kernel values may be used in indifferent iterations. This implies that some kernel values can be stored into the GPU memory with the aim of reducing the high latency memory and avoiding a large number of small read/write operations from the CPU memory. In this sense, all the kernel values related to the $n_B$ Lagrange multipliers are obtained, computing $n_B$ rows of the kernel matrix $\mathbf{K}$ through parallel matrix multiplications [77,78]:

$${\mathbf{K}}_B=\left(\begin{array}{cccc}K({\mathbf{x}}_1,{\mathbf{x}}_1)& K({\mathbf{x}}_1,{\mathbf{x}}_2)& \cdots & K({\mathbf{x}}_1,{\mathbf{x}}_{n_t})\\ K({\mathbf{x}}_2,{\mathbf{x}}_1)& K({\mathbf{x}}_2,{\mathbf{x}}_2)& \cdots & K({\mathbf{x}}_2,{\mathbf{x}}_{n_t})\\ ⋮& ⋮& \ddots & ⋮\\ K({\mathbf{x}}_{n_B},{\mathbf{x}}_1)& K({\mathbf{x}}_{n_B},{\mathbf{x}}_2)& \cdots & K({\mathbf{x}}_{n_B},{\mathbf{x}}_{n_t})\end{array}\right)$$

In particular, the RBF-based ${\mathbf{K}}_B$ matrix is computed in parallel by the GPU and stored into the device’s global memory. Algorithm 1 provides the pseudo-code of the parallel kernel RBF function, which were implemented following the approximate RBF kernel form:

$$K({\mathbf{x}}_i,{\mathbf{x}}_j)=exp\left(-\gamma \Vert {\mathbf{x}}_i-{\mathbf{x}}_j{\Vert }^2\right)=exp\left(-\gamma \left(\Vert {\mathbf{x}}_i{\Vert }^2+{\Vert {\mathbf{x}}_j\Vert }^2-2{\mathbf{x}}_i{\mathbf{x}}_j\right)\right)$$

(20)

In this context, the input parameters $xx$ and $x2x$ contain the $\left|\right|{\mathbf{x}}_i{\left|\right|}^2$, $\forall i\in [1,\cdots ,n_B]$ and ${\mathbf{x}}_i{\mathbf{x}}_j$, $\forall i,j\in [1,\cdots ,n_B]$ values respectively, which were previously computed through parallel matrix multiplications [78]. Then, $n_B$ threads compute the desired $n_B$ rows of the kernel matrix ${\mathbf{K}}_B$:

Algorithm 1 Parallel Kernel RBF for HSI classification

Require:$xx$ matrix of $\left|\right|{\mathbf{x}}_i{\left|\right|}^2$ values,

$x2x$ matrix of ${\mathbf{x}}_i{\mathbf{x}}_j$ values,

$K_B$ resulting kernel matrix,

$n_B$ number of rows,

$n_t$ number of training samples.

$i=blockIdx.x\ast blockDim.x+threadIdx.x$

if $idx<n_B$ then

$j=0$

while $j<n_t$ do

$K_B[i,j]=exp(-\gamma (xx\left[i\right]+xx\left[j\right]-2\ast x2x[i,j]))$

$j++$

end while

end if

During the training stage, the kernel values are extracted from the global memory and gathered into the shared memory as they are needed, avoiding repeated computations.

Finally, the parallel SMO solver updates the optimality indicator vector $\mathbf{E}$ of the training instances by launching $n_t$ GPU threads that compute Equation (14) in parallel (step 3).

These training steps are sequentially repeated until the optimality condition is met or when the SVM classifier is not able to improve.

3.4. Parallel Classification during the Inference Stage

The proposed one-against-all SVM for HSI remote sensing data multi-class classification provides the corresponding label $y_i$ of a given test sample ${\mathbf{x}}_i$ by applying Equation (8) during the inference stage. In this sense, Equation (8) is computed in parallel, making use of the kernel values in $\mathbf{K}$ to reduce the latency memory and avoid the repeated computations. Also, from Equation (6) we can observe that $K({\mathbf{x}}_i,{\mathbf{x}}_j)$ is the same that $K({\mathbf{x}}_j,{\mathbf{x}}_i)$, where i and j are related to the number of test samples and support vectors, respectively. In this sense, we can reduce the number or read/copy operations into the GPU memory following two strategies. On the one hand, if the number of test samples is larger than the number of support vectors, we read all the rows of the kernel matrix $\mathbf{K}$ that correspond to the support vectors by reading the indexes respected to j. On the other hand, if the number of support vectors is larger than the number of test samples, those rows that correspond to the test samples will be read by reading the indexes respected to i.

4. Experimental Results

4.1. Experimental Environment

To evaluate the performance and the benefits of the proposed parallel SVM for HSI remote sensing data classification, several implementations of the proposed classifier were developed and tested over two different hardware platforms:

• Platform 1: it is composed by an Intel Core Coffee Lake Refresh i7-9750H processor, 32 GB of DDR4 RAM with 2667 MHz, and an NVIDIA GeForce RTX 2070 with 8 GB of RAM, graphic clock at 2100 MHz and 14,000 MHZ of memory transfer rate. It is equipped with 2304 CUDA cores. These processors were named CPU0 and GPU0.
• Platform 2: Intel i9-9940X processor, 128 GB of DDR4 RAM with 2100 MHz, and an NVIDIA GTX 1080Ti with 11 GB of RAM, 2037 MHz of graphic clock and 11,232 MHz of memory transfer rate. It is equipped with 3584 CUDA cores. These processors were named CPU1 and GPU1.

CPU1 will serve as the baseline for the performance comparisons that were conducted during the experimentation due to its characteristics. Moreover, both environments use Ubuntu 18.04.3 x64 as operating system.

4.2. Hyperspectral Datasets

Our experiments were conducted over six different and well-known HSI scenes: Indian Pines and Big Indian Pines, Pavia University, Salinas Valley and University of Houston. Figure 5 shows the ground truth and the number of pixels per class for each image. Below, the characteristics of each scene are provided.

• The first dataset is known as Indian Pines, which was collected by the Airborne Visible Infra-Red Imaging Spectrometer (AVIRIS) [79] over the Indian Pines test site in North-western Indiana, which is characterized by several agricultural crops and irregular forest and pasture areas. It has $145\times 145$ pixels, each of which has 224 spectral reflectance bands covering the wavelengths from 400 nm to 2500 nm. We remove the bands 104–108, 150–163 and 220 (water absorption and null bands), and keep 200 bands in our experiments. This scene has 16 different ground-truth classes (see Figure 5).
• Big Indian Pines is a larger version of the first dataset, which has $2678\times 614$ pixels with wavelengths ranging from 400 nm to 2500 nm. We also remove the water absorption and null bands, retaining 200 spectral bands in our experiments. This scene has 58 ground-truth classes (see Figure 5).
• The third dataset is the Pavia University scene, which was collected by the Reflective Optics Spectrographic Imaging System (ROSIS) [80] during a flight campaign over Pavia, nothern Italy. In this sense, it is characterized by being an urban area, with areas of buildings, roads and parking lots. In particular, the Pavia University scene has $610\times 340$ pixels, and its spatial resolution is 1.3 m. The original pavia dataset contains 115 bands in the spectral region of 0.43–0.86 $\mathsf{\mu }$m. We remove the water absorption bands, and retain 103 bands in our experiments. The number of classes in this scene is 9 (see Figure 5).
• The fourth dataset is Pavia Centre and was also gathered by ROSIS sensor. It is composed by $1096\times 1096$ pixels and 102 spectral bands. This scene also has 9 ground-truth classes from an urban area (see Figure 5).
• The fifth dataset is Houston University [81], which was acquired by the Compact Airborne Spectrographic Imager (CASI) sensor [82] over the Houston University campus in June 2012, collecting spectral information from an urban area. This scene has 114 bands and 349 × 1905 pixels with wavelengths ranging from 380nm to 1050nm. It comprises 15 ground-truth classes (see Figure 5).
• Finally, the sixth dataset is Salinas Valley, which was also acquired by AVIRIS sensor over an agricultural area. It has 512 ×217 pixels and covers Salinas Valley in California. We remove the water absorption bands 108–112, 154–167 and 224, and keep 204 bands in our experiments. This scene contains 16 classes (see Figure 5).

4.3. Performance Evaluation

With the aim of evaluating the computational performance obtained by the proposed GPU implementation of SVMs for HSI data classification, and making a thorough analysis of the implemented classifiers also in terms of accuracy, several experiments were carried out:

• The first experiment focuses on the classification accuracy obtained by our GPU implementation as compared to a standard (CPU) implementation in LibSVM [83]. In particular, proposed GPU-SVM was compared with its CPU counterpart, the random forest (RF) [40] and the multinomial logistic regression (MLR) [40].
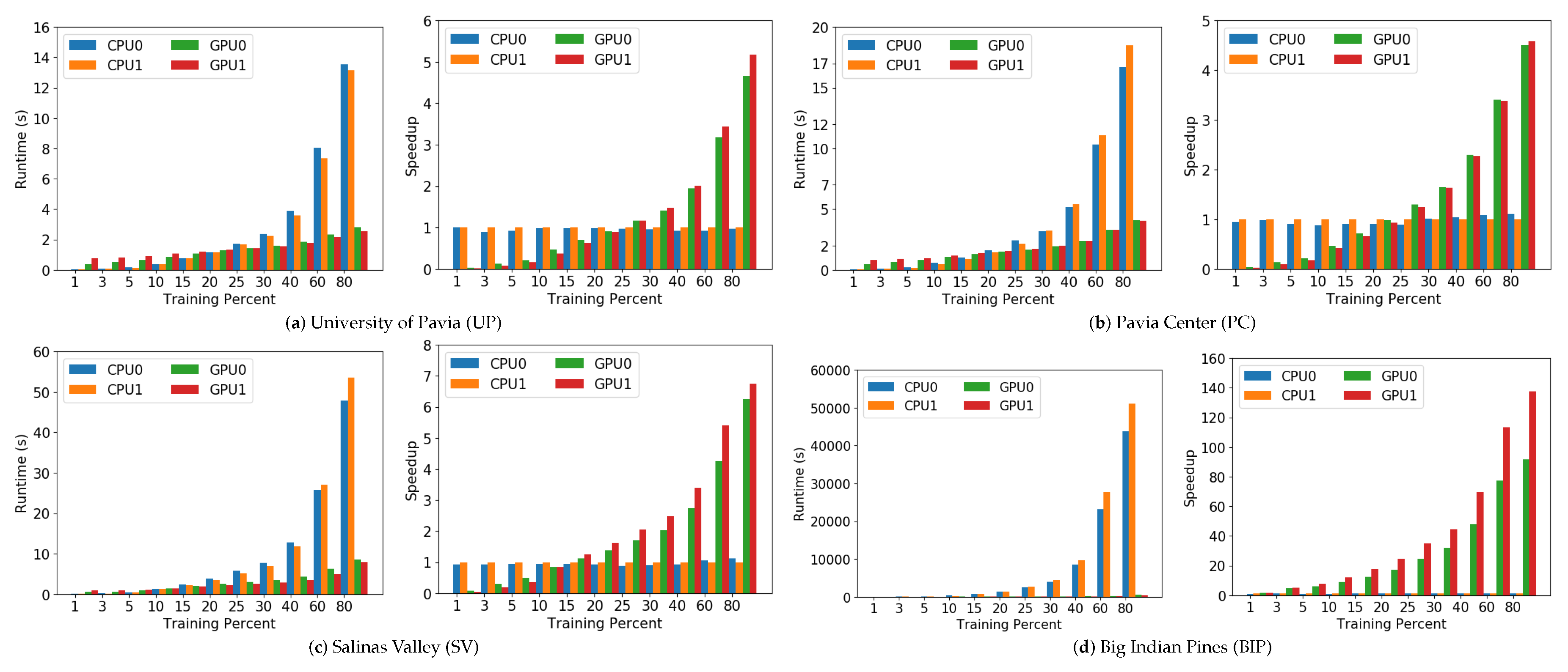
• The second experiment focuses on the scalability and speedups achieved by the GPU implementation with regards to the CPU implementation, from a global perspective. As we pointed before, CPU1 will be considered to be the baseline due its characteristics that make it the slowest device.
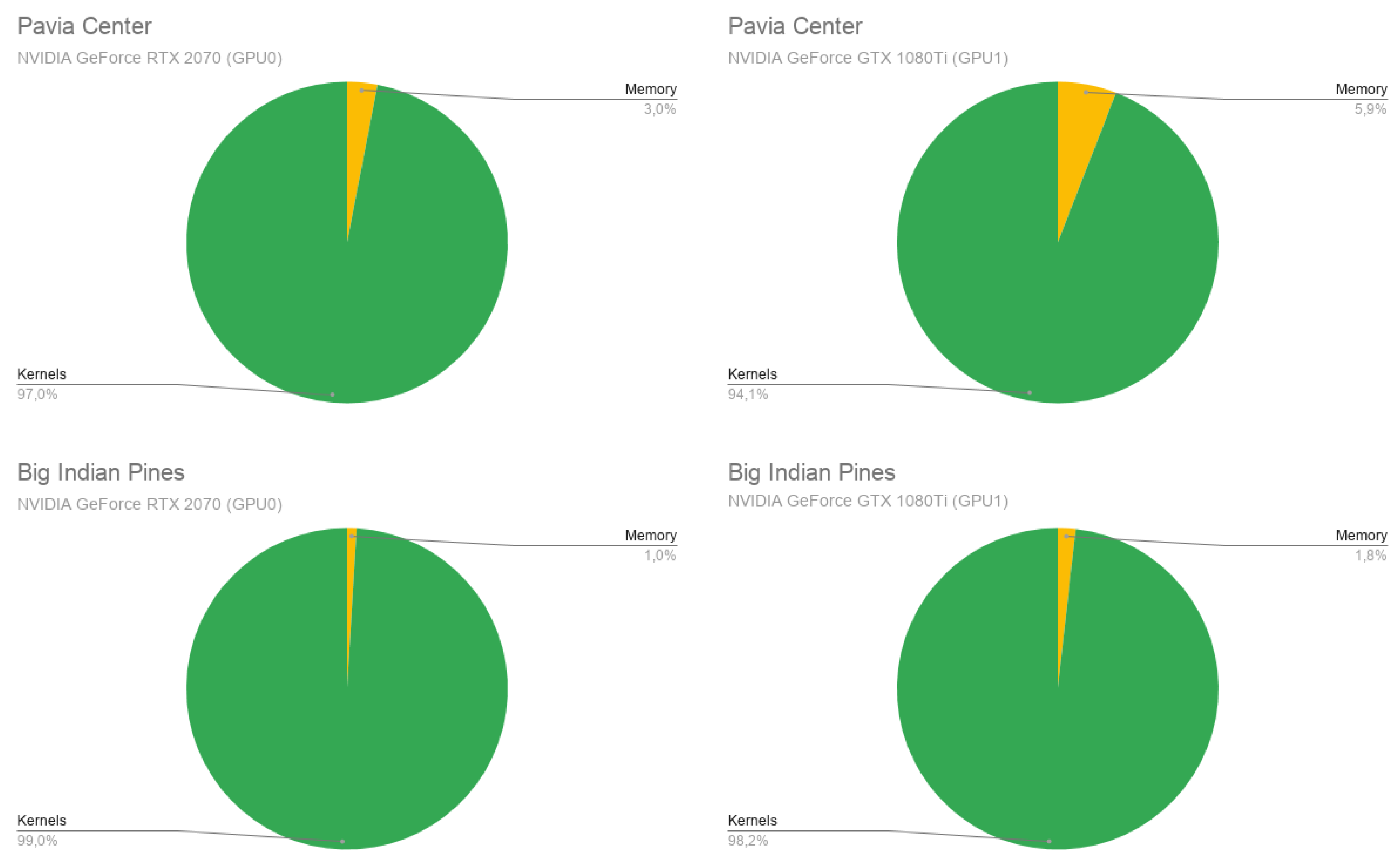
• The third and last experiment focuses on some specific aspects of the GPU implementation, including data-transfer times.

In the following, we describe in detail the results obtained in each of the aforementioned experiments.

4.3.1. Experiment 1: Accuracy Performance

In this experiment, we use the fixed training and test data for the AVIRIS Indian Pines image [displayed in Figure 6c,d], the ROSIS Pavia University image [displayed in Figure 7c,d] and the University of Houston image [Figure 8c,d]. These fixed training and test sets are publicly available online from the IEEE Geoscience and Remote Sensing Society (GRSS) data and algorithm evaluation website (DASE) at http://dase.grss-ieee.org. The main rationale for using these fixed training sets is that all algorithms can be compared in a fair way, regardless of random splits of training and test sets.

The obtained classification results can be graphically observed in Figure 6 and Figure 8. In particular, Figure 6a, Figure 7a and Figure 8a respectively show false color compositions of the aforementioned three images, while Figure 6b, Figure 7b and Figure 8b show the entire ground-truth data for each image. The results obtained by two well-known classifiers: RF [see Figure 6e, Figure 7e and Figure 8e] and the multinomial logistic regression (MLR) [see Figure 6f, Figure 7f and Figure 8f] are reported, together with the classification maps obtained by the CPU (LibSVM) implementation of the SVM [see Figure 6g, Figure 7g and Figure 8g] and our GPU implementation of SVM [see Figure 6h, Figure 7h and Figure 8h]. Although all classification maps have the typical “salt and pepper” noise of spectral classifiers, we can see that SVM classifiers achieve a higher quality map by classifying certain regions of the scenes more precisely, for instance the Soybeans-notill and Oats land-covers in Indian Pines scene or the the tree-line areas of Pavia University. Moreover, those classification maps obtained by CPU-based SVM and GPU-based SVM are quite similar.

The individual class accuracies are reported on

Table 2. Classification results obtained by different techniques for the Indian Pines, University of Pavia and University of Houston scenes, using the fixed training and test sets available for these datasets in http://dase.grss-ieee.org.

	Indian Pines				University of Pavia				Houston University
Class	RF	MLR			RF	MLR			RF	MLR
			SVM				SVM				SVM
	[40]	[40]	CPU	GPU	[40]	[40]	CPU	GPU	[40]	[40]	CPU	GPU
1	32.80	68.0	88.0	88.0	79.59	77.7	83.08	81.85	82.55	82.24	82.34	82.15
2	51.56	78.07	80.74	79.32	55.2	58.78	67.45	67.2	83.5	82.5	83.36	83.36
3	44.41	59.41	67.57	67.43	45.42	67.22	64.85	65.0	97.94	99.8	99.8	99.8
4	26.46	25.25	51.52	49.9	98.73	74.29	98.28	98.35	91.46	98.3	98.96	97.86
5	79.34	88.32	87.23	86.28	99.14	98.88	99.28	99.3	96.69	97.44	98.77	98.6
6	95.71	96.89	96.61	96.67	78.77	93.52	92.06	92.3	99.16	94.41	97.9	96.78
7	20.0	50.0	100.0	100.0	80.41	85.12	88.89	88.95	75.35	73.41	77.43	75.95
8	100.0	99.2	98.8	98.8	90.96	87.58	92.12	92.31	33.03	63.82	60.3	57.78
9	16.0	40.0	60.0	50.0	97.69	99.22	96.35	96.6	69.2	70.25	76.77	77.88
10	8.47	56.14	81.71	82.03					43.9	55.6	61.29	61.56
11	89.63	81.64	86.95	87.77					69.79	74.19	80.55	81.2
12	26.6	68.44	77.66	77.94					54.12	70.41	79.92	80.65
13	89.25	96.25	93.75	94.25					59.86	67.72	70.88	72.56
14	92.0	89.95	90.64	90.83					99.35	98.79	100.0	100.0
15	38.79	82.83	76.77	81.21					97.42	95.56	96.41	97.42
16	93.64	93.18	88.64	88.64
OA	65.69	78.16	84.21	84.25	70.15	72.23	78.91	78.67	72.97	78.98	81.86	81.69
AA	56.54	73.35	82.91	82.44	80.66	82.48	86.93	86.87	76.89	81.63	84.31	84.24
K(x100)	59.87	74.99	81.98	82.0	63.01	65.45	73.37	73.09	70.96	77.31	80.43	80.25

. Also the overall (OA), average (AA) accuracies and kappa coefficient are shown for each HSI dataset. We can observe that the CPU and GPU implementations of the SVM classifier reach the best OA and AA percentages in all datasets, exhibiting also the best kappa value. In particular, as shown in all cases, the OA obtained by our GPU implementation of SVM is very similar to that obtained by the corresponding CPU implementation, and superior to that obtained by other well-known classifiers such as RF and MLR.

4.3.2. Experiment 2: Scalability and Speedup

In this experiment, we used randomly selected training/test sets to evaluate the scalability of our GPU implementation as the amount of training becomes larger. In particular, 1%, 3%, 5%, 10%, 15%, 20%, 25%, 30%, 40%, 60% and 80% of training data were considered for the University of Pavia, Pavia Center, Salinas Valley and Big Indian Pines datasets.

Figure 9 reports the processing times (and speedups) measured in the considered CPUs (CPU0 in the first hardware platform and CPU1 in the second platform) and GPUs (GPU0 in the platform 1 and GPU1 in the platform 2) as the percentage of training increases. As we can observe in Figure 9, for all the considered images in this experiment (University of Pavia, Pavia Center, Salinas Valley and Big Indian Pines), the processing times increase as the percentage of training samples increases. This is expected, as the complexity of the classification problem becomes larger. However, we can also observe that the speedups obtained become more significant with the training size, particularly for the larger images. For instance, with University of Pavia (about 34,220 pixels when training with 80% of data) the implementation is able to reach a speedup of x6 with the fastest GPU, while with Big Indian Pines (around 1,315,433 samples when considering 80% of training data) is x140 faster than the baseline. This indicates that our newly developed GPU implementation of SVM scales with complexity and problem size, which is a highly desirable feature in parallel implementations.

4.3.3. Experiment 3: GPU Transfer-Memory and Kernel Runtimes

In this experiment, we fix the training percentage to 40% and study the memory transfers required by the proposed GPU implementation for different HSI datasets over GPU0 and GPU1 devices. Here, we specifically focus on the two largest datasets (Pavia Center and Big Indian Pines) and report the memory times consumed by the considered GPU platforms.

Table 3. Processing times (ms) obtained by our GPU implementation of the SVM algorithm on different platforms, using the datasets: Pavia Center and Big Indian Pines. The times indicate the transfers from host to device (HtoD), device to host (DtoH), device to device (DtoD) and the total processing times consumed by the kernels.

PAVIA CENTER
	NVIDIA GeForce RTX 2070 (Laptop)				NVIDIA GeForce GTX 1080Ti (Desktop)
Tr Percent	HtoD	DtoH	DtoD	Kernels	HtoD	DtoH	DtoD	Kernels
1	1.900800	1.008450	0.401280	89.683510	2.065540	0.909663	0.401824	53.969180
5	5.196410	1.211910	0.389169	342.75209	5.928330	1.308890	0.445162	192.82042
10	9.650360	1.710720	0.404029	588.11514	11.10364	1.798470	0.448121	292.20041
20	18.90792	2.658750	0.405595	845.38273	22.65927	2.731010	0.465384	503.46422
40	37.78842	4.761070	0.444797	1369.8100	45.99625	4.856580	0.505738	816.56403
60	56.83977	6.937100	0.483709	1924.3700	71.39292	6.930210	0.506987	1180.4300
80	77.18297	9.077530	0.476379	2425.9400	95.87500	9.032700	0.547660	1448.0500
BIG INDIAN PINES
	NVIDIA GeForce RTX 2070 (Laptop)				NVIDIA GeForce GTX 1080Ti (Desktop)
Tr Percent	HtoD	DtoH	DtoD	Kernels	HtoD	DtoH	DtoD	Kernels
1	72.270610	44.041780	20.12548	2167.8800	86.874980	45.894420	23.89330	2445.0100
5	189.45379	53.012700	21.65845	15000.320	215.96618	56.352320	25.65502	10679.120
10	345.04000	68.476270	23.63760	34717.630	395.10834	71.718340	27.34729	22486.610
20	683.13051	118.78844	29.17641	77072.650	813.34057	123.31494	32.40953	46963.590
40	1439.0210	296.14766	43.88958	184683.75	1703.9300	301.14840	46.36005	112824.33
60	2325.2100	579.43225	60.25476	335392.10	2868.1800	581.19374	61.65440	255449.66
80	3296.8700	969.39610	68.03797	519363.01	4077.2100	972.86474	77.46072	307944.21

provides a breakdown of the obtained processing times for different images and training percentages, indicating the transfer times from host to device (HtoD), device to host (DtoH), device to device (DtoD) and the time taken by the kernels. The times reported on Table 3 indicate that most of the time spent by our parallel implementation is consumed by kernels and not by data transfers, despite these transfers become more significant as the training percentage becomes larger (this does not affect scalability, as reported in Figure 9. We can graphically observe these results in Figure 10, where the amount of GPU video memory required by our implementation is very small in all cases (below 5.9%), which indicates that our implementation is efficient in terms of memory usage, even with large percentages of training.

5. Conclusions and Future Lines

This work presented a new GPU implementation of the well-known SVM technique in the context of HSI remote sensing data classification, with the goal of reducing computation times by massively parallelizing operations across GPU threads, and reducing memory latencies by efficiently handling data read/write operations. Three experiments were conducted over six widely used and real HSI datasets, providing very heterogeneous information in terms of content (different land-cover classes extracted from agricultural and urban environments) and amount of data (different spatial sizes with also different spatial resolutions). These experiments show the effectiveness of our accelerated SVM implementation, which not only scales with data volume, but also with training percentage. This reveals that the acceleration is more effective when the classification problem is more complex. Moreover, the study of data transfer times and algorithmic computation times shows an efficient use of memory, where the kernel computations dominate the parallel processing times. In addition, the proposed GPU implementation achieves good performance in comparison with other popular SVM implementations, achieving similar accuracy results but with faster performance.

As with any new approach, there are some unresolved issues that may present challenges over time. In the future, we will improve our SVM implementation in order to reduce the accesses to global device memory and make a more efficient use of CUDA streams. In addition, we will use our accelerated SVM in conjunction with other techniques for HSI processing and classification (e.g., supervised and semi-supervised techniques) with the aim of improving even more the obtained classification results.