A New GPU Implementation of Support Vector Machines for Fast Hyperspectral Image Classification
Abstract
1. Introduction
- through HSI pixel vectors (coarse-grained pixel level parallelism),
- through spectral-band information (fine-grained spectral level parallelism), and
- through tasks (task-level parallelism).
2. Support Vector Machines (SVMs): A Review
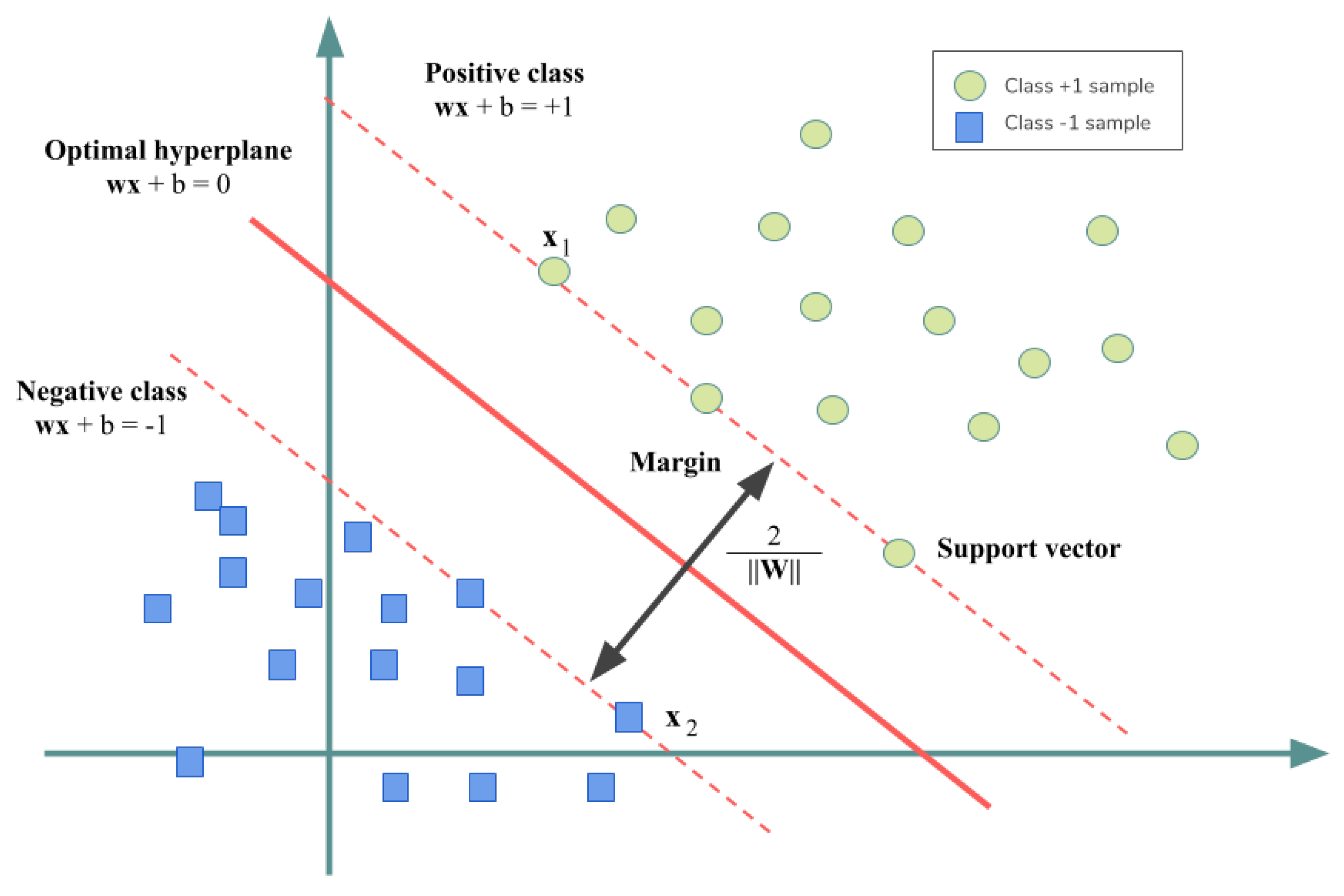
2.1. Linear SVM
2.2. Linear SVM for Linearly Nonseparable Data Classification
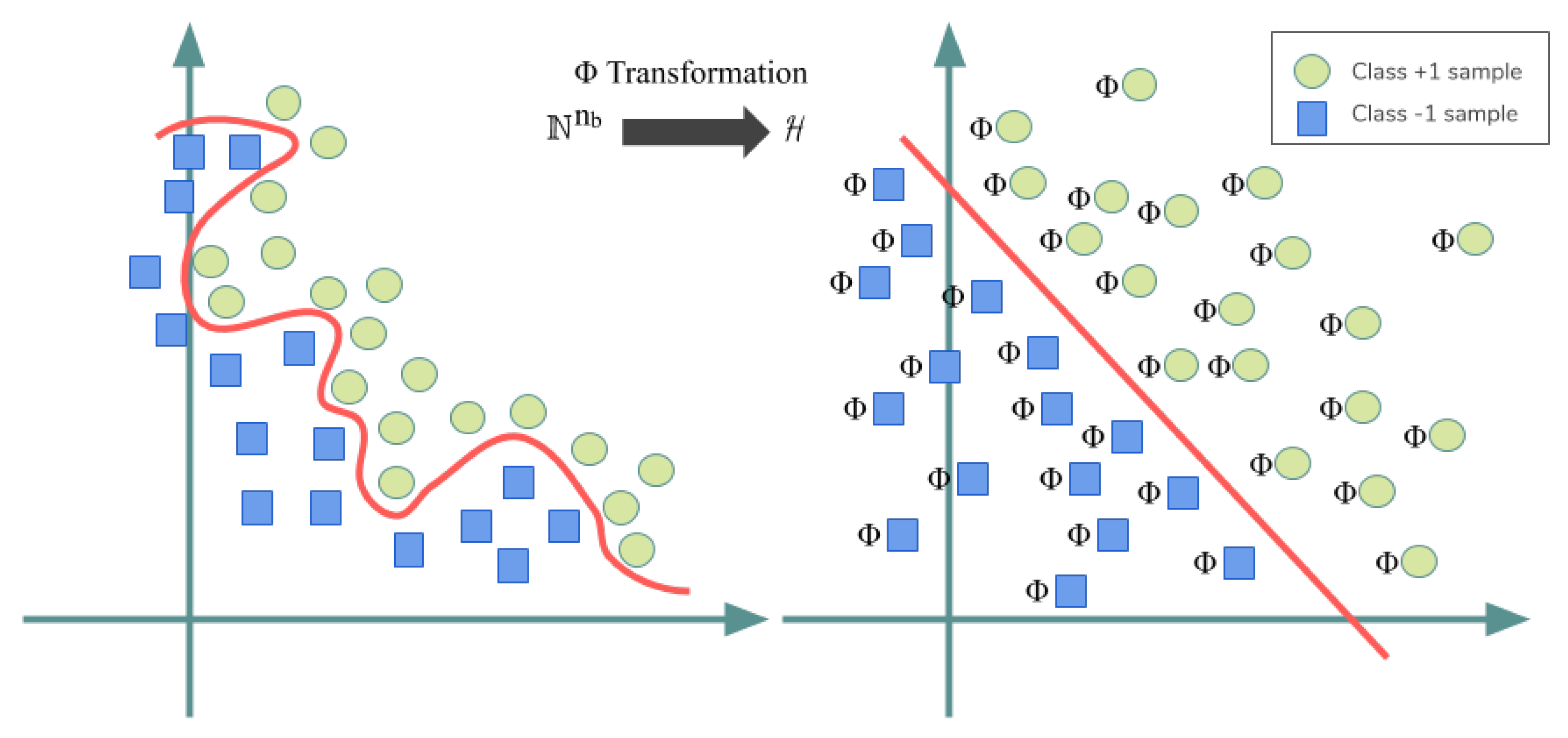
2.3. Kernel SVM for Non-Linear Data Classification
2.4. Multi-Class SVM
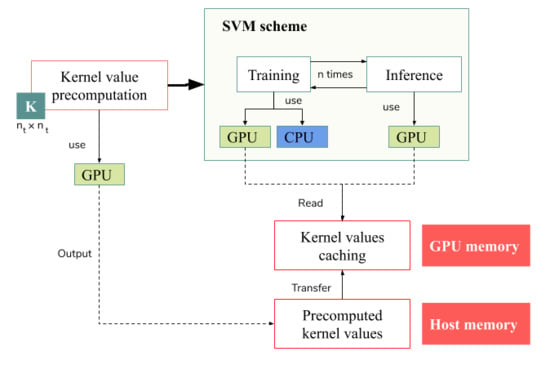
3. GPU-Accelerated SVM for HSI Data Classification
3.1. Previous Works and Proposal Overview
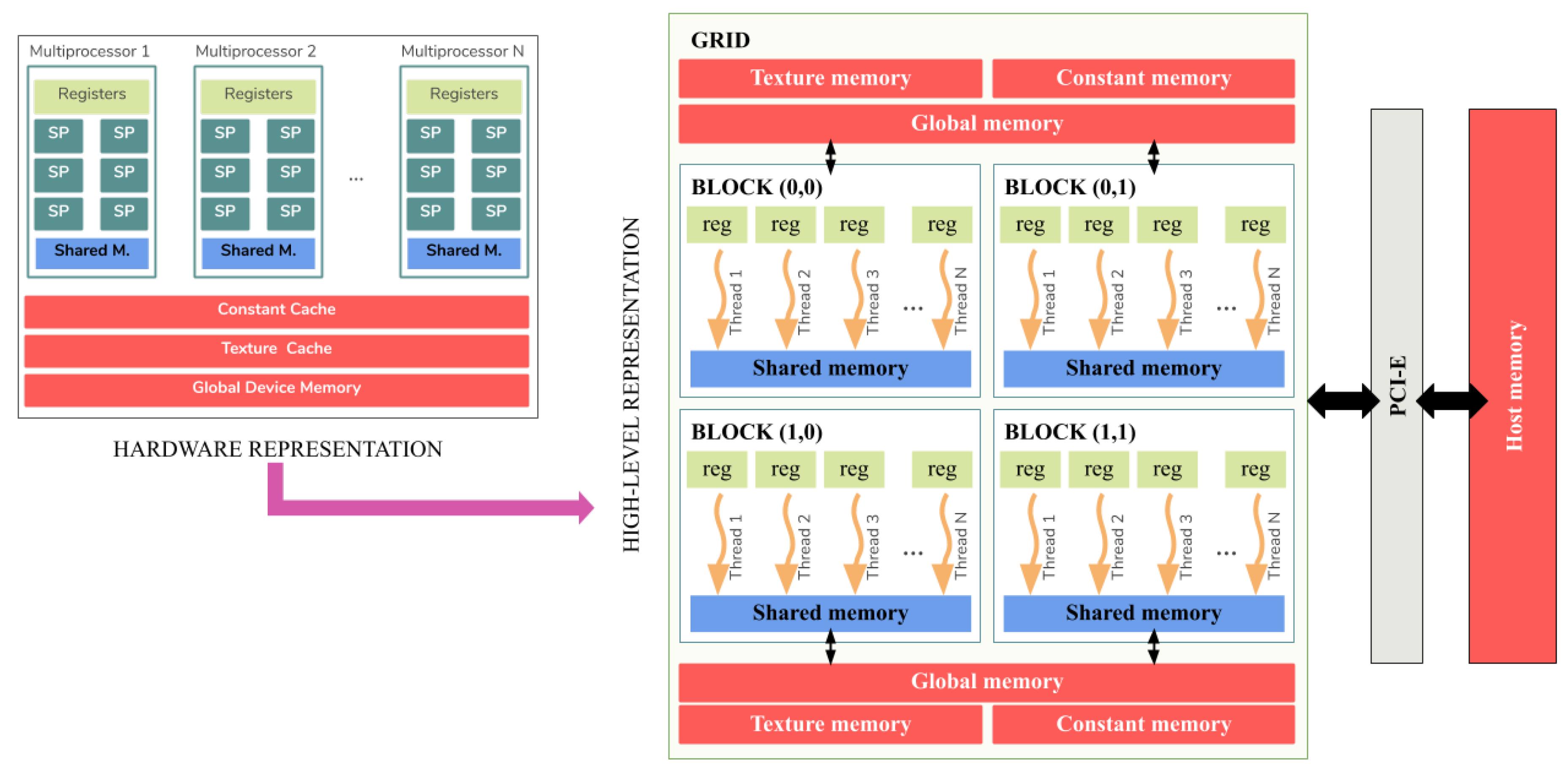
3.2. CUDA Platform
3.3. Parallel SMO during the Training Stage
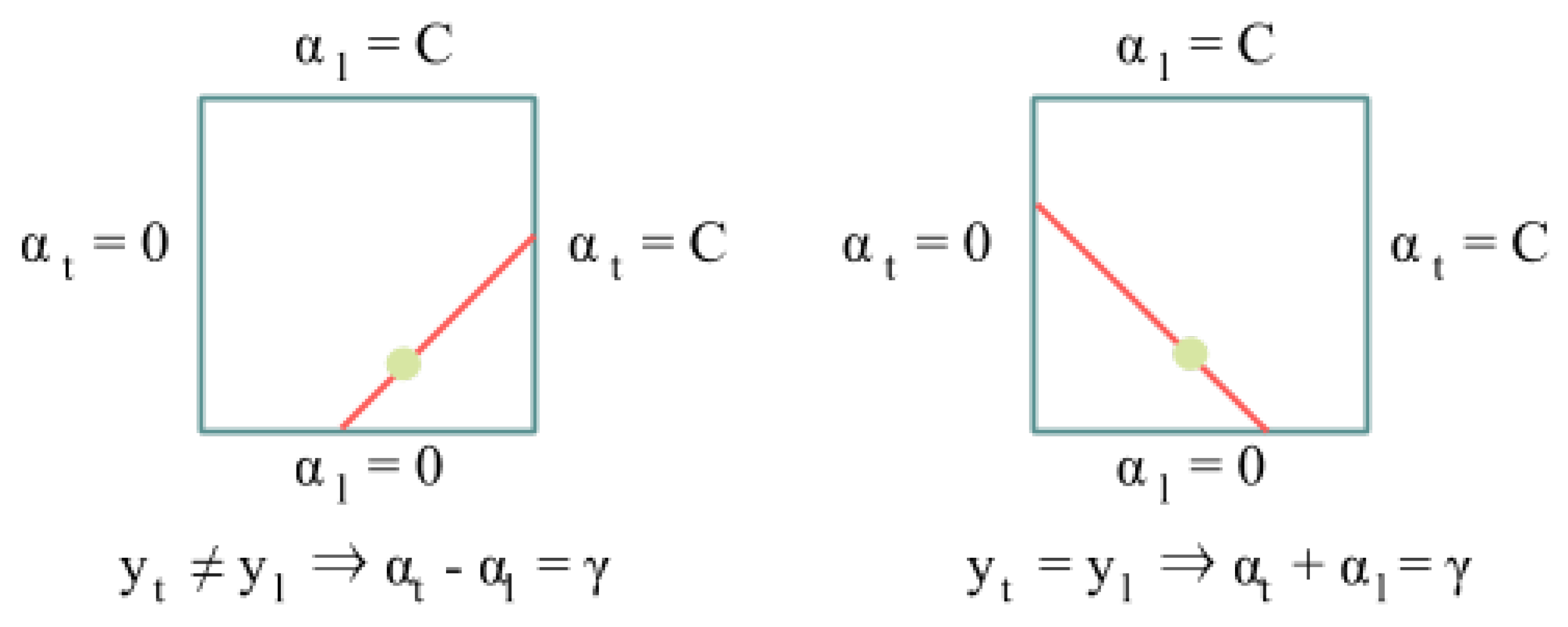
3.3.1. Previous Concepts about the SMO Algorithm
3.3.2. CUDA Optimization of SMO Algorithm
| Algorithm 1 Parallel Kernel RBF for HSI classification |
| Require: matrix of values, |
| matrix of values, |
| resulting kernel matrix, |
| number of rows, |
| number of training samples. |
| if then |
| while do |
| end while |
| end if |
3.4. Parallel Classification during the Inference Stage
4. Experimental Results
4.1. Experimental Environment
- Platform 1: it is composed by an Intel Core Coffee Lake Refresh i7-9750H processor, 32 GB of DDR4 RAM with 2667 MHz, and an NVIDIA GeForce RTX 2070 with 8 GB of RAM, graphic clock at 2100 MHz and 14,000 MHZ of memory transfer rate. It is equipped with 2304 CUDA cores. These processors were named CPU0 and GPU0.
- Platform 2: Intel i9-9940X processor, 128 GB of DDR4 RAM with 2100 MHz, and an NVIDIA GTX 1080Ti with 11 GB of RAM, 2037 MHz of graphic clock and 11,232 MHz of memory transfer rate. It is equipped with 3584 CUDA cores. These processors were named CPU1 and GPU1.
4.2. Hyperspectral Datasets
- The first dataset is known as Indian Pines, which was collected by the Airborne Visible Infra-Red Imaging Spectrometer (AVIRIS) [79] over the Indian Pines test site in North-western Indiana, which is characterized by several agricultural crops and irregular forest and pasture areas. It has pixels, each of which has 224 spectral reflectance bands covering the wavelengths from 400 nm to 2500 nm. We remove the bands 104–108, 150–163 and 220 (water absorption and null bands), and keep 200 bands in our experiments. This scene has 16 different ground-truth classes (see Figure 5).
- Big Indian Pines is a larger version of the first dataset, which has pixels with wavelengths ranging from 400 nm to 2500 nm. We also remove the water absorption and null bands, retaining 200 spectral bands in our experiments. This scene has 58 ground-truth classes (see Figure 5).
- The third dataset is the Pavia University scene, which was collected by the Reflective Optics Spectrographic Imaging System (ROSIS) [80] during a flight campaign over Pavia, nothern Italy. In this sense, it is characterized by being an urban area, with areas of buildings, roads and parking lots. In particular, the Pavia University scene has pixels, and its spatial resolution is 1.3 m. The original pavia dataset contains 115 bands in the spectral region of 0.43–0.86 m. We remove the water absorption bands, and retain 103 bands in our experiments. The number of classes in this scene is 9 (see Figure 5).
- The fourth dataset is Pavia Centre and was also gathered by ROSIS sensor. It is composed by pixels and 102 spectral bands. This scene also has 9 ground-truth classes from an urban area (see Figure 5).
- The fifth dataset is Houston University [81], which was acquired by the Compact Airborne Spectrographic Imager (CASI) sensor [82] over the Houston University campus in June 2012, collecting spectral information from an urban area. This scene has 114 bands and 349 × 1905 pixels with wavelengths ranging from 380nm to 1050nm. It comprises 15 ground-truth classes (see Figure 5).
- Finally, the sixth dataset is Salinas Valley, which was also acquired by AVIRIS sensor over an agricultural area. It has 512 ×217 pixels and covers Salinas Valley in California. We remove the water absorption bands 108–112, 154–167 and 224, and keep 204 bands in our experiments. This scene contains 16 classes (see Figure 5).
4.3. Performance Evaluation
- The first experiment focuses on the classification accuracy obtained by our GPU implementation as compared to a standard (CPU) implementation in LibSVM [83]. In particular, proposed GPU-SVM was compared with its CPU counterpart, the random forest (RF) [40] and the multinomial logistic regression (MLR) [40].
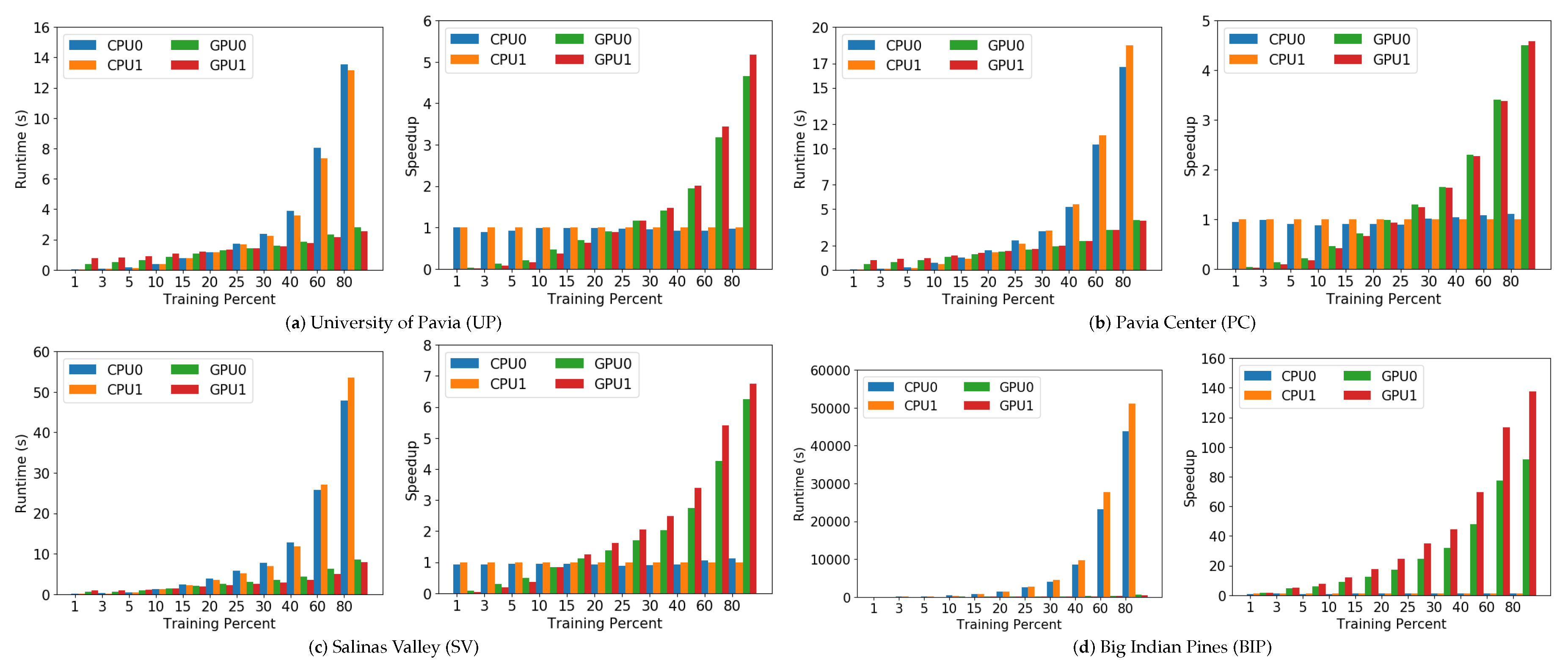
- The second experiment focuses on the scalability and speedups achieved by the GPU implementation with regards to the CPU implementation, from a global perspective. As we pointed before, CPU1 will be considered to be the baseline due its characteristics that make it the slowest device.
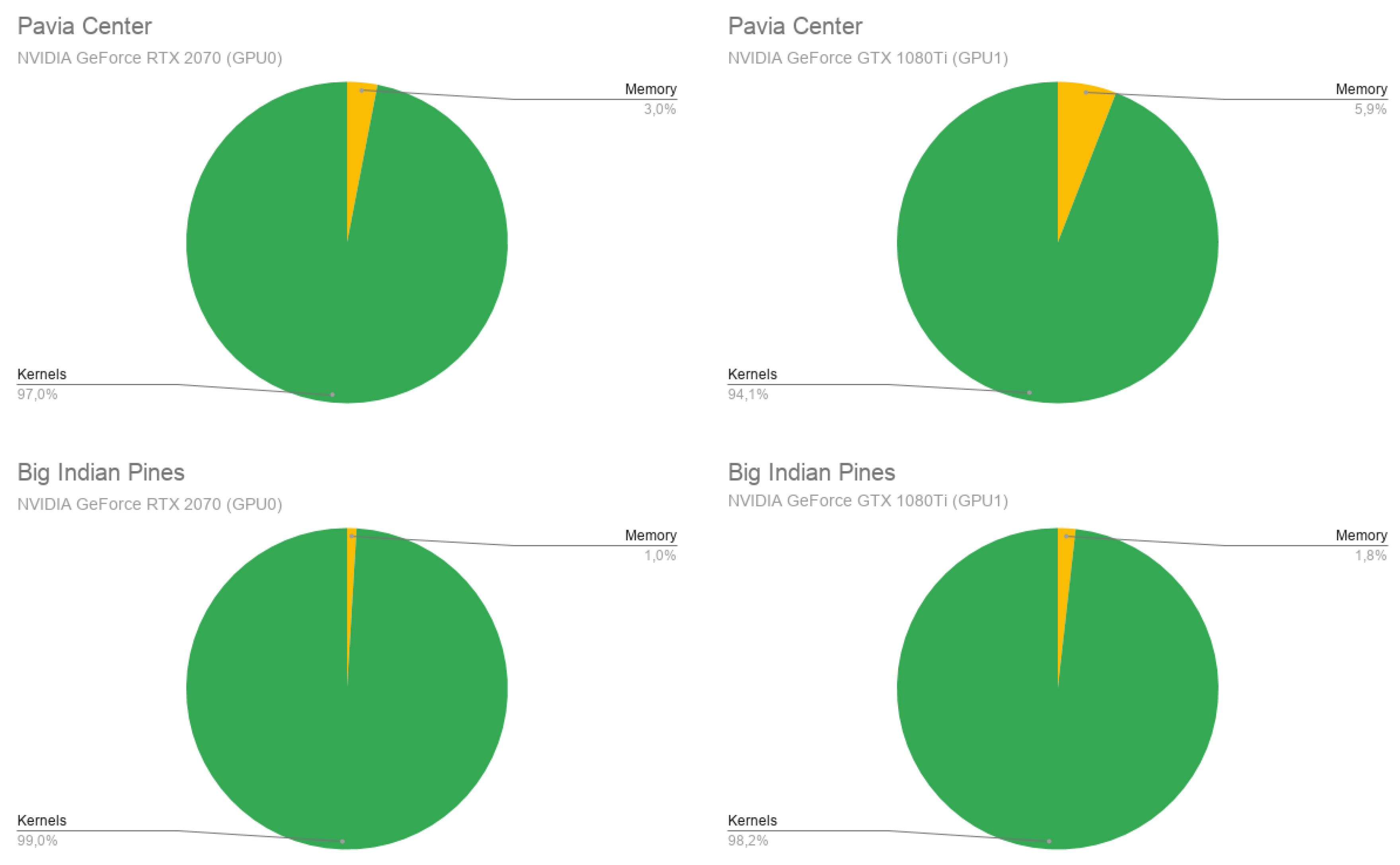
- The third and last experiment focuses on some specific aspects of the GPU implementation, including data-transfer times.
4.3.1. Experiment 1: Accuracy Performance
4.3.2. Experiment 2: Scalability and Speedup
4.3.3. Experiment 3: GPU Transfer-Memory and Kernel Runtimes
5. Conclusions and Future Lines
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Goetz, A.F.; Vane, G.; Solomon, J.E.; Rock, B.N. Imaging spectrometry for earth remote sensing. Science 1985, 228, 1147–1153. [Google Scholar] [CrossRef] [PubMed]
- Heldens, W.; Heiden, U.; Esch, T.; Stein, E.; Müller, A. Can the future EnMAP mission contribute to urban applications? A literature survey. Remote Sens. 2011, 3, 1817–1846. [Google Scholar] [CrossRef]
- Guanter, L.; Kaufmann, H.; Segl, K.; Foerster, S.; Rogass, C.; Chabrillat, S.; Kuester, T.; Hollstein, A.; Rossner, G.; Chlebek, C.; et al. The EnMAP spaceborne imaging spectroscopy mission for earth observation. Remote Sens. 2015, 7, 8830–8857. [Google Scholar] [CrossRef]
- Pignatti, S.; Palombo, A.; Pascucci, S.; Romano, F.; Santini, F.; Simoniello, T.; Umberto, A.; Vincenzo, C.; Acito, N.; Diani, M.; et al. The PRISMA hyperspectral mission: Science activities and opportunities for agriculture and land monitoring. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium-IGARSS, Melbourne, Australia, 21–26 July 2013; pp. 4558–4561. [Google Scholar]
- Chang, C.I. Hyperspectral Imaging: Techniques for Spectral Detection and Classification; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar] [CrossRef]
- Christophe, E.; Michel, J.; Inglada, J. Remote sensing processing: From multicore to GPU. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 643–652. [Google Scholar] [CrossRef]
- Messmer, P. High-Performance Computing in Earth- and Space-Science: An Introduction. In Applied Parallel Computing. State of the Art in Scientific Computing, Proceedings of the 7th International Workshop, PARA 2004, Lyngby, Denmark, 20–23 June 2004; Revised Selected Papers; Dongarra, J., Madsen, K., Waśniewski, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 527–529. [Google Scholar] [CrossRef]
- Plaza, A.J.; Chang, C.I. High Performance Computing in Remote Sensing; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Lee, C.A.; Gasster, S.D.; Plaza, A.; Chang, C.I.; Huang, B. Recent developments in high performance computing for remote sensing: A review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 508–527. [Google Scholar] [CrossRef]
- León, G.; Molero, J.M.; Garzón, E.M.; García, I.; Plaza, A.; Quintana-Ortí, E.S. Exploring the performance-power-energy balance of low-power multicore and manycore architectures for anomaly detection in remote sensing. J. Supercomput. 2015, 71, 1893–1906. [Google Scholar] [CrossRef]
- Plaza, A.; Benediktsson, J.A.; Boardman, J.W.; Brazile, J.; Bruzzone, L.; Camps-Valls, G.; Chanussot, J.; Fauvel, M.; Gamba, P.; Gualtieri, A.; et al. Recent advances in techniques for hyperspectral image processing. Remote Sens. Environ. 2009, 113, S110–S122. [Google Scholar] [CrossRef]
- Plaza, A.; Du, Q.; Chang, Y.L. High Performance Computing for Hyperspectral Image Analysis: Perspective and State-of-the-art. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009; pp. V-72–V-75. [Google Scholar] [CrossRef]
- Setoain, J.; Tenllado, C.; Prieto, M.; Valencia, D.; Plaza, A.; Plaza, J. Parallel Hyperspectral Image Processing on Commodity Graphics Hardware. In Proceedings of the 2006 International Conference on Parallel Processing Workshops (ICPPW’06), Columbus, OH, USA, 14–18 August 2006. [Google Scholar] [CrossRef]
- Setoain, J.; Prieto, M.; Tenllado, C.; Tirado, F. GPU for Parallel On-Board Hyperspectral Image Processing. Int. J. High Perform. Comput. Appl. 2008. [Google Scholar] [CrossRef]
- Plaza, A.; Valencia, D.; Plaza, J.; Martinez, P. Commodity cluster-based parallel processing of hyperspectral imagery. J. Parallel Distrib. Comput. 2006, 66, 345–358. [Google Scholar] [CrossRef]
- Plaza, J.; Pérez, R.; Plaza, A.; Martínez, P.; Valencia, D. Parallel Morphological/Neural Classification of Remote Sensing Images Using Fully Heterogeneous and Homogeneous Commodity Clusters. In Proceedings of the 2006 IEEE International Conference on Cluster Computing, Barcelona, Spain, 25–28 September 2006; pp. 1–10. [Google Scholar] [CrossRef]
- Aloisio, G.; Cafaro, M. A dynamic earth observation system. Parallel Comput. 2003, 29, 1357–1362. [Google Scholar] [CrossRef]
- Gorgan, D.; Bacu, V.; Stefanut, T.; Rodila, D.; Mihon, D. Grid based Satellite Image Processing Platform for Earth Observation Application Development. In Proceedings of the 2009 IEEE International Workshop on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications, Rende, Italy, 21–23 September 2009; Volume 21, pp. 247–252. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, N.; Yang, C.; Di, L. Cloud computing enabled web processing service for earth observation data processing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 1637–1649. [Google Scholar] [CrossRef]
- Wu, Z.; Li, Y.; Plaza, A.; Li, J.; Xiao, F.; Wei, Z. Parallel and Distributed Dimensionality Reduction of Hyperspectral Data on Cloud Computing Architectures. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2270–2278. [Google Scholar] [CrossRef]
- Haut, J.; Paoletti, M.; Plaza, J.; Plaza, A. Cloud implementation of the K-means algorithm for hyperspectral image analysis. J. Supercomput. 2017, 73. [Google Scholar] [CrossRef]
- Haut, J.M.; Gallardo, J.A.; Paoletti, M.E.; Cavallaro, G.; Plaza, J.; Plaza, A.; Riedel, M. Cloud deep networks for hyperspectral image analysis. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9832–9848. [Google Scholar] [CrossRef]
- Quirita, V.A.A.; Da Costa, G.A.O.P.; Happ, P.N.; Feitosa, R.Q.; Da Silva Ferreira, R.; Oliveira, D.A.B.; Plaza, A. A New Cloud Computing Architecture for the Classification of Remote Sensing Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 14, 409–416. [Google Scholar] [CrossRef]
- Zheng, X.; Xue, Y.; Guang, J.; Liu, J. Remote sensing data processing acceleration based on multi-core processors. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 641–644. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Plaza, J.; Plaza, A.; Liu, Q.; Hang, R. Multicore Implementation of the Multi-Scale Adaptive Deep Pyramid Matching Model for Remotely Sensed Image Classification. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium, Fort Worth, TX, USA, 23–28 July 2017; pp. 2247–2250. [Google Scholar]
- Sevilla, J.; Bernabe, S.; Plaza, A. Unmixing-based content retrieval system for remotely sensed hyperspectral imagery on GPUs. J. Supercomput. 2014, 70, 588–599. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, Q.; Plaza, A.; Li, J.; Wei, Z. Real-Time Implementation of the Sparse Multinomial Logistic Regression for Hyperspectral Image Classification on GPUs. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1456–1460. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Plaza, J.; Plaza, A. Scalable recurrent neural network for hyperspectral image classification. J. Supercomput. 2020, 1–17. [Google Scholar] [CrossRef]
- Jaramago, J.A.G.; Paoletti, M.E.; Haut, J.M.; Fernandez-Beltran, R.; Plaza, A.; Plaza, J. GPU Parallel Implementation of Dual-Depth Sparse Probabilistic Latent Semantic Analysis for Hyperspectral Unmixing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3156–3167. [Google Scholar] [CrossRef]
- Leeser, M.; Belanovic, P.; Estlick, M.; Gokhale, M.; Szymanski, J.J.; Theiler, J. Applying Reconfigurable Hardware to the Analysis of Multispectral and Hyperspectral Imagery. In Proceedings of the International Symposium on Optical Science and Technology, San Diego, CA, USA, 17 January 2002; pp. 100–107. [Google Scholar]
- Williams, J.A.; Dawood, A.S.; Visser, S.J. FPGA-based cloud detection for real-time onboard remote sensing. In Proceedings of the 2002 IEEE International Conference on FieId-Programmable Technology (FPT 2002), Hong Kong, China, 16–18 December 2002; pp. 110–116. [Google Scholar] [CrossRef]
- Nie, Z.; Zhang, X.; Yang, Z. An FPGA Implementation of Multi-Class Support Vector Machine Classifier Based on Posterior Probability. Int. Proc. Comput. Sci. Inf. Technol. 2012. [Google Scholar] [CrossRef]
- Gonzalez, C.; Sánchez, S.; Paz, A.; Resano, J.; Mozos, D.; Plaza, A. Use of FPGA or GPU-based architectures for remotely sensed hyperspectral image processing. Integration 2013, 46, 89–103. [Google Scholar] [CrossRef]
- González, C.; Bernabé, S.; Mozos, D.; Plaza, A. FPGA implementation of an algorithm for automatically detecting targets in remotely sensed hyperspectral images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4334–4343. [Google Scholar] [CrossRef]
- Torti, E.; Acquistapace, M.; Danese, G.; Leporati, F.; Plaza, A. Real-time identification of hyperspectral subspaces. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2680–2687. [Google Scholar] [CrossRef]
- Haut, J.M.; Bernabé, S.; Paoletti, M.E.; Fernandez-Beltran, R.; Plaza, A.; Plaza, J. Low–high-power consumption architectures for deep-learning models applied to hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2018, 16, 776–780. [Google Scholar] [CrossRef]
- Paz, A.; Plaza, A. Clusters versus GPUs for parallel target and anomaly detection in hyperspectral images. EURASIP J. Adv. Signal Process. 2010, 2010, 1–18. [Google Scholar] [CrossRef]
- Bernabe, S.; López, S.; Plaza, A.; Sarmiento, R. GPU implementation of an automatic target detection and classification algorithm for hyperspectral image analysis. IEEE Geosci. Remote Sens. Lett. 2012, 10, 221–225. [Google Scholar] [CrossRef]
- Santos, L.; Magli, E.; Vitulli, R.; López, J.F.; Sarmiento, R. Highly-parallel GPU architecture for lossy hyperspectral image compression. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 670–681. [Google Scholar] [CrossRef]
- Paoletti, M.; Haut, J.; Plaza, J.; Plaza, A. Deep learning classifiers for hyperspectral imaging: A review. ISPRS J. Photogramm. Remote Sens. 2019, 158, 279–317. [Google Scholar] [CrossRef]
- Agathos, A.; Li, J.; Petcu, D.; Plaza, A. Multi-GPU implementation of the minimum volume simplex analysis algorithm for hyperspectral unmixing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2281–2296. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Cristianini, N.; Shawe-Taylor, J. An Introduction to Support Vector Machines and other Kernel-Based Learning Methods; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Osuna, E.; Freund, R.; Girosi, F. An improved training algorithm for support vector machines. In Proceedings of the Neural Networks for Signal Processing VII. 1997 IEEE Signal Processing Society Workshop, Amelia Island, FL, USA, 24–26 September 1997; pp. 276–285. [Google Scholar]
- Platt, J. Fast Training of Support Vector Machines Using Sequential Minimal Optimization; Advances in Kernel Methods—Support Vector Learning; AJ, MIT Press: Cambridge, MA, USA, 1999; pp. 185–208. [Google Scholar]
- Fan, R.E.; Chen, P.H.; Lin, C.J. Working set selection using second order information for training support vector machines. J. Mach. Learn. Res. 2005, 6, 1889–1918. [Google Scholar]
- Tan, K.; Zhang, J.; Du, Q.; Wang, X. GPU parallel implementation of support vector machines for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4647–4656. [Google Scholar] [CrossRef]
- Li, Q.; Salman, R.; Kecman, V. An intelligent system for accelerating parallel SVM classification problems on large datasets using GPU. In Proceedings of the 2010 10th International Conference on Intelligent Systems Design and Applications, Cairo, Egypt, 29 November–1 December 2010; pp. 1131–1135. [Google Scholar]
- Wen, Z.; Shi, J.; Li, Q.; He, B.; Chen, J. ThunderSVM: A fast SVM library on GPUs and CPUs. J. Mach. Learn. Res. 2018, 19, 797–801. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Gale, D.; Kuhn, H.W.; Tucker, A.W. Linear programming and the theory of games. Act. Anal. Prod. Alloc. 1951, 13, 317–335. [Google Scholar]
- Platt, J. Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines; Technical Report MSR-TR-98-14; Microsoft Research: Redmond, WA, USA, 1998. [Google Scholar]
- Aiserman, M.; Braverman, E.M.; Rozonoer, L. Theoretical foundations of the potential function method in pattern recognition. Avtomat. I Telemeh 1964, 25, 917–936. [Google Scholar]
- Moreno, P.J.; Ho, P.P.; Vasconcelos, N. A Kullback-Leibler divergence based kernel for SVM classification in multimedia applications. In Proceedings of the Advances in Neural Information Processing Systems; 2004; pp. 1385–1392. Available online: https://dl.acm.org/doi/10.5555/2981345.2981516 (accessed on 16 April 2020).
- Mercer, J. Functions ofpositive and negativetypeand theircommection with the theory ofintegral equations. Philos. Trinsdictions Rogyal Soc. 1909, 209, 4–415. [Google Scholar]
- Hsu, C.W.; Lin, C.J. A comparison of methods for multiclass support vector machines. IEEE Trans. Neural Netw. 2002, 13, 415–425. [Google Scholar]
- Knerr, S.; Personnaz, L.; Dreyfus, G. Single-layer learning revisited: A stepwise procedure for building and training a neural network. In Neurocomputing; Springer: Berlin/Heidelberg, Germany, 1990; pp. 41–50. [Google Scholar]
- Platt, J.C.; Cristianini, N.; Shawe-Taylor, J. Large margin DAGs for multiclass classification. In Proceedings of the Advances in Neural Information Processing Systems; 2000; pp. 547–553. Available online: https://papers.nips.cc/paper/1773-large-margin-dags-for-multiclass-classification (accessed on 16 April 2020).
- Duan, K.B.; Rajapakse, J.C.; Nguyen, M.N. One-versus-one and one-versus-all multiclass SVM-RFE for gene selection in cancer classification. In Proceedings of the European Conference on Evolutionary Computation, Machine Learning and Data Mining in Bioinformatics, Valencia, Spain, 11–13 April 2007; pp. 47–56. [Google Scholar]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A training algorithm for optimal margin classifiers. In Proceedings of the Fifth Annual Workshop on Computational Learning Theory; 1992; pp. 144–152. Available online: https://dl.acm.org/doi/10.1145/130385.130401 (accessed on 16 April 2020).
- Chandra, R.; Dagum, L.; Kohr, D.; Menon, R.; Maydan, D.; McDonald, J. Parallel Programming in OpenMP; Morgan Kaufmann: San Mateo, CA, USA, 2001. [Google Scholar]
- Wu, Z.; Liu, J.; Plaza, A.; Li, J.; Wei, Z. GPU implementation of composite kernels for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1973–1977. [Google Scholar]
- Camps-Valls, G.; Gomez-Chova, L.; Muñoz-Marí, J.; Vila-Francés, J.; Calpe-Maravilla, J. Composite kernels for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2006, 3, 93–97. [Google Scholar] [CrossRef]
- Osuna, E.; Freund, R.; Girosit, F. Training support vector machines: An application to face detection. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Juan, PR, USA, 17–19 June 1997; pp. 130–136. [Google Scholar]
- Joachims, T. Making Large-Scale SVM Learning Practical; Technical Report; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Keerthi, S.S.; Shevade, S.K.; Bhattacharyya, C.; Murthy, K.R.K. Improvements to Platt’s SMO algorithm for SVM classifier design. Neural Comput. 2001, 13, 637–649. [Google Scholar] [CrossRef]
- Hsu, C.W.; Lin, C.J. A simple decomposition method for support vector machines. Mach. Learn. 2002, 46, 291–314. [Google Scholar] [CrossRef]
- Palagi, L.; Sciandrone, M. On the convergence of a modified version of SVM light algorithm. Optim. Methods Softw. 2005, 20, 317–334. [Google Scholar] [CrossRef]
- Glasmachers, T.; Igel, C. Maximum-gain working set selection for SVMs. J. Mach. Learn. Res. 2006, 7, 1437–1466. [Google Scholar]
- Bo, L.; Jiao, L.; Wang, L. Working set selection using functional gain for LS-SVM. IEEE Trans. Neural Netw. 2007, 18, 1541–1544. [Google Scholar] [CrossRef]
- Glasmachers, T.; Igel, C. Second-order SMO improves SVM online and active learning. Neural Comput. 2008, 20, 374–382. [Google Scholar] [CrossRef]
- Dogan, U.; Glasmachers, T.; Igel, C. Fast Training of Multi-Class Support Vector Machines; Faculty of Science, University of Copenhagen: Copenhagen, Denmark, 2011. [Google Scholar]
- Tuma, M.; Igel, C. Improved working set selection for LaRank. In Proceedings of the International Conference on Computer Analysis of Images and Patterns, Seville, Spain, 29–31 August 2011; pp. 327–334. [Google Scholar]
- Wu, H.C. The Karush–Kuhn–Tucker optimality conditions in an optimization problem with interval-valued objective function. Eur. J. Oper. Res. 2007, 176, 46–59. [Google Scholar] [CrossRef]
- Merrill, D. CUB v1. 5.3: CUDA Unbound, a library of warp-wide, blockwide, and device-wide GPU parallel primitives. NVIDIA Res. 2015. [Google Scholar]
- Nvidia, C. Cublas library. NVIDIA Corp. Santa Clara Calif. 2008, 15, 31. [Google Scholar]
- Naumov, M.; Chien, L.; Vandermersch, P.; Kapasi, U. Cusparse library. In Proceedings of the GPU Technology Conference, San Jose, CA, USA, 20–23 September 2010. [Google Scholar]
- Vane, G.; Green, R.O.; Chrien, T.G.; Enmark, H.T.; Hansen, E.G.; Porter, W.M. The airborne visible/infrared imaging spectrometer (AVIRIS). Remote Sens. Environ. 1993, 44, 127–143. [Google Scholar] [CrossRef]
- Kunkel, B.; Blechinger, F.; Lutz, R.; Doerffer, R.; van der Piepen, H.; Schroder, M. ROSIS (Reflective Optics System Imaging Spectrometer)—A candidate instrument for polar platform missions. In Proceedings of the SPIE 0868 Optoelectronic technologies for remote sensing from space, Cannes, France, 17–20 November 1988; p. 8. [Google Scholar] [CrossRef]
- Xu, X.; Lil, f.; Plaza, A. Fusion of hyperspectral and LiDAR data using morphological component analysis. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 3575–3578. [Google Scholar] [CrossRef]
- Babey, S.; Anger, C. A compact airborne spectrographic imager (CASI). In Quantitative Remote Sensing: An Economic Tool for the Nineties, Proceedings of the 12th IGARSS ’89 and Canadian Symposium on Remote Sensing, Vancouver, CO, Canada, 10–14 July 1989; Institute of Electrical and Electronics Engineers: New York, NY, USA, 1989; Volume 1, pp. 1028–1031. [Google Scholar]
- Chang, C.C.; Lin, C.J. LIBSVM: A Library for Support Vector Machines. ACM Trans. Intell. Syst. Technol. 2011, 2. [Google Scholar] [CrossRef]




| Linear | |
| Polynomial | |
| Gaussian | |
| Sigmoid | |
| Radial basis function (RBF) |
| Indian Pines | University of Pavia | Houston University | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Class | RF | MLR | RF | MLR | RF | MLR | ||||||
| SVM | SVM | SVM | ||||||||||
| [40] | [40] | CPU | GPU | [40] | [40] | CPU | GPU | [40] | [40] | CPU | GPU | |
| 1 | 32.80 | 68.0 | 88.0 | 88.0 | 79.59 | 77.7 | 83.08 | 81.85 | 82.55 | 82.24 | 82.34 | 82.15 |
| 2 | 51.56 | 78.07 | 80.74 | 79.32 | 55.2 | 58.78 | 67.45 | 67.2 | 83.5 | 82.5 | 83.36 | 83.36 |
| 3 | 44.41 | 59.41 | 67.57 | 67.43 | 45.42 | 67.22 | 64.85 | 65.0 | 97.94 | 99.8 | 99.8 | 99.8 |
| 4 | 26.46 | 25.25 | 51.52 | 49.9 | 98.73 | 74.29 | 98.28 | 98.35 | 91.46 | 98.3 | 98.96 | 97.86 |
| 5 | 79.34 | 88.32 | 87.23 | 86.28 | 99.14 | 98.88 | 99.28 | 99.3 | 96.69 | 97.44 | 98.77 | 98.6 |
| 6 | 95.71 | 96.89 | 96.61 | 96.67 | 78.77 | 93.52 | 92.06 | 92.3 | 99.16 | 94.41 | 97.9 | 96.78 |
| 7 | 20.0 | 50.0 | 100.0 | 100.0 | 80.41 | 85.12 | 88.89 | 88.95 | 75.35 | 73.41 | 77.43 | 75.95 |
| 8 | 100.0 | 99.2 | 98.8 | 98.8 | 90.96 | 87.58 | 92.12 | 92.31 | 33.03 | 63.82 | 60.3 | 57.78 |
| 9 | 16.0 | 40.0 | 60.0 | 50.0 | 97.69 | 99.22 | 96.35 | 96.6 | 69.2 | 70.25 | 76.77 | 77.88 |
| 10 | 8.47 | 56.14 | 81.71 | 82.03 | 43.9 | 55.6 | 61.29 | 61.56 | ||||
| 11 | 89.63 | 81.64 | 86.95 | 87.77 | 69.79 | 74.19 | 80.55 | 81.2 | ||||
| 12 | 26.6 | 68.44 | 77.66 | 77.94 | 54.12 | 70.41 | 79.92 | 80.65 | ||||
| 13 | 89.25 | 96.25 | 93.75 | 94.25 | 59.86 | 67.72 | 70.88 | 72.56 | ||||
| 14 | 92.0 | 89.95 | 90.64 | 90.83 | 99.35 | 98.79 | 100.0 | 100.0 | ||||
| 15 | 38.79 | 82.83 | 76.77 | 81.21 | 97.42 | 95.56 | 96.41 | 97.42 | ||||
| 16 | 93.64 | 93.18 | 88.64 | 88.64 | ||||||||
| OA | 65.69 | 78.16 | 84.21 | 84.25 | 70.15 | 72.23 | 78.91 | 78.67 | 72.97 | 78.98 | 81.86 | 81.69 |
| AA | 56.54 | 73.35 | 82.91 | 82.44 | 80.66 | 82.48 | 86.93 | 86.87 | 76.89 | 81.63 | 84.31 | 84.24 |
| K(x100) | 59.87 | 74.99 | 81.98 | 82.0 | 63.01 | 65.45 | 73.37 | 73.09 | 70.96 | 77.31 | 80.43 | 80.25 |
| PAVIA CENTER | ||||||||
| NVIDIA GeForce RTX 2070 (Laptop) | NVIDIA GeForce GTX 1080Ti (Desktop) | |||||||
| Tr Percent | HtoD | DtoH | DtoD | Kernels | HtoD | DtoH | DtoD | Kernels |
| 1 | 1.900800 | 1.008450 | 0.401280 | 89.683510 | 2.065540 | 0.909663 | 0.401824 | 53.969180 |
| 5 | 5.196410 | 1.211910 | 0.389169 | 342.75209 | 5.928330 | 1.308890 | 0.445162 | 192.82042 |
| 10 | 9.650360 | 1.710720 | 0.404029 | 588.11514 | 11.10364 | 1.798470 | 0.448121 | 292.20041 |
| 20 | 18.90792 | 2.658750 | 0.405595 | 845.38273 | 22.65927 | 2.731010 | 0.465384 | 503.46422 |
| 40 | 37.78842 | 4.761070 | 0.444797 | 1369.8100 | 45.99625 | 4.856580 | 0.505738 | 816.56403 |
| 60 | 56.83977 | 6.937100 | 0.483709 | 1924.3700 | 71.39292 | 6.930210 | 0.506987 | 1180.4300 |
| 80 | 77.18297 | 9.077530 | 0.476379 | 2425.9400 | 95.87500 | 9.032700 | 0.547660 | 1448.0500 |
| BIG INDIAN PINES | ||||||||
| NVIDIA GeForce RTX 2070 (Laptop) | NVIDIA GeForce GTX 1080Ti (Desktop) | |||||||
| Tr Percent | HtoD | DtoH | DtoD | Kernels | HtoD | DtoH | DtoD | Kernels |
| 1 | 72.270610 | 44.041780 | 20.12548 | 2167.8800 | 86.874980 | 45.894420 | 23.89330 | 2445.0100 |
| 5 | 189.45379 | 53.012700 | 21.65845 | 15000.320 | 215.96618 | 56.352320 | 25.65502 | 10679.120 |
| 10 | 345.04000 | 68.476270 | 23.63760 | 34717.630 | 395.10834 | 71.718340 | 27.34729 | 22486.610 |
| 20 | 683.13051 | 118.78844 | 29.17641 | 77072.650 | 813.34057 | 123.31494 | 32.40953 | 46963.590 |
| 40 | 1439.0210 | 296.14766 | 43.88958 | 184683.75 | 1703.9300 | 301.14840 | 46.36005 | 112824.33 |
| 60 | 2325.2100 | 579.43225 | 60.25476 | 335392.10 | 2868.1800 | 581.19374 | 61.65440 | 255449.66 |
| 80 | 3296.8700 | 969.39610 | 68.03797 | 519363.01 | 4077.2100 | 972.86474 | 77.46072 | 307944.21 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paoletti, M.E.; Haut, J.M.; Tao, X.; Miguel, J.P.; Plaza, A. A New GPU Implementation of Support Vector Machines for Fast Hyperspectral Image Classification. Remote Sens. 2020, 12, 1257. https://doi.org/10.3390/rs12081257
Paoletti ME, Haut JM, Tao X, Miguel JP, Plaza A. A New GPU Implementation of Support Vector Machines for Fast Hyperspectral Image Classification. Remote Sensing. 2020; 12(8):1257. https://doi.org/10.3390/rs12081257
Chicago/Turabian StylePaoletti, Mercedes E., Juan M. Haut, Xuanwen Tao, Javier Plaza Miguel, and Antonio Plaza. 2020. "A New GPU Implementation of Support Vector Machines for Fast Hyperspectral Image Classification" Remote Sensing 12, no. 8: 1257. https://doi.org/10.3390/rs12081257
APA StylePaoletti, M. E., Haut, J. M., Tao, X., Miguel, J. P., & Plaza, A. (2020). A New GPU Implementation of Support Vector Machines for Fast Hyperspectral Image Classification. Remote Sensing, 12(8), 1257. https://doi.org/10.3390/rs12081257