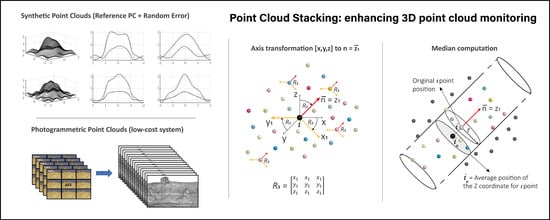
Point Cloud Stacking: A Workflow to Enhance 3D Monitoring Capabilities Using Time-Lapse Cameras
Abstract
1. Introduction
1.1. Photogrammetry vs. LiDAR 3D Point Cloud Errors
1.2. Landslide Monitoring Using Photogrammetry
1.3. Techniques for Image Stacking (2D)
1.4. Aim and Objectives
2. Materials and Methods
2.1. PCStacking Workflow
2.1.1. Automatic 3D Reconstruction from Time-Lapse Camera Systems
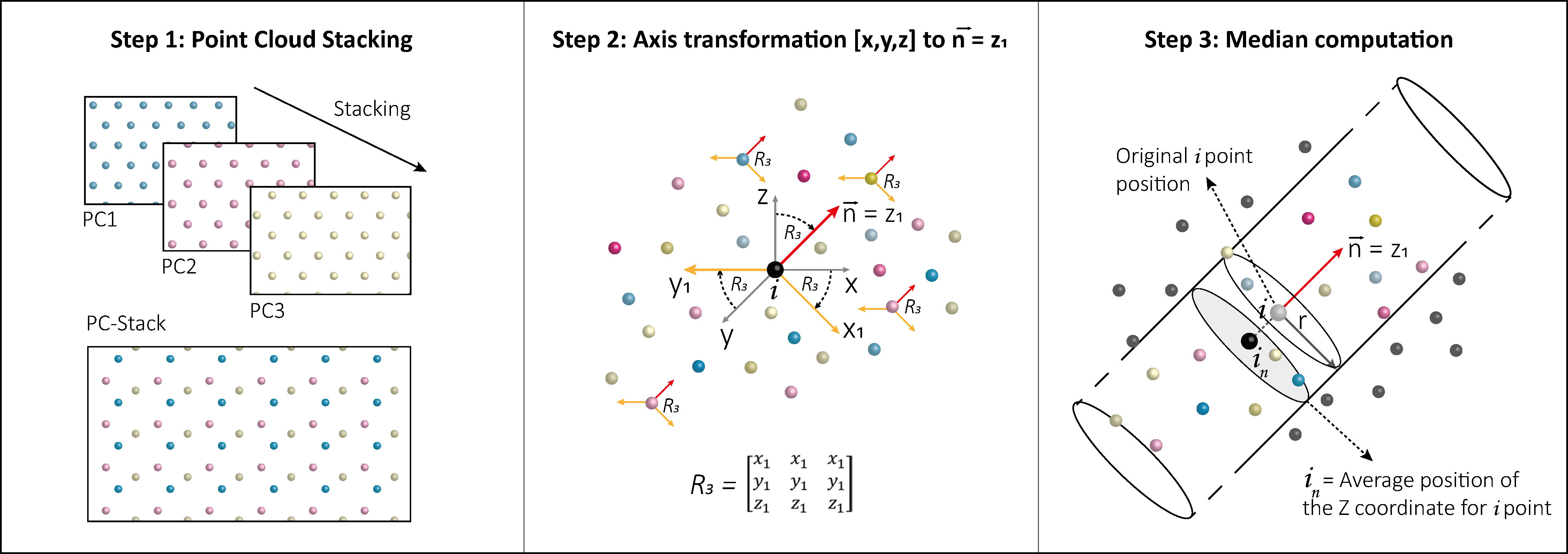
2.1.2. Point Cloud Stacking Algorithm
| Algorithm 1 PCStacking is |
| 1 Start |
| 2 get the number of Point Clouds (m) from a designated folder |
| 3 load m Point Clouds into the workspace |
| 4 merge all Point Clouds into a single matrix (PC-Stack) [step 1] |
| 5 input search radius value (r1) |
| 6 for each Point in PC-Stack |
| 7 create a subset1 of PC-Stack inside r1, with coordinates (x,y,z) |
| 8 apply axes transformation (PCA), being normal vector -> Z1 axes [step 2] |
| 9 compute median value of the subset1 along eigen vectors (X, Y, Z) [step 3] |
| 10 end |
| 11 output the mean coordinates of the stacked Point Cloud |
| 12 End |
2.2. Experimental Design (I): Synthetic Test
2.2.1. Synthetic Point Clouds Creation
2.2.2. PCStacking Application
- -
- Design a Reference PC (Ref-PC)
- -
- Create 20 Synthetic PCs (Synt-PC)
- -
- Application of the PCStacking algorithm: (n -> 2:20)
- o
- Input: n Synthetic PCs (Synt-PC)
- o
- Output: Enhanced PC (Enh-PCn)
- o
- Comparison between the Enhanced PCs (Enh-PCn) and the Reference PC (Ref-PC)
- -
- Analysis of computed differences
2.2.3. Redundancy Test
2.3. Experimental Design (II): 3D Reconstruction of a Rocky Cliff
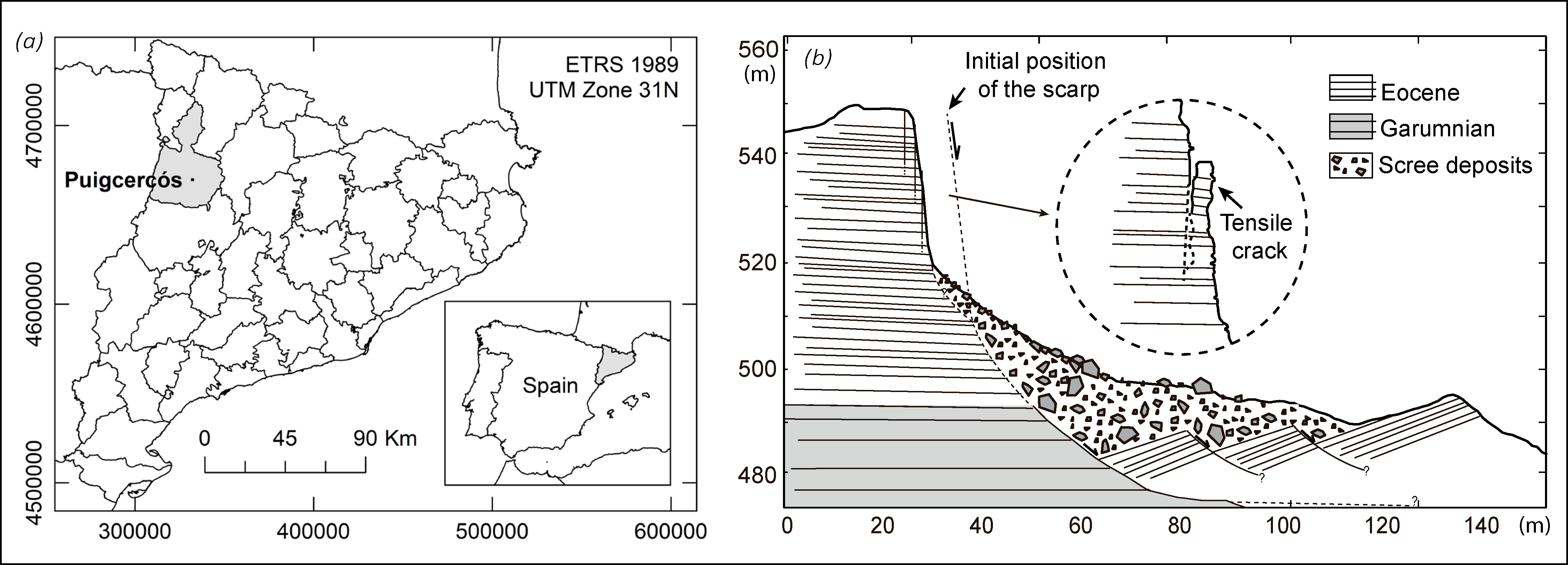
2.3.1. Pilot Study Area
2.3.2. Field Setup and Data Acquisition
2.3.3. Point Cloud Reconstruction
3. Results
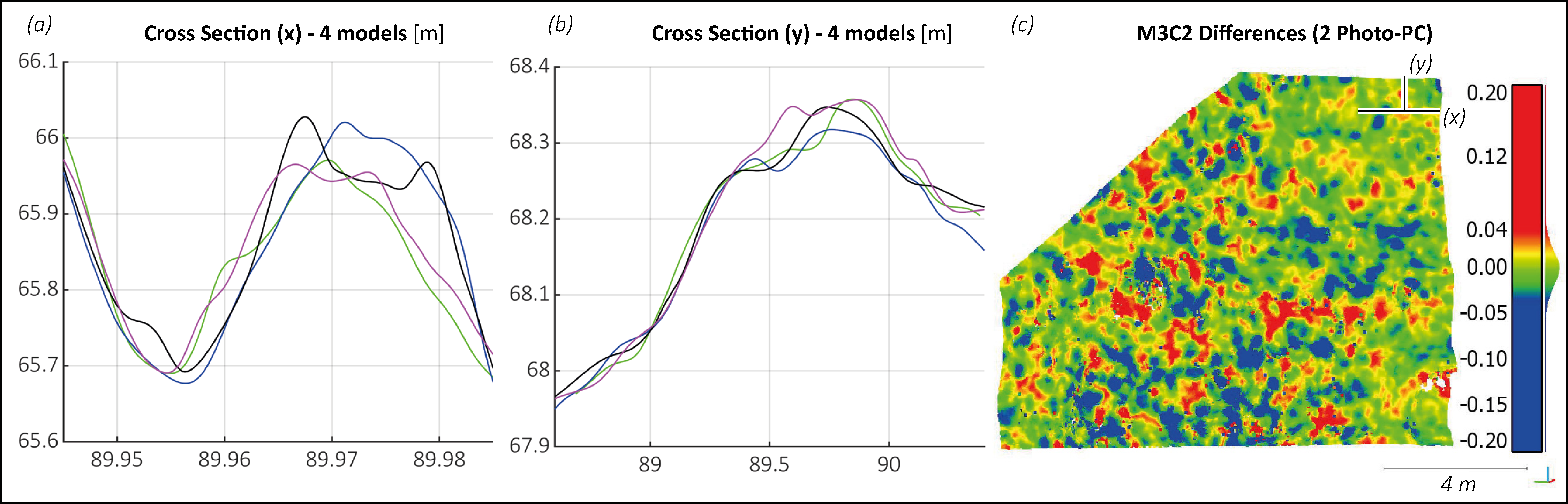
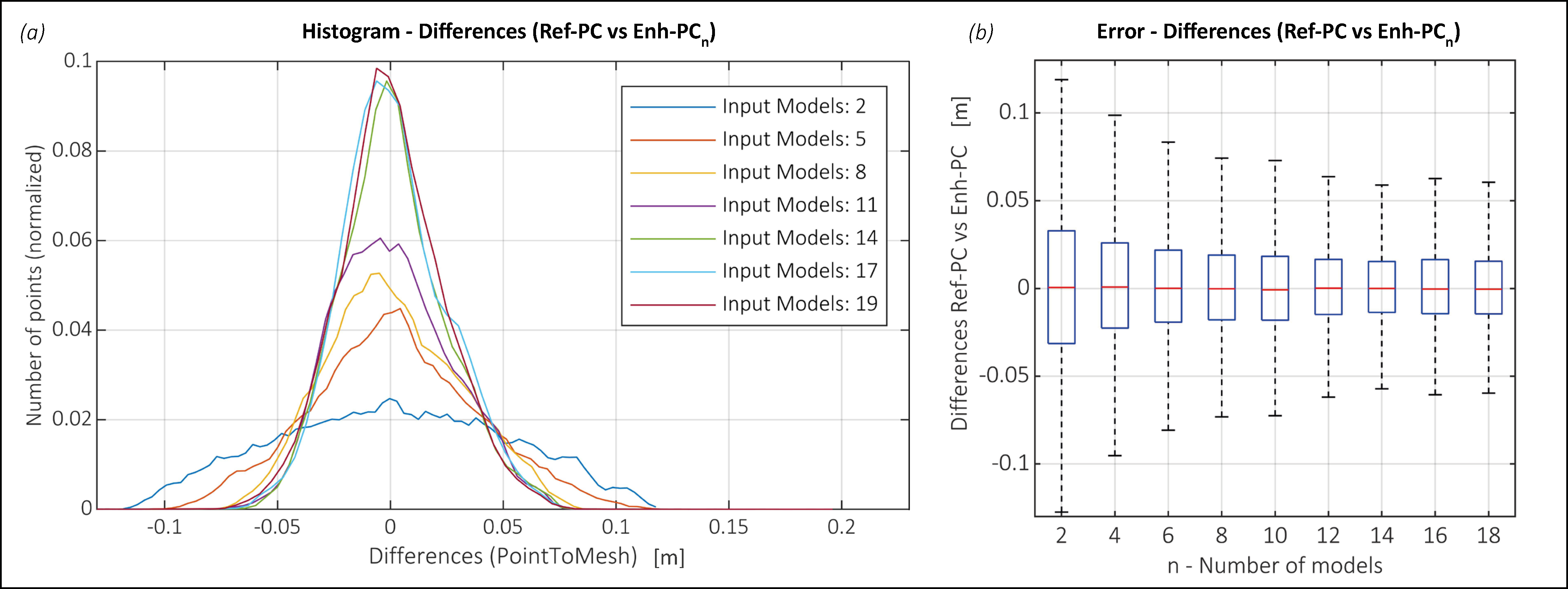
3.1. Synthetic Test
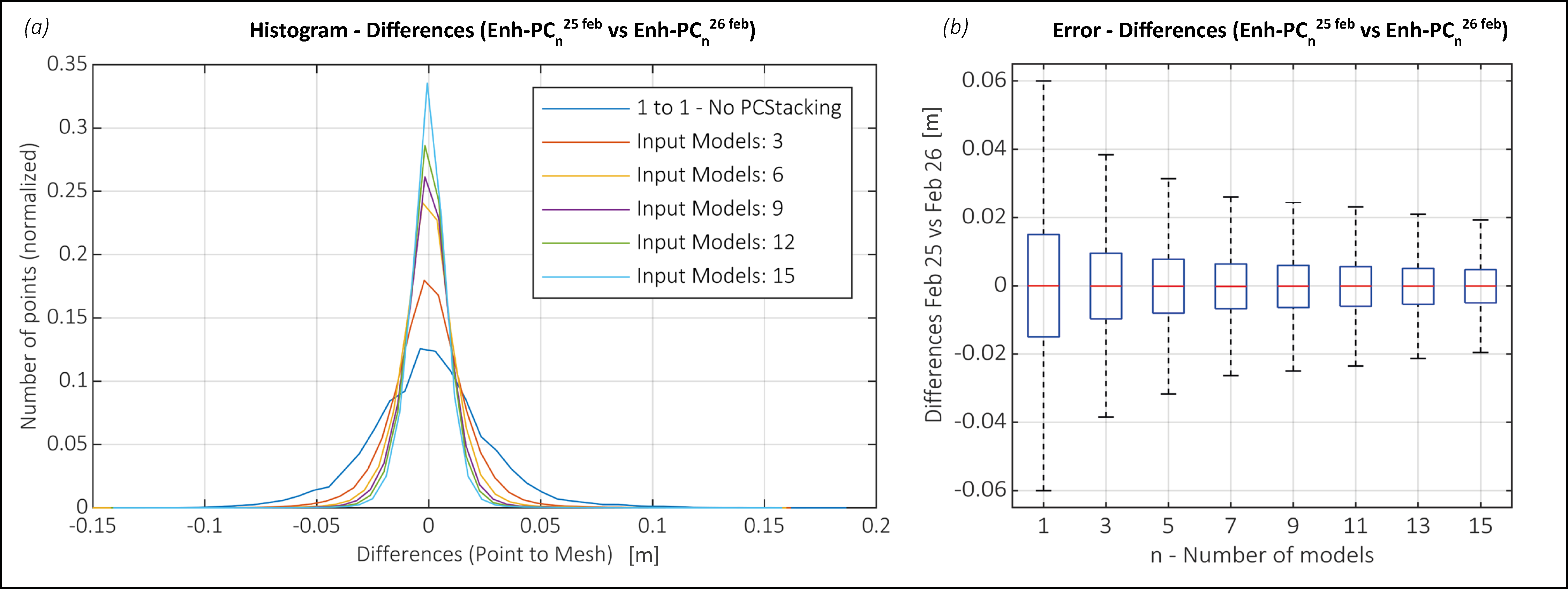
3.2. 3D Reconstruction on a Rocky Cliff
4. Discussion
4.1. Synthetic Test vs. Real Data
4.2. The PCStacking Method
4.3. Current Limits and Margins for Improvement
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dewez, T.J.B.; Rohmer, J.; Regard, V.; Cnudde, C. Probabilistic coastal cliff collapse hazard from repeated terrestrial laser surveys: Case study from Mesnil Val (Normandy, northern France). J. Coast. Res. 2016, 65, 702–707. [Google Scholar] [CrossRef]
- Eltner, A.; Kaiser, A.; Castillo, C.; Rock, G.; Neugirg, F.; Abellán, A. Image-based surface reconstruction in geomorphometry-merits, limits and developments. Earth Surf. Dyn. 2016, 4, 359–389. [Google Scholar] [CrossRef]
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. “Structure-from-Motion” photogrammetry: A low-cost, effective tool for geoscience applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef]
- Riquelme, A.J.; Abellán, A.; Tomás, R.; Jaboyedoff, M. A new approach for semi-automatic rock mass joints recognition from 3D point clouds. Comput. Geosci. 2014, 68, 38–52. [Google Scholar] [CrossRef]
- Derron, M.H.; Jaboyedoff, M. LIDAR and DEM techniques for landslides monitoring and characterization. Nat. Hazards Earth Syst. Sci. 2010, 10, 1877–1879. [Google Scholar] [CrossRef]
- Jaboyedoff, M.; Oppikofer, T.; Abellán, A.; Derron, M.H.; Loye, A.; Metzger, R.; Pedrazzini, A. Use of LIDAR in landslide investigations: A review. Nat. Hazards 2012, 61, 5–28. [Google Scholar] [CrossRef]
- García-Sellés, D.; Falivene, O.; Arbués, P.; Gratacos, O.; Tavani, S.; Muñoz, J.A. Supervised identification and reconstruction of near-planar geological surfaces from terrestrial laser scanning. Comput. Geosci. 2011, 37, 1584–1594. [Google Scholar] [CrossRef]
- Royán, M.J.; Abellán, A.; Jaboyedoff, M.; Vilaplana, J.M.; Calvet, J. Spatio-temporal analysis of rockfall pre-failure deformation using Terrestrial LiDAR. Landslides 2014, 11, 697–709. [Google Scholar] [CrossRef]
- Brodu, N.; Lague, D. 3D terrestrial lidar data classification of complex natural scenes using a multi-scale dimensionality criterion: Applications in geomorphology. ISPRS J. Photogramm. Remote Sens. 2012, 68, 121–134. [Google Scholar] [CrossRef]
- Abellán, A.; Vilaplana, J.M.; Calvet, J.; García-Sellés, D.; Asensio, E. Rockfall monitoring by Terrestrial Laser Scanning—Case study of the basaltic rock face at Castellfollit de la Roca (Catalonia, Spain). Nat. Hazards Earth Syst. Sci. 2011, 11, 829–841. [Google Scholar] [CrossRef]
- Kromer, R.A.; Abellán, A.; Hutchinson, D.J.; Lato, M.; Edwards, T.; Jaboyedoff, M. A 4D filtering and calibration technique for small-scale point cloud change detection with a terrestrial laser scanner. Remote Sens. 2015, 7, 13029–13058. [Google Scholar] [CrossRef]
- Jaboyedoff, M.; Demers, D.; Locat, J.; Locat, A.; Locat, P.; Oppikofer, T.; Robitaille, D.; Turmel, D. Use of terrestrial laser scanning for the characterization of retrogressive landslides in sensitive clay and rotational landslides in river banks. Can. Geotech. J. 2009, 46, 1379–1390. [Google Scholar] [CrossRef]
- Smith, M.W.; Carrivick, J.L.; Quincey, D.J. Structure from motion photogrammetry in physical geography. Prog. Phys. Geogr. 2015, 40, 247–275. [Google Scholar] [CrossRef]
- Lague, D.; Brodu, N.; Leroux, J. Accurate 3D comparison of complex topography with terrestrial laser scanner: Application to the Rangitikei canyon (N-Z). ISPRS J. Photogramm. Remote Sens. 2013, 82, 10–26. [Google Scholar] [CrossRef]
- Williams, J.G.; Rosser, N.J.; Hardy, R.J.; Brain, M.J.; Afana, A.A. Optimising 4-D surface change detection: An approach for capturing rockfall magnitude-frequency. Earth Surf. Dyn. 2018, 6, 101–119. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S. Straightforward reconstruction of 3D surfaces and topography with a camera: Accuracy and geoscience application. J. Geophys. Res. Earth Surf. 2012, 117, 1–17. [Google Scholar] [CrossRef]
- Eltner, A.; Schneider, D. Analysis of Different Methods for 3D Reconstruction of Natural Surfaces from Parallel-Axes UAV Images. Photogramm. Rec. 2015, 30, 279–299. [Google Scholar] [CrossRef]
- Parente, L.; Chandler, J.H.; Dixon, N. Optimising the quality of an SfM-MVS slope monitoring system using fixed cameras. Photogramm. Rec. 2019, 34, 408–427. [Google Scholar] [CrossRef]
- Petrie, G.; Toth, C. Introduction to Laser Ranging, Profiling, and Scanning. In Topographic Laser Ranging and Scanning; Shan, J., Toth, C.K., Eds.; CRC Press/Taylor & Francis: London, UK, 2008; pp. 1–28. [Google Scholar]
- Abellán, A.; Jaboyedoff, M.; Oppikofer, T.; Vilaplana, J.M. Detection of millimetric deformation using a terrestrial laser scanner: Experiment and application to a rockfall event. Nat. Hazards Earth Syst. Sci. 2009, 9, 365–372. [Google Scholar] [CrossRef]
- Kaiser, A.; Neugirg, F.; Rock, G.; Müller, C.; Haas, F.; Ries, J.; Schmidt, J. Small-scale surface reconstruction and volume calculation of soil erosion in complex moroccan Gully morphology using structure from motion. Remote Sens. 2014, 6, 7050–7080. [Google Scholar] [CrossRef]
- Castillo, C.; Pérez, R.; James, M.R.; Quinton, J.N.; Taguas, E.V.; Gómez, J.A. Comparing the accuracy of several field methods for measuring gully erosion. Soil Sci. Soc. Am. J. 2012, 76, 1319–1332. [Google Scholar] [CrossRef]
- Javernick, L.; Brasington, J.; Caruso, B. Modeling the topography of shallow braided rivers using Structure-from-Motion photogrammetry. Geomorphology 2014, 213, 166–182. [Google Scholar] [CrossRef]
- Pan, B. Digital image correlation for surface deformation measurement: Historical developments, recent advances and future goals. Meas. Sci. Technol. 2018, 29, 1–32. [Google Scholar] [CrossRef]
- Gabrieli, F.; Corain, L.; Vettore, L. A low-cost landslide displacement activity assessment from time-lapse photogrammetry and rainfall data: Application to the Tessina landslide site. Geomorphology 2016, 269, 56–74. [Google Scholar] [CrossRef]
- Travelletti, J.; Delacourt, C.; Allemand, P.; Malet, J.P.; Schmittbuhl, J.; Toussaint, R.; Bastard, M. Correlation of multi-temporal ground-based optical images for landslide monitoring: Application, potential and limitations. ISPRS J. Photogramm. Remote Sens. 2012, 70, 39–55. [Google Scholar] [CrossRef]
- Stumpf, A.; Malet, J.P.; Allemand, P.; Pierrot-Deseilligny, M.; Skupinski, G. Ground-based multi-view photogrammetry for the monitoring of landslide deformation and erosion. Geomorphology 2015, 231, 130–145. [Google Scholar] [CrossRef]
- Cardenal, J.; Mata, E.; Delgado, J.; Hernandez, M.A.; Gonzalez, A. Close Range Digital Photogrammetry Techniques Applied To. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, XXXVI, 235–240. [Google Scholar]
- Kromer, R.; Walton, G.; Gray, B.; Lato, M.; Group, R. Development and Optimization of an Automated Fixed-Location Time Lapse Photogrammetric Rock Slope Monitoring System. Remote Sens. 2019, 11, 1890. [Google Scholar] [CrossRef]
- Manconi, A.; Kourkouli, P.; Caduff, R.; Strozzi, T.; Loew, S. Monitoring surface deformation over a failing rock slope with the ESA sentinels: Insights from Moosfluh instability, Swiss Alps. Remote Sens. 2018, 10, 672. [Google Scholar] [CrossRef]
- Tannant, D. Review of Photogrammetry-Based Techniques for Characterization and Hazard Assessment of Rock Faces. Int. J. Geohazards Environ. 2015, 1, 76–87. [Google Scholar] [CrossRef]
- Eltner, A.; Kaiser, A.; Abellan, A.; Schindewolf, M. Time lapse structure-from-motion photogrammetry for continuous geomorphic monitoring. Earth Surf. Process. Landf. 2017, 42, 2240–2253. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S.; d’Oleire-Oltmanns, S.; Niethammer, U. Optimising UAV topographic surveys processed with structure-from-motion: Ground control quality, quantity and bundle adjustment. Geomorphology 2017, 280, 51–66. [Google Scholar] [CrossRef]
- Santise, M.; Thoeni, K.; Roncella, R.; Sloan, S.W.; Giacomini, A. Preliminary tests of a new low-cost photogrammetric system. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. -ISPRS Arch. 2017, 42, 229–236. [Google Scholar] [CrossRef]
- Wilkinson, M.W.; Jones, R.R.; Woods, C.E.; Gilment, S.R.; McCaffrey, K.J.W.; Kokkalas, S.; Long, J.J. A comparison of terrestrial laser scanning and structure-frommotion photogrammetry as methods for digital outcrop acquisition. Geosphere 2016, 12, 1865–1880. [Google Scholar] [CrossRef]
- Sturzenegger, M.; Yan, M.; Stead, D.; Elmo, D. Application and limitations of ground-based laser scanning in rock slope characterization. In Proceedings of the 1st Canada—U.S. Rock Mechanics Symposium, Simon Fraser University, Burnaby, BC, Canada, 27–31 May 2007; Volume 1, pp. 29–36. [Google Scholar]
- Nouwakpo, S.K.; Weltz, M.A.; McGwire, K. Assessing the performance of structure-from-motion photogrammetry and terrestrial LiDAR for reconstructing soil surface microtopography of naturally vegetated plots. Earth Surf. Process. Landf. 2016, 41, 308–322. [Google Scholar] [CrossRef]
- Verma, A.K.; Bourke, M.C. A method based on structure-from-motion photogrammetry to generate sub-millimetre-resolution digital elevation models for investigating rock breakdown features. Earth Surf. Dyn. 2019, 7, 45–66. [Google Scholar] [CrossRef]
- Bin, W.; Hai-bin, Z.; Bin, L. Detection of Faint Asteroids Based on Image Shifting and Stacking Method. Chin. Astron. Astrophys. 2018, 42, 433–447. [Google Scholar] [CrossRef]
- Kurczynski, P.; Gawiser, E. A simultaneous stacking and deblending algorithm for astronomical images. Astron. J. 2010, 139, 1592–1599. [Google Scholar] [CrossRef]
- Zhang, C.; Bastian, J.; Shen, C.; Van Den Hengel, A.; Shen, T. Extended depth-of-field via focus stacking and graph cuts. In Proceedings of the 2013 IEEE International Conference on Image Processing, Melbourne, Australia, 15–18 September 2013; pp. 1272–1276. [Google Scholar]
- Lato, M.J.; Bevan, G.; Fergusson, M. Gigapixel imaging and photogrammetry: Development of a new long range remote imaging technique. Remote Sens. 2012, 4, 3006–3021. [Google Scholar] [CrossRef]
- Selvakumaran, S.; Plank, S.; Geiß, C.; Rossi, C.; Middleton, C. Remote monitoring to predict bridge scour failure using Interferometric Synthetic Aperture Radar (InSAR) stacking techniques. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 463–470. [Google Scholar] [CrossRef]
- Liu, G.; Fomel, S.; Jin, L.; Chen, X. Stacking seismic data using local correlation. Geophysics 2009, 74, V43–V48. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Furukawa, Y.; Ponce, J. Accurate, dense, and robust multiview stereopsis. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1362–1376. [Google Scholar] [CrossRef] [PubMed]
- Furukawa, Y.; Curless, B.; Seitz, S.M.; Szeliski, R. Towards internet-scale multi-view stereo. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 1434–1441. [Google Scholar]
- Girardeau-Montaut, D. CloudCompare (version 2.x; GPL software), EDF R&D, Telecom ParisTech. Available online: http://www.cloudcompare.org/ (accessed on 20 January 2020).
- Hungr, O.; Leroueil, S.; Picarelli, L. The Varnes classification of landslide types, an update. Landslides 2014, 11, 167–194. [Google Scholar] [CrossRef]
- Vidal, L.M. Nota acerca de los hundimientos ocurridos en la Cuenca de Tremp (Lérida) en Enero de 1881. In Boletín de la Comisión del Mapa Geológico de España VIII; Madrid, Spain, 1881; pp. 113–129. [Google Scholar]
- Corominas, J.; Alonso, E. Inestabilidad de laderas en el Pirineo catalán. Ponen. y Comun. 1984. ETSICCP-UPC C.1–C.53. [Google Scholar]
- Abellán, A.; Calvet, J.; Vilaplana, J.M.; Blanchard, J. Detection and spatial prediction of rockfalls by means of terrestrial laser scanner monitoring. Geomorphology 2010, 119, 162–171. [Google Scholar] [CrossRef]
- Royán, M.J.; Abellán, A.; Vilaplana, J.M. Progressive failure leading to the 3 December 2013 rockfall at Puigcercós scarp (Catalonia, Spain). Landslides 2015, 12, 585–595. [Google Scholar] [CrossRef]
- Tonini, M.; Abellan, A. Rockfall detection from terrestrial LiDAR point clouds: A clustering approach using R. J. Spat. Inf. Sci. 2014, 8, 95–110. [Google Scholar] [CrossRef]





© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blanch, X.; Abellan, A.; Guinau, M. Point Cloud Stacking: A Workflow to Enhance 3D Monitoring Capabilities Using Time-Lapse Cameras. Remote Sens. 2020, 12, 1240. https://doi.org/10.3390/rs12081240
Blanch X, Abellan A, Guinau M. Point Cloud Stacking: A Workflow to Enhance 3D Monitoring Capabilities Using Time-Lapse Cameras. Remote Sensing. 2020; 12(8):1240. https://doi.org/10.3390/rs12081240
Chicago/Turabian StyleBlanch, Xabier, Antonio Abellan, and Marta Guinau. 2020. "Point Cloud Stacking: A Workflow to Enhance 3D Monitoring Capabilities Using Time-Lapse Cameras" Remote Sensing 12, no. 8: 1240. https://doi.org/10.3390/rs12081240
APA StyleBlanch, X., Abellan, A., & Guinau, M. (2020). Point Cloud Stacking: A Workflow to Enhance 3D Monitoring Capabilities Using Time-Lapse Cameras. Remote Sensing, 12(8), 1240. https://doi.org/10.3390/rs12081240