Abstract
Change detection (CD) networks based on supervised learning have been used in diverse CD tasks. However, such supervised CD networks require a large amount of data and only use information from current images. In addition, it is time consuming to manually acquire the ground truth data for newly obtained images. Here, we proposed a novel method for CD in case of a lack of training data in an area near by another one with the available ground truth data. The proposed method automatically entails generating training data and fine-tuning the CD network. To detect changes in target images without ground truth data, the difference images were generated using spectral similarity measure, and the training data were selected via fuzzy c-means clustering. Recurrent fully convolutional networks with multiscale three-dimensional filters were used to extract objects of various sizes from unmanned aerial vehicle (UAV) images. The CD network was pre-trained on labeled source domain data; then, the network was fine-tuned on target images using generated training data. Two further CD networks were trained with a combined weighted loss function. The training data in the target domain were iteratively updated using he prediction map of the CD network. Experiments on two hyperspectral UAV datasets confirmed that the proposed method is capable of transferring change rules and improving CD results based on training data extracted in an unsupervised way.
1. Introduction
Change detection (CD) is the process of identifying changes in land cover or land use in the same geographical area over time [1]. CD is one of the most important fields in remote sensing (RS) because it can be used with RS images in many real-world applications, such as the measurement of urban expansion [2], disaster evaluation [3], and crop monitoring [4].
As the availability of images from satellites and unmanned aerial vehicles (UAVs) with very-high resolution (VHR) cameras has increased, a large amount of data with a resolution of less than 1 m has been collated on regions of interest. More recently, smaller and lighter hyperspectral sensors have been developed that can be integrated with UAVs and provide hundreds of spectral bands. Hyperspectral UAV images can provide not only high levels of spatial detail but also rich spectral information about surface materials [5]. The detailed spectral signatures obtainable from hyperspectral images can help to identify finer spectral changes and therefore support more effective CD.
CD methods for analyzing VHR in both spatial and spectral images, such as those obtained from hyperspectral UAVs, encounter several issues, including high dimensionality and spatial and spectral complexity of images, geometric inconsistency between these images, and larger spectral variability which is the difference in spectral signatures caused by illumination and atmospheric conditions [6,7]. Various CD methods have been developed to solve these problems, which can be divided into unsupervised and supervised approaches. Unsupervised CD methods usually detect spectrally distinct pixels and are easily applied because they do not require prior knowledge of the region. Furthermore, they minimize the chances of human error. However, the changes identified can be spectrally grouped in classes that are not of interest to an analyst, for examples, spectral noise and shadow. On the other hand, supervised CD methods discriminate between changed and unchanged areas by using available training data, giving analysts control over the classes under scrutiny by defining the range of changes. However, it is difficult to collect extensive training data in the real world that will assist in the recognition of categories that are not represented in the training data itself [8,9].
Recently, deep learning methods, including supervised and unsupervised approaches, have been proven effective in image processing and CD [10]. Training data were generated using unsupervised methods, and deep learning networks based on a supervised learning approach were trained to produce change maps. Gong et al. [11] proposed a deep neural network, which includes unsupervised feature learning and supervised fine-tuning for the CD of synthetic aperture radar (SAR) data. This method can avoid the generation of difference images (DIs), which present differences between multi-temporal images of the same area, using a joint classifier for the temporal images. A restricted Boltzmann machine was used to apply CD to SAR images. Song et al. [12] also proposed using recurrent three-dimensional (3D) fully convolutional networks (FCNs) to effectively extract spectral-spatial-temporal features from hyperspectral images and preserve the spatial structure of feature maps. To train CD networks without prior information, training samples were generated automatically using principal component analysis and spectral correlation angles between temporal images. DIs of VHR satellite images were generated using deep features obtained from deep learning networks, and saliency detection was implemented to categorize these into three classes: changed, unchanged, and uncertain [13]. The changed and unchanged pixels were used as the training data for flexible convolutional neural network, and post-processing was implemented to generate change maps. Convolutional neural network (CNN) and change vector analysis were used as feature extractors to generate the predicted DI; then, the generative adversarial network (GAN) can build a model connecting the predicted DI and the original multispectral images [14]. By doing so, a better DI was generated, and GAN generator and fuzzy local information c-means clustering method were used to obtain the desired binary CD map. In addition, a deep Siamese convolutional network (DSCNN) with a recurrent neural network was developed to detect changes in both homogeneous optical images and heterogeneous data such as SAR and optical images [15]. To achieve this, DSCNN extracted the features map from homogeneous inputs with weight-sharing and when the inputs were heterogeneous, DSCNN was modified as a pseudo-Siamese network and two branches were designed with different convolution kernels and numbers.
Although the aforementioned methods are effective in the CD of various RS images, supervised deep learning networks require a large amount of training data and only use information from current images. To improve CD performance using additional knowledge from existing related images, CD methods involving transfer learning (TL) have been developed [16,17]. TL is a commonly used method for overcoming a lack of training data and utilizing knowledge acquired while solving one task to solve related ones. TL can be undertaken using pre-trained models as a starting point; however, when such information is reused, the effective transfer of learned information is a challenging issue in the RS field [18]. This is because it is difficult to reflect differences generated from sensor characteristics, noise, and distortions [16]. Yang et al. [16] linked a CD network with a reconstruction network to gain additional information from related temporal SAR images. The CD was conducted in the source domain with reference, and the reconstruction was performed in the target domain without reference. In the target domain, the DI was reconstructed by a log-ratio operator to consider the speckle noise of SAR images. The lower layers of the CD and reconstruction networks shared parameters, and, at the fine-tuning stage, the lower layers of the CD network were frozen, while the higher layers were fine-tuned for the target domain. Furthermore, CD methods using opensource datasets have been proposed [17]. For example, the ISPRS dataset, including VHR aerial images and labeled maps, was used to supervise semantic segmentation tasks. The pre-trained information in the ISPRS dataset can also be used for CD tasks involving VHR optical images. Liu et al. [17] first pre-trained a U-net model on the ISPRS dataset and minimize a designed loss function to combine high-level features from the pre-trained model with semantic information contained in the CD dataset. After that, they generated DIs using the log-ratio, and a CD map was produced by clustering DIs in post-processing. The previously mentioned CD methods that successfully used TL reused prior knowledge from the source domain, and DIs were generated as initial reference data to train the CD network.
Although supervised CD methods have been known to outperform unsupervised ones in terms of accuracy, the necessity of unsupervised approaches increases as huge amounts of data are accumulated [5,9]. Hence, it is important to transfer knowledge from pre-trained networks to other study sites where it is difficult to obtain information about changes. This paper proposes a CD method to transfer change rules obtained from supervised deep learning CD networks to other images without ground truth data. It automatically generates label data using spectral information from temporal hyperspectral images, and two recurrent FCNs are trained in parallel with a combined loss function. The proposed method provides the following three major contributions.
- (1)
- The method can be effectively applied to VHR in both spatial and spectral images by automatically generating initial label data from plentiful spectral bands and using multiscale 3D filters to extract various sized objects from the images.
- (2)
- Our method can improve the CD results of hyperspectral UAV images when using only label data obtained in an unsupervised way by transferring pre-trained information. In doing so, it possesses the advantages of both supervised and unsupervised approaches.
- (3)
- The proposed method can effectively transfer change rules using a combined weighted loss and detect changes with minimal additional training. Furthermore, the final CD map can be created without post-processing requirements, such as clustering and classification.
The rest of this paper is organized as follows. In Section 2, we present the proposed CD architecture. In Section 3, the data sets and the environmental conditions of the experiments are described. The results and discussion are addressed in Section 4 and Section 5, respectively. Finally, we draw our conclusions in Section 6.
2. Methods
The proposed method comprises two networks, and the final goal is detecting changes in temporal hyperspectral UAV images in the absence of ground truth data or prior knowledge regarding changes based on pre-trained supervised CD networks. Section 2.1 represents the overall architecture of the proposed CD methods. Section 2.2 and Section 2.3 explain the detailed structure of the CD network used in this paper and generation of label data, respectively. The ways of quality assessment are shown in the last subsection, Section 2.4. To simplify the expression, the acronyms used in this paper are given in Table 1.

Table 1.
The glossary of acronyms used in this paper.
2.1. Architecture of the Proposed Change Detection (CD) Methods
There are two CD networks as shown in Figure 1. One network was a CD network for images with ground truth data (which were called the labeled source dataset) and the other was a CD network for images without ground truth data (which was called the unlabeled target dataset). First, given two co-registered temporal images with ground truth data that were acquired over the same region but at two different times, the CD network of the first branch was trained on the source dataset. The network then generated a change map, which was composed of the set of classes of changed and unchanged areas. In this step, the training samples were randomly extracted from the ground truth data. Each training sample is a 3D patch of size . k is the length of the column and row and d is the number of spectral bands.
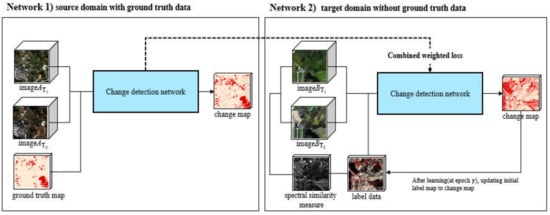
Figure 1.
Framework of the proposed method. First, network 1 is trained on the labeled source dataset, and network 2 is initialized as the pre-trained network 1. The automatically generated label data are fed into network 2 and the two networks are further trained by combined weighted loss. The label data is iteratively updated to change the map of network 2 at each defined epoch.
Second, after training the first CD network, the second CD network was initialized by the pre-trained network. The inputs to the second network were the unlabeled target images. To fine-tune the second CD network, initial label data were automatically generated using spectral similarity measures between the temporal images and a clustering algorithm. The detailed process of generating initial label data is explained in Section 2.3. The label data was composed of changed, non-changed, and background (null value) classes, and only the changed and non-changed classes were used as training data. After generating label data for the second CD network, the CD networks of both branches were further trained in parallel with combined loss which is defined as the weighted sum of losses of the two networks. The losses of the first and second networks are and , respectively, and the binary cross entropy loss can be defined as follows:
where, N is the number of samples. is ground truth value and is the predicted value. indicates 0 or 1, and they represent how far away from the true value. The prediction is for each class and averages of these class-wise errors to obtain the final loss. The combined loss is defined as follows:
where and are the weights of two networks. Because the pre-trained weights and biases were trained on labeled source dataset, the loss of the first network was small, and the loss of the second network was large at first. Therefore, was set at a higher rate than . For all experiments, and were set to 0.8 and at 0.2, respectively. As learning progressed through sharing , the loss of the second CD network was reduced based on the first CD network.
The initial label data of the target dataset included null values. When learning with the initial label data, it was impossible to train on the locations of pixels with null values. To train the CD networks for the entire regions of images, the training data were iteratively updated to the CD map of the second CD network at the defined epoch. In particular, it was important to update the initial training data with null values to the CD result map because the accuracy of the CD map affected the remaining training results. Therefore, the first updating period was relatively long at 100 epochs; after the first update, the updating cycle was set at a shorter period of 10 epochs.
2.2. CD Network for Very High-Resolution Hyperspectral UAV Images
UAV images with a resolution of 1 m or less contain objects of various sizes from very small neighborhoods to large regions composed of thousands of pixels. Smaller features, such as the edges of buildings and the texture of vegetation, tend to be extracted by small-scale convolutional filters, and the coarser general structures tend to respond to larger-scale convolutional filters [19]. In addition, hyperspectral UAV images can provide detailed spectral reflectance signatures, which show electromagnetic energy wavelengths. Analyzing spectral reflectance signatures makes it possible to identify different surface materials because the reflectance of different materials varies with the wavelength of the electromagnetic energy. Therefore, it is important to consider the spatial and spectral characteristics of surface objects as effective ways to analyze VHR hyperspectral UAV images.
This study used a CD network with multiscale 3D filters to extract various features, spatially and spectrally, from hyperspectral UAV images and detect changes by comparing these features. 3D filters can effectively extract spatial and spectral information of hyperspectral images, learning the local signal changes in both spatial and spectral dimensions of the feature cube [20]. Moreover, multiscale 3D filters can exploit the variously sized materials in high spatial resolution images [21].
The CD network was composed of 3D convolutional filters and convolutional long short-term memory (ConvLSTM) layers and generated binary change maps. The architecture of the CD network is shown in Figure 2.
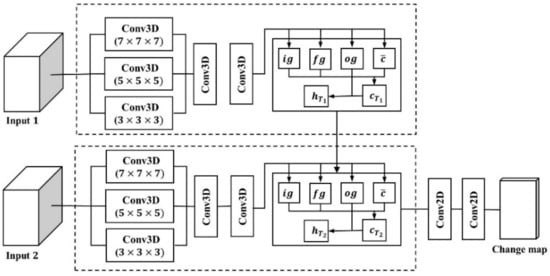
Figure 2.
Architecture of the CD network with multiscale 3D filters.
The size of the 3D patches was empirically set to in this work. The 3D patches were extracted along with the label data and central pixels of these cubes as the training samples. We randomly selected the center of each of the 40,000 pixels as training data, 20,000 pixels as validation data, and 30,000 pixels as testing data. Because convolutional layers exploited information from neighboring pixels and the training and validation pixels were extracted from the same image, their features were likely to overlap owing to the shared source of information [22]. Overlap between training and validation data can result in intrinsic positive bias in the CD result. However, in this paper, because the images of the study areas consist of relatively few pixels (e.g., pixels), the number of training patches was reduced when extracting without overlap. Therefore, data for network training were randomly extracted to increase the amount of training data.
After extracting the training samples, two patches captured from the same location in two temporal images were separately fed into the convolutional layer with different scale 3D filters in parallel. The size of 3D filters can be determined by the spatial and spectral resolution of the input images, and in this study, (, (, and ( 3D filters were used. Since the feature maps obtained from each convolutional filter were of different sizes, it was necessary to ensure each map was the same size before combining them into one joint feature map. Except for the number of channels used, the features in each map shared all relevant dimensions using padding and were collected in one tensor. The joint feature maps obtained from the convolutional layers were combined, and they passed through two more 3D convolutional layers. The filter size of these convolutional layers was (. ( is known as the best choice for 3D convolution in spatiotemporal feature learning [20]. After that, the spatial–spectral feature maps were fed into ConvLSTM layers to reflect temporal information and recode change rules. The outputs from the ConvLSTM layers were passed through 2D convolutional layers to generate a score map. The final number of feature maps equaled the number of classes. Finally, the pixels were classified into relevant classes according to the score map.
2.3. Generating Label Data
To train the CD network, label data was necessary because the loss is calculated based on the difference between predicted values and label data. Therefore, identification of areas where changes occurred and did not occur was necessary. In many studies [15,23,24], randomly selected samples from ground truth maps have been used as training data to calculate CD accuracies between prediction maps and ground truth maps. In this case, the accuracy of the training data was 100% because the training data were generated from ground truth data. Although this approach can evaluate the performance of the proposed method and detect changes within input sites, it is difficult to apply in real-world cases where it can be challenging to obtain prior information of changes at the sites under investigation. For practical reasons, there is a need for approaches that can be applied to a broad area with minimal training data because it is impossible to obtain training data with 100% accuracy covering the whole area of the sites under study. This study aimed to transfer pre-trained information from CD networks trained on data generated from the ground truth to other sites where there were no ground truth data. To achieve this, the label data were automatically generated using information from the input images.
Using DIs for CD is a well-known approach. DIs can show changed areas by highlighting the differences between two images of the same area. After DIs are generated, difference imaging analysis is performed to determine the nature of the changes. Recently, various deep learning-based CD networks have used DIs because they can indicate changes that have occurred and can be used as ground truth data for inputs without labeled data [14,16,17,21]. Therefore, the accuracy of CD results depends on the quality of DIs.
The log ratio is among the most classic algorithms that can produce a DI for each pair of pixels to examine speckle noise and it can be applied to both SAR and optical images. Liu et al. [17] generated DI from optical images using log ratio; then, a k-means clustering algorithm was applied to divide changed and unchanged pixels. Moreover, DIs based on log-ratio analysis were used as inputs for the reconstruction network to reconstruct the DIs for SAR images [16]. Feature maps obtained from convolutional layers could be used to generate DIs of optical images [14,25]. DIs defined by the absolute difference between two feature maps were created at each of the five levels of U-net model [25]. The DI then was used by the decoder in copy and concatenate operations instead of feature maps. Furthermore, feature maps were integrated by fully connected layers into a one-band feature map and the initial DI was generated using pre-prediction of the network [14]. The initial DI iteratively was updated until when below a threshold. The final CD map was generated by a fuzzy local information c-means algorithm.
Although previous studies effectively generated DIs for deep learning-based networks, the study of the utilization of spectral information of the original input data was insufficient. Hyperspectral images have a large amount of spectral information and they can provide more detailed spectral information about objects than multispectral images. Spectral information can be measured by spectral similarity measures, which calculate how close a given spectrum is to a specified reference spectrum and can indicate the presence of changes. In addition, calculating spectral similarities for CD has the advantage of reducing the CD problem to one dimension. It is relatively simple compared with kernel-based methods [26]. The computational cost of kernel-based methods is higher than the cost of direct comparison using similarity metrics. Therefore, a spectral similarity index allows easy application and interpretation of DIs [27].
This paper compares representative similarity indices to select an appropriate measure for CD of VHR hyperspectral images. DIs can be generated after the spectral similarity measure and automatic threshold are applied. Spectral similarity measures can be divided into two groups. One consists of original similarity indices such as spectral angle mapper (SAM), the spectral correlation angle (SCA), spectral information divergence (SID), and the Jeffries–Matusita (JM) distance; the other is a similarity index, which is defined by combining original single methods. They are effective in discriminating between spectral differences by overcoming the limitations of the original indices [28,29]. This study compared the various hybrid spectral similarity indices, e.g., SIDSAM (a combination of SID with SAM), SIDSCA (a combination of SID with SCA), and JMSAM (a combination of JM with SAM).
2.3.1. Difference Imaging Based on the Spectral Similarity Measures
Given two vectors of spectral signatures, such as and where L is the number of the spectral band and T denotes transposition, and are spectral signatures of the corresponding position in the temporal satellite images in the form of either radiation or reflectance values, respectively. SAM calculates the angle between two spectra and quantifies similarity. It is computationally simple and relatively insensitive to scale and illumination effects because the angle is invariant with respect to the length of the vectors. However, it has been regarded as unsuitable for spectrally similar objects [28,30]. The equation of SAM is as follows:
The spectral correlation measure (SCM) is the Pearson’s correlation coefficient between two spectra. Unlike SAM, SCM can discriminate between the negative and positive correlations between two spectra, and it is relatively insensitive to effects that are gained or offset [31,32]. SCM is calculated using Equation (4).
The SCM takes values between –1 and 1 and reflects the extent of linear relationships. To compare it with other similarity indices, the SCM can be represented as SCA with Equation (5).
SID is derived from the divergence information theory and models spectral band to band variability as a result of uncertainty caused by randomness [33,34]. SID considers geometrical information between two spectra and can be defined using the relative entropy and of with respect to and with respect to , respectively (Equations (6)–(8)).
where is the relative entropy with respect to band l. The probability mass functions, such as p and q, are defined as normalized pixel spectra such that and . and are self-information of and for band l, respectively, and they are defined as and . If the two spectra have distinct probability distributions, SID will tend to be large and is invariant with the scaling of spectral magnitude [35].
The JM distance measures the average distance between two class density functions. It can overcome the limitation of transformed divergence by exponentially decreasing weight to increase separation between the spectra [36].
and where are the mean vectors and and are the covariance matrices of signature and , respectively. is the determinant of . The value of the JM distance ranges between 0 and .
The limitations of original methods can be overcome using hybrid original indices such as SIDSAM, SIDSCA, and JMSAM. The hybrid methods can be calculated using both tan and sin versions. In this paper, the tan version of hybrid measures, such as , and were considered because the sine version has lower similarity values, and many studies have shown that the tan version showed superior performance [34,37].
SIDSAM and SIDSCA are formed by combining SID with SAM and SCA [31]. The SIDSAM mixed index can enable two similar spectra even more similar and two dissimilar spectra even more distinct (Equation (11)) [34].
SID-SCA is similar to SID-SCA but possesses the advantage of SCA in that it eliminates negative correlation and maintains the SAM characteristic of minimizing the shading effect. It is expressed as Equation (12) [34].
JM-SAM combines the stochastic JMD and SAM. The JM-SAM index can consider geometrical aspects such as angle and distance and band-information between two spectra. Therefore, it can discriminate more effectively than JM and SAM [36]. JM-SAM can be defined as Equation (13).
2.3.2. Sample Selection Using Fuzzy C-Means Clustering
After generating DI between two temporal images based on the hybrid spectral similarity index, DI was classified into changed/non-changed items using fuzzy c-means clustering (FCM) [38]. FCM is among the most widely used clustering method. It allows the pixels of whole images to belong to two or more clusters and can retain more information than hard clustering in some cases [11]. There are n pixels in , ,,. Fuzzy membership in FCM is achieved by computing the relative distance among the patterns and clustering centroids [39]. FCM aims at obtaining the membership probability of the pixel in DI for the jth cluster by minimizing the objective function J (U, V) [40].
where c is the number of clusters, m is the fuzzifier and represents different degrees, and V=[, ,,] is the matrix composed of c central values and cluster centroids and is defined using Equation (15).
Degree of membership is defined as follows:
FCM updates U and V iteratively to obtain an optimum solution. If for j = 1, …, c and i, then is assigned to cluster i.
If the pixel values of a DI are low (almost zero), there is a low possibility of changes, while high pixel values indicate a high possibility of changes because it means the pixel values at the corresponding locations are different. Generally, the number of clusters is set to two to make a binary map (changed and non-changed items). However, in this case, the uncertainty of training data can increase because there are pixels in the middle that cannot be determined to change or non-change. To reduce the uncertainty of training pixels and select training samples with pixels with a higher probability of changes and non-changes, we set c = 5 to cluster five classes, and then classes belonging to both extremes were set to changed and non-changed pixels, respectively. This is because it can be assumed that the pixels close to the maximum and minimum values of a DI have a high probability of showing changed and non-changed statuses, respectively. To determine the effectiveness of the hybrid spectral similarity measure, such as , , and , the accuracy of the training samples generated from each spectral similarity measure were compared; the best spectral similarity measure was selected for generating DIs.
2.4. Quality Assessment
There are many different ways to evaluate the accuracy of classification. In this paper, overall accuracy (OA), precision, recall, and the F1 score were used. OA represents the proportion of correctly classified observations compared with ground truth data and can be described as true positive (TP), true negative (TN), false negative (FN), and false positive (FP) (Equation (17)).
OA is simple and easy way to evaluate classification accuracy; however, when the class distribution is dissimilar, OA cannot appropriately show the effectiveness of the results. The F1 score is a better way to evaluate results when there are imbalanced classes as in the above case. The F1 score is the harmonic mean of the precision and recall values (Equation (18)). Precision and recall measures describe the score of correctly identified positive cases out of all predicted positive cases and all actual positive cases, respectively.
3. Datasets
Hyperspectral UAV images of two sites in Jeonju City in South Korea were used for CD. The dataset was acquired from the previous study [41]. The temporal hyperspectral UAV images were acquired on September 19, 2019 (), and October 16, 2019 (, respectively. They were acquired by a DJI Matrice 200 UAV equipped with hyperspectral sensors (Corning microHSI SHARK 410). This platform has accurate flight controls and inherent stability. The spatial resolution of the UAV sensor is 15 cm, and its spectral resolution is 4 nm over 150 bands ranging from 398.78 to 996.74 nm. The spatial resolution of the images was reduced to 60 cm to limit the number of classifications and reduce the memory requirements for deep learning. The flight path of the UAV was selected to follow the waypoint at a flying height of 200 m. The whole study area (covered in 15 passes. Study sites measuring , where errors associated with camera shaking and geometric problems were few, were selected from the whole area. The images were registered using the geographic map projection WGS-84. The center coordinates of sites 3 and 4 were (35°48′13″ N, 127°05′29″ E) and (35°47′19″ N, 127°07′26″ E), respectively (Figure 3). Prior to CD, the images were pre-processed by geometric and radiometric corrections based on the global navigation satellite system and field spectrometer data.
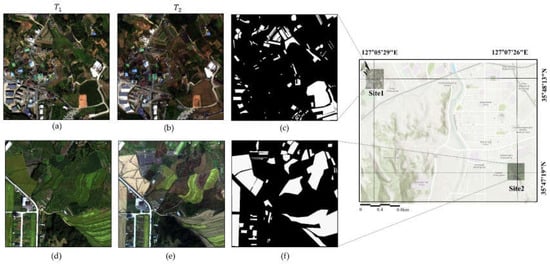
Figure 3.
Locations and hyperspectral UAV images of the two study sites. The upper images are of site 1 acquired at time (a) and (b) . The lower images are of site 2 acquired at time (d) and (e) . There are ground truth map (c) site1 and (f) site 2. The background map was obtained from the ArcGIS world map [42].
Ground truth data was created manually based on various web maps and field works. We defined the changes where the classes of land cover had changed, such as vegetation to bare soil. The classes of land cover in the study areas were defined as vegetation, bare soil, buildings, water, and roads. Colored roofs were all defined as “buildings.” “Bare soil” represented ground without buildings and vegetation, and “roads” encompassed asphalt roadways. Changes owing to the relief displacement and shadows were not counted as changes in the ground truth data. Moreover, the slight differences in vegetation vitality because of seasonal differences were not counted as changes.
4. Results
In this section, CD is conducted under four different conditions and CD accuracies are compared to evaluate the performance of the proposed method. In Section 4.1, we generate DIs using different hybrid spectral similarity measures such as SIDSAD, SIDSCA, and JMSAM, and initial label data are generated. CD accuracies when using the initial label data are compared to select the most suitable spectral similarity measure. In Section 4.2, to simultaneously confirm the effectiveness of using a pre-trained network and initial label data, various CD accuracies obtained using 1) training data randomly selected from the ground truth data and 2) a pre-trained network without additional training are compared. In the proposed method, a pre-trained network is used as the source domain and CD is conducted on the temporal images without ground truth data. In this case, we assumed that the target images had no associated ground truth data, so the generated label data in Section 4.1 are used as the initial ground truth map.
4.1. Label Data Generated from DIs
Figure 4 and Figure 5a–c show DIs from site 1 and site 2, respectively, that are the output of hybrid spectral similarity measures. The pixels with large differences in spectral reflectance between temporal images have high values (bright colors). For example, the regions that changed from bare soil to road or grass have bright colors in the DIs. The changes caused by shadows also appear bright although no meaningful changes actually occurred. However, the regions with little difference in spectral reflectance have values close to zero. SIDSAM and SIDSCA produced similar DIs. The regions where there were changes from bare soil and low vegetation to vegetation, changes from bare soil to newly constructed roads, and shadows were highlighted on DIs. JMSAM also identified the changed pixels; these changed pixels had higher values than in SID-based methods. However, in the DIs generated by JMSAM, the range of the changed pixels was wide and, in particular, not only changes in class types but also changes due to shadows were emphasized.

Figure 4.
DIs generated from (a) SIDSAM, (b) SIDCA, and (c) JMSAM; training samples generated from (d) SIDSAM, (e) SIDSCA, and (f) JMSAM; CD results using generated training samples (g) SIDSAM, (h) SIDSCA, and (i) JMSAM for site 1.


Figure 5.
DIs generated from (a) SIDSAM, (b) SIDCA, and (c) JMSAM; training samples generated from (d) SIDSAM, (e) SIDSCA, and (f) JMSAM; CD results using generated training samples (g) SIDSAM, (h) SIDSCA, and (i) JMSAM for site 2.
Figure 4 and Figure 5d–f show the training samples with three classes: changed (, non-changed (, and background with null values (. Although SIDSAM and SIDSCA produced similar DIs, SIDSCA seemed to be less affected by registration offset error. In the upper part of site 1, SIDSAM and JMSAM could not extract unchanged pixels properly because there was a difference in spectral reflectance when mosaicking the UAV images. SCA had the advantage of reducing the influence of gain and offset errors [30]. JMSAM could extract changed pixels, especially the distinct changes from bare soil to vegetation. However, the pixels where changes did not occur, i.e., those caused by shadow, were also extracted as training samples. Also, the areas of reduced vegetation vitality were classified into changed and non-changed data according to the degree of difference. For example, nearly all of the pixels in the upper left area in site 2, where there were changes from vegetation to bare soil, were identified as changed samples, but in the lower right area, the area with reduced vegetation was not extracted as changed pixels (Figure 5f).
To evaluate the effectiveness of the generated training data using various spectral similarity measures, the CD results using the training data were compared (Figure 4 and Figure 5g–i). Table 2 shows the accuracy of the CD maps. 3D patches randomly selected from and were fed into the CD network, which divided the whole study site area into two classes: changed and unchanged. In the training steps, was not used to train the CD network. JMSAM had the lowest CD accuracy for both site 1 and 2. The changed pixels were overestimated. In particular, the shadows caused by trees and buildings were classified as changed pixels. Although SIDSAM had a higher OA than SIDSCA at site 1, its F1 scores were lower than those of SIDSCA. It means that the change class could not be correctly classified. SIDSCA reported the highest F1 scores at both study sites. It shows that the training data generated from SIDSCA were more effective at detecting changes than other methods. However, some areas with changes in vegetation vitality were classified into unchanged classes. This is because the training data were selected from DIs that were calculated using spectral reflectance. According to the experimental results, we decided to use the training data generated from SIDSCA.

Table 2.
Accuracy of CD maps generated from various training data.
4.2. CD Results
The proposed method aimed to detect changes in temporal images without ground truth data based on pre-trained knowledge acquired from a nearby region with available training samples. We additionally conducted CD for two cases. The first case comprised CD of target images using the training samples obtained from ground truth data. In this study, although we assumed that target images have no ground truth or prior information, we compared the case in which ground truth data of target images exist to confirm the applicability of the proposed method. The second case comprised CD using only a pre-trained network, i.e., without additional training. There are two ways to detect change in target images without ground truth data using a supervised CD network, i.e., (1) generating label data in an unsupervised-manners, as in Section 4.1 and (2) using a pre-trained CD network trained on source data. Ideally, proper CD results are obtained when new input images are fed into an already learned network; however, for various reasons, it is difficult to properly detect changes using only a pre-trained CD network without adjustments and achieve the desired performance. The proposed method uses the pre-trained network as the initial value, but performs additional learning using the generated label data. To demonstrate the improvement of the proposed method, we compared it with the initial results of the pre-trained network without additional training.
The CD results obtained using the training samples selected from the ground truth data of sites 1 and 2 are presented in Figure 6a,d, respectively. The training samples were extracted using two methodologies. In the first method, 3D patches with label data were randomly extracted. In this case, the central pixels of these patches were independent; however, overlaps were observed between these patches. In the second method, the 3D patches were extracted such that they do not overlap. Because the image size is 600 600, 3,600 independent patches were generated. Although there was no overlap between these patches, the number of training samples was observed to decrease. Table 3 presents the accuracy of the CD results. The accuracy associated with the random selection of training data was considerably higher than that observed when the training samples were selected under non-overlapping conditions because the number of learnable patches decreased when cropping patches to maintain independence owing to the small-sized study area. The randomly selected OA scores were 0.9723 and 0.9757 at sites 1 and 2, respectively, and the F1 scores at sites 1 and 2 were 0.8978 and 0.9588, respectively. Based on these results, we used randomly selected 3D patches to train the CD network.

Figure 6.
CD results using (a) and (d), training samples randomly selected from the ground truth map; (b) and (e), using pre-trained CD networks at Epoch 0; and (c) and (f), the proposed CD methods at Epoch 200 for site 1 and 2, respectively.

Table 3.
Accuracy of the CD maps obtained using the randomly selected training samples and the samples selected under non-overlapping conditions from the ground truth map.
To transfer the pre-trained networks, if one dataset was the labeled source datasets, we assumed that the other dataset was the unlabeled target dataset. For example, in case 1, site 1 was the labeled source domain, and site 2 was the unlabeled target domain. In this case, the label data generated from SIDSCA was used to train the proposed CD network for site 2. In other words, the inputs of first CD network are site1 images and ground truth data, and the inputs of second CD network are site 2 images and automatically generated label data. Figure 6b,e show the CD results where the target domain images were fed into the pre-trained networks without any further training. Table 4 shows the accuracy of the CD results, and ‘Epoch 0’ represents CD results with no additional training. OA and F1 scores at sites 1 and 2 were 0.6337(OA) and 0.6273(OA) and 0.2998 (F1 score) and 0.4956 (F1 score), respectively. The changed areas were roughly identified in the CD maps. Although sites 1 and 2 were simultaneously obtained using the same sensor, it is not appropriate to detect changes for site 1 using the change rule of site 2 without additional fine-tuning because there are several differences between the spectral reflectance values, material types, and change patterns between the two sites. At both sites, the instances of precision were more frequent than the instances of recall. This means that the CD network returned very few results, but most of its predicted changes of class were correct when compared to the training data.

Table 4.
Accuracy of CD maps using pre-trained CD network and proposed CD methods.
The proposed CD method further trained two CD networks in parallel. There were two branches. The first CD network used the labeled source dataset and the second CD network used target images and the label data generated from SIDSCA. At first, the two networks were trained in parallel, sharing the weighted combined loss until Epoch 100. After training, the prediction map of the CD network in the second branch was used to update the label data for the target images. After that, the two networks were further trained, and the training data of the target images every tenth epoch were iteratively updated. Figure 7 shows F1 score and OA in each epoch for sites 1 and 2. The accuracy improvement in the proposed method became more apparent with increasing epoch number.
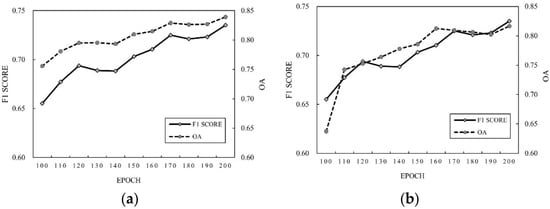
Figure 7.
CD F1 score and OA in each epoch at (a) site 1 (b) site 2.
In this study, the final epoch was set to 200 of Adam optimizer with a learning rate of and a batch size of 256. Figure 6c,f show the final CD results (Table 4). The proposed method could detect changes of class types compared with CD result on Epoch 0 (Figure 6b,e), and also, the CD results using label data generated from SIDSCA (Figure 4 and Figure 5h). It means that the proposed CD networks can effectively improve the CD results when using only the initial pre-trained network or automatically generated training samples. However, the changes caused by shadows were also included as the CD result. This is distinct at site 1 where there were many buildings. Therefore, the accuracies of site 1 measurements were lower than at site 2 (Table 4). The OA and F1 scores for site 1 and site 2 were 0.8164, 0.8391 and 0.4673 and 0.7351, respectively. Also, the areas with little change in vegetation vitality were classified as unchanged areas even though the areas were selected as changed classes in the training data.
5. Discussion
The proposed methods showed the improvements compared with other cases, but there are still limitations. In this section, we discuss the comparison with the output of each step, limitations, and future work.
5.1. Comparison with Output of Each Step
To evaluate the effectiveness of the proposed CD methods, a comparison was made between the CD results obtained from intermediate steps, which were the output of the CD network when using label data generated from SIDSCA, ground truth data, and pre-trained information in the source labeled dataset without additional training. Figure 8 shows the enlarged input images and CD results. Figure 8a,b show the subsets of site 1, and Figure 8c,d show the subsets of site 2. To show vegetation vitality, color-infrared (CIR) images were used. In the ground truth data, the vitality of the vegetation was significantly reduced so the area that appeared as bare soil in the RGB images was classified as a changed area. However, as we can see from the CIR images, vegetation was apparent to some extent and the DIs from SIDSCA were not recognized as changed areas from vegetation to bare soil (Figure 8a,d) This is because SIDSCA determines changes based on spectral similarity. Because the labeled source dataset (in this case, the labeled source domain was site 2 and the unlabeled target domain was site 1) trained these changes, the CD results of using pre-trained network without additional training showed those areas as changed areas, but the changed areas were overestimated. This method tended to extract area with little difference in spectral reflectance as changed pixels.


Figure 8.
Enlarged color-infrared hyperspectral UAV images, CD results using training data generated from SIDSCA, the ground truth, TL without further training, and the proposed method. (a) and (b) are subsets of site 1, and (c) and (d) are subsets of site 2.
The CD results of the proposed method shows the combined results when using the label data generated from SIDSCA and pre-trained network. It can identify changes caused by differences in vegetation vitality according the ground truth. However, shadows caused by trees were classified as changes because SIDSCA recognizes changes caused by shadows as changed pixels. Further, SIDSCA recognizes the spectral difference in relief displacement as changed pixels (Figure 8b). Since these changes were not actual changes in class type, the ground truth map does not include these pixels as training data representing changes. However, the proposed CD method tends to identify changes caused by relief displacement as unchanged classes compared with SIDSCA. In the subset image of site 2 (Figure 8c), the ground is covered with black vinyl and there are changes in the growth of crops. Although the ground truth data considers those areas as unchanged areas, SIDSCA classified the areas as changed areas because there were differences in spectral reflectance values. Also, since there were no training data related to these materials at site 1, CD results using pre-trained network without additional training could not properly classify the pixels into the unchanged class (in this case, site 1 was the labeled source domain and site 2 was the unlabeled target domain). The proposed CD method can improve CD results from SIDSCA and pre-trained network; however, it recognized the shadows caused by trees as changed areas.
5.2. Limitations and Future Work
The proposed method can detect changes in temporal images without ground truth data using automatically generated training data and a network pre-trained on labeled source data. Therefore, the advantage of the proposed method is that it can combine two approaches. For example, the changes caused by relief displacement can be recognized as unchanged pixels. However, there are limitations in using both approaches. For example, because the spectral similarity measures changes caused by shadows as real changes, the proposed CD method also classifies those pixels as changed areas even though the CD results of the pre-trained network and the ground truth do not define the shadows as changed pixels. In particular, the shadows cast by trees were classified as changed areas. Furthermore, the proposed CD method can be confusing where the criteria used to define changes are ambiguous, such as changes in vegetation vitality. For example, if there is no significant difference in spectral reflectance in DIs generated from SIDSCA, even though there are crop changes owing to harvesting, it is regarded as an unchanged region. This is because the proposed CD method uses training data generated from SIDSCA at the initial training stage. It means that the learning proceeds based on information that was initially defined.
To solve the aforementioned problems, the change criteria should be defined more clearly. For example, the change criteria for vegetation vitality can be defined based on differences in vegetation index values. Analysts should set clear criteria to prevent confusion between spectral similarity values and ground truth data when selecting the training data. If the two criteria coincide, the performance of the proposed CD method can be improved. Further, the increase in the amount of labeled source dataset will help reduce the impact of shadows. If the shadows are trained as unchanged areas in the large source domain dataset, the change rules for shadows could be learned. In the future, we will apply a large number of labeled source datasets to reduce the uncertainty effect of training data and develop algorithms to improve the quality of the training data.
6. Conclusions
In this paper, a novel CD method is proposed to detect changes in hyperspectral UAV images without ground truth data using pre-trained information from a labeled source dataset. The proposed method consists of automatically generating label data using SIDSCA and fine-tuning the CD network using combined weighted loss. SIDSCA generated DIs of two images, and the two clusters of FCM representing both extremes were selected as the training data. The CD network was then fine-tuned with a pre-trained network by training two networks in parallel. In the training, the training samples were iteratively updated using a prediction map of the CD network. Experiments on two hyperspectral UAV datasets confirmed that the proposed method is capable of transferring change rules and improving CD results based on the label data extracted in an unsupervised way. However, the performance of the proposed method is also dependent on the accuracy and the criteria of generated label data. Future work can be conducted to improve the accuracy of automatically generated training data.
Author Contributions
Conceptualization, Methodology, Software, Formal analysis, Investigation, A.S. and Y.K.; Resources, Validation, Data curation, Writing (original draft preparation), Funding acquisition, Visualization, A.S; Writing (review and editing), Supervision, Project administration Y.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2019R1A6A3A0109230211 and NRF-2019R1I1A2A01058144)
Acknowledgments
The authors would like to thank the anonymous reviewers for their very competent comments and helpful suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gong, J.; Sui, H.; Ma, G.; Zhou, Q. A review of multitemporal remote sensing data change detection algorithms. Proc. ISPRS 2008, 37, 757–762. [Google Scholar]
- Wang, S.; Ma, Q.; Ding, H.; Liang, H. Detection of urban expansion and land surface temperature change using multi-temporal Landsat images. Resour. Conserv. Recycl. 2018, 128, 526–534. [Google Scholar] [CrossRef]
- Washaya, P.; Balz, T.; Mohamadi, B. Coherence change-detection with sentinel-1 for natural and anthropogenic disaster monitoring in urban areas. Remote Sens. 2018, 10, 1026. [Google Scholar] [CrossRef]
- Schultz, M.; Shapiro, A.; Clevers, J.; Beech, C.; Herold, M. Forest cover and vegetation degradation detection in the Kavango Zambezi rransfrontier conservation area using BFAST monitor. Remote Sens. 2018, 10, 1850. [Google Scholar] [CrossRef]
- Adão, T.; Hruška, J.; Pádua, L.; Bessa, J.; Peres, E.; Morais, R.; Sousa, J.J. Hyperspectral imaging: A review on UAV-based sensors, data processing and applications for agriculture and forestry. Remote Sens. 2017, 9, 1110. [Google Scholar] [CrossRef]
- Dellinger, F.; Delon, J.; Gousseau, Y.; Michel, J.; Tupin, F. Change detection for high resolution satellite images, based on SIFT descriptors and an a contrario approach. In Proceedings of the 2014 IEEE International Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 1281–1284. [Google Scholar]
- Camacho, A.; Correa, C.V.; Arguello, H. An analysis of spectral variability in hyperspectral imagery: A case study of stressed oil palm detection in Colombia. Int. J. Remote Sens. 2019, 40, 7603–7623. [Google Scholar] [CrossRef]
- Wulder, M.A.; Ortlepp, S.M.; White, J.C.; Coops, N.C.; Coggins, S.B. Monitoring tree-level insect population dynamics with multi-scale and multi-source remote sensing. J. Spat. Sci. 2008, 53, 49–61. [Google Scholar] [CrossRef]
- Thomson, A.G.; Fuller, R.M.; Eastwoods, J.A. Supervised versus unsupervised methods for classification of coasts and river corridors from airborne remote sensing. Int. J. Remote Sens. 1998, 18, 3423–3431. [Google Scholar] [CrossRef]
- Liu, S.; Bruzzone, L. Hierarchical unsupervised change detection in multitemporal hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2015, 53, 244–260. [Google Scholar]
- Gong, M.; Zhao, J.; Liu, J.; Miao, Q.; Jiao, L. Change detection in synthetic aperture radar images based on deep neural networks. IEEE Trans. Neural Netw. 2016, 27, 125–138. [Google Scholar] [CrossRef]
- Song, A.; Choi, J.; Han, Y.; Kim, Y. Change detection in hyperspectral images using recurrent 3d fully convolutional networks. Remote Sens. 2018, 10, 1827. [Google Scholar] [CrossRef]
- Peng, D.; Guan, H. Unsupervised change detection method based on saliency analysis and convolutional neural network. J. Appl. Remote Sens. 2019, 13, 024512. [Google Scholar] [CrossRef]
- Gong, M.; Niu, X.; Zhang, P.; Li, Z. Generative adversarial networks for change detection in multi- spectral imagery. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2310–2314. [Google Scholar] [CrossRef]
- Chen, H.; Wu, C.; Du, B.; Zhang, L.; Wang, L. Change detection in multisource VHR images via deep Siamese convolutional multiple-layers recurrent neural network. IEEE Trans. Geosci. Remote Sens. 2019, 20, 1–17. [Google Scholar] [CrossRef]
- Yang, M.; Jiao, L.; Liu, F.; Hou, B.; Yang, S. Transferred deep learning-based change detection in remote sensing images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6960–6973. [Google Scholar] [CrossRef]
- Liu, J.; Chen, K.; Xu, G.; Sun, X.; Yan, M.; Diao, W.; Han, H. Convolutional neural network-based transfer learning for optical aerial images change detection. IEEE Geosci. Remote S. 2019, 17, 127–131. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Xue, X.; Jiang, Y.; Shen, Q. Deep learning for remote sensing image classification: A survey. In Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery; John Wiley & Sons: Hoboken, NJ, USA, 2018; p. e1264. [Google Scholar]
- Yuan, Q.; Wei, Y.; Meng, X.; Shen, H.; Zhang, L. A multiscale and multidepth convolutional neural network for remote sensing imagery pan-sharpening. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 978–989. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Shen, Q. Spectral-spatial classification of hyperspectral imagery with 3D convolutional neural network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef]
- Song, A.; Choi, J. Fully convolutional networks with multiscale 3D filters and transfer learning for change detection in high spatial resolution satellite images. Remote Sens. 2020, 12, 799. [Google Scholar] [CrossRef]
- Acquarelli, J.; Marchiori, E.; Buydens, L.M.C.; Tran, T.; van Laarhoven, T. Spectral-spatial classification of hyperspectral images: Three tricks and a new learning setting. Remote Sens. 2018, 10, 1156. [Google Scholar] [CrossRef]
- Lyu, H.; Lu, H.; Mou, L. Learning a transferable change rule from a recurrent neural network for land cover change detection. Remote Sens. 2016, 8, 506. [Google Scholar] [CrossRef]
- Mou, L.; Bruzzone, L.; Zhu, X.X. Learning spectral-spatial-temporal features via a recurrent convolutional neural network for change detection in multispectral imagery. IEEE Trans. Geosci. Remote Sens. 2019, 57, 924–935. [Google Scholar] [CrossRef]
- Jong, K.L.D.; Bosman, A.S. Unsupervised Change Detection in Satellite Images Using Convolutional Neural Networks. Available online: https://arxiv.org/abs/1812.05815?context=cs.NE (accessed on 30 March 2020).
- Bovolo, F.; Marchesi, S.; Bruzzone, L. A framework for automatic and unsupervised detection of multiple changes in multitemporal images. IEEE Trans. Geosci. Remote 2012, 50, 2196–2212. [Google Scholar] [CrossRef]
- Ramos, J.F.; Renza, D.; Ballesteros, L.; Dora, M. Evaluation of spectral similarity indices in unsupervised change detection approaches. Dyna 2018, 85, 117–126. [Google Scholar]
- Shanmugam, S.; SrinivasaPerumal, P. Spectral matching approaches in hyperspectral image processing. Int. J. Remote Sens. 2014, 35, 8217–8251. [Google Scholar] [CrossRef]
- Du, Y.; Chang, C.-I.; Ren, H.; Chang, C.-C.; Jensen, J.O.; D’Amico, F.M. New hyperspectral discrimination measure for spectral characterization. Opt. Eng. 2004, 43, 1777–1786. [Google Scholar]
- Kruse, F.A.; Lefkoff, A.B.; Boardman, J.W.; Heidebrecht, K.B.; Shapiro, A.T.; Barloon, P.J.; Goetz, A.F.H. The spectral image-processing system (SIPS)-interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
- Robila, S.A.; Gershman, A. Spectral matching accuracy in processing hyperspectral data. In Proceedings of the IEEE International Symposium on Signals, Circuits and Systems, ISSCS 2005, Iasi, Romania, 14–15 July 2005; Volume 1, pp. 165–166. [Google Scholar]
- Carvalho, O.A., Jr.; Guimaraes, R.F.; Gillespie, A.R.; Silva, N.C.; Gomes, R.A.T. A new approach to change vector analysis using distance and similarity measures. Remote Sens 2011, 3, 2473–2493. [Google Scholar] [CrossRef]
- Chang, C. An information theoretic-based approach to spectral variability, similarity and discriminability for hyperspectral image analysis. IEEE Trans. Inf. Theory 2000, 46, 1927–1932. [Google Scholar] [CrossRef]
- Kumar, M.N.; Seshasai, M.V.R.; Prasad, K.S.V. A new hybrid spectral similarity measure for discrimination among Vigna species. Int. J. Remote Sens. 2011, 32, 4041–4053. [Google Scholar] [CrossRef]
- Chen, B.; Vodacek, A.; Cahill, N.D. A novel adaptive scheme for evaluating spectral similarity in high-resolution urban scenes. IEEE J. Sel. Top. Appl. 2013, 6, 1376–1385. [Google Scholar] [CrossRef]
- Padma, S.; Sanjeevi, S. Jeffries Matusita based mixed-measure for improved spectral matching in hyperspectral image analysis. Int. J. Appl. Earth Obs. Geoinf. 2014, 32, 138–151. [Google Scholar] [CrossRef]
- Adep, R.N.; Vijayan, A.P.; Shetty, A.; Ramesh, H. Performance evaluation of hyperspectral classification algorithms on aviris mineral data. Perspect. Sci. 2016, 8, 722–726. [Google Scholar] [CrossRef]
- Dunn, J.C. A fuzzy relative of the ISODATA process and its use in detecting compact well-separated clusters. J. Cybern. 1974, 3, 32–57. [Google Scholar]
- Mai, D.S.; Long, T.N. Semi-Supervised Fuzzy C-Means Clustering for Change Detection from Multispectral Satellite Image. In Proceedings of the 2015 IEEE International Conference on Fuzzy Systems, Istanbul, Turkey, 2–5 August 2015. [Google Scholar]
- Hao, M.; Zhang, H.; Shi, W.; Deng, K. Unsupervised change detection using fuzzy c-means and MRF from remotely sensed images. Remote Sens. Lett. 2013, 4, 1185–1194. [Google Scholar] [CrossRef]
- Park, S.; Song, A. Discrepancy analysis for detecting candidate parcels requiring update of land category in cadastral map using hyperspectral UAV Images: A case study in Jeonju, South Korea. Remote Sens. 2020, 12, 354. [Google Scholar] [CrossRef]
- ArcGIS Webmap. Available online: https://www.arcgis.com/home/webmap/viewer.html (accessed on 28 January 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).