A Novel Stereo Matching Algorithm for Digital Surface Model (DSM) Generation in Water Areas
Abstract
1. Introduction
1.1. Background and Related Works
1.2. The Proposed Approach
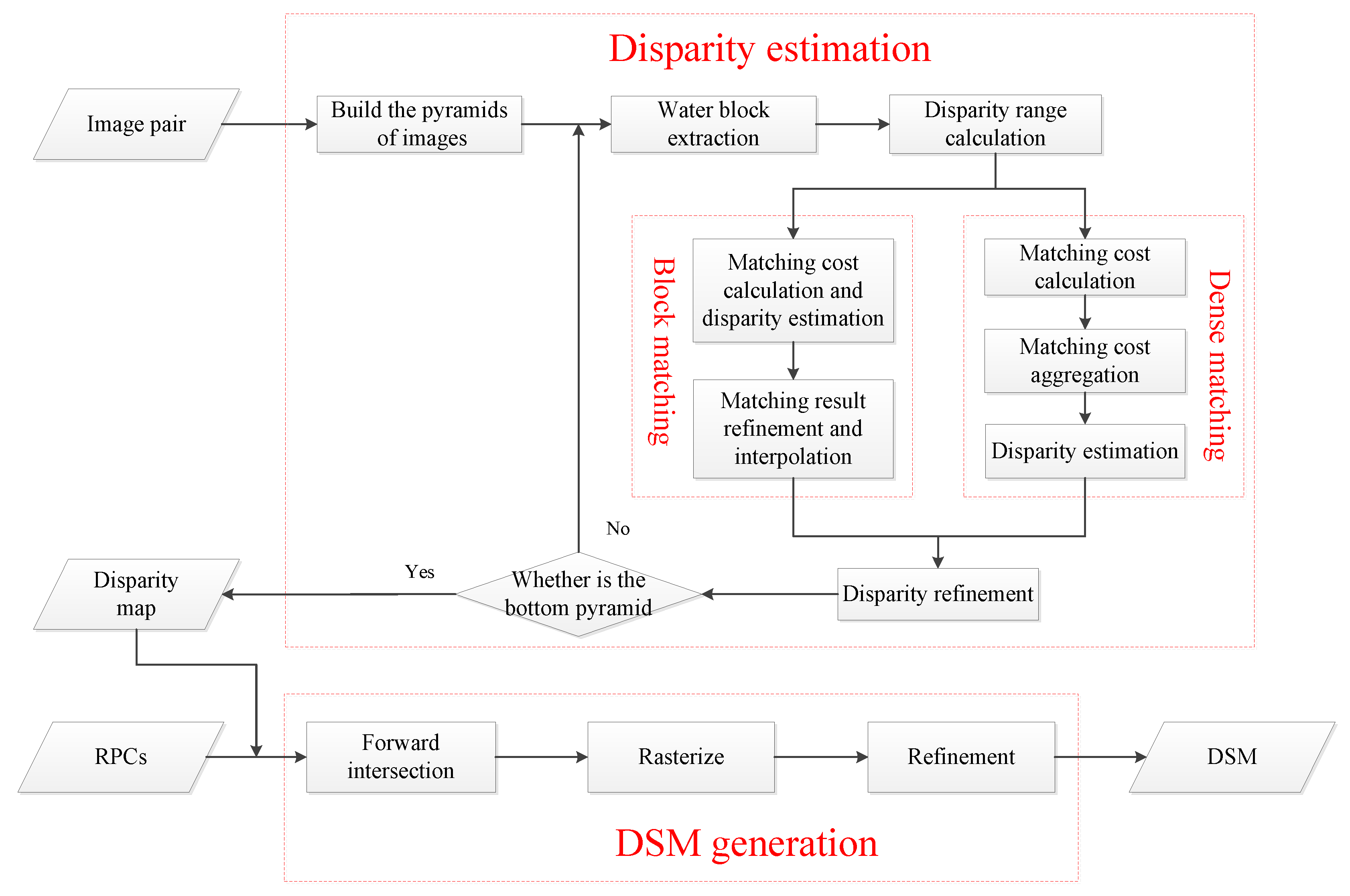
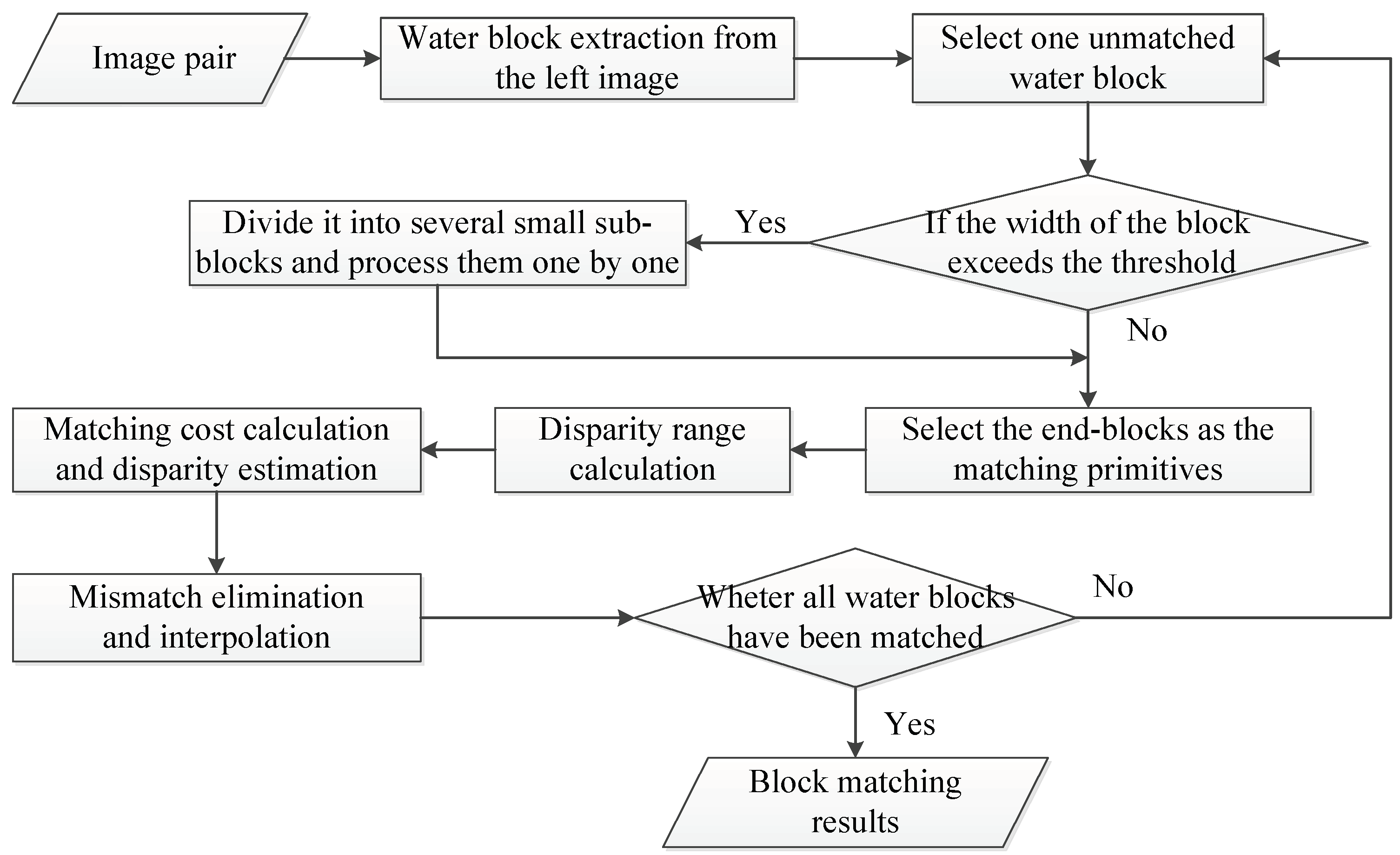
2. Method
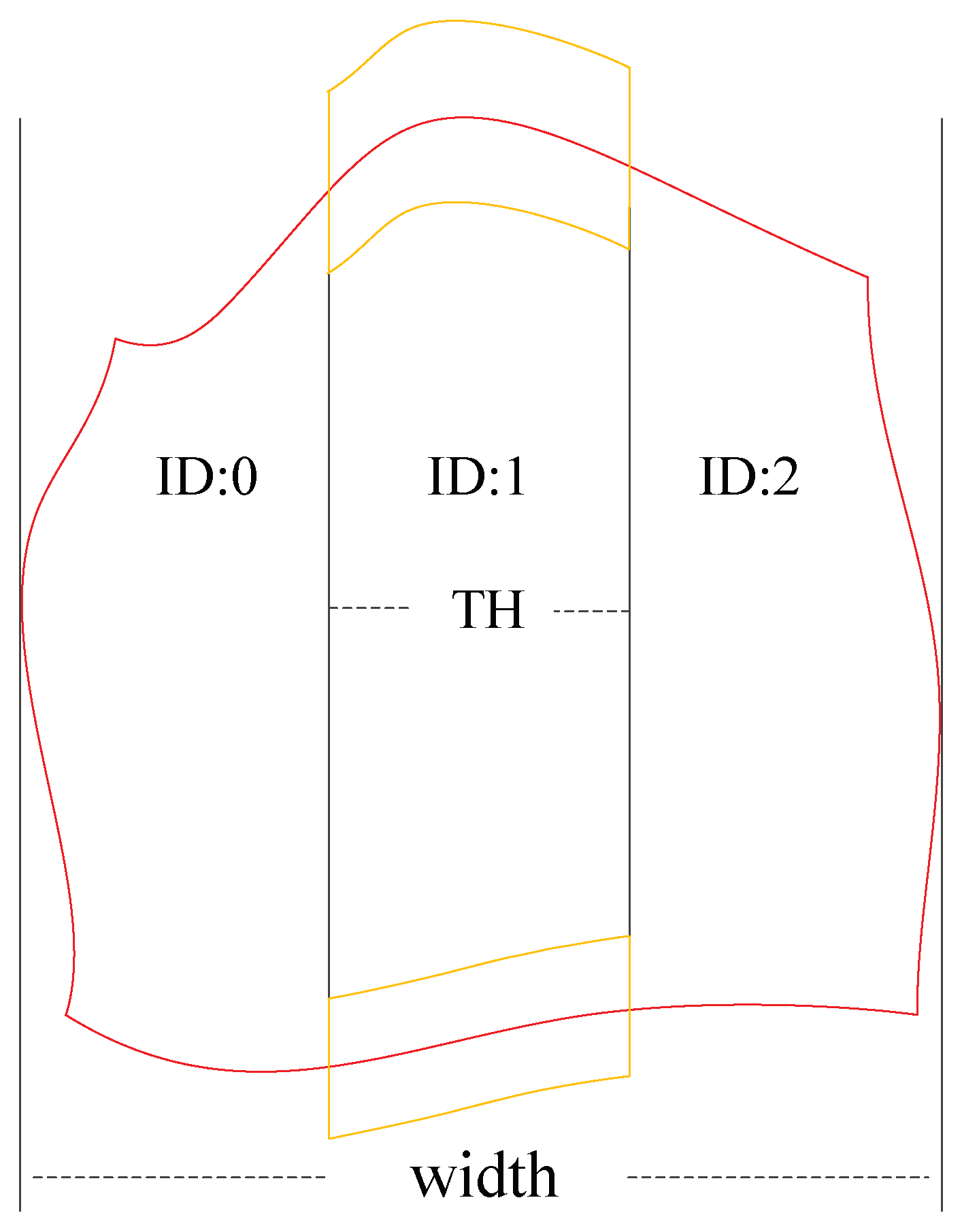
2.1. Water Block Extraction
- (1)
- Seed point detection is conducted on the whole image with a fixed sampling interval (set as 5), and then all detected seed points are recorded.
- (2)
- Seed point growth for all unprocessed seed points in turn to extract water blocks. If one seed point has been processed or belongs to a water block already detected, it will be marked as processed immediately.
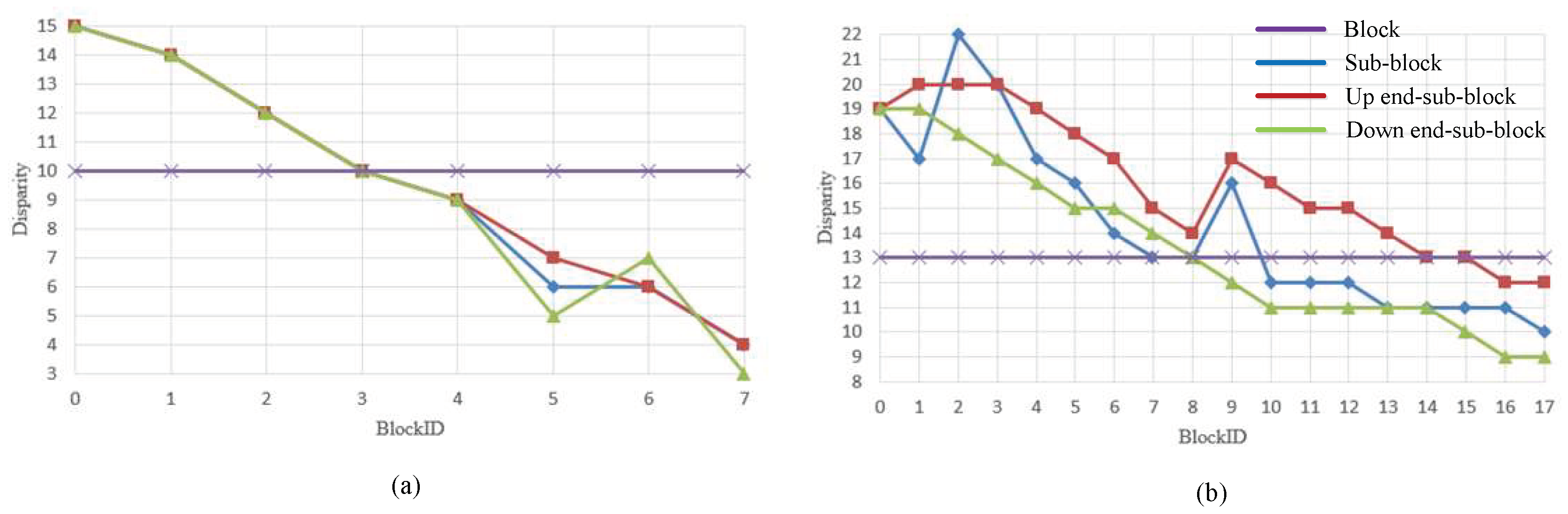
2.2. Disparity Range Calculation
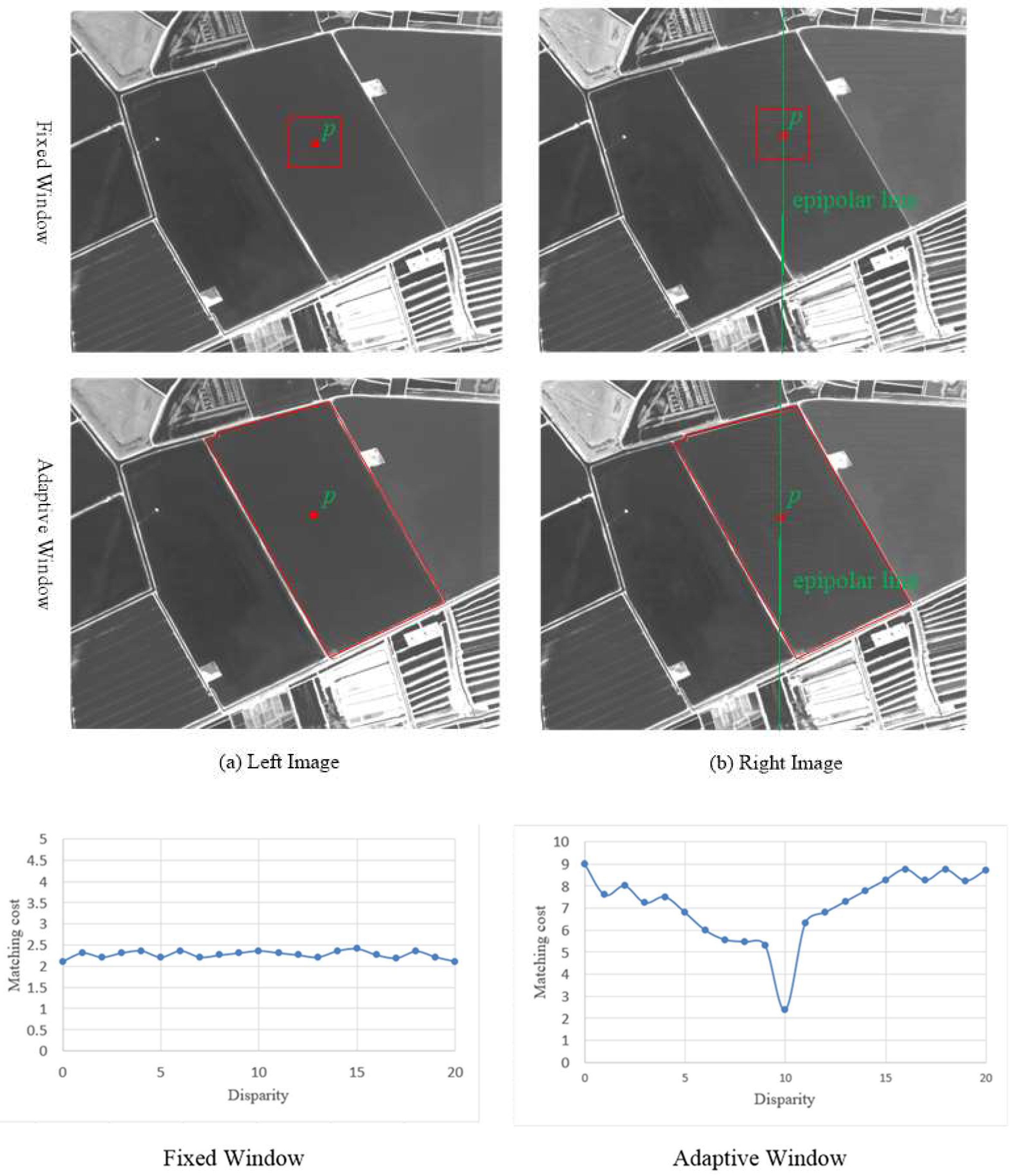
2.3. Block Matching
- (1)
- Considering that the water block should be a plane, it is reasonable to assume that all pixels belonging to the same block share the same disparity with high probability. Thus, it is natural to use the automatically detected blocks as the matching primitives in our method.
- (2)
- The image pair in this study has been already geometrically rectified, so it is allowed that the search space is limited to the one-dimension direction based on the epipolar constraint.
- (3)
- In this study block matching strategy is embedded into dense matching processing. Thus, a reasonable disparity range, which is crucial to low complexity and high accuracy, can be derived from the dense matching result.
- (4)
- Considering the two images of the image pair in this study are obtained by the same satellite simultaneously, it can be accepted that there is no complex but only linear radiation difference between them, which is very useful for reliable matching cost design.
2.3.1. Matching Cost Calculation and Disparity Estimation
2.3.2. Geometrical Deformation Process
2.3.3. Mismatch Elimination and Interpolation
2.4. Dense Matching
2.5. DSM Generation
3. Results
3.1. The Experimental Platform and Data
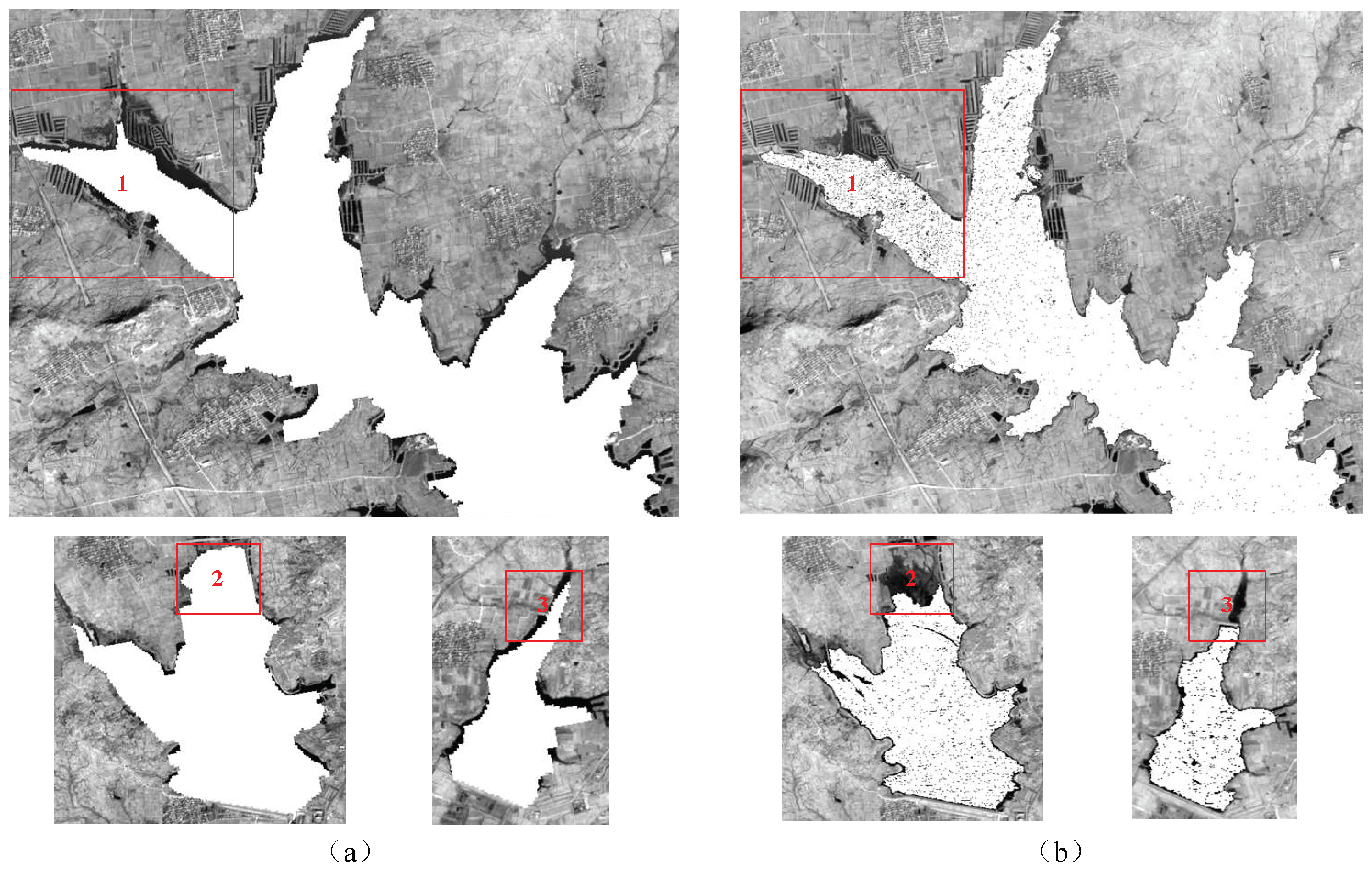
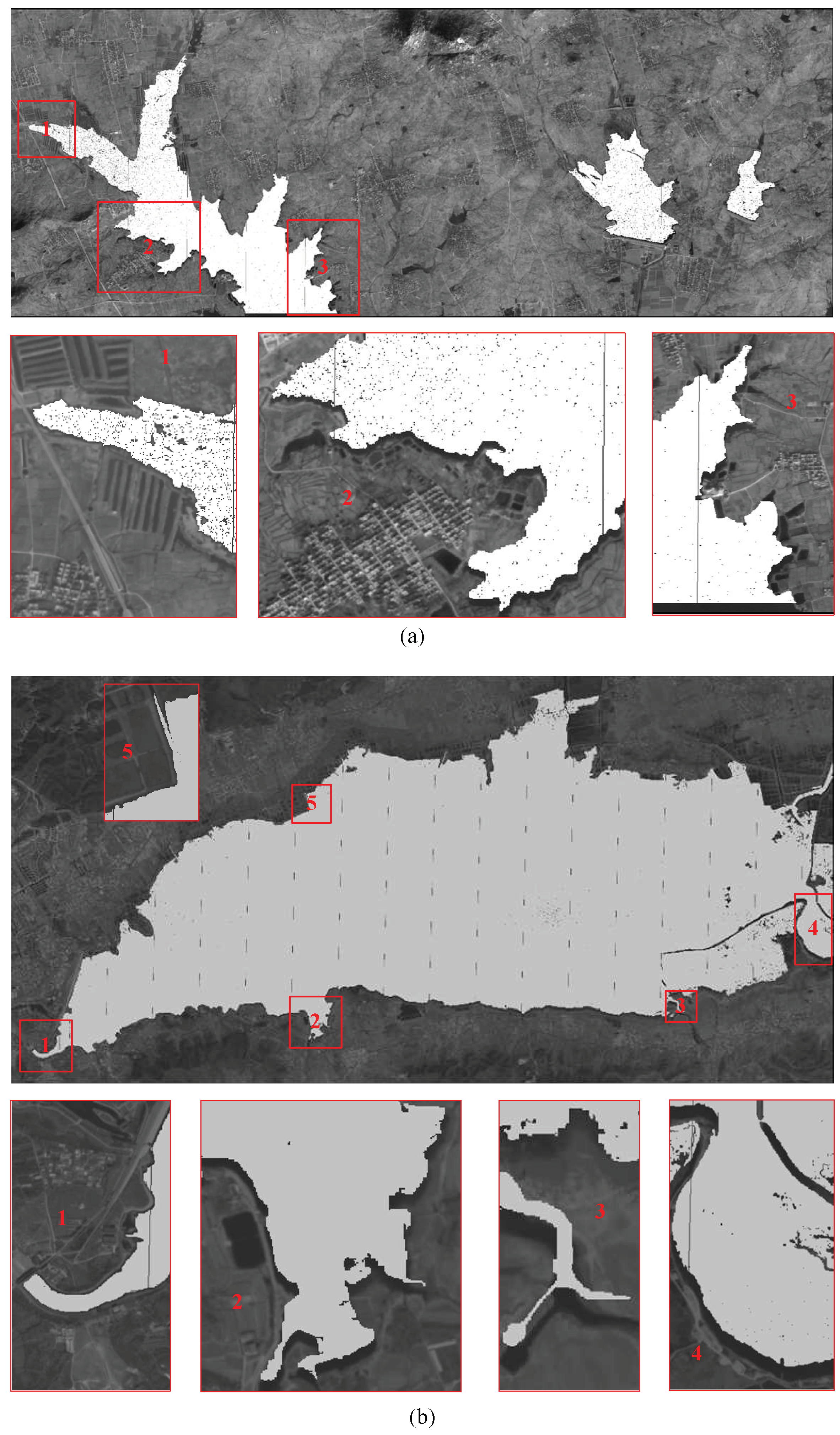
3.2. Experiment on Seed Point Extraction and ROI Extraction
3.3. Experiment on ROI Matching
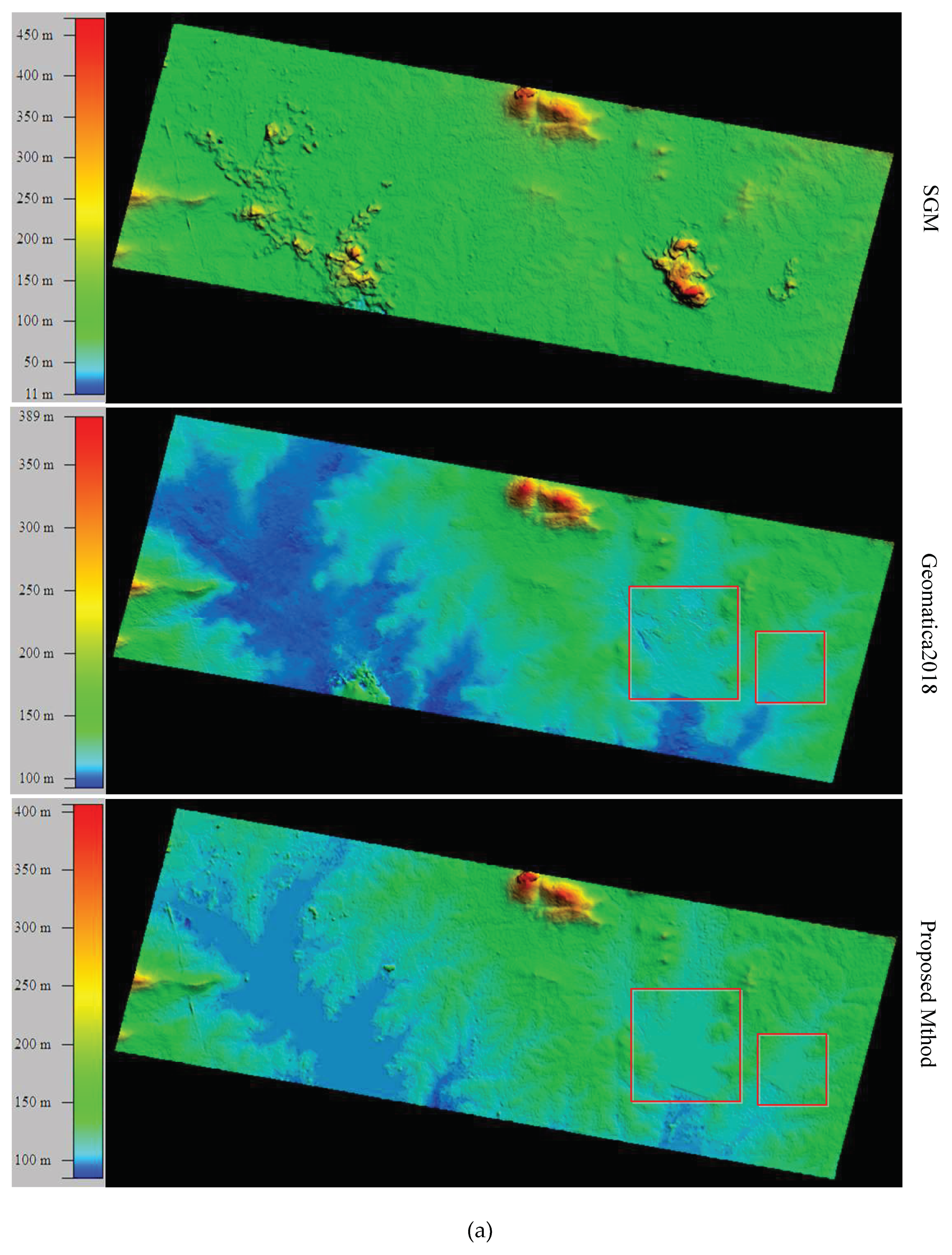
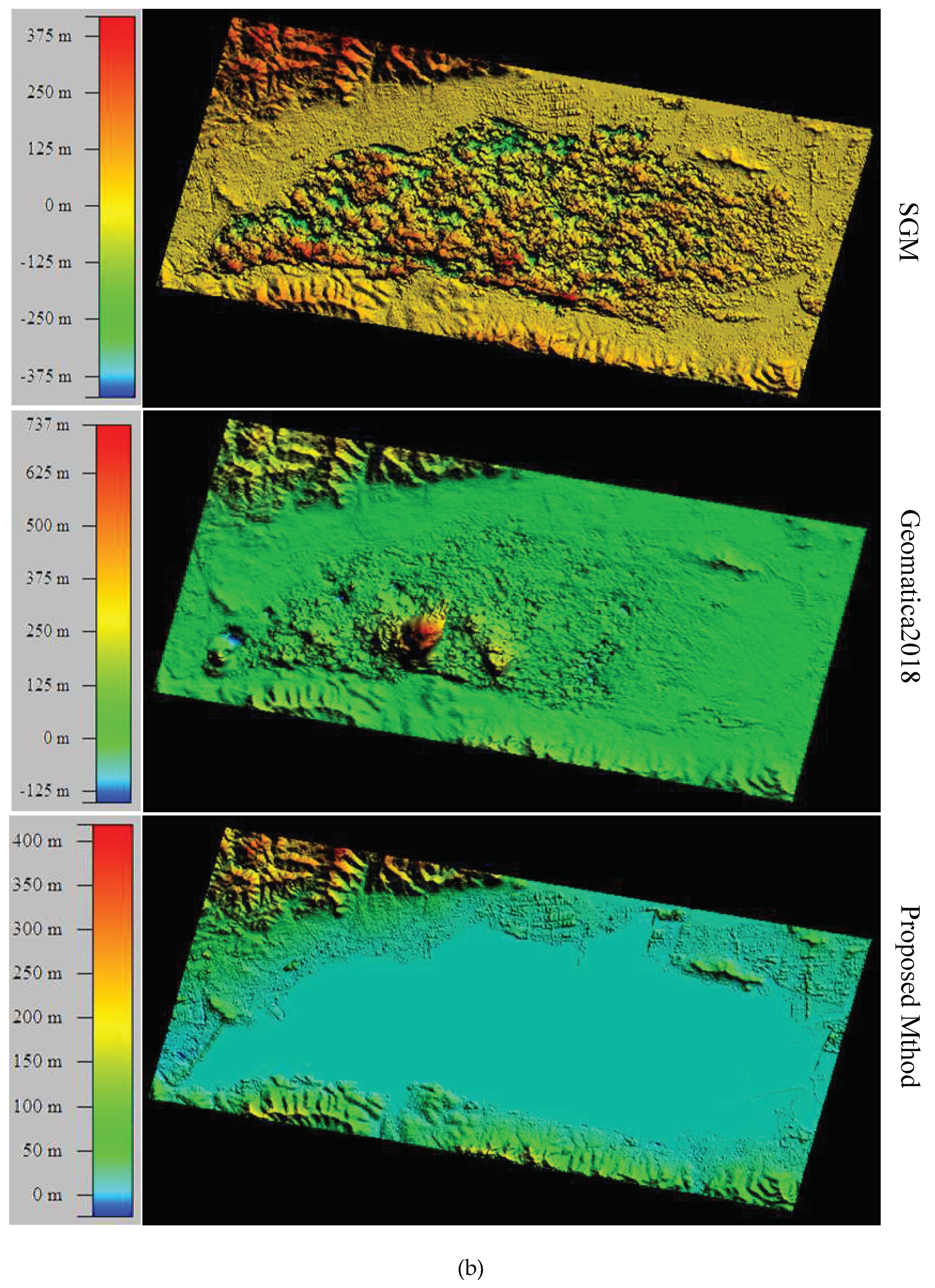
3.4. DSM Quality Assessment
4. Discussion
4.1. Advancements of The Proposed Method
4.2. Limitations of the Proposed Method
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rabus, B.; Eineder, M.; Roth, A.; Bamler, R. The shuttle radar topography mission-A new class of digital elevation models acquired by spaceborne radar. ISPRS J. Photogramm. Remote Sens. 2003, 57, 241–262. [Google Scholar] [CrossRef]
- Farr, T.G. The shuttle radar topography mission. Rev. Geophys. 2007, 45, 1–33. [Google Scholar] [CrossRef]
- Toutin, T. Comparison of stereo-extracted DTM from different high-resolution sensors: SPOT-5, EROS-a, IKONOS-II, and QuickBird. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2121–2129. [Google Scholar] [CrossRef]
- Aguilar, M.A.; Saldana, M.D.M.; Aguilar, F.J. Generation and Quality Assessment of Stereo-Extracted DSM from GeoEye-1 and WorldView-2 Imagery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1259–1271. [Google Scholar] [CrossRef]
- Xue, Y.; Xie, W.; Du, Q.; Sang, H. Performance evaluation of DSM extraction from ZY-3 three-line arrays imagery. ISPRS Arch. 2015, XL-7/W4, 247–253. [Google Scholar] [CrossRef]
- Scharstein, D.; Szeliski, R. A taxonomy and evaluation of dense two-frame stereo correspondence algorithms. Int. J. Comput. Vis. 2002, 47, 7–42. [Google Scholar] [CrossRef]
- Zhang, L.; Gruen, A. Multi-image matching for DSM generation from IKONOS imagery. ISPRS J. Photogramm. Remote Sens. 2006, 60, 195–211. [Google Scholar] [CrossRef]
- Hirschmüller, H. Stereo processing by semiglobal matching and mutual information. IEEE Trans. Pattern Anal. 2008, 30, 328–341. [Google Scholar] [CrossRef]
- Hu, T.; Guo, B.; Wu, H.; Gong, J.; Zhang, T. Dense corresponding pixel matching between aerial epipolar images using an RGB-belief propagation algorithm. IEEE Geosci. Remote Sens. Lett. 2012, 9, 1036–1040. [Google Scholar] [CrossRef]
- Labatut, P.; Pons, J.P.; Keriven, R. Efficient multi-view reconstruction of large-scale scenes using interest points, delaunay triangulation and graph cuts. In Proceedings of the International Conference on Computer Vision (ICCV), Rio De Janeiro, Brazil, 14–21 October 2007. [Google Scholar]
- Furukawa, Y.; Ponce, J. Accurate, dense, and robust multi-view stereopsis. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1362–1376. [Google Scholar] [CrossRef]
- GEOMATICA. Available online: https://www.nrcresearchpress.com/loi/cig (accessed on 15 September 2019).
- Trimbpe Inpho. Available online: https://geospatial.trimble.com/products-and-solutions/inpho (accessed on 10 October 2019).
- Zhang, Y.; Zhang, Y.; Mo, D.; Zhang, Y.; Li, X. Direct digital surface model generation by semi-global vertical line locus matching. Remote Sens. 2017, 9, 214. [Google Scholar] [CrossRef]
- Wu, B.; Zhang, Y.; Zhu, Q. Integrated point and edge matching on poor textural images constrained by self-adaptive triangulations. ISPRS J. Photogramm. Remote Sens. 2012, 68, 40–55. [Google Scholar] [CrossRef]
- Wang, D.; Liu, H.; Cheng, X. A Miniature Binocular Endoscope with Local Feature Matching and Stereo Matching for 3D Measurement and 3D Reconstruction. Sensors 2018, 18, 2243. [Google Scholar] [CrossRef] [PubMed]
- Mandlburger, G. A case study on through-water dense image matching. ISPRS Arch. 2018, XLII-2, 659–666. [Google Scholar] [CrossRef]
- Kanade, T.; Okutomi, M. A stereo matching algorithm with an adaptive window: Theory and experiment. In Proceedings of the IEEE International Conference on Robotics and Automation, Washington DC, USA, 10–17 May 2002. [Google Scholar]
- Ye, L.; Wu, B. Integrated image matching and segmentation for 3D surface reconstruction in urban areas. Photogramm. Eng Remote Sens. 2018, 84, 135–148. [Google Scholar] [CrossRef]
- Hu, H.; Rzhanov, Y.; Hatcher, P.J.; Bergeron, R.D. Binary adaptive semi-global matching based on image edges. In Proceedings of the 7th International Conference on Digital Image Processing, Los Angeles, CA, USA, 9–10 April 2015. [Google Scholar]
- Paris, S.; Durand, F. A fast approximation of the bilateral filter using a signal processing approach. In Proceedings of the European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Shan, Q.; Curless, B.; Furukawa, Y.; Hernandez, C.; Seitz, S.M. Occluding contours for multi-view stereo. In Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014. [Google Scholar]
- Shao, Z.F.; Yang, N.; Xiao, X.; Zhang, L.; Peng, Z. A multi-view dense point cloud generation algorithm based on low-altitude remote sensing images. Remote Sens. 2016, 8, 381. [Google Scholar] [CrossRef]
- Slater, J.A.; Garvey, G.; Johnston, C.; Haase, J.; Heady, B.; Kroenung, G.; Little, J. The srtm data “finishing” process and products. Photogramm. Eng. Remote Sens. 2006, 72, 237–247. [Google Scholar] [CrossRef]
- Reuter, H.I.; Nelson, A.; Jarvis, A. An evaluation of void-filling interpolation methods for SRTM data. Int. J. Geogr. Inf. Sci. 2007, 21, 983–1008. [Google Scholar] [CrossRef]
- Grimaldi, S.; Teles, V.; Bras, R.L. Sensitivity of a physically based method for terrain interpolation to initial conditions and its conditioning on stream location. Earth Surf Proc Land. 2004, 29, 587–597. [Google Scholar] [CrossRef]
- Grimaldi, S.; Teles, V.; Bras, R.L. Preserving first and second moments of the slope area relationship during the interpolation of digital elevation models. Adv. Water Resour. 2005, 28, 583–588. [Google Scholar] [CrossRef]
- Pekel, J.; Cottam, A.; Gorelick, N.; Belward, A.S. High-resolution mapping of global surface water and its long-term changes. Nature 2016, 540, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Feng, M.; Sexton, J.O.; Channan, S.; Townshend, J.R. A global, high-resolution (30-m) inland water body dataset for 2000: First results of a topographic-spectral classification algorithm. Int. J. Digit. Earth 2016, 9, 113–133. [Google Scholar] [CrossRef]
- Wang, Q.; Yuan, J.Y.; Li, B.-L. Matching algorithm integrated feature points and contour information. Appl. Res. Comput. 2014, 31, 3145–3147. [Google Scholar]
- Lowe, D.G. Distinctive image feartures from scal-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Gool, L.V. SURF: Speeded up robust features. Comput. Vis. Image Und. 2006, 110, 404–417. [Google Scholar]
- Perri, S.; Colonna, D.; Zicari, P.; Corsonello, P. SAD-based stereo matching circuit for FPGAs. In Proceedings of the 13th IEEE International Conference on Electronics, Circuits and Systems, Nice, France, 10–13 December 2006. [Google Scholar]
- Pourmohammad, A.; Poursajadi, S.; Karimifar, S. Scene matching NCC value improvement based on contrast matching. In Proceedings of the IEEE 8th Iranian Conference on Machine Vision and Image Processing, Zanjan, Iran, 10–12 September 2013. [Google Scholar]
- Bolles, R.C.; Fischler, M.A. A RANSAC-Based Approach to Model Fitting and Its Application to Finding Cylinders in Range Data. In Proceedings of the IJCAI, Vancouver, BC, Canada, 24–28 August 1981; Volume 1981, pp. 637–643. [Google Scholar]
- Humenberger, M.; Engelke, T.; Kubinger, W. A census-based stereo vision algorithm using modified semi-global matching and plane fitting to improve matching quality. In Proceedings of the Computer Vision and Pattern Recognition Workshops, San Francisco, CA, USA, 13–18 June 2010. [Google Scholar]
- Noh, M.J.; Howat, I.M. Automatic relative RPC image model bias compensation through hierarchical image matching for improving DEM quality. ISPRS J. Photogramm. Remote Sens. 2018, 136, 120–133. [Google Scholar] [CrossRef]
- China Centre for Resource Satellite Data and Application. Available online: http://www.cresda.com/CN/Satellite/3070.shtml (accessed on 10 April 2019).
- Gong, P.; Liu, H.; Zhang, M.; Li, C.; Wang, J.; Huang, H.; Clinton, N.; Ji, L.; Li, W.; Bai, Y.; et al. Stable classification with limited sample: Transferring a 30-m resolution sample set collected in 2015 to mapping 10-m resolution global land cover in 2017. Sci. Bull. 2019, 64, 370–373. [Google Scholar] [CrossRef]
- Finer Resolution Obsevation and Monitoring-Global Land Cover. Available online: http://data.ess.tsinghua.edu.cn/fromglc10_2017v01.html (accessed on 20 January 2020).
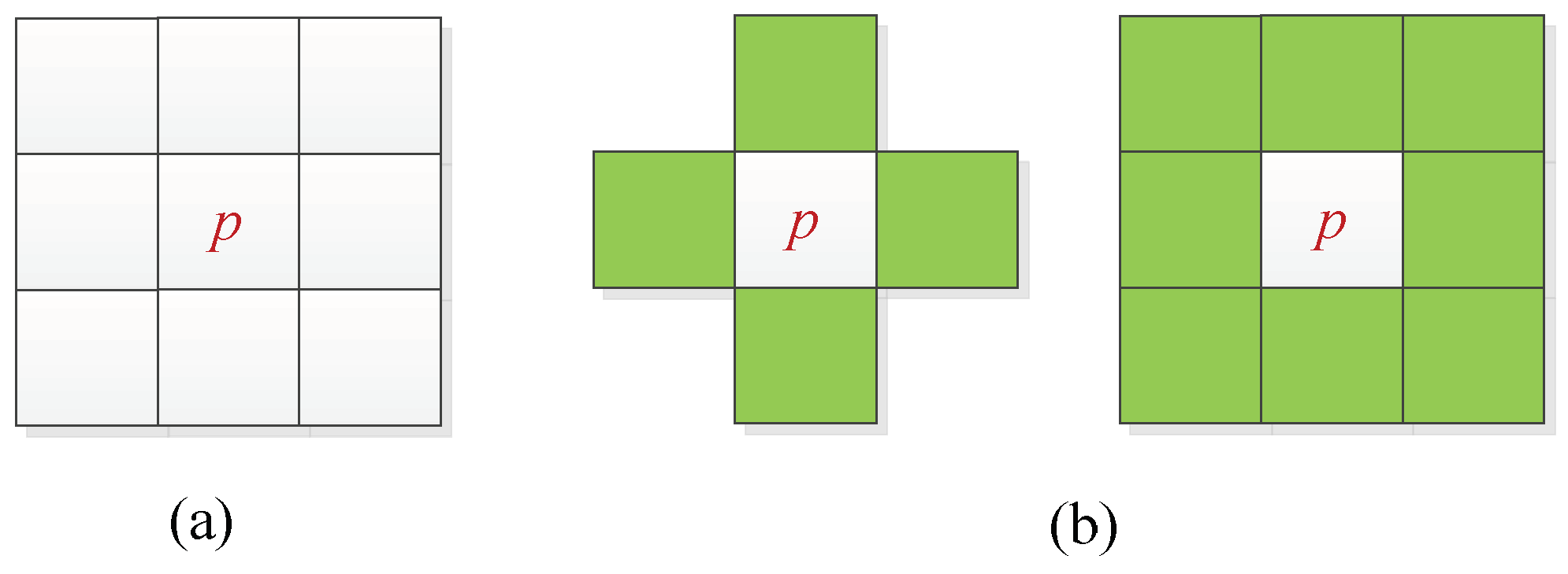





| Satellite Image Pairs | |
|---|---|
| Sensor | ZY-3 FWD/BWD |
| Image size(pixel) | 16281 16364 |
| Principal distance(mm) | 1700 |
| Pixel size(um) | 10 |
| Resolution(m) | 3.5 |
| Overlap | >90% |
| ROI | Pixels | Area (km2) | Height (m) |
|---|---|---|---|
| 1 | 34329 | 0.42 | 116.87 |
| 2 | 136791 | 1.68 | 115.11 |
| 3 | 484545 | 5.94 | 99.61 |
| 4 | 5376695 | 65.87 | 13.00 |
| Method | Indicator | Image Pair Block1 1510 pix | Image Pair Block2 2510 pix | ||
|---|---|---|---|---|---|
| ROI1 | ROI2 | ROI3 | ROI4 | ||
| SGM | RMSE/m | 25.31 | 125.85 | 51.26 | 84.65 |
| Variance/m | 19.14 | 86.42 | 37.92 | 83.05 | |
| Time/min | 6 | 14 | |||
| Geomatica2018 | RMSE/m | 2.13 | 2.87 | 11.68 | 79.71 |
| Variance/m | 1.36 | 2.34 | 10.09 | 73.92 | |
| Time/min | 2 | 4 | |||
| SGBM | RMSE/m | 0.33 | 0.54 | 0.38 | 0.28 |
| Variance/m | 0 | 0 | 0 | 0 | |
| Time/min | 4 | 9 | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, W.; Li, X.; Yang, B.; Fu, Y. A Novel Stereo Matching Algorithm for Digital Surface Model (DSM) Generation in Water Areas. Remote Sens. 2020, 12, 870. https://doi.org/10.3390/rs12050870
Yang W, Li X, Yang B, Fu Y. A Novel Stereo Matching Algorithm for Digital Surface Model (DSM) Generation in Water Areas. Remote Sensing. 2020; 12(5):870. https://doi.org/10.3390/rs12050870
Chicago/Turabian StyleYang, Wenhuan, Xin Li, Bo Yang, and Yu Fu. 2020. "A Novel Stereo Matching Algorithm for Digital Surface Model (DSM) Generation in Water Areas" Remote Sensing 12, no. 5: 870. https://doi.org/10.3390/rs12050870
APA StyleYang, W., Li, X., Yang, B., & Fu, Y. (2020). A Novel Stereo Matching Algorithm for Digital Surface Model (DSM) Generation in Water Areas. Remote Sensing, 12(5), 870. https://doi.org/10.3390/rs12050870






