Measuring the Urban Land Surface Temperature Variations Under Zhengzhou City Expansion Using Landsat-Like Data
Abstract
1. Introduction
2. Materials and Methods
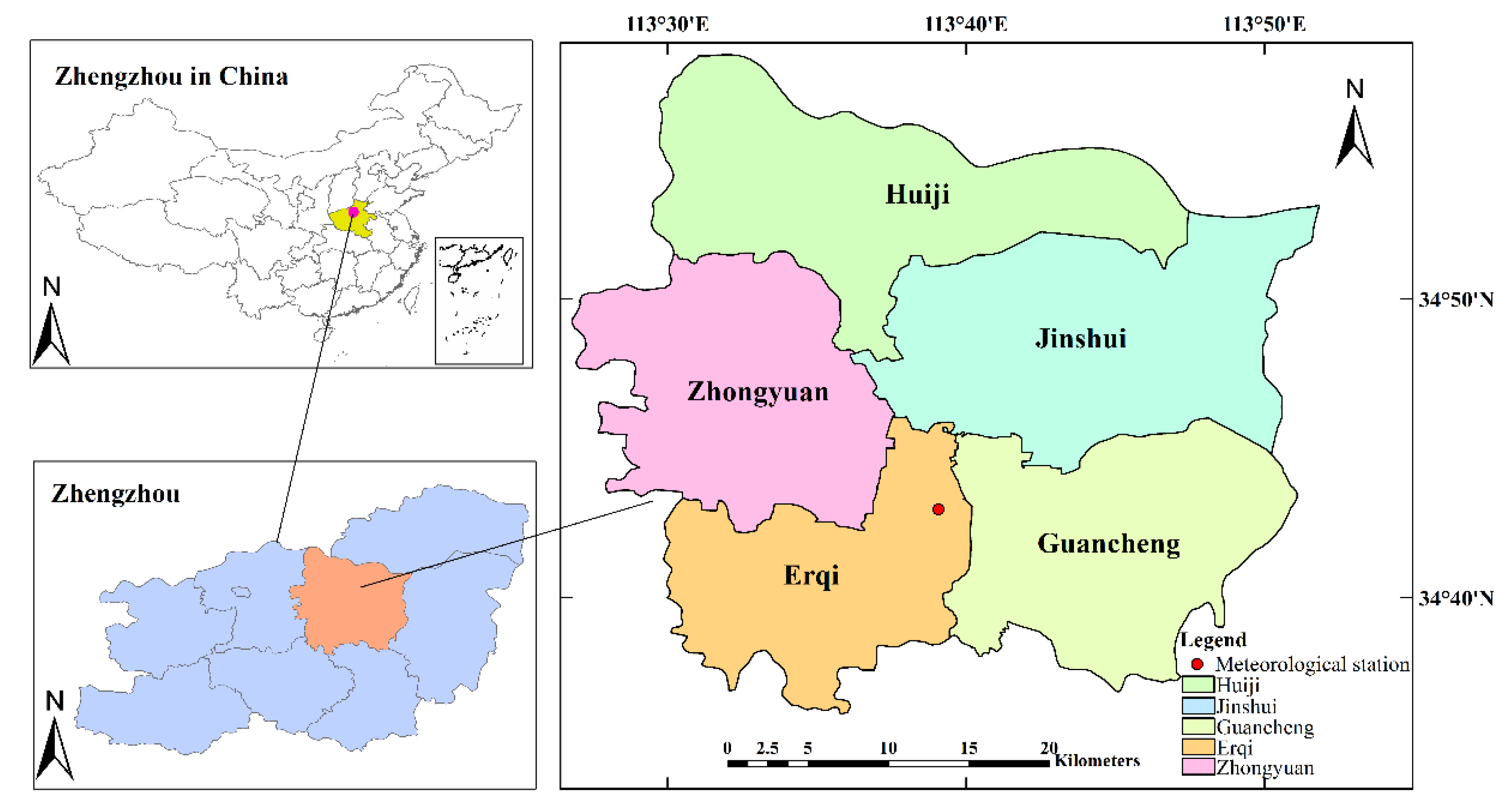
2.1. Materials
2.2. Methods
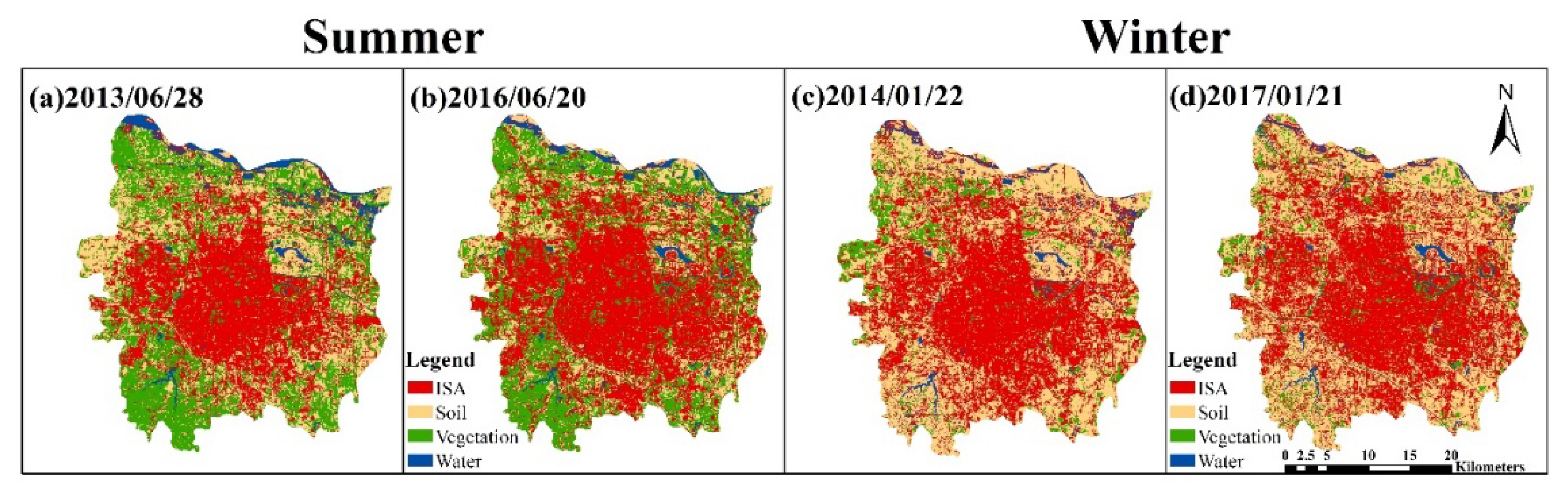
2.2.1. Data Preprocessing and Image Classification
2.2.2. Calculation of NDVI, NDBI, and LST
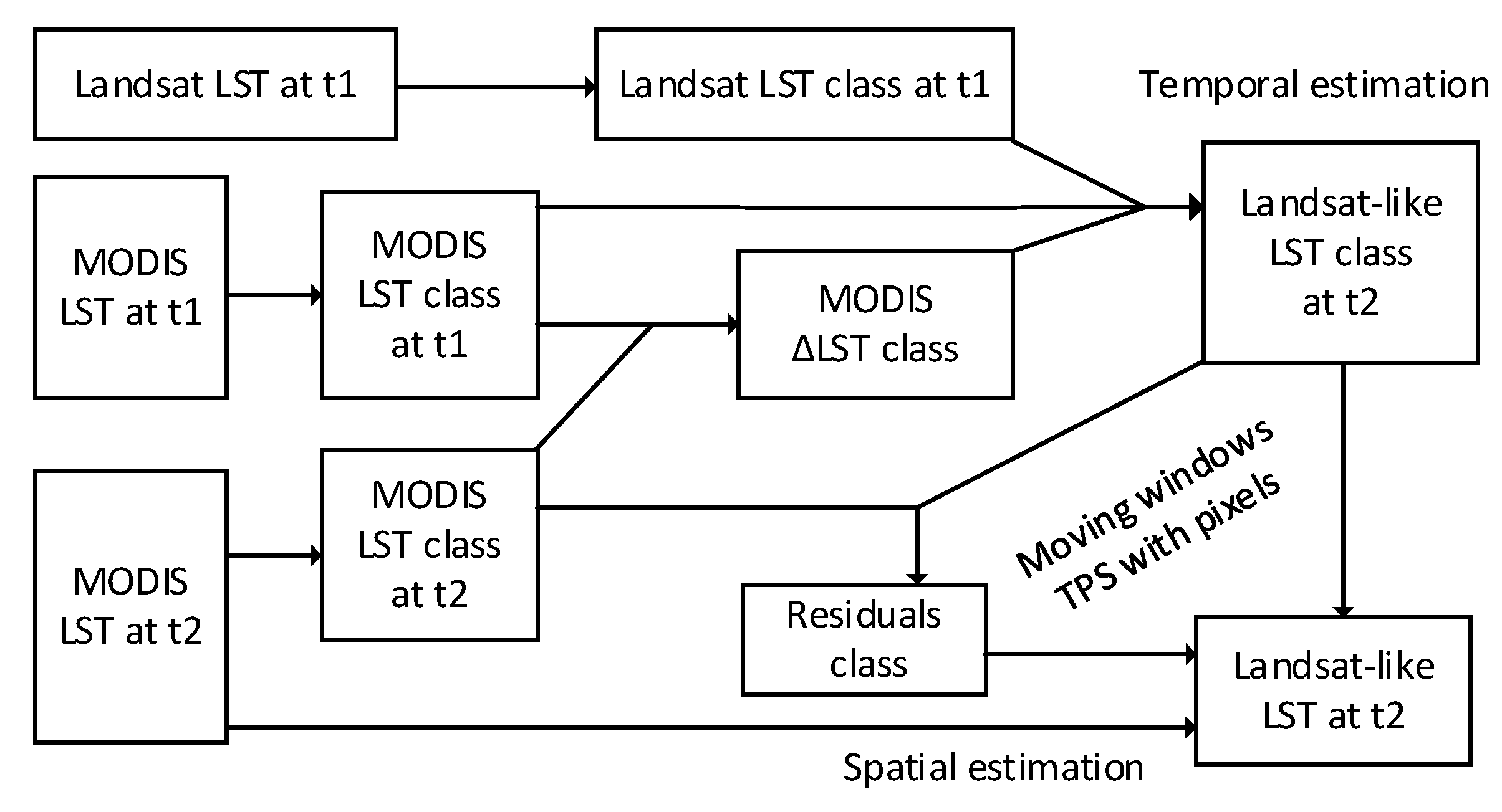
2.2.3. The Flexible Spatiotemporal Data Fusion Method
3. Results
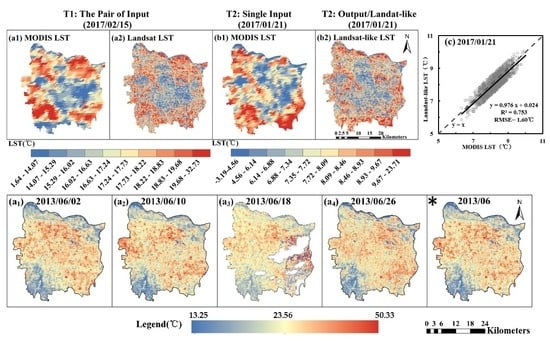
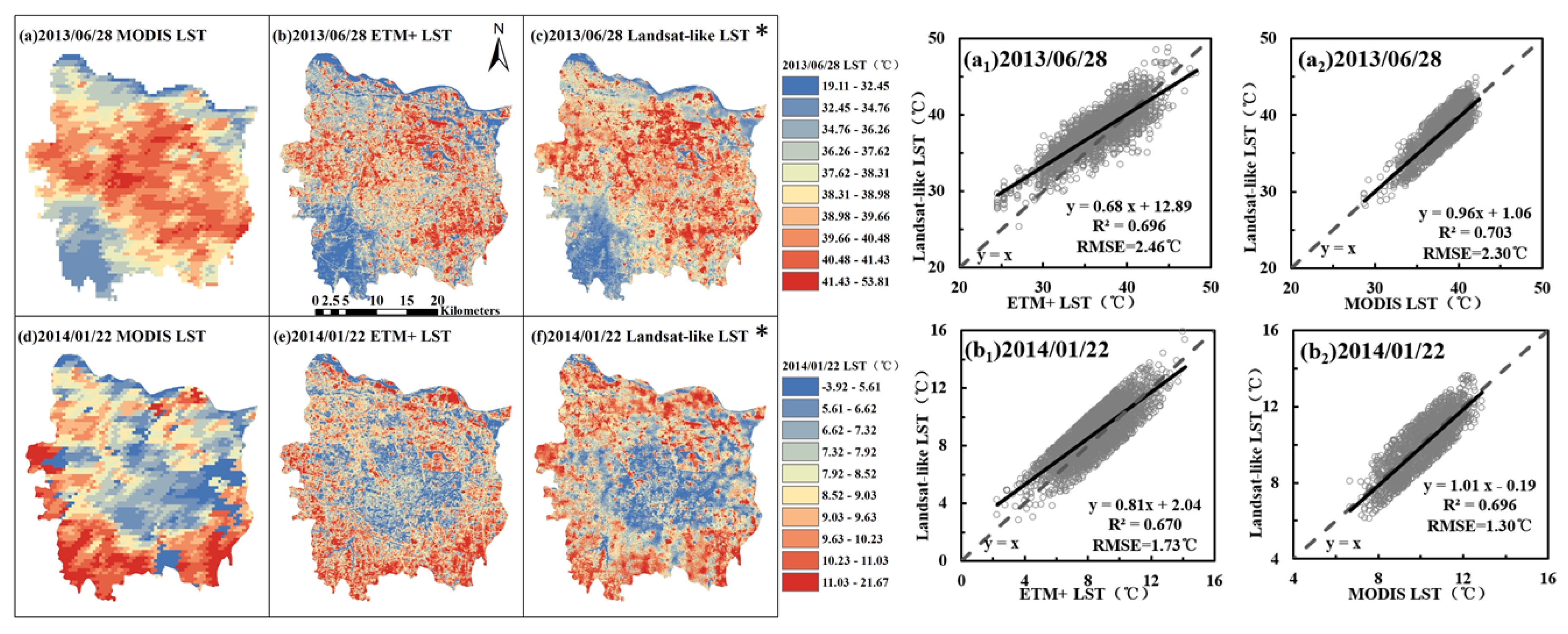
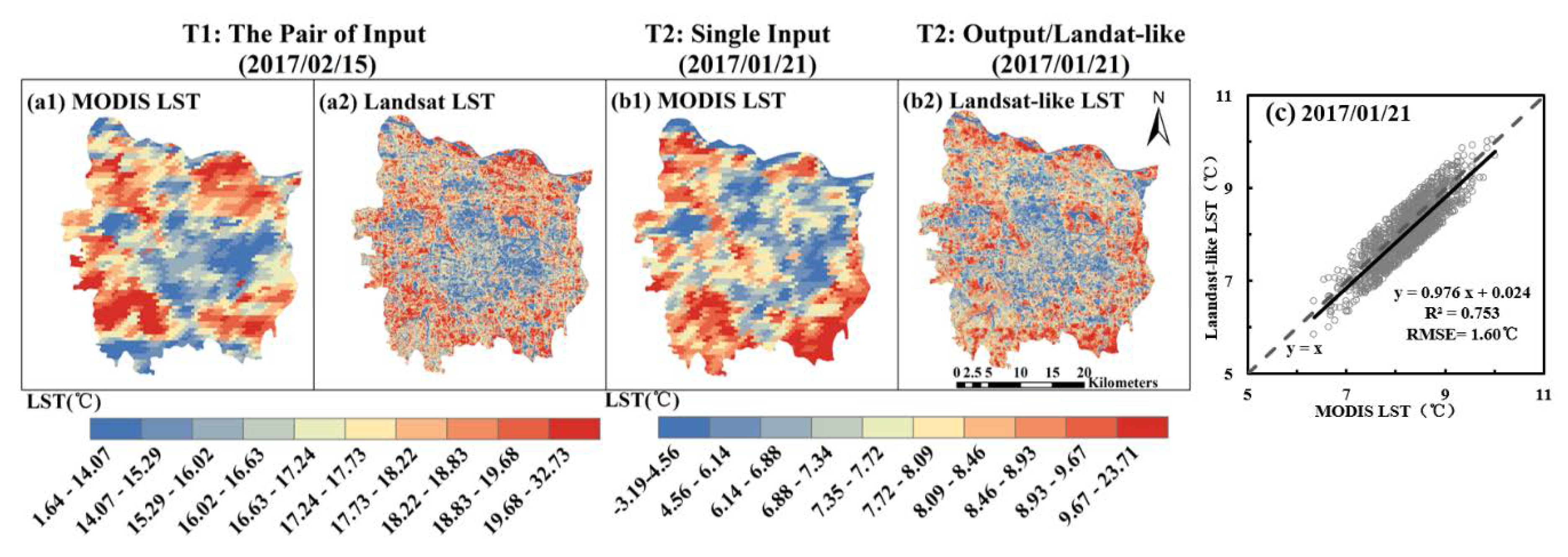
3.1. Land-like LST Accuracy Assessment
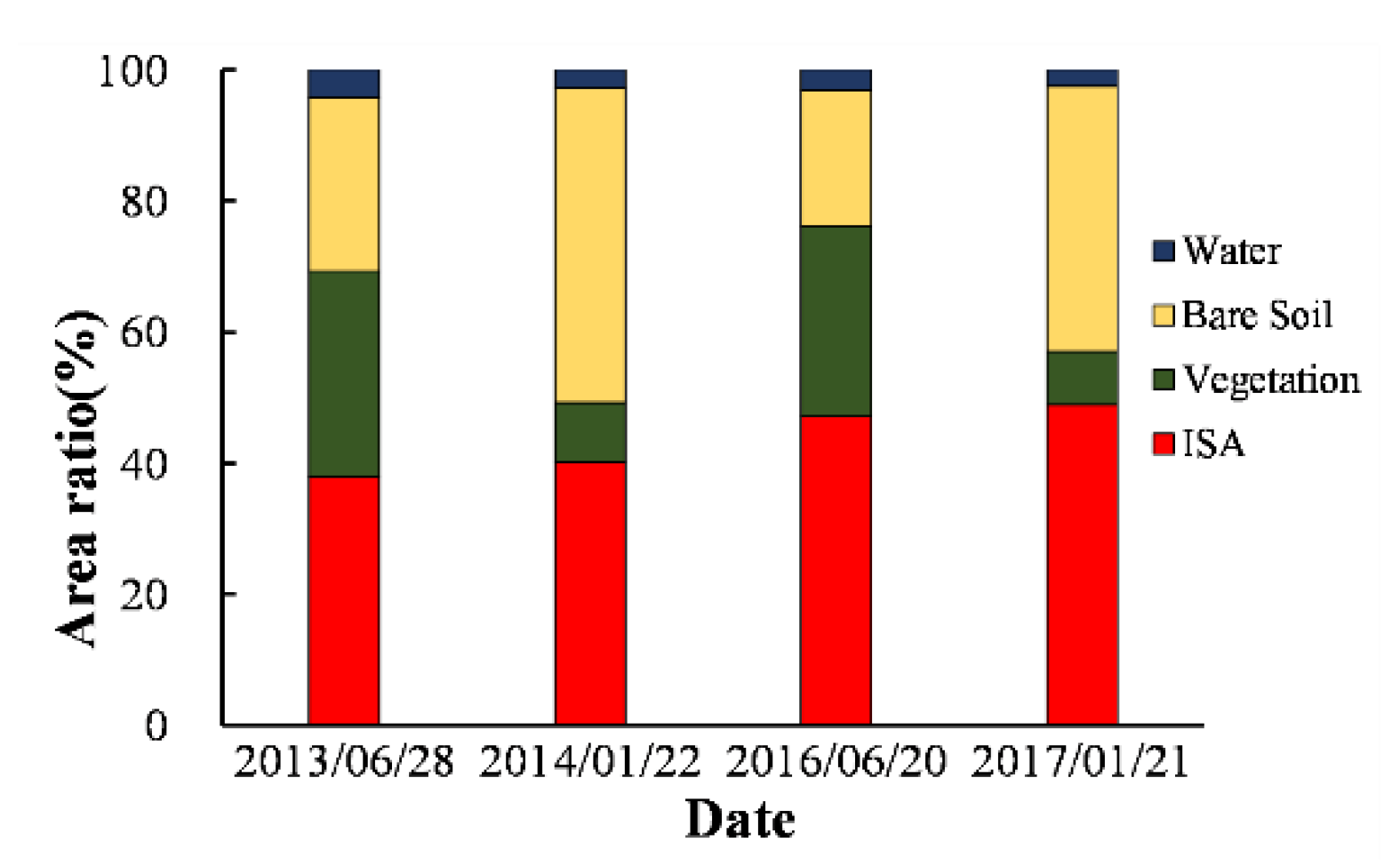
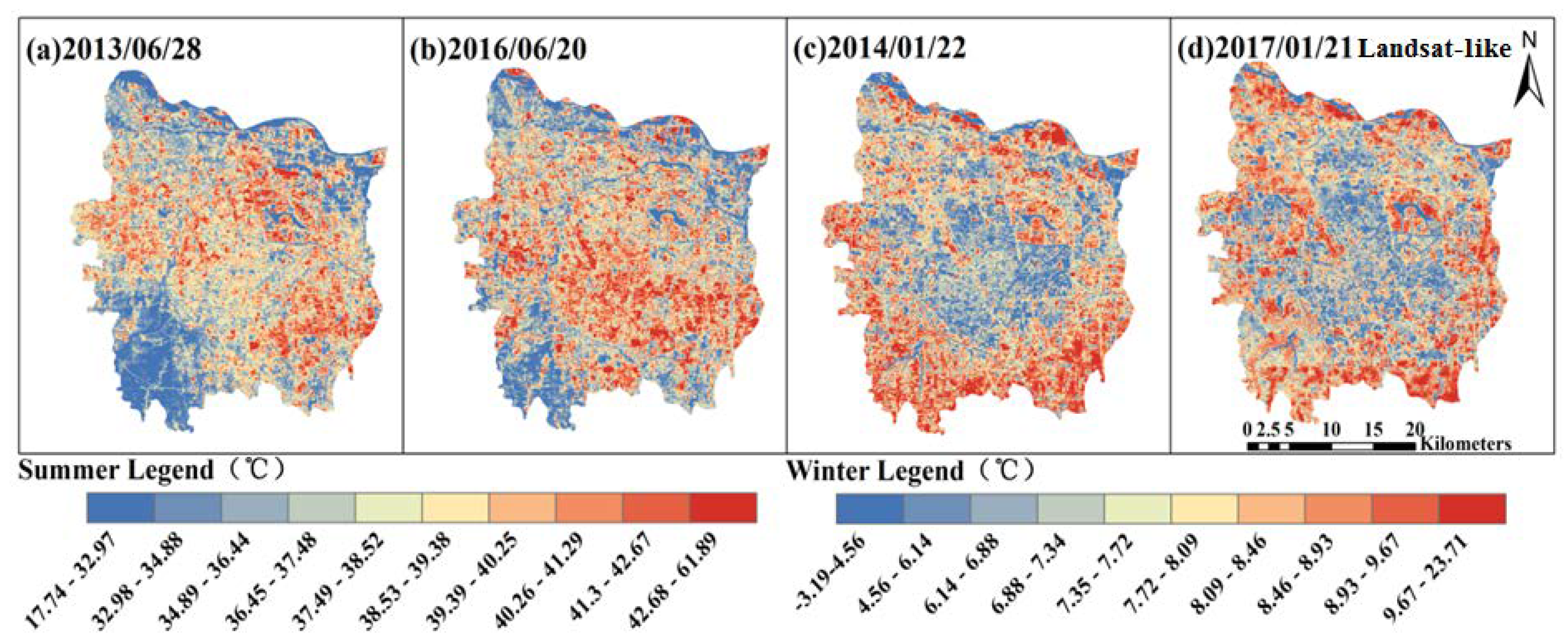
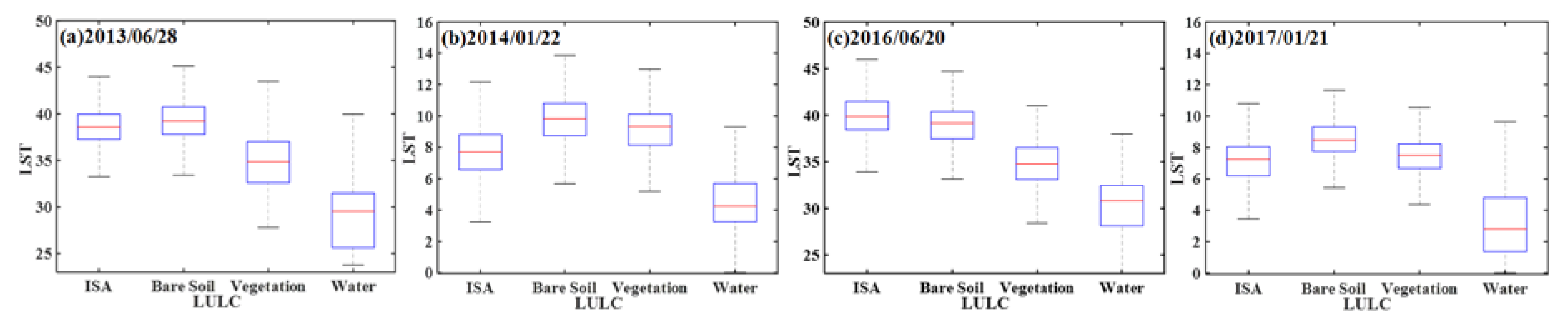
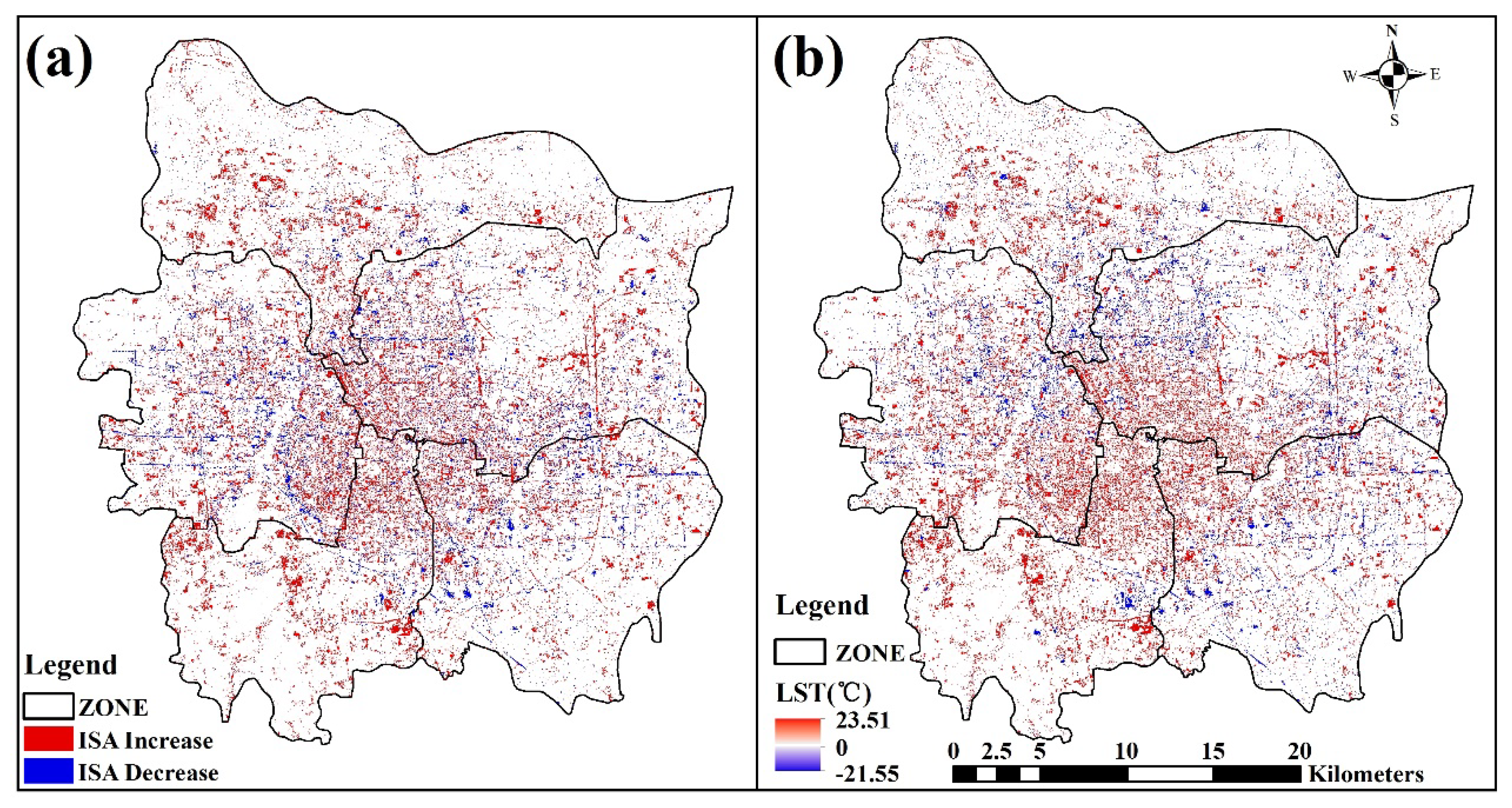
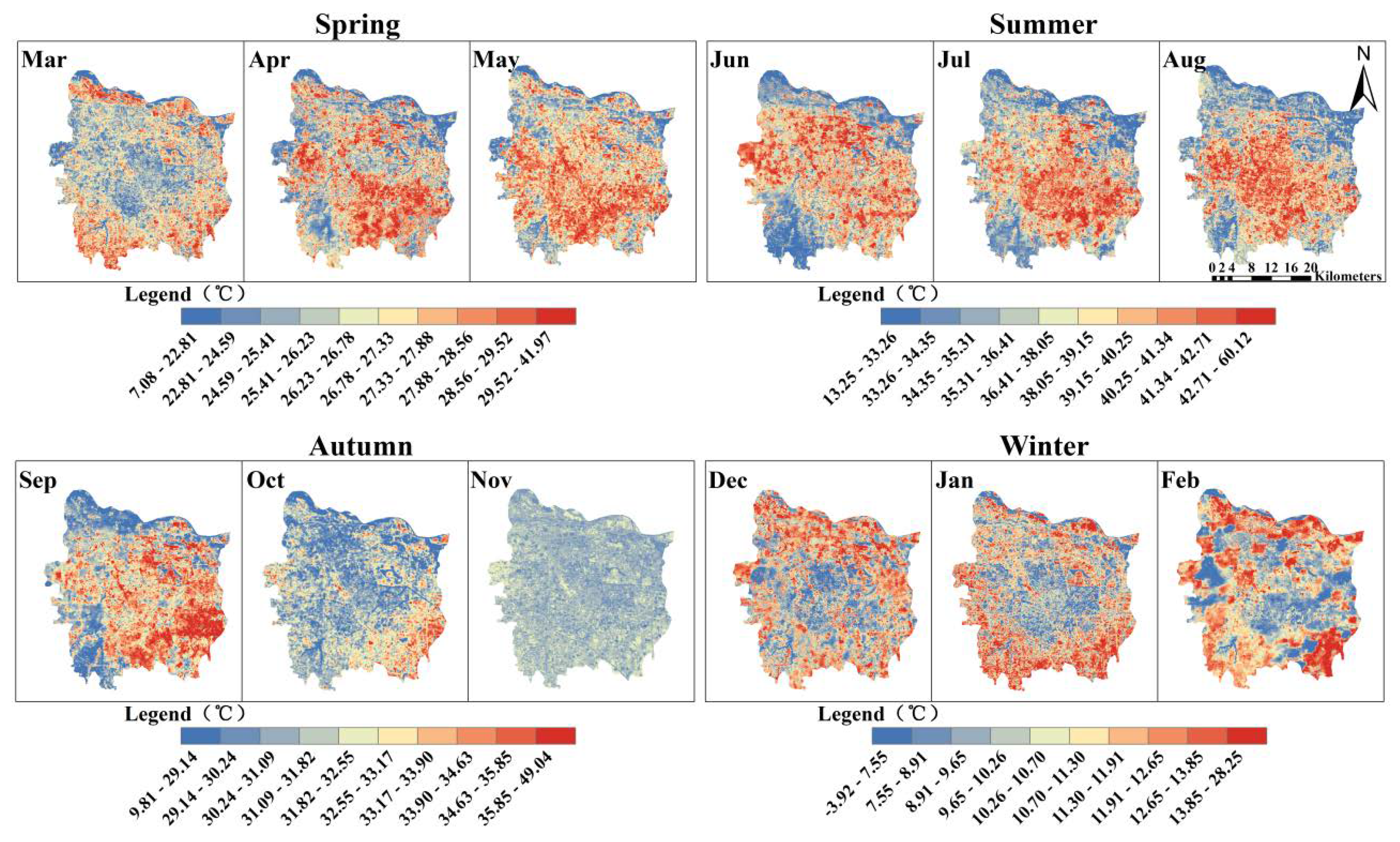
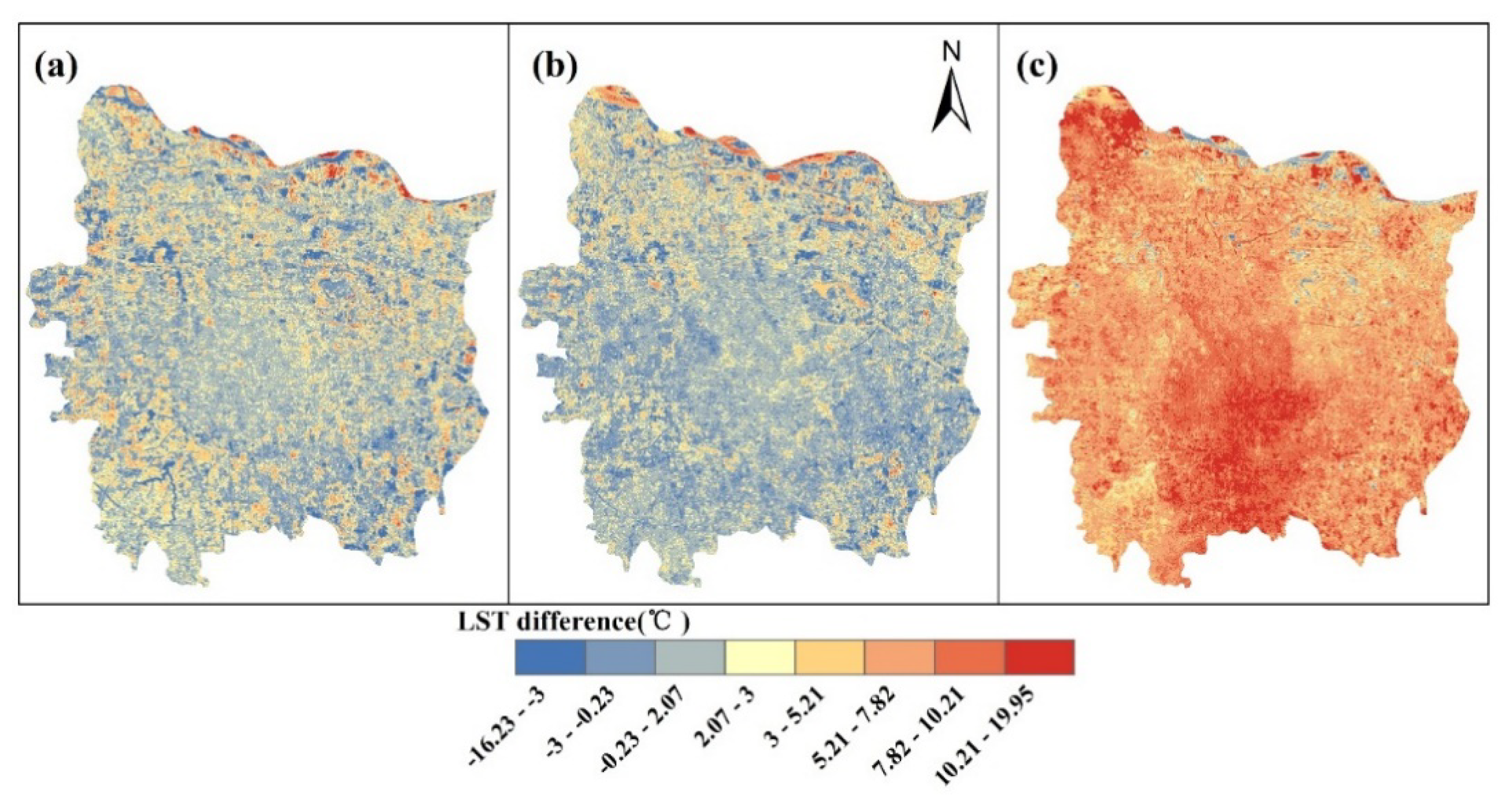
3.2. LST Variations under Urban Expansion
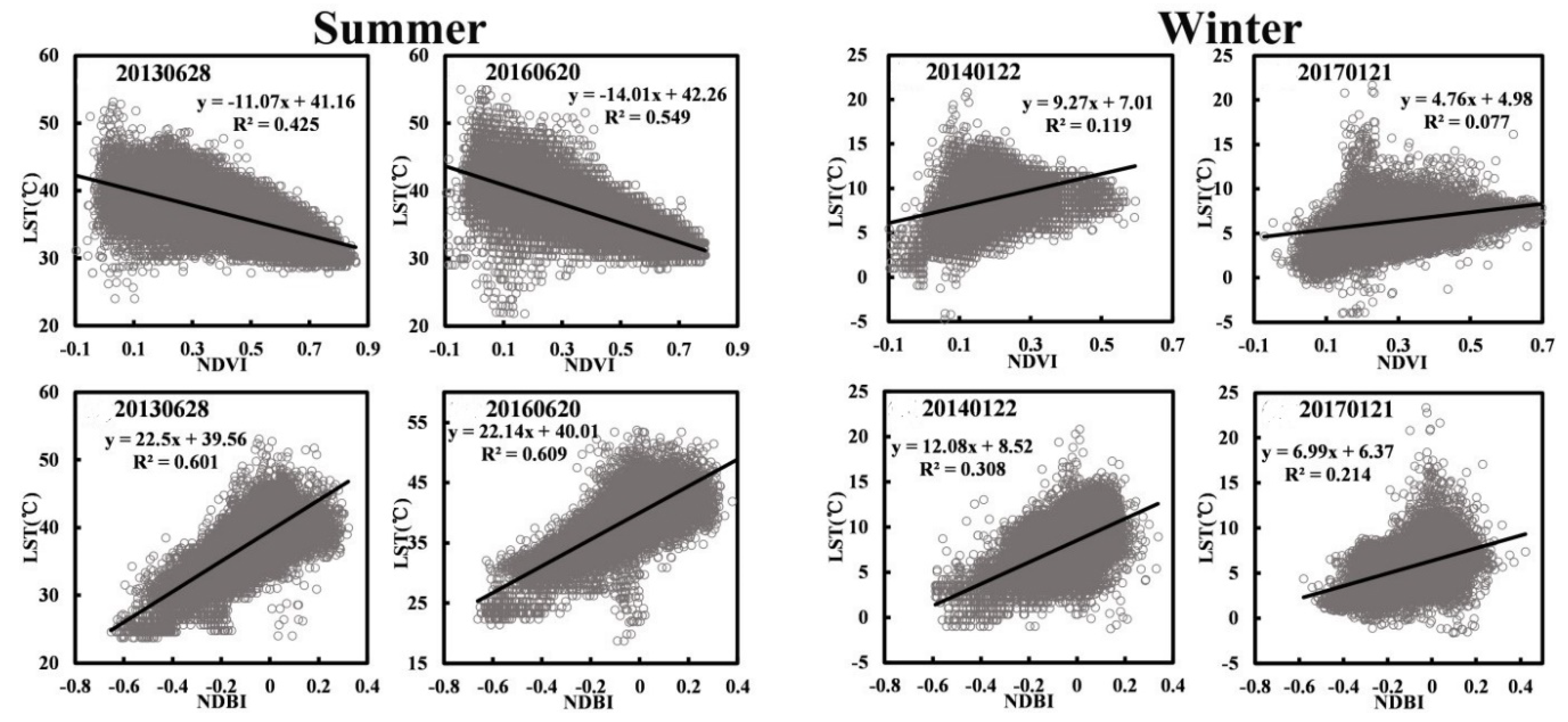
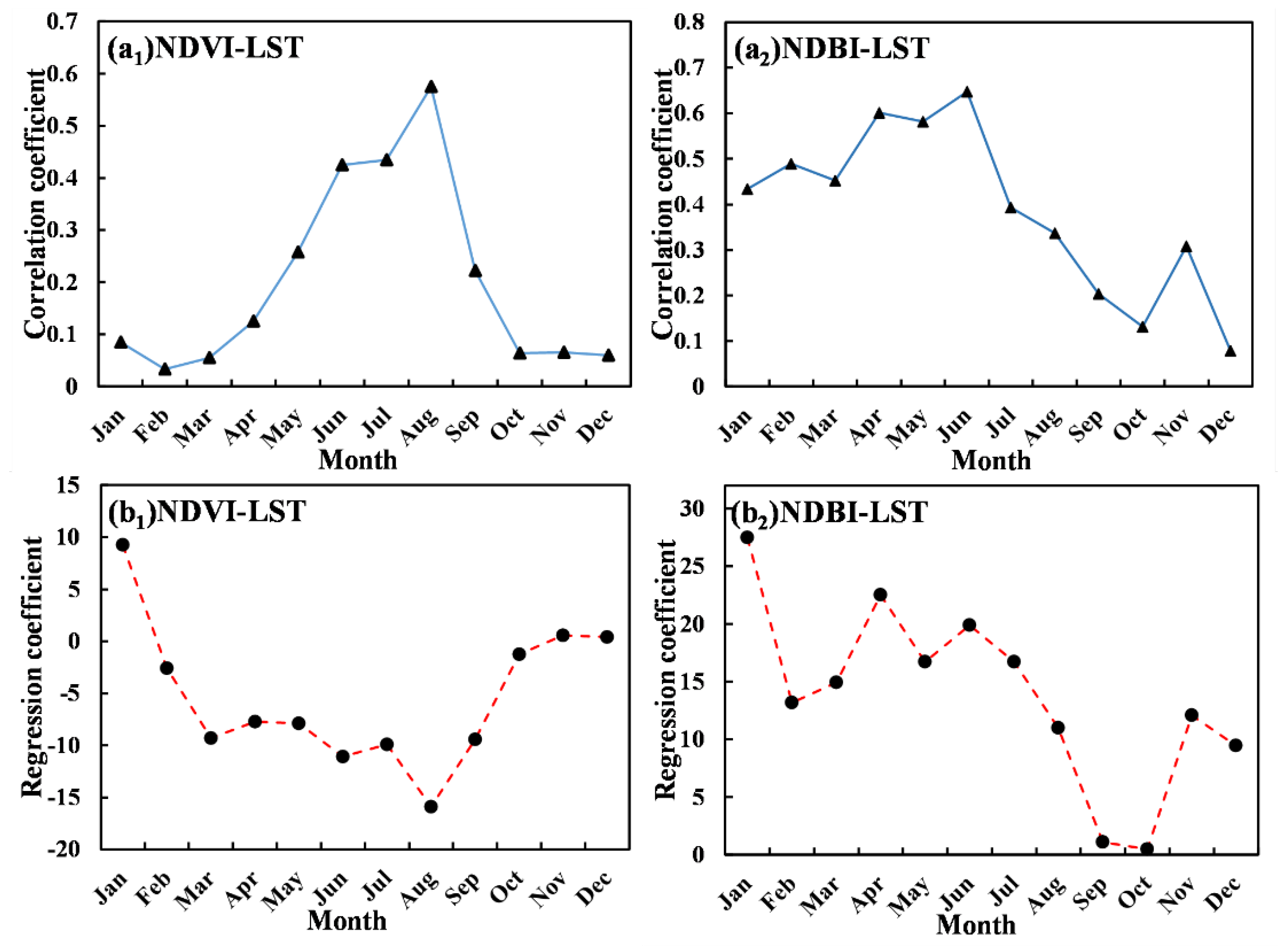
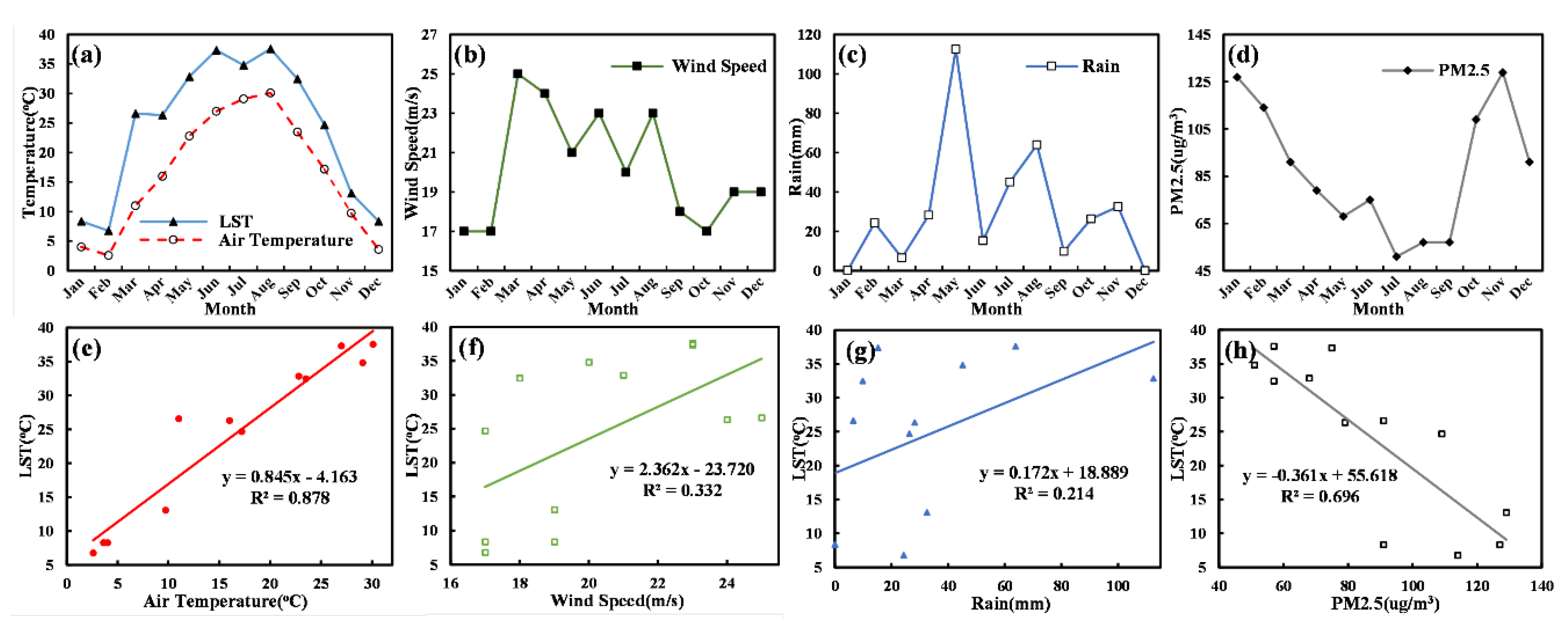
3.3. Driving Factors on LST
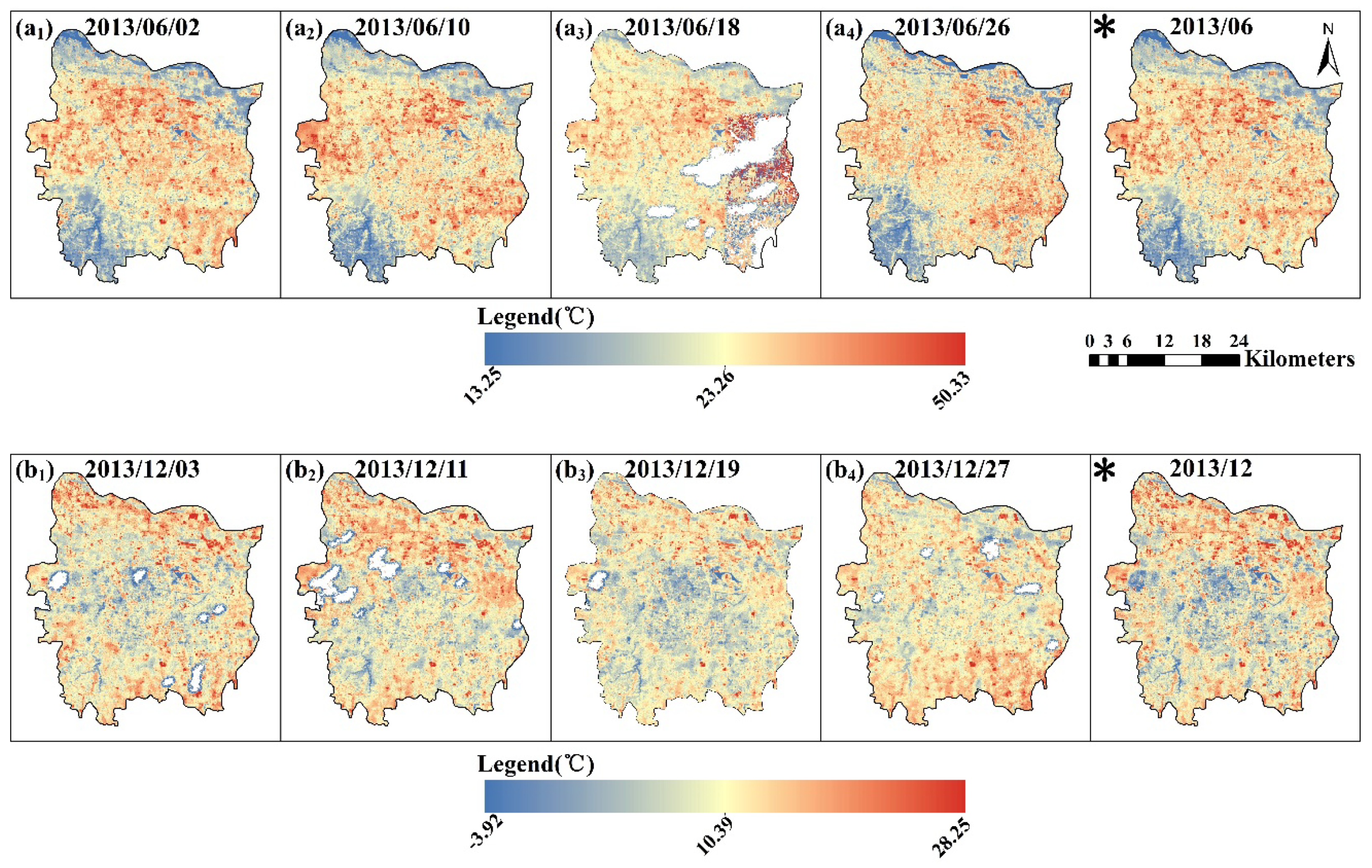
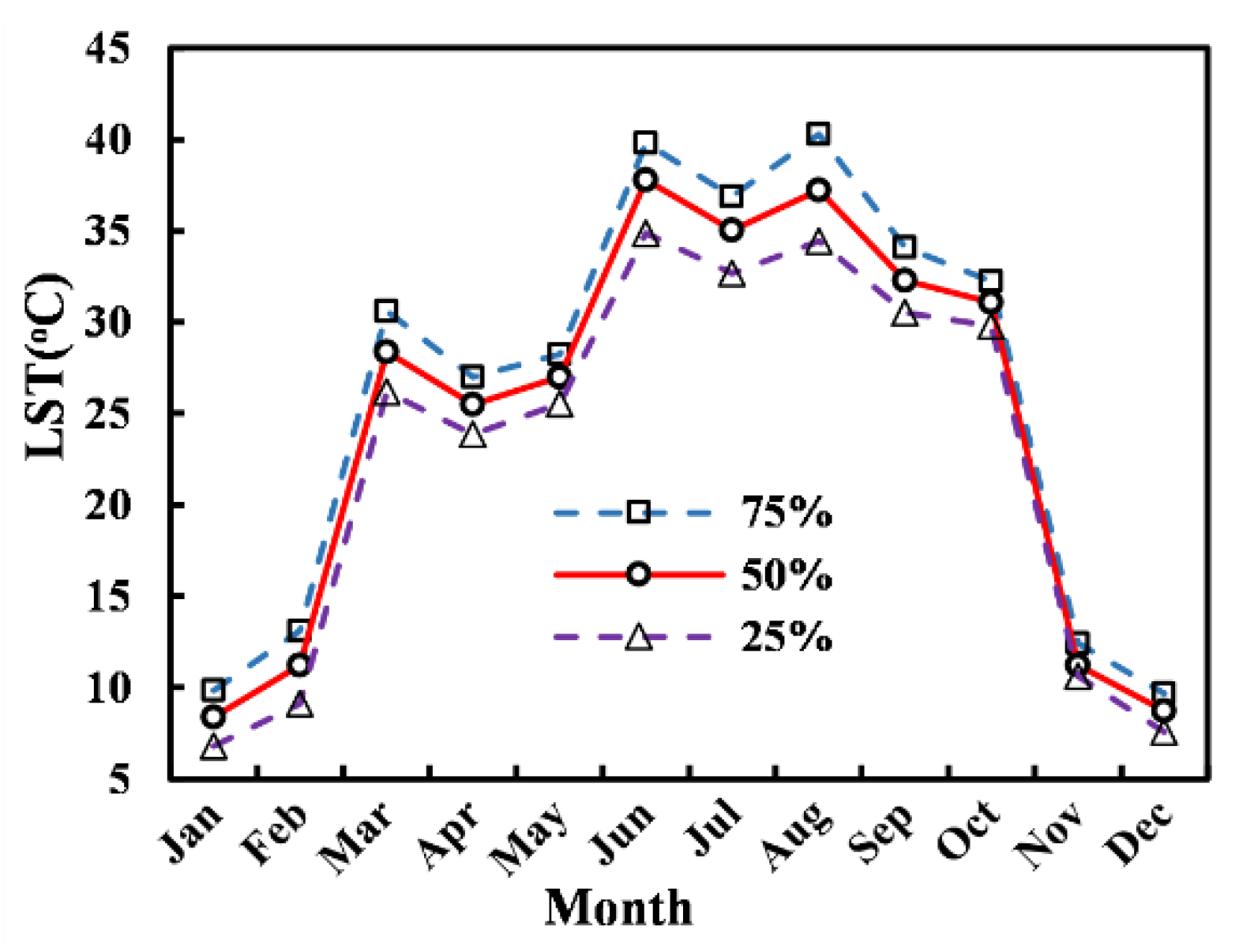
3.4. Integrated Monthly LST Dynamics Based on Landsat-like Data
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Feng, J.; Lichtenberg, E.; Ding, C. Balancing act: Economic incentives, administrative restrictions, and urban land expansion in China. China Econ. Rev. 2015, 36, 184–197. [Google Scholar] [CrossRef]
- Weilenmann, B.; Seidl, I.; Schulz, T. The socio-economic determinants of urban sprawl between 1980 and 2010 in Switzerland. Landsc. Urban Plan. 2017, 157, 468–482. [Google Scholar] [CrossRef]
- Kuang, W.; Chi, W.; Lu, D.; Dou, Y. A comparative analysis of megacity expansions in China and the U.S.: Patterns, rates and driving forces. Landsc. Urban Plan. 2014, 132, 121–135. [Google Scholar] [CrossRef]
- You, H.; Yang, X. Urban expansion in 30 megacities of China: Categorizing the driving force profiles to inform the urbanization policy. Land Use Policy 2017, 68, 531–551. [Google Scholar] [CrossRef]
- Division, P. World Urbanization Prospects: The 2014 Revision: Highlights; Rozenberg Publishers: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Yu, W.; Zhou, W. The Spatiotemporal Pattern of Urban Expansion in China: A Comparison Study of Three Urban Megaregions. Remote Sens. 2017, 9, 45. [Google Scholar] [CrossRef]
- Jenerette, G.D.; Harlan, S.L.; Buyantuev, A.; Stefanov, W.L.; Declet-Barreto, J.; Ruddell, B.L.; Soe, W.M.; Shai, K.; Li, X. Micro-scale urban surface temperatures are related to land-cover features and residential heat related health impacts in Phoenix, AZ USA. Landsc. Ecol. 2016, 31, 745–760. [Google Scholar]
- Miles, V.; Esau, I. Surface urban heat islands in 57 cities across different climates in northern Fennoscandia. Urban Clim. 2020, 31, 1–11. [Google Scholar] [CrossRef]
- Zhou, W.; Qian, Y.; Li, X.; Han, L. Relationships between land cover and the surface urban heat island: Seasonal variability and effects of spatial and thematic resolution of land cover data on predicting land surface temperatures. Landsc. Ecol. 2014, 29, 153–167. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Kainz, W. Monitoring patterns of urban heat islands of the fast-growing Shanghai metropolis, China: Using time-series of Landsat TM/ETM+ data. Int. J. Appl. Earth Obs. 2012, 19, 127–138. [Google Scholar] [CrossRef]
- Li, W.; Han, C.; Li, W.; Zhou, W.; Han, L. Multi-scale effects of urban agglomeration on thermal environment: A case of the Yangtze River Delta Megaregion, China. Sci. Total Environ. 2020, 713, 136556. [Google Scholar] [CrossRef]
- Yu, W.; Ma, M.; Hong, Y.; Tan, J.; Li, X. Supplement of the radiance-based method to validate satellite-derived land surface temperature products over heterogeneous land surfaces. Remote Sens. Environ. 2019, 230, 1–13. [Google Scholar] [CrossRef]
- Ichinose, T.; Shimodozono, K.; Hanaki, K. Impact of anthropogenic heat on urban climate in Tokyo. Atmos Environ. 1999, 33, 3897–3909. [Google Scholar] [CrossRef]
- Jin, M.; Dickinson, R.E.; Vogelmann, A.M. A Comparison of CCM2–BATS Skin Temperature and Surface-Air Temperature with Satellite and Surface Observations. J. Clim. 1997, 10, 1505–1524. [Google Scholar] [CrossRef]
- Jin, M.; Dickinson, R.E. Land surface skin temperature climatology: Benefitting from the strengths of satellite observations. Environ. Res. Lett. 2010, 5, 044004. [Google Scholar] [CrossRef]
- Jimenez-Munoz, J.C.; Sobrino, J.A. A Single-Channel Algorithm for Land-Surface Temperature Retrieval from ASTER Data. IEEE Geosci. Remote Sens. 2010, 7, 176–179. [Google Scholar] [CrossRef]
- Tang, H.; Bi, Y.; Li, Z.L.; Xia, J. Generalized split-window algorithm for estimate of land surface temperature from Chinese geostationary FengYun meteorological satellite (Fy-2C) data. Sensors 2008, 8, 933–951. [Google Scholar] [CrossRef]
- Wang, F.; Qin, Z.; Song, C.; Tu, L.; Karnieli, G.; Zhao, S. An Improved Mono-Window Algorithm for Land Surface Temperature Retrieval from Landsat 8 Thermal Infrared Sensor Data. Remote Sens. 2015, 7, 4268–4289. [Google Scholar] [CrossRef]
- Tang, H.; Shao, K.; Li, Z.L.; Wu, H.; Nerry, F.; Zhou, G. Estimation and validation of land surface temperature from Chinese second generation polar-orbiting FY-3A VIRR data. Remote Sens. 2015, 7, 3250–3273. [Google Scholar] [CrossRef]
- Qin, Z.H.; Karnieli, A.; Berliner, P. A mono-window algorithm for retrieving land surface temperature from Landsat TM data and its application to the Israel-Egypt border region. Int. J. Remote Sens. 2001, 22, 3719–3746. [Google Scholar] [CrossRef]
- Ouyang, X.Y.; Wang, N.; Wu, H.; Li, Z. Errors analysis on temperature and emissivity determination from hyperspectral thermal infrared data. Opt. Express. 2010, 18, 544–550. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, Y. Impacts of urban surface characteristics on spatiotemporal pattern of land surface temperature in Kunming of China. Sustain. Cities Soc. 2017, 32, 87–99. [Google Scholar] [CrossRef]
- Sheng, L.; Hu, H.; You, H.; Gu, Q.; Hu, H. Comparison of the urban heat island intensity quantified by using air temperature and Landsat land surface temperature in Hangzhou, China. Ecol. Indic. 2017, 72, 738–746. [Google Scholar] [CrossRef]
- Xiong, Y.; Huang, S.; Chen, F.; Ye, H.; Wang, C.; Zhu, C. The Impacts of Rapid Urbanization on the Thermal Environment: A Remote Sensing Study of Guangzhou, South China. Remote Sens. 2012, 4, 2033–2056. [Google Scholar] [CrossRef]
- Wang, S.; Ma, Q.; Ding, H.; Liang, H. Detection of urban expansion and land surface temperature change using multi-temporal landsat images. Resour. Conserv. Recycl. 2018, 128, 526–534. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Y.; Asrar, G.R.; Zhu, Z. Creating a seamless 1 km resolution daily land surface temperature dataset for urban and surrounding areas in the conterminous United States. Remote Sens. Environ. 2018, 206, 84–97. [Google Scholar] [CrossRef]
- Sun, L.; Chen, Z.; Gao, F.; Anderson, M.; Song, L.; Wang, L.; Hu, B.; Yang, Y. Reconstructing daily clear-sky land surface temperature for cloudy regions from MODIS data. Comput. Geosci.-UK 2017, 105, 10–20. [Google Scholar] [CrossRef]
- Jose, L.; Filho, A.; Karam, H. Estimation of long term low resolution surface urban heat island intensities for tropical cities using MODIS remote sensing data. Urban Clim. 2016, 17, 32–66. [Google Scholar] [CrossRef]
- Williamson, S.N.; Hik, D.S.; Gamon, J.A.; Jarosch, A.H.; Anslow, F.S.; Clarke, G.K.; Rupp, T.S. Spring and summer monthly MODIS LST is inherently biased compared to air temperature in snow covered sub-Arctic mountains. Remote Sens. Environ. 2017, 189, 14–24. [Google Scholar] [CrossRef]
- Haynes, M.; Horowitz, F.; Sambridge, M.; Gerner, E.; Beardsmore, G. Australian mean land-surface temperature. Geothermics 2018, 72, 156–162. [Google Scholar] [CrossRef]
- Eleftheriou, D.; Kiachidis, K.; Kalmintzis, G.; Kalea, A.; Bantasis, C.; Koumadoraki, P.; Spathara, M.E.; Tsolaki, A.; Tzampazidou, M.I.; Gemitzi, A. Determination of annual and seasonal daytime and nighttime trends of MODIS LST over Greece—Climate change implications. Sci. Total Environ. 2018, 616–617, 937–947. [Google Scholar] [CrossRef]
- Zhou, W.; Huang, G.; Cadenasso, M.L. Does spatial configuration matter? Understanding the effects of landcover pattern on land surface temperature in urban landscapes. Landsc. Urban Plan. 2011, 102, 54–63. [Google Scholar] [CrossRef]
- Larondelle, N.; Hamstead, Z.A.; Kremer, P.; Haase, D.; Macphearson, T. Applying a novel urban structure classification to compare the relationships of urban structure and surface temperature in Berlin and New York City. Appl. Geogr. 2014, 53, 427–437. [Google Scholar] [CrossRef]
- Chaudhuri, G.; Mishra, N.B. Spatio-temporal dynamics of land cover and land surface temperature in Ganges-Brahmaputra delta: A comparative analysis between India and Bangladesh. Appl. Geogr. 2016, 68, 68–83. [Google Scholar] [CrossRef]
- Mushore, T.D.; Mutanga, O.; Odindi, J.; Dube, T. Linking major shifts in land surface temperatures to long term land use and land cover changes: A case of Harare, Zimbabwe. Urban Clim. 2017, 20, 120–134. [Google Scholar] [CrossRef]
- Wu, M.; Li, H.; Huang, W.; Niu, Z.; Wang, C. Generating daily high spatial land surface temperatures by combining ASTER and MODIS land surface temperature products for environmental process monitoring. Environ Sci. Proc. Impact 2015, 17, 1396–1404. [Google Scholar] [CrossRef] [PubMed]
- Lu, D.; Weng, Q. Spectral mixture analysis of ASTER images for examining the relationship between urban thermal features and biophysical descriptors in Indianapolis, Indiana, USA. Remote Sens. Environ. 2006, 104, 157–167. [Google Scholar] [CrossRef]
- Soliman, A.; Duguay, C.; Hachem, S.; Saunders, W.; Luus, K. Pan-Arctic Land Surface Temperature from MODIS and AATSR: Product Development and Intercomparison. Remote Sens. 2012, 4, 3833–3856. [Google Scholar] [CrossRef]
- Yao, R.; Wang, L.; Huang, X.; Liu, F.; Wang, Q. Temporal trends of surface urban heat islands and associated determinants in major Chinese cities. Sci. Total Environ. 2017, 609, 742–754. [Google Scholar] [CrossRef]
- Zhou, D.; Zhao, S.; Liu, S.; Zhang, L.; Zhu, C. Surface urban heat island in China’s 32 major cities: Spatial patterns and drivers. Remote Sens. Environ. 2014, 152, 51–61. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar]
- Zhu, X.; Chen, J.; Gao, F.; Chen, X.; Masek, J. An enhanced spatial and temporal adaptive reflectance fusion model for complex heterogeneous regions. Remote Sens. Environ. 2010, 114, 2610–2623. [Google Scholar] [CrossRef]
- Xia, H.; Chen, Y.; Li, Y.; Quan, J. Combining kernel-driven and fusion-based methods to generate daily high-spatial-resolution land surface temperatures. Remote Sens. Environ. 2019, 224, 259–274. [Google Scholar] [CrossRef]
- Wang, J.; Schmitz, O.; Lu, M.; Karssenberg, D. Thermal unmixing based downscaling for fine resolution diurnal land surface temperature analysis. ISPRS J. Photogramm. 2020, 161, 76–89. [Google Scholar] [CrossRef]
- Shen, H.; Huang, L.; Zhang, L.; Wu, P.; Zeng, C. Long-term and fine-scale satellite monitoring of the urban heat island effect by the fusion of multi-temporal and multi-sensor remote sensed data: A 26-year case study of the city of Wuhan in China. Remote Sens. Environ. 2016, 172, 109–125. [Google Scholar] [CrossRef]
- Huang, B.; Wang, J.; Song, H.; Fu, D.; Wong, K. Generating High Spatiotemporal Resolution Land Surface Temperature for Urban Heat Island Monitoring. IEEE Geosci. Remote Sens. 2013, 10, 1011–1015. [Google Scholar] [CrossRef]
- Weng, Q.; Fu, P.; Gao, F. Generating daily land surface temperature at Landsat resolution by fusing Landsat and MODIS data. Remote Sens. Environ. 2014, 145, 55–67. [Google Scholar] [CrossRef]
- Wu, P.; Shen, H.; Zhang, L.; Göttsched, F. Integrated fusion of multi-scale polar-orbiting and geostationary satellite observations for the mapping of high spatial and temporal resolution land surface temperature. Remote Sens. Environ. 2015, 156, 169–181. [Google Scholar] [CrossRef]
- Zhu, X.; Helmer, E.H.; Gao, F.; Liu, D.; Chen, J.; Lefsky, M. A flexible spatiotemporal method for fusing satellite images with different resolutions. Remote Sens. Environ. 2016, 172, 165–177. [Google Scholar] [CrossRef]
- Zhang, L.; Weng, Q.; Shao, Z. An evaluation of monthly impervious surface dynamics by fusing Landsat and MODIS time series in the Pearl River Delta, China, from 2000 to 2015. Remote Sens. Environ. 2017, 201, 99–114. [Google Scholar] [CrossRef]
- Mu, B.; Mayer, A.L.; He, R.; Tian, G. Land use dynamics and policy implications in Central China: A case study of Zhengzhou. Cities 2016, 58, 39–49. [Google Scholar] [CrossRef]
- Gu, B.; Sheng, V.S. A Robust Regularization Path Algorithm for ν-Support Vector Classification. IEEE Trans. Neural Netw. Learn. 2016, 28, 1241–1248. [Google Scholar] [CrossRef] [PubMed]
- Colgan, M.S.; Baldeck, C.A.; Féret, J.-B.; Asner, G.P. Mapping Savanna Tree Species at Ecosystem Scales Using Support Vector Machine Classification and BRDF Correction on Airborne Hyperspectral and LiDAR Data. Remote Sens. 2012, 4, 3462–3480. [Google Scholar] [CrossRef]
- Bovolo, F.; Camps-Valls, G.; Bruzzone, L. A support vector domain method for change detection in multitemporal images. Pattern Recogn. Lett. 2010, 31, 1148–1154. [Google Scholar] [CrossRef]
- Barsi, J.A.; Barker, J.L.; Schott, J.R. An atmospheric correction parameter calculator for a single thermal band earth-sensing instrument. IEEE Int. Geosci. Remote Sens. Symp. 2003, 5, 3014–3016. [Google Scholar]
- Barsi, J.A.; Schott, J.R.; Palluconi, F.D.; Hook, S.J. Validation of a Web-Based Atmospheric Correction Tool for Single Thermal Band Instruments. SPIE 2005, 5882, 58820. [Google Scholar]
- Valor, E.; Caselles, V. Mapping land surface emissivity from NDVI: Application to European, African, and South American areas. Remote Sens. Environ. 1996, 57, 167–184. [Google Scholar] [CrossRef]
- Van de Griend, A.; Owe, M. On the relationship between thermal emissivity and the normalized difference vegetation index for natural surfaces. Int. J. Remote Sens. 1993, 14, 1119–1131. [Google Scholar] [CrossRef]
- Helder, D.L. Summary of current radiometric calibration coefficients for Landsat MSS, TM, ETM+, and EO-1 ALI sensors. Remote Sens. Environ. 2009, 113, 893–903. [Google Scholar]
- Hilker, T.; Wulder, M.A.; Coops, N.C.; Linke, J.; McDermid, G.; Masek, J.G.; Gao, F.; White, J.C. A new data fusion model for high spatial- and temporal-resolution mapping of forest disturbance based on Landsat and MODIS. Remote Sens. Environ. 2009, 113, 1613–1627. [Google Scholar] [CrossRef]
- Effat, H.A.; Hassan, O.A.K. Change detection of urban heat islands and some related parameters using multi-temporal Landsat images; a case study for Cairo city, Egypt. Urban Clim. 2014, 10, 171–188. [Google Scholar] [CrossRef]
- Holderness, T.; Barr, S.; Dawson, R.; Hall, J. An evaluation of thermal Earth observation for characterizing urban heatwave event dynamics using the urban heat island intensity metric. Int. J. Remote Sens. 2013, 34, 864–884. [Google Scholar] [CrossRef]
- Chen, B.; Huang, B.; Chen, L.; Xu, B. Spatially and temporally weighted regression: A novel method to produce continuous cloud-free Landsat imagery. IEEE Trans. Geosci. Remote Sens. 2017, 55, 27–37. [Google Scholar] [CrossRef]
- Fu, Y.; Wu, J. Expansion of Urbanization Based on Remote Sensing Technology Research to Zhengzhou City as an Example. Adv Mater Res. 2014, 926–930, 4242–4245. [Google Scholar] [CrossRef]
- Pan, C.; Wu, G. Study on the spatial expansion and optimization of Zhengzhou City base on GIS. In Proceedings of the 2011 International Symposium on Water Resource and Environmental Protection, Xi’an, China, 20–22 May 2011; pp. 2871–2875. [Google Scholar]
- Chen, L.; Li, M.; Huang, F.; Xu, S. Relationships of LST to NDBI and NDVI in Wuhan City Based on Landsat ETM+ Image. Int. Congr. Image Signal Process. 2013, 2, 840–845. [Google Scholar]
- Peng, J.; Jia, J.; Liu, Y.; Li, H.; Wu, J. Seasonal contrast of the dominant factors for spatial distribution of land surface temperature in urban areas. Remote Sens. Environ. 2018, 215, 255–267. [Google Scholar] [CrossRef]
- Sun, D.; Menas, K. Note on the NDVI-LST relationship and the use of temperature-related drought indices over North America. Geophys. Res. Lett. 2007, 34, 497–507. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, L. Spatial-temporal impacts of urban land use land cover on land surface temperature: Case studies of two Canadian urban areas. Int. J. Appl. Earth Obs. Geoinf. 2019, 75, 171–181. [Google Scholar] [CrossRef]
- Zhang, Y.; Balzter, H.; Zou, C.; Xu, H.; Tang, F. Characterizing bi-temporal patterns of land surface temperature using landscape metrics based on sub-pixel classifications from Landsat TM/ETM+. Int. J. Appl. Earth Obs. 2015, 42, 87–96. [Google Scholar] [CrossRef]
- Yang, J.; Jin, S.; Xiao, X.; Jin, C.; Xia, J.; Li, X.; Wang, S. Local climate zone ventilation and urban land surface temperatures: Towards a performance-based and wind-sensitive planning proposal in megacities. Sustain. Cities Soc. 2019, 47, 101487. [Google Scholar] [CrossRef]
- Wang, C.; Li, Y.; Myint, S.W.; Zhao, Q.; Went, Z.E. Impacts of spatial clustering of urban land cover on land surface temperature across Köppen climate zones in the contiguous United States. Landsc. Urban Plan. 2019, 192, 103668. [Google Scholar] [CrossRef]
- Rui, Y.; Lunche, W.; Xin, H.; Zhang, W.; Li, J.; Niu, Z. Interannual variations in surface urban heat island intensity and associated drivers in China. J. Environ. Manag. 2018, 222, 86–94. [Google Scholar]
- Zhu, W.; Lu, A.; Jia, S. Estimation of daily maximum and minimum air temperature using MODIS land surface temperature products. Remote Sens. Environ. 2013, 130, 62–73. [Google Scholar] [CrossRef]
- Cao, C.; Lee, X.; Liu, S.; Schultz, N.; Xiao, W.; Zhang, M.; Zhao, L. Urban heat islands in China enhanced by haze pollution. Nat. Commun. 2016, 7, 12509. [Google Scholar] [CrossRef] [PubMed]
- Ozelkan, E.; Bagis, S.; Ozelkan, E.; Ustundag, B.; Ormeci, C. Land Surface Temperature Retrieval for Climate Analysis and Association with Climate Data. Eur. J. Remote Sens. 2014, 47, 655–669. [Google Scholar] [CrossRef]
- Wang, K.; Liang, S. Evaluation of ASTER and MODIS land surface temperature and emissivity products using long-term surface longwave radiation observations at SURFRAD sites. Remote Sens. Environ. 2009, 113, 1556–1565. [Google Scholar] [CrossRef]
- Zhan, W.; Chen, Y.; Zhou, J.; Wang, J.; Liu, W.; Voogt, J.; Zhu, X.; Quan, J.; Li, J. Disaggregation of remotely sensed land surface temperature: Literature survey, taxonomy, issues, and caveats. Remote Sens. Environ. 2013, 131, 119–139. [Google Scholar] [CrossRef]


| LST Data Source | Spatial Resolution/ Temporal Resolution | Time Scale | Strength and Limitation | Reference |
|---|---|---|---|---|
| Landsat | 60 m (TM and ETM+) or 100 m (OLI-TIRS)/16 d | monthly | High spatial resolution, low frequency | Chen X, et al. [22] Sheng L, et al. [23] |
| annual | Xiong Y, et al. [24] Wang S, et al. [25] | |||
| MODIS | 1000 m/1 d | daily | High frequency, low spatial resolution | Li X, et al. [26] Sun L, et al. [27] |
| monthly | Jose L, et al. [28] Williamson S, et al. [29] | |||
| annual | Haynes M, et al. [30] Eleftheriou D, et al. [31] | |||
| Fusion data of Landsat and MODIS | 60 m (TM and ETM+) or 100 m (OLI-TIRS)/1 d | daily | High spatial resolution, high frequency | Huang B, et al. [46] Weng Q, et al. [47] |
| monthly | Zhang L, et al. [50] |
| Data | T1: The Pair of Inputs | T2: Single Input | T2: Output | |
|---|---|---|---|---|
| MODIS LST | Landsat LST | MODIS LST | Landsat-Like LST | |
| Verification | 4 June 2013 | 4 June 2013 | 28 June 2013 | 28 June 2013 |
| 13 December 2013 | 13 December 2013 | 22 January 2014 | 22 January 2014 | |
| Prediction | 15 February 2017 | 15 February 2017 | 21 January 2017 | 21 January 2017 |
| LULC Type | 28 June 2013 | 22 January 2014 | ||
|---|---|---|---|---|
| Landsat LST | MODIS LST | Landsat LST | MODIS LST | |
| ISA | 2.25 | 1.73 | 1.74 | 1.33 |
| Vegetation | 2.70 | 2.42 | 1.69 | 1.21 |
| Bare Soil | 2.22 | 1.69 | 1.70 | 1.27 |
| Water | 2.76 | 2.87 | 1.65 | 1.28 |
| The Number of Available Landsat Images | Month |
|---|---|
| 0 | April, July, and September of 2013, February of 2014 |
| 1 | November and December of 2013, January of 2014 |
| 2 | March, May, June, August, and October of 2013 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Xi, C.; Zhao, X.; Mao, P.; Wang, Z.; Shi, Y.; He, T.; Li, Z. Measuring the Urban Land Surface Temperature Variations Under Zhengzhou City Expansion Using Landsat-Like Data. Remote Sens. 2020, 12, 801. https://doi.org/10.3390/rs12050801
Yang H, Xi C, Zhao X, Mao P, Wang Z, Shi Y, He T, Li Z. Measuring the Urban Land Surface Temperature Variations Under Zhengzhou City Expansion Using Landsat-Like Data. Remote Sensing. 2020; 12(5):801. https://doi.org/10.3390/rs12050801
Chicago/Turabian StyleYang, Haibo, Chaofan Xi, Xincan Zhao, Penglei Mao, Zongmin Wang, Yong Shi, Tian He, and Zhenhong Li. 2020. "Measuring the Urban Land Surface Temperature Variations Under Zhengzhou City Expansion Using Landsat-Like Data" Remote Sensing 12, no. 5: 801. https://doi.org/10.3390/rs12050801
APA StyleYang, H., Xi, C., Zhao, X., Mao, P., Wang, Z., Shi, Y., He, T., & Li, Z. (2020). Measuring the Urban Land Surface Temperature Variations Under Zhengzhou City Expansion Using Landsat-Like Data. Remote Sensing, 12(5), 801. https://doi.org/10.3390/rs12050801