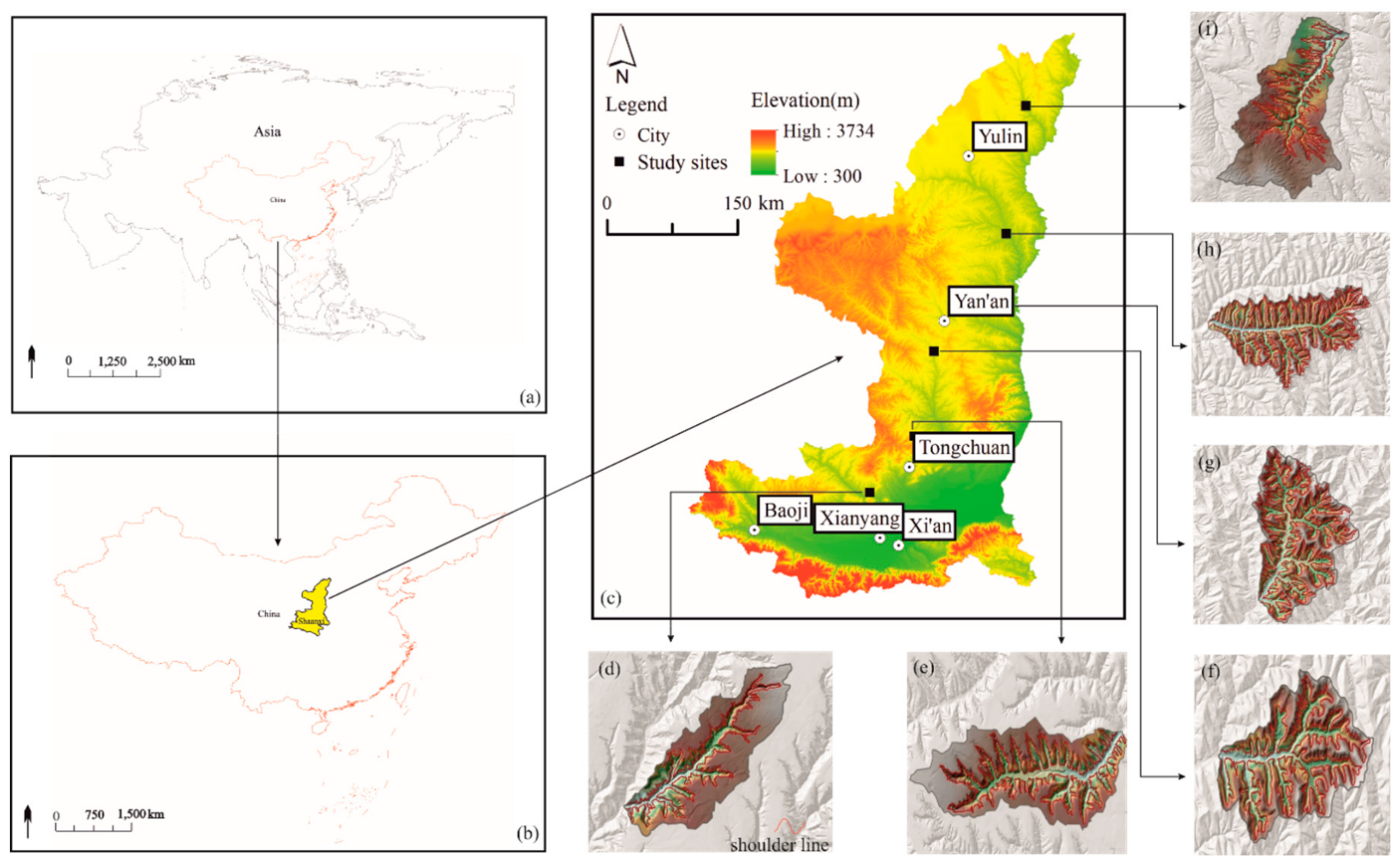
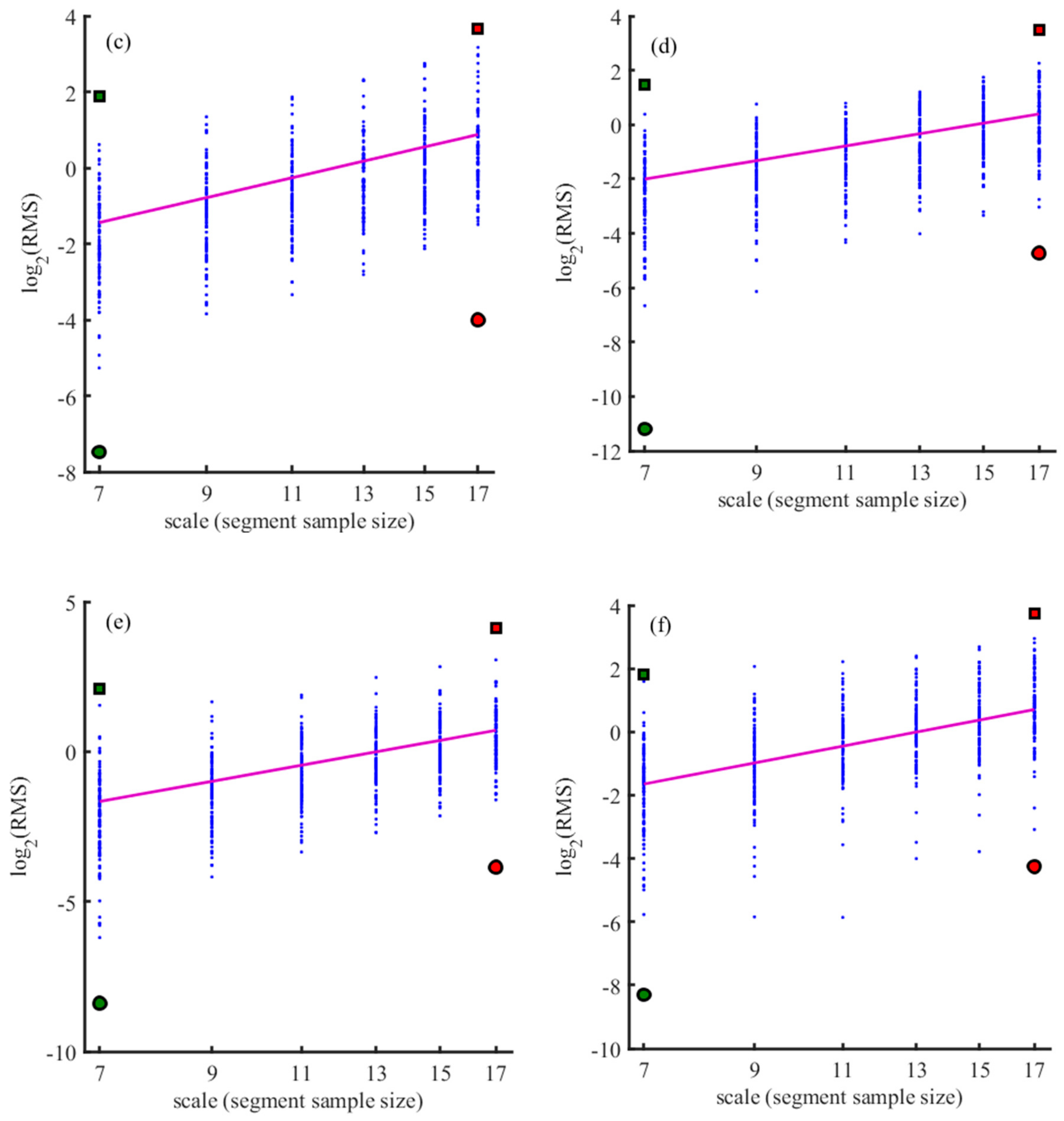
3.1. Multifractal Characteristics of the Profiles of Gully Shoulder Lines
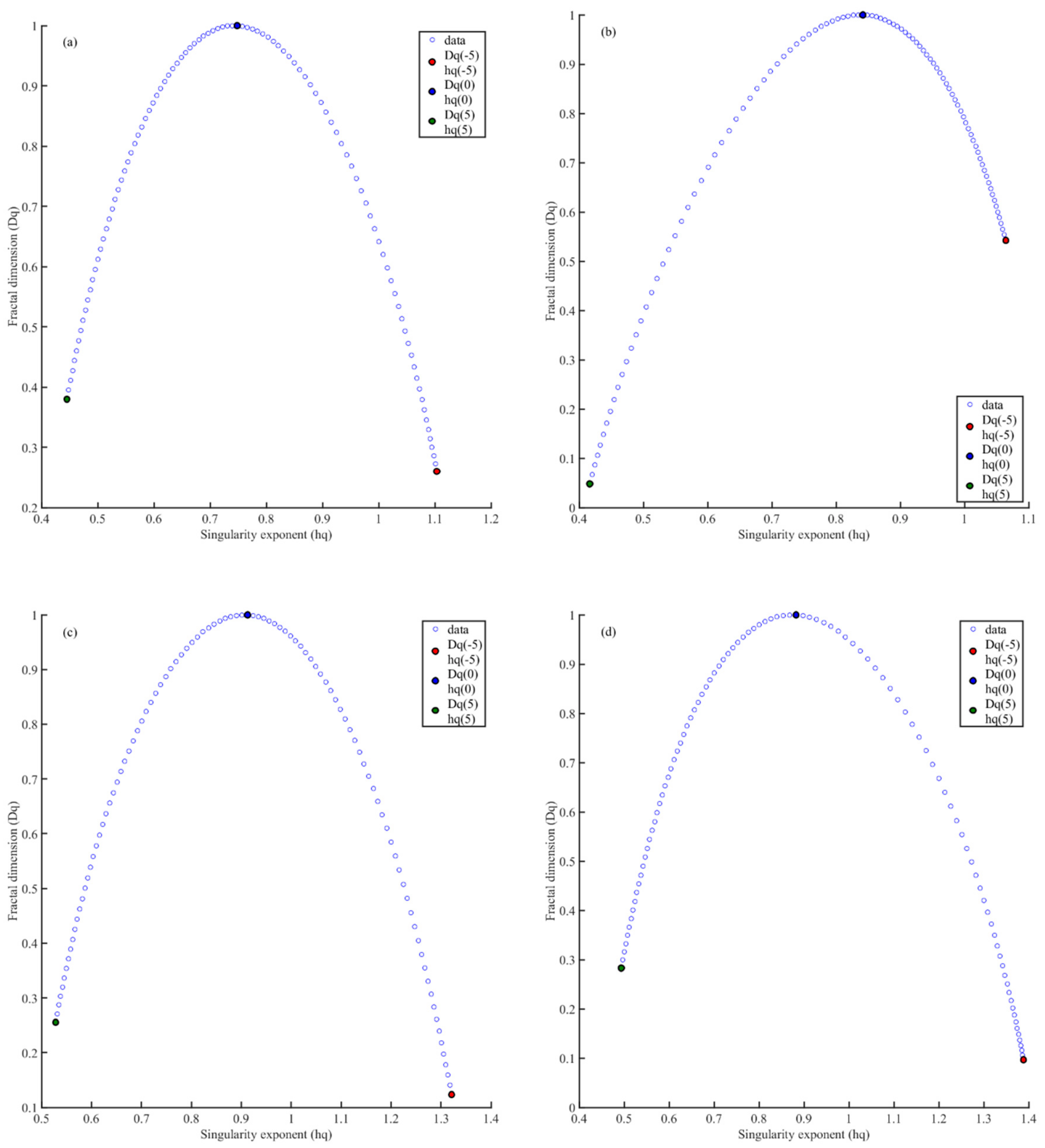
Figure 3 shows the multifractal spectrum
Dq −
hq relationship of the profiles of the gully shoulder lines in the six typical study sites, which were calculated using Equation (8). The figure also shows the singularity exponent
hq and fractal dimension
Dq. The singularity exponent
hq of the
q-order and its corresponding fractal dimension
Dq here are the same as the parameters α and f(α) of the multifractal spectrum in related literature [
23,
24]. The spatial distribution and scaling properties of these variables have multifractal properties which can be described in term of a multifractal spectrum. This curve provides a synthesized picture of the full complexity of the scaling structure [
25]. In addition, three parameters are very important to describe the complexity of the terrain profile. First, the width of the multifractal spectrum is Δ
hq. Second, the difference between the fractal dimensions of the maximum probability subset
Dqmin and the minimum
Dqmax. Third, the asymmetry of the curve. The width of the multifractal spectrum is Δ
hq (Δ
hq =
hqmax −
hqmin). The higher the Δ
hq, the wider the probability distribution as well as, the larger the difference between the highest elevation and the lowest elevation, so the “richer” the terrain profile in structure. The range of the fluctuation order in this study is (−5, 5) because the multifractal spectrum is most sensitive to fluctuation orders in this range and insensitive outside this range [
26]. According to
Figure 3, all the multifractal spectral curves are bell-shaped within the fluctuation order (−5, 5), which indicates that the changes in the gully shoulder line profiles show multifractal characteristics at all six study sites. The wider the spectral width of the multifractal spectrum, the more complex the dataset structure is. Corresponding to different topographic profiles along the shoulder line in the study site, this means that the fluctuations of the topographic profile along the shoulder line are dramatic and complex. Sites with complicated topographic reliefs must have a fragmented surface, be densely distributed gullies, and have active gully erosion. If the width of the multifractal spectrum is smaller, it means that the structure of the dataset is smoother. It indicates that the topographic fluctuations along the shoulder line in this area are stable, the ground surface is relatively flat, the gully distribution is sparse, and the gully erosion activity is weak. The △
hq parameter is the width of the multifractal spectrum and indicates the degree of multifractal strength. According to
Table 1, the six study sites are arranged in the following order according to their multifractal characteristics, from strong to weak: Ganquan, Yijun, Yanchuan, Chunhua, Shenmu, and Suide. The stronger the multifractal degree, the more drastic the profile fluctuation of the gully shoulder line and the greater the variation in gully shoulder lines, indicating serious and active gully erosion in the loess gullies.
As can be seen from
Figure 3d and
Table 1, the top of the multifractal spectrum curve of the gully shoulder line at the Ganquan study site is relatively flat, and the multifractal spectrum width △
hq is 0.8945, which is the largest among the six study sites; thus, the multifractal spectrum curve has a large distribution range. These characteristics show that the amplitude of the topographic fluctuation of the gully shoulder lines at Ganquan is relatively large and unevenly distributed. The difference between the fractal dimensions of the maximum probability subset (
Dqmin) and the minimum one (
Dqmax) is Δ
Dq (Δ
Dq =
Dqmin −
Dqmax).
Dqmin and
Dqmax reflect the number of the subset of the maximum and minimum probability, respectively. Thus, Δ
Dq < 0 represents that the chance of the terrain profile values lying at the lowest site is more than that at the highest site and vice versa. A right-skewed spectrum denotes the relatively strong dominance of high fractal exponents, corresponding to rough structures and a left-skewed spectrum indicate low ones (more smooth-looking). △
Dq = −0.1864, which is less than 0, indicates that most profile sample points of gully shoulder lines are at wave troughs, further indicating that many gullies exist at this site and that gully erosion is severe. The topographic relief (fluctuations) along the shoulder line in the Ganquan sampling site has a very complex structure, and the topography is dominated by dramatic fluctuations with small magnitudes. In the topographic fluctuations along the shoulder line, the proportion of the terrain profile values is much lower at the peak than at the bottom. This further proves that the long ridge loess landform gully erosion intensity is the largest, gully erosion is the most active, there are many gullies, the gully density is large, and the size of the formed gully is also large. The Ganquan study site is located in the central and southern part of the Loess Plateau in northern Shaanxi, which is characterized by a large amount of rainfall, particularly in summer, and severe erosion of the loess ridge landform by water. The △
hq value of the Yijun study site is 0.8674, second only to that at the Ganquan study site, and its gully shoulder line profile has strong fractal characteristics.
Figure 3e shows that the multifractal spectrum curve of the Yijun study site has a longer left tail, which indicates a multifractal structure that is insensitive to local small topographic fluctuations △
Dq = 0.1991, which is greater than 0, indicating that most of the sampling points of the gully shoulder lines are at wave peaks, with few loess gullies. Compared with the Ganquan sampling site, the topographic fluctuations along the shoulder line in the Yijun sampling site also have a complex structure, and the topographic fluctuations are also very strong. But the difference is that the topographic fluctuations of the Yijun sampling site are dominated by severe fluctuations with large magnitudes. In terrain relief profiles, the proportion at the peak is greater than at valleys. Because the Yijun sampling site is the loess fragmented tableland landform and is located in the southern part of the Loess Plateau, the annual precipitation is large, the rivers are numerous, and the gully erosion is active, but the gully erosion is basically in the head area of the ancient gullies.
Under the policy of returning farmland to forest land, vegetation restoration in the Loess Plateau is typically very good, whereas gully erosion is generally weak. The width of the multifractal spectrum at the Yanchuan study site is also large, with
△hq = 0.7929 (
Table 1), and the fractal characteristics of the gully shoulder line profile are also strong.
△Dq = −0.1321, which is less than 0, and the sampling points of the gully shoulder lines are mostly at wave troughs, which indicates that gully erosion of the shoulder lines is active at the Yanchuan study site and there are many gullies. The multifractal curve is similar to that of the Ganquan study site (
Figure 3c) and has the same structural characteristics. The fractal characteristics and gully erosion are slightly weaker than those of the Ganquan study site. The multifractal characteristics of the gully shoulder line profile in the Suide and Chunhua study sites are weak, with
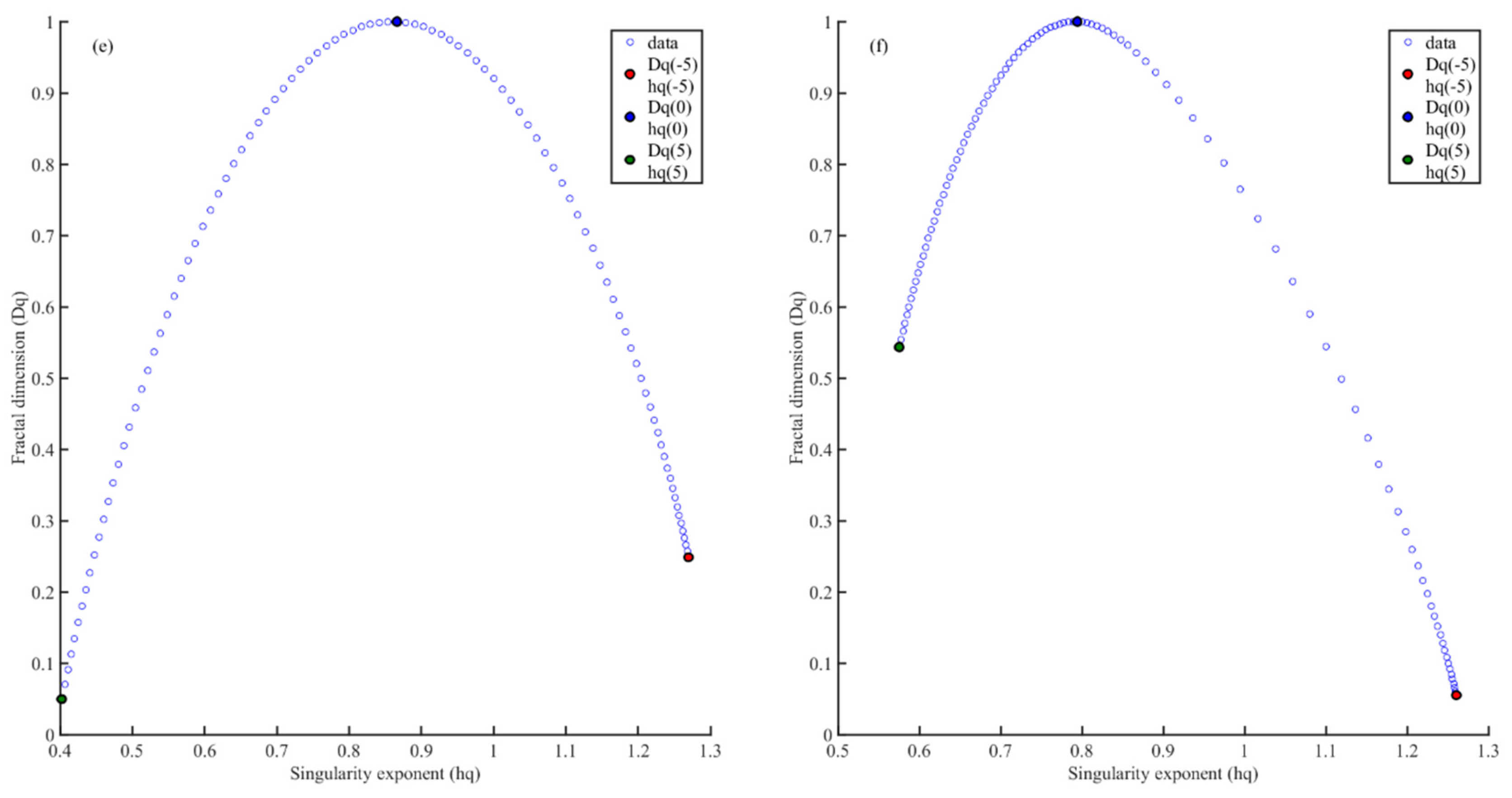
△hq values of 0.6479 and 0.6852, respectively, but the multifractal spectral structures of the two study sites are completely different. The multifractal spectrum at the Suide study site exhibits a right-sided structure, and the multifractal spectrum curve has a long left tail (
Figure 3b), which indicate that the gully shoulder line profile has multifractal structure characteristics that are insensitive to local small (or gentle) topographic relief. The width of the multifractal spectrum of the terrain profile along the shoulder line in Suide sampling site is the smallest, and the structure of the topographic relief dataset is relatively smooth. The topography is mainly stable, which indicates that the topographic relief is gentle, and the peak data has a higher proportion of the profile data. It further shows that the gully density in this site is relatively small, the gully erosion is relatively low and inactive. Because the Suide sampling site is located in the northern part of the Loess Plateau with less rain and drought, the erosion intensity is less than that of the sediment, so a loess hill landform with smooth topographic relief has been formed. Conversely, the multifractal spectrum at the Chunhua study site has a left-sided structure, and the multifractal spectrum curve has a long right tail (
Figure 3f), which indicate that the gully shoulder line profile has multifractal structural characteristics that are insensitive to local large (or severe) topographic fluctuations. The Chunhua sampling site with loess tableland landform has flat terrain without any fluctuation. Near the shoulder line, there are many gullies with relatively large depth and width. In this sampling site, gully erosion activity is relatively stable, and a few relatively active gully erosion sites caused by the transient runoff of heavy rain in summer. Comparing the study sites of Suide and Shenmu, gully erosion of shoulder lines at the Suide study site is more serious, and erosion of positive and negative topography is severe. Human activities (such as artificial terraces, warping dams, and other engineering measures) at the Suide study site have a greater impact on gully erosion. The Shenmu study site is a loess–aeolian and dune transition zone, with weak water erosion and wind erosion (
Table 1). The multifractal spectrum parameter △
hq = 0.6583, which indicates that the multifractal characteristics of the gully shoulder line profile are weak. The distribution of the multifractal spectrum curve is almost symmetrical, with no significant left or right deviation (
Figure 3a), which shows that the number of sampling points along the gully shoulder line profile is equal to the number of peaks and gullies, and gully erosion of the shoulder lines is relatively weak.
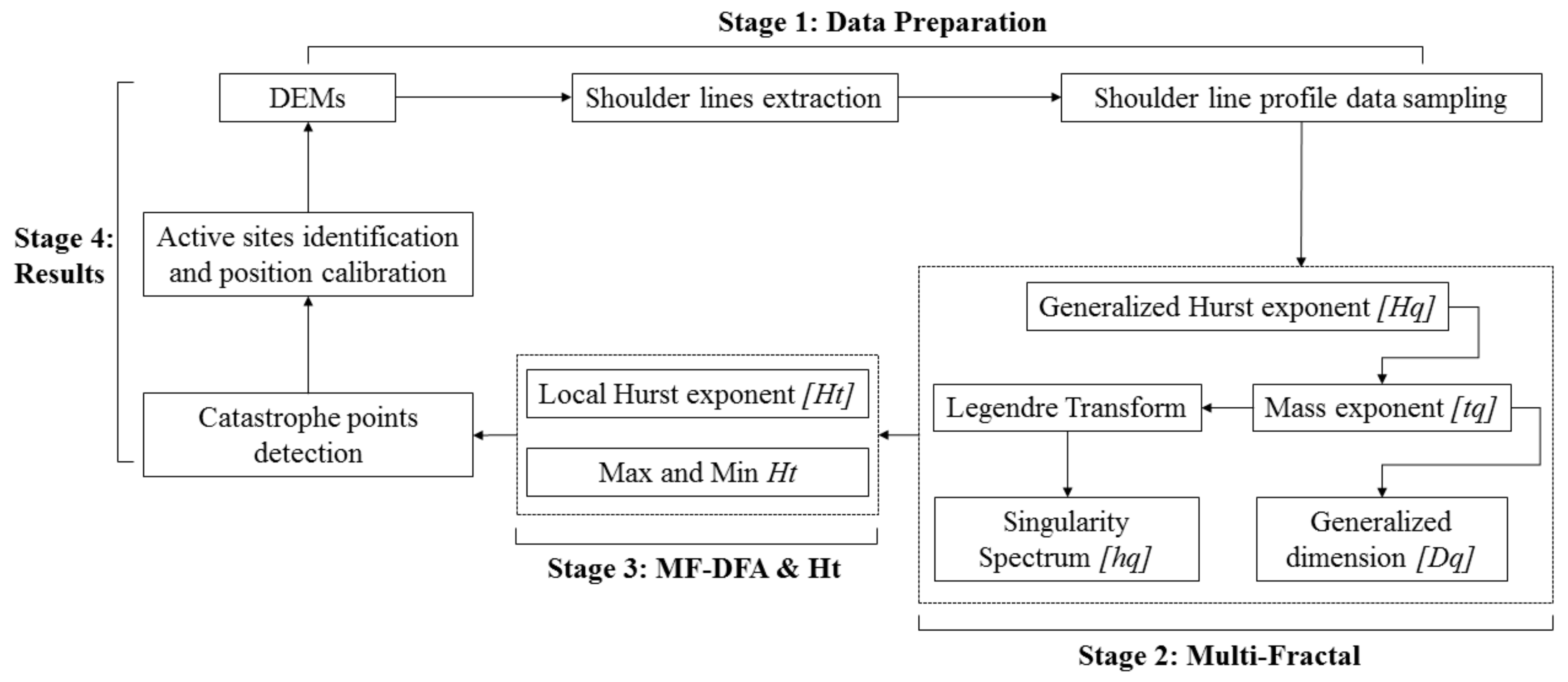
3.2. Identification of Points of Active Gully Erosion
The relevant parameters of the multifractal spectrum can only measure the gully erosion intensity of the gully shoulder line profile at each study site from a global perspective; they cannot identify local sites of active gully erosion or specific regions for soil and water conservation. However, the local Hurst exponent (also called the time Hurst exponent,
Ht), obtained using the multifractal generalized Hurst exponent, can solve this problem. The local Hurst exponent has an important feature when reflecting changes in the time series; it displays a mapping relationship between the position of the extreme point and the position corresponding to the original data series [
23]. Due to the erosion effect of surface runoff, the main form of gully erosion in the loess small watershed is fluvial incision and headward erosion [
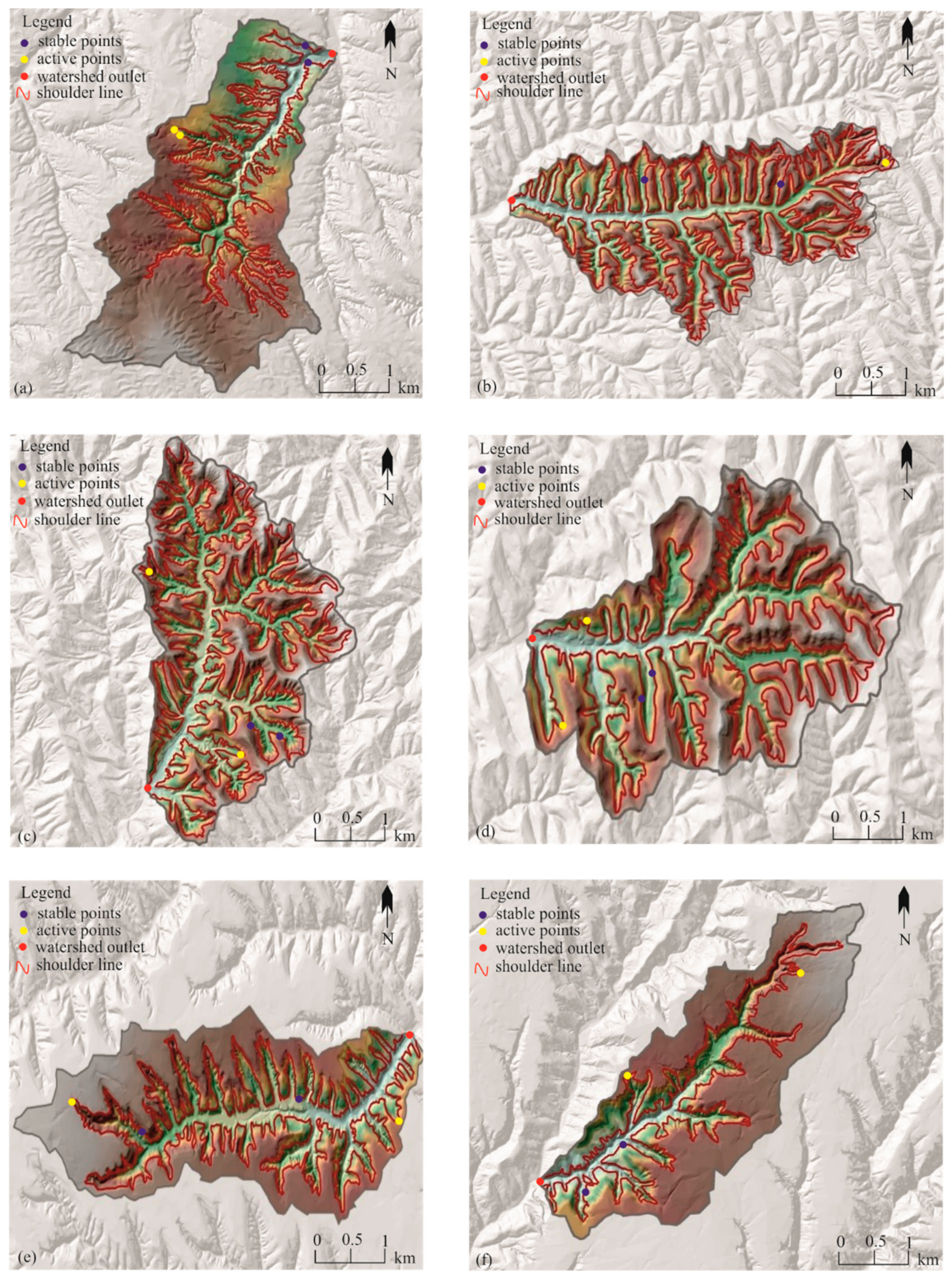
27]. The active gully erosion sites are mainly located along the shoulder line that is the boundary between positive and negative terrain. Where gully erosion is active, the frequency of material and energy exchange is relatively high, and a large variety of gullies of different sizes and grades will be formed along the shoulder line. The topography of this part will show complex relief features, and the ground surface will become rugged and fragmented. The correspondence relationship between the min, max values of the local Hurst exponent of the profile data along the shoulder line, and the original topographic profile is able to identify such complex relief features. The original data sequence position corresponding to the point position where
Ht reaches a maximum value must be the point at which the data do not fluctuate (data are stable), and the original data sequence corresponding to the point position where
Ht reaches a minimum value must be the point at which the data fluctuate most substantially [
26]. However, the local Hurst exponent obtained from the generalized Hurst exponent is affected by the analysis scale. That is, the overall average value of
Ht will not change (only the extreme value will change), the maximum value will decrease with increasing analysis scale, and the minimum value will change irregularly with increasing analysis scale. In addition to these changes, the spatial positions of extreme points used to obtain their spatial distribution patterns will also change. In this study, a minimum analysis scale of 7 and a maximum analysis scale of 17 were selected to determine the effect of the analysis scale (
Table 2).
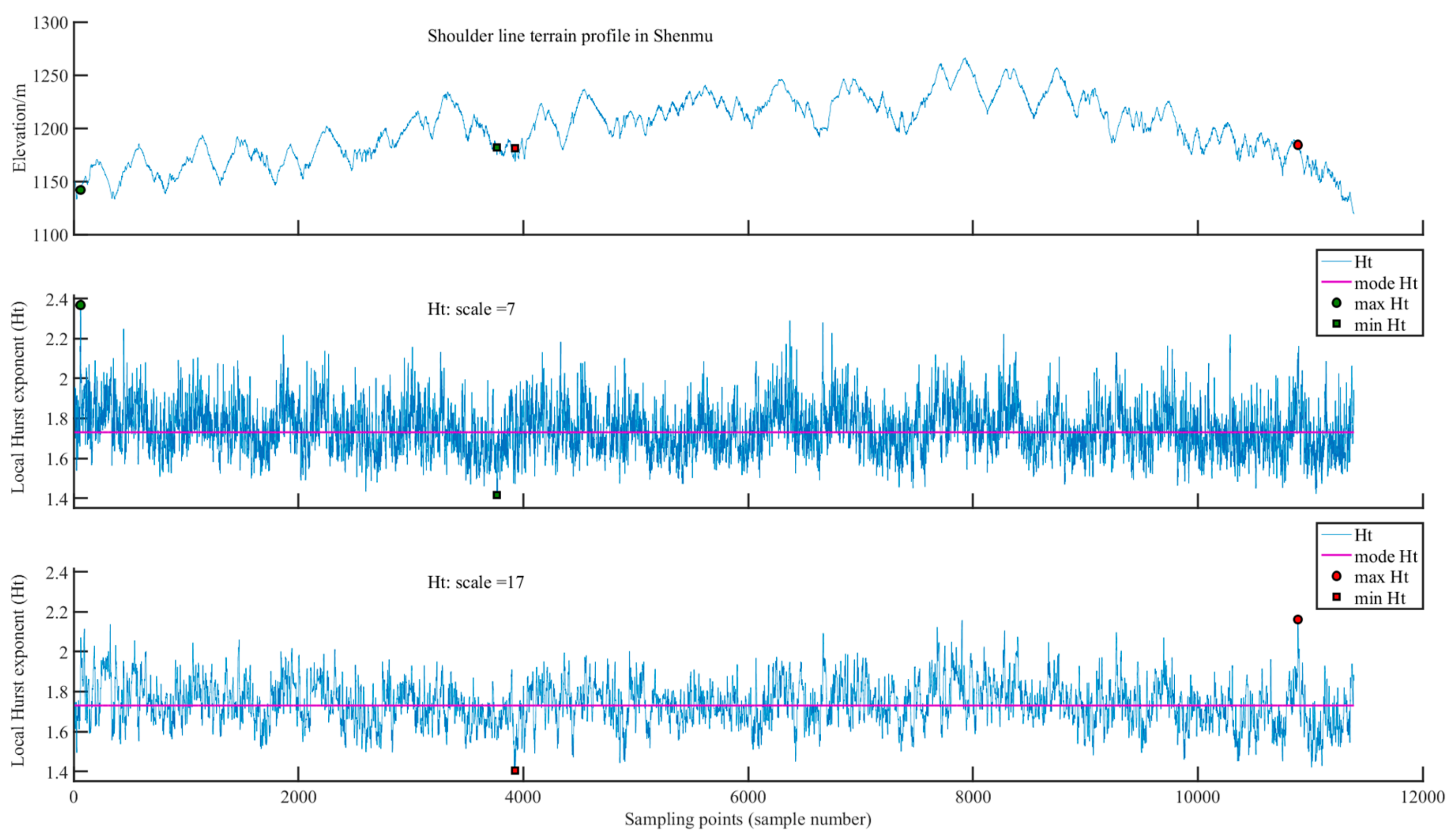
3.2.1. Shenmu Study Site
The average
Ht of the section gully shoulder lines at the Shenmu study site is 1.7302 (
Table 2). When the analysis scale is 7, the maximum
Ht of the gully shoulder line profile is 2.3688, and the point is located near the water outlet of the catchment at the study site, at the 54
th sample point. Here, topographic fluctuation of the gully shoulder line profile is stable (
Figure 4), and gully erosion is not significant and relatively stable. The minimum
Ht is 1.4171, located at the 3758
th sample point, which indicates that the topography of the gully shoulder line profile changes sharply near this point, corresponding to active gully erosion. When the analysis scale is 17, the maximum
Ht is 2.1617, located at the 10,884
th sample point, which is also located near the water outlet of the basin, further indicating that the terrain in this area is gentle and that gully erosion is not active. The minimum
Ht is 1.4026, located at the 3921
st sample point, which is very close to the minimum value sample point for an analysis scale of 7. This shows that the topography of the gully shoulder line profile fluctuates substantially in this area. The gully shoulder line of the Shenmu study site is an area with active gully erosion from sample points 3758 to 3921; thus, soil and water conservation should be emphasized in this area. Gully erosion is relatively stable near the watershed outlet in the Shenmu sampling site, and gully erosion is more active at the head of the gully located in the middle of the watershed.
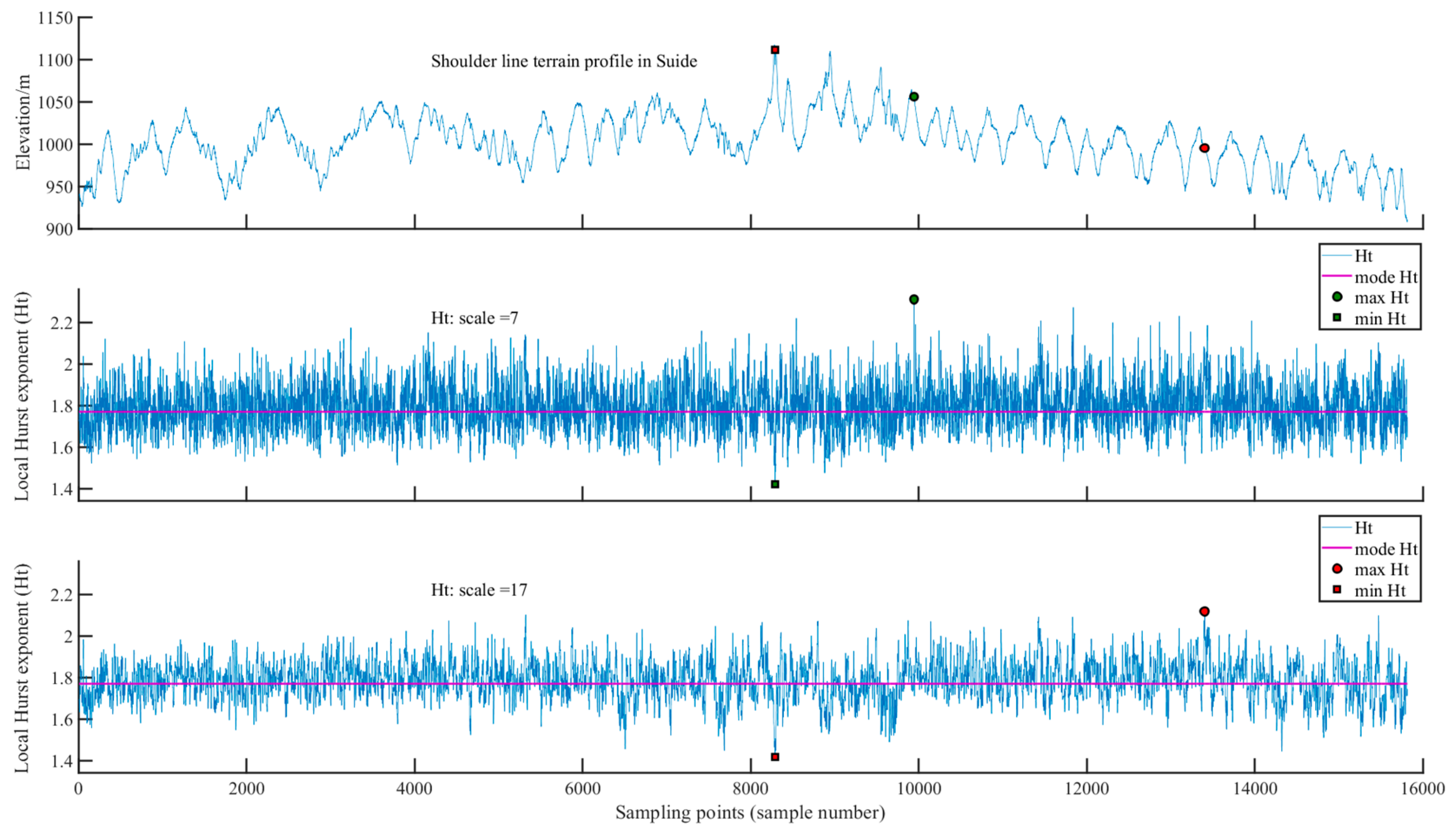
3.2.2. Suide Study Site
According to
Figure 5, when the analysis scale is 7, the maximum
Ht of the gully shoulder line profile at the Suide study site is 2.3106 (
Table 2), located at the 9937
th sample point, where the topographic change in gully shoulder lines is relatively small, which indicates that the terrain is gentle, gully erosion is not significant, and gully erosion activity is relatively stable. The minimum
Ht is 1.4204, which corresponds to the 8284
th sample point of the gully shoulder line profile. This suggests that the topography of the gully shoulder lines in this area varies substantially, landform erosion is serious, and gully development and erosion is severe. When the analysis scale is 17, the maximum
Ht is 2.1184, located at the 13,397
th sample point. The topographic fluctuation of the gully shoulder line at this site is relatively small, indicating that the terrain in the area is gentle and that gully erosion is not significant. However, the minimum
Ht is 1.4160, located at the 8284
th sample point, which is consistent with the location of the corresponding sample with an analysis scale of 7. This further indicates that the topography along the regional gully changes sharply and that gully development is relatively severe, representing the key area of active gully erosion at the Suide study site. The gully erosion active sites in the Suide sampling site are relatively concentrated, mainly distributed at the head of the gully in the upper reaches of the watershed, indicating that the gully is still growing.
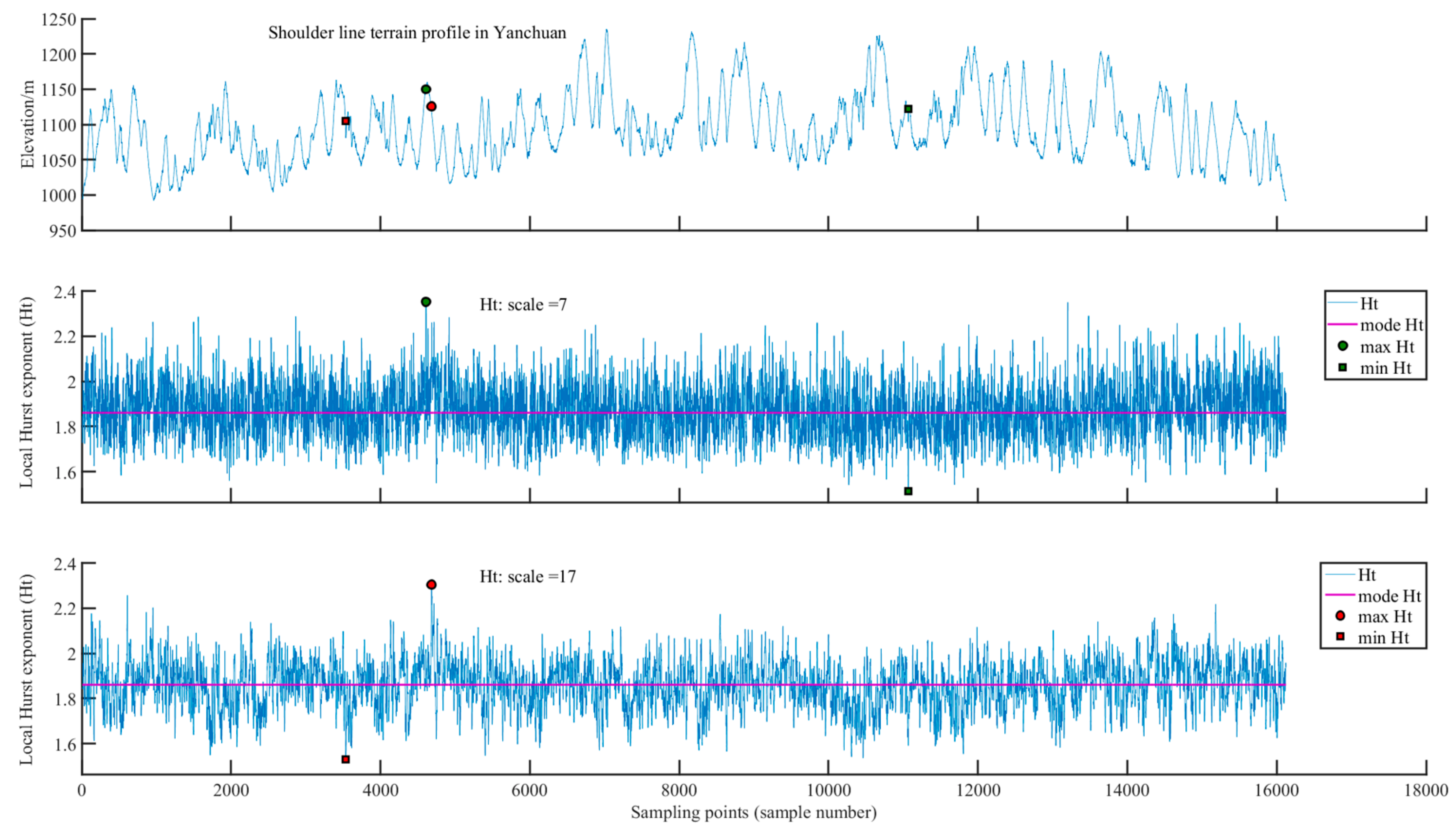
3.2.3. Yanchuan Study Site
For analysis scales of 7 and 17, the maximum
Ht values are 2.3522 and 2.3048 (
Table 2) and located at the 4603
rd and 4676
th sample points (
Figure 6), respectively, indicating that the topography of the gully shoulder line in this area is less undulating, the terrain is gentle, and gully erosion is relatively stable. The positions of the sample points corresponding to the minimum
Ht are quite different; the minimum
Ht values for analysis scales of 7 and 17 are 1.5147 and 1.5292, corresponding to the 11,060
th sample point and the 3529
th sample point, respectively. This shows that there are many gully shoulder line profiles at the Yanchuan study site, where gully erosion is active. The topography of the gully shoulder lines in these two areas changes sharply, and gully erosion is severe and active. This is likely because the predominant landform in the Yanchuan study site is hills with loess and ridges and belongs to a temperate continental monsoon climate. The rainfall is lower and concentrated in summer rainstorms, which leads to active gully erosion and continuous development of gully heads. The distribution of gully erosion active sites in the Yanchuan sampling site is scattered, but it is also at the gully head position, while the distribution of gully erosion stable sites is concentrated.
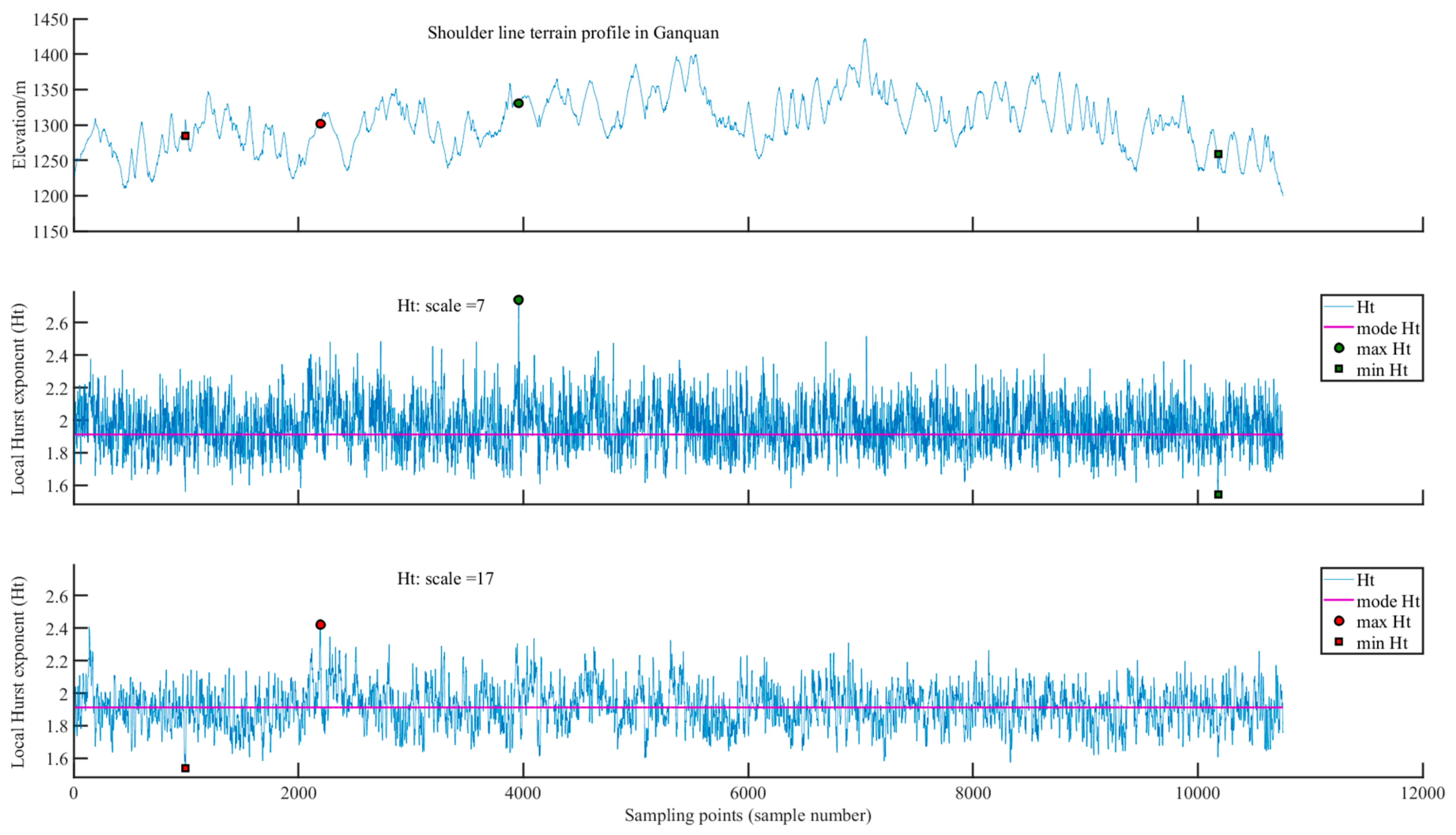
3.2.4. Ganquan Study Site
The extreme values of
Ht for the gully shoulder line profiles at the Ganquan study site exhibit different sample point positions corresponding to the two analysis scales. When the analysis scales are 7 and 17, the maximum
Ht values are 2.7400 and 2.4205 (
Table 2), corresponding to the 3951
st and 2188
th sampling points, respectively (
Figure 7). These points correspond to relatively small topographic fluctuations in the gully shoulder lines, which indicates gentle topography and relatively stable gully erosion. When the analysis scales are 7 and 17, the minimum
Ht values are 1.5425 and 1.5367 (
Table 2), corresponding to the 10,172
nd and 986
th sampling points, respectively (
Figure 7). This indicates a sharp change in the regional topography of gully shoulder lines, serious soil erosion, and active gully development. These two regions are located on the north–south symmetrical slope not far from the water outlet of the river basin, which may have a low erosion benchmark. The landform type of the study site is ridge-shaped loess hills and gullies, characterized by surface erosion on the slope, sharp downcutting of gullies and rivers between the ridge and the ground, and active gully erosion. The distribution of gully erosion active and stable sites in the Ganquan sampling site is relatively concentrated, and the gully erosion active sites are mainly located near the outlet of the watershed, which indicates that the gully erosion in the Ganquan sampling site is developed and evolved by means of fluvial incision.
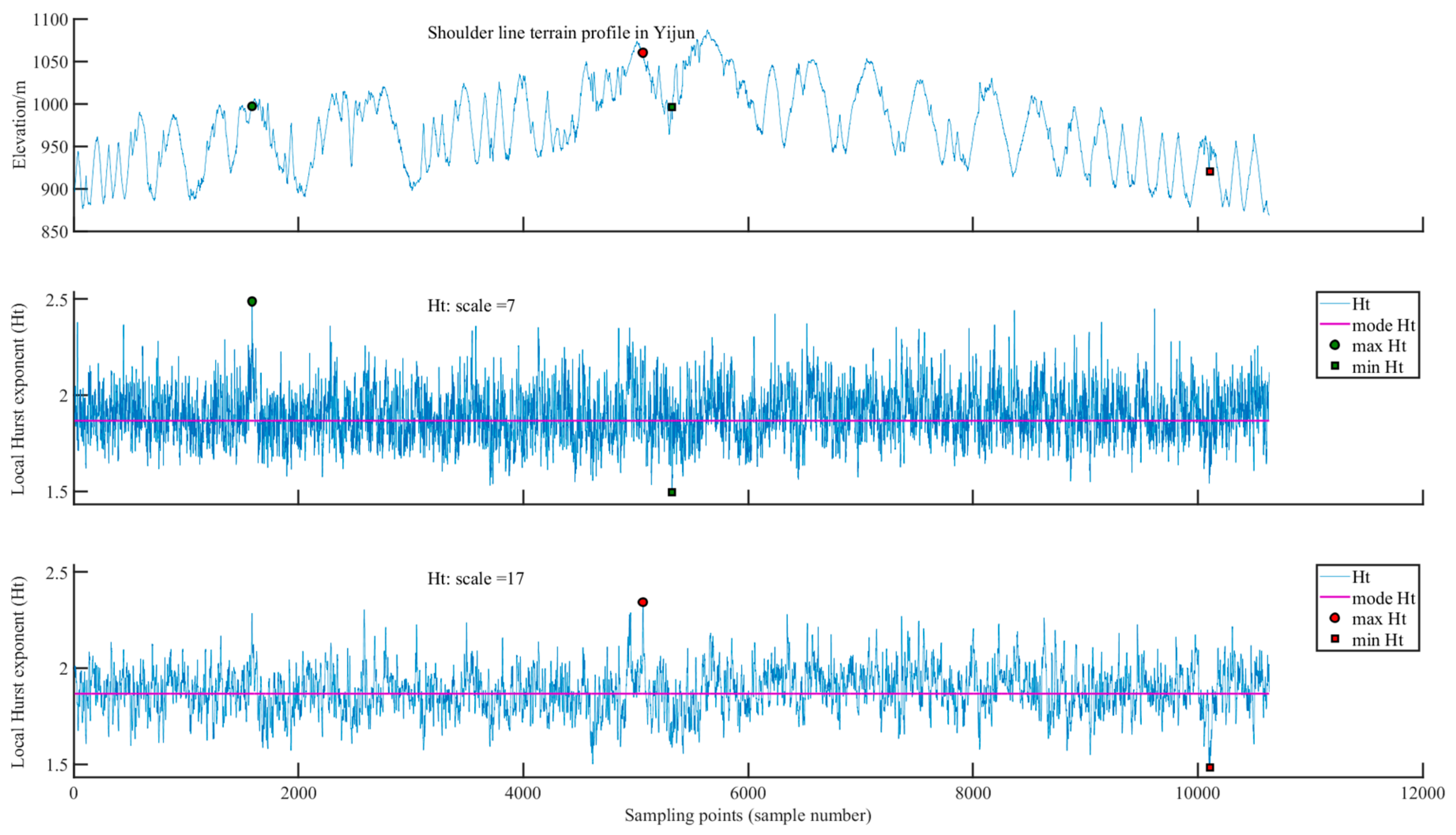
3.2.5. Yijun Study Site
The maximum
Ht values for gully shoulder line profiles at the Yijun study site are 2.4881 and 2.3426 for analysis scales of 7 and 17 (
Table 2), respectively. The corresponding sample points of gully shoulder lines are the 1580
th and 5057
th points (
Figure 8), respectively. These maximum values correspond to small topographic fluctuations, gentle topography, and stable gully erosion. For analysis scales are 7 and 17, the minimum
Ht values are 1.4962 and 1.4839 (
Table 2), located at the 5316
th and 10,101
st sample points (
Figure 8), respectively. The topography of the gully shoulder lines in the area near these two sample points varies greatly, which indicates that soil erosion is serious, and gully erosion is active. The area of stable gully erosion at an analysis scale of 17 and the area of active gully erosion at an analysis scale of 7 are spatially close but exhibit abrupt changes in gully erosion. The Yijun study site is predominantly loess gullies in long-ridge remnant tablelands, with substantial precipitation in the southern part of the Loess Plateau and gully erosion that is dominated by gravity erosion. The distribution of gully erosion active and stable sites in the Yijun sampling site is intertwined, which indicates that gully erosion activity in the loess fragmented landform is more complicated.
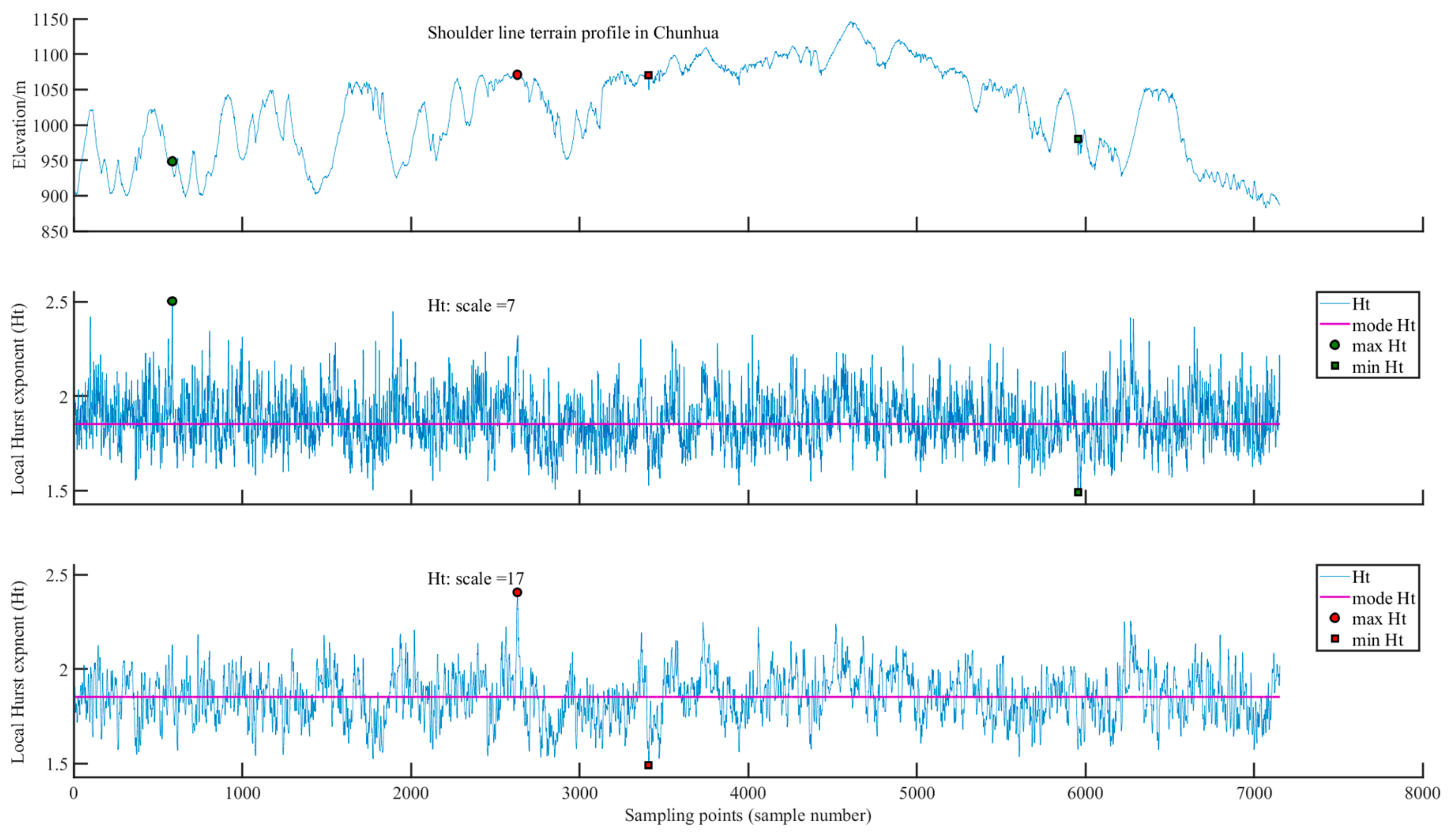
3.2.6. Chunhua Study Site
For analysis scales of 7 and 17, the maximum
Ht values at the Chunhua study site are 2.5029 and 2.4065 (
Table 2), corresponding to the 577
th and 2624
th sample points, respectively (
Figure 9). These two sample points are located on the sunny slope of the watershed. The topographic changes in the gully shoulder lines are small, the vegetation coverage is good, soil erosion is not significant, and gully erosion is relatively stable. The minimum
Ht values are 1.4896 and 1.4910 (
Table 2), located at the 5948
th and 3403
rd sample points, respectively (
Figure 9). These areas are located on the shady slope of the watershed, with sharp topographic fluctuations, severe soil erosion, and active gully development. The Chunhua study site is located in the southern part of the Loess Plateau. Annual precipitation is substantial and concentrated. The dominant landform type is loess tableland, and there is a large continuous tableland surface. The loess layer in the tableland area is thick, loose, and prone to collapse. Therefore, gravity erosion, hydraulic erosion, and headward erosion are severe. The surface of the tableland area is relatively complete, but the topography of the gully shoulder lines is relatively complex. The distribution of gully erosion active and stable sites in the Chunhua sampling site is also intertwined, which indicates that the gully erosion activity in the loess tableland landform is also complicated.