Abstract
Column-averaged dry air mole fraction of atmospheric CO2 (XCO2), obtained by multiple satellite observations since 2003 such as ENVISAT/SCIAMACHY, GOSAT, and OCO-2 satellite, is valuable for understanding the spatio-temporal variations of atmospheric CO2 concentrations which are related to carbon uptake and emissions. In order to construct long-term spatio-temporal continuous XCO2 from multiple satellites with different temporal and spatial periods of observations, we developed a precision-weighted spatio-temporal kriging method for integrating and mapping multi-satellite observed XCO2. The approach integrated XCO2 from different sensors considering differences in vertical sensitivity, overpass time, the field of view, repeat cycle and measurement precision. We produced globally mapped XCO2 (GM-XCO2) with spatial/temporal resolution of 1 × 1 degree every eight days from 2003 to 2016 with corresponding data precision and interpolation uncertainty in each grid. The predicted GM-XCO2 precision improved in most grids compared with conventional spatio-temporal kriging results, especially during the satellites overlapping period (0.3–0.5 ppm). The method showed good reliability with R2 of 0.97 from cross-validation. GM-XCO2 showed good accuracy with a standard deviation of bias from total carbon column observing network (TCCON) measurements of 1.05 ppm. This method has potential applications for integrating and mapping XCO2 or other similar datasets observed from multiple satellite sensors. The resulting GM-XCO2 product may be also used in different carbon cycle research applications with different precision requirements.
1. Introduction
Spatio-temporal variation of atmospheric CO2 concentration reflects the balance between anthropogenic carbon emissions and terrestrial and oceanic carbon uptake or emissions [1]. Increased fossil fuel emissions after the start of the Industrial Revolution contribute to the continuous growth of atmospheric CO2 concentrations [2] from 277 parts per million (ppm) in 1750 [3] to 407.4 ± 0.1 ppm in 2018 [4]. The growth rate of CO2 concentrations in the atmosphere is smaller than the rate of CO2 emitted by human activities because nearly 45% of the emissions are absorbed by oceans and the terrestrial biosphere each year [5]. The seasonal variations of terrestrial carbon uptake and emission contribute most to the seasonal cycle in atmospheric CO2 [6], which varies spatially due to non-uniform land-biosphere CO2 exchange [7]. In addition, there is spatial-temporal variability of atmospheric CO2 concentrations that can be used to study changes in regional land biosphere net CO2 fluxes, for example, seasonal cycle amplitude increase [8,9] and regional effects of extreme weather patterns like droughts [10,11]. Atmospheric CO2 concentrations have also been used for carbon flux or to estimate carbon uptake/emission changes using atmospheric inversion models [12,13] and a data-driven method [14]. The spatio-temporal variability of CO2 and related carbon sources/sinks distribution are still not fully understood [15,16]. A long time series of comparable global CO2 concentration datasets has the potential to improve our understanding of land-biosphere interactions and our ability to evaluate trends in regional terrestrial CO2 absorption capacity.
There are several methods to measure atmospheric CO2 concentrations, including surface measurements and satellite observations and approaches to estimate concentrations from model simulations. A network of surface CO2 monitoring station observations has been organized into the popular GLOBALVIEW-CO2 product and provides in situ measurements but is limited by station sparseness and the inherent spatial inhomogeneity of the surface atmosphere. Model simulations can provide continuous maps of CO2 using estimated surface fluxes and atmospheric mixing transport in addition to the previously noted sparse validation stations [17]. Satellite observations of atmospheric CO2 have the advantage of global coverage and high measurement density and can complement the surface network to advance our understandings of the carbon cycle and its changes [18,19]. With the development of remote sensing technology, there are several satellites used for atmospheric CO2 concentration observations [20,21]. Leveraging all available XCO2 datasets to construct a long time series, continuous, and comparable global CO2 concentrations would be useful.
Satellite-observed column-averaged dry air mole fraction of CO2 (XCO2) have been wildly used for carbon cycle studies, including CO2 enhancement detection induced by anthropogenic emissions [22,23], constraining model simulations of carbon fluxes [24,25], investigating carbon cycle responses to weather extremes [11,26], and improving understanding of vegetation uptake [27]. Satellites measuring XCO2 are the SCanning Imaging Absorption spectroMeter for Atmospheric CHartographY (SCIAMACHY) onboard the Environmental Satellite (ENVISAT) [28], Greenhouse Gases Observing Satellite (GOSAT) [29], and Orbiting Carbon Observatory-2 (OCO-2) [30]. They observe XCO2 but with different spatial/temporal resolution, prior vertical profile estimates, local overpass time, data precision, and observing gaps. As a result, there is an opportunity to generate a long time series of global XCO2 dataset starting from 2003 using XCO2 retrievals from these satellites with careful integration and gap-filling.
Gap-filling satellite-observed XCO2 has been investigated in several studies from different perspectives [31,32,33]. Geostatistical approaches, especially kriging, were widely used for GOSAT observed XCO2 Level 3 product production [17,34,35]. Spatial-only geostatistical methods do not take into account the temporal correlation structure of CO2 data [19], which may provide extra information. In order to make full use of spatio-tempal correlation of atmospheric CO2, a new spatio-temporal kriging method was developed for the global mapping of XCO2 [19,36]. Because these methods were previously used for observations from a single satellite, measurement error could be assumed to be uniform and not interfere with the kriging approach. In order to produce high spatio-temporal resolution and a long time series of XCO2 from multiple satellite observations, the precision of different datasets should be considered in this geostatistical method.
In this study, to create the longest possible time series of XCO2 and leverage multiple measurements to improve precision when possible, we developed a precision-weighted spatio-temporal kriging method for gap filling of integrated XCO2 from multiple satellite observations. Datasets used in this study and data preprocessing are described in Section 2. XCO2 integration methods and global mapping can be found in Section 3. Results of global mapped XCO2 and its validation are shown in Section 4 and data quality considerations are discussed in Section 5. Finally, conclusions are presented in Section 6.
2. Dataset
In this study, we collected atmospheric CO2 concentration datasets from multiple satellite-observations to produce a long time series of spatio-temporal continuous XCO2 from satellite observations, which was then evaluated by XCO2 from surface measurements and model simulations.
2.1. XCO2 from Multi-Satellite Observations
Atmospheric CO2 concentrations used here were the released Level 2 products that contain the full-physics retrievals of column-averaged CO2 in units of dry air mole fraction (XCO2). Satellite observations of XCO2 used here are from ENVISAT/SCIAMACHY, GOSAT, and OCO-2, which span from 2003 to 2016. XCO2 from SCIAMACHY onboard the European ENVISAT are obtained by the full-physics based Bremen Optimal Estimation–DOAS (BESD) algorithm (v02.01.01) [37], which span from January 2003 to March 2012 with a spatial/temporal resolution of 30x60 km every 35 days. XCO2 from GOSAT is produced by the algorithm of the Atmospheric CO2 Observations from Space (ACOS) team (v7.3 lite) [38], which span from June 2009 to May 2016 with spatial/temporal resolution of a diameter of 10.5 km every three days. XCO2 from OCO-2 is produced by the ACOS team (r9 lite) [39], which span from September 2014 to December 2016 with spatial/temporal resolution of 2.25 × 1.25 km every 16 days. Data quality was maximized by filtering XCO2 product by screening criteria specified by the corresponding user guides. Specifications of the three satellites that observed XCO2 are shown in Table 1. These satellites follow different orbits and have different gaps as shown in Figure 1. XCO2 retrievals from each satellite also have different data precision for different sensors, observation conditions, and retrieval methods. Therefore, we use different XCO2 precisions in time and space in the XCO2 integration and mapping with the spatio-temporal kriging method.

Table 1.
Specifications of multiple satellites that observed XCO2.
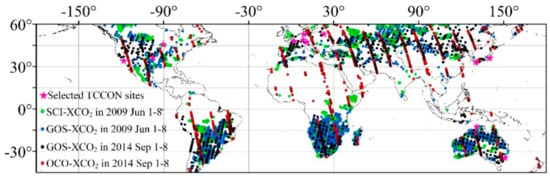
Figure 1.
Example of XCO2 from SCIAMACHY, GOSAT, and OCO-2. Green and blue points represent SCI-XCO2 and GOS-XCO2 from 1–8 June 2009. Black and red points are GOS-XCO2 and OCO-XCO2 from 1–8 September 2014. Total carbon column observing network (TCCON) sites used for validation are shown with a pink star.
2.2. The Total Carbon Column Observing Network
The total carbon column observing network (TCCON) are upward-looking terrestrial Fourier transform spectrometers established for measuring atmospheric XCO2 and other trace gases from the surface [40]. The instruments have high accuracy with approximately 0.25% error in XCO2 retrievals, which has been extensively used for validation of satellite observations [21,40,41]. In this study, we selected 12 TCCON sites within the mapping area as shown in Figure 1, with at least five years of coincidental measurements in the period from January 2003 to December 2016 for validating combined XCO2 products.
2.3. XCO2 from Model Simulation
CarbonTracker (CT) is a modeling system that assimilates global atmospheric CO2 observations from the ground, tall tower, and aircraft, coupled with an atmospheric transport model for simulating global distributions of atmospheric CO2 and tracking CO2 sources and sinks. Model-simulated atmospheric CO2 from CarbonTracker 2017 [42] was used in three steps of the integration and mapping method, primarily to normalize differences in altitude sensitivity and overpass time. First, we used CarbonTracker CO2 profiles in a grid of 2° × 3° (latitude x longitude) in 3-hour intervals as the common profile to align the a priori CO2 profiles and averaging kernels of multi-satellite observations. Second, we adopted diurnal patterns of CO2 concentrations in different pressure layers from CarbonTracker to unify the CO2 from satellite observations to 13:00 local time. XCO2 from CarbonTracker (CT-XCO2) was calculated from the model CO2 profile data with 25 layers at the local time 13:00 by using a pressure weighting average method [43]. Third, we used the CT-XCO2 for comparing with our new globally mapped XCO2 product.
3. Method
In this study, we developed a method for spatio-temporal integration and mapping of multi-satellite observed XCO2 considering variable data precision for producing globally mapped continuous XCO2 with spatial/temporal resolution of 1° × 1° every eight days from 2003 to 2016. We present the flow chart of global mapped XCO2 production and the precision weighted spatio-temporal kriging method in Figure 2. First, we adjusted a priori vertical CO2 profiles and averaging kernels of multiple satellite-observed XCO2 products to a common profile. Second, we corrected to a common local time and regularizing spatio-temporal scales of XCO2 from multiple satellites. Third, we used a modeled continuous XCO2 spatio-temporal random field for interpolation. Fourth, we developed a precision-weighted spatio-temporal kriging method for producing global maps of XCO2. Finally, we validated the new global mapped XCO2. We present details on developing the precision-weighted spatio-temporal kriging method including: (1) conventional spatio-temporal kriging method; (2) optimization of spatio-temporal correlation structure; (3) XCO2 prediction through integrating data precision, and; (4) uncertainty and precision of mapped XCO2.
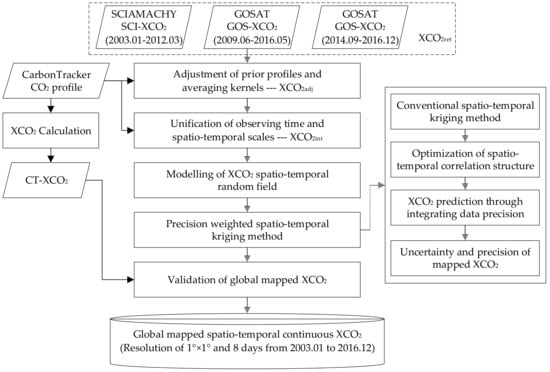
Figure 2.
Workflow chart of spatio-temporal integration of multi-satellite observed XCO2 using a precision-weighted kriging method.
3.1. Preprocessing
3.1.1. Adjustment of a Priori Vertical Profiles and Averaging Kernels
Each satellite has different measurement sensitivity at different altitudes through the atmospheric column and, therefore, they use different averaging kernels based on a priori assumptions of vertical CO2 profiles to account for senor sensitivities in XCO2 retrieval algorithms. The corrections are based on prior vertical profile layers as shown in Table 1. The a priori profiles from different satellite retrievals should be adjusted to a common profile when comparing XCO2 from different instruments. Additionally, the smoothing effect of the retrievals should be considered by applying the averaging kernels [44] to reduce the effects from different instruments on XCO2 retrievals [37,45]. In this study, we introduce a common a priori XCO2 profile from CT to integrate XCO2 retrievals from ENVISAT/ SCIAMACHY, GOSAT, and OCO-2 by using Equation (1).
where is the adjusted at observation time t, is the original XCO2 retrievals from satellites, h is a pressure-weighting vector, A is column-averaging kernels in the XCO2 retrieval algorithm, I is an identity matrix, is a set of common a priori CO2 profiles from CT, and is a set of a priori CO2 profiles used in XCO2 original satellite-specific retrieval algorithms. A priori CO2 profiles of each satellite, as shown in Table 1, were interpolated into the same 25 pressure layers of the CT model.
3.1.2. Unification of Observing Time and Spatio-Temporal Scales
The three satellites have different local overpass times: SCIAMACHY at 10:00, GOSAT at 13:00, and OCO-2 at 13:36 (Table 1). In order to reduce the effect of atmospheric CO2 concentrations diurnal variation [46,47], we introduce a correction coefficient to normalize the satellite observations local time to 13:00 based on diurnal variation of CT model simulations using Equation (2).
where is the converted at the reference time (rt, 13:00 local time); is the adjusted XCO2 derived from Equation (1) at satellite overpass time t; and are CO2 profiles from CT at times of rt and t, respectively; and is the pressure-weighting vector.
Moreover, XCO2 is affected by the different fields of view and observing dates as shown in Table 1. In order to reduce this effect, we integrate spatial and temporal scales of XCO2 retrievals using precision weighted averaging of within 30 km by 30 km every 8 days using Equations (3-1) and (3-2). This unification also reduces computational complexity and preserves local spatiotemporal patterns. A temporal resolution of 8 days is also well-suited for biosphere-atmosphere interaction analysis with other 8-day resolution datasets like vegetation indices from the Moderate Resolution Imaging Spectroradiometer (MODIS). An integrated XCO2 dataset at 30 km resolution every 8 days from 2003 to 2016 (integrated-XCO2) was generated.
where is the integrated combination of datasets, n is the number of observations in one unit, is converted satellite observed XCO2, is the weighting factor, which is determined by (data precision of ). is an arbitrary constant used for normalizing the data precision weighting factor. We adopted the data precision from these satellites observed XCO2 Level 2 product. The data precision in ACOS-GOSAT and OCO-2 is XCO2 posterior error, and that in BESD-SCIAMACHY is 1-sigma uncertainty of the retrieved XCO2.
3.2. Modeling XCO2 Spatio-Temporal Random Field for use in Kriging
XCO2 increases from year-to-year varies by latitude and has a significant seasonal cycle in most locations [48,49]. In order to interpret spatio-temporal geostatistics, we need to construct a second-order stationary random field represented by the stochastic residual component after removing inter-annual, latitudinal, and seasonal trends mentioned above, termed the deterministic mean. In this study, we adopted a fitting method for decomposing [50] the deterministic spatiotemporal mean and stochastic residual component of latitude-zonal XCO2. The fitting method is a combination of a linear function to fit the long-term increase and annual periodic function as shown in Equation (4).
where and T is the period of 46 time-units, t is the time in the time-unit, s represents the latitudinal zone, and , and are parameters to be estimated. is the cumulative annual increase for each time-unit determined by the Earth System Research Laboratory (ESRL) global annual CO2 growth rate [4]. The harmonic functions fit the annual cycle, semi-annual oscillation, seasonal variation and monthly variation of XCO2 [19]. represents the spatio-temporal residual component of satellite observed integrated XCO2, which will be used for interpretation.
3.3. Precision Weighted Spatio-Temporal Kriging
In the ordinary kriging method, a predicted value at an arbitrary target point is estimated by considering the statistical properties of a set of observed data. As a result, the predicted value () at point can be expressed as a weighted sum of the observational data as shown in Equation (5).
where is the weighting factor at the observation point , n is the total number of observational points to be used, and is the observed value at each point . The following subsections describe the precision-weighted spatio-temporal kriging method. Different kriging models were developed by adjusting the number of points ‘n’ and the weighting factor ‘’.
3.3.1. Conventional Spatio-Temporal Kriging
In spatio-temporal geostatistical analysis of XCO2, kriging prediction of Z(,) at a point (,) can be calculated as the linear weighted sum of the XCO2 values that minimizes the mean squared prediction error [19]. Weights of observations used for interpolation are determined by the geometry of observations and the spatio-temporal correlation structure of the data. Spatial and temporal information would be used for variogram modeling of the correlation structure [19,31] as shown in Equation (6).
where is an empirical variogram value at the lag (). is the observational data. is the number of data pairs within a distance of (). Once the empirical variogram has been constructed, we need to select a spatio-temporal variogram model to fit it. As shown in Zeng et al. [19,31], the spatio-temporal variogram model adopted here (Equation (7)) is a combination of the product-sum model [51,52] and an extra global nugget model to capture the nugget effect [53] (last term in Equation (7)).
We selected the exponential model for the marginal variogram model and as shown in Equation (8).
where and are the marginal spatial and temporal variograms, [,,] = [, , , , , ] are parameters to be estimated, and , C, and a are all greater than or equal to zero. In the exponential model, a, C and represent the influence range, partial sill, and nugget effects, respectively.
As a result, an arbitrary target point () to be estimated by using the spatio–temporal kriging method can be expressed as Equation (9).
where is the weight assigned to a known observation so as to minimize the prediction error variance while maintaining an unbiased prediction. The prediction error variance, which is a measurement of prediction uncertainty, is given by
where , =, and 1 is the n × 1 unit vector.
3.3.2. Optimization of Spatio-Temporal Correlation Structure
In a conventional spatio-temporal geostatistical analysis, all data pairs were used for spatio-temporal correlation structure using equal weight. XCO2 observations from different satellites/sensors, observing conditions and inversion methods have different data precision. So, the varying data precision should be considered in building the loss function for optimizing spatio-temporal correlation structure with precision weighting factor as shown in Equation (11).
where represents different weighting factors for data with different precisions. is the spatio-temporal variogram model shown in Equation (7). is the empirical variogram shown in Equation (6). and represent data precision and a normalization term.
The gradient descent method was used to calculate the optimal parameters. The partial derivative parameters (,, ,, , ) that need to be estimated are shown in Equations (12-1)–(12-6).
where are parameters waiting to be optimized. Parameters, ,, and , are the weighting factors (Equation (11-2)), exponential models (Equation (7) and Equation (8)) and empirical variogram values (Equation (6)), respectively.
We optimized the structure through minimizing . Initial parameters were obtained by using a least-squares approximation in the conventional spatio-temporal kriging method. Then, parameters were determined by a learning rate and partial derivative as shown in Equation (13).
where represents (. is the learning rate, usually in the range of . is the partial derivative parameter. We set the operating condition as a current change of less than 1% of all the changes in this adjustment. As a result, one example of optimized spatio-temporal semi-variogram surface is shown in Figure 3.
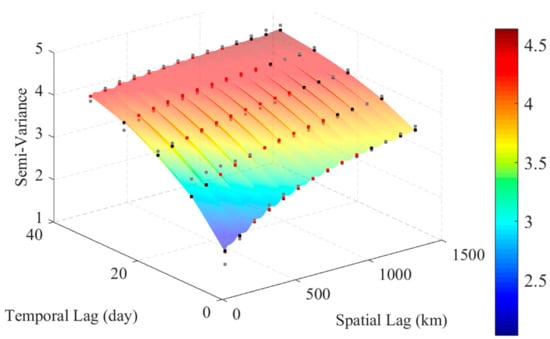
Figure 3.
One example of the optimized spatio-temporal semi-variogram surface (Zone 1: Latitude center: 55°N). Grey, black, and red points represent spatio-temporal semi-variogram that was calculated from experimental data, fitted models of the conventional and optimized correlation structure.
3.3.3. Integrating XCO2 Using Variable Data Precision
We estimated XCO2 in unobserved points using observational data and weighting factors from spatio-temporal correlation structure and data precision as shown in Equation (14).
where is the weighting factor from the spatio-temporal correlation structure and is from data precision. is observed XCO2 used for estimation. These two weighting factors were calculated by Equations (15-1) and (15-2).
where and are weighting factors in Equation (14). Equation (15-2) was used to control unbiased estimation. and … are spatio-temporal variograms for observations used for estimation of . is the polynomial residuals. can be achieved by Equation (16).
where , and are data precision, arbitrary constant and the number of used observational data.
We applied this method for global mapping of XCO2 (GM-XCO2), which provides a long time series of spatio-temporal continuous XCO2 dataset for global carbon cycle research.
3.3.4. Uncertainty and Precision of Mapped XCO2
We calculated data uncertainty and precision of the mapped XCO2 by using precision-weighted kriging. Uncertainty of predicted data from the spatio-temporal kriging method is shown in Equation (17)
where presents the prediction uncertainty, , and are the estimated weighting factor, spatio-temporal variograms, and polynomial residuals, respectively as shown in Equation (15).
In addition, the precision of GM-XCO2 integrated from the observed data is shown in Equation (18), according to the error transfer equation.
As a result, these two sources of uncertainty can be used for data screening in GM-XCO2 application.
3.4. Validation of Global Mapped XCO2
We validated the mapped GM-XCO2 product using cross-validation, compared to TCCON measurements and model simulation. Cross-validation has been used in accuracy assessments for spatio-temporal kriging methods [19,54]. In this study, we adopted cross-validation based on the Monte Carlo sampling method used in Zeng et al. [19]. As above, we used the satellite-observed integrated XCO2 dataset () for interpolation to GM-XCO2. The cross-validation was conducted by repeatedly (100 times) reserving 5% of the data for validation. Predicted GM-XCO2 was compared with the 5% reserved data in those corresponding spatio-temporal locations. We selected three statistical parameters for results evaluation: (1) the coefficient of determination (r2), (2) the root mean square error (RMSE), and (3) the percentage of estimation bias less than 1 or 2 times of data precision.
We compared GM-XCO2 with the XCO2 measured from TCCON (TCCON-XCO2) in 12 sites with more than 5 years of observation. TCCON-XCO2 was calculated with the pressure-averaged method [43] and data observed at a local time of 11:00 to 15:00. In addition, we did a comparison between GM-XCO2 and XCO2 from the CT model simulation in the spatio-temporal change over the global area.
4. Results
4.1. Integrated-XCO2 from Three Satellites
Here we presented latitudinal and temporal variability of the integrated XCO2 (top panel) and the difference between the integrated product and the original retrieval XCO2 values (bottom panel) from SCIAMACHY, GOSAT, and OCO-2 (Figure 4). The top panel shows XCO2 increased more than 30 ppm from 2003 to 2016 over most latitudes. Especially high XCO2 values occurred during the start of 2016 in the northern hemisphere (dark red). The bottom panel shows XCO2 adjustments, integrated XCO2 () minus original XCO2 () were mainly within −2.0 to 1.0 ppm and include seasonality, with high adjustment values in summer and low adjustment values in winter, except for some scattered grids in high or low latitudes. This could be caused by seasonal changes of the XCO2 averaging kernel (Appendix A: Figure A1) that was adopted for XCO2 adjustment in Equation (1). In addition, the adjustments decreased sharply in 2012 and 2016, with stability improvements of the newer satellite sensors.
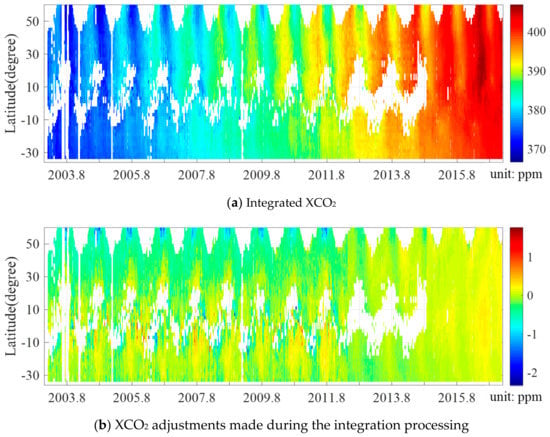
Figure 4.
Latitudinal-temporal change of integrated XCO2 (a) and XCO2 adjustments made during the integration processing, integrated XCO2 () minus original XCO2 () (b) from SCIAMACHY, GOSAT, and OCO-2.
4.2. Globally-Mapped XCO2
4.2.1. Latitudinal and Temporal Variability of Globally Mapped XCO2
The latitudinal and temporal variability of globally mapped XCO2 (GM-XCO2) and its prediction uncertainty and precision are shown in Figure 5. Comparing Figure 5a to gaps in Figure 4a show missing observations have been reasonably filled. GM-XCO2 also shows the yearly increase and seasonal variation from 2003 to 2016. GM-XCO2 is higher in the northern hemisphere compared to the southern hemisphere, and the annual maximum GM-XCO2 lasts longer in mid-latitudes than high/low latitudes.
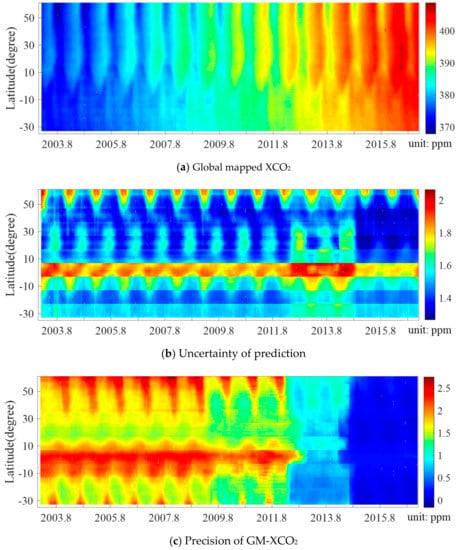
Figure 5.
Latitudinal and temporal variability of global mapped XCO2 (GM-XCO2, top panel), the uncertainty of the prediction (standard deviation, middle panel), and precision (bottom panel).
In the middle panel, kriging standard deviations (square root of in Equation 17) of the predicted GM-XCO2 represents the prediction uncertainty, which is determined by the available data around gaps. Higher uncertainty is shown in the tropic and high latitudes because of low numbers of robust observations in these latitudes corresponding to gaps in Figure 4a. The uncertainty also shows seasonal variation for different latitudes. In mid-high latitudes (35–60 °N), the uncertainty is high in winter for the observations affected by snow cover. In mid-low latitudes (extratropics within 35°N/°S), uncertainty is high in summer likely due to cloud contamination during the monsoon season.
In the bottom panel, GM-XCO2 precision is calculated from integrated XCO2 () precision. The precision is significantly improved from the middle of 2009 and 2014. It was 1.5 to 2.5 ppm before 2009, 0.5 to 1.5 from 2009 to 2014, and below 0.5 after 2014. That is because of the observing precision improvement of the newer sensors. Generally, the observed GM-XCO2 precision is better in mid-latitudes.
4.2.2. Comparison with Conventional Spatio-Temporal Kriging Results
The latitudinal and temporal differences between the results from the precision-weighted (this study) and conventional spatio-temporal kriging methods are shown in Figure 6. Precision (Figure 6c) of GM-XCO2 from precision weighted spatio-temporal kriging is improved for most of the predictions, especially for the SCIAMACHY and GOSAT overlapping periods (June 2009–March 2012) or GOSAT and OCO-2 overlaps (September 2014–May 2016). The precision improved by 0.3–0.5 ppm over latitudes with overlapping observations. GM-XCO2 (Figure 6a) is enhanced by 0.1–0.2 ppm for the summer of 2009 to 2011 and reduced by 0.2–0.3 for the summer of 2014 to 2016. Differences in the uncertainty of prediction (Figure 6b) are small for both kriging results (conventional and precision-weighted) because they are based on the same observations (), which results in a similar spatio-temporal correlation structure as shown in Figure 3.
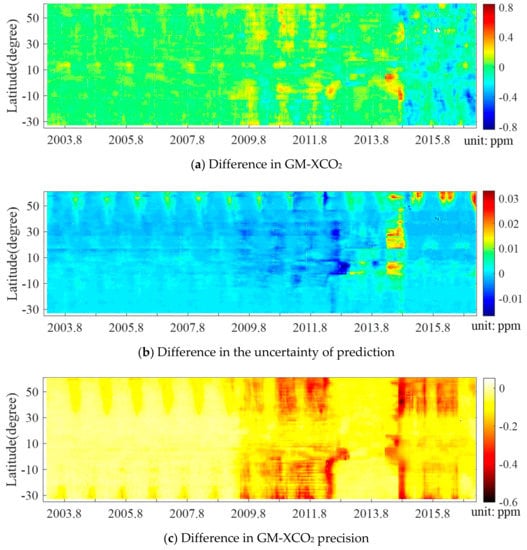
Figure 6.
Latitudinal and temporal difference between results from precision-weighted and conventional spatio-temporal kriging methods for global mapped XCO2 (GM-XCO2, top panel), the difference in the uncertainty of the prediction (standard deviation, middle panel) and the difference in GM-XCO2 precision (bottom panel). Positive values indicate precision-weighted results are higher and vice versa.
4.2.3. Spatial Distribution of GM-XCO2
GM-XCO2 provides important information about the mean spatial distribution and localized anomalies which could relate to local carbon uptake and emission. We present the spatial-temporal distribution of GM-XCO2 during different seasons in 2003, 2008, 2013, and 2015 (Figure 7). Seasonal patterns of GM-XCO2 were similar with an annual increase of approximately around 2.0 ppm. In spring, high GM-XCO2 appeared in northern Canada, the North China Plain, and the Arabian Peninsula. In summer, extremely low GM-XCO2 occurred in mid-high latitudes in the northern hemisphere. In autumn, the north-south hemispheric GM-XCO2 gradient relaxes. In winter, high XCO2 returns over the North China Plain and Central Africa.
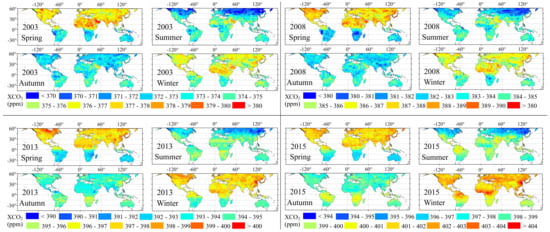
Figure 7.
Spatial-temporal distribution of mean seasonal globally-mapped XCO2 (GM-CO2) during spring (March, April, May), summer (June, July, August), autumn (September, October, November) and winter (December, January, Febryary) of 2003 (top-left), 2008 (top-right), 2013 (bottom-left), and 2015 (bottom-right). Color bars for different years assume an annual increase of 2 ppm.
In addition, we give out the global spatial distribution of mean XCO2 in 2016 shown in Figure 8. We can find that the main high XCO2 of 2016 is distributed in Eastern China, Southeast Asian regions, Amazon forest regions, African forest regions, south of the United States, the Arabian Peninsula, and India. These regions could be related to three main conditions, including (1) an industrial development zone inhabited by human beings; (2) a large area of tropical/subtropical rainforest area; (3) large agricultural regions.
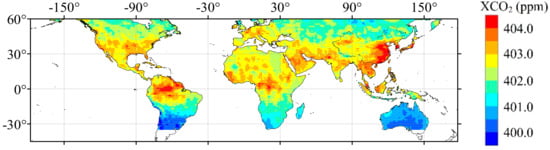
Figure 8.
Spatial-temporal distribution of mean GM-XCO2 in 2016.
4.3. GM-XCO2 Validation
4.3.1. Evaluation Using Cross-Validation
Results of cross-validation using the precision-weighted spatio-temporal kriging method are shown in Figure 9. Predicted XCO2 (GM-XCO2) agreed well with integrated XCO2 () with a high R2 of 0.97, showing the interpolation method retains much of the input signal. Total RMSE (root mean square error) between predicted GM-XCO2 and integrated XCO2 () is 1.36 ppm, which indicates good stability and the high precision of this method. Most of the predicted bias is within 1.0 ppm, except for some XCO2 data precision which is larger than 1.5 ppm (right panel). Specifically, 61% of the prediction bias is less than 1.0 ppm. Additionally, 70% and 80% of the predicted bias is within 1 and 2 times of XCO2 precision, respectively. Results from cross-validation suggest that this mapping method is effective and precise in gap-filling of multi-satellites observed XCO2, which could also be affected by original data precision.
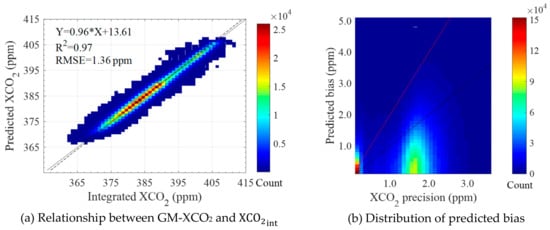
Figure 9.
Results of cross-validation using the precision-weighted spatio-temporal kriging method. The relationship between predicted XCO2 (GM-XCO2) and reserved integrated XCO2 () is shown in the left panel. The distribution of predicted bias (absolute difference between GM-XCO2 and reserved ) and precision is shown in the right panel. The black and red lines in the right panel represent the slope of 1 and 2.
4.3.2. Validation of GM-XCO2 with TCCON Measurements
High accuracy and continuous time series of XCO2 from TCCON measurements were used for validation of GM-XCO2 derived from satellite observations. In this study, we selected 12 sites with measurements for more than five years from 2003 to 2016 for comparison with GM-XCO2. and GM-XCO2 data within 500 km of each TCCON site was used for this comparison (Figure 10). GM-XCO2 retained information from satellite observations, which captured the annual increase and seasonal variation of XCO2 well. The temporal variation of GM-XCO2 is consistent with TCCON XCO2. Comparison statistics between GM-XCO2 and TCCON XCO2 are shown in Table 2. If we assume TCCON measurements are accurate, the accuracy of GM-XCO2 performs well with the total averaged bias of 0.01 ppm across 303 data pairs. The precision of GM-XCO2 in most TCCON sites (9/12) is within 1.0 ppm with an averaged absolute bias of 0.92 ppm. The mean value of the standard deviation of the bias over 12 sites is 1.05 ppm.
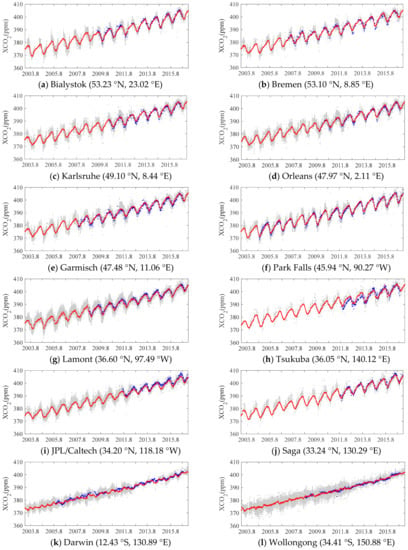
Figure 10.
Temporal variation comparison of GM-XCO2 at 12 TCCON sites. Grey, red, and blue points represent , GM-XCO2, and XCO2 from TCCON measurements, respectively. was retrieved within 500 km of TCCON sites. TCCON measurements from 11:00 to 15:00 local time were selected for comparison.

Table 2.
Comparison statistics between GM-XCO2 and TCCON XCO2. Bias is calculated using GM-XCO2 minus TCCON XCO2 for each coincident data pair and averaged for each site.
4.4. Comparison between GM-XCO2 and CarbonTracker Simulated XCO2
GM-XCO2, the spatial-temporal continuous XCO2 from satellite observations, can provide a detailed distribution of XCO2 over global or regional land areas. In order to explore the advantages and disadvantages of GM-XCO2, we present the latitudinal-temporal change comparison between GM-XCO2 with CT-XCO2 and their local temporal change comparison in the northern hemisphere.
4.4.1. Comparison with Latitudinal and Temporal Variability of CT-XCO2
The latitudinal and temporal variability of the difference between GM-XCO2 (Figure 5) and CT-XCO2 (Appendix A: Figure A2) and statistical summary are shown in Figure 11. The mean difference is 1.53 ± 0.80 ppm. XCO2 difference in the mid-latitudes showed better consistency with the mean value than that in low/high latitudes. The difference in high latitudes is smaller, especially for data before March 2012. In low latitudes, the difference varied with time, with lower values in summer and higher values in winter. The differences decreased with the satellite observations precision improvement from 2009 to 2016.
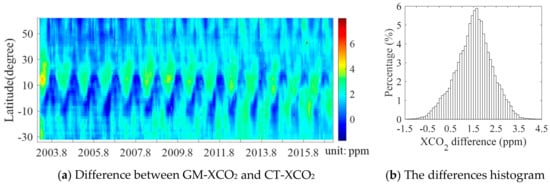
Figure 11.
Latitudinal and temporal variability of the difference between GM-XCO2 and CT-XCO2 (a): GM-XCO2 minus CT-XCO2) and a histogram of the differences (b).
XCO2 from low/high latitudes, especially for data before March 2012, shows the largest differences between GM-XCO2 and CT-XCO2. The potential reasons for this are: (1) Sparse satellite observation in high/low latitudes limited the accuracy of GM-XCO2; (2) Limited precision of XCO2 from SCIAMCHY contributed to large differences compared to CT-XCO2; (3) Lacking or limited surface measurements in low/high latitudes constrained the CT model and affected the simulation of accurate XCO2. GM-XCO2 provided spatial-temporal continuous XCO2 based on satellite observations that are different from the model simulation.
4.4.2. Temporal Variability of GM-XCO2 and CT-XCO2 in Mid-Latitudes
GM-XCO2 may provide insights into local carbon uptake and emission. We present the temporal variability of , GM-XCO2, and XCO2 from CarbonTracker (CT-XCO2) from 2003 to 2016 over mid-latitudes of North America and Eastern Asia (Figure 12). Mean GM-XCO2 kept the original XCO2 information from the satellites observation by kriging the . However, GM-XCO2 presented sharp changes in XCO2 during the peak and minimum of XCO2 in each year, which is not as smooth as that of CT-XCO2. In addition, the temporal variability of GM-XCO2 was more consistent with CT-XCO2 in Northern America than that of Eastern Asia. That could be attributed to the contribution from more surface measurements to constrain the models. As a result, GM-XCO2 might provide more information for areas with limited surface measurements, such as China.
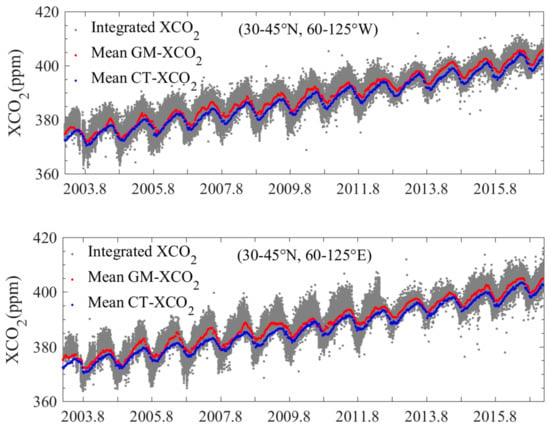
Figure 12.
Temporal variation of XCO2 from integrated and global mapped results (grey and red points) and CarbonTracker (blue points) over latitude in the range of 30 to 45°N and longitude of 60 to 125°W and 60 to 125°E.
5. Discussion
There are some advantages of GM-XCO2 used in global carbon cycle studies. GM-XCO2 provided spatial-temporal continuous XCO2 data from 2003 to 2016 which filled the gaps in observation as shown in Figure 1. It improved the data precision compared with XCO2 from conventional spatio-temporal kriging, especially for data in the satellites overlapping period. As a result, GM-XCO2 could help us understand the temporal and spatial changes in the global distribution of CO2 [17]. Because GM-XCO2 is from instantaneous satellite observations, it could capture detailed and abnormal XCO2 change which could be related to local carbon uptake and emission [10,55]. It could also be an important dataset for biosphere-atmosphere interactions by relating its changes to local biosphere parameter variations [7,11]. In addition, we provide XCO2 precision and interpolation uncertainty for each XCO2. Users can select different temporal and spatial segments of GM-XCO2 data for their specific application. As it was discussed that space-based XCO2 with precision (no bias) of 2.5 ppm could be used for matching ground-based network and precision within 1.0 ppm, it could help reduce inferred CO2 flux uncertainties significantly [56]. For anthropogenic CO2 monitoring, a precision requirement of GM-XCO2 must be better than 0.7 ppm [57].
However, there are also some challenges that need to be discussed. Prediction of GM-XCO2 in regions with little observations could have low precision and high interpolation uncertainty. GM-XCO2 in the tropical rainforest area and the winter in high latitudes should be used carefully as a few observations were limited by observing conditions [58,59]. The interpolation method might not describe the process of atmospheric transport perfectly, especially for regions with a complex climate like the Tibetan area. In addition, GM-XCO2 over a desert like the Sahara with an influence from high brightness reflection and complex dust for satellite observations inversion should also be used carefully [60].
6. Conclusions
In this study, we developed a precision-weighted spatio-temporal kriging interpolation method of multiple satellite observed XCO2. It not only used the spatio-temporal variability of XCO2, but also the precision of each observation for gap filling. The spatio-temporal correlation structure was optimized and the weighting of XCO2 with high precision was improved. The precision of predictions improved in most of the grids, especially for the satellites overlapping period (0.3 – 0.5 ppm). It would be useful for gap-filling of increasing satellite observations not only in XCO2 but also for other data observed by multiply satellites with different precision.
We also produced a spatial-temporal continuous XCO2 product, which provides the data precision and interpolation uncertainty of each grid. It is spatio-temporal continuous XCO2 from satellite observations which could capture the detailed change of XCO2. It could be an available dataset for global carbon cycle studies like biosphere-atmosphere interaction.
Author Contributions
L.L., and Z.H. conceived and designed the experiments; Z.H. performed the experiments; L.R.W., Z.H., and L.L. analyzed the data; C.W., M.S., Y.Z., L.L. and Z.-C.Z. contributed analysis tools; Z.H., and L.R.W. wrote the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Strategic Priority Research Program of the Chinese Academy of Sciences (XDA19080303), the Key Research Program of Chinese Academy of Sciences (ZDRW-ZS-2019-3) and the National Key Research and Development Program of China (2016YFA0600303).
Acknowledgments
We also thank ESA for sharing the SCIAMACHY BESD XCO2 level 2 data, the ACOS/OCO-2 project at JPL for sharing ACOS-GOSAT v7.3 and OCO-2 v9r data, NOAA ESRL for providing CarbonTracker CT2017 results. TCCON data were obtained from the TCCON Data Archive website at http://tccon.ornl.gov/.
Conflicts of Interest
No conflict.
Appendix A
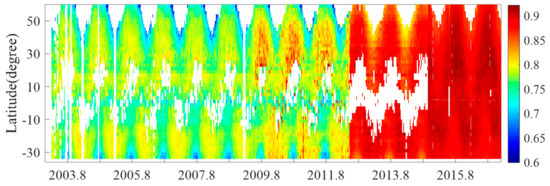
Figure A1.
Latitudinal-temporal change of mean XCO2 averaging kernel from SCIAMACHY (January–March 2003), GOSAT (June 2009–May 2014), and OCO-2 (September 2014.09–December 2016).
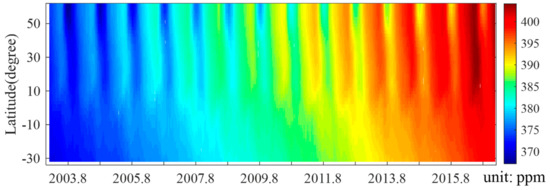
Figure A2.
Latitudinal-temporal change of CT-XCO2 from 2003 to 2016
Acronyms
| Acronyms | Full Names |
| XCO2 | Column-averaged dry air mole fraction of atmospheric CO2 |
| Original XCO2 retrievals from satellites | |
| Adjusted | |
| Converted | |
| Integrated combination of | |
| GM-XCO2 | Global mapped XCO2 |
| ENVISAT | Environmental Satellite |
| SCIAMACHY | SCanning Imaging Absorption spectroMeter for Atmospheric CHartographY |
| GOSAT | Greenhouse Gases Observing Satellite |
| OCO-2 | Orbiting Carbon Observatory-2 |
| BESD | Bremen Optimal Estimation–DOAS |
| ACOS | Atmospheric CO2 Observations from Space |
| TCCON | The total carbon column observing network |
| CT | CarbonTracker |
| r2 | the coefficient of determination |
| RMSE | the root mean square error |
| ESRL | Earth System Research Laboratory |
References
- Le Quéré, C.; Andrew, R.M.; Friedlingstein, P.; Sitch, S.; Hauck, J.; Pongratz, J.; Pickers, P.A.; Korsbakken, J.I.; Peters, G.P.; Canadell, J.G.; et al. Global Carbon Budget 2018. Earth Syst. Sci. Data 2018, 10, 2141–2194. [Google Scholar] [CrossRef]
- Stocker, T.; Qin, D.; Plattner, G.; Tignor, M.; Allen, S.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, B.; Midgley, B. IPCC, 2013: Climate Change 2013: The Physical Science Basis. In Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Fortunat, J.; Renato, S. Rates of change in natural and anthropogenic radiative forcing over the past 20,000 years. Proc. Natl. Acad. Sci. USA 2008, 105, 1425–1430. [Google Scholar]
- Dlugokencky, E.; Tans, P. Trends in Atmospheric Carbon Dioxide, National Oceanic & Atmospheric Administration, Earth System Research Laboratory (NOAA/ESRL). Available online: http://www.esrl.noaa.gov/gmd/ccgg/trends/global.html (accessed on 19 October 2019).
- Le Quéré, C.; Moriarty, R.; Andrew, R.M.; Canadell, J.G.; Sitch, S.; Korsbakken, J.I.; Friedlingstein, P.; Peters, G.P.; Andres, R.J.; Boden, T.A.; et al. Global Carbon Budget 2015. Earth Syst. Sci. Data 2015, 7, 349–396. [Google Scholar] [CrossRef]
- Randerson, J.T.; Thompson, M.V.; Conway, T.J.; Fung, I.Y.; Field, C.B. The contribution of terrestrial sources and sinks to trends in the seasonal cycle of atmospheric carbon dioxide. Glob. Biogeochem. Cycles 1997, 11, 535–560. [Google Scholar] [CrossRef]
- He, Z.; Zeng, Z.-C.; Lei, L.; Bie, N.; Yang, S. A Data-Driven Assessment of Biosphere-Atmosphere Interaction Impact on Seasonal Cycle Patterns of XCO2 Using GOSAT and MODIS Observations. Remote Sens. 2017, 9, 251. [Google Scholar] [CrossRef]
- Graven, H.D.; Keeling, R.F.; Piper, S.C.; Patra, P.K.; Stephens, B.B.; Wofsy, S.C.; Welp, L.R.; Sweeney, C.; Tans, P.P.; Kelley, J.J. Enhanced Seasonal Exchange of CO2 by Northern Ecosystems Since 1960. Science 2013, 341, 1085–1089. [Google Scholar] [CrossRef]
- Zeng, N.; Zhao, F.; Collatz, G.J.; Kalnay, E.; Salawitch, R.J.; West, T.O.; Guanter, L. Agricultural Green Revolution as a driver of increasing atmospheric CO2 seasonal amplitude. Nature 2014, 515, 394–397. [Google Scholar] [CrossRef]
- Detmers, R.G.; Hasekamp, O.; Aben, I.; Houweling, S.; van Leeuwen, T.T.; Butz, A.; Landgraf, J.; Köhler, P.; Guanter, L.; Poulter, B. Anomalous carbon uptake in Australia as seen by GOSAT. Geophys. Res. Lett. 2015, 42, 8177–8184. [Google Scholar] [CrossRef]
- He, Z.; Lei, L.; Welp, L.; Zeng, Z.-C.; Bie, N.; Yang, S.; Liu, L. Detection of Spatiotemporal Extreme Changes in Atmospheric CO2 Concentration Based on Satellite Observations. Remote Sens. 2018, 10, 839. [Google Scholar] [CrossRef]
- Chevallier, F.; Palmer, P.I.; Feng, L.; Boesch, H.; O’Dell, C.W.; Bousquet, P. Toward robust and consistent regional CO2 flux estimates from in situ and spaceborne measurements of atmospheric CO2. Geophys. Res. Lett. 2014, 41, 1065–1070. [Google Scholar] [CrossRef]
- Deng, F.; Jones, D.B.A.; Henze, D.K.; Bousserez, N.; Bowman, K.W.; Fisher, J.B.; Nassar, R.; O’Dell, C.; Wunch, D.; Wennberg, P.O.; et al. Inferring regional sources and sinks of atmospheric CO2 from GOSAT XCO2 data. Atmos. Chem. Phys. 2014, 14, 3703–3727. [Google Scholar] [CrossRef]
- Eldering, A.; Wennberg, P.O.; Crisp, D.; Schimel, D.S.; Gunson, M.R.; Chatterjee, A.; Liu, J.; Schwandner, F.M.; Sun, Y.; O’Dell, C.W. The Orbiting Carbon Observatory-2 early science investigations of regional carbon dioxide fluxes. Science 2017, 358, eaam5745. [Google Scholar] [CrossRef] [PubMed]
- Ciais, P.; Dolman, A.J.; Bombelli, A.; Duren, R.; Peregon, A.; Rayner, P.J.; Miller, C.; Gobron, N.; Kinderman, G.; Marland, G.; et al. Current systematic carbon-cycle observations and the need for implementing a policy-relevant carbon observing system. Biogeosciences 2014, 11, 3547–3602. [Google Scholar] [CrossRef]
- Heimann, M. Searching out the sinks. Nat. Geosci. 2009, 2, 3–4. [Google Scholar] [CrossRef]
- Watanabe, H.; Hayashi, K.; Saeki, T.; Maksyutov, S.; Nasuno, I.; Shimono, Y.; Hirose, Y.; Takaichi, K.; Kanekon, S.; Ajiro, M.; et al. Global mapping of greenhouse gases retrieved from GOSAT Level 2 products by using a kriging method. Int. J. Remote Sens. 2015, 36, 1509–1528. [Google Scholar] [CrossRef]
- Kathryn, M.K.; Wofsy, S.C.; Thomas, N.; Janusz, E.; Ehleringer, J.R.; Stephens, B.B. Assessment of ground-based atmospheric observations for verification of greenhouse gas emissions from an urban region. Proc. Natl. Acad. Sci. USA 2012, 109, 8423–8428. [Google Scholar]
- Zeng, Z.-C.; Lei, L.; Strong, K.; Jones, D.B.A.; Guo, L.; Liu, M.; Deng, F.; Deutscher, N.M.; Dubey, M.K.; Griffith, D.W.T.; et al. Global land mapping of satellite-observed CO2 total columns using spatio-temporal geostatistics. Int. J. Digit. Earth 2016. [Google Scholar] [CrossRef]
- Kataoka, F.; Crisp, D.; Taylor, T.E.; O’Dell, C.W.; Lee, R.A.M. The Cross-Calibration of Spectral Radiances and Cross-Validation of CO2 Estimates from GOSAT and OCO-2. Remote Sens. 2017, 9, 1158. [Google Scholar] [CrossRef]
- Heymann, J.; Reuter, M.; Hilker, M.; Buchwitz, M.; Schneising, O.; Bovensmann, H.; Burrows, J.P.; Kuze, A.; Suto, H.; Deutscher, N.M.; et al. Consistent satellite XCO2 retrievals from SCIAMACHY and GOSAT using the BESD algorithm. Atmos. Meas. Tech. 2015, 8, 2961–2980. [Google Scholar] [CrossRef]
- Hakkarainen, J.; Ialongo, I.; Tamminen, J. Direct space-based observations of anthropogenic CO2 emission areas from OCO-2. Geophys. Res. Lett. 2016, 43, 11400–411406. [Google Scholar] [CrossRef]
- Bovensmann, H.; Buchwitz, M.; Burrows, J.P.; Reuter, M. A remote sensing technique for global monitoring of power plant CO2 emissions from space and related applications. Atmos. Meas. Tech. 2010, 3, 55–110. [Google Scholar] [CrossRef]
- Schwandner, F.M.; Gunson, M.R.; Miller, C.E.; Carn, S.A.; Eldering, A.; Krings, T.; Verhulst, K.R.; Schimel, D.S.; Nguyen, H.M.; Crisp, D. Spaceborne detection of localized carbon dioxide sources. Science 2017, 358, eaam5782. [Google Scholar] [CrossRef] [PubMed]
- Nassar, R.; Hill, T.G.; Mclinden, C.A.; Wunch, D.; Jones, D.B.A.; Crisp, D.; Nassar, R.; Hill, T.G.; Mclinden, C.A.; Wunch, D. Quantifying CO2 emissions from individual power plants from space. Geophys. Res. Lett. 2017, 44, 10045–10053. [Google Scholar] [CrossRef]
- Liu, J.; Bowman, K.W.; Schimel, D.S.; Parazoo, N.C.; Jiang, Z.; Lee, M.; Bloom, A.A.; Wunch, D.; Frankenberg, C.; Sun, Y.; et al. Contrasting carbon cycle responses of the tropical continents to the 2015–2016 El Nino. Science 2017, 358. [Google Scholar] [CrossRef]
- Feng, L.; Palmer, P.I.; Parker, R.J.; Deutscher, N.M.; Feist, D.G.; Kivi, R.; Morino, I.; Sussmann, R. Estimates of European uptake of CO2 inferred from GOSAT XCO2 retrievals: Sensitivity to measurement bias inside and outside Europe. Atmos. Chem. Phys. 2016, 16, 1289–1302. [Google Scholar] [CrossRef]
- Bovensmann, H.; Burrows, J.P.; Buchwitz, M.; Frerick, J.; Noël, S.; Rozanov, V.V.; Chance, K.V.; Goede, A.P.H. SCIAMACHY: Mission Objectives and Measurement Modes. J. Atmos. Sci. 1999, 56, 125–150. [Google Scholar] [CrossRef]
- Yokota, T.; Yoshida, Y.; Eguchi, N.; Ota, Y.; Tanaka, T.; Watanabe, H.; Maksyutov, S. Global concentrations of CO2 and CH4 retrieved from GOSAT: First preliminary results. Sci. Online Lett. Atmos. 2009, 5, 160–163. [Google Scholar] [CrossRef]
- Boesch, H.; Baker, D.; Connor, B.; Crisp, D.; Miller, C. Global Characterization of CO2 Column Retrievals from Shortwave-Infrared Satellite Observations of the Orbiting Carbon Observatory-2 Mission. Remote Sens. 2011, 3, 270–304. [Google Scholar] [CrossRef]
- Zeng, Z.; Lei, L.; Hou, S.; Ru, F.; Guan, X.; Zhang, B. A Regional Gap-Filling Method Based on Spatiotemporal Variogram Model of Columns. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3594–3603. [Google Scholar] [CrossRef]
- Hammerling, D.M.; Michalak, A.M.; O’Dell, C.; Kawa, S.R. Global CO2 distributions over land from the Greenhouse Gases Observing Satellite (GOSAT). Geophys. Res. Lett. 2012, 39, 1–6. [Google Scholar] [CrossRef]
- Hai, N.; Katzfuss, M.; Cressie, N.; Braverman, A. Spatio-Temporal Data Fusion for Very Large Remote Sensing Datasets. Technometrics 2014, 56, 174–185. [Google Scholar]
- Liu, Y.; Wang, X.; Guo, M.; Tani, H. Mapping the FTS SWIR L2 product of XCO2 and XCH4 data from the GOSAT by the Kriging method—A case study in East Asia. Int. J. Remote Sens. 2012, 33, 3004–3025. [Google Scholar] [CrossRef]
- Jing, Y.; Shi, J.; Wang, T.; Sussmann, R. Mapping global atmospheric CO2 concentration at high spatiotemporal resolution. Atmosphere 2014, 5, 870–888. [Google Scholar] [CrossRef]
- Tadi, J.M.; Qiu, X.; Miller, S.; Michalak, A.M. Spatio-temporal approach to moving window block kriging of satellite data. Geosci. Model Dev. 2017, 10, 1–17. [Google Scholar] [CrossRef]
- Reuter, M.; Bovensmann, H.; Buchwitz, M.; Burrows, J.P.; Connor, B.J.; Deutscher, N.M.; Griffith, D.W.T.; Heymann, J.; Keppel-Aleks, G.; Messerschmidt, J.; et al. Retrieval of atmospheric CO2 with enhanced accuracy and precision from SCIAMACHY: Validation with FTS measurements and comparison with model results. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- O’Dell, C.W.; Connor, B.; Bösch, H.; O’Brien, D.; Frankenberg, C.; Castano, R.; Christi, M.; Eldering, D.; Fisher, B.; Gunson, M.; et al. The ACOS CO2 retrieval algorithm—Part 1: Description and validation against synthetic observations. Atmos. Meas. Tech. 2012, 5, 99–121. [Google Scholar] [CrossRef]
- Wunch, D.; Wennberg, P.O.; Osterman, G.; Fisher, B.; Naylor, B.; Roehl, C.M.; Dell, C.; Mandrake, L. Comparisons of the Orbiting Carbon Observatory-2 (OCO-2) XCO2 measurements with TCCON. Atmos. Meas. Tech. 2017, 10, 2209–2238. [Google Scholar] [CrossRef]
- Wunch, D.; Wennberg, P.O.; Toon, G.C.; Connor, B.J.; Fisher, B.; Osterman, G.B.; Frankenberg, C.; Mandrake, L.; O’Dell, C.; Ahonen, P.; et al. A method for evaluating bias in global measurements of CO2 total columns from space. Atmos. Chem. Phys. 2011, 11, 12317–12337. [Google Scholar] [CrossRef]
- Liang, A.; Gong, W.; Han, G.; Xiang, C. Comparison of Satellite-Observed XCO2 from GOSAT, OCO-2, and Ground-Based TCCON. Remote Sens. 2017, 9, 1033. [Google Scholar] [CrossRef]
- Peters, W.; Jacobson, A.R.; Sweeney, C.; Andrews, A.E.; Conway, T.J.; Masarie, K.; Miller, J.B.; Bruhwiler, L.M.; Petron, G.; Hirsch, A.I.; et al. An atmospheric perspective on North American carbon dioxide exchange: CarbonTracker. Proc. Natl. Acad. Sci. USA 2007, 104, 18925–18930. [Google Scholar] [CrossRef]
- Connor, B.J.; Boesch, H.; Toon, G.; Sen, B.; Miller, C.; Crisp, D. Orbiting Carbon Observatory: Inverse method and prospective error analysis. J. Geophys. Res. Atmos. 2008, 113, 1–14. [Google Scholar] [CrossRef]
- Rodgers, C.D.; Connor, B.J. Intercomparison of remote sounding instruments. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Wang, T.; Shi, J.; Jing, Y.; Zhao, T.; Ji, D.; Xiong, C. Combining XCO2 measurements derived from SCIAMACHY and GOSAT for potentially generating global CO2 maps with high spatiotemporal resolution. PLoS ONE 2014, 11, e0148152. [Google Scholar] [CrossRef] [PubMed]
- Olsen, S.C.; Randerson, J.T. Differences between surface and column atmospheric CO2 and implications for carbon cycle research. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Kevin Robert, G.; Law, R.M.; Scott, D.; Rayner, P.J.; David, B.; Philippe, B.; Lori, B.; Yu-Han, C.; Philippe, C.; Songmiao, F. Towards robust regional estimates of CO2 sources and sinks using atmospheric transport models. Nature 2002, 415, 626–630. [Google Scholar]
- Lindqvist, H.; O’Dell, C.W.; Basu, S.; Boesch, H.; Chevallier, F.; Deutscher, N.; Feng, L.; Fisher, B.; Hase, F.; Inoue, M.; et al. Does GOSAT capture the true seasonal cycle of carbon dioxide? Atmos. Chem. Phys. 2015, 15, 13023–13040. [Google Scholar] [CrossRef]
- Cogan, A.J.; Boesch, H.; Parker, R.J.; Feng, L.; Palmer, P.I.; Blavier, J.F.L.; Deutscher, N.M.; Macatangay, R.; Notholt, J.; Roehl, C.; et al. Atmospheric carbon dioxide retrieved from the Greenhouse gases Observing SATellite (GOSAT): Comparison with ground-based TCCON observations and GEOS-Chem model calculations. J. Geophys. Res. Atmos. 2012, 117, 1–17. [Google Scholar] [CrossRef]
- Kyriakidis, P.C.; Journel, A.G. Geostatistical Space–Time Models: A Review. Math. Geol. 1999, 31, 651–684. [Google Scholar] [CrossRef]
- De Iaco, S. Space–time correlation analysis: A comparative study. J. Appl. Stat. 2010, 37, 1027–1041. [Google Scholar] [CrossRef]
- Iaco, S.D.; Myers, D.E.; Posa, D. Space–time analysis using a general product–sum model. Stat. Probab. Lett. 2001, 52, 21–28. [Google Scholar] [CrossRef]
- Cressie, N.; Wikle, C.K. Statistics for Spatio-Temporal Data; Wily: New York, NY, USA, 2011. [Google Scholar]
- Liu, M.; Lei, L.; Liu, D.; Zeng, Z.-C. Geostatistical Analysis of CH4 Columns over Monsoon Asia Using Five Years of GOSAT Observations. Remote Sens. 2016, 8, 361. [Google Scholar] [CrossRef]
- Schneising, O.; Heymann, J.; Buchwitz, M.; Reuter, M.; Bovensmann, H.; Burrows, J.P. Anthropogenic carbon dioxide source areas observed from space: Assessment of regional enhancements and trends. Atmos. Chem. Phys. 2013, 13, 2445–2454. [Google Scholar] [CrossRef]
- Miller, C.E.; Crisp, D.; Decola, P.L.; Olsen, S.C.; Randerson, J.T.; Michalak, A.M.; Alkhaled, A.; Rayner, P.; Jacob, D.J.; Suntharalingam, P. Precision requirements for space-based XCO2 data. Ir. J. Psychol. Med. 2007, 29, 143–145. [Google Scholar]
- Wu, L.; aan de Brugh, J.; Meijer, Y.; Sierk, B.; Hasekamp, O.; Butz, A.; Landgraf, J. XCO2 observations using satellite measurements with moderate spectral resolution: Investigation using GOSAT and OCO-2 measurements. Atmos. Meas. Tech. Discuss. 2019, 2019, 1–23. [Google Scholar] [CrossRef]
- Belikov, D.A.; Bril, A.; Maksyutov, S.; Oshchepkov, S.; Saeki, T.; Takagi, H.; Yoshida, Y.; Ganshin, A.; Zhuravlev, R.; Aoki, S.; et al. Column-averaged CO2 concentrations in the subarctic from GOSAT retrievals and NIES transport model simulations. Polar Sci. 2014, 8, 129–145. [Google Scholar] [CrossRef]
- Kong, Y.; Chen, B.; Measho, S. Spatio-Temporal Consistency Evaluation of XCO2 Retrievals from GOSAT and OCO-2 Based on TCCON and Model Data for Joint Utilization in Carbon Cycle Research. Atmosphere 2019, 10, 354. [Google Scholar] [CrossRef]
- Yoshida, Y.; Kikuchi, N.; Morino, I.; Uchino, O.; Oshchepkov, S.; Bril, A.; Saeki, T.; Schutgens, N.; Toon, G.C.; Wunch, D.; et al. Improvement of the retrieval algorithm for GOSAT SWIR XCO2 and XCH4 and their validation using TCCON data. Atmos. Meas. Tech. 2013, 6, 1533–1547. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).