Finite Element Analysis based on A Parametric Model by Approximating Point Clouds
Abstract
1. Introduction
1.1. Background
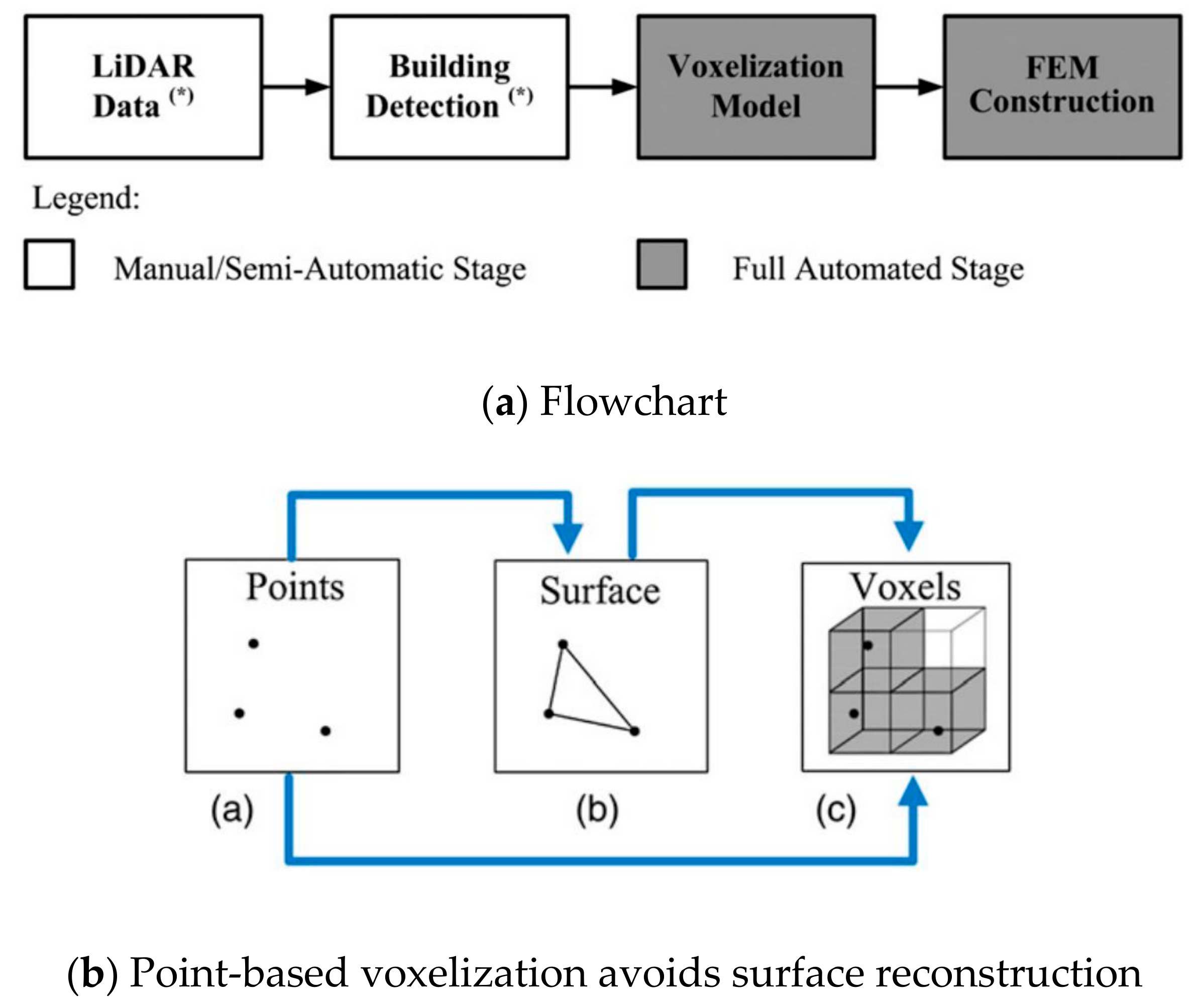
1.2. Geometric Model Generation Technologies
1.3. Geometric Information Acquisition from Sensors
1.4. Finite Element Analysis Model with High Accuracy
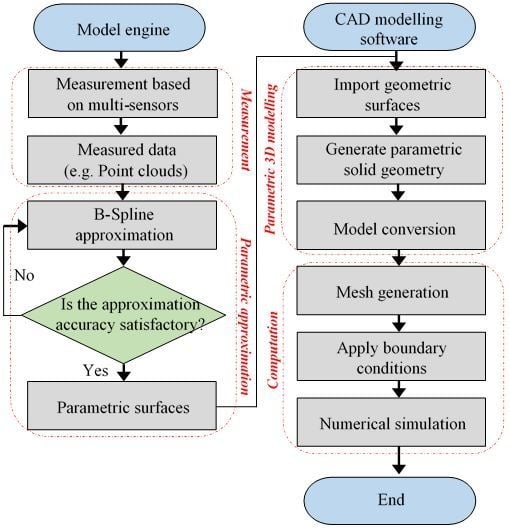
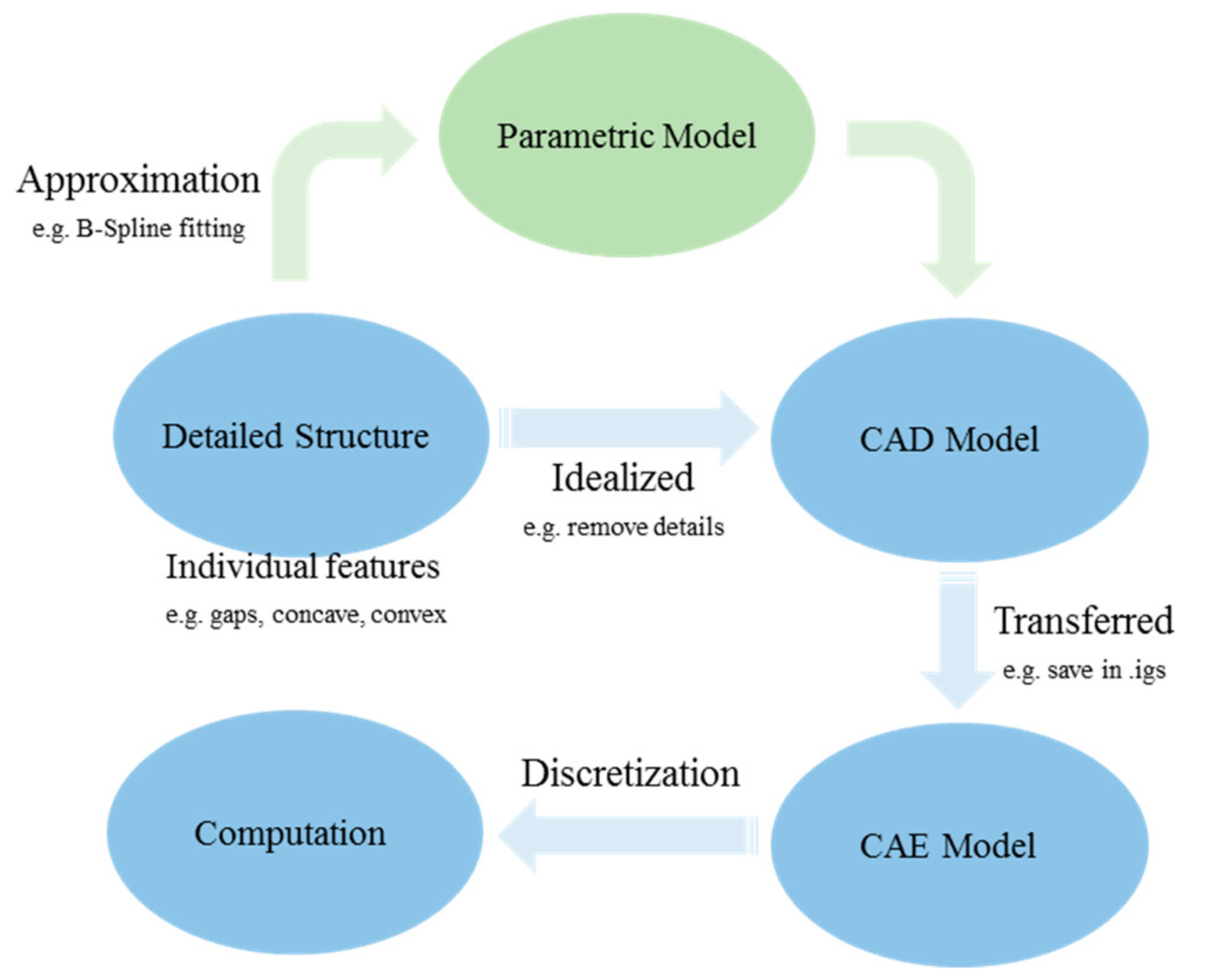
1.5. Motivation and Framework
2. Methodology of the Parametric Model
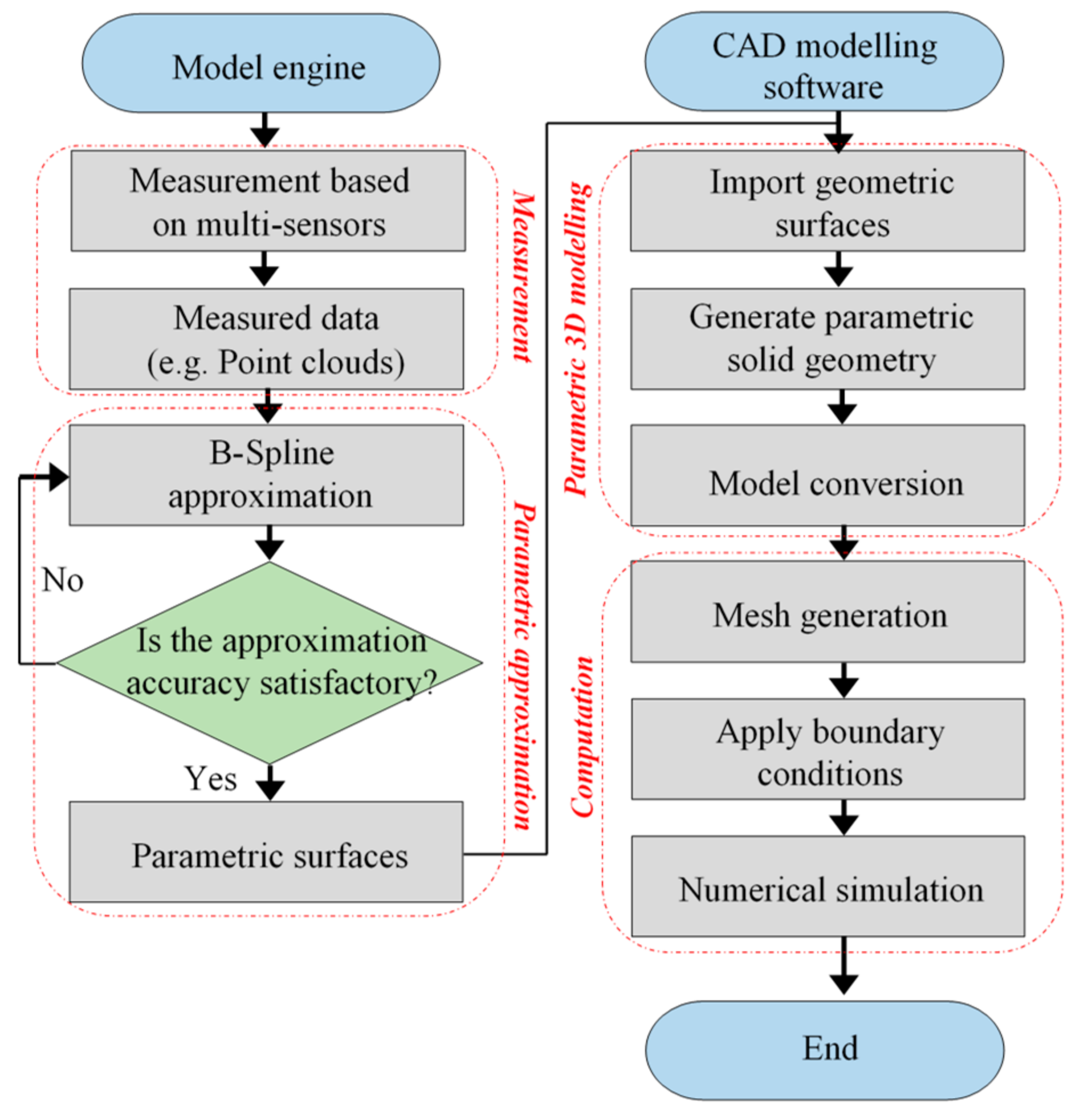
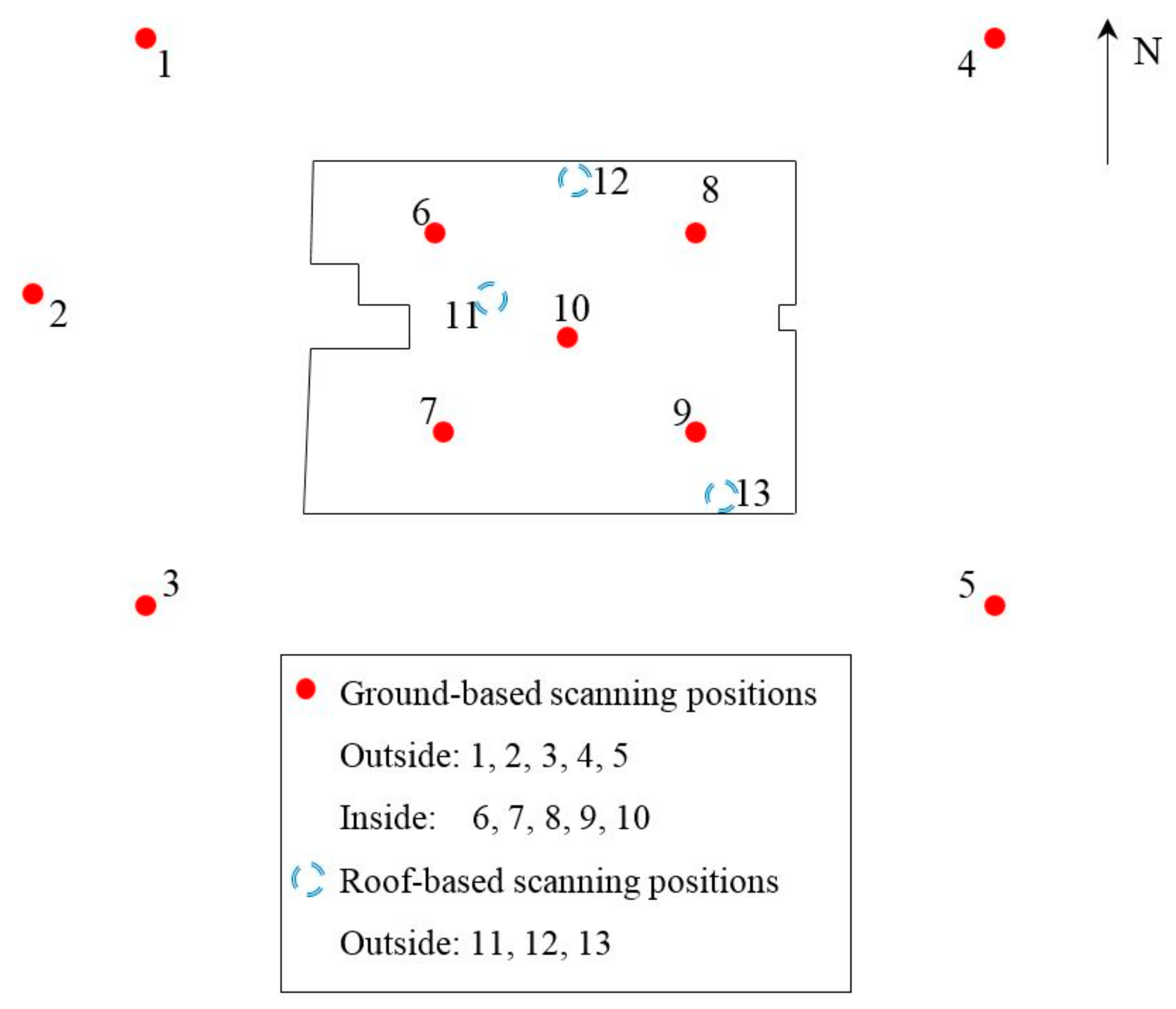
2.1. Feature Acquisition of the Object
2.2. B-Spline Approximation
2.2.1. B-Spline Basis Function
2.2.2. B-Spline Curves and Surfaces
2.2.3. B-Spline Approximation
3. Finite Element Method
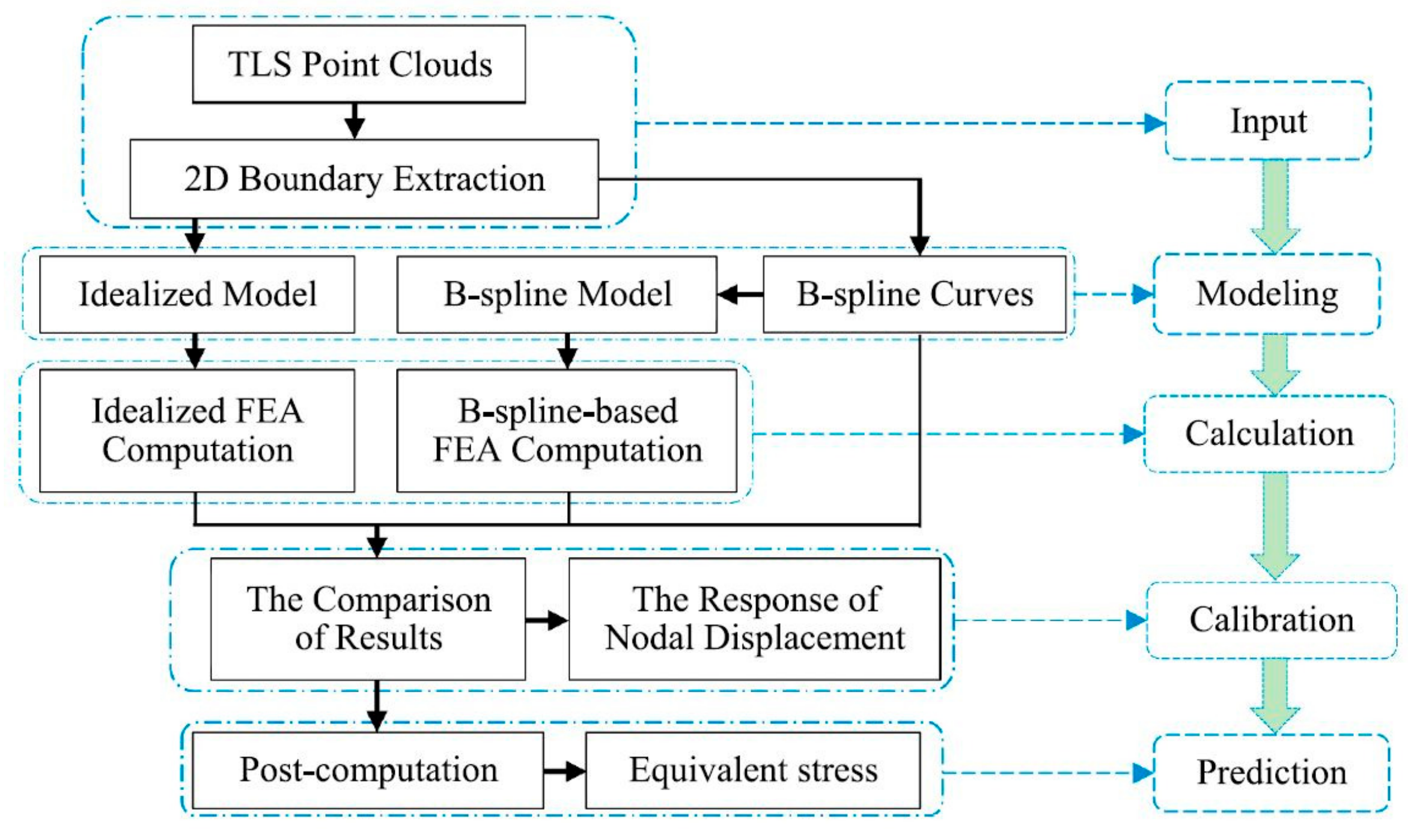
3.1. Computations
3.2. Static Computation Results
3.3. Dynamic Computation Results
4. Discussion and Analysis
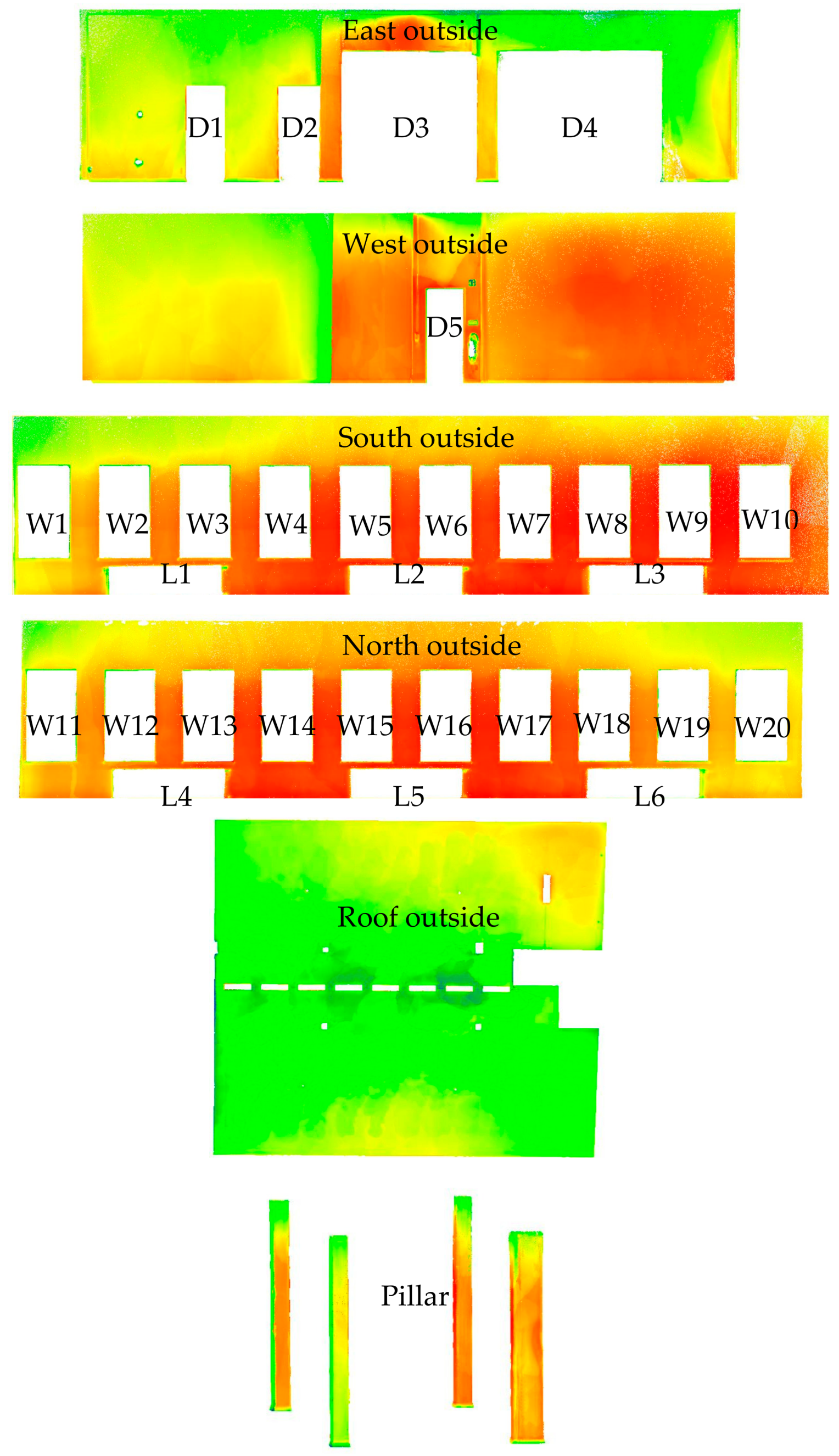
4.1. Model Quality Based on Measured Data
4.2. Deviation Analysis of Two Models
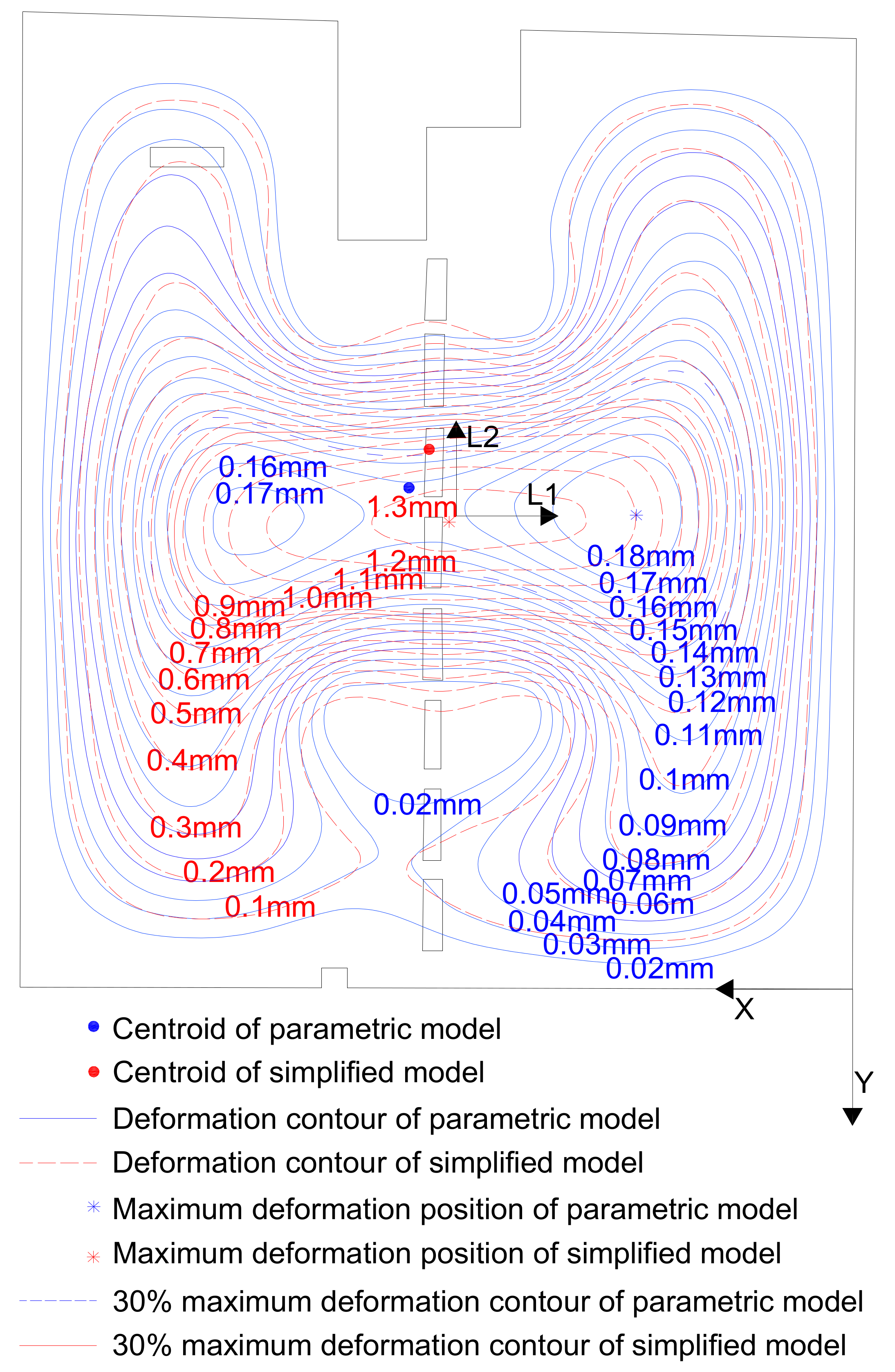
4.3. Deformation Analysis Based on Static Structure
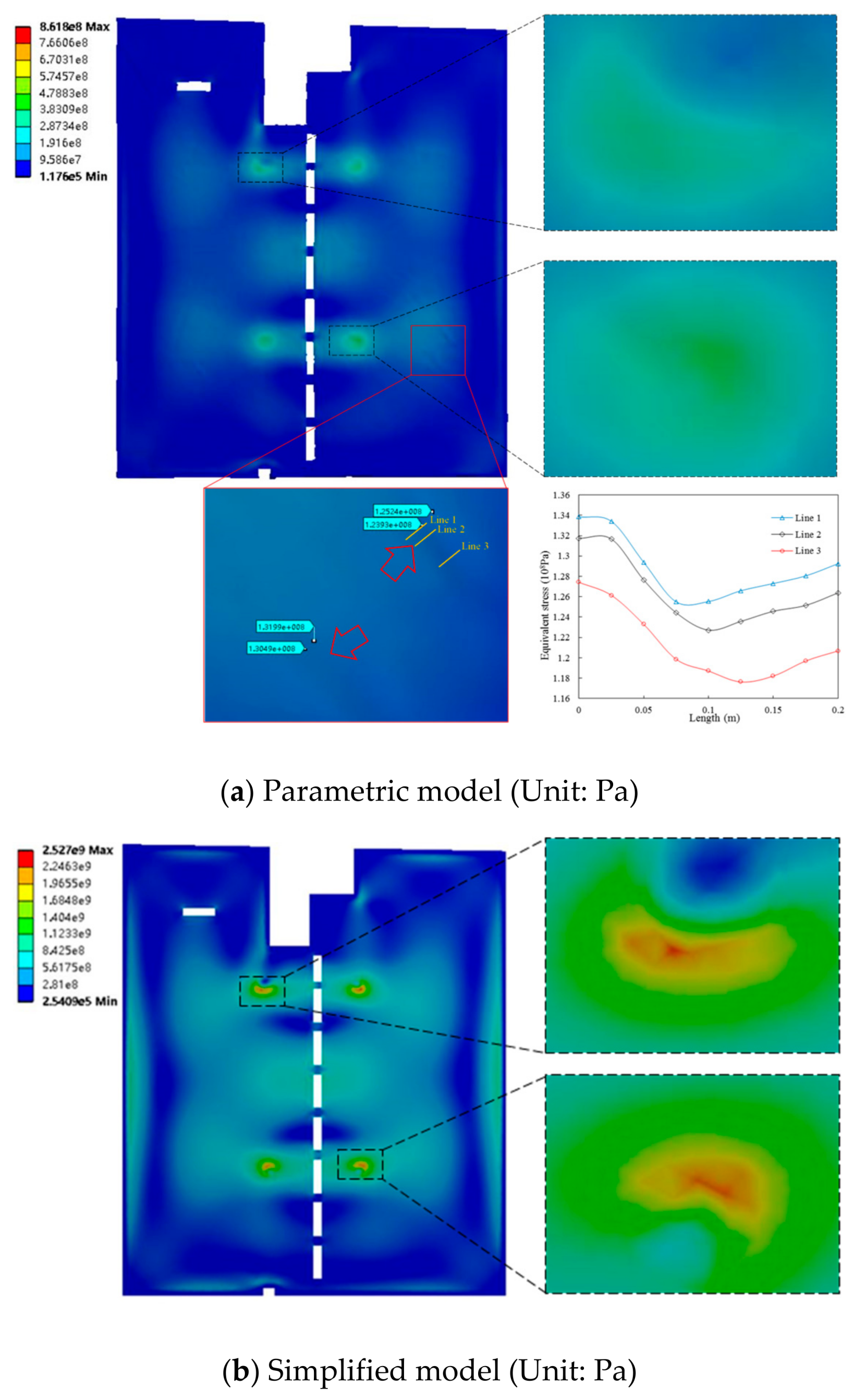
4.4. Stress Analysis Based on Static Process
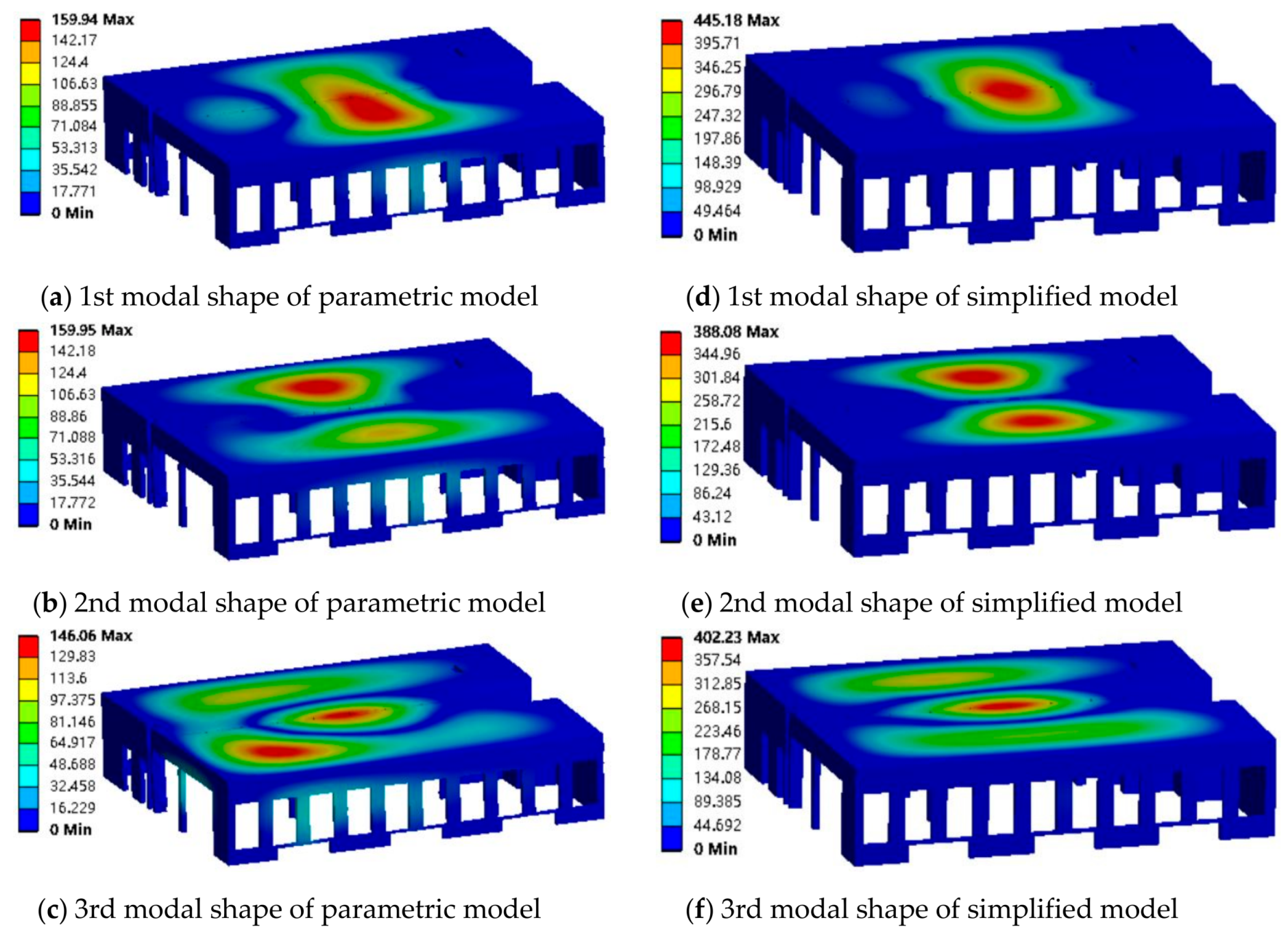
4.5. Vibration Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stefanou, G. The stochastic finite element method: Past, present and future. Comput. Methods Appl. Mech. Eng. 2009, 198, 1031–1051. [Google Scholar] [CrossRef]
- Hou, T.Y.; Wu, X.H. A multiscale finite element method for elliptic problems in composite materials and porous media. J. Comput. Phys. 1997, 134, 169–189. [Google Scholar] [CrossRef]
- Holzapfel, G.A.; Gasser, T.C.; Ogden, R.W. A new constitutive framework for arterial wall mechanics and a comparative study of material models. J. Elast. 2000, 61, 1–48. [Google Scholar] [CrossRef]
- Birman, V.; Byrd, L.W. Modeling and analysis of functionally graded materials and structures. Appl. Mech. Rev. 2007, 60, 195–216. [Google Scholar] [CrossRef]
- Pramod, A.L.N.; Ooi, E.T.; Song, C.; Natarajan, S. Numerical estimation of stress intensity factors in cracked functionally graded piezoelectric materials—A scaled boundary finite element approach. Compos. Struct. 2018, 206, 301–312. [Google Scholar] [CrossRef]
- Xu, W.; Xu, X.; Yang, H.; Neumann, I. Optimized finite element analysis model based on terrestrial laser scanning data. Compos. Struct. 2019, 207, 62–71. [Google Scholar] [CrossRef]
- Gómez, S.; Vlad, M.D.; López, J.; Fernández, E. Design and properties of 3D scaffolds for bone tissue engineering. Acta Biomater. 2016, 42, 341–350. [Google Scholar] [CrossRef]
- Peng, X.; Atroshchenko, E.; Kerfriden, P.; Bordas, S.P.A. Isogeometric boundary element methods for three dimensional static fracture and fatigue crack growth. Comput. Methods Appl. Mech. Eng. 2017, 316, 151–185. [Google Scholar] [CrossRef]
- Wang, D.; Hu, F.; Ma, Z.; Wu, Z.; Zhang, W. A CAD/CAE integrated framework for structural design optimization using sequential approximation optimization. Adv. Eng. Softw. 2014, 76, 56–68. [Google Scholar] [CrossRef]
- Breitenberger, M.; Apostolatos, A.; Philipp, B.; Wüchner, R.; Bletzinger, K.U. Analysis in computer aided design: Nonlinear isogeometric B-Rep analysis of shell structures. Comput. Methods Appl. Mech. Eng. 2015, 284, 401–457. [Google Scholar] [CrossRef]
- Montagnat, J.; Delingette, H.; Ayache, N. A review of deformable surfaces: Topology, geometry and deformation. Image Vis. Comput. 2001, 19, 1023–1040. [Google Scholar] [CrossRef]
- Piegl, L.; Tiller, W. The NURBS book, 2nd edition; Springer-Verleg: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Bureick, J.; Alkhatib, H.; Neumann, I. Robust Spatial Approximation of laser scanner point clouds by means of free-form curve approaches in deformation analysis. J. Appl. Geod. 2016, 10, 27–35. [Google Scholar] [CrossRef]
- Park, H.; Lee, J.H. B-spline curve fitting based on adaptive curve refinement using dominant points. CAD Comput. Aided Des. 2007, 39, 439–451. [Google Scholar] [CrossRef]
- Yoshihara, H.; Yoshii, T.; Shibutani, T.; Maekawa, T. Topologically robust B-spline surface reconstruction from point clouds using level set methods and iterative geometric fitting algorithms. Comput. Aided Geom. Des. 2012, 29, 422–434. [Google Scholar] [CrossRef]
- Yoo, D.J. Three-dimensional surface reconstruction of human bone using a B-spline based interpolation approach. CAD Comput. Aided Des. 2011, 43, 934–947. [Google Scholar] [CrossRef]
- Gálvez, A.; Iglesias, A.; Puig-Pey, J. Iterative two-step genetic-algorithm-based method for efficient polynomial B-spline surface reconstruction. Inf. Sci. 2012, 182, 56–76. [Google Scholar] [CrossRef]
- Louhichi, B.; Abenhaim, G.N.; Tahan, A.S. CAD/CAE integration: updating the CAD model after a FEM analysis. Int. J. Adv. Manuf. Technol. 2015, 76, 391–400. [Google Scholar] [CrossRef]
- He, Y.; Qin, H. Surface reconstruction with triangular b-splines. In Proceedings of the Geometric Modeling and Processing 2004, Beijing, China, 13–15 April 2004; pp. 279–287. [Google Scholar]
- Kiendl, J.; Bletzinger, K.U.; Linhard, J.; Wüchner, R. Isogeometric shell analysis with Kirchhoff-Love elements. Comput. Methods Appl. Mech. Eng. 2009, 198, 3902–3914. [Google Scholar] [CrossRef]
- Qian, X. Full analytical sensitivities in NURBS based isogeometric shape optimization. Comput. Methods Appl. Mech. Eng. 2010, 199, 2059–2071. [Google Scholar] [CrossRef]
- Zhang, Y.; Bazilevs, Y.; Goswami, S.; Bajaj, C.L.; Hughes, T.J.R. Patient-specific vascular NURBS modeling for isogeometric analysis of blood flow. Comput. Methods Appl. Mech. Eng. 2007, 196, 2943–2959. [Google Scholar] [CrossRef] [PubMed]
- Xia, Z.; Wang, Q.; Wang, Y.; Yu, C. A CAD/CAE incorporate software framework using a unified representation architecture. Adv. Eng. Softw. 2015, 87, 68–85. [Google Scholar] [CrossRef]
- Hughes, T.J.R.; Cottrell, J.A.; Bazilevs, Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput. Methods Appl. Mech. Eng. 2005, 194, 4135–4195. [Google Scholar] [CrossRef]
- Nguyen, V.P.; Anitescu, C.; Bordas, S.P.A.; Rabczuk, T. Isogeometric analysis: An overview and computer implementation aspects. Math. Comput. Simul. 2015, 117, 89–116. [Google Scholar] [CrossRef]
- Buffa, A.; Sangalli, G.; Vázquez, R. Isogeometric analysis in electromagnetics: B-splines approximation. Comput. Methods Appl. Mech. Eng. 2010, 199, 1143–1152. [Google Scholar] [CrossRef]
- Xu, G.; Mourrain, B.; Duvigneau, R.; Galligo, A. Analysis-suitable volume parameterization of multi-block computational domain in isogeometric applications. CAD Comput. Aided Des. 2013, 45, 395–404. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Calo, V.M.; Hughes, T.J.R.; Zhang, Y. Isogeometric fluid-structure interaction: Theory, algorithms, and computations. Comput. Mech. 2008, 43, 3–37. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Calo, V.M.; Cottrell, J.A.; Evans, J.A.; Hughes, T.J.R.; Lipton, S.; Scott, M.A.; Sederberg, T.W. Isogeometric analysis using T-splines. Comput. Methods Appl. Mech. Eng. 2010, 199, 229–263. [Google Scholar] [CrossRef]
- Benson, D.J.; Bazilevs, Y.; Hsu, M.C.; Hughes, T.J.R. Isogeometric shell analysis: The Reissner-Mindlin shell. Comput. Methods Appl. Mech. Eng. 2010, 199, 276–289. [Google Scholar] [CrossRef]
- Schillinger, D.; Dedè, L.; Scott, M.A.; Evans, J.A.; Borden, M.J.; Rank, E.; Hughes, T.J.R. An isogeometric design-through-analysis methodology based on adaptive hierarchical refinement of NURBS, immersed boundary methods, and T-spline CAD surfaces. Comput. Methods Appl. Mech. Eng. 2012, 249–252, 116–150. [Google Scholar] [CrossRef]
- Zang, Y.; Yang, B.; Li, J.; Guan, H. An accurate TLS and UAV image point clouds registration method for deformation detection of Chaotic hillside areas. Remote Sens. 2019, 11, 647. [Google Scholar] [CrossRef]
- Raumonen, P.; Kaasalainen, M.; Markku, Å.; Kaasalainen, S.; Kaartinen, H.; Vastaranta, M.; Holopainen, M.; Disney, M.; Lewis, P. Fast automatic precision tree models from terrestrial laser scanner data. Remote Sens. 2013, 5, 491–520. [Google Scholar] [CrossRef]
- Marchi, N.; Pirotti, F.; Lingua, E. Airborne and Terrestrial Laser Scanning Data for the Assessment of Standing and Lying Deadwood: Current Situation and New Perspectives. Remote Sens. 2018, 10, 1356. [Google Scholar] [CrossRef]
- Calders, K.; Origo, N.; Burt, A.; Disney, M.; Nightingale, J.; Raumonen, P.; Åkerblom, M.; Malhi, Y.; Lewis, P. Realistic Forest Stand Reconstruction from Terrestrial LiDAR for Radiative Transfer Modelling. Remote Sens. 2018, 10, 933. [Google Scholar] [CrossRef]
- Murphy, M.; McGovern, E.; Pavia, S. Historic Building Information Modelling - Adding intelligence to laser and image based surveys of European classical architecture. ISPRS J. Photogramm. Remote Sens. 2013, 76, 89–102. [Google Scholar] [CrossRef]
- Riveiro, B.; Morer, P.; Arias, P.; De Arteaga, I. Terrestrial laser scanning and limit analysis of masonry arch bridges. Constr. Build. Mater. 2011, 25, 1726–1735. [Google Scholar] [CrossRef]
- Tapete, D.; Casagli, N.; Luzi, G.; Fanti, R.; Gigli, G.; Leva, D. Integrating radar and laser-based remote sensing techniques for monitoring structural deformation of archaeological monuments. J. Archaeol. Sci. 2013, 40, 176–189. [Google Scholar] [CrossRef]
- Lambers, K.; Eisenbeiss, H.; Sauerbier, M.; Kupferschmidt, D.; Gaisecker, T.; Sotoodeh, S.; Hanusch, T. Combining photogrammetry and laser scanning for the recording and modelling of the Late Intermediate Period site of Pinchango Alto, Palpa, Peru. J. Archaeol. Sci. 2007, 34, 1702–1712. [Google Scholar] [CrossRef]
- Tong, X.; Liu, X.; Chen, P.; Liu, S.; Luan, K.; Li, L.; Liu, S.; Liu, X.; Xie, H.; Jin, Y.; et al. Integration of UAV-based photogrammetry and terrestrial laser scanning for the three-dimensional mapping and monitoring of open-pit mine areas. Remote Sens. 2015, 7, 6635–6662. [Google Scholar] [CrossRef]
- Lingua, A.; Piatti, D.; Rinaudo, F. Remote monitoring of landslide using an integration of GB-INSAR and Lidar techniques. ISPRS Intern. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, XXXVII, 133–139. [Google Scholar]
- Bardi, F.; Frodella, W.; Ciampalini, A.; Bianchini, S.; Del Ventisette, C.; Gigli, G.; Fanti, R.; Moretti, S.; Basile, G.; Casagli, N. Integration between ground based and satellite SAR data in landslide mapping: The San Fratello case study. Geomorphology 2014, 223, 45–60. [Google Scholar] [CrossRef]
- Yin, Y.; Zheng, W.; Liu, Y.; Zhang, J.; Li, X. Integration of GPS with InSAR to monitoring of the Jiaju landslide in Sichuan, China. Landslides 2010, 7, 359–365. [Google Scholar] [CrossRef]
- Bassier, M.; Hardy, G.; Bejarano-Urrego, L.; Drougkas, A.; Verstrynge, E.; Van Balen, K.; Vergauwen, M. Semi-automated creation of accurate FE meshes of heritage masonry walls from point cloud data. In RILEM Bookseries; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Chen, G.; Xu, W.; Zhao, J.; Zhang, H. Energy-Saving performance of flap-Adjustment-based centrifugal fan. Energies 2018, 11, 162. [Google Scholar] [CrossRef]
- Park, H.S.; Lee, H.M.; Adeli, H.; Lee, I. A new approach for health monitoring of structures: Terrestrial laser scanning. Comput. Civ. Infrastruct. Eng. 2007, 22, 19–30. [Google Scholar] [CrossRef]
- Castellazzi, G.; D’Altri, A.M.; Bitelli, G.; Selvaggi, I.; Lambertini, A. From laser scanning to finite element analysis of complex buildings by using a semi-automatic procedure. Sensors 2015, 15, 18360–18380. [Google Scholar] [CrossRef] [PubMed]
- Castellazzi, G.; D’Altri, A.M.; de Miranda, S.; Ubertini, F. An innovative numerical modeling strategy for the structural analysis of historical monumental buildings. Eng. Struct. 2017, 132, 229–248. [Google Scholar] [CrossRef]
- Hinks, T.; Carr, H.; Truong-Hong, L.; Laefer, D.F. Point cloud data conversion into solid models via point-based voxelization. J. Surv. Eng. 2012, 139, 72–83. [Google Scholar] [CrossRef]
- D’Altri, A.M.; Milani, G.; de Miranda, S.; Castellazzi, G.; Sarhosis, V. Stability analysis of leaning historic masonry structures. Autom. Constr. 2018, 92, 199–213. [Google Scholar] [CrossRef]
- Bassoli, E.; Vincenzi, L.; D’Altri, A.M.; de Miranda, S.; Forghieri, M.; Castellazzi, G. Ambient vibration-based finite element model updating of an earthquake-damaged masonry tower. Struct. Control Heal. Monit. 2018, 25, e2150. [Google Scholar] [CrossRef]
- Hamri, O.; Léon, J.C.; Giannini, F.; Falcidieno, B. Software environment for CAD/CAE integration. Adv. Eng. Softw. 2010, 41, 1211–1222. [Google Scholar] [CrossRef]
- Liu, G.R.; Nguyen-Thoi, T.; Lam, K.Y. An edge-based smoothed finite element method (ES-FEM) for static, free and forced vibration analyses of solids. J. Sound Vib. 2009, 320, 1100–1130. [Google Scholar] [CrossRef]
- Harper, P.W.; Hallett, S.R. Cohesive zone length in numerical simulations of composite delamination. Eng. Fract. Mech. 2008, 75, 4774–4792. [Google Scholar] [CrossRef]
- Nguyen-Xuan, H.; Rabczuk, T.; Nguyen-Thanh, N.; Nguyen-Thoi, T.; Bordas, S. A node-based smoothed finite element method with stabilized discrete shear gap technique for analysis of Reissner-Mindlin plates. Comput. Mech. 2010, 46, 679–701. [Google Scholar] [CrossRef]
- Temizer, I.; Wriggers, P.; Hughes, T.J.R. Contact treatment in isogeometric analysis with NURBS. Comput. Methods Appl. Mech. Eng. 2011, 200, 1100–1112. [Google Scholar] [CrossRef]
- Kang, M.J.; Kim, C.H. Analysis of laser and resistance spot weldments on press-hardened steel. Mater. Sci. Forum 2011, 695, 202–205. [Google Scholar] [CrossRef]
- Tserpes, K.I.; Koumpias, A.S. A numerical methodology for optimizing the geometry of composite structural parts with regard to strength. Compos. Part B Eng. 2015, 68, 176–184. [Google Scholar] [CrossRef]
- Chellini, G.; Nardini, L.; Pucci, B.; Salvatore, W.; Tognaccini, R. Evaluation of seismic vulnerability of Santa Maria del Mar in Barcelona by an integrated approach based on terrestrial laser scanner and finite element modeling. Int. J. Archit. Herit. 2014, 8, 795–819. [Google Scholar] [CrossRef]
- Monserrat, O.; Crosetto, M. Deformation measurement using terrestrial laser scanning data and least squares 3D surface matching. ISPRS J. Photogramm. Remote Sens. 2008, 63, 142–154. [Google Scholar] [CrossRef]
- Kaasalainen, S.; Jaakkola, A.; Kaasalainen, M.; Krooks, A.; Kukko, A. Analysis of incidence angle and distance effects on terrestrial laser scanner intensity: Search for correction methods. Remote Sens. 2011, 3, 2207–2221. [Google Scholar] [CrossRef]
- Kaasalainen, S.; Krooks, A.; Kukko, A.; Kaartinen, H. Radiometric calibration of terrestrial laser scanners withexternal reference targets. Remote Sens. 2009, 1, 144–158. [Google Scholar] [CrossRef]
- Zhao, X.; Kargoll, B.; Omidalizarandi, M.; Xu, X.; Alkhatib, H. Model selection for parametric surfaces approximating 3d point clouds for deformation analysis. Remote Sens. 2018, 10, 634. [Google Scholar] [CrossRef]
- Abellán, A.; Jaboyedoff, M.; Oppikofer, T.; Vilaplana, J.M. Detection of millimetric deformation using a terrestrial laser scanner: Experiment and application to a rockfall event. Nat. Hazards Earth Syst. Sci. 2009, 9, 365–372. [Google Scholar] [CrossRef]
- Fang, T.P.; Piegl, L.A. Delaunay triangulation using a uniform grid. IEEE Comput. Graph. Appl. 1993, 13, 36–47. [Google Scholar] [CrossRef]
- De Boor, C. On calculating with B-splines. J. Approx. Theory 1972, 6, 50–62. [Google Scholar] [CrossRef]
- Xu, X.; Zhao, X.; Yang, H.; Neumann, I. TLS-based feature extraction and 3D modeling for arch structures. J. Sensors 2017, 2017, 9124254. [Google Scholar] [CrossRef]
- Pal, P. Fast freeform hybrid reconstruction with manual mesh segmentation. Int. J. Adv. Manuf. Technol. 2012, 63, 1205–1215. [Google Scholar] [CrossRef]
- Di Carlo, F.; Meda, A.; Rinaldi, Z. Numerical evaluation of the corrosion influence on the cyclic behaviour of RC columns. Eng. Struct. 2017, 153, 264–278. [Google Scholar] [CrossRef]
- Greif, V.; Vlcko, J. Monitoring of post-failure landslide deformation by the PS-InSAR technique at Lubietova in Central Slovakia. Environ. Earth. Sci. 2012, 66, 1585–1595. [Google Scholar] [CrossRef]
- Li, Q.S.; Zhang, Y.H.; Wu, J.R.; Lin, J.H. Seismic random vibration analysis of tall buildings. Eng. Struct. 2004, 26, 1767–1778. [Google Scholar] [CrossRef]

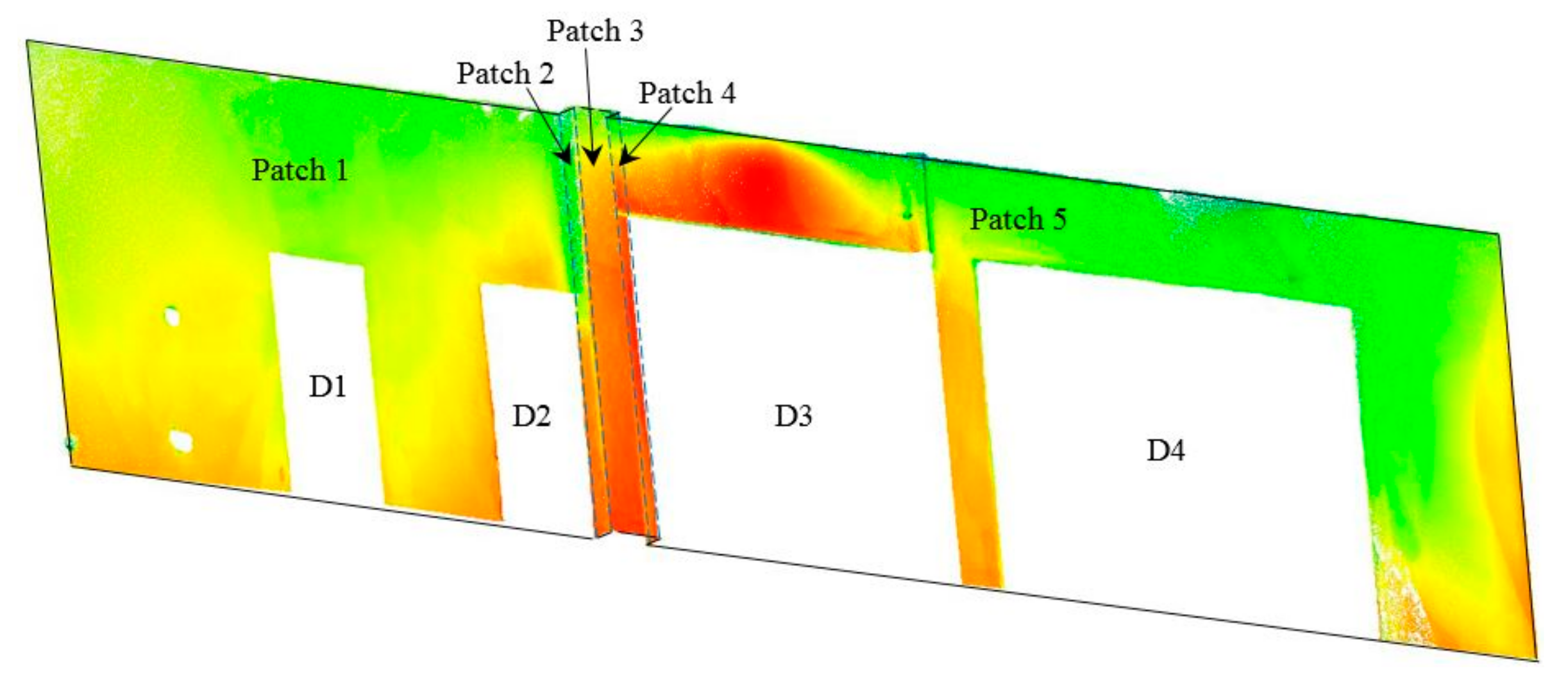

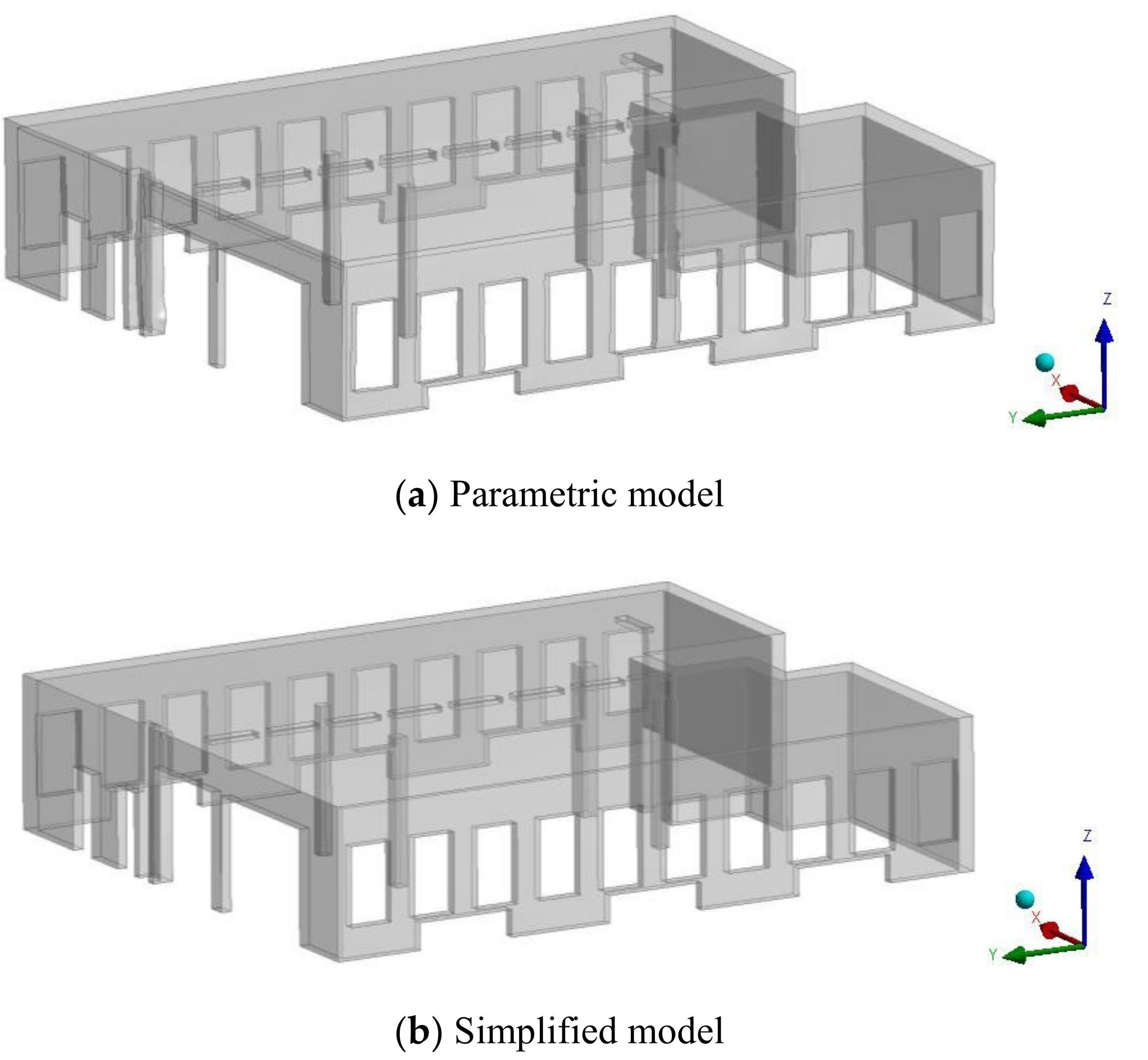
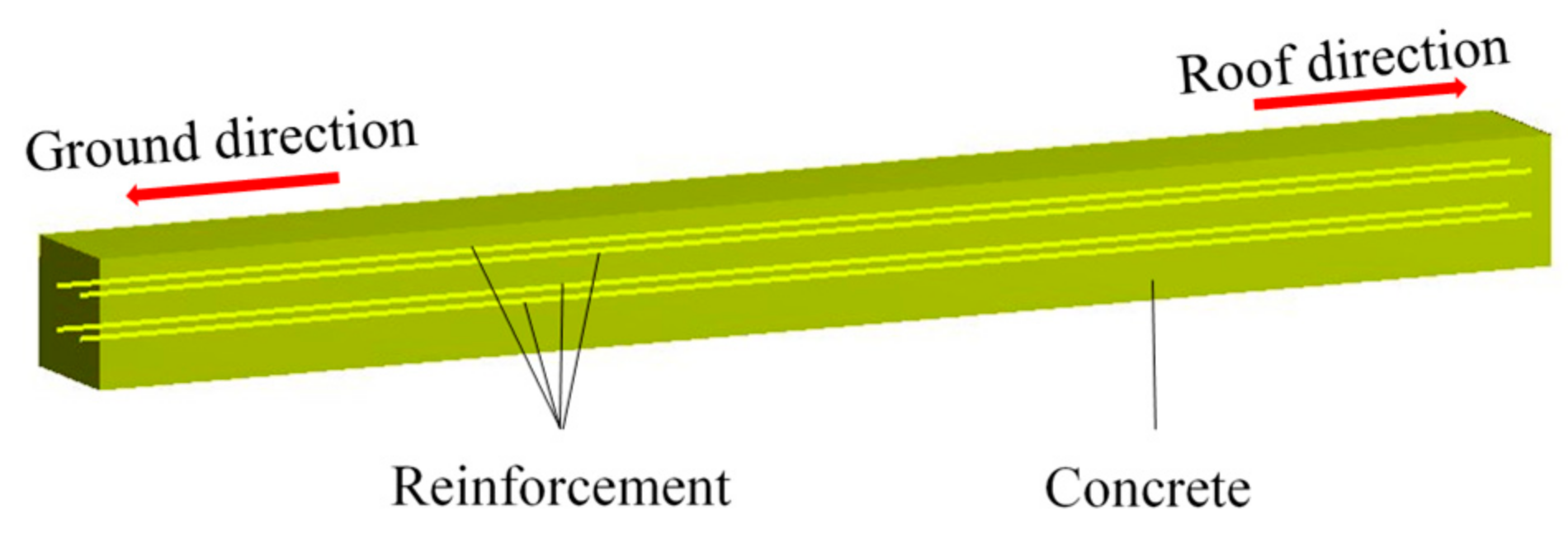
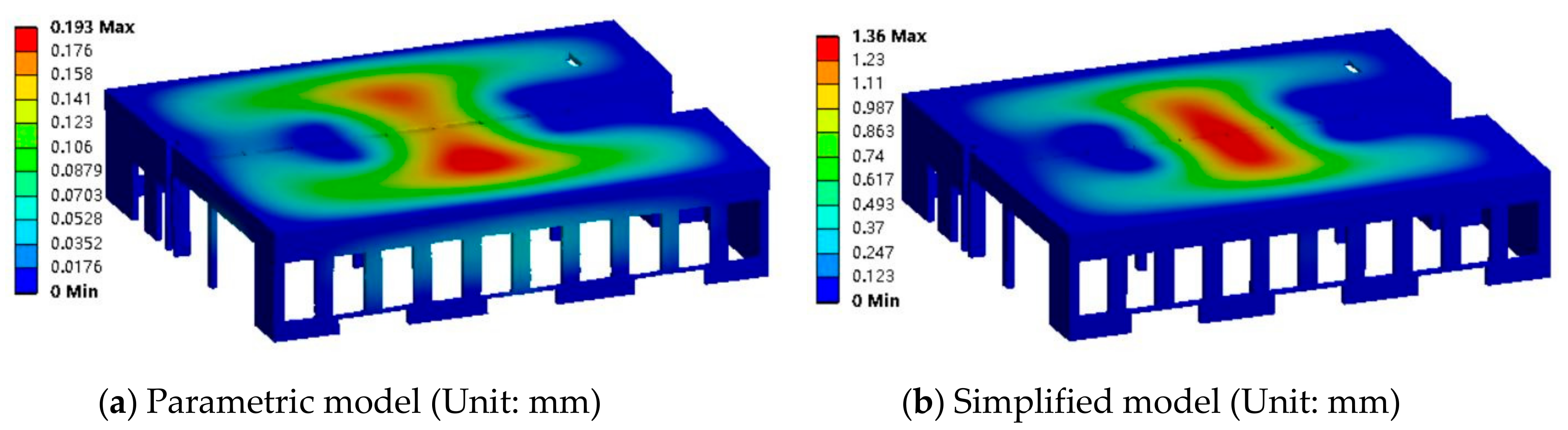
| Region | Side | n+1 | Region | Side | n+1 |
|---|---|---|---|---|---|
| D1 | Left | 20 | D3 | Upper | 30 |
| Upper | 9 | Right | 28 | ||
| Right | 20 | - | - | ||
| D2 | Left | 20 | D4 | Left | 28 |
| Upper | 9 | Upper | 36 | ||
| - | - | Right | 28 |
| (Concrete) | |
|---|---|
| Concrete density (kg/m3) | 2400 |
| Coefficient of the thermal expansion (1/°C) | 0.000014 |
| Reference temperature (°C) | 22 |
| Young’s modulus (GPa) | 30 |
| Poisson’s ratio | 0.18 |
| (Steel) | |
| Steel density (kg/m3) | 7850 |
| Young’s modulus (GPa) | 20 |
| Poisson’s ratio | 0.3 |
| Surfaces | Maximum Deviation (mm) | Standard Deviation (mm) |
|---|---|---|
| (Parametric model) | ||
| East outside | 37 | 1.07 |
| West outside | 34 | 0.65 |
| South outside | 26 | 1.15 |
| North outside | 27 | 1.09 |
| Roof outside | 26 | 0.94 |
| Pillar part | 51 | 0.82 |
| (Simplified model) | ||
| East outside | 55 | 15.13 |
| West outside | 51 | 10.58 |
| South outside | 46 | 21.38 |
| North outside | 48 | 22.56 |
| Roof outside | 43 | 14.59 |
| Pillar part | 53 | 18.23 |
| Parametric Model | Simplified Model | ||
|---|---|---|---|
| Mass volume (m3) | 76.5 | Mass volume (m3) | 67.8 |
| Local origin point X (m) | −21.2 | Local origin point X (m) | 0 |
| Local origin point Y (m) | −6.8 | Local origin point Y (m) | 10.1 |
| Local origin point Z (m) | 0.2 | Local origin point Z (m) | −9.9 |
| Centroid X (m) | −13.6 | Centroid X (m) | 7.2 |
| Centroid Y (m) | −15.4 | Centroid Y (m) | 1 |
| Centroid Z (m) | 2.96 | Centroid Z (m) | −7.4 |
| Relative centroid X (m) | 7.6 | Relative centroid X (m) | 7.2 |
| Relative centroid Y (m) | −8.6 | Relative centroid Y (m) | −9.1 |
| Relative centroid Z (m) | 2.76 | Relative centroid Z (m) | 2.5 |
| Moment of Inertia Ip1 (kgm2) | 5.99 | Moment of Inertia Ip1 (kgm2) | 5.7 |
| Moment of Inertia Ip2 (kgm2) | 4.3 | Moment of Inertia Ip2 (kgm2) | 4.01 |
| Moment of Inertia Ip3 (kgm2) | 9.9 | Moment of Inertia Ip3 (kgm2) | 9.3 |
| Mode | Max Deformation | Error 1 | Frequency | Error 2 |
|---|---|---|---|---|
| (Parametric model) | ||||
| 1 | 0.16 mm | - | 18.732 Hz | - |
| 2 | 0.16 mm | - | 21.174 Hz | - |
| 3 | 0.146 mm | - | 24.912 Hz | - |
| (Simplified model) | ||||
| 1 | 0.445 mm | 0.285 mm | 8.341 Hz | 10.391 Hz |
| 2 | 0.388 mm | 0.228 mm | 10.284 Hz | 10.89 Hz |
| 3 | 0.402 mm | 0.256 mm | 12.938 Hz | 11.974 Hz |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Neumann, I. Finite Element Analysis based on A Parametric Model by Approximating Point Clouds. Remote Sens. 2020, 12, 518. https://doi.org/10.3390/rs12030518
Xu W, Neumann I. Finite Element Analysis based on A Parametric Model by Approximating Point Clouds. Remote Sensing. 2020; 12(3):518. https://doi.org/10.3390/rs12030518
Chicago/Turabian StyleXu, Wei, and Ingo Neumann. 2020. "Finite Element Analysis based on A Parametric Model by Approximating Point Clouds" Remote Sensing 12, no. 3: 518. https://doi.org/10.3390/rs12030518
APA StyleXu, W., & Neumann, I. (2020). Finite Element Analysis based on A Parametric Model by Approximating Point Clouds. Remote Sensing, 12(3), 518. https://doi.org/10.3390/rs12030518