Quantifying Long-Term Land Surface and Root Zone Soil Moisture over Tibetan Plateau
Abstract
1. Introduction
2. Materials and Methods
2.1. Datasets
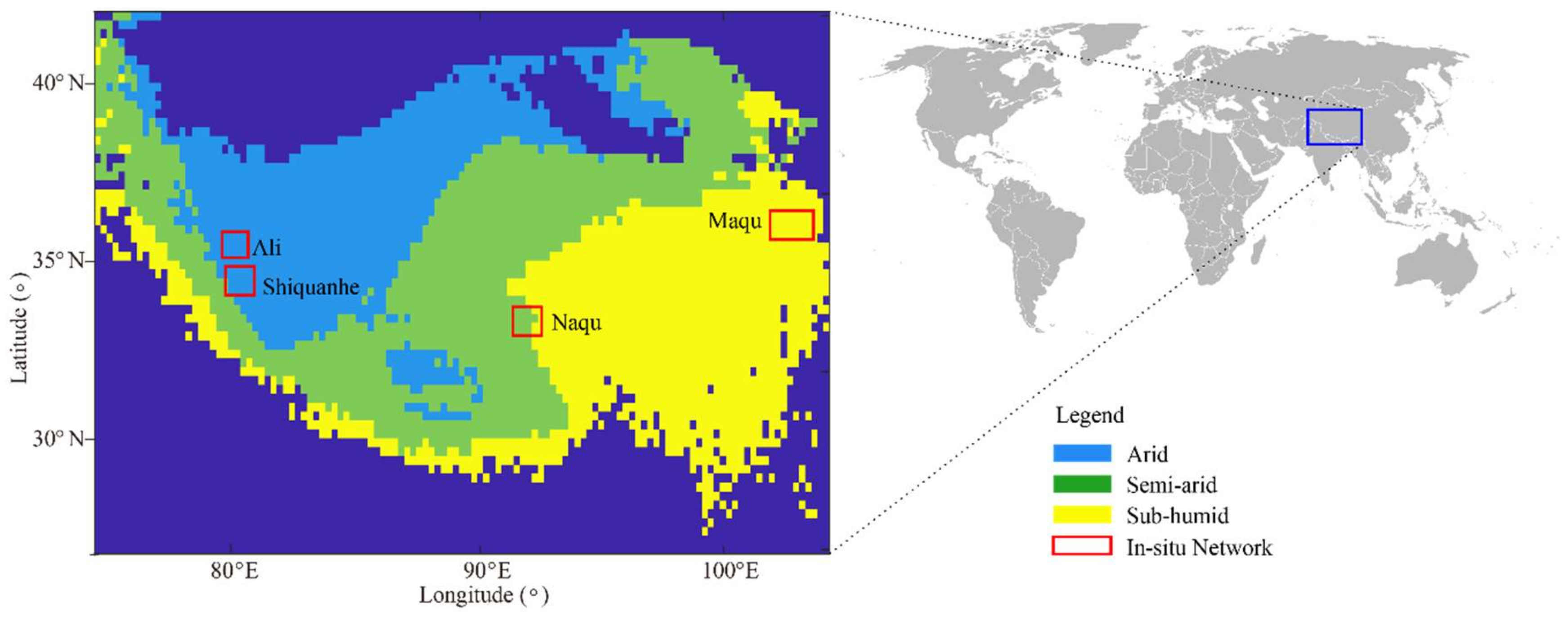
2.1.1. In-Situ Datasets
2.1.2. Satellite Datasets
2.1.3. Reanalysis Dataset
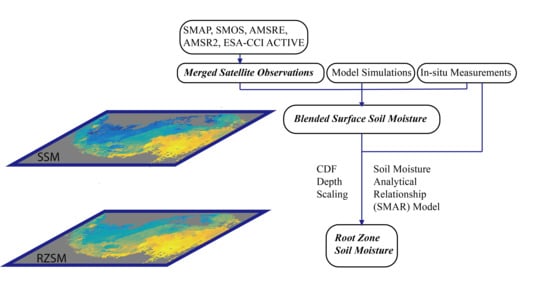
2.2. Methodology
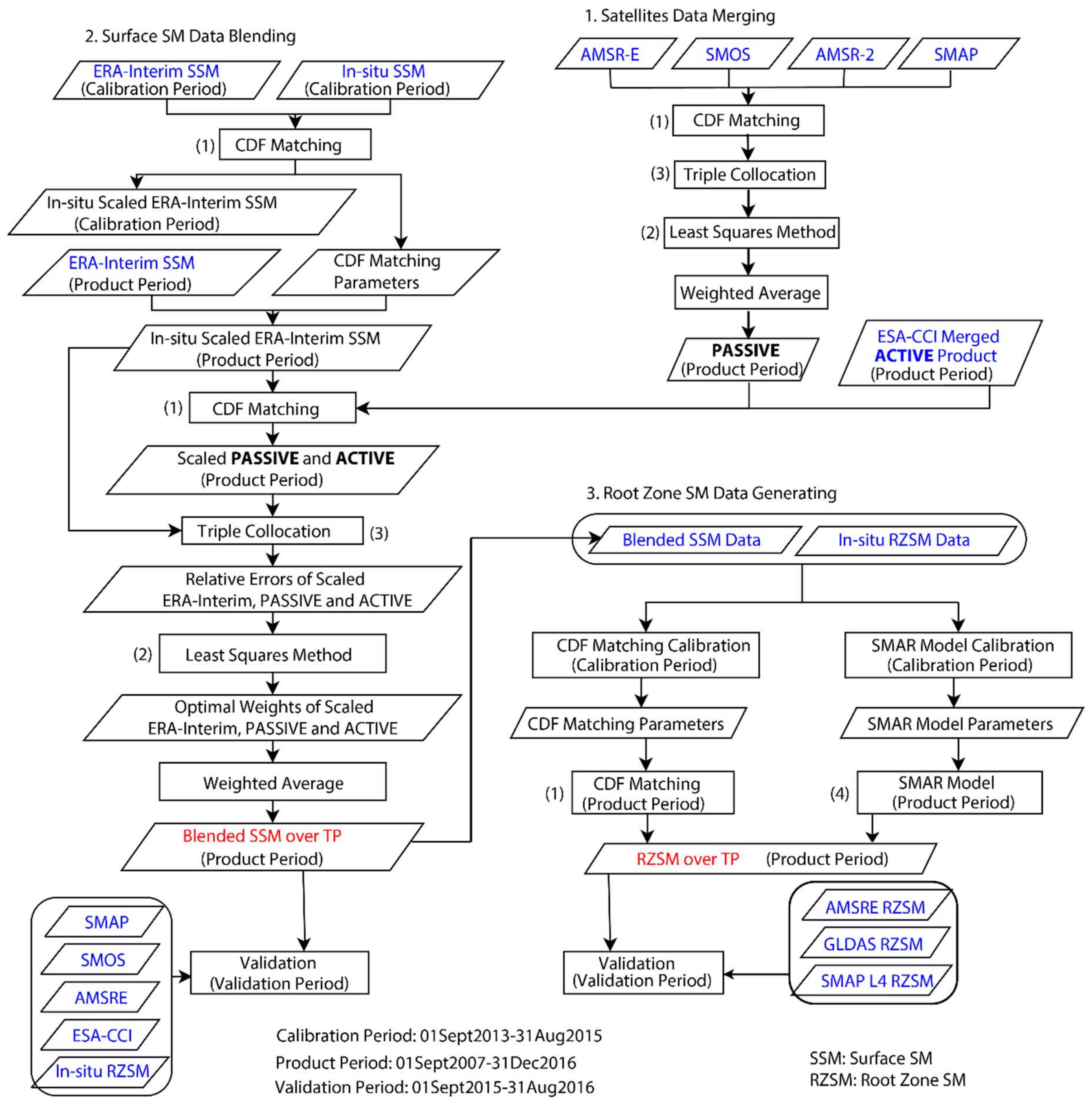
2.2.1. Methods Description
2.2.2. Processing Procedures
- Error Characterization using triple collocation
- The relative errors among the scaled PASSIVE, ACTIVE, and ERA-Interim products were calculated while using the triple collocation method, which used three collocated datasets to constrain the relative error variance determination without a manually decided reference.
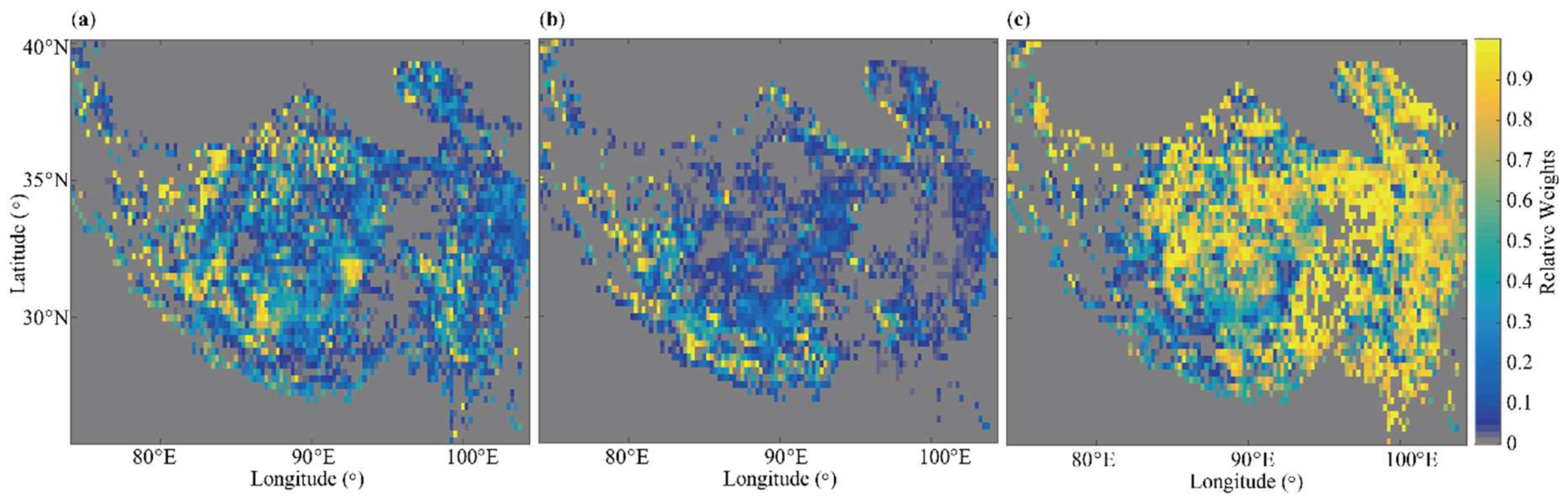
- Optimal weight calculation using the least-squares method and weighted averaging
- Similar with satellite data merging, a weighted average was used to merge scaled PASSIVE, ACTIVE, and ERA-Interim products over the Product Period and the optimal weights were obtained based on the relative errors while using least squares method.
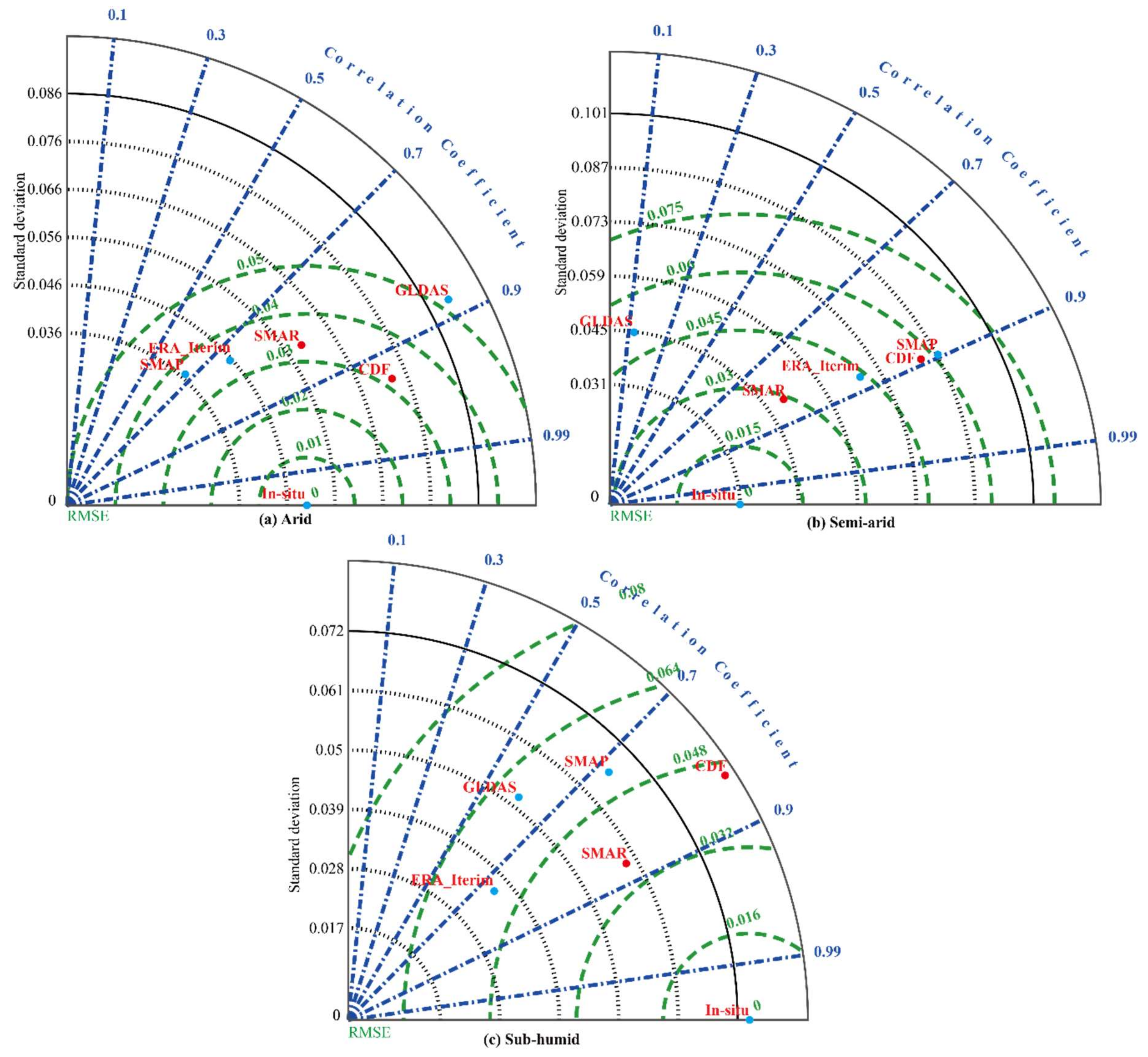
3. Results
3.1. SSM Product
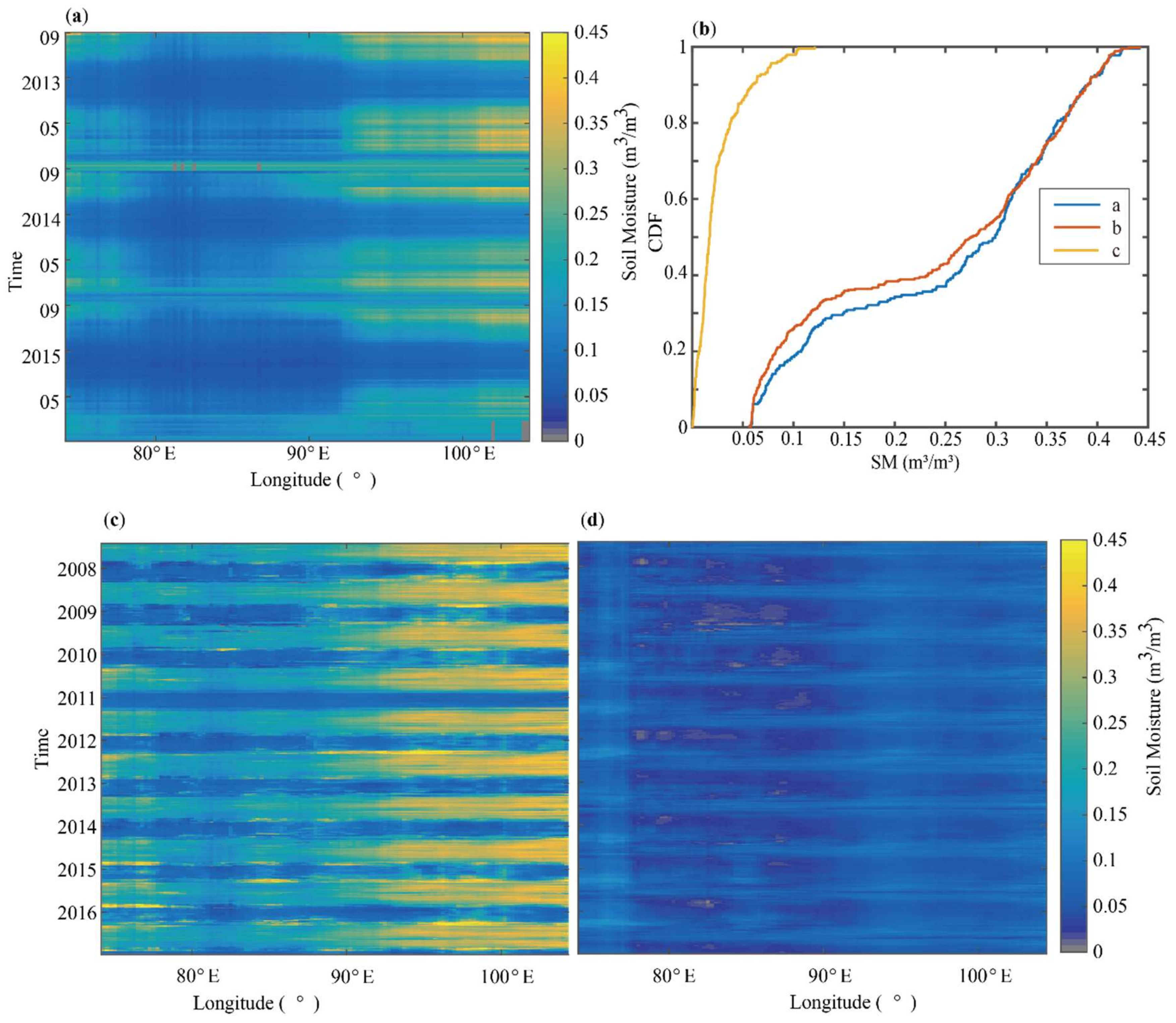
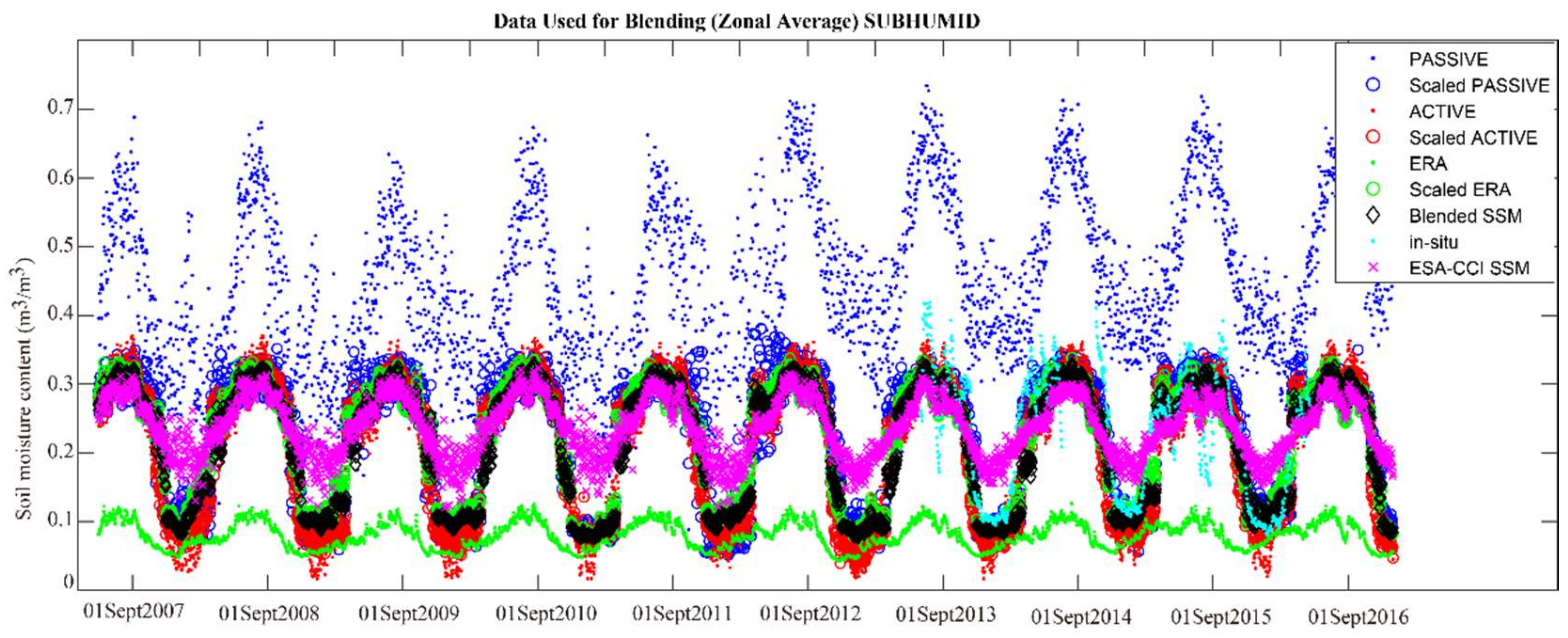
3.1.1. Merged Satellites SSM Product
3.1.2. Blended SSM Product
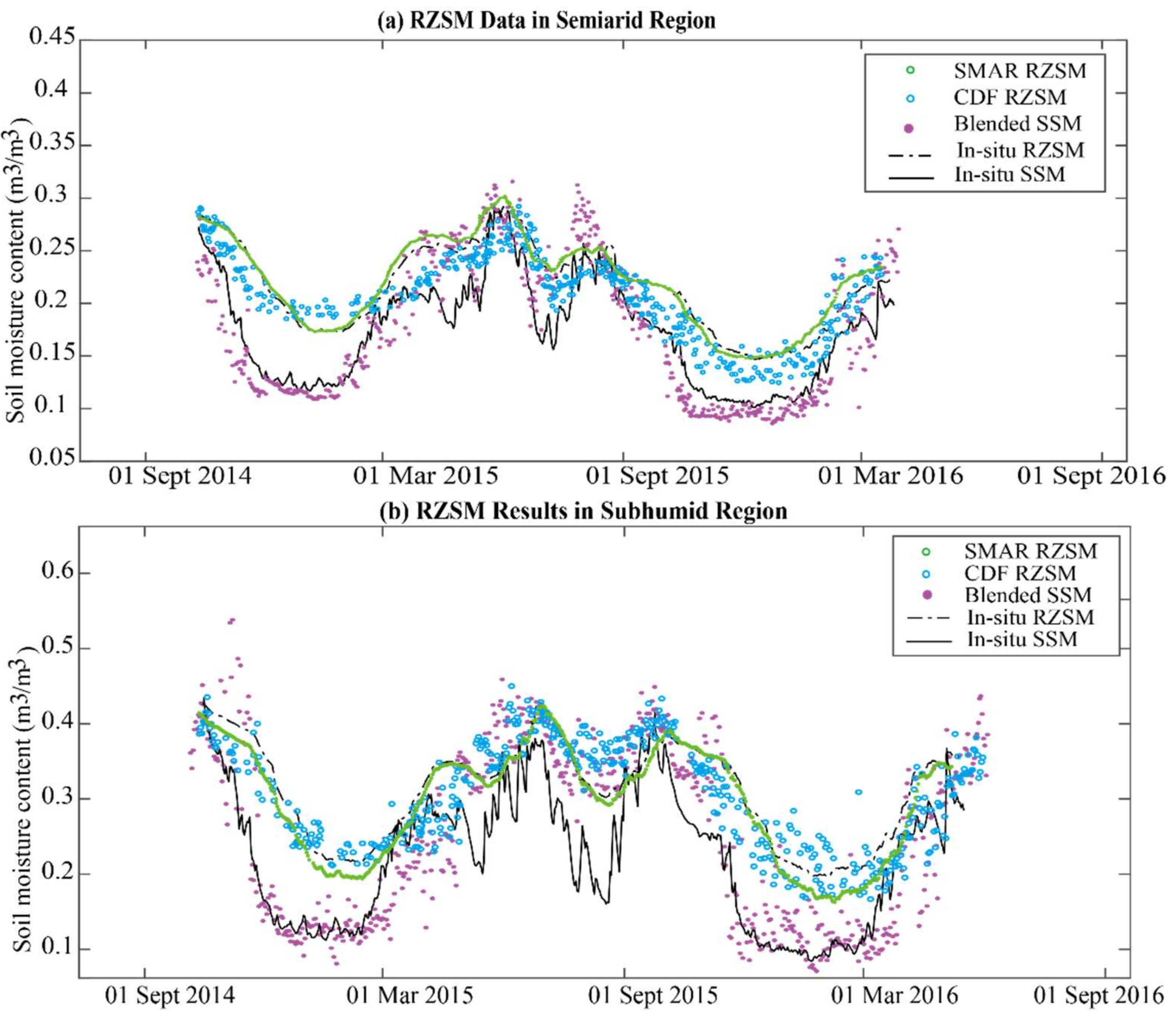
3.2. RZSM Product
4. Discussion
4.1. SSM Product
4.2. RZSM Product
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Su, Z.; Wen, J.; Dente, L.; van der Velde, R.; Wang, L.; Ma, Y.; Yang, K.; Hu, Z. The Tibetan Plateau observatory of plateau scale soil moisture and soil temperature (Tibet-Obs) for quantifying uncertainties in coarse resolution satellite and model products. Hydrol. Earth Syst. Sci. 2011, 15, 2303–2316. [Google Scholar] [CrossRef]
- Zeng, Y.; Su, Z.; Van Der Velde, R.; Wang, L.; Xu, K.; Wang, X.; Wen, J. Blending satellite observed, model simulated, and in situ measured soil moisture over Tibetan Plateau. Remote Sens. 2016, 8, 268. [Google Scholar] [CrossRef]
- Taylor, C.M.; de Jeu, R.A.M.; Guichard, F.; Harris, P.P.; Dorigo, W.A. Afternoon rain more likely over drier soils. Nature 2012, 489, 423–426. [Google Scholar] [CrossRef] [PubMed]
- Reynolds, C.A.; Jackson, T.J.; Rawls, W.J. Estimating soil water-holding capacities by linking the Food and Agriculture Organization soil map of the world with global pedon databases and continuous pedotransfer functions. Water Resour. Res. 2000, 36, 3653–3662. [Google Scholar] [CrossRef]
- Drusch, M.; Viterbo, P. Assimilation of Screen-Level Variables in ECMWF’s Integrated Forecast System: A Study on the Impact on the Forecast Quality and Analyzed Soil Moisture. Mon. Weather Rev. 2007, 135, 300–314. [Google Scholar] [CrossRef]
- Ma, Y.; Ma, W.; Zhong, L.; Hu, Z.; Li, M.; Zhu, Z.; Han, C.; Wang, B.; Liu, X. Monitoring and Modeling the Tibetan Plateau’s climate system and its impact on East Asia. Sci. Rep. 2017, 7, 1–6. [Google Scholar] [CrossRef]
- Bengtsson, L. The global atmospheric water cycle. Environ. Res. Lett. 2010, 5, 1–8. [Google Scholar] [CrossRef]
- Yang, K.; Wu, H.; Qin, J.; Lin, C.; Tang, W.; Chen, Y. Recent climate changes over the Tibetan Plateau and their impacts on energy and water cycle: A review. Glob. Planet. Chang. 2014, 112, 79–91. [Google Scholar] [CrossRef]
- Su, Z.; De Rosnay, P.; Wen, J.; Wang, L.; Zeng, Y. Evaluation of ECMWF’s soil moisture analyses using observations on the Tibetan Plateau. J. Geophys. Res. Atmos. 2013, 118, 5304–5318. [Google Scholar] [CrossRef]
- Zhao, H.; Zeng, Y.; Lv, S.; Su, Z. Analysis of Soil Hydraulic and Thermal Properties for Land Surface Modelling over the Tibetan Plateau. Earth Syst. Sci. Data 2018, 10, 1031–1061. [Google Scholar] [CrossRef]
- Ma, Y.; Kang, S.; Zhu, L.; Xu, B.; Tian, L.; Yao, T. Roof of the World: Tibetan observation and research platform. Bull. Am. Meteorol. Soc. 2008, 89, 1487–1492. [Google Scholar]
- Yang, K.; Qin, J. A Multiscale Soil Moisture and Freeze–Thaw Monitoring Network on the Third Pole. Bull. Am. Meteorol. Soc. 2013, 94, 1907–1916. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.-P.; Berger, M.; Martinuzzi, J.-M.; Font, J. Soil moisture retrieval from space: The Soil Moisture and Ocean Salinity (SMOS) mission. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1729–1735. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The Soil Moisture Active Passive (SMAP) Mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Owe, M.; de Jeu, R.; Holmes, T. Multisensor historical climatology of satellite-derived global land surface moisture. J. Geophys. Res. Earth Surf. 2008, 113, 1–17. [Google Scholar] [CrossRef]
- Wagner, W.; Hahn, S.; Kidd, R.; Melzer, T.; Bartalis, Z.; Hasenauer, S.; Figa-Saldaña, J.; De Rosnay, P.; Jann, A.; Schneider, S.; et al. The ASCAT soil moisture product: A review of its specifications, validation results, and emerging applications. Meteorol. Z. 2013, 22, 5–33. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Balsamo, G.; Albergel, C.; Beljaars, A.; Boussetta, S.; Brun, E.; Cloke, H.; Dee, D.; Dutra, E.; Munõz-Sabater, J.; Pappenberger, F.; et al. ERA-Interim/Land: A global land surface reanalysis data set. Hydrol. Earth Syst. Sci. 2015, 19, 389–407. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Wagner, W.; Dorigo, W.; De Jeu, R.; Fernandez, D.; Benveniste, J.; Haas, E.; Ertl, M. Fushion of ACTIVE and PASSIVE Microwave Observations to Create an Essential Climate Variable Data Record on Soil Moisture. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 7, 315–321. [Google Scholar]
- Dorigo, W.A.; Gruber, A.; De Jeu, R.A.M.; Wagner, W.; Stacke, T.; Loew, A.; Albergel, C.; Brocca, L.; Chung, D.; Parinussa, R.M.; et al. Evaluation of the ESA CCI soil moisture product using ground-based observations. Remote Sens. Environ. 2015, 162, 380–395. [Google Scholar] [CrossRef]
- Zhan, X.; Liu, J.; Zhao, L. Soil Moisture Operational Product System (SMOPS) Algorithm Theretical Basis Document. Available online: https://www.ospo.noaa.gov/Products/land/smops/algo.html (accessed on 17 August 2016).
- Naeimi, V.; Scipal, K.; Bartalis, Z.; Hasenauer, S.; Wagner, W. An improved soil moisture retrieval algorithm for ERS and METOP scatterometer observations. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1999–2013. [Google Scholar] [CrossRef]
- Manfreda, S.; Brocca, L.; Moramarco, T.; Melone, F.; Sheffield, J. A physically based approach for the estimation of root-zone soil moisture from surface measurements. Hydrol. Earth Syst. Sci. 2014, 18, 1199–1212. [Google Scholar] [CrossRef]
- Gao, X.; Wu, P.; Zhao, X.; Zhou, X.; Zhang, B.; Shi, Y.; Wang, J. Estimating soil moisture in gullies from adjacent upland measurements through different observation operators. J. Hydrol. 2013, 486, 420–429. [Google Scholar] [CrossRef]
- Han, E.; Merwade, V.; Heathman, G.C. Application of data assimilation with the Root Zone Water Quality Model for soil moisture profile estimation in the upper Cedar Creek, Indiana. Hydrol. Process. 2012, 26, 1707–1719. [Google Scholar] [CrossRef]
- Reichle, R.H.; Liu, Q.; Koster, R.D.; Crow, W.T.; De Lannoy, G.J.M.; Kimball, J.S.; Ardizzone, J.V.; Bosch, D.; Colliander, A.; Cosh, M.; et al. Version 4 of the SMAP Level-4 Soil Moisture Algorithm and Data Product. J. Adv. Model. Earth Syst. 2019, 11, 3106–3130. [Google Scholar] [CrossRef]
- Brocca, L.; Melone, F.; Moramarco, T.; Wagner, W.; Albergel, C. Scaling and Filtering Approaches for the Use of Satellite Soil Moisture Observations. In Remote Sensing of Energy Fluxes and Soil Moisture Content; CRC Press: Boca Raton, FL, USA, 2013; pp. 411–426. ISBN 978-1-4665-0578-0. [Google Scholar]
- Baldwin, D.; Manfreda, S.; Lin, H.; Smithwick, E.A.H. Estimating Root Zone Soil Moisture Across the Eastern United States with Passive Microwave Satellite Data and a Simple Hydrologic Model. Remote Sens. 2019, 11, 2013. [Google Scholar] [CrossRef]
- Gao, X.; Zhao, X.; Brocca, L.; Huo, G.; Lv, T.; Wu, P. Depth scaling of soil moisture content from surface to profile: Multistation testing of observation operators. Hydrol. Earth Syst. Sci. Discuss. 2017, 292, 1–25. [Google Scholar] [CrossRef]
- Reichle, R.H.; Koster, R.D. Bias reduction in short records of satellite soil moisture. Geophys. Res. Lett. 2004, 31, 2–5. [Google Scholar] [CrossRef]
- Drusch, M. Observation operators for the direct assimilation of TRMM microwave imager retrieved soil moisture. Geophys. Res. Lett. 2005, 32, L15403. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Parinussa, R.M.; Dorigo, W.A.; De Jeu, R.A.M.; Wagner, W.M.; Van Dijk, A.I.J.; McCabe, M.F.; Evans, J.P. Developing an improved soil moisture dataset by blending passive and active microwave satellite-based retrievals. Hydrol. Earth Syst. Sci. 2011, 15, 425–436. [Google Scholar] [CrossRef]
- Bankman, I.N. Handbook of Medical Image Processing and Analysis; Bronzino, J., Ed.; Elsevier/Academic Press: Amsterdam, The Netherlands, 2009; ISBN 9780123739049. [Google Scholar]
- Njoku, E.G.; Jackson, T.J.; Lakshmi, V.; Chan, T.K.; Nghiem, S.V. Soil moisture retrieval from AMSR-E. IEEE Trans. Geosci. Remote Sens. 2003, 41, 215–228. [Google Scholar] [CrossRef]
- Njoku, E.G.; Ashcroft, P.; Chan, T.K.; Li, L. Global survey and statistics of radio-frequency interference in AMSR-E land observations. IEEE Trans. Geosci. Remote Sens. 2005, 43, 938–946. [Google Scholar] [CrossRef]
- Njoku, E.G.; Chan, S.K. Vegetation and surface roughness effects on AMSR-E land observations. Remote Sens. Environ. 2006, 100, 190–199. [Google Scholar] [CrossRef]
- Imaoka, K.; Kachi, M.; Fujii, H.; Murakami, H.; Hori, M.; Ono, A.; Igarashi, T.; Nakagawa, K.; Oki, T.; Honda, Y.; et al. Global change observation mission (GCOM) for monitoring carbon, water cycles, and climate change. Proc. IEEE 2010, 98, 717–734. [Google Scholar] [CrossRef]
- Imaoka, K.; Maeda, T.; Kachi, M.; Kasahara, M.; Ito, N.; Nakagawa, K. Status of AMSR2 Instrument on GCOM-W1. Earth Observing Missions and Sensors: Development, Implementation, and Characterization II; Shimoda, H., Xiong, X., Cao, C., Gu, X., Kim, C., Kiran Kumar, A.S., Eds.; SPIE Asia-Pacific Remote Sensing: Kyoto, Japan, 2012; Volume 852815, pp. 1–6. [Google Scholar]
- Kerr, Y.H.; Waldteufel, P.; Richaume, P.; Wigneron, J.P.; Ferrazzoli, P.; Mahmoodi, A.; Al Bitar, A.; Cabot, F.; Gruhier, C.; Juglea, S.E.; et al. The SMOS Soil Moisture Retrieval Algorithm. Geosci. Remote Sens. 2012, 50, 1384–1403. [Google Scholar] [CrossRef]
- Wigneron, J.P.; Kerr, Y.H.; Waldteufel, P.; Saleh, K.; Escorihuela, M.J.; Richaume, P.; Ferrazzoli, P.; de Rosnay, P.; Gurney, R.; Calvet, J.C.; et al. L-band Microwave Emission of the Biosphere (L-MEB) Model: Description and calibration against experimental data sets over crop fields. Remote Sens. Environ. 2007, 107, 639–655. [Google Scholar] [CrossRef]
- Zeng, J.; Li, Z.; Chen, Q.; Bi, H.; Qiu, J.; Zou, P. Evaluation of remotely sensed and reanalysis soil moisture products over the Tibetan Plateau using in-situ observations. Remote Sens. Environ. 2015, 163, 91–110. [Google Scholar] [CrossRef]
- Colliander, A.; Jackson, T.J.; Bindlish, R.; Chan, S.; Das, N.; Kim, S.B.; Cosh, M.H.; Dunbar, R.S.; Dang, L.; Pashaian, L.; et al. Validation of SMAP surface soil moisture products with core validation sites. Remote Sens. Environ. 2017, 191, 215–231. [Google Scholar] [CrossRef]
- Gruber, A.; Dorigo, W.A.; Crow, W.; Wagner, W. Triple Collocation-Based Merging of Satellite Soil Moisture Retrievals. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6780–6792. [Google Scholar] [CrossRef]
- Gruber, A.; Scanlon, T.; Van Der Schalie, R.; Wagner, W.; Dorigo, W. Evolution of the ESA CCI Soil Moisture climate data records and their underlying merging methodology. Earth Syst. Sci. Data 2019, 11, 717–739. [Google Scholar] [CrossRef]
- Dorigo, W.; Wagner, W.; Albergel, C.; Albrecht, F.; Balsamo, G.; Brocca, L.; Chung, D.; Ertl, M.; Forkel, M.; Gruber, A.; et al. ESA CCI Soil Moisture for improved Earth system understanding: State-of-the art and future directions. Remote Sens. Environ. 2017, 203, 185–215. [Google Scholar] [CrossRef]
- Saxton, K.E.; Rawls, W.J. Soil Water Characteristic Estimates by Texture and Organic Matter for Hydrologic Solutions. Soil Sci. Soc. Am. J. 2006, 70, 1569. [Google Scholar] [CrossRef]
- Petropoulos, G.P. Remote Sensing of Energy Fluxes and Soil Moisture Content; CRC Press: Boca Raton, FL, USA, 2017; ISBN 9781138077577. [Google Scholar]
- Brocca, L.; Hasenauer, S.; Lacava, T.; Melone, F.; Moramarco, T.; Wagner, W.; Dorigo, W.; Matgen, P.; Martínez-Fernández, J.; Llorens, P.; et al. Soil moisture estimation through ASCAT and AMSR-E sensors: An intercomparison and validation study across Europe. Remote Sens. Environ. 2011, 115, 3390–3408. [Google Scholar] [CrossRef]
- Yilmaz, M.T.; Crow, W.T.; Anderson, M.C.; Hain, C. An objective methodology for merging satellite- and model-based soil moisture products. Water Resour. Res. 2012, 48, 1–15. [Google Scholar] [CrossRef]
- Stoffelen, A. Toward the true near-surface wind speed: Error modeling and calibration using triple collocation. J. Geophys. Res. Ocean. 1998, 103, 7755–7766. [Google Scholar] [CrossRef]
- Baldwin, D.; Manfreda, S.; Keller, K.; Smithwick, E.A.H. Predicting root zone soil moisture with soil properties and satellite near-surface moisture data across the conterminous United States. J. Hydrol. 2017, 546, 393–404. [Google Scholar] [CrossRef]
- Dorigo, W.A.; Scipal, K.; Parinussa, R.M.; Liu, Y.Y.; Wagner, W.; De Jeu, R.A.M.; Naeimi, V. Error characterisation of global active and passive microwave soil moisture datasets. Hydrol. Earth Syst. Sci. 2010, 14, 2605–2616. [Google Scholar] [CrossRef]
- Zwieback, S.; Scipal, K.; Dorigo, W.; Wagner, W. Structural and statistical properties of the collocation technique for error characterization. Nonlinear Process. Geophys. 2012, 19, 69–80. [Google Scholar] [CrossRef]
- Manfreda, S.; McCabe, M.F.; Fiorentino, M.; Rodríguez-Iturbe, I.; Wood, E.F. Scaling characteristics of spatial patterns of soil moisture from distributed modelling. Adv. Water Resour. 2007, 30, 2145–2150. [Google Scholar] [CrossRef]

| Data Sources | Datasets | Covered Time Range | Spatial and Temporal Resolution |
|---|---|---|---|
| In-situ Measurements | Tibet-Obs | 1-September-2013 to 31-August-2015 | Point; Every 15 min |
| 1-September-2015 to 31-August-2016 | |||
| Land Data Assimilation | ERA-Interim | 1-January-2007 to 31-December-2016 | 25 km; Daily |
| GLDAS | 1-September-2015 to 31-August-2016 | 25 km; Daily | |
| Satellites Observations (PASSIVE) | AMSRE | 1-January-2007 to 3-October-2011 | 25 km; Daily |
| SMOS | 1-June-2010 to 31-December-2016 | 30 km; Daily | |
| AMSR2 | 3-July-2012 to 31-December-2016 | 25 km; Daily | |
| SMAP | 31-March-2015 to 31-December-2016 | 36 km; Daily | |
| ESA-CCI PASSIVE | 1-January-2007 to 31-December-2016 | 25 km; Daily | |
| Satellites Observations (ACTIVE) | ESA-CCI ACTIVE | 1-January-2007 to 31-December-2016 | 25 km; Daily |
| Blended Product | ESA-CCI Soil Moisture | 1-January-2007 to 31-December-2016 | 25 km; Daily |
| Merging Period | Date | ||
|---|---|---|---|
| S1 | 1-June-2007 to 31-May-2010 | = 0.0023 | = 1 |
| S2 | 1-June-2010 to 3-October-2011 | = 0.0031 | = 0.613 |
| = 0.0068 | = 0.387 | ||
| S3 | 4-October-2011 to 2-July-2012 | = 0.0061 | = 1 |
| S4 | 3-July-2012 to 30-March-2015 | = 0.0085 | = 0.431 |
| = 0.0057 | = 0.569 | ||
| S5 | 31-March-2015 to 31-December-2016 | = 0.0074 | = 0.313 |
| = 0.0047 | = 0.395 | ||
| = 0.0065 | = 0.292 |
| Climate Zone | RMSE | ||||
|---|---|---|---|---|---|
| ARID: Ali | 0.0505 | 0.4967 | 0.3343 | 0.5020 | 0.0436 |
| SEMI-ARID: Naqu | 0.0230 | 0.1238 | 0.1987 | 0.1754 | 0.0274 |
| SUB-HUMID: Maqu | 0.0680 | 0.0602 | 0.0648 | 0.2582 | 0.0367 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuang, R.; Zeng, Y.; Manfreda, S.; Su, Z. Quantifying Long-Term Land Surface and Root Zone Soil Moisture over Tibetan Plateau. Remote Sens. 2020, 12, 509. https://doi.org/10.3390/rs12030509
Zhuang R, Zeng Y, Manfreda S, Su Z. Quantifying Long-Term Land Surface and Root Zone Soil Moisture over Tibetan Plateau. Remote Sensing. 2020; 12(3):509. https://doi.org/10.3390/rs12030509
Chicago/Turabian StyleZhuang, Ruodan, Yijian Zeng, Salvatore Manfreda, and Zhongbo Su. 2020. "Quantifying Long-Term Land Surface and Root Zone Soil Moisture over Tibetan Plateau" Remote Sensing 12, no. 3: 509. https://doi.org/10.3390/rs12030509
APA StyleZhuang, R., Zeng, Y., Manfreda, S., & Su, Z. (2020). Quantifying Long-Term Land Surface and Root Zone Soil Moisture over Tibetan Plateau. Remote Sensing, 12(3), 509. https://doi.org/10.3390/rs12030509