Arm Motion Classification Using Time-Series Analysis of the Spectrogram Frequency Envelopes
Abstract
1. Introduction
2. Materials and Methods
2.1. Radar MD Signature Representation
2.1.1. Time-Frequency Representations
2.1.2. Power Burst Curve (PBC)
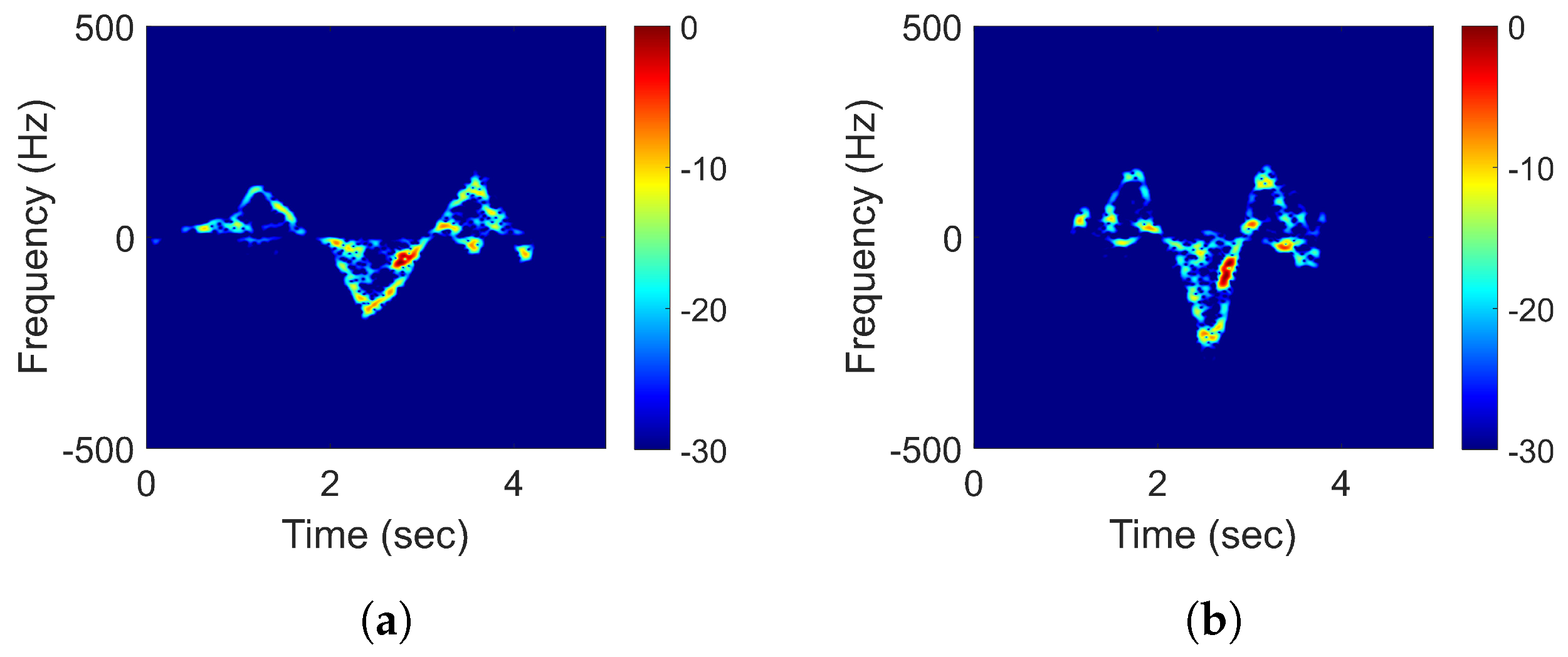
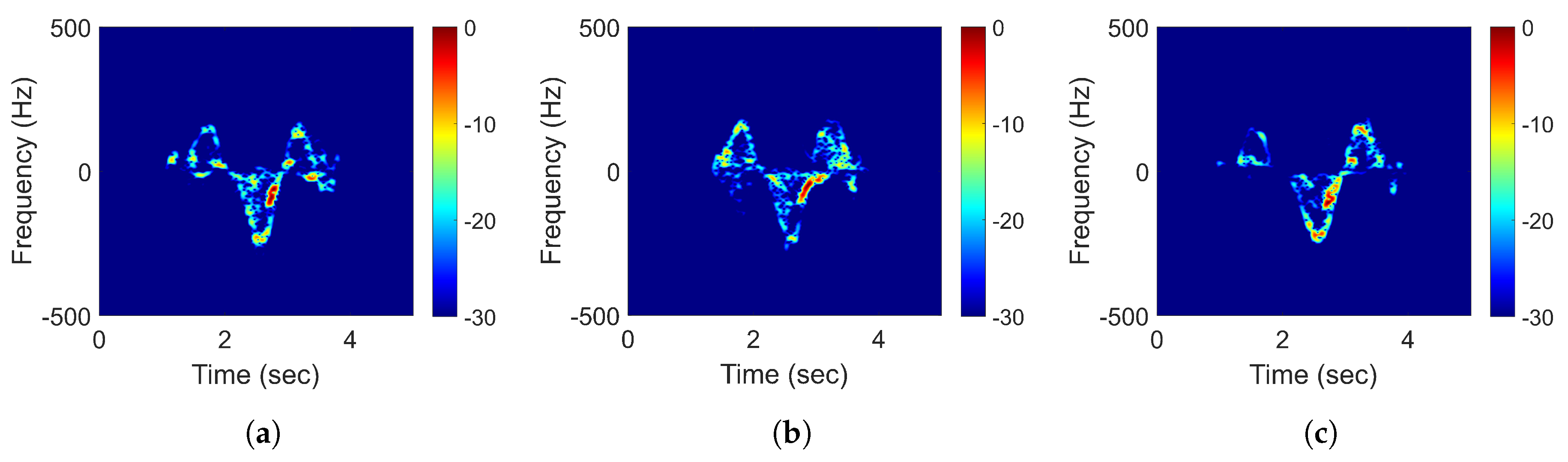
2.2. Extraction of the Maximum Instantaneous Doppler Frequency Signature
2.3. Time-Series Analysis Methods
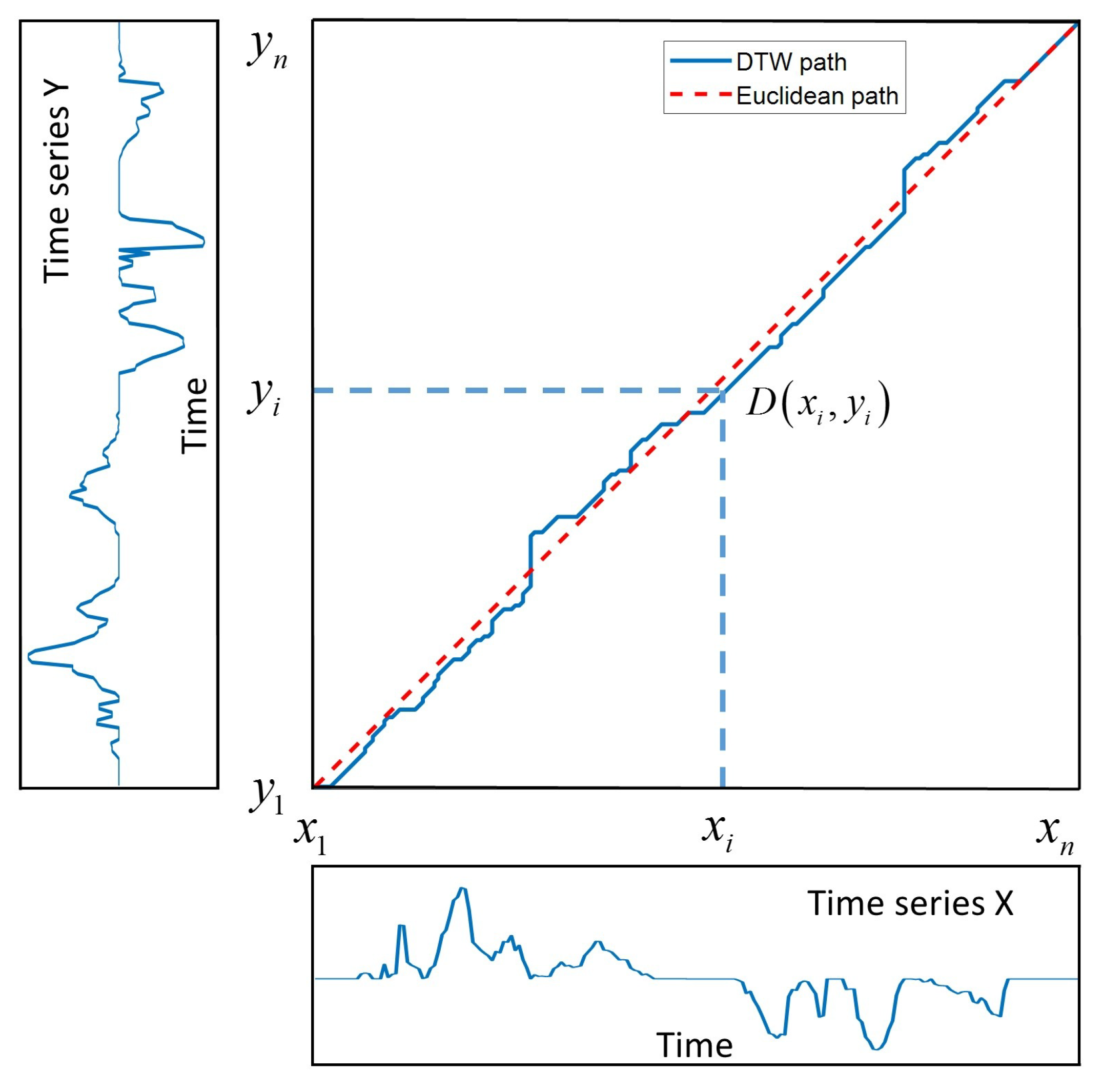
2.3.1. Dynamic Time Warping Method
- Boundary conditions: the beginning and end of the path are and , respectively;
- Monotonicity: given and where , we have ;
- Continuity: given and , we have .
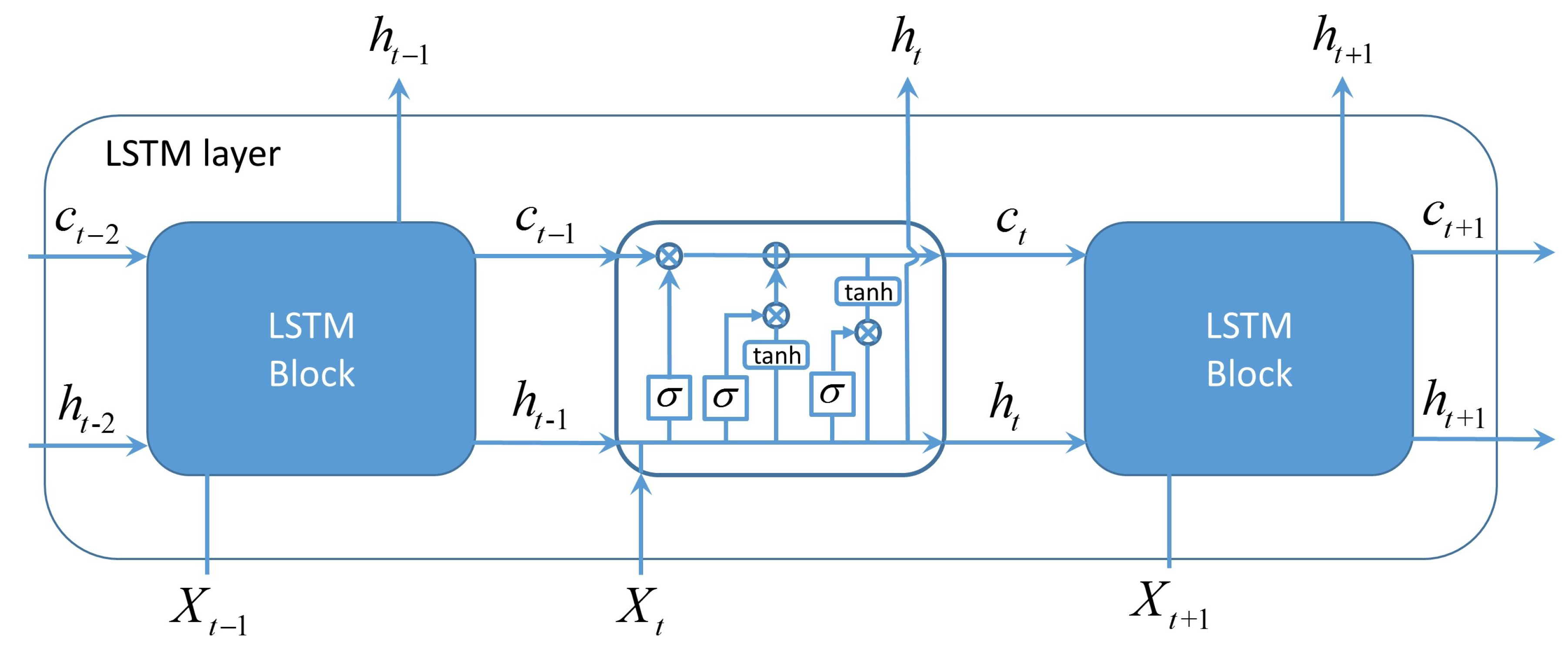
2.3.2. Long Short-Term Memory
3. Results
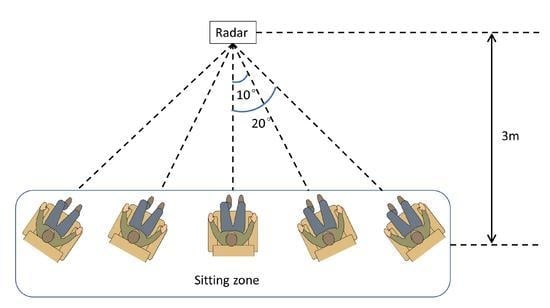
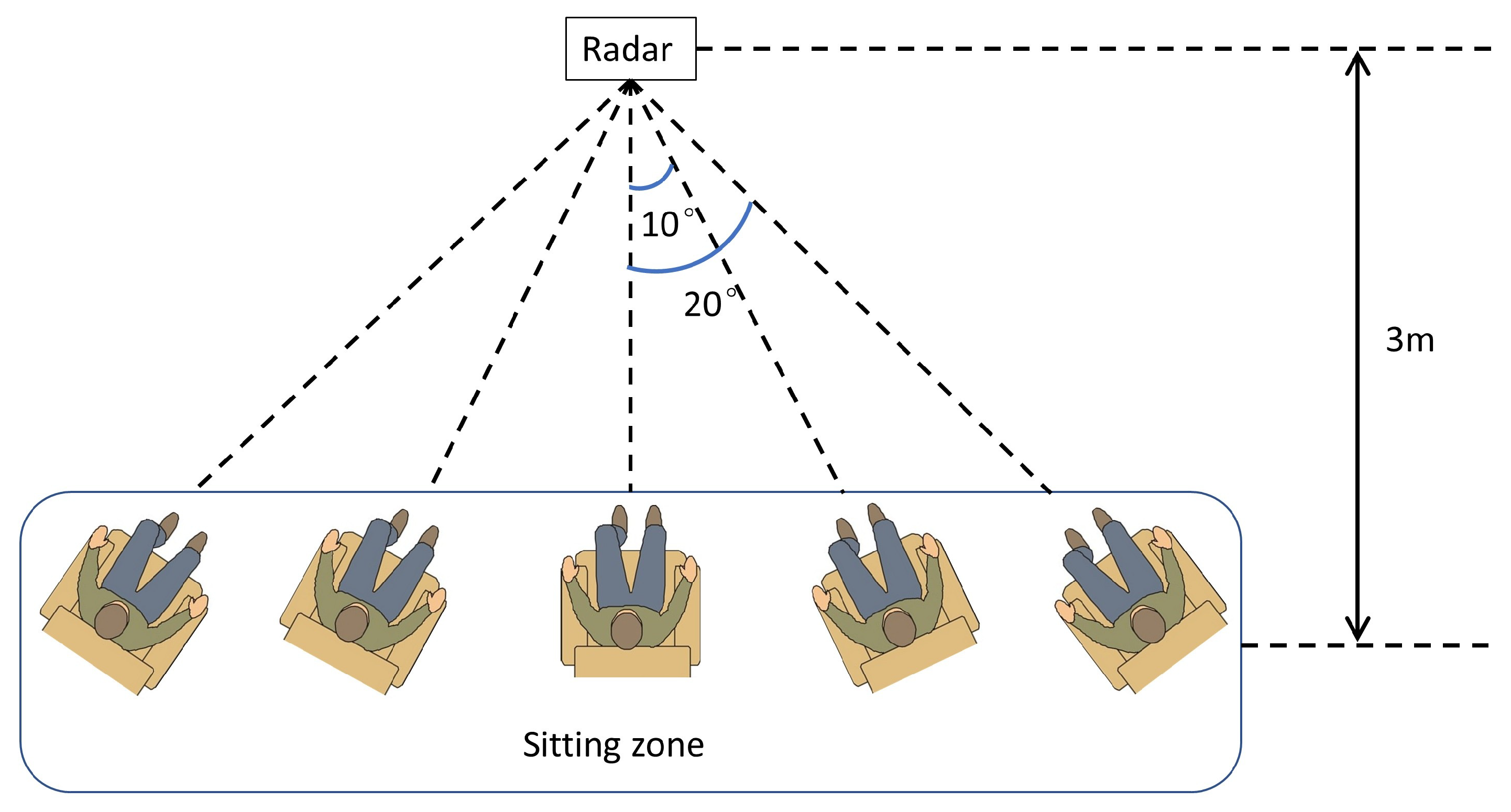
3.1. Arm Motion Experiments
3.2. Classification Results
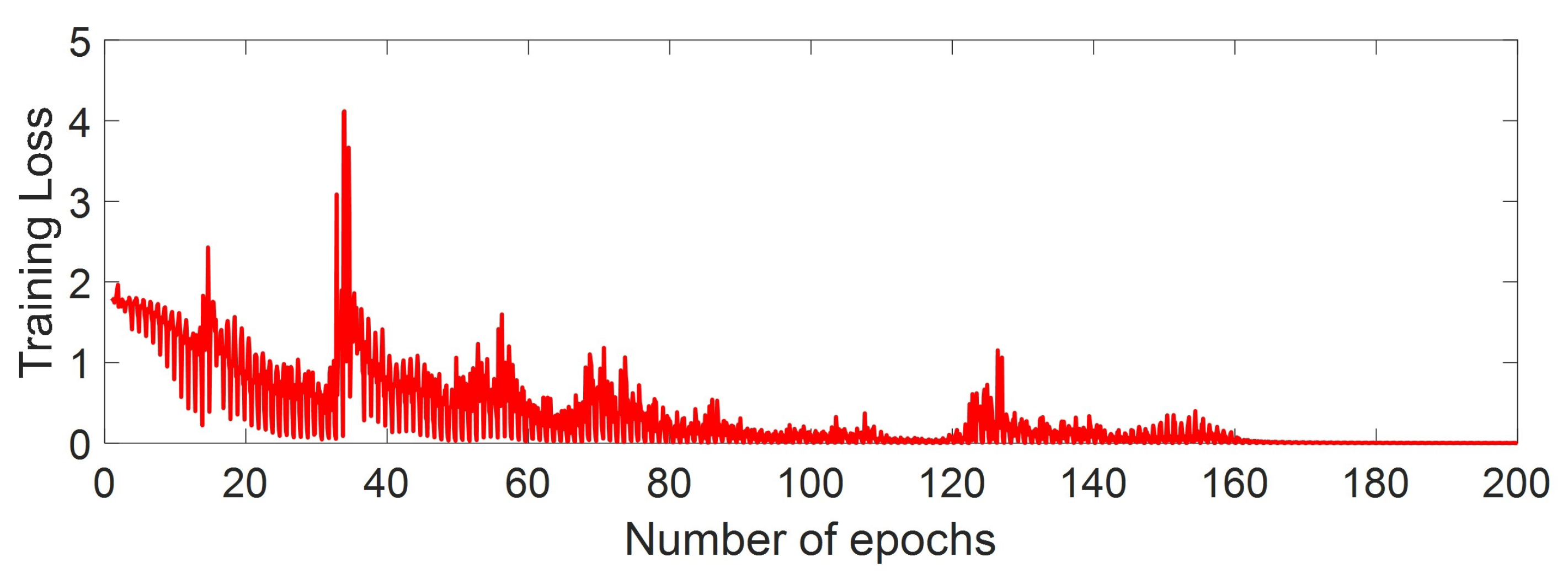
3.2.1. Classification Accuracy of the LSTM Method
3.2.2. Classification Accuracy of the DTW Method
4. Discussion
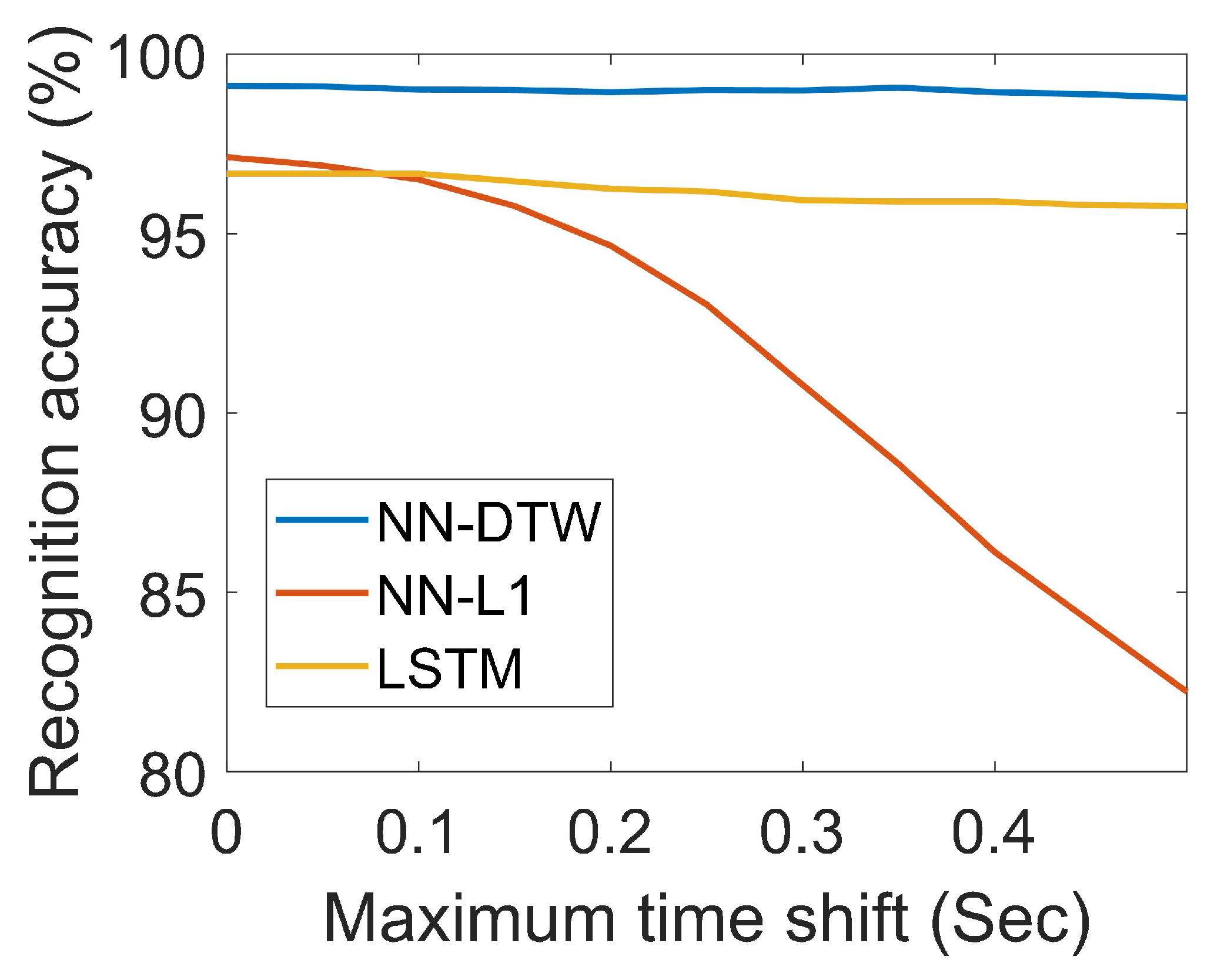
4.1. Analysis of the Classification Accuracy with Time Misalignment
4.2. Analysis of the Time Consumption
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| RF | Radio frequency |
| MD | Micro-Doppler |
| DTW | Dynamic time warping |
| LSTM | Long short-term memory |
| PCA | Prinicipal component analysis |
| TFR | Time-frequency representation |
| STFT | Short-time Fourier transform |
| PBC | Power burst curve |
| NN | Nearest neighbour |
| NN-DTW | NN classifier with the DTW distance) |
| STFT | Short-time Fourier transform |
| PBC | Power burst curve |
| CW | Continuous wave |
| ML | Machine learning |
| CNN | Convolutional neural network |
| RNN | Recurrent neural network |
References
- Li, G.; Zhang, R.; Ritchie, M.; Griffiths, H. Sparsity-driven micro-Doppler feature extraction for dynamic hand gesture recognition. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 655–665. [Google Scholar] [CrossRef]
- Kim, Y.; Toomajian, B. Hand gesture recognition using micro-Doppler signatures with convolutional neural network. IEEE Access 2016, 4, 7125–7130. [Google Scholar] [CrossRef]
- Wang, S.; Song, J.; Lien, J.; Poupyrev, I.; Hilliges, O. Interacting with Soli: Exploring fine-grained dynamic gesture recognition in the radio-frequency spectrum. In Proceedings of the 29th Annual Symposium on User Interface Software and Technology, Tokyo, Japan, 16–19 October 2016. [Google Scholar]
- Skaria, S.; Al-Hourani, A.; Lech, M.; Evans, R.J. Hand-gesture recognition using two-Antenna Doppler radar with deep convolutional neural networks. IEEE Sensors J. 2019, 19, 3041–3048. [Google Scholar] [CrossRef]
- Zhang, S.; Li, G.; Ritchie, M.; Fioranelli, F.; Griffiths, H. Dynamic hand gesture classification based on radar micro-Doppler signatures. In Proceedings of the 2016 CIE International Conference on Radar (RADAR), Guangzhou, China, 10–13 October 2016. [Google Scholar]
- Amin, M.G.; Zeng, Z.; Shan, T. Hand gesture recognition based on radar micro-Doppler signature envelopes. In Proceedings of the 2019 IEEE Radar Conference, Boston, MA, USA, 22–26 April 2019. [Google Scholar]
- Amin, M. Radar for Indoor Monitoring: Detection, Classification, and Assessment; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Amin, M.G.; Zhang, Y.D.; Ahmad, F.; Ho, K.D. Radar signal processing for elderly fall detection: The future for in-home monitoring. IEEE Signal Process. Mag. 2016, 33, 71–80. [Google Scholar] [CrossRef]
- Seifert, A.K.; Zoubir, A.M.; Amin, M.G. Detection of gait asymmetry using indoor Doppler radar. In Proceedings of the 2019 IEEE Radar Conference, Boston, MA, USA, 22–26 April 2019. [Google Scholar]
- Van Dorp, P.; Groen, F. Feature-based human motion parameter estimation with radar. IET Radar, Sonar Navig. 2008, 2, 135–145. [Google Scholar] [CrossRef]
- Kim, Y.; Ha, S.; Kwon, J. Human detection using Doppler radar based on physical characteristics of targets. IEEE Geosci. Remote. Sens. Lett. 2015, 12, 289–293. [Google Scholar]
- Mobasseri, B.G.; Amin, M.G. A time-frequency classifier for human gait recognition. Proc. SPIE 2009, 7306, 730628. [Google Scholar]
- Gurbuz, S.Z.; Clemente, C.; Balleri, A.; Soraghan, J.J. Micro-Doppler-based in-home aided and unaided walking recognition with multiple radar and sonar systems. IET Radar Sonar Navig. 2016, 11, 107–115. [Google Scholar] [CrossRef]
- Jokanović, B.; Amin, M. Fall detection using deep learning in range-Doppler radars. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 180–189. [Google Scholar] [CrossRef]
- Gurbuz, S.Z.; Amin, M.G. Radar-Based Human-Motion Recognition With Deep Learning: Promising applications for indoor monitoring. IEEE Signal Process. Mag. 2019, 36, 16–28. [Google Scholar] [CrossRef]
- Zeng, Z.; Amin, M.; Shan, T. Automatic arm motion recognition based on radar micro-Doppler signature envelopes. arXiv 2019, arXiv:1910.11176. [Google Scholar]
- Amin, M.; Zeng, Z.; Shan, T. Automatic arm motion recognition using radar for smart home technologies. In Proceedings of the 2019 International Radar Conference (RADAR), Toulon, France, 23–27 September 2019. [Google Scholar]
- Cui, Y.; Shi, J.; Wang, Z. Complex rotation quantum dynamic neural networks (CRQDNN) using Complex Quantum Neuron (CQN): Applications to time series prediction. Neural Netw. 2015, 71, 11–26. [Google Scholar] [CrossRef] [PubMed]
- Kadous, M.W. Temporal Classification: Extending the Classification Paradigm to Multivariate Time Series. Ph.D. Thesis, University of New South Wales Kensington, Sydney, Australia, 2002. [Google Scholar]
- Sharabiani, A.; Darabi, H.; Rezaei, A.; Harford, S.; Johnson, H.; Karim, F. Efficient classification of long time series by 3-d dynamic time warping. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 2688–2703. [Google Scholar] [CrossRef]
- Efrat, A.; Fan, Q.; Venkatasubramanian, S. Curve Matching, Time Warping, and Light Fields: New Algorithms for Computing Similarity between Curves. J. Math. Imaging Vis. 2007, 27, 203–216. [Google Scholar] [CrossRef]
- Buchin, K.; Buchin, M.; Wenk, C. Computing the Fréchet distance between simple polygons in polynomial time. In Proceedings of the Symposium on Computational Geometry, Sedona, AZ, USA, 5–7 June 2006. [Google Scholar]
- Alt, H.; Godau, M. Computing the Fréchet distance between two polygonal curves. Int. J. Comput. Geom. Appl. 1995, 5, 75–91. [Google Scholar] [CrossRef]
- Munich, M.E.; Perona, P. Continuous dynamic time warping for translation-invariant curve alignment with applications to signature verification. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–25 September 1999. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Welhenge, A.M.; Taparugssanagorn, A. Human activity classification using long short-term memory network. Signal Image Video Process. 2019, 13, 651–656. [Google Scholar] [CrossRef]
- Loukas, C.; Fioranelli, F.; Le Kernec, J.; Yang, S. Activity classification using raw range and I & Q radar data with long short term memory layers. In Proceedings of the 2018 IEEE 16th International Conference on Dependable, Autonomic and Secure Computing, 16th International Conference on Pervasive Intelligence and Computing, 4th International Conference on Big Data Intelligence and Computing and Cyber Science and Technology Congress (DASC/PiCom/DataCom/CyberSciTech), Athens, Greece, 12–15 August 2018. [Google Scholar]
- Klarenbeek, G.; Harmanny, R.; Cifola, L. Multi-target human gait classification using LSTM recurrent neural networks applied to micro-Doppler. In Proceedings of the 2017 European Radar Conference (EURAD), Nuremberg, Germany, 11–13 October 2017. [Google Scholar]
- Bemdt, D.J.; Clifford, J. Using dynamic time warping to find patterns in time series. In Proceedings of the AAAI-94 workshop on knowledge discovery in databases, Seattle, WA, USA, 31 July–1 August 1994. [Google Scholar]
- Salvador, S.; Chan, P. Toward accurate dynamic time warping in linear time and space. Intell. Data Anal. 2007, 11, 561–580. [Google Scholar] [CrossRef]
- Senin, P. Dynamic Time Warping Algorithm Review; Technical Report; Information and Computer Science Department, University of Hawaii at Manoa Honolulu: Honolulu, HI, USA, 2009. [Google Scholar]
- Gudmundsson, S.; Runarsson, T.P.; Sigurdsson, S. Support vector machines and dynamic time warping for time series. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–8 June 2008. [Google Scholar]
- Niennattrakul, V.; Ratanamahatana, C.A. On clustering multimedia time series data using k-means and dynamic time warping. In Proceedings of the 2007 International Conference on Multimedia and Ubiquitous Engineering (MUE’07), Seoul, Korea, 26–28 April 2007. [Google Scholar]
- Yu, F.; Dong, K.; Chen, F.; Jiang, Y.; Zeng, W. Clustering time series with granular dynamic time warping method. In Proceedings of the 2007 IEEE International Conference on Granular Computing (GRC 2007), Fremont, CA, USA, 2–4 November 2007. [Google Scholar]
- Czech, D.; Mishra, A.; Inggs, M. A CNN and LSTM-based approach to classifying transient radio frequency interference. Astron. Comput. 2018, 25, 52–57. [Google Scholar] [CrossRef]
- Zhao, Z.; Chen, W.; Wu, X.; Chen, P.C.; Liu, J. LSTM network: A deep learning approach for short-term traffic forecast. IET Intell. Transp. Syst. 2017, 11, 68–75. [Google Scholar] [CrossRef]
- Munir, K.; Elahi, H.; Ayub, A.; Frezza, F.; Rizzi, A. Cancer diagnosis using deep learning: A bibliographic review. Cancers 2019, 11, 1235. [Google Scholar] [CrossRef] [PubMed]
- Siddhartha; Lee, Y.H.; Moss, D.J.; Faraone, J.; Blackmore, P.; Salmond, D.; Boland, D.; Leong, P.H. Long short-term memory for radio frequency spectral prediction and its real-time FPGA implementation. In Proceedings of the MILCOM 2018-2018 IEEE Military Communications Conference (MILCOM), Los Angeles, CA, USA, 29–31 October 2008. [Google Scholar]
- Tan, B.; Woodbridge, K.; Chetty, K. A real-time high resolution passive WiFi Doppler-radar and its applications. In Proceedings of the 2014 International Radar Conference, Lille, France, 13–17 October 2014. [Google Scholar]
- Seifert, A.K.; Schäfer, L.; Amin, M.G.; Zoubir, A.M. Subspace Classification of Human Gait Using Radar Micro-Doppler Signatures. In Proceedings of the 26th European Signal Processing Conference (EUSIPCO), Rome, Italy, 3–7 September 2018. [Google Scholar]
- Amin, M.G. Time-Frequency Spectrum Analysis and Estimation for Nonstationary Random-Processes; Longman Cheshire (AUS): Melbourne, Australia, 1992. [Google Scholar]
- Cirillo, L.; Zoubir, A.; Amin, M. Parameter estimation for locally linear FM signals using a time-frequency Hough transform. IEEE Trans. Signal Process. 2008, 56, 4162–4175. [Google Scholar] [CrossRef]
- Setlur, P.; Amin, M.; Ahmad, F. Analysis of micro-Doppler signals using linear FM basis decomposition. In Radar Sensor Technology X; SPIE: Bellingham, WA, USA, 2006; p. 62100M. [Google Scholar]
- Erol, B.; Amin, M.G.; Boashash, B. Range-Doppler radar sensor fusion for fall detection. In Proceedings of the Radar Conference (RadarConf), Seattle, WA, USA, 9–12 May 2017. [Google Scholar]
- Amin, M.G.; Ravisankar, A.; Guendel, R.G. RF sensing for continuous monitoring of human activities for home consumer applications. In Proceedings of the SPIE Defense + Commercial Sensing, Baltimore, MD, USA, 13 May 2019. [Google Scholar]
- Ding, H.; Trajcevski, G.; Scheuermann, P.; Wang, X.; Keogh, E. Querying and mining of time series data: experimental comparison of representations and distance measures. Proc. Vldb Endow. 2008, 1, 1542–1552. [Google Scholar] [CrossRef]
- Graves, A.; Liwicki, M.; Fernández, S.; Bertolami, R.; Bunke, H.; Schmidhuber, J. A novel connectionist system for unconstrained handwriting recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 31, 855–868. [Google Scholar] [CrossRef] [PubMed]
- Graves, A.; Mohamed, A.r.; Hinton, G. Speech recognition with deep recurrent neural networks. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013. [Google Scholar]
- Müller, M. Dynamic Time Warping. In Information Retrieval for Music and Motion; Springer: Berlin/Heidelberg, Germany, 2007; pp. 69–84. [Google Scholar] [CrossRef]
- Sak, H.; Senior, A.; Beaufays, F. Long short-term memory recurrent neural network architectures for large scale acoustic modeling. In Proceedings of the Fifteenth Annual Conference of the International Speech Communication Association, Singapore, 14–18 September 2014. [Google Scholar]
- Deng, Z.; Zhu, X.; Cheng, D.; Zong, M.; Zhang, S. Efficient kNN classification algorithm for big data. Neurocomputing 2016, 195, 143–148. [Google Scholar] [CrossRef]
- Makkar, T.; Kumar, Y.; Dubey, A.K.; Rocha, Á.; Goyal, A. Analogizing time complexity of KNN and CNN in recognizing handwritten digits. In Proceedings of the 2017 Fourth International Conference on Image Information Processing (ICIIP), Shimla, India, 21–23 December 2017. [Google Scholar]
- Garcia, V.; Debreuve, E.; Nielsen, F.; Barlaud, M. K-nearest neighbor search: Fast GPU-based implementations and application to high-dimensional feature matching. In Proceedings of the 2010 IEEE International Conference on Image Processing, Hong Kong, China, 26–29 September 2010. [Google Scholar]
- Sakurai, Y.; Yoshikawa, M.; Faloutsos, C. FTW: fast similarity search under the time warping distance. In Proceedings of the twenty-fourth ACM SIGMOD-SIGACT-SIGART symposium on Principles of database systems, New York, NY, USA, 13–15 June 2005. [Google Scholar]
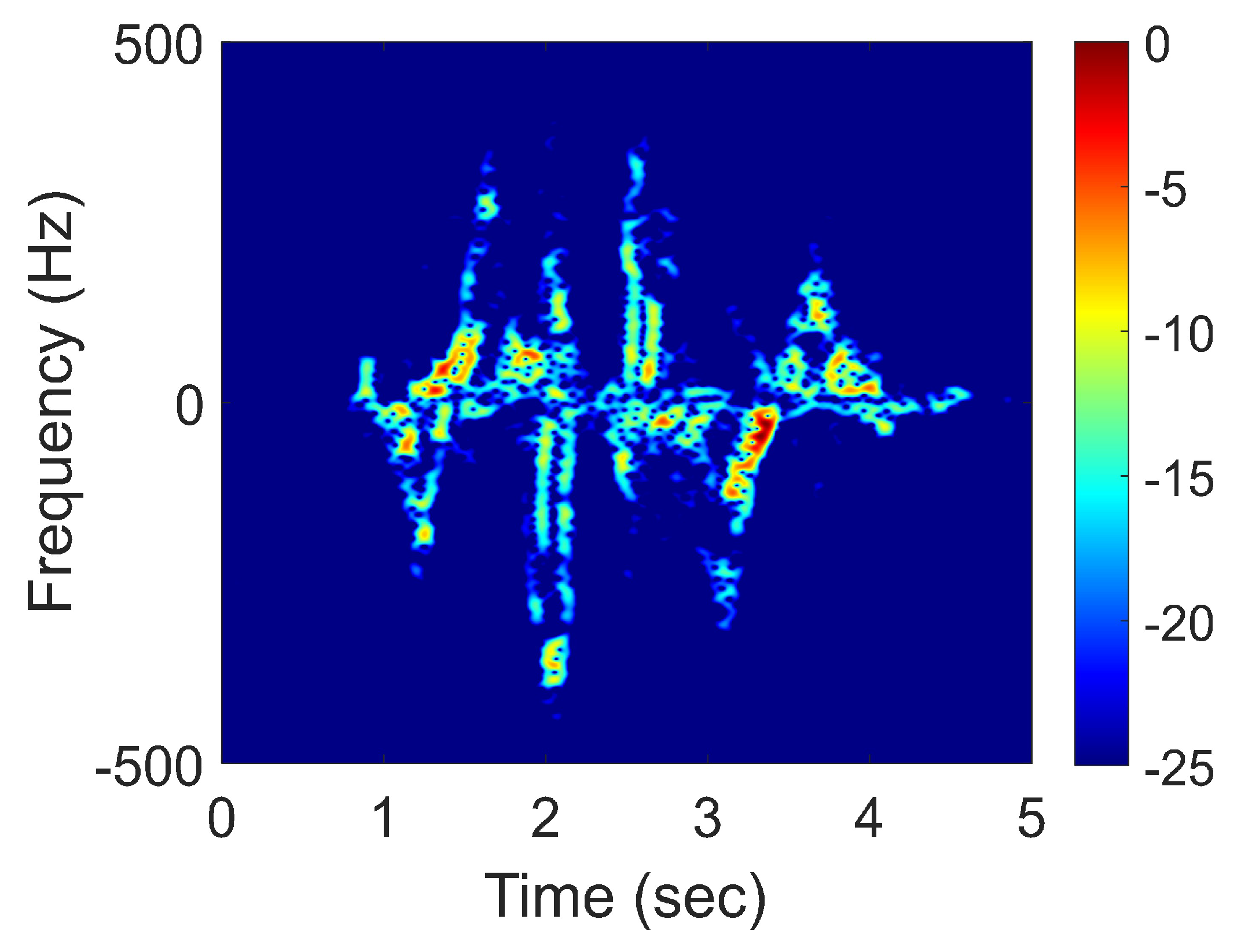
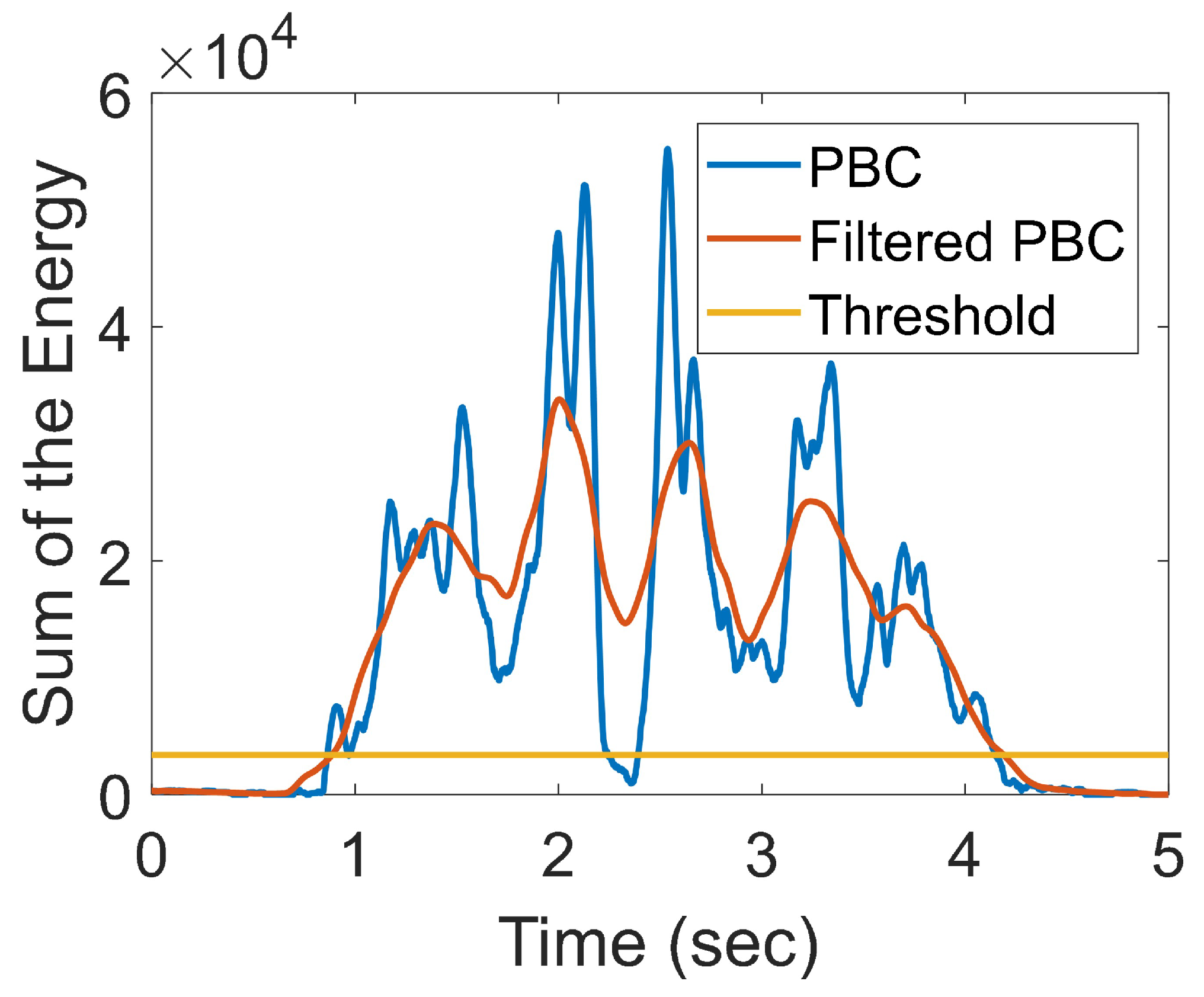

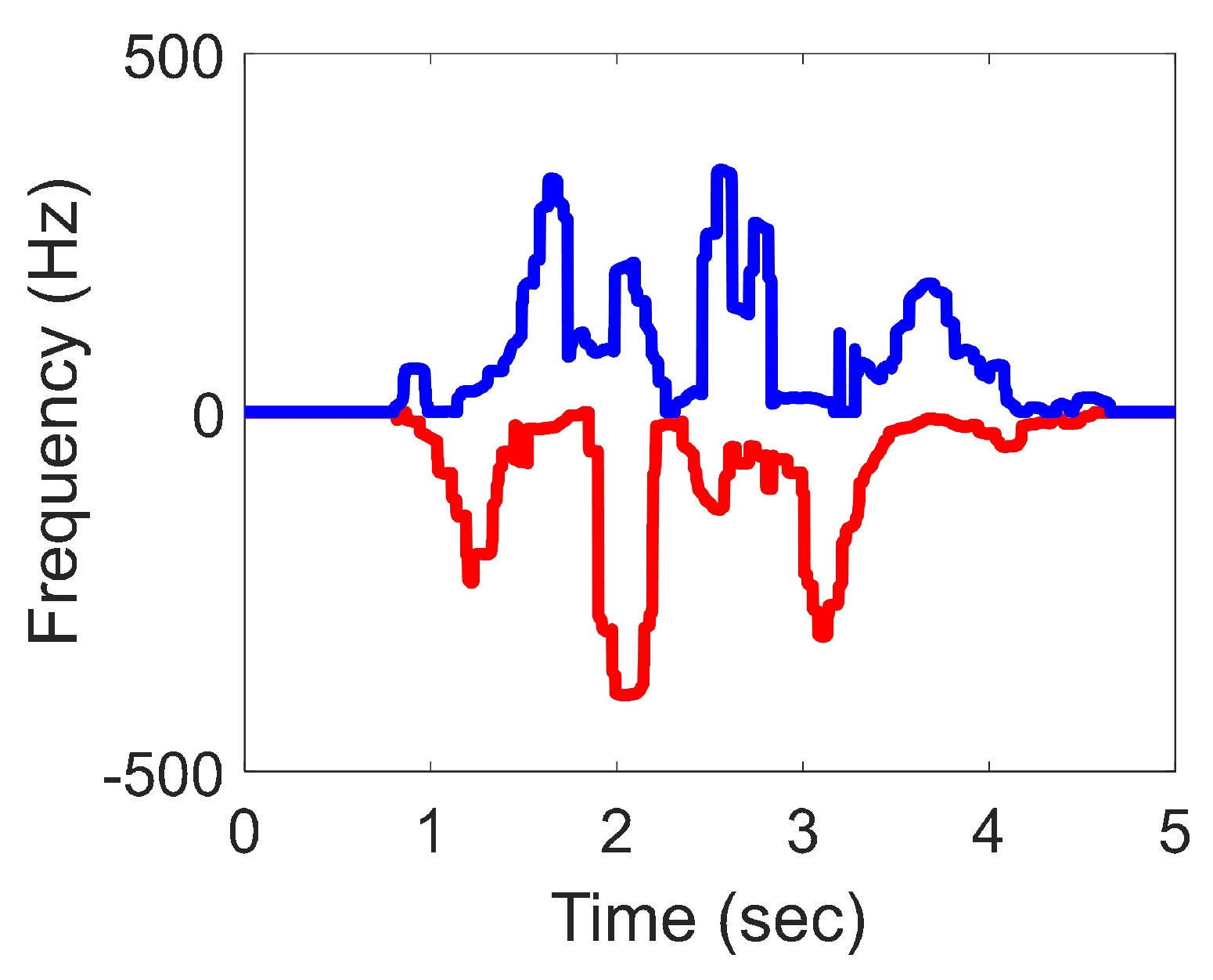


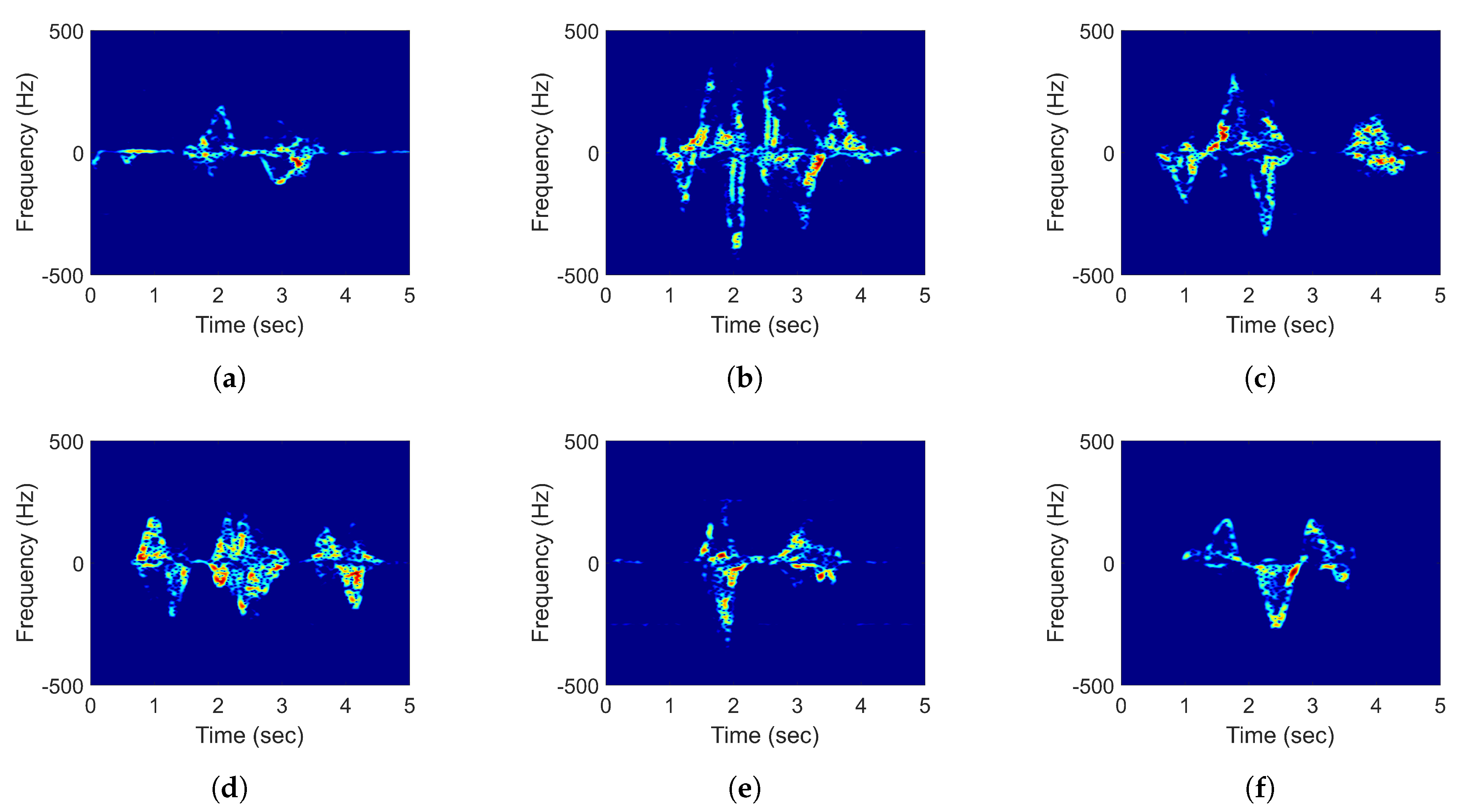






| a | b | c | d | e | f | |
|---|---|---|---|---|---|---|
| a | 95.77% | 0 | 0.59% | 1.73% | 1.49% | 0.42% |
| b | 0 | 98.38% | 0.40% | 0 | 0 | 1.22% |
| c | 0.89% | 2.02% | 93.22% | 1.37% | 2.02% | 0.48% |
| d | 2.02% | 0.06% | 0.84% | 96.97% | 0.11% | 0 |
| e | 1.31% | 0 | 1.94% | 0.44% | 96.12% | 0.19% |
| f | 0.25% | 0.63% | 0.13% | 0 | 0 | 98.99% |
| a | b | c | d | e | f | |
|---|---|---|---|---|---|---|
| a | 98.92% | 0 | 0.02% | 0.01% | 1.04% | 0.01% |
| b | 0.03% | 95.28% | 2.62% | 0.03% | 0.45% | 1.59% |
| c | 1.12% | 0.24% | 95.74% | 0.14% | 2.28% | 0.48% |
| d | 2.82% | 0 | 0.59% | 95.78% | 0.81% | 0 |
| e | 2.58% | 0 | 0.82% | 0 | 96.60% | 0 |
| f | 0.60% | 0.01% | 0.05% | 0 | 0.56% | 98.78% |
| a | b | c | d | e | f | |
|---|---|---|---|---|---|---|
| a | 96.96% | 0 | 0.02% | 0 | 2.79% | 0.23% |
| b | 0.03% | 98.70% | 0.71% | 0.07% | 0 | 0.45% |
| c | 0.28% | 0.38% | 97.87% | 0 | 1.39% | 0.08% |
| d | 1.02% | 0 | 1.42% | 96.82% | 0.59% | 0.15% |
| e | 0.17% | 0 | 0.48% | 0 | 99.09% | 0.26% |
| f | 0.13% | 0 | 0.04% | 0 | 0.69% | 98.14% |
| a | b | c | d | e | f | |
|---|---|---|---|---|---|---|
| a | 98.50% | 0 | 0.01% | 0 | 1.45% | 0.04% |
| b | 0.11% | 98.80% | 0.55% | 0.01% | 0 | 0.53% |
| c | 0.26% | 0.29% | 99.10% | 0 | 0.31% | 0.04% |
| d | 0.66% | 0 | 0.15% | 99.15% | 0.03% | 0 |
| e | 0.01% | 0 | 1.01% | 0 | 98.97% | 0.01% |
| f | 0.02% | 0 | 0.01% | 0 | 0.32% | 99.65% |
| Methods | Execution Time for Training | Execution Time for Test |
|---|---|---|
| LSTM | 2003.18 s | 1.68 s |
| NN-DTW | 0 s | 114.11 s |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Z.; Amin, M.G.; Shan, T. Arm Motion Classification Using Time-Series Analysis of the Spectrogram Frequency Envelopes. Remote Sens. 2020, 12, 454. https://doi.org/10.3390/rs12030454
Zeng Z, Amin MG, Shan T. Arm Motion Classification Using Time-Series Analysis of the Spectrogram Frequency Envelopes. Remote Sensing. 2020; 12(3):454. https://doi.org/10.3390/rs12030454
Chicago/Turabian StyleZeng, Zhengxin, Moeness G. Amin, and Tao Shan. 2020. "Arm Motion Classification Using Time-Series Analysis of the Spectrogram Frequency Envelopes" Remote Sensing 12, no. 3: 454. https://doi.org/10.3390/rs12030454
APA StyleZeng, Z., Amin, M. G., & Shan, T. (2020). Arm Motion Classification Using Time-Series Analysis of the Spectrogram Frequency Envelopes. Remote Sensing, 12(3), 454. https://doi.org/10.3390/rs12030454