Parametric Design of a Microwave Radiometer for Land Surface Temperature Retrieval from Moon-Based Earth Observation Platform
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Used
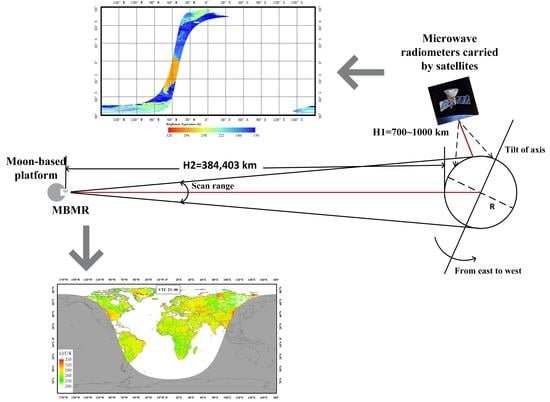
2.1.1. Moon-Based Microwave Radiation Simulation Data
2.1.2. LST Data from a Geostationary Satellite
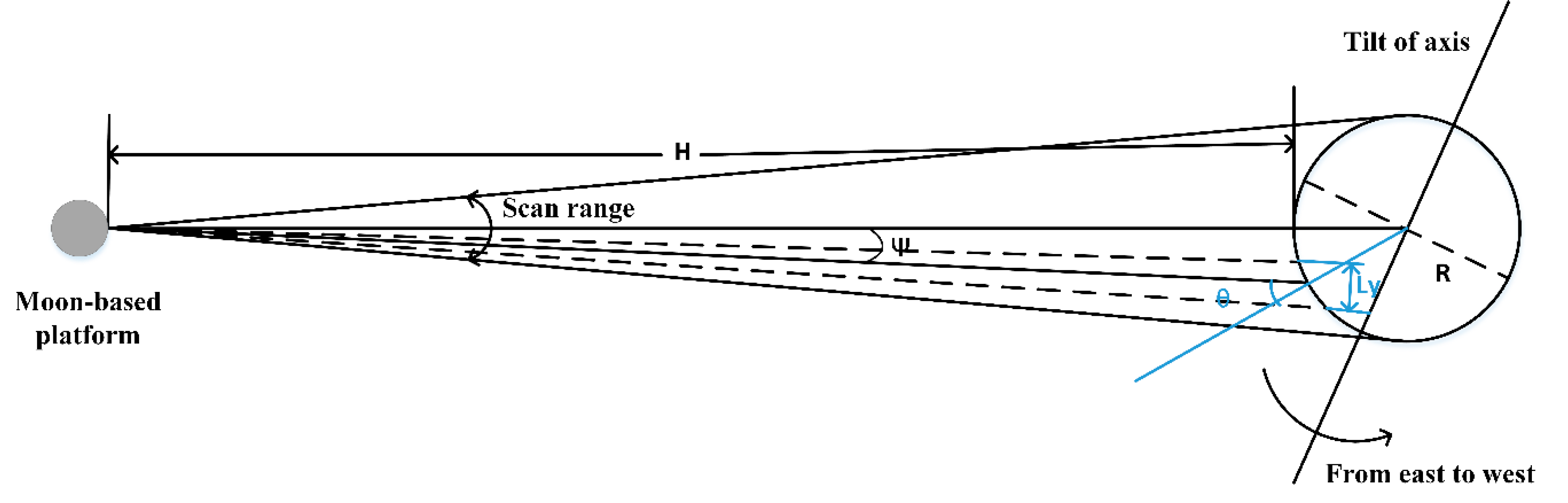
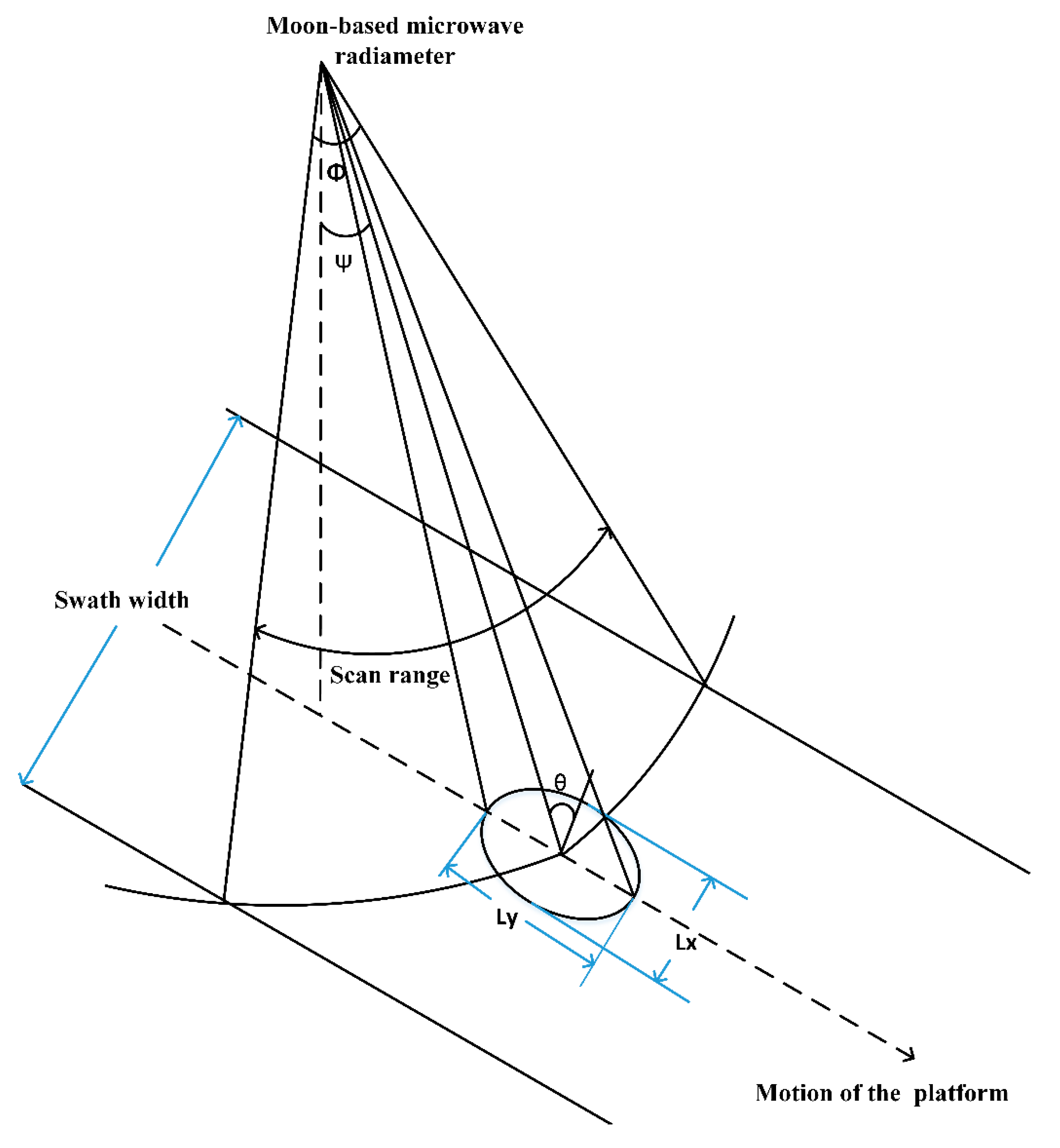
2.2. LST Retrieval from MEO Platform
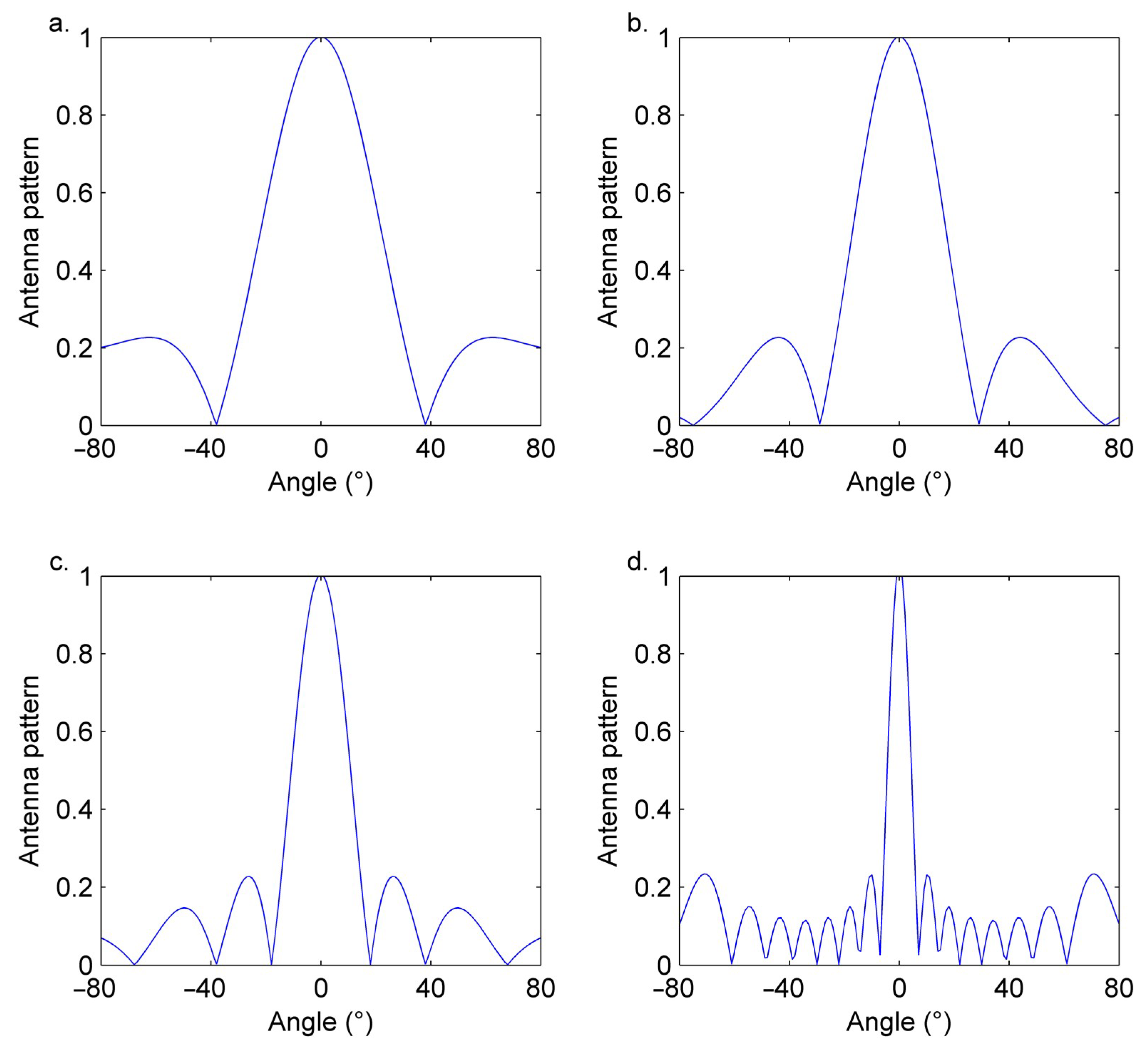
2.3. Optimization of MBMR Parameters
3. Results
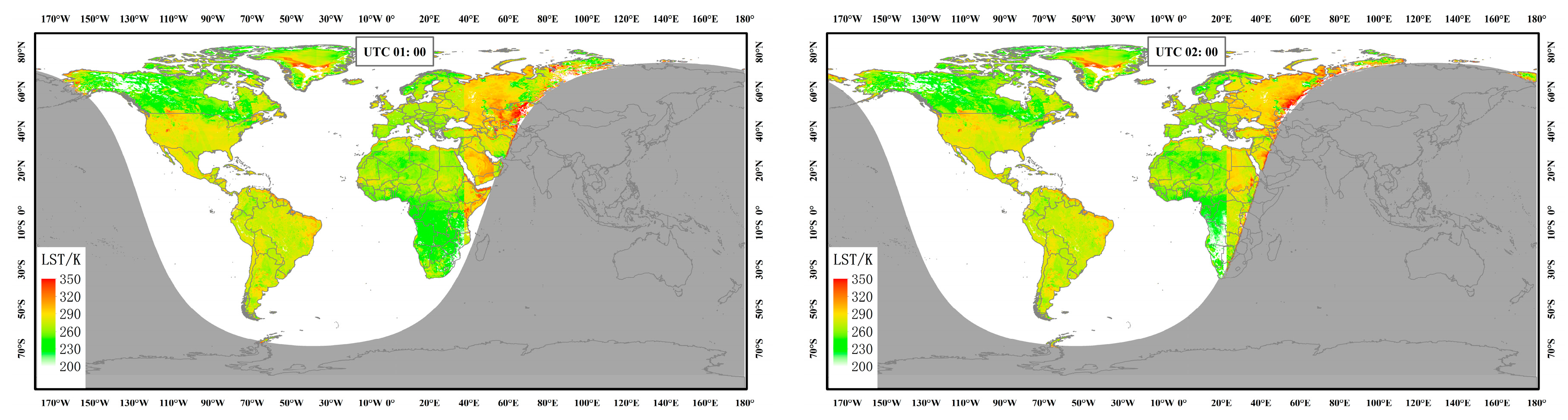
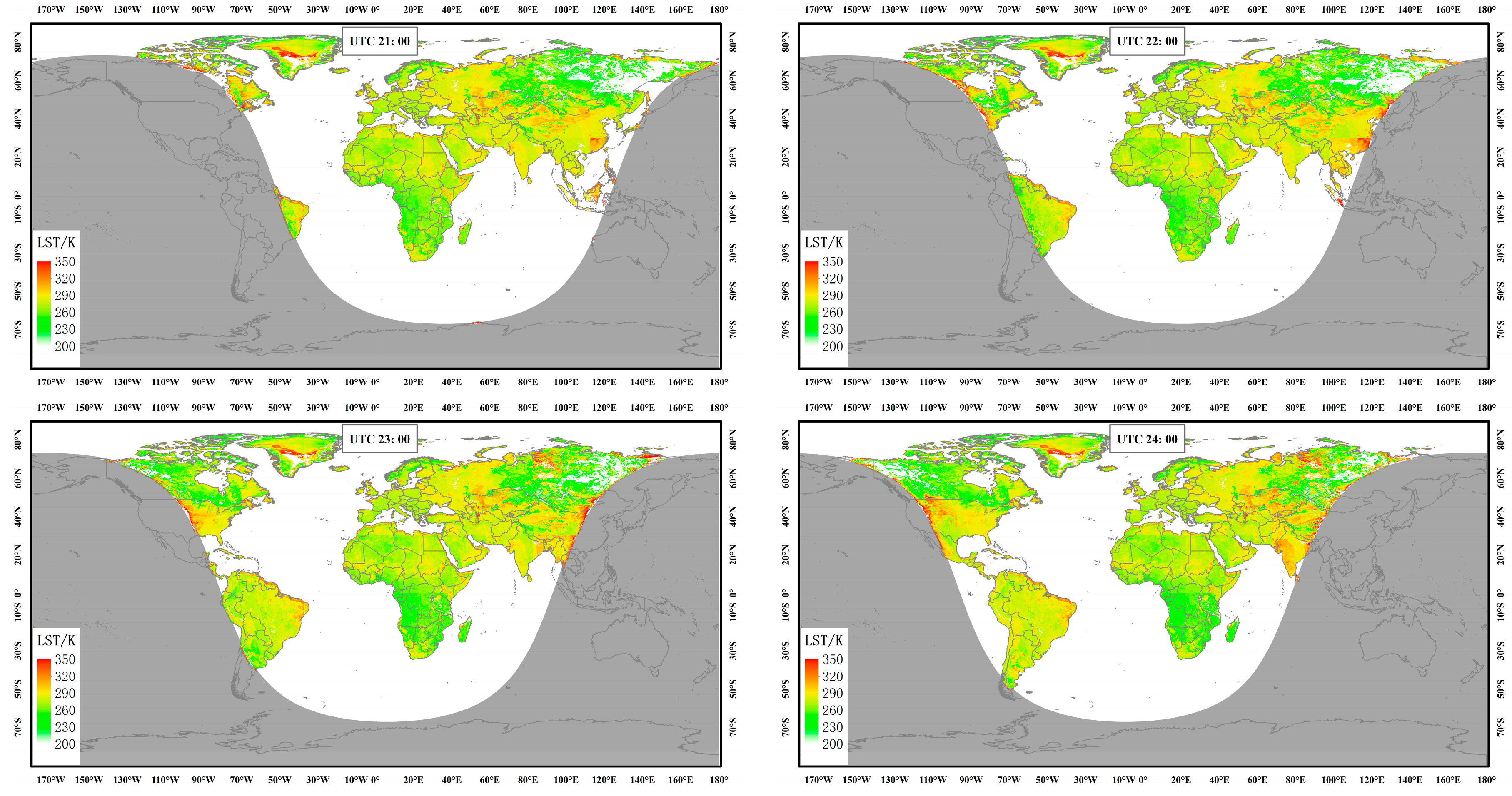
3.1. LST Estimations for MEO
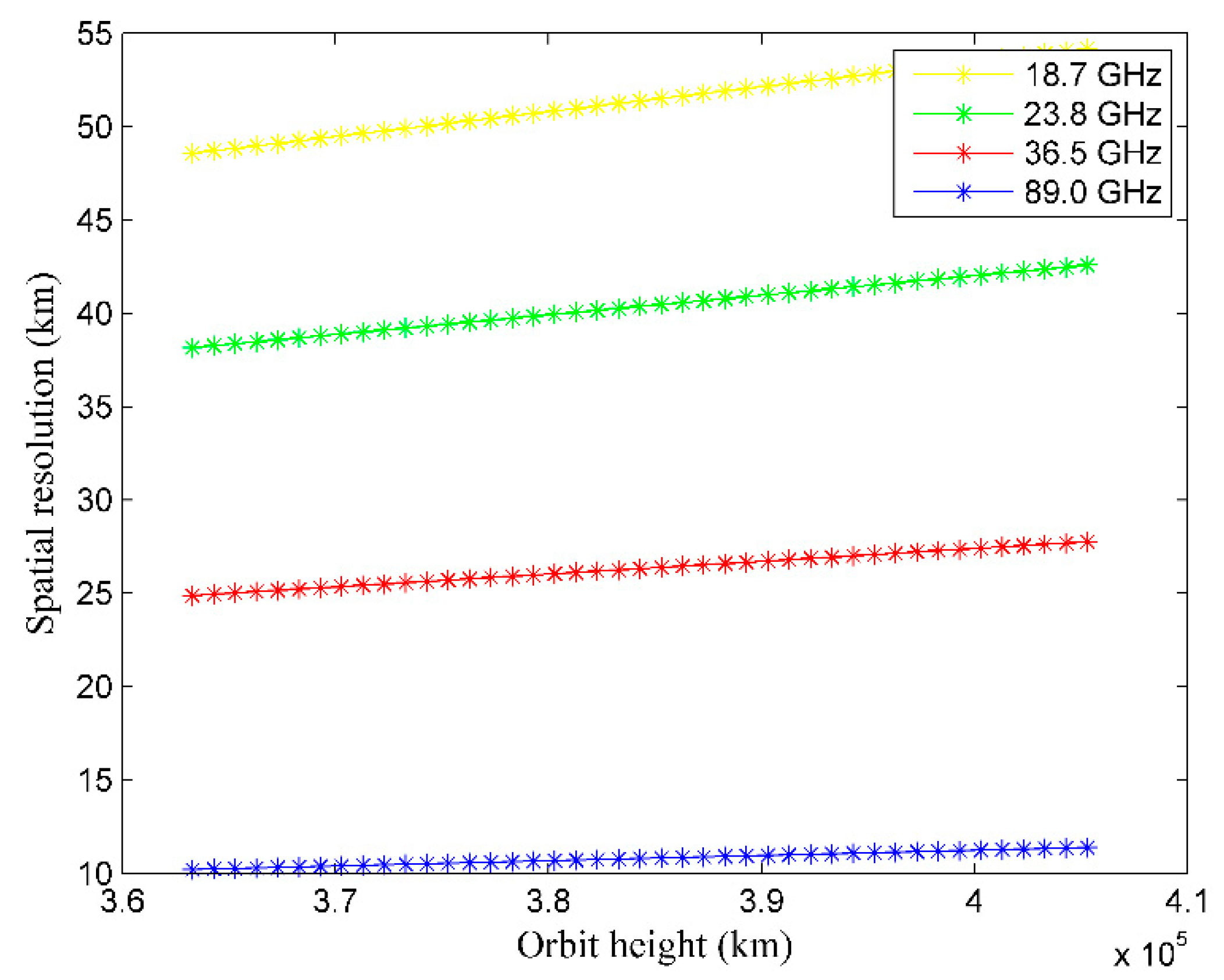
3.2. Parameter Analysis of MBMR Based on LST Estimations
4. Discussion
4.1. Comparison with the Existing Spaceborne Microwave Radiometers
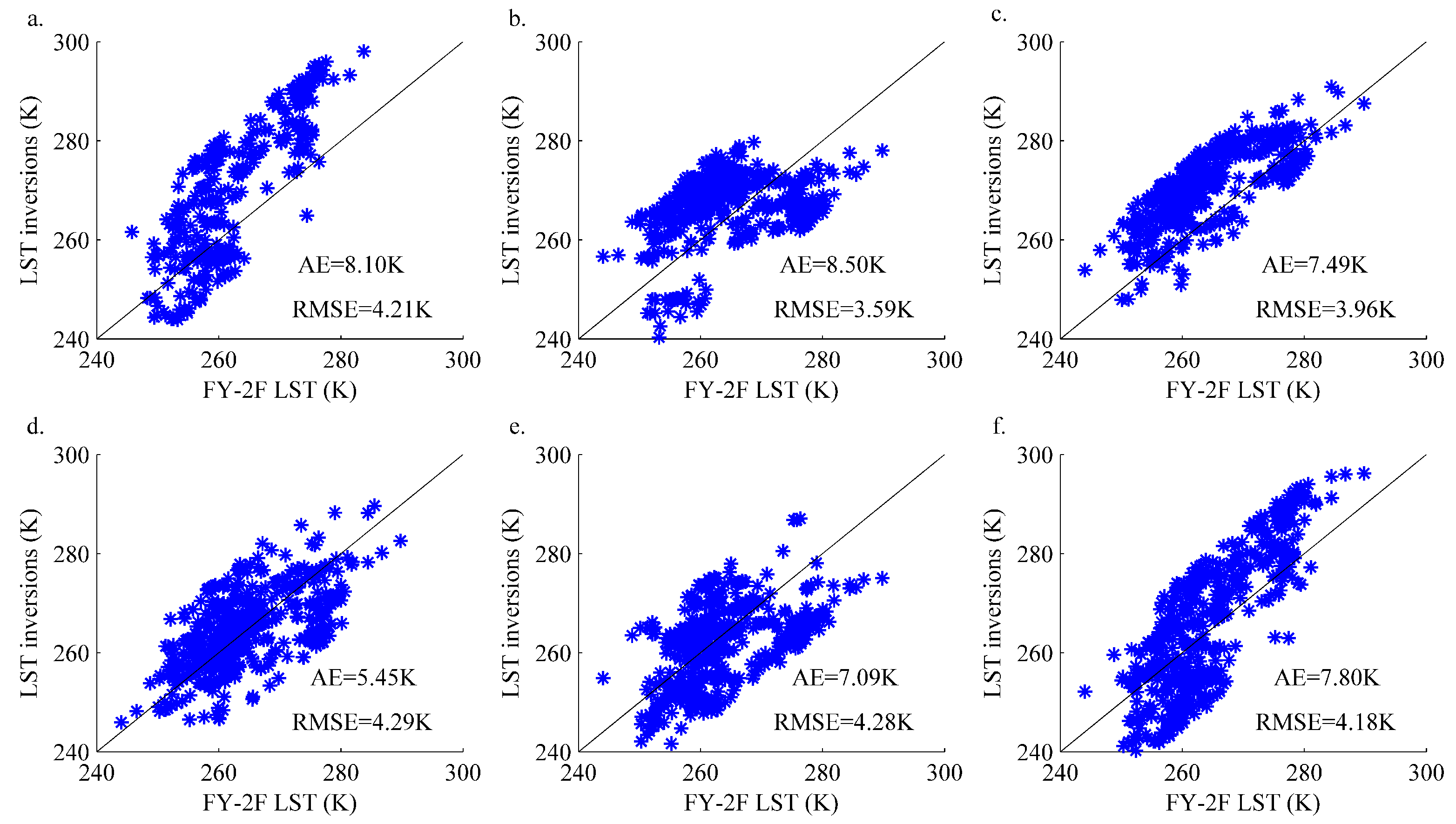
4.2. Comparison of LST Inversions between Spaceborne and Moon-Based Earth Observation Platforms
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Corradini, S.; Silvestri, M.; Musacchio, M.; Caltabiano, T.; Prestifilippo, M.; Guerrieri, L.; Stelitano, D.; Merucci, L.; Salerno, G.; Scollo, S.; et al. The Christmas 2018 Etna Eruption: Real Time Monitoring Using Geostationary and Polar Orbit Satellites Systems and Products Validation. In Proceedings of the IGARSS 2019-2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 9310–9313. [Google Scholar]
- Nie, C.; Liao, J.; Shen, G.; Duan, W. Simulation of the land surface temperature from moon-based Earth observations. Adv. Space Res. 2019, 63, 826–839. [Google Scholar] [CrossRef]
- Valero, F.P.; Herman, J.; Minnis, P. DSCOVR, a new approach to Earth Sciences from Space. Cosp 2006, 36, 1653. [Google Scholar]
- Valero, F.P. Lagrange Point Missions: The Key to Next-Generation Integrated Earth Observations. DSCOVR Innovation. AGUFM 2016, 2016, A21K-02. [Google Scholar]
- Zhang, D.W. Study on Moon-Earth Observation Methodology for Global Change. Ph.D. Thesis, East China Normal University, Shanghai, China, 2012. (In Chinese). [Google Scholar]
- Ding, Y.; Guo, H.; Liu, G. Potential applications of the moon based synthetic aperture radar for earth observation. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Melbourne, VIC, Australia, 21–26 July 2013; pp. 1767–1769. [Google Scholar] [CrossRef]
- Guo, H.; Liu, G.; Ding, Y.; Zou, Y.; Huang, S.; Jiang, L.; Gensuo, J.; Lv, M.; Ren, Y.; Ruan, Z.; et al. Moon-based earth observation for large scale geoscience phenomena. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 3705–3707. [Google Scholar] [CrossRef]
- Guo, H.; Liu, G.; Ding, Y. Moon-based Earth observation: Scientific concept and potential applications. Int. J. Digit. Earth 2018, 11, 546–557. [Google Scholar] [CrossRef]
- Ren, Y.; Guo, H.; Liu, G.; Ye, H. Simulation Study of Geometric Characteristics and Coverage for Moon-Based Earth Observation in the Electro-Optical Region. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2431–2440. [Google Scholar] [CrossRef]
- Ye, H.; Guo, H.; Liu, G. Observation parameters design of moon-based earth observation sensors for monitoring three-polar regions. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 5755–5758. [Google Scholar]
- Guo, H.; Ye, H.; Liu, G.; Dou, C.; Huang, J. Error analysis of exterior orientation elements on geolocation for a Moon-based Earth observation optical sensor. Int. J. Digit. Earth 2020, 13, 374–392. [Google Scholar] [CrossRef]
- Li, T.; Guo, H.; Zhang, L.; Nie, C.; Liao, J.; Liu, G. Simulation of Moon-based Earth observation optical image processing methods for global change study. Front. Earth Sci. 2019, 14, 236–250. [Google Scholar] [CrossRef]
- Yuan, L.; Liao, J. Exploring the influence of various factors on microwave radiation image simulation for Moon-based Earth observation. Front. Earth Sci. 2019, 14, 430–445. [Google Scholar] [CrossRef]
- Jiang, H.; Dong, J.; Jiang, L.; Li, D. Moon-Based SAR for Earth Observation and Its Spatial Baseline Decorrelation in Repeat-Pass Interferometry. In Proceedings of the IGARSS 2019-2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 1705–1708. [Google Scholar]
- Guo, H.; Ding, Y.; Liu, G.; Zhang, D.; Fu, W.; Zhang, L. Conceptual study of lunar-based SAR for global change monitoring. Sci. China Earth Sci. 2014, 57, 1771–1779. [Google Scholar] [CrossRef]
- Ren, Y.; Guo, H.; Liu, G.; Ye, H.; Ding, Y.; Zhang, D.; Ruan, Z.; Lv, M. Simulation of moon-based observation for large-scale Earth science phenomena. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 6253–6256. [Google Scholar] [CrossRef]
- Shen, G.; Guo, H.; Liu, G.; Zhang, L.; Huang, J. Geometry Numerical Simulation and Analysis for Moon-Based Earth Observation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 99, 1. [Google Scholar] [CrossRef]
- McFarland, M.J.; Miller, R.L.; Neale, C.M.U. Land surface temperature derived from the SSM/I passive microwave brightness temperatures. IEEE Trans. Geosci. Remote Sens. 1990, 28, 839–845. [Google Scholar] [CrossRef]
- Weng, F.; Grody, N.C. Physical retrieval of land surface temperature using the special sensor microwave imager. J. Geophys. Res. Space Phys. 1998, 103, 8839–8848. [Google Scholar] [CrossRef]
- Fily, M.; Royer, A.; Goïta, K.; Prigent, C. A simple retrieval method for LST and fraction of water surface determination from satellite microwave brightness temperatures in sub-arctic areas. Remote Sens. Environ. 2003, 85, 328–338. [Google Scholar] [CrossRef]
- Mao, K.; Shi, J.; Li, Z.; Qin, Z.; Jia, Y. Land surface temperature and emissivity retrieved from AMSR passive micro-wave data. IEEE Int. Geosci. Remote Sens. Symp. 2005, 4, 2247–2249. [Google Scholar] [CrossRef]
- Mao, K.; Shi, J.; Tang, H.; Guo, Y.; Qiu, Y.; Li, L. A neural-network technique for retrieving land surface temperature from AMSR-E passive microwave data. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 4422–4425. [Google Scholar] [CrossRef]
- Mao, K.B.; Shi, J.C.; Li, Z.L.; Qin, Z.H.; Li, M.C.; Xu, B. A physics-based statistical algorithm for retrieving LST from AMSR-E passive microwave data. Sci. China 2007, 50, 1115–1120. [Google Scholar] [CrossRef]
- Mao, K.; Tang, H.J.; Zhang, L.X.; Li, M.C.; Guo, Y.; Zhao, D.Z. A method for retrieving soil moisture in Tibet region by utilizing microwave index from TRMM/TMI data. Int. J. Remote Sens. 2008, 29, 2903–2923. [Google Scholar] [CrossRef]
- Gao, H.; Fu, R.; Dickinson, R.E.; Juarez, R.I.N. A practical method for retrieving LST from AMSR-E over the amazon forest. IEEE Trans. Geosci. Remote Sens. 2007, 46, 193–199. [Google Scholar] [CrossRef]
- Holmes, T.R.H.; De Jeu, R.A.M.; Owe, M.; Dolman, A.J. Land surface temperature from Ka band (37 GHz) passive microwave observations. J. Geophys. Res. Space Phys. 2009, 114, 04113. [Google Scholar] [CrossRef]
- Basist, A.; Grody, N.C.; Peterson, T.C.; Williams, C.N. Using the special sensor microwave/imager to monitor LSTs, wetness, and snow cover. J. Appl. Meteorol. Clim. 1998, 37, 888–911. [Google Scholar] [CrossRef]
- Zhou, F.-C.; Li, Z.-L.; Wu, H.; Duan, S.-B.; Song, X.; Yan, G. A Practical Two-Stage Algorithm for Retrieving Land Surface Temperature from AMSR-E Data—A Case Study Over China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1939–1948. [Google Scholar] [CrossRef]
- Huang, C.; Duan, S.-B.; Jiang, X.-G.; Han, X.-J.; Leng, P.; Gao, M.-F.; Li, Z.-L. A physically based algorithm for retrieving land surface temperature under cloudy conditions from AMSR2 passive microwave measurements. Int. J. Remote Sens. 2019, 40, 1828–1843. [Google Scholar] [CrossRef]
- Zhang, Q.; Cheng, J. An Empirical Algorithm for Retrieving Land Surface Temperature From AMSR-E Data Considering the Comprehensive Effects of Environmental Variables. Earth Space Sci. 2020, 7. [Google Scholar] [CrossRef]
- Yuan, L.; Liao, J. A Physical-Based Algorithm for Retrieving Land Surface Temperature from Moon-Based Earth Observation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1856–1866. [Google Scholar] [CrossRef]
- Ashkaliyev, Y.F. Radio-wave attenuation during propagation through the ionosphere in the 3 to 100 MHZ range. Geomagn. Aeron. 1972, 12, 309. [Google Scholar]
- Cai, W.X. Research on Propagation Characteristics of Radio Waves in Heating Ionosphere. Ph.D. Thesis, XIDIAN University, Xi’an China, 2015. [Google Scholar]
- Devi, M.I.; Khan, I.; Rao, D.N.M. A study of VLF wave propagation characteristics in the earth-ionosphere waveguide. Earth Planets Space 2008, 60, 737–741. [Google Scholar] [CrossRef]
- Lawrence, R.; Little, C.; Chivers, H. A survey of ionospheric effects upon earth-space radio propagation. Proc. IEEE 1964, 52, 4–27. [Google Scholar] [CrossRef]
- Li, J.T. Study on some Problems for Radio Wave Propagating and Scattering through Space Plasma. Ph.D. Thesis, Xi’an University, Xi’an, China, 2012. [Google Scholar]
- Lu, J.P. Absorption Attenuation of Electromagnetic Waves in Plasma. Ph.D. Thesis, Beijing Institute of Technology, Beijing, China, 2004. [Google Scholar]
- Chen, S.; Chen, X.-Z.; Chen, W.-Q.; Su, Y.; Li, D. A simple retrieval method of land surface temperature from AMSR-E passive microwave data—A case study over Southern China during the strong snow disaster of 2008. Int. J. Appl. Earth Obs. Geoinform. 2011, 13, 140–151. [Google Scholar] [CrossRef]
- Goïta, K.; Royer, A. Combination of passive microwave and thermal infrared for the retrieval and analysis of microwave emissivities and temperature. In Proceedings of the 2002 IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002. [Google Scholar] [CrossRef]
- Liu, Z.-L.; Wu, H.; Qiu, S.; Jia, Y.-Y.; Li, Z.-L. Determination of Land Surface Temperature from AMSR-E data for bare surfaces. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 3011–3014. [Google Scholar] [CrossRef]
- Royer, A.; Poirier, S. Surface temperature spatial and temporal variations in North America from homogenized satellite SMMR-SSM/I microwave measurements and reanalysis for 1979–2008. J. Geophys. Res. Space Phys. 2010, 115, 462–474. [Google Scholar] [CrossRef]
- Bergada, M.; Brotons, P.; Camacho, Y.; Díez, L.; Gamonal, A.; Garcia, J.L.; Gonzalez, R.; Pacheco, A.; Palacios, M.A.; Klein, U. Design and development of the Sentinel-3 Microwave Radiometer. Remote Sens. 2010, 7826. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, L.; Zhang, Z. Design and Test of a New Truck-Mounted Microwave Radiometer for Remote Sensing Research. In Proceedings of the 2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008. [Google Scholar] [CrossRef]
- Sun, J.; Zhao, K.; Jiang, T. A Multipoint Correction Method for Environmental Temperature Changes in Airborne Double-Antenna Microwave Radiometers. Sensors 2014, 14, 7820–7830. [Google Scholar] [CrossRef]
- Schwank, M.; Wiesmann, A.; Werner, C.; Mätzler, C.; Weber, D.; Murk, A.; Völksch, I.; Wegmüller, U. ELBARA II, an L-Band Radiometer System for Soil Moisture Research. Sensors 2010, 10, 584–612. [Google Scholar] [CrossRef] [PubMed]
- Wang, J. Research on the Key Technology of Miniaturized Microwave Radiometers for Microsatellites. Ph.D. Thesis, National Space Science Center, Chinese Academy of Sciences, Beijing, China, 2019. [Google Scholar]




| Bands (GHz) | 18.7 | 23.8 | 36.5 | 89 |
| Bandwidth (MHz) | 200 | 400 | 1000 | 3000 |
| Polarization | Horizontal and vertical polarization | |||
| Half power beam width (°) | 0.007 | 0.006 | 0.004 | 0.002 |
| Scanning angle (°) | 1.90 | |||
| Temperature sensitivity (K) | 0.7 | 0.6 | 0.7 | 1.2 |
| Antenna aperture size/diameter (m) | 120 | |||
| Spatial resolution (km) | 52 | 40 | 26 | 10 |
| Integration time (ms) | 0.19 | 0.12 | 0.03 | 0.01 |
| Parameters | SMMR 1 | SSM/I 2 | AMSR-E 3 | MWRI 4 | MBMR 5 |
|---|---|---|---|---|---|
| Frequency (GHz) | 6.6, 10.7, 18, 21, 37 | 19.3, 22.3, 37, 85.5 | 6.9, 10.7, 18.7, 23.8, 36.5, 89 | 10.7, 18.7, 23.8, 36.5, 89, 150 | 18.7, 23.8, 36.5, 89 |
| Polarization | Horizontal and vertical polarization | ||||
| Orbital height (km) | 955 | 860 | 705 | 836 | 384,400 |
| Viewing zenith angle (°) | 50.3 | 53.1 | 55 | 52–53 | 0–90 |
| Scan width (km) | 780 | 1400 | 1445 | 1400 | 20,000 |
| Antenna aperture size/diameter (m) | 0.79 | 0.6 | 1.6 | <2.0 | 120 |
| Spatial resolution (km) | 150 | 140 | 5–50 | 15~85 | 10~52 |
| Launch date | 1978 | 1987 | 2002 | 2008 | No |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, L.; Liao, J. Parametric Design of a Microwave Radiometer for Land Surface Temperature Retrieval from Moon-Based Earth Observation Platform. Remote Sens. 2020, 12, 4110. https://doi.org/10.3390/rs12244110
Yuan L, Liao J. Parametric Design of a Microwave Radiometer for Land Surface Temperature Retrieval from Moon-Based Earth Observation Platform. Remote Sensing. 2020; 12(24):4110. https://doi.org/10.3390/rs12244110
Chicago/Turabian StyleYuan, Linan, and Jingjuan Liao. 2020. "Parametric Design of a Microwave Radiometer for Land Surface Temperature Retrieval from Moon-Based Earth Observation Platform" Remote Sensing 12, no. 24: 4110. https://doi.org/10.3390/rs12244110
APA StyleYuan, L., & Liao, J. (2020). Parametric Design of a Microwave Radiometer for Land Surface Temperature Retrieval from Moon-Based Earth Observation Platform. Remote Sensing, 12(24), 4110. https://doi.org/10.3390/rs12244110