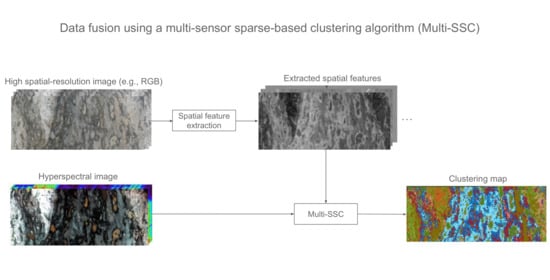
Data Fusion Using a Multi-Sensor Sparse-Based Clustering Algorithm
Abstract
1. Introduction
- 1.
- We propose a novel multi-sensor sparse-based clustering algorithm that describes the data at different levels of detail.
- 2.
- To the best of our knowledge, this is the first attempt to incorporate spatial information in the form of morphological-based profiles extracted from multi-sensor data sets in a hierarchical sparse-based clustering algorithm.
- 3.
- In the proposed algorithm, both spectral and spatial features equally contribute at each level of the tree.
- 4.
- The proposed algorithm is able to cluster large-scale data sets.
- 5.
- The proposed algorithm can be adapted to different ancillary remote sensing data sets (e.g., RGB, multi-spectral images, HSI, LiDAR, synthetic aperture radar).
2. Methodology
2.1. Spatial Feature Extraction
2.1.1. Morphological Profiles
2.1.2. Invariant Attribute Profiles
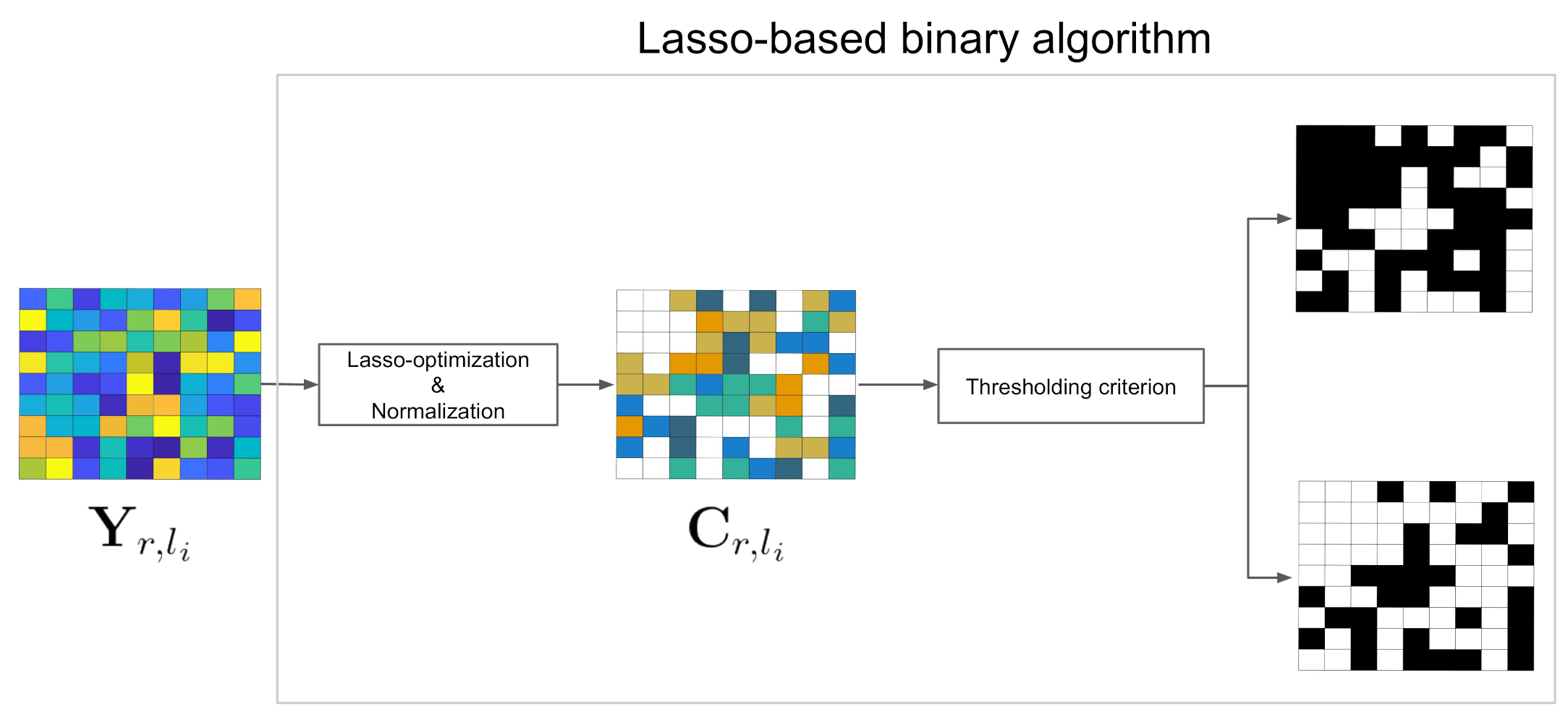
2.2. Sparse Subspace Clustering (SSC)
2.3. Hierarchical Sparse Subspace Clustering (HESSC)
2.4. Multi-Sensor Spectral-Spatial Sparse-Based Clustering (Multi-SSC)
3. Experiments
3.1. Data Acquisition and Description
- (1)
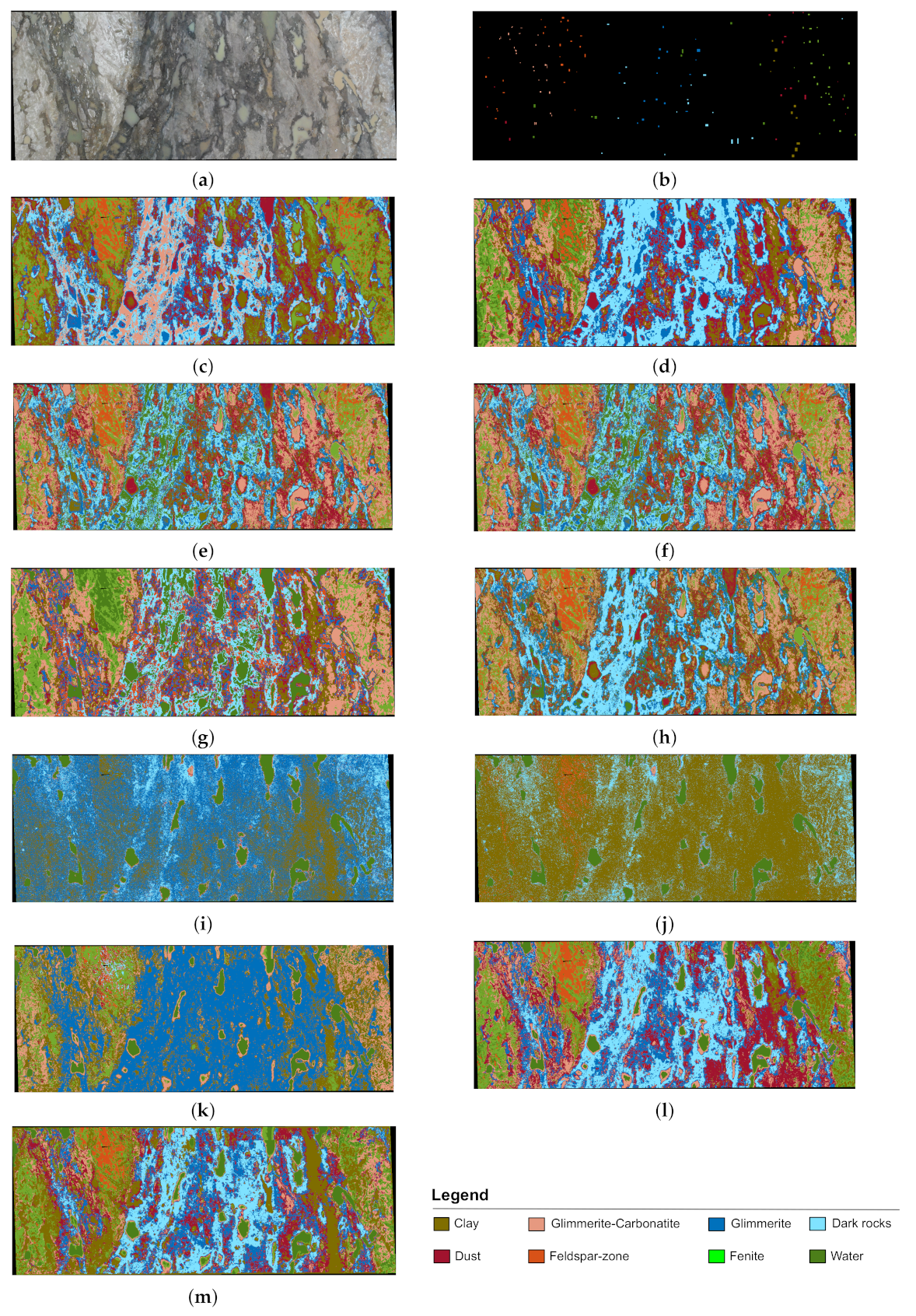
- Czech data : The first data set was acquired near the Litov tailing lake and its adjacent waste heap, situated in the Sokolov district of the Czech Republic. Both HSI and RGB images were acquired. The HSI was acquired by a hyperspectral frame-based camera (0.6 Mp Rikola Hyperspectral Imager), which was deployed on a hexacopter unmanned aerial vehicle (UAV; Aibotix Aibot X6v2) along with a pre-programmed stop-scan-motion flight plan to capture a complete set of HSIs for the subsequent image mosaicking. The RGB image was captured by employing a senseFly S.O.D.A. RGB camera, deployed on a fixed-wing UAV. The spatial resolution of the captured RGB image is 1.5 cm. It is downsampled to the size of the HSI data ( pixels), which has a spatial resolution of 3.3 cm and is composed of 50 spectral bands ranging from 0.50–0.90 m. Figure 3 illustrates the acquired RGB image of the Czech data set.
- (2)
- Finland data: The second data set was captured over an outcrop of the Archean Siilinjärvi glimmerite-carbonatite complex in Finland, which is currently mined for large phosphate-rich apatite occurrences used in fertilizer production [55]. In the Finland data set, the same instruments were employed to acquire the HSI and RGB data. The HSI and downsampled RGB images are composed of pixels. Figure 4 displays the acquired RGB image of the Finland data set.
- (3)
- Trento data: The third data set was captured over a rural area in the south of the city of Trento, Italy. It consists of LiDAR and HSI data that are composed of 600 by 166 pixels with a spatial sampling of 1 m. The HSI was acquired by the AISA Eagle sensor, and contains 63 spectral bands ranging between 0.40 and 0.98 m. The LiDAR data were captured by the Optech ALTM 3100EA sensor. The color-composite image of the HSI from the Trento data is shown in Figure 5.
3.2. Experimental Setup
3.3. Evaluation Metrics
3.4. Results and Discussion
3.4.1. The Czech Data Set
3.4.2. The Finland Data Set
3.4.3. The Trento Data Set
3.4.4. Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Meng, T.; Jing, X.; Yan, Z.; Pedrycz, W. A survey on machine learning for data fusion. Inf. Fusion 2020, 57, 115–129. [Google Scholar] [CrossRef]
- Goetz, A.F.; Vane, G.; Solomon, J.E.; Rock, B.N. Imaging Spectrometry for Earth Remote Sensing. Science 1985, 228, 1147–1153. [Google Scholar] [CrossRef] [PubMed]
- Orynbaikyzy, A.; Gessner, U.; Conrad, C. Crop type classification using a combination of optical and radar remote sensing data: A review. Int. J. Remote Sens. 2019, 40, 6553–6595. [Google Scholar] [CrossRef]
- Ghamisi, P.; Rasti, B.; Yokoya, N.; Wang, Q.; Hofle, B.; Bruzzone, L.; Bovolo, F.; Chi, M.; Anders, K.; Gloaguen, R.; et al. Multisource and Multitemporal Data Fusion in Remote Sensing: A Comprehensive Review of the State of the Art. IEEE Geosci. Remote Sens. Mag. 2019, 7, 6–39. [Google Scholar] [CrossRef]
- Lorenz, S.; Seidel, P.; Ghamisi, P.; Zimmermann, R.; Tusa, L.; Khodadadzadeh, M.; Contreras, I.C.; Gloaguen, R. Multi-Sensor Spectral Imaging of Geological Samples: A Data Fusion Approach Using Spatio-Spectral Feature Extraction. Sensors 2019, 19, 2787. [Google Scholar] [CrossRef] [PubMed]
- Tusa, L.; Andreani, L.; Khodadadzadeh, M.; Contreras, C.; Ivascanu, P.; Gloaguen, R.; Gutzmer, J. Mineral Mapping and Vein Detection in Hyperspectral Drill-Core Scans: Application to Porphyry-Type Mineralization. Minerals 2019, 9, 122. [Google Scholar] [CrossRef]
- Cho, M.A.; Skidmore, A.; Corsi, F.; van Wieren, S.E.; Sobhan, I. Estimation of green grass/herb biomass from airborne hyperspectral imagery using spectral indices and partial least squares regression. Int. J. Appl. Earth Obs. Geoinf. 2007, 9, 414–424. [Google Scholar] [CrossRef]
- Tuşa, L.; Khodadadzadeh, M.; Contreras, C.; Rafiezadeh Shahi, K.; Fuchs, M.; Gloaguen, R.; Gutzmer, J. Drill-Core Mineral Abundance Estimation Using Hyperspectral and High-Resolution Mineralogical Data. Remote Sens. 2020, 12, 1218. [Google Scholar] [CrossRef]
- Hughes, G. On the mean accuracy of statistical pattern recognizers. IEEE Trans. Inf. Theory 1968, 55–63. [Google Scholar] [CrossRef]
- Ghamisi, P.; Yokoya, N.; Li, J.; Liao, W.; Liu, S.; Plaza, J.; Rasti, B.; Plaza, A. Advances in Hyperspectral Image and Signal Processing: A Comprehensive Overview of the State of the Art. IEEE Geosci. Remote Sens. Mag. 2017, 5, 37–78. [Google Scholar] [CrossRef]
- Ghamisi, P.; Maggiori, E.; Li, S.; Souza, R.; Tarablaka, Y.; Moser, G.; De Giorgi, A.; Fang, L.; Chen, Y.; Chi, M.; et al. New Frontiers in Spectral-Spatial Hyperspectral Image Classification: The Latest Advances Based on Mathematical Morphology, Markov Random Fields, Segmentation, Sparse Representation, and Deep Learning. IEEE Geosci. Remote Sens. Mag. 2018, 6, 10–43. [Google Scholar] [CrossRef]
- Ghamisi, P.; Plaza, J.; Chen, Y.; Li, J.; Plaza, A.J. Advanced Spectral Classifiers for Hyperspectral Images: A review. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–32. [Google Scholar] [CrossRef]
- He, L.; Li, J.; Liu, C.; Li, S. Recent Advances on Spectral–Spatial Hyperspectral Image Classification: An Overview and New Guidelines. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1579–1597. [Google Scholar] [CrossRef]
- You, C.; Li, C.; Robinson, D.P.; Vidal, R. Self-Representation Based Unsupervised Exemplar Selection in a Union of Subspaces. arXiv 2020, arXiv:2006.04246. [Google Scholar] [CrossRef] [PubMed]
- Arthur, D.; Vassilvitskii, S. k-Means plus plus: The advantages of careful seeding. In Proceedings of the Eighteenth Annual Acm-Siam Symposium on Discrete Algorithms, New Orleans, LA, USA, 7–9 January 2007; pp. 1027–1035. [Google Scholar]
- Bezdek, J.C. Pattern Recognition with Fuzzy Objective Function Algorithms; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Elhamifar, E.; Vidal, R. Sparse Subspace Clustering: Algorithm, Theory, and Applications. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2765–2781. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Ghamisi, P.; Soergel, U.; Zhu, X.X. Hyperspectral and lidar fusion using deep three-stream convolutional neural networks. Remote Sens. 2018, 10, 1649. [Google Scholar] [CrossRef]
- Rasti, B.; Ghamisi, P. Remote sensing image classification using subspace sensor fusion. Inf. Fusion 2020, 64, 121–130. [Google Scholar] [CrossRef]
- Rasti, B.; Ghamisi, P.; Gloaguen, R. Hyperspectral and LiDAR Fusion Using Extinction Profiles and Total Variation Component Analysis. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3997–4007. [Google Scholar] [CrossRef]
- Hartling, S.; Sagan, V.; Sidike, P.; Maimaitijiang, M.; Carron, J. Urban Tree Species Classification Using a WorldView-2/3 and LiDAR Data Fusion Approach and Deep Learning. Sensors 2019, 19, 1284. [Google Scholar] [CrossRef]
- Yokoya, N.; Grohnfeldt, C.; Chanussot, J. Hyperspectral and Multispectral Data Fusion: A comparative review of the recent literature. IEEE Geosci. Remote Sens. Mag. 2017, 5, 29–56. [Google Scholar] [CrossRef]
- Pelizari, P.A.; Spröhnle, K.; Geiß, C.; Schoepfer, E.; Plank, S.; Taubenböck, H. Multi-sensor feature fusion for very high spatial resolution built-up area extraction in temporary settlements. Remote Sens. Environ. 2018, 209, 793–807. [Google Scholar] [CrossRef]
- Sellami, A.; Abbes, A.B.; Barra, V.; Farah, I.R. Fused 3-D spectral-spatial deep neural networks and spectral clustering for hyperspectral image classification. Pattern Recognit. Lett. 2020, 138, 594–600. [Google Scholar] [CrossRef]
- Pourkamali-Anaraki, F.; Folberth, J.; Becker, S. Efficient Solvers for Sparse Subspace Clustering. Signal Process. 2020, 172, 107548. [Google Scholar] [CrossRef]
- Zhang, H.; Zhai, H.; Zhang, L.; Li, P. Spectral–Spatial Sparse Subspace Clustering for Hyperspectral Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3672–3684. [Google Scholar] [CrossRef]
- You, C.; Vidal, R. Sparse Subspace Clustering by Orthogonal Matching Pursuit. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 3918–3927. [Google Scholar]
- Rafiezadeh Shahi, K.; Khodadadzadeh, M.; Tusa, L.; Ghamisi, P.; Tolosana-Delgado, R.; Gloaguen, R. Hierarchical Sparse Subspace Clustering (HESSC): An Automatic Approach for Hyperspectral Image Analysis. Remote Sens. 2020, 12, 2421. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, Y.; Blum, R.S.; Han, J.; Tao, D. Sparse representation based multi-sensor image fusion for multi-focus and multi-modality images: A review. Inf. Fusion 2018, 40, 57–75. [Google Scholar] [CrossRef]
- Shahi, K.R.; Khodadadzadeh, M.; Tolosana-delgado, R.; Tusa, L.; Gloaguen, R. The Application Of Subspace Clustering Algorithms In Drill-Core Hyperspectral Domaining. In Proceedings of the 2019 10th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS), Amsterdam, The Netherlands, 24–26 September 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Rafiezadeh Shahi, K.; Ghamisi, P.; Jackisch, R.; Khodadadzadeh, M.; Lorenz, S.; Gloaguen, R. A new spectral-spatial subspace clustering algorithm for hyperspectral image analysis. ISPRS Ann. Photogramm. Remote. Sens. Spat. Inf. Sci. 2020, 3, 185–191. [Google Scholar] [CrossRef]
- Vidal, R. Subspace Clustering. IEEE Signal Process. Mag. 2011, 28, 52–68. [Google Scholar] [CrossRef]
- Cai, D.; Chen, X. Large scale spectral clustering via landmark-based sparse representation. IEEE Trans. Cybern. 2014, 45, 1669–1680. [Google Scholar]
- Dyer, E.; Sankaranarayanan, A.; Baraniuk, R. Greedy feature selection for subspace clustering. J. Mach. Learn. Res. 2013, 14, 2487–2517. [Google Scholar]
- Guo, Y.; Gao, J.; Li, F. Spatial subspace clustering for drill hole spectral data. J. Appl. Remote Sens. 2014, 8, 1–20. [Google Scholar] [CrossRef]
- Hinojosa, C.; Bacca, J.; Arguello, H. Coded Aperture Design for Compressive Spectral Subspace Clustering. IEEE J. Sel. Top. Signal Process. 2018, 12, 1589–1600. [Google Scholar] [CrossRef]
- Pesaresi, M.; Benediktsson, J.A. A new approach for the morphological segmentation of high-resolution satellite imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 309–320. [Google Scholar] [CrossRef]
- Benediktsson, J.A.; Palmason, J.A.; Sveinsson, J.R. Classification of hyperspectral data from urban areas based on extended morphological profiles. IEEE Trans. Geosci. Remote Sens. 2005, 43, 480–491. [Google Scholar] [CrossRef]
- Dalla Mura, M.; Benediktsson, J.A.; Waske, B.; Bruzzone, L. Morphological Attribute Profiles for the Analysis of Very High Resolution Images. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3747–3762. [Google Scholar] [CrossRef]
- Dalla Mura, M.; Villa, A.; Benediktsson, J.A.; Chanussot, J.; Bruzzone, L. Classification of Hyperspectral Images by Using Extended Morphological Attribute Profiles and Independent Component Analysis. IEEE Geosci. Remote Sens. Lett. 2011, 8, 542–546. [Google Scholar] [CrossRef]
- Huang, X.; Guan, X.; Benediktsson, J.A.; Zhang, L.; Li, J.; Plaza, A.; Dalla Mura, M. Multiple Morphological Profiles From Multicomponent-Base Images for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4653–4669. [Google Scholar] [CrossRef]
- Ghamisi, P.; Dalla Mura, M.; Benediktsson, J.A. A Survey on Spectral–Spatial Classification Techniques Based on Attribute Profiles. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2335–2353. [Google Scholar] [CrossRef]
- Hong, D.; Wu, X.; Ghamisi, P.; Chanussot, J.; Yokoya, N.; Zhu, X.X. Invariant Attribute Profiles: A Spatial-Frequency Joint Feature Extractor for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3791–3808. [Google Scholar] [CrossRef]
- Liu, K.; Skibbe, H.; Schmidt, T.; Blein, T.; Palme, K.; Brox, T.; Ronneberger, O. Rotation-invariant HOG descriptors using Fourier analysis in polar and spherical coordinates. Int. J. Comput. Vis. 2014, 106, 342–364. [Google Scholar] [CrossRef]
- Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Süsstrunk, S. SLIC Superpixels Compared to State-of-the-Art Superpixel Methods. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2274–2282. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends® Mach. Learn. 2011, 3, 1–122. [Google Scholar]
- Von Luxburg, U. A tutorial on spectral clustering. Stat. Comput. 2007, 17, 395–416. [Google Scholar] [CrossRef]
- Ng, A.Y.; Jordan, M.I.; Weiss, Y. On spectral clustering: Analysis and an algorithm. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 9–14 December 2002; pp. 849–856. [Google Scholar]
- Chen, X.; Cai, D. Large scale spectral clustering with landmark-based representation. In Proceedings of the Twenty-Fifth AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 7–11 August 2011. [Google Scholar]
- Efron, B.; Hastie, T.; Johnstone, I.; Tibshirani, R. Least angle regression. Ann. Statist. 2004, 32, 407–499. [Google Scholar]
- Liu, H.; Zhao, R.; Fang, H.; Cheng, F.; Fu, Y.; Liu, Y.Y. Entropy-based consensus clustering for patient stratification. Bioinformatics 2017, 33, 2691–2698. [Google Scholar] [CrossRef]
- Wu, T.; Gurram, P.; Rao, R.M.; Bajwa, W.U. Hierarchical union-of-subspaces model for human activity summarization. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Santiago, Chile, 11–12 December 2015; pp. 1–9. [Google Scholar]
- Gu, Y.; Zhang, Y.; Zhang, J. Integration of Spatial–Spectral Information for Resolution Enhancement in Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1347–1358. [Google Scholar]
- Gillmann, C.; Arbelaez, P.; Hernandez, J.T.; Hagen, H.; Wischgoll, T. An uncertainty-aware visual system for image pre-processing. J. Imaging 2018, 4, 109. [Google Scholar] [CrossRef]
- O’Brien, H.; Heilimo, E.; Heino, P. Chapter 4.3—The Archean Siilinjärvi Carbonatite Complex. In Mineral Deposits of Finland; Maier, W.D., Lahtinen, R., O’Brien, H., Eds.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 327–343. [Google Scholar] [CrossRef]
- Jakob, S.; Zimmermann, R.; Gloaguen, R. The Need for Accurate Geometric and Radiometric Corrections of Drone-Borne Hyperspectral Data for Mineral Exploration: MEPHySTo—A Toolbox for Pre-Processing Drone-Borne Hyperspectral Data. Remote Sens. 2017, 9, 88. [Google Scholar] [CrossRef]
- Jackisch, R.; Lorenz, S.; Zimmermann, R.; Möckel, R.; Gloaguen, R. Drone-Borne Hyperspectral Monitoring of Acid Mine Drainage: An Example from the Sokolov Lignite District. Remote Sens. 2018, 10, 385. [Google Scholar] [CrossRef]
- Jackisch, R.; Lorenz, S.; Kirsch, M.; Zimmermann, R.; Tusa, L.; Pirttijaervi, M.; Saartenoja, A.; Ugalde, H.; Madriz, Y.; Savolainen, M.; et al. Integrated Geological and Geophysical Mapping of a Carbonatite-Hosting Outcrop in Siilinjärvi, Finland, Using Unmanned Aerial Systems. Remote Sens. 2020, 12, 2998. [Google Scholar] [CrossRef]
- Rezaei, M.; Fränti, P. Set Matching Measures for External Cluster Validity. IEEE Trans. Knowl. Data Eng. 2016, 28, 2173–2186. [Google Scholar] [CrossRef]
- Hubert, L.; Arabie, P. Comparing partitions. J. Classif. 1985, 2, 193–218. [Google Scholar] [CrossRef]
- Wu, J.; Xiong, H.; Chen, J. Adapting the Right Measures for K-means Clustering. In Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Paris, France, 28 June–1 July 2009; pp. 877–886. [Google Scholar] [CrossRef]






| Class | No. Ground Truth Samples | K-means | K-means | K-means | FCM | FCM | FCM | LSC | LSC | LSC | ESC | ESC | ESC | HESSC | HESSC | Multi-SSC (MPs) | Multi-SSC (IAPs) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1018 | 50.49 | 87.92 | 91.06 | 36.05 | 84.87 | 44.40 | 100 | 93.42 | 80.35 | 100 | 99.71 | 98.04 | 63.06 | 89.00 | 55.50 | 97.05 |
| 2 | 901 | 98.67 | 93.01 | 88.67 | 97.34 | 10.54 | 66.89 | 0.00 | 0.11 | 99.00 | 99.00 | 99.67 | 53.50 | 66.26 | 26.53 | 77.36 | 99.67 |
| 3 | 1119 | 73.73 | 71.40 | 71.94 | 63.81 | 71.67 | 46.85 | 50.67 | 79.54 | 67.74 | 41.82 | 0.54 | 41.82 | 22.88 | 0.00 | 51.03 | 36.73 |
| 4 | 874 | 52.86 | 0.00 | 3.43 | 65.90 | 29.18 | 60.64 | 64.30 | 16.82 | 65.22 | 0.57 | 2.17 | 94.16 | 47.94 | 86.61 | 80.32 | 56.86 |
| 5 | 838 | 97.61 | 99.05 | 87.61 | 96.06 | 98.69 | 86.42 | 95.94 | 97.02 | 0.12 | 41.77 | 80.19 | 0.00 | 65.75 | 68.50 | 56.44 | 85.68 |
| 6 | 863 | 31.29 | 66.74 | 68.25 | 58.86 | 42.53 | 59.10 | 35.57 | 42.41 | 47.74 | 0.12 | 86.33 | 0.00 | 12.05 | 98.73 | 86.79 | 29.66 |
| 7 | 777 | 38.74 | 49.55 | 35.39 | 35.91 | 46.72 | 35.65 | 35.39 | 55.08 | 33.33 | 10.29 | 0.00 | 11.45 | 65.89 | 16.22 | 28.06 | 32.95 |
| 8 | 785 | 0.00 | 7.39 | 31.97 | 4.59 | 2.55 | 4.59 | 8.54 | 19.75 | 9.94 | 43.95 | 51.72 | 79.36 | 43.82 | 38.85 | 17.71 | 80.13 |
| OA | 56.85 | 61.06 | 61.37 | 58.00 | 50.08 | 56.70 | 50.17 | 52.28 | 55.68 | 43.05 | 52.42 | 45.45 | 47.74 | 52.13 | 57.34 | 64.85 | |
| AA | 55.42 | 59.38 | 59.79 | 57.31 | 48.34 | 50.57 | 48.80 | 50.51 | 50.43 | 42.19 | 52.54 | 47.29 | 48.45 | 53.05 | 56.65 | 64.84 | |
| 0.50 | 0.55 | 0.58 | 0.51 | 0.42 | 0.48 | 0.42 | 0.45 | 0.45 | 0.34 | 0.45 | 0.48 | 0.40 | 0.46 | 0.51 | 0.59 | ||
| 0.50 | 0.47 | 0.49 | 0.41 | 0.42 | 0.36 | 0.37 | 0.45 | 0.33 | 0.22 | 0.36 | 0.53 | 0.31 | 0.35 | 0.53 | 0.54 | ||
| 0.63 | 0.62 | 0.63 | 0.54 | 0.56 | 0.51 | 0.53 | 0.58 | 0.51 | 0.41 | 0.55 | 0.62 | 0.50 | 0.52 | 0.64 | 0.66 | ||
| t (seconds) | 1.16 | 1.01 | 1.66 | 145.12 | 187.09 | 196.62 | 34.65 | 34.94 | 35.01 | 13,387.00 | 9859.00 | 11,130.00 | 3562.80 | 3557.20 | 3086.51 | 3114.80 | |
| Class | No. Ground Truth Samples | K-means | K-means | K-means | FCM | FCM | FCM | LSC | LSC | LSC | ESC | ESC | ESC | HESSC | HESSC | Multi-SSC (MPs) | Multi-SSC (IAPs) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1062 | 53.58 | 54.43 | 71.28 | 48.96 | 49.81 | 66.20 | 68.17 | 50.85 | 31.17 | 77.78 | 95.67 | 13.75 | 54.90 | 75.33 | 56.97 | 100 |
| 2 | 791 | 0.00 | 25.92 | 20.86 | 0.00 | 0.00 | 0.00 | 3.92 | 1.64 | 9.99 | 1.39 | 1.90 | 41.09 | 22.12 | 4.23 | 8.34 | 2.28 |
| 3 | 1048 | 54.48 | 65.55 | 61.45 | 31.58 | 32.44 | 55.15 | 41.70 | 37.40 | 52.86 | 71.28 | 0.00 | 7.63 | 0.00 | 89.50 | 53.34 | 71.18 |
| 4 | 994 | 50.80 | 94.16 | 55.33 | 43.86 | 44.47 | 52.11 | 47.38 | 56.94 | 66.90 | 0.00 | 0.80 | 0.00 | 96.38 | 24.14 | 85.92 | 85.01 |
| 5 | 964 | 56.64 | 45.33 | 65.66 | 61.51 | 62.14 | 68.67 | 40.87 | 39.63 | 43.57 | 1.04 | 0.00 | 45.75 | 0.21 | 7.57 | 3.01 | 12.34 |
| 6 | 1061 | 88.22 | 69.18 | 87.75 | 86.90 | 86.71 | 88.03 | 0.00 | 89.44 | 94.25 | 0.19 | 30.73 | 26.86 | 42.79 | 82.75 | 83.69 | 71.25 |
| 7 | 1065 | 35.87 | 58.59 | 0.00 | 37.84 | 38.12 | 11.87 | 70.05 | 30.42 | 16.42 | 34.46 | 37.46 | 94.96 | 57.46 | 15.83 | 98.22 | 56.81 |
| 8 | 1011 | 0.00 | 10.29 | 68.83 | 37.29 | 38.67 | 57.28 | 85.66 | 29.28 | 37.93 | 100 | 100 | 19.15 | 88.82 | 33.71 | 49.11 | 91.10 |
| OA | 43.88 | 53.84 | 53.15 | 44.80 | 45.36 | 51.62 | 45.89 | 43.30 | 44.68 | 37.19 | 34.70 | 40.71 | 46.05 | 44.56 | 56.49 | 63.43 | |
| AA | 42.45 | 52.93 | 53.90 | 43.49 | 44.05 | 49.91 | 44.72 | 41.95 | 44.14 | 35.77 | 33.32 | 31.15 | 45.34 | 41.63 | 54.82 | 61.25 | |
| 0.35 | 0.47 | 0.48 | 0.36 | 0.37 | 0.44 | 0.38 | 0.35 | 0.37 | 0.27 | 0.24 | 0.21 | 0.38 | 0.42 | 0.50 | 0.58 | ||
| 0.27 | 0.38 | 0.32 | 0.28 | 0.27 | 0.36 | 0.30 | 0.27 | 0.33 | 0.16 | 0.11 | 0.28 | 0.34 | 0.23 | 0.41 | 0.46 | ||
| 0.42 | 0.52 | 0.49 | 0.43 | 0.42 | 0.51 | 0.49 | 0.42 | 0.51 | 0.37 | 0.35 | 0.38 | 0.51 | 0.42 | 0.55 | 0.57 | ||
| t (seconds) | 27.81 | 54.56 | 55.45 | 318.40 | 339.15 | 338.18 | 52.05 | 57.71 | 71.11 | 100,890.00 | 100,210.00 | 110,700.00 | 12,085.00 | 70,492.00 | 90,436.00 | 98,752.00 | |
| Clusters | No. Ground Truth Samples | K-means | K-means | K-means | FCM | FCM | FCM | LSC | LSC | LSC | ESC | ESC | ESC | HESSC | HESSC | Multi-SSC (MPs) | Multi-SSC (IAPs) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 4034 | 70.91 | 38.34 | 59.67 | 75.90 | 24.86 | 55.35 | 60.13 | 43.27 | 55.33 | 10.55 | 26.82 | 2.78 | 0.00 | 45.70 | 29.30 | 0.00 |
| 2 | 2903 | 89.25 | 98.97 | 0.55 | 84.46 | 99.44 | 0.65 | 0.00 | 35.59 | 2.17 | 10.08 | 99.22 | 64.17 | 80.26 | 81.46 | 36.33 | 68.55 |
| 3 | 479 | 0.00 | 15.64 | 30.90 | 59.46 | 59.67 | 32.36 | 10.77 | 16.16 | 24.84 | 42.78 | 4.13 | 63.67 | 21.71 | 25.65 | 9.60 | 26.72 |
| 4 | 9123 | 57.07 | 86.35 | 99.93 | 0.00 | 69.86 | 99.91 | 56.70 | 68.82 | 99.62 | 34.35 | 74.15 | 54.58 | 91.69 | 70.65 | 99.95 | 90.57 |
| 5 | 10,501 | 42.79 | 48.68 | 69.05 | 39.18 | 22.42 | 68.50 | 35.81 | 36.88 | 60.01 | 69.37 | 44.05 | 73.32 | 43.70 | 39.11 | 59.26 | 94.47 |
| 6 | 3174 | 31.23 | 15.72 | 52.96 | 53.09 | 7.63 | 53.02 | 94.72 | 90.65 | 70.01 | 83.81 | 46.84 | 50.50 | 55.45 | 34.00 | 82.89 | 44.83 |
| OA | 51.97 | 59.52 | 63.22 | 53.88 | 54.21 | 58.65 | 47.71 | 52.96 | 63.76 | 46.34 | 63.95 | 54.13 | 56.76 | 52.09 | 65.12 | 71.90 | |
| AA | 48.54 | 50.61 | 52.18 | 51.18 | 44.77 | 51.63 | 43.02 | 49.23 | 52.00 | 41.82 | 49.20 | 51.50 | 48.80 | 49.43 | 52.89 | 54.19 | |
| 0.46 | 0.46 | 0.53 | 0.43 | 0.42 | 0.54 | 0.37 | 0.45 | 0.54 | 0.27 | 0.50 | 0.51 | 0.41 | 0.49 | 0.55 | 0.61 | ||
| 0.27 | 0.16 | 0.50 | 0.28 | 0.16 | 0.51 | 0.28 | 0.18 | 0.42 | 0.21 | 0.30 | 0.32 | 0.37 | 0.36 | 0.44 | 0.53 | ||
| 0.43 | 0.25 | 0.54 | 0.46 | 0.25 | 0.54 | 0.45 | 0.26 | 0.56 | 0.37 | 0.44 | 0.38 | 0.49 | 0.46 | 0.58 | 0.64 | ||
| t (seconds) | 2.55 | 2.73 | 3.01 | 21.69 | 20.42 | 11.60 | 3.86 | 2.48 | 2.96 | 763.52 | 118.92 | 764.79 | 478.94 | 576.11 | 407.49 | 518.63 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rafiezadeh Shahi, K.; Ghamisi, P.; Rasti, B.; Jackisch, R.; Scheunders, P.; Gloaguen, R. Data Fusion Using a Multi-Sensor Sparse-Based Clustering Algorithm. Remote Sens. 2020, 12, 4007. https://doi.org/10.3390/rs12234007
Rafiezadeh Shahi K, Ghamisi P, Rasti B, Jackisch R, Scheunders P, Gloaguen R. Data Fusion Using a Multi-Sensor Sparse-Based Clustering Algorithm. Remote Sensing. 2020; 12(23):4007. https://doi.org/10.3390/rs12234007
Chicago/Turabian StyleRafiezadeh Shahi, Kasra, Pedram Ghamisi, Behnood Rasti, Robert Jackisch, Paul Scheunders, and Richard Gloaguen. 2020. "Data Fusion Using a Multi-Sensor Sparse-Based Clustering Algorithm" Remote Sensing 12, no. 23: 4007. https://doi.org/10.3390/rs12234007
APA StyleRafiezadeh Shahi, K., Ghamisi, P., Rasti, B., Jackisch, R., Scheunders, P., & Gloaguen, R. (2020). Data Fusion Using a Multi-Sensor Sparse-Based Clustering Algorithm. Remote Sensing, 12(23), 4007. https://doi.org/10.3390/rs12234007