An Assessment of the Hydrological Trends Using Synergistic Approaches of Remote Sensing and Model Evaluations over Global Arid and Semi-Arid Regions
Abstract
1. Introduction
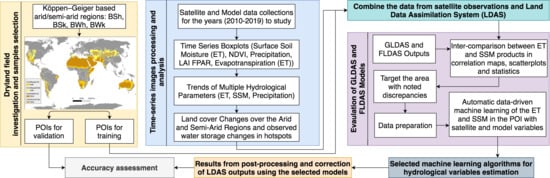
2. Materials and Methods
2.1. Study Area
2.2. Data
2.2.1. Data from Remote Sensing Observations
- Precipitation Data
- Surface Soil Moisture Data
- Water Storage Data
- Vegetation Indices Data
2.2.2. Data from Process-Based Models
2.3. Methods
2.3.1. Harmonic Analysis
2.3.2. Correlational Analysis
2.3.3. Data-Driven Modelling of Selected Variables
2.3.4. Model Accuracy Assessment
3. Results
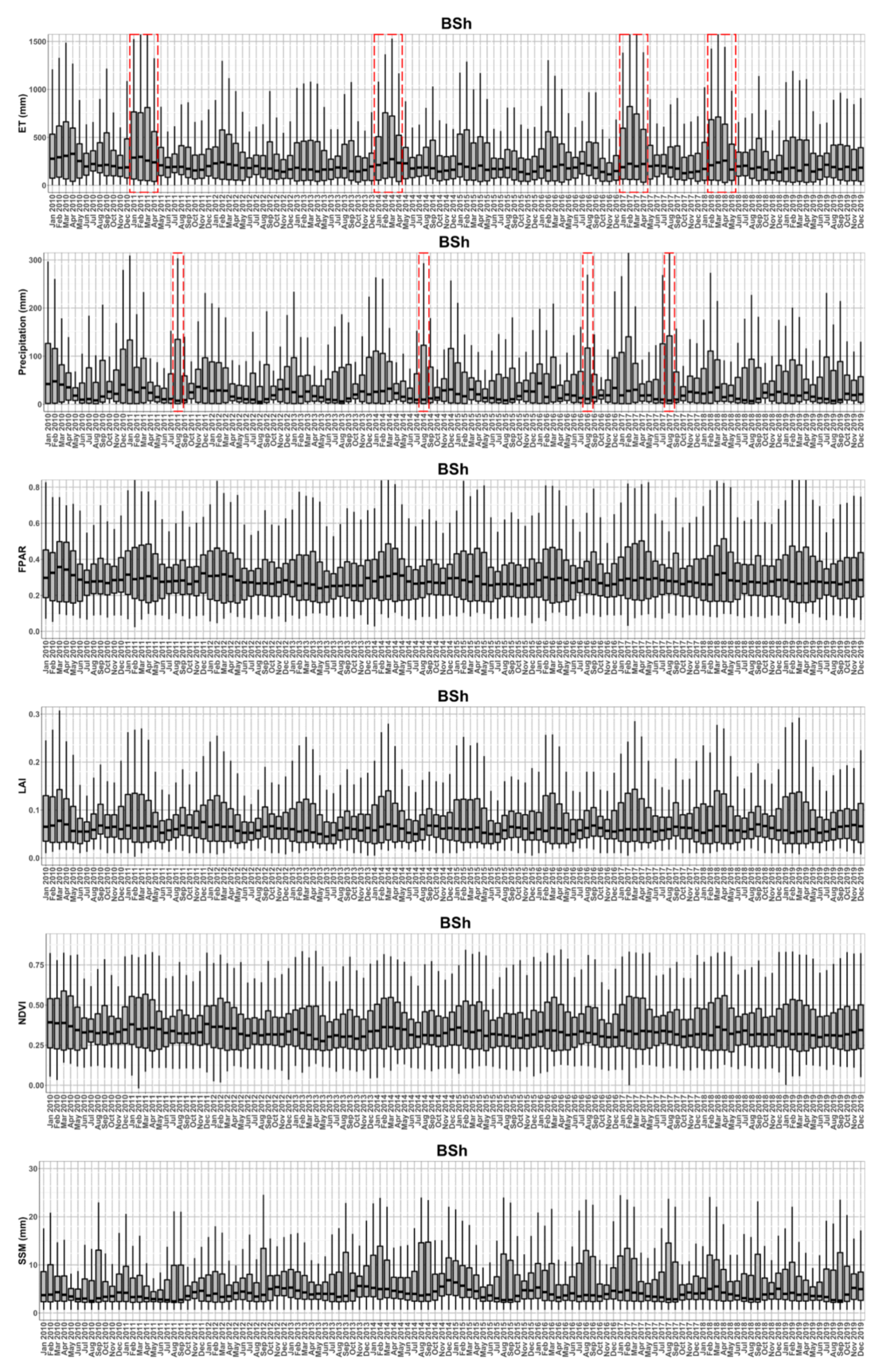
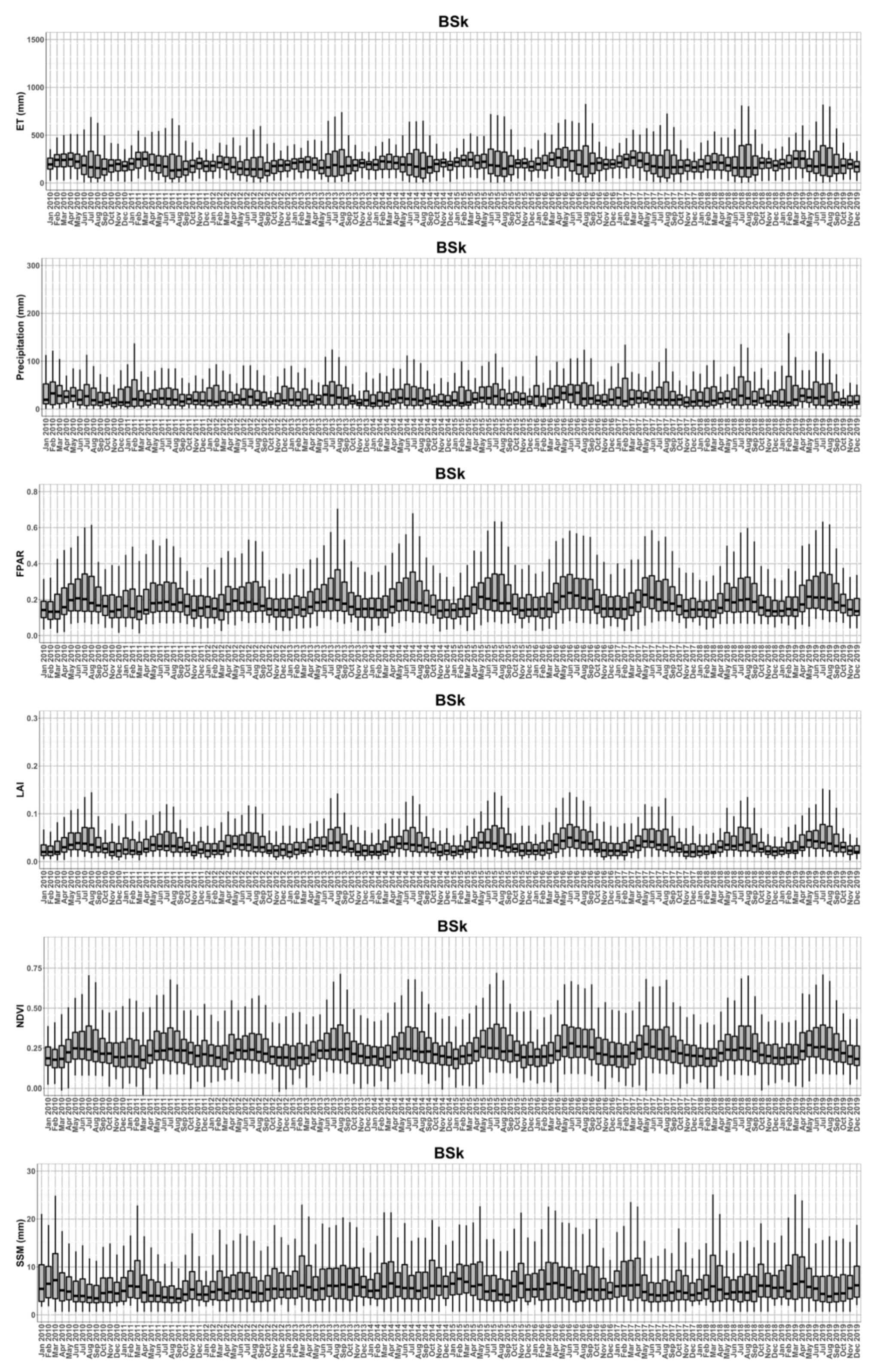
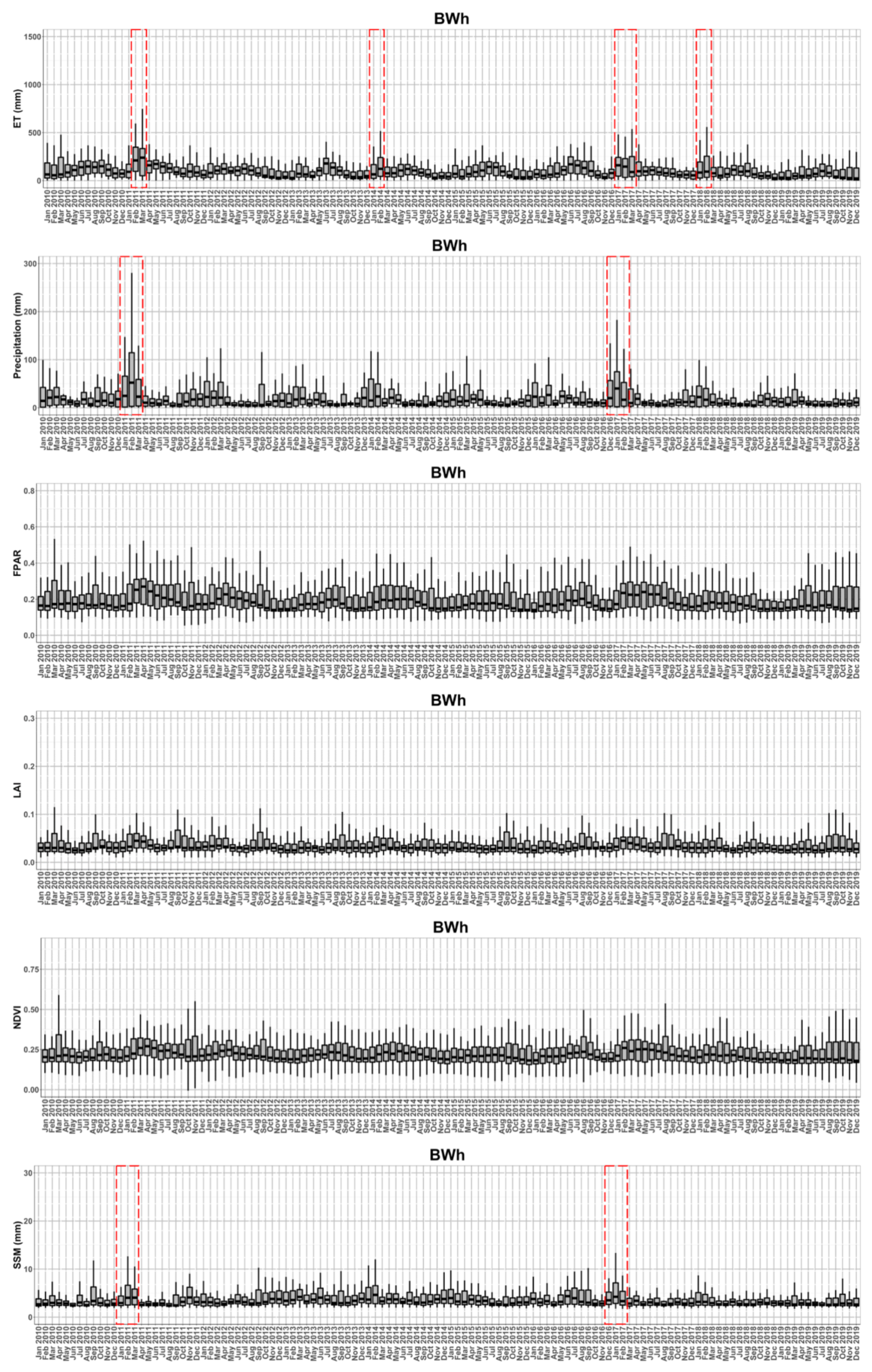
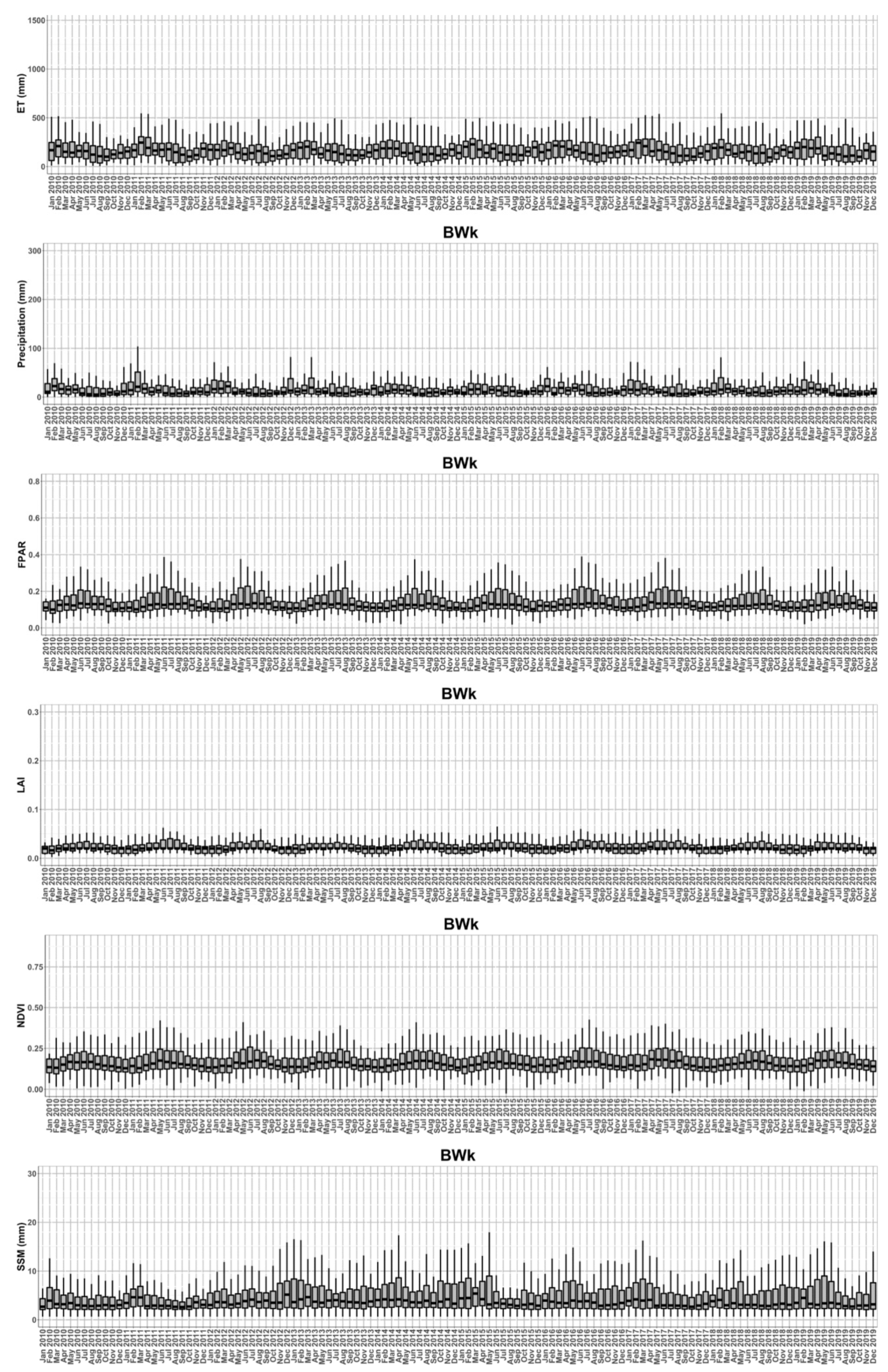
3.1. The Time Series of Multiple Hydrological Parameters
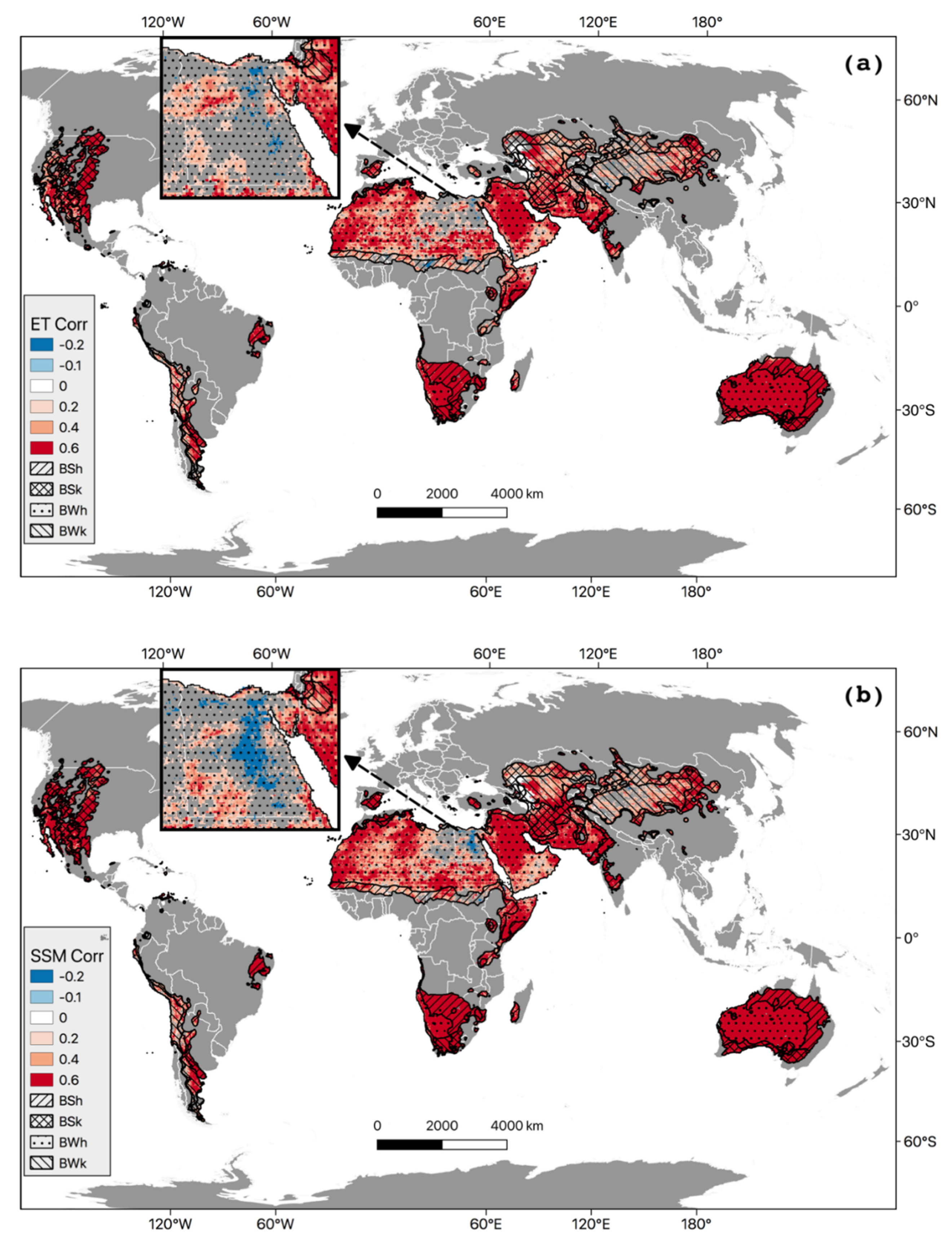
3.2. Trends of Multiple Hydrological Parameters
3.3. The Landcover and Water Storage Changes
3.4. The Comparison and Modeling of FLDAS and GLDAS ET and SSM Products
4. Discussions
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Assessment, M.E. Dryland Systems, Ecosystems and Human Well-Being: Current State and Trends; Island Press: Washington, DC, USA, 2005. [Google Scholar]
- Ahlstrom, A.; Raupach, M.R.; Schurgers, G.; Smith, B.; Arneth, A.; Jung, M.; Reichstein, M.; Canadell, J.G.; Friedlingstein, P.; Jain, A.K.; et al. The dominant role of semi-arid ecosystems in the trend and variability of the land CO2 sink. Science 2015, 348, 895–899. [Google Scholar] [CrossRef]
- Biederman, J.A.; Scott, R.L.; Bell, T.W.; Bowling, D.R.; Dore, S.; Garatuza-Payan, J.; Kolb, T.E.; Krishnan, P.; Krofcheck, D.J.; Litvak, M.E.; et al. CO2 exchange and evapotranspiration across dryland ecosystems of southwestern North America. Glob. Chang. Biol. 2017, 23, 4204–4221. [Google Scholar] [CrossRef]
- Humphrey, V.; Zscheischler, J.; Ciais, P.; Gudmundsson, L.; Sitch, S.; Seneviratne, S.I. Sensitivity of atmospheric CO2 growth rate to observed changes in terrestrial water storage. Nature 2018, 560, 628–631. [Google Scholar] [CrossRef]
- Poulter, B.; Frank, D.; Ciais, P.; Myneni, R.B.; Andela, N.; Bi, J.; Broquet, G.; Canadell, J.G.; Chevallier, F.; Liu, Y.Y.; et al. Contribution of semi-arid ecosystems to interannual variability of the global carbon cycle. Nature 2014, 509, 600–603. [Google Scholar] [CrossRef]
- Huang, J.; Guan, X.; Ji, F. Enhanced cold-season warming in semi-arid regions. Atmos. Chem. Phys. 2012, 12, 5391–5398. [Google Scholar] [CrossRef]
- Huang, J.; Yu, H.; Guan, X.; Wang, G.; Guo, R. Accelerated dryland expansion under climate change. Nat. Clim. Chang. 2016, 6, 166–171. [Google Scholar] [CrossRef]
- Cayan, D.R.; Das, T.; Pierce, D.W.; Barnett, T.P.; Tyree, M.; Gershunov, A. Future dryness in the southwest US and the hydrology of the early 21st century drought. Proc. Natl. Acad. Sci. USA 2010, 107, 21271–21276. [Google Scholar] [CrossRef] [PubMed]
- Cook, B.I.; Ault, T.R.; Smerdon, J.E. Unprecedented 21st century drought risk in the American Southwest and Central Plains. Sci. Adv. 2015, 1, e1400082. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Yu, H.; Dai, A.; Wei, Y.; Kang, L. Drylands face potential threat under 2 °C global warming target. Nat. Clim. Chang. 2017, 7, 417–422. [Google Scholar] [CrossRef]
- D’Odorico, P.; Porporato, A. (Eds.) Dryland Ecohydrology; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2006; ISBN 978-1-4020-4259-1. [Google Scholar]
- Scott, R.L.; Huxman, T.E.; Barron-Gafford, G.A.; Darrel Jenerette, G.; Young, J.M.; Hamerlynck, E.P. When vegetation change alters ecosystem water availability. Glob. Chang. Biol. 2014, 20, 2198–2210. [Google Scholar] [CrossRef] [PubMed]
- Noy-Meir, I. Desert Ecosystems: Environment and Producers. Annu. Rev. Ecol. Syst. 1973, 4, 25–51. [Google Scholar] [CrossRef]
- Reynolds, J.F.; Smith, D.M.S.; Lambin, E.F.; Turner, B.L.; Mortimore, M.; Batterbury, S.P.J.; Downing, T.E.; Dowlatabadi, H.; Fernandez, R.J.; Herrick, J.E.; et al. Global Desertification: Building a Science for Dryland Development. Science 2007, 316, 847–851. [Google Scholar] [CrossRef]
- Nagler, P.L.; Nguyen, U.; Bateman, H.L.; Jarchow, C.J.; Glenn, E.P.; Waugh, W.J.; van Riper, C. Northern tamarisk beetle (Diorhabda carinulata) and tamarisk (Tamarix spp.) interactions in the Colorado River basin: Northern tamarisk beetle and tamarisk interactions. Restor. Ecol. 2018, 26, 348–359. [Google Scholar] [CrossRef]
- Nagler, P.L.; Jarchow, C.J.; Glenn, E.P. Remote sensing vegetation index methods to evaluate changes in greenness and evapotranspiration in riparian vegetation in response to the Minute 319 environmental pulse flow to Mexico. Proc. IAHS 2018, 380, 45–54. [Google Scholar] [CrossRef][Green Version]
- Fisher, J.B.; Melton, F.; Middleton, E.; Hain, C.; Anderson, M.; Allen, R.; McCabe, M.F.; Hook, S.; Baldocchi, D.; Townsend, P.A.; et al. The future of evapotranspiration: Global requirements for ecosystem functioning, carbon and climate feedbacks, agricultural management, and water resources: The Future of Evapotranspiration. Water Resour. Res. 2017, 53, 2618–2626. [Google Scholar] [CrossRef]
- Baldocchi, D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R.; et al. FLUXNET: A new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Novick, K.A.; Biederman, J.A.; Desai, A.R.; Litvak, M.E.; Moore, D.J.P.; Scott, R.L.; Torn, M.S. The AmeriFlux network: A coalition of the willing. Agric. For. Meteorol. 2018, 249, 444–456. [Google Scholar] [CrossRef]
- Mirtl, M.; Borer, E.T.; Djukic, I.; Forsius, M.; Haubold, H.; Hugo, W.; Jourdan, J.; Lindenmayer, D.; McDowell, W.H.; Muraoka, H.; et al. Genesis, goals and achievements of Long-Term Ecological Research at the global scale: A critical review of ILTER and future directions. Sci. Total Environ. 2018, 626, 1439–1462. [Google Scholar] [CrossRef]
- Schimel, D.; Hargrove, W.; Hoffman, F.; MacMahon, J. NEON: A hierarchically designed national ecological network. Front. Ecol. Environ. 2007, 5, 59. [Google Scholar] [CrossRef]
- Kowalik, W.S.; Marsh, S.E.; Lyon, R.J.P. A relation between landsat digital numbers, surface reflectance, and the cosine of the solar zenith angle. Remote Sens. Environ. 1982, 12, 39–55. [Google Scholar] [CrossRef]
- Marsh, S.E.; Lyon, R.J.P. Quantitative relationships of near-surface spectra to Landsat radiometric data. Remote Sens. Environ. 1980, 10, 241–261. [Google Scholar] [CrossRef]
- Rouse, J., Jr. Contractor Report (CR): Monitoring the Vernal Advancement and Retrogradation (Green Wave Effect) of Natural Vegetation; NTRS—NASA Technical Reports Server: Washington, DC, USA, 1974.
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Anyamba, A.; Tucker, C.J. Analysis of Sahelian vegetation dynamics using NOAA-AVHRR NDVI data from 1981–2003. J. Arid Environ. 2005, 63, 596–614. [Google Scholar] [CrossRef]
- Donohue, R.J.; McVicar, T.R.; Roderick, M.L. Climate-related trends in Australian vegetation cover as inferred from satellite observations, 1981–2006. Glob. Chang. Biol. 2009, 15, 1025–1039. [Google Scholar] [CrossRef]
- Fensholt, R.; Rasmussen, K. Analysis of trends in the Sahelian ‘rain-use efficiency’ using GIMMS NDVI, RFE and GPCP rainfall data. Remote Sens. Environ. 2011, 115, 438–451. [Google Scholar] [CrossRef]
- Donohue, R.J.; Roderick, M.L.; McVicar, T.R.; Farquhar, G.D. Impact of CO2 fertilization on maximum foliage cover across the globe’s warm, arid environments: CO2 Fertilization and Foliage Cover. Geophys. Res. Lett. 2013, 40, 3031–3035. [Google Scholar] [CrossRef]
- Fensholt, R.; Langanke, T.; Rasmussen, K.; Reenberg, A.; Prince, S.D.; Tucker, C.; Scholes, R.J.; Le, Q.B.; Bondeau, A.; Eastman, R.; et al. Greenness in semi-arid areas across the globe 1981–2007—An Earth Observing Satellite based analysis of trends and drivers. Remote Sens. Environ. 2012, 121, 144–158. [Google Scholar] [CrossRef]
- Helldén, U.; Tottrup, C. Regional desertification: A global synthesis. Glob. Planet. Chang. 2008, 64, 169–176. [Google Scholar] [CrossRef]
- Kolby Smith, W.; Reed, S.C.; Cleveland, C.C.; Ballantyne, A.P.; Anderegg, W.R.L.; Wieder, W.R.; Liu, Y.Y.; Running, S.W. Large divergence of satellite and Earth system model estimates of global terrestrial CO2 fertilization. Nat. Clim. Chang. 2016, 6, 306–310. [Google Scholar] [CrossRef]
- Zhu, Z.; Piao, S.; Myneni, R.B.; Huang, M.; Zeng, Z.; Canadell, J.G.; Ciais, P.; Sitch, S.; Friedlingstein, P.; Arneth, A.; et al. Greening of the Earth and its drivers. Nat. Clim. Chang. 2016, 6, 791–795. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- El-Nadry, M.; Li, W.; El-Askary, H.; Awad, M.A.; Mostafa, A.R. Urban Health Related Air Quality Indicators over the Middle East and North Africa Countries Using Multiple Satellites and AERONET Data. Remote Sens. 2019, 11, 2096. [Google Scholar] [CrossRef]
- Maneja, R.H.; Miller, J.D.; Li, W.; El-Askary, H.; Flandez, A.V.B.; Dagoy, J.J.; Alcaria, J.F.A.; Basali, A.U.; Al-Abdulkader, K.A.; Loughland, R.A.; et al. Long-term NDVI and recent vegetation cover profiles of major offshore island nesting sites of sea turtles in Saudi waters of the northern Arabian Gulf. Ecol. Indic. 2020, 117, 106612. [Google Scholar] [CrossRef]
- Li, W.; El-Askary, H.; Qurban, M.A.; Li, J.; ManiKandan, K.P.; Piechota, T. Using multi-indices approach to quantify mangrove changes over the Western Arabian Gulf along Saudi Arabia coast. Ecol. Indic. 2019, 102, 734–745. [Google Scholar] [CrossRef]
- Li, W.; El-Askary, H.M.; Qurban, M.; Allali, M.; Manikandan, K. On the drying trends over the MENA countries using harmonic analysis of the enhanced vegetation index. In Advances in Remote Sensing and Geo Informatics Applications; El-Askary, H.M., Lee, S., Heggy, E., Pradhan, B., Eds.; Springer: Cham, Switzerland, 2019; pp. 243–245. ISBN 978-3-030-01439-1. [Google Scholar]
- Li, W.; El-Askary, H.; Lakshmi, V.; Piechota, T.; Struppa, D. Earth Observation and Cloud Computing in Support of Two Sustainable Development Goals for the River Nile Watershed Countries. Remote Sens. 2020, 12, 1391. [Google Scholar] [CrossRef]
- Li, W.; Ali, E.; Abou El-Magd, I.; Mourad, M.M.; El-Askary, H. Studying the Impact on Urban Health over the Greater Delta Region in Egypt Due to Aerosol Variability Using Optical Characteristics from Satellite Observations and Ground-Based aeronet Measurements. Remote Sens. 2019, 11, 1998. [Google Scholar] [CrossRef]
- Bastin, J.-F.; Berrahmouni, N.; Grainger, A.; Maniatis, D.; Mollicone, D.; Moore, R.; Patriarca, C.; Picard, N.; Sparrow, B.; Abraham, E.M.; et al. The extent of forest in dryland biomes. Science 2017, 356, 635–638. [Google Scholar] [CrossRef]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and future Köppen-Geiger climate classification maps at 1-km resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef]
- Hengl, T.; Walsh, M.G.; Sanderman, J.; Wheeler, I.; Harrison, S.P.; Prentice, I.C. Global mapping of potential natural vegetation: An assessment of Machine Learning algorithms for estimating land potential. PeerJ 2018, 6, e5457. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef]
- Bolten, J.D.; Crow, W.T.; Zhan, X.; Jackson, T.J.; Reynolds, C.A. Evaluating the Utility of Remotely Sensed Soil Moisture Retrievals for Operational Agricultural Drought Monitoring. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 57–66. [Google Scholar] [CrossRef]
- Mladenova, I.E.; Bolten, J.D.; Crow, W.T.; Anderson, M.C.; Hain, C.R.; Johnson, D.M.; Mueller, R. Intercomparison of Soil Moisture, Evaporative Stress, and Vegetation Indices for Estimating Corn and Soybean Yields Over the U.S. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1328–1343. [Google Scholar] [CrossRef]
- Mohammed, I.; Bolten, J.; Srinivasan, R.; Lakshmi, V. Improved Hydrological Decision Support System for the Lower Mekong River Basin Using Satellite-Based Earth Observations. Remote Sens. 2018, 10, 885. [Google Scholar] [CrossRef] [PubMed]
- Kerr, Y.H.; Levine, D. Foreword to the Special Issue on the Soil Moisture and Ocean Salinity (SMOS) Mission. IEEE Trans. Geosci. Remote Sens. 2008, 46, 583–585. [Google Scholar] [CrossRef]
- Landerer, F.W.; Swenson, S.C. Accuracy of scaled GRACE terrestrial water storage estimates: Accuracy of GRACE-TWS. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. 2006, 33, L08402. [Google Scholar] [CrossRef]
- Swenson, S. GRACE Monthly Land Water Mass Grids Netcdf Release 5.0; PO.DAAC: Pasadena, CA, USA, 2012.
- Mu, Q.; Zhao, M.; Running, S.W. MODIS Global Terrestrial Evapotranspiration (ET) Product (NASA MOD16A2/A3) Collection 5. NASA Headquarters; Report; Numerical Terradynamic Simulation Group Publications: Missoula, MT, USA, 2013. [Google Scholar]
- Didan, K. MOD13A2 MODIS/Terra Vegetation Indices 16-Day L3 Global 1 km SIN Grid V006; NASA LP DAAC: Washington, DC, USA, 2015. [CrossRef]
- Myneni, R. MOD15A2H MODIS/Terra Leaf Area Index/FPAR 8-Day L4 Global 500 m SIN Grid V006; NASA LP DAAC: Washington, DC, USA, 2015. [CrossRef]
- Chen, J.M.; Black, T.A. Defining leaf area index for non-flat leaves. Plant Cell Environ. 1992, 15, 421–429. [Google Scholar] [CrossRef]
- Fensholt, R.; Sandholt, I.; Rasmussen, M.S. Evaluation of MODIS LAI, fAPAR and the relation between fAPAR and NDVI in a semi-arid environment using in situ measurements. Remote Sens. Environ. 2004, 91, 490–507. [Google Scholar] [CrossRef]
- McNally, A.; Arsenault, K.; Kumar, S.; Shukla, S.; Peterson, P.; Wang, S.; Funk, C.; Peters-Lidard, C.D.; Verdin, J.P. A land data assimilation system for sub-Saharan Africa food and water security applications. Sci. Data 2017, 4, 170012. [Google Scholar] [CrossRef]
- Derber, J.C.; Parrish, D.F.; Lord, S.J. The new global operational analysis system at the National Meteorological Center. Weather Forecast. 1991, 6, 538–547. [Google Scholar] [CrossRef]
- Adler, R.F.; Huffman, G.J.; Chang, A.; Ferraro, R.; Xie, P.-P.; Janowiak, J.; Rudolf, B.; Schneider, U.; Curtis, S.; Bolvin, D.; et al. The version-2 global precipitation climatology project (GPCP) monthly precipitation analysis (1979–present). J. Hydrometeorol. 2003, 4, 1147–1167. [Google Scholar] [CrossRef]
- NASA GSFC Hydrological Sciences Laboratory (HSL). FLDAS Noah Land Surface Model L4 Global Monthly 0.1 × 0.1 Degree (MERRA-2 and CHIRPS) V001; Amy McNally NASA/GSFC/HSL: Greenbelt, MD, USA, 2018.
- Xie, P.; Arkin, P.A. Global precipitation: A 17-year monthly analysis based on gauge observations, satellite estimates, and numerical model outputs. Bull. Am. Meteorol. Soc. 1997, 78, 2539–2558. [Google Scholar] [CrossRef]
- Sheffield, J.; Goteti, G.; Wood, E.F. Development of a 50-Year High-Resolution Global Dataset of Meteorological Forcings for Land Surface Modeling. J. Clim. 2006, 19, 3088–3111. [Google Scholar] [CrossRef]
- Li, W.; El-Askary, H.; Qurban, M.; Proestakis, E.; Garay, M.; Kalashnikova, O.; Amiridis, V.; Gkikas, A.; Marinou, E.; Piechota, T.; et al. An Assessment of Atmospheric and Meteorological Factors Regulating Red Sea Phytoplankton Growth. Remote Sens. 2018, 10, 673. [Google Scholar] [CrossRef]
- Li, W.; El-Askary, H.; ManiKandan, K.; Qurban, M.; Garay, M.; Kalashnikova, O. Synergistic Use of Remote Sensing and Modeling to Assess an Anomalously High Chlorophyll-a Event during Summer 2015 in the South Central Red Sea. Remote Sens. 2017, 9, 778. [Google Scholar] [CrossRef]
- Xu, Q.-S.; Liang, Y.-Z. Monte Carlo cross validation. Chemom. Intell. Lab. Syst. 2001, 56, 1–11. [Google Scholar] [CrossRef]
- Tiwari, S.P.; Sarma, Y.V.B.; Kurten, B.; Ouhssain, M.; Jones, B.H. An Optical Algorithm to Estimate Downwelling Diffuse Attenuation Coefficient in the Red Sea. IEEE Trans. Geosci. Remote Sens. 2018, 56, 7174–7182. [Google Scholar] [CrossRef]
- Zhang, R.; Xu, Z.; Zuo, D.; Ban, C. Hydro-Meteorological Trends in the Yarlung Zangbo River Basin and Possible Associations with Large-Scale Circulation. Water 2020, 12, 144. [Google Scholar] [CrossRef]
- Ahmed, K.; Shahid, S.; Wang, X.; Nawaz, N.; Najeebullah, K. Evaluation of Gridded Precipitation Datasets over Arid Regions of Pakistan. Water 2019, 11, 210. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H.; Papalexiou, S.M.; Langousis, A.; Khatami, S.; Volpi, E.; Grimaldi, S. Global-scale massive feature extraction from monthly hydroclimatic time series: Statistical characterizations, spatial patterns and hydrological similarity. arXiv 2020, arXiv:2010.12833. [Google Scholar]
- Yan, D.; Scott, R.L.; Moore, D.J.P.; Biederman, J.A.; Smith, W.K. Understanding the relationship between vegetation greenness and productivity across dryland ecosystems through the integration of PhenoCam, satellite, and eddy covariance data. Remote Sens. Environ. 2019, 223, 50–62. [Google Scholar] [CrossRef]
- Vanleeuwen, W.; Huete, A.; Duncan, J.; Franklin, J. Radiative transfer in shrub savanna sites in Niger: Preliminary results from HAPEX-Sahel. 3. Optical dynamics and vegetation index sensitivity to biomass and plant cover. Agric. For. Meteorol. 1994, 69, 267–288. [Google Scholar] [CrossRef]
- Houborg, R.; McCabe, M.F. Adapting a regularized canopy reflectance model (REGFLEC) for the retrieval challenges of dryland agricultural systems. Remote Sens. Environ. 2016, 186, 105–120. [Google Scholar] [CrossRef]
- Middleton, E.M.; Deering, D.W.; Ahmad, S.P. Surface anisotropy and hemispheric reflectance for a semiarid ecosystem. Remote Sens. Environ. 1987, 23, 193–212. [Google Scholar] [CrossRef]
- van Leeuwen, W.J.D.; Huete, A.R. Effects of standing litter on the biophysical interpretation of plant canopies with spectral indices. Remote Sens. Environ. 1996, 55, 123–138. [Google Scholar] [CrossRef]
- Huete, A.R.; Jackson, R.D. Suitability of spectral indices for evaluating vegetation characteristics on arid rangelands. Remote Sens. Environ. 1987, 23, 213-IN8. [Google Scholar] [CrossRef]
- Huete, A.R.; Tucker, C.J. Investigation of soil influences in AVHRR red and near-infrared vegetation index imagery. Int. J. Remote Sens. 1991, 12, 1223–1242. [Google Scholar] [CrossRef]
- Baret, F.; Guyot, G. Potentials and limits of vegetation indices for LAI and APAR assessment. Remote Sens. Environ. 1991, 35, 161–173. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Lyon, R.J.P. Influence of rock-soil spectral variation on the assessment of green biomass. Remote Sens. Environ. 1985, 17, 265–279. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Myneni, R.B.; Hoffman, S.; Knyazikhin, Y.; Privette, J.L.; Glassy, J.; Tian, Y.; Wang, Y.; Song, X.; Zhang, Y.; Smith, G.R.; et al. Global products of vegetation leaf area and fraction absorbed PAR from year one of MODIS data. Remote Sens. Environ. 2002, 83, 214–231. [Google Scholar] [CrossRef]
- Owuor, S.O.; Butterbach-Bahl, K.; Guzha, A.C.; Rufino, M.C.; Pelster, D.E.; Díaz-Pinés, E.; Breuer, L. Groundwater recharge rates and surface runoff response to land use and land cover changes in semi-arid environments. Ecol. Process. 2016, 5, 16. [Google Scholar] [CrossRef]
- Siebert, S.; Burke, J.; Faures, J.-M.; Frenken, K.; Hoogeveen, J.; Döll, P.; Portmann, F.T. Groundwater use for irrigation—A global inventory. Hydrol. Earth Syst. Sci. 2010, 14, 1863–1880. [Google Scholar] [CrossRef]
- Santoni, C.S.; Jobbágy, E.G.; Contreras, S. Vadose zone transport in dry forests of central Argentina: Role of land use. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Jassas, H.; Kanoua, W.; Merkel, B. Actual Evapotranspiration in the Al-Khazir Gomal Basin (Northern Iraq) Using the Surface Energy Balance Algorithm for Land (SEBAL) and Water Balance. Geosciences 2015, 5, 141–159. [Google Scholar] [CrossRef]
- Mohamed, M.A.; Anders, J.; Schneider, C. Monitoring of Changes in Land Use/Land Cover in Syria from 2010 to 2018 Using Multitemporal Landsat Imagery and GIS. Land 2020, 9, 226. [Google Scholar] [CrossRef]
- Hassen, B.A.; Minch, A. GIS Based Groundwater Recharge Estimation: The Case of Shinile Sub-Basin; Arba Minch University: Arba Minch, Ethiopia, 2018. [Google Scholar]
- Manandhar, R.; Odeh, I.O.A.; Pontius, R.G. Analysis of twenty years of categorical land transitions in the Lower Hunter of New South Wales, Australia. Agric. Ecosyst. Environ. 2010, 135, 336–346. [Google Scholar] [CrossRef]
- Amdan, M.L.; Aragón, R.; Jobbágy, E.G.; Volante, J.N.; Paruelo, J.M. Onset of deep drainage and salt mobilization following forest clearing and cultivation in the Chaco plains (Argentina). Water Resour. Res. 2013, 49, 6601–6612. [Google Scholar] [CrossRef]
- Nosetto, M.D.; Jobbágy, E.G.; Brizuela, A.B.; Jackson, R.B. The hydrologic consequences of land cover change in central Argentina. Agric. Ecosyst. Environ. 2012, 154, 2–11. [Google Scholar] [CrossRef]
- Nosetto, M.D.; Acosta, A.M.; Jayawickreme, D.H.; Ballesteros, S.I.; Jackson, R.B.; Jobbágy, E.G. Land-use and topography shape soil and groundwater salinity in central Argentina. Agric. Water Manag. 2013, 129, 120–129. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, K.; Qin, J.; Zhao, L.; Tang, W.; Han, M. Evaluation of AMSR-E retrievals and GLDAS simulations against observations of a soil moisture network on the central Tibetan Plateau: Evaluate soil moisture products on tibet. J. Geophys. Res. Atmos. 2013, 118, 4466–4475. [Google Scholar] [CrossRef]
- Wang, L.; Caylor, K.K.; Villegas, J.C.; Barron-Gafford, G.A.; Breshears, D.D.; Huxman, T.E. Partitioning evapotranspiration across gradients of woody plant cover: Assessment of a stable isotope technique: Isotopic evapotranspiration partitioning. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Li, W.; Tiwari, S.P.; ManiKandan, K.P.; El-Askary, H. Ocean colormodeling in the central red sea using oceanographical obser-vation and simulated parameters. In Proceedings of the 2020 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Waikoloa, HI, USA, 26 September–2 October 2020; pp. 5620–5623. [Google Scholar]
- Nile Basin Initiative. In The Nile Basin Water Resources Atlas; Nile Basin Initiative: Entebbe, Uganda, 2016. [Google Scholar]
- Montanari, A.; Koutsoyiannis, D. A blueprint for process-based modeling of uncertain hydrological systems: Stochastic process-based modeling. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Todini, E. Hydrological catchment modelling: Past, present and future. Hydrol. Earth Syst. Sci. 2007, 11, 468–482. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H.; Langousis, A.; Jayawardena, A.W.; Sivakumar, B.; Mamassis, N.; Montanari, A.; Koutsoyiannis, D. Probabilistic Hydrological Post-Processing at Scale: Why and How to Apply Machine-Learning Quantile Regression Algorithms. Water 2019, 11, 2126. [Google Scholar] [CrossRef]
- Montanari, A. Uncertainty of hydrological predictions. In Treatise on Water Science 2; Wilderer, P.A., Ed.; Elsevier: Amsterdam, The Netherlands, 2011; pp. 459–478. [Google Scholar]
- Smith, W.K.; Dannenberg, M.P.; Yan, D.; Herrmann, S.; Barnes, M.L.; Barron-Gafford, G.A.; Biederman, J.A.; Ferrenberg, S.; Fox, A.M.; Hudson, A.; et al. Remote sensing of dryland ecosystem structure and function: Progress, challenges, and opportunities. Remote Sens. Environ. 2019, 233, 111401. [Google Scholar] [CrossRef]


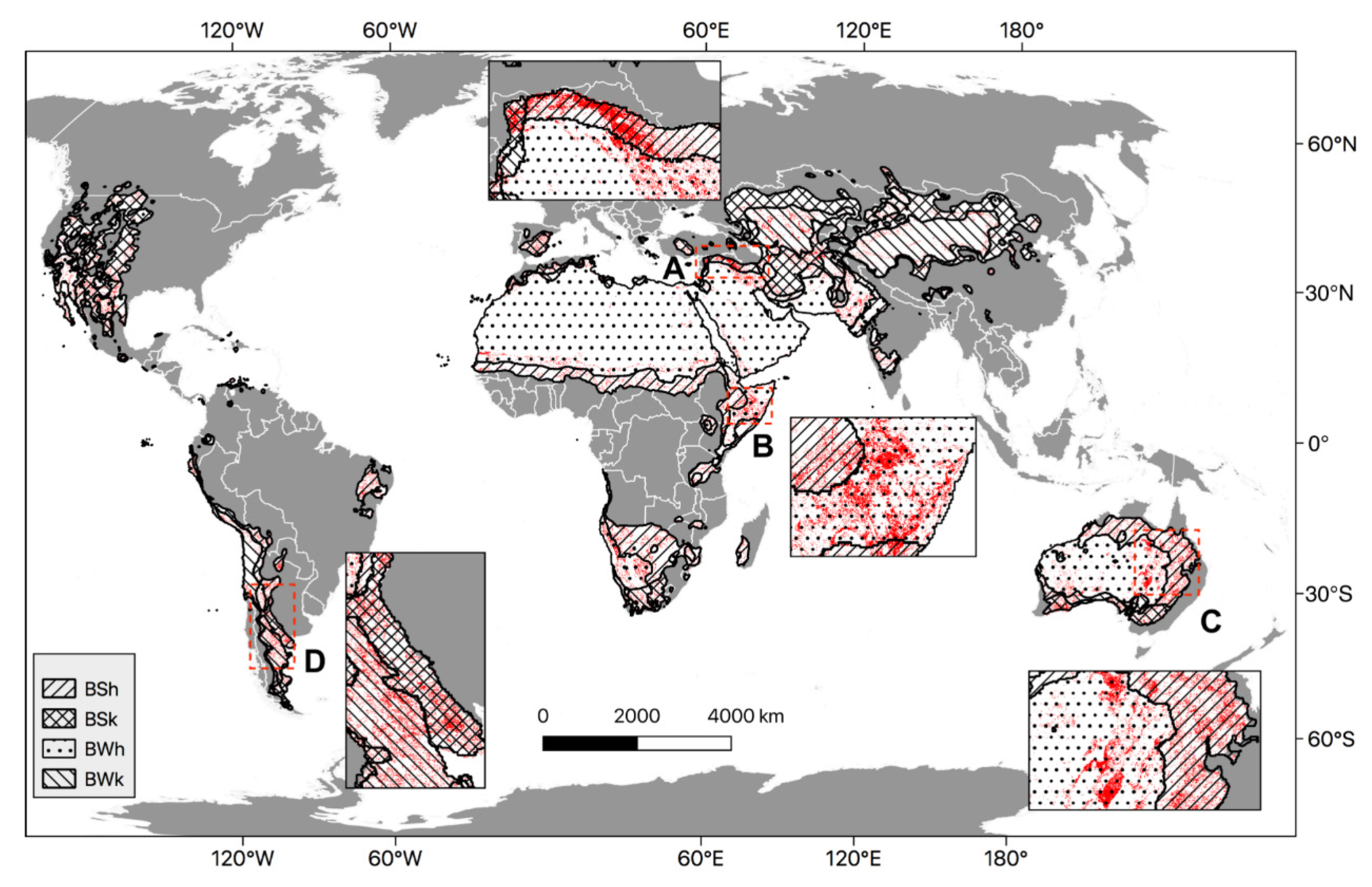





| Climate Type | Not Changed Landcover (Pixel Count) | Changed Landcover (Pixel Count) | Changed Landcover (Percentage) |
|---|---|---|---|
| BSh | 1,972,365 | 233,177 | 10.57% |
| BSk | 2,043,856 | 154,848 | 7.04% |
| BWh | 4,997,033 | 203,959 | 3.92% |
| BWk | 1,392,325 | 89,749 | 6.06% |
| Total | 10,405,579 | 681,733 | 6.15% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; El-Askary, H.; Thomas, R.; Tiwari, S.P.; Manikandan, K.P.; Piechota, T.; Struppa, D. An Assessment of the Hydrological Trends Using Synergistic Approaches of Remote Sensing and Model Evaluations over Global Arid and Semi-Arid Regions. Remote Sens. 2020, 12, 3973. https://doi.org/10.3390/rs12233973
Li W, El-Askary H, Thomas R, Tiwari SP, Manikandan KP, Piechota T, Struppa D. An Assessment of the Hydrological Trends Using Synergistic Approaches of Remote Sensing and Model Evaluations over Global Arid and Semi-Arid Regions. Remote Sensing. 2020; 12(23):3973. https://doi.org/10.3390/rs12233973
Chicago/Turabian StyleLi, Wenzhao, Hesham El-Askary, Rejoice Thomas, Surya Prakash Tiwari, Karuppasamy P. Manikandan, Thomas Piechota, and Daniele Struppa. 2020. "An Assessment of the Hydrological Trends Using Synergistic Approaches of Remote Sensing and Model Evaluations over Global Arid and Semi-Arid Regions" Remote Sensing 12, no. 23: 3973. https://doi.org/10.3390/rs12233973
APA StyleLi, W., El-Askary, H., Thomas, R., Tiwari, S. P., Manikandan, K. P., Piechota, T., & Struppa, D. (2020). An Assessment of the Hydrological Trends Using Synergistic Approaches of Remote Sensing and Model Evaluations over Global Arid and Semi-Arid Regions. Remote Sensing, 12(23), 3973. https://doi.org/10.3390/rs12233973