Modeling Gross Primary Production of Midwestern US Maize and Soybean Croplands with Satellite and Gridded Weather Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Site Summary
2.2. Input Data
2.2.1. Daymet Data
2.2.2. MODIS Data
2.2.3. AmeriFlux Data
2.3. GPP Modeling Approach
2.4. Calibration and Validation
- (1)
- Field Year Selection. For statistical purposes, 75% of field years were chosen randomly without replacement (i.e., 47 out of the 65 total field years) to calibrate the model (Table 2), to ensure at least one field year was reserved for each crop type for validation purposes for a total of 18 field years (Table 3).
- (2)
- LUEc Calibration. The iterative training process using an R script as described in Nguy-Robertson et al. [13] was used to determine ε0, β, σWscalar, and σPscalar values for irrigated and nonirrigated maize and soybean crops. The training utilized input values from the selected calibration field year flux data, Daymet derived Tavg, VPD, APAR, and Tscalar, and remotely-derived gLAI. The iterative process trained the parameters using a step-by-step method in which each scalar was estimated one at a time. During the iteration in which a parameter is calculated, assumptions are made about the other parameters to mimic optimal field conditions. Once the parameters are calculated, the iterations are repeated using the entire calibration dataset to produce ε0, β, σWscalar, and σPscalar values with corresponding standard deviations. The calibrated dataset includes AmeriFlux-derived GPP, Daymet-derived Tavg, VPD, CC, APAR, and Tscalar, and remotely derived gLAI data. Additionally, gLAImax values for irrigated and rainfed soybean and maize were estimated from MODIS-derived gLAI data (Equations (5) and (6)). From these outputs, scalars were calculated (Equations (8)–(15)).
- (3)
- Daily GPP Estimation. Data from validation field year datasets (Table 3) and parameters derived from the iterative process along with specified constants (Table 4), were used to calculate daily values of the scalars, Cscalar, Wscalar, and Pscalar (Equations (11), (14), and (15)) and APAR (Equation (10)), from which daily GPP values were estimated (Equation (8)).
- (4)
- LUEc Validation. The estimated daily GPP values were compared to the observed AmeriFlux determined daily GPP using linear regression (α = 0.05), with corresponding R2, root mean square error (RMSE), and mean normalized bias (MNB).
3. Results
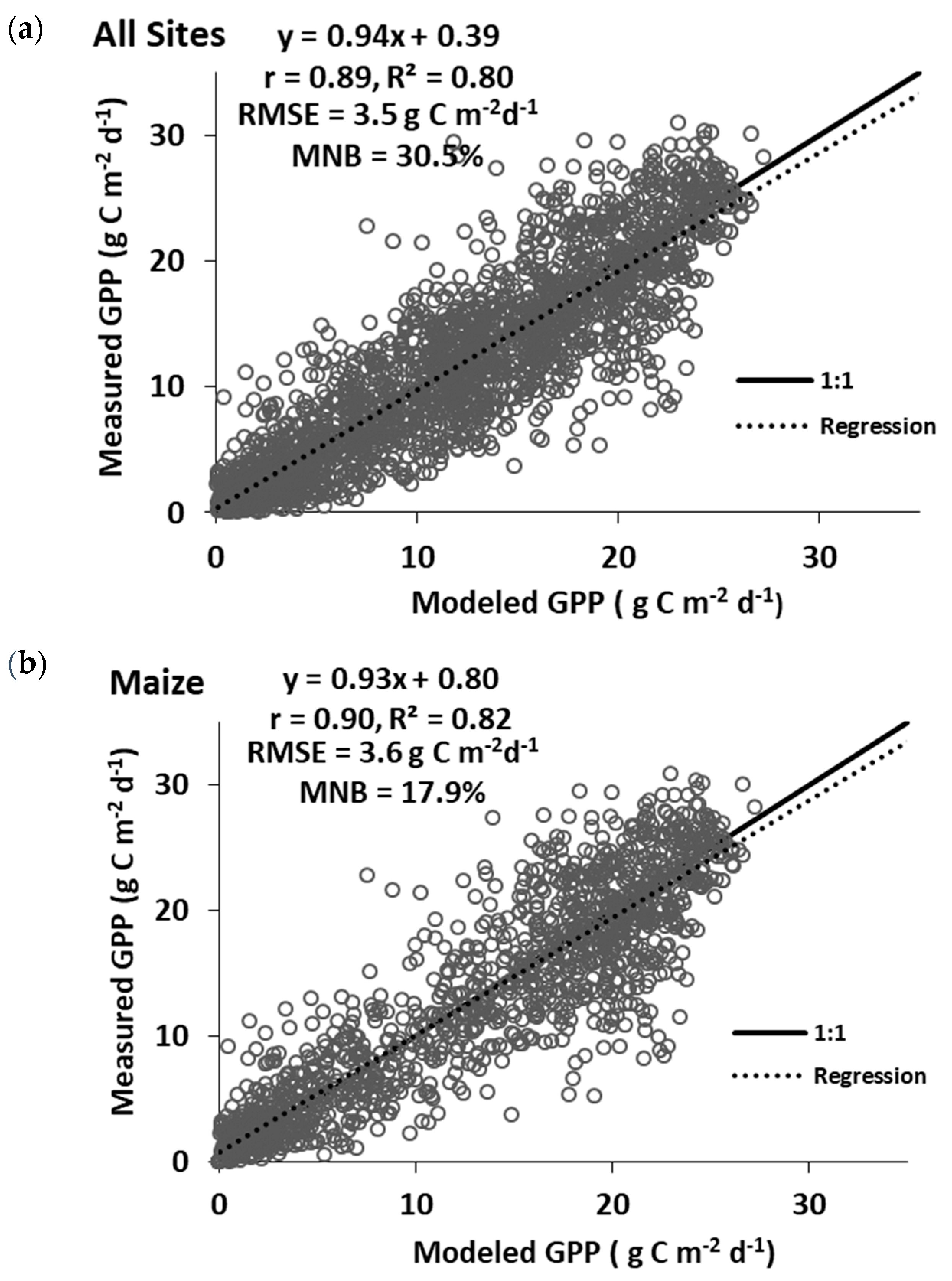
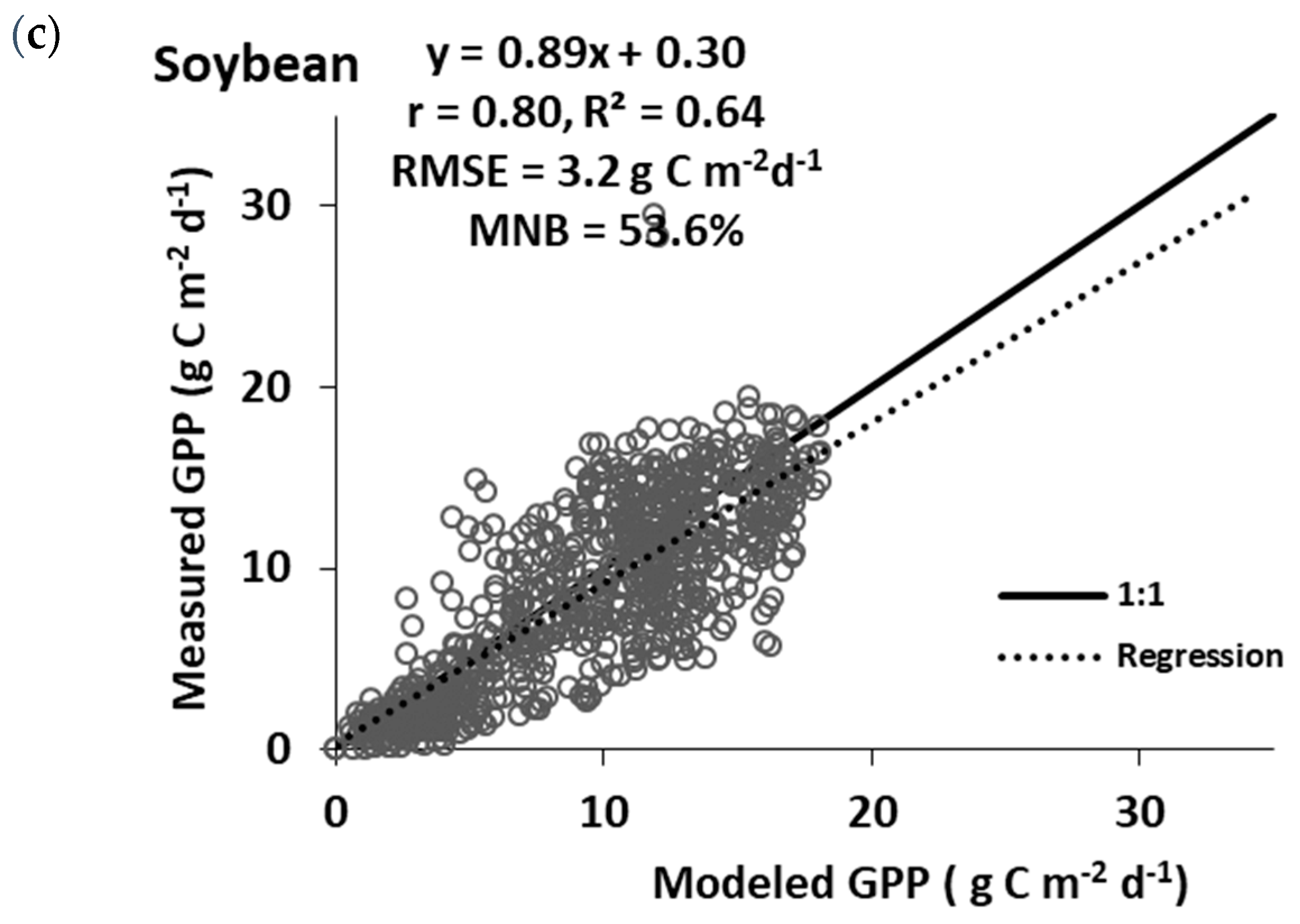
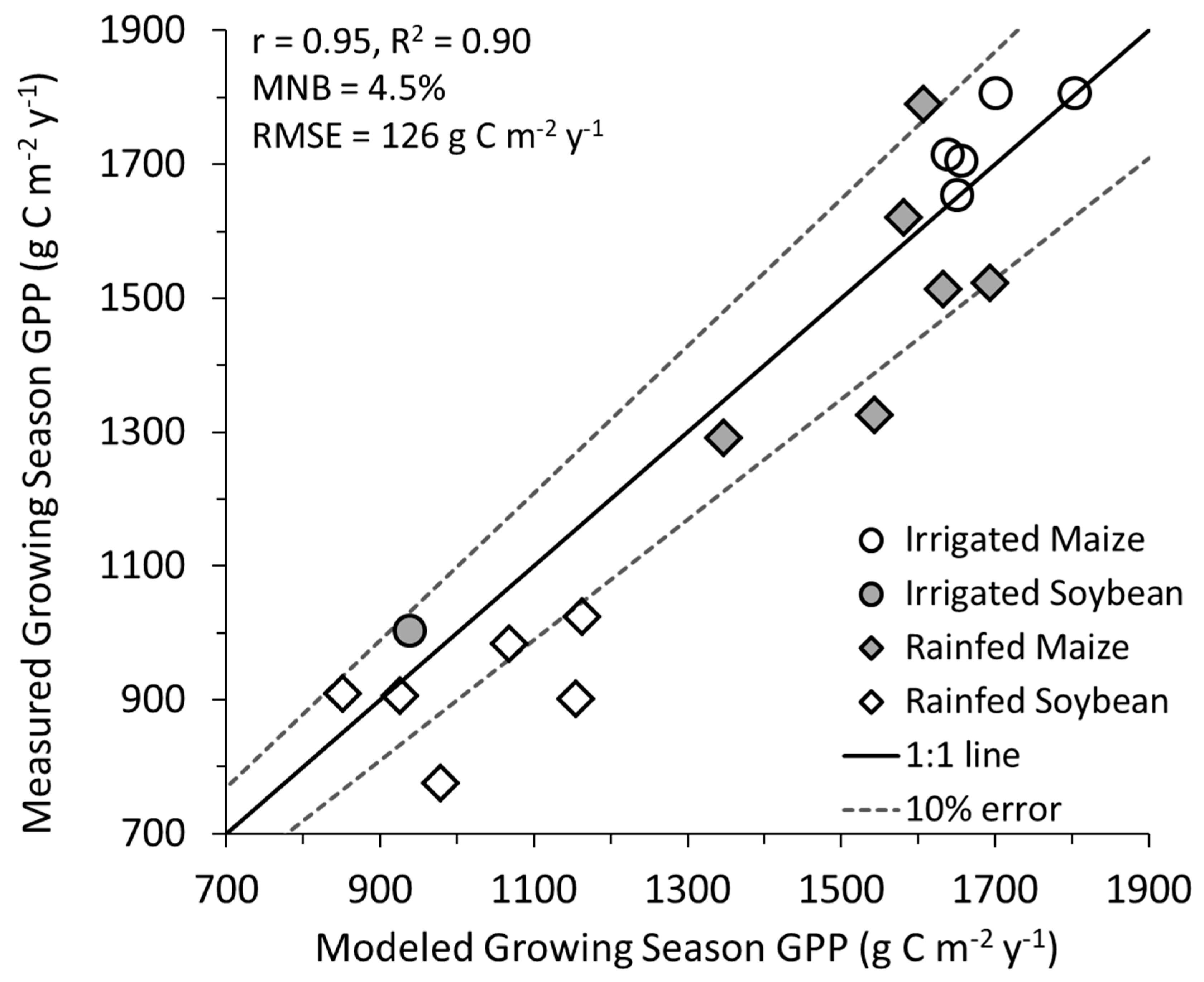
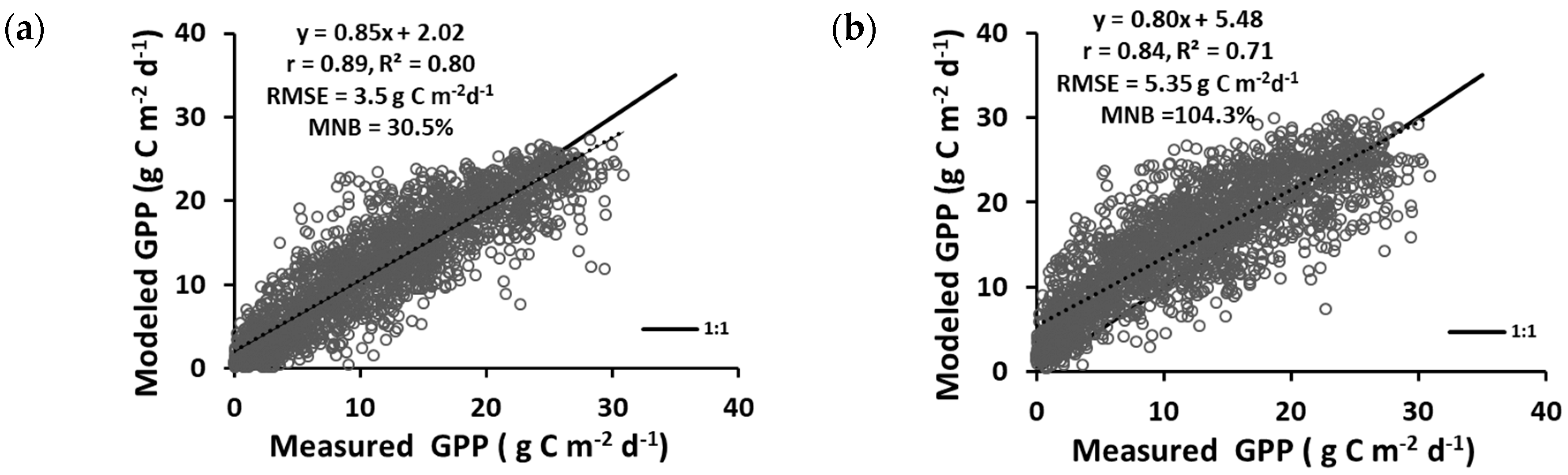
3.1. All Sites Years Combined
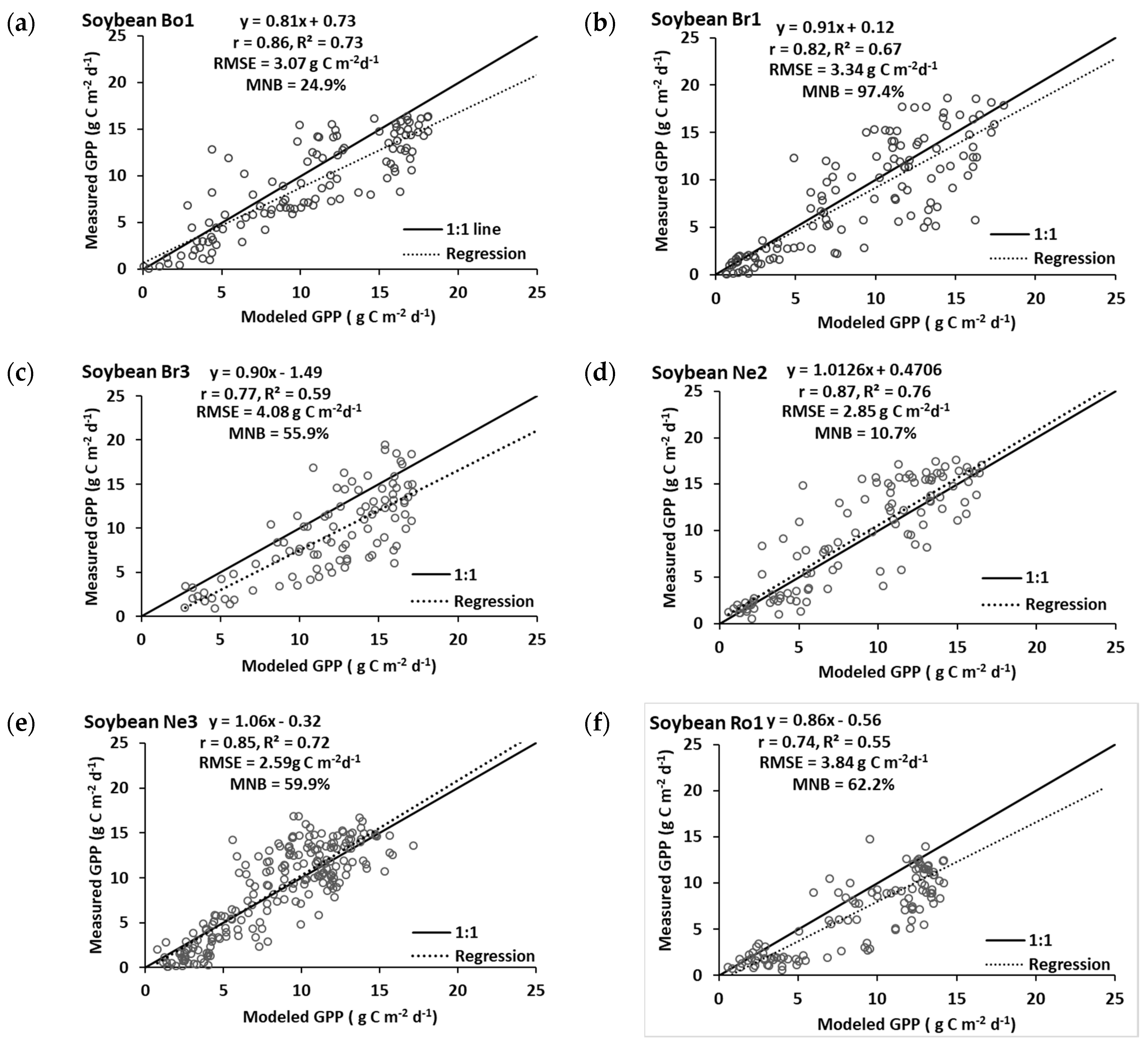
3.2. Maize and Soybean Field Years
4. Discussion
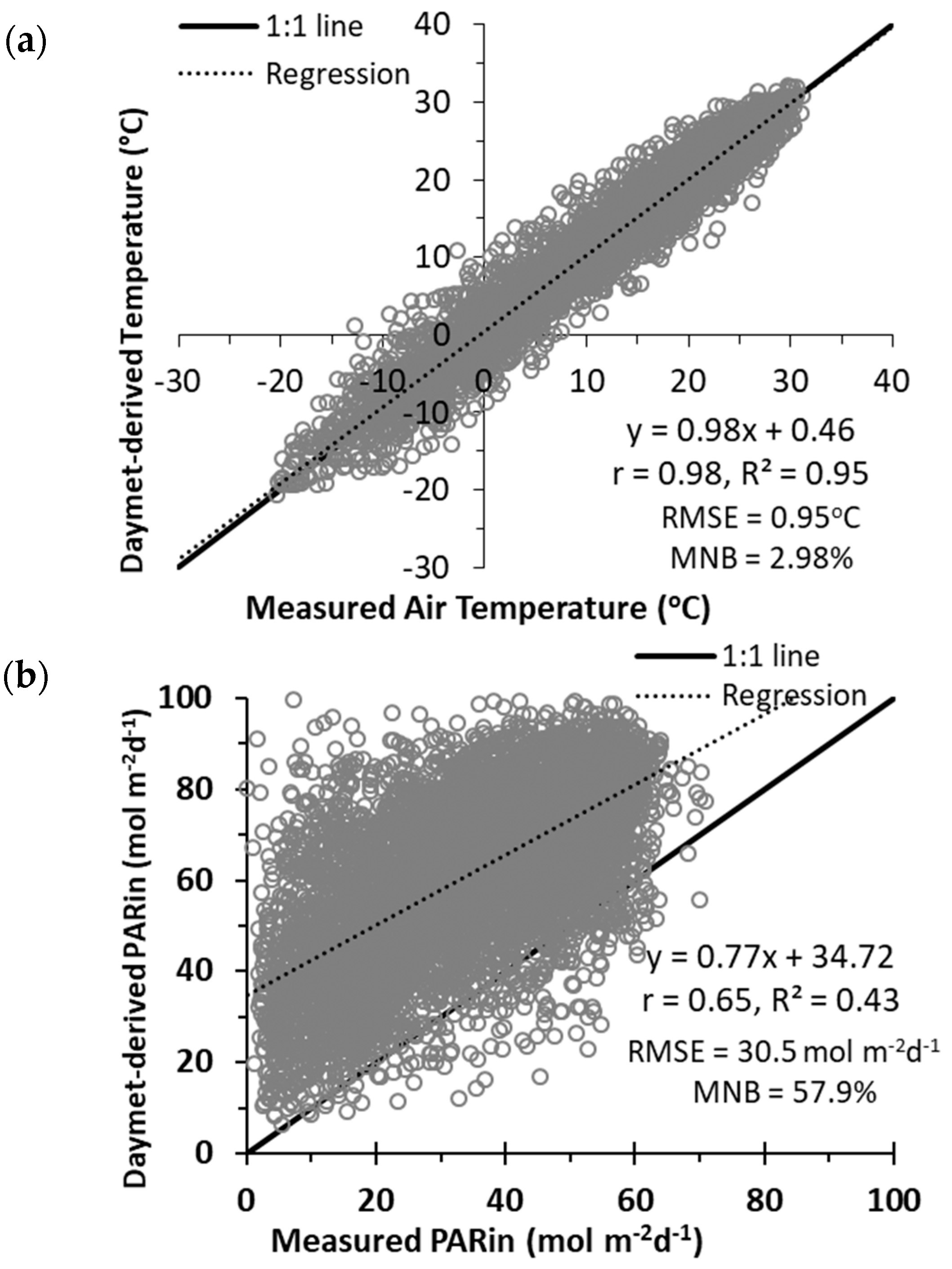
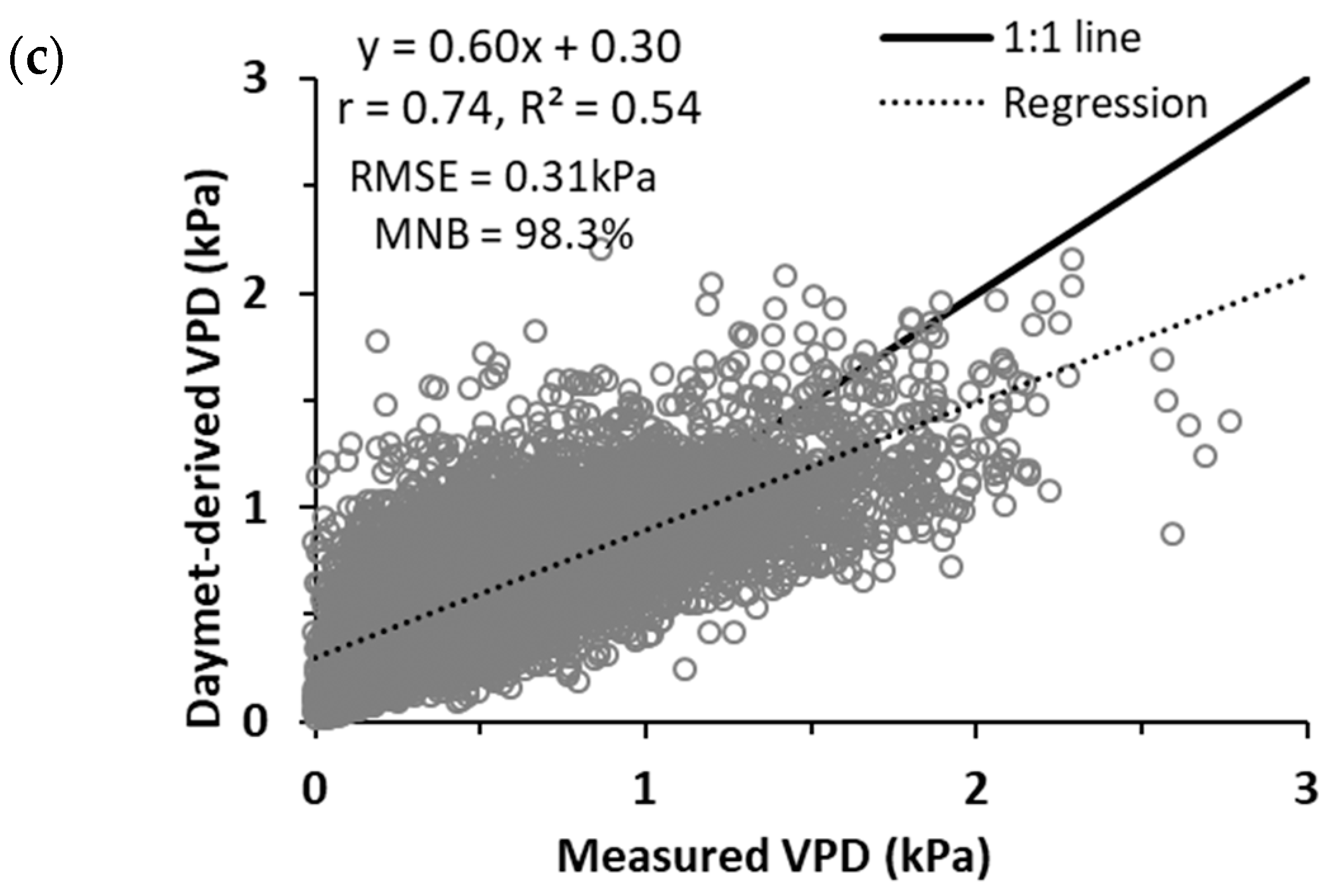
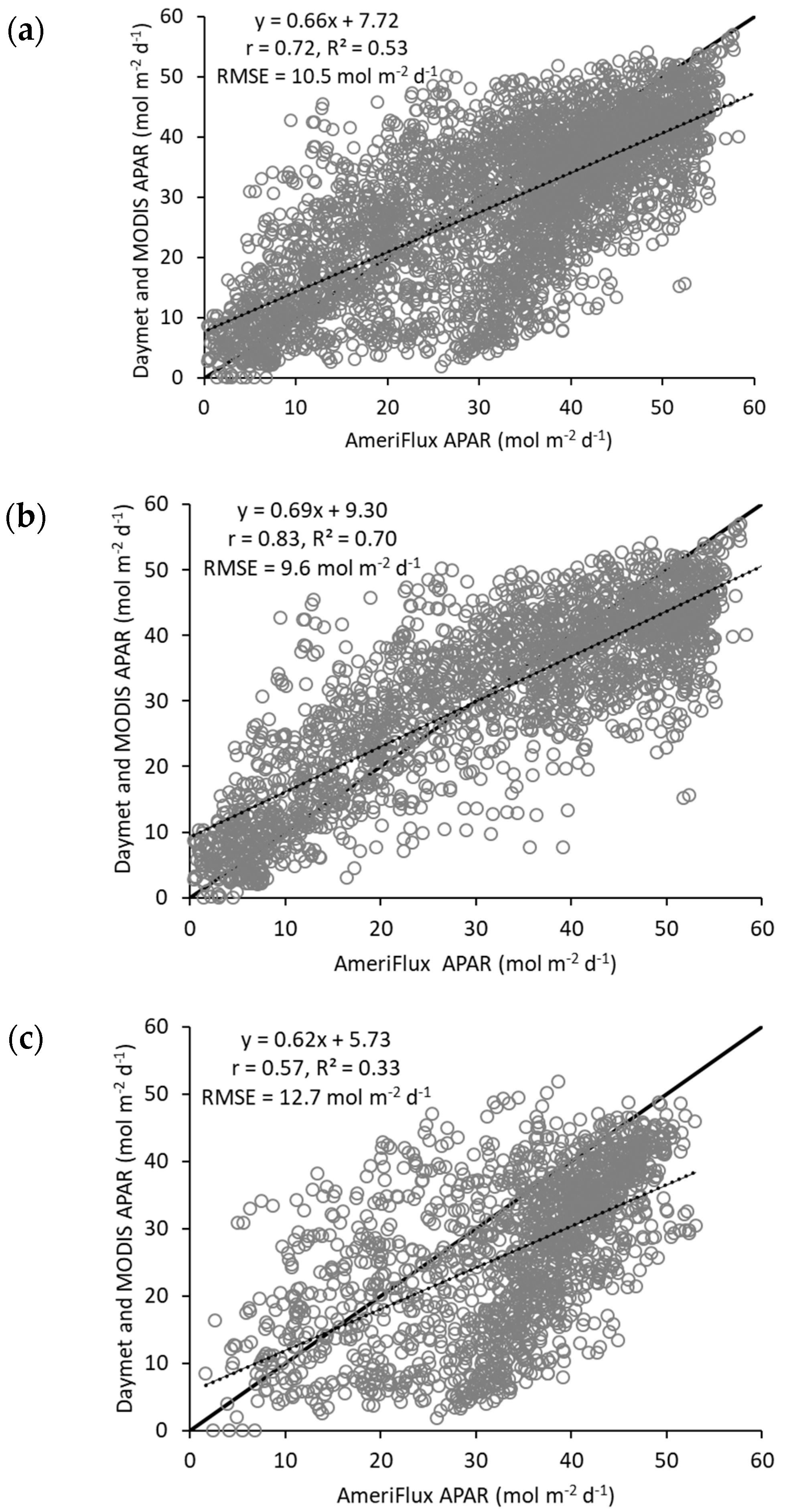
4.1. Daymet-Derived PARin and VPD
4.2. LUEc Scalars
4.3. gLAI Estimates
4.4. APAR Importance in GPP Estimates
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cui, T.; Wang, Y.; Sun, R.; Qiao, C.; Fan, W.; Jiang, G.; Hao, L.; Zhang, L. Estimating vegetation primary production in the heihe river basin of China with multi-source and multi-scale data. PLoS ONE 2016. [Google Scholar] [CrossRef] [PubMed]
- Beer, C.; Reichstein, M.; Tomelleri, E.; Ciais, P.; Jung, M.; Carvalhais, N.; Rödenbeck, C.; Arain, M.A.; Baldocchi, D.; Bonan, G.B.; et al. Terrestrial gross carbon dioxide uptake: Global distribution and covariation with climate. Science 2010. [Google Scholar] [CrossRef] [PubMed]
- Suyker, A.E.; Verma, S.B. Gross primary production and ecosystem respiration of irrigated and rainfed maize-soybean cropping systems over 8 years. Agric. For. Meteorol. 2012. [Google Scholar] [CrossRef]
- Matsushita, B.; Tamura, M. Integrating remotely sensed data with an ecosystem model to estimate net primary productivity in East Asia. Remote Sens. Environ. 2002. [Google Scholar] [CrossRef]
- Heinsch, F.; Reeves, M.; Votava, P.; Kang, S.; Cristina, M.; Zhao, M.; Glassy, J.; Jolly, W.; Loehman, R.; Bowker, C.F.; et al. User’s Guide GPP and NPP (MOD17A2/A3) Products NASA MODIS Land Algorithm. Version 2.0; University of Montana: Missoula, MT, USA, 2003. [Google Scholar]
- Heinsch, F.A.; Zhao, M.; Running, S.W.; Kimball, J.S.; Nemani, R.R.; Davis, K.J.; Bolstad, P.V.; Cook, B.D.; Desai, A.R.; Ricciuto, D.M.; et al. Evaluation of remote sensing based terrestrial productivity from MODIS using regional tower eddy flux network observations. IEEE Trans. Geosci. Remote Sens. 2006. [Google Scholar] [CrossRef]
- Xiao, X.; Hollinger, D.; Aber, J.; Goltz, M.; Davidson, E.A.; Zhang, Q.; Moore, B. Satellite-based modeling of gross primary production in an evergreen needleleaf forest. Remote Sens. Environ. 2004. [Google Scholar] [CrossRef]
- Tramontana, G.; Ichii, K.; Camps-Valls, G.; Tomelleri, E.; Papale, D. Uncertainty analysis of gross primary production upscaling using Random Forests, remote sensing and eddy covariance data. Remote Sens. Environ. 2015. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiao, X.; Wu, X.; Zhou, S.; Zhang, G.; Qin, Y.; Dong, J. A global moderate resolution dataset of gross primary production of vegetation for 2000–2016. Sci. Data 2017. [Google Scholar] [CrossRef]
- Yuan, W.; Cai, W.; Xia, J.; Chen, J.; Liu, S.; Dong, W.; Merbold, L.; Law, B.; Arain, A.; Beringer, J.; et al. Global comparison of light use efficiency models for simulating terrestrial vegetation gross primary production based on the LaThuile database. Agric. For. Meteorol. 2014. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, C.; Sun, G.; Band, L.E.; McNulty, S.; Noormets, A.; Zhang, Q.; Zhang, Z. Development of a coupled carbon and water model for estimating global gross primary productivity and evapotranspiration based on eddy flux and remote sensing data. Agric. For. Meteorol. 2016. [Google Scholar] [CrossRef]
- Running, S.; Zhao, M. Daily GPP and Annual NPP (MOD17A2/A3) Products NASA Earth Observing System MODIS Land Algorithm. In MOD17 User’s Guide; 2015; Available online: https://www.ntsg.umt.edu/files/modis/MOD17UsersGuide2015_v3.pdf (accessed on 9 October 2020).
- Nguy-Robertson, A.; Suyker, A.; Xiao, X. Modeling gross primary production of maize and soybean croplands using light quality, temperature, water stress, and phenology. Agric. For. Meteorol. 2015. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Arkebauer, T.J.; Suyker, A.E. Convergence of daily light use efficiency in irrigated and rainfed C3 and C4 crops. Remote Sens. Environ. 2018. [Google Scholar] [CrossRef]
- Li, A.; Bian, J.; Lei, G.; Huang, C. Estimating the maximal light use efficiency for different vegetation through the CASA model combined with time-series remote sensing data and ground measurements. Remote Sens. 2012, 4, 3857–3876. [Google Scholar] [CrossRef]
- Thornton, P.E.; Thornton, M.M.; Mayer, B.W.; Wilhelmi, N.; Wei, Y.; Devarakonda, R.; Cook, R.B. Daymet: Daily Surface Weather Data on a 1-km Grid for North America, Version 2; Data Set; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2014. [CrossRef]
- Weiss, A.; Norman, J.M. Partitioning solar radiation into direct and diffuse, visible and near-infrared components. Agric. For. Meteorol. 1985. [Google Scholar] [CrossRef]
- Biggs, W. Radiation Measurement. In Advanced Agricultural Instrumentation; Gensler, W.G., Ed.; Springer: Dordrecht, The Netherlands, 1986; pp. 3–20. ISBN 978-94-009-4404-6. [Google Scholar]
- Gitelson, A.A. Wide Dynamic Range Vegetation Index for Remote Quantification of Biophysical Characteristics of Vegetation. J. Plant Physiol. 2004. [Google Scholar] [CrossRef] [PubMed]
- Nguy-Robertson, A.L.; Gitelson, A.A. Algorithms for estimating green leaf area index in C3 and C4 crops for MODIS, Landsat TM/ETM+, MERIS, Sentinel MSI/OLCI, and Venμs sensors. Remote Sens. Lett. 2015. [Google Scholar] [CrossRef]
- Monteith, J.L. Solar Radiation and Productivity in Tropical Ecosystems. J. Appl. Ecol. 1972. [Google Scholar] [CrossRef]
- Raich, J.W. Potential net primary productivity in South America: Application of a global model. Ecol. Appl. 1991. [Google Scholar] [CrossRef]
- Kalfas, J.L.; Xiao, X.; Vanegas, D.X.; Verma, S.B.; Suyker, A.E. Modeling gross primary production of irrigated and rain-fed maize using MODIS imagery and CO2 flux tower data. Agric. For. Meteorol. 2011. [Google Scholar] [CrossRef]
- Wu, W.X.; Wang, S.Q.; Xiao, X.M.; Yu, G.R.; Fu, Y.L.; Hao, Y. Bin Modeling gross primary production of a temperate grassland ecosystem in Inner Mongolia, China, using MODIS imagery and climate data. Sci. China Ser. D Earth Sci. 2008. [Google Scholar] [CrossRef]
- Maselli, F.; Papale, D.; Puletti, N.; Chirici, G.; Corona, P. Combining remote sensing and ancillary data to monitor the gross productivity of water-limited forest ecosystems. Remote Sens. Environ. 2009. [Google Scholar] [CrossRef]
- Gilmanov, T.G.; Wylie, B.K.; Tieszen, L.L.; Meyers, T.P.; Baron, V.S.; Bernacchi, C.J.; Billesbach, D.P.; Burba, G.G.; Fischer, M.L.; Glenn, A.J.; et al. CO2 uptake and ecophysiological parameters of the grain crops of midcontinent North America: Estimates from flux tower measurements. Agric. Ecosyst. Environ. 2013. [Google Scholar] [CrossRef]
- Reich, P.B.; Walters, M.B.; Ellsworth, D.S. Leaf age and season influence the relationships between leaf nitrogen, leaf mass per area and photosynthesis in maple and oak trees. Plant Cell Environ. 1991. [Google Scholar] [CrossRef]
- Field, C.; Mooney, H.A. Leaf age and seasonal effects on light, water, and nitrogen use efficiency in a California shrub. Oecologia 1983. [Google Scholar] [CrossRef]
- Mourtzinis, S.; Rattalino Edreira, J.I.; Conley, S.P.; Grassini, P. From grid to field: Assessing quality of gridded weather data for agricultural applications. Eur. J. Agron. 2017. [Google Scholar] [CrossRef]
- Nguy-Robertson, A.; Peng, Y.; Arkebauer, T.; Scoby, D.; Schepers, J.; Gitelson, A. Using a Simple Leaf Color Chart to Estimate Leaf and Canopy Chlorophyll a Content in Maize (Zea mays). Commun. Soil Sci. Plant Anal. 2015. [Google Scholar] [CrossRef]
- Gilabert, M.A.; Moreno, A.; Maselli, F.; Martínez, B.; Chiesi, M.; Sánchez-Ruiz, S.; García-Haro, F.J.; Pérez-Hoyos, A.; Campos-Taberner, M.; Pérez-Priego, O.; et al. Daily GPP estimates in Mediterranean ecosystems by combining remote sensing and meteorological data. ISPRS J. Photogramm. Remote Sens. 2015, 102, 184–197. [Google Scholar] [CrossRef]
- Nasahara, K.N. Simple algorithm for estimation of photosynthetically active radiation (PAR) using satellite data. Sci. Online Lett. Atmos. 2009. [Google Scholar] [CrossRef]
- Sakamoto, T.; Gitelson, A.A.; Wardlow, B.D.; Verma, S.B.; Suyker, A.E. Estimating daily gross primary production of maize based only on MODIS WDRVI and shortwave radiation data. Remote Sens. Environ. 2011. [Google Scholar] [CrossRef]
- Daly, C.; Halbleib, M.; Smith, J.I.; Gibson, W.P.; Doggett, M.K.; Taylor, G.H.; Curtis, J.; Pasteris, P.P. Physiographically sensitive mapping of climatological temperature and precipitation across the conterminous United States. Int. J. Climatol. 2008, 28, 2031–2064. [Google Scholar] [CrossRef]
- Hazarika, M.K.; Yasuoka, Y.; Ito, A.; Dye, D. Estimation of net primary productivity by integrating remote sensing data with an ecosystem model. Remote Sens. Environ. 2005. [Google Scholar] [CrossRef]
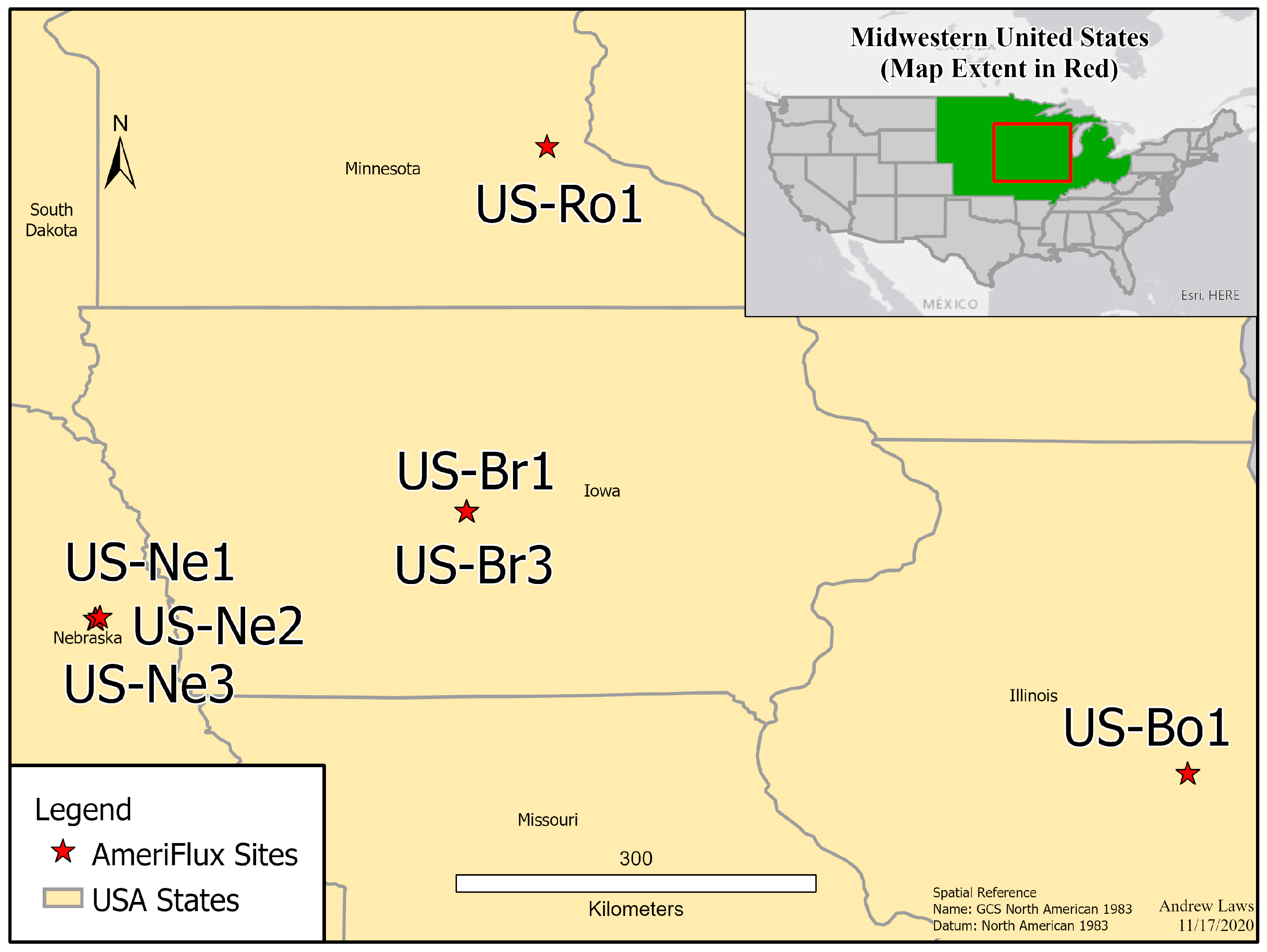
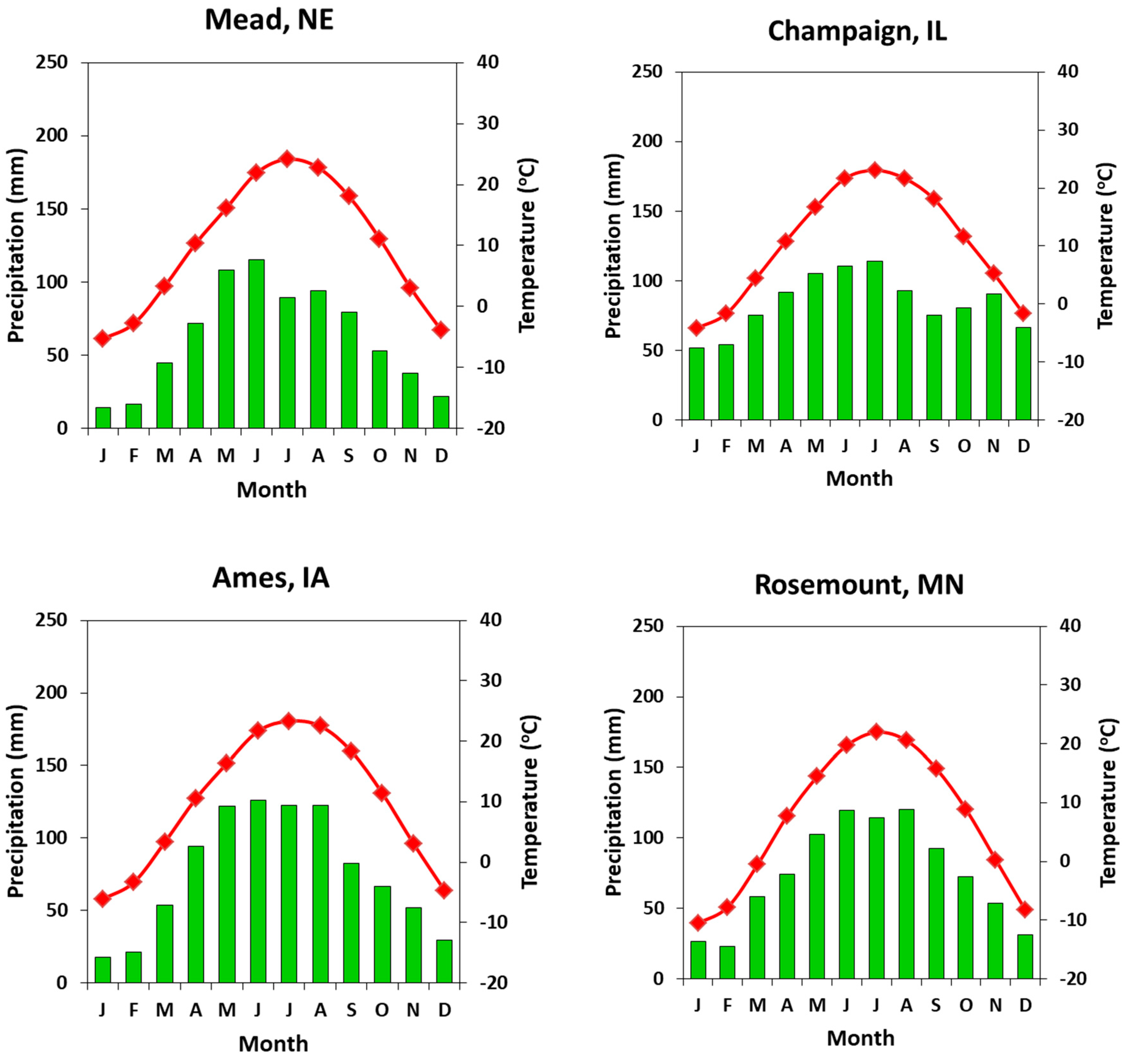

| Approximate Field Site Location | AmeriFlux Site | Latitude, Longitude, Elevation | Management | Maize Crop | Soybean Crop | Mean Annual Temperature (°C) | Mean Annual Precipitation [+Irrigation] (mm) | Area (ha) |
|---|---|---|---|---|---|---|---|---|
| Mead, NE | US-Ne1 | 41.1650° N, 96.4766° W, 361 m | Irrigated | 2002–2013 | -- | 10 | 790 [+242] | 49.8 |
| US-Ne2 | 41.1650° N, 96.4700° W, 362 m | Irrigated | 2003–2013 Odd years; 2010, 2012 | 2002–2008 Even years | 10 | 790 [+214] | 53.5 | |
| US-Ne3 | 41.1797° N, 96.4396° W, 363 m | Rainfed | 2003–2013 Odd years | 2002–2012 Even years | 10 | 790 | 66.2 | |
| Brooks Field, near Ames, IA | US-Br1 | 41.9749° N, 93.6906° W, 313 m | Rainfed | 2005–2011 Odd years | 2006–2010 Even years | 9 | 845 | 30.8 |
| US-Br3 | 41.9747° N, 93.6935° W, 313 m | Rainfed | 2006–2010 Even years | 2005–2011 Odd years | 9 | 845 | 18.1 | |
| Bondville, IL | US-Bo1 | 40.0062° N, 88.2904° W, 219 m | Rainfed | 2001–2007 Odd years | 2002–2006 Even years | 11 | 991 | 31.7 |
| Rosemount, MN | US-Ro1 | 44.7143° N, 93.0898° W; 290 m | Rainfed | 2005–2011 Odd years | 2006–2012 Even years | 6 | 879 | 17.7 |
| Calibration Years | ||
|---|---|---|
| Site | Maize | Soybean |
| US-Ne1 (NE—irrigated) | 2002–2005, 2007, 2009–2012 | -- |
| US-Ne2 (NE—irrigated) | 2003, 2005, 2007, 2009, 2010, 2013 | 2002, 2004, 2008 |
| US-Ne3 (NE) | 2003, 2005, 2011, 2013 | 2006, 2008, 2010, 2012 |
| US-Br1 (IA) | 2005, 2007, 2009 | 2006,2008 |
| US-Br3 (IA) | 2006, 2010 | 2007, 2009, 2011 |
| US-Bo1 (IL) | 2001, 2005, 2007 | 2002, 2004 |
| US-Ro1 (MN) | 2005, 2009, 2011 | 2006, 2010, 2012 |
| Field Years | 30 | 17 |
| Validation Years | ||
|---|---|---|
| Site | Maize | Soybean |
| US-Ne1 (NE—irrigated) | 2006, 2008, 2013 | N/A |
| US-Ne2 (NE—irrigated) | 2011, 2012 | 2006 |
| US-Ne3 (NE) | 2007, 2009 | 2002, 2004 |
| US-Br1 (IA) | 2011 | 2010 |
| US-Br3 (IA) | 2008 | 2005 |
| US-Bo1 (IL) | 2003 | 2006 |
| US-Ro1 (MN) | 2007 | 2008 |
| Field Years | 11 | 7 |
| Nguy-Robertson et al. [13] | This Study | ||||||
|---|---|---|---|---|---|---|---|
| Variables | Symbol | Equation | Units | Maize | Soybean | Maize | Soybean |
| Derived through iterative process: | |||||||
| Maximal light use efficiency | ε0 | (8) | g C mol−1 | 0.526 ± 0.007 | 0.374 ± 0.005 | 0.573 ± 0.002 | 0.407 ± 0.002 |
| Sensitivity of ε to diffuse light | β | (11) | unitless | 0.347 ± 0.051 | 0.411 ± 0.056 | 0.181 ± 0.014 | 0.294 ± 0.020 |
| Water stress curvature parameter | σWscalar | (14) | kPa | 6 ± 0.25 | 4 ± 0 | 6 ± 0 | 4 ± 0 |
| Phenology curvature parameter | σPscalar | (15) | m2 m−2 | 18 ± 4.59 | 18 ± 7.15 | 7 ± 0 | 8 ± 0 |
| Calculated | |||||||
| Maximal green leaf area index [irrigated] | gLAImax | (10), (15) | m2 m−2 | 4.93 [6.78] | 4.63 [6.15] | 5.04 [5.14] | 3.86 [4.25] |
| Constants | |||||||
| Light extinction coefficient | k | (10) | unitless | 0.443 | 0.601 | 0.443 | 0.601 |
| Minimum temperature for physiological activity | Tmin constant | (1), (13) | °C | 10 | 10 | 10 | 10 |
| Maximum temperature for physiological activity | Tmax constant | (1), (13) | °C | 48 | 48 | 48 | 48 |
| Optimal temperature for physiological activity | Topt constant | (13) | °C | 28 | 28 | 28 | 28 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malek-Madani, G.; Walter-Shea, E.A.; Nguy-Robertson, A.L.; Suyker, A.; Arkebauer, T.J. Modeling Gross Primary Production of Midwestern US Maize and Soybean Croplands with Satellite and Gridded Weather Data. Remote Sens. 2020, 12, 3956. https://doi.org/10.3390/rs12233956
Malek-Madani G, Walter-Shea EA, Nguy-Robertson AL, Suyker A, Arkebauer TJ. Modeling Gross Primary Production of Midwestern US Maize and Soybean Croplands with Satellite and Gridded Weather Data. Remote Sensing. 2020; 12(23):3956. https://doi.org/10.3390/rs12233956
Chicago/Turabian StyleMalek-Madani, Gunnar, Elizabeth A. Walter-Shea, Anthony L. Nguy-Robertson, Andrew Suyker, and Timothy J. Arkebauer. 2020. "Modeling Gross Primary Production of Midwestern US Maize and Soybean Croplands with Satellite and Gridded Weather Data" Remote Sensing 12, no. 23: 3956. https://doi.org/10.3390/rs12233956
APA StyleMalek-Madani, G., Walter-Shea, E. A., Nguy-Robertson, A. L., Suyker, A., & Arkebauer, T. J. (2020). Modeling Gross Primary Production of Midwestern US Maize and Soybean Croplands with Satellite and Gridded Weather Data. Remote Sensing, 12(23), 3956. https://doi.org/10.3390/rs12233956





